SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



En in het verlengde kun je dan de middelwaardestelling en de maximum/minimum stelling bewijzen.quote:Op donderdag 27 februari 2014 11:43 schreef -J-D- het volgende:
[..]
Zeker. Dat moet zeker onderdeel zijn van de lessen. Buigpunten berekenen en dergelijke kunnen ze op een gegeven moment wel, maar dat onderdeel smeekt er haast om om wat dieper uitgespit te worden.


Heeft iemand een idee van wie de definitie van de determinant van nxn matrices is? Ik weet dat Cauchy in 1812 een verhandeling over determinanten heeft geschreven en het woord "determinant" in zijn huidige betekenis heeft ingevoerd. Ik weet alleen niet of hij ook de definitie
heeft ingevoerd. Ook verwijzingen naar bronnen waar ik misschien het antwoord kan vinden zijn welkom
heeft ingevoerd. Ook verwijzingen naar bronnen waar ik misschien het antwoord kan vinden zijn welkom


De formule die je geeft wordt wel toegeschreven aan Leibniz (echter niet in deze notatie) en is dus ouder dan Cauchy. Er is een artikel van Binet geschreven in 1812 maar gepubliceerd in 1813 (lees online) waarin hij de vermenigvuldiging van determinanten bespreekt, maar niet in de thans gebruikelijke notatie. In de daarop volgende jaargang van hetzelfde tijdschrift staat de verhandeling van Cauchy die je kennelijk bedoelt (lees online), eveneens geschreven in 1812 en voorgedragen op dezelfde dag als die van Binet, maar pas gepubliceerd in 1815. In dit artikel introduceert Cauchy de moderne rangschikking van de elementen van een determinant in een vierkant en de dubbele subscript notatie. Hij gebruikt alleen nog niet de verticale strepen, die werden in 1841 geïntroduceerd door Cayley. De scan van het artikel van Cauchy is helaas slecht te lezen, maar de passage waarin hij het woord determinant in de huidige betekenis introduceert staat op p. 51:quote:Op dinsdag 4 maart 2014 08:01 schreef woop_woop_woop het volgende:
Heeft iemand een idee van wie de definitie van de determinant van nxn matrices is? Ik weet dat Cauchy in 1812 een verhandeling over determinanten heeft geschreven en het woord "determinant" in zijn huidige betekenis heeft ingevoerd. Ik weet alleen niet of hij ook de definitie
[ afbeelding ]
heeft ingevoerd. Ook verwijzingen naar bronnen waar ik misschien het antwoord kan vinden zijn welkom
M. Gauss s'en est servi avec avantage dans ses Recherches analytiques, pour découvrir les propriétés générales des formes du second degré, c'est-à-dire, des polynomes du second degré à deux ou à plusieurs variables; et il a désigné ces mêmes fonctions sous le nom de déterminans. Je conserverai cette dénomination qui fournit un moyen facile d'énoncer les résultats; j'observerai seulement qu'on donne aussi quelquefois aux fonctions dont il s'agit le nom de résultantes à deux ou à plusieurs lettres. Ainsi les deux expressions suivantes, déterminant et résultante, devront être regardées comme synonymes.
Cauchy verwijst dus naar Gauss (om precies te zijn, naar diens Disquisitiones arithmeticae, § 154, lees online).
Er zijn erg veel mensen die bijdragen hebben geleverd aan de theorie van de determinanten, te veel om hier de revue te laten passeren. Het standaardwerk op dit gebied is Thomas Muir, The Theory of Determinants in the Historical Order of Development, 1906-1923, 4 vols. Samen meer dan duizend bladzijden(!) en ook beschikbaar als Dover reprint (1960). Aangezien er geen copyright meer op dit werk rust, is het ook legaal beschikbaar via archive.org (lees online of download als PDF of als DjVu).
Een overzicht vind je verder in Morris Kline, Mathematical Thought from Ancient to Modern Times, 1972, vol. 2, hoofdstuk 33: Determinants and Matrices. Beslist raadplegen, hier vind je veel verwijzingen naar primaire bronnen die je in de meeste gevallen ook weer online kunt vinden.
[ Bericht 0% gewijzigd door Riparius op 06-03-2014 06:04:24 ]


@riparius, compleet off topic ( of tenminste een beetje ) een vraag uit nieuwsgierigheid: wat voor soort onderzoek, werk of studie houd je je mee bezig? Je weet wel heel erg veel van een brede range aan beta onderwerpen 
Winnaar wielerprono 2006 en biatlon wk prono 2016


Ik ben zijn secretaresse niet, maar hij beantwoordt geen privé vragen (tot op heden). Lees zijn PoHi maar eens door, dan kun je je antwoord zelf verzinnen.quote:


dan zal hij dat wel niet willen vertellen, en dat betekent ook dat ik er geen vraag meer over stel. Duidelijk is voor mij wel dat we het niet over de gemiddelde wiskunde student hebben en meer richting gepromoveerde wiskundige met geschiedkundige interesses moeten denken.quote:Op dinsdag 4 maart 2014 18:45 schreef Amoeba het volgende:
[..]
Ik ben zijn secretaresse niet, maar hij beantwoordt geen privé vragen (tot op heden). Lees zijn PoHi maar eens door, dan kun je je antwoord zelf verzinnen.
Winnaar wielerprono 2006 en biatlon wk prono 2016


En juist daar trek je te snel conclusies.quote:Op dinsdag 4 maart 2014 18:50 schreef komrad het volgende:
[..]
dan zal hij dat wel niet willen vertellen, en dat betekent ook dat ik er geen vraag meer over stel. Duidelijk is voor mij wel dat we het niet over de gemiddelde wiskunde student hebben en meer richting gepromoveerde wiskundige met geschiedkundige interesses moeten denken.


prima, ik neem dat van je aan maar laten we het daar bij houden. Ter voorkoming van verdere topicvervuiling en ivm mogelijke privacywens.quote:Op dinsdag 4 maart 2014 18:52 schreef Amoeba het volgende:
[..]
En juist daar trek je te snel conclusies.
Winnaar wielerprono 2006 en biatlon wk prono 2016


Hallo allemaal,
Zij
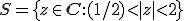
en
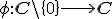
gegeven door
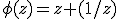 .
.
Mijn opdracht is om het beeld van S onder phi te vinden. Omdat
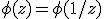
hoef ik (1/2,1) niet te bekijken, en verder vond ik dat
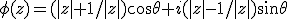 ,
,
wat ellipsen zijn als je |z| vast neemt en theta laat lopen. Als |z| = 1 krijgen we als beeld het interval [2,-2] en als |z| = 2 krijgen we een ellips waar alle andere ellipsen binnen liggen. Het is nu intuitief wel duidelijk uit de continuiteit van phi dat alle punten binnen die grote ellips in phi(S) liggen, maar is er een elegante manier om dit hard te maken? Een stelling uit de topologie misschien? Ik heb nog nauwelijks topologie gehad, en ik heb het gevoel dat dit er mee te maken heeft. Ik vind het vrij vervelend om voor elk punt een ellips in het beeld waar dat punt op ligt te construeren...
[ Bericht 0% gewijzigd door JWF op 04-03-2014 20:31:36 ]
Zij
en
gegeven door
Mijn opdracht is om het beeld van S onder phi te vinden. Omdat
hoef ik (1/2,1) niet te bekijken, en verder vond ik dat
wat ellipsen zijn als je |z| vast neemt en theta laat lopen. Als |z| = 1 krijgen we als beeld het interval [2,-2] en als |z| = 2 krijgen we een ellips waar alle andere ellipsen binnen liggen. Het is nu intuitief wel duidelijk uit de continuiteit van phi dat alle punten binnen die grote ellips in phi(S) liggen, maar is er een elegante manier om dit hard te maken? Een stelling uit de topologie misschien? Ik heb nog nauwelijks topologie gehad, en ik heb het gevoel dat dit er mee te maken heeft. Ik vind het vrij vervelend om voor elk punt een ellips in het beeld waar dat punt op ligt te construeren...
[ Bericht 0% gewijzigd door JWF op 04-03-2014 20:31:36 ]


Daar moeten cirkels uit komen, geen 'algemene' ellipsen.quote:Op dinsdag 4 maart 2014 19:43 schreef JWF het volgende:
Hallo allemaal,
Zij
en
gegeven door.
Mijn opdracht is om het beeld van S onder phi te vinden. Omdat
hoef ik (1/2,1) niet te bekijken, en verder vond ik dat,
wat ellipsen zijn als je |z| vast neemt en theta laat lopen. Als |z| = 1 krijgen we als beeld het interval [2,-2] en als |z| = 2 krijgen we een ellips waar alle andere ellipsen binnen liggen. Het is nu intuitief wel duidelijk uit de continuiteit van phi dat alle punten binnen die grote ellips in phi(S) liggen, maar is er een elegante manier om dit hard te maken? Een stelling uit de topologie misschien? Ik heb nog nauwelijks topologie gehad, en ik heb het gevoel dat dit er mee te maken heeft. Ik vind het vrij vervelend om voor elk punt een ellips in het beeld waar dat punt op ligt te construeren...


Hoe dat zo? Je hebt toch
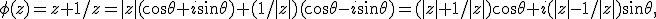
(met theta natuurlijk het argument en |z| de modulus). Er gaat dan hierboven iets fout, want dat zijn echt geen cirkels.
(met theta natuurlijk het argument en |z| de modulus). Er gaat dan hierboven iets fout, want dat zijn echt geen cirkels.


Als je hebtquote:Op dinsdag 4 maart 2014 20:33 schreef JWF het volgende:
Hoe dat zo? Je hebt toch
(met theta natuurlijk het argument en |z| de modulus). Er gaat dan hierboven iets fout, want dat zijn echt geen cirkels.
w = z + 1/z
dan is
w = (r + 1/r)·cos φ + i·(r − 1/r)·sin φ
voor
z = r·eiφ
Als je r constant houdt, dan krijg je voor r ≠ 1 en tevens r ≠ 0 inderdaad een ellips in het w-vlak als beeld van z = r·eiφ, als je φ het interval [0, 2π] laat doorlopen, terwijl de eenheidscirkel in het w-vlak wordt afgebeeld op het reële interval [−2, 2]. Houd je daarentegen φ constant dan geeft z = r·eiφ in het w-vlak een hyperbool als je r het interval (0, ∞) laat doorlopen mits φ ≠ k·½π, k ∈ Z. Zo geeft je polaire grid in het z-vlak dus een set ellipsen en een set hyperbolen in het w-vlak die elkaar allemaal loodrecht snijden en die ook allemaal dezelfde brandpunten hebben, namelijk de beeldpunten van −2 en 2.


Laat maar, ik had de vraag verkeerd gelezen.quote:Op dinsdag 4 maart 2014 20:33 schreef JWF het volgende:
Hoe dat zo? Je hebt toch
(met theta natuurlijk het argument en |z| de modulus). Er gaat dan hierboven iets fout, want dat zijn echt geen cirkels.


Top, fantastische post! In de laatste referentie die je noemt staat inderdaad een Franse brief + vertaling van Leibniz waarin hij inderdaad een determinant lijkt te berekenen. Dit wil natuurlijk niet zeggen dat hij ook de eerste is die die formule bedacht heeft (of dat hij überhaupt die formule bedacht heeft), maar maakt het wel aannemelijk dat hij er een aandeel in heeft gehad.quote:Op dinsdag 4 maart 2014 16:20 schreef Riparius het volgende:
[..]
Een overzicht vind je verder in Morris Kline, Mathematical Thought from Ancient to Modern Times, 1972, vol. 2, hoofdstuk 33: Determinants and Matrices. Beslist raadplegen, hier vind je veel verwijzingen naar primaire bronnen die je in de meeste gevallen ook weer online kunt vinden.
Dat is inderdaad het artikel waar ik het over had
In het boek wat ik voor het vak "History of Mathematics" gebruik ("A History of Mathematics" van Uta Merzbach en Carl Boyer), werden deze artikelen genoemd. Voor de rest staat er helaas niet zoveel in over determinanten.
Ik zal vooral de laatste bron gebruiken, mijn Frans is helaas onder middelbare-school niveau


Dat snap ik, maar de rekenkundige bewerking vind ik lastig. Hoe maak ik dit stap voor stap kleiner?quote:
1/ 3 ^3sqrtu^2 * (3x^2+3)


Je bedoelde kennelijk dit, maar je herleiding klopt niet. Ga eerst maar eens deze cursus doorwerken.quote:


Volgens mij hoort die drie in de noemer bij de wortel. Dan klopt 't toch wel?quote:Op vrijdag 7 maart 2014 20:05 schreef Riparius het volgende:
[..]
Je bedoelde kennelijk dit, maar je herleiding klopt niet. Ga eerst maar eens deze cursus doorwerken.
[ Bericht 4% gewijzigd door #ANONIEM op 07-03-2014 20:56:25 ]


Had m'n bericht al aangepast.quote:Op vrijdag 7 maart 2014 20:56 schreef Amoeba het volgende:
[..]
Kijk zelf even. Iets met delen door 3 enzo


Dat staat er niet. Zet dan haken, maak zorg dat de gebruikte notatie voor geen enkele verwarring kan zorgen.quote:Op vrijdag 7 maart 2014 20:57 schreef 2thmx het volgende:
[..]
Had m'n bericht al aangepast.Denk dat 'rareziekte' de derdemachtswortel bedoelt, in de noemer.


Da's waar. Maar omdat'ie "Gevonden" typte, neem ik aan dat'ie bedoelt dat'ie het juiste antwoord (het antwoord uit het antwoordenboek o.i.d.) heeft "gevonden". Dan hoort de drie kennelijk bij de wortelquote:Op vrijdag 7 maart 2014 20:59 schreef Amoeba het volgende:
[..]
Dat staat er niet. Zet dan haken, maak zorg dat de gebruikte notatie voor geen enkele verwarring kan zorgen.


Dan is de volgende les dat hij ook op het internet eenduidige notatie gebruikt.quote:Op vrijdag 7 maart 2014 21:01 schreef 2thmx het volgende:
[..]
Da's waar. Maar omdat'ie "Gevonden" typte, neem ik aan dat'ie bedoelt dat'ie het juiste antwoord (het antwoord uit het antwoordenboek o.i.d.) heeft "gevonden". Dan hoort de drie kennelijk bij de wortel.


Zo blijft het raden wat de vragensteller bedoelt, en kennelijk ziet hij zelf ook niet in dat zijn notatie ambigu of domweg fout is. In ieder geval mag je niet sqrt(u) schrijven als je cbrt(u) bedoelt. Dan wil hij dus dit aangeven in plaats van dit.quote:Op vrijdag 7 maart 2014 21:01 schreef 2thmx het volgende:
[..]
Da's waar. Maar omdat'ie "Gevonden" typte, neem ik aan dat'ie bedoelt dat'ie het juiste antwoord (het antwoord uit het antwoordenboek o.i.d.) heeft "gevonden". Dan hoort de drie kennelijk bij de wortel.


Beste mensen,
Kan iemand mij helpen met de volgende opgave:
-Waar ik dus niet uitkom is het volgende; ik weet niet waar "b" voor staat
-Steeds probeer ik met her Cartesisch product van A te werken A²= 49 elementen {[1,1], [1,2], .....[7,7]
-De kardinaliteit is eveneens [49]
-R is een deelverzameling van A²
Verder kom ik echt niet..
Hopelijk is er iemand die mij wat wegwijs kan maken.
De uitleg die ik hier heb behelst maar 5 regels, verder kom ik geen stap vooruit.
Frustrerend!
Bij voorbaat dank!!
Kan iemand mij helpen met de volgende opgave:
-Waar ik dus niet uitkom is het volgende; ik weet niet waar "b" voor staat
-Steeds probeer ik met her Cartesisch product van A te werken A²= 49 elementen {[1,1], [1,2], .....[7,7]
-De kardinaliteit is eveneens [49]
-R is een deelverzameling van A²
Verder kom ik echt niet..
Hopelijk is er iemand die mij wat wegwijs kan maken.
De uitleg die ik hier heb behelst maar 5 regels, verder kom ik geen stap vooruit.
Frustrerend!
Bij voorbaat dank!!


Misschien moet je je leerboek eens beter bestuderen, of zelf even op het net op zoek gaan naar wat een binaire relatie nu eigenlijk is. De binaire relatie R is hier een deelverzameling van A × A en a en b stellen elementen voor van A. Gegeven is dat aRb oftewel (a,b) ∈ R dan en slechts dan als b − a = 1. Dan is het toch niet moeilijk alle elementen van R te geven?quote:Op donderdag 13 maart 2014 16:11 schreef maaktniksuit het volgende:
Beste mensen,
Kan iemand mij helpen met de volgende opgave:
[ afbeelding ]
-Waar ik dus niet uitkom is het volgende; ik weet niet waar "b" voor staat
-Steeds probeer ik met her Cartesisch product van A te werken A²= 49 elementen {[1,1], [1,2], .....[7,7]
-De kardinaliteit is eveneens [49]
-R is een deelverzameling van A²
Verder kom ik echt niet..
Hopelijk is er iemand die mij wat wegwijs kan maken.
De uitleg die ik hier heb behelst maar 5 regels, verder kom ik geen stap vooruit.
Frustrerend!
Bij voorbaat dank!!


Ik heb het allemaal even op een rijtje gezet, ik kom hier uit:quote:Op donderdag 13 maart 2014 17:54 schreef Riparius het volgende:
[..]
Misschien moet je je leerboek eens beter bestuderen, of zelf even op het net op zoek gaan naar wat een binaire relatie nu eigenlijk is. De binaire relatie R is hier een deelverzameling van A × A en a en b stellen elementen voor van A. Gegeven is dat aRb oftewel (a,b) ∈ R dan en slechts dan als b − a = 1. Dan is het toch niet moeilijk alle elementen van R te geven?
{[2,1], [3,2], [4,3], [5,4], [6,5], [7,6]}
In de veronderstelling dat b - a steeds 1 moet zijn?


Nee, je hebt a en b omgewisseld, oftewel je doet nu net of aRb dan en slechts dan als b − a = −1. Gebruik verder ronde haakjes om geordende paren aan te geven.quote:Op donderdag 13 maart 2014 18:02 schreef maaktniksuit het volgende:
[..]
Ik heb het allemaal even op een rijtje gezet, ik kom hier uit:
{[2,1], [3,2], [4,3], [5,4], [6,5], [7,6]}
In de veronderstelling dat b - a steeds 1 moet zijn?


Mijn docent stuurt me net ter ondersteuning:
"A^2 bevat 49 tweetallen.
R is een relatie op A^2, en bevat juist die tweetallen (a,b) zodanig dat b - a = 1.
Voor welke tweetallen uit A^2 geldt dat laatste?"
Ik houd voor a, b telkens verzameling A aan.
Aangezien ik in mijn votige post a en heb heb omgewisseld,
{{1,2}, (2,3), (4,5), (6,7)}
Sorry van de rechte haakjes, dit is de manier waarop ik het online moet invoeren, vandaar.
Ik voel me echt een uilskuiken op dit moment, dit jaar ga ik na 4 jaar weer een opleiding volgen

"A^2 bevat 49 tweetallen.
R is een relatie op A^2, en bevat juist die tweetallen (a,b) zodanig dat b - a = 1.
Voor welke tweetallen uit A^2 geldt dat laatste?"
Ik houd voor a, b telkens verzameling A aan.
Aangezien ik in mijn votige post a en heb heb omgewisseld,
{{1,2}, (2,3), (4,5), (6,7)}
Sorry van de rechte haakjes, dit is de manier waarop ik het online moet invoeren, vandaar.
Ik voel me echt een uilskuiken op dit moment, dit jaar ga ik na 4 jaar weer een opleiding volgen


Je vergeet nu ook nog twee elementen van R op te schrijven.quote:Op donderdag 13 maart 2014 18:21 schreef maaktniksuit het volgende:
Ik voel me echt een uilskuiken op dit moment, dit jaar ga ik na 4 jaar weer een opleiding volgen


Ik heb nu volgens mij het juiste antwoord:quote:Op donderdag 13 maart 2014 18:27 schreef Riparius het volgende:
[..]
Je vergeet nu ook nog twee elementen van R op te schrijven.
{(1,2, (2,3), (3,4), (4,5), (5,6), (6,7)}
Ik moet nog wennen aan de manier waarop je bij wiskunde dient te denken, pfff


Ja, dat is het, afgezien van een vergeten haakje. Maar dit was toch doodsimpel? Voor welke opleiding is dit als ik vragen mag?quote:Op donderdag 13 maart 2014 19:18 schreef maaktniksuit het volgende:
[..]
Ik heb nu volgens mij het juiste antwoord:
{(1,2), (2,3), (3,4), (4,5), (5,6), (6,7)}
Ik moet nog wennen aan de manier waarop je bij wiskunde dient te denken, pfff


Dit is voor de opleiding Bedrijfskundige Informatica.quote:Op donderdag 13 maart 2014 19:24 schreef Riparius het volgende:
[..]
Ja, dat is het, afgezien van een vergeten haakje. Maar dit was toch doodsimpel? Voor welke opleiding is dit als ik vragen mag?
Ik ben voornemens in september te starten, ik volg nu een cursus waarbij ik de wiskundestof uit de propedeuse behandel.
Indien ik voor alle tentamens een voldoende haal, heb ik tijdens de propedeuse vrijstelling voor het vak wiskunde.


Grapje ik weet het al. Ik had een tabel met z-scores nodig. #delete
[ Bericht 31% gewijzigd door rick949 op 22-03-2014 19:58:41 ]
[ Bericht 31% gewijzigd door rick949 op 22-03-2014 19:58:41 ]


Vraagje.
Zij f: [a,b] -> R Riemann integreerbaar op [a.b], waar [a,b] een gesloten interval op R is. Verder zij a∫bf(x)dx > 0.
Bewijs de volgende bewering: Er is een interval I binnen [a,b] met lengte groter dan 0, er is een eps z.d.d. f(x) > eps voor alle x in I.
Nu heb ik dit:
Maar ik vrees dat mijn keuze voor een partitie Q om deze als een oneindige vereniging te definiëren misschien niet helemaal juist is..
[ Bericht 0% gewijzigd door #ANONIEM op 22-03-2014 18:22:22 ]
Zij f: [a,b] -> R Riemann integreerbaar op [a.b], waar [a,b] een gesloten interval op R is. Verder zij a∫bf(x)dx > 0.
Bewijs de volgende bewering: Er is een interval I binnen [a,b] met lengte groter dan 0, er is een eps z.d.d. f(x) > eps voor alle x in I.
Nu heb ik dit:
Maar ik vrees dat mijn keuze voor een partitie Q om deze als een oneindige vereniging te definiëren misschien niet helemaal juist is..
[ Bericht 0% gewijzigd door #ANONIEM op 22-03-2014 18:22:22 ]


Je mag je partitie inderdaad niet oneindig kiezen. In Riemann integratie is een partitie eindig. Je kiest het eindig en kan het eventueel later in het bewijs willekeurig groot (wel aftelbaar!) maken.quote:Op zaterdag 22 maart 2014 18:19 schreef Amoeba het volgende:
Vraagje.
Zij f: [a,b] -> R Riemann integreerbaar op [a.b], waar [a,b] een gesloten interval op R is. Verder zij a∫bf(x)dx > 0.
Bewijs de volgende bewering: Er is een interval I binnen [a,b] met lengte groter dan 0, er is een eps z.d.d. f(x) > eps voor alle x in I.
Nu heb ik dit:
[ afbeelding ]
Maar ik vrees dat mijn keuze voor een partitie Q om deze als een oneindige vereniging te definiëren misschien niet helemaal juist is..
[ Bericht 2% gewijzigd door Mathemaat op 22-03-2014 23:29:45 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Het supremum van alle ondersommen genomen over alle eindige partities is gelijk aan de integraal, die groter dan 0 is. Er is dus een partitie waarvoor de ondersom groter dan 0 is. Die partitie moet minstens 1 interval hebben waarvoor de onderwaarde (infimum) groter dan 0 is.


Ohja, even supremum noemen. Foutje.quote:Op zondag 23 maart 2014 00:37 schreef thabit het volgende:
Het supremum van alle ondersommen genomen over alle eindige partities is gelijk aan de integraal, die groter dan 0 is. Er is dus een partitie waarvoor de ondersom groter dan 0 is. Die partitie moet minstens 1 interval hebben waarvoor de onderwaarde (infimum) groter dan 0 is.
Ik denk dat ik het wel weet dan. Even een kwestie van iets anders opschrijven.
Dank.


Maar dan mag ik niet meer spreken van L(Q,f) = sup(L(P,f) | P een partitie)quote:Op zaterdag 22 maart 2014 23:23 schreef Mathemaat het volgende:
[..]
Je mag je partitie inderdaad niet oneindig kiezen. In Riemann integratie is een partitie eindig. Je kiest het eindig en kan het eventueel later in het bewijs willekeurig groot (wel aftelbaar!) maken.
Nee dit moet anders en ik zie al hoe.


Inderdaad je Q is geen partitie. Maar je hoeft geen specifieke partitie te kiezen, gebruik het antwoord van Thabit.quote:Op zondag 23 maart 2014 07:47 schreef Amoeba het volgende:
[..]
Maar dan mag ik niet meer spreken van L(Q,f) = sup(L(P,f) | P een partitie)
Nee dit moet anders en ik zie al hoe.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Ga ik doen.quote:Op zondag 23 maart 2014 12:11 schreef Mathemaat het volgende:
[..]
Inderdaad je Q is geen partitie. Maar je hoeft geen specifieke partitie te kiezen, gebruik het antwoord van Thabit.





 Op
Op  Op
Op 
