SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
OP
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
Ah, tuurlijk. Bedanktquote:Op zondag 23 mei 2010 14:54 schreef Riparius het volgende:
[..]
Als je aanneemt dat f'(x0) > 0 dan kun je een omgeving van x0 (minus x0 zelf) kiezen waarin het differentiequotiënt (f(x) - f(x0))/(x - x0) positief is, en dat is strijdig met de aanname dat f bij x0 een maximum of minimum heeft. Maar deze omgeving (x0-δ, x0+δ) van x0 moet wel binnen het gegeven interval (a,b) liggen, dus
a < x0 - δ < x0 + δ < b
Je hebt hier een paar rekenregels nodig. Misschien gaat er wel een lampje branden als ik zeg:
(a b)^n = ...
(a/b)^n = ...
(a b)^n = ...
(a/b)^n = ...
Hoe krijg ik de inverse functie van 2 / (1 + e-x) 
Edit: Heb het denk het -ln ((2/y) -1)
[ Bericht 31% gewijzigd door Diabox op 25-05-2010 22:24:07 ]
Edit: Heb het denk het -ln ((2/y) -1)
[ Bericht 31% gewijzigd door Diabox op 25-05-2010 22:24:07 ]
Ik heb een Excel-vraag. Ik moet 3 (!!) functies combineren in 1 functie zegmaar:
- Vert.zoeken
- Als functie
- Isfout functie
=VERT.ZOEKEN(D2;'voorraadlijst hal C'!A2;1;ONWAAR) (de Vert.zoeken functie)
= ALS(ISFOUT(G14);"Fout";"Goed") (de ALS/ISfout functie)
Gewoon erachter plakken lukt niet
Alvast bedankt!
- Vert.zoeken
- Als functie
- Isfout functie
=VERT.ZOEKEN(D2;'voorraadlijst hal C'!A2;1;ONWAAR) (de Vert.zoeken functie)
= ALS(ISFOUT(G14);"Fout";"Goed") (de ALS/ISfout functie)
Gewoon erachter plakken lukt niet
Alvast bedankt!
Ik heb een vraag of ik dit goed aanpak:
Zie vraag 11 (blz. 998) 6e druk Calculus.
Ik moet een triple integral berekenen van (integraal = { )
{ { { 6xy dV, waar E onder het vlak , z=1+x+y and boven het gebied die door het xy-vlak is begrensd door y=wortel(x) , y=0 en x=1
Nu heb ik het zo aangepakt. Ik heb ten eerste dit gebied als een type 1 en het vlak als een type II behandeld, waardoor ik op de volgende triple integraal som kom:
1{0, y2 {0 , (1+x+y) { 0 : 6xy dz dx dy
(dus 1 is boven en 0 is onder. y^2 is boven en is onder etc.
Zie vraag 11 (blz. 998) 6e druk Calculus.
Ik moet een triple integral berekenen van (integraal = { )
{ { { 6xy dV, waar E onder het vlak , z=1+x+y and boven het gebied die door het xy-vlak is begrensd door y=wortel(x) , y=0 en x=1
Nu heb ik het zo aangepakt. Ik heb ten eerste dit gebied als een type 1 en het vlak als een type II behandeld, waardoor ik op de volgende triple integraal som kom:
1{0, y2 {0 , (1+x+y) { 0 : 6xy dz dx dy
(dus 1 is boven en 0 is onder. y^2 is boven en is onder etc.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Niemand antwoord? 
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Hey, ik heb de afgelopen paar uur getracht een definitie te begrijpen, maar vanwege weinig voorbeelden/concretisering van de variabelen zit ik beetje in het duisternis te zoeken... op google vind ik enkel papers en wederom weinig voorbeelden die me goed aantonen tot wat precies alle variabelen verhouden.
De stof die ik gebruik is:
http://homepages.cwi.nl/~apt/stra/ch11.pdf
Het gaat over Pre-Bayesian games.
Als je een goeie site weet waar ik meer over Pre-Bayesian Games kan leren met wat voorbeelden is dat meer dan genoeg!
Th = theta
nou heb ik wel ongeveer een clou wat in grote lijnen gebeurt, maar er wordt niet echt goed alles stap voor stap uitgelegd terwijl ik dat wel even nodig heb.
Mijn grootste probleem is de 'best-response' en 'dominant' definities op pagina 103 (2 van de pdf).
Ik zie niet goed welke cijfers ik nu precies met elkaar moet vergelijken.
Wat ik denk dat ik moet doen is voor elke type kijken of de gekozen si( . ) een hogere of gelijke payoff heeft als een andere action van player i. Maar mijn probleem is of ik s-i(th-i) moet instantiseren naar slechts 1 actie en in principe dat ik slechts één Th-game check. Op dezelfde pagina onderaan staat Example 24, dus moet ik s-i(Th-i) als de keuze van player 2 de actie F kiezen, om vervolgens tot de conclusie te komen dat si(Thi) dus F moet zijn (want payoff groter dan als player 1 B zou kiezen)?
Kortom de vraag is, als ik example 24 gebruik, of ik in meerdere Th-games moet checken?
Hoe bepaal ik wat een best-response si( . ) is?
Andere vraag, si( . ) houdt dus in dat ik voor alle types een actie heb (/moet hebben)?
Is in example 24, s1(U) = B, s1(D) = F, s2(L) = B en s2(R) = F, ook een ex-post equilibrium?
Wat is de precieze reden dat de Nash Equilibrium (NE) in elke th-game voor dezelfde acties moeten staan voor de spelers als in de andere games, alvorens het een ex-post equilibrium wordt genoemd?
Anders gezegd, waarom is example 25 geen ex-post equilibrium vanwege de positionering van de NE's? Aan welke eis wordt niet voldaan?
Ik en anderen van me studiegroepje zullen je enorm dankbaar zijn met wat dan ook voor hulp.
De stof die ik gebruik is:
http://homepages.cwi.nl/~apt/stra/ch11.pdf
Het gaat over Pre-Bayesian games.
Als je een goeie site weet waar ik meer over Pre-Bayesian Games kan leren met wat voorbeelden is dat meer dan genoeg!
Th = theta
nou heb ik wel ongeveer een clou wat in grote lijnen gebeurt, maar er wordt niet echt goed alles stap voor stap uitgelegd terwijl ik dat wel even nodig heb.
Mijn grootste probleem is de 'best-response' en 'dominant' definities op pagina 103 (2 van de pdf).
Ik zie niet goed welke cijfers ik nu precies met elkaar moet vergelijken.
Wat ik denk dat ik moet doen is voor elke type kijken of de gekozen si( . ) een hogere of gelijke payoff heeft als een andere action van player i. Maar mijn probleem is of ik s-i(th-i) moet instantiseren naar slechts 1 actie en in principe dat ik slechts één Th-game check. Op dezelfde pagina onderaan staat Example 24, dus moet ik s-i(Th-i) als de keuze van player 2 de actie F kiezen, om vervolgens tot de conclusie te komen dat si(Thi) dus F moet zijn (want payoff groter dan als player 1 B zou kiezen)?
Kortom de vraag is, als ik example 24 gebruik, of ik in meerdere Th-games moet checken?
Hoe bepaal ik wat een best-response si( . ) is?
Andere vraag, si( . ) houdt dus in dat ik voor alle types een actie heb (/moet hebben)?
Is in example 24, s1(U) = B, s1(D) = F, s2(L) = B en s2(R) = F, ook een ex-post equilibrium?
Wat is de precieze reden dat de Nash Equilibrium (NE) in elke th-game voor dezelfde acties moeten staan voor de spelers als in de andere games, alvorens het een ex-post equilibrium wordt genoemd?
Anders gezegd, waarom is example 25 geen ex-post equilibrium vanwege de positionering van de NE's? Aan welke eis wordt niet voldaan?
Ik en anderen van me studiegroepje zullen je enorm dankbaar zijn met wat dan ook voor hulp.
Wat is E? En je kan het beter typen in Latex, nogal onoverzichtelijk zo. Dan heb je meer kans dat iemand reageertquote:Op vrijdag 28 mei 2010 20:20 schreef Burakius het volgende:
Ik heb een vraag of ik dit goed aanpak:
Zie vraag 11 (blz. 998) 6e druk Calculus.
Ik moet een triple integral berekenen van (integraal = { )
{ { { 6xy dV, waar E onder het vlak , z=1+x+y and boven het gebied die door het xy-vlak is begrensd door y=wortel(x) , y=0 en x=1
Nu heb ik het zo aangepakt. Ik heb ten eerste dit gebied als een type 1 en het vlak als een type II behandeld, waardoor ik op de volgende triple integraal som kom:
1{0, y2 {0 , (1+x+y) { 0 : 6xy dz dx dy
(dus 1 is boven en 0 is onder. y^2 is boven en is onder etc.
E is gewoon een gebiedje ( dus in dit geval is E= 6xy )quote:Op zondag 30 mei 2010 23:45 schreef BasementDweller het volgende:
[..]
Wat is E? En je kan het beter typen in Latex, nogal onoverzichtelijk zo. Dan heb je meer kans dat iemand reageert
Verder kun je het gewoon op klad herschrijven. Ik kan geen latex gedoe doen.... { = een integraal. Wat er vóór staat is de bovengrens, wat erna staat is de ondergrens.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Is dit een goed bewijs:
Stelling: (ab)A = a(bA)
Waarbij a en b scalars zijn, A is een willekeurige matrix.
Ik wil bewijzen dat elke row i gelijk is aan beide kanten, dus:
(ab)A = (ab) [Ai1,Ai2,Ai3,...]
= [abAi1,abAi2,abAi3,...]
= a[bAi1,bAi2,bAi3,...]
= a(bA)
Stelling: (ab)A = a(bA)
Waarbij a en b scalars zijn, A is een willekeurige matrix.
Ik wil bewijzen dat elke row i gelijk is aan beide kanten, dus:
(ab)A = (ab) [Ai1,Ai2,Ai3,...]
= [abAi1,abAi2,abAi3,...]
= a[bAi1,bAi2,bAi3,...]
= a(bA)
Hoe bewijs je dat R samenhangend is? Een direct bewijs lijkt me moeilijk. Misschien via contradictie? Dus uitgaan van nietsamenhangend en laten zien dat dit tot een contradictie leidt?
-
Stel je hebt een opdeling van R in twee disjuncte open deelverzamelingen U en V. Dan kun je een functie f: R -> R definieren door f(x) = 0 voor x in U en f(x) = 1 voor x in V te definieren, maar deze functie voldoet niet aan de tussenwaardestelling.quote:Op maandag 31 mei 2010 19:27 schreef gaussie het volgende:
Hoe bewijs je dat R samenhangend is? Een direct bewijs lijkt me moeilijk. Misschien via contradictie? Dus uitgaan van nietsamenhangend en laten zien dat dit tot een contradictie leidt?
.
Volgens mij kloppen je grenzen niet. Ik zou zeggen dit:quote:Op maandag 31 mei 2010 00:57 schreef Burakius het volgende:
[..]
E is gewoon een gebiedje ( dus in dit geval is E= 6xy )
Verder kun je het gewoon op klad herschrijven. Ik kan geen latex gedoe doen.... { = een integraal. Wat er vóór staat is de bovengrens, wat erna staat is de ondergrens.
maar ik weet ook niet precies wat je gedaan hebt omdat ik niet weet wat je bedoelt met type I en type II.
Latex is trouwens echt een aanrader. Als je bijvoorbeeld wilt typen de integraal van a tot b van f(x) dx, dan is de code heel simpel: \int_a^b f(x) dx. Ook voor breuken is Latex vaak handig, dan kan je \frac{a}{b} gebruiken voor a/b boven elkaar (probeer maar). Dit kan je hier typen: http://betahw.mine.nu/index.php , en je krijgt direct de output als plaatje.
Heeft iemand hier een idee hoe ik het volgende lower en upperbound grenzen bereken van het volgende vraagstuk? Ik zit zelf namelijk vast tijdens de voorbereiding voor een tentamen met dit geval.
Obtain an interval that with a confidence of 95% contains the mean labour hours of moves of 500 cubic feet with 3 pieces of large furniture where and elevator can be used.
Ik heb een SPSS tabel met Hours, Feet, Large Furniture en Elevator(dummy yes/no = 1/0)
Ik kom er maar niet uit met welke formule ik aan de slag moet.. Iemand een idee?
Obtain an interval that with a confidence of 95% contains the mean labour hours of moves of 500 cubic feet with 3 pieces of large furniture where and elevator can be used.
Ik heb een SPSS tabel met Hours, Feet, Large Furniture en Elevator(dummy yes/no = 1/0)
Ik kom er maar niet uit met welke formule ik aan de slag moet.. Iemand een idee?
Liever eigenwijs dan helemaal geen zelfvertrouwen.
Een standaard regressiemodel volstaat waarschijnlijk al. Heb je eenmaal de parameters geschat, dan is het niet moelijk het gevraagde CI te bepalen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb een vraag over compactheid. Waarom is een open interval (a,b) niet compact? Volgens de stelling van heine borel is een subset van R^n compact if it is closed and bounded. Een open interval is natuurlijk niet gesloten. Maar formeel wordt een topologische ruimte compact genoemd, indien elk van haar open dekkingen een eindige deeldekking heeft.
Waarom heeft een open interval geen eindige deeldekking en een gesloten interval wel?
Waarom heeft een open interval geen eindige deeldekking en een gesloten interval wel?
-
Een open overdekking van (0,1) die geen eindige deeloverdekking heeft is bijvoorbeeld {(1/n, 1)}, waarbij n de natuurlijke getallen groter dan 1 doorloopt.
Elke open overdekking van [0,1] heeft een eindige deeloverdekking. Dus als pathologisch voorbeeld neem ik dan maar {[0,1]}.
Misschien een wat minder triviaal voorbeeld: het voorbeeld bij (0,1) werkt kennelijk niet bij [0,1], want { (1/n,1] } mist het punt 0. Er zou dus nog een deel [0, a) in moeten zitten, maar dan kun je de (1/n, 1] met n > 1/a wegflikkeren uit je overdekking en hou je een eindige deeloverdekking over.
Ik ben een beetje in de war met grenzen van dubbele integralen.
Simultane dichtheid van X en Y is
f(x,y) = k voor
0<x<5
0<y<9
y<x^2
Bereken k.
Nu heb ik de grenzen als volgt vastgelegd:
y van 0 tot x
x van 0 tot 3
+
y van 0 tot 9
x van 3 tot 5
Krijg wel het goede antwoord maar heb't gevoel dat het makkelijker kan, is dat zo?
[ Bericht 1% gewijzigd door andrew.16 op 03-06-2010 18:36:31 ]
Simultane dichtheid van X en Y is
f(x,y) = k voor
0<x<5
0<y<9
y<x^2
Bereken k.
Nu heb ik de grenzen als volgt vastgelegd:
y van 0 tot x
x van 0 tot 3
+
y van 0 tot 9
x van 3 tot 5
Krijg wel het goede antwoord maar heb't gevoel dat het makkelijker kan, is dat zo?
[ Bericht 1% gewijzigd door andrew.16 op 03-06-2010 18:36:31 ]
f(x,y) = 0 anders? Nee, dat kan niet makkelijker. Ja je kunt het gebied tekenen en de oppervlakte berekenen. Omdat de hoogte overal hetzelfde is, kun je zo snel de inhoud bepalen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Waarvoor dient de formule (x-µ)/o- = z? Het heeft met statistiek te maken, en ik heb het al eerder geleerd, maar ik vergeet die rommel altijd. 
Ik ben aan het leren voor een tentamen, maar omdat ik sinds de middelbare school geen analytische wiskunde meer heb gehad, schort er heel wat aan mijn wiskunde.
Best beschamend eigenlijk, maar kan iemand mij helpen met het vinden van x in de volgende som en dit uitleggen?
2 * (x / 105,99) + (1,372 - x) / 84,01 = 0,02138
Het antwoord moet zijn: x = 0,724
Best beschamend eigenlijk, maar kan iemand mij helpen met het vinden van x in de volgende som en dit uitleggen?
2 * (x / 105,99) + (1,372 - x) / 84,01 = 0,02138
Het antwoord moet zijn: x = 0,724
This isn't even my final form.
Helemaal niet slordig, ik snap hem. Heel erg bedankt!quote:Op zaterdag 5 juni 2010 16:57 schreef JoPiDo het volgende:
[ afbeelding ]
beetje slordig uitgelegd, ben bang dat je niet elke stap begrijpt
This isn't even my final form.
Voor het normaliseren van een normale verdeling. Met de standaard normale verdeling kun je kijken welke waarden bij een bepaalde z-waarde horen.quote:Op zaterdag 5 juni 2010 16:31 schreef pagadder het volgende:
Waarvoor dient de formule (x-µ)/o- = z? Het heeft met statistiek te maken, en ik heb het al eerder geleerd, maar ik vergeet die rommel altijd.
"Reality is an illusion created by a lack of alcohol."
Ik heb de formule:
x - x
x(x+h) x(x+h)
Volgens de uitwerkingen wordt het:
-h
x(x+h)
(het gaat dus om een deling). Waarom gaat dit zo?
x - x
x(x+h) x(x+h)
Volgens de uitwerkingen wordt het:
-h
x(x+h)
(het gaat dus om een deling). Waarom gaat dit zo?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
kun je dit iets duidelijker opschrijven? ik kan hier geen wijs uitquote:Op zondag 6 juni 2010 14:00 schreef kanovinnie het volgende:
Ik heb de formule:
x - x
x(x+h) x(x+h)
Volgens de uitwerkingen wordt het:
-h
x(x+h)
(het gaat dus om een deling). Waarom gaat dit zo?
volgens mij bedoel je:
maar daar komt 0 uit
Ja dat dus, maar dan nog gedeeld door h. Het is trouwens een limietberekening waar H>0quote:Op zondag 6 juni 2010 14:17 schreef JoPiDo het volgende:
[..]
kun je dit iets duidelijker opschrijven? ik kan hier geen wijs uit
volgens mij bedoel je:
[ afbeelding ]
maar daar komt 0 uit
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
Ik zie dat er een foutje ingeslopen is, de tweede deling zou x-h gedeeltdoor x(x+h) moeten zijn.
Hoe kom je zo snel aan die plaatjes trouwens?
Hoe kom je zo snel aan die plaatjes trouwens?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
op het eind -h dan toch? En nu snap ik em.
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
Dat is gek. in de uitwerkingen van mijn leraar staat dat het -h wordt.
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
quote:Op zondag 6 juni 2010 14:34 schreef kanovinnie het volgende:
[..]
Ja dat dus, maar dan nog gedeeld door h. Het is trouwens een limietberekening waar H>0
gast, WTF
maak anders een foto van de hele opgave dan werk ik hem voor je uit
quote:Op zondag 6 juni 2010 15:19 schreef JoPiDo het volgende:
[..]
gast, WTF
maak anders een foto van de hele opgave dan werk ik hem voor je uit
Stap 2-3 is dus onduidenlijk voor mij.
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
http://www.youtube.com/jopido#p/a/u/1/0poefZx7RAoquote:Op zondag 6 juni 2010 16:08 schreef kanovinnie het volgende:
[..]
[ afbeelding ]
Stap 2-3 is dus onduidenlijk voor mij.
omdat bij de breuk de onderkant aan elkaar gelijk is gemaakt, kun je ze direct bij elkaar optellen
Delen door een breuk is vermenigvuldigen met het omgekeerde. Bij de laatste stap deel je boven- en onderkant door h.
[ Bericht 13% gewijzigd door 123hopsaflops op 06-06-2010 16:39:49 ]
Ok, dat snap ik. Nu nog een vraagje.
x^0,5, gediffrentieerd. Dan wordt dat toch 0.5x^-0,5?
x^0,5, gediffrentieerd. Dan wordt dat toch 0.5x^-0,5?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
quote:Op zondag 6 juni 2010 16:48 schreef kanovinnie het volgende:
Ok, dat snap ik. Nu nog een vraagje.
x^0,5, gediffrentieerd. Dan wordt dat toch 0.5x^-0,5?
net als:
Op je formule-blad staat:
Invullen voor jouw som geeft: a=1 en b=0.5, dus:
Op mijn formuleblad staat gewoonquote:Op zondag 6 juni 2010 16:55 schreef JoPiDo het volgende:
[..]
[ afbeelding ]
net als:
[ afbeelding ]
Op je formule-blad staat:
[ afbeelding ]
Invullen voor jouw som geeft: a=1 en b=0.5, dus:
[ afbeelding ]
x^n=n*x^n-1.
Dus had ik het goed. Bedankt!
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
quote:Op zondag 6 juni 2010 17:00 schreef kanovinnie het volgende:
[..]
Op mijn formuleblad staat gewoon
x^n=n*x^n-1.
Dus had ik het goed. Bedankt!
dat is hetzelfde, maar niet helemaal compleet
Wel compleet in combinatie met de regelquote:Op zondag 6 juni 2010 17:01 schreef JoPiDo het volgende:
[..]
dat is hetzelfde, maar niet helemaal compleet
d(f a)/dx = a df/dx (a=constant),
die waarschijnlijk apart vermeld staat.
Ik heb gewoon een formuleblad gemaakt met alle standaartafgeleides.
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
quote:Op zondag 6 juni 2010 17:09 schreef kanovinnie het volgende:
Ik heb gewoon een formuleblad gemaakt met alle standaartafgeleides.
als het goed is heeft de school waar je de toets voor moet maken ook een formule-blad waar dit al op staat en die je bovendien kunt gebruiken op toetsen/tentamens, als je daar tijdens het huiswerk maken al mee oefent, is de toets/tentamen een eitje
Nog beter als je ze gewoon uit je hoofd kentquote:Op zondag 6 juni 2010 22:36 schreef JoPiDo het volgende:
[..]
als het goed is heeft de school waar je de toets voor moet maken ook een formule-blad waar dit al op staat en die je bovendien kunt gebruiken op toetsen/tentamens, als je daar tijdens het huiswerk maken al mee oefent, is de toets/tentamen een eitje
quote:Op zondag 6 juni 2010 23:12 schreef BasementDweller het volgende:
[..]
Nog beter als je ze gewoon uit je hoofd kent
ik denk dat iemand die 'standaard' niet kan spellen, beter niet dingen uit zijn hoofd moet gaan zitten leren
Ja. Want spelling heeft zoveel met wiskunde te maken. Toch leuk van iemand te horen die zelf geen hoofdletters en punten gebruikt.quote:Op zondag 6 juni 2010 23:23 schreef JoPiDo het volgende:
[..]
ik denk dat iemand die 'standaard' niet kan spellen, beter niet dingen uit zijn hoofd moet gaan zitten leren
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
De grootheden X en Y hebben een simultane verdeling gedefinieerd door de kansdichtheid:
f(x, y) = x op het gebied: 0 < x < 2 en 0 < y < 3 - x
Bepaal de marginale dichtheid van Y.
Marginale dichtheid van x snap ik, maar ik zie niet hoe ik de marginale dichtheid van y zou moeten bepalen.
Ik doe altijd: f(y)= (integraal van 0 tot 2) x dx
Maar daar klopt neem ik aan geen hout van. Ik heb altijd problemen met de grenzen van de marginale dichtheid van y, geen idee hoe ik het zou moeten aanpakken.
f(x, y) = x op het gebied: 0 < x < 2 en 0 < y < 3 - x
Bepaal de marginale dichtheid van Y.
Marginale dichtheid van x snap ik, maar ik zie niet hoe ik de marginale dichtheid van y zou moeten bepalen.
Ik doe altijd: f(y)= (integraal van 0 tot 2) x dx
Maar daar klopt neem ik aan geen hout van. Ik heb altijd problemen met de grenzen van de marginale dichtheid van y, geen idee hoe ik het zou moeten aanpakken.
je moet de x eruit integreren, maar je moet x niet van 0 t/m 2 laten lopen want 3-x moet groter zijn dan y.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus dan moet x lopen van 0 tot 3-y?quote:Op dinsdag 8 juni 2010 00:23 schreef GlowMouse het volgende:
je moet de x eruit integreren, maar je moet x niet van 0 t/m 2 laten lopen want 3-x moet groter zijn dan y.
Ja, tenzij 3-y groter is dan 2, dan loopt x maar tot 2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik ben op zoek naar een wiskunde boek dat geschikt is voor zelfstudie. Ik heb havo gedaan met Wiskunde B1 en 2. Maar veel is weggezakt en ik was er toen ook al niet goed in.
Ik heb al gekeken naar:
- Wiskunde voor het hoger onderwijs
- Basisboek wiskunde
Welk boek raden jullie aan?
Ik heb al gekeken naar:
- Wiskunde voor het hoger onderwijs
- Basisboek wiskunde
Welk boek raden jullie aan?
"Everything we are, we are when we're alone."
Ik ken het eerste boek niet, maar Basisboek wiskunde (van Van de Craats, toch?) heeft iig veel opgaves om mee te oefenen. Deze is overigens ook voor een heel groot deel online in te zien (http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)quote:Op dinsdag 8 juni 2010 17:15 schreef Meursault het volgende:
Ik ben op zoek naar een wiskunde boek dat geschikt is voor zelfstudie. Ik heb havo gedaan met Wiskunde B1 en 2. Maar veel is weggezakt en ik was er toen ook al niet goed in.
Ik heb al gekeken naar:
- Wiskunde voor het hoger onderwijs
- Basisboek wiskunde
Welk boek raden jullie aan?
Om het patroon goed te krijgen. (Net als bij e; e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, ...] = [1; 0, 1, 1, 2, 1, 1, 4, 1, 1, 6, 1, ...])
e^2 = [7; 2, 1, 1, 3, 18, 5, 1, 1, 6, 30, 8, 1, ...] = [1, 0, 6, 2, 1, 1, 3, 18, 5, 1, 1, 6, 30, 8, 1, ...]
De waardes van p en q zouden op deze manier toch alleen moeten opschuiven? Ik heb nu q0 = 7, maar bij die tweede kettingbreuk heb ik nergens een 7 staan. Bij p kloppen de waardes (tot p7) wel.
Ik zie niet waarom er een 7 bij de q's zou moeten komen. Bij de eerste beginnen de q's met 1, 2, 3, 5, ... en bij de tweede met 1, 0, 1, 2, 3, 5, ...
Oh, ja, damn, ik zie het. Hier begin ik met tellen bij 0 natuurlijk, maar mathematica vindt niet dat lijsten beginnen met een 0e element. Ik heb blijkbaar daar iets verkeerds mee gedaan :p
Gevonden!
Gevonden!
Over de kettingbreuk van e (http://arxiv.org/PS_cache/math/pdf/0601/0601660v3.pdf)
Stelling is e = [1, 0, 1, 1, 2, 1, 1, 4, 1, 1,6, 1, ...]. Om dit te bewijzen moet worden laten zien dat lim pi/qi = e. Daarvoor worden 3 integralen gedefinieerd, namelijk:
[img][/img].
Omdat de limiet van An, Bn en Cn 0 is volgt dus dat lim qie-pi=0.
Zijn het 3 integralen omdat er ook drie verschillende "mogelijkheden" zijn voor p en q? Dus omdat de ontwikkeling van de kettingbreuk zich na 3 keer herhaalt? (En dus voor e^2 zullen er vijf integralen moeten zijn, als dat bewijs tenminste op dezelfde manier gaat?)
Omdat qi >= 1 als i >= 2 is het zo dat e = lim pi/qi.
Klinkt logisch, maar wat zou er precies fout gaan als q kleiner dan 1 was?
Verder wil ik bewijzen dat dit gelijk is aan 0:
[img][/img]
Het artikel zegt hierover "To prove (2) integrate both sides of
[img][/img]."
Ik heb geen idee echter hoe ik de linkerkant moet integreren.
[ Bericht 6% gewijzigd door Hanneke12345 op 14-06-2010 16:59:50 ]
Stelling is e = [1, 0, 1, 1, 2, 1, 1, 4, 1, 1,6, 1, ...]. Om dit te bewijzen moet worden laten zien dat lim pi/qi = e. Daarvoor worden 3 integralen gedefinieerd, namelijk:
[img][/img].
Omdat de limiet van An, Bn en Cn 0 is volgt dus dat lim qie-pi=0.
Zijn het 3 integralen omdat er ook drie verschillende "mogelijkheden" zijn voor p en q? Dus omdat de ontwikkeling van de kettingbreuk zich na 3 keer herhaalt? (En dus voor e^2 zullen er vijf integralen moeten zijn, als dat bewijs tenminste op dezelfde manier gaat?)
Omdat qi >= 1 als i >= 2 is het zo dat e = lim pi/qi.
Klinkt logisch, maar wat zou er precies fout gaan als q kleiner dan 1 was?
Verder wil ik bewijzen dat dit gelijk is aan 0:
[img][/img]
Het artikel zegt hierover "To prove (2) integrate both sides of
[img][/img]."
Ik heb geen idee echter hoe ik de linkerkant moet integreren.
[ Bericht 6% gewijzigd door Hanneke12345 op 14-06-2010 16:59:50 ]
Ja, dat zijn inderdaad 3 integralen vanwege het patroon in de kettingbreuk.
In die laatste formule horen geen integraaltekens te staan. Dan staat er een identiteit van functies en integreren levert dan dus een uitdrukking voor de som van de integralen.
In die laatste formule horen geen integraaltekens te staan. Dan staat er een identiteit van functies en integreren levert dan dus een uitdrukking voor de som van de integralen.
voor een sinusvormige wisselspanning geldt:
U(t) = 50 * sin (200pi*t)
Op welk tijdstip is er precies 1 periode voorbij?
Hoe bereken je dit?
U(t) = 50 * sin (200pi*t)
Op welk tijdstip is er precies 1 periode voorbij?
Hoe bereken je dit?
Die 50 maakt het bereik 50x groter, dus daar hoef je voor de periode niet naar te kijken. Als er zou staan sin(2x) dan zou de periode 2 keer zo klein worden, omdat x twee keer zo 'snel' gaat. De 'normale' periode van sin(x) is 2pi, dus van sin(2x) wordt de periode 1pi. Van sin(200pi maal x) wordt de periode dus 200pi zo klein: 2pi delen door 200pi geeft 1/100. De periode wordt dus 1/100.
Klopt met het antwoord, super bedanktquote:Op zondag 13 juni 2010 17:29 schreef JoPiDo het volgende:
Die 50 maakt het bereik 50x groter, dus daar hoef je voor de periode niet naar te kijken. Als er zou staan sin(2x) dan zou de periode 2 keer zo klein worden, omdat x twee keer zo 'snel' gaat. De 'normale' periode van sin(x) is 2pi, dus van sin(2x) wordt de periode 1pi. Van sin(200pi maal x) wordt de periode dus 200pi zo klein: 2pi delen door 200pi geeft 1/100. De periode wordt dus 1/100.
Het is 'geldt'.
heb je een tegenvoorbeeld voor die eerste?
heb je een tegenvoorbeeld voor die eerste?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dan heeft het antwoordvel het fout; beide stellingen zijn nl. FALSE (fout dus). Even informeel gezegd loopt 3x minder hard omhoog dan 4x als je x naar +oneindig laat lopen. Omgekeerd geldt dus ook; als je x naar -oneindig laat lopen zal 3x minder hard omlaag naar 0 naderen dan 4x, en zal 3x dus groter zijn dan 4x voor elke x kleiner dan 0. Bedenk ook dat je e-x en 10-x als 1/ex en 1/10x kunt schrijven (let op het wegvallen van het minteken in de exponent doordat je je macht nu in breukvorm schrijft)quote:Op zondag 13 juni 2010 20:07 schreef vault_tec het volgende:
[ afbeelding ]
Moet toch allebei niet waar zijn? antwoorden vel zegt dat de eerste wel klopt ¬¬
[ Bericht 1% gewijzigd door ErictheSwift op 13-06-2010 20:32:39 ]
Bedankt, wordt morgen een 10 
Maar als ik getallen in ga vullen voor x komt er toch uit dat de 3 > 4 is.
Maar als ik getallen in ga vullen voor x komt er toch uit dat de 3 > 4 is.
Het wordt duidelijker door links en rechts te delen door het positieve getal 4^x, dan krijg je links 0.75^x en rechts 1. Ze zijn gelijk in het geval x=0, en de functie f gedefinieerd door f(x) = 0.75^x is afnemend.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dank u, snap het al... Ik heb ook kwadraten P-1 maar die staan tussen 2 strepen
2 Ip-1I (of het maar even uit te beelden)
Hoe kan je dit berekenen... Heel deze periode geen wiskunde gehad en nu wel alsnog een toets krijgen
2 Ip-1I (of het maar even uit te beelden)
Hoe kan je dit berekenen... Heel deze periode geen wiskunde gehad en nu wel alsnog een toets krijgen
even ervan uitgaande dat het absoluutstrepen betreft; dan moet je je functie of vgl. opdelenquote:Op zondag 13 juni 2010 20:44 schreef vault_tec het volgende:
Dank u, snap het al... Ik heb ook kwadraten P-1 maar die staan tussen 2 strepen
2 Ip-1I (of het maar even uit te beelden)
Hoe kan je dit berekenen... Heel deze periode geen wiskunde gehad en nu wel alsnog een toets krijgen
2|p-1| = 2p-2 voor elke x => 0
2|p-1| = 2 - 2p voor elke x < 0 (vermenigvuldig je oorsponkelijke functie/vgl. met -1 ; plot anders ff |X| uit dan zie gelijk waarom)
Ik snap het nietquote:Op zondag 13 juni 2010 20:49 schreef ErictheSwift het volgende:
[..]
even ervan uitgaande dat het absoluutstrepen betreft; dan moet je je functie of vgl. opdelen
2|p-1| = 2p-2 voor elke x => 0
2|p-1| = 2 - 2p voor elke x < 0 (vermenigvuldig je oorsponkelijke functie/vgl. met -1 ; plot anders ff |X| uit dan zie gelijk waarom)
|x| betekent het minteken eraf hakken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, hij hakt het minteken van p-1. Dus als p = -10 is, dan staat er 11.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Glowmouse, da's wel een heel foute uitleg van het begrip absolute waarde. Foei, jij als local fok! maths geek zijnde zou beter moeten weten 
.
@Vault_tec: mss dat onderstaande plaatje het 1 en ander verduidelijkt.
snap je nu waarom ik schreef:
|x| = x voor elke x groter dan of gelijk aan 0
|x| = -x voor elke x kleiner dan 0
en x kan je dus vervangen door een willekeurige functie, dus ook 2p-2.
.@Vault_tec: mss dat onderstaande plaatje het 1 en ander verduidelijkt.
snap je nu waarom ik schreef:
|x| = x voor elke x groter dan of gelijk aan 0
|x| = -x voor elke x kleiner dan 0
en x kan je dus vervangen door een willekeurige functie, dus ook 2p-2.
quote:Op zondag 13 juni 2010 21:18 schreef ErictheSwift het volgende:
Glowmouse, da's wel een heel foute uitleg van het begrip absolute waarde. Foei, jij als local fok! maths geek zijnde zou beter moeten weten
@Vault_tec: mss dat onderstaande plaatje het 1 en ander verduidelijkt.
[ afbeelding ]
snap je nu waarom ik schreef:
|x| = x voor elke x groter dan of gelijk aan 0
|x| = -x voor elke x kleiner dan 0
en x kan je dus vervangen door een willekeurige functie, dus ook 2p-2.
Klopt het dat de surface integral van een curl vector field altijd 0 is vanwege de stelling van Gauss?
Dus
0 omdat de divergentie van curl altijd 0 is.
Lijkt me onwaarschijnlijk dat dit klopt, maar wat doe ik dan fout?
Dus
0 omdat de divergentie van curl altijd 0 is.
Lijkt me onwaarschijnlijk dat dit klopt, maar wat doe ik dan fout?
... en dan te bedenken dat ik nooit echt hoog heb gestaan voor wiskunde (kijkt met schuin oog naar Huyssequote:
)
quote:Op zondag 13 juni 2010 20:07 schreef vault_tec het volgende:
[ afbeelding ]
Moet toch allebei niet waar zijn? antwoorden vel zegt dat de eerste wel klopt ¬¬
Voor x<0 geldt:
en:
Omdat 1/3 > 1/4, geldt:
Dus de eerste is niet waar. De tweede lijkt me duidelijk.
[ Bericht 1% gewijzigd door 123hopsaflops op 13-06-2010 21:37:42 ]
En waarom niet-gehele getallen niet zouden werken, zie ik niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:Op zondag 13 juni 2010 21:33 schreef GlowMouse het volgende:
En waarom niet-gehele getallen niet zouden werken, zie ik niet.
ohja, ik was in de war met tot de macht een breuk en wortels
dan klopt mijn hele verhaal dus gewoon
Nee, voor x<0quote:Op zondag 13 juni 2010 21:37 schreef JoPiDo het volgende:
[..]
ohja, ik was in de war met tot de macht een breuk en wortels
dan klopt mijn hele verhaal dus gewoon
Want stel dat het wel waar is en x=-1, dan
quote:Op zondag 13 juni 2010 21:40 schreef BasementDweller het volgende:
[..]
Nee, voor x<0
[ afbeelding ]
Want stel dat het wel waar is en x=-1, dan
[ afbeelding ]
ga nog maar eens goed lezen wat en hoe ik het allemaal opschrijf
Gedaan. Ik snap wel wat je bedoelt alleen je schrijft het gewoon fout opquote:Op zondag 13 juni 2010 21:41 schreef JoPiDo het volgende:
[..]
ga nog maar eens goed lezen wat en hoe ik het allemaal opschrijf
quote:Op zondag 13 juni 2010 21:42 schreef BasementDweller het volgende:
[..]
Gedaan. Ik snap wel wat je bedoelt alleen je schrijft het gewoon fout op
ik schrijf het helemaal perfect op
quote:Op zondag 13 juni 2010 21:44 schreef BasementDweller het volgende:
[..]
Wat snap je niet aan mijn tegenvoorbeeld
nu mag je je arrogante smoelwerkje weer houden
quote:Op zondag 13 juni 2010 21:36 schreef BasementDweller het volgende:
Maar weet je geen antwoord op mijn vraag, Glowmouse?
Nee, ik doe niet aan dat soort integralen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Jongens jongens toch, hou het een beetje vriendelijk OK? Dit is geen wedstrijdje E-fallus-oppompen.quote:Op zondag 13 juni 2010 21:45 schreef JoPiDo het volgende:
[..]
nu mag je je arrogante smoelwerkje weer houden
Erg arrogant inderdaad, iemand op een fout wijzen
Nogmaals mijn vraag:
Klopt het dat de surface integral van een curl vector field altijd 0 is vanwege de stelling van Gauss?
Dus
0 omdat de divergentie van curl altijd 0 is.
Lijkt me onwaarschijnlijk dat dit klopt, anders is de stelling van stokes nogal zinloos, maar wat doe ik dan fout?
Nogmaals mijn vraag:
Klopt het dat de surface integral van een curl vector field altijd 0 is vanwege de stelling van Gauss?
Dus
0 omdat de divergentie van curl altijd 0 is.
Lijkt me onwaarschijnlijk dat dit klopt, anders is de stelling van stokes nogal zinloos, maar wat doe ik dan fout?
Terechtquote:Op zondag 13 juni 2010 21:50 schreef GlowMouse het volgende:
[..]
Nee, ik doe niet aan dat soort integralen.
Lijkt me wel dat dit klopt als V en S voldoende 'mooi' zijn (compact en glad is ongetwijfeld voldoende).quote:Op zondag 13 juni 2010 21:26 schreef BasementDweller het volgende:
Klopt het dat de surface integral van een curl vector field altijd 0 is vanwege de stelling van Gauss?
Dus
[ afbeelding ]
0 omdat de divergentie van curl altijd 0 is.
Lijkt me onwaarschijnlijk dat dit klopt, maar wat doe ik dan fout?
Ja, in de opgave waar ik mee bezig ben is V het volume van een bol en S de oppervlakte ervan. F is ook goed gedefinieerd en af te leiden.quote:Op zondag 13 juni 2010 21:54 schreef thabit het volgende:
[..]
Lijkt me wel dat dit klopt als V en S voldoende 'mooi' zijn (compact en glad is ongetwijfeld voldoende).
Maar waarom zou je dan ooit de stelling van Stokes gebruiken (als er altijd 0 uit zou moeten komen)?
De stelling van Stokes drukt eigenlijk de dualiteit tussen singuliere homologie en de Rham cohomologie uit. Dat is toch wel behoorlijk fundamenteel.
Ongetwijfeld, maar volgens mij mis je mijn punt. Als de dubbele integraal van curl altijd nul is vanwege de stelling van gauss, heeft het geen zin om het om te zetten in een enkele kringintegraal met de stelling van Stokes en dan uit te rekenen. Verspilde moeite als het toch altijd nul is.quote:Op zondag 13 juni 2010 21:59 schreef thabit het volgende:
De stelling van Stokes drukt eigenlijk de dualiteit tussen singuliere homologie en de Rham cohomologie uit. Dat is toch wel behoorlijk fundamenteel.
Bij Stokes heb je andere voorwaarden. Daar gaat het om een oppervlak met rand. Bij Gauss is het oppervlak de rand, en die rand heeft op zijn beurt geen rand, dus een integraal daarover is dan ook 0.
Om het even te concretiseren, het gaat om deze vraag.
Evaluate
, where F=(x^2+y-4, 3xy, 2xz+z^2) and S is the surface 
met 
using Stokes' theorem
. (unit normal upward pointing)
Met Gauss' theorem krijg ik dus 0. Het oppervlak S is de rand van een halve bol. En bij stokes moet je integreren over het pad, de rand van het oppervlak (x²+y²=16). Dit heb ik geparametriseerd door c(t)=(cos(t), sin(t)) en geëvalueerd. Dit levert echter 16 pi en dus geen 0.
En mijn punt is dus ook dat het oppervlak (als rand) zelf ook een rand heeft in dit geval, of zie ik dat fout?
Evaluate
. (unit normal upward pointing)
Met Gauss' theorem krijg ik dus 0. Het oppervlak S is de rand van een halve bol. En bij stokes moet je integreren over het pad, de rand van het oppervlak (x²+y²=16). Dit heb ik geparametriseerd door c(t)=(cos(t), sin(t)) en geëvalueerd. Dit levert echter 16 pi en dus geen 0.
En mijn punt is dus ook dat het oppervlak (als rand) zelf ook een rand heeft in dit geval, of zie ik dat fout?
Met de stelling van Gauss krijg je hier geen 0, want de rand van de halve bol heeft ook nog een schijf aan de onderkant zitten en die zit niet in S.
Kan je dit verder toelichten? Wat maakt het uit dat die schijf niet in S zit?quote:Op zondag 13 juni 2010 22:47 schreef thabit het volgende:
Met de stelling van Gauss krijg je hier geen 0, want de rand van de halve bol heeft ook nog een schijf aan de onderkant zitten en die zit niet in S.
Gauss relateert een integraal over een (voldoende 'mooie' maar daar is hier wel aan voldaan) driedimensionale vorm aan een integraal over de rand van die vorm. Een halve bol heeft als rand een half boloppervlak aan de bovenkant plus een cirkelschijf aan de onderkant. Als je alleen maar over het halve boloppervlak integreert, dan neem je de cirkelschijf dus niet mee. Dus je kunt Gauss niet op die manier toepassen omdat je niet over de hele rand integreert.
Ah, duidelijk. Het moet natuurlijk een gesloten oppervlak zijn.quote:Op zondag 13 juni 2010 23:40 schreef thabit het volgende:
Gauss relateert een integraal over een (voldoende 'mooie' maar daar is hier wel aan voldaan) driedimensionale vorm aan een integraal over de rand van die vorm. Een halve bol heeft als rand een half boloppervlak aan de bovenkant plus een cirkelschijf aan de onderkant. Als je alleen maar over het halve boloppervlak integreert, dan neem je de cirkelschijf dus niet mee. Dus je kunt Gauss niet op die manier toepassen omdat je niet over de hele rand integreert.
Ik doe nog iets fout met de stelling van stokes of directe evaluatie. Bij directe evaluatie krijg ik namelijk wel 0 (en 16pi met stokes). (dus als iemand zich geroepen voelt om het na te rekenen, graag
)
Ik denk toch dat het dan mis moet gaan bij de directe evaluatie.
Wat moet je hier als dS nemen? Mijn boek zegt
,
alleen dan zit ik nog met x, y en z in de integrand terwijl er dphi dtheta achter staat. Kan ik dan zomaar voor x,y en z spherical coordinates invullen?
Ik krijg:quote:Evaluate
. (unit normal upward pointing)
Wat moet je hier als dS nemen? Mijn boek zegt
alleen dan zit ik nog met x, y en z in de integrand terwijl er dphi dtheta achter staat. Kan ik dan zomaar voor x,y en z spherical coordinates invullen?
Ik vul in:
x=4cos(th)sin(phi)
y=4sin(th)sin(phi)
z=cos(phi)
Dan krijg ik dit als integrand:
4 Sin[\[Phi]] (-32 Cos[\[Phi]] Sin[\[Theta]] Sin[\[Phi]] + 4 Cos[\[Phi]] (-1 + 12 Sin[\[Theta]] Sin[\[Phi]]))
en als ik dat door mathematica laat integreren (phi van 0 tot pi en theta van 0 tot 2pi), dan krijg ik 0 en geen -16pi.
[ Bericht 5% gewijzigd door BasementDweller op 14-06-2010 16:38:50 ]
x=4cos(th)sin(phi)
y=4sin(th)sin(phi)
z=cos(phi)
Dan krijg ik dit als integrand:
4 Sin[\[Phi]] (-32 Cos[\[Phi]] Sin[\[Theta]] Sin[\[Phi]] + 4 Cos[\[Phi]] (-1 + 12 Sin[\[Theta]] Sin[\[Phi]]))
en als ik dat door mathematica laat integreren (phi van 0 tot pi en theta van 0 tot 2pi), dan krijg ik 0 en geen -16pi.
[ Bericht 5% gewijzigd door BasementDweller op 14-06-2010 16:38:50 ]
Als dS neem ik gewoon (x,y,z) sinphi dphi dtheta.
Het inproduct geeft: -2 z y + z (3 y - 1) R sinphi dphi dtheta met R=4, en dan y en z substitueren en integreren...
Het inproduct geeft: -2 z y + z (3 y - 1) R sinphi dphi dtheta met R=4, en dan y en z substitueren en integreren...
Bij z moet je natuurlijk ook niet de factor 4 vergeten, maar dat zal wel een tikfout zijn. Probeer het eens uit te schrijven in termen van dx, dy en dz en daarna pas te substitueren, want ik zie niet helemaal waar die uitdrukking voor dS vandaan komt.
Dat was een typfout. Maar oké, ze zeggen dus datquote:Op zaterdag 12 juni 2010 22:55 schreef thabit het volgende:
Ja, dat zijn inderdaad 3 integralen vanwege het patroon in de kettingbreuk.
In die laatste formule horen geen integraaltekens te staan. Dan staat er een identiteit van functies en integreren levert dan dus een uitdrukking voor de som van de integralen.
En dus ?
? (Of nouja, als onbepaalde integraal, dus de rechterkant op het interval [0,1].)
Maar dan nog snap ik niet waarom de eerste vergelijking waar is. "which follows immediately from the product rule for dervatives", volgens 't artikel. Maar ik zie het nog niet.
Ik zou niet weten hoe ik het in dxdydz moet uitschrijven... dS is gewoon de jacobiaan die je krijgt door sferische substitutie.quote:Op maandag 14 juni 2010 16:58 schreef thabit het volgende:
Bij z moet je natuurlijk ook niet de factor 4 vergeten, maar dat zal wel een tikfout zijn. Probeer het eens uit te schrijven in termen van dx, dy en dz en daarna pas te substitueren, want ik zie niet helemaal waar die uitdrukking voor dS vandaan komt.
In mijn boek staat vector surface element for a sphere:
Dit kan je wel uitrekenen door te parametriseren en het uitproduct te nemen van de afgeleides naar phi en theta (als het goed is).
Ik snap alleen niet waarom er R^2 bij die laatste staat en R bij die andere twee, tikfoutje?
Kan iemand me even helpen.
Evaluate
, where E lies between the spheres x2 + y2 + z2 = 1 and x2 + y2 + z2 = 4 in the first octant.
Dit moet allemaal in spherical coordinates.
Nou heb ik natuurlijk al gevonden dat
. en
Nu moet ik alleen nog de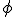
vinden (dit is de hoek tussen Z en X)
Maar ja, ik weet natuurlijk een aantal dingen ( bijvoorbeeld z = cos(phi) etc.) Maar goed ik kom er niet uit. Kan iemand me helpen?
[ Bericht 4% gewijzigd door Burakius op 15-06-2010 00:13:36 ]
Evaluate
Dit moet allemaal in spherical coordinates.
Nou heb ik natuurlijk al gevonden dat
Nu moet ik alleen nog de
Maar ja, ik weet natuurlijk een aantal dingen ( bijvoorbeeld z = cos(phi) etc.) Maar goed ik kom er niet uit. Kan iemand me helpen?
[ Bericht 4% gewijzigd door Burakius op 15-06-2010 00:13:36 ]
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Waarom loopt O tussen 0 en 2pi als je maar één octant wilt?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oja goede vraag. Dan moet hij natuurlijk tot pi/2 . Stom even over heen gezienquote:Op dinsdag 15 juni 2010 00:07 schreef GlowMouse het volgende:
Waarom loopt O tussen 0 en 2pi als je maar één octant wilt?
Ik heb even geedit: (met latex, thats a first).
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zou ik het ook met cilinder coordinaten kunnen doen?
waarbij theta dan tussen pi/2 en 0 zit. r tussen 2 en 1 en z dan tussen 4 en 1 ??
waarbij theta dan tussen pi/2 en 0 zit. r tussen 2 en 1 en z dan tussen 4 en 1 ??
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zeg eens in woorden welk gebied ze precies bedoelen. Volgens mij heb je dat verkeerd voor je.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb gewoon precies omschreven wat de vraag is. Ik moet alleen die klote PHI nog vinden om de som te maken. Help alsjeblieftquote:Op dinsdag 15 juni 2010 00:19 schreef GlowMouse het volgende:
Zeg eens in woorden welk gebied ze precies bedoelen. Volgens mij heb je dat verkeerd voor je.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Heb het antwoord al. Omdat phi ook tot de eerste octant gaat is het ook natuurlijk gewoon van 0 tot pi/2
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Lol dat is precies het antwoord wat ik zocht terwijl je een andere vraag vroeg hahahaha.quote:Op maandag 14 juni 2010 17:24 schreef BasementDweller het volgende:
I got it!!!!!!!!
Ik moet natuurlijk phi integreren van 0 tot pi/2 en niet van 0 tot pi
Volgend paragraaf moet ik ook aan de Jacobian
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Use a triple integral to find the volume of the solid enclosed by the cylinder x = y2 and the planes z=0 and x+z=1.
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Om te beginnen zou ik een plaatje tekenen.quote:Op dinsdag 15 juni 2010 09:16 schreef Jac0bus het volgende:
Use a triple integral to find the volume of the solid enclosed by the cylinder x = y2 and the planes z=0 and x+z=1.
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
Als ik een vlak heb gegeven door x+y+z=1 met restrictie x² + 2y² =< 1, kan je dan nog poolcoördinaten gebruiken voor de oppervlakte-integraal? Wat zijn dan de grenzen van r?
Andere vraag:
Opgave:
Let
and D the unit disk in the u,v-plane. Find the area of Phi(D).
De unit disk is: u² + v² =< 1. De integraal die we moeten berekenen is:
.
Waarbij T_x = partiële afgeleide van phi naar x, en T_y partiële naar y.
Dus
.
Substitutie van poolcoördinaten geeft:
Het antwoord zou moeten zijn,
.
Waar gaat het fout ?
Opgave:
Let
De unit disk is: u² + v² =< 1. De integraal die we moeten berekenen is:
Waarbij T_x = partiële afgeleide van phi naar x, en T_y partiële naar y.
Dus
Substitutie van poolcoördinaten geeft:
Het antwoord zou moeten zijn,
Waar gaat het fout
?
Ik zie het al... vergeten de ondergrens er vanaf te trekken. Bah, ik maak altijd van die lame foutjes met integreren
Gedaan, zowel 3d als 2d, ik zie alleen totaal niet hoe dat object er uit zou moeten zien, iets wat mijn grootste probleem is met die integralen. Zo zijn de integralen ook veel lastiger op te stellen.quote:Op dinsdag 15 juni 2010 11:43 schreef thabit het volgende:
[..]
Om te beginnen zou ik een plaatje tekenen.
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Ik neem aan dat je de unit cilinder bedoelt (straal =1) ?quote:Op dinsdag 15 juni 2010 09:16 schreef Jac0bus het volgende:
Use a triple integral to find the volume of the solid enclosed by the cylinder x = y2 and the planes z=0 and x+z=1.
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
x=y² is een gekantelde parabool
z=0 is het xy-vlak
x+z=1 is een vlak, wat je kan tekenen door het x,z vlak te nemen (want in y is die constant) en z=1-x te tekenen, en die lijn dan "uit te rekken" in de y-richting.
Ik heb het heel groot getekend en ik denk dat eruit moet komen:
(< en > betekenen groter of gelijk)
0 < x < 1
-wortel (x) < y < wortel (x)
0 < z < 1-x
Maar ik ben hier ook niet supergoed in, dus onder voorbehoud.
In dit geval integreer je dan eerst over z of y omdat die uitgedrukt zijn in andere variabelen. Tot slot integreer je over x.
(< en > betekenen groter of gelijk)
0 < x < 1
-wortel (x) < y < wortel (x)
0 < z < 1-x
Maar ik ben hier ook niet supergoed in, dus onder voorbehoud.
In dit geval integreer je dan eerst over z of y omdat die uitgedrukt zijn in andere variabelen. Tot slot integreer je over x.
Probeer eerst eens y = te vinden. Teken die. Daarna ga je tekenen wat je weet van z = ....quote:Op dinsdag 15 juni 2010 13:26 schreef Jac0bus het volgende:
[..]
Gedaan, zowel 3d als 2d, ik zie alleen totaal niet hoe dat object er uit zou moeten zien, iets wat mijn grootste probleem is met die integralen. Zo zijn de integralen ook veel lastiger op te stellen.
Ten slotte zou je x = kunnen vinden.
Waar het hierom draait is dat het slim is als je eerst 3 onafhankelijke tekening maakt voor de xy-plane, yz-plane en xz- plane. Zodoende kun je het vaak wel vinden.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Geen idee over die cylinder, zoals ik de vraag typte is hij letterlijk zoals hij in het boek staat. Het antwoord is 8/15 btw.quote:Op dinsdag 15 juni 2010 13:38 schreef BasementDweller het volgende:
[..]
Ik neem aan dat je de unit cilinder bedoelt (straal =1) ?
x=y² is een gekantelde parabool
z=0 is het xy-vlak
x+z=1 is een vlak, wat je kan tekenen door het x,z vlak te nemen (want in y is die constant) en z=1-x te tekenen, en die lijn dan "uit te rekken" in de y-richting.
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Als je mijn boundaries gebruikt kom je inderdaad op 8/15 (met de unit cilinder dus).quote:Op dinsdag 15 juni 2010 13:44 schreef Jac0bus het volgende:
[..]
Geen idee over die cylinder, zoals ik de vraag typte is hij letterlijk zoals hij in het boek staat. Het antwoord is 8/15 btw.
Druk eerst x^-2.25 uit in een getal.quote:
Neem de reciproke van beide kanten, en doe beide kanten tot de 4e macht. Trek nu de 9e machtswortel aan beide kanten.
Sense?quote:Op dinsdag 15 juni 2010 17:21 schreef BasementDweller het volgende:
[..]
Druk eerst x^-2.25 uit in een getal.
Neem de reciproke van beide kanten, en doe beide kanten tot de 4e macht. Trek nu de 9e machtswortel aan beide kanten.
Ik zou zeggen probeer het eens. Als je met je rekenmachine ook de 2.25e machtswortel kan berekenen kan je dat tot de 4e verheffen weglaten.quote:
-2.25 machtswortel ((11/0,37)) = -4.516quote:
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik zoek een internetsite die vertelt wat de simple continued fraction van e^2 is, een andere dan wikipedia. M'n googleskills laten het hierin even afweten (zoeken op e is al heel vervelend, laat staan op e^2).
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Mja, zat ik aan te denken, maar ik wil iets dat echt vertelt dat er regelmaat in zit. We hebben al wel mooie plaatjes, maar dat is niet afdoende bewijs ("Is de regelmaat die in deze plaatjes te zien is voor $e^2$ er ook echt, en kunnen wij dit bewijzen?
Deze regelmaat is er echt, en dat is ook wel te bewijzen. Op dit moment is dat bewijs nog in progress, maar kunnen we ons wel beroepen op andere bronnen.", wikipedia is geen bron
)
Deze regelmaat is er echt, en dat is ook wel te bewijzen. Op dit moment is dat bewijs nog in progress, maar kunnen we ons wel beroepen op andere bronnen.", wikipedia is geen bron
)
Je wil dus zeg maar een algemene formule die de kettingbreuk geeft ipv dat het eindigt in "...."? En die formule dan bewijzen.
En het bewijs in dat ene artikel, kun je niet kijken hoe je de technieken aldaar kunt toepassen op e2?
De formule heb ik al. Het bewijs ben ik nog mee bezig (alleen snap ik nog niet helemaal hoe ze aan de integralen komen, en dat is zeg maar het meest essentiele deel van het bewijs). Maar los daarvan hoopte ik een site te vinden die de formule bevestigd. Als bron waar ik me op beroep in die zin, dus. ;o
Toffe plaatjes . Vind het altijd bijzonder dat e en pi van die regelmatige kettingbreuken hebben, maar heb me er nooit echt in verdiept.
. Vind het altijd bijzonder dat e en pi van die regelmatige kettingbreuken hebben, maar heb me er nooit echt in verdiept.
Ja hè, groepsgenootje die met mathematica om kan gaan (Y)
Overigens hebben we door zulke plaatjes ook besloten dat er geen regelmaat in e^3 zit, wat de "bronnen"(wikipedia, dus :p) ook lijken te bevestigen.
Maar dat geheel terzijde!
(Y) Overigens hebben we door zulke plaatjes ook besloten dat er geen regelmaat in e^3 zit, wat de "bronnen"(wikipedia, dus :p) ook lijken te bevestigen.
Maar dat geheel terzijde!
Hier staan ook wat links naar bronnen voor e2: http://www.research.att.com/~njas/sequences/?q=7%2C+2%2C+1%2C+1%2C+3%2C+18&sort=0&fmt=0&language=english&go=Search
Uit het ongerijmde. Kies maar een epsilon (bijvoorbeeld 1 om het simpel te houden), dan zou er een delta moeten zijn zodat blabla, maar als je x heel groot maakt, dan zie je dat dat niet kan.quote:Op woensdag 16 juni 2010 00:17 schreef BasementDweller het volgende:
Hoe kan ik bewijzen dat x³ niet uniform continu is op R?
Ah, merci.quote:Op woensdag 16 juni 2010 00:26 schreef thabit het volgende:
Hier staan ook wat links naar bronnen voor e2: http://www.research.att.com/~njas/sequences/?q=7%2C+2%2C+1%2C+1%2C+3%2C+18&sort=0&fmt=0&language=english&go=Search
Ik zou als ik jou was beginnen met het bekende artikel van Euler over kettingbreuken. Het origineel staat hier en een Engelse vertaling (met annotaties en bibliografie) vind je hier. Lees ook even wat Ed Sandifer hier over dit artikel van Euler heeft te zeggen. Euler leidt in zijn artikel o.m. een kettingbreuk af voor e2p/a. Er is dus wel een regelmatige kettingbreuk te geven voor bijv. e3, alleen zijn de elementen daarvan dan niet louter integers.quote:Op dinsdag 15 juni 2010 23:26 schreef Hanneke12345 het volgende:
Mja, zat ik aan te denken, maar ik wil iets dat echt vertelt dat er regelmaat in zit. We hebben al wel mooie plaatjes, maar dat is niet afdoende bewijs ("Is de regelmaat die in deze plaatjes te zien is voor $e^2$ er ook echt, en kunnen wij dit bewijzen?
Deze regelmaat is er echt, en dat is ook wel te bewijzen. Op dit moment is dat bewijs nog in progress, maar kunnen we ons wel beroepen op andere bronnen.", wikipedia is geen bron
Dat idee had ik al, maar het netjes opschrijven lukte nog niet.quote:Op woensdag 16 juni 2010 00:29 schreef thabit het volgende:
[..]
Uit het ongerijmde. Kies maar een epsilon (bijvoorbeeld 1 om het simpel te houden), dan zou er een delta moeten zijn zodat blabla, maar als je x heel groot maakt, dan zie je dat dat niet kan.
Kies e=1 en zij d>0. Kies x,y zo dat d(x,y) < d en
| f(x) - f(y) | = | x³ - y³ | >= ... > e.
Wat moet er op de puntjes?
Het is duidelijk dat als je x en y groot genoeg kies dat het altijd groter dan 1 is, maar ik weet niet of ze daar op een tentamen alle punten voor geven.
schrijf x³ - y³ = (x-y)(x² + xy + y²)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Vraag was: Sketch the solid whose volume is given by the integral and evaluate it. Integraal zelf staat dus onderaan in het plaatje. Maar ik snap totaal niet waarom dat volume twee verschillende delen heeft? r=2 en theta = pi/2 kan ik zo uit het plaatje opmaken, maar vanwaar die twee verschillende delen(dus 1 cylinder en 1 parabool 9-r2)?
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Ook dat had ik zelf al bedacht (quote:Op donderdag 17 juni 2010 13:13 schreef GlowMouse het volgende:
schrijf x³ - y³ = (x-y)(x² + xy + y²)
), alleen ik wist niet wat je daarmee moest doen omdat |x-y|<d en je wil juist een '>' teken krijgen.edit:
Je kan wel zeggen x³ - y³ = (x-y)(x² + xy + y²) > (x-y)(xy) = x²y - y²x... maar dan...
Dus x²y - y²x = y(y+d/2)² - y²(y+d/2) = y³ + dy² + d²/4 - y³ - y²d/2 = dy² + d²/4 - y²d/2
Als y>1, dan dy² + d²/4 - y²d/2 > d + d²/4 - d/2 = d/2 + d²/4
Als je e de helft neemt van d/2 + d²/4 dan is x³-y³>e.
Ik denk dat dit wel goed is uitgewerkt zo.
Als y>1, dan dy² + d²/4 - y²d/2 > d + d²/4 - d/2 = d/2 + d²/4
Als je e de helft neemt van d/2 + d²/4 dan is x³-y³>e.
Ik denk dat dit wel goed is uitgewerkt zo.
Wat bedoel je met twee verschillende delen?quote:Op donderdag 17 juni 2010 16:07 schreef Jac0bus het volgende:
[ afbeelding ]
Vraag was: Sketch the solid whose volume is given by the integral and evaluate it. Integraal zelf staat dus onderaan in het plaatje. Maar ik snap totaal niet waarom dat volume twee verschillende delen heeft? r=2 en theta = pi/2 kan ik zo uit het plaatje opmaken, maar vanwaar die twee verschillende delen(dus 1 cylinder en 1 parabool 9-r2)?
Als je bedoelt waarom die parabool opeens ophoudt en overgaat in de cilinder... dat heeft er mee te maken dat de gedefinieerde verzameling uit punten bestaat waar voor (x,y,z) binnen de cilinder én binnen de paraboloïde ligt.
Nee. e moet je vantevoren kiezen en dan moet het daarna voor elke d fout gaan.quote:Op donderdag 17 juni 2010 18:25 schreef BasementDweller het volgende:
Dus x²y - y²x = y(y+d/2)² - y²(y+d/2) = y³ + dy² + d²/4 - y³ - y²d/2 = dy² + d²/4 - y²d/2
Als y>1, dan dy² + d²/4 - y²d/2 > d + d²/4 - d/2 = d/2 + d²/4
Als je e de helft neemt van d/2 + d²/4 dan is x³-y³>e.
Ik denk dat dit wel goed is uitgewerkt zo.
Ik neem e dus (d/2 + d²/4) / 2, en dan gaat het voor iedere d fout in die zin dat x³-y³>e, maar ik moet e dus vast kiezen? e=1 ofzo
Je zou ook een algemene redenering kunnen opzetten voor een willekeurige ε > 0 en aan de hand van de definitie van uniforme continuïteit laten zien dat de aanname dat je functie f(x) = x3 uniform continu is tot een tegenstrijdigheid leidt omdat er wel degelijk getallen x en y zijn met |x - y| < δ zodanig dat |f(x) - f(y)| > ε.quote:Op donderdag 17 juni 2010 18:45 schreef BasementDweller het volgende:
Ik neem e dus (d/2 + d²/4) / 2, en dan gaat het voor iedere d fout in die zin dat x³-y³>e, maar ik moet e dus vast kiezen? e=1 ofzo
Kies e=1/2. Zij d>0 willekeurig. Neem y>0 zo, dat y²=1/d en laat x=y+d/2 (dus y=x-d/2). Er is voldaan aan |x-y|<d en
|x³-y³| = |(x-y)(x²+2xy+y²)| = |d/2 (x²+2xy+y²) | > d |xy| > d y² = 1 > 1/2 = e
Zo goed? :p
[ Bericht 0% gewijzigd door BasementDweller op 17-06-2010 19:27:27 ]
|x³-y³| = |(x-y)(x²+2xy+y²)| = |d/2 (x²+2xy+y²) | > d |xy| > d y² = 1 > 1/2 = e
Zo goed? :p
[ Bericht 0% gewijzigd door BasementDweller op 17-06-2010 19:27:27 ]
Dus omdat de radius niet hoger mag zijn dan 2 zegmaar? Dat hij dan overgaat op een cylinder, omdat de paraboloïde anders er overheen zou gaan?quote:Op donderdag 17 juni 2010 18:28 schreef BasementDweller het volgende:
[..]
Wat bedoel je met twee verschillende delen?
Als je bedoelt waarom die parabool opeens ophoudt en overgaat in de cilinder... dat heeft er mee te maken dat de gedefinieerde verzameling uit punten bestaat waar voor (x,y,z) binnen de cilinder én binnen de paraboloïde ligt.
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Precies, de paraboloïde valt daar buiten de (x,y,z) waarvoor r<2.quote:Op donderdag 17 juni 2010 19:50 schreef Jac0bus het volgende:
[..]
Dus omdat de radius niet hoger mag zijn dan 2 zegmaar? Dat hij dan overgaat op een cylinder, omdat de paraboloïde anders er overheen zou gaan?
Dank, nu snap ik hemquote:Op donderdag 17 juni 2010 19:53 schreef BasementDweller het volgende:
[..]
Precies, de paraboloïde valt daar buiten de (x,y,z) waarvoor r<2.
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Laten we eens aannemen dat de functie f(x) = x3 wel uniform continu zou zijn. Dan zou er volgens de definitie van uniforme continuïteit bij elke ε > 0 een δ > 0 moeten bestaan zodanig datquote:Op donderdag 17 juni 2010 19:45 schreef BasementDweller het volgende:
Zou iemand voor me willen opschrijven hoe het wel moet?
(1) | f(x) - f(y) | < ε voor elke x en y die voldoen aan | x - y | < δ
Kies nu een ε > 0, dan is er volgens onze aanname een δ > 0 die aan (1) voldoet. Kies nu verder een positief getal h zodanig dat:
(2) 0 < h < δ
Kies verder:
(3) x > √(ε/3h)
En:
(4) y = x + h,
Zodat:
(5) | x - y | = h
Uit (2) volgt dan dat x en y voldoen aan | x - y | < δ terwijl uit (3) en (4) volgt dat ook geldt:
(6) y > √(ε/3h)
Nu volgt uit (3) en (6) dat geldt:
(7) x2 > ε/3h, xy > ε/3h, y2 > ε/3h,
en dus ook:
(8) | x2 + xy + y2 | > ε/h
Maar aangezien geldt:
(9) | f(x) - f(y) | = | x3 - y3 | = | x - y |∙| x2 + xy + y2 |
Volgt nu uit (9) met behulp van (5) en (8) dat:
(10) | f(x) - f(y) | > ε,
en dit is in tegenspraak met de aanname dat f(x) uniform continu zou zijn. De aanname voert dus tot een tegenstrijdigheid, zodat de conclusie is dat f(x) niet uniform continu is.
Als f* de conjugate functie is van f (f* (s) = sup(st - f(t)), weet iemand toevallig hoe f* heet en hoe het gedefinieerd is?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ok mensen, Integreren voor gevorderden..
Ik ben dus met een integraal gestrand waarvan ik gehoord heb dat er een gesloten uitdrukking voor te vinden is, maar ik kom er niet aan uit. Het gaat om de volgende integraal:
}{x})dx)
Allereerst schrijf ik het probleem om naar:
)dx-\int%20ln(x)dx)
Die tweede integraal geloof ik wel, maar de eerste probeer ik via partieel integreren:
)dx%20%3D%20xln(ln(x))%20-%20\int\frac{1}{ln(x)}dx)
Substitutie geeft:
%20\Rightarrow%20e^{u}%3Dx%20\Rightarrow%20e^{u}du%20%3D%20dx)
waardoor de integraal overgaat in:
Deze integraal kan ik zelf alleen oplossen met behulp van een Taylorreeks, maar dan wordt de uiteindelijke oplossing een oneindige sommatie van natuurlijke logaritmes en daar word ik niet zo blij van. Heeft iemand nog andere suggesties?
Ik ben dus met een integraal gestrand waarvan ik gehoord heb dat er een gesloten uitdrukking voor te vinden is, maar ik kom er niet aan uit. Het gaat om de volgende integraal:
Allereerst schrijf ik het probleem om naar:
Die tweede integraal geloof ik wel, maar de eerste probeer ik via partieel integreren:
Substitutie geeft:
waardoor de integraal overgaat in:
Deze integraal kan ik zelf alleen oplossen met behulp van een Taylorreeks, maar dan wordt de uiteindelijke oplossing een oneindige sommatie van natuurlijke logaritmes en daar word ik niet zo blij van. Heeft iemand nog andere suggesties?
Ik heb zo'n oude witte casio geleend van een vriend (mijne is kapot) en ik had de volgende vraag.
Ik moet de normalcdf plotten in een grafiek, maar ik heb geen idee hoe dit op deze rekenmachine moet, kan iemand mij helpen?
Ik moet de normalcdf plotten in een grafiek, maar ik heb geen idee hoe dit op deze rekenmachine moet, kan iemand mij helpen?
mundus vult decipi
differentieer 2x/ln(x) naar x and watch the magic work:quote:
( 2x/ln(x) )' =
2/ln(x) + 2x*(1/x)*(-1/ln2(x)) =
2/ln(x) -2/ln2(x) =
2/ln(x) -2/2ln(x)
4/2ln(x) - 2/2ln(x) =
(4-2)/2ln(x) =
2/2ln(x) =
1/ln(x)
[ Bericht 9% gewijzigd door ErictheSwift op 19-06-2010 21:40:02 ]
quote:Op zaterdag 19 juni 2010 21:34 schreef ErictheSwift het volgende:
[..]
differentieer 2x/Ln(x) naar x and watch the magic work:
( 2x/ln(x) )' =
2/ln(x) + 2x*(1/x)*(-1/ln2 x)
waar zit nu de magie?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
[snip]quote:Op zaterdag 19 juni 2010 21:34 schreef ErictheSwift het volgende:
[..]
differentieer 2x/ln(x) naar x and watch the magic work:
( 2x/ln(x) )' =
Dit is fout, de afgeleide is niet 1/ln(x) maar 2/ln(x) - 2/(ln(x))2
Je verdoet trouwens je tijd, een primitieve van 1/ln(x) is niet in elementaire functies uit te drukken.
Dat laatste wist ik ja, maar zijn er wellicht andere, hippe trucjes om dat te omzeilen?quote:Op zaterdag 19 juni 2010 22:30 schreef Riparius het volgende:
[..]
[snip]
Dit is fout, de afgeleide is niet 1/ln(x) maar 2/ln(x) - 2/(ln(x))2
Je verdoet trouwens je tijd, een primitieve van 1/ln(x) is niet in elementaire functies uit te drukken.
Nee die zijn er niet. Er zijn zat functies die geen primitieve hebben, exp(x²) is er een ander voorbeeld van.
(a) is me gelukt, maar heb hulp nodig bij (b). Hoe kan ik dit aanpakken?
Wat ik zelf al geprobeerd heb:
Voor x in I geldt volgens Taylor: f'(x)=f'(0)+ x f''(x) + x²f'''(x)/2 + O(3) = x f''(x) + x²f'''(x)/2 + O(3)
We weten dat als x in I zit dat f''(x)>0 voor x>0 en f''(x)<0 voor x<0, dus x f''(x) > 0 voor x ongelijk aan 0. Voor x in I geldt ook f"'(x)>0, dus x² f"'(x)/2 >0. Dus f'(x)>0 zo lang O(3) niet voor problemen zorgt, maar hoe bewijs ik dit?
Intuïtief snap ik wel dat als je het interval I maar klein genoeg maakt dat die hogere orde termen er steeds minder invloed hebben, maar ik weet dus niet hoe ik kan bewijzen dat die invloed klein genoeg is.
Ja, ook als je een primitieve niet in elementaire functies kunt uitdrukken zijn er soms mogelijkheden om een bepaalde (definiete) integraal exact te berekenen, bijvoorbeeld door gebruik te maken van reeksontwikkelingen of door gebruik te maken van de residuenstelling uit de complexe analyse.quote:Op zondag 20 juni 2010 11:23 schreef Don_Vanelli het volgende:
[..]
Dat laatste wist ik ja, maar zijn er wellicht andere, hippe trucjes om dat te omzeilen?
Mja, berekeningen mbv complexe integratie zijn doorgaans alleen nuttig als je integratiegrenzen hebt. Zonder integratiegrenzen heb je geen singulieren punten he.quote:Op zondag 20 juni 2010 18:05 schreef Riparius het volgende:
[..]
Ja, ook als je een primitieve niet in elementaire functies kunt uitdrukken zijn er soms mogelijkheden om een bepaalde (definiete) integraal exact te berekenen, bijvoorbeeld door gebruik te maken van reeksontwikkelingen of door gebruik te maken van de residuenstelling uit de complexe analyse.
Dat bedoel ik, daarom spreek ik ook over definiete (bepaalde) integralen. Maar wie heeft jou wijsgemaakt dat er een gesloten uitdrukking zou zijn voor de primitieve van de functie die je wilde integreren?quote:Op zondag 20 juni 2010 18:22 schreef Don_Vanelli het volgende:
[..]
Mja, berekeningen mbv complexe integratie zijn doorgaans alleen nuttig als je integratiegrenzen hebt. Zonder integratiegrenzen heb je geen singuliere punten he.
Niemand, maar ik hoopte dat er toch over nagedacht zou kunnen wordenquote:Op zondag 20 juni 2010 18:28 schreef Riparius het volgende:
[..]
Dat bedoel ik, daarom spreek ik ook over definiete (bepaalde) integralen. Maar wie heeft jou wijsgemaakt dat er een gesloten uitdrukking zou zijn voor de primitieve van de functie die je wilde integreren?
Daar is al lang diep over nagedacht. Het is ook mogelijk te bewijzen dat primitieven van functies als 1/ln(x) of ex/x niet in elementaire functies kunnen worden uitgedrukt. Verder vind ik vreemd dat je nu weer ontkent wat je hierboven schrijft, namelijk dat je van iemand 'gehoord' had dat je functie wel te primitiveren was middels elementaire functies. Dus wat wil je nu eigenlijk?quote:Op zondag 20 juni 2010 18:37 schreef Don_Vanelli het volgende:
[..]
Niemand, maar ik hoopte dat er toch over nagedacht zou kunnen worden
Gebruik de middelwaardestelling om te laten zien dat f'(x) < 0 of f'(x) = 0 voor elke x uit I ongelijk nul tot een tegenstrijdigheid leidt.quote:Op zondag 20 juni 2010 14:22 schreef BasementDweller het volgende:
[ link | afbeelding ]
(a) is me gelukt, maar heb hulp nodig bij (b). Hoe kan ik dit aanpakken?
Wat ik zelf al geprobeerd heb:
Voor x in I geldt volgens Taylor: f'(x)=f'(0)+ x f''(x) + x²f'''(x)/2 + O(3) = x f''(x) + x²f'''(x)/2 + O(3)
We weten dat als x in I zit dat f''(x)>0 voor x>0 en f''(x)<0 voor x<0, dus x f''(x) > 0 voor x ongelijk aan 0. Voor x in I geldt ook f"'(x)>0, dus x² f"'(x)/2 >0. Dus f'(x)>0 zo lang O(3) niet voor problemen zorgt, maar hoe bewijs ik dit?
Intuïtief snap ik wel dat als je het interval I maar klein genoeg maakt dat die hogere orde termen er steeds minder invloed hebben, maar ik weet dus niet hoe ik kan bewijzen dat die invloed klein genoeg is.
Ik heb een vraag over een statistiek tentamenvraag, in dit geval vooral kansrekenen.
Het volgende is gegeven:
Normaal verdeelde populatie. mu=80 en o=10 (standaardafwijking). Het gaat hier om aantal uren dat men leert (tentamen voorbereid)
De vraag:
Bereken de kans dat je een student vindt die meer dan 96 uur heeft besteed aan het voorbereiden van het tentamen.
Uitvoering:
Berekenen Z-waarde.
96-80
-------- = 1.6
10.
Vervolgens staat er: opzoeken in tabel levert een kans op van 0.0548. Hoe moet ik dit opzoeken????
Ik moet deze tabel gebruiken: [url=http://www.pearsoneducation.nl/mcclave/index1.html]http://www.pearsoneducation.nl/mcclave/index1.html [/url]de bovenste. Kan iemand mij helpen
Edit: link werkt niet helemaal zoals ik wel. Op de pagina op nummer 6 klikken, dan bovenste tabel.
Het volgende is gegeven:
Normaal verdeelde populatie. mu=80 en o=10 (standaardafwijking). Het gaat hier om aantal uren dat men leert (tentamen voorbereid)
De vraag:
Bereken de kans dat je een student vindt die meer dan 96 uur heeft besteed aan het voorbereiden van het tentamen.
Uitvoering:
Berekenen Z-waarde.
96-80
-------- = 1.6
10.
Vervolgens staat er: opzoeken in tabel levert een kans op van 0.0548. Hoe moet ik dit opzoeken????
Ik moet deze tabel gebruiken: [url=http://www.pearsoneducation.nl/mcclave/index1.html]http://www.pearsoneducation.nl/mcclave/index1.html [/url]de bovenste. Kan iemand mij helpen
Edit: link werkt niet helemaal zoals ik wel. Op de pagina op nummer 6 klikken, dan bovenste tabel.
Links lees je de eerste decimaal af, dan pak je de kolom voor de tweede decimaal.
Hier geldt dus: P(0 <= Z <= 1.6) = 0,4452. Van daaruit kun je P(Z > 1.6 bepalen).
Hier geldt dus: P(0 <= Z <= 1.6) = 0,4452. Van daaruit kun je P(Z > 1.6 bepalen).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja aflezen lukt mij nog wel. maar ik vraag mij af hoe men de z-waarde van 1.6 (0.4452) ineens op 0.0548 komt. De kans dat die iemand meer dan 96 uur leert.quote:Op maandag 21 juni 2010 22:41 schreef GlowMouse het volgende:
Links lees je de eerste decimaal af, dan pak je de kolom voor de tweede decimaal.
Hier geldt dus: P(0 <= Z <= 1.6) = 0,4452. Van daaruit kun je P(Z > 1.6 bepalen).
Z-waarde gaat over een normale verdeling met mu=0 en sigma=1quote:Op maandag 21 juni 2010 22:53 schreef VinceMega het volgende:
[..]
Ja aflezen lukt mij nog wel. maar ik vraag mij af hoe men de z-waarde van 1.6 (0.4452) ineens op 0.0548 komt. De kans dat die iemand meer dan 96 uur leert.
P(Z>0)=P(Z<0)=0.5
Nu zou het toch moeten lukken
Als je hebt
.
Bestaat er notatie om de stapgrootte (bijvoorbeeld 2) in deze sommatie aan te geven?
Ik heb deze sommatie slechts als voorbeeld gebruikt. Het gaat me niet om het antwoord van dit specifieke voorbeeld.
Bestaat er notatie om de stapgrootte (bijvoorbeeld 2) in deze sommatie aan te geven?
Ik heb deze sommatie slechts als voorbeeld gebruikt. Het gaat me niet om het antwoord van dit specifieke voorbeeld.
Nee, dan moet je met 2i en |_ b/2 _| + (a mod 2) werken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hallo,
Ik vraag me af hoe je de vergelijking van een raaklijn kan uitrekenen met derive.
De functie: f(x)=x√x
en de punten waar je de vergelijking van moet maken zijn (4,8)
Of als iemand het weet met wolfram mag van mij ook
Ik vraag me af hoe je de vergelijking van een raaklijn kan uitrekenen met derive.
De functie: f(x)=x√x
en de punten waar je de vergelijking van moet maken zijn (4,8)
Of als iemand het weet met wolfram mag van mij ook
De raaklijn g in een punt a wordt gegeven door: g(x)= f(a) + f'(a) (x-a).
f(x)=x^(3/2), dus f'(x) = 3/2 x^(1/2) => f'(4)=3
Dus g(x) = f(4)+f'(4)(x-4) = 8+3(x-4) = 3x-4.
Kan dus makkelijk uit je hoofd. Met Wolfram alpha kan je ook wel afgeleides uitrekenen, met D[x^(3/2),x] bijvoorbeeld.
f(x)=x^(3/2), dus f'(x) = 3/2 x^(1/2) => f'(4)=3
Dus g(x) = f(4)+f'(4)(x-4) = 8+3(x-4) = 3x-4.
Kan dus makkelijk uit je hoofd. Met Wolfram alpha kan je ook wel afgeleides uitrekenen, met D[x^(3/2),x] bijvoorbeeld.
Nog 1 klein vraagje:
Hoe kom je opeens aan die 8 en 3 bij 8+3(x-4)?
Is die 8 f + f' maar waar komt die 3 dan opeens vandaan?
Dus g(x) = f(4)+f'(4)(x-4) = 8+3(x-4) = 3x-4.
Hoe kom je opeens aan die 8 en 3 bij 8+3(x-4)?
Is die 8 f + f' maar waar komt die 3 dan opeens vandaan?
Dus g(x) = f(4)+f'(4)(x-4) = 8+3(x-4) = 3x-4.
kijk eens hoe de haakjes staan; f+f' is niet (f+f').
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hallo,
Ben nu bij Calculus bij een hoofdstuk over parametric equations.
Je moet daar een booglengte bepalen, maar kom hier niet uit.
x=sin 2t y=cos 2t 0<t<2 pi (groter gelijk)
Nu staat er
integraal van 0 tot 2 pi van sqrt ( 4 cos^2 2t + 4 sin^2 2t) dt .
Tot hier begrijp ik het nog
Nu komt dit uit op integraal van 0 tot 2pi van 2 dt. Komt dit op omdat 4 cos^2 2t + 4 sin^2 2t 4 is?
(want cos^2 t +sin^2 t=1)
Dank
Ben nu bij Calculus bij een hoofdstuk over parametric equations.
Je moet daar een booglengte bepalen, maar kom hier niet uit.
x=sin 2t y=cos 2t 0<t<2 pi (groter gelijk)
Nu staat er
integraal van 0 tot 2 pi van sqrt ( 4 cos^2 2t + 4 sin^2 2t) dt .
Tot hier begrijp ik het nog
Nu komt dit uit op integraal van 0 tot 2pi van 2 dt. Komt dit op omdat 4 cos^2 2t + 4 sin^2 2t 4 is?
(want cos^2 t +sin^2 t=1)
Dank
Nog een vraagje
x= cos 2t y= cos t
find dy/dx en d2y/dx2
dy/dx is -sin t / -2 sin 2t (weet niet hoe ik dit verder moet vereenvoudigen)
d2y/dx2 bepalen is dan ook lastig (kan natuurlijk wel met quotientregel maar ik denk dat je dy/dx nog wel kan vereenvoudigen, maar weet niet hoe
x= cos 2t y= cos t
find dy/dx en d2y/dx2
dy/dx is -sin t / -2 sin 2t (weet niet hoe ik dit verder moet vereenvoudigen)
d2y/dx2 bepalen is dan ook lastig (kan natuurlijk wel met quotientregel maar ik denk dat je dy/dx nog wel kan vereenvoudigen, maar weet niet hoe
Denk voor de vereenvoudiging van je quotiënt eens aan goniometrische identiteiten, bijvoorbeeld de formule voor de sinus van de dubbele hoek:quote:Op donderdag 24 juni 2010 12:34 schreef martijnnum1 het volgende:
Nog een vraagje
x= cos 2t y= cos t
find dy/dx en d2y/dx2
dy/dx is -sin t / -2 sin 2t (weet niet hoe ik dit verder moet vereenvoudigen)
d2y/dx2 bepalen is dan ook lastig (kan natuurlijk wel met quotientregel maar ik denk dat je dy/dx nog wel kan vereenvoudigen, maar weet niet hoe
sin 2α = 2∙sin α∙cos α
Verder maak je een denkfout als je meent dat je d2y/dx2 zou kunnen bepalen door de uitdrukking voor dy/dx in t te differentiëren naar t.
Hallo,
Ik zoek de partieel afgeleiden van
x*sin(y-z)
Nu krijg ik
Respect to x: sin (y-z)
y: x cos (y-z)
z: -x cos (y-z)
Maar dit zijn de uitkomsten
to x:
-sin(z - y)
to y:
x⋅cos(z - y)
to z:
-x⋅cos(z - y)
Waarom is het ineens binnen de haakjes z-y ipv y-z?
En vanwaar die - van -sin(z-y) bij diff naar x.
Dankje
Ik zoek de partieel afgeleiden van
x*sin(y-z)
Nu krijg ik
Respect to x: sin (y-z)
y: x cos (y-z)
z: -x cos (y-z)
Maar dit zijn de uitkomsten
to x:
-sin(z - y)
to y:
x⋅cos(z - y)
to z:
-x⋅cos(z - y)
Waarom is het ineens binnen de haakjes z-y ipv y-z?
En vanwaar die - van -sin(z-y) bij diff naar x.
Dankje
Ken je je goniometrische identiteiten eigenlijk wel?quote:Op vrijdag 25 juni 2010 15:04 schreef martijnnum1 het volgende:
Hallo,
Ik zoek de partieel afgeleiden van
x*sin(y-z)
Nu krijg ik
Respect to x: sin (y-z)
y: x cos (y-z)
z: -x cos (y-z)
Maar dit zijn de uitkomsten
to x:
-sin(z - y)
to y:
x⋅cos(z - y)
to z:
-x⋅cos(z - y)
Waarom is het ineens binnen de haakjes z-y ipv y-z?
En vanwaar die - van -sin(z-y) bij diff naar x.
Dankje
cos(-α) = cos α
sin(-α) = -sin α
Ik vermoed dat je een computerprogramma hebt gebruikt om de afgeleiden te controleren en dat dit programma om de een of andere reden (y - z) vervangt door (z - y).
En heb je de opgave die je hier gisteren postte wel op kunnen lossen?
Ja, van gisteren is me gelukt.
Snap de stof die ik nu moet leren opzich ook allemaal wel, maar zoals je ziet zit bepaalde basiskennis er nog niet helemaal goed in (vooral goniometrische identiteiten inderdaad, heb ze nooit echt goed geleerd op de middelbare).
Bedankt in ieder geval.
Snap de stof die ik nu moet leren opzich ook allemaal wel, maar zoals je ziet zit bepaalde basiskennis er nog niet helemaal goed in (vooral goniometrische identiteiten inderdaad, heb ze nooit echt goed geleerd op de middelbare).
Bedankt in ieder geval.
OK. Je hebt gevonden dat d2y/dx2 = -1/(16∙cos3t) hoop ik?quote:Op vrijdag 25 juni 2010 16:00 schreef martijnnum1 het volgende:
Ja, van gisteren is me gelukt.
Kijk even op Wikipedia voor een overzicht, hier bijvoorbeeld.quote:Snap de stof die ik nu moet leren opzich ook allemaal wel, maar zoals je ziet zit bepaalde basiskennis er nog niet helemaal goed in (vooral goniometrische identiteiten inderdaad, heb ze nooit echt goed geleerd op de middelbare).
Bedankt in ieder geval.
Hallo,
Ik kan de integraal van cos(x) *esin x dx niet bepalen. Hij moet esin(x) zijn, maar weet niet hoe ik dat moet verkrijgen.
Kan iemand mij dit uitleggen.
Dankje!
Ik kan de integraal van cos(x) *esin x dx niet bepalen. Hij moet esin(x) zijn, maar weet niet hoe ik dat moet verkrijgen.
Kan iemand mij dit uitleggen.
Dankje!
substitueer y = sinx.
[ Bericht 2% gewijzigd door GlowMouse op 26-06-2010 17:45:49 ]
[ Bericht 2% gewijzigd door GlowMouse op 26-06-2010 17:45:49 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Opgave 3.1 (Algemeen dagblad, 29 september 2005)
De gemiddelde prijs van een ‘boekenpakket’ van schoolboeken in de bovenbouw van het voortgezet onderwijs kost ¤ 395. Uit een steekproef onder 10 scholen blijkt zo’n pakket echter ¤ 410 te kosten. Neem aan dat de standaardafwijking ¤ 15 is.
Toets of de gemiddelde prijs van het beschreven boekenpakket groter is dan ¤ 395 (α = 0,05).
Uitwerking 3.1.
1. H0: μ = 395 (of μ ≤395) toetsen tegen H1: μ > 395 (euro)
2. α=0,05; een rechtseenzijdige toets.
3. Toetsingsgrootheid: 10=steekproefgemiddelde ~ N(395; 15(wortel)10)= N(300; 4,74...) .
4. Is 410 significant? Met p-waarde: P(x > 4102) = P(z>(410 – 395)/4,74...)) =P(z>3,16)= 0,0008, dus (zeer) significant.
5. Conclusie: H0 verwerpen. Boekenpakket duurder dan ¤ 395.
Ik volg dit niet. Ze doen toch met Normal CDF op de GRM? Hoe voer je dit in, ik snap niet waar ze die 0,00008 vandaan halen.
De gemiddelde prijs van een ‘boekenpakket’ van schoolboeken in de bovenbouw van het voortgezet onderwijs kost ¤ 395. Uit een steekproef onder 10 scholen blijkt zo’n pakket echter ¤ 410 te kosten. Neem aan dat de standaardafwijking ¤ 15 is.
Toets of de gemiddelde prijs van het beschreven boekenpakket groter is dan ¤ 395 (α = 0,05).
Uitwerking 3.1.
1. H0: μ = 395 (of μ ≤395) toetsen tegen H1: μ > 395 (euro)
2. α=0,05; een rechtseenzijdige toets.
3. Toetsingsgrootheid: 10=steekproefgemiddelde ~ N(395; 15(wortel)10)= N(300; 4,74...) .
4. Is 410 significant? Met p-waarde: P(x > 4102) = P(z>(410 – 395)/4,74...)) =P(z>3,16)= 0,0008, dus (zeer) significant.
5. Conclusie: H0 verwerpen. Boekenpakket duurder dan ¤ 395.
Ik volg dit niet. Ze doen toch met Normal CDF op de GRM? Hoe voer je dit in, ik snap niet waar ze die 0,00008 vandaan halen.
Blues ain't nothing but a good man feeling bad...
Volgens mij is dat de kans dat iets meer dan 3.16 SD's afwijkt, als ik het goed lees.quote:Op zaterdag 26 juni 2010 18:07 schreef GoodGawd het volgende:
Opgave 3.1 (Algemeen dagblad, 29 september 2005)
De gemiddelde prijs van een ‘boekenpakket’ van schoolboeken in de bovenbouw van het voortgezet onderwijs kost ¤ 395. Uit een steekproef onder 10 scholen blijkt zo’n pakket echter ¤ 410 te kosten. Neem aan dat de standaardafwijking ¤ 15 is.
Toets of de gemiddelde prijs van het beschreven boekenpakket groter is dan ¤ 395 (α = 0,05).
Uitwerking 3.1.
1. H0: μ = 395 (of μ ≤395) toetsen tegen H1: μ > 395 (euro)
2. α=0,05; een rechtseenzijdige toets.
3. Toetsingsgrootheid: 10=steekproefgemiddelde ~ N(395; 15(wortel)10)= N(300; 4,74...) .
4. Is 410 significant? Met p-waarde: P(x > 4102) = P(z>(410 – 395)/4,74...)) =P(z>3,16)= 0,0008, dus (zeer) significant.
5. Conclusie: H0 verwerpen. Boekenpakket duurder dan ¤ 395.
Ik volg dit niet. Ze doen toch met Normal CDF op de GRM? Hoe voer je dit in, ik snap niet waar ze die 0,00008 vandaan halen.
normalcdf(410, 1E99, 395, 15/sqrt(10))
[ Bericht 1% gewijzigd door GlowMouse op 27-06-2010 12:20:35 ]
[ Bericht 1% gewijzigd door GlowMouse op 27-06-2010 12:20:35 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
yep :p, 4102 zal wel typo zijnquote:Op zaterdag 26 juni 2010 20:52 schreef GlowMouse het volgende:
normalcdf(410, 1E99, 395, 15/sqrt(10))
Waarom uitstellen tot morgen als je het overmorgen nog kunt doen?
Stochastiek. Ik heb echt geen idee heo ik deze sommen - eigenlijk allemaal - moet maken ;(
X~nbin(n1, p) en Y~nbin(n2, p) onafhankelijk van elkaar.
-Bepaal de verdeling van X+Y
Klinkt als iets wat ik echt zo zou moeten kunnen, maar ik kan het niet vinden in de syllabus en weet ook niet goed hoe ik dit moet doen. Wat betekent X+Y eigenlijk precies? Ik weet dat met één stochast dan geldt P(X=x)=P({w|X(w)=x). Het verschil tussen X en Y is hoeveel successen er zijn. Moet P(X+Y) dan de kans zijn dat er n1 óf n2 successen zijn?
Overigens als dit zo zou zijn (geen idee, het is maar een gok), is de verdeling dan gewoon nbin(min{n1, n2, p)?
X~nbin(n1, p) en Y~nbin(n2, p) onafhankelijk van elkaar.
-Bepaal de verdeling van X+Y
Klinkt als iets wat ik echt zo zou moeten kunnen, maar ik kan het niet vinden in de syllabus en weet ook niet goed hoe ik dit moet doen. Wat betekent X+Y eigenlijk precies? Ik weet dat met één stochast dan geldt P(X=x)=P({w|X(w)=x). Het verschil tussen X en Y is hoeveel successen er zijn. Moet P(X+Y) dan de kans zijn dat er n1 óf n2 successen zijn?
Overigens als dit zo zou zijn (geen idee, het is maar een gok), is de verdeling dan gewoon nbin(min{n1, n2, p)?
X is een stochast; een functie op een kansruimte waar een reëel getal uitkomt. Getallen kun je optellen.
Als X~BIN(1,1/6) en Y~BIN(1,1/6) dan is X+Y het aantal keren zes als je twee keer met een dobbelsteen gooit.
Je kunt de convolutie nemen; P(X+Y = x) = sum{k=0 t/m x} P(X=k en Y=x-k}. Maar bij verdelingen als bin en nbin kun je beter beredeneren.
Als X~BIN(1,1/6) en Y~BIN(1,1/6) dan is X+Y het aantal keren zes als je twee keer met een dobbelsteen gooit.
Je kunt de convolutie nemen; P(X+Y = x) = sum{k=0 t/m x} P(X=k en Y=x-k}. Maar bij verdelingen als bin en nbin kun je beter beredeneren.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus, in dit geval X~nbin(n1p), Y~nbin(n2, p) - X, Y het aantal so herhalingen om resp. n1, n2 successen te behalen. Dan betekent X+Y het aantal so herhalingen om n1+n2 successen te hebben, en dus X+Y~nbin(n1+n2, p)?
[ Bericht 1% gewijzigd door Hanneke12345 op 29-06-2010 02:23:21 ]
[ Bericht 1% gewijzigd door Hanneke12345 op 29-06-2010 02:23:21 ]
En voor de variantie (ik ben die pagina kwijt in m'n syllabus, en kan de syllabus ook niet online vinden ;x). Wikipedia zegt dat zowel E(X-EX)2 als EX2-(EX)2 gebruikt kunnen worden, maar welke is ook alweer gebruikelijker?
Bij negatief-binomiaal zegt wikipedia dat EX = n/p, hoe komen ze hier precies aan? M'n syllabus zegt wel dat als P(X in S) = 1 met S eindig, dan is de verwachting EX = Som{x in S} xP(X=x), maar dat is hier (bij nbin) niet van toepassing, toch?
Bij negatief-binomiaal zegt wikipedia dat EX = n/p, hoe komen ze hier precies aan? M'n syllabus zegt wel dat als P(X in S) = 1 met S eindig, dan is de verwachting EX = Som{x in S} xP(X=x), maar dat is hier (bij nbin) niet van toepassing, toch?
Weten jullie misschien een leuk wiskunde leesboek om de vakantie mee door te komen? (niveau: ik ga nu naar 2e jaar wiskunde aan de uni)
Die tweede en aftelbaarheid ipv eindigheid is voldoende.quote:Op maandag 28 juni 2010 12:56 schreef Hanneke12345 het volgende:
En voor de variantie (ik ben die pagina kwijt in m'n syllabus, en kan de syllabus ook niet online vinden ;x). Wikipedia zegt dat zowel E(X-EX)2 als EX2-(EX)2 gebruikt kunnen worden, maar welke is ook alweer gebruikelijker?
Bij negatief-binomiaal zegt wikipedia dat EX = n/p, hoe komen ze hier precies aan? M'n syllabus zegt wel dat als P(X in S) = 1 met S eindig, dan is de verwachting EX = Som{x in S} xP(X=x), maar dat is hier (bij nbin) niet van toepassing, toch?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik faal echt heel hard in deze opdrachten.
Homogene of uniforme verdeling: (toch even latex maar ;x)
Ik snap niet goed hoe ze aan de FX komen. Volgens mij is fX altijd constant (0 als x niet uit (a,b), 1/(b-a) als x in (a,b) ).
Verder is in de vraag het interval [-1,1], een gesloten of open interval maakt denk ik weinig uit? (Als in; ik kan net als vaak bij analyse gebeurd zeggen "uniform op [-1, 1] dus zeker op (-1, 1) en dan daarmee verder gaan)
Homogene of uniforme verdeling: (toch even latex maar ;x)
Ik snap niet goed hoe ze aan de FX komen. Volgens mij is fX altijd constant (0 als x niet uit (a,b), 1/(b-a) als x in (a,b) ).
Verder is in de vraag het interval [-1,1], een gesloten of open interval maakt denk ik weinig uit? (Als in; ik kan net als vaak bij analyse gebeurd zeggen "uniform op [-1, 1] dus zeker op (-1, 1) en dan daarmee verder gaan)
Dat is niet constant, aangezien hij 2 verschillende waarden kan aannemen. Teken eens een grafiekje zou ik zeggen.quote:Op maandag 28 juni 2010 14:30 schreef Hanneke12345 het volgende:
Ik faal echt heel hard in deze opdrachten.
Homogene of uniforme verdeling: (toch even latex maar ;x)
[ afbeelding ]
Ik snap niet goed hoe ze aan de FX komen. Volgens mij is fX altijd constant (0 als x niet uit (a,b), 1/(b-a) als x in (a,b) ).
Oh, ja ik zie 't al. Ik zat omgekeerd te denken (FX = d/dx fX ipv andersom). En bovendien moet het natuurlijk voldoen aan de limieten naar 0 en 1.
Ik moet nu de verdelingsfunctie bepalen van Y = sqrt(1+Z) en Z is uniform op [-1, 1]. Moet dan als Y = k dus sqrt(1+Z) = k dus Z = k2+1?
EX als X Pascal(p) verdeeld is snap ik toch niet helemaal
EX = som{k=1 tot oneindig}k(1-p)k-1p = p lim som {k = 1 tot K} - d/dp(1-p)k
Dat p ervoor kan worden gezet snap ik, dat je van een som naar oneindig een limiet maakt ook. Maar de -d/dp niet. Als ik het goed heb moet -d/dp dus gelijk zijn aan k/(1-p). Maar verder kom ik niet.
Ik moet nu de verdelingsfunctie bepalen van Y = sqrt(1+Z) en Z is uniform op [-1, 1]. Moet dan als Y = k dus sqrt(1+Z) = k dus Z = k2+1?
EX als X Pascal(p) verdeeld is snap ik toch niet helemaal
EX = som{k=1 tot oneindig}k(1-p)k-1p = p lim som {k = 1 tot K} - d/dp(1-p)k
Dat p ervoor kan worden gezet snap ik, dat je van een som naar oneindig een limiet maakt ook. Maar de -d/dp niet. Als ik het goed heb moet -d/dp dus gelijk zijn aan k/(1-p). Maar verder kom ik niet.
Klopt dan dit?
Althans, als Z uniform op (-1, 1) zou zijn?
En voor [-1, 1] moet ik denk ik alleen wat groter dan / kleiner dan veranderen in groter of gelijk etc?
Waarom kom ik niet uit op de goede variantie voor X(~nbin(n, p)?
EX = n/p
EX2 = n2/p
EX2 - (EX)2 = (n2p - n2) / p2 = (n2(p-1))/p2
Moet zijn: (np-n)/p2.
Ik heb dus een n teveel, als ik het goed zie.
Althans, als Z uniform op (-1, 1) zou zijn?
En voor [-1, 1] moet ik denk ik alleen wat groter dan / kleiner dan veranderen in groter of gelijk etc?
Waarom kom ik niet uit op de goede variantie voor X(~nbin(n, p)?
EX = n/p
EX2 = n2/p
EX2 - (EX)2 = (n2p - n2) / p2 = (n2(p-1))/p2
Moet zijn: (np-n)/p2.
Ik heb dus een n teveel, als ik het goed zie.
Er gaat wat mis in je plaatje. Als x²<0.25 dan -0.5<x<0.5. Jij meldt nu alleen de bovengrens. Dat gaat een aantal keer fout. En de laatste stap is echt fout; nu bij x=1.1 krijg je een raar resultaat.
En als EX = n/p dan zal je EX² wel fout zijn.
[ Bericht 16% gewijzigd door GlowMouse op 28-06-2010 21:54:42 ]
En als EX = n/p dan zal je EX² wel fout zijn.
[ Bericht 16% gewijzigd door GlowMouse op 28-06-2010 21:54:42 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik begin me steeds stommer te voelen Waar komt die wortel-half nu precies vandaan? En mag FX zomaar "gaten" hebben? (Als in: er is nu geen x zodat FX(x) is tussen 0 en 0.25).
Wat moet ik hier precies doen voor EY? Ik weet .
Maar is die laatste integraal niet oneindig?
Die ander - is het niet zo dat als X is het aantal herhalingen dat je moet doen om n successen te krijgen, dan is X^2 het aantal herhalingen voor n^2 successen en dus X^2 ~ nbin(n^2, p)?
Ik probeer via Pascalverdeling op de verwachting voor de negatief-binomiaal uit te komen, maar het lukt me echt niet. Wat moet ik doen met dingen als som{k=1 tot oneindig} (k-1)-boven-(n-1)?
God, dit zijn alleen nog maar de eerste twee sommen
Waar komt die wortel-half nu precies vandaan? En mag FX zomaar "gaten" hebben? (Als in: er is nu geen x zodat FX(x) is tussen 0 en 0.25). Wat moet ik hier precies doen voor EY? Ik weet .
Maar is die laatste integraal niet oneindig?
Die ander - is het niet zo dat als X is het aantal herhalingen dat je moet doen om n successen te krijgen, dan is X^2 het aantal herhalingen voor n^2 successen en dus X^2 ~ nbin(n^2, p)?
Ik probeer via Pascalverdeling op de verwachting voor de negatief-binomiaal uit te komen, maar het lukt me echt niet. Wat moet ik doen met dingen als som{k=1 tot oneindig} (k-1)-boven-(n-1)?
God, dit zijn alleen nog maar de eerste twee sommen
fX is de afgeleide van FX. En die absoluutstrepen horen er ook niet te staan.quote:Op dinsdag 29 juni 2010 02:22 schreef Hanneke12345 het volgende:
Ik begin me steeds stommer te voelen
Wat moet ik hier precies doen voor EY? Ik weet [ afbeelding ].
Maar is die laatste integraal niet oneindig?
Nee, 't is het kwadraat van het aantal herhalingen voor n successen.quote:Op dinsdag 29 juni 2010 02:22 schreef Hanneke12345 het volgende:
Die ander - is het niet zo dat als X is het aantal herhalingen dat je moet doen om n successen te krijgen, dan is X^2 het aantal herhalingen voor n^2 successen en dus X^2 ~ nbin(n^2, p)?
FX is een (niet-dalende) functie van R naar [0,1].quote:Op dinsdag 29 juni 2010 02:22 schreef Hanneke12345 het volgende:
Ik begin me steeds stommer te voelen
Ik neem aan dat daar nog een factor xk oid bij zit. Tja, dat manipuleren met reeksen moet je een beetje in de vingers hebben. In dit geval volstaat het denk ik om de reeks te schrijven als een zoveelste afgeleide van een andere reeks. Vaak kun je ook gebruiken dat n boven k de k-de danwel (n-k)-de coefficient in (1+x)n is, of zelfs het residu van (1+z)n/zk+1 bij z=0, en zo zijn er nog wel een paar andere truuks.quote:Op dinsdag 29 juni 2010 02:22 schreef Hanneke12345 het volgende:
Ik probeer via Pascalverdeling op de verwachting voor de negatief-binomiaal uit te komen, maar het lukt me echt niet. Wat moet ik doen met dingen als som{k=1 tot oneindig} (k-1)-boven-(n-1)?
Het begint langzaam iets helderder te worden allemaal. ;x (Dat wordt tijd )
Laatste keer dan nog;
Kansdichtheid van X en Y wordt gegeven door: fX,Y(x,y) = cx^2y^2 als x in [-1, 1], y in [-1, x]
Teken in R^2 het gebied waarop fX, Y(x,y) > 0.
- Is dat gewoon in het x,y-vlak en dan een soort driehoek met hoekpunten (-1, -1) (1,1) en (1, -1), maar dan zonder punt (0,0)?
Bepaal C
- Hoe kan ik met deze informatie C bepalen?
Bepaal de dichtheid en verdelingsfunctie van X
- Hoe kan ik hieruit X halen?
Ik ben bang dat deze opgave werkt met dubbelintegralen, klopt mijn vermeoden?
)Laatste keer dan nog;
Hoe dan, en waarom kan ik bij X+Y wel gewoon zeggen nbin(n_1+n_2,p)? Ik neem aan dat 't uiteindelijk toch op dezelfde manier werkt?quote:Op dinsdag 29 juni 2010 08:49 schreef thabit het volgende:
[..]
Nee, 't is het kwadraat van het aantal herhalingen voor n successen.
Kansdichtheid van X en Y wordt gegeven door: fX,Y(x,y) = cx^2y^2 als x in [-1, 1], y in [-1, x]
Teken in R^2 het gebied waarop fX, Y(x,y) > 0.
- Is dat gewoon in het x,y-vlak en dan een soort driehoek met hoekpunten (-1, -1) (1,1) en (1, -1), maar dan zonder punt (0,0)?
Bepaal C
- Hoe kan ik met deze informatie C bepalen?
Bepaal de dichtheid en verdelingsfunctie van X
- Hoe kan ik hieruit X halen?
Ik ben bang dat deze opgave werkt met dubbelintegralen, klopt mijn vermeoden?
Dat dat zo werkt in dit geval, dat is gewoon toeval. Het werkt zeg maar niet per definitie zo, maar het komt in dit speciale geval zo uit.quote:Op dinsdag 29 juni 2010 16:28 schreef Hanneke12345 het volgende:
Het begint langzaam iets helderder te worden allemaal. ;x (Dat wordt tijd
Laatste keer dan nog;
[..]
Waarom kan ik bij X+Y wel gewoon zeggen nbin(n_1+n_2, p)?
Ja.quote:Op dinsdag 29 juni 2010 16:28 schreef Hanneke12345 het volgende:
Kansdichtheid van X en Y wordt gegeven door: fX,Y(x,y) = cx^2y^2 als x in [-1, 1], y in [-1, x]
Teken in R^2 het gebied waarop fX, Y(x,y) > 0.
- Is dat gewoon in het x,y-vlak en dan een soort driehoek met hoekpunten (-1, -1) (1,1) en (1, -1), maar dan zonder punt (0,0)?
De integraal van fX,Y over R2 moet 1 zijn.quote:Bepaal C
- Hoe kan ik met deze informatie C bepalen?
De dichtheid is een gevaarlijk begrip want een kansverdeling hoeft geen dichtheid te hebben en als-ie dat wel heeft is de dichtheid iha niet uniek (de dichtheid kun je bijvoorbeeld in 1 punt veranderen, dan verandert de verdeling daarmee niet). Ik zou dus beginnen met de verdeling, die kun je schrijven als een integraal.quote:Bepaal de dichtheid en verdelingsfunctie van X
- Hoe kan ik hieruit X halen?
Jaquote:Ik ben bang dat deze opgave werkt met dubbelintegralen, klopt mijn vermeoden?
.
Hoeveel driehoeken kun je vinden in de complete graaf van zeg 6 punten?
Ik dacht zelf aan het volgende:
Je hebt (6*5 /2 =) 15 verschillende kanten. Met elk van die 15 kanten kun je (6-2=) 4 verschillende driehoeken maken. Dus zodoende heb je 60 driehoeken, maar omdat je nu alles 3 voudig telt, deel je door drie op om 20 te komen.
En algemeen voor Kn: n(n-1)/2 * (n-2)/3.
Klopt dat?
Ik dacht zelf aan het volgende:
Je hebt (6*5 /2 =) 15 verschillende kanten. Met elk van die 15 kanten kun je (6-2=) 4 verschillende driehoeken maken. Dus zodoende heb je 60 driehoeken, maar omdat je nu alles 3 voudig telt, deel je door drie op om 20 te komen.
En algemeen voor Kn: n(n-1)/2 * (n-2)/3.
Klopt dat?
⎝⏠⏝⏠⎠
De complete graaf toch wel. Je snapt wel wat ik bedoel toch? Kijkend naar de kantenverzameling, etc.
Maar ik heb het antwoord al. 't Is goed.
Maar ik heb het antwoord al. 't Is goed.
⎝⏠⏝⏠⎠
Ik vind zowel je vraagstelling onjuist als je redenering onduidelijk. Je vraag zou moeten luiden: hoeveel verschillende driehoeken kun je maken met 6 punten in het platte vlak waarvan er geen drie op één rechte lijn liggen?quote:Op woensdag 30 juni 2010 15:03 schreef Huehueteotl het volgende:
Hoeveel driehoeken kun je vinden in de complete graaf van zeg 6 punten?
Ik dacht zelf aan het volgende:
Je hebt (6*5 /2 =) 15 verschillende kanten. Met elk van die 15 kanten kun je (6-2=) 4 verschillende driehoeken maken. Dus zodoende heb je 60 driehoeken, maar omdat je nu alles 3 voudig telt, deel je door drie op om 20 te komen.
En algemeen voor Kn: n(n-1)/2 * (n-2)/3.
Klopt dat?
Dan is de beantwoording van de vraag een kwestie van eenvoudige combinatoriek. Voor het eerste hoekpunt van een driehoek heb je de keuze uit zes mogelijkheden, voor het tweede hoekpunt kun je dan nog uit 5 mogelijkheden kiezen, en voor het derde hoekpunt uit de resterende 4 mogelijkheden. Het aantal combinaties is dus 6 over 3 oftewel (6∙5∙4)/(1∙2∙3) = 20.
Veel simpeler zo, inderdaadquote:Op woensdag 30 juni 2010 15:36 schreef Riparius het volgende:
[..]
Ik vind zowel je vraagstelling onjuist als je redenering onduidelijk. Je vraag zou moeten luiden: hoeveel verschillende driehoeken kun je maken met 6 punten in het platte vlak waarvan er geen drie op één rechte lijn liggen?
Dan is de beantwoording van de vraag een kwestie van eenvoudige combinatoriek. Voor het eerste hoekpunt van een driehoek heb je de keuze uit zes mogelijkheden, voor het tweede hoekpunt kun je dan nog uit 5 mogelijkheden kiezen, en voor het derde hoekpunt uit de resterende 4 mogelijkheden. Het aantal combinaties is dus 6 over 3 oftewel (6∙5∙4)/(1∙2∙3) = 20.
Bedankt. 't Is allemaal aardig weggezakt bij me.
Hoeveel verschillende drietallen van zijden zijn er in een volledige graaf met 5 punten (reguliere graaf)?
Volgens mijn boek 120....
Ik zou zelf denken 5*4/2, 10 verschillende kanten.
En dan dus voor de drietallen 10 * 9 * 8 / 3 = 240 het dubbele dus, wat tel ik nu dubbel?
⎝⏠⏝⏠⎠
Het aantal is 10 over 3, en dat is (10∙9∙8)/(1∙2∙3) = 120.quote:Op woensdag 30 juni 2010 15:43 schreef Huehueteotl het volgende:
[..]
Veel simpeler zo, inderdaad
Bedankt. 't Is allemaal aardig weggezakt bij me.
Hoeveel verschillende drietallen van zijden zijn er in een volledige graaf met 5 punten (reguliere graaf)?
Volgens mijn boek 120....
Ik zou zelf denken 5*4/2, 10 verschillende kanten.
En dan dus voor de drietallen 10 * 9 * 8 / 3 = 240 het dubbele dus, wat tel ik nu dubbel?
Heb morgen een economietoets voor de proefwerweek en snap alles, behalve 1 ding.
het hoofdstuk belasting betalen
het hoofdstuk belasting betalen
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.andere foto:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Het gaat om de som 2, misschien staat er nog iets over som 1 maar gewoon negeren.
Mijn vraag is: hoe kom ik te weten hoeveel schijven ik moet plaatsen?
De leraar is een aantal weken afwezig geweest, hij was er 2 lessen.
En nu heeft hij gezegd dat hij voldoende heeft uitgelegd maar dat is natuurlijk niet zo anders snapte ik het wel.
Leren in de proefwerkweek in dit weerKijk de wolken zijn de golven van de zee, dus ik moet zwemmen om te zorgen dat ik leef.
Bedankt riparius.
'Absoluut', of wat is je vraag?quote:Op woensdag 30 juni 2010 16:02 schreef FastFox91 het volgende:
[ afbeelding ]
Weet iemand een term voor dat | |?
⎝⏠⏝⏠⎠
Ik kwam het tegen en wist niet wat het was. Doormiddel van het antwoord kon ik uitvogelen wat het ongeveer deed. Maar nu met de term kan ik op googlen zoeken naar meer informatie. Geen vragen verder. Bedankt.quote:
Je kunt dit het eenvoudigst in omgekeerde richting inzien. Om 1/i af te trekken van 1/(i-1) moet je de breuken eerst gelijknamig maken. Dat doe je door teller en noemer van 1/(i-1) met i en teller en noemer van 1/i met (i-1) te vermenigvuldigen. Aangenomen dat je met i de imaginaire eenheid bedoelt kun je deze uitdrukkingen trouwens ook herleiden tot -½ +½ ∙i.quote:Op woensdag 30 juni 2010 17:12 schreef Siddartha het volgende:
Ik heb er een tijdje uitgelegen, maar waarom is
1 / i ( i - 1)
gelijk aan:
1/ (i-1) - 1/i
?
Ah, duidelijk!quote:Op woensdag 30 juni 2010 17:36 schreef Riparius het volgende:
[..]
Je kunt dit het eenvoudigst in omgekeerde richting inzien. Om 1/i af te trekken van 1/(i-1) moet je de breuken eerst gelijknamig maken. Dat doe je door teller en noemer van 1/(i-1) met i en teller en noemer van 1/i met (i-1) te vermenigvuldigen. Aangenomen dat je met i de imaginaire eenheid bedoelt kun je deze uitdrukkingen trouwens ook herleiden tot -½ +½ ∙i.
Bedankt.
Verder moet ik met die identiteit het volgende bewijzen (Hoe gebruik je trouwens het sommatie-teken in latex?):
Bewijs dat de som van alle n, zonder n=1 (onder de S staat i= 2, erboven staat 'n'), van de functie:
1/ i (i-1)
gelijk is aan
1 - 1/n
Pff, het moet allemaal vrij simpel zijn maar ik kom er gewoon niet op.
Oh, op die manier. Negeer mijn opmerking over complexe getallen, i is hier een index. Als elke term van je som van de gedaantequote:Op woensdag 30 juni 2010 18:17 schreef Siddartha het volgende:
[..]
Ah, duidelijk!
Bedankt.
Verder moet ik met die identiteit het volgende bewijzen (Hoe gebruik je trouwens het sommatie-teken in latex?):
Bewijs dat de som van alle n, zonder n=1 (onder de S staat i= 2, erboven staat 'n'), van de functie:
1/ i (i-1)
gelijk is aan
1 - 1/n
Pff, het moet allemaal vrij simpel zijn maar ik kom er gewoon niet op.
1/ (i-1) - 1/i
is, dan zullen de meeste termen tegen elkaar wegvallen. Te beginnen met i = 2 krijg je immers:
(1/1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + ...
Je houdt dan alleen de eerste term 1/1 en de laatste term -1/n over, zodat de som voor i = 2 .. n inderdaad gelijk is aan
1/1 - 1/n
Met dit resultaat kun je gemakkelijk bewijzen dat de reeks:
1/(1∙2) + 1/(2∙3) + 1/(3∙4) + ...
convergeert naar 1.
hmm, dat moest ik dus zien door wat getallen in te vullen of is er een betere manier?quote:Op woensdag 30 juni 2010 18:45 schreef Riparius het volgende:
[..]
Oh, op die manier. Negeer mijn opmerking over complexe getallen, i is hier een index. Als elke term van je som van de gedaante
1/ (i-1) - 1/i
is, dan zullen de meeste termen tegen elkaar wegvallen. Te beginnen met i = 2 krijg je immers:
(1/1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + ...
Je houdt dan alleen de eerste term 1/1 en de laatste term -1/n over, zodat de som voor i = 2 .. n inderdaad gelijk is aan
1/1 - 1/n
Met dit resultaat kun je gemakkelijk bewijzen dat de reeks:
1/(1∙2) + 1/(2∙3) + 1/(3∙4) + ...
convergeert naar 1.
Vaak helpt het om die sigma weg te werken en de som uit te schrijven. Dat geeft meer inzicht in wat er nou eigenlijk staat. Op die manier zie je al direct waarom het klopt... er is geen andere manier in dit geval denk ik.quote:Op woensdag 30 juni 2010 18:54 schreef Siddartha het volgende:
[..]
hmm, dat moest ik dus zien door wat getallen in te vullen of is er een betere manier?
Voor een som in LaTeX, schrijf bijvoorbeeld \sum_{i=1}^k a_i voor
Nee, dat was niet direct de strekking van mijn uitleg, ik wilde het alleen even aanschouwelijk maken. Het is trouwens een heel bekende methode om sommige reeksen te sommeren, wat je hier hebt is een telescoopreeks.quote:Op woensdag 30 juni 2010 18:54 schreef Siddartha het volgende:
[..]
hmm, dat moest ik dus zien door wat getallen in te vullen
Uiteraard, maar wat heet beter? Als je bedoelt strenger, dan zou je kunnen denken aan een bewijs met volledige inductie.quote:of is er een betere manier?
Denk dat ik gewoon nog wat moet oefenen met reeksen, weet er nog zeer weinig van.
Maar die telescoopreeks gebruik je dus vooral als je een vermoeden hebt dat er ook daadwerkelijk wat valt weg te strepen? Wanneer je bijv. een functie min een functie moet doen die erop lijkt, oid?
@Basementdweller, bedankt!
Maar die telescoopreeks gebruik je dus vooral als je een vermoeden hebt dat er ook daadwerkelijk wat valt weg te strepen? Wanneer je bijv. een functie min een functie moet doen die erop lijkt, oid?
@Basementdweller, bedankt!
Het telescoopprincipe om de som van een (oneindige) reeks te bepalen is uiteraard maar in zeer bepaalde gevallen bruikbaar, maar theoretisch is het van groot belang. Lees ook even het artikel in de Duitse Wikipedia.quote:Op woensdag 30 juni 2010 20:21 schreef Siddartha het volgende:
Denk dat ik gewoon nog wat moet oefenen met reeksen, weet er nog zeer weinig van.
Maar die telescoopreeks gebruik je dus vooral als je een vermoeden hebt dat er ook daadwerkelijk wat valt weg te strepen? Wanneer je bijv. een functie min een functie moet doen die erop lijkt, oid?
Als je bijvoorbeeld weet dat de reeks:
1/(1∙2) + 1/(2∙3) + 1/(3∙4) + ...
convergeert (naar 1), dan kun je al meteen concluderen dat bijvoorbeeld de reeks:
1/12 + 1/22 + 1/32 + 1/42 + ...
ook convergent moet zijn en dat de som (c.q. limiet) hiervan tussen 1 en 2 ligt (waarom?).
Omgekeerd is het mogelijk om met het resultaat dat je hebt gevonden te bewijzen dat de harmonische reeks:
1/1 + 1/2 + 1/3 + 1/4 + ...
juist divergeert.
[ Bericht 0% gewijzigd door Riparius op 01-07-2010 15:18:11 ]
Even een noobvraag, hetis herhaling en ik ben het vergeten.
Als de functie f(x)= -2xsquared + 8px + 12p
Voor welke waarde van p is de extreem (ik heb de engelse variant, ik weet niet wat de correcte hollandsche termen zijn) minder dan 20?
In dit hoofdstuk komt vooral discriminant en extreem (-(b/2a)) in basisvorm voor.
Spoed.
Als de functie f(x)= -2xsquared + 8px + 12p
Voor welke waarde van p is de extreem (ik heb de engelse variant, ik weet niet wat de correcte hollandsche termen zijn) minder dan 20?
In dit hoofdstuk komt vooral discriminant en extreem (-(b/2a)) in basisvorm voor.
Spoed.
extreem is gewoon maximum lijkt me,quote:Op donderdag 1 juli 2010 17:46 schreef Lespaulspelert het volgende:
Even een noobvraag, hetis herhaling en ik ben het vergeten.
Als de functie f(x)= -2xsquared + 8px + 12p
Voor welke waarde van p is de extreem (ik heb de engelse variant, ik weet niet wat de correcte hollandsche termen zijn) minder dan 20?
In dit hoofdstuk komt vooral discriminant en extreem (-(b/2a)) in basisvorm voor.
Spoed.
wat je dan doet is afgeleide gelijkstellen aan 0 om het maximum te berekenen:
f(x) = -2x^2 +8px +12p
f'(x) = -4x + 8p
gelijkstellen aan 0 geeft : 8p = 4x oftewel x = 2p.
dat invullen in functie geeft -8p^2 + 16p^2 +12p , die aan 20 gelijkstellen en je krijgt
8p^2 +12p - 20 = 0, levert p=1 v p = -2,5 .. Dan zit het maximum onder de 20 wanneer -2.5<p<1
nu wel goed ? :p
[ Bericht 5% gewijzigd door Baszh op 01-07-2010 20:07:43 ]
Waarom uitstellen tot morgen als je het overmorgen nog kunt doen?
Ik neem aan dat je de volgende kwadratische functie bedoelt (s.v.p. superscript gebruiken):quote:Op donderdag 1 juli 2010 17:46 schreef Lespaulspelert het volgende:
Even een noobvraag, hetis herhaling en ik ben het vergeten.
Als de functie f(x)= -2xsquared + 8px + 12p
Voor welke waarde van p is de extreem (ik heb de engelse variant, ik weet niet wat de correcte hollandsche termen zijn) minder dan 20?
In dit hoofdstuk komt vooral discriminant en extreem (-(b/2a)) in basisvorm voor.
Spoed.
f(x) = -2x2 + 8px + 12p
De algemene gedaante van een kwadratische functie is:
(1) f(x) = ax2 + bx + c,
waarbij we a ongelijk aan nul mogen veronderstellen (anders is het geen kwadratische functie meer). Deze functie bereikt een extreme waarde voor:
(2) x = -b/2a,
en dit extremum zelf is:
(3) -D/4a,
waarbij
(4) D = b2 - 4ac
de discriminant wordt genoemd van het kwadratisch polynoom ax2 + bx + c. De extreme waarde is een minimum indien a > 0 en een maximum indien a < 0.
Voor jouw functie is a = -2, b = 8p, c = 12p. Substitueer nu deze waarden voor a,b en c in (3) om je opgave op te lossen.
Dit is helemaal fout. Als je het zelf niet weet, kun je beter niet posten.quote:Op donderdag 1 juli 2010 19:06 schreef Baszh het volgende:
[..]
extreem is gewoon maximum lijkt me,
wat je dan doet is afgeleide gelijkstellen aan 0 om het maximum te berekenen:
f(x) = -2x^2 +8px +12p
f'(x) = -4x + 8p
gelijkstellen aan 0 geeft : 8p = 4x(max) oftewel x(max) = 2p.
Dus x(max) is minder dan 20 wanneer p minder is dan 20/2 = 10.
quote:
[..]
Dit is helemaal fout. Als je het zelf niet weet, kun je beter niet posten.
Dat is wel overdreven, alleen de laatste regel klopt niet. Je moet naar de functiewaarde kijken ipv naar x.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
aja kut sorry, ik edit em welquote:Op donderdag 1 juli 2010 19:21 schreef GlowMouse het volgende:
[..]
Dat is wel overdreven, alleen de laatste regel klopt niet. Je moet naar de functiewaarde kijken ipv naar x.
Waarom uitstellen tot morgen als je het overmorgen nog kunt doen?
Kan iemand even (2n)! omschrijven tot iets? (net zoals dat (n+1)! --> (n+1)*n!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |