SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Kan je dit verder toelichten? Wat maakt het uit dat die schijf niet in S zit?quote:Op zondag 13 juni 2010 22:47 schreef thabit het volgende:
Met de stelling van Gauss krijg je hier geen 0, want de rand van de halve bol heeft ook nog een schijf aan de onderkant zitten en die zit niet in S.
Gauss relateert een integraal over een (voldoende 'mooie' maar daar is hier wel aan voldaan) driedimensionale vorm aan een integraal over de rand van die vorm. Een halve bol heeft als rand een half boloppervlak aan de bovenkant plus een cirkelschijf aan de onderkant. Als je alleen maar over het halve boloppervlak integreert, dan neem je de cirkelschijf dus niet mee. Dus je kunt Gauss niet op die manier toepassen omdat je niet over de hele rand integreert.
Ah, duidelijk. Het moet natuurlijk een gesloten oppervlak zijn.quote:Op zondag 13 juni 2010 23:40 schreef thabit het volgende:
Gauss relateert een integraal over een (voldoende 'mooie' maar daar is hier wel aan voldaan) driedimensionale vorm aan een integraal over de rand van die vorm. Een halve bol heeft als rand een half boloppervlak aan de bovenkant plus een cirkelschijf aan de onderkant. Als je alleen maar over het halve boloppervlak integreert, dan neem je de cirkelschijf dus niet mee. Dus je kunt Gauss niet op die manier toepassen omdat je niet over de hele rand integreert.
Ik doe nog iets fout met de stelling van stokes of directe evaluatie. Bij directe evaluatie krijg ik namelijk wel 0 (en 16pi met stokes). (dus als iemand zich geroepen voelt om het na te rekenen, graag
)
Ik denk toch dat het dan mis moet gaan bij de directe evaluatie.
Wat moet je hier als dS nemen? Mijn boek zegt
,
alleen dan zit ik nog met x, y en z in de integrand terwijl er dphi dtheta achter staat. Kan ik dan zomaar voor x,y en z spherical coordinates invullen?
Ik krijg:quote:Evaluate, where F=(x^2+y-4, 3xy, 2xz+z^2) and S is the surface
met
using Stokes' theorem
. (unit normal upward pointing)
Wat moet je hier als dS nemen? Mijn boek zegt
alleen dan zit ik nog met x, y en z in de integrand terwijl er dphi dtheta achter staat. Kan ik dan zomaar voor x,y en z spherical coordinates invullen?
Ik vul in:
x=4cos(th)sin(phi)
y=4sin(th)sin(phi)
z=cos(phi)
Dan krijg ik dit als integrand:
4 Sin[\[Phi]] (-32 Cos[\[Phi]] Sin[\[Theta]] Sin[\[Phi]] + 4 Cos[\[Phi]] (-1 + 12 Sin[\[Theta]] Sin[\[Phi]]))
en als ik dat door mathematica laat integreren (phi van 0 tot pi en theta van 0 tot 2pi), dan krijg ik 0 en geen -16pi.
[ Bericht 5% gewijzigd door BasementDweller op 14-06-2010 16:38:50 ]
x=4cos(th)sin(phi)
y=4sin(th)sin(phi)
z=cos(phi)
Dan krijg ik dit als integrand:
4 Sin[\[Phi]] (-32 Cos[\[Phi]] Sin[\[Theta]] Sin[\[Phi]] + 4 Cos[\[Phi]] (-1 + 12 Sin[\[Theta]] Sin[\[Phi]]))
en als ik dat door mathematica laat integreren (phi van 0 tot pi en theta van 0 tot 2pi), dan krijg ik 0 en geen -16pi.
[ Bericht 5% gewijzigd door BasementDweller op 14-06-2010 16:38:50 ]
Als dS neem ik gewoon (x,y,z) sinphi dphi dtheta.
Het inproduct geeft: -2 z y + z (3 y - 1) R sinphi dphi dtheta met R=4, en dan y en z substitueren en integreren...
Het inproduct geeft: -2 z y + z (3 y - 1) R sinphi dphi dtheta met R=4, en dan y en z substitueren en integreren...
Bij z moet je natuurlijk ook niet de factor 4 vergeten, maar dat zal wel een tikfout zijn. Probeer het eens uit te schrijven in termen van dx, dy en dz en daarna pas te substitueren, want ik zie niet helemaal waar die uitdrukking voor dS vandaan komt.
Dat was een typfout. Maar oké, ze zeggen dus datquote:Op zaterdag 12 juni 2010 22:55 schreef thabit het volgende:
Ja, dat zijn inderdaad 3 integralen vanwege het patroon in de kettingbreuk.
In die laatste formule horen geen integraaltekens te staan. Dan staat er een identiteit van functies en integreren levert dan dus een uitdrukking voor de som van de integralen.
En dus ?
? (Of nouja, als onbepaalde integraal, dus de rechterkant op het interval [0,1].)
Maar dan nog snap ik niet waarom de eerste vergelijking waar is. "which follows immediately from the product rule for dervatives", volgens 't artikel. Maar ik zie het nog niet.
Ik zou niet weten hoe ik het in dxdydz moet uitschrijven... dS is gewoon de jacobiaan die je krijgt door sferische substitutie.quote:Op maandag 14 juni 2010 16:58 schreef thabit het volgende:
Bij z moet je natuurlijk ook niet de factor 4 vergeten, maar dat zal wel een tikfout zijn. Probeer het eens uit te schrijven in termen van dx, dy en dz en daarna pas te substitueren, want ik zie niet helemaal waar die uitdrukking voor dS vandaan komt.
In mijn boek staat vector surface element for a sphere:
Dit kan je wel uitrekenen door te parametriseren en het uitproduct te nemen van de afgeleides naar phi en theta (als het goed is).
Ik snap alleen niet waarom er R^2 bij die laatste staat en R bij die andere twee, tikfoutje?
Kan iemand me even helpen.
Evaluate
, where E lies between the spheres x2 + y2 + z2 = 1 and x2 + y2 + z2 = 4 in the first octant.
Dit moet allemaal in spherical coordinates.
Nou heb ik natuurlijk al gevonden dat
. en
Nu moet ik alleen nog de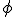
vinden (dit is de hoek tussen Z en X)
Maar ja, ik weet natuurlijk een aantal dingen ( bijvoorbeeld z = cos(phi) etc.) Maar goed ik kom er niet uit. Kan iemand me helpen?
[ Bericht 4% gewijzigd door Burakius op 15-06-2010 00:13:36 ]
Evaluate
Dit moet allemaal in spherical coordinates.
Nou heb ik natuurlijk al gevonden dat
Nu moet ik alleen nog de
Maar ja, ik weet natuurlijk een aantal dingen ( bijvoorbeeld z = cos(phi) etc.) Maar goed ik kom er niet uit. Kan iemand me helpen?
[ Bericht 4% gewijzigd door Burakius op 15-06-2010 00:13:36 ]
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Waarom loopt O tussen 0 en 2pi als je maar één octant wilt?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oja goede vraag. Dan moet hij natuurlijk tot pi/2 . Stom even over heen gezienquote:Op dinsdag 15 juni 2010 00:07 schreef GlowMouse het volgende:
Waarom loopt O tussen 0 en 2pi als je maar één octant wilt?
Ik heb even geedit: (met latex, thats a first).
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zou ik het ook met cilinder coordinaten kunnen doen?
waarbij theta dan tussen pi/2 en 0 zit. r tussen 2 en 1 en z dan tussen 4 en 1 ??
waarbij theta dan tussen pi/2 en 0 zit. r tussen 2 en 1 en z dan tussen 4 en 1 ??
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zeg eens in woorden welk gebied ze precies bedoelen. Volgens mij heb je dat verkeerd voor je.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb gewoon precies omschreven wat de vraag is. Ik moet alleen die klote PHI nog vinden om de som te maken. Help alsjeblieftquote:Op dinsdag 15 juni 2010 00:19 schreef GlowMouse het volgende:
Zeg eens in woorden welk gebied ze precies bedoelen. Volgens mij heb je dat verkeerd voor je.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Heb het antwoord al. Omdat phi ook tot de eerste octant gaat is het ook natuurlijk gewoon van 0 tot pi/2
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Lol dat is precies het antwoord wat ik zocht terwijl je een andere vraag vroeg hahahaha.quote:Op maandag 14 juni 2010 17:24 schreef BasementDweller het volgende:
I got it!!!!!!!!
Ik moet natuurlijk phi integreren van 0 tot pi/2 en niet van 0 tot pi
Volgend paragraaf moet ik ook aan de Jacobian
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Use a triple integral to find the volume of the solid enclosed by the cylinder x = y2 and the planes z=0 and x+z=1.
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
