SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik vul in:
x=4cos(th)sin(phi)
y=4sin(th)sin(phi)
z=cos(phi)
Dan krijg ik dit als integrand:
4 Sin[\[Phi]] (-32 Cos[\[Phi]] Sin[\[Theta]] Sin[\[Phi]] + 4 Cos[\[Phi]] (-1 + 12 Sin[\[Theta]] Sin[\[Phi]]))
en als ik dat door mathematica laat integreren (phi van 0 tot pi en theta van 0 tot 2pi), dan krijg ik 0 en geen -16pi.
[ Bericht 5% gewijzigd door BasementDweller op 14-06-2010 16:38:50 ]
x=4cos(th)sin(phi)
y=4sin(th)sin(phi)
z=cos(phi)
Dan krijg ik dit als integrand:
4 Sin[\[Phi]] (-32 Cos[\[Phi]] Sin[\[Theta]] Sin[\[Phi]] + 4 Cos[\[Phi]] (-1 + 12 Sin[\[Theta]] Sin[\[Phi]]))
en als ik dat door mathematica laat integreren (phi van 0 tot pi en theta van 0 tot 2pi), dan krijg ik 0 en geen -16pi.
[ Bericht 5% gewijzigd door BasementDweller op 14-06-2010 16:38:50 ]
Als dS neem ik gewoon (x,y,z) sinphi dphi dtheta.
Het inproduct geeft: -2 z y + z (3 y - 1) R sinphi dphi dtheta met R=4, en dan y en z substitueren en integreren...
Het inproduct geeft: -2 z y + z (3 y - 1) R sinphi dphi dtheta met R=4, en dan y en z substitueren en integreren...
Bij z moet je natuurlijk ook niet de factor 4 vergeten, maar dat zal wel een tikfout zijn. Probeer het eens uit te schrijven in termen van dx, dy en dz en daarna pas te substitueren, want ik zie niet helemaal waar die uitdrukking voor dS vandaan komt.
Dat was een typfout. Maar oké, ze zeggen dus datquote:Op zaterdag 12 juni 2010 22:55 schreef thabit het volgende:
Ja, dat zijn inderdaad 3 integralen vanwege het patroon in de kettingbreuk.
In die laatste formule horen geen integraaltekens te staan. Dan staat er een identiteit van functies en integreren levert dan dus een uitdrukking voor de som van de integralen.
En dus ?
? (Of nouja, als onbepaalde integraal, dus de rechterkant op het interval [0,1].)
Maar dan nog snap ik niet waarom de eerste vergelijking waar is. "which follows immediately from the product rule for dervatives", volgens 't artikel. Maar ik zie het nog niet.
Ik zou niet weten hoe ik het in dxdydz moet uitschrijven... dS is gewoon de jacobiaan die je krijgt door sferische substitutie.quote:Op maandag 14 juni 2010 16:58 schreef thabit het volgende:
Bij z moet je natuurlijk ook niet de factor 4 vergeten, maar dat zal wel een tikfout zijn. Probeer het eens uit te schrijven in termen van dx, dy en dz en daarna pas te substitueren, want ik zie niet helemaal waar die uitdrukking voor dS vandaan komt.
In mijn boek staat vector surface element for a sphere:
Dit kan je wel uitrekenen door te parametriseren en het uitproduct te nemen van de afgeleides naar phi en theta (als het goed is).
Ik snap alleen niet waarom er R^2 bij die laatste staat en R bij die andere twee, tikfoutje?
Kan iemand me even helpen.
Evaluate
, where E lies between the spheres x2 + y2 + z2 = 1 and x2 + y2 + z2 = 4 in the first octant.
Dit moet allemaal in spherical coordinates.
Nou heb ik natuurlijk al gevonden dat
. en
Nu moet ik alleen nog de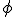
vinden (dit is de hoek tussen Z en X)
Maar ja, ik weet natuurlijk een aantal dingen ( bijvoorbeeld z = cos(phi) etc.) Maar goed ik kom er niet uit. Kan iemand me helpen?
[ Bericht 4% gewijzigd door Burakius op 15-06-2010 00:13:36 ]
Evaluate
Dit moet allemaal in spherical coordinates.
Nou heb ik natuurlijk al gevonden dat
Nu moet ik alleen nog de
Maar ja, ik weet natuurlijk een aantal dingen ( bijvoorbeeld z = cos(phi) etc.) Maar goed ik kom er niet uit. Kan iemand me helpen?
[ Bericht 4% gewijzigd door Burakius op 15-06-2010 00:13:36 ]
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Waarom loopt O tussen 0 en 2pi als je maar één octant wilt?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oja goede vraag. Dan moet hij natuurlijk tot pi/2 . Stom even over heen gezienquote:Op dinsdag 15 juni 2010 00:07 schreef GlowMouse het volgende:
Waarom loopt O tussen 0 en 2pi als je maar één octant wilt?
Ik heb even geedit: (met latex, thats a first).
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zou ik het ook met cilinder coordinaten kunnen doen?
waarbij theta dan tussen pi/2 en 0 zit. r tussen 2 en 1 en z dan tussen 4 en 1 ??
waarbij theta dan tussen pi/2 en 0 zit. r tussen 2 en 1 en z dan tussen 4 en 1 ??
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zeg eens in woorden welk gebied ze precies bedoelen. Volgens mij heb je dat verkeerd voor je.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb gewoon precies omschreven wat de vraag is. Ik moet alleen die klote PHI nog vinden om de som te maken. Help alsjeblieftquote:Op dinsdag 15 juni 2010 00:19 schreef GlowMouse het volgende:
Zeg eens in woorden welk gebied ze precies bedoelen. Volgens mij heb je dat verkeerd voor je.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Heb het antwoord al. Omdat phi ook tot de eerste octant gaat is het ook natuurlijk gewoon van 0 tot pi/2
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Lol dat is precies het antwoord wat ik zocht terwijl je een andere vraag vroeg hahahaha.quote:Op maandag 14 juni 2010 17:24 schreef BasementDweller het volgende:
I got it!!!!!!!!
Ik moet natuurlijk phi integreren van 0 tot pi/2 en niet van 0 tot pi
Volgend paragraaf moet ik ook aan de Jacobian
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Use a triple integral to find the volume of the solid enclosed by the cylinder x = y2 and the planes z=0 and x+z=1.
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Om te beginnen zou ik een plaatje tekenen.quote:Op dinsdag 15 juni 2010 09:16 schreef Jac0bus het volgende:
Use a triple integral to find the volume of the solid enclosed by the cylinder x = y2 and the planes z=0 and x+z=1.
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
Als ik een vlak heb gegeven door x+y+z=1 met restrictie x² + 2y² =< 1, kan je dan nog poolcoördinaten gebruiken voor de oppervlakte-integraal? Wat zijn dan de grenzen van r?
Andere vraag:
Opgave:
Let
and D the unit disk in the u,v-plane. Find the area of Phi(D).
De unit disk is: u² + v² =< 1. De integraal die we moeten berekenen is:
.
Waarbij T_x = partiële afgeleide van phi naar x, en T_y partiële naar y.
Dus
.
Substitutie van poolcoördinaten geeft:
Het antwoord zou moeten zijn,
.
Waar gaat het fout ?
Opgave:
Let
De unit disk is: u² + v² =< 1. De integraal die we moeten berekenen is:
Waarbij T_x = partiële afgeleide van phi naar x, en T_y partiële naar y.
Dus
Substitutie van poolcoördinaten geeft:
Het antwoord zou moeten zijn,
Waar gaat het fout
?
Ik zie het al... vergeten de ondergrens er vanaf te trekken. Bah, ik maak altijd van die lame foutjes met integreren
Gedaan, zowel 3d als 2d, ik zie alleen totaal niet hoe dat object er uit zou moeten zien, iets wat mijn grootste probleem is met die integralen. Zo zijn de integralen ook veel lastiger op te stellen.quote:Op dinsdag 15 juni 2010 11:43 schreef thabit het volgende:
[..]
Om te beginnen zou ik een plaatje tekenen.
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Ik neem aan dat je de unit cilinder bedoelt (straal =1) ?quote:Op dinsdag 15 juni 2010 09:16 schreef Jac0bus het volgende:
Use a triple integral to find the volume of the solid enclosed by the cylinder x = y2 and the planes z=0 and x+z=1.
Iemand enig idee? Ik weet dat het een triple integraal van 1 is maar ik heb ontzettende moeite met boundaries in problemen als dit. Hoe moet ik dit aanpakken als ik wil weten van waar naar waar de integralen gaan en in welke volgorde?
x=y² is een gekantelde parabool
z=0 is het xy-vlak
x+z=1 is een vlak, wat je kan tekenen door het x,z vlak te nemen (want in y is die constant) en z=1-x te tekenen, en die lijn dan "uit te rekken" in de y-richting.
Ik heb het heel groot getekend en ik denk dat eruit moet komen:
(< en > betekenen groter of gelijk)
0 < x < 1
-wortel (x) < y < wortel (x)
0 < z < 1-x
Maar ik ben hier ook niet supergoed in, dus onder voorbehoud.
In dit geval integreer je dan eerst over z of y omdat die uitgedrukt zijn in andere variabelen. Tot slot integreer je over x.
(< en > betekenen groter of gelijk)
0 < x < 1
-wortel (x) < y < wortel (x)
0 < z < 1-x
Maar ik ben hier ook niet supergoed in, dus onder voorbehoud.
In dit geval integreer je dan eerst over z of y omdat die uitgedrukt zijn in andere variabelen. Tot slot integreer je over x.
Probeer eerst eens y = te vinden. Teken die. Daarna ga je tekenen wat je weet van z = ....quote:Op dinsdag 15 juni 2010 13:26 schreef Jac0bus het volgende:
[..]
Gedaan, zowel 3d als 2d, ik zie alleen totaal niet hoe dat object er uit zou moeten zien, iets wat mijn grootste probleem is met die integralen. Zo zijn de integralen ook veel lastiger op te stellen.
Ten slotte zou je x = kunnen vinden.
Waar het hierom draait is dat het slim is als je eerst 3 onafhankelijke tekening maakt voor de xy-plane, yz-plane en xz- plane. Zodoende kun je het vaak wel vinden.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Geen idee over die cylinder, zoals ik de vraag typte is hij letterlijk zoals hij in het boek staat. Het antwoord is 8/15 btw.quote:Op dinsdag 15 juni 2010 13:38 schreef BasementDweller het volgende:
[..]
Ik neem aan dat je de unit cilinder bedoelt (straal =1) ?
x=y² is een gekantelde parabool
z=0 is het xy-vlak
x+z=1 is een vlak, wat je kan tekenen door het x,z vlak te nemen (want in y is die constant) en z=1-x te tekenen, en die lijn dan "uit te rekken" in de y-richting.
I had this song playing when Mary Ellen was born. Had her right there on the pool table, and they didn't stop the game...
Als je mijn boundaries gebruikt kom je inderdaad op 8/15 (met de unit cilinder dus).quote:Op dinsdag 15 juni 2010 13:44 schreef Jac0bus het volgende:
[..]
Geen idee over die cylinder, zoals ik de vraag typte is hij letterlijk zoals hij in het boek staat. Het antwoord is 8/15 btw.
Druk eerst x^-2.25 uit in een getal.quote:
Neem de reciproke van beide kanten, en doe beide kanten tot de 4e macht. Trek nu de 9e machtswortel aan beide kanten.
Sense?quote:Op dinsdag 15 juni 2010 17:21 schreef BasementDweller het volgende:
[..]
Druk eerst x^-2.25 uit in een getal.
Neem de reciproke van beide kanten, en doe beide kanten tot de 4e macht. Trek nu de 9e machtswortel aan beide kanten.
Ik zou zeggen probeer het eens. Als je met je rekenmachine ook de 2.25e machtswortel kan berekenen kan je dat tot de 4e verheffen weglaten.quote:
-2.25 machtswortel ((11/0,37)) = -4.516quote:
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik zoek een internetsite die vertelt wat de simple continued fraction van e^2 is, een andere dan wikipedia. M'n googleskills laten het hierin even afweten (zoeken op e is al heel vervelend, laat staan op e^2).
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Mja, zat ik aan te denken, maar ik wil iets dat echt vertelt dat er regelmaat in zit. We hebben al wel mooie plaatjes, maar dat is niet afdoende bewijs ("Is de regelmaat die in deze plaatjes te zien is voor $e^2$ er ook echt, en kunnen wij dit bewijzen?
Deze regelmaat is er echt, en dat is ook wel te bewijzen. Op dit moment is dat bewijs nog in progress, maar kunnen we ons wel beroepen op andere bronnen.", wikipedia is geen bron
)
Deze regelmaat is er echt, en dat is ook wel te bewijzen. Op dit moment is dat bewijs nog in progress, maar kunnen we ons wel beroepen op andere bronnen.", wikipedia is geen bron
)
Je wil dus zeg maar een algemene formule die de kettingbreuk geeft ipv dat het eindigt in "...."? En die formule dan bewijzen.
En het bewijs in dat ene artikel, kun je niet kijken hoe je de technieken aldaar kunt toepassen op e2?
De formule heb ik al. Het bewijs ben ik nog mee bezig (alleen snap ik nog niet helemaal hoe ze aan de integralen komen, en dat is zeg maar het meest essentiele deel van het bewijs). Maar los daarvan hoopte ik een site te vinden die de formule bevestigd. Als bron waar ik me op beroep in die zin, dus. ;o
