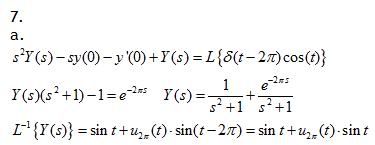SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
| ❤ | Triquester... | ツ Met een accént aigu
Gisteravond tijdens een personeelsfeest urenlang naar een discussie geluisterd wat de uitkomst moest zijn van 10 : 2 x 5
Erg vermakelijk.
(tvp)
Erg vermakelijk.
(tvp)
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Niet alleen vermakelijk, maar ook verwarrend. Ik weet niet hoe goed jijzelf en je gesprekspartners waren ingevoerd, maar het idiote is dat de uitkomst vroeger anders was dan nu, als gevolg van andere regels.quote:Op donderdag 19 november 2009 18:29 schreef -J-D- het volgende:
Gisteravond tijdens een personeelsfeest urenlang naar een discussie geluisterd wat de uitkomst moest zijn van 10 : 2 x 5
Erg vermakelijk.
(tvp)
Gelijkwaardige bewerkingen worden van links naar rechts uitgevoerd. 
Goed dat ze het veranderd hebben. Nu kan ik het zelfs onthouden.
Goed dat ze het veranderd hebben. Nu kan ik het zelfs onthouden.
Hetgeen bewezen en beklonken moest worden.
25 lijkt mij conceptueel gezien het beste antwoord.quote:Op donderdag 19 november 2009 18:29 schreef -J-D- het volgende:
Gisteravond tijdens een personeelsfeest urenlang naar een discussie geluisterd wat de uitkomst moest zijn van 10 : 2 x 5
Erg vermakelijk.
(tvp)
Tot zover mijn boerenverstand.quote:Op donderdag 19 november 2009 18:43 schreef thabit het volgende:
[..]
25 lijkt mij conceptueel gezien het beste antwoord.
10 : (2x5) = 1
| ❤ | Triquester... | ツ Met een accént aigu
Niet iedereen was ervan overtuigd dat de uitkomst vroeger anders was dan nuquote:Op donderdag 19 november 2009 18:38 schreef Riparius het volgende:
[..]
Niet alleen vermakelijk, maar ook verwarrend. Ik weet niet hoe goed jijzelf en je gesprekspartners waren ingevoerd, maar het idiote is dat de uitkomst vroeger anders was dan nu, als gevolg van andere regels.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Delen is het "omgekeerde" van vermenigvuldigen, daarom zijn ze gelijkwaardig.quote:
[..]
Tot zover mijn boerenverstand.
10 : (2x5) = 1
Van links naar rechts dus uitvoeren, dus 25.
En met die haken verander je dus de som.
Hetgeen bewezen en beklonken moest worden.
Ja, 25. Dat weet ik, maar zoals hij er bij mij staat had anders ook nog GEKUND... Want als je hem noemt: '10 gedeeld door 2 maal 5' dan noem je woordelijk de haken niet, maar zo kan je hem wel invullen.quote:
[..]
Delen is het "omgekeerde" van vermenigvuldigen, daarom zijn ze gelijkwaardig.
Van links naar rechts dus uitvoeren, dus 25.
Ik ga me er nu al aan irriteren dat ik dit topic in mijn MyAT heb staan
| ❤ | Triquester... | ツ Met een accént aigu
waar komt die "=" vandaan?quote:
[..]
Maar dat doe ik toch?
2^k x 2 = (k+2)!
Rechterkant wordt dan: (k+2)((k+1)!
En dan hoef ik alleen te bewijzen dat 2 kleiner gelijk (k+2)
die doe je niet algebraïsch.quote:
Ik word helemaal gek.. hoe kan ik deze vergelijking oplossen, weet iemand dat??
x0.5 - 0.75(x + 720)0.5 = 9
heb de wortels voor het gemak even vervangen door een 0.5de macht. Ik heb echt al van alles geprobeerd, maar ik weet niet hoe ik dit moet aanpakken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
numeriek, elke gekke methode voldoet welquote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hij kan volgens mij wel algebraisch opgelost worden.
Haal eerst 1 van de twee worteltermen naar 1 kant toe, kwadrateer de vergelijking, dan heb je nog 1 wortelterm over, die kun je op dezelfde manier wegkwadrateren.
Haal eerst 1 van de twee worteltermen naar 1 kant toe, kwadrateer de vergelijking, dan heb je nog 1 wortelterm over, die kun je op dezelfde manier wegkwadrateren.
8 } aan elkaar vast.
Ik moet de rest van de toetsencombinaties nog hebben. (a.u.b.)
Ik moet de rest van de toetsencombinaties nog hebben. (a.u.b.)
Hetgeen bewezen en beklonken moest worden.
Ik volg momenteel een vak: gewone differentiaalvergelijkingen, de opvolger op t vak: nummerieke methode waar ik zojuist een 3 van terug heb:( Die natuurkunde-achtige vakken liggen me niet zo.
Een vraag waar ik helemaal niks van kon maken:
Exercise 1.9. Solutions may cease to exist because u'(t) tends to infinity without blow-up of u.
(a)Derive the solutions of u'=2t/(u-1). On what interval I do they exsist?
Make a sketch of the solutions in the (t,u)-plane.
(b) Do the same fot the differential equation u'=-t/u
Hoe pak je zoiets aan??
Een vraag waar ik helemaal niks van kon maken:
Exercise 1.9. Solutions may cease to exist because u'(t) tends to infinity without blow-up of u.
(a)Derive the solutions of u'=2t/(u-1). On what interval I do they exsist?
Make a sketch of the solutions in the (t,u)-plane.
(b) Do the same fot the differential equation u'=-t/u
Hoe pak je zoiets aan??
Dat weet je toch wel ?? (wat heb je anders gedaan als voorbereiding).quote:Op donderdag 19 november 2009 22:44 schreef marleenhoofd- het volgende:
hoe?
Je hebt:
u' = 2t/(u-1)
Hiervoor is te schrijven:
du/dt = 2t/(u-1)
En dus ook:
(u-1)du = 2tdt
Nu beide leden integreren en je krijgt:
½u2 - u = t2 + c
Nu wil je u uitdrukken als functie van t, dus moet je hieruit u oplossen. Nu jij weer.
Dankjewel, als voorbereiding heb ik het dictaat doorgespit, maar dat laat nogal de wensen aan zich over. Ik weet bijna niks van differentiaal vergelijkingen. Je snappen zijn echter simpel, hier kom ik uiteraard wel uit.quote:Op donderdag 19 november 2009 22:48 schreef Riparius het volgende:
[..]
Dat weet je toch wel ?? (wat heb je anders gedaan als voorbereiding).
Je hebt:
u' = 2t/(u-1)
Hiervoor is te schrijven:
du/dt = 2t/(u-1)
En dus ook:
(u-1)du = 2tdt
Nu beide leden integreren en je krijgt:
½u2 - u = t2 + c
Nu wil je u uitdrukken als functie van t, dus moet je hieruit u oplossen. Nu jij weer.
Nog een wellicht simpele vraag waar ik niet uitkom:
Exercise 1.5. Find explicit solutions of u'=(u-a)(u-b), by transforming it to a Bernoulli type equation.
Ik denk dat dit de Bernoulli type is (gewoon haakjes uitsschrijven) u'=p(t)u + q(t)u2 + ab
met p(t)=-a-b q(t)=1, maar mag die +ab er zomaar bij?
en hoe los je dit dan op??
Ik verwacht overigens niet dat jullie hier veel tijd in gaan stoppen want dat heb ik zelf nog niet genoeg gedaan. Maar mocht t ook weer zo simpel zijn:O
Exercise 1.5. Find explicit solutions of u'=(u-a)(u-b), by transforming it to a Bernoulli type equation.
Ik denk dat dit de Bernoulli type is (gewoon haakjes uitsschrijven) u'=p(t)u + q(t)u2 + ab
met p(t)=-a-b q(t)=1, maar mag die +ab er zomaar bij?
en hoe los je dit dan op??
Ik verwacht overigens niet dat jullie hier veel tijd in gaan stoppen want dat heb ik zelf nog niet genoeg gedaan. Maar mocht t ook weer zo simpel zijn:O
Ik neem aan dat a en b hier constanten zijn. Nee, die ab mag er niet 'zomaar' bij want dan is het geen Bernoulli dv meer. Simple as that. Je moet dus iets anders verzinnen, en het wordt ook gesuggereerd wat. Je moet de dv eerst transformeren door een geschikte substitutie toe te passen, zodat ie wel de gewenste vorm krijgt.quote:Op donderdag 19 november 2009 23:03 schreef marleenhoofd- het volgende:
Nog een wellicht simpele vraag waar ik niet uitkom:
Exercise 1.5. Find explicit solutions of u'=(u-a)(u-b), by transforming it to a Bernoulli type equation.
Ik denk dat dit de Bernoulli type is (gewoon haakjes uitsschrijven) u'=p(t)u + q(t)u2 + ab
met p(t)=-a-b q(t)=1, maar mag die +ab er zomaar bij?
en hoe los je dit dan op??
Neem bijvoorbeeld:
v = u - b,
waarbij v je nieuwe afhankelijke variabele is. Aangezien functies die slechts een constante verschillen dezelfde afgeleide hebben, geldt u' = v', en dus krijgen we dan:
v' = (v + b - a)v
v' = v2 + (b-a)v
v' + (a-b)v = v2
Voila.
Gewoon een beetje creatief zijn.quote:Ik verwacht overigens niet dat jullie hier veel tijd in gaan stoppen want dat heb ik zelf nog niet genoeg gedaan. Maar mocht t ook weer zo simpel zijn:O
hier ga ik even een tvp plaatsen, de tentamenweken komen er toch alweer aan 
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
hij is uiteindelijk toch algebraisch opgelostquote:Op donderdag 19 november 2009 19:41 schreef GlowMouse het volgende:
[..]
waar komt die "=" vandaan?
[..]
die doe je niet algebraïsch.
ik ben het mannetje in de chinese kamer
Van Wikipedia:quote:Op donderdag 19 november 2009 16:36 schreef GoodGawd het volgende:
[ afbeelding ]
Vraag:
De 4e regel zie je dat -y'' (0)
Waarom is dat?
Algemeen voor hogere afgeleiden:
Hij was maar een clown...
Zijn er eigenlijk efficiëntere kortstepad-algoritmen dan het kortstepad-algoritme van Dijkstra? Google geeft in dit geval weinig tot geen uitsluitsel.
Voor zover ik weet niet, maar als je negatieve lengtes hebt of een korste pad wilt weten van elk punt naar elk ander punt dan is Dijkstra niet te gebruiken of niet het snelste.quote:
Zijn er eigenlijk efficiëntere kortstepad-algoritmen dan het kortstepad-algoritme van Dijkstra? Google geeft in dit geval weinig tot geen uitsluitsel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kan iemand mij uitleggen waarom de steekproefmediaan niet precies is, met de empirische verdelingsfunctie?
Ik zat vandaag op school wiskunde sommen te maken en was op een gegeven moment dergelijke huisjes aan het tekenen:
De kunst van deze huisjes is dat ze op een paar manieren getekend kunnen worden zonder je pen van het papier te halen. Hierover heb ik twee vraagjes waar jullie misschien wel antwoord op hebben:
1) Hoe heet een dergelijk huisje? Dan kan ik het tenminste googlen
2) Is dit ooit al eens wiskundig vraagstuk geweest van een bekende wiskundige? Ik moet een PO maken die ik hier eventueel over kan houden. Ik weet dat Euler wel een dergelijk vraagstuk heeft opgelost met bruggen in Kralinigrad, maar of dat onder dezelfde noemer valt, weet ik niet.
Alvast thnx voor jullie antwoord
p.s. Don't mention mijn teken skillz0rz
De kunst van deze huisjes is dat ze op een paar manieren getekend kunnen worden zonder je pen van het papier te halen. Hierover heb ik twee vraagjes waar jullie misschien wel antwoord op hebben:
1) Hoe heet een dergelijk huisje? Dan kan ik het tenminste googlen
2) Is dit ooit al eens wiskundig vraagstuk geweest van een bekende wiskundige? Ik moet een PO maken die ik hier eventueel over kan houden. Ik weet dat Euler wel een dergelijk vraagstuk heeft opgelost met bruggen in Kralinigrad, maar of dat onder dezelfde noemer valt, weet ik niet.
Alvast thnx voor jullie antwoord
p.s. Don't mention mijn teken skillz0rz
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
- de mediaan hoeft niet te bestaanquote:
Kan iemand mij uitleggen waarom de steekproefmediaan niet precies [ afbeelding ] is, met [ afbeelding ] de empirische verdelingsfunctie?
[ afbeelding ]
- F is niet strict stijgend, hoe definieer de inverse?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dit is precies het probleem van de Zeven bruggen van Koningsbergen.quote:Op vrijdag 20 november 2009 22:03 schreef beertenderrr het volgende:
Ik zat vandaag op school wiskunde sommen te maken en was op een gegeven moment dergelijke huisjes aan het tekenen:
[ afbeelding ]
De kunst van deze huisjes is dat ze op een paar manieren getekend kunnen worden zonder je pen van het papier te halen. Hierover heb ik twee vraagjes waar jullie misschien wel antwoord op hebben:
1) Hoe heet een dergelijk huisje? Dan kan ik het tenminste googlen
2) Is dit ooit al eens wiskundig vraagstuk geweest van een bekende wiskundige? Ik moet een PO maken die ik hier eventueel over kan houden. Ik weet dat Euler wel een dergelijk vraagstuk heeft opgelost met bruggen in Kralinigrad, maar of dat onder dezelfde noemer valt, weet ik niet.
Alvast thnx voor jullie antwoord
p.s. Don't mention mijn teken skillz0rz
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Waarom tel ik dan vijf hoekpuntenquote:
[..]
Dit is precies het probleem van de Zeven bruggen van Koningsbergen.
Hetgeen bewezen en beklonken moest worden.
Dat het probleem hetzelfde is, betekent toch niet dat de instance ook hetzelfde is?quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat is een semantisch probleem.quote:
[..]
Dat het probleem hetzelfde is, betekent toch niet dat de instance ook hetzelfde is?
Dit is geen huisje.
Hetgeen bewezen en beklonken moest worden.
Ok, dan neem ik dat mee voor mijn opdrachtquote:Op vrijdag 20 november 2009 23:03 schreef GlowMouse het volgende:
[..]
Dit is precies het probleem van de Zeven bruggen van Koningsbergen.
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
1) Wanneer bestaat de mediaan dan niet?quote:Op vrijdag 20 november 2009 23:01 schreef GlowMouse het volgende:
[..]
1) de mediaan hoeft niet te bestaan
2) F is niet strict stijgend, hoe definieer de inverse?
2) hoeft niet uniek te zijn.
De strekking van het (deel van het) artikel is volgens mij dat F-1(0.5) de mediaan van de populatieverdeling is en dat niet altijd de mediaan van de steekproefverdeling is.
Stel dat we in het geval dat niet uniek is, het midden van het interval als mediaan definiëren.
Wanneer is dan niet de steekproefmediaan?
1. wat is de mediaan van de waarnemingen 1 en 2? Ieder getal tussen 1 en 2 voldoet.
2. wat gebeurt er bij een even aantal waarnemingen?
2. wat gebeurt er bij een even aantal waarnemingen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Van het vierkant ABCD met zijde 6 worden bij de hoekpunten driehoeken weggelaten zodat een regelmatige achthoek ontstaat. Bereken exact de zijde van de achthoek.
Oke nu staat er bij de antwoorden (ik kwam zelf niet erg ver) dat bij de driehoekjes verhoudingen zijn van 1 : 1 : wortel 2 (schuine zijde)
Vanwaar die wortel 2? Kan iemand me dat uitleggen?
Oke nu staat er bij de antwoorden (ik kwam zelf niet erg ver) dat bij de driehoekjes verhoudingen zijn van 1 : 1 : wortel 2 (schuine zijde)
Vanwaar die wortel 2? Kan iemand me dat uitleggen?
Ik raak echt heel erg in de war van deze som:
"Laat I = [-1,1]. Schrijf P2(I) voor de vectorruimte van kwadratische polynomen op I. Op P2 definiëren we het standaardinproduct,
We schrijven P0(I) voor de lineaire deelruimte van P2(I) van polynomen van graad nul op I
a. Geef twee verschillende orthonormale bases van P0(I) "
Een polynoom van graad nul, dat is toch gewoon alleen een los getal? Een basis moet het totale bereik van P0 dan omspannen. Maar P0 is volgens mij ééndimensionaal, dus hoeft de basis ook maar één element te bevatten? Is elke basis dan orthogonaal? En is dus de enige eis dat de norm van het element dat je kiest voor de basis 1 is?
Ik heb zo het vermoeden dat dit niet klopt, want het wordt zo'n gekke som dan. ;x
"Laat I = [-1,1]. Schrijf P2(I) voor de vectorruimte van kwadratische polynomen op I. Op P2 definiëren we het standaardinproduct,
We schrijven P0(I) voor de lineaire deelruimte van P2(I) van polynomen van graad nul op I
a. Geef twee verschillende orthonormale bases van P0(I) "
Een polynoom van graad nul, dat is toch gewoon alleen een los getal? Een basis moet het totale bereik van P0 dan omspannen. Maar P0 is volgens mij ééndimensionaal, dus hoeft de basis ook maar één element te bevatten? Is elke basis dan orthogonaal? En is dus de enige eis dat de norm van het element dat je kiest voor de basis 1 is?
Ik heb zo het vermoeden dat dit niet klopt, want het wordt zo'n gekke som dan. ;x
Onder orthogonaal wordt inderdaad vaak norm 1 verstaan, dus je hebt twee verschillende orthogonale bases. Merk op dat je wel de coëfficienten van de x² en de x moet vermelden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik krijg dan dus en de tweede is hetzelfde maar dan met -wortel(0,5)?
Ik vind een ééndimensionale basis nog een beetje gek. Hoewel een basis voor de nullspace vaak ook ééndimensionaal was natuurlijk.
Ik vind een ééndimensionale basis nog een beetje gek. Hoewel een basis voor de nullspace vaak ook ééndimensionaal was natuurlijk.
Sowieso zijn elementen van deze vectorruimte polynomen en geen kolomvector oid. Een kolomvector wordt het pas als je een basis hebt gekozen.quote:Op zondag 22 november 2009 17:36 schreef Hanneke12345 het volgende:
Ik krijg dan dus [ afbeelding ] en de tweede is hetzelfde maar dan met -wortel(0,5)?
Ik vind een ééndimensionale basis nog een beetje gek. Hoewel een basis voor de nullspace vaak ook ééndimensionaal was natuurlijk.
De norm moet 1 izijn. Het inproduct dus |1|
p(x), q(x) = a
a2*1 - a2*-1 = |1|
2a2=|1|
a2=|1/2|
Toch?
[ Bericht 6% gewijzigd door Hanneke12345 op 22-11-2009 18:09:06 ]
p(x), q(x) = a
a2*1 - a2*-1 = |1|
2a2=|1|
a2=|1/2|
Toch?
[ Bericht 6% gewijzigd door Hanneke12345 op 22-11-2009 18:09:06 ]
Ohja, andersom. Zal het even editten. ;x
Eerste keer dat ik integralen maak in latex, ging er vanuit dat je eerst de bovenste zou moeten noemen.
Eerste keer dat ik integralen maak in latex, ging er vanuit dat je eerst de bovenste zou moeten noemen.
Ik kom er even niet uit, zal waarschijn ergens iets simpels over het hoofd zien.
Vind de Laplace transformatie van de functie: f(t) = t2
1. Ten eerste vraag ik me af of ik dan met een onbepaalde integraal moet gaan rekenen, of zoals letterlijk elk voorbeeld uit mijn schrift en uit het boek met een integraal van 0 tot oneindig?
2.
Ik heb basically het volgende gedaan: integraal teken = $ hahaha
$ t2 * e-st
En die heb ik lopen integreren (Wat me niet helemaal lukte moet ik zeggen, want ik ging twee keer integreren etc. werd moeilijker dan dat het zou moeten zijn denk ik. En hij staat ook niet in een standaardtabel (voor zover ik kan zien).
Vind de Laplace transformatie van de functie: f(t) = t2
1. Ten eerste vraag ik me af of ik dan met een onbepaalde integraal moet gaan rekenen, of zoals letterlijk elk voorbeeld uit mijn schrift en uit het boek met een integraal van 0 tot oneindig?
2.
Ik heb basically het volgende gedaan: integraal teken = $ hahaha
$ t2 * e-st
En die heb ik lopen integreren (Wat me niet helemaal lukte moet ik zeggen, want ik ging twee keer integreren etc. werd moeilijker dan dat het zou moeten zijn denk ik. En hij staat ook niet in een standaardtabel (voor zover ik kan zien).
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zoals ik al zei, dat wou me niet echt lukken. Ondertussen heb ik al een moeilijker probleem:
f(t) = t * sin (at) ... En dan doen net alsof de functie stapsgewijs continu is. Geen idee hoe je nou dit moet doen. Moet ik iets met die tabel doen. Ik zag ook iets met k(f)t ofzo.. loop helemaal vast.
f(t) = t * sin (at) ... En dan doen net alsof de functie stapsgewijs continu is. Geen idee hoe je nou dit moet doen. Moet ik iets met die tabel doen. Ik zag ook iets met k(f)t ofzo.. loop helemaal vast.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Wacht even, je gooit nu heel veel vragen op het forum. Ik kan hieruit niet goed afleiden waar je nu precies mee vastloopt.
Maar i.e.g. de integraal van t2*e-2t. Deze lijkt erop dat je die met partieël integreren kunt oplossen.
Maar i.e.g. de integraal van t2*e-2t. Deze lijkt erop dat je die met partieël integreren kunt oplossen.
kloep kloep
google op eulergrafen ofzo. Het heeft te maken met het aantal wegen dat bij elk kruispunt bij elkaar komt, ik heb nu even geen tijd maar met simpele grafentheorie is dit wel op te lossen.quote:Op vrijdag 20 november 2009 22:03 schreef beertenderrr het volgende:
Ik zat vandaag op school wiskunde sommen te maken en was op een gegeven moment dergelijke huisjes aan het tekenen:
[ afbeelding ]
De kunst van deze huisjes is dat ze op een paar manieren getekend kunnen worden zonder je pen van het papier te halen. Hierover heb ik twee vraagjes waar jullie misschien wel antwoord op hebben:
1) Hoe heet een dergelijk huisje? Dan kan ik het tenminste googlen
2) Is dit ooit al eens wiskundig vraagstuk geweest van een bekende wiskundige? Ik moet een PO maken die ik hier eventueel over kan houden. Ik weet dat Euler wel een dergelijk vraagstuk heeft opgelost met bruggen in Kralinigrad, maar of dat onder dezelfde noemer valt, weet ik niet.
Alvast thnx voor jullie antwoord
p.s. Don't mention mijn teken skillz0rz
De functie die je moet integreren over het interval [0, ∞) is t2∙e-st, waarbij de t de onafhankelijke variabele is. Een primitieve van deze functie is:quote:Op zondag 22 november 2009 19:22 schreef Burakius het volgende:
Ik kom er even niet uit, zal waarschijn ergens iets simpels over het hoofd zien.
Vind de Laplace transformatie van de functie: f(t) = t2
1. Ten eerste vraag ik me af of ik dan met een onbepaalde integraal moet gaan rekenen, of zoals letterlijk elk voorbeeld uit mijn schrift en uit het boek met een integraal van 0 tot oneindig?
2.
Ik heb basically het volgende gedaan: integraal teken = $ hahaha
$ t2 * e-st
En die heb ik lopen integreren (Wat me niet helemaal lukte moet ik zeggen, want ik ging twee keer integreren etc. werd moeilijker dan dat het zou moeten zijn denk ik. En hij staat ook niet in een standaardtabel (voor zover ik kan zien).
-s-3∙(s2∙t2 +2∙s∙t + 2)∙e-st
Integreren van t2∙e-st met als variabele t over het interval [0, ∞) levert dan 2∙s-3, aangezien -s-3∙(s2∙t2 +2∙s∙t + 2)∙e-st nadert tot 0 voor t → ∞, mits s > 0.
[ Bericht 0% gewijzigd door Riparius op 22-11-2009 20:39:25 ]
Je beseft dat dat niet zo makkelijk te primitiveren is he? Je schudt het nu wel even uit je mouw
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Tja, oefening baart kunst. Partieel integreren inderdaad, maar je kunt ook uitgaan van het het product van een algemeen kwadratisch polynoom in t en e-st en dan door differentiëren de juiste coëfficiënten van het polynoom bepalen.quote:Op zondag 22 november 2009 20:43 schreef Burakius het volgende:
Je beseft dat dat niet zo makkelijk te primitiveren is he? Je schudt het nu wel even uit je mouw
Geloof me ik kan goed partieel integreren, maar deze kwam ik toch niet uit....quote:Op zondag 22 november 2009 21:10 schreef Riparius het volgende:
[..]
Tja, oefening baart kunst. Partieel integreren inderdaad, maar je kunt ook uitgaan van het het product van een algemeen kwadratisch polynoom in t en e-st en dan door differentiëren de juiste coëfficiënten van het polynoom bepalen.
ik bleef bij: t^2* -1/s * e^-st - 2 $ t*-1/s *e^-st dt
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Je moet hier herhaald partieel integeren. Kijk even hier voor een voorbeeld waarbij x3∙e-x wordt geïntegreerd.quote:Op zondag 22 november 2009 21:12 schreef Burakius het volgende:
[..]
Geloof me ik kan goed partieel integreren, maar deze kwam ik toch niet uit....
ik bleef bij: t^2* -1/s * e^-st - 2 $ t*-1/s *e^-st dt
Ja dat kan ik ook. Ik geef het op. Dit is echt mijn anti-wiskunde dag. Niets lukt.quote:Op zondag 22 november 2009 21:16 schreef Riparius het volgende:
[..]
Je moet hier herhaald partieel integeren. Kijk even hier voor een voorbeeld waarbij x3∙e-x wordt geïntegreerd.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Kan iemand mij helpen met het volgende? Het gaat over oscillatie.
Stel je hebt het volgende:
Je hebt een muur met een veer eraan (k1), aan die veer zit een massa (m1). Aan deze massa zit weer een veer (k2) met een massa (m2). Elke vorm van wrijving is verwaarloosbaar klein.
(alles is horizontaal, alsof er een tafel onder staat).
|---@----@ (muur->veer->blok->veer->blok)
Zoek nu een berekening om de beweging van beide te berekenen.
Is er iemand in de zaal die natuurkunde of wiskunde heeft gestudeerd/studeert en die een idee heeft hoe we dit kunnen doen?
Stel je hebt het volgende:
Je hebt een muur met een veer eraan (k1), aan die veer zit een massa (m1). Aan deze massa zit weer een veer (k2) met een massa (m2). Elke vorm van wrijving is verwaarloosbaar klein.
(alles is horizontaal, alsof er een tafel onder staat).
|---@----@ (muur->veer->blok->veer->blok)
Zoek nu een berekening om de beweging van beide te berekenen.
Is er iemand in de zaal die natuurkunde of wiskunde heeft gestudeerd/studeert en die een idee heeft hoe we dit kunnen doen?
Op weg naar sint juttemes.
staat dat rechterblok stil ofzo? En waardoor zou het gaan bewegen?
Ik zou beginnen met het opstellen van een differentiaalvergelijking.
Ik zou beginnen met het opstellen van een differentiaalvergelijking.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, hij staat niet stil. Het gaat er meer om dat je waarschijnlijk de formule van de eerste oscillatie (de linker) in de tweede oscillatie moet gaan zetten. Maar ik heb geen idee hoe dit in zijn werk gaat. (evenals de differentiaalvergelijking overigens). Kun je een duwtje in de richting geven?quote:Op zondag 22 november 2009 23:15 schreef GlowMouse het volgende:
staat dat rechterblok stil ofzo? En waardoor zou het gaan bewegen?
Ik zou beginnen met het opstellen van een differentiaalvergelijking.
Op weg naar sint juttemes.
Hey ik moet het "initial value vinden door middel van Laplace. Nu ben ik bezig, maar ik zie één ding wat fout kan zijn in het boek.. of ik zie het echt niet meer.:
Hoe maakt het boek nou van s2 L(y) - s y(0) - y'(0) - s L (y) - y(0) - 2 L (y) = 0
Ook daarna vervangt het boek die L(y) door Y(s) . Nou goed vind ik best. Daarna herschrijft het de formule om Y(s) te vinden. Nou ook niet moeilijk:
(s2 -s -2) Y(s) + (1-s) y(0) - y'(0) = 0
Het gaat om het vetgedrukte. Want als ik dit uitschrijf zet ik daar toch echt (-1 - s ) y(0) .
Is dit een fout van het boek. Lijkt me zeer onwaarschijnlijk. Desondanks moet er toch echt -1 staan om - y(0) te krijgen...
Hoe maakt het boek nou van s2 L(y) - s y(0) - y'(0) - s L (y) - y(0) - 2 L (y) = 0
Ook daarna vervangt het boek die L(y) door Y(s) . Nou goed vind ik best. Daarna herschrijft het de formule om Y(s) te vinden. Nou ook niet moeilijk:
(s2 -s -2) Y(s) + (1-s) y(0) - y'(0) = 0
Het gaat om het vetgedrukte. Want als ik dit uitschrijf zet ik daar toch echt (-1 - s ) y(0) .
Is dit een fout van het boek. Lijkt me zeer onwaarschijnlijk. Desondanks moet er toch echt -1 staan om - y(0) te krijgen...
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Een beetje googelen (en kennis van het Engels) kan geen kwaad. Zoek even op coupled spring-mass system, dan vind je (bijvoorbeeld) dit, waar alles zo'n beetje wordt voorgekauwd.quote:Op zondag 22 november 2009 23:13 schreef kloontje_de_reuzekloon het volgende:
Kan iemand mij helpen met het volgende? Het gaat over oscillatie.
Stel je hebt het volgende:
Je hebt een muur met een veer eraan (k1), aan die veer zit een massa (m1). Aan deze massa zit weer een veer (k2) met een massa (m2). Elke vorm van wrijving is verwaarloosbaar klein.
(alles is horizontaal, alsof er een tafel onder staat).
|---@----@ (muur->veer->blok->veer->blok)
Zoek nu een berekening om de beweging van beide te berekenen.
Is er iemand in de zaal die natuurkunde of wiskunde heeft gestudeerd/studeert en die een idee heeft hoe we dit kunnen doen?
ik vind jou best een toffe kerelquote:Op maandag 23 november 2009 00:45 schreef Riparius het volgende:
[..]
Een beetje googelen (en kennis van het Engels) kan geen kwaad. Zoek even op coupled spring-mass system, dan vind je (bijvoorbeeld) dit, waar alles zo'n beetje wordt voorgekauwd.
heb me helemaal scheel lopen zoeken op internet, alleen blijkbaar met de verkeerde keywords. Bedankt
Op weg naar sint juttemes.
Hey allemaal ,
Ik had in een ander topic de volgende uitwerking gekregen (vergelijking):
5x-y=7
2x+6y=-4
30x-6y=42
2x+6y=-4
----------------------
32+0=38
toen zei hij X is 38/32 en dat is dan weer 19/16 maar waarom moet je dat dan gedeeld door 2 doen ?
en om y uit rekenen werd het volgende geformuleerd:
y=7-95/16 en dat werd dan weer 17/16
hoe kan dat dan opeens 17/16 worden ??
(Het antwoord op y is uiteindelijk -17/16) ???
de vergelijking op zich snap ik wel maar hoe die breuken opeens veranderen snap ik niet.
Bij voorbaat dank.
[ Bericht 67% gewijzigd door CRONALDO7 op 23-11-2009 18:45:02 ]
, Ik had in een ander topic de volgende uitwerking gekregen (vergelijking):
5x-y=7
2x+6y=-4
30x-6y=42
2x+6y=-4
----------------------
32+0=38
toen zei hij X is 38/32 en dat is dan weer 19/16 maar waarom moet je dat dan gedeeld door 2 doen ?
en om y uit rekenen werd het volgende geformuleerd:
y=7-95/16 en dat werd dan weer 17/16
hoe kan dat dan opeens 17/16 worden ?? (Het antwoord op y is uiteindelijk -17/16) ???
de vergelijking op zich snap ik wel maar hoe die breuken opeens veranderen snap ik niet.
Bij voorbaat dank.
[ Bericht 67% gewijzigd door CRONALDO7 op 23-11-2009 18:45:02 ]
Dat delen door 2 doe je in feite niet... het is enkel een breuk vereenvoudigen.
5x-y=7
2x+6y=-4 dit is jouw stelsel
bovenste maal 6:
30x-6y=42
2x+6y=-4
Nu deze optellen:
32x = 38
en x dus gelijk aan 38/32 = 19/16
als x bekend is vul je deze in bij een van de gegeven vergelijkingen uit het stelsel.
Dan hou je een vergelijking met één onbekende over en kun je y uitrekenen. Laat dat nog eens zien.
5x-y=7
2x+6y=-4 dit is jouw stelsel
bovenste maal 6:
30x-6y=42
2x+6y=-4
Nu deze optellen:
32x = 38
en x dus gelijk aan 38/32 = 19/16
als x bekend is vul je deze in bij een van de gegeven vergelijkingen uit het stelsel.
Dan hou je een vergelijking met één onbekende over en kun je y uitrekenen. Laat dat nog eens zien.
kloep kloep
OK bedankt man.
Ja bij die andere gaf die deze berekening:
Vul de gevonden waarden van x in dan krijg je:
5* 19/16-y=7→-y=7-95/16=17/16
We vinden dus Y=-17/16
Hier snap ik het dus helemaal niet want als ik 7-95/16 op mijn calculatot typ krijg ik 1 1/16 dus als iemand mij dit kan uitleggen zal ik dat heel erg apprecieren.
Ja bij die andere gaf die deze berekening:
Vul de gevonden waarden van x in dan krijg je:
5* 19/16-y=7→-y=7-95/16=17/16
We vinden dus Y=-17/16
Hier snap ik het dus helemaal niet want als ik 7-95/16 op mijn calculatot typ krijg ik 1 1/16 dus als iemand mij dit kan uitleggen zal ik dat heel erg apprecieren.
Je moet niet meteen jouw rekenmachine pakken. Op papier uitwerken dan weet je tenminste wat je aan het doen bent.
Afijn, x=19/16 had jij als oplossing.
Jouw stelsel:
5x=y=7
2x+6y=-4
Neem bv de bovenste en vul daar x=19/16 in. Dit levert op:
5*(19/16) -y =7
naar de andere kant brengen
y=5*(19/16)-7
Uitwerken met breuken levert dan y=-17/16.
De gevonden waarden x=19/16 en y=-17/16 kun je invullen in de tweede vergelijking van het stelsel om te zien of jouw oplossingen kloppen. En inderdaad dit klopt.
Mocht het breuken uitwerken niet lukken laat het dan nog even weten.
Afijn, x=19/16 had jij als oplossing.
Jouw stelsel:
5x=y=7
2x+6y=-4
Neem bv de bovenste en vul daar x=19/16 in. Dit levert op:
5*(19/16) -y =7
naar de andere kant brengen
y=5*(19/16)-7
Uitwerken met breuken levert dan y=-17/16.
De gevonden waarden x=19/16 en y=-17/16 kun je invullen in de tweede vergelijking van het stelsel om te zien of jouw oplossingen kloppen. En inderdaad dit klopt.
Mocht het breuken uitwerken niet lukken laat het dan nog even weten.
kloep kloep
Om even te refereren naar een vorige post..
Beide (onder en boven de zwarte lijn) vind ik namelijk wel goed. Is het alleen de Ln of Log?
Had alleen nog wat vraagjes, de standard error is gewoon Ln alpha/log alpha right?
En het is toch een lineaire formule? (vanwege de 2 variabelen?). Ik dacht namelijk dat een least squares methode moest voldoen aan onderstaand. Waar dus slechts 1 variabele inzit, en niet 2.
En wat is eigenlijk de vuistregel dat je de formule moet omturnen naar een logaritme zodat hij aan de Least squares methode voldoet?
Ik kan dat niet in mn boek terugvinden 
quote:Op maandag 9 november 2009 00:54 schreef sitting_elfling het volgende:
Kan iemand me hier helpen met een opstapje? Heb een vaag idee waar ik ong. moet uitkomen in de stappen die ik moet doen, maar weet absoluut niet hoe ik moet beginnen. Hoe turn ik het zo om dat het berekend kan worden door de LSR?
[ ]
]Ik vraag me af of ik in de juiste richting zit te denken?quote:
Beide (onder en boven de zwarte lijn) vind ik namelijk wel goed. Is het alleen de Ln of Log?
Had alleen nog wat vraagjes, de standard error is gewoon Ln alpha/log alpha right?
En het is toch een lineaire formule? (vanwege de 2 variabelen?). Ik dacht namelijk dat een least squares methode moest voldoen aan onderstaand. Waar dus slechts 1 variabele inzit, en niet 2.
En wat is eigenlijk de vuistregel dat je de formule moet omturnen naar een logaritme zodat hij aan de Least squares methode voldoet?
Ik kan dat niet in mn boek terugvinden
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
log is ln.
De standard error in het normale model kun je niet meer bepalen.
LS is b0 + b1x1 + b2x2 + ... + bnxn. Mogen best veel x'en in terugkomen, mits allemaal lineair.
En de logaritme werkt bij functies die eruit zien zoals de jouwe.
De standard error in het normale model kun je niet meer bepalen.
LS is b0 + b1x1 + b2x2 + ... + bnxn. Mogen best veel x'en in terugkomen, mits allemaal lineair.
En de logaritme werkt bij functies die eruit zien zoals de jouwe.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ja, je bewijs klopt, maar je zou t een stuk eenvoudiger en overzichtelijker op kunnen schrijven.quote:Op vrijdag 20 november 2009 19:46 schreef Siddartha het volgende:
Nieuwe rondes, nieuwe kansen!
Het bewijs, voor x>-1 en n bestaat uit alleen uit natuurlijke getallen, dat
[ afbeelding ]
We nemen aan dat P(k) waar is (vervang n door k).
Dan kijken we of het ook voor elk volgende k waar is, dus voor P(k+1).
Als we P(k+1) in de linkerkant invullen, zien we dat we het ook anders kunnen schrijven:
[ afbeelding ]
De factor om k+1 te krijgen is (1+x), dus kunnen we de rechterkant daarmee ook vermenigvuldigen en als het bewijs klopt, kan je de rechterkant tot deze vorm omschrijven (wanneer je gewoon (k+1) had ingevuld):
[ afbeelding ]
Of de uitkomst die je dan krijgt moet groter zijn dat bovenstaande vergelijking, omdat we niet willen weten of ze gelijk aan elkaar zijn maar groter/gelijk.
Dus:
[ afbeelding ]
Dat kun je zo opschrijven:
[ afbeelding ]
Dan zie je dat het eerste deel gelijk is aan gewoon p(k+1) invullen, maar dan staat er nog kx^2 achter.
En omdat kx^2 in dit geval altijd groter/gelijk is aan 0, moet deze verandering dus groter/gelijk zijn aan
[ afbeelding ]
Dan volgt alleen nog P(k) te controleren voor een willekeurig getal, P(1) klopt.
Dus, het bewijs klopt.
( Sorry dat ik zo langdradig/uitgebreid schrijf, maar ik wil graag weten of de stappen die ik neem kloppen.)
+1 for stupidquote:Op maandag 23 november 2009 22:10 schreef GlowMouse het volgende:
log is ln.
Dom, dom. Ik heb continu een verschil tussen die 2 in mn hoofd. Begrijp ik nu iig Waarom kun je de standard error niet meer bepalen? Kun je niet gewoon zeggen dat Ln Alpha de standard error is?quote:De standard error in het normale model kun je niet meer bepalen.
LS is b0 + b1x1 + b2x2 + ... + bnxn. Mogen best veel x'en in terugkomen, mits allemaal lineair.
En de logaritme werkt bij functies die eruit zien zoals de jouwe.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ja uiteraard, maar met normaal bedoel ik het oorspronkelijke model.quote:
[..]
Waarom kun je de standard error niet meer bepalen? Kun je niet gewoon zeggen dat Ln Alpha de standard error is?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik doe een HBO opleiding en daar wordt alle stof nog eens behandeld van het voortgezet onderwijs. Nu zit ik mijn hersenen al de hele avond te pijnigen op iets wat ik altijd behoorlijk simpel vond, wie kan deze vraag uitleggen?
Het volgende wordt gevraagd: Bepaal de vergelijking y = ax^2 + bx + c van de parabool
Gegeven zijn de top (2,-1) en het punt waar de grafiek doorheen gaat (1,1).
Wie kan dit uitleggen?
Het volgende wordt gevraagd: Bepaal de vergelijking y = ax^2 + bx + c van de parabool
Gegeven zijn de top (2,-1) en het punt waar de grafiek doorheen gaat (1,1).
Wie kan dit uitleggen?
Als je de punten gewoon invult, welke twee vergelijkingen heb je dan?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ken je de formule voor de x-coordinaat van de top nog? x=2 daar invullen, krijg je een vgl voor a, b en c. Verder ken je 2 punten, die allebei invullen => nog twee vgl'en voor a, b en c. Drie vergelijkingen, 3 onbekenden.
Inderdaad. En laat ik dat nu allemaal al voor hem gedaan hebben ook, dus ik begrijp de behoefte van Siddhartha aan een nieuwe ronde niet zo.quote:Op maandag 23 november 2009 22:26 schreef marleenhoofd- het volgende:
[..]
ja, je bewijs klopt, maar je zou t een stuk eenvoudiger en overzichtelijker op kunnen schrijven.
Begin even met het doornemen van deze uitwerking. Niet helemaal hetzelfde type opgave als jouw opgave, maar je kunt er wel ideeën uit opdoen over manieren waarop je te werk kunt gaan.quote:Op maandag 23 november 2009 22:41 schreef Babbbe het volgende:
Ik doe een HBO opleiding en daar wordt alle stof nog eens behandeld van het voortgezet onderwijs. Nu zit ik mijn hersenen al de hele avond te pijnigen op iets wat ik altijd behoorlijk simpel vond, wie kan deze vraag uitleggen?
Het volgende wordt gevraagd: Bepaal de vergelijking y = ax^2 + bx + c van de parabool
Gegeven zijn de top (2,-1) en het punt waar de grafiek doorheen gaat (1,1).
Wie kan dit uitleggen?
Ja klopt maar dit begrijp ik juist niet:
y=5*(19/16)-7
Uitwerken met breuken levert dan y=-17/16.
Wat doet u precies om op 17/16 uit te komen ? 19-7+5 ofzo ?
y=5*(19/16)-7
Uitwerken met breuken levert dan y=-17/16.
Wat doet u precies om op 17/16 uit te komen ? 19-7+5 ofzo ?
quote:Op maandag 23 november 2009 20:46 schreef Borizzz het volgende:
Je moet niet meteen jouw rekenmachine pakken. Op papier uitwerken dan weet je tenminste wat je aan het doen bent.
Afijn, x=19/16 had jij als oplossing.
Jouw stelsel:
5x=y=7
2x+6y=-4
Neem bv de bovenste en vul daar x=19/16 in. Dit levert op:
5*(19/16) -y =7
naar de andere kant brengen
y=5*(19/16)-7
Uitwerken met breuken levert dan y=-17/16.
De gevonden waarden x=19/16 en y=-17/16 kun je invullen in de tweede vergelijking van het stelsel om te zien of jouw oplossingen kloppen. En inderdaad dit klopt.
Mocht het breuken uitwerken niet lukken laat het dan nog even weten.
Ja klopt maar dit begrijp ik juist niet:
y=5*(19/16)-7
Uitwerken met breuken levert dan y=-17/16.
Wat doet u precies om op 17/16 uit te komen ? 19-7+5 ofzo ?
Dit is echt gewoon lagere school werk (rekenen met breuken). Ik zie trouwens dat je meer dan twee maanden geleden ook al vragen had over precies dezelfde opgave en ook toen kon je al niet overweg met breuken. Dat betekent dus dat je al die tijd geen enkele vordering hebt gemaakt. Dat is vrij treurig, en dan druk ik me nog eufemistisch uit. Hoeveel uren heb je de afgelopen 2½ maand aan wiskunde besteed?quote:Op dinsdag 24 november 2009 00:49 schreef CRONALDO7 het volgende:
Ja klopt maar dit begrijp ik juist niet:
y=5*(19/16)-7
Uitwerken met breuken levert dan y=-17/16.
Wat doet u precies om op 17/16 uit te komen ? 19-7+5 ofzo ?
We hadden al gevonden dat:
x = 19/16
Volgens de eerste vergelijking geldt ook:
5x - y = 7,
en dus ook:
y = 5x - 7
Invullen van x = 19/16 geeft dan:
y = 5∙(19/16) - 7
En dus:
y = 95/16 - 7
Nu moet je het getal 7 schrijven als een breuk met noemer 16 om dit van 95/16 af te kunnen trekken. We hebben 7∙16 = 112, en dus 7 = 112/16. Zodoende krijgen we dan:
y = 95/16 - 112/16
y = (95 - 112)/16
y = -17/16
Excuses daarvoor, maar ik probeerde puur voor mezelf de logica achter de stappen te zien. En wilde graag weten of die logica goed was. Ik had misschien beter een ander bewijs kunnen nemen, maar omdat ik toch al een hele tijd met dat bezig was...quote:Op maandag 23 november 2009 22:46 schreef Riparius het volgende:
[..]
Inderdaad. En laat ik dat nu allemaal al voor hem gedaan hebben ook, dus ik begrijp de behoefte van Siddhartha aan een nieuwe ronde niet zo.
Nogmaals erg bedankt voor je heldere uitleg, nu snap ik het
.
Dank!quote:Op maandag 23 november 2009 22:34 schreef GlowMouse het volgende:
[..]
Ja uiteraard, maar met normaal bedoel ik het oorspronkelijke model.
Maakt het overigens nog uit, of je van een 2d of 3d lineair model uitgaat? Of is dat laatste hier niet van toepassing?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ja, daar had iemand het over. Die twijfelde over of je nu een 2d of 3d model moest toepassen. Ik was niet eens bekend met die termenquote:
Dit is pas mijn 1e periode met econometrie, alles nieuw. Men verwacht hier dat zo'n 35% a 45% hier faalt op het econometrie vak. Met een professor die verder geen erg duidelijke antwoorden geeft hoe je de vragen correct moet beantwoorden
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ik kan niet vinden wat nu precies het verschil is tussen het cartesisch product en een concatenatie in de logica. Iemand hier die me kan helpen?
Dankjewel Riparius!quote:Begin even met het doornemen van deze uitwerking. Niet helemaal hetzelfde type opgave als jouw opgave, maar je kunt er wel ideeën uit opdoen over manieren waarop je te werk kunt gaan.
Je hebt:quote:Op woensdag 25 november 2009 17:09 schreef poesemuis het volgende:
(1/3)^x . (1/3)^(-2) = 1/ (3^x) . 9
zou iemand deze stap voor me op kunnen helderen? alvast bedankt
(1/3)x∙(1/3)-2
Dit is een kwestie van wat elementaire rekenregels voor machten en breuken toepassen, meer niet.
Voor de eerste factor maak je gebruik van:
(a/b)p = ap/bp
Dus krijg je: (1/3)x = 1x/3x = 1/3x (want 1x = 1).
Voor de tweede factor zou je hetzelfde kunnen doen, dus:
(1/3)-2 = 1-2/3-2 = 1/3-2. Nu kun je teller en noemer van deze breuk nog vermenigvuldigen met 32 om die 3-2 in de noemer kwijt te raken. Daarbij maken we gebruik van de regenregel:
ap∙aq = ap+q
In de noemer van de breuk krijg je dan 1, want 3-2∙32 = 30 = 1. Dus hebben we:
1/3-2 = 32/1 = 9/1 = 9.
[ Bericht 0% gewijzigd door Riparius op 25-11-2009 17:48:42 ]
differentier : 1/ x(ln x) ^p
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Begin even met hiervoor te schrijven:quote:Op woensdag 25 november 2009 18:11 schreef Burakius het volgende:
differentieer : 1/ x(ln x) ^p
x-1∙(ln x)-p
(Tenminste, ik neem aan dat je oorspronkelijke notatie hiermee equivalent is). Dan gewoon productregel en kettingregel toepassen.
Hey Riparius,
Hartelijk bedankt voor je uitgebreide hulp !!
En om even terug te komen op je vraag:
Het ligt allemaal vrij gecompliceerd, ik studeer namelijk Management, Economie en Recht, ik zit nu in jaar 2 maar ik heb een tentamen uit jaar 1 niet gehaald en dat vak heet Kwantitatieve Methoden waar al mijn vragen dus op gebasseerd zijn, aan het eind van deze periode heb ik een herkansing van dit vak mocht ik hem dan nog niet halen dan heb ik nog een kans maar als die 2e kans dan onvoldoende is, dan krijg ik een SBA ( Studie Bindend Advies) in dit geval moet ik van school af.
Daarom is het voor mij zaak om alle details te weten over die sommen, en ik heb geen les meer in dit vak dus daarom heb ik er niet veel tijd aan besteed in de door jou genoemde intervalperiode, mede doordat ik ook gewoon tentamens en projecten in het 2e jaar moet leren/maken. En breuken heb ik nooit goed onder de knie gehad, maar dat was je vast al duidelijk: ik ben meer van de ''letters''
Dus dat is eigenlijk de situatie in een notendop, ik hoop dat je het een beetje begrijpt.
Met vriendelijke groet,
Mitch.
Hartelijk bedankt voor je uitgebreide hulp !!
En om even terug te komen op je vraag:
Het ligt allemaal vrij gecompliceerd, ik studeer namelijk Management, Economie en Recht, ik zit nu in jaar 2 maar ik heb een tentamen uit jaar 1 niet gehaald en dat vak heet Kwantitatieve Methoden waar al mijn vragen dus op gebasseerd zijn, aan het eind van deze periode heb ik een herkansing van dit vak mocht ik hem dan nog niet halen dan heb ik nog een kans maar als die 2e kans dan onvoldoende is, dan krijg ik een SBA ( Studie Bindend Advies) in dit geval moet ik van school af.
Daarom is het voor mij zaak om alle details te weten over die sommen, en ik heb geen les meer in dit vak dus daarom heb ik er niet veel tijd aan besteed in de door jou genoemde intervalperiode, mede doordat ik ook gewoon tentamens en projecten in het 2e jaar moet leren/maken. En breuken heb ik nooit goed onder de knie gehad, maar dat was je vast al duidelijk: ik ben meer van de ''letters''
Dus dat is eigenlijk de situatie in een notendop, ik hoop dat je het een beetje begrijpt.
Met vriendelijke groet,
Mitch.
Ah, zo. Ik vermoedde al dat je het tentamen waar die lineaire vergelijkingen bij te pas komen moest herkansen. Maar het heeft weinig zin om steeds dezelfde paar opgaven te blijven herkauwen. Probeer wat meer oude tentamens te pakken te krijgen en ga daarmee oefenen. Of verzin zelf wat stelsels van lineaire vergelijkingen en probeer die dan op te lossen. Lees ook even dit artikel door (hoewel dat veel te ver gaat voor jouw doeleinden). Als je wil controleren of je de juiste oplossing hebt gevonden kun je een stelsel lineaire vergelijkingen ook hier invoeren. En ja, of het nou zo verstandig is om een studie met economie erin te kiezen als je meer van de letteren bent ... Dan lijkt me een typische α-studie toch een stuk bevredigender.quote:Op donderdag 26 november 2009 01:11 schreef CRONALDO7 het volgende:
Hey Riparius,
Hartelijk bedankt voor je uitgebreide hulp !!
En om even terug te komen op je vraag:
Het ligt allemaal vrij gecompliceerd, ik studeer namelijk Management, Economie en Recht, ik zit nu in jaar 2 maar ik heb een tentamen uit jaar 1 niet gehaald en dat vak heet Kwantitatieve Methoden waar al mijn vragen dus op gebasseerd zijn, aan het eind van deze periode heb ik een herkansing van dit vak mocht ik hem dan nog niet halen dan heb ik nog een kans maar als die 2e kans dan onvoldoende is, dan krijg ik een SBA ( Studie Bindend Advies) in dit geval moet ik van school af.
Daarom is het voor mij zaak om alle details te weten over die sommen, en ik heb geen les meer in dit vak dus daarom heb ik er niet veel tijd aan besteed in de door jou genoemde intervalperiode, mede doordat ik ook gewoon tentamens en projecten in het 2e jaar moet leren/maken. En breuken heb ik nooit goed onder de knie gehad, maar dat was je vast al duidelijk: ik ben meer van de ''letters''
Dus dat is eigenlijk de situatie in een notendop, ik hoop dat je het een beetje begrijpt.
Met vriendelijke groet,
Mitch.
De afgeleide van f(x) = xe^x + 4 is volgens mijn antwoorden e^x(x+1)
terwijl het volgens mij moet zijn:
f'(x) = 1(e^x + 4) + x(e^x)
= e^x + 4 + xe^x
in de antwoorden wordt de +4 zeg maar volledig genegeerd. is dit een of andere regel en zie ik iets over het hoofd of heeft het antwoordenboekje het fout?
terwijl het volgens mij moet zijn:
f'(x) = 1(e^x + 4) + x(e^x)
= e^x + 4 + xe^x
in de antwoorden wordt de +4 zeg maar volledig genegeerd. is dit een of andere regel en zie ik iets over het hoofd of heeft het antwoordenboekje het fout?
Als er x(e^x + 4) stond, had je gelijk. Nu heb je f(x)g(x)+4 met f(x)=x en g(x)=e^x. De afgeleide is dus de afgeleide van f(x)g(x) plus de afgeleide van 4.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
nee dat stond er niet, geen haakjes in de originele formule. dus altijd als je een formule hebt met e en een x en een +(normaal getal) kun je dat gewoon buiten beschouwing laten (aangezien de afgeleide daarvan altijd 0 is) en hoef je die niet te betrekken in f(x) of g(x)? want als je de productregel toepast op een formule zonder e doe je dat wel toch?quote:Op donderdag 26 november 2009 21:45 schreef GlowMouse het volgende:
Als er x(e^x + 4) stond, had je gelijk. Nu heb je f(x)g(x)+4 met f(x)=x en g(x)=e^x. De afgeleide is dus de afgeleide van f(x)g(x) plus de afgeleide van 4.
dat is 3x^5 + 4 en heeft afgeleide 15x^4.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kansrekeningvraagje, nouja een klein onderdeel ervan...
Je hebt een vaas met een rode en een blauwe knikker, als je rood pakt ben je klaar, als je blauw pakt moet je hem terugleggen met nog een blauwe erbij. De kans dat je na 1 keer trekken klaar bent is dus 1/2, dat je met precies 2 keer trekken klaar bent (1-1/2)*(1/3) = 1/6, de kans dat je na 3 keer trekken klaar bent is (1-(1/2+1/6))*(1/4) enzovoorts. Nu moet ik aantonen dat de kans dat je in n keer klaar bent gelijk is aan 1/(n(n+1)). Die 1/(n+1) is logisch, dat is de kans dat je als je in die positie bent beland je een rode bal trekt. Die 1/n is de kans dat je nog niet klaar was bij de eerste n-1 trekkingen, dit is opgebouwd uit:
1 - (1/2 + 1/6 + 1/10 ...) = 1 - Som van i=1 tot n ( 1 / (4i - 2 ) ) en dit moet dus gelijk zijn aan 1/n, maar hier kom ik niet uit. Hoe kan ik dit aantonen?
Je hebt een vaas met een rode en een blauwe knikker, als je rood pakt ben je klaar, als je blauw pakt moet je hem terugleggen met nog een blauwe erbij. De kans dat je na 1 keer trekken klaar bent is dus 1/2, dat je met precies 2 keer trekken klaar bent (1-1/2)*(1/3) = 1/6, de kans dat je na 3 keer trekken klaar bent is (1-(1/2+1/6))*(1/4) enzovoorts. Nu moet ik aantonen dat de kans dat je in n keer klaar bent gelijk is aan 1/(n(n+1)). Die 1/(n+1) is logisch, dat is de kans dat je als je in die positie bent beland je een rode bal trekt. Die 1/n is de kans dat je nog niet klaar was bij de eerste n-1 trekkingen, dit is opgebouwd uit:
1 - (1/2 + 1/6 + 1/10 ...) = 1 - Som van i=1 tot n ( 1 / (4i - 2 ) ) en dit moet dus gelijk zijn aan 1/n, maar hier kom ik niet uit. Hoe kan ik dit aantonen?
"Reality is an illusion created by a lack of alcohol."
dat doe je snelquote:Op donderdag 26 november 2009 21:58 schreef GlowMouse het volgende:
dat is 3x^5 + 4 en heeft afgeleide 15x^4.
. oke dus dan laat je ook die +4 buiten beschouwing tenzij het tussen haakjes staat.oh wacht, dat was natuurlijk een stom voorbeeld omdat je die kon vereenvoudigen waar je bij staat
Gewoon uitvermenigvuldigen poesemuis, en dan differentieer je de 4 maar aangezien dat een constante is gaat die gewoon naar 0.
"Reality is an illusion created by a lack of alcohol."
Je doet het verkeerd. De kans dat je 2x blauw achter elkaar trekt is 1/2 * 2/3. 3x blauw achter elkaar gaat met kans 1/2*2/3*3/4.quote:
Kansrekeningvraagje, nouja een klein onderdeel ervan...
Je hebt een vaas met een rode en een blauwe knikker, als je rood pakt ben je klaar, als je blauw pakt moet je hem terugleggen met nog een blauwe erbij. De kans dat je na 1 keer trekken klaar bent is dus 1/2, dat je met precies 2 keer trekken klaar bent (1-1/2)*(1/3) = 1/6, de kans dat je na 3 keer trekken klaar bent is (1-(1/2+1/6))*(1/4) enzovoorts. Nu moet ik aantonen dat de kans dat je in n keer klaar bent gelijk is aan 1/(n(n+1)). Die 1/(n+1) is logisch, dat is de kans dat je als je in die positie bent beland je een rode bal trekt. Die 1/n is de kans dat je nog niet klaar was bij de eerste n-1 trekkingen, dit is opgebouwd uit:
1 - (1/2 + 1/6 + 1/10 ...) = 1 - Som van i=1 tot n ( 1 / (4i - 2 ) ) en dit moet dus gelijk zijn aan 1/n, maar hier kom ik niet uit. Hoe kan ik dit aantonen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ah. Stom dat ik dat niet zag, lange dag achter de rug. Thanks!
"Reality is an illusion created by a lack of alcohol."
oja als er geen haakjes en geen e in je formule staan kun je hem gewoon vereenvoudigen/differentieren.
als er wel haakjes staan kun je de productregel gebruiken.
en als je geen haakjes hebt en een e en een x, dan ga je haakjes zetten en laat je de eventuele +/-(normaal getal) gewoon buiten beschouwing, heb ik het zo goed?
als er wel haakjes staan kun je de productregel gebruiken.
en als je geen haakjes hebt en een e en een x, dan ga je haakjes zetten en laat je de eventuele +/-(normaal getal) gewoon buiten beschouwing, heb ik het zo goed?
Niet echt, je kunt gewoon alles doen zolang het logisch is Bijvoorbeeld
x^2 . 3x^3 + 4
kan ook met de productregel:
2x * 3x^3 + x^2 * 9x^2
= 6x^4 + 9x^4
= 15x^4.
Bijvoorbeeldx^2 . 3x^3 + 4
kan ook met de productregel:
2x * 3x^3 + x^2 * 9x^2
= 6x^4 + 9x^4
= 15x^4.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oja, ja, ik denk dat ik het wel begrijp nu, en dat je een normaal getal alleen hoeft op te nemen in de afgeleide als hij tussen haakjes staat. en bij bvquote:Op donderdag 26 november 2009 22:16 schreef GlowMouse het volgende:
Niet echt, je kunt gewoon alles doen zolang het logisch is
x^2 . 3x^3 + 4
kan ook met de productregel:
2x * 3x^3 + x^2 * 9x^2
= 6x^4 + 9x^4
= 15x^4.
l(x) = (2wortelx / x^2 + 2)
dan moet je de 2 wel meenemen omdat hij meedoet aan de deling, toch?
als die +2 onder de deelstreep staat wel ja.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ja, daar staat ie. oke bedankt voor je hulpquote:Op donderdag 26 november 2009 22:24 schreef GlowMouse het volgende:
als die +2 onder de deelstreep staat wel ja.
ik vind dit soort topics echt geweldig, ik doe vwo n&g profiel in 1 jaar en het is veel zelfstudie, en dat ik hier af en toe een vraag kan stellen die dan ook meteen beantwoord wordt is echt heel handig. dank aan alle slimmerikken hier
Ik heb een inproductruimte en een lineaire afbeelding. Vraag is "laat zien dat een zelfgeadjungeerde afbeelding normaal is", kan ik dit doen met representatieve matrix? Dus L=L* en LL*=L*L? Het wordt nogal triviaal op die manier, geloof ik. Of moet ik dit doen met de inproductruimte dat L<x,y>=<x,Ly>? `
Het is inderdaad zo triviaal als je hier beweert.quote:Op vrijdag 27 november 2009 22:38 schreef Hanneke12345 het volgende:
Ik heb een inproductruimte en een lineaire afbeelding. Vraag is "laat zien dat een zelfgeadjungeerde afbeelding normaal is", kan ik dit doen met representatieve matrix? Dus L=L* en LL*=L*L? Het wordt nogal triviaal op die manier, geloof ik. Of moet ik dit doen met de inproductruimte dat L<x,y>=<x,Ly>? `
Toch even een tvp.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
(zag dat ik het in het verkeerde topic had gepost)
Glowmouse, kan ik je een vraag stellen over EViews? Het heeft namelijk betrekking tot de logaritmische functie die ik eerder toegepast heb, die Cobb Douglas functie, waarvan ik de formule moet toepassen (en dan de statistische waarden moet opzoeken) in EViews maar zover kom ik nog niet ..
Glowmouse, kan ik je een vraag stellen over EViews? Het heeft namelijk betrekking tot de logaritmische functie die ik eerder toegepast heb, die Cobb Douglas functie, waarvan ik de formule moet toepassen (en dan de statistische waarden moet opzoeken) in EViews maar zover kom ik nog niet ..
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Kun je onder estimate niet direct LOG(Y) = b0 + b1*LOG(X1) + ... invullen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hetgeen wat ik tot nu toe heb gedaan was..quote:Op zondag 29 november 2009 01:53 schreef GlowMouse het volgende:
Kun je onder estimate niet direct LOG(Y) = b0 + b1*LOG(X1) + ... invullen?
genr lnY=log(y)
genr lnK=log(k)
genr lnL=log(L)
Invullen op dat witte gedeelte, in die bovenste balk.
En dan uitgaan van naar estimate equation gaan en heb daar dit ingevuld
| 1 2 3 4 5 6 7 | ========================= LS LNY C LNK LNL Estimation Equation: ========================= LNY = C(1) + C(2)*LNK + C(3)*LNL |
Een vriend van me zei alleen dat dit wat vaag was, omdat je immers van de Cobb Douglas functie een lineair regressie model maakt en dus ook de alfa een log maakt, maar dat je dit niet invoert bij de formule.
Wat doe ik hier fout?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Dit gaat toch helemaal goed? Die vriend van je heeft half gelijk, met de errorterm gebeuren vreemde dingen (in je logmodel is de errorterm normaal verdeeld, in je CD-model vermenigvuldig je met de logaritme daarvan). Dat kun je niet rechtpraten met een lineair regressiemodel, maar dit is voor zover ik weet wel de standaard schatmethode.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dan houd ik het maar zo. Wij hebben tot nu toe alleen nog gewerkt met EViews(nog niet met spss). Het knaagt alleen ontzettend dat ik geen log voor alpha kan zetten omdat hij die natuurlijk niet ondersteunt. Dan maar een goede onderbouwing geven dat het voor de significantie van het toepasbare model niet uitmaakt, immers de vraag was dat het moest voldoen aan lineaire regressie, en dan moet het wel op deze logaritmische manier.quote:Op zondag 29 november 2009 02:03 schreef GlowMouse het volgende:
Dit gaat toch helemaal goed? Die vriend van je heeft half gelijk, met de errorterm gebeuren vreemde dingen (in je logmodel is de errorterm normaal verdeeld, in je CD-model vermenigvuldig je met de logaritme daarvan). Dat kun je niet rechtpraten met een lineair regressiemodel, maar dit is voor zover ik weet wel de standaard schatmethode.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
L is een lineaire afbeelding, dus L(x)=Ax=(Ax)*=A*x*quote:Op vrijdag 27 november 2009 22:38 schreef Hanneke12345 het volgende:
Ik heb een inproductruimte en een lineaire afbeelding. Vraag is "laat zien dat een zelfgeadjungeerde afbeelding normaal is", kan ik dit doen met representatieve matrix? Dus L=L* en LL*=L*L? Het wordt nogal triviaal op die manier, geloof ik. Of moet ik dit doen met de inproductruimte dat L<x,y>=<x,Ly>? `
Maar dan volgt daaruit niet dat A=A* toch? Die vector x zit me dwars. ;(
Want L ◦ L* = AA*x* = AAx = L◦L
En L* ◦ L = A* (Ax)* = A*A*x* = A*Ax
Maar als x een vector is, dan is Ax dat ook, en dan kan Ax nooit gelijk zijn aan (Ax)T, toch? Of betekent dit dat een lineaire afbeelding alleen zelfgeadjungeerd is als x ook een vierkante matrix is?
Als S de matrix is die het inproduct beschrijft, dan geldt S = S* en
xSA*y[/sup]*[/sup] = xASy*
voor alle x en y (hier is x een rijvector en y* een kolomvector en ik laat voor het gemak A rechts op x werken).
Waarschijnlijk is het handiger om hier in termen van lineaire afbeeldingen ipv matrices te denken.
xSA*y[/sup]*[/sup] = xASy*
voor alle x en y (hier is x een rijvector en y* een kolomvector en ik laat voor het gemak A rechts op x werken).
Waarschijnlijk is het handiger om hier in termen van lineaire afbeeldingen ipv matrices te denken.
Edit.
Inproduct is een bilineaire afbeelding en dus <x,y> = xSy*, (normale standaardinproduct is xyT, dan is S dus matrix van eenheidsvectoren?). (Dit is vooralsnog of niet vertelt in de colleges of mij volledig ontgaan)
Dan is x |-> Ax,
<x,y> |-> A<x,y> = <Ax,y> = <x,Ay> dus AxSy* = xSA*y* ?
Maar waarom xA en niet Ax?
L◦L*: x|-> AA*x*
<x,y>|-> <Ax,Ay>* ?
Waarom is deze som opeens moeilijk en eerst zo makkelijk. x;
[ Bericht 66% gewijzigd door Hanneke12345 op 29-11-2009 15:12:14 ]
Inproduct is een bilineaire afbeelding en dus <x,y> = xSy*, (normale standaardinproduct is xyT, dan is S dus matrix van eenheidsvectoren?). (Dit is vooralsnog of niet vertelt in de colleges of mij volledig ontgaan)
Dan is x |-> Ax,
<x,y> |-> A<x,y> = <Ax,y> = <x,Ay> dus AxSy* = xSA*y* ?
Maar waarom xA en niet Ax?
L◦L*: x|-> AA*x*
<x,y>|-> <Ax,Ay>* ?
Waarom is deze som opeens moeilijk en eerst zo makkelijk. x;
[ Bericht 66% gewijzigd door Hanneke12345 op 29-11-2009 15:12:14 ]
Hoe zit het met vaste verhoudingen in driehoeken? Hoe weet je bv dat van een bepaalde driehoek de verhoudingen van de zijdes 1:2:wortel 3 zijn?
Vanwege sinus/cosinus/tangens. Er is bekend dat b.v. sin(30°) = 1/2 en cos(30°) = √3/2, en zo heb je met een driehoek met zijden 1/2 en √3 en de stelling van Pythagoras dat deze schuine zijde 2 heeft.quote:
Hoe zit het met vaste verhoudingen in driehoeken? Hoe weet je bv dat van een bepaalde driehoek de verhoudingen van de zijdes 1:2:wortel 3 zijn?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
nou, ik zal het proberen, maar meetkunde vind ik echt een hocus pocus.quote:Op maandag 30 november 2009 20:56 schreef thabit het volgende:
Kun je iets concreter zijn met je vraagstelling?
oke, stel je hebt een zeshoek met zijde a.
punt P en S zijn middens van zijden en liggen recht tegenover elkaar, druk deze afstand uit in a
dus eerst de 0,5xPS, de halve afstand, berekenen mbv een driehoek, een rechthoekige driehoek met 90, 60 en 30 graden in de hoeken.
en nu is het blijkbaar duidelijk dat de verhoudingen in deze driehoek 1:2:wortel 3 zijn, maar hoe is dit duidelijk?
Stel hoek A is de hoek van 60 graden en zijde a is de zijde tegenover hoek A (of als je een Belg bent: hoek a en zijde A). Laten we meteen ook maar de hoek van 30 graden B noemen en de hoek van 90 graden C (met tegenoverliggende zijdes b en c respectievelijk).
Als je nu de driehoek spiegelt in zijde a, dan krijg je een gelijkzijdige driehoek (teken maar eens). Nu is a een zijde hiervan, maar ook 2b. Dus zijde a is tweemaal zo groot als zijde b. De wortel 3 krijg je nu met Pythagoras.
Als je nu de driehoek spiegelt in zijde a, dan krijg je een gelijkzijdige driehoek (teken maar eens). Nu is a een zijde hiervan, maar ook 2b. Dus zijde a is tweemaal zo groot als zijde b. De wortel 3 krijg je nu met Pythagoras.
oke ik heb het getekend en begrijp het nu wat meer, maar.. moet zijde c dan niet ipv wortel 3 wortel 5 zijn?quote:Op maandag 30 november 2009 21:15 schreef thabit het volgende:
Stel hoek A is de hoek van 60 graden en zijde a is de zijde tegenover hoek A (of als je een Belg bent: hoek a en zijde A). Laten we meteen ook maar de hoek van 30 graden B noemen en de hoek van 90 graden C (met tegenoverliggende zijdes b en c respectievelijk).
Als je nu de driehoek spiegelt in zijde a, dan krijg je een gelijkzijdige driehoek (teken maar eens). Nu is a een zijde hiervan, maar ook 2b. Dus zijde a is tweemaal zo groot als zijde b. De wortel 3 krijg je nu met Pythagoras.
want 1^2 + 2^2 = 5 = c^2?
ja kloptquote:
Ohnee foutje, AM moet 2 zijn en MP 'wortel 3?'
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
jawel toch,quote:Op maandag 30 november 2009 22:02 schreef GlowMouse het volgende:
[..]
AM is 2 inderdaad, maar dan krijg je geen wortel3.
als AM=2 dan
AP^2 + MP^2 = AM^2
1^2 + x^2 = 2^2
x^2 = 3
x= wortel 3
oh faal, zit nog met die wortel5 in mijn hoofd, klopt inderdaad
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
maar is het iedere keer zo'n karweitje om de verhoudingen te berekenen of zijn er vaste verhoudingen bekend bij bepaalde driehoeken?
1-2-wortel3 is wel bekend, en 1-1-wortel2 ook wel. En het karweitje kost steeds minder tijd als je het vaak doet.quote:
maar is het iedere keer zo'n karweitje om de verhoudingen te berekenen of zijn er vaste verhoudingen bekend bij bepaalde driehoeken?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ik kom niet uit bij de d/dx 2x(^3)√x , ik voel me echt een aap
het antwoord moet zijn 7x^2,5
het antwoord moet zijn 7x^2,5
Deathlift or Die.
Dat antwoord klopt, dus je bent er wel degelijk uitgekomen!quote:Op dinsdag 1 december 2009 11:15 schreef Ethanolic het volgende:
ik kom niet uit bij de d/dx 2x(^3)√x , ik voel me echt een aap
het antwoord moet zijn 7x^2,5
stond in het antwoordenboek, maar ik heb niets aan overschrijven.quote:Op dinsdag 1 december 2009 11:17 schreef thabit het volgende:
[..]
Dat antwoord klopt, dus je bent er wel degelijk uitgekomen!
Deathlift or Die.
ja dat snap ikquote:
en ik weet ook dat d/dx wortel x = 1/2x^(-1/2) = 1/(2 wortel x)
Deathlift or Die.
dankjewel, ik gebruikte de product regel vanaf x3wortel(x)quote:
Je kunt x3wortel(x) dan schrijven als x7/2
echt stom.
Deathlift or Die.
Had ook gekund, maar vereist wat extra stappen.quote:Op dinsdag 1 december 2009 11:55 schreef Ethanolic het volgende:
[..]
dankjewel, ik gebruikte de product regel vanaf x3wortel(x)
nu heb ik nog een vraagje.
ik krijg een rij met breuken in 1 formule
f = - (2/x3) + 4/x4 - 1/x4
nu gebruik ik de qoutient regel
f/g => (f'g - g'f) / g2
dat maakt
- (0*x3 - 3x2*2)/(x6)
oftewel
- (0 - 3x2*2)/(x6)
- (-6x2)/(x6)
nu streep ik de x2 weg
- (-6
laat maar ik ben er al uit toch maar even gepost voor de moeite met de supjes enzo haha
als je het zo uittypt zie je het probleem wel inene.
[ Bericht 3% gewijzigd door Ethanolic op 01-12-2009 12:12:23 ]
ik krijg een rij met breuken in 1 formule
f = - (2/x3) + 4/x4 - 1/x4
nu gebruik ik de qoutient regel
f/g => (f'g - g'f) / g2
dat maakt
- (0*x3 - 3x2*2)/(x6)
oftewel
- (0 - 3x2*2)/(x6)
- (-6x2)/(x6)
nu streep ik de x2 weg
- (-6
laat maar ik ben er al uit
toch maar even gepost voor de moeite met de supjes enzo hahaals je het zo uittypt zie je het probleem wel inene.
[ Bericht 3% gewijzigd door Ethanolic op 01-12-2009 12:12:23 ]
Deathlift or Die.
Ik heb zo m’n twijfels over de uitwerking, en je hoeft ook de quotientregel niet te gebruiken: weten dat 1/xn = x-n helpt je al een stuk verder.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het klopt wel. Ik moet het ook met de quotientregel doen om er mee te oefenen.quote:
Ik heb zo m’n twijfels over de uitwerking, en je hoeft ook de quotientregel niet te gebruiken: weten dat 1/xn = x-n helpt je al een stuk verder.
Deathlift or Die.
Oké, je hebt dus expres de berekening beperkt tot de eerste term en van dat antwoord alleen de teller opgeschreven?quote:
[..]
Het klopt wel. Ik moet het ook met de quotientregel doen om er mee te oefenen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het zit zo dat ik bij dequote:
[..]
Oké, je hebt dus expres de berekening beperkt tot de eerste term en van dat antwoord alleen de teller opgeschreven?
- (-6/x4)
de voorste min had weggelaten in mn schrift
daar kwam ik dus achter terwijl ik het hier uittypte.
antwoord op je vraag, ja dus
Deathlift or Die.
Oké, dan gaat er inderdaad niets mis, maar dat had ik even niet door.quote:
[..]
Het zit zo dat ik bij de
- (-6/x4)
de voorste min had weggelaten in mn schrift
daar kwam ik dus achter terwijl ik het hier uittypte.
antwoord op je vraag, ja dus
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Maak vooral domme foutjes, over dingen heenlezen enzo.quote:
[..]
Oké, dan gaat er inderdaad niets mis, maar dat had ik even niet door.
Maar het gaat top verder
Deathlift or Die.
om DC te berekenen moet je eerst AE en FB berekenen en dat getal van 10 aftrekken.
maar waarom kun je niet gewoon direct DC uitrekenen, DCE is toch ook een verhoudingsdriehoek waarvan je weet dat de lange zijde 4 is?
oja en nog een klein vraagje erbij: kan iemand me misschien uitleggen waarom je x/wortel 3 ook kunt schrijven als 1/3 . x . wortel 3
Dat partieel integeren...
Intergreer ln(x)2.
ln(x) * (x ln(x) - x) ∫ 1/x * (x ln x -x) dx
= x ln(x)2 - x ln(x) - ∫ ln(x) - 1 dx
= x ln(x)2 - x ln(x) - 1/x + x
Wat doe ik fout?
Intergreer ln(x)2.
ln(x) * (x ln(x) - x) ∫ 1/x * (x ln x -x) dx
= x ln(x)2 - x ln(x) - ∫ ln(x) - 1 dx
= x ln(x)2 - x ln(x) - 1/x + x
Wat doe ik fout?
Ik volg niet direct wat je wilt doen. Zijn dit alle gegevens die je hebt?quote:
[ afbeelding ]
om DC te berekenen moet je eerst AE en FB berekenen en dat getal van 10 aftrekken.
maar waarom kun je niet gewoon direct DC uitrekenen, DCE is toch ook een verhoudingsdriehoek waarvan je weet dat de lange zijde 4 is?
Vermenigvuldig teller en noemer met √3:quote:oja en nog een klein vraagje erbij: kan iemand me misschien uitleggen waarom je x/wortel 3 ook kunt schrijven als 1/3 . x . wortel 3
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Nu is het een paint-topic!!!quote:
[ afbeelding ]
om DC te berekenen moet je eerst AE en FB berekenen en dat getal van 10 aftrekken.
maar waarom kun je niet gewoon direct DC uitrekenen, DCE is toch ook een verhoudingsdriehoek waarvan je weet dat de lange zijde 4 is?
oja en nog een klein vraagje erbij: kan iemand me misschien uitleggen waarom je x/wortel 3 ook kunt schrijven als 1/3 . x . wortel 3
Hetgeen bewezen en beklonken moest worden.
oja, ik snap hetquote:Op dinsdag 1 december 2009 16:37 schreef Iblis het volgende:
[..]
Ik volg niet direct wat je wilt doen. Zijn dit alle gegevens die je hebt?
[..]
Vermenigvuldig teller en noemer met √3:
[ afbeelding ]
ik wil de opp van de trapezium berekenen en daarvoor heb ik DC nodig. sorry de rest van de gegevens: AB=10 en hoek A = 60 en hoek B = 45. en wat ik me afvraag is of DCE ook niet een verhoudingsdriehoek is met 1:2:wortel 3, want dan zou je DC toch in 1x kunnen berekenen?
Waar zou je dat uit op willen maken?quote:
[..]
oja, ik snap het
ik wil de opp van de trapezium berekenen en daarvoor heb ik DC nodig. sorry de rest van de gegevens: AB=10 en hoek A = 60 en hoek B = 45. en wat ik me afvraag is of DCE ook niet een verhoudingsdriehoek is met 1:2:wortel 3, want dan zou je DC toch in 1x kunnen berekenen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Dat ∫ln(x) niet 1/x is.quote:
Dat partieel integeren...
Intergreer ln(x)2.
ln(x) * (x ln(x) - x) ∫ 1/x * (x ln x -x) dx
= x ln(x)2 - x ln(x) - ∫ ln(x) - 1 dx
= x ln(x)2 - x ln(x) - 1/x + x
Wat doe ik fout?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
ik weet het niet, ik dacht dat een rechthoekige driehoek altijd zulke verhoudingen heeft? volgens mijn antwoorden heeft AED wel zulke verhoudingen, 1:2:wortel 3 en dan DCE blijkbaar niet, maar waarom niet?quote:Op dinsdag 1 december 2009 16:45 schreef Iblis het volgende:
[..]
Waar zou je dat uit op willen maken?
Omdat dat van de precieze hoek afhangt. /_ CED kan natuurlijk vanalles zijn afhankelijk van hoe breed DC is. Je kunt het denk ik zo zien: als de breedte van het trapezium 9,5 was, dan had je de som ook kunnen oplossen (probeer maar). Je kunt dat middenstuk veranderen zonder dat je die driehoeken aan de zijkant verandert, en dan veranderen natuurlijk ook hoek /_ CED en /_ ECD mee.quote:
[..]
ik weet het niet, ik dacht dat een rechthoekige driehoek altijd zulke verhoudingen heeft? volgens mijn antwoorden heeft AED wel zulke verhoudingen, 1:2:wortel 3 en dan DCE blijkbaar niet, maar waarom niet?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
aha, en is het dan een regel dat een rechthoekige driehoek een hoek van 60 (en 30) graden moet hebben om de verhoudingen 1:2:wortel 3 te hebben?quote:Op dinsdag 1 december 2009 16:53 schreef Iblis het volgende:
[..]
Omdat dat van de precieze hoek afhangt. /_ CED kan natuurlijk vanalles zijn afhankelijk van hoe breed DC is. Je kunt het denk ik zo zien: als de breedte van het trapezium 9,5 was, dan had je de som ook kunnen oplossen (probeer maar). Je kunt dat middenstuk veranderen zonder dat je die driehoeken aan de zijkant verandert, en dan veranderen natuurlijk ook hoek /_ CED en /_ ECD mee.
Vraagje over inductie, ik moet bewijzen dat 32n - 1 deelbaar is door 2n+2. Voor n=1 klopt het, en als we even stellen: an = 32n - 1 dan kom ik na invullen van n+1 met wat klooien op het volgende:
32(n+1) - 1 is deelbaar door 2n+3 = 2 * 2n+2
32 * 32n - 1
32n - 1 + 8 * 32n
an + 8 * 32n
Hierna kom ik niet verder (ik weet uberhaubt niet of ik wel de goede richting op ga) wie kan mij verder helpen?
32(n+1) - 1 is deelbaar door 2n+3 = 2 * 2n+2
32 * 32n - 1
32n - 1 + 8 * 32n
an + 8 * 32n
Hierna kom ik niet verder (ik weet uberhaubt niet of ik wel de goede richting op ga) wie kan mij verder helpen?
"Reality is an illusion created by a lack of alcohol."
Laten we voor de gein eens n=3 invullen. 36-1 = 26 * 28 = 23 * 7 * 13 is niet deelbaar door 25. Waarschijnlijk bedoel je dan ook 32^n - 1 in plaats van 32n - 1.quote:Op woensdag 2 december 2009 12:01 schreef Dzy het volgende:
Vraagje over inductie, ik moet bewijzen dat 32n - 1 deelbaar is door 2n+2. Voor n=1 klopt het, en als we even stellen: an = 32n - 1 dan kom ik na invullen van n+1 met wat klooien op het volgende:
32(n+1) - 1 is deelbaar door 2n+3 = 2 * 2n+2
32 * 32n - 1
32n - 1 + 8 * 32n
an + 8 * 32n
Hierna kom ik niet verder (ik weet uberhaubt niet of ik wel de goede richting op ga) wie kan mij verder helpen?
D'oh. Niet goed gelezen. Dan ga ik het nog maar een keer zelf proberen. Was er eigenlijk gewoon vanuit gegaan dat het wel zou kloppen. Nou ik ga het weer proberen, thanks!
"Reality is an illusion created by a lack of alcohol."
Ik heb volgens mij nu net bewezen dat het niet kan kloppen, maar ik moet bewijzen dat het wel klopt dus er moet ergens een foutje zitten:
We stellen an = 3n^2 - 1 dit moet dus deelbaar zijn door 2n+2
We vullen in n+1:
32^(n+1) - 1 moet deelbaar zijn door 2n+3 = 2 * 2n+2
32^n * 2 - 1 = 32^n * 32^n - 1
Hier loop ik een beetje vast, je zou iets van de vorm:
an(32^n) + 32^n
kunnen construeren maar ik zie niet zo goed wat ik daarmee opschiet.
We stellen an = 3n^2 - 1 dit moet dus deelbaar zijn door 2n+2
We vullen in n+1:
32^(n+1) - 1 moet deelbaar zijn door 2n+3 = 2 * 2n+2
32^n * 2 - 1 = 32^n * 32^n - 1
Hier loop ik een beetje vast, je zou iets van de vorm:
an(32^n) + 32^n
kunnen construeren maar ik zie niet zo goed wat ik daarmee opschiet.
"Reality is an illusion created by a lack of alcohol."
Rechts staat een verschil van 2 kwadraten. Doe daar wat mee.quote:Op woensdag 2 december 2009 12:30 schreef Dzy het volgende:
Ik heb volgens mij nu net bewezen dat het niet kan kloppen, maar ik moet bewijzen dat het wel klopt dus er moet ergens een foutje zitten:
We stellen an = 3n^2 - 1 dit moet dus deelbaar zijn door 2n+2
We vullen in n+1:
32^(n+1) - 1 moet deelbaar zijn door 2n+3 = 2 * 2n+2
32^n * 2 - 1 = 32^n * 32^n - 1
Ik moet het volgende lineare systeem oplossen:
2x-3y=-2
2x+y= 1
3x+2y=1
Ik kwam zelf uit op:
1 0 1/8
0 1 3/4
0 0 1
Dus, x=1/8 en y=3/4.
Maar dit klopt niet, alleen voor de eerste 2 regels. Wat heb ik fout gedaan?
(Excuses voor deze waarschijnlijk zeer simpele vraag, maar ik ben zelfstanding een linear algebra boek door het nemen...Maar ik snap er nog erg weinig van. Bovendien heb ik geen antwoorden voor de opgaven.)
2x-3y=-2
2x+y= 1
3x+2y=1
Ik kwam zelf uit op:
1 0 1/8
0 1 3/4
0 0 1
Dus, x=1/8 en y=3/4.
Maar dit klopt niet, alleen voor de eerste 2 regels. Wat heb ik fout gedaan?
(Excuses voor deze waarschijnlijk zeer simpele vraag, maar ik ben zelfstanding een linear algebra boek door het nemen...Maar ik snap er nog erg weinig van. Bovendien heb ik geen antwoorden voor de opgaven.)
Je hebt niets fout gedaan, behalve concluderen dat je iets fout hebt gedaan. De conclusie had moeten zijn dat het stelsel dus geen oplossingen heeft.quote:Op woensdag 2 december 2009 16:08 schreef Siddartha het volgende:
Ik moet het volgende lineare systeem oplossen:
2x-3y=-2
2x+y= 1
3x+2y=1
Ik kwam zelf uit op:
1 0 1/8
0 1 3/4
0 0 1
Dus, x=1/8 en y=3/4.
Maar dit klopt niet, alleen voor de eerste 2 regels. Wat heb ik fout gedaan?
Ah natuurlijk!quote:Op woensdag 2 december 2009 16:13 schreef thabit het volgende:
[..]
Je hebt niets fout gedaan, behalve concluderen dat je iets fout hebt gedaan. De conclusie had moeten zijn dat het stelsel dus geen oplossingen heeft.
Leuk dat zoiets de eerste opgave is na een hele uitleg over hoe je zo'n stelsel oplost (met alleen maar voorbeelden van wél oplosbare stelsels).
Bedankt !
Meteen dan nog maar een vraag, de volgende opgave:
4x-8y = 12
3x-6y=9
-2x+4y=-6
Kan dus ook niet opgelost worden? (Ik krijg lege vectoren in de 2de en 3de rij)
[ Bericht 13% gewijzigd door Siddartha op 02-12-2009 16:20:50 ]
Alle drie de vergelijkingen zeggen hetzelfde, er zijn dus oneindig mogelijke oplossingen, namelijk x = 2y+3
"Reality is an illusion created by a lack of alcohol."
Het zal er wel mee te maken hebben dat ik vandaag al veel te lang bezig ben en ik ziek aan het worden ben maar wat bedoel je precies?quote:Op woensdag 2 december 2009 14:27 schreef thabit het volgende:
[..]
Rechts staat een verschil van 2 kwadraten. Doe daar wat mee.
"Reality is an illusion created by a lack of alcohol."
Wel, 32^n * 32^n is een kwadraat. En 1 is ook een kwadraat. Dus 32^n * 32^n - 1 is het verschil van twee kwadraten.
(a - b)(a + b) = a2 - b2, als je nu eens 1 als 12 opvat.quote:
[..]
Het zal er wel mee te maken hebben dat ik vandaag al veel te lang bezig ben en ik ziek aan het worden ben maar wat bedoel je precies?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik had hem al voor Iblis trouwens, even in my defense nu aan de besliskunde, weer even genoeg bewezen.
nu aan de besliskunde, weer even genoeg bewezen.
"Reality is an illusion created by a lack of alcohol."
Als dit 'niveau' van vragen niet gewenst is, hoor ik het graag.
Maar stel je hebt een systeem van vergelijkingen die allemaal uitkomen op 0. Hoe
kan je die dan oplossen?
Voorbeeld:
2x-y-3z=0
-x+2y-3z= 0
x+y+4z=0
Dus:
2 -1 -3 0
-1 2 -3 0
1 1 4 0
Dan kom ik uiteindelijk uit op:
1 0 0 0
0 1 0 0
0 0 1 0
Wat nergens op slaat....
Maar stel je hebt een systeem van vergelijkingen die allemaal uitkomen op 0. Hoe
kan je die dan oplossen?
Voorbeeld:
2x-y-3z=0
-x+2y-3z= 0
x+y+4z=0
Dus:
2 -1 -3 0
-1 2 -3 0
1 1 4 0
Dan kom ik uiteindelijk uit op:
1 0 0 0
0 1 0 0
0 0 1 0
Wat nergens op slaat....
Alle vragen zijn welkom hoor (tenzij mensen echt geen moeite doen om zelf een vinger uit te steken).quote:
Als dit 'niveau' van vragen niet gewenst is, hoor ik het graag.
Jawel, dit zegt dat x=y=z=0 de enige oplossing x. Je kiest x zo dat 1*x = 0. 0 dus.quote:Dan kom ik uiteindelijk uit op:
1 0 0 0
0 1 0 0
0 0 1 0
Wat nergens op slaat....
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het geitenprobleem:
Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
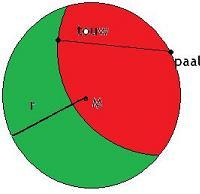
Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
Ik moet op basis van het
Ln Y = Ln α + K^β1 + L^β2 model, de capital en labour intensive formule ontrekken.
Uitgaande van Labour intensive, is de formule daarvan Log ( Y / L ) = Log ( K / L ). Nu moet ik aangeven waarom ik op Log K / L uitkom en vroeg me af of onderstaande methode ook maar enigszins in de buurt komt ?
Ln Y = Ln α + K^β1 + L^β2 model, de capital en labour intensive formule ontrekken.
Uitgaande van Labour intensive, is de formule daarvan Log ( Y / L ) = Log ( K / L ). Nu moet ik aangeven waarom ik op Log K / L uitkom en vroeg me af of onderstaande methode ook maar enigszins in de buurt komt ?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ln Y = Ln α + K^β1 + L^β2
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik zie inderdaad net dat ik een aantal stappen heb overgeslagen,quote:Op woensdag 2 december 2009 23:15 schreef GlowMouse het volgende:
Ln Y = Ln α + K^β1 + L^β2
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ik weet niet hoe je het wilt doen, maar het antwoord is nee.quote:
als je hebt
e^(-x+1) = ln e^2
mag je deze e's dan tegen elkaar wegstrepen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
In het algemeen mag dat niet (al komt er hier toevallig wel het goede antwoord uit).quote:Op donderdag 3 december 2009 14:29 schreef poesemuis het volgende:
als je hebt
e^(-x+1) = ln e^2
mag je deze e's dan tegen elkaar wegstrepen?
ja daaromquote:Op donderdag 3 december 2009 14:44 schreef thabit het volgende:
[..]
In het algemeen mag dat niet (al komt er hier toevallig wel het goede antwoord uit).
mijn wiskundeleraar deed het op deze manier, ik vond het al vreemd
Er geldt ln ea = a, dus er staat, als je dat meeneemt: e-x+1 = 2, dat los je op door links en rechts de logaritme te nemen, en dan krijg je -x + 1 = ln 2.quote:
[..]
ja daarom
Maar ‘wegstrepen’ is dus niet echt het geval, doch het komt inderdaad, zoals thabit zegt hier toevallig goed uit.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(ex-1) dx (van 0 --> ln2)
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen
Probeer eens u = v2 + 1 te substitueren (dan gaat in elk geval de wortel weg).quote:Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(ex-1) dx (van 0 --> ln2)
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen
Je moet natuurlijk die wortel zien kwijt te raken, en daarvoor moet je een geschiktere substitutie bedenken. Wat we willen is de uitdrukking onder het wortelteken omvormen tot een kwadraat, omdat de wortel uit het kwadraat van een grootheid die grootheid zelf is, of het tegendeel daarvan. Dus willen we een substitutie zodanig dat:quote:Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(ex-1) dx (van 0 --> ln2)
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen
(1) u2 = ex - 1
Oplossen voor x geeft dan:
(2) x = ln(u2 + 1)
En dus hebben we ook:
(3) dx/du = 2u/(u2 + 1)
En dus:
(4) dx = 2u/(u2 + 1)∙du
We hebben nu:
(5) ∫ √(ex - 1)∙dx = ∫ 2u2/(u2 + 1)∙du
Nu heb je ook
(6) 2u2/(u2 + 1) = (2(u2 + 1) - 2)/(u2 + 1) = 2 - 2/(u2 + 1)
En dus:
(7) ∫ 2u2/(u2 + 1)∙du = ∫ (2 - 2/(u2 + 1))∙du = 2u - 2∙arctan u + C
Uit (5) en (7) volgt dan na terugsubstitueren van u = √(ex - 1) dat:
(8) ∫ √(ex - 1)∙dx = 2∙√(ex - 1) - 2∙arctan(√(ex - 1)) + C
Voor de waarde van de bepaalde integraal over het interval [0, ln 2] vinden we dan 2∙(1 - arctan 1) = 2∙(1 - π/4) = 2 - π/2.
[ Bericht 0% gewijzigd door Riparius op 03-12-2009 21:31:01 ]
Bedankt! Was er nooit zelf op gekomen om u2 te doen.quote:Op donderdag 3 december 2009 21:19 schreef Riparius het volgende:
-Knip-
Je kunt ook opmerken: √2·√2 = 2, dus 2/√2 = √2, m.a.w. er staat dus gewoon (√2√3)3 = (√6)3 = 6√6.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
zit een typo in inderdaad; ik gebruik dat √(6/4) = √6 / √4 = √6 / 2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(ex-1) dx (van 0 --> ln2)
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen
Als je echt je antwoord wil controleren, probeer dan je antwoorden te checken op Wolframalpha.
Het is af en toe at kutten om de juiste input te vinden, maar er staan genoeg examples op de site hoe de invoer werkt.
In jouw geval is het:
http://www.wolframalpha.c(...)m+x%3D0+to+LN%282%29
Kom ook eens spammen in mijn fotoboek :') **En ja, ik zie er goed uit dat hoef je niet nog eens te vermelden! ** ( hihi )
quote:Op zaterdag 5 december 2009 21:30 schreef Illuminator het volgende:
Met behulp van jullie antwoorden en wat gepuzzel van mijn kant ben ik tot het volgende resultaat gekomen. Volgens mij klopt dit en is het ook de beoogde rekenwijze van het boek.
[ afbeelding ]
Opmerkingen?
---
@GlowMouse: de eerste helft van je uitleg snap ik, maar vanaf het onderstaande stuk volg ik het niet meer:
[ afbeelding ]
Hoe kom je van het linker resultaat bij het rechter resultaat? En waarom gebruik je 6/4 in plaats van 3/2? Het antwoord lijkt ook niet helemaal te kloppen, maar misschien zie ik iets over het hoofd.
@Iblis: die methode maakt de som drastisch eenvoudiger. Erg leuk. Jammer genoeg niet altijd toepasbaar bij soortgelijke sommen.
---
In ieder geval erg bedankt voor de uitleg.
En voor jou geldt:
http://www.wolframalpha.c(...)8sqrt%282%29^3%29%29
Heb het topic niet gelezen, maar dus ik weet niet of hier scholieren of studenten zitten,
Ik wil het volgende alleen even meegeven: Een echte beta is lui, en laat de som voor zich uitrekenen en hoeft slechts te weten hoe, en hoe die het toe moet passen
Kom ook eens spammen in mijn fotoboek :') **En ja, ik zie er goed uit dat hoef je niet nog eens te vermelden! ** ( hihi )
Ik zou het niet echt een methode willen noemen, het is gewoon opmerken dat als de teller x bevat en de noemer √x dat je dan in feite gewoon √x in de teller hebt staan. Dat zie je inderdaad niet altijd, maar vaak wel.quote:
@Iblis: die methode maakt de som drastisch eenvoudiger. Erg leuk. Jammer genoeg niet altijd toepasbaar bij soortgelijke sommen.
De iets algemenere methode is teller en noemer met de wortel in de noemer vermenigvuldigen. Ik zou b.v. niet eerst die derde macht nemen, maar dan dit doen:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Van die editor word ik niet veel wijzer, dan maar even zo.
(20-0,64√L)200/√L wordt 4000/√L – 128
Hoe? ik kom er niet uit.
edit: opgelost (20-0,64√L) eerst maal 200 en dan delen door wortel L. Bleef maar puzzelen maar iemand heeft me geholpen..
[ Bericht 41% gewijzigd door borisz op 06-12-2009 17:32:37 ]
(20-0,64√L)200/√L wordt 4000/√L – 128
Hoe? ik kom er niet uit.
edit: opgelost (20-0,64√L) eerst maal 200 en dan delen door wortel L. Bleef maar puzzelen maar iemand heeft me geholpen.
. [ Bericht 41% gewijzigd door borisz op 06-12-2009 17:32:37 ]
winnaar wielerprono 2007 :) Last.FM
Heren , waarom wordt die cost niet meegenomen in de Laplace transformatie (die cost, waar die dirac functie in het begin mee wordt vermenigvuldigd). Dank u wel.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Utgaande van bijv. een null hypothesis waar bij
h0: B1+b2=1
h1: b1+b2 niet gelijk aan 1
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?
h0: B1+b2=1
h1: b1+b2 niet gelijk aan 1
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
je hypothesen sluiten elkaar niet uit?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oeps, sorry. Ik bedoelde niet kleiner dan 1 maar gelijk aan 1.quote:Op maandag 7 december 2009 00:58 schreef GlowMouse het volgende:
je hypothesen sluiten elkaar niet uit?
Utgaande van bijv. een null hypothesis waar bij
h0: B1+b2=1
h1: b1+b2 niet gelijk aan 1
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Bij een lage p-waarde verwerp je de nulhypothese ja. De F-test komt van een regressiemodel? Dan krijg je bij een hoge F-waarde een lage p-waarde.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bij gelijkblijvende vrijheidsgraden is er gewoon een vaste relatie tussen de P-waarde en de waarde die uit de F-toets naar voren komt. Het maakt dus niet uit of je op basis van een kritische waarde van de F-toets de nulhypothese verwerpt of op basis van de P-waarde. Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese (bij een kritische P-waarde van 0,05 en een gevonden P-waarde van 0,0499 is de verwerping minder krachtig dan bij een gevonden P-waarde 0,0001).quote:Op maandag 7 december 2009 01:01 schreef sitting_elfling het volgende:
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?
[ Bericht 4% gewijzigd door Bolkesteijn op 07-12-2009 01:21:44 ]
Ik hoop toch dat je het significantieniveau vantevoren kiest; de p-waarde zegt helemaal niks over de significantie van de verwerping, alleen over de kans op een type-2 fout.quote:Op maandag 7 december 2009 01:16 schreef Bolkesteijn het volgende:
[..]
Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hij komt inderdaad van een regressie model. Je doet de calculaties, krijgt een hoge F waarde, alleen moet je de mate van kans significantie zelf kiezen. En dan is er de vraag of je de null hypothese verwerpt of niet. Maar sinds P miniem laag is, wordt hij dus verworpen.quote:Op maandag 7 december 2009 01:03 schreef GlowMouse het volgende:
Bij een lage p-waarde verwerp je de nulhypothese ja. De F-test komt van een regressiemodel? Dan krijg je bij een hoge F-waarde een lage p-waarde.
Bedankt!
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Maar het is toch zo uitgaande van een regressie model dat bij hoge F er dus een kleine P is, en als die kleine P < 0.05 is h0 wordt verworpen, en vice versa. Dus bij lage F sowieso een hoge p zit?quote:Op maandag 7 december 2009 01:16 schreef Bolkesteijn het volgende:
[..]
Bij gelijkblijvende vrijheidsgraden is er gewoon een vaste relatie tussen de P-waarde en de waarde die uit de F-toets naar voren komt. Het maakt dus niet uit of je op basis van een kritische waarde van de F-toets de nulhypothese verwerpt of op basis van de P-waarde. Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese (bij een kritische P-waarde van 0,05 en een gevonden P-waarde van 0,0499 is de verwerping minder krachtig dan bij een gevonden P-waarde 0,0001).
Ik moet maar eens een ander econometrie boek aanschaffen.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Begin met Bain & Engelhardt, Introduction to Probability and Mathematical Statistics; staat genoeg in over kansrekening en standaard toetstheorie.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het significantieniveau hangt toch gewoon af van de betrouwbaarheid die je wenselijk acht? Wat heeft de volgorde er mee te maken? Indien je gevonden P-waarde maar minimaal onder de kritische P-waarde zit is er sprake van een minder krachtige verwerping van H0, dan als de gevonden P-waarde vrijwel gelijk is aan nul en dus ruim onder de kritische P-waarde zit. Zo heb ik het tenminste altijd geinterpreteerd, immers dan zou je ook in het geval van een nog lagere kritische P-waarde H0 verwerpen.quote:Op maandag 7 december 2009 01:18 schreef GlowMouse het volgende:
Ik hoop toch dat je het significantieniveau vantevoren kiest; de p-waarde zegt helemaal niks over de significantie van de verwerping, alleen over de kans op een type-2 fout.
juistquote:
[..]
Het significantieniveau hangt toch gewoon af van de betrouwbaarheid die je wenselijk acht?
Je moet niet je significantieniveau kiezen op basis van je data, anders krijg je gekke dingen.quote:Wat heeft de volgorde er mee te maken?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh, zo, ja dat snap ik. Dan ga je jezelf 'rijk rekenen'.quote:Op maandag 7 december 2009 01:35 schreef GlowMouse het volgende:
Je moet niet je significantieniveau kiezen op basis van je data, anders krijg je gekke dingen.
Ik ga d'r vanuit dat die prima is, dus zal hem aanschaffen voor mn examens later in Januari.quote:Op maandag 7 december 2009 01:28 schreef GlowMouse het volgende:
Begin met Bain & Engelhardt, Introduction to Probability and Mathematical Statistics; staat genoeg in over kansrekening en standaard toetstheorie.
Wij hebben hier als hoofdboek Essentials of Econometrics van Gujarati en Porter. En dat boek werkt niet motiverend
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Oke, dat was echt helemaal fout, na vandaag weer ploeteren kom ik op het volgende uit. Maakt het nu wel sense?quote:Op woensdag 2 december 2009 23:15 schreef GlowMouse het volgende:
Ln Y = Ln α + K^β1 + L^β2
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.
Is het stap per stap nu wel goed? Dus de stappen uitleggen van het initiele Cobb Douglas model naar log Y/L = log K/L
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Bij kansrekening een tijd gediscussieerd over het volgende vraagstuk. Hoe stom ook, maar wij kwamen er niet uit. Kan iemand mij een beetje de goede kant opsturen? Alvast bedankt.
Voor een bepaalde plaats en tijd doen 2 weerstations, I en II, een weersvoorspelling: regen of zon.
Bekend is dat I in 9 van de 10 gevallen goed voorspelt, en II in 4 van de 5 gevallen.
Vraag: Als I regen voorspelt en II zon, wat is dan de kans op regen?
Voor een bepaalde plaats en tijd doen 2 weerstations, I en II, een weersvoorspelling: regen of zon.
Bekend is dat I in 9 van de 10 gevallen goed voorspelt, en II in 4 van de 5 gevallen.
Vraag: Als I regen voorspelt en II zon, wat is dan de kans op regen?
kun je niet zeggenquote:
Bij kansrekening een tijd gediscussieerd over het volgende vraagstuk. Hoe stom ook, maar wij kwamen er niet uit. Kan iemand mij een beetje de goede kant opsturen? Alvast bedankt.
Voor een bepaalde plaats en tijd doen 2 weerstations, I en II, een weersvoorspelling: regen of zon.
Bekend is dat I in 9 van de 10 gevallen goed voorspelt, en II in 4 van de 5 gevallen.
Vraag: Als I regen voorspelt en II zon, wat is dan de kans op regen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De rol van u_i in regel 1 is twijfelachtig, verder ziet het er goed uit.quote:
[..]
Oke, dat was echt helemaal fout, na vandaag weer ploeteren kom ik op het volgende uit. Maakt het nu wel sense?
Is het stap per stap nu wel goed? Dus de stappen uitleggen van het initiele Cobb Douglas model naar log Y/L = log K/L
[ afbeelding ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
omdat afhankelijkheid een grote rol speelt.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Zal je dat nader kunnen toelichten, denk dat ik het niet helemaal volgquote:Op maandag 7 december 2009 18:58 schreef GlowMouse het volgende:
[..]
omdat afhankelijkheid een grote rol speelt.
Als die twee weerstations in dezelfde plek staan (wat ze doen) dan hebben ze hetzelfde weer. Het is waarschijnlijk dat alleen in twijfelgevallen een fout gemaakt wordt. Station II doet het vaker fout dan Station I, dus het zou best kunnen dat als Station I het fout heeft, II het ook zeker fout heeft, en II ook soms anders afwijkt.quote:
[..]
Zal je dat nader kunnen toelichten, denk dat ik het niet helemaal volg
Met die logica is station I dus ‘leidinggevend’ en zou je die gewoon altijd moeten volgen en is het 9/10 keer correct.
Maar dat is waarschijnlijk niet wat ze bedoelen, ze bedoelen waarschijnlijk dat er helemaal geen verband zit tussen de momenten waarop ze het fout doen. Dat ze het onafhankelijk van elkaar fout doen. Maar je moet je ernstig afvragen of dat wel een realistische situatie is.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Wat ' ze' bedoelen was nou net de vraag. Oorspronkelijk was het een hoogleraar wiskunde die ermee kwam en toen is een professor kansrekening een beetje uit zijn slof geschoten. De vraag was waarom. En dit is het antwoord dus. Bedankt!quote:Op maandag 7 december 2009 19:18 schreef Iblis het volgende:
[..]
Als die twee weerstations in dezelfde plek staan (wat ze doen) dan hebben ze hetzelfde weer. Het is waarschijnlijk dat alleen in twijfelgevallen een fout gemaakt wordt. Station II doet het vaker fout dan Station I, dus het zou best kunnen dat als Station I het fout heeft, II het ook zeker fout heeft, en II ook soms anders afwijkt.
Met die logica is station I dus ‘leidinggevend’ en zou je die gewoon altijd moeten volgen en is het 9/10 keer correct.
Maar dat is waarschijnlijk niet wat ze bedoelen, ze bedoelen waarschijnlijk dat er helemaal geen verband zit tussen de momenten waarop ze het fout doen. Dat ze het onafhankelijk van elkaar fout doen. Maar je moet je ernstig afvragen of dat wel een realistische situatie is.
Tja, met de extra aanname van onafhankelijkheid is de som wel op te lossen op zich. Maar dan moet je dat even melden. Zo gegeven is er geen oplossing om bovenstaande dus.quote:
[..]
Wat ' ze' bedoelen was nou net de vraag. Oorspronkelijk was het een hoogleraar wiskunde die ermee kwam en toen is een professor kansrekening een beetje uit zijn slof geschoten. De vraag was waarom. En dit is het antwoord dus. Bedankt!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Nee het ging puur om dit vraagstuk(letterlijk). Want als ze wel onderling afhankelijk zijn met elkaar, wat zal het dan worden ?quote:Op maandag 7 december 2009 19:32 schreef Iblis het volgende:
[..]
Tja, met de extra aanname van onafhankelijkheid is de som wel op te lossen op zich. Maar dan moet je dat even melden. Zo gegeven is er geen oplossing om bovenstaande dus.
Er kan echt vanalles uitkomen, je hebt de simultane kansverdeling nodig. En dat wist die professor ook best.quote:
[..]
Nee het ging puur om dit vraagstuk(letterlijk). Want als ze wel onderling afhankelijk zijn met elkaar, wat zal het dan worden ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Niemand hier nog een antwoord op?quote:Op zondag 6 december 2009 23:40 schreef Burakius het volgende:
[ afbeelding ]
Heren , waarom wordt die cost niet meegenomen in de Laplace transformatie (die cost, waar die dirac functie in het begin mee wordt vermenigvuldigd). Dank u wel.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
| 1 2 3 | -------- - ---------------------------------------------- 2^16 2^I |
Hoe zou je bovenstaande kunnen vereenvoudigen tot een enkele formule? Als ik het plot is het bijna een e-macht, afgezien dat de uitkomst bij I > 16 natuurlijk 0 is. Oftewel: is afkappen wiskundig te benaderen?
'To alcohol, the cause of and the solution to all of life's problems' - Homer J. Simpson
Ik besef me net dat ik eigenlijk geen fuck snap van de letter 'd' in de differentiaalrekening. Het is echt een chinees voor mij die notaties. Heeft iemand toevallig een duidelijke uitleg wat die letter nou in alle gevallen betekent? De andere notaties van functies en afgeleiden etc. snap ik eigenlijk ook niet goed.
Wat ik nu weet:
d betekent soms dat het gaat om een oneindig klein interval. Dus als je dan dy/dx hebt, geeft je daarmee de exacte richtingscoefficient op een bepaalde plek aan, of de functie van alle richtingscoefficienten -> de afgeleide.
Volgens mijn boek is dit dan weer uit te leggen doordat je dx als een 'independent variable' neemt en dy als een 'dependent variable' afhankelijk van dx als volgt: dy = dy/dx * dx = f'(x) * dx
Wat ik nou niet begrijp is waar die dy nou voor staat. Ik kan me er geen beeld bij vormen, algebraisch is het wel logisch, maar wat is nou het nu van het aangeven een 'dy' dan uberhaupt?
En dan beginnen ze vervolgens ook nog die d voor allemaal verschillende soorten elementen te zetten.
Bijv. U = lnx , dU = dx/x
Dat klopt algebraisch, maar wat is die dU dan uberhaupt? De afgeleide van U? Dat kan weer niet want dat is dU/dx al right? De richtingscoefficient van U bij x misschien? En wat is het verschil dan tussen U en U(x)?
Ik ben echt totaal het overzicht kwijt
Wat ik nu weet:
d betekent soms dat het gaat om een oneindig klein interval. Dus als je dan dy/dx hebt, geeft je daarmee de exacte richtingscoefficient op een bepaalde plek aan, of de functie van alle richtingscoefficienten -> de afgeleide.
Volgens mijn boek is dit dan weer uit te leggen doordat je dx als een 'independent variable' neemt en dy als een 'dependent variable' afhankelijk van dx als volgt: dy = dy/dx * dx = f'(x) * dx
Wat ik nou niet begrijp is waar die dy nou voor staat. Ik kan me er geen beeld bij vormen, algebraisch is het wel logisch, maar wat is nou het nu van het aangeven een 'dy' dan uberhaupt?
En dan beginnen ze vervolgens ook nog die d voor allemaal verschillende soorten elementen te zetten.
Bijv. U = lnx , dU = dx/x
Dat klopt algebraisch, maar wat is die dU dan uberhaupt? De afgeleide van U? Dat kan weer niet want dat is dU/dx al right? De richtingscoefficient van U bij x misschien? En wat is het verschil dan tussen U en U(x)?
Ik ben echt totaal het overzicht kwijt
Veel van die trucs van dy/dx zijn algebraïsch van aard inderdaad en volgen uit Leibniz’ dy/dx notatie. Die ‘werken’, maar er is soms moeilijk een interpretatie aan te geven, daarom houdt ook niet iedereen ervan.
Het is m.i een beetje een notatietruc (maar wel een handige). In principe kan het ook zonder, maar dat is vaak wel omslachtiger noteren.
Het is m.i een beetje een notatietruc (maar wel een handige). In principe kan het ook zonder, maar dat is vaak wel omslachtiger noteren.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Een e-macht? Ik snap hem niet volgens mij.quote:Op dinsdag 8 december 2009 14:49 schreef MichielPH het volgende:
[ code verwijderd ]
Hoe zou je bovenstaande kunnen vereenvoudigen tot een enkele formule? Als ik het plot is het bijna een e-macht, afgezien dat de uitkomst bij I > 16 natuurlijk 0 is. Oftewel: is afkappen wiskundig te benaderen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Hmm das lekkerquote:Op dinsdag 8 december 2009 17:19 schreef Iblis het volgende:
Veel van die trucs van dy/dx zijn algebraïsch van aard inderdaad en volgen uit Leibniz’ dy/dx notatie. Die ‘werken’, maar er is soms moeilijk een interpretatie aan te geven, daarom houdt ook niet iedereen ervan.
Het is m.i een beetje een notatietruc (maar wel een handige). In principe kan het ook zonder, maar dat is vaak wel omslachtiger noteren.
Vooral aangezien we er ook mee moeten rekenen bljikbaar. Wat ik dan nog steeds niet begrijp is het verschil tussen bijvoorbeeld een functie U, U(x), U' en U'(x).
Destemeer omdat je bijv. bij partiële zon vage notatie hebt.
Formule voor partiële integratie:
- Integraal (UdV) = UV - Integraal (dUV)
De notatie voor de afgeleide van U is dU/dx right?
Dus dU is niet gelijk aan U' maar aan U'dx, maar als je de formule gebruikt doe je wel gewoon
integraal(f(x)g'(x)) = f(x)g(x) - integraal (f'(x)g(x)) in plaats van
integraal( f(x) (g'(X)/dx) ) = f(x)g(x) - integraal( ((f'(x)/dx) g(x) )
Stom van me, het grondtal is natuurlijk gewoon 2:quote:Op dinsdag 8 december 2009 17:23 schreef Iblis het volgende:
[..]
Een e-macht? Ik snap hem niet volgens mij.
Eerste vergelijking:
| 1 2 3 | -------- - ---------------------------------------------- 2^16 2^I |
Dit valt namelijk te herschrijven tot
Tweede vergelijing:
| 1 2 3 | --------------- = 2^(-i) - 2^-16 2^16 |
Ik ben aan de tweede vergelijking gekomen door de eerste vergelijkingen domweg in te vullen en met de getallen de tweede vergelijking te bedenken. Nu is de vraag: Is de tweede vergelijking ook te herleiden zonder getallen in te hoeven vullen?
'To alcohol, the cause of and the solution to all of life's problems' - Homer J. Simpson
Het is een traditionele notatie die teruggaat op Leibniz en dateert uit de tijd dat men nog geen streng limietbegrip had. Omdat men met dx, dy, althans oorspronkelijk, 'oneindig kleine' grootheden bedoelde aan te geven sprak men dan ook van infinitesimaalrekening.quote:Op dinsdag 8 december 2009 16:28 schreef synthesix het volgende:
Ik besef me net dat ik eigenlijk geen fuck snap van de letter 'd' in de differentiaalrekening. Het is echt een chinees voor mij die notaties. Heeft iemand toevallig een duidelijke uitleg wat die letter nou in alle gevallen betekent? De andere notaties van functies en afgeleiden etc. snap ik eigenlijk ook niet goed.
Over welk boek heb je het hier?quote:Wat ik nu weet:
d betekent soms dat het gaat om een oneindig klein interval. Dus als je dan dy/dx hebt, geeft je daarmee de exacte richtingscoefficient op een bepaalde plek aan, of de functie van alle richtingscoefficienten -> de afgeleide.
Volgens mijn boek is dit dan weer uit te leggen doordat je dx als een 'independent variable' neemt en dy als een 'dependent variable' afhankelijk van dx als volgt: dy = dy/dx * dx = f'(x) * dx
De notaties van Leibniz zijn om allerlei redenen erg nuttig, denk alleen maar aan de kettingregel of de substitutiemethode in de integraalrekening. De notatie ∫f(x)dx is trouwens ook van Leibniz afkomstig. Hij correspondeerde veel met de broers Jacob en Johann Bernoulli, die zijn notatie overnamen. Johann Bernoulli gaf Leonard Euler les in zijn jonge jaren, zodat Euler de notatie ook overnam. And the rest, as they say, is history ...quote:Wat ik nou niet begrijp is waar die dy nou voor staat. Ik kan me er geen beeld bij vormen, algebraisch is het wel logisch, maar wat is nou het nu van het aangeven een 'dy' dan uberhaupt?
In Engeland bleven ze overigens nog een eeuw doorprutsen met de onhandige notatie van Newton, dit als gevolg van de grote controverse rond de ontdekking van de infinitesimaalrekening. Maar het resultaat daarvan was dat de Britse wiskunde enorm achterop raakte.
Je kunt bij dx en dy het best de overeenkomst met Δx en Δy in gedachten houden. Als x je onafhankelijke variabele is en y de daarvan afhankelijke variabele, dan is Δy dus het increment van de afhankelijke variabele y als gevolg van het increment Δx in de onafhankelijke variabele x. Evenzo voor dy en dx, zij het dat men zich oorspronkelijk voorstelde dat het hier ging om 'oneindig kleine' (infinitesimale) grootheden.quote:
En dan beginnen ze vervolgens ook nog die d voor allemaal verschillende soorten elementen te zetten.
Bijv. U = lnx , dU = dx/x
Dat klopt algebraisch, maar wat is die dU dan uberhaupt? De afgeleide van U? Dat kan weer niet want dat is dU/dx al right? De richtingscoefficient van U bij x misschien? En wat is het verschil dan tussen U en U(x)?
De notatie U(x) geeft alleen expliciet aan dat een variabele U afhangt van (dus een functie is van ) een variabele x. We noemen x dan de onafhankelijke variabele en U de (daarvan) afhankelijke variabele. Niettemin is hier sprake van een conceptuele verwarring tussen de naam van een functie en de naam van de afhankelijke variabele van die functie, dat is immers niet hetzelfde: je kunt een functie f hebben met als functievoorschrift y = f(x). Dan is y de afhankelijke variabele, maar de functie zelf wordt toch echt aangeduid met f, niet met y.
Ga eens even lekker grasduinen in Wikipedia. De raison d'être van de diverse notaties wordt je dan wel duidelijk.quote:Ik ben echt totaal het overzicht kwijt
Thanks ^^ het begon al een beetje duidelijker te worden onderhand, ik snap het idee van de notatie nu wel ongeveer. Het gaat trouwens om "Calculus: A complete course van Robert Adams, Christopher Essex (et al. ?)"quote:Op dinsdag 8 december 2009 18:15 schreef Riparius het volgende:
[..]
Het is een traditionele notatie die teruggaat op Leibniz en dateert uit de tijd dat men nog geen streng limietbegrip had. Omdat men met dx, dy, althans oorspronkelijk, 'oneindig kleine' grootheden bedoelde aan te geven sprak men dan ook van infinitesimaalrekening.
[..]
Over welk boek heb je het hier?
[..]
De notaties van Leibniz zijn om allerlei redenen erg nuttig, denk alleen maar aan de kettingregel of de substitutiemethode in de integraalrekening. De notatie ∫f(x)dx is trouwens ook van Leibniz afkomstig. Hij correspondeerde veel met de broers Jacob en Johann Bernoulli, die zijn notatie overnamen. Johann Bernoulli gaf Leonard Euler les in zijn jonge jaren, zodat Euler de notatie ook overnam. And the rest, as they say, is history ...
In Engeland bleven ze overigens nog een eeuw doorprutsen met de onhandige notatie van Newton, dit als gevolg van de grote controverse rond de ontdekking van de infinitesimaalrekening. Maar het resultaat daarvan was dat de Britse wiskunde enorm achterop raakte.
[..]
Je kunt bij dx en dy het best de overeenkomst met Δx en Δy in gedachten houden. Als x je onafhankelijke variabele is en y de daarvan afhankelijke variabele, dan is Δy dus het increment van de afhankelijke variabele y als gevolg van het increment Δx in de onafhankelijke variabele x. Evenzo voor dy en dx, zij het dat men zich oorspronkelijk voorstelde dat het hier ging om 'oneindig kleine' (infinitesimale) grootheden.
De notatie U(x) geeft alleen expliciet aan dat een variabele U afhangt van (dus een functie is van ) een variabele x. We noemen x dan de onafhankelijke variabele en U de (daarvan) afhankelijke variabele. Niettemin is hier sprake van een conceptuele verwarring tussen de naam van een functie en de naam van de afhankelijke variabele van die functie, dat is immers niet hetzelfde: je kunt een functie f hebben met als functievoorschrift y = f(x). Dan is y de afhankelijke variabele, maar de functie zelf wordt toch echt aangeduid met f, niet met y.
[..]
Ga eens even lekker grasduinen in Wikipedia. De raison d'être van de diverse notaties wordt je dan wel duidelijk.
(Ik zat ook al te grasduinen in google, blijkt dat ik niet de enige ben met dit probleem trouwens
)Wat ik nog steeds niet echt begrijp is die notatie van functies:
Je geeft met U(x) dus aan dat de waarde van U afhankelijk is van x, maar als je bijvoorbeeld dU/dx noteert, dan is U nog steeds afhankelijk van x. Waarom gebruik je dan gewoon U ipv U(x)?
dU/dx wordt gehanteerd als er geen verwarring is, net als b.v. met f', je ziet soms f'(x), soms f'. Er is (meestal) geen verschil.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
ik heb een vraag over een 5 x 5 matrix. (voordat iemand meteen verwijst naar een internetpagina, ze gaan allemaal over een matrix met nullen aan het begin, en die zijn anders).
Ik heb de volgende matrix:
1 2 4 0 1
2 4 0 1 1
4 0 1 1 2
0 1 1 2 4
1 1 2 4 0
Kan iemand mij vertellen hoe ik hier de determined van moet vinden?
Alvast bedankt!!
Kloontje
Ik heb de volgende matrix:
1 2 4 0 1
2 4 0 1 1
4 0 1 1 2
0 1 1 2 4
1 1 2 4 0
Kan iemand mij vertellen hoe ik hier de determined van moet vinden?
Alvast bedankt!!
Kloontje
Op weg naar sint juttemes.
Wat je je eerst moet beseffen is dat dit een vierkante matrix is, en dat je daarom de determinant kunt bepalen. Er zijn meerdere manieren om de determinant te bepalen, waarvan ik er drie zal uitlichten.
1:Ontwikkelen
Je moet een kolom of rij kiezen die je wilt gebruiken. Kies een rij of een kolom uit waarin de meeste nullen zitten. In dit geval maakt het niet veel uit. Stel we kiezen de eerste rij om de determinant mee te bepalen.
Dit betekent dat we met de 1ste rij gaan "ontwikkelen".
Je pakt de eerste " set " die je gaat uitrekenen: [1 2 , 2 4] (een , betekent dat het eronder ligt, ik ben niet goed met de layout etc.) Je moet je beseffen dat er een schaakbord patroon aanwezig is van + en - . D.w.z. : +1 -2 +4 -0 +1 etc. Het eerste cijfer van je rij is +1. Dus je neemt + 1. Wat je daarna doet is een soort van eigen methode die ik heb bedacht. Je kruist in gedachte de eerste rij weg en de eerste kolom (omdat je dus de 1ste rij hebt gekozen). Wat je overhoudt, daar moet je die + 1 mee vermenigvuldigen. Dus dat wordt:
+1 *
| 4 0 1 1 |
| 0 1 1 2 |
| 1 1 2 4 |
| 1 2 4 0 |
Daarna ga je verder met de volgende cijfer van je rij:
+ (-2) *
| etc. etc. |
Deze methode duurt mij eigenlijk te lang.
Wat je kunt doen is een bovendriehoeksmatrix of een onderdriehoeksmatrix vinden. De diagonaal daarvan (vermenigvuldigd) is ook de determinant.
Mijn rekenmachine geeft als det: 1048 op, maar ik weet niet of ik dit nu goed heb gedaan. Iemand die het wil verifieren.
1:Ontwikkelen
Je moet een kolom of rij kiezen die je wilt gebruiken. Kies een rij of een kolom uit waarin de meeste nullen zitten. In dit geval maakt het niet veel uit. Stel we kiezen de eerste rij om de determinant mee te bepalen.
Dit betekent dat we met de 1ste rij gaan "ontwikkelen".
Je pakt de eerste " set " die je gaat uitrekenen: [1 2 , 2 4] (een , betekent dat het eronder ligt, ik ben niet goed met de layout etc.) Je moet je beseffen dat er een schaakbord patroon aanwezig is van + en - . D.w.z. : +1 -2 +4 -0 +1 etc. Het eerste cijfer van je rij is +1. Dus je neemt + 1. Wat je daarna doet is een soort van eigen methode die ik heb bedacht. Je kruist in gedachte de eerste rij weg en de eerste kolom (omdat je dus de 1ste rij hebt gekozen). Wat je overhoudt, daar moet je die + 1 mee vermenigvuldigen. Dus dat wordt:
+1 *
| 4 0 1 1 |
| 0 1 1 2 |
| 1 1 2 4 |
| 1 2 4 0 |
Daarna ga je verder met de volgende cijfer van je rij:
+ (-2) *
| etc. etc. |
Deze methode duurt mij eigenlijk te lang.
Wat je kunt doen is een bovendriehoeksmatrix of een onderdriehoeksmatrix vinden. De diagonaal daarvan (vermenigvuldigd) is ook de determinant.
Mijn rekenmachine geeft als det: 1048 op, maar ik weet niet of ik dit nu goed heb gedaan. Iemand die het wil verifieren.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Je kunt ook met rijoperaties de matrix in driehoeksvorm brengen, als je bijhoudt hoe de determinant dan verandert.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja zolang hij niet rijen verwisseld of vermenigvuldigd, veranderd er toch niks als het goed is? Zoiets was het.quote:Op woensdag 9 december 2009 15:48 schreef Iblis het volgende:
Je kunt ook met rijoperaties de matrix in driehoeksvorm brengen, als je bijhoudt hoe de determinant dan verandert.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
zou je dat misschien uit kunnen leggen?quote:Op woensdag 9 december 2009 15:48 schreef Iblis het volgende:
Je kunt ook met rijoperaties de matrix in driehoeksvorm brengen, als je bijhoudt hoe de determinant dan verandert.
Ik heb de bovenstaande methode geprobeerd. Alleen vraag ik me af hoe het volgende moet:
stel ik heb
1*
2 4 0 1
4 0 1 1
0 1 1 2
1 1 2 4
Moet ik dan ( (2)(0) + (4)(4) ) + ( (0)(1) + (1)(1) ) uitrekenen? Dus als het ware steeds 4 cijfers nemen en die pakken.. of hoe moet het?
Op weg naar sint juttemes.
Ja, maar ook al doet hij dat wel, dan kan het nog.quote:
[..]
Ja zolang hij niet rijen verwisseld of vermenigvuldigd, veranderd er toch niks als het goed is? Zoiets was het.
Als je een rij met c vermenigvuldigd, moet je de determinant daarna ook door c delen, en als je twee rijen verwisselt met -1 vermenigvuldigen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Kloontje, mijn uitleg is niet super ik weet het. Het is echter een dermate grote matrix, dat ik je aanraad om gewoon een driehoeksvorm matrix te krijgen. En zoals Ibo zegt, als je tijdens dat proces vermenigvuldigd met c, dan moet je de determinant daarna ook met c delen. En als je twee rijen verwisselt, moet je met -1 vermenigvuldigen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
ok, thx. Ik zal even uit gaan zoeken hoe ik aan een driehoeksmatrix kom.quote:Op woensdag 9 december 2009 15:59 schreef Burakius het volgende:
Kloontje, mijn uitleg is niet super ik weet het. Het is echter een dermate grote matrix, dat ik je aanraad om gewoon een driehoeksvorm matrix te krijgen. En zoals Ibo zegt, als je tijdens dat proces vermenigvuldigd met c, dan moet je de determinant daarna ook met c delen. En als je twee rijen verwisselt, moet je met -1 vermenigvuldigen.
Op weg naar sint juttemes.
Ik weet niet wat je allemaal als voorkennis hebt, je kunt natuurlijk ook beide combineren. B.v. eerst één kolom allemaal 0-en maken op 1 na, en dan de cofactoren van Burakus kiezen. En zo voort.quote:
[..]
ok, thx. Ik zal even uit gaan zoeken hoe ik aan een driehoeksmatrix kom.
Dan werk je uiteindelijk naar een 2x2 matrix toe.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
a = 40+0,1 x (50 + 0,05a + 0,05 x (60 + 0,05a)) + 0,05 x (60 + 0,05a)
a = 48,7
Kan iemand mij vertellen hoe men a berekent? Zonder GR dan.
a = 48,7
Kan iemand mij vertellen hoe men a berekent? Zonder GR dan.
Gewoon haakjes uitwerken (zoals hier boven al staat), dan lost het zichzelf op. Ik denk alleen wel dat je een foutje hebt gemaakt met de 0'en in je berekening?quote:Op woensdag 9 december 2009 17:38 schreef Snuf. het volgende:
a = 40+0,1 x (50 + 0,05a + 0,05 x (60 + 0,05a)) + 0,05 x (60 + 0,05a)
a = 48,7
Kan iemand mij vertellen hoe men a berekent? Zonder GR dan.
Op weg naar sint juttemes.
Ik ben echt vet slecht in Wiskunde, maar is dit de uitwerking na de haakjes?
2000 x 0,1 + 2a + 120 + 0.1a
Ik denk het niet eigenlijk
2000 x 0,1 + 2a + 120 + 0.1a
Ik denk het niet eigenlijk
Ik zie geen =-teken meer in je uitwerking, dus nee, dit is zeker niet goed. Komop, iets beter je best doen. Nu lijkt het er teveel op dat je maar iets opschrijft in de hoop dat een ander zegt nee, dit is niet goed en je dan alles gaat voorkauwen.quote:Op woensdag 9 december 2009 18:26 schreef Snuf. het volgende:
Ik ben echt vet slecht in Wiskunde, maar is dit de uitwerking na de haakjes?
2000 x 0,1 + 2a + 120 + 0.1a
Ik denk het niet eigenlijk
Heey mensen,
Hier wordt de ratio test gebruikt, om te weten of het convergeert of divergeert. Nou geen probleem zou je zeggen. Nou an+1 / an etc. En dan delen is hetzelfde als vermenigvuldigen etc. En dan komt het stuk waarin opeens die -3 (n+2) opeens een 3 wordt en er doodleuk een 3 weggaat.
Nu heb ik dit eerder wel weten op te lossen, maar kom er nu niet op. Het zal vast iets met kruislings vermenigvuldigen zijn ofzo? Wie kan me helpen.
(dus het laatste deel dat onder absoluut strepen staat, dat snap ik niet, hoe dat zo is gekomen).
Hier wordt de ratio test gebruikt, om te weten of het convergeert of divergeert. Nou geen probleem zou je zeggen. Nou an+1 / an etc. En dan delen is hetzelfde als vermenigvuldigen etc. En dan komt het stuk waarin opeens die -3 (n+2) opeens een 3 wordt en er doodleuk een 3 weggaat.
Nu heb ik dit eerder wel weten op te lossen, maar kom er nu niet op. Het zal vast iets met kruislings vermenigvuldigen zijn ofzo? Wie kan me helpen.
(dus het laatste deel dat onder absoluut strepen staat, dat snap ik niet, hoe dat zo is gekomen).
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
2^3(n+1) wordt 2^(3n) * 2^3, en die -3 valt weg vanwege a^b / a^c = a^(b-c).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb een concreet probleem waarbij ik moeite heb te zien hoe ik dit wiskundig kan oplossen.
Ik moet bepalen wat de gunstigste plek is voor twee noodgevallencentra (politie/brandweer/etc.). Ik heb een veld van 5 bij 10 "huizenblokken" met wegen ertussen. Van ieder blok is het aantal ongevallen bekend uit een eerder jaar. Zo'n centrum komt op hoek van zo'n blok. Ik mag aannemen dat de ongelukken in het midden van een blok gebeuren. Verder doet een wagen er gemiddeld 15 seconden over om een blok in N-Z richting te passeren en gemiddeld 20 seconden in O-W richting.
Iemand die me een een duwtje in de goede richting kan geven?
Ik moet bepalen wat de gunstigste plek is voor twee noodgevallencentra (politie/brandweer/etc.). Ik heb een veld van 5 bij 10 "huizenblokken" met wegen ertussen. Van ieder blok is het aantal ongevallen bekend uit een eerder jaar. Zo'n centrum komt op hoek van zo'n blok. Ik mag aannemen dat de ongelukken in het midden van een blok gebeuren. Verder doet een wagen er gemiddeld 15 seconden over om een blok in N-Z richting te passeren en gemiddeld 20 seconden in O-W richting.
Iemand die me een een duwtje in de goede richting kan geven?
Is er een bepaald onderwerp waarmee je bezig bent? Want dit probleem laat zich wel op meerdere manieren modelleren (of zelfs gewoon met brute kracht uitrekenen op een beperkte dataset), maar meestal heeft men wel een model in gedachten afhankelijk van de stof die behandeld wordt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het is voor het vak Modelleren, de eerste opdracht. Ik moet dus eigenlijk zelf een manier gaan bedenken, bronnen zoeken die me een manier geven ofzo.
Of bedoel je dat ik maar in de boeken van andere vakken moet gaan zoeken?quote:
Iemand die me een een duwtje in de goede richting kan geven?
Nee, nou, tja, ik vind het wat lastig om echt wat aan te raden omdat ik niet weet welke vakken je gehad hebt. Ik zou beginnen met een soort coördinatensysteem te maken voor de locaties en de centra, en dan b.v. een formule te bedenken die aanrijdtijd geeft voor een centra-locatie en een ongevallocatie.quote:
[..]
Of bedoel je dat ik maar in de boeken van andere vakken moet gaan zoeken?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
De vraag:
Toon aan dat de volgende Quine-variant van de Russell-formule geen modellen heeft:
∃x ∀y (Rxy ↔ ¬R2yy)
met R2uv ↔ ∃s (Rus ∧ Rsv).
Wat ik er niet van snap:
Wat is 'n "Quine-variant", wat is 'n "Russell-formule", wat wordt er precies bedoelt met 'n model?
Toon aan dat de volgende Quine-variant van de Russell-formule geen modellen heeft:
∃x ∀y (Rxy ↔ ¬R2yy)
met R2uv ↔ ∃s (Rus ∧ Rsv).
Wat ik er niet van snap:
Wat is 'n "Quine-variant", wat is 'n "Russell-formule", wat wordt er precies bedoelt met 'n model?
Quine was ook een logicus, dat is verder irrelevant voor de vraag. Maar de Russellformule wordt ook eerder in het boek gegeven (voorbeeld 7.3) en wat een model is, dat moet je inmiddels wel weten, dat is anders opnieuw het hoofdstuk lezen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik dacht al aan zoiets, mijn eerdere idee was een soort graaf., alleen dan weet ik niet hoe ik die aantal ongevallen uit een eerder jaar erin moet verwerken.
Ik ga er wel mee spelen en misschien valt dan van alles vanzelf op zijn plek. Had het makkelijker gevonden als precies was gezegd waar ik op moest optimaliseren ofzo.
Thanks iig.
Ik ga er wel mee spelen en misschien valt dan van alles vanzelf op zijn plek. Had het makkelijker gevonden als precies was gezegd waar ik op moest optimaliseren ofzo.
Thanks iig.
Ja ik weet dat 'n model bestaat uit een domein en een interpretatiefunctie. Maar ik snap niet wat ze hiermee precies willen met deze vraag. Ik heb echt geen idee hoe ik moet aantonen dat iets geen modellen heeft.
In het model moet je ook de interpretatie geven. Zou je dan niet kunnen zeggen dat als het in het ene model niet waar is, je een model kan geven waar de interpretatie van R' "¬R" is, waardoor je er dus altijd iig een model is waarbij het waar is? (Tegenovergestelde van wat je moet aantonen, dus een vraag aan Iblis. )
)
Hallo allemaal,
Ik zit in de knoop met de volgende som, misschien is er iemand die me kan helpen?
Ik heb een matrix:
| -1 -1 |
| 6 4 |
De bedoeling is dat ik hem diagonalizeer (CDC^-1)
Kortom, ik heb de eigenvalues en de eigenvectors nodig. Geen probleem opzich, ware het niet dat het me niet lukt!
Dit heb ik:
| -1 -1 | - | x 0 |
| 6 4 | - | 0 x |
| -1-x -1 |
| 6 4-x|
(x is lamda)
Nu is de enige uitleg die in mijn handout staat een 2 x 2 matrix waarbij je linksonder nul kunt maken (en dat kan hier niet toch? Ik dacht aan C1=C1-C2 en dan R2=R2-R1 en nog een keer R2=R2-R1, maar dat werkt niet).
Is er iemand die een makkelijkere manier heeft? Het gaat puur om de eigenvalue's, de rest weet ik.
Alvast bedankt!
PS: ik zat te denken om misschien rechtsboven nul te maken, door C2=C2-C1. Maar dan heb ik 3 eigenvalues, mag dat?
Ik zit in de knoop met de volgende som, misschien is er iemand die me kan helpen?
Ik heb een matrix:
| -1 -1 |
| 6 4 |
De bedoeling is dat ik hem diagonalizeer (CDC^-1)
Kortom, ik heb de eigenvalues en de eigenvectors nodig. Geen probleem opzich, ware het niet dat het me niet lukt!
Dit heb ik:
| -1 -1 | - | x 0 |
| 6 4 | - | 0 x |
| -1-x -1 |
| 6 4-x|
(x is lamda)
Nu is de enige uitleg die in mijn handout staat een 2 x 2 matrix waarbij je linksonder nul kunt maken (en dat kan hier niet toch? Ik dacht aan C1=C1-C2 en dan R2=R2-R1 en nog een keer R2=R2-R1, maar dat werkt niet).
Is er iemand die een makkelijkere manier heeft? Het gaat puur om de eigenvalue's, de rest weet ik.
Alvast bedankt!
PS: ik zat te denken om misschien rechtsboven nul te maken, door C2=C2-C1. Maar dan heb ik 3 eigenvalues, mag dat?
Op weg naar sint juttemes.
Eigenwaarden bereken je door de determinant van
gelijk te stellen aan nul. Determinant bereken je door x11x22-x21x12. In dit geval dus (-1-x)(4-x)-(6*-1)
gelijk te stellen aan nul. Determinant bereken je door x11x22-x21x12. In dit geval dus (-1-x)(4-x)-(6*-1)
Oftwel -4-+x-4x-x^2 - (-6)quote:Op donderdag 10 december 2009 20:32 schreef Hanneke12345 het volgende:
Eigenwaarden bereken je door de determinant van
[ afbeelding ]
gelijk te stellen aan nul. Determinant bereken je door x11x22-x21x12. In dit geval dus (-1-x)(4-x)-(6*-1)
2 - x - 4x + x^2
Oh wacht even! het wordt dus x^2 - 3 x + 2, ABC formule?
= 2 of 1
Thanks!!
Op weg naar sint juttemes.
Ik zou gewoon een tegenspraak afleiden, lijkt me wel het makkelijkst. Als een formule tot een tegenspraak leidt, heeft-ie ook geen modellen.quote:Op donderdag 10 december 2009 19:36 schreef Diabox het volgende:
Ja ik weet dat 'n model bestaat uit een domein en een interpretatiefunctie. Maar ik snap niet wat ze hiermee precies willen met deze vraag. Ik heb echt geen idee hoe ik moet aantonen dat iets geen modellen heeft.
Ik vertypte me, ik bedoelde voorbeeld 7.13, mijn excuses. Ik heb het even uit Google books gepikt:quote:
Ja ik weet dat 'n model bestaat uit een domein en een interpretatiefunctie. Maar ik snap niet wat ze hiermee precies willen met deze vraag. Ik heb echt geen idee hoe ik moet aantonen dat iets geen modellen heeft.
Dat is een belangrijke aanwijzing, ik weet niet of je dat volgt?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik volg het voorbeeld, ik snap nu ook wat beter wat ze met de vraag willen/bedoelen, maar;quote:Op donderdag 10 december 2009 22:11 schreef Iblis het volgende:
[..]
Ik vertypte me, ik bedoelde voorbeeld 7.13, mijn excuses. Ik heb het even uit Google books gepikt:
[ afbeelding ]
Dat is een belangrijke aanwijzing, ik weet niet of je dat volgt?
Het dikgedrukte snap ik niet helemaal.quote:Toon aan dat de volgende Quine-variant van de Russell-formule geen modellen heeft:
∃x ∀y (Rxy ↔ ¬R2yy)
met R2uv ↔ ∃s (Rus ∧ Rsv).
Verder heb ik nog een andere vraag. Bij het opstellen van een semantische tableau moet(en) vaak (?altijd?) domein(en) worden toegekend. Mijn probleem is;
1. Ik snap niet waarom er een domein moet worden toegekend
2. Ik weet niet wanneer ik maar 1, of meerdere domeinen moet toekennen. Als ik een x zie maak ik hier domein d1 van en als ik een y zie maar ik hier domein d2 van, dit is in sommige gevallen (al dan niet toevallig) goed, maar in andere gevallen kon ik voor beide x hetzelfde domein d1 gebruiken.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Edit:
Oke hier even 'n uitwerking van zo'n semantisch tableau met cijfertjes toegevoegd op de punten waar ik niet snap wat er nu precies gebeurt:
http://i45.tinypic.com/2yuc9pc.jpg
1. Waarom kennen ze d1 ook toe aan y?
2. Waarom kennen ze d1 ook toe aan z?
3. Waarom kennen ze hier dan weer d2 toe aan z?
4. Waarom laten ze eerst dit zien en dan pas 5? Andersom mag ook? En hoezo is die <-> er weer?
5. Zie 4.
6. Wat gebeurt hier, 4x R(domein, domein), met verschillende combinaties van domeinen zeg maar
[ Bericht 9% gewijzigd door Diabox op 10-12-2009 23:16:18 ]
Heey,
Ik heb een probleempje met het vinden van een geschikte elliptische kromme E. Gegeven een natuurlijk getal N van ongeveer 8 cijfers wil ik een elliptische kromme E en een priemgetal p vinden met de eigenschap:
#E(Fp)=N.
Wat ik heb gedaan is het volgende, ik kies een priemgetal p in het Hasse interval
[N-2sqrt(N),N +2sqrt(N)] het liefst dichtbij de grenzen N+/- 2sqrt(N). Daarna vind ik een geheel getal t met de eigenschap N=p+1-t en D:=t^2-4p < 0. Ook wens ik dat |D| in de buurt van 0 ligt of dat D deelbaar is door een relatief grote kwadraat, dus D=k^2D' met |D'| veel kleiner is dan |D|.
Dit kan allemaal gedaan worden met for-loops op maple en/of magma/sage. Voor het negatieve getal D (of D') ga ik vervolgens het Hilbert polynoom HD uitrekenen. Als het goed is, ontbindt dit polynoom zich in lineaire factoren in Fp[X]. Een van de nulpunten noem ik j_0. Blijkbaar
kan ik een elliptische kromme over Fp van de vorm y2=x3+cx+c en waarvan
de j-invariant is gelijk aan j_0. Ik kan met gemak c uitrekenen en deze kromme zou dan het gewenste aantal punten N moeten hebben.
Ik heb nu een probeem dat mijn Hilbert polynoom niet ontbonden wordt in lineaire factoren... ik heb het gevoel dat ik iets fouts doe!
Kan iemand even kijken waar het misgaat bij dit algortime? Kan het beter/sneller?
Ik heb een probleempje met het vinden van een geschikte elliptische kromme E. Gegeven een natuurlijk getal N van ongeveer 8 cijfers wil ik een elliptische kromme E en een priemgetal p vinden met de eigenschap:
#E(Fp)=N.
Wat ik heb gedaan is het volgende, ik kies een priemgetal p in het Hasse interval
[N-2sqrt(N),N +2sqrt(N)] het liefst dichtbij de grenzen N+/- 2sqrt(N). Daarna vind ik een geheel getal t met de eigenschap N=p+1-t en D:=t^2-4p < 0. Ook wens ik dat |D| in de buurt van 0 ligt of dat D deelbaar is door een relatief grote kwadraat, dus D=k^2D' met |D'| veel kleiner is dan |D|.
Dit kan allemaal gedaan worden met for-loops op maple en/of magma/sage. Voor het negatieve getal D (of D') ga ik vervolgens het Hilbert polynoom HD uitrekenen. Als het goed is, ontbindt dit polynoom zich in lineaire factoren in Fp[X]. Een van de nulpunten noem ik j_0. Blijkbaar
kan ik een elliptische kromme over Fp van de vorm y2=x3+cx+c en waarvan
de j-invariant is gelijk aan j_0. Ik kan met gemak c uitrekenen en deze kromme zou dan het gewenste aantal punten N moeten hebben.
Ik heb nu een probeem dat mijn Hilbert polynoom niet ontbonden wordt in lineaire factoren... ik heb het gevoel dat ik iets fouts doe!
Kan iemand even kijken waar het misgaat bij dit algortime? Kan het beter/sneller?
De j-invariant van een elliptische kromme bepaalt z'n isomorfieklasse slechts over een algebraisch afgesloten lichaam. Het zou kunnen dat je nog een twist moet toepassen op de verkregen kromme om het gewenste resultaat te krijgen. Maar goed, dat verklaart verder niet wat er misgaat met H_D.
Kun je posten wat je allemaal hebt (dus N, p, D H_D etc?) want ik kan niet zo een twee drie ruiken wat er aan de hand is.
Kun je posten wat je allemaal hebt (dus N, p, D H_D etc?) want ik kan niet zo een twee drie ruiken wat er aan de hand is.
Om het eenvoudig te houden:quote:Op zaterdag 12 december 2009 20:13 schreef thabit het volgende:
De j-invariant van een elliptische kromme bepaalt z'n isomorfieklasse slechts over een algebraisch afgesloten lichaam. Het zou kunnen dat je nog een twist moet toepassen op de verkregen kromme om het gewenste resultaat te krijgen. Maar goed, dat verklaart verder niet wat er misgaat met H_D.
Kun je posten wat je allemaal hebt (dus N, p, D H_D etc?) want ik kan niet zo een twee drie ruiken wat er aan de hand is.
N=101
p=83
D=-43
H_d= x + 884736000 dus H_d= x-10 mod 83
J_0=10
J(y^2=x^3+cx+c)=1728*4c/(4c+27) dus c moet zijn 135/3436 en in F83 is c=72.
Nu is het aantal punten op y^2=x^3-11x-11 gelijk aan 67 en dat is niet 101.
Okee, dan moet je dus de kwadratische twist van die kromme nemen. Het spoor t van de Frobenius is voor jouw kromme gelijk aan 84-67 = 17. Neem je z'n kwadratische twist dan krijg je een kromme met Frobeniusspoor -t = -17 en dus met 84+17 = 101 rationale punten.
Het is me gelukt! Ik koos een niet kwadraat in het eindige lichaam en uiterdaad voldoet de 'twisted' kromme aan de eisen.
Even een vraagje of ik de volgende formule zo goed heb omgezet. Ik wil n weten.
wordt
Ik twijfel nogal en weet ook niet of het in 1 stap kan. Ik hoop van wel, dan kan ik die methode gewoon aanhouden. Anders zal ik wel via die formule (buiten het delen door 2 en het aftrekken van 1) het antwoord gelijk kunnen stellen aan 2n-1 en dan eerst die 1 aan de andere kant erbij tellen, om vervolgens door 2 te delen, toch?
Alvast bedankt voor de replies
wordt
Ik twijfel nogal
en weet ook niet of het in 1 stap kan. Ik hoop van wel, dan kan ik die methode gewoon aanhouden. Anders zal ik wel via die formule (buiten het delen door 2 en het aftrekken van 1) het antwoord gelijk kunnen stellen aan 2n-1 en dan eerst die 1 aan de andere kant erbij tellen, om vervolgens door 2 te delen, toch?Alvast bedankt voor de replies
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
Nee, is niet goed. Je hebt de volgorde van twee bewerkingen omgekeerd.quote:Op zondag 13 december 2009 17:36 schreef beertenderrr het volgende:
Even een vraagje of ik de volgende formule zo goed heb omgezet. Ik wil n weten.
[ afbeelding ]
wordt
[ afbeelding ]
Ik twijfel nogal
Alvast bedankt voor de replies
welke precies en hoe zou het dan moeten zijn?quote:Op zondag 13 december 2009 17:39 schreef Riparius het volgende:
[..]
Nee, is niet goed. Je hebt de volgorde van twee bewerkingen omgekeerd.
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
Je hebt:quote:Op zondag 13 december 2009 17:42 schreef beertenderrr het volgende:
[..]
welke precies en hoe zou het dan moeten zijn?
f = (2n - 1)v/4l
Beide leden met 4l/v vermenigvuldigen geeft:
4fl/v = 2n - 1
Bij beide leden 1 optellen geeft:
4fl/v + 1 = 2n
En dus krijgen we na beide leden door 2 te delen:
n = (4fl/v + 1)/2
ahh oke, duidelijk, thnxquote:Op zondag 13 december 2009 17:56 schreef Riparius het volgende:
[..]
Je hebt:
f = (2n - 1)v/4l
Beide leden met 4l/v vermenigvuldigen geeft:
4fl/v = 2n - 1
Bij beide leden 1 optellen geeft:
4fl/v + 1 = 2n
En dus krijgen we na beide leden door 2 te delen:
n = (4fl/v + 1)/2
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
Ik wil even een bedankje doen aan de mensen die me hebben geholpen met die paar logica vragen die ik had, ik heb net mijn tentamen gemaakt en die is sowieso hoger dan een 9 
"Reality is an illusion created by a lack of alcohol."
hee allemaal,
Ik heb een dringende vraag over wiskunde/natuurkunde...
Ik moet het toerental van een automotor berekenen in rpm
ik heb de volgende gegevens:
diameter wiel 59,18 cm
snelheid 6,9m/s
massa 175 kg
Tcontinu =2,90988
Tacceleratie=8,846
ik weet niet of deze gegevens allemaal nodig zijn, als iemand maar weet hoe ik de rpm kan berekenen.
(T = koppel)
help me
Ik heb een dringende vraag over wiskunde/natuurkunde...
Ik moet het toerental van een automotor berekenen in rpm
ik heb de volgende gegevens:
diameter wiel 59,18 cm
snelheid 6,9m/s
massa 175 kg
Tcontinu =2,90988
Tacceleratie=8,846
ik weet niet of deze gegevens allemaal nodig zijn, als iemand maar weet hoe ik de rpm kan berekenen.
(T = koppel)
help me
ik heb deze som al eens eerder opgelost, maar nu kom ik er gewoon niet op.
Ik heb deze formule:
Q= 100P^(-2)
En moet dan wiskundig laten zien dat de prijs elasticiteit altijd -2 is.
Ik heb deze formule:
Q= 100P^(-2)
En moet dan wiskundig laten zien dat de prijs elasticiteit altijd -2 is.
Wat is dQ/dP? En wat krijg je als je dat *P/Q doet?quote:
ik heb deze som al eens eerder opgelost, maar nu kom ik er gewoon niet op.
Ik heb deze formule:
Q= 100P^(-2)
En moet dan wiskundig laten zien dat de prijs elasticiteit altijd -2 is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ok, dan krijg ik de -2.quote:Op dinsdag 15 december 2009 17:26 schreef GlowMouse het volgende:
[..]
Wat is dQ/dP? En wat krijg je als je dat *P/Q doet?
Maar hoe kom je bij die formule? Elasticiteit is richtingscoeficient x p/q. Waarom kan je dan nu de afgeleide gebruiken?
De richtingscoefficient is natuurlijk de afgeleide van een functie.
"Reality is an illusion created by a lack of alcohol."
DOH!quote:Op dinsdag 15 december 2009 17:36 schreef Dzy het volgende:
De richtingscoefficient is natuurlijk de afgeleide van een functie.
Hoe kan ik dat nou gemist hebben.
Glowmouse en Dzy, bedankt voor de snelle antwoorden op deze domme vraag
.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |
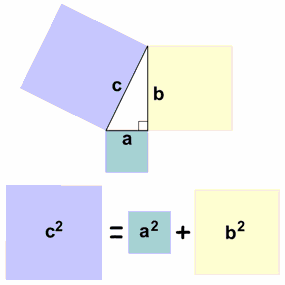