Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
.Maar hoe integreer je dit, voor een algemene n?
7 minuten is niet echt snelquote:
Lukt dit niet met 2x partiëel en daarna een vergelijking oplossen?quote:Op zondag 9 januari 2011 19:53 schreef BasementDweller het volgende:
Ik wil de Fourierreeks van cos(x)^n bepalen. Voor de coëfficiënten c_k geldt
[ afbeelding ]
Maar hoe integreer je dit, voor een algemene n?
Hoe bepaal je ze dan?quote:
Ik zou cos(x) gewoon als (e^(ix) + e^(-ix)) / 2 schrijven. Dan hoef je niet eens te integreren om de Fouriercoëfficiënten te bepalen.
Met het binomium van Newton.quote:
Heb het al, krijg als coëfficiënten c_k:
Bedankt
Lijkt me overigens met partiëel integreren (haast) ondoenbaar.
[ Bericht 33% gewijzigd door BasementDweller op 09-01-2011 22:52:49 ]
je linkt werkt niet bij mensen die geen 182 posts op één pagina hebben; [Bèta wiskunde] Huiswerk-en-vragentopic werkt wel.quote:
Thabit, hoe zit het hiermee: [Bèta wiskunde] Huiswerk-en-vragentopic ?
Sjongejonge, slecht ontwerp.quote:
[..]
je linkt werkt niet bij mensen die geen 182 posts op één pagina hebben; [Bèta wiskunde] Huiswerk-en-vragentopic werkt wel.
.Calculator die integralen kan uitrekenen, kan differentieren en nog meer. Ook een om met matrices te rekenen, best handig.
Dan een simpel (?) vraagje:
Ik probeer de homotopische equivalentie van een aantal verzamelingen te laten zien. Ik weet wel welke afbeeldingen daarvoor zorgen, alleen ik krijg ze niet formeel geschreven. Volgens mij is het vrij elementaire calculus, maar daar ben ik dus echt slecht in.
Hieronder wat ik zelf voor elkaar krijg:
1)Homotopische equivalentie van een ring in R2 en de eenheidscirkel.
2)Open schijf met weggelaten punt {z: 0<|z|<1 } in C en de eenheidscirkel
3)Rn\{0} en Sn
Dus wat ik graag zou weten is, hoe ik die functies netjes beschrijf en hoe ik eraan kom. Ik zie bijvoorbeeld bij 2, dat je met de functie z/|z| wel alle punten van de schijf op de eenheidscirkel krijgt.
Bij 3. wordt het iets van x/||x|| en de gewone inclusie voor de andere kant...
Denk niet dat het (veel) beter is dan wolframalpha.comquote:
Misschien iets voor in de OP: http://wims.unice.fr/wims/en_home.html
Ik zie niet zo gauw hoe dat zonder goniometrie kan. Moet ongetwijfeld wel mogelijk zijn.quote:
Thabit, hoe zit het hiermee: [Bèta wiskunde] Huiswerk-en-vragentopic ?
quote:
[..]
Ik zie niet zo gauw hoe dat zonder goniometrie kan. Moet ongetwijfeld wel mogelijk zijn.
het ging om post #182: [Bèta wiskunde] Huiswerk-en-vragentopicAh, zo, ik keek naar de post eronder.quote:
[..]
.In de formule e1T(e2A) =/= (e1Te2)A is e2A helemaal niet gedefinieerd.
Pardon?quote:Op woensdag 12 januari 2011 00:17 schreef thabit het volgende:
Tja, analyse, da's ook meer natuurkunde dan wiskunde.
Nou kom ik uit op de breuk 3p³+p / p³+p.
Hoe kan ik deze verder vereenvoudigen? Het antwoordmodel zegt namelijk 3 - 2/p²+1 ?
e2t * e-t
Ben even roestig weer. Thx
exp(t)quote:
Wat krijg je van:
e2t * e-t
Ben even roestig weer. Thx
Ik kom er zelfs met wat je zegt niet uit (heb totaal geen wiskundig inzichtquote:
gebruik dat (a+b)/c = a/c + b/c en schrijf 3p² = 2p² + p² en schrijf p³+p = p(p²+1)
), kan je het wat uitgebreider uitleggen en ook uitleggen hoe je weet dat je dat moet doen?Je kijkt er nog geen 10 minuten naar. Heb je al pen en papier gepakt, alles opgeschreven, en geprobeerd wat ik zei?quote:
[..]
Ik kom er zelfs met wat je zegt niet uit (heb totaal geen wiskundig inzicht
Zoiets weet je door ervaring.
Heb al 2 kantjes van een kladblok vol met probeersels en geen enkele komt uit op de goede vereenvoudiging...quote:Op woensdag 12 januari 2011 18:57 schreef GlowMouse het volgende:
[..]
Je kijkt er nog geen 10 minuten naar. Heb je al pen en papier gepakt, alles opgeschreven, en geprobeerd wat ik zei?
Zoiets weet je door ervaring.
Hoe kom je hierop? Misschien is dat al fout...quote:
Nou kom ik uit op de breuk 3p³+p / p³+p.
Elasticiteit = deltaQ/deltaP * P/Q. y (p) = p³+pquote:
[..]
Hoe kom je hierop? Misschien is dat al fout...
Elasticiteit = (3p²+1) * P / p³+p = p(3p²+1) / p³+p = 3p³+p / p³+p = ?
Dat is toch goed of niet?
Daar kom ik ook niet op uit, maar weer even verder puzzelen..quote:
Misschien klopt het antwoord wel niet. Ik kom op 1 + ( 2p² / (p²+1) )
Elasticiteit = (3p²+1) * p/q = p(3p²+1)/(p³+p) = (3p³+p)/(p³+p) = (p³+p)/(p³+p) + 2p³/(p³+p) = 1 + 2p²/(p²+1) . Zelfde als GM...
Dan klopt het antwoord inderdaad gewoon niet. Bedankt jongens, dit maakt een hoop duidelijk.quote:
Dus eigenlijk bedoel je met y(p), q(p). Afgeleide klopt, alleen je vergeet wat haakjes:
Elasticiteit = (3p²+1) * p/q = p(3p²+1)/(p³+p) = (3p³+p)/(p³+p) = (p³+p)/(p³+p) + 2p³/(p³+p) = 1 + 2p²/(p²+1) . Zelfde als GM...
Het antwoord dat je eerst zelf gaf (uit het antwoordenboekje) klopt wel als vereenvoudiging van de breuk die je zelf geeft, dus je trekt de verkeerde conclusie. Heb je wel eens iets aan breuken gedaan op de lagere school?quote:
[..]
Dan klopt het antwoord inderdaad gewoon niet. Bedankt jongens, dit maakt een hoop duidelijk.
Grappig.quote:
[..]
Het antwoord dat je eerst zelf gaf (uit het antwoordenboekje) klopt wel, dus je trekt de verkeerde conclusie. Heb je wel eens iets aan breuken gedaan op de lagere school?
Leg eens uit dan waarom het wel klopt en waarom GM en BD daar ook niet op uitkomen?
Waar wij op uitkomen kun je herschrijven naar het antwoord. Als je aan het antwoord twijfelt, kun je een paar p's invullen en vergelijken met jouw antwoord.quote:
[..]
Grappig.
Leg eens uit dan waarom het wel klopt en waarom GM en BD daar ook niet op uitkomen?
Je wilde weten waarom (3p³+p)/(p³+p) gelijk is aan 3 - 2/(p²+1).quote:
[..]
Grappig.
Leg eens uit dan waarom het wel klopt en waarom GM en BD daar ook niet op uitkomen?
(3p³+p)/(p³+p) = (3(p³+p) - 2p) / (p³+p) = 3 - 2p/(p³+p) = 3 - 2/(p²+1).
Als je haakjes plaatst dan klopt het antwoord wel, dus ik hoop dat ze in je antwoordenboekje wel haakjes gebruiken.
Als ik het nu hierboven zie lijkt het heel logisch, maar als ik dat zelf moet bedenken kom ik daar echt nooit op..quote:
Zo kan je het ook vereenvoudigen idd:
(3p³+p)/(p³+p) = (3(p³+p) - 2p) / (p³+p) = 3 - 2p/(p³+p) = 3 - 2/(p²+1).
Als je haakjes plaatst dan klopt het antwoord wel, dus ik hoop dat ze in je antwoordenboekje wel haakjes gebruiken.
Blij dat het tentamen gewoon open vragen zijn, dan krijg je tenminste punten als je de berekening grotendeels goed doet, de tussentoetsen waren MC.
quote:
[..]
Als je aan het antwoord twijfelt, kun je een paar p's invullen en vergelijken met jouw antwoord.
Als je gestopt was bij (3p³+p)/(p³+p) dan zou je (wat mij betreft) alle punten moeten krijgen, alleen omdat teller en noemer nogal op elkaar lijken ligt vereenvoudigen nog wel voor de hand hier.quote:
[..]
Als ik het nu hierboven zie lijkt het heel logisch, maar als ik dat zelf moet bedenken kom ik daar echt nooit op..
Blij dat het tentamen gewoon open vragen zijn, dan krijg je tenminste punten als je de berekening grotendeels goed doet, de tussentoetsen waren MC.
MC vragen bij berekeningen is wel erg triest trouwens
. Doe dan: laat zien dat de elasticiteit =... , of doe gewoon "bereken de elasticiteit".Had ik even gemist, maar dat gebruik ik inderdaad ook wel. Ik kon er alleen niet over uit dat ik de verdere vereenvoudiging niet snapte.quote:
[..]
Als je aan het antwoord twijfelt, kun je een paar p's invullen en vergelijken met jouw antwoord.
Ja, en dan bij antwoord E neerzetten "Geen van bovenstaande antwoorden is correct.".quote:
[..]
Als je gestopt was bij (3p³+p)/(p³+p) dan zou je (wat mij betreft) alle punten moeten krijgen, alleen omdat teller en noemer nogal op elkaar lijken ligt vereenvoudigen nog wel voor de hand hier.
MC vragen bij berekeningen is wel erg triest trouwens
En dan stuk voor stuk na moeten gaan of jou antwoord omgeschreven kan worden naar A,B,C of Dquote:
Ja, en dan bij antwoord E neerzetten "Geen van bovenstaande antwoorden is correct.".
Jup.quote:
[..]
En dan stuk voor stuk na moeten gaan of jou antwoord omgeschreven kan worden naar A,B,C of D
1 / (1-x) + 1 / (1+x) = 3
Alvast erg bedankt
Hmm
Stel je vermenigvuldigt met (1-x) dan krijg je (1-x) / (1-x) + (1-x) / (1+x) = 3(1-x)
En daar kwam dacht ik 1 - x = 3 - 3x
Waar zit de fout?
Laat zien of de volgende lineaire afbeeldingen injectief, surjectief of bijectief is:
f: R3->R2 : (x,y,z) |--> (x-y,2z)
Injectief:
Nee, want voor elke x,y in R, met x=/ 0, en x=y geldt voor z=0
f(x,y,z) = (0,0)
Aangezien x=y=/0, is deze afbeelding dus niet injectief.
Surjectief:
f(1,0,0) = (1,0) =f(v1)
f(0,1,0) = (-1,0)= f(v2)
f(0,0,1)= (0,1) = f(v3)
We zien dus dat L(f(v1),f(v3))= R2. Aangezien voor elke x,y,z in R (x-y,2z) een element uit R2 is, is f dus surjectief.
Je laatste zin snap ik niet (wat is L?). Surjectief toon je aan dat elk element uit R² bereikt kan worden, en dat volgt idd uit lineariteit, f(v1) en f(v3).
Klopt, dat was een typefoutje.quote:
f(v3) is geen (0,1) maar (0,2).
Je laatste zin snap ik niet (wat is L?). Surjectief toon je aan dat elk element uit R² bereikt kan worden, en dat volgt idd uit lineariteit, f(v1) en f(v3).
Met L(f(v1),f(v3)) bedoel ik het lineaire opspansel van f(v1),f(v3).
Dit stukje vind ik ook een beetje vaag. Bedoel je met de laatste zin misschien: aangezien f(0,0,0)=(0,0) is de afbeelding niet injectief?quote:
Kan iemand hierheen kijken?
Laat zien of de volgende lineaire afbeeldingen injectief, surjectief of bijectief is:
f: R3->R2 : (x,y,z) |--> (x-y,2z)
Injectief:
Nee, want voor elke x,y in R, met x=/ 0, en x=y geldt voor z=0
f(x,y,z) = (0,0)
Aangezien x=y=/0, is deze afbeelding dus niet injectief.
Ik zou het zo doen:
Injectief betekent f(x)=f(y) => x=y. Het is makkelijk om met tegenspraak te laten zien dat ie niet injectief is; Stel f is injectief. Dan volgt uit f(0,0,1)=f(1,1,1)=(0,2), dat (0,0,1)=(1,1,1) (tegenspraak).
Ik maak gebruik van het gegeven dat als Ker f = 0 dan en alleen dan is f injectief.quote:
[..]
Dit stukje vind ik ook een beetje vaag. x mag ook best nul zijn, want dan is x-y ook nog nul als x=y.
Ik zou het zo doen:
Injectief betekent f(x)=f(y) => x=y. Het is makkelijk om met tegenspraak te laten zien dat ie niet injectief is; Stel f is injectief. Dan volgt uit f(0,0,1)=f(1,1,1)=(0,0,2), dat (0,0,1)=(1,1,1) (tegenspraak).
Bewijs:
Stel alleen f(0)=0
Dan voor f(v)=f(v') , dan f(v-v')=f(0) betekent dat v=v'.
Oftewel de definitie van injectief.
Ah ja, zo kan het ookquote:
[..]
Ik maak gebruik van het gegeven dat als Ker f = 0 dan en alleen dan is f injectief.
Bewijs:
Stel alleen f(0)=0
Dan voor f(v)=f(v') , dan f(v-v')=f(0) betekent dat v=v'.
Oftewel de definitie van injectief.
Het klinkt stom, maar kan iemand me een voorbeeld geven van een niet surjectieve afbeelding?quote:
Op En belangrijker, hoe bewijs je dat?
f: R-> R , f(x)=x²quote:
[..]
Het klinkt stom, maar kan iemand me een voorbeeld geven van een niet surjectieve afbeelding?
En belangrijker, hoe bewijs je dat?
f is niet surjectief omdat f(x)=/ -1 voor alle x in het domein van f (een kwadraat is altijd niet-negatief). Dus -1 ligt wel in het codomein maar wordt niet bereikt => niet surjectief.
Maar het codomein wordt dus niet beschreven door, in dit geval, x2, maar is gewoon R ?quote:Op donderdag 13 januari 2011 14:22 schreef BasementDweller het volgende:
[..]
f: R-> R , f(x)=x²
f is niet surjectief omdat f(x)=/ -1 voor alle x (een kwadraat is altijd niet-negatief). Dus -1 ligt wel in het codomein maar wordt niet bereikt => niet surjectief.
Ja. Het codomein mag je eigenlijk zelf kiezen, zo lang het bereik van de functie er maar een deelverzameling van is.quote:
[..]
Maar het codomein wordt dus niet beschreven door, in dit geval, x2, maar is gewoon R ?
Als je dezelfde functie had genomen met als codomein: alle niet-negatieve reële getallen, dan was ie wel surjectief geweest.
Ik zie net je edit:quote:
[..]
Ja. Het codomein mag je eigenlijk zelf kiezen, zo lang het bereik van de functie er maar een deelverzameling van is.
Als je dezelfde functie had genomen met als codomein: alle niet-negatieve reële getallen, dan was ie wel surjectief geweest.
Alles mbt surjectieviteit word meteen een stuk duidelijker.
Bedankt!
N=natuurlijke getallen? Dan heb je je functie niet goed gedefiniëerd, want dan heeft f(1/2) geen uitkomst, want (1/2)^2 = 1/4 (niet in N).quote:
[..]
Dus als het codomein N, domein gewoon R laten, in dit geval was geweest, was de functie wél surjectief?
Klopt, ik merkte het al toen ik op invoeren drukte.quote:
[..]
N=natuurlijke getallen? Dan heb je je functie niet goed gedefiniëerd, want dan heeft f(1/2) geen uitkomst, want (1/2)^2 = 1/4 (niet in N).
0,05 is hetzelfde als 20-1
0,05t is hetzelfde als 20-1t
Nu gaan we integraal nemen:
f 0,05t = 0,025t2 toch?
f 20-1t = 20
Ben ik nou gek v_v?
Bedoel je met 'f' een primitieve? Een primitieve van 20^(-1)*t is bijv. 20^(-1)*t^2/2, in ieder geval niet 20.quote:
Ik zit met iets.
0,05 is hetzelfde als 20-1
0,05t is hetzelfde als 20-1t
Nu gaan we integraal nemen:
f 0,05t = 0,025t2 toch?
f 20-1t = 20
Ben ik nou gek v_v?
f ( 0,05t) dt= 0,025t2
f ( 20-1t) dt = 20
Ik wil deze snelheids vector omzetten naar een positie vector, dus v integreren naar s.
Dus 75cos(0,05t) als je dat integreert word het 75sin(0,05t) MAAL de integraal van 0,05t. Product regels is dat geloof ik he. En toen zag ik dat de uitkomst daarvan 20 is.
Zoals gezegd, die tweede klopt niet.quote:
Moet een integraal teken voorstellen.
f ( 0,05t) dt= 0,025t2
f ( 20-1t) dt = 20
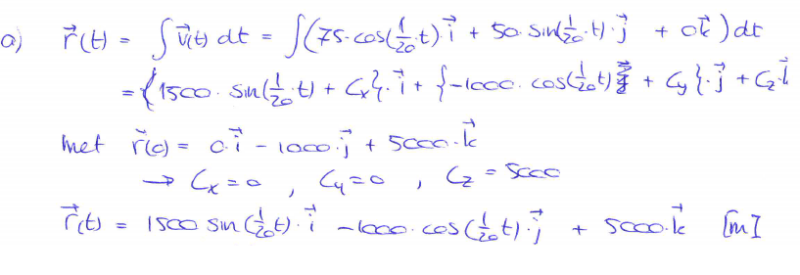
Zoals je ziet staat er 1500. Dat betekent dus dat 75 met 20 is vermenigvuldigd. Waar komt die 20 dan vandaan?
SPOILERantwoorden tentamen
Nee, de integraal van v(s) = 75*cos(0.05*s) voor s van 0 tot t wordt (75/0.05)*sin(0.05t).quote:
v(t) = 75cos(0,05t)
Ik wil deze snelheids vector omzetten naar een positie vector, dus v integreren naar s.
Dus 75cos(0,05t) als je dat integreert word het 75sin(0,05t) MAAL de integraal van 0,05t. Product regels is dat geloof ik he. En toen zag ik dat de uitkomst daarvan 20 is.
De kettingregel, differentieren van (75/0.05)*sin(0.05t) geeft (75/0.05)*cos(0.05*t)*0.05 = 75*cos(0.05*t).quote:
Wat voor een rekenregel is dit dan?
Moeilijke integralen hebben vaak een uitkomst die simpel te differentieren valt.quote:
Wat voor een rekenregel is dit dan?
Gebruik dat dan om te controleren of je ook echt de goede integraal hebt.
[ Bericht 0% gewijzigd door Siddartha op 13-01-2011 18:01:43 ]
Waar baseer je dat op? Ik ken genoeg 'eenvoudige' functies waarvan een primitieve niet in elementaire functies is uit te drukken, maar daaruit volgt niet dat omgekeerd 'moeilijke' functies eenvoudig te primitiveren zouden zijn.quote:
[..]
Moeilijke integralen hebben vaak een uitkomst die simpel te integreren valt.
Hij bedoelt denk ik dat de uitkomst van moeilijke integralen soms makkelijk te differentieren is als controle.quote:Op donderdag 13 januari 2011 17:52 schreef Riparius het volgende:
[..]
Waar baseer je dat op? Ik ken genoeg 'eenvoudige' functies waarvan een primitieve niet in elementaire functies is uit te drukken, maar daaruit volgt niet dat omgekeerd 'moeilijke' functies eenvoudig te primitiveren zouden zijn.
Differentieren bedoel ik.quote:
[..]
Waar baseer je dat op? Ik ken genoeg 'eenvoudige' functies waarvan een primitieve niet in elementaire functies is uit te drukken, maar daaruit volgt niet dat omgekeerd 'moeilijke' functies eenvoudig te primitiveren zouden zijn.
Zo had hij dat de integraal van 20^-1 een getal was. Je ziet meteen dat zoiets niet kan.
Ik probeer de homotopische equivalentie van een aantal verzamelingen te laten zien. Ik weet wel welke afbeeldingen daarvoor zorgen, alleen ik krijg ze niet formeel geschreven. Volgens mij is het vrij elementaire calculus, maar daar ben ik dus echt slecht in.
Hieronder wat ik zelf voor elkaar krijg:
1)Homotopische equivalentie van een ring in R2 en de eenheidscirkel.
[ afbeelding ]
2)Open schijf met weggelaten punt {z: 0<|z|<1 } in C en de eenheidscirkel
3)Rn\{0} en Sn
Dus wat ik graag zou weten is, hoe ik die functies netjes beschrijf en hoe ik eraan kom. Ik zie bijvoorbeeld bij 2, dat je met de functie z/|z| wel alle punten van de schijf op de eenheidscirkel krijgt.
Bij 3. wordt het iets van x/||x|| en de gewone inclusie voor de andere kant...
Lijkt me toch prima zo? Bij 2 kun je van de cirkel naar de schijf gaan door z naar z/2 te sturen.quote:
Dan een simpel (?) vraagje:
Ik probeer de homotopische equivalentie van een aantal verzamelingen te laten zien. Ik weet wel welke afbeeldingen daarvoor zorgen, alleen ik krijg ze niet formeel geschreven. Volgens mij is het vrij elementaire calculus, maar daar ben ik dus echt slecht in.
Hieronder wat ik zelf voor elkaar krijg:
1)Homotopische equivalentie van een ring in R2 en de eenheidscirkel.
[ afbeelding ]
2)Open schijf met weggelaten punt {z: 0<|z|<1 } in C en de eenheidscirkel
3)Rn\{0} en Sn
Dus wat ik graag zou weten is, hoe ik die functies netjes beschrijf en hoe ik eraan kom. Ik zie bijvoorbeeld bij 2, dat je met de functie z/|z| wel alle punten van de schijf op de eenheidscirkel krijgt.
Bij 3. wordt het iets van x/||x|| en de gewone inclusie voor de andere kant...
Je moet nog wel aantonen dat het homotopie-equivalenties zijn natuurlijk.
Ja, dat het homotopie-equivalenties zijn lukt me wel, 't zijn die elementaire dingen die me altijd buggen. Had je bij wijze van voorbeeld en om het te vatten ook gewoon elke z naar z/3 of z/4 kunnen sturen in jouw functie?Uiteraard had dat zo gekund, die dingen zijn allemaal homotoop met elkaar.quote:
Oké bedankt
Volgens mij zijn die ''deelrijen'' officieel geel deelrijen omdat ik ook termen verander...
, maar zie het dan maar gewoon als 'nieuwe' rijen.Een oneindige som is een limiet van eindige sommen. Als er negatieve termen zijn, dan kan de limiet afhangen van de sommatievolgorde.quote:
Wat kan er dan fout gaan als sommige termen <0 zijn?
Als A een n*m-matrix is, en B een n*n-matrix, dan is A*B alleen gedefinieerd indien n gelijk is aan m.quote:
Als ik de matrixen A en C weet met A*B = C, B = n*n matrix en A en C een n*m matrix... is het dan mogelijk om achter matrix B uit te rekenen?
Is echter A een m*n-matrix, dan is de vermenigvuldiging wel goed gedefinieerd. Je kan B kolomsgewijs uitrekenen, als v de i-de kolom is van B en w de i-de kolom is van C, dan moet je dus het stelsel A*v = w oplossen en dat zo voor i van 1 t/m n.
1) If f is measurable and f = g except on a set of measure zero, show that g is also measurable.
2)voor meetbare f:
Hoe bewijs ik dat?
Ze zijn me alle twee overigens intuitief totaal begrijpelijk.
[ Bericht 100% gewijzigd door BasementDweller op 16-01-2011 21:37:15 ]
Je kan het voorstellen door zo'n lijn:
1 ------------------------ 2
Als je dan spiegelt of of pi rad draait dan heeft dat hetzelfde effect, dus s=r, dus {e,r,s,sr}={e,r,r,r^2} = {e,r} ~= Z/Z2. Waarom klopt dit niet?
In het bewijs is alfa zo gekozen dat het buiten S ligt. Ze maken er een bolletje omheen met een straal > 0 zodat het hele bolletje buiten S ligt. Omdat de rij naar alfa convergeert, komen de punten in die rij willekeurig dicht bij alfa voor voldoende grote n, en dus ook in het deltabolletje, en dus allemaal buiten S.
[ Bericht 7% gewijzigd door BasementDweller op 16-01-2011 23:23:02 ]
p en alpha zijn dus in principe hetzelfde punt toch? Waarom is het dan nodig om nog een punt p te kiezen?quote:
Als een rij convergeert naar alfa dan is alfa een limietpunt. Ze laten zien dat zo'n limietpunt tot S behoort. Omdat dit argument opgaat voor een willekeurig limietpunt, behoort ieder limietpunt tot S en dan is S per definitie gesloten.
In het bewijs is alfa zo gekozen dat het buiten S ligt. Ze maken er een bolletje omheen met een straal > 0 zodat het hele bolletje buiten S ligt. Omdat de rij naar alfa convergeert, komen de punten in die rij willekeurig dicht bij alfa voor voldoende grote n, en dus ook in het deltabolletje, en dus allemaal buiten S.
Nee p is een punt in het deltabolletje rond alfa. Die delta kiezen ze zo dat ieder punt p in dat bolletje niet in S ligt. Dus dat hele bolletje ligt niet in S (preciezer: de doorsnede van het bolletje en S is leeg).quote:
[..]
p en alpha zijn dus in principe hetzelfde punt toch? Waarom is het dan nodig om nog een punt p te kiezen?
Ze kiezen dus een alpha waar de rij x(n) naar toe convergeert. Ze nemen aan dat alpha buiten S ligt. Ze tekenen een bol om alpha met straal delta zo dat de hele bol niet in S ligt. Omdat alpha het middelpunt is van het bolletje, zou x(n) ook in het bolletje moeten zitten, dit is niet zo, dus alpha is binnen S, dus S is closed.quote:
[..]
Nee p is een punt in het deltabolletje rond alfa. Die delta kiezen ze zo dat ieder punt p in dat bolletje niet in S ligt. Dus dat hele bolletje ligt niet in S (preciezer: de doorsnede van het bolletje en S is leeg).
Klopt dat cursieve deel?
Nee, niet iedere x(n) hoeft in het bolletje te zitten. Zie je waarom?quote:
[..]
Ze kiezen dus een alpha waar de rij x(n) naar toe convergeert. Ze nemen aan dat alpha buiten S ligt. Ze tekenen een bol om alpha met straal delta zo dat de hele bol niet in S ligt. Omdat alpha het middelpunt is van het bolletje, zou x(n) ook in het bolletje moeten zitten, dit is niet zo, dus alpha is binnen S, dus S is closed.
Klopt dat cursieve deel?
Dat zeg je eigenlijk zelf ook al.
Pas als n groot genoeg is zit hij in het bolletje (schrijf anders eens met de definitie van de limiet op wat het betekent dat a_n naar alfa convergeert als n naar oneindig gaat!!).
Dan heb je dus een heel deel van de rij wat buiten S ligt, dus is de rij geen deelverzameling van S, in tegenspraak met hoe je die rij gekozen had.
[ Bericht 10% gewijzigd door BasementDweller op 16-01-2011 23:50:31 ]
Ahaa, dankjewel voor je snelle en goede hulp!quote:
[..]
Nee, niet iedere x(n) hoeft in het bolletje te zitten. Zie je waarom?
Dat zeg je eigenlijk zelf ook al.
Pas als n groot genoeg is zit hij in het bolletje (schrijf anders eens met de definitie van de limiet op wat het betekent dat a_n naar alfa convergeert als n naar oneindig gaat!!).
Dan heb je dus een heel deel van de rij wat buiten S ligt, dus is de rij geen deelverzameling van S, in tegenspraak met hoe je die rij gekozen had.
Kan ik weer even verder Is f positief? In dat geval is het triviaal dat m(f(x)=\inf)>0 => \int_{\Omega} f \geq \int_{f^{-1}(\inf)} f = \inf. Anders moet je f opbreken in negatieve en positieve delen en hetzelfde doen, rekening houdend met het feit dat de aanname dat \int_{\Omega} f < \inf i.h.b. betekent dat de integraal welgedefinieerd is, dus het kan niet zo zijn dat (JPB-smiley) beide delen een oneindige integraal hebben.quote:
Lebesgue Integratie:
1) If f is measurable and f = g except on a set of measure zero, show that g is also measurable.
2)voor meetbare f:
[ afbeelding ]
Hoe bewijs ik dat?
Ze zijn me alle twee overigens intuitief totaal begrijpelijk.
[ afbeelding ]
Antwoord zegt f(3) = 1
Ik begrijp dat de afgeleiden van g in 3, gelijk is aan 3. Maar er valt geen kwartje wat ik met die afgeleiden moet doen. Blijkbaar is de limiet naar 3 van g(x) = 4.
g(3) ~ 4
g'(3) = 3
Definitie
lim = (f(x+delta x) + f(x)) / delta x
delta x-> 0
Helaas begrijp ik ook niet wat je met geheel vereenvoudigen bedoeld. Ik heb geprobeerd om formule te differentieren, en dat gelijk te stellen aan 3 in de hoop hier iets mee te kunnen. Helaas lukt dat ook niet.
. (ik heb alfa als a geschreven)1. sin a = 1/6.
bereken: cos a
2. bereken: arcsin - 1/2 wortel 2
Ik hoop dat iemand me kan helpen!
bedankt alvast!
het gaat over de afgeleide van gquote:
Bedankt voor je hulp, alleen heb ik geen idee waar je naar toe wilt gaan.
Definitie
lim = (f(x+delta x) + f(x)) / delta x
delta x-> 0
Helaas begrijp ik ook niet wat je met geheel vereenvoudigen bedoeld. Ik heb geprobeerd om formule te differentieren, en dat gelijk te stellen aan 3 in de hoop hier iets mee te kunnen. Helaas lukt dat ook niet.
1. gebruik sin²x + cos²x = 1.quote:
Ik heb morgen tentamen basis wiskunde, maar ik kom er nu achter dat ik ook nog goniometrie moet leren. En ik snap een gedeelte totaal niet
1. sin a = 1/6.
bereken: cos a
2. bereken: arcsin - 1/2 wortel 2
Ik hoop dat iemand me kan helpen!
bedankt alvast!
2. teken een eenheidscirkel met daarin deze vraag, en gebruik sin(pi/4) = 1/2 wortel 2.
alleen 2. nog niet..
moet ik iets in die formule invullen waarna het antwoord eruit rolt?
het antwoord op de vraag is btw -1/4pi
mijn paint?quote:
er staat geen plaatje bij de opgave, het zijn alleen cijfers en tekens.
Gewoon even 2 driehoekjes uit je hoofdleren...quote:
Ik heb morgen tentamen basis wiskunde, maar ik kom er nu achter dat ik ook nog goniometrie moet leren. En ik snap een gedeelte totaal niet
1. sin a = 1/6.
bereken: cos a
2. bereken: arcsin - 1/2 wortel 2
Ik hoop dat iemand me kan helpen!
bedankt alvast!
In deze driehoek
alfa = pi/6
beta = pi/2
gamma = pi/3
Dan nog tweede driehoek met AB = BC = 1 en AC dus wortel 2
Met alfa = pi/4
beta = pi/2
gamma = pi/4
Dingen uit je hoofd leren bij wiskunde is over het algemeen niet verstandig. Maar als je dan toch een ezelsbruggetje wil hebben, kun je beter het volgende onthouden:quote:Op maandag 17 januari 2011 20:44 schreef Dale. het volgende:
[..]
Gewoon even 2 driehoekjes uit je hoofdleren...
De 'standaard' hoeken zijn 0, 30, 45, 60 en 90 graden en de sinus van deze hoeken is resp. ½√0, ½√1, ½√2, ½√3, ½√4. Voor de cosinus hetzelfde rijtje in omgekeerde volgorde, en de tangens is uiteraard het quotiënt van sinus en cosinus.
Hiermee wel lijkt me. Anders moet je zelf afleiden wat de taylorpolynoom is van een sinus (want die moet je dan ook niet uit je hoofd leren), en dan vervolgens die oneindige som berekenen?quote:
[..]
Dingen uit je hoofd leren bij wiskunde is over het algemeen niet verstandig.
Ik vind zelf die twee driehoekjes zelf makkelijker te onthouden, daar kan weinig fout gaan.
ik voel mij alles behalve slim op dit moment
Maar vraag 2. is me nog niet duidelijk zou iemand het kunnen uitwerken?
Voor welke x is sin(x) = - wortel(2)/2 ?
En dat kan je afleiden uit dit (lelijke) standaarddriehoekje:
Waaromquote:
Het is een vrij nieuw gebied; het is niet moeilijk om met een nieuw idee te komen en dat te laten publiceren. Daarom is het theoretisch weinig interessant. Daarnaast is het nergens toepasbaar.quote:
Er is ook maar één universiteit echt mee bezig hier in Nederland.
quote:
[..]
Daarnaast is het nergens toepasbaar.
Gevraagd is met de kettingregel dz/dt te vinden.
Uit dz/dt=(dz/dx)(dx/dt)+(dz/dy)(dy/dt) volgt dan toch:
dz/dt = (2xy+y2)(4t3)+(x2+2xy)(-3t3)
Is dit dan het goede antwoord of moet je x en y ook nog invullen ofzo?
Het is wel zo. Zelfs van convexe analyse, dat veel theoretischer lijkt, heb ik meer toepassingen gezien.quote:
Het laatste stukje moet -3t² zijn. Invullen lijkt me mooier, maar niet noodzakelijk.quote:
Stel z=x2y+xy2, x = 2+t4, y = 1-t3
Gevraagd is met de kettingregel dz/dt te vinden.
Uit dz/dt=(dz/dx)(dx/dt)+(dz/dy)(dy/dt) volgt dan toch:
dz/dt = (2xy+y2)(4t3)+(x2+2xy)(-3t3)
Is dit dan het goede antwoord of moet je x en y ook nog invullen ofzo?
Zij W een lineaire deelruimte van V die U bevat, d.w.z U is een deelruimte van W.
Laat zien dat in dit geval W/U= {w+U| w uit W} een lineaire deelruimte van V/U is.
Ik dacht het volgende:
W is een lineaire deelruimte van V, en W/U is dan simpel de begrenzing van V/U op W.
Aangezien W lineair is, is W/U dat dan ook en dus een lineaire deelruimte van V/U.
Mijn vraag is of dit klopt en hoe kan ik dit het beste formuleren?
Tevens, kan ik dit ook bewijzen door te stellen dat W/U = W ( want {w+U | w uit W} =W omdat W lineair is en U een deelverzameling van W)
In zekere zin klopt dit idee, het handigst is het om gewoon formeel de axioma's van een deelruimte na te gaan. Wees er dan vooral op bedacht dat je toch ergens moet gebruiken dat U een deelruimte van W is.quote:
Zij U een lineaire deelruimte van V en zij V/U de quotientenruimte van U in V.
Zij W een lineaire deelruimte van V die U bevat, d.w.z U is een deelruimte van W.
Laat zien dat in dit geval W/U= {w+U| w uit W} een lineaire deelruimte van V/U is.
Ik dacht het volgende:
W is een lineaire deelruimte van V, en W/U is dan simpel de begrenzing van V/U op W.
Aangezien W lineair is, is W/U dat dan ook en dus een lineaire deelruimte van V/U.
Mijn vraag is of dit klopt en hoe kan ik dit het beste formuleren?
Nee, W/U is niet W.quote:Tevens, kan ik dit ook bewijzen door te stellen dat W/U = W ( want {w+U | w uit W} =W omdat W lineair is en U een deelverzameling van W)
Neem w1+U,w2+U in W/U.quote:
[..]
In zekere zin klopt dit idee, het handigst is het om gewoon formeel de axioma's van een deelruimte na te gaan. Wees er dan vooral op bedacht dat je toch ergens moet gebruiken dat U een deelruimte van W is.
[..]
Nee, W/U is niet W.
Dan (w1+U) + (w2+U) = w1+w2+U een element van W/U want:
W is een lineaire deelruimte, dus w1+ w2 is een element van W.
Hetzelfde principe voor scalaire vermenigvuldiging.
Oftewel, W/U is een lineaire deelruimte.
Waarom klopt W/U= W niet?
Laat u een element van U zijn, dan is u ook een element van W ( U is een deelgroep van W).
Dan is de verzameling van alle u+w voor w in W toch gelijk aan W? W is een lineaire deelgroep.
n=120
p=0,38
standaardafwijking=0,05
Het gaat om een tweezijdige binomiale toets. De linkerzijde wordt dan berekend met
binomcdf (120, 0.38, g) kleiner of gelijk dan 0,025
dan moet je aflezen in de tabel op de GR welke waarde g is. Dat begrijp ik.
De rechterzijde wordt berekend als
1-binomcdf(120, 0.38, g-1) kleiner of gelijk dan 0,025
ook weer aflezen in de tabel om te kijken welke waarde g heeft. Ik begrijp alleen niet waarom er -1 staat (en waarom dus, als de g is berekend, er 1 bij opgeteld moet worden). Ik snap ten eerste het hele idee hierachter niet en ten tweede bereken je met de GR toch g en niet g-1? Wat er wordt gedaan in de voorbeeldopgave is g-1=56 is dus g=57. Ik snap er de ballen van.
P(X groter of gelijk 10) = 1 - P(X kleiner of gelijk 9) ?
Als g=10 staat dat er ja.quote:
Ooh. heeft het te maken met het regeltje:
P(X groter of gelijk 10) = 1 - P(X kleiner of gelijk 9) ?
Nu is de vraag "Bepaal alle oplossingen van dit stelsel als p != 0 en p != 1."
Nu staat in de uitwerkingen het volgende:
Nu is mijn vraag wat gebeurt er in de laatste stap?
Ik geloof dat men eerst p = 0 stelt en daarna de rijen verwisseld... In ieder geval rij 2 in de voorlaatste matrix is gelijk aan rij 1 in de laatste matrix... Maar dan duikt bij mij de vraag op waarom p gelijk gesteld mag worden aan 0? Terwijl in de vraag gezegd wordt p != 0.
Ik dacht zelf omdat men nu zeg maar 2 rijen hebt waarbij a + b + c = 3 en b + c = 3 waardoor je een soort gevalsonderscheid krijgt waarbij je echter p niet precies hebt vastgelegd... immers a + b + c != b + c? Of zit ik nu onzin te verkondigen
?Is W/U een deelverzameling van V/U? Is de optelling goed gedefinieerd (onafhankelijk van gekozen representanten)?quote:
[..]
Neem w1+U,w2+U in W/U.
Dan (w1+U) + (w2+U) = w1+w2+U een element van W/U want:
W is een lineaire deelruimte, dus w1+ w2 is een element van W.
Hetzelfde principe voor scalaire vermenigvuldiging.
Oftewel, W/U is een lineaire deelruimte.
W/U bestaat uit nevenklassen. Elk element van W/U wordt door een element van W gerepresenteerd, maar sommige elementen van W representeren hetzelfde element van W/U: voor elke u in U is w + U hetzelfde element van W/U als w + u + U, terwijl w niet gelijk is aan w + u (als u niet 0 is).quote:Waarom klopt W/U= W niet?
Laat u een element van U zijn, dan is u ook een element van W ( U is een deelgroep van W).
Dan is de verzameling van alle u+w voor w in W toch gelijk aan W? W is een lineaire deelgroep.
Die laatste stap klopt niet. Op positie (1,2) hoort een p. Als je dan gewoon verderveegt dan krijg je op (2,2) een 1-p. Onder de aanname p!=1 kun je die mooi als pivot nemen. Als je goed doorveegt, kom je uiteindelijk op [1 0 0 0; 0 1 0 3+2/p; 0 0 1 -2/p].quote:
Ik heb het stelsel...
[ [url=http://latex.codecogs.com/gif.latex?\left[\begin{matrix}%20p%20&%201%20&%201%20\%20p+1%20&%202%20&%202%20\%200%20&%203%20&%203+p%20\end{matrix}\right.%20\left|\begin{matrix}%20\%203%20\%20\%20\%206%20\%20\%20\%207%20\%20\end{matrix}\right]]afbeelding[/url] ]
Nu is de vraag "Bepaal alle oplossingen van dit stelsel als p != 0 en p != 1."
Nu staat in de uitwerkingen het volgende:
[ [url=http://latex.codecogs.com/gif.latex?\left[\begin{matrix}%20p%20&%201%20&%201%20\%20p+1%20&%202%20&%202%20\%200%20&%203%20&%203+p%20\end{matrix}\right.%20\left|\begin{matrix}%20\%203%20\%20\%20\%206%20\%20\%20\%207%20\%20\end{matrix}\right]%20\sim%20\left[\begin{matrix}%20p%20&%201%20&%201%20\%201%20&%201%20&%201%20\%200%20&%203%20&%203+p%20\end{matrix}\right.%20\left|\begin{matrix}%20\%203%20\%20\%20\%203%20\%20\%20\%207%20\%20\end{matrix}\right]%20\sim%20\left[\begin{matrix}%201%20&%201%20&%201%20\%200%20&%201%20&%201%20\%200%20&%203%20&%203+p%20\end{matrix}\right.%20\left|\begin{matrix}%20\%203%20\%20\%20\%203%20\%20\%20\%207%20\%20\end{matrix}\right]]afbeelding[/url] ]
Nu is mijn vraag wat gebeurt er in de laatste stap?
Ik geloof dat men eerst p = 0 stelt en daarna de rijen verwisseld... In ieder geval rij 2 in de voorlaatste matrix is gelijk aan rij 1 in de laatste matrix... Maar dan duikt bij mij de vraag op waarom p gelijk gesteld mag worden aan 0? Terwijl in de vraag gezegd wordt p != 0.
Ik dacht zelf omdat men nu zeg maar 2 rijen hebt waarbij a + b + c = 3 en b + c = 3 waardoor je een soort gevalsonderscheid krijgt waarbij je echter p niet precies hebt vastgelegd... immers a + b + c != b + c? Of zit ik nu onzin te verkondigen
Sorry maar zou je dat doorvegen kunnen laten zien? Ik ben dus nu gaan rekenen met op (1,2) p maar echt verder kom ik niet... ik blijf met 2 p's in me maag zitten.quote:
[..]
Die laatste stap klopt niet. Op positie (1,2) hoort een p. Als je dan gewoon verderveegt dan krijg je op (2,2) een 1-p. Onder de aanname p!=1 kun je die mooi als pivot nemen. Als je goed doorveegt, kom je uiteindelijk op [1 0 0 0; 0 1 0 3+2/p; 0 0 1 -2/p].
SPOILER
In dit geval vraag ik me af of de 'tweede' (de gebonden) x dezelfde waarde moet hebben als de eerste x om de formule waar te laten zijn.
Dus, concreet voorbeeld: zou de formule waar zijn als x = 5, y = 5, R(5, 5) = waar, P(4) = waar, maar P is niet waar voor alle andere waarden? Is de formule dan waar?
(Ik neem aan van wel, maar ik vind het gek dat x in dezelfde formule twee verschillende waarden kan hebben...)
De tweede x is inderdaad een "andere" x dan de eerste x. In jouw voorbeeld is de formule inderdaad waar.quote:
Ik heb een kleine vraag over gebonden en ongebonden variabelen in logische formules:
[ afbeelding ]
In dit geval vraag ik me af of de 'tweede' (de gebonden) x dezelfde waarde moet hebben als de eerste x om de formule waar te laten zijn.
Dus, concreet voorbeeld: zou de formule waar zijn als x = 5, y = 5, R(5, 5) = waar, P(4) = waar, maar P is niet waar voor alle andere waarden? Is de formule dan waar?
(Ik neem aan van wel, maar ik vind het gek dat x in dezelfde formule twee verschillende waarden kan hebben...)
ok, hartelijk dankquote:
[..]
De tweede x is inderdaad een "andere" x dan de eerste x. In jouw voorbeeld is de formule inderdaad waar.
Aangezien W een deelverzameling van V is en U weer een deelverzameling van W, lijkt me het voldoende om te bewijzen dat W lineair is. Dat elke representant van W/U ook in V/U zit, geeft aan dat W/U een deelverzameling is van V/U, het bewijsquote:
[..]
Is W/U een deelverzameling van V/U? Is de optelling goed gedefinieerd (onafhankelijk van gekozen representanten)?
geeft aan dat W/U een lineaire deelruimte is van V/U.quote:Neem w1+U,w2+U in W/U.
Dan (w1+U) + (w2+U) = w1+w2+U een element van W/U want:
W is een lineaire deelruimte, dus w1+ w2 is een element van W.
Hetzelfde principe voor scalaire vermenigvuldiging.
Oftewel, W/U is een lineaire deelruimte.
Toch?
Maar elke u is in W ( U is een deelruimte van W), en W is een lineaire deelruimte, dus zit w+u wél in W. Noem 'w+u' : y, dan is y een element van W en zit y+U voor elke u in W weer in W, want dan krijg je weer y+u ( met u uit U), waar u ook in W zit.quote:W/U bestaat uit nevenklassen. Elk element van W/U wordt door een element van W gerepresenteerd, maar sommige elementen van W representeren hetzelfde element van W/U: voor elke u in U is w + U hetzelfde element van W/U als w + u + U, terwijl w niet gelijk is aan w + u (als u niet 0 is).
Voor de eerste (f(x)) wil ik als norm gebruiken alle elementen uit de matrix bij elkaar opgeteld. Omdat ik weet dat cos en sin continu is zou ik 't daarmee makkelijk moeten kunnen.
Het probleem is daarbij vooral dat ik weet dat voor alle epsilon is er een delta zodat |x-a| < delta dan |sin x - sin a| < epsilon. Dus stel uiteindelijk kies ik x = (r, phi) en a = (q, psi) dan weet ik dat voor epsilon/4 is er een delta zodat |phi - psi| < delta dan |sin phi - sin psi| < epsilon/4. Maar ik wil krijgen dat ||x-a|| dus ||(r-q, phi-psi)|| < delta dan |sin phi - sin psi| < epsilon/4.
Bij de tweede wilde ik dezelfde norm gaan gebruiken (leek me makkelijker dan met kwadraten en wortels werken sowieso) dan krijg ik \frac{x_1 + x_2 + 2}{x_1^2 +x_2^2} < epsilon. Vanaf daar kwam ik ook niet echt verder.
Edit: negeer die laatste alinea maar, daar klopt sowieso niks van
[ Bericht 7% gewijzigd door Hanneke12345 op 19-01-2011 22:16:05 ]
Veronderstel dat de Fourier-reeks uniform convergeert naar de continue functie f. Dan geldt voor ieder geheel getal k dat
Maar hoe kan je bepalen of de Fourier-reeks uniform naar f convergeert als je nog bezig bent met de coëfficiënten te bepalen?
De tweede term kan ik afschatten door y_1^2+y_2^2 te vervangen voor (y_1+y_2)^2. Maar bij de eerste kan ik dat niet doen omdat 't hele ding dan kleiner wordt.
Of ik zat te denken ik kan van de min een plus maken, dan wordt het ook groter. Maar hoe dan verder..
Ik begrijp eigenlijk niet zo goed wat je wilt? Je kijkt naar de totale afgeleide, een functie die afbeeldt op een matrixruimte. Als je het over continuiteit daarvan wilt hebben, moet je een norm gebruiken. Je hebt het over "alle elementen van de matrix optellen", maar dat is niet zo handig omdat je dan matrices hebt die ongelijk 0 zijn maar wel norm 0 hebben. Dan moet je het op z'n minst over de som van de absolute waarden hebben. Maar dan kijk je naar de som van 4 reeelwaardige functies waarvan van elk meteen duidelijk is dat ze continu zijn, daar valt toch niets te bewijzen?quote:
Probleem wat ik wel heb bij de tweede (f^{-1}) is dat ik niet goed weet hoe ik het moet gaan afschatten. Ik kom tot
[ afbeelding ]
De tweede term kan ik afschatten door y_1^2+y_2^2 te vervangen voor (y_1+y_2)^2. Maar bij de eerste kan ik dat niet doen omdat 't hele ding dan kleiner wordt.
Of ik zat te denken ik kan van de min een plus maken, dan wordt het ook groter. Maar hoe dan verder..
)(ik vind btw de methode die we nu gebruiken zwaar ruk. We hebben geen reader maar moeten alles leren uit losse pdf bestanden, voornamelijk gejat van andere universiteiten die wel dictaten aan hun studenten geven, die door de leraar van internet zijn geplukt en op geen enkele manier samenhangend zijn, of zelfs maar in dezelfde taal. maar goed ik stop want dit is klb niet
)Om even in de context te plaatsen:
Deze formules laten mij vermoeden dat phi en die andere griekse letter helemaal geen x mogen bevatten. Anders zouden de formules toch niet waar zijn?
Ik had al gezocht in het bestand maar niets gevonden. Pdf's doen soms raar met zoeken (ik zocht op 'vrij' wat daar wel degelijk stond)... Anyway ik kan mijn laatste post opeens niet meer zien dus een losse post dan maar.
O, het stond op een nieuwe pagina
ik drukte wel op >> in my active topics... Wat een faal allemaal .Dan zou ik voor die tweede bijv. gewoon gebruiken dat als teller en noemer conrinu zijn, het quotient dat ook is (module noemer=0 en zo), of wil je dat soort regels ook niet gebruiken? Voor de eerste moret je continuiteit van sinus en cosinus hebben, als je wel wilt aannemen dat ze continu in 0 zijn kun je dat bijv. met van die ik-weet-niet-meer-hoe-ze-heten formules a la sin(a+b) = ... doen. Continuiteit in 0 zou je evt. kunnen bewijzen vanuit de def.quote:
Som van absolute waardes inderdaad, excuses. Verder "direct duidelijk dat ze continu zijn", maar ik probeer 't toch zo te bewijzen (wnat dat zou dan ook moeten kunnen. Ik zou van de afzonderlijke functies waarschijnlijk ook nog niet kunnen bewijzen dat ze continu zijn
Tijd voor koffie.quote:
EDIT: Al gevonden, excuses, het stond wel in het bestand, zij het pas een paar bladzijden na het gebruik van het woord. Het gaat om een variabele die onafhankelijk is van kwantoren...
Ik had al gezocht in het bestand maar niets gevonden. Pdf's doen soms raar met zoeken (ik zocht op 'vrij' wat daar wel degelijk stond)... Anyway ik kan mijn laatste post opeens niet meer zien dus een losse post dan maar.
O, het stond op een nieuwe pagina
. Voor mijn opleiding gebruik ik "Calculus a complete course" van Adams en Essex maar om eerlijk te zijn komt dat niet helemaal over Wat zijn andere goede boeken die calculus op een duidelijke manier uiteenzetten? Liefst met genoeg en goede voorbeelden? Ik heb zelf al even op Amazon en bol gekeken, maar het aanbod is zo groot dat ik het moeilijk vind een goede keuze te maken
Bij onze opleiding gebruiken we "Calculus, Early Transcendentals" van James Stewart. Naar mijn mening wel een goed boek.quote:
Ik ben op zoek naar een nieuw calculusboek op WO-niveau
Wat zijn andere goede boeken die calculus op een duidelijke manier uiteenzetten? Liefst met genoeg en goede voorbeelden? Ik heb zelf al even op Amazon en bol gekeken, maar het aanbod is zo groot dat ik het moeilijk vind een goede keuze te maken
Ja dat boek is vrijwel hetzelfde. Elke WO studie met wiskunde gebruikt een van die twee boeken.quote:Op donderdag 20 januari 2011 18:20 schreef Fsmxi het volgende:
[..]
Bij onze opleiding gebruiken we "Calculus, Early Transcendentals" van James Stewart. Naar mijn mening wel een goed boek.
MWP wat is precies je probleem dan?
Ik heb wel de uitwerkingen van Adams, misschien dat je daar wat aan hebt.
Lineair bij een productie (X) = 200 hoort kosten (Y) = 575
bij een productie (X) = 460 hoort kosten (Y) = 1030
Dat is toch een schuin oplopende lijn (ziet er uit als ' / ' ) ? (van links onder naar rechtsboven)
Waarom zegt mijn antwoordenboek dan [DELTA] Y / [DELTA] X = (575 - 1030) / (200-460) instead of (1030 - 575) / (460 - 200)
?????????? :$
Maakt geen fuck uit, is precies hetzelfde.quote:
Y = AX + B met A = [DELTA] Y / [DELTA] X
Lineair bij een productie (X) = 200 hoort kosten (Y) = 575
bij een productie (X) = 460 hoort kosten (Y) = 1030
Dat is toch een schuin oplopende lijn (ziet er uit als ' / ' ) ? (van links onder naar rechtsboven)
Waarom zegt mijn antwoordenboek dan [DELTA] Y / [DELTA] X = (575 - 1030) / (200-460) instead of (1030 - 575) / (460 - 200)
?????????? :$
Tja, daar zijn stellingen voor. "Als f aan die-en-die voorwaarden voldoet, dan convergeert de Fourierreeks uniform naar f".quote:
In mijn dictaat staat de volgende stelling:
Veronderstel dat de Fourier-reeks uniform convergeert naar de continue functie f. Dan geldt voor ieder geheel getal k dat [ afbeelding ]
Maar hoe kan je bepalen of de Fourier-reeks uniform naar f convergeert als je nog bezig bent met de coëfficiënten te bepalen?
Het probleem is vooral dat ik Adams te abstract vind en de stof van elk hoofdstuk snel de diepte in gaat.quote:
[..]
Ja dat boek is vrijwel hetzelfde. Elke WO studie met wiskunde gebruikt een van die twee boeken.
MWP wat is precies je probleem dan?
Ik heb wel de uitwerkingen van Adams, misschien dat je daar wat aan hebt.
Ook vind ik het boek niet zo overzichtelijk, in die zin dat er weinig concrete voorbeelden in staan.
Nou doe ik twee studies, bedrijfskunde en scheikunde, dus ik kan vergelijken. Voor lineaire algebra hadden we ook Adams. Uiteindelijk snapte ik er niets van en heb ik het boek "Essential Mathematics for Economic Analysis" gebruikt (van bedrijfskunde). Laatstgenoemde legt alles wat mij betreft veel beter uit. Besteed misschien minder aandacht aan de theorie erachter en meer aan praktische toepassingen, maar daardoor leer je in principe wel de algemene vaardigheden die nodig zijn.
Misschien dat een Calculus-boek toegespitst op alpha-studenten wat geschikter voor mij is (hoewel ze bij Econometrie ook al Adams gebruiken
)Enig idee? Of vraag ik iets onmogelijks?
Gisteravond niet meer verder naar gekeken maar zit nu weer even te stoeien en lukt nog steeds nietquote:
Je moet die 1 linksboven gebruiken om te vegen. Dus van rij2 trek je p keer rij1 af.
Wat ik nu heb is...
SPOILERRij operaties vanaf de 3de samengestelde matrix:
- rij2 = rij2 - p*rij1
- rij3 = rij3 - 3*rij2
- rij2 = 3*rij2 + rij3
- rij3 = rij3/p
- rij2 = rij2 - rij3
... maja dan
Wat betekenen in beide gevallen deze twee laatste symbolen? Ben maar een VWO-6er'tje en kom deze symbolen voor het eerst tegen in m'n boek. Ik hoop trouwens dat die Z en R de juiste symbolen zijn aangezien ze toch een beetje anders uitzien in m'n boek.
Bedoel je nietquote:
[ afbeelding ] en [ afbeelding ]
Wat betekenen in beide gevallen deze twee laatste symbolen? Ben maar een VWO-6er'tje en kom deze symbolen voor het eerst tegen in m'n boek. Ik hoop trouwens dat die Z en R de juiste symbolen zijn aangezien ze toch een beetje anders uitzien in m'n boek.
Ja klopt, die twee zijn het.quote:
[..]
Bedoel je niet [ afbeelding ] en [ afbeelding ]? In dat geval zijn het de gehele getallen en reeele getallen.
Ik bedoelde eigenlijk wat het betekent wanneer dat symbool, die \epsilon, voor die R en Z geplaatst wordt.Ah, het is geen \epsilon maar een \in, geeft de relatie "is een element van" aan.quote:
[..]
Ja klopt, die twee zijn het.
Ok, bedankt.quote:
[..]
Ah, het is geen \epsilon maar een \in, geeft de relatie "is een element van" aan.
Producten van groepen vat ik, afbeeldingen tussen groepen vat ik, ondergroepen, normale groepen, etc. etc. maar factorgroepen/quotiëntgroepen?
Iemand die er eens wat verfrissend licht over kan schijnen? Met voorbeelden evt.
Het voorbeeld op wikipedia illustreert wel goed wat er gebeurt: http://en.wikipedia.org/wiki/Quotient_group#Definition .quote:Op vrijdag 21 januari 2011 21:28 schreef TheLoneGunmen het volgende:
De definities en opgaven ten spijt, kan ik intuïtief niets voorstellen bij factorgroepen.
Producten van groepen vat ik, afbeeldingen tussen groepen vat ik, ondergroepen, normale groepen, etc. etc. maar factorgroepen/quotiëntgroepen?
Iemand die er eens wat verfrissend licht over kan schijnen? Met voorbeelden evt.
Je hebt een groep van, in dat geval, 6 elementen. Je "deelt" door een normale ondergroep van 2 elementen, en je krijgt een partitie van de gehele groep bestaande uit 6/2=3 elementen.
De vraag was om te bewijzen dat sigma(|B) = sigma(O^n) en of ook geldt sigma(|B')=sigma(O^n). Dit is een bewijs:
Ik snap de zin die begint met "Since #|B'..." niet. Waarom is de cardinaliteit belangrijk, en waarom geldt volgens (*) dan die implicatie?
De cardinaliteit is belangrijk omdat sigma-algebra's gesloten zijn onder aftelbare verenigingen (dat is ook de reden om die B' te introduceren naast B, aftelbaarheid van Q gebruiken). Wat is O^n?quote:
Ik heb zelf ook een vraagje.
De vraag was om te bewijzen dat sigma(|B) = sigma(O^n) en of ook geldt sigma(|B')=sigma(O^n). Dit is een bewijs:
[ afbeelding ]
Ik snap de zin die begint met "Since #|B'..." niet. Waarom is de cardinaliteit belangrijk, en waarom geldt volgens (*) dan die implicatie?
Dat wist ik, maar ik zie niet hoe ze dat hier gebruiken...?quote:
[..]
De cardinaliteit is belangrijk omdat sigma-algebra's gesloten zijn onder aftelbare verenigingen (dat is ook de reden om die B' te introduceren naast B, aftelbaarheid van Q gebruiken). Wat is O^n?
O^n is de family of open sets in R^n
Ik begrijp je vraag geloof ik niet. Het doel van (*) is om te bewijzen dat U \in O^n => U \in \sigma(B') (**). Dit impliceert immers \sigma(O^n) \subset \sigma(B'), en omdat je al had \sigma(B') \subset \sigma(B) \subset \sigma(O^n) volgt de conclusie \sigma(B')=\sigma(B) = \sigma(O^n). Om (**) te bewijzen begin je met een U uit O^n, en gebruik je de definitie van open vz. en de dichtheid van Q in R om (*) af te leiden. Maar het rechterlid van (*) is een aftelbare vereniging van elementen uit B', en is dus een element van \sigma(B'). Dus ook U \in \sigma(B'), en hiermee is (**) bewezen.quote:
[..]
Dat wist ik, maar ik zie niet hoe ze dat hier gebruiken...?
O^n is de family of open sets in R^n
Ah, bij dat dikgedrukte zat het probleem. Ik snap het nu, bedanktquote:
[..]
Ik begrijp je vraag geloof ik niet. Het doel van (*) is om te bewijzen dat U \in O^n => U \in \sigma(B') (**). Dit impliceert immers \sigma(O^n) \subset \sigma(B'), en omdat je al had \sigma(B') \subset \sigma(B) \subset \sigma(O^n) volgt de conclusie \sigma(B')=\sigma(B) = \sigma(O^n). Om (**) te bewijzen begin je met een U uit O^n, en gebruik je de definitie van open vz. en de dichtheid van Q in R om (*) af te leiden. Maar het rechterlid van (*) is een aftelbare vereniging van elementen uit B', en is dus een element van \sigma(B'). Dus ook U \in \sigma(B'), en hiermee is (**) bewezen.
tan(2x)=sin(2x)/cos(2x)
Een breuk, dus (nat-tan)/(n^2)
nat = sin(2x)*-2sin(2x)
tan = cos(2x)*2cos(2x)
(nat-tan)/n^2 = (-2sin2(2x) - 2cos2(2x))/(cos2(2x)
Alleen is dit niet goed aldus wolfram alpha. Alleen werkt wolfram alpha ook met de sec etc. en daar snap ik niets van, dus kan iemand uitleggen waar het fout gaat?
Je bent bijna klaar, je kunt nog gebruiken dat sin^2(x)+cos^2(x)=1 en dan komt jouw uitdrukking uit op 2/cos^2(2x) (je doet de quotientregel verkeerd om waardoor je een extra minteken hebt) en dat klopt (want sec(x)=1/cos(x)).quote:
De afgeleide van tan(2x)
tan(2x)=sin(2x)/cos(2x)
Een breuk, dus (nat-tan)/(n^2)
nat = sin(2x)*-2sin(2x)
tan = cos(2x)*2cos(2x)
(nat-tan)/n^2 = (-2sin2(2x) - 2cos2(2x))/(cos2(2x)
Alleen is dit niet goed aldus wolfram alpha. Alleen werkt wolfram alpha ook met de sec etc. en daar snap ik niets van, dus kan iemand uitleggen waar het fout gaat?
[ Bericht 0% gewijzigd door keesjeislief op 22-01-2011 11:48:17 ]
Teken het toenamendiagram op [-1,5] met stapgrootte 1
(klik om te vergroten)
waarom is delta-y 3 bij x=0 en y=4?
waarom is delya-y 1 bij x=1 en y=5
enz.
Het gaat om de scheve asymptoten van deze functie, volgens mij zijn die
en
maar volgens het antwoordmodel zijn die y=x+6 en y=-x-6.
Als ik ze plot lijkt het echter ook y=x en y=-x te zijn, zit ik ergens helemaal fout, of klopt het antwoordmodel niet? (het is een antwoordmodel voor een tentamen van vorig jaar, je zou toch mogen verwachten dat dat klopt..)
Delta-y is gelijk aan ynieuw - youd, dat geeft bij x=1 dus ynieuw (dat is de huidige y, hier dus 5) minus youd (dat is de vorige y-waarde, hier dus 4) dus 5-4=1quote:
Gegeven is de formule y= -x2+2x+4
Teken het toenamendiagram op [-1,5] met stapgrootte 1
[ link | afbeelding ]
(klik om te vergroten)
waarom is delta-y 3 bij x=0 en y=4?
waarom is delya-y 1 bij x=1 en y=5
enz.
Haha nu snap ik het, bedankt!quote:
[..]
Delta-y is gelijk aan ynieuw - youd, dat geeft bij x=1 dus ynieuw (dat is de huidige y, hier dus 5) minus youd (dat is de vorige y-waarde, hier dus 4) dus 5-4=1
Voor de intercept b kijk je naar lim(x-> oo) (x+1)(x+2)/(x-3) - x = lim(x-> oo) (x²+3x-6)/x - x²/x = lim(x-> oo) (3x-6)/x = 3. Ik zou daarom zeggen y = x+3 ipv y = x+6.quote:
Even een kort vraagje over deze formule:
[ afbeelding ]
Het gaat om de scheve asymptoten van deze functie, volgens mij zijn die
[ afbeelding ]
en
[ afbeelding ]
maar volgens het antwoordmodel zijn die y=x+6 en y=-x-6.
Als ik ze plot lijkt het echter ook y=x en y=-x te zijn, zit ik ergens helemaal fout, of klopt het antwoordmodel niet? (het is een antwoordmodel voor een tentamen van vorig jaar, je zou toch mogen verwachten dat dat klopt..)
Ik heb die wat anders gedaan, namelijk lim(x-> oo) (x2+3x+2)/(x-3)-x(x-3)/(x-3)=lim(x-> oo) 2/(3-x)=0quote:
[..]
Voor de intercept b kijk je naar lim(x-> oo) (x+1)(x+2)/(x-3) - x = lim(x-> oo) (x²+3x-6)/x - x²/x = lim(x-> oo) (3x-6)/x = 3. Ik zou daarom zeggen y = x+3 ipv y = x+6.
Hoe kom ik van
1 - 1 / (1+x)
naar
x / (1+x)
?
1=(1+x)/(1+x)quote:Op woensdag 26 januari 2011 12:57 schreef Quyxz_ het volgende:
Ik zit even vast...
Hoe kom ik van
1 - 1 / (1+x)
naar
x / (1+x)
?
Tuurlijk!quote:
Bedankt.
Ik kom er zelf niet uit want ik vind het totaal niet logisch, waarom wordt de 144 gedeeld door 2 en dus 72 van gemaakt, en waarom wordt er van 54 90 gemaakt, is mij totaal onduidelijk. Iemand die dit kan toelichten?
Ja dit dacht ik in het begin dus ook, maar blijkbaar moet het wel zo. Onderbouwen kan ik het idd niet. Volgens mij doen ze * de afgeleide van 6y3, en y3 is constant dus nog een keer maal 6?quote:
Of ik kan het niet meer, of dat programma van je faalt al op de eerste regel./
[ afbeelding ]
Alle tussenstappen in je screenshot zijn fout, alleen het eindantwoord klopt. Welke joker heeft dit geschreven?quote:
Ik heb een probleempje met de afgeleide, ik snap niet hoe ze bij de volgende vraag aan dat antwoord komen.
Ik kom er zelf niet uit want ik vind het totaal niet logisch, waarom wordt de 144 gedeeld door 2 en dus 72 van gemaakt, en waarom wordt er van 54 90 gemaakt, is mij totaal onduidelijk. Iemand die dit kan toelichten?
[ afbeelding ]
www.mathxl.comquote:
[..]
Alle tussenstappen in je screenshot zijn fout, alleen het eindantwoord klopt. Welke joker heeft dit geschreven?
Integreer de functie: x2e-x
Dat wordt -x2e-x- Integraal(-2xe-x).
Integraal(-2xe-x) wordt -2e-x+2xe-x.
Dus de gezochte integraal is:
-x2e-x + 2e-x-2xe-x.
Kijken of hij aan de eigenschappen van een cdf voldoet, en misschien wat invullen ja.quote:
Algemeen vraagje. Als je een pdf of CDF van een X is gegeven en dan een Y die een functie is van X met de vraag wat de pdf of CDF van die Y is... nou dan zijn daar wel bepaalde technieken voor, maar hoe controleer je nu snel of je gevonden antwoord goed is? Door iets in te vullen ergens wellich?
Klopt niet.quote:
Integraal(-2xe-x) wordt -2e-x+2xe-x.
Ah, ik zie het al. Ik had -2 uit de integraal gehaald, maar het tweede min-teken niet veranderd.quote:
Bedankt!
Niet geheel waar... enigste wat fout is is dat ze vanquote:
[..]
Alle tussenstappen in je screenshot zijn fout, alleen het eindantwoord klopt. Welke joker heeft dit geschreven?
Wat is wat?quote:
[..]
Kijken of hij aan de eigenschappen van een cdf voldoet, en misschien wat invullen ja.
Als je 1 dobbelsteen hebt, kun 1 t/m 6 gooien, elk met evenveel kans. Heb je twee dobbelstenen, dan kun je ze, zoals bij Monopoly, bij elkaar optellen, maar je kunt ze ook met elkaar vermenigvuldigen. Dan gooi je minimaal 1 en maximaal 36, en nog wat waarden die daartussen zitten met een bepaalde kans.quote:
D'accord. Maar het product van stochasten>? Ik weet wel dat omdat ze onafhankelijk zijn, dat de verwachting dan gewoon het product van de verwachtingen is.... Maar de verdeling?En los daarvan, wat moet ik me eigenlijk voorstellen bij een product van onafhankelijke stochasten?
... (en toch druk ik er elke keer op)http://lmgtfy.com/?q=Ti-83+ERR%3AARCHIVEDquote:
Vraagje... ik heb een probleem met me TI-83... Wanneer ik ALPHA - A. Dus de letter A typ op de TI83. dan krijg ik ERR:ARCHIVED... Ik heb hem al gereset maar het probleem blijft... iemand enig idee?
Inverse functie van: f(x)= 3x + 6 / x + 1
stap 1: f(x+1) = 3x+6
stap 2: fx + f = 3x + 6
stap 3: fx - 3x = -f + 6
stap 4: x(f-3) = -f + 6
stap 5: x = f-3 / -f+6
(Ben maar een beetje aan het proberen, op gevoel .. weet niet of het goed is)
stap 5: x = -f+6 / f-3
En even letten op het domein. (x=/=-1)
Hoe bedoel je domein? Hoezo mag het geen -1 zijn?quote:
En even letten op het domein. (x=/=-1)
Zou je de uitwerking kunnen geven?quote:
Als je in je oorspronkelijke formule voor f(x) x=-1 invult, moet je door 0 delen en dat kan niet.quote:
[..]
Hoe bedoel je domein? Hoezo mag het geen -1 zijn?
"delen door nul is flauwekul"quote:
[..]
Als je in je oorspronkelijke formule voor f(x) x=-1 invult, moet je door 0 delen en dat kan niet.
TnxHeb morgen een tentamen, dus zal nog wel met meer vragen komen.
quote:
[..]
"delen door nul is flauwekul"
Heb morgen een tentamen, dus zal nog wel met meer vragen komen.
quote:
2Log ( x - 3) + 2Log ( x - 1) = 3
Stap 1: 2Log ( x-3 * x - 1) = 3
Stap 2: 2Log ( x2 - x - 3x + 3) = 3
Klopt het tot nu toe?
jaquote:
Next!
2Log ( x - 3) + 2Log ( x - 1) = 3
Stap 1: 2Log ( x-3 * x - 1) = 3
Stap 2: 2Log ( x2 - x - 3x + 3) = 3
Klopt het tot nu toe?
verder kom ik ook nietquote:
....
2Log ( x2 - 4x + 3) = 3
23 = x2 - 4x + 3
5 = x2 - 4x
Haakjes? Heb daar nog problemen mee.quote:
x2-4x-5=(x+1)(x-5)=0, hieruit kan je makkelijk de nulpunten (x=-1 en x=5) aflezenquote:
[..]
Haakjes? Heb daar nog problemen mee.
Daar ontbreken haakjes. En wat M.rak zegt.quote:
Ja. Maar merk op dat ook x > 3 moet zijn, zodat alleen de oplossing x = 5 voldoet.quote:
[..]
x2-4x-5=(x+1)(x-5)=0, hieruit kan je makkelijk de nulpunten (x=-1 en x=5) aflezen
Kan ook met de ABC formule toch? ( ABCquote:
[..]
x2-4x-5=(x+1)(x-5)=0, hieruit kan je makkelijk de nulpunten (x=-1 en x=5) aflezen
) 2Log ( (x-3) * (x - 1)) = 3quote:[quote] Op donderdag 27 januari 2011 19:08 schreef GlowMouse het volgende:
[..]
Daar ontbreken haakjes. En wat M.rak zegt.
(?)Dat kan ook ja, maar in principe lijkt het me makkelijker om te ontbindenquote:
[..]
Kan ook met de ABC formule toch? ( ABC
.Die klopt helemaal.quote:[..]
2Log ( (x-3) * (x - 1)) = 3
Ontbinden kan ik nietquote:
[..]
Dat kan ook ja, maar in principe lijkt het me makkelijker om te ontbinden
[..]
Die klopt helemaal.
Nog even een vraagje, maakt het uit als je bij de inverse functie de f(x) veranderd in y?
(Zie foto)
Ik heb de kansverdelingSPOILER
Nu moet ik
Nu zie ik boven de tabel, zie foto, Zo'n omrekening staan...
Nu is mijn vraag hoe doe ik dit voor P(Bin(5,3/4) <= 0) en P(Bin(5,3/4) <= -1)?
Ik heb bijvoorbeeld bij P(Bin(5,3/4) <= 0) = P(Bin(5;0,25) >= 0) ((3/4)/3 = 0,25 en 0 * 3 = 0) is dus 1 - P(Bin(5;0,25) <= 0)
ps. de goeie waardes zouden moeten zijn... P(Bin(5,3/4) <= 0) = 1 en P(Bin(5,3/4) <= -1) = 0,9990
[ Bericht 1% gewijzigd door Dale. op 27-01-2011 23:16:16 ]
Definieer Y = 5-X. Dan Y~BIN(5,1/4). Dit kun je zien via de pdf, maar ook met de uitleg dat de binomiale verdeling het aantal successen telt.
[ Bericht 26% gewijzigd door GlowMouse op 27-01-2011 23:24:55 ]
Tuurlijk kun je dat wel. Je hebt:quote:
(x + a)(x + b) = x2 + (a+b)x + ab
Als je dus x2 - 4x - 5 wil ontbinden, dan zoek je twee getallen waarvan de som -4 is en het product -5. Het is gemakkelijk te zien dat de gezochte getallen +1 en -5 zijn, zodat we dus hebben:
x2 - 4x - 5 = (x + 1)( x - 5)
Dat maakt wel uit maar niet veel aangezien de afhankelijke variabele bij een reële functie van x gewoonlijk inderdaad wordt aangeduid met y. Het is iets handzamer qua notatie als je de inverse van een functie y = f(x) wil bepalen.quote:Nog even een vraagje, maakt het uit als je bij de inverse functie de f(x) verandert in y?
Die 1/4 komt van (1-p) gewoon? Maar dus... P(Bin(5,3/4) <= 0) = P(Bin(5,1/4) <= 5) en P(Bin(5,3/4) <= -1) = P(Bin(5,1/4) <= 4)... En dat klopt ook volgens de tabel.quote:
Je zult wel X~BIN(5, 3/4) bedoelen. Aangezien X>=0 met kans 1, kun je volstaan met P(X<=0).
Definieer Y = 5-X. Dan Y~BIN(5,1/4).
Maar even een ander voorbeeldje dat ik heb... X~BIN(15,1/3)... en Dan P(BIN(15,1/3) = 0) = P(BIN(15,1/3) <= 0) - P(BIN(15,1/3) <= -1).
Definieer Y = 15-X. Dan wordt...
P(BIN(15,2/3) <= 15) - P(BIN(15,2/3) <= 14)... maar 2/3 staat weer niet in me tabel
Die als volgt is gegeven
8.Carton contains 144 balls each of which has a mean weight of 5 ounces and a standard deviation of 2/5 ounces. Use the CENTRAL LIMIT THEOREM to approximate the probability that the total weight of the baseballs in the carton is a maximum of 725 ounces.
Ik snap dat sigma=2/5 n=144 mu=5... maar dan?
(somX_i - 144*5)/(12*2/5) ~ N(0,1)
invullen: P(somX_i <= 725) = .... = P((somX_i - 144*5)/(12*2/5) <= ....) = ..
En dan?
Ik snap wel wat je moet doen, alleen zie ik dat niet zo snel.quote:
[..]
Tuurlijk kun je dat wel. Je hebt:
(x + a)(x + b) = x2 + (a+b)x + ab
Als je dus x2 - 4x - 5 wil ontbinden, dan zoek je twee getallen waarvan de som -4 is en het product -5. Het is gemakkelijk te zien dat de gezochte getallen +1 en -5 zijn, zodat we dus hebben:
x2 - 4x - 5 = (x + 1)( x - 5)
[..]
Dat maakt wel uit maar niet veel aangezien de afhankelijke variabele bij een reële functie van x gewoonlijk inderdaad wordt aangeduid met y. Het is iets handzamer qua notatie als je de inverse van een functie y = f(x) wil bepalen.
Ik ken nu bijna alle vragen, alleen moet ik deze nog:
vraag 1.Bereken de extreme waarden van f(x) = x3 + 3x2
Stap 1: Afgeleide: 3x2 + 6x
Stap 2: Afgeleide gelijkstellen aan 0 > 3x2 + 6x = 0
Maar hoe nu verder? Ik kan geen ABC toepassen.. zo misschien:
Stap 3: x (3x+6) = 0 -> x=0 v 3x + 6=0 (x=-2)
vraag2. Los de vergelijkingen op:
Stap 1: 4x = 1/8 * 5Wortel2
Stap 2: 4x = 1/8 * 2(1/5)
Stap 3: 4x = 1/8 * 11/5
Stap 4: 4Log (1/8 * 11/5)
Stap 5: 4Log 11/40 = x
Hoe nu verder? zo misschien?
Stap 6: 11/40 = 4x en dan delen door 4?
Op de plek van de puntjes in mijn post 244. Daar staat geen 725.quote:Op donderdag 27 januari 2011 23:52 schreef TheLoneGunmen het volgende:
Ja maar dat snap ik niet met mijn pindabrein... wat je dan moet doen om uiteindelijk de kans te krijgen. Want dan moet je toch in zo'n standaard z tabel kijken, maar bij welke waarde? Niet 725 in ieder geval.
= P(somX_i - 144*5 <= 725 - 144*5)
etc. tot je uitkomt op
P((somX_i - 144*5)/(12*2/5) <= ....)
De abc-formule is uiteraard altijd toepasbaar om een kwadratische vergelijking op te lossen, maar je kunt hier veel eenvoudiger ontbinden in factoren, zoals je nu ook hebt gedaan. Maar je opgave is hiermee nog lang niet klaar, want er wordt gevraagd naar de extrema van f(x), en niet naar de waarde(n) van x waarbij die extrema worden bereikt. Bovendien moet je van elke extreme waarde aangeven of het een (locaal) minimum of een (locaal) maximum betreft.quote:
[..]
Ik snap wel wat je moet doen, alleen zie ik dat niet zo snel.
Ik ken nu bijna alle vragen, alleen moet ik deze nog:
vraag 1.Bereken de extreme waarden van f(x) = x3 + 3x2
Stap 1: Afgeleide: 3x2 + 6x
Stap 2: Afgeleide gelijkstellen aan 0 > 3x2 + 6x = 0
Maar hoe nu verder? Ik kan geen ABC toepassen.. zo misschien:
Stap 3: x (3x+6) = 0 -> x=0 v 3x + 6=0 (x=-2)
Gebruik superscript consequent, dat heeft FOK niet voor niets, dit is erg onduidelijk. Je bedoelt kennelijk:quote:vraag2. Los de vergelijkingen op:
Stap 1: 4x = 1/8 * 5Wortel2
Stap 2: 4x = 1/8 * 2(1/5)
4x = 1/8*21/5
Dit gaat helemaal niet goed, mede door je eigen onduidelijke notatie.quote:Stap 3: 4x = 1/8 * 11/5
Stap 4: 4Log (1/8 * 11/5)
Stap 5: 4Log 11/40 = x
Hoe nu verder? zo misschien?
Stap 6: 11/40 = 4x en dan delen door 4?
Nja dit bedoel ik.
Voila, een wortelteken: √quote:Op vrijdag 28 januari 2011 00:33 schreef ajacied4lf het volgende:
Ik zal het proberen, maar het is een beetje lastig zonder worteltekens etc.
Nja dit bedoel ik.
[ afbeelding ]
Handig tnxquote:
Zie hem niet, weet alleen dat ik hem kan omzetten in een logaritme.quote:
de rechterkant kun je ook schrijven als 4iets.
GlowMouse zet je een beetje op het verkeerde been, want het is niet handig om 1/8 om te zetten in een macht van 4. We kunnen beter alles omzetten in machten van 2. Dus:quote:
[..]
Handig tnx
[..]
Zie hem niet, weet alleen dat ik hem kan omzetten in een logaritme.
4x = 1/8*21/5
22x = 2-3*21/5
22x = 2-14/5
Zie je nu hoe je verder kunt gaan, zonder gebruik van logaritmen?
Delen door 2:quote:
[..]
GlowMouse zet je een beetje op het verkeerde been, want het is niet handig om 1/8 om te zetten in een macht van 4. We kunnen beter alles omzetten in machten van 2. Dus:
4x = 1/8*21/5
22x = 2-3*21/5
22x = 2-14/5
Zie je nu hoe je verder kunt gaan, zonder gebruik van logaritmen?
2x = -14/5
x = -1,4
Maar weet niet zeker, heb het nooit zo gehad.
Inderdaad, dit is juist.quote:
[..]
Delen door 2:
2x = -14/5
x = -1,4
Maar weet niet zeker, heb het nooit zo gehad.
Behalve dat je niet door 2 deelt, maar de machten gewoon aan elkaar gelijk zijn omdat de grondtallen ook hetzelfde zijn.quote:
Ik doelde op de uitkomst, die is juist. En in 2x = -14/5 moet je toch beide leden door 2 delen om x te verkrijgen?quote:
[..]
Behalve dat je niet door 2 deelt, maar de machten gewoon aan elkaar gelijk zijn omdat de grondtallen ook hetzelfde zijn.
Daar wel ja, maar het is niet zo dat je het grondtal wegdeelt of zo, die indruk kreeg ikquote:
[..]
Ik doelde op de uitkomst, die is juist. En in 2x = -14/5 moet je toch beide leden door 2 delen om x te verkrijgen?
Maar hoe weet je dat 1/8 gelijk is aan 2-3
In het algemeen geldt a-n = 1/(an)quote:
Ok mooi
Maar hoe weet je dat 1/8 gelijk is aan 2-3
Wel, 8 = 2*2*2 = 23, en ook is 1/ap = a-p, dus 1/8 = 1/23 = 2-3.quote:
Ok mooi
Maar hoe weet je dat 1/8 gelijk is aan 2-3
-14/5?
Elementaire rekenregels voor machten:quote:
Ohja, hoe kom je aan 22x = 2-14/5
-14/5?
(ap)q = apq
ap*aq = ap+q
Dus:
4x = (22)x = 22x
En ook:
2-3*21/5 = 2-15/5*21/5 = 2-15/5 + 1/5 = 2-14/5
Heb hem vandaag gehad, ging wel lekker (heb een voldoende)quote:
[..]
Elementaire rekenregels voor machten:
(ap)q = apq
ap*aq = ap+q
Dus:
4x = (22)x = 22x
En ook:
2-3*21/5 = 2-15/5*21/5 = 2-15/5 + 1/5 = 2-14/5
Sterker nog, ik zou eerst beginnen met te bepalen voor welke x-waarden deze vgl. valide isquote:
[..]
Ja. Maar merk op dat ook x > 3 moet zijn, zodat alleen de oplossing x = 5 voldoet.
2Log ( x - 3) + 2Log ( x - 1) = 3
de logaritme is in R alleen gedefinieerd voor x > 0, dus we moeten oplossen:
x - 3 > 0 => x > 3
en
x - 1 > 0 => x > 1
hieruit volgt dus dat x sowieso groter dan 3 moet zijn
Had de laatste log-term nou Log(1-x) geweest en je had klakkeloos de rekenregels voor logaritmen toegepast, dat had je voor lelijke verrassingen (lees: dikke rode streep) komen te staan.
Nee, dit is niet zo. Als je namelijk in bovenstaande vergelijking (x - 1) vervangt door (1 - x), dan resulteert een vierkantsvergelijking met een negatieve discriminant, en die heeft sowieso geen reële oplossingen. Het probleem dat je denkt te zien bestaat dus niet. Een beetje snuggere leerling ziet trouwens direct dat bovenstaande vergelijking dan geen reële oplossingen kan hebben omdat er geen reële getallen zijn die voldoen aan x > 3 en tevens x < 1. Minder snuggere leerlingen zullen wel gaan rekenen en pas als ze ontdekken dat de resulterende vierkantsvergelijking een negatieve discriminant heeft tot de conclusie komen dat de oorspronkelijke vergelijking geen reële oplossing(en) heeft.quote:
[..]
Sterker nog, ik zou eerst beginnen met te bepalen voor welke x-waarden deze vgl. valide is
2Log ( x - 3) + 2Log ( x - 1) = 3
de logaritme is in R alleen gedefinieerd voor x > 0, dus we moeten oplossen:
x - 3 > 0 => x > 3
en
x - 1 > 0 => x > 1
hieruit volgt dus dat x sowieso groter dan 3 moet zijn
Had de laatste log-term nou Log(1-x) geweest en je had klakkeloos de rekenregels voor logaritmen toegepast, dat had je voor lelijke verrassingen (lees: dikke rode streep) komen te staan.
Je hebt gelijk.... in dit geval. Maar het is niet zo gek moeilijk om situaties te bedenken waarbij er maar 1 v/d 2 wortels uit de resulterende vierkantsvgl voldoet aan de domein-eisen van beide logtermen. En daar wou ik even voor waarschuwen; mn vroegere wiskundeleraar was gèk op dat soort death traps.quote:
[..]
Nee, dit is niet zo. Als je namelijk in bovenstaande vergelijking (x - 1) vervangt door (1 - x), dan resulteert een vierkantsvergelijking met een negatieve discriminant, en die heeft sowieso geen reële oplossingen. Het probleem dat je denkt te zien bestaat dus niet. Een beetje snuggere leerling ziet trouwens direct dat bovenstaande vergelijking dan geen reële oplossingen kan hebben omdat er geen reële getallen zijn die voldoen aan x > 3 en tevens x < 1. Minder snuggere leerlingen zullen wel gaan rekenen en pas als ze ontdekken dat de resulterende vierkantsvergelijking een negatieve discriminant heeft tot de conclusie komen dat de oorspronkelijke vergelijking geen reële oplossing(en) heeft.
[Bèta overig] Huiswerk- en vragentopic
xy / (x2+xy+y2)
gelijk is aan R2 \ {(0, 0)} ?
de epsilon delta definitie waarmee oa de formele definitie van een limiet wordt beschrevenquote:
Wat is dan de epsilon delta methode?
quote:
Wat heeft dit dan met een limiet te maken?
euhm.. moet ik nu de zaken gaan uitleggen terwijl ik met een vraag kom die ik al lastig vind?quote:
Wat heeft dit dan met een limiet te maken?
Je wilt een domein bepalen mbv een delta/epsilon bewijs? Kan je me hier een simpel voorbeeld van geven?quote:
[..]
[..]
euhm.. moet ik nu de zaken gaan uitleggen terwijl ik met een vraag kom die ik al lastig vind?
Het grootst mogelijke domein kan je wel bepalen. Dat is hier natuurlijk de bedoeling.quote:
Het domein is een eigenschap van een functie, niet iets wat je kunt bepalen.
Dat zal ook niet de bedoeling zijn, want ik mis imaginaire getallen (oa.).quote:
[..]
Het grootst mogelijke domein kan je wel bepalen. Dat is hier natuurlijk de bedoeling.
... in R^2quote:
[..]
Dat zal ook niet de bedoeling zijn, want ik mis imaginaire getallen (oa.).
Ja inderdaad. Dat bedoelde ik. Kan iemand mij dat uitleggen misschien?quote:
Ik denk dat het de bedoeling is te bewijzen dat de limiet (x,y) -> (0,0) van die functie niet bestaat.
Bedoel je dat?
Hmm nee. Het gaat om het aantonen van het groots mogelijk domein gelijk aan R2/{(0,0)}quote:
Die functie lijkt wel verdacht veel op een voorbeeldfunctie waarmee je een eigenschap van limieten kunt laten zien. Zoals de limiet van xy is de limiet van x keer de limiet van y, etc.
Bedoel je dat?
Als je y=0 invult, staat er 0/x2 en dat is 0 voor x != 0, dus de limiet zou 0 moeten zijn als die bestaat. Vul je y=x in, dan staat er x2/3x2 en dat is 1/3 voor x!=0 dus zou de limiet 1/3 moeten zijn. Het kan het niet allebei zijn, dus bestaat de limiet niet.quote:
[..]
Ja inderdaad. Dat bedoelde ik. Kan iemand mij dat uitleggen misschien?
Sorry, daar kwam ik uit. Maar niet hoe je laat zien dat het grootst mogelijke domein gelijk is aan R2/{(0,0)}quote:
[..]
Als je y=0 invult, staat er 0/x2 en dat is 0 voor x != 0, dus de limiet zou 0 moeten zijn als die bestaat. Vul je y=x in, dan staat er x2/3x2 en dat is 1/3 voor x!=0 dus zou de limiet 1/3 moeten zijn. Het kan het niet allebei zijn, dus bestaat de limiet niet.
Schrijf de noemer als som van 2 kwadraten. Zo laat je zien dat-ie niet 0 is voor (x,y) != (0,0).quote:
[..]
Sorry, daar kwam ik uit. Maar niet hoe je laat zien dat het grootst mogelijke domein gelijk is aan R2/{(0,0)}
En dat heeft toch echt niets met definitie van de limiet te makenquote:
[..]
Schrijf de noemer als som van 2 kwadraten. Zo laat je zien dat-ie niet 0 is voor (x,y) != (0,0).
Hmmz die begrijp ik niet helemaal.. Hoe schrijf je iets als som van 2 kwadraten?quote:
[..]
Schrijf de noemer als som van 2 kwadraten. Zo laat je zien dat-ie niet 0 is voor (x,y) != (0,0).
(x+y/2)² + 3y²/4 = ...quote:
[..]
Hmmz die begrijp ik niet helemaal.. Hoe schrijf je iets als som van 2 kwadraten?
e^(x+1)-e^x=3
[ Bericht 65% gewijzigd door hello_moto1992 op 03-02-2011 14:30:02 ]
Ohja, natuurlijk. Daar gaat weer een puntje.quote:
Schrijf het linkerlid als product en neem aan beide kanten de natuurlijke logaritme
Jammer manquote:
[..]
Ohja, natuurlijk. Daar gaat weer een puntje.
Stel w1,w2,... is een rijtje punten in W dat convergeert naar a in Rn. Laat zien dat a in W zit.
Ik probeerde het op deze manier:
Dan is er een e>0 zodat w1,w2,... elementen zijn van Be(a).
Stel nu dat a een element is van Rn\W ( die dus open is), dan is er
een d zodat Bd(a) een deelruimte in Rn\W.
Dan zijn er twee mogelijkheden:
Be(a) is een deelruimte van Bd(a): Maar dan zijn w1,w2,... elementen uit Rn\W. Klopt niet.
Of
Bd(a) is een deelruimte van Be(a): Maar dan...
En hier kom ik niet verder.
Stel a zit niet in W, dan zit a in in de open verzameling R^n\W. Hij zit dus in een bolletje met straal d>0 dat bevat is in R^n\W. Omdat de rij (w) convergeert naar a is er voor een willekeurige e>0 een rangnummer K zodat voor alle k>K w_k in B_e(a) zit. Dus ook voor e=d.
Dit leidt direct tot tegenspraak
Hmm, ik was er niet zeker van of ik wk willekeurig dicht bij a kon kiezen. Maar dat is dus inbegrepen in de definitie van 'convergeren'?quote:
Je begint een beetje onhandig met die e zo te kiezen, maar je bent al een end op weg.
Stel a zit niet in W, dan zit a in in de open verzameling R^n\W. Hij zit dus in een bolletje met straal d>0 dat bevat is in R^n\W. Omdat de rij (w) convergeert naar a is er voor een willekeurige e>0 een rangnummer K zodat voor alle k>K w_k in B_e(a) zit. Dus ook voor e=d.
Dit leidt direct tot tegenspraak
Jazeker, want dat een rij convergeert naar een punt a betekent dat de limiet van de rij als de index naar oneindig gaat gelijk is aan a. Dit kan je uitschrijven met de definitie van de limiet.quote:
[..]
Hmm, ik was er niet zeker van of ik wk willekeurig dicht bij a kon kiezen. Maar dat is dus inbegrepen in de definitie van 'convergeren'?