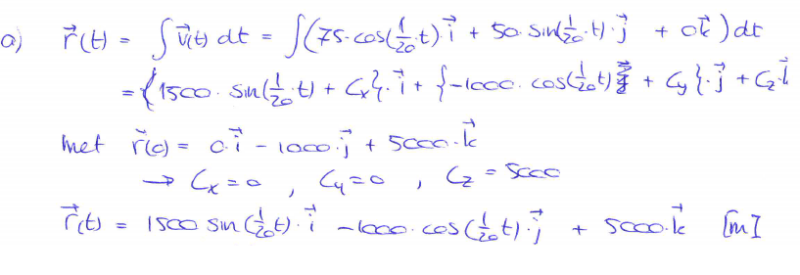SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk-en-vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oeps. Jij bent wel erg snel GM. 
.
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Ik wil de Fourierreeks van cos(x)^n bepalen. Voor de coëfficiënten c_k geldt
%5En%20e%5E%7B-i%20k%20x%7D%20dx%20)
Maar hoe integreer je dit, voor een algemene n?
Maar hoe integreer je dit, voor een algemene n?
7 minuten is niet echt snelquote:
Lukt dit niet met 2x partiëel en daarna een vergelijking oplossen?quote:Op zondag 9 januari 2011 19:53 schreef BasementDweller het volgende:
Ik wil de Fourierreeks van cos(x)^n bepalen. Voor de coëfficiënten c_k geldt
[ afbeelding ]
Maar hoe integreer je dit, voor een algemene n?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik zou cos(x) gewoon als (e^(ix) + e^(-ix)) / 2 schrijven. Dan hoef je niet eens te integreren om de Fouriercoëfficiënten te bepalen.
Hoe bepaal je ze dan?quote:
Ik zou cos(x) gewoon als (e^(ix) + e^(-ix)) / 2 schrijven. Dan hoef je niet eens te integreren om de Fouriercoëfficiënten te bepalen.
Ja oke, dan heb je een uitdrukking voor [(e^(ix) + e^(-ix)) / 2]^n, maar daarmee nog geen Fourriercoëfficiënten...
Heb het al, krijg als coëfficiënten c_k:
%20k%7D%7B2%5En%7D%20e%5E%7B-ix(n-k)%7D)
Bedankt
Lijkt me overigens met partiëel integreren (haast) ondoenbaar.
[ Bericht 33% gewijzigd door BasementDweller op 09-01-2011 22:52:49 ]
Heb het al, krijg als coëfficiënten c_k:
Bedankt
Lijkt me overigens met partiëel integreren (haast) ondoenbaar.
[ Bericht 33% gewijzigd door BasementDweller op 09-01-2011 22:52:49 ]
Thabit, hoe zit het hiermee: [Bèta wiskunde] Huiswerk-en-vragentopic ?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
je linkt werkt niet bij mensen die geen 182 posts op één pagina hebben; [Bèta wiskunde] Huiswerk-en-vragentopic werkt wel.quote:
Thabit, hoe zit het hiermee: [Bèta wiskunde] Huiswerk-en-vragentopic ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Sjongejonge, slecht ontwerp.quote:
[..]
je linkt werkt niet bij mensen die geen 182 posts op één pagina hebben; [Bèta wiskunde] Huiswerk-en-vragentopic werkt wel.
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Misschien iets voor in de OP: http://wims.unice.fr/wims/en_home.html
Calculator die integralen kan uitrekenen, kan differentieren en nog meer. Ook een om met matrices te rekenen, best handig.
Dan een simpel (?) vraagje:
Ik probeer de homotopische equivalentie van een aantal verzamelingen te laten zien. Ik weet wel welke afbeeldingen daarvoor zorgen, alleen ik krijg ze niet formeel geschreven. Volgens mij is het vrij elementaire calculus, maar daar ben ik dus echt slecht in.
Hieronder wat ik zelf voor elkaar krijg:
1)Homotopische equivalentie van een ring in R2 en de eenheidscirkel.
2)Open schijf met weggelaten punt {z: 0<|z|<1 } in C en de eenheidscirkel
3)Rn\{0} en Sn
Dus wat ik graag zou weten is, hoe ik die functies netjes beschrijf en hoe ik eraan kom. Ik zie bijvoorbeeld bij 2, dat je met de functie z/|z| wel alle punten van de schijf op de eenheidscirkel krijgt.
Bij 3. wordt het iets van x/||x|| en de gewone inclusie voor de andere kant...
Calculator die integralen kan uitrekenen, kan differentieren en nog meer. Ook een om met matrices te rekenen, best handig.
Dan een simpel (?) vraagje:
Ik probeer de homotopische equivalentie van een aantal verzamelingen te laten zien. Ik weet wel welke afbeeldingen daarvoor zorgen, alleen ik krijg ze niet formeel geschreven. Volgens mij is het vrij elementaire calculus, maar daar ben ik dus echt slecht in.
Hieronder wat ik zelf voor elkaar krijg:
1)Homotopische equivalentie van een ring in R2 en de eenheidscirkel.
2)Open schijf met weggelaten punt {z: 0<|z|<1 } in C en de eenheidscirkel
3)Rn\{0} en Sn
Dus wat ik graag zou weten is, hoe ik die functies netjes beschrijf en hoe ik eraan kom. Ik zie bijvoorbeeld bij 2, dat je met de functie z/|z| wel alle punten van de schijf op de eenheidscirkel krijgt.
Bij 3. wordt het iets van x/||x|| en de gewone inclusie voor de andere kant...
Denk niet dat het (veel) beter is dan wolframalpha.comquote:
Misschien iets voor in de OP: http://wims.unice.fr/wims/en_home.html
Ik zie niet zo gauw hoe dat zonder goniometrie kan. Moet ongetwijfeld wel mogelijk zijn.quote:
Thabit, hoe zit het hiermee: [Bèta wiskunde] Huiswerk-en-vragentopic ?
quote:
[..]
Ik zie niet zo gauw hoe dat zonder goniometrie kan. Moet ongetwijfeld wel mogelijk zijn.
het ging om post #182: [Bèta wiskunde] Huiswerk-en-vragentopic
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ah, zo, ik keek naar de post eronder.quote:
[..]
.In de formule e1T(e2A) =/= (e1Te2)A is e2A helemaal niet gedefinieerd.
Daarom juist. De conventie dat een 1x1 matrix een getal is, breekt associativiteit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
O, zo. Een 1x1-matrix is geen getal. Een inproduct is dat wel. xTy is dan ook niet het inproduct van x en y, maar de 1x1-matrix die het inproduct <x,y> als element heeft.
Maar 'iedereen' schrijft xTy wel als getal, zelfs mijn analyseboek 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Pardon?quote:Op woensdag 12 januari 2011 00:17 schreef thabit het volgende:
Tja, analyse, da's ook meer natuurkunde dan wiskunde.
Beschouw de vraagfunctie y(p) = p³ + p. De prijselasticiteit van de vraag is...
Nou kom ik uit op de breuk 3p³+p / p³+p.
Hoe kan ik deze verder vereenvoudigen? Het antwoordmodel zegt namelijk 3 - 2/p²+1 ?
Nou kom ik uit op de breuk 3p³+p / p³+p.
Hoe kan ik deze verder vereenvoudigen? Het antwoordmodel zegt namelijk 3 - 2/p²+1 ?
gebruik dat (a+b)/c = a/c + b/c en schrijf 3p² = 2p² + p² en schrijf p³+p = p(p²+1)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wat krijg je van:
e2t * e-t
Ben even roestig weer. Thx
e2t * e-t
Ben even roestig weer. Thx
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
exp(t)quote:
Wat krijg je van:
e2t * e-t
Ben even roestig weer. Thx
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik kom er zelfs met wat je zegt niet uit (heb totaal geen wiskundig inzichtquote:
gebruik dat (a+b)/c = a/c + b/c en schrijf 3p² = 2p² + p² en schrijf p³+p = p(p²+1)
), kan je het wat uitgebreider uitleggen en ook uitleggen hoe je weet dat je dat moet doen?
Je kijkt er nog geen 10 minuten naar. Heb je al pen en papier gepakt, alles opgeschreven, en geprobeerd wat ik zei?quote:
[..]
Ik kom er zelfs met wat je zegt niet uit (heb totaal geen wiskundig inzicht
Zoiets weet je door ervaring.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Heb al 2 kantjes van een kladblok vol met probeersels en geen enkele komt uit op de goede vereenvoudiging...quote:Op woensdag 12 januari 2011 18:57 schreef GlowMouse het volgende:
[..]
Je kijkt er nog geen 10 minuten naar. Heb je al pen en papier gepakt, alles opgeschreven, en geprobeerd wat ik zei?
Zoiets weet je door ervaring.
Misschien klopt het antwoord wel niet. Ik kom op 1 + ( 2p² / (p²+1) )
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe kom je hierop? Misschien is dat al fout...quote:
Nou kom ik uit op de breuk 3p³+p / p³+p.
Elasticiteit = deltaQ/deltaP * P/Q. y (p) = p³+pquote:
[..]
Hoe kom je hierop? Misschien is dat al fout...
Elasticiteit = (3p²+1) * P / p³+p = p(3p²+1) / p³+p = 3p³+p / p³+p = ?
Dat is toch goed of niet?
Daar kom ik ook niet op uit, maar weer even verder puzzelen..quote:
Misschien klopt het antwoord wel niet. Ik kom op 1 + ( 2p² / (p²+1) )
Dus eigenlijk bedoel je met y(p), q(p). Afgeleide klopt, alleen je vergeet wat haakjes:
Elasticiteit = (3p²+1) * p/q = p(3p²+1)/(p³+p) = (3p³+p)/(p³+p) = (p³+p)/(p³+p) + 2p³/(p³+p) = 1 + 2p²/(p²+1) . Zelfde als GM...
Elasticiteit = (3p²+1) * p/q = p(3p²+1)/(p³+p) = (3p³+p)/(p³+p) = (p³+p)/(p³+p) + 2p³/(p³+p) = 1 + 2p²/(p²+1) . Zelfde als GM...
Dan klopt het antwoord inderdaad gewoon niet. Bedankt jongens, dit maakt een hoop duidelijk.quote:
Dus eigenlijk bedoel je met y(p), q(p). Afgeleide klopt, alleen je vergeet wat haakjes:
Elasticiteit = (3p²+1) * p/q = p(3p²+1)/(p³+p) = (3p³+p)/(p³+p) = (p³+p)/(p³+p) + 2p³/(p³+p) = 1 + 2p²/(p²+1) . Zelfde als GM...
Het antwoord dat je eerst zelf gaf (uit het antwoordenboekje) klopt wel als vereenvoudiging van de breuk die je zelf geeft, dus je trekt de verkeerde conclusie. Heb je wel eens iets aan breuken gedaan op de lagere school?quote:
[..]
Dan klopt het antwoord inderdaad gewoon niet. Bedankt jongens, dit maakt een hoop duidelijk.
Grappig.quote:
[..]
Het antwoord dat je eerst zelf gaf (uit het antwoordenboekje) klopt wel, dus je trekt de verkeerde conclusie. Heb je wel eens iets aan breuken gedaan op de lagere school?
Leg eens uit dan waarom het wel klopt en waarom GM en BD daar ook niet op uitkomen?
Waar wij op uitkomen kun je herschrijven naar het antwoord. Als je aan het antwoord twijfelt, kun je een paar p's invullen en vergelijken met jouw antwoord.quote:
[..]
Grappig.
Leg eens uit dan waarom het wel klopt en waarom GM en BD daar ook niet op uitkomen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je wilde weten waarom (3p³+p)/(p³+p) gelijk is aan 3 - 2/(p²+1).quote:
[..]
Grappig.
Leg eens uit dan waarom het wel klopt en waarom GM en BD daar ook niet op uitkomen?
Zo kan je het ook vereenvoudigen idd:
(3p³+p)/(p³+p) = (3(p³+p) - 2p) / (p³+p) = 3 - 2p/(p³+p) = 3 - 2/(p²+1).
Als je haakjes plaatst dan klopt het antwoord wel, dus ik hoop dat ze in je antwoordenboekje wel haakjes gebruiken.
(3p³+p)/(p³+p) = (3(p³+p) - 2p) / (p³+p) = 3 - 2p/(p³+p) = 3 - 2/(p²+1).
Als je haakjes plaatst dan klopt het antwoord wel, dus ik hoop dat ze in je antwoordenboekje wel haakjes gebruiken.
Als ik het nu hierboven zie lijkt het heel logisch, maar als ik dat zelf moet bedenken kom ik daar echt nooit op..quote:
Zo kan je het ook vereenvoudigen idd:
(3p³+p)/(p³+p) = (3(p³+p) - 2p) / (p³+p) = 3 - 2p/(p³+p) = 3 - 2/(p²+1).
Als je haakjes plaatst dan klopt het antwoord wel, dus ik hoop dat ze in je antwoordenboekje wel haakjes gebruiken.
Blij dat het tentamen gewoon open vragen zijn, dan krijg je tenminste punten als je de berekening grotendeels goed doet, de tussentoetsen waren MC.
quote:
[..]
Als je aan het antwoord twijfelt, kun je een paar p's invullen en vergelijken met jouw antwoord.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Als je gestopt was bij (3p³+p)/(p³+p) dan zou je (wat mij betreft) alle punten moeten krijgen, alleen omdat teller en noemer nogal op elkaar lijken ligt vereenvoudigen nog wel voor de hand hier.quote:
[..]
Als ik het nu hierboven zie lijkt het heel logisch, maar als ik dat zelf moet bedenken kom ik daar echt nooit op..
Blij dat het tentamen gewoon open vragen zijn, dan krijg je tenminste punten als je de berekening grotendeels goed doet, de tussentoetsen waren MC.
MC vragen bij berekeningen is wel erg triest trouwens
. Doe dan: laat zien dat de elasticiteit =... , of doe gewoon "bereken de elasticiteit".
Had ik even gemist, maar dat gebruik ik inderdaad ook wel. Ik kon er alleen niet over uit dat ik de verdere vereenvoudiging niet snapte.quote:
[..]
Als je aan het antwoord twijfelt, kun je een paar p's invullen en vergelijken met jouw antwoord.
Ja, en dan bij antwoord E neerzetten "Geen van bovenstaande antwoorden is correct.".quote:
[..]
Als je gestopt was bij (3p³+p)/(p³+p) dan zou je (wat mij betreft) alle punten moeten krijgen, alleen omdat teller en noemer nogal op elkaar lijken ligt vereenvoudigen nog wel voor de hand hier.
MC vragen bij berekeningen is wel erg triest trouwens
En dan stuk voor stuk na moeten gaan of jou antwoord omgeschreven kan worden naar A,B,C of Dquote:
Ja, en dan bij antwoord E neerzetten "Geen van bovenstaande antwoorden is correct.".
Jup.quote:
[..]
En dan stuk voor stuk na moeten gaan of jou antwoord omgeschreven kan worden naar A,B,C of D
Ik heb morgen een toets wiskunde, maar uit een volgens mij relatief eenvoudig sommetje kom ik niet uit. Ik weet niet hoe ik het moet aanpakken, maar moet het 1x weten en dan lukt het wel (hoop ik). Is er iemand die deze even voor kan doen?
1 / (1-x) + 1 / (1+x) = 3
Alvast erg bedankt
1 / (1-x) + 1 / (1+x) = 3
Alvast erg bedankt
zorg dat je de breuken kwijtraakt; vermenigvuldig bv. eerst met (1-x).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Als ik dat doe komt er bij mij x=1 uit, maar dat kan niet want dan krijg je iets delen door 0.
Hmm
Stel je vermenigvuldigt met (1-x) dan krijg je (1-x) / (1-x) + (1-x) / (1+x) = 3(1-x)
En daar kwam dacht ik 1 - x = 3 - 3x
Waar zit de fout?
Hmm
Stel je vermenigvuldigt met (1-x) dan krijg je (1-x) / (1-x) + (1-x) / (1+x) = 3(1-x)
En daar kwam dacht ik 1 - x = 3 - 3x
Waar zit de fout?
Kan iemand hierheen kijken?
Laat zien of de volgende lineaire afbeeldingen injectief, surjectief of bijectief is:
f: R3->R2 : (x,y,z) |--> (x-y,2z)
Injectief:
Nee, want voor elke x,y in R, met x=/ 0, en x=y geldt voor z=0
f(x,y,z) = (0,0)
Aangezien x=y=/0, is deze afbeelding dus niet injectief.
Surjectief:
f(1,0,0) = (1,0) =f(v1)
f(0,1,0) = (-1,0)= f(v2)
f(0,0,1)= (0,1) = f(v3)
We zien dus dat L(f(v1),f(v3))= R2. Aangezien voor elke x,y,z in R (x-y,2z) een element uit R2 is, is f dus surjectief.
Laat zien of de volgende lineaire afbeeldingen injectief, surjectief of bijectief is:
f: R3->R2 : (x,y,z) |--> (x-y,2z)
Injectief:
Nee, want voor elke x,y in R, met x=/ 0, en x=y geldt voor z=0
f(x,y,z) = (0,0)
Aangezien x=y=/0, is deze afbeelding dus niet injectief.
Surjectief:
f(1,0,0) = (1,0) =f(v1)
f(0,1,0) = (-1,0)= f(v2)
f(0,0,1)= (0,1) = f(v3)
We zien dus dat L(f(v1),f(v3))= R2. Aangezien voor elke x,y,z in R (x-y,2z) een element uit R2 is, is f dus surjectief.
f(v3) is geen (0,1) maar (0,2).
Je laatste zin snap ik niet (wat is L?). Surjectief toon je aan dat elk element uit R² bereikt kan worden, en dat volgt idd uit lineariteit, f(v1) en f(v3).
Je laatste zin snap ik niet (wat is L?). Surjectief toon je aan dat elk element uit R² bereikt kan worden, en dat volgt idd uit lineariteit, f(v1) en f(v3).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Klopt, dat was een typefoutje.quote:
f(v3) is geen (0,1) maar (0,2).
Je laatste zin snap ik niet (wat is L?). Surjectief toon je aan dat elk element uit R² bereikt kan worden, en dat volgt idd uit lineariteit, f(v1) en f(v3).
Met L(f(v1),f(v3)) bedoel ik het lineaire opspansel van f(v1),f(v3).
Dit stukje vind ik ook een beetje vaag. Bedoel je met de laatste zin misschien: aangezien f(0,0,0)=(0,0) is de afbeelding niet injectief?quote:
Kan iemand hierheen kijken?
Laat zien of de volgende lineaire afbeeldingen injectief, surjectief of bijectief is:
f: R3->R2 : (x,y,z) |--> (x-y,2z)
Injectief:
Nee, want voor elke x,y in R, met x=/ 0, en x=y geldt voor z=0
f(x,y,z) = (0,0)
Aangezien x=y=/0, is deze afbeelding dus niet injectief.
Ik zou het zo doen:
Injectief betekent f(x)=f(y) => x=y. Het is makkelijk om met tegenspraak te laten zien dat ie niet injectief is; Stel f is injectief. Dan volgt uit f(0,0,1)=f(1,1,1)=(0,2), dat (0,0,1)=(1,1,1) (tegenspraak).
Ik maak gebruik van het gegeven dat als Ker f = 0 dan en alleen dan is f injectief.quote:
[..]
Dit stukje vind ik ook een beetje vaag. x mag ook best nul zijn, want dan is x-y ook nog nul als x=y.
Ik zou het zo doen:
Injectief betekent f(x)=f(y) => x=y. Het is makkelijk om met tegenspraak te laten zien dat ie niet injectief is; Stel f is injectief. Dan volgt uit f(0,0,1)=f(1,1,1)=(0,0,2), dat (0,0,1)=(1,1,1) (tegenspraak).
Bewijs:
Stel alleen f(0)=0
Dan voor f(v)=f(v') , dan f(v-v')=f(0) betekent dat v=v'.
Oftewel de definitie van injectief.
Ah ja, zo kan het ookquote:
[..]
Ik maak gebruik van het gegeven dat als Ker f = 0 dan en alleen dan is f injectief.
Bewijs:
Stel alleen f(0)=0
Dan voor f(v)=f(v') , dan f(v-v')=f(0) betekent dat v=v'.
Oftewel de definitie van injectief.
Het klinkt stom, maar kan iemand me een voorbeeld geven van een niet surjectieve afbeelding?quote:
Op En belangrijker, hoe bewijs je dat?
f: R-> R , f(x)=x²quote:
[..]
Het klinkt stom, maar kan iemand me een voorbeeld geven van een niet surjectieve afbeelding?
En belangrijker, hoe bewijs je dat?
f is niet surjectief omdat f(x)=/ -1 voor alle x in het domein van f (een kwadraat is altijd niet-negatief). Dus -1 ligt wel in het codomein maar wordt niet bereikt => niet surjectief.
Maar het codomein wordt dus niet beschreven door, in dit geval, x2, maar is gewoon R ?quote:Op donderdag 13 januari 2011 14:22 schreef BasementDweller het volgende:
[..]
f: R-> R , f(x)=x²
f is niet surjectief omdat f(x)=/ -1 voor alle x (een kwadraat is altijd niet-negatief). Dus -1 ligt wel in het codomein maar wordt niet bereikt => niet surjectief.
Ja. Het codomein mag je eigenlijk zelf kiezen, zo lang het bereik van de functie er maar een deelverzameling van is.quote:
[..]
Maar het codomein wordt dus niet beschreven door, in dit geval, x2, maar is gewoon R ?
Als je dezelfde functie had genomen met als codomein: alle niet-negatieve reële getallen, dan was ie wel surjectief geweest.
Ik zie net je edit:quote:
[..]
Ja. Het codomein mag je eigenlijk zelf kiezen, zo lang het bereik van de functie er maar een deelverzameling van is.
Als je dezelfde functie had genomen met als codomein: alle niet-negatieve reële getallen, dan was ie wel surjectief geweest.
Alles mbt surjectieviteit word meteen een stuk duidelijker.
Bedankt!
N=natuurlijke getallen? Dan heb je je functie niet goed gedefiniëerd, want dan heeft f(1/2) geen uitkomst, want (1/2)^2 = 1/4 (niet in N).quote:
[..]
Dus als het codomein N, domein gewoon R laten, in dit geval was geweest, was de functie wél surjectief?
Klopt, ik merkte het al toen ik op invoeren drukte.quote:
[..]
N=natuurlijke getallen? Dan heb je je functie niet goed gedefiniëerd, want dan heeft f(1/2) geen uitkomst, want (1/2)^2 = 1/4 (niet in N).
Ik zit met iets.
0,05 is hetzelfde als 20-1
0,05t is hetzelfde als 20-1t
Nu gaan we integraal nemen:
f 0,05t = 0,025t2 toch?
f 20-1t = 20
Ben ik nou gek v_v?
0,05 is hetzelfde als 20-1
0,05t is hetzelfde als 20-1t
Nu gaan we integraal nemen:
f 0,05t = 0,025t2 toch?
f 20-1t = 20
Ben ik nou gek v_v?
Blues ain't nothing but a good man feeling bad...
Bedoel je met 'f' een primitieve? Een primitieve van 20^(-1)*t is bijv. 20^(-1)*t^2/2, in ieder geval niet 20.quote:
Ik zit met iets.
0,05 is hetzelfde als 20-1
0,05t is hetzelfde als 20-1t
Nu gaan we integraal nemen:
f 0,05t = 0,025t2 toch?
f 20-1t = 20
Ben ik nou gek v_v?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Moet een integraal teken voorstellen.
f ( 0,05t) dt= 0,025t2
f ( 20-1t) dt = 20
f ( 0,05t) dt= 0,025t2
f ( 20-1t) dt = 20
Blues ain't nothing but a good man feeling bad...
v(t) = 75cos(0,05t)
Ik wil deze snelheids vector omzetten naar een positie vector, dus v integreren naar s.
Dus 75cos(0,05t) als je dat integreert word het 75sin(0,05t) MAAL de integraal van 0,05t. Product regels is dat geloof ik he. En toen zag ik dat de uitkomst daarvan 20 is.
Ik wil deze snelheids vector omzetten naar een positie vector, dus v integreren naar s.
Dus 75cos(0,05t) als je dat integreert word het 75sin(0,05t) MAAL de integraal van 0,05t. Product regels is dat geloof ik he. En toen zag ik dat de uitkomst daarvan 20 is.
Blues ain't nothing but a good man feeling bad...
Zoals gezegd, die tweede klopt niet.quote:
Moet een integraal teken voorstellen.
f ( 0,05t) dt= 0,025t2
f ( 20-1t) dt = 20
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Hier gaat het om:
Zoals je ziet staat er 1500. Dat betekent dus dat 75 met 20 is vermenigvuldigd. Waar komt die 20 dan vandaan?
Zoals je ziet staat er 1500. Dat betekent dus dat 75 met 20 is vermenigvuldigd. Waar komt die 20 dan vandaan?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Blues ain't nothing but a good man feeling bad...
Nee, de integraal van v(s) = 75*cos(0.05*s) voor s van 0 tot t wordt (75/0.05)*sin(0.05t).quote:
v(t) = 75cos(0,05t)
Ik wil deze snelheids vector omzetten naar een positie vector, dus v integreren naar s.
Dus 75cos(0,05t) als je dat integreert word het 75sin(0,05t) MAAL de integraal van 0,05t. Product regels is dat geloof ik he. En toen zag ik dat de uitkomst daarvan 20 is.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
De kettingregel, differentieren van (75/0.05)*sin(0.05t) geeft (75/0.05)*cos(0.05*t)*0.05 = 75*cos(0.05*t).quote:
Wat voor een rekenregel is dit dan?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Moeilijke integralen hebben vaak een uitkomst die simpel te differentieren valt.quote:
Wat voor een rekenregel is dit dan?
Gebruik dat dan om te controleren of je ook echt de goede integraal hebt.
[ Bericht 0% gewijzigd door Siddartha op 13-01-2011 18:01:43 ]
Waar baseer je dat op? Ik ken genoeg 'eenvoudige' functies waarvan een primitieve niet in elementaire functies is uit te drukken, maar daaruit volgt niet dat omgekeerd 'moeilijke' functies eenvoudig te primitiveren zouden zijn.quote:
[..]
Moeilijke integralen hebben vaak een uitkomst die simpel te integreren valt.
Hij bedoelt denk ik dat de uitkomst van moeilijke integralen soms makkelijk te differentieren is als controle.quote:Op donderdag 13 januari 2011 17:52 schreef Riparius het volgende:
[..]
Waar baseer je dat op? Ik ken genoeg 'eenvoudige' functies waarvan een primitieve niet in elementaire functies is uit te drukken, maar daaruit volgt niet dat omgekeerd 'moeilijke' functies eenvoudig te primitiveren zouden zijn.
WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.
Arguing on the Internet is like running in the Special Olympics.
Differentieren bedoel ik.quote:
[..]
Waar baseer je dat op? Ik ken genoeg 'eenvoudige' functies waarvan een primitieve niet in elementaire functies is uit te drukken, maar daaruit volgt niet dat omgekeerd 'moeilijke' functies eenvoudig te primitiveren zouden zijn.
Zo had hij dat de integraal van 20^-1 een getal was. Je ziet meteen dat zoiets niet kan.
Dan een simpel (?) vraagje:
Ik probeer de homotopische equivalentie van een aantal verzamelingen te laten zien. Ik weet wel welke afbeeldingen daarvoor zorgen, alleen ik krijg ze niet formeel geschreven. Volgens mij is het vrij elementaire calculus, maar daar ben ik dus echt slecht in.
Hieronder wat ik zelf voor elkaar krijg:
1)Homotopische equivalentie van een ring in R2 en de eenheidscirkel.
[ afbeelding ]
2)Open schijf met weggelaten punt {z: 0<|z|<1 } in C en de eenheidscirkel
3)Rn\{0} en Sn
Dus wat ik graag zou weten is, hoe ik die functies netjes beschrijf en hoe ik eraan kom. Ik zie bijvoorbeeld bij 2, dat je met de functie z/|z| wel alle punten van de schijf op de eenheidscirkel krijgt.
Bij 3. wordt het iets van x/||x|| en de gewone inclusie voor de andere kant...
Ik probeer de homotopische equivalentie van een aantal verzamelingen te laten zien. Ik weet wel welke afbeeldingen daarvoor zorgen, alleen ik krijg ze niet formeel geschreven. Volgens mij is het vrij elementaire calculus, maar daar ben ik dus echt slecht in.
Hieronder wat ik zelf voor elkaar krijg:
1)Homotopische equivalentie van een ring in R2 en de eenheidscirkel.
[ afbeelding ]
2)Open schijf met weggelaten punt {z: 0<|z|<1 } in C en de eenheidscirkel
3)Rn\{0} en Sn
Dus wat ik graag zou weten is, hoe ik die functies netjes beschrijf en hoe ik eraan kom. Ik zie bijvoorbeeld bij 2, dat je met de functie z/|z| wel alle punten van de schijf op de eenheidscirkel krijgt.
Bij 3. wordt het iets van x/||x|| en de gewone inclusie voor de andere kant...
Lijkt me toch prima zo? Bij 2 kun je van de cirkel naar de schijf gaan door z naar z/2 te sturen.quote:
Dan een simpel (?) vraagje:
Ik probeer de homotopische equivalentie van een aantal verzamelingen te laten zien. Ik weet wel welke afbeeldingen daarvoor zorgen, alleen ik krijg ze niet formeel geschreven. Volgens mij is het vrij elementaire calculus, maar daar ben ik dus echt slecht in.
Hieronder wat ik zelf voor elkaar krijg:
1)Homotopische equivalentie van een ring in R2 en de eenheidscirkel.
[ afbeelding ]
2)Open schijf met weggelaten punt {z: 0<|z|<1 } in C en de eenheidscirkel
3)Rn\{0} en Sn
Dus wat ik graag zou weten is, hoe ik die functies netjes beschrijf en hoe ik eraan kom. Ik zie bijvoorbeeld bij 2, dat je met de functie z/|z| wel alle punten van de schijf op de eenheidscirkel krijgt.
Bij 3. wordt het iets van x/||x|| en de gewone inclusie voor de andere kant...
Je moet nog wel aantonen dat het homotopie-equivalenties zijn natuurlijk.
Oké bedankt Ja, dat het homotopie-equivalenties zijn lukt me wel, 't zijn die elementaire dingen die me altijd buggen. Had je bij wijze van voorbeeld en om het te vatten ook gewoon elke z naar z/3 of z/4 kunnen sturen in jouw functie?
Ja, dat het homotopie-equivalenties zijn lukt me wel, 't zijn die elementaire dingen die me altijd buggen. Had je bij wijze van voorbeeld en om het te vatten ook gewoon elke z naar z/3 of z/4 kunnen sturen in jouw functie?
Uiteraard had dat zo gekund, die dingen zijn allemaal homotoop met elkaar.quote:
Oké bedankt
Kan iemand mijn bewijs checken? l^1 betekent absoluut optelbaar, en l^2 kwadratisch optelbaar:
Volgens mij zijn die ''deelrijen'' officieel geel deelrijen omdat ik ook termen verander...
, maar zie het dan maar gewoon als 'nieuwe' rijen.
Volgens mij zijn die ''deelrijen'' officieel geel deelrijen omdat ik ook termen verander...
, maar zie het dan maar gewoon als 'nieuwe' rijen.
Dat ziet er wel correct uit. Misschien kun je nog even opmerken dat het nemen van oneindige sommen in dit geval geoorloofd is omdat de termen allemaal >= 0 zijn.
Een oneindige som is een limiet van eindige sommen. Als er negatieve termen zijn, dan kan de limiet afhangen van de sommatievolgorde.quote:
Wat kan er dan fout gaan als sommige termen <0 zijn?
Als ik de matrixen A en C weet met A*B = C, B = n*n matrix en A en C een n*m matrix... is het dan mogelijk om achter matrix B uit te rekenen?
Als A een n*m-matrix is, en B een n*n-matrix, dan is A*B alleen gedefinieerd indien n gelijk is aan m.quote:
Als ik de matrixen A en C weet met A*B = C, B = n*n matrix en A en C een n*m matrix... is het dan mogelijk om achter matrix B uit te rekenen?
Is echter A een m*n-matrix, dan is de vermenigvuldiging wel goed gedefinieerd. Je kan B kolomsgewijs uitrekenen, als v de i-de kolom is van B en w de i-de kolom is van C, dan moet je dus het stelsel A*v = w oplossen en dat zo voor i van 1 t/m n.
Als A=C=O (de all-0 matrix), dan kun je B nooit meer precies bepalen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Lebesgue Integratie:
1) If f is measurable and f = g except on a set of measure zero, show that g is also measurable.
2)voor meetbare f:
Hoe bewijs ik dat?
Ze zijn me alle twee overigens intuitief totaal begrijpelijk.
1) If f is measurable and f = g except on a set of measure zero, show that g is also measurable.
2)voor meetbare f:
Hoe bewijs ik dat?
Ze zijn me alle twee overigens intuitief totaal begrijpelijk.
Waarom is de dihedrale groep D_2 niet isomorf aan Z/Z2?
Je kan het voorstellen door zo'n lijn:
1 ------------------------ 2
Als je dan spiegelt of of pi rad draait dan heeft dat hetzelfde effect, dus s=r, dus {e,r,s,sr}={e,r,r,r^2} = {e,r} ~= Z/Z2. Waarom klopt dit niet?
Je kan het voorstellen door zo'n lijn:
1 ------------------------ 2
Als je dan spiegelt of of pi rad draait dan heeft dat hetzelfde effect, dus s=r, dus {e,r,s,sr}={e,r,r,r^2} = {e,r} ~= Z/Z2. Waarom klopt dit niet?
Je moet het zien als een "tweehoek". Er gaat als het ware een zijde van 1 naar 2 onderlangs en een zijde van 2 naar 1. Spiegelen is dan iets anders dan roteren: spiegelen verwisselt boven en onder niet, maar roteren wel.
Als een rij convergeert naar alfa dan is alfa een limietpunt. Ze laten zien dat zo'n limietpunt tot S behoort. Omdat dit argument opgaat voor een willekeurig limietpunt, behoort ieder limietpunt tot S en dan is S per definitie gesloten.
In het bewijs is alfa zo gekozen dat het buiten S ligt. Ze maken er een bolletje omheen met een straal > 0 zodat het hele bolletje buiten S ligt. Omdat de rij naar alfa convergeert, komen de punten in die rij willekeurig dicht bij alfa voor voldoende grote n, en dus ook in het deltabolletje, en dus allemaal buiten S.
[ Bericht 7% gewijzigd door BasementDweller op 16-01-2011 23:23:02 ]
In het bewijs is alfa zo gekozen dat het buiten S ligt. Ze maken er een bolletje omheen met een straal > 0 zodat het hele bolletje buiten S ligt. Omdat de rij naar alfa convergeert, komen de punten in die rij willekeurig dicht bij alfa voor voldoende grote n, en dus ook in het deltabolletje, en dus allemaal buiten S.
[ Bericht 7% gewijzigd door BasementDweller op 16-01-2011 23:23:02 ]
p en alpha zijn dus in principe hetzelfde punt toch? Waarom is het dan nodig om nog een punt p te kiezen?quote:
Als een rij convergeert naar alfa dan is alfa een limietpunt. Ze laten zien dat zo'n limietpunt tot S behoort. Omdat dit argument opgaat voor een willekeurig limietpunt, behoort ieder limietpunt tot S en dan is S per definitie gesloten.
In het bewijs is alfa zo gekozen dat het buiten S ligt. Ze maken er een bolletje omheen met een straal > 0 zodat het hele bolletje buiten S ligt. Omdat de rij naar alfa convergeert, komen de punten in die rij willekeurig dicht bij alfa voor voldoende grote n, en dus ook in het deltabolletje, en dus allemaal buiten S.
Nee p is een punt in het deltabolletje rond alfa. Die delta kiezen ze zo dat ieder punt p in dat bolletje niet in S ligt. Dus dat hele bolletje ligt niet in S (preciezer: de doorsnede van het bolletje en S is leeg).quote:
[..]
p en alpha zijn dus in principe hetzelfde punt toch? Waarom is het dan nodig om nog een punt p te kiezen?
Ze kiezen dus een alpha waar de rij x(n) naar toe convergeert. Ze nemen aan dat alpha buiten S ligt. Ze tekenen een bol om alpha met straal delta zo dat de hele bol niet in S ligt. Omdat alpha het middelpunt is van het bolletje, zou x(n) ook in het bolletje moeten zitten, dit is niet zo, dus alpha is binnen S, dus S is closed.quote:
[..]
Nee p is een punt in het deltabolletje rond alfa. Die delta kiezen ze zo dat ieder punt p in dat bolletje niet in S ligt. Dus dat hele bolletje ligt niet in S (preciezer: de doorsnede van het bolletje en S is leeg).
Klopt dat cursieve deel?
Nee, niet iedere x(n) hoeft in het bolletje te zitten. Zie je waarom?quote:
[..]
Ze kiezen dus een alpha waar de rij x(n) naar toe convergeert. Ze nemen aan dat alpha buiten S ligt. Ze tekenen een bol om alpha met straal delta zo dat de hele bol niet in S ligt. Omdat alpha het middelpunt is van het bolletje, zou x(n) ook in het bolletje moeten zitten, dit is niet zo, dus alpha is binnen S, dus S is closed.
Klopt dat cursieve deel?
Dat zeg je eigenlijk zelf ook al.
Pas als n groot genoeg is zit hij in het bolletje (schrijf anders eens met de definitie van de limiet op wat het betekent dat a_n naar alfa convergeert als n naar oneindig gaat!!).
Dan heb je dus een heel deel van de rij wat buiten S ligt, dus is de rij geen deelverzameling van S, in tegenspraak met hoe je die rij gekozen had.
[ Bericht 10% gewijzigd door BasementDweller op 16-01-2011 23:50:31 ]
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |