SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
OP
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Shit, gooi ik met die nutteloze post ook het topic nog dicht. In de herkansing dan maar:
Deze post bij gebrek aan openstaande wiskundevragen, zoals al lange tijd steeds het geval is als ik in dit topic kijk. .
.
Edit: even googlen levert bijv. het volgende op, uit een "Samenvatting Wiskunde Leerboek 1 getal en ruimte examenstof": "Het open interval <6,13> is het gedeelte van de getallenlijn tussen 6 en 13.". Het lijkt dus inderdaad om notatie uit (in ieder geval) Getal & Ruimte te gaan.
[ Bericht 6% gewijzigd door keesjeislief op 14-09-2009 01:56:15 ]
Ik herinner me die notatie wel ergens van, waarschijnlijk van mijn middelbare schooltijd, wij gebruikten Getal & Ruimte, misschien dat het daar (o.a.) vandaan komt?quote:Op zondag 13 september 2009 21:50 schreef Iblis het volgende:
[..]
Goede vraag. Ik denk dat ik dat per ongeluk fout heb ingesteld op m’n toetsenbord. Alhoewel ik meestal \rangle gebruik: [ afbeelding ]. Bij de volgende revisie zal ik dat fiksen.
Deze post bij gebrek aan openstaande wiskundevragen, zoals al lange tijd steeds het geval is als ik in dit topic kijk.
Edit: even googlen levert bijv. het volgende op, uit een "Samenvatting Wiskunde Leerboek 1 getal en ruimte examenstof": "Het open interval <6,13> is het gedeelte van de getallenlijn tussen 6 en 13.". Het lijkt dus inderdaad om notatie uit (in ieder geval) Getal & Ruimte te gaan.
[ Bericht 6% gewijzigd door keesjeislief op 14-09-2009 01:56:15 ]
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Klopt, daar wordt dat zo gebruikt.quote:Op maandag 14 september 2009 01:40 schreef keesjeislief het volgende:
Shit, gooi ik met die nutteloze post ook het topic nog dicht. In de herkansing dan maar:
[..]
Ik herinner me die notatie wel ergens van, waarschijnlijk van mijn middelbare schooltijd, wij gebruikten Getal & Ruimte, misschien dat het daar (o.a.) vandaan komt?
Deze post bij gebrek aan openstaande wiskundevragen, zoals al lange tijd steeds het geval is als ik in dit topic kijk..
Edit: even googlen levert bijv. het volgende op, uit een "Samenvatting Wiskunde Leerboek 1 getal en ruimte examenstof": "Het open interval <6,13> is het gedeelte van de getallenlijn tussen 6 en 13.". Het lijkt dus inderdaad om notatie uit (in ieder geval) Getal & Ruimte te gaan.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Weer wat geleerd. Ik heb in ieder geval m’n keyboard layout aangepast, zodat ik ⟨–∞,+∞⟩ de juiste haakjes kan gebruiken en Riparius me niet meer hoeft te corrigeren. 
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Hoop dat iemand me een zetje in de goede richting kan geven, weet namelijk echt niet waar ik moet beginnen.
Gegeven een iteratieproces van een vispopulatie:
t(n+1) = t(n) * e^(k(a-t(n)))
Laat zien dat de geschaalde variabele y(n) = t(n) / a voldoet aan:
y(n+1) = y(n) * e^(K(1-y(n)))
(K is hier een andere variabele dan k in de eerste vergelijking)
(Heb het geprobeerd in het latex ding van glowmouse te zetten maar daar kwam de macht niet echt lekker uit)
Gegeven een iteratieproces van een vispopulatie:
t(n+1) = t(n) * e^(k(a-t(n)))
Laat zien dat de geschaalde variabele y(n) = t(n) / a voldoet aan:
y(n+1) = y(n) * e^(K(1-y(n)))
(K is hier een andere variabele dan k in de eerste vergelijking)
(Heb het geprobeerd in het latex ding van glowmouse te zetten maar daar kwam de macht niet echt lekker uit)


Je moest waarschijnlijk e^{...} typen, om aan te geven wat allemaal in de exponent moest. Hoe dan ook als y(n) = t(n)/a, dan krijg je:
Bovenstaande hebben we gewoon verkregen door y(n) door t(n)/a te vervangen. Nu gaan we in de exponent eens die 1/a buiten haakjes halen, dan krijgen we:
Ik neem aan dat K/a = k, dus dat we dat kunnen vervangen, en dan krijgen we:
En laat de rechterkant nu precies gelijk zijn aan t(n + 1)/a:
Bovenstaande hebben we gewoon verkregen door y(n) door t(n)/a te vervangen. Nu gaan we in de exponent eens die 1/a buiten haakjes halen, dan krijgen we:
Ik neem aan dat K/a = k, dus dat we dat kunnen vervangen, en dan krijgen we:
En laat de rechterkant nu precies gelijk zijn aan t(n + 1)/a:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


[edit] Laat maar, zie het al  bedankt! [/edit]
bedankt! [/edit]
[ Bericht 70% gewijzigd door woopehh op 14-09-2009 12:45:01 ]
[ Bericht 70% gewijzigd door woopehh op 14-09-2009 12:45:01 ]


De exponenten zijn hetzelfde. Als je met de bovenste begint, deel dan K door a en vermenigvuldig 1-t(n)/a met a om bij de onderste uit te komen. Je haalt een 1/a buiten haakjes, om het anders te zeggen.quote:Op maandag 14 september 2009 12:39 schreef woopehh het volgende:
Bedankt, snap alleen niet echt hoe je van:
[ afbeelding ]
naar
[ afbeelding ]
gaat, zou je dat nog kunnen toelichten?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Indien verdeeld is, voor welke waarde van x geldt dat de kans
Ik heb het geprobeerd met z-transformatie, maar dat lukt me niet:
(kortom, ik hou weer gewoon -x+2 over...)
Ik snap er echt helemaal niets van!
Ik heb het geprobeerd met z-transformatie, maar dat lukt me niet:
(kortom, ik hou weer gewoon -x+2 over...)
Ik snap er echt helemaal niets van!


Maar je hebt nu een andere x. Nu moet je in een tabel de z-waarde opzoeken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ohja, vergeten te zeggen.. Dat heb ik gedaan, maar de tabel die ik erbij heb gekregen gaat maar tot z=3,0...quote:Op dinsdag 15 september 2009 18:51 schreef GlowMouse het volgende:
Maar je hebt nu een andere x. Nu moet je in een tabel de z-waarde opzoeken.
Ik dacht eerst dat ik moest kijken bij z=5 (van 5%) maar dat staat dus niet in de tabel...


Je zoekt nu op P(Z < 0.95). Ik wil c zodanig dat P(Z<c) = 0.95.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Uh.. ja dat snap ik, dat was ook de opgave: ..quote:Op dinsdag 15 september 2009 19:21 schreef GlowMouse het volgende:
Ik wil c zodanig dat P(Z<c) = 0.95.
Ik heb alleen dus echt geen flauw idee hoe ik dat doe...


Je weet toch hoe deze curve werkt?quote:Op dinsdag 15 september 2009 19:26 schreef Booomer het volgende:
[..]
Uh.. ja dat snap ik, dat liet ik hier al zien [ afbeelding ]..
Ik heb alleen dus echt geen flauw idee hoe ik dat doe...
Bron: Wikimedia Commons. Maker: Jeremy Kemp. Licentie: CC-BY.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja, ik moet het punt (-x+2) vinden waarop 95% binnen de curve valt.. Maar hoe weet ik dus niet, zoals ik nu al meerdere keren heb gezegd. Kan niemand het nou gewoon even uitleggen? 
[ Bericht 33% gewijzigd door Booomer op 15-09-2009 19:51:52 ]
[ Bericht 33% gewijzigd door Booomer op 15-09-2009 19:51:52 ]


Gewoon opzoeken in een tabel: http://www.math.unb.ca/~knight/utility/NormTble.htm.quote:Op dinsdag 15 september 2009 19:46 schreef Booomer het volgende:
Ja, ik moet het punt (-x+2) vinden waarop 95% binnen de curve valt.. Maar hoe weet ik dus niet, zoals ik nu al meerdere keren heb gezegd. Kan niemand het nou gewoon even uitleggen?
Kijk voor welke waarde van Z je een kans 0.95 krijgt.
Je gaat eerst naar beneden in de tabel, verticaal dus. Dan zie je dat je voor Z=1.6 de waarde 0.9452 krijgt en voor Z=1.7 de waarde 0.9554. De laatste waarde is te hoog, dus zoek je verder in de rij van Z=1.6. Je gaat nu dus horizontaal kijken. Dan zie je dat je voor Z=1.64 de waarde 0.9495 en voor Z=1.65 de waarde 0.9505 krijgt. De gevraagde kans van 0.95 ligt hier precies tussen in dus neem je als benadering Z=1.645.
Nu geldt: Z = -x + 2
x = 2 - 1.645 = 0.355


Huh, dat is een hele andere tabel als die ik erbij heb gekregen. Die van mij loopt bij z=0,00 (0,5000) af naar z=3,09 (0,0010). Hierin kan ik dus niet eens een kans 0,95 opzoeken. 


Maar wat zégt die tabel? Waarnaar gelinkt wordt geeft de ‘Probability content from -∞ to Z’. Die van jou van Z naar +∞ waarschijnlijk. Want z = 3,09 geeft 0,9990 in die tabel, en 0,0010 + 0,9990 = 1. Daarom mijn vraag: weet je hoe die curve werkt?quote:Op dinsdag 15 september 2009 20:07 schreef Booomer het volgende:
Huh, dat is een hele andere tabel als die ik erbij heb gekregen. Die van mij loopt bij z=0,00 (0,5000) af naar z=3,09 (0,0010). Hierin kan ik dus niet eens een kans 0,95 opzoeken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ben ik alweer, mis jammer genoeg nog steeds wat colleges door ziekte en wil niet graag achter komen 
Teken een blok waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.
Nu de misschien heel domme vraag.. wat bedoelen ze in hemelsnaam met dat blok? Misschien dat ik dan de rest van de vraag wel snap
Misschien dat ik dan de rest van de vraag wel snap 
Teken een blok waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.
Nu de misschien heel domme vraag.. wat bedoelen ze in hemelsnaam met dat blok?


Denk het. Heel die curve = 1, en gevraagd werd op welk punt je 95% hebt. Bedankt mrbombastic, dankzij jou ben ik eruit gekomen!quote:Op dinsdag 15 september 2009 20:11 schreef Iblis het volgende:
[..]
Maar wat zégt die tabel? Waarnaar gelinkt wordt geeft de ‘Probability content from -∞ to Z’. Die van jou van Z naar +∞ waarschijnlijk. Want z = 3,09 geeft 0,9990 in die tabel, en 0,0010 + 0,9990 = 1. Daarom mijn vraag: weet je hoe die curve werkt?



Die notatie is echt zo? Ik zit ook even te twijfelen, maar bedoelen ze niet gewoon wat ik een balk zou noemen?quote:Op dinsdag 15 september 2009 20:13 schreef woopehh het volgende:
Ben ik alweer, mis jammer genoeg nog steeds wat colleges door ziekte en wil niet graag achter komen
Teken een blok [ afbeelding ] waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.
Nu de misschien heel domme vraag.. wat bedoelen ze in hemelsnaam met dat blok?Misschien dat ik dan de rest van de vraag wel snap
Bron: Wikimedia Commons. Maker: Svdmolen. Publiek Domein.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Maar snap je ook hoe je nu jouw tabel kunt gebruiken om het op te zoeken? Want je krijgt meestal maar een halve tabel, zogezegd, omdat die curve symmetrisch is.quote:Op dinsdag 15 september 2009 20:16 schreef Booomer het volgende:
[..]
Denk het. Heel die curve = 1, en gevraagd werd op welk punt je 95% hebt. Bedankt mrbombastic, dankzij jou ben ik eruit gekomen! [ afbeelding ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja, ik zoek dus niet op een kans van 0,95 maar op een kans van 0,05. Maarja, hoe moest ik dat ruiken?quote:Op dinsdag 15 september 2009 20:17 schreef Iblis het volgende:
[..]
Maar snap je ook hoe je nu jouw tabel kunt gebruiken om het op te zoeken? Want je krijgt meestal maar een halve tabel, zogezegd, omdat die curve symmetrisch is.
Btw, die site uit de OP (http://betahw.mine.nu/index.php) doet het niet...


Nou, omdat er waarschijnlijk staat wat jouw tabel aangeeft.quote:Op dinsdag 15 september 2009 20:24 schreef Booomer het volgende:
[..]
Ja, ik zoek dus niet op een kans van 0,95 maar op een kans van 0,05. Maarja, hoe moest ik dat ruiken?
Op 0,0000 geven beide tabellen 0,5 aan. Logisch, want de helft van de oppervlakte zit links van het midden en de andere helft rechts. Dan kijk je bij 0,6 en zie je dat jouw tabel minder dan 0,5 aangeeft. Eigenlijk weet je dan ook al dat de tabel dus de oppervlakte rechts van het punt aangeeft.
Het maakt in feite niet uit echter, want je weet dat de totale oppervlakte 1 moet zijn. Wil je dus weten op welk punt de oppervlakte links ervan 0,95 is, en je hebt alleen een tabel zoals jij hebt, dan zoek je dus naar 0,05, want dat moet de oppervlakte rechts van dat punt zijn.
Daarom: Weet je hoe die curve werkt?
Ik vraag dat niet om irritant te doen, maar omdat deze constatering wel van belang was. De eerste keer dat ik die tabel zag vond ik ’m ook ontzagwekkend.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


GlowMouse er is iets stuk!quote:Op dinsdag 15 september 2009 20:24 schreef Booomer het volgende:
Btw, die site uit de OP (http://betahw.mine.nu/index.php) doet het niet...
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja nog even gecontroleerd en het staat er toch echt zo.. jammer genoeg snap ik nog steeds niet wat ik moet doen nu. De eerste vraag is:quote:Op dinsdag 15 september 2009 20:16 schreef Iblis het volgende:
[..]
Die notatie is echt zo? Ik zit ook even te twijfelen, maar bedoelen ze niet gewoon wat ik een balk zou noemen?
[ link | afbeelding ]
Bron: Wikimedia Commons. Maker: Svdmolen. Publiek Domein.
Druk het volgende uit in a, b en c:
De vector die hoort bij het snijpunt P van AE en DR
Zou iemand me een zetje in de goede richting kunnen geven?


Heb je een PDF waarin je de opgave leest? Dit is wat speculatief, maar ik denk dat het toch een balk is, dat die 8 letters de hoekpunten zijn, maar dat er wat mis is met de fonts, waardoor je een ’ ziet en geen lijntje.quote:Op dinsdag 15 september 2009 20:31 schreef woopehh het volgende:
[..]
Ja nog even gecontroleerd en het staat er toch echt zo.. jammer genoeg snap ik nog steeds niet wat ik moet doen nu. De eerste vraag is:
Druk het volgende uit in a, b en c:
De vector die hoort bij het snijpunt P van AE en DR
Zou iemand me een zetje in de goede richting kunnen geven?
Ik heb wel eens zo’n kapotte PDF gezien. Goed, zoals gezegd, speculatief, maar het zou de rest van de vraag niet per se onzinnig maken, als je maar wist welke letter precies waar zit op de balk.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Neuh staat gewoon in het boek.. en geen klasgenootjes op msn en uitleggen over de telefoon blijft toch pittig :pquote:Op dinsdag 15 september 2009 20:36 schreef Iblis het volgende:
[..]
Heb je een PDF waarin je de opgave leest? Dit is wat speculatief, maar ik denk dat het toch een balk is, dat die 8 letters de hoekpunten zijn, maar dat er wat mis is met de fonts, waardoor je een ’ ziet en geen lijntje.
Ik heb wel eens zo’n kapotte PDF gezien. Goed, zoals gezegd, speculatief, maar het zou de rest van de vraag niet per se onzinnig maken, als je maar wist welke letter precies waar zit op de balk.Is er geen studiegenoot die je even kunt vragen?
Kan wel het antwoord geven maar daar kom je in dit geval waarschijnlijk ook niet echt verder mee :p


Meer: misschien heeft de docent tijdens college gezegd dat die vraag niet klopt o.i.d. Dan kun je dat even checken.quote:Op dinsdag 15 september 2009 20:40 schreef woopehh het volgende:
[..]
Neuh staat gewoon in het boek.. en geen klasgenootjes op msn en uitleggen over de telefoon blijft toch pittig :p
Kan wel het antwoord geven maar daar kom je in dit geval waarschijnlijk ook niet echt verder mee :p
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


O zo, zal even kijkenquote:Op dinsdag 15 september 2009 20:43 schreef Iblis het volgende:
[..]
Meer: misschien heeft de docent tijdens college gezegd dat die vraag niet klopt o.i.d. Dan kun je dat even checken.


Nou ik heb er weer een.. Heb geprobeerd de Z-waarde op te zoeken, maar volgens mij doe ik het weer helemaal verkeerd.. 


quote:Op dinsdag 15 september 2009 20:44 schreef woopehh het volgende:
[..]
O zo, zal even kijkenLaat het nog wel even weten als ik erachter ben, bedankt iig
Toch nog even mee doorgegaan, beetje koppig
Als ik er dit figuur van maak:
Bron: Wikimedia Commons. Maker: Svdmolen. Publiek Domein.
Krijg ik bij alle vragen (en het zijn er 6 dus lijkt me sterk dat het toeval is..) het goede antwoord


Als jij zo’n figuur bewerkt zit er jouw auteursrecht op.quote:Op dinsdag 15 september 2009 21:12 schreef woopehh het volgende:
Toch nog even mee doorgegaan, beetje koppig
Als ik er dit figuur van maak:
Bron: Wikimedia Commons. Maker: Svdmolen. Publiek Domein.
Krijg ik bij alle vragen (en het zijn er 6 dus lijkt me sterk dat het toeval is..) het goede antwoordbedankt Iblis!
Maar, goed bezig!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Waarom vul je die 5 in?quote:Op dinsdag 15 september 2009 21:08 schreef Booomer het volgende:
Nou ik heb er weer een.. Heb geprobeerd de Z-waarde op te zoeken, maar volgens mij doe ik het weer helemaal verkeerd..
[ afbeelding ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Hopelijk zet je dat lang genoeg aan het denken, hier de uitleg. Gegeven een standaard normaalverdeling, met en kun je gebruik maken van je tabel om zoiets te vinden. Als je dus hebt , en men vraagt, voor welke G' geldt , dan kunnen we dat opzoeken, en dan vinden we dat dit geldt voor G' = 1,645, dat hebben we bij de vorige vraag uitgevonden.
Daarbij, omdat de kromme symmetisch is, kunnen we ook concluderen dat dus .
Nu zijn we al redelijk ver. Zou je verdeling dus standaard normaalverdeeld zijn, dan heb je het antwoord. Maar je verdeling is dat niet. Echter, wat nu zo handig is, is, dat als je hebt dat , met willekeurige μ en σ, dat dan geldt dat:
wél normaal verdeeld is. Die twee ideeën combineren we. We weten dat voor z < -1,645 geldt dat de kans erop 5% is, maar dat dit een standaard normaalverdeelde z is, en we weten hoe we onze x ook standaard normaalverdeeld maken, dus, we vullen dat in:
Als je dit oplost krijg je x - 1015 < -19,74, ofwel x < 995,26. Dus die lichtste 5% weegt hooguit 995,26 gram, wat een logisch antwoord lijkt.
[ Bericht 1% gewijzigd door Iblis op 15-09-2009 22:46:22 (Ontlelijkt.) ]
Daarbij, omdat de kromme symmetisch is, kunnen we ook concluderen dat dus .
Nu zijn we al redelijk ver. Zou je verdeling dus standaard normaalverdeeld zijn, dan heb je het antwoord. Maar je verdeling is dat niet. Echter, wat nu zo handig is, is, dat als je hebt dat , met willekeurige μ en σ, dat dan geldt dat:
wél normaal verdeeld is. Die twee ideeën combineren we. We weten dat voor z < -1,645 geldt dat de kans erop 5% is, maar dat dit een standaard normaalverdeelde z is, en we weten hoe we onze x ook standaard normaalverdeeld maken, dus, we vullen dat in:
Als je dit oplost krijg je x - 1015 < -19,74, ofwel x < 995,26. Dus die lichtste 5% weegt hooguit 995,26 gram, wat een logisch antwoord lijkt.
[ Bericht 1% gewijzigd door Iblis op 15-09-2009 22:46:22 (Ontlelijkt.) ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Nee, absoluut niet. Als je dat zo invult, dan heb je het eerlijk gezegd echt niet begrepen. Hopelijk snap je het na mijn uitleg wel. Ik leg het gerust nog duidelijker uit. Geen probleem.quote:
Die x is je stochastische variabele. Er wordt juist gevraagd naar de waarde ervan, die wordt niet gegeven.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Heel erg bedankt voor je hulp Iblis! Ik geloof meteen dat je antwoord goed is, alleen het is echt abracadabra voor me.. Al zou ik nu een zelfde vraag alleen moeten oplossen zou ik het weer niet weten, omdat ik gewoon niet weet wat ik aan het doen ben. 



Ik moet ook zeggen dat ik niet bepaald netjes te werk ging. Hopelijk is m’n herziene versie een stuk duidelijker. Wat nog even de moeite van het zeggen waard is, je rekent niet een specifieke waarde voor x uit. x is namelijk een toevalsvariabele. Die kun je in feite alleen ‘uitlezen’ of inspecteren.quote:Op dinsdag 15 september 2009 22:12 schreef Booomer het volgende:
Heel erg bedankt voor je hulp Iblis! Ik geloof meteen dat je antwoord goed is, alleen het is echt abracadabra voor me.. Al zou ik nu een zelfde vraag alleen moeten oplossen zou ik het weer niet weten, omdat ik gewoon niet weet wat ik aan het doen ben. [ afbeelding ]
De vraag die je eigenlijk altijd stelt is bijvoorbeeld ‘wat is de kans dat als ik x uitlees x kleiner is dan 1’? Dat noteer je als:
En doorgaans wordt de functie Φ gebruikt om de waarde daarvan te bepalen, dus: Φ(1) geeft aan wat de kans erop is. En omdat die functie niet gemakkelijk uit te rekenen is, heb je daar die tabel voor.
Die tabel kun je echter ook ‘andersom’ gebruiken. Als men vraagt:
,
dan vraagt men voor welke y dit geldt. In de vorige vraag vraagt men bijvoorbeeld voor welk gewicht G geldt dat als je x uitleest de kans dat x minder is dan G 5% is.
Men vraagt dus eigenlijk:
.
En dan moet je dit omtoveren in een z die wel normaal verdeeld is, zodat je je uitleestabel kunt gebruiken. En dat doe je eigenlijk als je de voorgaande vraag omschrijft in:
Omdat je nu weet dat wél standaard normaal verdeeld is, kun je bepalen dat G' gelijk aan -1,645 moet zijn (en G' = (G - 1015)/12).
Ik hoop dat dit een beetje helpt. Maar als je het niet snapt, laat iemand anders het je uitleggen, in mijn ervaring zijn er altijd meerdere wegen die tot begrip leiden, en ik ben niet beledigd als het de mijne niet is.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik heb de volgende vraag vanuit de verzamelingenleer(hoop dat ik hier dan goed zit):
V = {{∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}}.
Uit hoeveel elementen bestaat de machtverzameling P(V )?
Hierbij wordt met het teken ∅ een lege verzameling bedoelt.
Nu weet ik dat als het aantal elementen van een verzameling n is, dat het aantal elementen van de machtverzameling 2 tot de macht n is.
Volgens mij bestaat deze verzameling uit 3 elementen, dus dat zal betekenen 2³=8
Kan iemand dit verifiëren of zie ik dit helemaal verkeerd ..
V = {{∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}}.
Uit hoeveel elementen bestaat de machtverzameling P(V )?
Hierbij wordt met het teken ∅ een lege verzameling bedoelt.
Nu weet ik dat als het aantal elementen van een verzameling n is, dat het aantal elementen van de machtverzameling 2 tot de macht n is.
Volgens mij bestaat deze verzameling uit 3 elementen, dus dat zal betekenen 2³=8
Kan iemand dit verifiëren of zie ik dit helemaal verkeerd ..


Klopt, zoals GlowMouse zegt, en de elementen zijn getallen 1, 2 en 3, volgens een veel gebruikte constructie van de natuurlijke getallen, zoals door Von Neumann bedacht. Dit ter info.quote:Op woensdag 16 september 2009 16:05 schreef Hap_Slik het volgende:
Volgens mij bestaat deze verzameling uit 3 elementen, dus dat zal betekenen 2³=8
Kan iemand dit verifiëren of zie ik dit helemaal verkeerd ..
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Beide dank. Ik heb de gebruikte stelling nog niet hoeven bewijzen, maar dat moet niet zo moeilijk zijn. Nu had ik nog één afsluitende vraag.quote:Op woensdag 16 september 2009 16:12 schreef Iblis het volgende:
[..]
Klopt, zoals GlowMouse zegt, en de elementen zijn getallen 1, 2 en 3, volgens een veel gebruikte constructie van de natuurlijke getallen, zoals door Von Neumann bedacht. Dit ter info.
Ik weet dat: ∅ ⊂ V altijd een deelverzameling is van een verzameling(in dit voorbeeld dus V). Nu lijkt de volgende propositie mij onjuist:
{∅} ⊂ V
Dit omdat er geen 'losse' lege verzameling opgenomen is als element in V. Klopt dit dan ook?


Door op te zoeken waaraan iets moet voldoen wil het een lineaire deelruimte zijn en dan te checken of het daaraan voldoet.quote:Op woensdag 16 september 2009 19:22 schreef woopehh het volgende:
Toch weer een vraagje:
A = {x in R2 | x1 - 2x2 = 0}
Hoe bepaal ik of dit een lineaire deelruimte is?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ben nu bezig met het begin van getaltheorie.
Ik heb nog moeite met de manier van bewijzen in dit vak gebied. Ik sta nu voor een aantal ogenschijnlijk gemakkelijke opdrachten, maar ik heb, na bestudering van de theorie, nog geen idee hoe dit aan te pakken.
Ik zet er even 2 opdrachten neer:
1.Bewijs: Elk natuurlijk getal groter dan 1 is te schrijven als som van priemgetallen.
2=2, 3=1+2, 4=2+2,5=3+2, 11=2+2+7
Ik had het idee te beginnen met het idee dat 2 het enige even priemgetal is. Door er een oneven getal bij op te tellen kun je alle gewenste getallen bereiken....
2. Bewijs als ggd(a,c)=1 en b|c, dan ggd(a,b)=1.
a en c zijn relatief priem. Dus 1=m*a+n*c. Dus een lineaire combinatie, met m,n geheel getal.
dit houdt in dat a en c veelvouden zijn van 1.
b|c, dus c=e*a met e=geheel getal.
Dit zijn zaken die je uit het gegeven kunt afleiden, maar het leidt me nog niet bepaald naar het antwoord.
Ik heb nog moeite met de manier van bewijzen in dit vak gebied. Ik sta nu voor een aantal ogenschijnlijk gemakkelijke opdrachten, maar ik heb, na bestudering van de theorie, nog geen idee hoe dit aan te pakken.
Ik zet er even 2 opdrachten neer:
1.Bewijs: Elk natuurlijk getal groter dan 1 is te schrijven als som van priemgetallen.
2=2, 3=1+2, 4=2+2,5=3+2, 11=2+2+7
Ik had het idee te beginnen met het idee dat 2 het enige even priemgetal is. Door er een oneven getal bij op te tellen kun je alle gewenste getallen bereiken....
2. Bewijs als ggd(a,c)=1 en b|c, dan ggd(a,b)=1.
a en c zijn relatief priem. Dus 1=m*a+n*c. Dus een lineaire combinatie, met m,n geheel getal.
dit houdt in dat a en c veelvouden zijn van 1.
b|c, dus c=e*a met e=geheel getal.
Dit zijn zaken die je uit het gegeven kunt afleiden, maar het leidt me nog niet bepaald naar het antwoord.
kloep kloep


Dat had ik er wel even bij kunnen zetten idd, ik weet dat:quote:Op woensdag 16 september 2009 19:31 schreef Iblis het volgende:
[..]
Door op te zoeken waaraan iets moet voldoen wil het een lineaire deelruimte zijn en dan te checken of het daaraan voldoet.
1. De nulvector 0 zit in A
2. Voor alle x in A en y in A zit x+y in A
3. Voor alle x in A en elke u in R zit ux in A
Maar hoe ik dan verder moet..


Een inductie bewijs moet toch nog wel lukken? Zeker als er geen grenzen zitten aan het aantal keer dat je een priemgetal mag gebruiken lijkt me dat niet zo moeilijk.quote:Op woensdag 16 september 2009 19:37 schreef Borizzz het volgende:
1.Bewijs: Elk natuurlijk getal groter dan 1 is te schrijven als som van priemgetallen.
2=2, 3=1+2, 4=2+2,5=3+2, 11=2+2+7
Ik had het idee te beginnen met het idee dat 2 het enige even priemgetal is. Door er een oneven getal bij op te tellen kun je alle gewenste getallen bereiken....
Doe inductie eventueel alleen voor de oneven getallen. Want de even heb je natuurlijk echt zo.
a → b ⇔ ¬b → ¬a, dus stel, ggd(a, b) > 1.quote:2. Bewijs als ggd(a,c)=1 en b|c, dan ggd(a,b)=1.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Das lang geleden. Ik moet ook weer even bij het begin beginnen.quote:Op woensdag 16 september 2009 19:43 schreef Iblis het volgende:
Een inductie bewijs moet toch nog wel lukken? Zeker als er geen grenzen zitten aan het aantal keer dat je een priemgetal mag gebruiken lijkt me dat niet zo moeilijk.
Doe inductie eventueel alleen voor de oneven getallen. Want de even heb je natuurlijk echt zo.
inductie wil volgens mij zeggen dat je aantoont dat iets waar is voor n=1. Vervolgens veronderstel je n=k en dat redeneer je door naar n=k+1.
dus...
de bewering klopt voor n=2. maar n=k??
maar ik weet niet meer hoe je dit dan verder doet.
Je bedoelt hier de contrapositie?quote:a → b ⇔ ¬b → ¬a, dus stel, ggd(a, b) > 1.
dus ggd(a,b)>1. dan geldt zowel ggd(a,c) niet 1 en b geen deler van c?
dus a>b, en ggd(a,b) niet 1??
Ik heb wel gehoord van deze bewijstechnieken, maar ik kan ze nog niet zomaar uitvoeren..
[ Bericht 1% gewijzigd door Borizzz op 16-09-2009 19:55:40 ]
kloep kloep


Gewoon invullen, je hebt dus:quote:Op woensdag 16 september 2009 19:39 schreef woopehh het volgende:
[..]
Dat had ik er wel even bij kunnen zetten idd, ik weet dat:
1. De nulvector 0 zit in A
2. Voor alle x in A en y in A zit x+y in A
3. Voor alle x in A en elke u in R zit ux in A
Maar hoe ik dan verder moet..
A = {x in R2 | x1 - 2x2 = 0}
1) Zit (0, 0) erin? Nou, vul in: 0 - 2*0 = 0, dus, voldoet aan de voorwaarde, zit in a.
2) Neem aan dat x, y ∈ A, dan weet je dus dat x1 - 2x2 = 0, en verder dat y1 - 2y2 = 0. Definieer z = x + y, dan is de vraag z1 - 2z2 = 0? Volgens mij is dat niet zo moeilijk als je dat invult.
3) Neem x ∈ A, dan geldt dus weer x1 - 2x2 = 0, anders had x niet in A gezeten, dan is de vraag dus ux, voldoet dat ook aan de voorwaarde? M.a.w. ux = (ux1, ux2), en geldt ux1 - 2(ux2) = 0 inderdaad?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Wat is het toch altijd logisch als je het zietquote:Op woensdag 16 september 2009 19:50 schreef Iblis het volgende:
[..]
Gewoon invullen, je hebt dus:
A = {x in R2 | x1 - 2x2 = 0}
1) Zit (0, 0) erin? Nou, vul in: 0 - 2*0 = 0, dus, voldoet aan de voorwaarde, zit in a.
2) Neem aan dat x, y ∈ A, dan weet je dus dat x1 - 2x2 = 0, en verder dat y1 - 2y2 = 0. Definieer z = x + y, dan is de vraag z1 - 2z2 = 0? Volgens mij is dat niet zo moeilijk als je dat invult.
3) Neem x ∈ A, dan geldt dus weer x1 - 2x2 = 0, anders had x niet in A gezeten, dan is de vraag dus ux, voldoet dat ook aan de voorwaarde? M.a.w. ux = (ux1, ux2), en geldt ux1 - 2(ux2) = 0 inderdaad?


Inductie werkt als volgt. Je neemt aan dat als het voor n geldt dat het dan ook voor b.v. n + 1 geldt (of voor n + 2 in dit geval).quote:Op woensdag 16 september 2009 19:49 schreef Borizzz het volgende:
das lang geleden.
inductie wil volgens mij zeggen dat je aantoont dat iets waar is voor n=1. Vervolgens veronderstel je n=k en dat redeneer je door naar n=k+1.
dus...
de bewering klopt voor n=2. maar n=k??
maar ik weet niet meer hoe je dit dan verder doet.
Neem aan dat n op enige wijze reeds te schrijven is als som van priemgetallen p1, p2, …, pn. Wat kun je dan over n + 2 zeggen? Het staat er eigenlijk al.
Rest je alleen nog aan om daadwerkelijk een n te vinden waarvoor dit geldt, wel nu, dat is evident. Immers, als je het rond krijgt, dan kun je dus zeggen het geldt voor 2, dus geldt het voor 4, en dus voor 6, en dus voor 8, etc. Idem met 3.
Dus ggd(a, b) ≠ 1. Zeg dus ggd(a, b) = z, met z > 1. Wat weet je dan over ggd(a, c) als je weet dat b|c?quote:Je bedoelt hier de contrapositie?
dus ggd(a,b)=1. dan geldt zowel ggd(a,c) niet 1 en b geen deler van c?
Hoe laat je dit zien? Of moet er dan een "of" staan?
Ik heb wel gehoord van deze bewijstechnieken, maar ik kan ze nog niet zomaar uitvoeren..
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Zoiets schreef ik toch ook?quote:Op woensdag 16 september 2009 19:54 schreef Iblis het volgende:
Inductie werkt als volgt. Je neemt aan dat als het voor n geldt dat het dan ook voor b.v. n + 1 geldt (of voor n + 2 in dit geval).
Dus ik stel dat het geldt voor voor een priegetal n.quote:Neem aan dat n op enige wijze reeds te schrijven is als som van priemgetallen p1, p2, …, pn. Wat kun je dan over n + 2 zeggen? Het staat er eigenlijk al.
Rest je alleen nog aan om daadwerkelijk een n te vinden waarvoor dit geldt, wel nu, dat is evident. Immers, als je het rond krijgt, dan kun je dus zeggen het geldt voor 2, dus geldt het voor 4, en dus voor 6, en dus voor 8, etc. Idem met 3.
Dan geldt n=P1+P2+P3...+PN.
Dan geldt ook n+1=P1+P2+P3...+PN+1.
maar is P1+P2+P3...+PN+1 dan wel een priemgetal?
ggd(a,b)=z en z groter dan 1. Maar als je de ontkenning wil van b|c, dan mag je toch niet gebruiken dat b|c?quote:Dus ggd(a, b) ≠ 1. Zeg dus ggd(a, b) = z, met z > 1. Wat weet je dan over ggd(a, c) als je weet dat b|c?
Of maak ik nu de ontkenning verkeerd?
kloep kloep


b|c betekent: er is een k met c = b * k. We hebben nu 1 = m*a + n*c = m*a + (n*k)*b.quote:Op woensdag 16 september 2009 19:37 schreef Borizzz het volgende:
Ben nu bezig met het begin van getaltheorie.
Ik heb nog moeite met de manier van bewijzen in dit vak gebied. Ik sta nu voor een aantal ogenschijnlijk gemakkelijke opdrachten, maar ik heb, na bestudering van de theorie, nog geen idee hoe dit aan te pakken.
Ik zet er even 2 opdrachten neer:
2. Bewijs als ggd(a,c)=1 en b|c, dan ggd(a,b)=1.
a en c zijn relatief priem. Dus 1=m*a+n*c. Dus een lineaire combinatie, met m,n geheel getal.
dit houdt in dat a en c veelvouden zijn van 1.
b|c, dus c=e*a met e=geheel getal.
Dit zijn zaken die je uit het gegeven kunt afleiden, maar het leidt me nog niet bepaald naar het antwoord.


Tja, maar hiermee kom ik toch niet verder?quote:Op woensdag 16 september 2009 20:02 schreef thabit het volgende:
[..]
b|c betekent: er is een k met c = b * k. We hebben nu 1 = m*a + n*c = m*a + (n*k)*b.
kloep kloep


Maar zoiets is vaak niet goed genoeg in de wiskunde.quote:
Het geldt zelfs voor elk getal n. Dat was de vraag toch ook? Immers, om te beginnen, als n even is, dan heb je simpel weg:quote:Dus ik stel dat het geldt voor voor een priegetal n.
Dan geldt n=P1+P2+P3...+PN.
Dan geldt ook n+1=P1+P2+P3...+PN+1.
maar is P1+P2+P3...+PN+1 dan wel een priemgetal?
Omdat 2 een priemgetal is, ben je klaar voor de even getallen.
In feite is het nu simpel, want 3 is ook een priemgetal dus voor oneven n ≥ 3 kun je zeggen:
Eigenlijk heb je niet eens inductie nodig als je dat heel lastig vindt.
Gegeven b|c wil jij bewijzen dat ggd(a, c) = 1 → ggd(a, b) = 1. Je kunt het rechtstreeks doen, dat geeft thabit, mijn redenering komt in principe op hetzelfde neer. Zij nog steeds b|c dan passen we contrapositie toe (dit is echt logisch equivalent), en neem aan dat ggd(a, b) niet gelijk is aan 1, er dus een getal k waardoor zowel a als b deelbaar is. Omdat b een deler is van c, en k van b is k ook een deler van c. Dit kun je nog formeel maken: b = n·k, c = m·b, dus c = m·n·k, klaar. Dus ggd(a, c) is dan ook zeker geen 1.quote:ggd(a,b)=z en z groter dan 1. Maar als je de ontkenning wil van b|c, dan mag je toch niet gebruiken dat b|c?
Of maak ik nu de ontkenning verkeerd?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Bézout's identityquote:Op woensdag 16 september 2009 20:08 schreef Borizzz het volgende:
[..]
Tja, maar hiermee kom ik toch niet verder?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik moet het toch gewoon kunnen hoor.quote:Op woensdag 16 september 2009 20:12 schreef Iblis het volgende:
Eigenlijk heb je niet eens inductie nodig als je dat heel lastig vindt.
Ik heb het dus altijd zo geleerd: eerst aannemen voor n, dan door doorrekenen iets vinden voor n+1.quote:Dus ik stel dat het geldt voor voor een priegetal n.
Dan geldt n=P1+P2+P3...+PN.
Dan geldt ook n+1=P1+P2+P3...+PN+1.
maar is P1+P2+P3...+PN+1 dan wel een priemgetal?
Naar mijn idee moest dit wel goed zijn?:{
je zegt dus dan c=m*n*k en a=a? De rekenarij volg ik wel.quote:Gegeven b|c wil jij bewijzen dat ggd(a, c) = 1 → ggd(a, b) = 1. Je kunt het rechtstreeks doen, dat geeft thabit, mijn redenering komt in principe op hetzelfde neer. Zij nog steeds b|c dan passen we contrapositie toe (dit is echt logisch equivalent), en neem aan dat ggd(a, b) niet gelijk is aan 1, er dus een getal k waardoor zowel a als b deelbaar is. Omdat b een deler is van c, en k van b is k ook een deler van c. Dit kun je nog formeel maken: b = n·k, c = m·b, dus c = m·n·k, klaar. Dus ggd(a, c) is dan ook zeker geen 1.
c bestaat dus uit meerdere factoren en a is niet over bekend.
Dan kun je toch niet conclueren dan dan ggd(a,c)=1?
t wordt nog wat die getaltheorie...maar ja alle begin is moeilijk.
kloep kloep


Waarom n + 1, dat is alleen maar onhandig, kies toch n + 2. Volledige inductie is niet beperkt tot n + 1, maar werkt met het idee dat als het voor n geldt dat als je kunt bewijzen dat het dan ook ‘voor de volgende in de reeks’ geldt en je hebt een beginpunt, dat je dan je hele reeks hebt.quote:Op woensdag 16 september 2009 20:21 schreef Borizzz het volgende:
Ik heb het dus altijd zo geleerd: eerst aannemen voor n, dan door doorrekenen iets vinden voor n+1.
Naar mijn idee moest dit wel goed zijn?:{
a = a is een waarheid als een koe. Ik begin dus met de aanname dat ggd(a, b) = k > 1, dan is k natuurlijk automatisch ook een deler van a. Immers, het is een gemene deler. Dan zeg ik, omdat k een deler van b is, en b weer van c is k ook een deler van c. Met a is nog steeds niets veranderd, dus k is ook nog een deler van a. Kortom, ggd(a, c) zal zeker geen 1 zijn, omdat k zowel een deler van a als van c is, en k > 1 (dat is de aanname).quote:je zegt dus dan c=m*n*k en a=a? De rekenarij volg ik wel.
c bestaat dus uit meerdere factoren en a is niet over bekend.
Dan kun je toch niet conclueren dan dan ggd(a,c)=1?
t wordt nog wat die getaltheorie...maar ja alle begin is moeilijk.
Daarmee is de contrapositie bewezen en is je bewijs rond. Ik kan het echt niet veel duidelijker maken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


OK. Dank je wel! Wat er staat klinkt allemaal wel logisch. Maar om er zelf op te komen is nog een ander verhaal.quote:Op woensdag 16 september 2009 20:27 schreef Iblis het volgende:
[..]
Waarom n + 1, dat is alleen maar onhandig, kies toch n + 2. Volledige inductie is niet beperkt tot n + 1, maar werkt met het idee dat als het voor n geldt dat als je kunt bewijzen dat het dan ook ‘voor de volgende in de reeks’ geldt en je hebt een beginpunt, dat je dan je hele reeks hebt.
[..]
a = a is een waarheid als een koe. Ik begin dus met de aanname dat ggd(a, b) = k > 1, dan is k natuurlijk automatisch ook een deler van a. Immers, het is een gemene deler. Dan zeg ik, omdat k een deler van b is, en b weer van c is k ook een deler van c. Met a is nog steeds niets veranderd, dus k is ook nog een deler van a. Kortom, ggd(a, c) zal zeker geen 1 zijn, omdat k zowel een deler van a als van c is, en k > 1 (dat is de aanname).
Daarmee is de contrapositie bewezen en is je bewijs rond. Ik kan het echt niet veel duidelijker maken.
Het duizelde me even omdat ik ook veel nieuwe theorie in 1x wil doen en ik geef mezelf te weinig tijd om het te snappen. Ik ga eerst weer even de boeken in.
kloep kloep


Je kunt het ook uit het ongerijmde doen, komt eigenlijk op hetzelfde neer, maar misschien dat het beter valt. Begin dus met ggd(a, c) = 1, en b|c. Dan weten we b·k = c, dat is immers wat ‘deler van’ inhoudt.
Neem nu aan (voor het ongerijmde) dat ggd(a, b) > 1. Zeg dat die gemene deler d is. Dan weten we, a valt te schrijven als a = d·n, en b = d·m. Omdat c = k·b, dus ook c=k·d·m. Hé, maar dan zien we dat d dus blijkbaar ook een deler van c is (en nog steeds van a). Tegenspraak.
Het is 95% hetzelfde als contrapositie, maar misschien dat deze ‘flow’ van gedachten je beter ligt.
Neem nu aan (voor het ongerijmde) dat ggd(a, b) > 1. Zeg dat die gemene deler d is. Dan weten we, a valt te schrijven als a = d·n, en b = d·m. Omdat c = k·b, dus ook c=k·d·m. Hé, maar dan zien we dat d dus blijkbaar ook een deler van c is (en nog steeds van a). Tegenspraak.
Het is 95% hetzelfde als contrapositie, maar misschien dat deze ‘flow’ van gedachten je beter ligt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Hmm... dus uit het feit dat a=d*n en c=k*d*n concludeer jij dat d een deler is van zowel a als c.quote:Op woensdag 16 september 2009 20:40 schreef Iblis het volgende:
Je kunt het ook uit het ongerijmde doen, komt eigenlijk op hetzelfde neer, maar misschien dat het beter valt. Begin dus met ggd(a, c) = 1, en b|c. Dan weten we b·k = c, dat is immers wat ‘deler van’ inhoudt.
Neem nu aan (voor het ongerijmde) dat ggd(a, b) > 1. Zeg dat die gemene deler d is. Dan weten we, a valt te schrijven als a = d·n, en b = d·m. Omdat c = k·b, dus ook c=k·d·m. Hé, maar dan zien we dat d dus blijkbaar ook een deler van c is (en nog steeds van a). Tegenspraak.
Het is 95% hetzelfde als contrapositie, maar misschien dat deze ‘flow’ van gedachten je beter ligt.
Terwijl we aannamen dat ggd(a,c)=1.
Tegenspraak dus.
kloep kloep


Dat is zo ongeveer de definitie van deler van, dus dat lijkt me een geldige conclusie.quote:Op woensdag 16 september 2009 20:48 schreef Borizzz het volgende:
Hmm... dus uit het feit dat a=d*n en c=k*d*n concludeer jij dat d een deler is van zowel a als c.
Nee, zo moet je het niet uitleggen (ik ben wat aan het muggenziften hoor, maar toch, getaltheorie is precies werk).quote:Terwijl we aannamen dat ggd(a,c)=1.
Tegenspraak dus.
We willen bewijzen:
ggd(a, c) = 1, en b | c betekent dat ook ggd(a, b) = 1. Die eerste twee dingen mogen we dus als waar beschouwen. Dat is ons uitgangspunt.
Dan komt pas onze verdere aanname, en die is dat het toch mogelijk is dat is ggd(a, b) > 1. Deze aanname leidt tot een tegenspraak met het gegeven dat ggd(a, c) = 1. Die tegenspraak betekent dat onze aanname incorrect is. Dus dat het tegengestelde van de aanname wel waar moet zijn, namelijk ggd(a, b) = 1.
Misschien moet je er anders nu even niet te hard over nadenken, maar op de manier waarop je het zegt kreeg ik niet het gevoel dat je het 100% snapte. Maar nachtrust doet ook wonderen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Kan het ook zo:
Opgave is ggd(a,c)=1 en b|c. Bewijs dat ggd(a,b)=1.
Veronderstel: ggd(a,c)=1 en b|c.
iedere ggd is te schrijven als lin. combinatie van a en c en dus 1=ma+nc, met m en n geheel getal.
b|c levert c=d*b met d een geheel getal.
we gaan substitueren:
1=ma+nc
1=ma+ndb
nd is een geheel getal.
1=(m)a+(nd)b.
met de theorie over ggd en lin.conbinatie mag ik nu concluderen:
ggd(a,b)=1.
[ Bericht 1% gewijzigd door Borizzz op 16-09-2009 21:08:03 ]
Opgave is ggd(a,c)=1 en b|c. Bewijs dat ggd(a,b)=1.
Veronderstel: ggd(a,c)=1 en b|c.
iedere ggd is te schrijven als lin. combinatie van a en c en dus 1=ma+nc, met m en n geheel getal.
b|c levert c=d*b met d een geheel getal.
we gaan substitueren:
1=ma+nc
1=ma+ndb
nd is een geheel getal.
1=(m)a+(nd)b.
met de theorie over ggd en lin.conbinatie mag ik nu concluderen:
ggd(a,b)=1.
[ Bericht 1% gewijzigd door Borizzz op 16-09-2009 21:08:03 ]
kloep kloep


Dat is wat thabit je reeds zei, maar ik dacht dat die manier je niet zo lag. Het is een prima oplossing, maar ik heb een kanttekening: als je zulk soort dingen lastig vindt, dan is dit, denk ik, meer een oplossing die ‘werkt’ omdat je de goede dingen combineert, maar verder niet zo intuïtief is.quote:Op woensdag 16 september 2009 20:55 schreef Borizzz het volgende:
Kan het ook zo:
Opgave is ggd(a,c)=1 en b|c. Bewijs dat ggd(a,b)=1.
Veronderstel: ggd(a,c)=1 en b|c.
iedere ggd is te schrijven als lin. combinatie van a en c en dus 1=ma+nb.
b|c levert c=d*b met d een geheel getal.
we gaan substitueren:
1=ma+nb
1=ma+nbc
nb is een geheel getal.
1=(m)a+(nc)b.
met de theorie over ggd en lin.conbinatie mag ik nu concluderen:
ggd(a,b)=1.
Als je die theorie helemaal in de vingers hebt, prima, gebruik ze. Heb je dat niet, dan hanteer je eigenlijk een gereedschap dat je niet helemaal doorziet. Voor je begrip is dat niet zo handig.
Mocht je doel alleen zijn dat je de vraag wilt beantwoorden, dan heb ik niets gezegd.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Iblis, ik heb nog wat lettertjes in het bewijs veranderd, ik was niet zo precies geweest. Wil je even checken in mijn vorige post of het goed is?quote:Op woensdag 16 september 2009 20:58 schreef Iblis het volgende:
[..]
Dat is wat thabit je reeds zei, maar ik dacht dat die manier je niet zo lag. Het is een prima oplossing, maar ik heb een kanttekening: als je zulk soort dingen lastig vindt, dan is dit, denk ik, meer een oplossing die ‘werkt’ omdat je de goede dingen combineert, maar verder niet zo intuïtief is.
Als je die theorie helemaal in de vingers hebt, prima, gebruik ze. Heb je dat niet, dan hanteer je eigenlijk een gereedschap dat je niet helemaal doorziet. Voor je begrip is dat niet zo handig.
Mocht je doel alleen zijn dat je de vraag wilt beantwoorden, dan heb ik niets gezegd.
Het gaat er mij niet om of een redenering mij ligt of niet. Ik wil vaak meerdere invalshoeken zien, voordat ik het snap. Ik heb in de theorie een bewijs gezien over lineaire combinatie en gemene delers. Door thabit kwam ik op het idee dat je dit kunt toepassen. Jouw bewijs richtte zich meer op definitie van (gemende)deler. Ik kwam nog niet op het idee dat als je stelt ggd(a,b)=k dat dan volgt k|a en k|b. Te logisch voor woorden maar ja...
En bijv ook als d|a en c|d dat dan volgt c|a.
Al deze dingen heb ik gezien en bewezen, maar het idee hebben om het te gebruiken, en toe te passen gaat nog niet zo vanzelf.
kloep kloep


Lijkt me prima. Ik vind het zelf, eerlijk gezegd, ietwat vreemd dat je de conclusie ‘als k de grootste gemene deler van a en b is’ dat dan k een deler van a en b is, niet trok. Wat is dan je voorstelling van die functie?
Maar daarom vraag ik me ook af, hoe thabits benadering je dan wél wat zegt.
Ik kan me moeilijk verplaatsen in wat voor jou dan vanzelfsprekend is, en wat niet (wat op zich niet erg is, maar mijn keus voor uitleg misschien niet de gelukkigste maakt in jouw geval). Maar goed, zoals het bewijs nu staat klopt het.
Maar daarom vraag ik me ook af, hoe thabits benadering je dan wél wat zegt.
Ik kan me moeilijk verplaatsen in wat voor jou dan vanzelfsprekend is, en wat niet (wat op zich niet erg is, maar mijn keus voor uitleg misschien niet de gelukkigste maakt in jouw geval). Maar goed, zoals het bewijs nu staat klopt het.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Tja, dat vraag ik me zelf ook af.quote:Op woensdag 16 september 2009 21:11 schreef Iblis het volgende:
Lijkt me prima. Ik vind het zelf, eerlijk gezegd, ietwat vreemd dat je de conclusie ‘als k de grootste gemene deler van a en b is’ dat dan k een deler van a en b niet trok. Wat is dan je voorstelling van die functie?
Maar daarom vraag ik me ook af, hoe thabits benadering je dan wél wat zegt.
Ik kan me moeilijk verplaatsen in wat voor jou dan vanzelfsprekend is, en wat niet. Maar goed, zoals het bewijs nu staat klopt het.
Het ligt ook zo voor de hand. Het duizelde allemaal wat, daar zal het wel aan liggen én het feit dat ik het allemaal snel wil snappen. Geduld lijkt me dan ook een schone zaak.
Bovendien is dit het laatste vak dat ik moet doen, heb er wel wat angst voor. Dit lijkt me het moeilijkste vak uit de opleiding, al heb ik ook al aardig wat lastige vakken achter de rug.
kloep kloep


Op zich is getaltheorie vaak vrij elementair. Het hangt ervanaf hoe het gegeven wordt, maar meestal kun je met heel basale middelen vrij ver komen. Dat zie je ook in deze opgaven. Ik suggereerde eerste volledige inductie, maar dat heb je niet eens nodig. Dat is ook wel fijn aan zo’n vak, ook al ben je de impliciete functiestelling vergeten, weet je niet meer hoe die Borel-σ algebra nu precies werkte of hoe die ene partiële differentiaalvergelijking opgelost moest worden, nu zit je weer bij de basis met delers.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Dát doet me weer denken aan projectieve meetkunde: een prachtig vak. Moeilijk dat wel, maar ook door vol te houden heb ik dit ook behaald. Projectieve meetkunde is ook een vak waar je met heel weinig middelen (bv de dubbelverhouding, enkele contstructies) heel ver kunt doorredeneren.quote:Op woensdag 16 september 2009 21:18 schreef Iblis het volgende:
Op zich is getaltheorie vaak vrij elementair. Het hangt ervanaf hoe het gegeven wordt, maar meestal kun je met heel basale middelen vrij ver komen. Dat zie je ook in deze opgaven. Ik suggereerde eerste volledige inductie, maar dat heb je niet eens nodig. Dat is ook wel fijn aan zo’n vak, ook al ben je de impliciete functiestelling vergeten, weet je niet meer hoe die Borel-σ algebra nu precies werkte of hoe die ene partiële differentiaalvergelijking opgelost moest worden, nu zit je weer bij de basis met delers.
Ik hoop dat ik je in de toekomst nog ns met wat getaltheorie probleempjes mag lastigvallen.
kloep kloep


Dat zou ik toch niet helemaal willen beweren. Uiteraard bestaat er elementaire getaltheorie, wat je kunt doen zonder veel theoretische kennis te hebben, maar als je wat verder wilt komen dan komt er toch een hoop bij kijken.quote:Op woensdag 16 september 2009 21:18 schreef Iblis het volgende:
Op zich is getaltheorie vaak vrij elementair.


Heb je helemaal gelijk in, maar ik bedoel, een vak zoals Borizzz dat volgt, waarbij je met deze dingen begint. Ik weet niet hoe ver het de diepte in gaat, maar het is doorgaans niet een vak dat bij uitstek voortbouwt op veel andere vakken.quote:Op woensdag 16 september 2009 21:26 schreef thabit het volgende:
[..]
Dat zou ik toch niet helemaal willen beweren. Uiteraard bestaat er elementaire getaltheorie, wat je kunt doen zonder veel theoretische kennis te hebben, maar als je wat verder wilt komen dan komt er toch een hoop bij kijken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik hoop dat ik ze kan beantwoorden.quote:Op woensdag 16 september 2009 21:23 schreef Borizzz het volgende:
Ik hoop dat ik je in de toekomst nog ns met wat getaltheorie probleempjes mag lastigvallen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Als je een beetje serieuze getaltheorie wilt doen, dan heb je wel een hoop algebra (groepen, ringen, lichamen, Galoistheorie etc), meetkunde en complexe analyse nodig.quote:Op woensdag 16 september 2009 21:28 schreef Iblis het volgende:
[..]
Heb je helemaal gelijk in, maar ik bedoel, een vak zoals Borizzz dat volgt, waarbij je met deze dingen begint. Ik weet niet hoe ver het de diepte in gaat, maar het is doorgaans niet een vak dat bij uitstek voortbouwt op veel andere vakken.


Vastwel! Ik ben al blij met alle moeite die (vrijwillig en laten we dat niet vergeten!) gestoken wordt in het helpen van users.quote:Op woensdag 16 september 2009 21:28 schreef Iblis het volgende:
[..]
Ik hoop dat ik ze kan beantwoorden.
Even opgezocht:quote:Op woensdag 16 september 2009 21:43 schreef thabit het volgende:
[..]
Als je een beetje serieuze getaltheorie wilt doen, dan heb je wel een hoop algebra (groepen, ringen, lichamen, Galoistheorie etc), meetkunde en complexe analyse nodig.
congruenties, hoofdstelling, algoritme van euclides, fermat en euler, congruentievergelijkingen, kwadratische reciprociteit komt nog aan bod.
kloep kloep


Dat zijn allemaal nog elementaire onderwerpen, daar hoef je geen zware wiskunde voor te doen. Vooral die kwadratische reciprociteit is een hele mooie stelling die iets bovennatuurlijks in zich lijkt te hebben.quote:Op woensdag 16 september 2009 21:45 schreef Borizzz het volgende:
[..]
Even opgezocht:
congruenties, hoofdstelling, algoritme van euclides, fermat en euler, congruentievergelijkingen, kwadratische reciprociteit komt nog aan bod.


Ben benieuwdquote:Op woensdag 16 september 2009 21:58 schreef thabit het volgende:
[..]
Dat zijn allemaal nog elementaire onderwerpen, daar hoef je geen zware wiskunde voor te doen. Vooral die kwadratische reciprociteit is een hele mooie stelling die iets bovennatuurlijks in zich lijkt te hebben.
Maar alles op z'n tijd. Ik werk rustig aan de theorie en opgaven.
Bedankt voor nu!
kloep kloep


Ik heb geprobeerd een antwoord te geven op 2 vraagstukken (oa eentje van gisteren).
Kun je even kijken of deze beter zijn?
1.
Bewijs dat elk natuurlijk getal te schrijven is als som van priemgetallen.
- Vast staat dat 2 en 3 priemgetallen zijn.
Er geldt: 2+k*2 geeft alle even getallen (k=nat. getal).
Er geldt 3+k*2 geeft alle oneven getallen (k=nat. getal).
Dus: elk getal is de som van in ieder geval tweeen en drieeen en dus ook de som van priemgetallen.
2.
Bewijs dat elk natuurlijk getal groter dan 7 te schrijven is als som van drieen en vijven.
- Hier pak ik een zelfde type redenering. Maar nu werk ik met 3*k en 5*k, dus drie- en vijfvouden.
Er geldt: 8=3+5, 9=3+3, 10=5+5.
8,9 en 10 zijn dus opgebouwd uit drieeen en vijven.
3-vouden liggen altijd 3 van elkaar op de getallenlijn.
dus met 8+k*3+l*5 en 9+k*3+l*5 en 10+k*3+l*5 worden alle getallen groter dan 7 bereikt.
Deze getallen zijn dan ook opgebouwd uit enkel drieen en vijven.
Kun je even kijken of deze beter zijn?
1.
Bewijs dat elk natuurlijk getal te schrijven is als som van priemgetallen.
- Vast staat dat 2 en 3 priemgetallen zijn.
Er geldt: 2+k*2 geeft alle even getallen (k=nat. getal).
Er geldt 3+k*2 geeft alle oneven getallen (k=nat. getal).
Dus: elk getal is de som van in ieder geval tweeen en drieeen en dus ook de som van priemgetallen.
2.
Bewijs dat elk natuurlijk getal groter dan 7 te schrijven is als som van drieen en vijven.
- Hier pak ik een zelfde type redenering. Maar nu werk ik met 3*k en 5*k, dus drie- en vijfvouden.
Er geldt: 8=3+5, 9=3+3, 10=5+5.
8,9 en 10 zijn dus opgebouwd uit drieeen en vijven.
3-vouden liggen altijd 3 van elkaar op de getallenlijn.
dus met 8+k*3+l*5 en 9+k*3+l*5 en 10+k*3+l*5 worden alle getallen groter dan 7 bereikt.
Deze getallen zijn dan ook opgebouwd uit enkel drieen en vijven.
kloep kloep


>> dus met 8+k*3+l*5 en 9+k*3+l*5 en 10+k*3+l*5 worden alle getallen groter dan 7 bereikt.
Daarvan zou ik maken: met 5 + k*3, 3*3*3 + (k-1)*3 en 2*5 + (k-1)*3 (k in N) worden alle getallen groter dan 7 bereikt. Die I*5 heb je niet nodig.
Daarvan zou ik maken: met 5 + k*3, 3*3*3 + (k-1)*3 en 2*5 + (k-1)*3 (k in N) worden alle getallen groter dan 7 bereikt. Die I*5 heb je niet nodig.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Klopt, vijfvouden heb ik niet echt nodig, omdat je met de drievouden alles al dekt. Maar goed voor de volledigheidquote:Op donderdag 17 september 2009 14:55 schreef GlowMouse het volgende:
>> dus met 8+k*3+l*5 en 9+k*3+l*5 en 10+k*3+l*5 worden alle getallen groter dan 7 bereikt.
Daarvan zou ik maken: met 5 + k*3, 3*3*3 + (k-1)*3 en 2*5 + (k-1)*3 (k in N) worden alle getallen groter dan 7 bereikt. Die I*5 heb je niet nodig.
Kloppen ze beide een beetje?
kloep kloep


Alle natuurlijke even getallen (m.u.v. 0 eventueel als je die erbij rekent), en alle natuurlijke oneven getallen groter dan 1. Als je precies wilt zijn.quote:Op donderdag 17 september 2009 14:48 schreef Borizzz het volgende:.
Bewijs dat elk natuurlijk getal te schrijven is als som van priemgetallen.
- Vast staat dat 2 en 3 priemgetallen zijn.
Er geldt: 2+k*2 geeft alle even getallen (k=nat. getal).
Er geldt 3+k*2 geeft alle oneven getallen (k=nat. getal).
Dus: elk getal is de som van in ieder geval tweeen en drieeen en dus ook de som van priemgetallen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik heb ook geprobeerd om een bewijs van de hoofdstelling op te schrijven.
Ik heb getracht om het in mijn eigen woorden, correct weer te geven.
Kan deze ook door de beugel?
Bewijs loopt via volledige inductie.
Te bew: elk natuurlijk getal heeft unieke priemf. ontbinding.
Bestaan:
-a=2 heeft unieke priemf. ontbinding.
nu een redenering met volledige inductie van a-1 naar a.
-Veronderstel: alle getallen kleiner dan a hebben unieke priemf. ontbinding.
voor het getal a zijn er dan 2 mogelijkheden: a=priem of a=niet priem.
als a priem is, dan heeft ook a een unieke priemf. ontbinding. Klaar.
als a niet priem is, dan is a samengesteld. Dus a=a1*a2. Door dit feit geldt ook a1 en a2 kleiner dan a.
Door mijn veronderstelling hebben a1 en a2 een unieke priemf. ontbinding. En dus heeft a1*a2=a dit ook. Klaar.
Uniciteit
a=2 is weer een unieke priemf. ontbinding.
weer een redenering van a-1 naar a.
Neem a groter gelijk 3.
Veronderstel: priemfactor ontbinding van alle getallen kleiner dan a is uniek.
Stel a heeft 2 unieke priemf. ontbindingen: p1*p2*...pR en q1*q2*...*qS.
Dus a=p1*p2*...pR = q1*q2*...*qS.
Met de theorie van deler volgt p1|q1*q2*...*qS.
Er geldt p1|qi. p1 is dus deler van een van de factoren q. (hiervoor heb ik een apart bewijs).
Door de volgorde te wisselen mag je ook stellen dat p1|q1 (volgorde in een priemf. ontbinding niet belangrijk).
Aangezien p1 en q1 beide priemgetallen zijn en ook p1|q1 moet gelden p1=q1.
Dan geldt ook a/p1=q2*q3*...qS=p2*p3*..pR.
Met mijn eerdere veronderstelling (priemf. ontbindingen van getallen kleiner dan a uniek) moet gelden
q2*q3*...qS=p2*p3*..pR.
met p1=q1 volgt nu
p1*p2*...pR = q1*q2*...*qS en R=S, dus de priemf. ontbindingen zijn volledig gelijk.
En a heeft dus maar 1 priemfactorontbinding.
(met name R=S moet worden aangetoond, anders was je met p1*p2*...pR = q1*q2*...*qS al veel eerder klaar geweest).
[ Bericht 2% gewijzigd door Borizzz op 17-09-2009 16:19:09 ]
Ik heb getracht om het in mijn eigen woorden, correct weer te geven.
Kan deze ook door de beugel?
Bewijs loopt via volledige inductie.
Te bew: elk natuurlijk getal heeft unieke priemf. ontbinding.
Bestaan:
-a=2 heeft unieke priemf. ontbinding.
nu een redenering met volledige inductie van a-1 naar a.
-Veronderstel: alle getallen kleiner dan a hebben unieke priemf. ontbinding.
voor het getal a zijn er dan 2 mogelijkheden: a=priem of a=niet priem.
als a priem is, dan heeft ook a een unieke priemf. ontbinding. Klaar.
als a niet priem is, dan is a samengesteld. Dus a=a1*a2. Door dit feit geldt ook a1 en a2 kleiner dan a.
Door mijn veronderstelling hebben a1 en a2 een unieke priemf. ontbinding. En dus heeft a1*a2=a dit ook. Klaar.
Uniciteit
a=2 is weer een unieke priemf. ontbinding.
weer een redenering van a-1 naar a.
Neem a groter gelijk 3.
Veronderstel: priemfactor ontbinding van alle getallen kleiner dan a is uniek.
Stel a heeft 2 unieke priemf. ontbindingen: p1*p2*...pR en q1*q2*...*qS.
Dus a=p1*p2*...pR = q1*q2*...*qS.
Met de theorie van deler volgt p1|q1*q2*...*qS.
Er geldt p1|qi. p1 is dus deler van een van de factoren q. (hiervoor heb ik een apart bewijs).
Door de volgorde te wisselen mag je ook stellen dat p1|q1 (volgorde in een priemf. ontbinding niet belangrijk).
Aangezien p1 en q1 beide priemgetallen zijn en ook p1|q1 moet gelden p1=q1.
Dan geldt ook a/p1=q2*q3*...qS=p2*p3*..pR.
Met mijn eerdere veronderstelling (priemf. ontbindingen van getallen kleiner dan a uniek) moet gelden
q2*q3*...qS=p2*p3*..pR.
met p1=q1 volgt nu
p1*p2*...pR = q1*q2*...*qS en R=S, dus de priemf. ontbindingen zijn volledig gelijk.
En a heeft dus maar 1 priemfactorontbinding.
(met name R=S moet worden aangetoond, anders was je met p1*p2*...pR = q1*q2*...*qS al veel eerder klaar geweest).
[ Bericht 2% gewijzigd door Borizzz op 17-09-2009 16:19:09 ]
kloep kloep


wat voor fout maak ik dan? ik bedoelde uiteraard "er is er maar 1".quote:Op donderdag 17 september 2009 16:16 schreef thabit het volgende:
Misschien kun je het woord 'uniek' even opzoeken in een woordenboek.
kloep kloep


Waar staat 15.27 voor? Is dat de stelling die zegt als p priem p|ab dan p|a of p|b? Dat is de belangrijkste stap in het hele bewijs, dus die kun je beter maar wel snappen.


Ja, dat heb ik inmiddels weggehaald, stond idd voor die stelling.quote:Op donderdag 17 september 2009 16:19 schreef thabit het volgende:
Waar staat 15.27 voor? Is dat de stelling die zegt als p priem p|ab dan p|a of p|b? Dat is de belangrijkste stap in het hele bewijs, dus die kun je beter maar wel snappen.
Voor p|ab dan p|a of p|b heb ik een bewijs met inductie, die ik wel snapte. (moet haast wel).
kloep kloep


quote:Op donderdag 17 september 2009 16:13 schreef Borizzz het volgende:
Stel a heeft 2 unieke priemf. ontbindingen


Hier toon je nog helemaal niks unieks aan, het woord uniek kan dus overal weg.quote:Op donderdag 17 september 2009 16:13 schreef Borizzz het volgende:
Ik heb ook geprobeerd om een bewijs van de hoofdstelling op te schrijven.
Ik heb getracht om het in mijn eigen woorden, correct weer te geven.
Kan deze ook door de beugel?
Bewijs loopt via volledige inductie.
Te bew: elk natuurlijk getal heeft unieke priemf. ontbinding.
Bestaan:
-a=2 heeft unieke priemf. ontbinding.
nu een redenering met volledige inductie van a-1 naar a.
-Veronderstel: alle getallen kleiner dan a hebben unieke priemf. ontbinding.
voor het getal a zijn er dan 2 mogelijkheden: a=priem of a=niet priem.
als a priem is, dan heeft ook a een unieke priemf. ontbinding. Klaar.
als a niet priem is, dan is a samengesteld. Dus a=a1*a2. Door dit feit geldt ook a1 en a2 kleiner dan a.
Door mijn veronderstelling hebben a1 en a2 een unieke priemf. ontbinding. En dus heeft a1*a2=a dit ook. Klaar.
Twee unieke priemfactorontbindingen, dat kan niet.quote:Uniciteit
a=2 is weer een unieke priemf. ontbinding.
weer een redenering van a-1 naar a.
Neem a groter gelijk 3.
Veronderstel: priemfactor ontbinding van alle getallen kleiner dan a is uniek.
Stel a heeft 2 unieke priemf. ontbindingen: p1*p2*...pR en q1*q2*...*qS.
Hier zou ik opmerken dat de ontbindingen q2 * ... * qS en p2 * ... * pR hetzelfde zijn.quote:Dus a=p1*p2*...pR = q1*q2*...*qS.
Met de theorie van deler volgt p1|q1*q2*...*qS.
Er geldt p1|qi. p1 is dus deler van een van de factoren q. (hiervoor heb ik een apart bewijs).
Door de volgorde te wisselen mag je ook stellen dat p1|q1 (volgorde in een priemf. ontbinding niet belangrijk).
Aangezien p1 en q1 beide priemgetallen zijn en ook p1|q1 moet gelden p1=q1.
Dan geldt ook a/p1=q2*q3*...qS=p2*p3*..pR.
Met mijn eerdere veronderstelling (priemf. ontbindingen van getallen kleiner dan a uniek) moet gelden
q2*q3*...qS=p2*p3*..pR.
quote:met p1=q1 volgt nu
p1*p2*...pR = q1*q2*...*qS en R=S, dus de priemf. ontbindingen zijn volledig gelijk.
En a heeft dus maar 1 priemfactorontbinding.
(met name R=S moet worden aangetoond, anders was je met p1*p2*...pR = q1*q2*...*qS al veel eerder klaar geweest).


Hoe heb je dat bewezen dan?quote:Op donderdag 17 september 2009 16:21 schreef Borizzz het volgende:
[..]
Ja, dat heb ik inmiddels weggehaald, stond idd voor die stelling.
Voor p|ab dan p|a of p|b heb ik een bewijs met inductie, die ik wel snapte. (moet haast wel).


Als volgt:quote:
Laat a,b geheel getal en p priem. Te bew als p|ab dan p|a of p|b.
Gegeven p|ab.
Veronderstel dat p geen deler is dan b.
Omdat p priem is heeft het geen echte delers.
dus ggd(b,p)=1.
Met theorie over lineaire combinatie geldt: 1=xb+yp (x,y geheel).
dan geldt ook a=axb+ayp
ander geschreven a=x(ab) + p(ay).
p|ab (gegeven) en p|p(ay)
dus ook p|(x(ab) + p(ay).
dus ook p|a.
Leek me een heel eind in de goede richting.
Dit is volgens mij ook uit te breiden naar factoren met meer dan 2 termen.
kloep kloep


Klopte, op jouw opmerking na, dat bewijs van de hoofdstelling een beetje verder?quote:Op donderdag 17 september 2009 16:40 schreef thabit het volgende:
Okee, dat lijkt me dan verder wel correct.
Ik kon dat toch redelijk volgen (vergeleken met gister).
kloep kloep


Ja.quote:Op donderdag 17 september 2009 16:42 schreef Borizzz het volgende:
[..]
Klopte, op jouw opmerking na, dat bewijs van de hoofdstelling een beetje verder?
Ik kon dat toch redelijk volgen (vergeleken met gister).


ben ik weer. Klein dingetje uit de theorie, bij het bewijs van algoritme van euclides.
er staat a,b,c,r geheel en a=c*b+r en 0<r<b. Dan ggd(a,b)=ggd(b,r).
Omdat r=a-cb geldt ggd(a,b)|r. Dit gaat me ietsje snel.
Heeft dit te maken met het feit dat door r=a-cb r in feite een lineaire combinatie is van a en b.? Dan is automatisch r een veelvoud van de ggd(a,b).
Vervolg:
ggd(a,b)|r en ggd(a,b)|b dus ggd(a,b) is deler van zowel r als b.
dus uiteindelijk laat je dan zien ggd(a,b)=ggd(b,r).
er staat a,b,c,r geheel en a=c*b+r en 0<r<b. Dan ggd(a,b)=ggd(b,r).
Omdat r=a-cb geldt ggd(a,b)|r. Dit gaat me ietsje snel.
Heeft dit te maken met het feit dat door r=a-cb r in feite een lineaire combinatie is van a en b.? Dan is automatisch r een veelvoud van de ggd(a,b).
Vervolg:
ggd(a,b)|r en ggd(a,b)|b dus ggd(a,b) is deler van zowel r als b.
dus uiteindelijk laat je dan zien ggd(a,b)=ggd(b,r).
kloep kloep


ggd(a,b) deelt b dus het deelt ook (-c) * bquote:Op donderdag 17 september 2009 20:45 schreef Borizzz het volgende:
ben ik weer. Klein dingetje uit de theorie, bij het bewijs van algoritme van euclides.
er staat a,b,c,r geheel en a=c*b+r en 0<r<b. Dan ggd(a,b)=ggd(b,r).
Omdat r=a-cb geldt ggd(a,b)|r. Dit gaat me ietsje snel.
Heeft dit te maken met het feit dat door r=a-cb r in feite een lineaire combinatie is van a en b.? Dan is automatisch r een veelvoud van de ggd(a,b).
Vervolg:
ggd(a,b)|r en ggd(a,b)|b dus ggd(a,b) is deler van zowel r als b.
dus uiteindelijk laat je dan zien ggd(a,b)=ggd(b,r).
ggd(a,d) deelt a en (-c)*b dus deelt het ook de som van beiden, wat dus r is
goh, getaltheorie, lang geleden, was wel een van de leukste vakken.


De conclusie ggd(a,b)|r. Of dit volgt uit het feit dat r lin. combinatie van a en b is.quote:
kloep kloep


Ja, dat volgt daaruit.quote:Op donderdag 17 september 2009 21:24 schreef Borizzz het volgende:
[..]
De conclusie ggd(a,b)|r. Of dit volgt uit het feit dat r lin. combinatie van a en b is.


Ik snap nog altijd niet goed wat een parametervoorstelling nou is.
[vraag] Het standaarinproduct tussen twee vectoren x, y uit R^n is gedefinieerd als <x,y>=x1y1+x2y2+....+xnyn. We zeggen dat x en y oodrecht op elkaar staan als <x,y>=0
Schrijf V voor het valk door de oorsprong van R^3 dat loodrecht staat op z uit R^3, waarbij
Met andere woorden V bestaat uit alle vectoren in R^3 die loodrecht op z staan.
a) geef een vergelijking voor V.
Volgens mij gewoon v1+v2+v3=0, toch?
b) leid ook een parametervoorstelling af voor V.
Deze weet ik dus niet hoe dat moet. Als ik alleen v1+v2=0 ofzo zou ehbben zou ik dan geloof ik kunnen zeggen stel v2=n dan v1=-n?
[vraag] Het standaarinproduct tussen twee vectoren x, y uit R^n is gedefinieerd als <x,y>=x1y1+x2y2+....+xnyn. We zeggen dat x en y oodrecht op elkaar staan als <x,y>=0
Schrijf V voor het valk door de oorsprong van R^3 dat loodrecht staat op z uit R^3, waarbij
Met andere woorden V bestaat uit alle vectoren in R^3 die loodrecht op z staan.
a) geef een vergelijking voor V.
Volgens mij gewoon v1+v2+v3=0, toch?
b) leid ook een parametervoorstelling af voor V.
Deze weet ik dus niet hoe dat moet. Als ik alleen v1+v2=0 ofzo zou ehbben zou ik dan geloof ik kunnen zeggen stel v2=n dan v1=-n?


als ggd(a,b)=1 en ggd(a,c)=1 dan te bew is ggd(a,bc=1).
Dit moet dan vlg mij ook kunnen met lineaire combinaties:
ggd(a,b)=1 dus 1=ma+nb
ggd(a,c)=1 dus 1=ka+lc.
Dus nu moet ik dit zien om te werken naar iets van de vorm: 1=(x)a+(y)bc.
Maar ik zie nog niet goed hoe:
ik maakte ma+nb=ka+lc
ma-ka+nb-lc=0
maar dit voelt al niet zo lekker...
Dit moet dan vlg mij ook kunnen met lineaire combinaties:
ggd(a,b)=1 dus 1=ma+nb
ggd(a,c)=1 dus 1=ka+lc.
Dus nu moet ik dit zien om te werken naar iets van de vorm: 1=(x)a+(y)bc.
Maar ik zie nog niet goed hoe:
ik maakte ma+nb=ka+lc
ma-ka+nb-lc=0
maar dit voelt al niet zo lekker...
kloep kloep


ggd(a,b)=1 dus 1=ma+nb
Als a=7 en b=8, wat zijn m en n dan?
Als a=7 en b=8, wat zijn m en n dan?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


n=1 en a=-1.quote:Op zaterdag 19 september 2009 17:57 schreef GlowMouse het volgende:
ggd(a,b)=1 dus 1=ma+nb
Als a=7 en b=8, wat zijn m en n dan?
kloep kloep


Hmm ok, daar ben ik het wel mee eens dat je het zo kunt bewijzen. Ik had dat nog niet eerder gezien.
(nl)(bc) = nb * lc = (1-ma)(1-ka) = 1+(kma-m-k)a.
Dat die a terugkomt in de factor lijkt mij geen bezwaar.
[ Bericht 9% gewijzigd door GlowMouse op 19-09-2009 18:56:13 ]
(nl)(bc) = nb * lc = (1-ma)(1-ka) = 1+(kma-m-k)a.
Dat die a terugkomt in de factor lijkt mij geen bezwaar.
[ Bericht 9% gewijzigd door GlowMouse op 19-09-2009 18:56:13 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


kun je dit even in wat meer stapjes opschrijven? Dit gaat me te snel, en ik zie hier ook nog geen bewijs in.quote:Op zaterdag 19 september 2009 18:05 schreef GlowMouse het volgende:
Hmm ok, daar ben ik het wel mee eens dat je het zo kunt bewijzen. Ik had dat nog niet eerder gezien.
(nl)(bc) = nb * lc = (1-ma)(1-ka) = 1+(a-m-k)a.
Dat die a terugkomt in de factor lijkt mij geen bezwaar.
ik had tot nu toe 1=ma+nb en 1=ka+lb. Dit volgt uit het gegeven.
En volgens mij moet het nu naar de vorm 1=(x)a+(y)bc, want dan mag je concluderen dat de ggd(a,bc) 1 is.
[ Bericht 0% gewijzigd door Borizzz op 19-09-2009 18:58:19 ]
kloep kloep


Ik heb tot nu toe dit:
(1) 1=ma+nb
(2) 1=ka+lc
c=cma+nbc volgt uit (1)
lc=1-ka (volgt uit (2)
c=(1-ka)/l
(1-ka)/l=cma+nbc
1=cmal +ka +nbcl
1=(cma)a + (nl)bc
en dan ben je op zich klaar
maar wat ik "zwak" vindt is het delen in deze uitwerking. Je gaat uit van gehele getallen, en door te delen (en de verz. gehele getallen is niet gesloten mbt delen) ben je vlg mij niet zeker dan
cma en nl gehele getallen zijn.
(1) 1=ma+nb
(2) 1=ka+lc
c=cma+nbc volgt uit (1)
lc=1-ka (volgt uit (2)
c=(1-ka)/l
(1-ka)/l=cma+nbc
1=cmal +ka +nbcl
1=(cma)a + (nl)bc
en dan ben je op zich klaar
maar wat ik "zwak" vindt is het delen in deze uitwerking. Je gaat uit van gehele getallen, en door te delen (en de verz. gehele getallen is niet gesloten mbt delen) ben je vlg mij niet zeker dan
cma en nl gehele getallen zijn.
kloep kloep


Afgezien van nb vervangen door 1-ma en lc door 1-ka doe ik niet zo gek veel.
Er staat dat 1 = (nl)(bc) + (k+m-a)a.
Er staat dat 1 = (nl)(bc) + (k+m-a)a.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik zie nog steeds niet wat je doetquote:Op zaterdag 19 september 2009 18:52 schreef GlowMouse het volgende:
Afgezien van nb vervangen door 1-ma en lc door 1-ka doe ik niet zo gek veel.
Er staat dat 1 = (nl)(bc) + (k+m-a)a.
1=ma+nb en 1=ka+lc.
en dan?
kloep kloep


edit: ga maar een uurtje puzzelen, hier moet je uit kunnen komen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ok, ik heb m al Glowmouse. Achteraf gezien wel logisch omdat je een uitdrukking wil hebben waar de factor bc in zit, dat zou de hint op moeten leveren dat je nb*lc moet gaan doen.
Ik heb nog 2 opdrachten waar ik mee bezig ben, maar de oplossing nog niet helemaal gevonden heb,
Bv deze:
ax2+bx+c=0, met a,b,c geheel en oneven. Bew. dat er dan geen oplossing is.
Ik neem dan a=2k+1, b=2m+1 en c=2l+1, met k,m,l geheel.
Zo ben ik zeker dat de coefficienten a,b,c inderdaad altijd oneven zijn.
Omdat er geen oplossingen mogen zijn moet gelden: discriminant <0.
dus
(2m+1)2-4(2k+1)(2l+1) = discr.
4m2+4m+1-8kl-8l-8k-4
4m2+4m -8kl -8l -8k -3
4(m2+m -2kl -2l -2k) -3
discriminant is een viervoud -3,
en ik had hier gehoopt hier een uitdrukking te vinden waarbij je kon concluderen dat het negatief was.
.. waar zit de (denk)fout?
Ik heb nog 2 opdrachten waar ik mee bezig ben, maar de oplossing nog niet helemaal gevonden heb,
Bv deze:
ax2+bx+c=0, met a,b,c geheel en oneven. Bew. dat er dan geen oplossing is.
Ik neem dan a=2k+1, b=2m+1 en c=2l+1, met k,m,l geheel.
Zo ben ik zeker dat de coefficienten a,b,c inderdaad altijd oneven zijn.
Omdat er geen oplossingen mogen zijn moet gelden: discriminant <0.
dus
(2m+1)2-4(2k+1)(2l+1) = discr.
4m2+4m+1-8kl-8l-8k-4
4m2+4m -8kl -8l -8k -3
4(m2+m -2kl -2l -2k) -3
discriminant is een viervoud -3,
en ik had hier gehoopt hier een uitdrukking te vinden waarbij je kon concluderen dat het negatief was.
.. waar zit de (denk)fout?
kloep kloep


hoe zit het met bijvoorbeeld x² + x - 1 = 0?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja dan is de discriminant 5. Tegenvoorbeeld?quote:Op zaterdag 19 september 2009 19:21 schreef GlowMouse het volgende:
hoe zit het met bijvoorbeeld x² + x - 1 = 0?
Dit wil zeggen dat de bewering dus onwaar is??
En mijn uitwerking, op zich goed, maar niet nodig..
kloep kloep


Ze zullen wel geheeltallige x bedoelen, maar dan is pariteit een betere aanpak.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nou de laatste waar ik niet geheel uitkwam:
bew dat voor iedere n (geheeltallig) dat 10n +3*4n+2 +5 een negenvoud is.
Dit wilde ik doen met volledige inductie.
dussss
1. bewering is waar voor n=1 want 9|207.
2. Veronderstel: bew. waar voor n=k.
Dus er geldt 10k +3*4k+2 +5 = 0 (mod 9)
(te bew: dit geldt ook voor n=k+1).
10k +3*4k+2 = -5 (mod 9)
10k +3*4k+2 = 4 (mod 9)
10k+1=10*10k
4k+2=42*4k
dus
10k+1 + 10*3*4k = 40 (mod 9)
16*10k+1 + 10*3*4k+1 = 640 (mod 9)
en ja.. dan kom ik eigenlijk niet zoveel verder meer...
ik wil toe naar iets als
10k+1 +3*4k+1 = 0 (mod 9),
moet ik de 10 en 4 (die allebij tot de macht k zijn, samennemen? hoe?
of zit ik op een geheel verkeerd spoor.
[ Bericht 0% gewijzigd door Borizzz op 19-09-2009 19:52:48 ]
bew dat voor iedere n (geheeltallig) dat 10n +3*4n+2 +5 een negenvoud is.
Dit wilde ik doen met volledige inductie.
dussss
1. bewering is waar voor n=1 want 9|207.
2. Veronderstel: bew. waar voor n=k.
Dus er geldt 10k +3*4k+2 +5 = 0 (mod 9)
(te bew: dit geldt ook voor n=k+1).
10k +3*4k+2 = -5 (mod 9)
10k +3*4k+2 = 4 (mod 9)
10k+1=10*10k
4k+2=42*4k
dus
10k+1 + 10*3*4k = 40 (mod 9)
16*10k+1 + 10*3*4k+1 = 640 (mod 9)
en ja.. dan kom ik eigenlijk niet zoveel verder meer...
ik wil toe naar iets als
10k+1 +3*4k+1 = 0 (mod 9),
moet ik de 10 en 4 (die allebij tot de macht k zijn, samennemen? hoe?
of zit ik op een geheel verkeerd spoor.
[ Bericht 0% gewijzigd door Borizzz op 19-09-2009 19:52:48 ]
kloep kloep


Ik zou 10^n gelijk vervangen door 1 (mod 9).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoezo geldt dit?quote:Op zaterdag 19 september 2009 19:52 schreef GlowMouse het volgende:
Ik zou 10^n gelijk vervangen door 1 (mod 9).
En klopt de berekening een beetje? Want op t einde zit ik dus wel vast.
kloep kloep


Omdat 10 = 1 (mod 9).
En je moet deze stap sowieso ergens zetten.
En je moet deze stap sowieso ergens zetten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Tja dan krijg ik dit
10k+3*4k+2 +5 = 0 (mod 9)
1 + 3*4k+2 +5 = 0 (mod 9)
3*4k+2 +6 = 0 (mod 9)
3*4k+2 =3 (mod 9)
4k+3 = 4*4k+2
4k+3 = 12 (mod 9)
... weer vast.
10k+3*4k+2 +5 = 0 (mod 9)
1 + 3*4k+2 +5 = 0 (mod 9)
3*4k+2 +6 = 0 (mod 9)
3*4k+2 =3 (mod 9)
4k+3 = 4*4k+2
4k+3 = 12 (mod 9)
... weer vast.
kloep kloep


Je aanpak is dan ook abominabel en slecht te volgen. Je begint gewoon met 10^(k+1) + 3*4^(k+3) + 5, en schrijft dan net zo lang = ... = ... tot je op = 0 uitkomt. Dan zie je tenminste wat er gebeurt. Nu is het bij jou elk regeltje maar weer raden wat je aan het doen bent.
10^(k+1) + 3*4^(k+3) + 5
= 10^k + 4 * 3*4^(k+2) + 5 (mod 9)
= 10^k + 3*4^(k+2) + 5 + [vul zelf maar in, wat ben ik vergeten]
= [gewoon overnemen] (mod 9)
= ...
[ Bericht 0% gewijzigd door GlowMouse op 19-09-2009 20:23:15 ]
10^(k+1) + 3*4^(k+3) + 5
= 10^k + 4 * 3*4^(k+2) + 5 (mod 9)
= 10^k + 3*4^(k+2) + 5 + [vul zelf maar in, wat ben ik vergeten]
= [gewoon overnemen] (mod 9)
= ...
[ Bericht 0% gewijzigd door GlowMouse op 19-09-2009 20:23:15 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


je moet toch van k naar k+1 redeneren?
en je haalt een factor 4 eruit, daar deel je door...? en 10^n blijft staan? dat kan toch niet?
en je haalt een factor 4 eruit, daar deel je door...? en 10^n blijft staan? dat kan toch niet?
kloep kloep


Dat doe ik op regel 4, daar gebruik ik dat de uitspraak waar is voor n=k.quote:Op zaterdag 19 september 2009 20:21 schreef Borizzz het volgende:
je moet toch van k naar k+1 redeneren?
En ik deel nergens door, ik trek er wat af dat ik er later weer bijtel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik volg het nog niet, maar even opnieuw beginnen
10^k + 3*4^(k+2) +5 = 0 (mod 9)
10^k = 1 (mod 9)
1 + 3*4^(k+2) +5 = 0 (mod 9)
3* 4^(k+2) +6 = 0 (mod 9)
3* 4^(k+2) = 3 (mod 9)
nu van k+2 naar k+3, dus voor de inductie 1 stap verder, dus beide zijdne maal 4 doen...
3* 4^(k+3) = 12 (mod 9)
nu delen door 3
4^(k+3) = 4 (mod 9)
maar =0 zie ik nog nergens ...?
10^k + 3*4^(k+2) +5 = 0 (mod 9)
10^k = 1 (mod 9)
1 + 3*4^(k+2) +5 = 0 (mod 9)
3* 4^(k+2) +6 = 0 (mod 9)
3* 4^(k+2) = 3 (mod 9)
nu van k+2 naar k+3, dus voor de inductie 1 stap verder, dus beide zijdne maal 4 doen...
3* 4^(k+3) = 12 (mod 9)
nu delen door 3
4^(k+3) = 4 (mod 9)
maar =0 zie ik nog nergens ...?
kloep kloep


hier haal je een factor 4 ineens weg.quote:Op zaterdag 19 september 2009 20:10 schreef GlowMouse het volgende:
= 10^k + 4 * 3*4^(k+2) + 5 (mod 9)
= 10^k + 3*4^(k+2) + 5 + [vul zelf maar in, wat ben ik vergeten]
Maar dan 10^k/4 en 5/4?
kloep kloep


Ik deel helemaal niks door 4, want dan zou ik alles voor het =-teken ook door 4 moeten delen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zucht... ik snap m niet, terwijl ik dit toch al vaker gedaan heb.
Volgens mij start ik hier:
10k +3*4k+2 +5 = 0 (mod 9)
en met inductie moet dit ook gaan gelden voor k+1 dus
10 k+1 +3*4 k+3 +5 = 0 (mod 9) en dit moet ik bewijzen.
10k +3*4k+2 +5 = 0 (mod 9)
10k = 1 (mod 9)
dus
1 +3*4k+2 +5 = 0 (mod 9)
3*4k+2 +6 = 0 (mod 9)
3*4k+2 = 3 (mod 9)
tot zover moet t kloppen toch?
Volgens mij start ik hier:
10k +3*4k+2 +5 = 0 (mod 9)
en met inductie moet dit ook gaan gelden voor k+1 dus
10 k+1 +3*4 k+3 +5 = 0 (mod 9) en dit moet ik bewijzen.
10k +3*4k+2 +5 = 0 (mod 9)
10k = 1 (mod 9)
dus
1 +3*4k+2 +5 = 0 (mod 9)
3*4k+2 +6 = 0 (mod 9)
3*4k+2 = 3 (mod 9)
tot zover moet t kloppen toch?
kloep kloep


quote:Op zaterdag 19 september 2009 20:10 schreef GlowMouse het volgende:
Je aanpak is dan ook abominabel en slecht te volgen. Je begint gewoon met 10^(k+1) + 3*4^(k+3) + 5, en schrijft dan net zo lang = ... = ... tot je op = 0 uitkomt. Dan zie je tenminste wat er gebeurt. Nu is het bij jou elk regeltje maar weer raden wat je aan het doen bent.
10^(k+1) + 3*4^(k+3) + 5
= 10^k + 4 * 3*4^(k+2) + 5 (mod 9)
= 10^k + 3*4^(k+2) + 5 + [vul zelf maar in, wat ben ik vergeten]
= [gewoon overnemen] (mod 9)
= ...
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Daar kan ik helemaal niets mee, terwijl mijn methode iets is, wat ik een jaar of wat geleerd had op de opleiding...quote:
Volgens mij moet je er op 'mijn manier' ook kunnen komen.
kloep kloep


Slaap er anders een nachtje over, ik kan me niet voorstellen dat ze iemand tot chaoot opleiden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Naja laat maar dan.
Maar toch, ik heb m oude aantekeningen erbij gepakt, en daar staat in dat ik van k naar k+1 moet redeneren.
...
ik kan niet veel fouts vinden in mijn post van hierboven.
3*4k+2 = 3 (mod 9) klopt gewoon, dus dan moet je toch wel verder kunnen komen.
Maar toch, ik heb m oude aantekeningen erbij gepakt, en daar staat in dat ik van k naar k+1 moet redeneren.
...
ik kan niet veel fouts vinden in mijn post van hierboven.
3*4k+2 = 3 (mod 9) klopt gewoon, dus dan moet je toch wel verder kunnen komen.
kloep kloep


Nee, je moet aannemen dat het waar is van k, en dan bewijzen dat het ook geldt voor k+1. Jij pakt de bewering voor k en schrijft het om tot iets onbruikbaars.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Kijk eens naar machten van 4 modulo 9, dus 4 (mod 9), 42 (mod 9), 43 (mod 9), 44 (mod 9). Er staat echter 3·4k+2, dus kijk ook eens naar 3·4, 3·42, enz (alles modulo 9).
Het patroon moet duidelijk zijn lijkt me, en dan moet je dat ook wel in een (inductie)bewijs kunnen omzetten.
[ Bericht 3% gewijzigd door Iblis op 19-09-2009 21:01:45 (ik ben niet aan het programmeren natuurlijk) ]
Het patroon moet duidelijk zijn lijkt me, en dan moet je dat ook wel in een (inductie)bewijs kunnen omzetten.
[ Bericht 3% gewijzigd door Iblis op 19-09-2009 21:01:45 (ik ben niet aan het programmeren natuurlijk) ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Nou als ik aanneem dat het geldt voor k dan is het dus
10k +3*4k+2 +5 = 0 (mod 9)
nu laten zien dat dit ook waar is voor k+1.
10k + 3*4*4k+1 +5 =0 (mod 9)
10k +3*4k+1 +5 +3*4k+1 = 0 (mod 9)
zoiets had je volgens mij.
10k +3*4k+2 +5 = 0 (mod 9)
nu laten zien dat dit ook waar is voor k+1.
10k + 3*4*4k+1 +5 =0 (mod 9)
10k +3*4k+1 +5 +3*4k+1 = 0 (mod 9)
zoiets had je volgens mij.
kloep kloep


machten van 4 modulo 9...
4 - 13 - 22 - 31
16 -23 -32 - 41
64-73-82-91
oke, een patroon maar helpt dit mij verder?
4 - 13 - 22 - 31
16 -23 -32 - 41
64-73-82-91
oke, een patroon maar helpt dit mij verder?
kloep kloep


Ik slaap hier nog wel even een nachtje over.
Ik heb het echt heel mooi gekund vroeger, maar nu bij deze wil het gewoon niet, terwijl het idee van inductiebewijzen mij echt wel duidelijk is.
Iets anders dan
ggd(a,b)=x en ggd(a-b,b)=y.
a) x| (a-b)
hier heb ik dit:
x|a dus a=kx en x|b dus b=lx
a-b = kx-lx
a-b = (k-l)x
dus x|(a-b).
Op zich ok, had ik een paar dagen geleden nog niet gekund. Dus: ben wel stukje verder.
b) bewijs x|y.
er geldt a-b=(k-l)x
ook geldt y|(a-b)
dus y|(k-l)x
.. en dan heb ik eigenlijk bewezen dat y een veelvoud van x deelt, maar nog niet x zelf.
c) bew ggd(a-b,b)=ggd(a,b)
dit zie ik dan nog niet helemaal
stel ggd(a,b)=d
dan d|a en d|b.
stel ook c|a en c|b, dan geldt d>c.
...
Ik heb het echt heel mooi gekund vroeger, maar nu bij deze wil het gewoon niet, terwijl het idee van inductiebewijzen mij echt wel duidelijk is.
Iets anders dan
ggd(a,b)=x en ggd(a-b,b)=y.
a) x| (a-b)
hier heb ik dit:
x|a dus a=kx en x|b dus b=lx
a-b = kx-lx
a-b = (k-l)x
dus x|(a-b).
Op zich ok, had ik een paar dagen geleden nog niet gekund. Dus: ben wel stukje verder.
b) bewijs x|y.
er geldt a-b=(k-l)x
ook geldt y|(a-b)
dus y|(k-l)x
.. en dan heb ik eigenlijk bewezen dat y een veelvoud van x deelt, maar nog niet x zelf.
c) bew ggd(a-b,b)=ggd(a,b)
dit zie ik dan nog niet helemaal
stel ggd(a,b)=d
dan d|a en d|b.
stel ook c|a en c|b, dan geldt d>c.
...
kloep kloep


Hoe je erop komt… en welk patroon je denkt te zien… neem nu eens de rest na deling door 9, dat is immers wat je met 10k ook doet, en dat geeft doorgaans het best beeld. Ja, 43 (mod 9) ≡ 91, maar dat helpt toch niemand verder?quote:Op zaterdag 19 september 2009 21:08 schreef Borizzz het volgende:
machten van 4 modulo 9...
4 - 13 - 22 - 31
16 -23 -32 - 41
64-73-82-91
oke, een patroon maar helpt dit mij verder?
41 (mod 9) ≡ 4
42 (mod 9) ≡ 7
43 (mod 9) ≡ 1
44 (mod 9) ≡ 4
Enz. Nu nog eens keer 3, en het wordt echt interessant modulo 9. Volgens mij kun je dan wel wat voor 3·4k + 2 (mod 9) stellen. In het algemeen dus. Dan weet je dus wat 10k (mod 9) is, wat 3·4k + 2 (mod 9) is, en dan zou het toch echt moeten lukken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


dus 3*4k+2 is 3 mod 9?
waren a) en b) dan goed?
maar y deelt dan toch een veelvoud van x?
dan heb ik nog niet bewezen dat y|x.
waren a) en b) dan goed?
maar y deelt dan toch een veelvoud van x?
dan heb ik nog niet bewezen dat y|x.
kloep kloep


Ik had gehoopt dat je dat niet meer had hoeven te vragen. Maar, ja. Als je graag een inductie bewijs wilt: neem aan dat het geldt voor k, dan k + 1 = 4 * 3 (mod 9) = 12 (mod 9) = 3. En voor k = 0 geldt het natuurlijk want 48 (mod 9) = 3. Klaar. Maar het kan directer als je zoals thabit doet van de rekenregels van modulo gebruik maakt.quote:
Eigenlijk zijn die 3 alle drie heel makkelijk doen met een bekende eigenschap van de ggd.quote:waren a) en b) dan goed?
maar y deelt dan toch een veelvoud van x?
dan heb ik nog niet bewezen dat y|x.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik denk dat ik er beter mee kan stoppen vanavond.
Belooft niet veel goeds voor dit vak als het zolang duurt voordat ik het ook een keer doorheb.
Aan de andere kant moet ik ook niet te veel en te snel willen, ik ben pas 3 dagen echt bezig met dit vak.
Belooft niet veel goeds voor dit vak als het zolang duurt voordat ik het ook een keer doorheb.
Aan de andere kant moet ik ook niet te veel en te snel willen, ik ben pas 3 dagen echt bezig met dit vak.
kloep kloep


Je bedoelt lineaire combinatie?quote:Op zaterdag 19 september 2009 21:41 schreef Iblis het volgende:
Eigenlijk zijn die 3 alle drie heel makkelijk doen met een bekende eigenschap van de ggd.
kloep kloep


Naja, eigenlijk denk ik dat je die niet kent, want dan zou het te makkelijk zijn, maar i.h.a. geldt ggd(a + mb, b) = ggd(a, b) met m een geheel getal. Dus x = y.quote:Op zaterdag 19 september 2009 21:46 schreef Borizzz het volgende:
[..]
Je bedoelt lineaire combinatie?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


heeey!!
Ik heb een vraagje over elliptische krommen. Zij f : P --> P1(C) een niet constante meromorfe functie die gedefinieerd is op een 'fundamenteel parallalogram' P. We nemen aan dat f minstens 1 pole heeft. Ik moet laten zien dat dat deze surjectief is. Dus het beeld is hele P1(C) (projectieve ruimte over het lichaam van complexe getallen).
je kunt P1(C) zien als C verenigd met een punt in het oneindig. Oneindig bereiken is niet het probleem, het probleem is nu dat ieder ander element in P1(C) bereikt wordt. Ik dacht het volgende: Stel er is een element a in P1(C) dat niet bereikt wordt. Bekijk g:1/(f-a).
Daarna probeerde ik iets zinnigs te zeggen over g maar ik kwam er niet uit.
Trouwens deze functie f --> P(C) is toch continu? ook al zijn er polen aangezien P1(C)
--> P(C) is toch continu? ook al zijn er polen aangezien P1(C)
oneindig bevat...?
alvast bedankt!!
Ik heb een vraagje over elliptische krommen. Zij f : P --> P1(C) een niet constante meromorfe functie die gedefinieerd is op een 'fundamenteel parallalogram' P. We nemen aan dat f minstens 1 pole heeft. Ik moet laten zien dat dat deze surjectief is. Dus het beeld is hele P1(C) (projectieve ruimte over het lichaam van complexe getallen).
je kunt P1(C) zien als C verenigd met een punt in het oneindig. Oneindig bereiken is niet het probleem, het probleem is nu dat ieder ander element in P1(C) bereikt wordt. Ik dacht het volgende: Stel er is een element a in P1(C) dat niet bereikt wordt. Bekijk g:1/(f-a).
Daarna probeerde ik iets zinnigs te zeggen over g maar ik kwam er niet uit.
Trouwens deze functie f
oneindig bevat...?
alvast bedankt!!


Ik kom niet uit een oplossing dit is de vraag:
De vraagfunctie naar EPO luidt: Q = 147-P^2 (Q=epo; P= prijs van EPO)
Uiteindelijk dient de elasticiteit berekent te worden en dan komen ze tot de volgende formule:
Ed = (elasticiteit demand) (delta Q / Q) / (delta P / P ) = (Delta Q / Delta P) * P / Q = -2P * (P/147-P^2)
Ed = -2P^2 / 147 - P^2
Kan iemand mij uitleggen hoe zij komen tot deze berekening? Kom er niet uit
De vraagfunctie naar EPO luidt: Q = 147-P^2 (Q=epo; P= prijs van EPO)
Uiteindelijk dient de elasticiteit berekent te worden en dan komen ze tot de volgende formule:
Ed = (elasticiteit demand) (delta Q / Q) / (delta P / P ) = (Delta Q / Delta P) * P / Q = -2P * (P/147-P^2)
Ed = -2P^2 / 147 - P^2
Kan iemand mij uitleggen hoe zij komen tot deze berekening? Kom er niet uit


dQ/dP * P / Q moet je onthouden als definitie van elasticiteit. En het is de afgeleide, geen 'delta'. En dan is het verder makkelijk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


f is meromorf dus continu naar P1(C), inderdaad. Met 'gedefinieerd op een fundamenteel parallellogram' bedoel je dat het gedefinieerd is op P = C/L, met L een rooster?quote:Op zondag 20 september 2009 12:23 schreef Optimistic1 het volgende:
heeey!!
Ik heb een vraagje over elliptische krommen. Zij f : P --> P1(C) een niet constante meromorfe functie die gedefinieerd is op een 'fundamenteel parallalogram' P. We nemen aan dat f minstens 1 pole heeft. Ik moet laten zien dat dat deze surjectief is. Dus het beeld is hele P1(C) (projectieve ruimte over het lichaam van complexe getallen).
je kunt P1(C) zien als C verenigd met een punt in het oneindig. Oneindig bereiken is niet het probleem, het probleem is nu dat ieder ander element in P1(C) bereikt wordt. Ik dacht het volgende: Stel er is een element a in P1(C) dat niet bereikt wordt. Bekijk g:1/(f-a).
Daarna probeerde ik iets zinnigs te zeggen over g maar ik kwam er niet uit.
Trouwens deze functie f--> P(C) is toch continu? ook al zijn er polen aangezien P1(C)
oneindig bevat...?
alvast bedankt!!
Na een coordinaattransformatie op P^1(C) mag je aannemen dat a het punt op oneindig is. Dan is f dus gewoon een holomorfe functie van P=C/L naar C, en dus te liften naar een holomorfe functie C->C. Nu is C/L compact dus het beeld van f is dat ook. Dat betekent dat f begrensd moet zijn; Liouville zegt dan dat f constant is, maar een van de aannames is dat f dat niet is.


Uiterdaad, het is C/L met L een rooster.
Ik zie het nu, dank je wel!
Over roosters gesproken. Dit zijn discrete ondergroupen van C. Ze hebben de vorm L={0}, L=Z.l of L=Z.l1 ( + ) Z.l2. Ik wil laten zien als je minstens 3 verschillende l's hebt dan krijg je niet meer een rooster. Dus dan krijg je niet een discrete verzameling.
Is het een kwestie van uitschrijven of kan het veel handiger?
Ik zie het nu, dank je wel!
Over roosters gesproken. Dit zijn discrete ondergroupen van C. Ze hebben de vorm L={0}, L=Z.l of L=Z.l1 ( + ) Z.l2. Ik wil laten zien als je minstens 3 verschillende l's hebt dan krijg je niet meer een rooster. Dus dan krijg je niet een discrete verzameling.
Is het een kwestie van uitschrijven of kan het veel handiger?


Als je 3 vectoren hebt, Z-linear onafhankelijk (dus ook Q-lineair onafhankelijk), dan is er wel altijd een lineaire combinatie over R te vinden. Met een ladenprincipe-argument oid kun je wel laten zien dat er dan altijd lineaire combinaties gemaakt kunnen worden die willekeurig dicht bij elkaar liggen. Dat toont dan aan dat de zaak niet discreet is.


| 1 7 0 0 1 = 3 |
| 0 0 1 0 2 = 2 |
| 0 0 0 1 1 = 1 |
"vegen" moet ik..
| 0 0 1 0 2 = 2 |
| 0 0 0 1 1 = 1 |
"vegen" moet ik..
Herb is the healing of a nation, alcohol is the destruction.


nbiet zo - bijdehand he, ik word helemaal para van die shit, is toch onmogelijk deze? 
[ Bericht 1% gewijzigd door GlowMouse op 21-09-2009 21:44:17 ]
[ Bericht 1% gewijzigd door GlowMouse op 21-09-2009 21:44:17 ]
Herb is the healing of a nation, alcohol is the destruction.


je weet wat vegen is, of je weet het niet 
maar ik heb ergens een stukje theorie gevonden, dus ik ga het proberen toe te passen
maar ik heb ergens een stukje theorie gevonden, dus ik ga het proberen toe te passen
Herb is the healing of a nation, alcohol is the destruction.


e^(6x-1) = 8/7
6x-1 = ln(8/7)
6x= ln(8/7) +1
en dan? ik moet een exact antwoord krijgen.
en nog een vraagje:
6^(-8x+2)=4/3
ln(6) * (-8x+2) = ln(4/3)
-8x+2 = ln(4/3) / ln(6)
en hier kom ik ook niet verder, ik moet ook weer een exact antwoord krijgen.
Wie kan mij helpen?


6x= ln(8/7) +1
Delen door 6: x = (ln(8/7) +1)/6
Delen door 6: x = (ln(8/7) +1)/6
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Laat maar die 2e vraag. ik moest 8 van de 10 vragen goed hebben (internettoets) en ik heb de 2 laatste open gelaten. Ik had de rest dus allemaal goed.  ook het antwoord van mijn 1e vraag was goed.
ook het antwoord van mijn 1e vraag was goed.
Dankje GlowMouse
Hier het antwoord van de 2e vraag, voor wie het interesseert.
Dankje GlowMouse
Hier het antwoord van de 2e vraag, voor wie het interesseert.


Hey,
Ik heb een vraagje wat voor mij (te) lang geleden is:
You add up two pure sinusoids of 1000Hz and 40 dB SPL with a phase difference of 0 'graden'.
How much db SPL is the result?
Dezelfde vraag is dan voor 90 graden en 180 graden.
Kunnen jullie mij in ieder geval wat op weg helpen?
Alvast bedankt
Ik heb een vraagje wat voor mij (te) lang geleden is:
You add up two pure sinusoids of 1000Hz and 40 dB SPL with a phase difference of 0 'graden'.
How much db SPL is the result?
Dezelfde vraag is dan voor 90 graden en 180 graden.
Kunnen jullie mij in ieder geval wat op weg helpen?
Alvast bedankt


SPL = sound pressure levelquote:
Is gerelateerd aan een vast referentie 'level' van de druk die het geluid te weeg brengt.
Maar volgens mij heeft dat eigenlijk geen invloed op het antwoord.


't Is natuurlijk wel handig om te weten hoe een dB SPL is uitgedrukt in termen van de golf. Zeker omdat het hier het wiskundetopic is. Als je dat niet kunt vertellen, dan moet je in het andere betatopic wezen.


Volgens mij moet het zijn: x=1/4 - 1/8(ln(4)/ln(6) - ln(3)/ln(6))quote:Op maandag 21 september 2009 22:17 schreef P1N00 het volgende:
Laat maar die 2e vraag. ik moest 8 van de 10 vragen goed hebben (internettoets) en ik heb de 2 laatste open gelaten. Ik had de rest dus allemaal goed.ook het antwoord van mijn 1e vraag was goed.
Dankje GlowMouse
Hier het antwoord van de 2e vraag, voor wie het interesseert.
[ afbeelding ]


Da's natuurlijk hetzelfde, alleen minder vereenvoudigd opgeschreven.quote:Op dinsdag 22 september 2009 12:09 schreef lyolyrc het volgende:
[..]
Volgens mij moet het zijn: x=1/4 - 1/8(ln(4)/ln(6) - ln(3)/ln(6))


Ik snapte al niet waar de 2 vandaan kwam, maar het is natuurlijk heel simpel:quote:Op dinsdag 22 september 2009 12:11 schreef thabit het volgende:
Da's natuurlijk hetzelfde, alleen minder vereenvoudigd opgeschreven.
1/8*ln(4)/ln(6) = 1/8*ln(22)/ln(6) = 2/8*ln(2)/ln(6) = 1/4*ln(2)/ln(6)


Hoe bereken ik de limit van een functie met behulp van een Taylor-reeks? En wanneer mag dit? In mijn boek staat alleen een voorbeeld en daar kom ik niet echt verder mee.


Oneindige taylorreeks? Ander is het heel flauw.quote:Op dinsdag 22 september 2009 15:03 schreef woopehh het volgende:
Hoe bereken ik de limit van een functie met behulp van een Taylor-reeks? En wanneer mag dit? In mijn boek staat alleen een voorbeeld en daar kom ik niet echt verder mee.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Eerste 3 termen zouden genoeg moeten zijn geloof ik..quote:Op dinsdag 22 september 2009 15:08 schreef GlowMouse het volgende:
[..]
Oneindige taylorreeks? Ander is het heel flauw.


Waar neem je dan de limiet naar toe?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Limiet x->0 van:quote:Op dinsdag 22 september 2009 15:15 schreef GlowMouse het volgende:
Waar neem je dan de limiet naar toe?
Plaatje werkt niet echt lekker, de functie is:
(1 - cos(2x)) / x2
[ Bericht 10% gewijzigd door motorbloempje op 01-09-2013 21:29:05 ]


Moet je \frac{teller}{noemer} gebruiken, anders heeft het geen voordeel om tex te gebruiken.
En rond welk punt had je die taylorbenadering?
En rond welk punt had je die taylorbenadering?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Tja, als je gewoon Taylort vind je dat:
De reeksontwikkeling is rond x = 0 (gejat trouwens van: Wolfram Alpha).
En dan is het denk ik niet zo moeilijk om de limiet te nemen…
De reeksontwikkeling is rond x = 0 (gejat trouwens van: Wolfram Alpha).
En dan is het denk ik niet zo moeilijk om de limiet te nemen…
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Iblis, hoe maak jij een taylorreeks om een punt waarop de functie niet gedefinieerd is?
Gezond verstand gebruiken; kijk eens naar die functie die Iblis geeft, denk je dat dat goed gaat?quote:Op dinsdag 22 september 2009 15:37 schreef woopehh het volgende:
Ok, bedanktMaar kan ik taylorreeksen bijvoorbeeld ook gebruiken voor limieten naar oneindig?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op dinsdag 22 september 2009 15:42 schreef GlowMouse het volgende:
Iblis, hoe maak jij een taylorreeks om een punt waarop de functie niet gedefinieerd is?
[..]
Gezond verstand gebruiken; kijk eens naar die functie die Iblis geeft, denk je dat dat goed gaat?
Wat denk ik de bedoeling is, maar wat ik niet zo netjes zei: is dat je cos(2x) Taylort, dat geeft:
Die prop je in de teller, die 1 valt weg, dan deel je x2 eruit en ga je de limiet nemen naar 0 (of je neemt eerste de limiet en deelt dan x2 eruit, wat netter is). Nu lijkt het inderdaad alsof je eerste die functie al evalueert voor x = 0.
Overigens is L’Hôpital gebruiken in dit geval denk ik net zo gemakkelijk.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Helemaal niemand?quote:Op dinsdag 22 september 2009 11:32 schreef Gordon__Gekko het volgende:
Hey,
Ik heb een vraagje wat voor mij (te) lang geleden is:
You add up two pure sinusoids of 1000Hz and 40 dB SPL with a phase difference of 0 'graden'.
How much db SPL is the result?
Dezelfde vraag is dan voor 90 graden en 180 graden.
Kunnen jullie mij in ieder geval wat op weg helpen?
Alvast bedankt


Als je twee sinusvormige signalen die dezelfde frequentie en amplitude hebben en bovendien in fase zijn bij elkaar optelt, dan is de resultante een sinusvormig signaal met dezelfde frequentie maar met de dubbele amplitude. Dat had je toch wel door hoop ik?quote:
Een verdubbeling van de amplitude komt overeen met een toename van (ongeveer) 6 dB.
Bekijk nu eerst eens de situatie waarin de twee sinusvormige signalen met gelijke frequentie en amplitude 180 graden in fase verschillen. Dan zijn de signalen precies in tegenfase, want:
sin (t + π) = - sin t
Het resultaat is nu dus dat de signalen elkaar precies uitdoven.
Nu mag je zelf even proberen te bedenken wat het resultaat is bij een faseverschil van 90 graden. Dat is overigens wel iets lastiger ...


bij een supermarkt komen op een middag:
563 volwassenen
414 vrouwen
310 personen alleen
296 volwassen vrouwen
213 volwassenen alleen
124 vrouwen alleen
92 volwassen vrouwen alleen
54 personen noch volwassen, noch vrouw, noch alleen
hoeveel personen zijn in totaal naar de supermarkt geweest?
dat zijn dus:
563 volwassenen m+v
414 - 296 = 118 onvolwassen vrouwen
onvolwassen mannen: 54 + (aantal onvolwassen mannen niet alleen)
en dat laatste, hoe die rest van de onvolwassen mannen te berekenen, daar kom ik niet uit, jullie misschien? het goede antwoord is 800, dus we komen nog 65 tekort, alvast bedankt
563 volwassenen
414 vrouwen
310 personen alleen
296 volwassen vrouwen
213 volwassenen alleen
124 vrouwen alleen
92 volwassen vrouwen alleen
54 personen noch volwassen, noch vrouw, noch alleen
hoeveel personen zijn in totaal naar de supermarkt geweest?
dat zijn dus:
563 volwassenen m+v
414 - 296 = 118 onvolwassen vrouwen
onvolwassen mannen: 54 + (aantal onvolwassen mannen niet alleen)
en dat laatste, hoe die rest van de onvolwassen mannen te berekenen, daar kom ik niet uit, jullie misschien? het goede antwoord is 800, dus we komen nog 65 tekort, alvast bedankt


Het makkelijkste is dit met een Venn-diagram te tekenen. Je tekent drie cirkels die elkaar allemaal overlappen, voor Volwassen, Vrouwen, Alleenstaanden. Ik duid volwassen met een V aan, vrouwen met F, en alleen staanden met A.
Je hebt het middelste gebied waar ze allemaal overlappen (V+F+A), daar zitten er 92 in. Dat is gegeven. Dan heb je het gebied F+A, dus vrouwen alleen, maar zonder degenen die ook in V+F+A zitten, dat zijn er 124 - 92 = 32. Dan heb je nog V+F, dat is 296 - 92 = 204. Houd je in totaal voor alleen F (dus niet in V of A) 86 over.
Nu voor de alleenstaanden: V+F+A heb je al, F+A ook, nu V+A, dat zijn er 213 - 92 (die in V+F+A zitten) = 121.
Degenen die alleen in A zitten zijn er nu: 310 - 121 - 92 - 32 (resp. V+A, V+F+A, F+A) = 65 (het aantal dat je mist).
Voor V houd je nog over 563 - 121 - 92 - 204 = 146.
Heb je in totaal 7 vakjes, + 54 die nergens bijhoren, en als je dat optelt krijg je: 146+86+65+121+92+32+204+54 = 800.
Ik hoop dat het zo duidelijk is, tekenen is nog veel duidelijker. Maar dat is me even te veel werk.
Je hebt het middelste gebied waar ze allemaal overlappen (V+F+A), daar zitten er 92 in. Dat is gegeven. Dan heb je het gebied F+A, dus vrouwen alleen, maar zonder degenen die ook in V+F+A zitten, dat zijn er 124 - 92 = 32. Dan heb je nog V+F, dat is 296 - 92 = 204. Houd je in totaal voor alleen F (dus niet in V of A) 86 over.
Nu voor de alleenstaanden: V+F+A heb je al, F+A ook, nu V+A, dat zijn er 213 - 92 (die in V+F+A zitten) = 121.
Degenen die alleen in A zitten zijn er nu: 310 - 121 - 92 - 32 (resp. V+A, V+F+A, F+A) = 65 (het aantal dat je mist).
Voor V houd je nog over 563 - 121 - 92 - 204 = 146.
Heb je in totaal 7 vakjes, + 54 die nergens bijhoren, en als je dat optelt krijg je: 146+86+65+121+92+32+204+54 = 800.
Ik hoop dat het zo duidelijk is, tekenen is nog veel duidelijker. Maar dat is me even te veel werk.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


ahh dankjewel, ik snap hetquote:Op donderdag 24 september 2009 11:08 schreef Iblis het volgende:
Het makkelijkste is dit met een Venn-diagram te tekenen. Je tekent drie cirkels die elkaar allemaal overlappen, voor Volwassen, Vrouwen, Alleenstaanden. Ik duid volwassen met een V aan, vrouwen met F, en alleen staanden met A.
Je hebt het middelste gebied waar ze allemaal overlappen (V+F+A), daar zitten er 92 in. Dat is gegeven. Dan heb je het gebied F+A, dus vrouwen alleen, maar zonder degenen die ook in V+F+A zitten, dat zijn er 124 - 92 = 32. Dan heb je nog V+F, dat is 296 - 92 = 204. Houd je in totaal voor alleen F (dus niet in V of A) 86 over.
Nu voor de alleenstaanden: V+F+A heb je al, F+A ook, nu V+A, dat zijn er 213 - 92 (die in V+F+A zitten) = 121.
Degenen die alleen in A zitten zijn er nu: 310 - 121 - 92 - 32 (resp. V+A, V+F+A, F+A) = 65 (het aantal dat je mist).
Voor V houd je nog over 563 - 121 - 92 - 204 = 146.
Heb je in totaal 7 vakjes, + 54 die nergens bijhoren, en als je dat optelt krijg je: 146+86+65+121+92+32+204+54 = 800.
Ik hoop dat het zo duidelijk is, tekenen is nog veel duidelijker. Maar dat is me even te veel werk.


en als je een vierkant of een rechthoekige figuur hebt met hokjes, laten we zeggen 5 bij 7 hokjes, dan is het aantal wegen er doorheen 12Combinatie5 of 12 Combinatie7.
Maar als je dan een driehoekige figuur hebt, bv de helft van een figuur van 5 bij 5 hokjes, hoeveel wegen zijn er dan van het hoekpunt naar de middellijn, het antwoord is 2^5 wegen er doorheen, maar ik begrijp niet helemaal waarom dit zo is, ik zou denken misschien 10C5:2 of 15^2 omdat je 15 kruispunten hebt. kan iemand me dit misschien uitleggen?
Maar als je dan een driehoekige figuur hebt, bv de helft van een figuur van 5 bij 5 hokjes, hoeveel wegen zijn er dan van het hoekpunt naar de middellijn, het antwoord is 2^5 wegen er doorheen, maar ik begrijp niet helemaal waarom dit zo is, ik zou denken misschien 10C5:2 of 15^2 omdat je 15 kruispunten hebt. kan iemand me dit misschien uitleggen?


oja tuurlijk, dankjewelquote:Op donderdag 24 september 2009 12:08 schreef thabit het volgende:
Je moet 5 stappen doen en bij elke stap heb je 2 keuzes: naar links of naar rechts. Zo kom je op 25


laat mbv de definitie zien dat 
(Het is n --> oneindig maar heb geen flauw idee hoe ik dat op moet schrijven )
)
Dus eerst |1/(2n+3) - L(=0) | < ε
En dit heb ik vereenvouwdigd naar n = 1/2ε -3/2
Maar wat moet ik nu doen?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:29:12 ]
(Het is n --> oneindig maar heb geen flauw idee hoe ik dat op moet schrijven
Dus eerst |1/(2n+3) - L(=0) | < ε
En dit heb ik vereenvouwdigd naar n = 1/2ε -3/2
Maar wat moet ik nu doen?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:29:12 ]


Eerst zorgen dat we je plaatje te zien krijgen (of het gewoon in je post opnemen) want zo is je vraag niet te beantwoorden.quote:Op donderdag 24 september 2009 16:21 schreef andrew.16 het volgende:
laat mbv de definitie zien dat [ afbeelding ]
(Het is n --> oneindig maar heb geen flauw idee hoe ik dat op moet schrijven)
Dus eerst |1/(2n+3) - L(=0) | < ε
En dit heb ik vereenvouwdigd naar n = 1/2ε -3/2
Maar wat moet ik nu doen?


Z’n vermoedelijke plaatje aan de hand van de URL:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Laat met behulp van de definitie zien dat:
Volgens de definitie moet
Dus
Dit heb ik vereenvoudigd naar
Maar heb nu dus geen flauw idee wat ik verder moet doen..
Volgens de definitie moet
Dus
Dit heb ik vereenvoudigd naar
Maar heb nu dus geen flauw idee wat ik verder moet doen..


Ik kom niet uit de partieel afgeleiden van de volgende functie: U = SC + 10(S+C)
Nu moet ik de partieel afgeleide MUs genaamd vinden en MUc.
De antwoorden zijn: MUs = C+10 en MUc = S+10, met die algemene formule van partieel diffierentieren waarbij je er 1 constant zet kom ik niet uit. Heeft een idee hoe dit op te lossen?
Nu moet ik de partieel afgeleide MUs genaamd vinden en MUc.
De antwoorden zijn: MUs = C+10 en MUc = S+10, met die algemene formule van partieel diffierentieren waarbij je er 1 constant zet kom ik niet uit. Heeft een idee hoe dit op te lossen?


Ik vind je beschrijving heel moeilijk te volgen, maar ik snap niet precies waarom het zo moeilijk is, als je U = SC + 10(S + C) neemt, en even de haakjes uitschrijft, dan krijg je dus U = SC + 10S + 10C.
Als je deze afleidt naar S, dus C constant neemt, dan krijg je toch C + 10? SC wordt C namelijk, net zoals 2x als je dat naar x afleidt 2 wordt, 10C is een constante, die verdwijnt en 10S wordt 10.
Voor afleiden naar C krijg je in feite hetzelfde verhaal maar dan met S en C verwisseld.
Als je deze afleidt naar S, dus C constant neemt, dan krijg je toch C + 10? SC wordt C namelijk, net zoals 2x als je dat naar x afleidt 2 wordt, 10C is een constante, die verdwijnt en 10S wordt 10.
Voor afleiden naar C krijg je in feite hetzelfde verhaal maar dan met S en C verwisseld.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Kom er nog niet uit, heb nu veel met U = X + Y gewerkt en nu komen er ineens 3 delen in de vergelijking voor.
Zo zou ik hem oplossen (hierbij maak ik gebruik met de ''formule'' van partieel differentiëren z = x + y:
Stel dat zie s als x, dan betekent dit dat ik de y'tjes (C's) constant zet?
Dan doe ik als volgt:
U = SC + 10S + 10C
MUs = dan C constant houden
Dan heb ik zeg maar U = S + 10S over, dit los ik dan op met normaal differentiëren (formule n * a * x^n-1)
Dan valt S weg en wordt 10S 10. Nu tel ik daar de constanten bij op en kom ik op S + 10 + 10C.
Kun je misschien uitleggen waar het bij mij fout gaat?
Zo zou ik hem oplossen (hierbij maak ik gebruik met de ''formule'' van partieel differentiëren z = x + y:
Stel dat zie s als x, dan betekent dit dat ik de y'tjes (C's) constant zet?
Dan doe ik als volgt:
U = SC + 10S + 10C
MUs = dan C constant houden
Dan heb ik zeg maar U = S + 10S over, dit los ik dan op met normaal differentiëren (formule n * a * x^n-1)
Dan valt S weg en wordt 10S 10. Nu tel ik daar de constanten bij op en kom ik op S + 10 + 10C.
Kun je misschien uitleggen waar het bij mij fout gaat?


In alle eerlijkheid, je terminologie is héél erg niet duidelijk. Hier heb je een teken voor partieel differentiëren: ∂, kopieer en plak dat anders om het iets duidelijker te maken.quote:Op zondag 27 september 2009 10:30 schreef Matr het volgende:
Kom er nog niet uit, heb nu veel met U = X + Y gewerkt en nu komen er ineens 3 delen in de vergelijking voor.
Zo zou ik hem oplossen (hierbij maak ik gebruik met de ''formule'' van partieel differentiëren z = x + y:
Als je bedoelt met ‘s als x zien’ dat je s als variabele neemt, dan betekent het inderdaad dat je de y’s, of C’s in dit geval als constant beschouwt. Constant is dus vast maar onbekend.quote:Stel dat zie s als x, dan betekent dit dat ik de y'tjes (C's) constant zet?
Nee, met C constant houden heb je nog steds U = SC + 10S + 10C over. Immers, als je een formule als ax2 + bx + c hebt, met a, b en c constant, dan haal je die toch ook niet weg? Wat jij doet is C gewoon weghalen. Dat slaat nergens op want dan krijg je een heel andere formule. Ik heb het gevoel dat als ik vraag of je cx + 10x + 10c wilt differentiëren naar x, dat dat prima lukt, en dat je direct ziet dat dat x + 10 is.quote:Dan doe ik als volgt:
U = SC + 10S + 10C
MUs = dan C constant houden
Dan heb ik zeg maar U = S + 10S over, dit los ik dan op met normaal differentiëren (formule n * a * x^n-1)
Hoe je ooit bedacht dat dit een goed idee was is me ook niet duidelijk, er is toch geen moment in het differentiëren dat je constanten weer terughaalt?quote:Dan valt S weg en wordt 10S 10. Nu tel ik daar de constanten bij op en kom ik op S + 10 + 10C.
Bedenk wat differentiëren zegt: het bepaalt de richting van de raaklijn. Voor een functie die constant is, is die richting natuurlijk altijd 0 (horizontaal in een grafiek), vandaar dat die constante termen verdwijnen als je differentieert.
Als je dus: SC + 10S + 10C hebt dan verdwijnt de constante term (10C als je naar S afleidt), als je het volledig zou willen uitschrijven volgens jouw formules zou je kunnen zeggen:
∂U/∂S = ∂(SC + 10S + 10C)/∂S = 1*C*S0 + 1*10*S0 + 0 = C + 10.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Oke ik denk dat ik het al begrijp ik heb alleen iets verkeerd geleerd.
Dat kwam omdat ik telkens maal functies had dus bijvoorbeeld:
U = X^4 * Y
∂U / ∂X
Berekende ik dan als volgt (ik zette Y constant en haalde ik later terug)
U = X^4 , dan gebruikte ik N*A*X^n-1 = 4 * 1 * X^4-1 = 4X^3, dan haalde ik de constante terug en had kreeg ik 4X^3 * Y wat dan de afgeleide was. Maar jij zegt dus dat dit helemaal fout is want een constante mag je niet terug halen. De Y in deze functie is dus helemaal geen constante, kun jij mij misschien vertellen wat een contante is, ik zie het nu gewoon als dat wanneer X of Y apart staan, dus niet als product van elkaar, dat dit een constante is klopt dit?
Met jou uitleg en de door mijn 'gebruikte formules' kan ik die vorige vergelijking nu oplossen ik denk dan als volgt. S*C (staat er als ware bij die eerste) Ik zie dan C als constante (wat dan waarschijnlijk fout is maar zo kan ik hem op mijn manier wel oplossen) dan doe ik weer mijn formule N*A*X^N-1 = 1*1*S^1-1 = 0 en valt weg dan houdt ik C over. 10C zie ik dan vanaf nu als een ''echte'' constante en die valt gewoon weg.
10S los ik op als N*A*X^N-1 = 1*10*S^1-1 = 10. En dan kom ik op C + 10 als afgeleide. Leer ik het zo helemaal fout of zou ik met deze manier gewoon door kunnen werken?
[ Bericht 1% gewijzigd door Matr op 27-09-2009 12:24:33 ]
Dat kwam omdat ik telkens maal functies had dus bijvoorbeeld:
U = X^4 * Y
∂U / ∂X
Berekende ik dan als volgt (ik zette Y constant en haalde ik later terug)
U = X^4 , dan gebruikte ik N*A*X^n-1 = 4 * 1 * X^4-1 = 4X^3, dan haalde ik de constante terug en had kreeg ik 4X^3 * Y wat dan de afgeleide was. Maar jij zegt dus dat dit helemaal fout is want een constante mag je niet terug halen. De Y in deze functie is dus helemaal geen constante, kun jij mij misschien vertellen wat een contante is, ik zie het nu gewoon als dat wanneer X of Y apart staan, dus niet als product van elkaar, dat dit een constante is klopt dit?
Met jou uitleg en de door mijn 'gebruikte formules' kan ik die vorige vergelijking nu oplossen ik denk dan als volgt. S*C (staat er als ware bij die eerste) Ik zie dan C als constante (wat dan waarschijnlijk fout is maar zo kan ik hem op mijn manier wel oplossen) dan doe ik weer mijn formule N*A*X^N-1 = 1*1*S^1-1 = 0 en valt weg dan houdt ik C over. 10C zie ik dan vanaf nu als een ''echte'' constante en die valt gewoon weg.
10S los ik op als N*A*X^N-1 = 1*10*S^1-1 = 10. En dan kom ik op C + 10 als afgeleide. Leer ik het zo helemaal fout of zou ik met deze manier gewoon door kunnen werken?
[ Bericht 1% gewijzigd door Matr op 27-09-2009 12:24:33 ]


Ik vind je aanpak een beetje vreemd met dat ‘constantes weghalen en terughalen’. In principe zeg ik gewoon (a·xn)' = a·(n)·xn-1, je laat die constante in feite gewoon staan.
Dus de afgeleide (naar x) van a·x2 is a·2·x = 2ax. En dat doe je hier ook. Verder denk ik dat als je x2 + a afleidt naar x, dat je dan direct 2x opschrijft en dat je die a ook niet ‘terughaalt’.
Ik hoop dat dit een beetje je vraag beantwoordt, want de methode die jij hanteert snap ik niet helemaal.
[ Bericht 0% gewijzigd door Iblis op 27-09-2009 13:29:02 ]
Dus de afgeleide (naar x) van a·x2 is a·2·x = 2ax. En dat doe je hier ook. Verder denk ik dat als je x2 + a afleidt naar x, dat je dan direct 2x opschrijft en dat je die a ook niet ‘terughaalt’.
Ik hoop dat dit een beetje je vraag beantwoordt, want de methode die jij hanteert snap ik niet helemaal.
[ Bericht 0% gewijzigd door Iblis op 27-09-2009 13:29:02 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Bedankt voor de uitleg, denk dat ik er nu wel uitkom. Mocht dat niet zo zijn dan zal ik weer in dit topic reageren 


Ik zie ’m.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Find a 3 x 3 matrix A such that
Hoe werkt dat?
| 1 2 3 4 5 6 7 8 9 10 11 | A |0| = |2| |0| |3| |0| |4| A |1| = |5| |0| |6| |0| |7| A |0| = |8| |1| |9| |
Hoe werkt dat?
Herb is the healing of a nation, alcohol is the destruction.


Pak a eens de matrix [a b c; d e f; g h i] en kijk wat ze nu eigenlijk zeggen 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


| 1 2 3 | A |4 5 6| |7 8 9| |
leek mij te makkelijk..
ik snap die shit niet
Herb is the healing of a nation, alcohol is the destruction.


| 1 2 3 | |d e f|*|0| = |g h i| |0| |
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


1 4 7
2 5 8
3 6 9
dan? die getallen moeten wel terugkomen toch? je neemt namelijk het product met 1 telkens.
2 5 8
3 6 9
dan? die getallen moeten wel terugkomen toch? je neemt namelijk het product met 1 telkens.
Herb is the healing of a nation, alcohol is the destruction.


Ben voor school bezig met varianties, maar snap niet echt hoe ik deze som moet berekenen omdat ik niet snap wat mijn Xi reeks nu wordt. Kan iemand hem misschien voordoen? Thanks!
Voor een productieorder moeten 10 producten achtereenvolgens worden bewerkt. de gemiddelde bewerkingstijd per product bedraagt 5 min. Elke bewerking is echter onzeker qua tijdsduur: er geldt een variatiecoëfficiënt van 0,8.
Gevraagd: de variatiecoëfficiënt van de totale bewerkingstijd voor een productieorder.
Voor een productieorder moeten 10 producten achtereenvolgens worden bewerkt. de gemiddelde bewerkingstijd per product bedraagt 5 min. Elke bewerking is echter onzeker qua tijdsduur: er geldt een variatiecoëfficiënt van 0,8.
Gevraagd: de variatiecoëfficiënt van de totale bewerkingstijd voor een productieorder.


variatiecoefficiént is sigma/mu.
Per stap geldt dus een sigma van 5*0,8 = 4, ofwel een sigma^2 van 16.
Omdat niet gegeven is wat de afhankelijkheid is tussen de stappen, kun je de sigma^2 van het totaal niet berekenen. Anders zou je de wortel daarvan nemen en delen door 10*5.
Per stap geldt dus een sigma van 5*0,8 = 4, ofwel een sigma^2 van 16.
Omdat niet gegeven is wat de afhankelijkheid is tussen de stappen, kun je de sigma^2 van het totaal niet berekenen. Anders zou je de wortel daarvan nemen en delen door 10*5.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Thanks voor het snelle antwoord!quote:Op zondag 27 september 2009 15:49 schreef GlowMouse het volgende:
variatiecoefficiént is sigma/mu.
Per stap geldt dus een sigma van 5*0,8 = 4, ofwel een sigma^2 van 16.
Omdat niet gegeven is wat de afhankelijkheid is tussen de stappen, kun je de sigma^2 van het totaal niet berekenen. Anders zou je de wortel daarvan nemen en delen door 10*5.
Som is dus niet op te lossen met de gegeven informatie?:S


kloptquote:Op zondag 27 september 2009 15:54 schreef habbekratz het volgende:
[..]
Thanks voor het snelle antwoord!
Som is dus niet op te lossen met de gegeven informatie?:S
Iemand een bron dat x geen betekenis heeft?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Beide betekenissen waren foutgekeurd
Met hun vage definities wil ik functie en primitieve ook wel verdedigen (constante functie en primitieve van de nulfunctie)
let niet op rood/zwart
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik begrijp de in de afbeelding gegeven definitie van cumulatief dagelijks temperatuurgemiddelde al niet. Als namelijk T(t) een temperatuur voorstelt op tijdstip t, dan kan de gegeven integraal, en daarmee Tcum(D), niet dezelfde (fysische) dimensie hebben als T(t) en daarmee ook geen temperatuur voorstellen.quote:Op zondag 27 september 2009 17:17 schreef GlowMouse het volgende:
[ afbeelding ]
Beide betekenissen waren foutgekeurd
Met hun vage definities wil ik functie en primitieve ook wel verdedigen (constante functie en primitieve van de nulfunctie)
let niet op rood/zwart


Ik zou de integraal ook door D delen met deze definitie, maar ze werken hiemree omdat het verder in de opgave gebruikt wordt als een maat voor wanneer een plant gaat bloeien.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Puur mathematisch is x inderdaad een dummyvariabele, maar je zou er natuurlijk een fysische interpretatie aan kunnen geven. Wikipedia vermeldt (zonder bron overigens):quote:Op zondag 27 september 2009 17:06 schreef GlowMouse het volgende:
[..]
klopt
[ afbeelding ]
Iemand een bron dat x geen betekenis heeft?
quote:The variable of integration dx has different interpretations depending on the theory being used. For example, it can be seen as strictly a notation indicating that x is a dummy variable of integration, as a reflection of the weights in the Riemann sum, a measure (in Lebesgue integration and its extensions), an infinitesimal (in non-standard analysis) or as an independent mathematical quantity: a differential form. More complicated cases may vary the notation slightly.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Misschien een hele domme vraag, maar ik kom niet uit de volgende opdracht:
Tim rijdt op de fiets in a minuten van Amsterdam naar Leiden. Yeliz rijdt in haar auto langs
dezelfde weg in b minuten van Leiden naar Amsterdam [b < a]. Tim en Yeliz vertrekken op
hetzelfde moment.
(a) Na hoeveel minuten komen Tim en Yeliz elkaar tegen?

Iemand enig idee hoe dit aan te pakken is ?!
Alvast bedankt
Tim rijdt op de fiets in a minuten van Amsterdam naar Leiden. Yeliz rijdt in haar auto langs
dezelfde weg in b minuten van Leiden naar Amsterdam [b < a]. Tim en Yeliz vertrekken op
hetzelfde moment.
(a) Na hoeveel minuten komen Tim en Yeliz elkaar tegen?
Iemand enig idee hoe dit aan te pakken is ?!
Alvast bedankt


Je weet de afstand van de route toch niet ?! Deze heb je toch nodig, anders heb je toch niet genoeg informatie ?! Of zie ik nou echt iets over het hoofd 


De afstand is 1 quirk, waarbij de quirk een oude afstandsmaat is, gebaseerd op de afstand tussen Leiden en Amsterdam. Snelheden meten we in quirks per minuut.


Stel x=aantal km van A'dam naar Leiden.quote:Op maandag 28 september 2009 18:55 schreef thabit het volgende:
De afstand is 1 quirk, waarbij de quirk een oude afstandsmaat is, gebaseerd op de afstand tussen Leiden en Amsterdam. Snelheden meten we in quirks per minuut.
Dan is volgens mij A=X*(A/X) en B=X*(B/X), maar goed hoe ik dit dan weer in de vergelijking moet gieten die opgelost moet worden is dan nog de vraag .. Ik voel me nu echt zo dom


Op het moment dat ze elkaar tegenkomen hebben ze bijelkaar afstand 1 afgelegd. Tim gaat met een snelheid van 1/a en die griet met een snelheid van 1/b. Bij elkaar opgeteld hebben ze een snelheid van 1/a + 1/b. Nu jij weer.


Voor a en b kun je nu de formules invullen, dus dan krijg je 1/(x*(a/x))+1/(x*(b/x)). Dit is dus de snelheid die ze hebben. Wordt de formule dan niet 1-1/(x*(a/x))=1/(x*(b/x)) ?!quote:Op maandag 28 september 2009 19:19 schreef thabit het volgende:
Op het moment dat ze elkaar tegenkomen hebben ze bijelkaar afstand 1 afgelegd. Tim gaat met een snelheid van 1/a en die griet met een snelheid van 1/b. Bij elkaar opgeteld hebben ze een snelheid van 1/a + 1/b. Nu jij weer.


Wel, als ze bij elkaar een afstand van 1 afleggen en met een totale snelheid van 1/a + 1/b, dan is de tijd die ze daarover gedaan hebben gelijk aan 1 / (1/a + 1/b) = ab/(a+b).


Als je in een matrix (4 x 5 matrix) een 0-rij krijgt met rijvegen, kan 'ie dan nog geschreven worden in echelonvorm?
(Ik dacht dat een echelon elke kolom de pivot-positie een rij verder zit (mag je dat zo noemen?), maar mag de onderste rij dan ook 0 zijn?)
(Ik dacht dat een echelon elke kolom de pivot-positie een rij verder zit (mag je dat zo noemen?), maar mag de onderste rij dan ook 0 zijn?)


Ja dat kan, ja dat mag.
quote:Een matrix is in rij-echelonvorm, standaard-rijvorm of rij-trapvorm als elke volgende rij met meer nullen begint dan de voorgaande, tenzij deze [de voorgaande dus] een nulrij is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ja, bijvoorbeeld als je de 4x5 matrix waar je mee begon uit alleen maar enen bestond.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


klopt, elke matrix is equivalent met een matrix in echelonvorm, en met een unieke matrix in gereduceerde echelonvorm
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Aight. Gereduceerd is vast iets dat er op de pivotposities een 1 staat ofzo? Dan begrijp ik dit stuk in ieder geval geloof ik 


Het lukt me nog niet helemaal om de kleine stelling van Fermat te bewijzen met inductie.
Ik heb t tot zover: Met "=" bedoel ik in dit geval "komt overeen met".
ap=a (mod p) is te bewijzen.
1. Bewering waar als p=2. a2-1=a.
2.
Nu de inductieveronderstelling. Stel het is waar voor ak=a (mod k), met k priem.
Dan moet ik bewijzen dat het ook geldt voor 1 priemgetal verder?
.. maar dit krijg ik niet goed geschreven.
Ik leerde eerder dat met voll. inductie het volgende moet worden bewezen: a k+1 = a (mod k). Maar dit lijkt me in dit geval (los van t feit dat t niet uitkomt) niet juist omdat de exponent bij a priem moet zijn.
Ik heb t tot zover: Met "=" bedoel ik in dit geval "komt overeen met".
ap=a (mod p) is te bewijzen.
1. Bewering waar als p=2. a2-1=a.
2.
Nu de inductieveronderstelling. Stel het is waar voor ak=a (mod k), met k priem.
Dan moet ik bewijzen dat het ook geldt voor 1 priemgetal verder?
.. maar dit krijg ik niet goed geschreven.
Ik leerde eerder dat met voll. inductie het volgende moet worden bewezen: a k+1 = a (mod k). Maar dit lijkt me in dit geval (los van t feit dat t niet uitkomt) niet juist omdat de exponent bij a priem moet zijn.
kloep kloep


Hoe gaat dat dan?quote:Op woensdag 30 september 2009 14:26 schreef thabit het volgende:
Ik zou inductie naar a gebruiken, niet naar p.
Bedoel je: veronderstel ak = a (mod k)
en herschrijven tot (a+1)k = a+1 (mod k)
Dus meer een handige truc: inductie naar p is lastig omdat p+1 niet priem hoeft te zijn, dat je daarom inductie naar t grondtal a gaat nemen...
[ Bericht 14% gewijzigd door Borizzz op 30-09-2009 14:38:27 ]
kloep kloep


Nog een vraag:
Inkomensvraagfunctie, Q1 als functie van I
P1Q1 = 2P2Q2
P2Q2 = 0,5P1Q1
I = P1Q1 + P2Q2
I = P1Q1 + 0,5P1Q1
I = 1,5P1Q1
Q = I / 1,5 PI
Q1 = 2/3 / I
Ik snap niet hoe ze van de een na laatste regel tot de laatste komen. Welke rekenregel mis ik?
Inkomensvraagfunctie, Q1 als functie van I
P1Q1 = 2P2Q2
P2Q2 = 0,5P1Q1
I = P1Q1 + P2Q2
I = P1Q1 + 0,5P1Q1
I = 1,5P1Q1
Q = I / 1,5 PI
Q1 = 2/3 / I
Ik snap niet hoe ze van de een na laatste regel tot de laatste komen. Welke rekenregel mis ik?


1/1,5 = 2/3quote:Op donderdag 1 oktober 2009 16:31 schreef Matr het volgende:
Nog een vraag:
Inkomensvraagfunctie, Q1 als functie van I
P1Q1 = 2P2Q2
P2Q2 = 0,5P1Q1
I = P1Q1 + P2Q2
I = P1Q1 + 0,5P1Q1
I = 1,5P1Q1
Q = I / 1,5 PI
Q1 = 2/3 / I
Ik snap niet hoe ze van de een na laatste regel tot de laatste komen. Welke rekenregel mis ik?
Doe verder eens wat aan je notatie. Gebruik subscript voor indices bijvoorbeeld. Zo is het nauwelijks te lezen.
Lagere school gemist soms?


Ik moet van de volgende functies het richtingscoefficient berekenen, maar heb geen idee meer hoe dat ook alweer moest.
x=2y
-3x=-y+3
Hoop dat iemand me wil helpen.
x=2y
-3x=-y+3
Hoop dat iemand me wil helpen.


Weet je nog hoe je een afgeleide moet berekenen en wat de betekenis van een afgeleide (in een bepaald punt) is?quote:Op vrijdag 2 oktober 2009 11:11 schreef Jahr00n het volgende:
Ik moet van de volgende functies het richtingscoefficient berekenen, maar heb geen idee meer hoe dat ook alweer moest.
x=2y
-3x=-y+3
Hoop dat iemand me wil helpen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Niet echt eigenlijk, m'n wiskunde is compleet weggezakt.quote:Op vrijdag 2 oktober 2009 11:13 schreef Iblis het volgende:
[..]
Weet je nog hoe je een afgeleide moet berekenen en wat de betekenis van een afgeleide (in een bepaald punt) is?


Dan is dat hetgeen wat je moet opzoeken. Dat is me even wat te veel werk om nu allemaal uit te leggen. Kijk in je boek zou ik zeggen.quote:Op vrijdag 2 oktober 2009 11:15 schreef Jahr00n het volgende:
[..]
Niet echt eigenlijk, m'n wiskunde is compleet weggezakt.
Of als je dat niet hebt: kijk b.v. eens in de WisFAQ, ook bij de Applets en misschien bij de definitie of bij de uitgebreide uitleg op Wetenschapsforum en misschien op Wikipedia, alhoewel dat misschien al te technisch is.
Het is een heel fundamenteel begrip, dus je doet er echt goed aan om het op te halen, ook al kost het wat leeswerk.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Dat heb je toch allemaal niet nodig om de rico van een rechte te bepalen, afgeleiden en zo.
Gewoon omvormen naar y = ....
en dan neem je de coëfficiënt van x
dus als y = ax+b dan is a de rico a
in het eerste voorbeeld wordt dat y= 1/2 x dus rico = 1/2
Dat leren ze bij ons al in het derde (België), terwijl afgeleiden pas voor het vijfde zijn.
Gewoon omvormen naar y = ....
en dan neem je de coëfficiënt van x
dus als y = ax+b dan is a de rico a
in het eerste voorbeeld wordt dat y= 1/2 x dus rico = 1/2
Dat leren ze bij ons al in het derde (België), terwijl afgeleiden pas voor het vijfde zijn.


Daar heb je gelijk in. In mijn hoofd zijn afgeleide en richtingscoëfficiënt aardig hard gekoppeld.quote:Op vrijdag 2 oktober 2009 11:53 schreef Beregd het volgende:
Dat heb je toch allemaal niet nodig om de rico van een rechte te bepalen, afgeleiden en zo.
Gewoon omvormen naar y = ....
en dan neem je de coëfficiënt van x
dus als y = ax+b dan is a de rico a
in het eerste voorbeeld wordt dat y= 1/2 x dus rico = 1/2
Dat leren ze bij ons al in het derde (België), terwijl afgeleiden pas voor het vijfde zijn.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Nu wordt het wat duidelijker, maar hoe kom je dan aan die 1?quote:Op vrijdag 2 oktober 2009 11:53 schreef Beregd het volgende:
Dat heb je toch allemaal niet nodig om de rico van een rechte te bepalen, afgeleiden en zo.
Gewoon omvormen naar y = ....
en dan neem je de coëfficiënt van x
dus als y = ax+b dan is a de rico a
in het eerste voorbeeld wordt dat y= 1/2 x dus rico = 1/2
Dat leren ze bij ons al in het derde (België), terwijl afgeleiden pas voor het vijfde zijn.


Wat dacht je van zelf omschrijven naar y=...?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hallo, ik ben bezig met een hoofdstuk over de afgeleide functie en je kan volgens mijn boek met de grafische rekenmachine een raaklijn krijgen in graph en in table kun je ook de helling krijgen. alleen ik krijg beide niet voor elkaar op mijn grm. ik heb een casio CFX-9850GB PLUS, ik geloof dat het in graph iets te maken heeft met de d/dx toets, en die krijg ik nog wel tevoorschijn, maar wat er dan achter te zetten? en iets van derivetive spookt door mijn hoofd. als iemand me kan helpen hiermee, heel erg bedankt 


Hallo!  Ik heb voor het vak 'logica en taalanalyse 1' de voorbeeldtussentoets gemaakt die op BlackBoard stond. Het gaat over filosofische logica (vertalen), propositielogica, semantische tableaux en waarheidstafels. Zou iemand deze voor mij na kunnen kijken en feedback kunnen leveren? Bedankt!
Ik heb voor het vak 'logica en taalanalyse 1' de voorbeeldtussentoets gemaakt die op BlackBoard stond. Het gaat over filosofische logica (vertalen), propositielogica, semantische tableaux en waarheidstafels. Zou iemand deze voor mij na kunnen kijken en feedback kunnen leveren? Bedankt!
De voorbeeldtussentoets
Mijn antwoorden
De voorbeeldtussentoets
Mijn antwoorden


Bij vraag 1c is me niet helemaal duidelijk wat je doet. Je hebt daar P ← (Q ∨ R) en (Q ∨ R) → P staan. Het gebruik van ← is niet helemaal standaard. Als je dat hebt geleerd als ‘alleen als’, dan lijkt het me goed, anders niet per se. (Q ∨ R) → P laat echter de mogelijkheid open dat hij niet slaagt, noch in juni, noch in augustus, maar toch hard heeft gewerkt. Ik zou zeggen dat men eerder op zoek is naar een equivalentie: P ↔ (Q ∨ R). (Of iets uitgebreider (P → (Q ∨ R)) ∧ (¬P → ¬(Q ∨ R)), maar die zijn aan elkaar gelijk. Overigens worden namen van maanden in het Nederlands niet met hoofdletters geschreven, maar dat doet de vraagsteller ook fout.quote:Op zaterdag 3 oktober 2009 02:10 schreef Friek_ het volgende:
Hallo!Ik heb voor het vak 'logica en taalanalyse 1' de voorbeeldtussentoets gemaakt die op BlackBoard stond. Het gaat over filosofische logica (vertalen), propositielogica, semantische tableaux en waarheidstafels. Zou iemand deze voor mij na kunnen kijken en feedback kunnen leveren? Bedankt!
En 1d mist? Of ligt dat aan mijn Open Office?
Bij 2 heb je niet expliciet antwoord gegeven op c) en d)? Dat valt af te leiden natuurlijk doordat a & d en b & c elkaar uitsluiten.
Die tableaus moet ik straks even naar kijken.
Wat 6 betreft: deze is heel flauw. De bedoeling is dat je gewoon een beetje knoeit, totdat je een formule met ∨ en ∧ en → hebt die klopt. Je ziet dat er heel veel F is, dus je zou b.v. kunnen beginnen met (φ ∧ ψ ∧ χ), maar dan voldoe je niet aan rij 6. Dus voeg je nog toe: (φ ∧ ψ ∧ χ) ∨ (¬φ ∧ ψ ∧ ¬χ).
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Vraag 3 is overigens ook juist, nu die tableaus:
Bij tableau kun je iets slimmer zijn denk ik. Je splitst Q ∨ R op en dan heb je de R-tak, waarbij je nog ¬P ∨ ¬Q en ¬P ∨ ¬R hebt, waarom kies je er niet voor als eerste ¬P ∨ ¬R te splitsen? De volgorde maakt niet uit immers, en als je dat doet sluit die tak eerder.
Dit geldt ook voor tableau 5.
Verder zijn ze juist.
Wat 6 betreft, volgens mij kun je daar ook nog (φ ↔ χ) ∧ ψ van maken. (Als je die uitschrijft blijkt dat het hetzelfde is).
Bij tableau kun je iets slimmer zijn denk ik. Je splitst Q ∨ R op en dan heb je de R-tak, waarbij je nog ¬P ∨ ¬Q en ¬P ∨ ¬R hebt, waarom kies je er niet voor als eerste ¬P ∨ ¬R te splitsen? De volgorde maakt niet uit immers, en als je dat doet sluit die tak eerder.
Dit geldt ook voor tableau 5.
Verder zijn ze juist.
Wat 6 betreft, volgens mij kun je daar ook nog (φ ↔ χ) ∧ ψ van maken. (Als je die uitschrijft blijkt dat het hetzelfde is).
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Wanneer er in de natuurlijke taal 'alleen als' voorkomt heb ik van de docent geleerd dat ik het connectief → diende om te draaien. Alleen als φ, ψ drukt juist uit ψ → φ. Ik heb even de collegesheet opgezocht waarin dit werd uitgelegd:quote:Op zaterdag 3 oktober 2009 09:19 schreef Iblis het volgende:
[..]
Bij vraag 1c is me niet helemaal duidelijk wat je doet. Je hebt daar P ← (Q ∨ R) en (Q ∨ R) → P staan. Het gebruik van ← is niet helemaal standaard. Als je dat hebt geleerd als ‘alleen als’, dan lijkt het me goed, anders niet per se. (Q ∨ R) → P laat echter de mogelijkheid open dat hij niet slaagt, noch in juni, noch in augustus, maar toch hard heeft gewerkt. Ik zou zeggen dat men eerder op zoek is naar een equivalentie: P ↔ (Q ∨ R). (Of iets uitgebreider (P → (Q ∨ R)) ∧ (¬P → ¬(Q ∨ R)), maar die zijn aan elkaar gelijk. Overigens worden namen van maanden in het Nederlands niet met hoofdletters geschreven, maar dat doet de vraagsteller ook fout.
Je zou inderdaad zeggen dat 'alleen als' een soort 'dan en slechts dan'-connectief (de equivalentie) uitdrukt; deze opmerking had ik ook geplaatst toen hij over de materiële implicatie sprak. Helaas ben ik alweer vergeten wat hij voor reactie gaf.
quote:En 1d mist? Of ligt dat aan mijn Open Office?
Maar daar hoort volgens mij (P & ¬Q) → R te staan.
P: Jan werkt hard
Q: Jan slaagt in Juni voor Logica
R: Jan slaagt in Augustus voor Logica
Even weer een collegesheet erbij:quote:Bij 2 heb je niet expliciet antwoord gegeven op c) en d)? Dat valt af te leiden natuurlijk doordat a & d en b & c elkaar uitsluiten.
Uit deze collegesheet had ik drie mogelijkheden afgeleid:
Tautologie + consistent (alleen maar W's of 1'en)
Inconsistent/contradictie (alleen maar F's of 0'en)
Contingent + consistent (zowel W's als F's of 0'en als 1'en)
Zodoende had ik dus beredeneerd dat hij zowel contingent als consistent moest zijn (er is immers één mogelijkheid waarin hij helemaal waar is).
Hier moet ik nog eens over gaan zitten volgens mij. De basale concepten van de propositielogica snap ik nu wel, maar de eigenschappen vind ik persoonlijk iets lastiger. Iets zegt me dat je die hiervoor moet kennen.quote:Wat 6 betreft: deze is heel flauw. De bedoeling is dat je gewoon een beetje knoeit, totdat je een formule met ∨ en ∧ en → hebt die klopt. Je ziet dat er heel veel F is, dus je zou b.v. kunnen beginnen met (φ ∧ ψ ∧ χ), maar dan voldoe je niet aan rij 6. Dus voeg je nog toe: (φ ∧ ψ ∧ χ) ∨ (¬φ ∧ ψ ∧ ¬χ).
[ Bericht 0% gewijzigd door #ANONIEM op 03-10-2009 13:52:04 ]


Hmm, klopt helemaal. Zal volgende keer wat efficiënter te werk gaan wanneer ik zoiets uitschrijf.quote:Op zaterdag 3 oktober 2009 10:03 schreef Iblis het volgende:
Bij tableau kun je iets slimmer zijn denk ik. Je splitst Q ∨ R op en dan heb je de R-tak, waarbij je nog ¬P ∨ ¬Q en ¬P ∨ ¬R hebt, waarom kies je er niet voor als eerste ¬P ∨ ¬R te splitsen? De volgorde maakt niet uit immers, en als je dat doet sluit die tak eerder.


Ik zie nu trouwens pas dat opgave 4 en 5 echt vrijwel identiek zijn, maar dat de ene net een redenering is door dat 'conclusie'-teken. 
Overigens bedoelde ik bij opgave 3 de vierde, zesde en de achtste regel! Weer een foutje.
[ Bericht 30% gewijzigd door #ANONIEM op 03-10-2009 14:03:58 ]
Overigens bedoelde ik bij opgave 3 de vierde, zesde en de achtste regel! Weer een foutje.
[ Bericht 30% gewijzigd door #ANONIEM op 03-10-2009 14:03:58 ]


Ja, ik vind die ook niet heel sterk, maar vooruit, gewoon met je docent meegaan.quote:Op zaterdag 3 oktober 2009 13:50 schreef Friek_ het volgende:
Je zou inderdaad zeggen dat 'alleen als' een soort 'dan en slechts dan'-connectief (de equivalentie) uitdrukt; deze opmerking had ik ook geplaatst toen hij over de materiële implicatie sprak. Helaas ben ik alweer vergeten wat hij voor reactie gaf.
Lijkt me correct.quote:Maar daar hoort volgens mij (P & ¬Q) → R te staan.
P: Jan werkt hard
Q: Jan slaagt in Juni voor Logica
R: Jan slaagt in Augustus voor Logica
Snap ik, maar ik zou dan (in het geval van een echte toets) expliciet zeggen dat die andere twee niet opgaan.quote:Even weer een collegesheet erbij:
[ afbeelding ]
Uit deze collegesheet had ik drie mogelijkheden afgeleid:
Tautologie + consistent (alleen maar W's of 1'en)
Inconsistent/contradictie (alleen maar F's of 0'en)
Contingent + consistent (zowel W's als F's of 0'en als 1'en)
Zodoende had ik dus beredeneerd dat hij zowel contingent als consistent moest zijn (er is immers één mogelijkheid waarin hij helemaal waar is).
Je kunt dit op twee manieren aanpaken, ik kopieer even die tafel (ik gebruik die regelnummers niet hieronder, dus met Geval 1 bedoel ik het geval op regel 2):quote:Hier moet ik nog eens over gaan zitten volgens mij. De basale concepten van de propositielogica snap ik nu wel, maar de eigenschappen vind ik persoonlijk iets lastiger. Iets zegt me dat je die hiervoor moet kennen.
| 1 2 3 4 5 6 7 8 9 | T T T | T T T F | F T F T | F T F F | F F T T | F F T F | T F F T | F F F F | F |
Je kunt dit heel mechanisch (d.w.z. zonder inzicht) doen in feite, dat is een truc die met elke waarheidstafel werkt.
Je ziet dat deze in geval 1 en 6 waar is. Dus dan zeg je, de formule is:
(Geval 1) ∨ (Geval 6)
Nu kijken we even wat Geval 1 inhoudt, dat is: (φ ∧ ψ ∧ χ) – alledrie waar. En wat Geval 6 inhoudt, dat is: (¬φ ∧ ψ ∧ ¬χ), dus φ en χ niet waar en ψ wel, dat staat er immers letterlijk. Als je dat in z’n geheel neemt krijg je:
(φ ∧ ψ ∧ χ) ∨ (¬φ ∧ ψ ∧ ¬χ)
Stel dat je b.v. deze tafel krijgt:
| 1 2 3 4 5 6 7 8 9 | T T T | T T T F | F T F T | F T F F | T F T T | F F T F | T F F T | F F F F | T |
Dan kun je zeggen, die is waar als:
(Geval 1) ∨ (Geval 4) ∨ (Geval 6) ∨ (Geval 8)
Nu, vul maar in:
| 1 2 | (φ ∧ ψ ∧ χ) ∨ (φ ∧ ¬ψ ∧ ¬χ) ∨ (¬φ ∧ ψ ∧ ¬χ) ∨ (¬φ ∧ ¬ψ ∧ ¬χ) |
Daar komt helemaal geen inzicht bij kijken. In de oorspronkelijke vraag, het eerste geval, is er dus ook een iets kortere oplossing mogelijk, namelijk: (φ ↔ χ) ∧ ψ
Die moet je wel even ‘zien’. Als je naar de tabel kijkt zie je dat die in twee gevallen waar is (te weten 1 & 6), en in beide gevallen geldt dat φ en χ aan elkaar gelijk zijn dus: (φ ↔ χ). Dit geldt in nog twee gevallen, namelijk 4 & 8, maar het verschil tussen 4 & 8 en 1 & 6 is dat ψ in het geval van 1 & 6 wél waar is, dus je formule wordt: (φ ↔ χ) ∧ ψ.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Iblis, ontzettend bedankt tot zover. Ik heb nu even geen tijd om uitgebreid te reageren, dus ik zal morgen weer even er voor gaan zitten. 
[ Bericht 4% gewijzigd door #ANONIEM op 04-10-2009 01:09:02 ]
[ Bericht 4% gewijzigd door #ANONIEM op 04-10-2009 01:09:02 ]


En ga ook voor dat andere topic zitten, je hebt er zelfs geen tvp meer 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik zit nu in VWO5 en heb een hoofdstuk met hellingen. Dus ik moet een grafiek bij een grafiek maken met daar de hellingen in.
Dan moet ik op mn rekenmachine ook de Y1 en Y2 invoeren, maar zoals in het boek staat lijkt het niet gewoon de losse letter Y met een 1 erachter maar echt een Y en dan zo'n klein 1tje ernaast.
Ik heb een TI-83
Dan moet ik op mn rekenmachine ook de Y1 en Y2 invoeren, maar zoals in het boek staat lijkt het niet gewoon de losse letter Y met een 1 erachter maar echt een Y en dan zo'n klein 1tje ernaast.
Ik heb een TI-83


Druk op de linker blauwe knop onder het scherm.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


edit
of toch niet.
of toch niet.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


2nd bedoel je?quote:Op zondag 4 oktober 2009 16:10 schreef GlowMouse het volgende:
Druk op de linker blauwe knop onder het scherm.


Ja, dan krijg ik de Y1=
Y2=
etc.
te zien waar je de formule in kunt vullen. Maar ik moet dus ook daar een y1 in kunnen vullen.
Y2=
etc.
te zien waar je de formule in kunt vullen. Maar ik moet dus ook daar een y1 in kunnen vullen.


Oh, dan moet je wel onder vars kijken  sorry JD
sorry JD 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zondag 4 oktober 2009 16:24 schreef GlowMouse het volgende:
Oh, dan moet je wel onder vars kijkensorry JD
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Oh weer een probleempje. Nu kan ik in de tabel alleen de functie die ik bij Y1 óf die van Y2 zien, maar ik moet ze allebei tegelijk zien.


Laat Mnxn de vectorruimte van n x n matrices zijn.
a) laat zien dat de symetrische n x n matrices een lineaire deelruimte van M n x n vormen.
1. Matrix met alleen maar nullen is altijd symetrisch.
2. Als je twee symetrische matrices bij elkaar optelt kom je op een symetrische matrix. Maar ik heb geen idee hoe ik dit goed kan laten zien. Is het genoeg als ik het met een 3 x 3 matrix zou laten zien?
3. "Als elk element in de matrix wordt vermenigvuldigd met dezelfde a, blijft de matrix symetrisch" <- zou dat genoeg antwoord zijn, of is dat slechts herhaling van de stelling / vraag?
a) laat zien dat de symetrische n x n matrices een lineaire deelruimte van M n x n vormen.
1. Matrix met alleen maar nullen is altijd symetrisch.
2. Als je twee symetrische matrices bij elkaar optelt kom je op een symetrische matrix. Maar ik heb geen idee hoe ik dit goed kan laten zien. Is het genoeg als ik het met een 3 x 3 matrix zou laten zien?
3. "Als elk element in de matrix wordt vermenigvuldigd met dezelfde a, blijft de matrix symetrisch" <- zou dat genoeg antwoord zijn, of is dat slechts herhaling van de stelling / vraag?


Ja, het 0-element zit er in dus.quote:Op zondag 4 oktober 2009 18:55 schreef Hanneke12345 het volgende:
Laat Mnxn de vectorruimte van n x n matrices zijn.
a) laat zien dat de symetrische n x n matrices een lineaire deelruimte van M n x n vormen.
1. Matrix met alleen maar nullen is altijd symetrisch.
Nee, dat geeft wel het idee natuurij, maar dat is niet genoeg. Je kunt echter makkelijk aantonen dat als je een aij hebt uit een symmetrische Matrix en net zo’n bij, dat dan ook aij + bij = aji + bji.quote:2. Als je twee symetrische matrices bij elkaar optelt kom je op een symetrische matrix. Maar ik heb geen idee hoe ik dit goed kan laten zien. Is het genoeg als ik het met een 3 x 3 matrix zou laten zien?
Iets formeler: aij = aji in een Matrix dan ook α·aij = α·aji. (α ∈ ℝ waarschijnlijk).quote:3. "Als elk element in de matrix wordt vermenigvuldigd met dezelfde a, blijft de matrix symetrisch" <- zou dat genoeg antwoord zijn, of is dat slechts herhaling van de stelling / vraag?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Aight.
Begrippen basis, kern (nullspace) en bereik (columnspace) snap ik nog niet echt;
"b) destileer hieruit een basis voor de kern van A.
Merk op: Ax = 0 dan en slechts dan als Ex = 0 (E is de echelonvorm van A). Dus, als een kolom van E lineair van zekere andere kolommen van E afhangt geldt hetzelfde voor de overeenkomstige kolommen van A.
c)Geef een selectie van kolommen van E die een basis vormt voor het bereik van E
d)Geef een selectie van kolommen van A die een basis vormt voor het bereik van A"
Dat stuk over Ax=0 dus Ex=0 heeft toch meer betrekking op vraag b dan op c en d, want voor de kern geldt Ax=0?
Er staat ook Kern = {x∈ℝn | T(x) = 0}, deze definitie heeft toch alleen betekenis als je een formule hebt, en niet als je een matrix hebt?
Begrippen basis, kern (nullspace) en bereik (columnspace) snap ik nog niet echt;
"b) destileer hieruit een basis voor de kern van A.
Merk op: Ax = 0 dan en slechts dan als Ex = 0 (E is de echelonvorm van A). Dus, als een kolom van E lineair van zekere andere kolommen van E afhangt geldt hetzelfde voor de overeenkomstige kolommen van A.
c)Geef een selectie van kolommen van E die een basis vormt voor het bereik van E
d)Geef een selectie van kolommen van A die een basis vormt voor het bereik van A"
Dat stuk over Ax=0 dus Ex=0 heeft toch meer betrekking op vraag b dan op c en d, want voor de kern geldt Ax=0?
Er staat ook Kern = {x∈ℝn | T(x) = 0}, deze definitie heeft toch alleen betekenis als je een formule hebt, en niet als je een matrix hebt?


Je formule is nu T(x) = Ax.
De opmerking is relevant voor a, maar ook voor d.
De opmerking is relevant voor a, maar ook voor d.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Is een lineaire deelruimte iets anders dan gewoon een deelruimte?
Laat I = [-2,2]. Schrijf P3(I) voor de vectorruimte van polynomen van graad ten hoogste drie op I, dus:
P3(I)={p:I--> R: x ->a+bx+cx2+dx3 | a,b,c,d ∈ℝ}
Definieer
V = {p∈P3(I)|p(0)=0}
a)Bewijs dat V een lineaire deelruimte is van P3(I)
0)p(x)=0+0x+02+0x3=0 dus p(0)=0
1)p(x)∈V, p(0)=0 en q(x)∈V q(0)=0
stel r(x) = p(x)+q(x)
Dan r(0)=p(0)+q(0)=0+0=0
dus r(x)∈V
2)p(x)∈V, p(0)=0
Stel r(x) = a*p(x)
Dan r(0) = a*p(0) = a*0 = 0
dus r(x)∈V
Definieer nu ook W = {p∈P3(I) | p(1) =0}
Is W een lineaire deelruimte van P3(I)?
Dan zou je toch de hele redenatie die ik bij a heb hier kunnen herhalen, of zie ik iets over het hoofd?
Laat I = [-2,2]. Schrijf P3(I) voor de vectorruimte van polynomen van graad ten hoogste drie op I, dus:
P3(I)={p:I--> R: x ->a+bx+cx2+dx3 | a,b,c,d ∈ℝ}
Definieer
V = {p∈P3(I)|p(0)=0}
a)Bewijs dat V een lineaire deelruimte is van P3(I)
0)p(x)=0+0x+02+0x3=0 dus p(0)=0
1)p(x)∈V, p(0)=0 en q(x)∈V q(0)=0
stel r(x) = p(x)+q(x)
Dan r(0)=p(0)+q(0)=0+0=0
dus r(x)∈V
2)p(x)∈V, p(0)=0
Stel r(x) = a*p(x)
Dan r(0) = a*p(0) = a*0 = 0
dus r(x)∈V
Definieer nu ook W = {p∈P3(I) | p(1) =0}
Is W een lineaire deelruimte van P3(I)?
Dan zou je toch de hele redenatie die ik bij a heb hier kunnen herhalen, of zie ik iets over het hoofd?


>> Is een lineaire deelruimte iets anders dan gewoon een deelruimte?
voor zover ik weet niet
>> Dan zou je toch de hele redenatie die ik bij a heb hier kunnen herhalen, of zie ik iets over het hoofd?
je ziet niks over het hoofd
voor zover ik weet niet
>> Dan zou je toch de hele redenatie die ik bij a heb hier kunnen herhalen, of zie ik iets over het hoofd?
je ziet niks over het hoofd
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dit was mijn vraag
Daarnaast heb ik een negatieve t-score gekregen van -2,81. Het getal dat uit de tabel komt zou nu 1.96 zijn. Is mijn t-score nu kleiner dan 1.96, of moet je deze positief maken?
En de laatste vraag, ik heb een tweezijdige toets, moet ik de df dan bereken met n - 1 of n - 2?
[ Bericht 6% gewijzigd door Siniti op 04-10-2009 21:22:18 ]
Dit was het antwoord:quote:Op zondag 4 oktober 2009 21:06 schreef Siniti het volgende:
Ik moet de df weten om achterin dat spss-boek in die tabel te kunnen zoeken, maar hoe bereken je dit ding? Overal staat N-1 maar dan zou mijn df in de honderden lopen
Betekent dit dus dat de df score in de tabel te vinden is bij het oneindig tekentje?quote:Op zondag 4 oktober 2009 21:08 schreef GlowMouse het volgende:
degrees of freedom van je error (DFE) kan in de honderden lopen, dat is geen probleem.
Daarnaast heb ik een negatieve t-score gekregen van -2,81. Het getal dat uit de tabel komt zou nu 1.96 zijn. Is mijn t-score nu kleiner dan 1.96, of moet je deze positief maken?
En de laatste vraag, ik heb een tweezijdige toets, moet ik de df dan bereken met n - 1 of n - 2?
[ Bericht 6% gewijzigd door Siniti op 04-10-2009 21:22:18 ]


Mn x n zijn alle symetrische n x n matrices. Nu moet ik een basis voor deze ruimte vinden (/geven)
Dus {v1,v2...,vn zodanig dat.
1) v1, v2,...,vn ∈ℝn (toch? Ik ben in de war doordat ik niet gewoon een Rn heb waar ik de basis voor moet zoeken. Maar ik neem aan dat ik Mn x n moet zien als meerdere vectoren uit de ℝn?)
2) v1, v2,...vn zijn lineair onafhankelijk. (dus te schrijven als identiteitsmatrix, dacht ik? Een identiteitsmatrix is symetrisch, maar ik denk niet dat elke symetrische matrix te schrijven is als I, ik weet vooral inet hoe ik dit zou moeten noteren.)
3)span Mn x n = {v1, v2...vn (deze weet ik niet goed hoe ik dit kan vinden en wat span precies inhoudt.)
Dus {v1,v2...,vn zodanig dat.
1) v1, v2,...,vn ∈ℝn (toch? Ik ben in de war doordat ik niet gewoon een Rn heb waar ik de basis voor moet zoeken. Maar ik neem aan dat ik Mn x n moet zien als meerdere vectoren uit de ℝn?)
2) v1, v2,...vn zijn lineair onafhankelijk. (dus te schrijven als identiteitsmatrix, dacht ik? Een identiteitsmatrix is symetrisch, maar ik denk niet dat elke symetrische matrix te schrijven is als I, ik weet vooral inet hoe ik dit zou moeten noteren.)
3)span Mn x n = {v1, v2...vn (deze weet ik niet goed hoe ik dit kan vinden en wat span precies inhoudt.)


De ruimte van alle nxn matrices heeft dimensie n2 over R. De ruimte van symmetrische matrices is daar een deelruimte van.


Hmm, ik kom daar geloof ik niet echt verder mee. dat van die deelruimte was ik ook al achter. Ik kijk sowieso morgen even verder naar die som.
Ik weet ook niet echt wat ik me bij deze formule moet voorstellen;
Die laatste met L1 dus. De rest kwam ik nog wel uit. Maar wat ze bedoelen met f->f(0) en f(1) etc. ontgaat me.
Ik weet ook niet echt wat ik me bij deze formule moet voorstellen;
Die laatste met L1 dus. De rest kwam ik nog wel uit. Maar wat ze bedoelen met f->f(0) en f(1) etc. ontgaat me.


denk hetquote:Op zondag 4 oktober 2009 21:11 schreef Siniti het volgende:
Dit was mijn vraag
[..]
Betekent dit dus dat de df score in de tabel te vinden is bij het oneindig tekentje?
positief maken als je een tweezijdige toets hebt (maar daar had je de 1.96 al voor gepakt)quote:Daarnaast heb ik een negatieve t-score gekregen van -2,81. Het getal dat uit de tabel komt zou nu 1.96 zijn. Is mijn t-score nu kleiner dan 1.96, of moet je deze positief maken?
df is alleen van belang bij de toets op modelreductie (F-toets) en daar heb je geen onderscheid eenzijdig/tweezijdigquote:En de laatste vraag, ik heb een tweezijdige toets, moet ik de df dan bereken met n - 1 of n - 2?
[ Bericht 2% gewijzigd door GlowMouse op 04-10-2009 23:11:32 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je weet wel wat C0(I) betekent?quote:Op zondag 4 oktober 2009 23:03 schreef Hanneke12345 het volgende:
Hmm, ik kom daar geloof ik niet echt verder mee. dat van die deelruimte was ik ook al achter. Ik kijk sowieso morgen even verder naar die som.
Ik weet ook niet echt wat ik me bij deze formule moet voorstellen;
[ afbeelding ]
Die laatste met L1 dus. De rest kwam ik nog wel uit. Maar wat ze bedoelen met f->f(0) en f(1) etc. ontgaat me.


Is goed, zal ik doen. Lijkt me ook wijs.quote:Op zaterdag 3 oktober 2009 14:09 schreef Iblis het volgende:
[..]
Snap ik, maar ik zou dan (in het geval van een echte toets) expliciet zeggen dat die andere twee niet opgaan.
Hmm, het kwartje begint wel heel langzaam te vallen. Volgens mij kun je dit namelijk ook terugvinden in de tableau's bij de regels voor afleiding. In feite kunnen eigenlijk alle connectieven (equivalentie, materiele implicatie) herschreven worden met behulp van enkel de negatie, disjunctie en conjunctie. Bij φ → ψ is ¬φ v ψ het geval; bij φ ↔ ψ weer (¬φ v ¬ψ) v (φ v ψ). Zodoende kun je ook (φ v ψ v χ) ∨ (¬φ v ψ v ¬χ) herschrijven tot (φ ↔ χ) v ψ.quote:[..]
Je kunt dit op twee manieren aanpaken, ik kopieer even die tafel (ik gebruik die regelnummers niet hieronder, dus met Geval 1 bedoel ik het geval op regel 2):
[ code verwijderd ]
Je kunt dit heel mechanisch (d.w.z. zonder inzicht) doen in feite, dat is een truc die met elke waarheidstafel werkt.
Je ziet dat deze in geval 1 en 6 waar is. Dus dan zeg je, de formule is:
(Geval 1) ∨ (Geval 6)
Nu kijken we even wat Geval 1 inhoudt, dat is: (φ ∧ ψ ∧ χ) – alledrie waar. En wat Geval 6 inhoudt, dat is: (¬φ ∧ ψ ∧ ¬χ), dus φ en χ niet waar en ψ wel, dat staat er immers letterlijk. Als je dat in z’n geheel neemt krijg je:
(φ ∧ ψ ∧ χ) ∨ (¬φ ∧ ψ ∧ ¬χ)
Stel dat je b.v. deze tafel krijgt:
[ code verwijderd ]
Dan kun je zeggen, die is waar als:
(Geval 1) ∨ (Geval 4) ∨ (Geval 6) ∨ (Geval 8)
Nu, vul maar in:
[ code verwijderd ]
Daar komt helemaal geen inzicht bij kijken. In de oorspronkelijke vraag, het eerste geval, is er dus ook een iets kortere oplossing mogelijk, namelijk: (φ ↔ χ) ∧ ψ
Die moet je wel even ‘zien’. Als je naar de tabel kijkt zie je dat die in twee gevallen waar is (te weten 1 & 6), en in beide gevallen geldt dat φ en χ aan elkaar gelijk zijn dus: (φ ↔ χ). Dit geldt in nog twee gevallen, namelijk 4 & 8, maar het verschil tussen 4 & 8 en 1 & 6 is dat ψ in het geval van 1 & 6 wél waar is, dus je formule wordt: (φ ↔ χ) ∧ ψ.
Even een alternatief voorbeeld om te kijken of ik het daadwerkelijk snap:
Hij is in zes gevallen waar. Dus de gezochte formule moet zijn:
(Geval 3) v (Geval 4) v (Geval 5) v (Geval 6) v (Geval 7) v (Geval 8)
(¬A v B v ¬C) v (¬A v B v C) v (A v ¬B v ¬C) v (A v ¬B v C) v (A v B v ¬C) v (A v B v C)
Volgens mij kun je dit ook herschrijven tot iets anders, maar ik zie even niet wat.


Let op: Binnen die gevallen moet je én gebruiken. Dus (¬A ∧ B ∧ ¬C) ∨ (¬A ∧ B ∧ C) en zo voort.quote:Op maandag 5 oktober 2009 01:03 schreef Friek_ het volgende:
Even een alternatief voorbeeld om te kijken of ik het daadwerkelijk snap:
[ afbeelding ]
Hij is in zes gevallen waar. Dus de gezochte formule moet zijn:
(Geval 3) v (Geval 4) v (Geval 5) v (Geval 6) v (Geval 7) v (Geval 8)
(¬A v B v ¬C) v (¬A v B v C) v (A v ¬B v ¬C) v (A v ¬B v C) v (A v B v ¬C) v (A v B v C)
Je kunt bij deze formule ook A ∨ B zeggen. Immers, deze alleen niet waar als A en B beide niet waar zijn (eerste twee gevallen). Als A wel waar is (laatste 4) of B is waar (geval 3 en 4) is de formule waar.quote:Volgens mij kun je dit ook herschrijven tot iets anders, maar ik zie even niet wat.
Dat kun je afleiden uit bovenstaande formule door een boel herschrijven en vereenvoudigen, máár het is makkelijker om het even te zien. En dat zien, dat is niet helemaal uit te leggen. Je kijkt in feite ‘wat hebben de ware gevallen met elkaar gemeen’, of juist ‘wat missen ze’. En op grond daarvan maak je je formule.
[ Bericht 25% gewijzigd door Iblis op 05-10-2009 08:52:32 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


En die eerste betreft Polynomen van graad 1, ax + b dus, en je ziet een manier om een continue functie af te beelden op zo’n polynoom, met behulp van ϕ0 en ϕ1.quote:Op maandag 5 oktober 2009 08:55 schreef Hanneke12345 het volgende:
[..]
"vectorruimte van continue functies", min of meer dus.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik lees in het topic vooral heel veel erg moeilijke vragen. Volgens mij is mijn vraag dan een eitje voor het gros van jullie 
Fietsenverhuurbedrijf Wadtrappers, gevestigd op een van de waddeneilanden, verhuurt fietsen per dag. Ondanks de opkomst van de anti-lekfietsbanden blijkt, als gevolg van de vele schelpenpaden op het eiland, dat de kans op een lekke band op een zekere dag 3% (0,03) bedraagt.
a. Als een groep van 7 fietsers op een dag de fietsen terugbezorgt, bereken dan de kans dat precies 1 van de 7 fietsen een lekke band blijkt te hebben.
b. Op een mooie dag zijn 250 fietsen verhuurd. Benader door de normale verdeling de kans dat er bij meer dan 11 fietsen een lekke band wordt aangetroffen.
Ik hoop dat jullie het mij uit kunnen leggen.
Fietsenverhuurbedrijf Wadtrappers, gevestigd op een van de waddeneilanden, verhuurt fietsen per dag. Ondanks de opkomst van de anti-lekfietsbanden blijkt, als gevolg van de vele schelpenpaden op het eiland, dat de kans op een lekke band op een zekere dag 3% (0,03) bedraagt.
a. Als een groep van 7 fietsers op een dag de fietsen terugbezorgt, bereken dan de kans dat precies 1 van de 7 fietsen een lekke band blijkt te hebben.
b. Op een mooie dag zijn 250 fietsen verhuurd. Benader door de normale verdeling de kans dat er bij meer dan 11 fietsen een lekke band wordt aangetroffen.
Ik hoop dat jullie het mij uit kunnen leggen.


Eerst even een zeuropmerking: Je moet je wel vergewissen van onderlinge onafhankelijkheid. Je kunt je afvragen of dit realistisch is. Stel, er ligt ergens glas op de weg, of er zijn ergens nieuwe schelpen neergelegd, dan is het goed mogelijk dat een groepje dat daarlangs fietst buitenproportioneel getroffen wordt, terwijl een groepje dat daar niet langs fietst, in het geheel geen problemen heeft.quote:Op maandag 5 oktober 2009 11:17 schreef Thije het volgende:
Ik lees in het topic vooral heel veel erg moeilijke vragen. Volgens mij is mijn vraag dan een eitje voor het gros van jullie
Fietsenverhuurbedrijf Wadtrappers, gevestigd op een van de waddeneilanden, verhuurt fietsen per dag. Ondanks de opkomst van de anti-lekfietsbanden blijkt, als gevolg van de vele schelpenpaden op het eiland, dat de kans op een lekke band op een zekere dag 3% (0,03) bedraagt.
Om de vragen te kunnen beantwoorden moet je die onderlinge onafhankelijkheid wel aannemen – maar eigenlijk moet de vraagsteller dat expliciet vermelden, anders is er geen zinnig woord over te zeggen.
Ik geef niet direct het antwoord: Maar je moet dit als Bernoulli-pogingen zien. Dus je doet in feite 7 pogingen met een succeskans van 3%. Kun je dan zelf de uitdrukking vinden?quote:a. Als een groep van 7 fietsers op een dag de fietsen terugbezorgt, bereken dan de kans dat precies 1 van de 7 fietsen een lekke band blijkt te hebben.
Ook deze is niet bijster lastig, maar denk aan de continuïteitscorrectie. Wat denk je dat de bijpassende normale verdeling is, en wat wil je dan precies weten? Kun je dat zelf al formuleren?quote:b. Op een mooie dag zijn 250 fietsen verhuurd. Benader door de normale verdeling de kans dat er bij meer dan 11 fietsen een lekke band wordt aangetroffen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


"de kans op een zekere dag is 3%" slaat sowieso nergens op.
De frequentie kan 3% zijn, maar de kans op een specifieke dag, daar kun je niets mee, zoals Iblis aangeeft.
a) is trouwens het gemakkelijkste als je het omgekeerd benadert, dus de kans dat niemand van de zeven lek rijdt.
De frequentie kan 3% zijn, maar de kans op een specifieke dag, daar kun je niets mee, zoals Iblis aangeeft.
a) is trouwens het gemakkelijkste als je het omgekeerd benadert, dus de kans dat niemand van de zeven lek rijdt.


Er staat toch precies 1 van de 7? Wat jij wilt is toch vooral handig als je wilt weten wat de kans is dat minstens 1 van de 7 lek rijdt?quote:Op maandag 5 oktober 2009 11:40 schreef Beregd het volgende:
"de kans op een zekere dag is 3%" slaat sowieso nergens op.
De frequentie kan 3% zijn, maar de kans op een specifieke dag, daar kun je niets mee, zoals Iblis aangeeft.
a) is trouwens het gemakkelijkste als je het omgekeerd benadert, dus de kans dat niemand van de zeven lek rijdt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik ben echt een leek, ik ga straks proberen thuis, samen met mn rekenboek, tot een redelijk antwoord te komen. Bedankt alvast.quote:Ik geef niet direct het antwoord: Maar je moet dit als Bernoulli-pogingen zien. Dus je doet in feite 7 pogingen met een succeskans van 3%. Kun je dan zelf de uitdrukking vinden?
Ook hier moet ik je nu het antwoord schuldig blijven..quote:Ook deze is niet bijster lastig, maar denk aan de continuïteitscorrectie. Wat denk je dat de bijpassende normale verdeling is, en wat wil je dan precies weten? Kun je dat zelf al formuleren?


Maar eigenlijk, en dat is geen schande hoor, heb je dus geen idee hoe je het moet aanpakken? Als ik dan een antwoord neergooi denk ik dat je er nog niet heel veel mee opschiet.quote:Op maandag 5 oktober 2009 13:35 schreef Thije het volgende:
[..]
Ik ben echt een leek, ik ga straks proberen thuis, samen met mn rekenboek, tot een redelijk antwoord te komen. Bedankt alvast.
[..]
Ook hier moet ik je nu het antwoord schuldig blijven..
Ik zou je dan willen aanraden het zelf eerst te lezen, het dan te proberen, en dan als je ergens concreet vast zit, of denkt: ‘volgens mij moet het zo’ (en met reden) het weer te vragen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Oh weer een probleempje. Nu kan ik in de tabel alleen de functie die ik bij Y1 óf die van Y2 zien, maar ik moet ze allebei tegelijk zien.


’t Is nog steeds geen 24 uur, maar ik denk dat men het gewoon niet weet, vraag je docent anders?quote:Op maandag 5 oktober 2009 15:13 schreef Gitaarmat het volgende:
Oh weer een probleempje. Nu kan ik in de tabel alleen de functie die ik bij Y1 óf die van Y2 zien, maar ik moet ze allebei tegelijk zien.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Hier verder: [Bèta wiskunde] Huiswerk- en vragentopic
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.

 verdeeld is, voor welke waarde van x geldt dat de kans
verdeeld is, voor welke waarde van x geldt dat de kans 
 (kortom, ik hou weer gewoon -x+2 over...)
(kortom, ik hou weer gewoon -x+2 over...)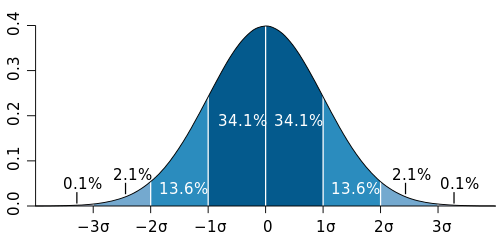
 waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.
waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.












