SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vorige deel: [Bèta wiskunde] 'Huiswerk- en vragentopic'.
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Wiskunde
Natuurkunde
Informatica
Scheikunde
Biologie
Algemene Natuurwetenschappen
... en alles wat verder in de richting komt.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Wiskundig inhoudelijk:
http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
OP
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Wiskundig inhoudelijk:
OP
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


De titel is verkeerd… dit had natuurlijk Bèta wiskunde moeten zijn… even niet opgelet bij copy & pasten; ik pas ook even de wiki aan.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Je kan in je definitie f natuurlijk naar een willekeurige vectorruimte laten gaan (lijkt me conceptueel beter). De beide definities zijn equivalent met elkaar: f:VxV->E wordt vastgelegd door z'n samenstellingen met de projecties van E naar eendimensionale deelruimten (elke vectorruimte heeft immers een basis).quote:Op zondag 30 november 2008 19:12 schreef zuiderbuur het volgende:
[..]
Ben je daar zeker van? Hoe werkt dat dan? f moest een functionaal zijn naar het veld waarover we de ruimte V beschouwen.


Heey,
Ik moet laten zien dat voor een I een Z[a]-ideaal met a integraal over Z van graad n dat I-1=It met t:Q(a)--> Q een Q-lineaire afbeelding sum(bi ai,i=0...n-1) ---> bn-1. Dus dat I-1 de t-duale is van I waarbij je dus I ziet als lattice.
De inclusie I-1 < It heb ik al. De tweede valt een beetje tegen.
Als x zit in It dan geldt t(xI) zit in Z maar volgt dan direct hieruit dat xI zit in Z[a]? Ik zie het niet zo.
Alvast bedankt
Ik moet laten zien dat voor een I een Z[a]-ideaal met a integraal over Z van graad n dat I-1=It met t:Q(a)--> Q een Q-lineaire afbeelding sum(bi ai,i=0...n-1) ---> bn-1. Dus dat I-1 de t-duale is van I waarbij je dus I ziet als lattice.
De inclusie I-1 < It heb ik al. De tweede valt een beetje tegen.
Als x zit in It dan geldt t(xI) zit in Z maar volgt dan direct hieruit dat xI zit in Z[a]? Ik zie het niet zo.
Alvast bedankt
verlegen :)


Als x = som(b_i a^i) niet in Z[a] zit, neem dan de hoogste index i met b_i niet in Z. Dan is t(an-1-ix) niet geheel.


heey. Ik zie het nu. Dank je wel.quote:Op donderdag 4 december 2008 21:01 schreef thabit het volgende:
Als x = som(b_i a^i) niet in Z[a] zit, neem dan de hoogste index i met b_i niet in Z. Dan is t(an-1-ix) niet geheel.
verlegen :)


Vraagje:
Ik heb nu een hoofdstuk van machtsfuncties en dergelijke, met allerlei rekenregels als:
iets tot de macht a x iets tot de macht b, dat moet je dan bij elkaar optellen.
maar wat als er staat iets tot de macht a-iets tot de macht b dus bijvoorbeeld x3-x2 wat wordt het dan?
en die vraag heb ik ook voor +. wat als x3+x2 er staat, en de 3 en 2 zijn machten alleen ik weet niet hoe je dat doet op de pc.
Ik heb nu een hoofdstuk van machtsfuncties en dergelijke, met allerlei rekenregels als:
iets tot de macht a x iets tot de macht b, dat moet je dan bij elkaar optellen.
maar wat als er staat iets tot de macht a-iets tot de macht b dus bijvoorbeeld x3-x2 wat wordt het dan?
en die vraag heb ik ook voor +. wat als x3+x2 er staat, en de 3 en 2 zijn machten alleen ik weet niet hoe je dat doet op de pc.
"De kabel aan je gitaar is als de band onder je auto: Klein stukje rubber en wat metaal maar o zo belangrijk..."


Schrijf het gewoon uit. Je hebt b.v. a3*a2 = a*a*a * a*a = a*a*a*a*a = a5.quote:Op vrijdag 12 december 2008 17:21 schreef matjuhhh007 het volgende:
Vraagje:
Ik heb nu een hoofdstuk van machtsfuncties en dergelijke, met allerlei rekenregels als:
iets tot de macht a x iets tot de macht b, dat moet je dan bij elkaar optellen.
maar wat als er staat iets tot de macht a-iets tot de macht b dus bijvoorbeeld x3-x2 wat wordt het dan?
en die vraag heb ik ook voor +. wat als x3+x2 er staat, en de 3 en 2 zijn machten alleen ik weet niet hoe je dat doet op de pc.
Maar in het geval van a*a*a - a*a heb je niet zoiets. Stel a = 3, dan heb je 3*3*3 - 3*3 = 27 - 9 = 18. Maar 18 is geen macht van drie, dus daar kun je nooit iets moois van maken. Dus, a3 - a2 valt in z'n algemeenheid niet te vereenvoudigen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Oh, dat kan je dus niet schrijfen als een magtsvunksie!
"De kabel aan je gitaar is als de band onder je auto: Klein stukje rubber en wat metaal maar o zo belangrijk..."


Opgelost! 
Het posten alleen is schijnbaar voldoende!
[ Bericht 15% gewijzigd door Borizzz op 14-12-2008 09:54:58 ]
Het posten alleen is schijnbaar voldoende!
[ Bericht 15% gewijzigd door Borizzz op 14-12-2008 09:54:58 ]
kloep kloep


Een vriend van me is nogal wiskundig aangelegd, en als ik vragen heb ga ik vaak naar hem toe. Het dwingt me om het probleem goed te omschrijven en dat geeft vaak al heel veel duidelijkheid. Soms ben ik net na de vraagstelling al bijna bij het antwoord, zonder dat-ie z'n mond nog heeft opengetrokkenquote:Op vrijdag 12 december 2008 21:44 schreef Borizzz het volgende:
Opgelost!
Het posten alleen is schijnbaar voldoende!
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Dat ervaar ik vaak ook als ik hier iets post. Meestal ben ik door het posten opzich al een stap verder.quote:Op zondag 14 december 2008 20:22 schreef Haushofer het volgende:
[..]
Een vriend van me is nogal wiskundig aangelegd, en als ik vragen heb ga ik vaak naar hem toe. Het dwingt me om het probleem goed te omschrijven en dat geeft vaak al heel veel duidelijkheid. Soms ben ik net na de vraagstelling al bijna bij het antwoord, zonder dat-ie z'n mond nog heeft opengetrokken
kloep kloep


Avond!
Zonet even bezig met mijn huiswerk voor Wiskunde. Hierin wordt het volgende gevraagd:
Voor het aantal personenauto's A dat per dag gebruik maakt van een nieuwe stuk tolweg hanteert een adviesbureau het model A=aT^2+bT+60000. Hierin is T het toltarief in euro's, waarbij T maximaal ¤7,00 is.
Onderzoek wijst uit dat bij een tarief van ¤2,50 dagelijks 40.000 personenauto's van de weg gebruik zullen maken. Dit aantal neemt af tot 25000 bij een tarief van ¤5,00.
Nu heb ik het tot meerdere keren toe uitgerekend en ik krijg a = 6000 en b = -23000.
Mijn uitwerkingenboekje beweert echter dat het moet zijn a = 400 en b = -9000
Antwoordenboekje:
Hierin staat op een gegeven moment **** geeft **** -40.000 en daaronder staat -35000
Dit trekken ze van elkaar af (hihi, aftrekken!) en dan wordt de uitkomst -50000?
Kan iemand mij wat uitleg geven, ik snap het niet.
ps: Havo 4 Wiskunde B
Zonet even bezig met mijn huiswerk voor Wiskunde. Hierin wordt het volgende gevraagd:
Voor het aantal personenauto's A dat per dag gebruik maakt van een nieuwe stuk tolweg hanteert een adviesbureau het model A=aT^2+bT+60000. Hierin is T het toltarief in euro's, waarbij T maximaal ¤7,00 is.
Onderzoek wijst uit dat bij een tarief van ¤2,50 dagelijks 40.000 personenauto's van de weg gebruik zullen maken. Dit aantal neemt af tot 25000 bij een tarief van ¤5,00.
Nu heb ik het tot meerdere keren toe uitgerekend en ik krijg a = 6000 en b = -23000.
Mijn uitwerkingenboekje beweert echter dat het moet zijn a = 400 en b = -9000
Antwoordenboekje:
Hierin staat op een gegeven moment **** geeft **** -40.000 en daaronder staat -35000
Dit trekken ze van elkaar af (hihi, aftrekken!) en dan wordt de uitkomst -50000?
Kan iemand mij wat uitleg geven, ik snap het niet.
ps: Havo 4 Wiskunde B


Als je daar -5000 leest dan kopt het verder 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja, maar hoe komt dit uitwerkingenboekje in vredesnaam aan die -50000, want ik kom daar aan -75000quote:Op maandag 15 december 2008 19:27 schreef GlowMouse het volgende:
Als je daar -5000 leest dan kopt het verder
Edit:
En als -12,5a = -50000 zou zijn.
Dan kan a nooit 400 zijn.


Avond 
Ik heb 2 vragen mbt integreren
f(x)=3(4+2x)5-4x2
Ik kom op F(x)=0,5(4+2x)6-4/3x3+c
Het antwoord is F(x)=0,25(4+2x)6-4/3x3+c
Nu weet ik dat ik iets met compensatie moet doen, maar ik weet niet precies hoe, vandaar het verkeerde antwoord.
Nog een:
f(x)= -4(5x-6)*SQRT(5x-6)
F(x)= -8/5*(5x-6)2*SQRT(5x-6)
Het antwoord is -8/25*(5x-6)2*SQRT(5x-6)
Zelfde probleem eigenlijk, maar dat compenseren gaat nog niet helemaal lekker.
Iemand die mij dat kan uitleggen?
[ Bericht 0% gewijzigd door Niconigger op 16-12-2008 20:52:17 ]
Ik heb 2 vragen mbt integreren
f(x)=3(4+2x)5-4x2
Ik kom op F(x)=0,5(4+2x)6-4/3x3+c
Het antwoord is F(x)=0,25(4+2x)6-4/3x3+c
Nu weet ik dat ik iets met compensatie moet doen, maar ik weet niet precies hoe, vandaar het verkeerde antwoord.
Nog een:
f(x)= -4(5x-6)*SQRT(5x-6)
F(x)= -8/5*(5x-6)2*SQRT(5x-6)
Het antwoord is -8/25*(5x-6)2*SQRT(5x-6)
Zelfde probleem eigenlijk, maar dat compenseren gaat nog niet helemaal lekker.
Iemand die mij dat kan uitleggen?
[ Bericht 0% gewijzigd door Niconigger op 16-12-2008 20:52:17 ]


tvp
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Dat compenseren: het is niet zo erg om steeds op jouw antwoord uit te komen, zo begint iedereen  Wat je vervolgens doet, is differentiëren. Bij je eerste zie je dan dat door de kettingregel er nog een factor 2 (afgeleide van 2x) bij komt. Om daarvoor te compenseren deel je die 0,5 nog eens door 2.
Wat je vervolgens doet, is differentiëren. Bij je eerste zie je dan dat door de kettingregel er nog een factor 2 (afgeleide van 2x) bij komt. Om daarvoor te compenseren deel je die 0,5 nog eens door 2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt  .
.
Want bij die tweede als ik dan -8/5 door 5 deel (want 5x) dan kom ik op een heel ander getal uit. Hoe zit dat dan?
Sorry, verkeerde antwoord het klopt wel als je deelt door 5.
Dus dat geldt voor alle sommen, zo ja dan weet ik hoe ik verder moet
Want bij die tweede als ik dan -8/5 door 5 deel (want 5x) dan kom ik op een heel ander getal uit. Hoe zit dat dan?
Sorry, verkeerde antwoord het klopt wel als je deelt door 5.
Dus dat geldt voor alle sommen, zo ja dan weet ik hoe ik verder moet


Als je het 'antwoord' met 8/25 zou differentiëren, komt daar 4*(5x-6)*SQRT(5x-6) uit. Dat 'antwoord' kopt dus niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hee, jij wijzigt gauw je post; moet nog een minteken bij en dan klopt het dus.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Sorry, ik had het antwoord verkeerd gelezen.
Ik zie nu ook dat de min niet in het antwoord staat, foutje in het boek dus.
Bedankt
Ik zie nu ook dat de min niet in het antwoord staat, foutje in het boek dus.
Bedankt


Standaard-normale verdelingen
Je hebt een standaarddeviatie van 20 gram, en je wilt dat 80% van je broden minimaal 800 gram weegt. Wat moet het gemiddelde gewicht van een brood zijn dan?
Uitrekenen lukt wel alleen is dit omslachtig via een tabellenpapier, hoe moet dit op een grafische rekenmachine? (dus welke formule invoeren)
Je hebt een standaarddeviatie van 20 gram, en je wilt dat 80% van je broden minimaal 800 gram weegt. Wat moet het gemiddelde gewicht van een brood zijn dan?
Uitrekenen lukt wel alleen is dit omslachtig via een tabellenpapier, hoe moet dit op een grafische rekenmachine? (dus welke formule invoeren)


z = invNorm(0.20)
daarna (800-mu)/20 = z oplossen.
daarna (800-mu)/20 = z oplossen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Heey ik heb moeite met het boek van Algebraic Geometry (Robin HAG) en dus ging voor het boek An Introduction to Computational Algebraic Geometry and Commutative Algebra van o.a David Cox.
Is het een goed boek voor beginners?
Een van de vragen is: bewijs dat de verzameling D={(x,x) met x in R}\{1,1} (dus diagonaal behalve (1,1) ) geen varieteit is... Ik heb al een schets van een bewijs geschreven alleen ik heb moeite met de precieze formulering... Heeft iemand een oplossing?
Is het een goed boek voor beginners?
Een van de vragen is: bewijs dat de verzameling D={(x,x) met x in R}\{1,1} (dus diagonaal behalve (1,1) ) geen varieteit is... Ik heb al een schets van een bewijs geschreven alleen ik heb moeite met de precieze formulering... Heeft iemand een oplossing?
verlegen :)


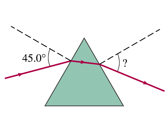
hoi ik zat net een in mijn natuurkunde examenbundel te kijken en ik kom er echt niet uit hoe ze aan die 3,9cm komen?
als ik het uit de examenbundel opmeet krijg ik 3,1 cm
ik heb de vraag op internet gevonden met uitwerking.
zou iemand het me aub kunnen uitleggen hoe ze aan die 3,9cm komen,
Vraag 16
http://www.havovwo.nl/vwo/vna/bestanden/vna103iiopg5.pdf
uitwerking
http://www.havovwo.nl/vwo/vna/bestanden/vna103iiopl5.pdf
als ik het uit de examenbundel opmeet krijg ik 3,1 cm
ik heb de vraag op internet gevonden met uitwerking.
zou iemand het me aub kunnen uitleggen hoe ze aan die 3,9cm komen,
Vraag 16
http://www.havovwo.nl/vwo/vna/bestanden/vna103iiopg5.pdf
uitwerking
http://www.havovwo.nl/vwo/vna/bestanden/vna103iiopl5.pdf
I wake up after only seeing the beginning of my dream...but I will grasp what happens after that with my arms


Ik denk dat het op een ander formaat afgedrukt is; het maakt ook niet zoveel uit, waar het om gaat is hoe de somkracht qua lengte zich verhoudt tot de losse krachten. Als jij 3,1 cm meet, en je meet dat de somkracht 5,7cm is, dan kom je alsnog op (5,35/3,1) * 5,7 = 9,9 kN uit.quote:Op maandag 29 december 2008 20:25 schreef nourguy01 het volgende:
hoi ik zat net een in mijn natuurkunde examenbundel te kijken en ik kom er echt niet uit hoe ze aan die 3,9cm komen?
als ik het uit de examenbundel opmeet krijg ik 3,1 cm
ik heb de vraag op internet gevonden met uitwerking.
zou iemand het me aub kunnen uitleggen hoe ze aan die 3,9cm komen,
Vraag 16
http://www.havovwo.nl/vwo/vna/bestanden/vna103iiopg5.pdf
uitwerking
http://www.havovwo.nl/vwo/vna/bestanden/vna103iiopl5.pdf
Het is eigenlijk wat misleidend dat ze die maten zo expliciet gebruiken; het gaat namelijk alleen om de verhoudingen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


dank u wel 
I wake up after only seeing the beginning of my dream...but I will grasp what happens after that with my arms


Probleem:
Een project bestaat uit dertig deelprojecten die aan aannemers worden uitbesteed. Voor elk deelproject kunnen max. 7 aannemers zich aanmelden. In totaal melden zich 50 aannemers aan. Van die aannemers zijn er
-5 die op 10 deelprojecten inschrijven,
-5 die op 8 deelprojecten inschrijven
-20 die op 3 deelprojecten inschrijven.
-De overige 20 schrijven op 2 projecten in.
Er wordt niet meer dan één deelproject aan een aannemer toegeschreven.
Gezocht: een ondergrens voor het maximale deelprojecten dat tegelijkertijd kan worden gedaan.
Ik heb t grafentheoretisch aangepakt. maar zit nu flink vast. Wie kan me wat op weg helpen?
Een project bestaat uit dertig deelprojecten die aan aannemers worden uitbesteed. Voor elk deelproject kunnen max. 7 aannemers zich aanmelden. In totaal melden zich 50 aannemers aan. Van die aannemers zijn er
-5 die op 10 deelprojecten inschrijven,
-5 die op 8 deelprojecten inschrijven
-20 die op 3 deelprojecten inschrijven.
-De overige 20 schrijven op 2 projecten in.
Er wordt niet meer dan één deelproject aan een aannemer toegeschreven.
Gezocht: een ondergrens voor het maximale deelprojecten dat tegelijkertijd kan worden gedaan.
Ik heb t grafentheoretisch aangepakt. maar zit nu flink vast. Wie kan me wat op weg helpen?
kloep kloep


De vraag is onduidelijk: wanneer kunnen projecten tegelijk worden gedaan, en wanneer na elkaar?
In het slechtste geval schrijven ze zich allemaal in op (een deel van) dezelfde 10 projecten, en dan is het maximum dus 10. Of kan het nog slechter?
In het slechtste geval schrijven ze zich allemaal in op (een deel van) dezelfde 10 projecten, en dan is het maximum dus 10. Of kan het nog slechter?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik had eerst een apart topic geopend, maar die is alweer gesloten.
Na mijn Hbo P ben ik Rechten gaan studeren op de uni maar dat beviel mij niet. Dus nu wil ik Economie of Bedrijfskunde gaan doen maar omdat ik geen vwo diploma heb moet ik een Wiskunde toelatingstoets maken op de EUR. Basisboek Wiskunde heb ik al aangeschaft en ik ben al aan de slag ermee gegaan. Maar op het internet heb ik ook een voorbeeldtoets + uitwerkingen aangetroffen. Zijn er misschien mensen hier die mij met de uitwerkingen kunnen helpen ?(Dus de antwoorden toelichten en niet alleen het antwoord zelf) Aan de hand daarvan zou ik zelfstandig de meeste dingen uit basisboek kunnen maken.
En matrices/kans en opgave B staan niet eens in het basisboek. Dus ook help daarbij is welkom.
Ik ben natuurlijk zelf ook al met 't basisboek bezig maar ook in dat boek staan alleen de antwoorden en niet de uitwerkingen erbij. Dat is soms heel erg lastig als je er dan niet uit kan komen.
Het gaat om deze voorbeeldtoets + uitwerkingen:
http://www.rsm.nl/portal/(...)beeldtoets%20A12.pdf
http://www.rsm.nl/portal/(...)2%20uitwerkingen.pdf
[ Bericht 3% gewijzigd door farinos op 05-01-2009 21:40:29 ]
Na mijn Hbo P ben ik Rechten gaan studeren op de uni maar dat beviel mij niet. Dus nu wil ik Economie of Bedrijfskunde gaan doen maar omdat ik geen vwo diploma heb moet ik een Wiskunde toelatingstoets maken op de EUR. Basisboek Wiskunde heb ik al aangeschaft en ik ben al aan de slag ermee gegaan. Maar op het internet heb ik ook een voorbeeldtoets + uitwerkingen aangetroffen. Zijn er misschien mensen hier die mij met de uitwerkingen kunnen helpen ?(Dus de antwoorden toelichten en niet alleen het antwoord zelf) Aan de hand daarvan zou ik zelfstandig de meeste dingen uit basisboek kunnen maken.
En matrices/kans en opgave B staan niet eens in het basisboek. Dus ook help daarbij is welkom.
Ik ben natuurlijk zelf ook al met 't basisboek bezig maar ook in dat boek staan alleen de antwoorden en niet de uitwerkingen erbij. Dat is soms heel erg lastig als je er dan niet uit kan komen.
Het gaat om deze voorbeeldtoets + uitwerkingen:
http://www.rsm.nl/portal/(...)beeldtoets%20A12.pdf
http://www.rsm.nl/portal/(...)2%20uitwerkingen.pdf
[ Bericht 3% gewijzigd door farinos op 05-01-2009 21:40:29 ]


Welke opgaven wil je uitgewerkt hebben? Veel zou je na doorwerken van het basisboek wel moeten kunnen namelijk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Over het tegelijk uitvoeren van projecten wordt niets genoemd. Dan ga ik er van uit dat ze in principe alle projecten gelijktijdig zouden kunnen als er 30 aannemers waren geweest die op de verschillende projecten kunnen zitten.
En ik zocht een ondergrens voor het aantal gelijktijdige projecten.
En ik zocht een ondergrens voor het aantal gelijktijdige projecten.
kloep kloep


Ik interpreteer de vraag nu als "hoeveel projecten kunnen er in het slechtste geval worden toegewezen", en dat zijn er 10.quote:Op maandag 5 januari 2009 21:36 schreef Borizzz het volgende:
Over het tegelijk uitvoeren van projecten wordt niets genoemd. Dan ga ik er van uit dat ze in principe alle projecten gelijktijdig zouden kunnen als er 30 aannemers waren geweest die op de verschillende projecten kunnen zitten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat klopt. Opgave 9, 11, 12, 13, 14 en Opgave B staan niet in het basisboek. Zou iemand mijn in ieder geval daarmee kunnen helpen ? En ook met opgave 7 als het kan die probeerde ik net op te lossen maar ik kom er niet uit.quote:Op maandag 5 januari 2009 21:35 schreef GlowMouse het volgende:
Welke opgaven wil je uitgewerkt hebben? Veel zou je na doorwerken van het basisboek wel moeten kunnen namelijk.


7a. x = [ x^(2/3) ] ^(3/2)
7b: logaritme
7c: als 7a
9a: http://nl.wikipedia.org/wiki/Matrixvermenigvuldiging
je krijgt linksboven p+2q = p+10 ofwel q = 5
je krijgt linksonder 2p+15 = 5+22 ofwel p = 6
9b: http://nl.wikipedia.org/wiki/Determinant (alleen leren voor 2x2)
11 gebruik K(t) = K * 1,04^15
12 logisch nadenken of een Venn-diagram tekenen
13a ze kiezen 0 als waarde voor t, dus gewoon invullen
13b gebruik logaritme
14a (1/6)^6
14b lees http://nl.wikipedia.org/wiki/Binomiale_verdeling
Ba A = 30100, dus opbrengst = A*2 = 60200
Bb afgeleide op 0 stellen: d/dT T*(400T²-9150T+4600) = 1200T² - 18300T + 4600 = 0 => abc-formule
Bc A berekenen als T=2,40, A berekenen als T = 2,40*1,05, en het procentuele verschil bepalen
Bd noem dat tarief t. We weten dat (400t²-9150t + 46800)*0.975 = 400(t*1.06)²-9150(t*1.06) + 46800
7b: logaritme
7c: als 7a
9a: http://nl.wikipedia.org/wiki/Matrixvermenigvuldiging
je krijgt linksboven p+2q = p+10 ofwel q = 5
je krijgt linksonder 2p+15 = 5+22 ofwel p = 6
9b: http://nl.wikipedia.org/wiki/Determinant (alleen leren voor 2x2)
11 gebruik K(t) = K * 1,04^15
12 logisch nadenken of een Venn-diagram tekenen
13a ze kiezen 0 als waarde voor t, dus gewoon invullen
13b gebruik logaritme
14a (1/6)^6
14b lees http://nl.wikipedia.org/wiki/Binomiale_verdeling
Ba A = 30100, dus opbrengst = A*2 = 60200
Bb afgeleide op 0 stellen: d/dT T*(400T²-9150T+4600) = 1200T² - 18300T + 4600 = 0 => abc-formule
Bc A berekenen als T=2,40, A berekenen als T = 2,40*1,05, en het procentuele verschil bepalen
Bd noem dat tarief t. We weten dat (400t²-9150t + 46800)*0.975 = 400(t*1.06)²-9150(t*1.06) + 46800
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Er zit ook meer achter volgens mij, want:quote:Op maandag 5 januari 2009 21:42 schreef Borizzz het volgende:
Hmm, in dat geval zou ik t wel erg makkelijk vinden ineens.
Er zit meer achter denk ik
Dus stel dat de 5 die zich voor 8 projecten aanmelden dat alle 8 op hetzelfde project doen; dan neem je die 5 die zich voor 10 projecten inschrijven: slechts 2 van die 5 kunnen ook die eerste 8 projecten doen. 3 van die 5 moeten sowieso heel andere projecten kiezen.quote:Voor elk deelproject kunnen max. 7 aannemers zich aanmelden.
Ik moet wel even piekeren over wat de geijkte oplossing hier is…
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja hij is lastig. Ben er niet voor niets al een week zoet mee.
Ik heb een graaf ervan gemaakt en dan koppelingen maken.
Vergeet niet dat 1 project maar door 1 aannemer wordt gedaan en dat een aannemer ook niet meer dan een project krijgt.
Ik heb een graaf ervan gemaakt en dan koppelingen maken.
Vergeet niet dat 1 project maar door 1 aannemer wordt gedaan en dat een aannemer ook niet meer dan een project krijgt.
kloep kloep


Ah, dat is de lastigheid. Als je alleen het antwoord wilt weten, kun je hem als MIP formuleren en oplossen. Anders zat ik in de richting van laatjes te denken, maar dat werd hem ook niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Koppelingen (of matchings, zoals ik ze altijd noem...) lijken me wel de manier, maar ik zit er niet meer goed genoeg in om met zekerheid te stellen: Ja, dit is de oplossing. Matchings kunnen ook als LP worden opgelost, maar dat lijkt me voor Borizzz' vak niet de bedoeling. 
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Nouja.. ik kijk wel ff nog. Heb vandaag iig wel een ander lastig probleem getackeld 
Ieks... npg 3 weken voor het tentamen
Ieks... npg 3 weken voor het tentamen
kloep kloep


Je kunt het formuleren als een max-flow probleem. Vanuit de bron lopen er kanten met capaciteit [10/8/3/2] naar de 50 aannemers, van elke aannemer loopt er een kant met capaciteit 1 naar elk project, en van elk project loopt er een kant met capaciteit 7 naar de put. Pak eerst een klein aantal projecten, en vergroot het steeds totdat je een flow van 5*10+5*8+20*3+20*2 kunt maken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


En dan? Met een bron en een put had ik ook al geprobeerd., maar bij het vergroten liep ik steeds vast....
kloep kloep


Waarom loop je vast? Je kunt toch een willekeurig max-flow algoritme pakken?quote:Op maandag 5 januari 2009 22:41 schreef Borizzz het volgende:
En dan? Met een bron en een put had ik ook al geprobeerd., maar bij het vergroten liep ik steeds vast....
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hey bedankt!quote:Op maandag 5 januari 2009 21:59 schreef GlowMouse het volgende:
7a. x = [ x^(2/3) ] ^(3/2)
7b: logaritme
7c: als 7a
9a: http://nl.wikipedia.org/wiki/Matrixvermenigvuldiging
je krijgt linksboven p+2q = p+10 ofwel q = 5
je krijgt linksonder 2p+15 = 5+22 ofwel p = 6
9b: http://nl.wikipedia.org/wiki/Determinant (alleen leren voor 2x2)
11 gebruik K(t) = K * 1,04^15
12 logisch nadenken of een Venn-diagram tekenen
13a ze kiezen 0 als waarde voor t, dus gewoon invullen
13b gebruik logaritme
14a (1/6)^6
14b lees http://nl.wikipedia.org/wiki/Binomiale_verdeling
Ba A = 30100, dus opbrengst = A*2 = 60200
Bb afgeleide op 0 stellen: d/dT T*(400T²-9150T+4600) = 1200T² - 18300T + 4600 = 0 => abc-formule
Bc A berekenen als T=2,40, A berekenen als T = 2,40*1,05, en het procentuele verschil bepalen
Bd noem dat tarief t. We weten dat (400t²-9150t + 46800)*0.975 = 400(t*1.06)²-9150(t*1.06) + 46800
Alleen de helft van de antwoorden snap k nog niet echt..dat wordt dus een hoop op internet gaan zoeken en graven en werken in het wiskunde basisboek.


pfff de kerstvakantie heeft mijn algebra weer flink toegetakeld 
Het gaat om het volgende
2 vergelijkingen met 2 onbekenden

en

Hoe los je ook alweer zoiets op? Ik ben het helemaal kwijt
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:22:45 ]
Het gaat om het volgende
2 vergelijkingen met 2 onbekenden
en
Hoe los je ook alweer zoiets op? Ik ben het helemaal kwijt
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:22:45 ]
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Je kunt { en } gebruiken als je één heel ding in een exponent wilt hebben.


Kijk eens of je hier wat mee kunt:
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:22:53 ]
Kijk eens of je hier wat mee kunt:
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:22:53 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Sorry ik zie het nog steeds niet, wat slecht van me 
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Links staat een getal dat je uit kunt rekenen, rechts zet je ook een breuk maar vervang je die getallen door de uitdrukkingen in x en y. Vereenvoudigen levert aan de rechterkant een 
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:22:59 ]
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:22:59 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb het nu ja, ik dacht weer veel te moeilijk na en vergat wat basisregels van wegstrepen 
bedankt
bedankt
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Vraagje:
Iteratie van f(x) = a ( sqrt ( 1/4 - (x-1/2)^2))
Voor welke waarde van a is er een overgang van het gedrag met periode 1 naar gedrag met periode 2? Ik ben al bijna anderhalf uur bezig maar kom er maar niet uit.
Graag wat hulp
Iteratie van f(x) = a ( sqrt ( 1/4 - (x-1/2)^2))
Voor welke waarde van a is er een overgang van het gedrag met periode 1 naar gedrag met periode 2? Ik ben al bijna anderhalf uur bezig maar kom er maar niet uit.
Graag wat hulp


@ Borizzz
Ligt het aan mij of kom ik een aantal projecten tekort?
Want er zijn 30 deelprojecten en de som waarvoor aannemers zich hebben ingeschreven is 23, of worden deze 7 niet uitgevoerd?
En misschien kun je er een rooster bij/van maken ofzo (de rooster methode heb ik gekregen met discrete optimalisering, waarbij je vanuit een graaf een rooster maakt)
[ Bericht 17% gewijzigd door PAAC op 08-01-2009 11:31:54 ]
Ligt het aan mij of kom ik een aantal projecten tekort?
Want er zijn 30 deelprojecten en de som waarvoor aannemers zich hebben ingeschreven is 23, of worden deze 7 niet uitgevoerd?
En misschien kun je er een rooster bij/van maken ofzo (de rooster methode heb ik gekregen met discrete optimalisering, waarbij je vanuit een graaf een rooster maakt)
[ Bericht 17% gewijzigd door PAAC op 08-01-2009 11:31:54 ]


PAAC: 30 projecten en 50 aannemers. Een project kan wel door meerdere aannemers worden gedaan, maar elke aannemer heeft maar 1 project.
Alle projecten worden uitgevoerd.
Alle projecten worden uitgevoerd.
kloep kloep


Leuke editor heb je daar, GlowMousequote:Op dinsdag 6 januari 2009 18:14 schreef GlowMouse het volgende:
Links staat een getal dat je uit kunt rekenen, rechts zet je ook een breuk maar vervang je die getallen door de uitdrukkingen in x en y. Vereenvoudigen levert aan de rechterkant een [ afbeelding ]
ff wachten nog


Jij kunt hem ook gebruiken, zie de OPquote:Op donderdag 8 januari 2009 22:47 schreef Game_Error het volgende:
[..]
Leuke editor heb je daar, GlowMouse
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je kan me zeker niet de graaf laten zien die je dan hebt gemaakt?quote:Op donderdag 8 januari 2009 16:01 schreef Borizzz het volgende:
PAAC: 30 projecten en 50 aannemers. Een project kan wel door meerdere aannemers worden gedaan, maar elke aannemer heeft maar 1 project.
Alle projecten worden uitgevoerd.
Want als je 50(5 + 5 + 20 + 20) aannemers hebt, die zich voor maar 23(10 + 8 + 3 + 2) deelprojecten inschrijven. Wordt er voor 7 deelprojecten niet ingeschreven, hoe worden deze dan uitgevoerd?
Dat een project door meerdere aannemers gedaan kan worden maakt niets uit, omdat er maar 23 inschrijvingen zijn van de 30 projecten.
[EDIT]
Krijg ineens een "ingeving" om 1 uur s'nachts
Is het zo dat als 5 aannemers zich inschrijven voor 10 projecten, ze zich niet alle 5 inschrijven voor 10 dezelfde projecten? Want dan wordt het volledig afhankelijk voor welke projecten de aannemers zich inschrijven.
(Ik ben nu zelf ook wel geintereseerd in het antwoord, aangezien ik volgende week een toets heb over een soortgelijk onderwerp
[ Bericht 15% gewijzigd door PAAC op 09-01-2009 01:08:47 ]


Ik heb wel een graaf hoor, PM me maar even.
En de aannemers schrijven zich in voor 10 projecten. Die hoeven niet per se dezelfde te zijn, 10 verschillende kan ook.
En de aannemers schrijven zich in voor 10 projecten. Die hoeven niet per se dezelfde te zijn, 10 verschillende kan ook.
kloep kloep


Iemand die mij kan helpen hiermee?quote:Op woensdag 7 januari 2009 22:09 schreef McGilles het volgende:
Vraagje:
Iteratie van f(x) = a ( sqrt ( 1/4 - (x-1/2)^2))
Voor welke waarde van a is er een overgang van het gedrag met periode 1 naar gedrag met periode 2? Ik ben al bijna anderhalf uur bezig maar kom er maar niet uit.
Graag wat hulp


Ik had hem al gevonden via de URL van de functiequote:Op donderdag 8 januari 2009 22:49 schreef GlowMouse het volgende:
[..]
Jij kunt hem ook gebruiken, zie de OP
ff wachten nog


Geef eens een voorbeeld van een a en een x zodat je 'gedrag met periode 1' krijgt. Ik snap de vraagstelling namelijk niet.quote:Op vrijdag 9 januari 2009 12:07 schreef McGilles het volgende:
[..]
Iemand die mij kan helpen hiermee?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het is de letterlijke vraagstelling uit m'n boek, dus kan er ook niks aan doen, ben met jou eens dat het vaag is.quote:Op vrijdag 9 januari 2009 17:53 schreef GlowMouse het volgende:
[..]
Geef eens een voorbeeld van een a en een x zodat je 'gedrag met periode 1' krijgt. Ik snap de vraagstelling namelijk niet.
Voorbeeld met a = 1/2 en x = 1/2
Dan neigt de iteratie naar 1/2*(sqrt (1/4 - (x-1/2)^2) = x dus x = 1/5
Dit is gedrag met periode 1. Echter zijn er bepaalde waarden van 'a' te verzinnen zodat dit niet het geval is, maar dat er gedrag met periode 2 is, bijvoorbeeld xn = 0.2, xn+1 = 0.7 en xn+2 = xn = 0.2


f is een cirkel om (0,1/2) met straal 1/2 die in de y-richting met een factor a wordt uitgerekt.
De vraag zou volgens mij moeten zijn 'voor welke a is er gedrag met periode 2 mogelijk?'
Met een webgrafiek en a=2 zie je gedrag met periode 2 als je bij 0.96 begint. Zolang a>1 kun je via hetzelfde trucje gedrag met periode 2 krijgen. Sluitend is het niet, maar de vergelijking die je op moet lossen worden dan te complex. Je wilt eigenlijk weten voor welke a de vergelijking f(a,f(a,x))=x meer dan 2 oplossingen heeft.
De vraag zou volgens mij moeten zijn 'voor welke a is er gedrag met periode 2 mogelijk?'
Met een webgrafiek en a=2 zie je gedrag met periode 2 als je bij 0.96 begint. Zolang a>1 kun je via hetzelfde trucje gedrag met periode 2 krijgen. Sluitend is het niet, maar de vergelijking die je op moet lossen worden dan te complex. Je wilt eigenlijk weten voor welke a de vergelijking f(a,f(a,x))=x meer dan 2 oplossingen heeft.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hallo ik ben bezig met een hoofdstuk over Statistische verwerking, en ik ben bij een vraag aangekomen waar je de standaarddeviatie (standaardafwijking) moet berekenen adhv een lijst van de salarissen van de medewerkers van een bedrijf.
Als ik op mijn rekenmachine de maandsalarasissen in L1 invul en de frequenties in L2. En vervolgens op Stat > Calc > 1-Var Stars druk krijg ik de lijst met het gemiddelde en de standaarddeviatie. Voor het gemm. krijg ik 2000 en voor de standaardev. 690.4105059. Ik heb het idee dat hij de L2 lijst met de frequenties (dus hoeveel mensen in welke salarisgroep zitten) niet meerekent, want als ik die L2 lijst weer leegmaak en het nog een keer uitreken krijg ik hetzelfde resultaat.
Weet iemand wat ik fout doe?
Als ik op mijn rekenmachine de maandsalarasissen in L1 invul en de frequenties in L2. En vervolgens op Stat > Calc > 1-Var Stars druk krijg ik de lijst met het gemiddelde en de standaarddeviatie. Voor het gemm. krijg ik 2000 en voor de standaardev. 690.4105059. Ik heb het idee dat hij de L2 lijst met de frequenties (dus hoeveel mensen in welke salarisgroep zitten) niet meerekent, want als ik die L2 lijst weer leegmaak en het nog een keer uitreken krijg ik hetzelfde resultaat.
Weet iemand wat ik fout doe?


Je moet 1-Var Stats L1,L2 doen. En je schat dan trouwens de standaardafwijking van de populatie werknemers onder de aanname dat je een aselecte steekproef hebt. En die heb je niet, dus de uitkomst is redelijk nutteloos.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Van de GR weet ik niks, kan je het niet op papier doen? Dan kan je haast geen fouten makenquote:Op zaterdag 10 januari 2009 16:22 schreef julian6 het volgende:
Hallo ik ben bezig met een hoofdstuk over Statistische verwerking, en ik ben bij een vraag aangekomen waar je de standaarddeviatie (standaardafwijking) moet berekenen adhv een lijst van de salarissen van de medewerkers van een bedrijf.
[ afbeelding ]
Als ik op mijn rekenmachine de maandsalarasissen in L1 invul en de frequenties in L2. En vervolgens op Stat > Calc > 1-Var Stars druk krijg ik de lijst met het gemiddelde en de standaarddeviatie. Voor het gemm. krijg ik 2000 en voor de standaardev. 690.4105059. Ik heb het idee dat hij de L2 lijst met de frequenties (dus hoeveel mensen in welke salarisgroep zitten) niet meerekent, want als ik die L2 lijst weer leegmaak en het nog een keer uitreken krijg ik hetzelfde resultaat.
Weet iemand wat ik fout doe?


Als ik lijsten L1 en L2 heb ik gevuld met de klassenmiddens van de salarisgroepen in L1 en de frequenties in L2 dan ga ik naar Stat > Calc > 1-Var Stats en vervolg achtereenvolgens L1 L2 invul en op enter druk krijg ik een Syntax error.quote:Op zaterdag 10 januari 2009 16:40 schreef GlowMouse het volgende:
Je moet 1-Var Stats L1,L2 doen. En je schat dan trouwens de standaardafwijking van de populatie werknemers onder de aanname dat je een aselecte steekproef hebt. En die heb je niet, dus de uitkomst is redelijk nutteloos.
edit: Als ik een komma ertussengooi komt er wel een lijst. Maar nu komen de gemiddeldes en de standaarddev niet overeen met die in het antwoordenboekje
Dankje voor je hulp


Dat betekent dat ja. Het betekent overigens ook dat je schatter voor de standaardafwijking heel onzuiver wordt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Waarom doe je het niet even op papierquote:Op zaterdag 10 januari 2009 16:48 schreef julian6 het volgende:
[..]
Als ik lijsten L1 en L2 heb ik gevuld met de klassenmiddens van de salarisgroepen in L1 en de frequenties in L2 dan ga ik naar Stat > Calc > 1-Var Stats en vervolg achtereenvolgens L1 L2 invul en op enter druk krijg ik een Syntax error.
edit: Als ik een komma ertussengooi komt er wel een lijst. Maar nu komen de gemiddeldes en de standaarddev niet overeen met die in het antwoordenboekjeBij vraag A staat toch echt 'gebruik daarvoor de klassenmiddens' dat betekend toch dat ik het midden moet nemen van de salarisgroepen (Dus 900 bij 1, 100 bij 2 etc)
Dankje voor je hulp
Kolommen: x-gem, x - x-gem, (x - x-gem)^2, etc
Ben je zo klaar mee en heb je ook dat domme apparaat niet bij nodig


Maar hoe verklaar je dan dat de uitkomst niet overeenkomt met het antwoordenboek? De standaarddev komt uit op 460 en in het antwoordenboek staat 400 
Edit: Blijkt dat ik de verkeerde L lijst had gekozen & de waardes stonden verkeerd. Het antwoord klopt nu wel, bedankt GlowMouse
[ Bericht 20% gewijzigd door julian6 op 10-01-2009 17:06:24 ]
Edit: Blijkt dat ik de verkeerde L lijst had gekozen & de waardes stonden verkeerd. Het antwoord klopt nu wel, bedankt GlowMouse
[ Bericht 20% gewijzigd door julian6 op 10-01-2009 17:06:24 ]


Vraagje: als je een box plot moet tekenen, moet je dan ook de kwartielen aangeven dmv Q1 en Q3 en de mediaan ook?


Glowmouse, ik heb een somfrequentietabel gemaakt met de somfrequenties in %. Nu moet ik die data in mijn GR invoeren en een somfrequentiepolygoon tevoorschijn toveren. Heb jij enig idee hoe ik dat aanpak?


Pen en papierquote:Op zondag 11 januari 2009 16:58 schreef julian6 het volgende:
Glowmouse, ik heb een somfrequentietabel gemaakt met de somfrequenties in %. Nu moet ik die data in mijn GR invoeren en een somfrequentiepolygoon tevoorschijn toveren. Heb jij enig idee hoe ik dat aanpak?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Maar van mn leraar moet je het met de rekenmachine doen (en dat lijkt me zelf ook het beste); Weet jij hoe ik die kan maken met de GR?


Zie de handleiding van je rekenmachine.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Met Google kan ik zo de handleiding van elke gangbare rekenmachine vinden hoor 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Om de studie van hun kinderen te kunnen betalen hebben de ouders maandelijks een bedrag van ¤ 200,- op een rekening gezet. De eerste storting vond plaats op 1 augustus 1995 en de laatste storting op 1 juli 2007. De intrest bedroeg van 1 augustus 1995 tot en met 31 juli 2007 0,4% per maand, daarna 5% per jaar. Vanaf 1 september 2013 willen ze 7 jaar lang een vast bedrag per maand van deze rekening opnemen.
a. Bereken het saldo van de rekening op 1 augustus 2007.
E PRE = 200 x 1.004 x (1.004 tot de 144 -1) : 0.004 = 38.998.67
b. Bereken het saldo van de rekening op 1 augustus 2013.
E = 38.998,67 * 1,05 tot de 6 = 52.261,94
c. Bereken het bedrag dat de ouders maandelijks op kunnen nemen.
CW POST = 52.261,94 = T x 1 – 1,004074124 tot de – 84 : 0.004074124 . T = 735.94
Vraagje, bij antwoord C gebruiken ze 1.004074124, maar hoe komen ze aan dit getal?
a. Bereken het saldo van de rekening op 1 augustus 2007.
E PRE = 200 x 1.004 x (1.004 tot de 144 -1) : 0.004 = 38.998.67
b. Bereken het saldo van de rekening op 1 augustus 2013.
E = 38.998,67 * 1,05 tot de 6 = 52.261,94
c. Bereken het bedrag dat de ouders maandelijks op kunnen nemen.
CW POST = 52.261,94 = T x 1 – 1,004074124 tot de – 84 : 0.004074124 . T = 735.94
Vraagje, bij antwoord C gebruiken ze 1.004074124, maar hoe komen ze aan dit getal?
Sjakie Wolfs 1931-2008
Bobby Haarms 1934-2009
Michael Jackson 1958-2009
Bobby Haarms 1934-2009
Michael Jackson 1958-2009


Dat is de 5% rente als je die omrekent naar een samengestelde rente per maand (1.05 tot de macht (1/12)).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zondag 11 januari 2009 21:33 schreef GlowMouse het volgende:
Dat is de 5% rente als je die omrekent naar een samengestelde rente per maand (1.05 tot de macht (1/12)).
Sjakie Wolfs 1931-2008
Bobby Haarms 1934-2009
Michael Jackson 1958-2009
Bobby Haarms 1934-2009
Michael Jackson 1958-2009


100 leerlingen van een school doen mee aan een test waarbij max. 100 punten kunnen worden behaald. De resultaten van de test staan in de somfrequentiepolygoon hierboven.
a Hoeveel leerlingen behaalden meer dan 55 punten?
Dat is 45 toch? Antwoordenmodel op internet & het boekje wat ik hier heb zegt 55. Ligt het nou aan mij, of klopt dat niet?


Er staat zelfs een stipje waar je het af moet lezen 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja die heb ik d'r gezet, maar ik kijk er al 10 min naar maar het resterende is toch echt 45
dus 45 leerlingen behaalde meer dan 55 punten
denk ik. of ben ik echt zo dom
antwoordmodel:
"T-5a Ongeveer 55 leerlingen behaalden een score van meer dan 55 punten."
dus 45 leerlingen behaalde meer dan 55 punten
denk ik. of ben ik echt zo dom
antwoordmodel:
"T-5a Ongeveer 55 leerlingen behaalden een score van meer dan 55 punten."


Ja en?quote:Op zondag 11 januari 2009 21:44 schreef GlowMouse het volgende:
Er staat zelfs een stipje waar je het af moet lezen
Ik heb nog nooit van een somfrequentiepolygoon gehoord, maar ik zou denken dat je 55 van de 100 leerlingen af moet trekken, dus ook op 45 uitkomen.


quote:
Ik ga die knakkers bellen van Wolters noordhoff. Beetje verkeerde informatie de wereld insturen.
Maar ik ben niet scheel dus, dat is mooi


Ik zit met een probleempje en ik kijk ergens overheen.
De volgende som binair talstelsel:
11010110 -
01111111 =
01010111 is de goede oplossing.
maar met de regels :
0-0=0
1-0=1
1-1=0
0-1=1 (een lenen)
1-1-1=1 (een lenen)
kom ik op 01100111 als uitkomst (wat niet goed is). Het gaat fout bij de 5e "1" . Volgens mij staat daar 1-1 =0 maar moet blijkbaar 1 uitkomen. Wat doe ik fout?
De volgende som binair talstelsel:
11010110 -
01111111 =
01010111 is de goede oplossing.
maar met de regels :
0-0=0
1-0=1
1-1=0
0-1=1 (een lenen)
1-1-1=1 (een lenen)
kom ik op 01100111 als uitkomst (wat niet goed is). Het gaat fout bij de 5e "1" . Volgens mij staat daar 1-1 =0 maar moet blijkbaar 1 uitkomen. Wat doe ik fout?
no time to waste


Ik snap niet waarom jij met 0-0 begint. Je zet ze onder elkaar, en begint rechts.
0-1 = 1, 1 lenen
1-1-1 = 1, 1 lenen
1-1-1 = 1, 1 lenen
0-1-1 = 0, 1 lenen
1-1-1 = 1, 1 lenen
0-1-1 = 0, 1 lenen
1-1-1 = 1, 1 lenen
1-0-1 = 0
Waarbij de extra -1 steeds komt van de geleende 1.
| 1 2 3 | 01111111 ------------ |
0-1 = 1, 1 lenen
1-1-1 = 1, 1 lenen
1-1-1 = 1, 1 lenen
0-1-1 = 0, 1 lenen
1-1-1 = 1, 1 lenen
0-1-1 = 0, 1 lenen
1-1-1 = 1, 1 lenen
1-0-1 = 0
Waarbij de extra -1 steeds komt van de geleende 1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik kom niet uit de volgende integraal:
y(t) = exp(-t) * cos(t)
Ik heb het geprobeerd via partieel integreren, alleen kom niet echt veel verder. Kan iemand het uitleggen?
y(t) = exp(-t) * cos(t)
Ik heb het geprobeerd via partieel integreren, alleen kom niet echt veel verder. Kan iemand het uitleggen?


Partieel integreren waarbij je eerst exp primitiveert en cos differentieert. Bij die nieuwe integraal primitiveer je eerst cos en differentieer je exp (weer partieel dus). Je hebt dan een mooie vergelijking met links en rechts dezelfde integraalquote:Op maandag 12 januari 2009 20:23 schreef WyBo het volgende:
Ik kom niet uit de volgende integraal:
y(t) = exp(-t) * cos(t)
Ik heb het geprobeerd via partieel integreren, alleen kom niet echt veel verder. Kan iemand het uitleggen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb het geprobeerd, maar het is niet gelukt hor. Wat jij dus beweerd is dat als jij 2x partieel integreert je het sommetje op kunt lossen?quote:Op maandag 12 januari 2009 20:31 schreef GlowMouse het volgende:
[..]
Partieel integreren waarbij je eerst exp primitiveert en cos differentieert. Bij die nieuwe integraal primitiveer je eerst cos en differentieer je exp (weer partieel dus). Je hebt dan een mooie vergelijking met links en rechts dezelfde integraal
Maar als ik 2x partieel integreer kom ik op hetzelfde uit namelijk dat de
integraal van exp(-t) * cos(t) gelijk is aan de integraal van exp(-t) * cos(t)
Zo kom je dus toch niet verder of doe ik iets fout?


Zul je zien dat ik het net verkeerd zei. Wat je in de eerste stap als eerste primitiveert maakt eigenlijk niet zoveel uit, zolang je bij de tweede keer partieel integreren maar zorgt dat je bij het primitiveren niet dezelfde term krijgt die je al had.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Modelleer het probleem als een max flow zoals GlowMouse al eerder heeft uitgelegd. Je wilt nu een toewijzing vinden waarbij het aantal kanten naar de put met positieve flow zo klein mogelijk is. Dit kun je doen door kosten toe te wijzen aan deze kanten: kant i krijgt kosten 8i. Nu bereken je met behulp van een max flow min cost de minimale kosten C. Het aantal niet 0 cijfers in de octale representatie van C is nu je gewenste antwoord. Deze niet 0 dingen zullen allemaal op de minst significante posities staan, omdat je anders door verwisseling van de corresponderende deelprojecten de kosten lager kunt krijgen. Het kan ook helemaal niet met minder projecten omdat je dan ook lagere kosten zult krijgen.quote:Op maandag 5 januari 2009 21:22 schreef Borizzz het volgende:
Probleem:
Een project bestaat uit dertig deelprojecten die aan aannemers worden uitbesteed. Voor elk deelproject kunnen max. 7 aannemers zich aanmelden. In totaal melden zich 50 aannemers aan. Van die aannemers zijn er
-5 die op 10 deelprojecten inschrijven,
-5 die op 8 deelprojecten inschrijven
-20 die op 3 deelprojecten inschrijven.
-De overige 20 schrijven op 2 projecten in.
Er wordt niet meer dan één deelproject aan een aannemer toegeschreven.
Gezocht: een ondergrens voor het maximale deelprojecten dat tegelijkertijd kan worden gedaan.
Ik heb t grafentheoretisch aangepakt. maar zit nu flink vast. Wie kan me wat op weg helpen?
Het zou me eigenlijk niet verbazen als er een combinatorisch antwoord is, maar deze truc werkt altijd wel.
Hmmzzz.. bij nader inzien klopt dit algoritme toch niet helemaal. Het geeft een subgraaf met zo min mogelijk opdrachten, maar er kan best een kleinere maximale matching zijn.
[ Bericht 4% gewijzigd door Wolfje op 12-01-2009 22:51:29 (dom!) ]


Dat is een veel mooiere oplossing 
[ Bericht 25% gewijzigd door GlowMouse op 12-01-2009 21:41:47 ]
[ Bericht 25% gewijzigd door GlowMouse op 12-01-2009 21:41:47 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dus als ik het nu goed begrijp, ga je 2x partieel integreren, doe je het vervolgens weer vanaf het begin alleen dan in de andere volgorde, kan je vervolgens de integralen wegstrepen en hou je de oplossing over?quote:Op maandag 12 januari 2009 21:33 schreef GlowMouse het volgende:
Dat is een veel mooiere oplossing
[ afbeelding ]


Als je goed kijkt zie je dat ik twee keer dezelfde term primitiveer 
Welke integralen wil je 'tegen elkaar wegstrepen'?
Welke integralen wil je 'tegen elkaar wegstrepen'?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je hebt op de eerste regel exp(-t) * cos(t) geprimitiveert, en op de tweede ook, alleen in andere volgorde.
Exp(-t) * Cos(t) = [blabla1] - { exp(-t) * cos(t) (eerste regel)
Exp(-t) * Cos(t) = [blabla2] - { exp(-t) * cos (t) (tweede regel)
Je kunt die twee aan elkaar gelijkstellen, de twee integralen op het einde wegstrepen en dan hou je over [blabla1] = [blabla2]
En dan heb je de oplossing?
Exp(-t) * Cos(t) = [blabla1] - { exp(-t) * cos(t) (eerste regel)
Exp(-t) * Cos(t) = [blabla2] - { exp(-t) * cos (t) (tweede regel)
Je kunt die twee aan elkaar gelijkstellen, de twee integralen op het einde wegstrepen en dan hou je over [blabla1] = [blabla2]
En dan heb je de oplossing?


Kijk eens goed, blabla1 = blabla2 en dat wist je al. In principe heb je aan één regel voldoende. Dit was alleen om te laten zien dat het niet uitmaakt hoe je begint.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Kijk maar goed wat er op de eerste regel staat 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Integraal = iets - zelfde integraal. Maar dan kun je de integraal bepalen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Duidelijke vraagquote:Op woensdag 14 januari 2009 12:27 schreef AryaMehr het volgende:
Iemand ervaring met Excel? Moet namelijk morgen een PO Wiskunde inleveren.
Ja, er zitten hier mensen die het wel eens opgestart hebben en er wel eens mee gewerkt hebben
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Gebruik gewoon Mathematica voor wiskunde POs samen met LaTeX, dat werkt een stuk efficiënter dan excel gok ik. 
ff wachten nog


Hangt ervan af waarvoor, ik denk dat je Excel een beetje onderschat.
"Reality is an illusion created by a lack of alcohol."


Vraag over (standaard) multiple regressie analyse
Ik heb één afhankelijke variabele en meerdere onafhankelijke variablen. Alle onafhankelijke variablen zijn gedefinieerd als dummies, en kunnen de waarde 1 of 0 aannemen. Een onafhankelijke variabele is een categorische variabele met 4 mogelijkheden welke is opgedeeld in 3 dummy-variabelen (allen op 0 is de vierde variabele).
Het mag duidelijk zijn dat ik de parameter voor deze dummyvariabelen graag wil gaan berekenen. Nou heb ik echter de volgende vraag:
De onafhankelijke variabelen komen ook gelijktijdig voor, in verschillende combinaties. Als ik de regressie draai komt er een enkele parameter uit voor elke onafhankelijke variabele en niet voor combinaties van variabelen.
Willekeurig voorbeeld ter illustratie:
Het berekenen van de invloed van het gebruik van posters, online bannering, en/of emailcampagne op de verkoopcijfers van concertkaartjes.
De drie onafhankelijke variabelen worden als dummies gemodelleerd (wel of niet aanwezig, intensiteit van campagne laten we even buiten beschouwing). Na standaardregressie krijg ik parameters voor de drie dummies, maar weet bijvoorbeeld nu niet of email en bannering samen méér doen dan wanneer je email en bannering als losstaande acties zou doen.
Vraag:
Mijn oplossing zou zijn om alle voorkomende configuraties elk één dummyvariabele toe te kennen. Dan komen er geen combinaties meer voor in de regressie. Volgens een docent is dit niet nodig, en kan je ook op de eerstgenoemde manier de combinaties en de eventueel daarbij behorende synergieverschijnselen te verklaren; zelfs het geven van een schatting voor combinaties die niet voorkomen in de praktijk.
Wie begrijpt wat ik bedoel, en heeft een idee waar mijn docent op doelt?
Ik heb één afhankelijke variabele en meerdere onafhankelijke variablen. Alle onafhankelijke variablen zijn gedefinieerd als dummies, en kunnen de waarde 1 of 0 aannemen. Een onafhankelijke variabele is een categorische variabele met 4 mogelijkheden welke is opgedeeld in 3 dummy-variabelen (allen op 0 is de vierde variabele).
Het mag duidelijk zijn dat ik de parameter voor deze dummyvariabelen graag wil gaan berekenen. Nou heb ik echter de volgende vraag:
De onafhankelijke variabelen komen ook gelijktijdig voor, in verschillende combinaties. Als ik de regressie draai komt er een enkele parameter uit voor elke onafhankelijke variabele en niet voor combinaties van variabelen.
Willekeurig voorbeeld ter illustratie:
Het berekenen van de invloed van het gebruik van posters, online bannering, en/of emailcampagne op de verkoopcijfers van concertkaartjes.
De drie onafhankelijke variabelen worden als dummies gemodelleerd (wel of niet aanwezig, intensiteit van campagne laten we even buiten beschouwing). Na standaardregressie krijg ik parameters voor de drie dummies, maar weet bijvoorbeeld nu niet of email en bannering samen méér doen dan wanneer je email en bannering als losstaande acties zou doen.
Vraag:
Mijn oplossing zou zijn om alle voorkomende configuraties elk één dummyvariabele toe te kennen. Dan komen er geen combinaties meer voor in de regressie. Volgens een docent is dit niet nodig, en kan je ook op de eerstgenoemde manier de combinaties en de eventueel daarbij behorende synergieverschijnselen te verklaren; zelfs het geven van een schatting voor combinaties die niet voorkomen in de praktijk.
Wie begrijpt wat ik bedoel, en heeft een idee waar mijn docent op doelt?


Wat is je vraag?quote:Op woensdag 14 januari 2009 12:56 schreef Dzy het volgende:
Hangt ervan af waarvoor, ik denk dat je Excel een beetje onderschat.


Synergieverschijnselen kun je niet verklaren met de output die je nu hebt. En het lijkt me ook volkomen logisch dat dat ook niet lukt voor combinaties waarvoor je geen waarnemingen hebt.
Maar onder de aanname dat je dat verschijnsel niet hebt, is je output natuurlijk wel nuttig.
Maar onder de aanname dat je dat verschijnsel niet hebt, is je output natuurlijk wel nuttig.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Synergie zou je natuurlijk wel tot op zekere hoogte kunnen aantonen door combinaties als één variabele te analyseren. Als het effect dan groter is dan wanneer je de variabelen onafhanklijk zou meten, dan is er wel sprake van synergie.quote:Op woensdag 14 januari 2009 15:16 schreef GlowMouse het volgende:
Synergieverschijnselen kun je niet verklaren met de output die je nu hebt. En het lijkt me ook volkomen logisch dat dat ook niet lukt voor combinaties waarvoor je geen waarnemingen hebt.
Maar onder de aanname dat je dat verschijnsel niet hebt, is je output natuurlijk wel nuttig.
Dat je niet-bestaande combinaties zou kunnen verklaren klonk mij ook wat onwaarschijnlijk, maar dat zou kunnen duiden op een miscommunicatie tussen mij en docent.


Vlak voor mijn tentamen nog een stukje grafentheorie. De opgave lijkt makkelijk, maar heb ik toch flink moeite mee.
Gegeven is een boom met p punten. De vraag is hoeveel lijnen men moet toevoegen om er een maximaal vlakke graaf van te maken.
Mijn opl.
Vlakke graaf is een graaf zonder snijdende lijnen. Een graaf is maximaal vlak als er na toevoeging van een nieuwe lijn aan deze graaf een eerste snijdende lijn moet komen.
Een boom is per definitie vlak. P punten en dan is q (aantal lijnen) gelijk aan p-1. Ook voldoet een boom omdat die vlak is aan euler, dus p-q+f=2. Maar op zich brengt dat me nog niet veel verder.
Ga ik het uittekenen in enkele concrete bomen.
Bij p=5 heb ik 4 lijnen. Als ik er 6 lijnen bijzet is ie maximaal vlak.
Bij p=6 heb ik 5 lijnen. Als ik ook hier 6 lijnen erbij zit is het maximaal vlak.
Bij p=7 heb ik 6 lijnen. 8 lijnen erbij totdat die maximaal vlak is.
Ik zie hier nog niet veel in. Iemand die kan helpen? Moet het op een andere manier benaderd worden?

Gegeven is een boom met p punten. De vraag is hoeveel lijnen men moet toevoegen om er een maximaal vlakke graaf van te maken.
Mijn opl.
Vlakke graaf is een graaf zonder snijdende lijnen. Een graaf is maximaal vlak als er na toevoeging van een nieuwe lijn aan deze graaf een eerste snijdende lijn moet komen.
Een boom is per definitie vlak. P punten en dan is q (aantal lijnen) gelijk aan p-1. Ook voldoet een boom omdat die vlak is aan euler, dus p-q+f=2. Maar op zich brengt dat me nog niet veel verder.
Ga ik het uittekenen in enkele concrete bomen.
Bij p=5 heb ik 4 lijnen. Als ik er 6 lijnen bijzet is ie maximaal vlak.
Bij p=6 heb ik 5 lijnen. Als ik ook hier 6 lijnen erbij zit is het maximaal vlak.
Bij p=7 heb ik 6 lijnen. 8 lijnen erbij totdat die maximaal vlak is.
Ik zie hier nog niet veel in. Iemand die kan helpen? Moet het op een andere manier benaderd worden?
kloep kloep


Hmm, dit is ook meer een interesse punt.
Maar heb je een voorbeeld van een maximaal vlakke graaf, want ik heb kon er niets over terug vinden in mijn Dictaat van grafentheorie en op wiki/google kan ik de term ook niet vinden...
Maar heb je een voorbeeld van een maximaal vlakke graaf, want ik heb kon er niets over terug vinden in mijn Dictaat van grafentheorie en op wiki/google kan ik de term ook niet vinden...


Dat is een graaf waarbij je geen nieuwe kanten meer toe kunt voegen zonder een niet-vlakke graaf te krijgen. En een graaf is vlak wanneer je hem in het vlak kunt tekenen zonder dat kanten elkaar kruisen.quote:Op woensdag 14 januari 2009 23:55 schreef PAAC het volgende:
Maar heb je een voorbeeld van een maximaal vlakke graaf
Een voorbeeld is de complete graaf op 4 knopen waarbij je één kant weglaat.
Opgave 43 suggereert dat je 3n-6 kanten krijgt.
[ Bericht 7% gewijzigd door GlowMouse op 15-01-2009 00:15:35 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zonder visuele hulp wordt het er voor mij niet veel duidelijker op... (en dan te bedenken dat ik van plan ben over 2 jaar master (technische) wiskunde wil gaan doen... )quote:Op woensdag 14 januari 2009 23:58 schreef GlowMouse het volgende:
[..]
Dat is een graaf waarbij je geen nieuwe kanten meer toe kunt voegen zonder een niet-vlakke graaf te krijgen. En een graaf is vlak wanneer je hem in het vlak kunt tekenen zonder dat kanten elkaar kruisen.
Een voorbeeld is de complete graaf op 4 knopen waarbij je één kant weglaat.
Opgave 43 suggereert dat je 3n-6 kanten krijgt.


Toch is deze opgave 43 volgens mij (ongeveer) hetgeen je hebben moet. Je weet dat p - q + f = 2. Je kunt een eenvoudige observatie m.b.t. de facetten of mazen maken van de graaf voor p > 3, namelijk elke maas wordt omsloten door minstens drie kanten, anderzijds geldt dat elke kant maximaal deel is van twee mazen (soms ook van 1). Daaruit kun je afleiden, met de eerste formule dat moet gelden: q <= 3p - 6.quote:Op donderdag 15 januari 2009 00:59 schreef PAAC het volgende:
[..]
Zonder visuele hulp wordt het er voor mij niet veel duidelijker op... (en dan te bedenken dat ik van plan ben over 2 jaar master (technische) wiskunde wil gaan doen... )
Hieruit volgt dat je maximale planariteit bereikt door q = 3p - 6.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Mensen ik heb echt dringend hulp nodig.
Ik moet vandaag mijn PO Wiskunde inleveren maar ik kom er niet uit bij de laatste vraag:
Opdracht 5:
a) De kracht van aardbevingen wordt uitgedrukt in getallen van Richter. Maak een omrekingstabel van Richter naar SI eenheden (m/s (binas)) waarbij elke waarde door interpolatie uit te lezen is.
b) Laat aan de hand een grafiek zien of er sprake is van een exponentieel, lineair of machts verband
Een soort gelijke grafiek als het kan:
Als iemand me hiermee kan helpen ben ik hem echt dankbaar. Kom op mensen!
[ Bericht 6% gewijzigd door AryaMehr op 15-01-2009 13:05:52 ]
Ik moet vandaag mijn PO Wiskunde inleveren maar ik kom er niet uit bij de laatste vraag:
Opdracht 5:
a) De kracht van aardbevingen wordt uitgedrukt in getallen van Richter. Maak een omrekingstabel van Richter naar SI eenheden (m/s (binas)) waarbij elke waarde door interpolatie uit te lezen is.
b) Laat aan de hand een grafiek zien of er sprake is van een exponentieel, lineair of machts verband
Een soort gelijke grafiek als het kan:
Als iemand me hiermee kan helpen ben ik hem echt dankbaar. Kom op mensen!
[ Bericht 6% gewijzigd door AryaMehr op 15-01-2009 13:05:52 ]


Schaal van Richter. Let op de exponenten!quote:Op donderdag 15 januari 2009 13:00 schreef AryaMehr het volgende:
Mensen ik heb echt dringend hulp nodig.
Ik moet vandaag mijn PO Wiskunde inleveren maar ik kom er niet uit bij de laatste vraag:
Opdracht 5:
a) De kracht van aardbevingen wordt uitgedrukt in getallen van Richter. Maak een omrekingstabel van Richter naar SI eenheden (m/s (binas)) waarbij elke waarde door interpolatie uit te lezen is.
b) Laat aan de hand een grafiek zien of er sprake is van een exponentieel, lineair of machts verband
Als iemand me hiermee kan helpen ben ik hem echt dankbaar. Kom op mensen!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik denk dat je toch echt zelf wat meer inzet moet tonen dan dit. Je knalt twee vragen online zonder dat je ook maar enige info geeft over waar het niet lukt.quote:Op donderdag 15 januari 2009 13:00 schreef AryaMehr het volgende:
Mensen ik heb echt dringend hulp nodig.
Ik moet vandaag mijn PO Wiskunde inleveren maar ik kom er niet uit bij de laatste vraag:
Opdracht 5:
a) De kracht van aardbevingen wordt uitgedrukt in getallen van Richter. Maak een omrekingstabel van Richter naar SI eenheden (m/s (binas)) waarbij elke waarde door interpolatie uit te lezen is.
b) Laat aan de hand een grafiek zien of er sprake is van een exponentieel, lineair of machts verband
Als iemand me hiermee kan helpen ben ik hem echt dankbaar. Kom op mensen!


De andere vier vragen snap ik wel, alleen kom ik bij de laatste vraag er niet uit. De omrekeningstabel voor Richter naar SI eenheden heb ik al wel, alleen lukt het me maar niet om daar een grafiek van te maken?quote:Op donderdag 15 januari 2009 13:05 schreef TheSilverSpoon het volgende:
[..]
Ik denk dat je toch echt zelf wat meer inzet moet tonen dan dit. Je knalt twee vragen online zonder dat je ook maar enige info geeft over waar het niet lukt.
Misschien dat iemand me kan helpen? Ik snap niks van Excel.


Gewoon een aantal waarden naast elkaar zetten en hier een spreidingsdiagram van tekenen met lineaire regressielijn.
"Reality is an illusion created by a lack of alcohol."


The Richter magnitude scale, or more correctly local magnitude ML scale, assigns a single number to quantify the amount of seismic energy released by an earthquake. It is a base-10 logarithmic scale obtained by calculating the logarithm of the combined horizontal amplitude of the largest displacement from zero on a Wood–Anderson torsion seismometer output. So, for example, an earthquake that measures 5.0 on the Richter scale has a shaking amplitude 10 times larger than one that measures 4.0. The effective limit of measurement for local magnitude is about ML = 6.8.quote:Op donderdag 15 januari 2009 13:36 schreef AryaMehr het volgende:
[..]
De andere vier vragen snap ik wel, alleen kom ik bij de laatste vraag er niet uit. De omrekeningstabel voor Richter naar SI eenheden heb ik al wel, alleen lukt het me maar niet om daar een grafiek van te maken?
Misschien dat iemand me kan helpen? Ik snap niks van Excel.


Voor het tekenen van een grafiek moet je ook echt even in de F1 (Help) van Excel zijn. Het lijkt me niet dat het Bèta Huiswerk- en vragentopic daar de plek voor is, zeker omdat je kennelijk wel de tabel al hebt.quote:Op donderdag 15 januari 2009 14:11 schreef AryaMehr het volgende:
Nou, ik heb het geprobeerd, maar het wil me maar niet lukken met de grafiek.
Het grafiektype dat hiervoor geschikt is, is een spreidingsgrafiek met vloeiende lijn. Als je deze tekent van 0-12 op de schaal van Richter, dan kan je alle tussenliggende waardes aflezen. Je ziet vanzelf wat voor een vorm de grafiek heeft, al kan je dat na de aanwijzingen ook al zien aan de tekst van bijv. wiki.


Waarom pak je meters per seconde? Er zijn meer SI-eenheden hoor, zoals Joule. Daarbij heb je in je tabel intervallen staan bij één punt op de schaal van Richter. Dat kan natuurlijk nooit! Bij elk punt op de schaal van Richter hoort één waarde van de eenheid waarin je het omrekent. Bijvoorbeeld:quote:Op donderdag 15 januari 2009 14:33 schreef AryaMehr het volgende:
De omrekeningstabel:
[ afbeelding ]
Welk grafiek moet ik hier voor gebruiken? Logaritmisch? Maar dan lukt het niet?
0 Kelvin -273,15 Graden Celcius
etc.
Zoals in de eerder geplaatste grafiek dus.
Als je een goede tabel hebt vult Excel zelf de punten in.
Uit nieuwsgierigheid, bij welke klas, vak (A1,2 B1,2) en opleidingsniveau hoort dit?
[ Bericht 0% gewijzigd door TheSilverSpoon op 15-01-2009 16:04:32 ]


Nog even terug naar mijn vraag over grafen.
Gegeven is een boom met p punten. De vraag is hoeveel lijnen men moet toevoegen om er een maximaal vlakke graaf van te maken.
Hoe ik het nu begrijp is dat omdat een boom vlak is dat er geldt p-q+f=2, volgens de formule van Euler. Bij een boom met p punten zet ik nu er steeds lijnen bij zodat het een graaf wordt. Ik vul de graaf net zo lang met lijnen totdat het maximaal vlak geworden is. Uiteraard ontstaan er dan facetten. Bij een boom geldt f=1, bij de maximale graaf is dat een getal groter dan 1.
Bij een maximaal vlakke graaf is elk facet een driehoek. Elk facet heeft dus 3 lijnen en elke lijn grenst aan twee facetten. Hoe komen jullie dan aan q=3p-6?! Ik neem aan dat jullie iets met die voorwaarden doen die ik net opschreef, en dan is het volgens mij nog geen antwoord op de vraag.....
[ Bericht 6% gewijzigd door Borizzz op 15-01-2009 16:11:48 ]
Gegeven is een boom met p punten. De vraag is hoeveel lijnen men moet toevoegen om er een maximaal vlakke graaf van te maken.
Hoe ik het nu begrijp is dat omdat een boom vlak is dat er geldt p-q+f=2, volgens de formule van Euler. Bij een boom met p punten zet ik nu er steeds lijnen bij zodat het een graaf wordt. Ik vul de graaf net zo lang met lijnen totdat het maximaal vlak geworden is. Uiteraard ontstaan er dan facetten. Bij een boom geldt f=1, bij de maximale graaf is dat een getal groter dan 1.
Bij een maximaal vlakke graaf is elk facet een driehoek. Elk facet heeft dus 3 lijnen en elke lijn grenst aan twee facetten. Hoe komen jullie dan aan q=3p-6?! Ik neem aan dat jullie iets met die voorwaarden doen die ik net opschreef, en dan is het volgens mij nog geen antwoord op de vraag.....
[ Bericht 6% gewijzigd door Borizzz op 15-01-2009 16:11:48 ]
kloep kloep


Bij een maximaal vlakke graaf is inderdaad elk facet een driehoek. Stel dat het meer was dan een driehoek, een facet zou door vier punten omgeven worden zodat elk paar punten een buur was, dan zou je 'midden in dit facet' een vijfde punt kunnen tekenen en met de overige vier verbinden en had je K5 in het platte vlak ingebed, terwijl K5 niet-planair (vlak) is, dus dat kan niet. Ergo, als een facet dus al omgegeven wordt door vier lijnen (b.v. een vierkant), dan heb je twee punten die geen buur zijn waartussen je een extra lijn kunt trekken, zo trianguleer je de graaf.quote:Op donderdag 15 januari 2009 16:01 schreef Borizzz het volgende:
Nog even terug naar mijn vraag over grafen.
Gegeven is een boom met p punten. De vraag is hoeveel lijnen men moet toevoegen om er een maximaal vlakke graaf van te maken.
Hoe ik het nu begrijp is dat omdat een boom vlak is dat er geldt p-q+f=2, volgens de formule van Euler. Bij een boom met p punten zet ik nu er steeds lijnen bij zodat het een graaf wordt. Ik vul de graaf net zo lang met lijnen totdat het maximaal vlak geworden is. Uiteraard ontstaan er dan facetten. Bij een boom geldt f=1, bij de maximale graaf is dat een getal groter dan 1.
Bij een maximaal vlakke graaf is elk facet een driehoek. Elk facet heeft dus 3 lijnen en elke lijn grenst aan twee facetten. Hoe komen jullie dan aan q=3p-6?! Ik neem aan dat jullie iets met die voorwaarden doen die ik net opschreef, en dan is het volgens mij nog geen antwoord op de vraag…
Maar nu even terug, we hebben dus dat elke lijn van zo'n driehoek aan 2 facetten grenst, en elk facet aan omgeven wordt door drie lijnen, daaruit volgt: 3f = 2q. Als we dan p - q + f nemen, dan vinden we: 3p - 3q + 3f = 6, dan vullen we in: 3f = 2q, dus: 3p - 3q + 2q = 6, dus 3p - q = 6, ofwel: q = 3p - 6.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Hmm, dat houdt dus in dat je in het algemeen aan een boom 3p-6 lijnen toevoegdt om een maximaal vlakke graaf te maken.
Op zich niet eens zo heel lastig. Maar als zo vaak: hoe kom je erop!
Op zich niet eens zo heel lastig. Maar als zo vaak: hoe kom je erop!
kloep kloep


Ik zou zeggen, je boom heeft nu p punten, en p-1 lijnen, en je moet hebben dat je 3p - 6 lijnen hebt, ofwel, (3p - 6) - (p - 1) = 2p - 5 om erbij te tekenen. Neem b.v. 3 punten: 6 - 5 = 1. neem 4 punten: 8 - 5 = 3. Neem 5 punten: 10 - 5 = 5. (Jij zei gister 6, maar als ik het teken kom ik ook op 5).quote:Op donderdag 15 januari 2009 16:19 schreef Borizzz het volgende:
Hmm, dat houdt dus in dat je in het algemeen aan een boom 3p-6 lijnen toevoegdt om een maximaal vlakke graaf te maken.
Op zich niet eens zo heel lastig. Maar als zo vaak: hoe kom je erop!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik zie idd ook geen logische connectie tussen de Schaal van Richter en snelheid.quote:Op donderdag 15 januari 2009 14:54 schreef TheSilverSpoon het volgende:
[..]
Waarom pak je meters per seconde?
While we're living, the dreams we have as children fade away
AFC Ajax | Borussia Mönchengladbach] | Kansas City Chiefs | Alabama Crimson Tide
AFC Ajax | Borussia Mönchengladbach] | Kansas City Chiefs | Alabama Crimson Tide


Nou dan zal ik die boom met 5 punten wel verkeerd getekend hebben....
Maar bedankt, Iblis! Over twee weekjes tentamen
Over twee weekjes tentamen 
Afgezien van een paar vraagstukken vond ik dit onderdeel makkelijker dan die complexe analyse.
Maar bedankt, Iblis!
Afgezien van een paar vraagstukken vond ik dit onderdeel makkelijker dan die complexe analyse.
kloep kloep


Zijn er wellicht nog inzichten omtrent een mogelijke analyse die tot een antwoord leidt met betrekking tot mijn vraagstuk? Zelf kom ik niet verder dan de mogelijkheid om een beperkt aantal 'profielen' op te stellen uit de combinaties van independent variables die voorkomen in de praktijk, teneinde daar een antwoord op te geven. Maar goed, dan verlies ik gelijk inzicht in de individuele variabelen die ik wel voor handen heb. Om deze reden heb ik al indirect aangedragen dat hij Joule kan gebruiken, want daarin valt Richter wel uit te drukken.
Om deze reden heb ik al indirect aangedragen dat hij Joule kan gebruiken, want daarin valt Richter wel uit te drukken.
Ik vrees dat de vraagsteller denkt dat m/s dé (enige) SI- eenheid is. Overigens knap dat hij toch de tabel met m/s en de schaal van Richter weet te vullen...quote:Op donderdag 15 januari 2009 16:31 schreef zjroentje het volgende:
Ik zie idd ook geen logische connectie tussen de Schaal van Richter en snelheid.


Het is al te laat.quote:Op donderdag 15 januari 2009 16:35 schreef TheSilverSpoon het volgende:
Ik vrees dat de vraagsteller denkt dat m/s dé (enige) SI- eenheid is. Overigens knap dat hij toch de tabel met m/s en de schaal van Richter weet te vullen...Om deze reden heb ik al indirect aangedragen dat hij Joule kan gebruiken, want daarin valt Richter wel uit te drukken.


Ik zou vrolijk de schaal van Richter uitzetten tegen de uitslag van de amplitude van de meetapparatuur.quote:Op donderdag 15 januari 2009 16:35 schreef TheSilverSpoon het volgende:
Ik vrees dat de vraagsteller denkt dat m/s dé (enige) SI- eenheid is. Overigens knap dat hij toch de tabel met m/s en de schaal van Richter weet te vullen...Om deze reden heb ik al indirect aangedragen dat hij Joule kan gebruiken, want daarin valt Richter wel uit te drukken.


Amplitude van de meetapparatuur (in absolute zin) is natuurlijk afhankelijk van de meetapparatuur.quote:Op donderdag 15 januari 2009 19:25 schreef McGilles het volgende:
[..]
Ik zou vrolijk de schaal van Richter uitzetten tegen de uitslag van de amplitude van de meetapparatuur.


Relatieve amplitude danquote:Op donderdag 15 januari 2009 22:58 schreef TheSilverSpoon het volgende:
[..]
Amplitude van de meetapparatuur (in absolute zin) is natuurlijk afhankelijk van de meetapparatuur.


ik loop steeds vast op het omzetten van machten.
zo zou 12,0cm2 hetzelfde moeten zijn als 12,0 x 10^-4 m2, maar ik snap niet hoe het werkt met machten en verschillende inhoudsmaten etc.. wie kan opheldering geven??
zo zou 12,0cm2 hetzelfde moeten zijn als 12,0 x 10^-4 m2, maar ik snap niet hoe het werkt met machten en verschillende inhoudsmaten etc.. wie kan opheldering geven??


12,0 cm² = 12,0 * (m/100)² = 12,0 * m² / 100² = 12,0 * m² * 10-4 = 12,0 * 10-4 m².
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je kunt gebruik maken van het regeltjequote:Op vrijdag 16 januari 2009 14:21 schreef hupseflupse het volgende:
ik loop steeds vast op het omzetten van machten.
zo zou 12,0cm2 hetzelfde moeten zijn als 12,0 x 10^-4 m2, maar ik snap niet hoe het werkt met machten en verschillende inhoudsmaten etc.. wie kan opheldering geven??
(a*b)m = am * bm
waarbij a en b van alles kunnen zijn.
Dus ( 1 centimeter )2 = ( 0,01 meter )2 = (0,01)2 (meter)2 = 10-4m2
Of,
(1 milliliter )3 = (0,001 liter )3 = (0,001)3 (liter)3
= 10-9 L3
Hierbij kun je dan weer gebruik maken van
(am)n = am*n
Dus bijvoorbeeld
(10-2)3 = 10-6
Zo vind ik het altijd handig onthouden
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


thanks! het begint al een beetje te dagen nu 
maar begrijp je deze dan? ;
58940589 mm2 = 5,89 10^7 mm2
= 1,26 10^7 10^-6 m2
= 1,26 10^1 m
stond ergens in een voorbeeld.
(sorry voor het Noob gehalte, ben hier erg slecht in)
maar begrijp je deze dan? ;
58940589 mm2 = 5,89 10^7 mm2
= 1,26 10^7 10^-6 m2
= 1,26 10^1 m
stond ergens in een voorbeeld.
(sorry voor het Noob gehalte, ben hier erg slecht in)


Je hebt 1,26*10^7 mm2quote:Op vrijdag 16 januari 2009 15:55 schreef hupseflupse het volgende:
thanks! het begint al een beetje te dagen nu
maar begrijp je deze dan? ;
58940589 mm2 = 5,89 10^7 mm2
= 1,26 10^7 10^-6 m2
= 1,26 10^1 m
stond ergens in een voorbeeld.
(sorry voor het Noob gehalte, ben hier erg slecht in)
van mm2 naar m2 is 3 stappen (dus 10^-6)
Omdat je 10^7 vermenigvuldigt met 10^- 6 moet je de machten bij elkaar optellen (7+-6= 7-6 =1)
Het antwoord is dus 1,26*10^1


Die tweede regel is gek, je komt niet zomaar op 1,26. Het moet zijn:
58.940.589 mm² = 5,89 107 mm² = 5,89 107 (m/1000)² = 5,89 107 m² / 1000² = 5,89 107 m² *10-6 = 5,89 101 m² = 58,9 m².
58.940.589 mm² = 5,89 107 mm² = 5,89 107 (m/1000)² = 5,89 107 m² / 1000² = 5,89 107 m² *10-6 = 5,89 101 m² = 58,9 m².
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hallo, nog wat over grafentheorie.
In de Petersen-graaf zit de K5 verstopt.
Die is gemakkelijk te zien.
Maar er moet ook de K3,3 inzitten. Deze zie ik niet.
Wie kan me helpen hiermee?
In de Petersen-graaf zit de K5 verstopt.
Die is gemakkelijk te zien.
Maar er moet ook de K3,3 inzitten. Deze zie ik niet.
Wie kan me helpen hiermee?


Je definitie van verstoppen is wat vreemd, maar op wikipedia staat het antwoord.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik kom hier even niet uit. Lineaire algrabra
Laat gegeven zijn het vlak W in R3 met vergelijking x1 + 3x2 - x3 = 0.
(a) Construeer een orthogonale basis van W.
antwoord:
Ik zie wel dat w1 en w2 nulruimten zijn van (1 3 -1 | 0 )
Maar dan? Dan snap ik er niks meer van.
Laat gegeven zijn het vlak W in R3 met vergelijking x1 + 3x2 - x3 = 0.
(a) Construeer een orthogonale basis van W.
antwoord:
Ik zie wel dat w1 en w2 nulruimten zijn van (1 3 -1 | 0 )
Maar dan? Dan snap ik er niks meer van.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Ik weet wat ze bedoelen met contracting, maar dit kan ik niet volgen.quote:Op zondag 18 januari 2009 17:27 schreef GlowMouse het volgende:
Je definitie van verstoppen is wat vreemd, maar op wikipedia staat het antwoord.
Jij wel?
Want ik had wikipedia ook al gevonden, maar kwam toch niet verder.
Wat moet je precies op wat leggen?


Ze maken een vector w2' die loodrecht staat op w1. Andersom kan ook: een vector w1' maken die loodrecht staat op w2.quote:
En zij gebruiken dat de loodrechte projectie van w2 op w1 gegeven wordt door w1Tw2/(w1Tw1) * w1 = -3/2 w1. Het stuk van w2 dat loodrecht op w1 staat, wordt dus gegeven door w2 - (-3/2)w1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Sorry ik snap het antwoord nog helemaal niet, wat is nou eigenlijk het antwoord?quote:Op zondag 18 januari 2009 17:40 schreef GlowMouse het volgende:
[..]
Ze maken een vector w2' die loodrecht staat op w1. Andersom kan ook: een vector w1' maken die loodrecht staat op w2.
En zij gebruiken dat de loodrechte projectie van w2 op w1 gegeven wordt door w1Tw2/(w1Tw1) * w1 = -3/2 w1. Het stuk van w2 dat loodrecht op w1 staat, wordt dus gegeven door w2 - (-3/2)w1.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Het antwoord gaf je zelf al, maar loodrecht projecteren is dus het tussenstapje.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je definitie van 'verstoppen' vond ik nogal vreemd, maar het is een minor zoals uiteengezet op http://en.wikipedia.org/wiki/Minor_(graph_theory)quote:Op zondag 18 januari 2009 18:19 schreef Beo_beo het volgende:
GlowMouse, waarom mag dat punt zomaar verwijden?
Dat is toch geen contractie dan?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoi Allen.
Hier een vraagje over statistiek. Heb daar al jaren niet echt meer iets mee gedaan, dus dat is een beetje weggezakt. Ik heb een bepaald experiment op twee verschillende manieren uitgevoerd en heb daarmee twee datasets vergaard (een lijstje gemiddeldes). Wat ik nu wil weten is of de ene methode beter is dan de andere, oftewel, ik wel weten of er een significant verschil zit tussen de twee datasets.
Welke statistische toets kan ik hiervoor het best gebruiken? Ik heb dus gemiddelde A (gebaseerd op 10 datapunten) en gemiddelde B (ook gebaseerd op 10 datapunten) en ik wil dus weten of A en B significant van elkaar verschillen.
Wie kan mijn geheugen even opfrissen?
EDIT: Diep in mijn geheugen graven leverde de t-toets op. Is dit een goede test om te gebruiken? En zo ja, hoe gebruik je deze ook weer? Als ik in de tabel opzoek bij 9 vrijheidsgraden en 0.05 dan vind ik een t-waarde van 1.833. Als ik de t-waarde van mijn toets uitrekenen, is het verschil dan signicant als "berekende waarde > tabelwaarde" of juist andersom?
[ Bericht 20% gewijzigd door Bioman_1 op 19-01-2009 10:29:18 ]
Hier een vraagje over statistiek. Heb daar al jaren niet echt meer iets mee gedaan, dus dat is een beetje weggezakt. Ik heb een bepaald experiment op twee verschillende manieren uitgevoerd en heb daarmee twee datasets vergaard (een lijstje gemiddeldes). Wat ik nu wil weten is of de ene methode beter is dan de andere, oftewel, ik wel weten of er een significant verschil zit tussen de twee datasets.
Welke statistische toets kan ik hiervoor het best gebruiken? Ik heb dus gemiddelde A (gebaseerd op 10 datapunten) en gemiddelde B (ook gebaseerd op 10 datapunten) en ik wil dus weten of A en B significant van elkaar verschillen.
Wie kan mijn geheugen even opfrissen?
EDIT: Diep in mijn geheugen graven leverde de t-toets op. Is dit een goede test om te gebruiken? En zo ja, hoe gebruik je deze ook weer? Als ik in de tabel opzoek bij 9 vrijheidsgraden en 0.05 dan vind ik een t-waarde van 1.833. Als ik de t-waarde van mijn toets uitrekenen, is het verschil dan signicant als "berekende waarde > tabelwaarde" of juist andersom?
[ Bericht 20% gewijzigd door Bioman_1 op 19-01-2009 10:29:18 ]
Theories come and theories go. The frog remains


Je moet je eerst afvragen wat beter is. Hoger gemiddelde, grotere mediaan, kleinere variantie, etc.
De two-sample t-test is een goede test op het gemiddelde wanneer je niets over de variantie weet, maar daarvoor moeten de waarnemingen wel uit een normale verdeling komen. Omdat je maar 10 waarnemingen hebt is die aanname erg cruciaal. Wie zegt anders immers dat de verwachting bestaat? Je bent dan aangewezen op een parametervrije toets.
De two-sample t-test is een goede test op het gemiddelde wanneer je niets over de variantie weet, maar daarvoor moeten de waarnemingen wel uit een normale verdeling komen. Omdat je maar 10 waarnemingen hebt is die aanname erg cruciaal. Wie zegt anders immers dat de verwachting bestaat? Je bent dan aangewezen op een parametervrije toets.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


tnx. Ik zat ook al te denken over de "normale verdeling aanname". Ik denk dat de Wilcoxon signed-rank test het best werkt voor wat ik wil doen. Zal daar eens verder naar kijken.quote:Op maandag 19 januari 2009 11:33 schreef GlowMouse het volgende:
Je moet je eerst afvragen wat beter is. Hoger gemiddelde, grotere mediaan, kleinere variantie, etc.
De two-sample t-test is een goede test op het gemiddelde wanneer je niets over de variantie weet, maar daarvoor moeten de waarnemingen wel uit een normale verdeling komen. Omdat je maar 10 waarnemingen hebt is die aanname erg cruciaal. Wie zegt anders immers dat de verwachting bestaat? Je bent dan aangewezen op een parametervrije toets.
Theories come and theories go. The frog remains


Dat lijkt me een goede keus. Houd er alleen rekening mee dat parametervrije toetsen een onjuiste nulhypothese niet zo snel verwerpen, dus zolang je niet verwerpt heb je niet zo'n sterke uitspraak.quote:Op maandag 19 januari 2009 11:41 schreef Bioman_1 het volgende:
[..]
tnx. Ik zat ook al te denken over de "normale verdeling aanname". Ik denk dat de Wilcoxon signed-rank test het best werkt voor wat ik wil doen. Zal daar eens verder naar kijken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Licht valt onder een hoek van 45 graden in op een gelijkzijdig (alle hoeken 60 graden) prisma. De brekingsindex van het prisma bedraagt 1,54.
Bereken onder welke hoek het licht het prisma verlaat.
---
Mijn idee:
Je begint natuurlijk met theta = arcsin(sin[45]*1,54). theta = 27,33 graden.
Dan beredeneer ik:
Licht valt loodrecht in, dus 90 graden - 27,33 graden = 62,66 graden aan het linkerbeen in de driehoek die aan de top van de prisma wordt gevormd.
Een driehoek heeft 180 graden, dus 180 - (60+62,66) = 57,33 graden voor het rechterbeen van de driehoek. Daar valt het licht loodrecht uit (in een hoek met 90 graden dus), en 90 - 57,33 = 32,66 voor de hoek van 'inval' als ik opnieuw de wet van snellius ga toepassen.
Dit geeft voor de hoek van uitval: theta = arcsin(sin[32,33]*1,54) = 55,44 graden.
Maar het antwoord is 56,3 graden. Maak ik een fout of is dit een kwestie van afronding?
[ Bericht 1% gewijzigd door Koewam op 20-01-2009 23:19:23 ]


1. dit is het wiskunde-topic, niet voor natuurkunde dus
2. arcsin(sin[32,66]*1,54) geeft bij mij een juist antwoord
3. die hoek vind je sneller door de beide normalen te tekenen en te gebruiken dat de som van hoeken in een vierhoek 360 graden is
2. arcsin(sin[32,66]*1,54) geeft bij mij een juist antwoord
3. die hoek vind je sneller door de beide normalen te tekenen en te gebruiken dat de som van hoeken in een vierhoek 360 graden is
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


1. Wist nog niet dat dit gesplitst was, bedankt.
2. Ah gos ja, overtikfout. Bedankt.
3. Is de hoek die de twee normalen op het snijpunt maakt 90 graden? Tophoek 60, twee hoeken in de normalen 90 + 90, opgeteld is dat 240. 360 - 240 = 120. Ik snap niet hoe dat werkt.
2. Ah gos ja, overtikfout. Bedankt.
3. Is de hoek die de twee normalen op het snijpunt maakt 90 graden? Tophoek 60, twee hoeken in de normalen 90 + 90, opgeteld is dat 240. 360 - 240 = 120. Ik snap niet hoe dat werkt.


90 graden inderdaad want het is een normaal. Dan kom je op 120 graden uit voor de onderste hoek. Dan gebruik je de driehoek waarvan één zijde gegeven wordt door de lichtstraal en de andere twee door de normalen om die 32,66 graden te vinden. Scheelt 1x rekenen en is denk ik ook makkelijker uit te tekenen en begrijpbaar te maken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik ben niet van 't kansrekenen en statistiek en ik kom niet uit deze simpele vraagstelling.
"Uit een onderzoek op basis van een steekproef met omvang 25 bleek een gemiddelde van 76 met een foutmarge van 12 voor een betrouwbaarheid van 95%. Vermeld het 95% betrouwbaarheidsinterval."
Er moet 64 tot 88 uitkomen maar hoe? Geen idee, ik heb hier nooit les in gehad..
"Uit een onderzoek op basis van een steekproef met omvang 25 bleek een gemiddelde van 76 met een foutmarge van 12 voor een betrouwbaarheid van 95%. Vermeld het 95% betrouwbaarheidsinterval."
Er moet 64 tot 88 uitkomen maar hoe? Geen idee, ik heb hier nooit les in gehad..
Ik ben een superster want ik drink jupiler!


Een betrouwbaarheidsinterval is een interval dat, wanneer telkens op dezelfde wijze geconstrueerd, naar verwachting in een vast percentage van de gevallen (hier: 95%) de juiste parameter bevat. Die parameter is hier de verwachting. Het begrip foutmarge ken ik niet, maar is blijkbaar op analoge wijze gedefinieerd. Daar het gemiddelde een schatter is voor de verwachting (mits de verwachting bestaat), zijn de grenzen van het betrouwbaarheidsinterval 76 +/- 12.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Potdomme dat was wel erg simpel, maar ik snap er nu wat meer van. Dankjewel.
Ik ben een superster want ik drink jupiler!


Dilemma hiero:
TEG x sin(30) - TEC cos(45) = 0
TEG x cos(30) - TEC sin(45) - 20 = 0
*met sin(30) bedoel ik sinus 30 graden enz.
Ik moet TEC en TEG weten dmv substitueren oid
woensdag tentamen!
[ Bericht 7% gewijzigd door Marthh op 25-01-2009 12:59:31 ]
TEG x sin(30) - TEC cos(45) = 0
TEG x cos(30) - TEC sin(45) - 20 = 0
*met sin(30) bedoel ik sinus 30 graden enz.
Ik moet TEC en TEG weten dmv substitueren oid
woensdag tentamen!
[ Bericht 7% gewijzigd door Marthh op 25-01-2009 12:59:31 ]


schrijf bijvoorbeeld de eerste vergelijking als TEG = TEC cos(45) / sin(30).quote:Op zondag 25 januari 2009 12:45 schreef Marthh het volgende:
Dilemma hiero:
TEG x sin(30) - TEC cos(45) = 0
TEG x cos(30) - TEC sin(45) - 20 = 0
*met sin(30) bedoel ik sinus 30 graden enz.
Ik moet TEC en TEG weten dmv substitueren oid
woensdag tentamen!
Dit vul je dan in de 2e vergelijking in, zodat de 2e vergelijking alleen nog maar de variabele TEC bevat. Die kan je oplossen, en de gevonden waarde voor TEC vul je dan weer in de eerste vergelijking in om de oplossing voor de andere variabele te vinden.
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


quote:Op zondag 25 januari 2009 20:57 schreef Pietjuh het volgende:
[..]
schrijf bijvoorbeeld de eerste vergelijking als TEG = TEC cos(45) / sin(30).
Dit vul je dan in de 2e vergelijking in, zodat de 2e vergelijking alleen nog maar de variabele TEC bevat. Die kan je oplossen, en de gevonden waarde voor TEC vul je dan weer in de eerste vergelijking in om de oplossing voor de andere variabele te vinden.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik snap de methode, maar waarom is TEG = TEC cos(45) / sin(30)?quote:Op zondag 25 januari 2009 20:57 schreef Pietjuh het volgende:
[..]
schrijf bijvoorbeeld de eerste vergelijking als TEG = TEC cos(45) / sin(30).
Dit vul je dan in de 2e vergelijking in, zodat de 2e vergelijking alleen nog maar de variabele TEC bevat. Die kan je oplossen, en de gevonden waarde voor TEC vul je dan weer in de eerste vergelijking in om de oplossing voor de andere variabele te vinden.


Elementaire algebra, brugklas niveau. Als geldt ab - cd = 0 en b is ongelijk aan 0, dan geldt a = cd/b.quote:Op maandag 26 januari 2009 21:26 schreef Marthh het volgende:
[..]
Ik snap de methode, maar waarom is TEG = TEC cos(45) / sin(30)?
Overigens geldt sin 30° = ½ en sin 45° = cos 45° = ½√2, dus daar zou ik even mee beginnen.


Okee snapquote:Op maandag 26 januari 2009 22:20 schreef Riparius het volgende:
[..]
Elementaire algebra, brugklas niveau. Als geldt ab - cd = 0 en b is ongelijk aan 0, dan geldt a = cd/b.
Overigens geldt sin 30° = ½ en sin 45° = cos 45° = ½√2, dus daar zou ik even mee beginnen.
eindelijk


Ik heb twee vraagjes:
1)
F*cos(30)=0,2*(400+F*sin(30))
Hoe bereken ik F uit? Antwoord is 104,4N.
2)
Je hebt twee vectoren:
V1=
(x4+x2-1/2d)cos(...)
(x4+x2-1/2d)sin(...)
0
Fz=
0
-mg
0
Wat is dan V1*Fz? Hoe moet je dat doen? Het antwoord is:
V1*Fz:
0
0
-(x4+x2-1/2d)cos(...)mg
Alvast bedankt
[ Bericht 37% gewijzigd door BK89 op 27-01-2009 12:45:21 ]
1)
F*cos(30)=0,2*(400+F*sin(30))
Hoe bereken ik F uit? Antwoord is 104,4N.
2)
Je hebt twee vectoren:
V1=
(x4+x2-1/2d)cos(...)
(x4+x2-1/2d)sin(...)
0
Fz=
0
-mg
0
Wat is dan V1*Fz? Hoe moet je dat doen? Het antwoord is:
V1*Fz:
0
0
-(x4+x2-1/2d)cos(...)mg
Alvast bedankt
[ Bericht 37% gewijzigd door BK89 op 27-01-2009 12:45:21 ]


je haalt alles met een F erin naar de linker kant, dan krijg je
F*cos(30)-,2*F*sin(30)=80
F(cos(30)-,2*sin(30))=80
F=80/(cos(30)-,2*sin(30))=104,35 (niet gelet op significantie)
En van die vectoren heb ik ook geen idee, bedoel je die * als een dot-product of niet?
Ik zou zeggen dat het overigens
0
-(x4+x2-1/2d)sin(...)mg
0
zou worden
F*cos(30)-,2*F*sin(30)=80
F(cos(30)-,2*sin(30))=80
F=80/(cos(30)-,2*sin(30))=104,35 (niet gelet op significantie)
En van die vectoren heb ik ook geen idee, bedoel je die * als een dot-product of niet?
Ik zou zeggen dat het overigens
0
-(x4+x2-1/2d)sin(...)mg
0
zou worden
ff wachten nog


Bedankt voor het uitleg van vraag 1, zal zo ff proberenquote:Op dinsdag 27 januari 2009 13:32 schreef Game_Error het volgende:
je haalt alles met een F erin naar de linker kant, dan krijg je
F*cos(30)-,2*F*sin(30)=80
F(cos(30)-,2*sin(30))=80
F=80/(cos(30)-,2*sin(30))=104,35 (niet gelet op significantie)
En van die vectoren heb ik ook geen idee, bedoel je die * als een dot-product of niet?
Ik zou zeggen dat het overigens
0
-(x4+x2-1/2d)sin(...)mg
0
zou worden


Er is een andere optie voor vraag 1 die ik kan bedenken, en dat is dat ze het cross-product nemen, deze methode is bedoelt om een vector te vinden die orthogonaal staat op de originele 2 vectoren, in de geval levert dat dus:
0
0
-(x4+x2-1/2d)cos(...)mg
Precies wat jij zocht.
0
0
-(x4+x2-1/2d)cos(...)mg
Precies wat jij zocht.
ff wachten nog


Inmiddels ben ik wat stappen verder met eerdere vragen die nog onbeantwoord waren gebleven. Echter, nu doet het volgende zich voor.
Bij een normale multiple regressie bekijk ik de verkoop van verschillende producten als afhankelijke variabele en gebruik verschillende marketingacties als onafhankelijke factoren (dummyvariabelen). Aangezien de producten onderling nogal verscihllen in hun standaardverkoopvolume (sommige bijv. 100stuks/mnd en andere 500st/mnd compenseer ik daarvoor door voor ieder product een dummyvariabele aan te maken in de regressie (eigenlijk een dummy minder, omdat allemaal 0 het referentieproduct is). Het model heeft een behoorlijke fit en de parameters zijn nagenoeg allemaal significant.
Stel, de waarde voor de constante is 1000 (dus 1000 stuks per maand), en de waarde voor drie parameters die staan voor een actie zijn respectievelijk 200, 400 en 300.
Dan is mijn interpretatie dat het individueel uitvoeren van deze acties dezelfde toename aan verkoop veroorzaken. Actie 1: 1200 totaal ; Actie 2 1400 totaal; Actie 3 1300 totaal.
Nou is bijvoorbeeld de parameter voor de dummy van product X= -500 (de basisverkoop van product X ligt dus zo'n 500 producten/mnd lager), het lijkt me dan niet redelijk om aan te nemen dat de verkoop toeneemt met 200 als je actie 1 uitvoert. Mag ik wel de relatieve toename van de constante icm een actie (bijv 20% voor actie 1) gebruiken om het effect van actie 1 op product X uit te drukken? Dat zou dan betekenen dat de verwachting is dat actie 1 icm met product x een verkoop van ongeveer 600 producten zou opleveren.
Bij een normale multiple regressie bekijk ik de verkoop van verschillende producten als afhankelijke variabele en gebruik verschillende marketingacties als onafhankelijke factoren (dummyvariabelen). Aangezien de producten onderling nogal verscihllen in hun standaardverkoopvolume (sommige bijv. 100stuks/mnd en andere 500st/mnd compenseer ik daarvoor door voor ieder product een dummyvariabele aan te maken in de regressie (eigenlijk een dummy minder, omdat allemaal 0 het referentieproduct is). Het model heeft een behoorlijke fit en de parameters zijn nagenoeg allemaal significant.
Stel, de waarde voor de constante is 1000 (dus 1000 stuks per maand), en de waarde voor drie parameters die staan voor een actie zijn respectievelijk 200, 400 en 300.
Dan is mijn interpretatie dat het individueel uitvoeren van deze acties dezelfde toename aan verkoop veroorzaken. Actie 1: 1200 totaal ; Actie 2 1400 totaal; Actie 3 1300 totaal.
Nou is bijvoorbeeld de parameter voor de dummy van product X= -500 (de basisverkoop van product X ligt dus zo'n 500 producten/mnd lager), het lijkt me dan niet redelijk om aan te nemen dat de verkoop toeneemt met 200 als je actie 1 uitvoert. Mag ik wel de relatieve toename van de constante icm een actie (bijv 20% voor actie 1) gebruiken om het effect van actie 1 op product X uit te drukken? Dat zou dan betekenen dat de verwachting is dat actie 1 icm met product x een verkoop van ongeveer 600 producten zou opleveren.


Dan heb je je regressiemodel verkeerd gespecificeerd.quote:Op dinsdag 27 januari 2009 21:00 schreef TheSilverSpoon het volgende:
Nou is bijvoorbeeld de parameter voor de dummy van product X= -500 (de basisverkoop van product X ligt dus zo'n 500 producten/mnd lager), het lijkt me dan niet redelijk om aan te nemen dat de verkoop toeneemt met 200 als je actie 1 uitvoert.
Nee.quote:Mag ik wel de relatieve toename van de constante icm een actie (bijv 20% voor actie 1) gebruiken om het effect van actie 1 op product X uit te drukken? Dat zou dan betekenen dat de verwachting is dat actie 1 icm met product x een verkoop van ongeveer 600 producten zou opleveren.
[ Bericht 0% gewijzigd door GlowMouse op 27-01-2009 21:22:20 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op dinsdag 27 januari 2009 21:11 schreef GlowMouse het volgende:
Dan heb je je regressiemodel verkeerd gespecificeertd.
Door de producten als binaire variabelen mee te nemen in de regressievergelijking compenseer ik voor het verkoopvolume dat veroorzaakt wordt door het product zelf. Deze werkwijze is mij nota bene door een docent aangeraden, en we hebben het samen ook doorgelopen. Zelf had ik meer met het idee om de verschillende producten aan te duiden (nesten) in de termen van de dummies. Dus product i in week t.
Dat de parameter voor de constante (een product met baseline rond de 1000) hoger is dan een ander product is niet gek. Als de parameter voor een ander product lager is, dan is daar niets geks aan als die parameter negatief is. Dus iets meer argumentatie zou welkom zijn
De fit van het model is zoals gezegd ook hoog, R square rond de 0,8 en adjusted R square rond de 0,77.


Als jij je model specificeert als verkoop = b0 + b1*actie1 + b2*actie2 + b3*actie3 + b4*product1 + b5*product2 + b6*product 3 + b7*product4 + ... + eps, dan geef je daarmee aan dat je verwacht dat de verkopen van een willekeurig product ceteris paribus met b1 toenemen wanneer je actie1 laat lopen voor dat product. Zeg je vervolgens dat je niet denkt dat dat het geval is, is je model onjuist gespecificeerd. Dan zul je kruistermen mee moeten nemen tussen producten en acties en een grote R² dat dat gaat geven!.quote:Op dinsdag 27 januari 2009 21:20 schreef TheSilverSpoon het volgende:
[..]
Door de producten als binaire variabelen mee te nemen in de regressievergelijking compenseer ik voor het verkoopvolume dat veroorzaakt wordt door het product zelf. Deze werkwijze is mij nota bene door een docent aangeraden, en we hebben het samen ook doorgelopen. Zelf had ik meer met het idee om de verschillende producten aan te duiden (nesten) in de termen van de dummies. Dus product i in week t.
Een hoge (adjusted) R² zegt niet zoveel. Zeker hier, waar je een groot deel 'verklaart' met de juiste dummycategorie.quote:De fit van het model is zoals gezegd ook hoog, R square rond de 0,8 en adjusted R square rond de 0,77.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Op de wijze die jij schetst heb ik het inderdaad ingevoerd.quote:Op dinsdag 27 januari 2009 21:29 schreef GlowMouse het volgende:
[..]
Als jij je model specificeert als verkoop = b0 + b1*actie1 + b2*actie2 + b3*actie3 + b4*product1 + b5*product2 + b6*product 3 + b7*product4 + ... + eps, dan geef je daarmee aan dat je verwacht dat de verkopen van een willekeurig product ceteris paribus met b1 toenemen wanneer je actie1 laat lopen voor dat product. Zeg je vervolgens dat je niet denkt dat dat het geval is, is je model onjuist gespecificeerd. Dan zul je kruistermen mee moeten nemen tussen producten en acties en een grote R² dat dat gaat geven!.
Ik laat het model uiteindelijk draaien in 4 sets (productcategorieën) omdat ik verwacht dat daar wel verschillen optreden, en doe inderdaad daarmee de aanname dat het effect voor de verschillende producten gelijk is. Let wel, ik verwacht dat het relatieve effect gelijk is voor verschillende producten. Volgens jou kan ik dat nooit op deze wijze berekenen?
Stel: Product X (basisverkoop van 100) en product Y is de constante met een basisverkoop van 400.
Als ik de fomule bekijk, dan wordt inderdaad het effect van de basisverkoop opgevangen door de productdummy. Dat is vrij simpel. Maar, als ik het goed begrijp (en zie), dan levert een actie bij product X met een toename van 10%, maar een hele kleine bijdrage aan de parameter vergeleken met een actie van product Y met dezelfde relatieve toename. Respectievelijk 10 en 40. Dit is dan ook de reden dat je hier niet de toename van de verkoop uit kan halen voor verschillende producten.
Wat zou jij suggereren? Een model met 'nested' variabelen, waarbij ik het product opneem in de parameter; dus bijv: Dummy voor actie 1, voor product i in week t
Dat is ook helemaal waar, zeker aangezien het om ongeveer 27 producten gaat, en slechts 8 andere dummies.quote:Een hoge (adjusted) R² zegt niet zoveel. Zeker hier, waar je een groot deel 'verklaart' met de juiste dummycategorie.


Als je relatieve veranderingen wilt bekijken, moet je logaritmen in je model opnemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Mmm, daar heb ik al wat van gezien inderdaad. Maar de huidige specificatie van het model geeft ook niet eens de absolute verandering aan als ik het goed zie, zoals ik probeerde te verwoorden in vorige post, n´est pas?quote:Op dinsdag 27 januari 2009 22:05 schreef GlowMouse het volgende:
Als je relatieve veranderingen wilt bekijken, moet je logaritmen in je model opnemen.


Waarom je de week toe wilt voegen snap ik niet, maar afgezien daarvan is het wat ik eerder bedoelde met kruistermen. Je voegt als regressoren actie1*product1, actie1*product2, etc toe. Je verlaat daarmee wel de gedachte van de gelijke relatieve verandering voor ieder product, hoewel dat met wat lineaire restricties op de regressiecoëfficienten wel te verhelpen is.quote:Op dinsdag 27 januari 2009 22:23 schreef TheSilverSpoon het volgende:
[..]
Mmm, daar heb ik al wat van gezien inderdaad. Maar de huidige specificatie van het model geeft ook niet eens de absolute verandering aan als ik het goed zie, zoals ik probeerde te verwoorden in vorige post, n´est pas?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


(Vergeet ik nog te zeggen, maar bedankt voor je input! Zit nu in 't buitenland zonder boeken, en kan derhalve ook niet de slag maken die ik gedacht had te maken. Ik lijk redelijk op 't verkeerde been gezet door de docent, zeker omdat hij weet waar ik naar toe werk.)quote:Op dinsdag 27 januari 2009 22:25 schreef GlowMouse het volgende:
Waarom je de week toe wilt voegen snap ik niet, maar afgezien daarvan is het wat ik eerder bedoelde met kruistermen. Je voegt als regressoren actie1*product1, actie1*product2, etc toe. Je verlaat daarmee wel de gedachte van de gelijke relatieve verandering voor ieder product, hoewel dat met wat lineaire restricties op de regressiecoëfficienten wel te verhelpen is.
Week voeg ik toe omdat het belangrijk is. In het model is het dan ook eigenlijk:
Verkoop(product i, week t) = b0 + b1*actie1(product i week t) + b2*actie2(product i week t) + b3*actie3(product i week t) + b4*product1 + b5*product2(product i week t) + b6*product 3(product i week t) + b7*product4(product i week t) + ... + eps
In woorden: de aanwezigheid van de acties is afhankelijk van de week en het product. Voor alle producten heb ik tientallen weken aan data. Week is niet zozeer belangrijk voor de tijd als wel om elke 'case' de juiste dummywaarden mee te geven op basis van het weeknummer.
Mmm, gelijke relatieve verandering wil ik juist wel aanhouden, op z'n minst per productgroep (bestaande uit zo'n 5-8 producten).
Bovenstaande formule komt uit een gelijksoortig onderzoek. In dit geval wordt er gepooled over de verschillende winkels (waar ongetwijfeld ook andere baseline sales zijn), ik zou dan kunnen poolen over de productsoorten. (Later wordt nog een formule gegeven voor de omrekening van de parameter naar het percentage toename dat een actie veroorzaakt.
Overigens worden acties hier wel als combinatie gezien, en niet los behandeld.


t heeft bij jouw de functie van wat je normaal als i hebt: je onderscheid er de cases mee. Echte mensen werken met vectornotatie en vermelden daarmee alle cases in 1x zodat je die t niet hoeft te noemen. Zolang t maar niet in je regressoren terugkomt is het goed.
Als prod1 dan 2x zoveel verkocht wordt als prod2 bijvoorbeeld, kun je zeggen dat de coefficient bij prod1*actie1 tweemaal zo groot moet zijn als bij prod1*actie2. Met zulke lineaire restricties is een model nog eenvoudig te schatten.
Als prod1 dan 2x zoveel verkocht wordt als prod2 bijvoorbeeld, kun je zeggen dat de coefficient bij prod1*actie1 tweemaal zo groot moet zijn als bij prod1*actie2. Met zulke lineaire restricties is een model nog eenvoudig te schatten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De restricties zijn dan weer discutabel, temeer omdat de baseline sales mede-afhankelijk is van het effect van de parameters. Vicieuze cirkel zou ik denken?quote:Op dinsdag 27 januari 2009 23:07 schreef GlowMouse het volgende:
t heeft bij jouw de functie van wat je normaal als i hebt: je onderscheid er de cases mee. Echte mensen werken met vectornotatie en vermelden daarmee alle cases in 1x zodat je die t niet hoeft te noemen. Zolang t maar niet in je regressoren terugkomt is het goed.
Als prod1 dan 2x zoveel verkocht wordt als prod2 bijvoorbeeld, kun je zeggen dat de coefficient bij prod1*actie1 tweemaal zo groot moet zijn als bij prod1*actie2. Met zulke lineaire restricties is een model nog eenvoudig te schatten.
Zal m'n docent eens aanschrijven, en zal 't resultaat dan we weer posten. Je suggesties en uitleg worden meegenomen.


Je wilt het toch proportioneel aan de verkopen? Wat loop je dan met de baseline sales, die zijn daarvoor helemaal niet van belang.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat is ook zo, ik leg het als leek ook niet al te best uit (uiteindelijke interesse ligt ook meer in de implicaties vande uitkomst dan de weg er naar toe).quote:Op dinsdag 27 januari 2009 23:30 schreef GlowMouse het volgende:
Je wilt het toch proportioneel aan de verkopen? Wat loop je dan met de baseline sales, die zijn daarvoor helemaal niet van belang.
Ik noem de baseline sales steeds omdat het model daar nu op stukloopt. Als dat allemaal gelijk was geweest, en de aanname dat activiteiten gelijke impact hadden voor de verschillende producten, dan had ik het wel kunnen toepassen.


Ik heb een testmodel gemaakt met daarin gefingeerde waardes zodat ik voor mijzelf wat meer begrip kreeg over de betekenis en effect van een en ander. Op de huidige manier liep het model compleet mank op het moment dat de basisverkoop van de producten onderling sterk uiteenliep.
Door de ln toe te passen op de verkoopcijfers krijg ik een parameter die ik middels een formule terug kan rekenen naar een percentage (relatieve toename). Het testmodel laat een fit van (niet gek) R square=1 zien, en de omgerekende parameters geven exact de groei aan die ik gegeven heb tijdens actieperiodes.
Dit heb ik ook toegepast op mijn eigen model en data, en de fit is daarmee weer een stuk toegenomen, nu tot zo'n 0,85R square. Ook de significantie van de 'acties' is sterk toegenomen hierdoor.
Hiermee lijkt mijn probleem opgelost.
[ Bericht 8% gewijzigd door TheSilverSpoon op 28-01-2009 08:19:05 ]
Door de ln toe te passen op de verkoopcijfers krijg ik een parameter die ik middels een formule terug kan rekenen naar een percentage (relatieve toename). Het testmodel laat een fit van (niet gek) R square=1 zien, en de omgerekende parameters geven exact de groei aan die ik gegeven heb tijdens actieperiodes.
Dit heb ik ook toegepast op mijn eigen model en data, en de fit is daarmee weer een stuk toegenomen, nu tot zo'n 0,85R square. Ook de significantie van de 'acties' is sterk toegenomen hierdoor.
Hiermee lijkt mijn probleem opgelost.
[ Bericht 8% gewijzigd door TheSilverSpoon op 28-01-2009 08:19:05 ]


Als je een hoge R² zoekt, heb ik nog wel een programma dat alle combinaties van regressoren en kruistermen afgaat en zo naar de beste fit zoekt 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Kan iemand mij uitleggen stapgewijs hoe je dit naar echelon vorm moet vegen:
1 -3 4 -4
3 -7 7 -8
-4 6 -1 4
En hoe kan je daarna zien of er oneindig veel oplossing zijn of niet?
Alvast bedankt
1 -3 4 -4
3 -7 7 -8
-4 6 -1 4
En hoe kan je daarna zien of er oneindig veel oplossing zijn of niet?
Alvast bedankt


drie keer de eerste rij van de tweede rij aftrekken
1 -3 4 -4
0 2 -5 4
-4 5 -1 4
vier keer de eerste rij bij de derde rij optellen
1 -3 4 -4
0 2 -5 4
0 -6 15 -12
tweede rij door twee delen
1 -3 4 -4
0 1 -5/2 2
0 -6 15 -12
tweede rij 3x bij de eerste/6x bij de derde optellen
1 0 -7/2 2
0 1 -5/2 2
0 0 0 0
Nu heb je x1 - 7/2 x3 = 2 en x2 -5/2 x3 = 2. Als je x3 vrij kiest, liggen x1 en x2 vast: x1 = 2 + 7/2 x3 en x2 = 2 + 5/2 * x3.
1 -3 4 -4
0 2 -5 4
-4 5 -1 4
vier keer de eerste rij bij de derde rij optellen
1 -3 4 -4
0 2 -5 4
0 -6 15 -12
tweede rij door twee delen
1 -3 4 -4
0 1 -5/2 2
0 -6 15 -12
tweede rij 3x bij de eerste/6x bij de derde optellen
1 0 -7/2 2
0 1 -5/2 2
0 0 0 0
Nu heb je x1 - 7/2 x3 = 2 en x2 -5/2 x3 = 2. Als je x3 vrij kiest, liggen x1 en x2 vast: x1 = 2 + 7/2 x3 en x2 = 2 + 5/2 * x3.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik moet m.b.v. Six Sigma een verbeterplan maken om de uitval van studenten in jaar 1 te verbeteren. Ik heb geen idee hoe en waar ik moet beginnen. Moet ik gewoon het DMAIC schema invullen? Hiervoor heb ik niet alle gegevens en deze worden ook niet verstrekt. Wie o wie kan me hierbij helpen?? Bij voorbaat dank!


Dit is een wiskundeotopic, je kunt beter naar een ander huiswerktopic gaan.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt, volgens mij lukt het nu met de echelon vorm zoekenquote:Op woensdag 28 januari 2009 13:19 schreef GlowMouse het volgende:
drie keer de eerste rij van de tweede rij aftrekken
1 -3 4 -4
0 2 -5 4
-4 5 -1 4
vier keer de eerste rij bij de derde rij optellen
1 -3 4 -4
0 2 -5 4
0 -6 15 -12
tweede rij door twee delen
1 -3 4 -4
0 1 -5/2 2
0 -6 15 -12
tweede rij 3x bij de eerste/6x bij de derde optellen
1 0 -7/2 2
0 1 -5/2 2
0 0 0 0
Nu heb je x1 - 7/2 x3 = 2 en x2 -5/2 x3 = 2. Als je x3 vrij kiest, liggen x1 en x2 vast: x1 = 2 + 7/2 x3 en x2 = 2 + 5/2 * x3.


Zoek eens op wat vrije variabelen zijn en hoe zich dat in deze matrix laat vertalen naar oneindig veel oplossingen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Lekker cynisch... Het model dat ik gebruik is een model dat meer gebruikt wordt in het onderzoeksgebied. Dat de fit niet heilig is heb ik al eerder bevestigd, in dit geval is het model wel verbeterd door de toevoeging die ik heb gedaan.quote:Op woensdag 28 januari 2009 09:50 schreef GlowMouse het volgende:
Als je een hoge R² zoekt, heb ik nog wel een programma dat alle combinaties van regressoren en kruistermen afgaat en zo naar de beste fit zoekt


In mijn boek wordt een punt op een lijn genoemd (x,x/(1+x)) Ik snap niet precies wat er met deze notatie genoemd wordt, dit is toch geen punt?


Een coordinaat bestaat normaal uit een x- en y-coordinaat. Bv (2,3)
Nu is de x coordinaat gewoon x.
De y coordinaat is nu x/(1+x)
De formule van dit verhaal is dus y = x/(1+x) als ik je verhaal goed begrijp.
Nu is de x coordinaat gewoon x.
De y coordinaat is nu x/(1+x)
De formule van dit verhaal is dus y = x/(1+x) als ik je verhaal goed begrijp.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


En jij doet Harvard?quote:Op zaterdag 31 januari 2009 23:06 schreef nickybol het volgende:
In mijn boek wordt een punt op een lijn genoemd (x,x/(1+x)) Ik snap niet precies wat er met deze notatie genoemd wordt, dit is toch geen punt?
IL-uni's zijn ook niet meer wat het geweest is.
Ten percent faster with a sturdier frame


Ik hoop dat iemand mij even wil helpen.
Mijn neefje heeft een proeftoets meegekregen voor wiskunde en er is mij gevraagd om hem hiermee te helpen (echter kom ik niet uit onderstaande).
Kan iemand mij helpen?
Ik kan onderstaande niet vinden op zijn rekenmachine (type FX-82MS). Al reeds op google gekeken, echter niks kunnen vinden. Wellicht dat één van jullie dit weet.
Tevens bij opdracht 3 kom ik er niet uit met de uitkomst.
Bij onderstaande 3 kom ik er helemaal niet uit.
Wellicht "NEWBIE" vragen maar mij lukt het niet en uit het boek (Basis Wiskunde van Kees van den Hoek wordt ik al helemaal niks wijzer)..
Alvast bedankt voor de hulp
Mijn neefje heeft een proeftoets meegekregen voor wiskunde en er is mij gevraagd om hem hiermee te helpen (echter kom ik niet uit onderstaande).
Kan iemand mij helpen?
Ik kan onderstaande niet vinden op zijn rekenmachine (type FX-82MS). Al reeds op google gekeken, echter niks kunnen vinden. Wellicht dat één van jullie dit weet.
Tevens bij opdracht 3 kom ik er niet uit met de uitkomst.
Bij onderstaande 3 kom ik er helemaal niet uit.
Wellicht "NEWBIE" vragen maar mij lukt het niet en uit het boek (Basis Wiskunde van Kees van den Hoek wordt ik al helemaal niks wijzer)..
Alvast bedankt voor de hulp


Welke 'onderstaande 3'? Er staan er helemaal geen 3 onder waar je dat zegt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


2a: 1.06^(-20)
2b: Vlak onder on zit het knopje voor de derdemachtswortel. Vierdemachtswortel gaat via 4[shift]^170.
2c: log(89)/log(3)
2b: Vlak onder on zit het knopje voor de derdemachtswortel. Vierdemachtswortel gaat via 4[shift]^170.
2c: log(89)/log(3)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Super hier kan ik iets mee!!!quote:Op zondag 1 februari 2009 12:37 schreef GlowMouse het volgende:
2a: 1.06^(-20)
2b: Vlak onder on zit het knopje voor de derdemachtswortel. Vierdemachtswortel gaat via 4[shift]^170.
2c: log(89)/log(3)


Ah shit, gewoon een afleesfoutje. Ik ben nog steeds in de war met die punten en die komma's sinds ik hier in Amerika ben aangekomen en zit weer veel te moeilijk te denken. Gewoon een simpel coordinaat dus.. Thanks anywayquote:Op zaterdag 31 januari 2009 23:18 schreef -J-D- het volgende:
Een coordinaat bestaat normaal uit een x- en y-coordinaat. Bv (2,3)
Nu is de x coordinaat gewoon x.
De y coordinaat is nu x/(1+x)
De formule van dit verhaal is dus y = x/(1+x) als ik je verhaal goed begrijp.


Nee, eerder een interpretatiefout. Daarom kun je ook beter een puntkomma gebruiken als scheidingsteken bij coördinaten, dus bijv. (2;3) en (0,5;1,5). Bijna niemand die het doet, terwijl het toch zo'n voor de hand liggende oplossing is. Maar het lost de verwarring rond het gebruik van de punt en de komma als decimaal scheidingsteken natuurlijk niet op. In Nederland gebruikt niemand een komma als scheidingsteken voor duizendtallen maar wel een punt, en dus zou het oprukkende Angelsaksische gebruik van de punt als decimaal scheidingsteken in ieder geval in Nederland ontmoedigd moeten worden.quote:Op zondag 1 februari 2009 19:56 schreef nickybol het volgende:
[..]
Ah shit, gewoon een afleesfoutje. Ik ben nog steeds in de war met die punten en die komma's sinds ik hier in Amerika ben aangekomen en zit weer veel te moeilijk te denken. Gewoon een simpel coordinaat dus.. Thanks anyway


Is het internationaal niet meestal een punt als decimaal scheidingsteken in plaats van een komma? Hier in Amerika is het alleen maar een punt als decimaal scheidingsteken, en wordt een komma gebruikt voor duizendtallen.


Nullen kun je beter schrappen door te vermenigvuldigen met machten van 10. Zodoende blijft alleen het decimale scheidingsteken over, dat punt of komma, dat maakt zoveel niet uit. Een voordeel van deze notatie is dat je geen onterechte nauwkeurigheid aan een waarde koppelt.quote:Op maandag 2 februari 2009 04:41 schreef nickybol het volgende:
Is het internationaal niet meestal een punt als decimaal scheidingsteken in plaats van een komma? Hier in Amerika is het alleen maar een punt als decimaal scheidingsteken, en wordt een komma gebruikt voor duizendtallen.


quote:Op maandag 2 februari 2009 04:41 schreef nickybol het volgende:
Is het internationaal niet meestal een punt als decimaal scheidingsteken in plaats van een komma? Hier in Amerika is het alleen maar een punt als decimaal scheidingsteken, en wordt een komma gebruikt voor duizendtallen.
Blauw is punt, groen is komma, rood is iets Arabisch. In veel wetenschappelijke literatuur vind je wel de '.'. Let overigens op de briljante situatie in Canada.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Opgave 3a of heel opgave 3?quote:Op zondag 1 februari 2009 12:31 schreef peter070 het volgende:
Tevens bij opdracht 3 kom ik er niet uit met de uitkomst.
anyways, bij opgave 3 ga je eerst buiten haakjes werken en dan krijg je
| 1 |
Vervolgens weet ik niet meer wat de officiele stap is dat je moet doen, wiskunde is iets te lang geleden, maar mijn instinct zegt dat je eerst de vergelijking uitrekent (waarbij zijn de twee kanten gelijk), en vervolgens pak je een getal net boven en en net daaronder, waardoor je weet wanneer de vergelijking klopt..
| 1 2 3 4 5 6 7 8 | -3x - 12 = 2x +1/2 0 = x + 12 1/2 x = -12 1/2 als je dan uitrekent voor x = -13 komt er uit 27 < 26.5, en voor x = -12 24 < 24.5 -13 < -12, dus de uitkomst is x => -12 1/2 |
Mijn wiskunde is te ver weggezakt en dit kan vast veel sneller en makkelijker


quote:Op zondag 1 februari 2009 12:31 schreef peter070 het volgende:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | a) q(a) = 5 - 1 = 4000 kg b) evenwicht = q(a) = q(v) => -2 1/2p + 20 = p -1 => 0 = 3.5p - 21 => 21 = 3.5p => p = 6 evenwichtsprijs = 6 euro evenwichtshoeveelheid = 5000 kilo c) aanbodsoverschot van 3500 kg => q(a) - q(v) = 3.5 p-1 - (-2.5p + 20) = 3.5 p -1 +2.5p -20 = 3.5 3.5p -21 = 3.5 3.5p = 24.5 p = 7 euro even controleren aanbod = 7-1 = 6000 kilo vraag = -2.5 x 7 + 20 = 2500 kilo d) deze vraag begrijp ik ook niet :P |


d: q_v = -2.5 * 5.5 + 20 = 6250 kg ; q_a = 4500 kg. Het verschil, 1750 kg, zal de overheid moeten importeren voor 12250 euro.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik begreep voornamelijk de vraagstelling nietquote:Op maandag 2 februari 2009 11:30 schreef GlowMouse het volgende:
d: q_v = -2.5 * 5.5 + 20 = 6250 kg ; q_a = 4500 kg. Het verschil, 1750 kg, zal de overheid moeten importeren voor 12250 euro.


Ik begrijp hem ook niet maar het is het enige dat je kan doenquote:Op maandag 2 februari 2009 11:35 schreef Stranger het volgende:
[..]
Ik begreep voornamelijk de vraagstelling nietZe moeten wiskunde niet te praktijkgericht proberen te maken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | 6 3 96 2 6 72 1 1 18 640 560 b) W = 640x + 560y c) 6x + 3y <= 96 (constructie), wordt versimpeld tot 2x + y <= 32 2x + 6y <= 72 (bekleding), wordt versimpeld tot x + 3y <= 36 x + y <= 18 (vewerking) d) het toegestane gebied teken je in een assenstelsel. Mijn paint skillss zijn niet zo goed, maar om je een beeld te geven, het ziet er ongeveer zo uit: |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | Roze = Bekleding Rood = afwerking Groen = de niveaulijn gevraagd bij e) f) Zoals je in de grafiek ziet, zijn er 4 hoekpunten, namelijk (16,0), (0,12) en de snijpunten van rood en roze en rood en blauw, welke, als je de grafiek goed tekent, (9,9) en (14,4) zijn. Je vult dit allemaal in de formule voor W in en dan krijg je op (16,0) = 10240 (0,12) = 6720 (9,9) = 10800 (14,4) = 11200 Dus bij 14 fauteuils en 4 sofa's is de maximale winst g) Ik denk dat je hier de tabel opnieuw moet invullen maar dan verrekend met het aantal fauteuils en sofa's dat je maakt 84 uur 12 uur 96 uur 28 uur 24 uur 52 uur 14 uur 4 uur 18 uur 8960 2240 11200 h) uit de tabel af te lezen: bekleding, houdt 20 uur over. |


Even logica:
Gewoon een puzzeltje. Ben benieuwd of iemand de oplossing ziet!
Hier staan 10 genummerde beweringen. Hoeveel ervan zijn waar?
1. Precies één van deze beweringen is onwaar.
2. Precies twee van deze beweringen zijn onwaar.
3. Precies drie van deze beweringen zijn onwaar.
4. Precies vier van deze beweringen zijn onwaar.
5. Precies vijf van deze beweringen zijn onwaar.
6. Precies zes van deze beweringen zijn onwaar.
7. Precies zeven van deze beweringen zijn onwaar.
8. Precies acht van deze beweringen zijn onwaar.
9. Precies negen van deze beweringen zijn onwaar.
10. Precies tien van deze beweringen zijn onwaar.
Gewoon een puzzeltje. Ben benieuwd of iemand de oplossing ziet!
Hier staan 10 genummerde beweringen. Hoeveel ervan zijn waar?
1. Precies één van deze beweringen is onwaar.
2. Precies twee van deze beweringen zijn onwaar.
3. Precies drie van deze beweringen zijn onwaar.
4. Precies vier van deze beweringen zijn onwaar.
5. Precies vijf van deze beweringen zijn onwaar.
6. Precies zes van deze beweringen zijn onwaar.
7. Precies zeven van deze beweringen zijn onwaar.
8. Precies acht van deze beweringen zijn onwaar.
9. Precies negen van deze beweringen zijn onwaar.
10. Precies tien van deze beweringen zijn onwaar.
kloep kloep


Ik gok dat 1 bewering waar is, namelijk: 9. Precies negen van deze beweringen zijn onwaar.
ff wachten nog


Er kan er duidelijk ten hoogste één waar zijn, en dan zijn er dus tenminste negen onwaar.
Maar het antwoord van Game_Error heeft toch geen onderbouwing nodig? Of wil je dat hij nog aanwijst welke 9 er dan onwaar zijn
Maar het antwoord van Game_Error heeft toch geen onderbouwing nodig? Of wil je dat hij nog aanwijst welke 9 er dan onwaar zijn
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Game_error zijn antwoord is prima inderdaad. Ik heb nog een vraagje, ik moet met behulp van Maple op twee manieren differentiëren, namelijk met de definitie (lim h->0 van (f(x-h)-f(x))/h) en gewoon met diff. Hier komen twee voor mijn oog verschillende functies uit, maar deze horen natuurlijk hetzelfde te zijn. Dit moet ik ook aantonen, maar hoe doe ik dit? (Ben nog niet zo skilled in Maple..)
"Reality is an illusion created by a lack of alcohol."


Allebei vereenvoudigen? De verschilfunctie vereenvoudigen en op de nulfunctie uitkomen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


je kunt vlg mij niet voorkomen dat maple soms een 'rare' output geeft voor twee dezelfde uitkomsten.
kun je niet gewoon beide uitkomsten plotten en over elkaar heenleggen?
welke maple invoer heb je gebruikt?
kun je niet gewoon beide uitkomsten plotten en over elkaar heenleggen?
welke maple invoer heb je gebruikt?
kloep kloep


Om welke functie gaat het?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Het gaat om de functie:
f(x) = (sqrt(x) * ln(1+x^2)) / (2 + cos(x))
ik ga er morgen mee verder ik ben bekaf en maple even goed zat nu... ik heb al duizend wazige errors gehad.
f(x) = (sqrt(x) * ln(1+x^2)) / (2 + cos(x))
ik ga er morgen mee verder ik ben bekaf en maple even goed zat nu... ik heb al duizend wazige errors gehad.
"Reality is an illusion created by a lack of alcohol."


Mijn maple-sessie.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | |\^/| Maple 12 (X86 64 LINUX) ._|\| |/|_. Copyright (c) Maplesoft, a division of Waterloo Maple Inc. 2008 \ MAPLE / All rights reserved. Maple is a trademark of <____ ____> Waterloo Maple Inc. | Type ? for help. > f := x -> (sqrt(x) * ln(1+x^2)) / (2 + cos(x)); 2 sqrt(x) ln(1 + x ) f := x -> ------------------ 2 + cos(x) > r1 := simplify(diff(f(x), x)); 2 2 2 2 r1 := 1/2 (2 ln(1 + x ) + 2 ln(1 + x ) x + ln(1 + x ) cos(x) 2 2 2 2 2 + ln(1 + x ) cos(x) x + 8 x + 4 x cos(x) + 2 x ln(1 + x ) sin(x) 3 2 / 1/2 2 2 + 2 x ln(1 + x ) sin(x)) / (x (1 + x ) (4 + 4 cos(x) + cos(x) )) / > r2 := simplify(limit((f(x + h)-f(x))/(h), h=0)); 2 2 2 2 r2 := 1/2 (2 ln(1 + x ) + 2 ln(1 + x ) x + ln(1 + x ) cos(x) 2 2 2 2 2 + ln(1 + x ) cos(x) x + 8 x + 4 x cos(x) + 2 x ln(1 + x ) sin(x) 3 2 / 1/2 + 2 x ln(1 + x ) sin(x)) / (x / 2 2 2 2 2 (4 + 4 cos(x) + cos(x) + 4 x + 4 x cos(x) + x cos(x) )) > simplify(r1 - r2); 0 > QED |
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Maple TA, wat een ramp was dat programma zeg, ik ben blij dat we er maar 4 weken mee hebben moeten werken... 
En over die logica, 9 is gewoon de enige die kan kloppen als je ze nagaat, ik heb geen idee hoe ik dat moet bewijzen. Logica is nooit mijn sterkste kant geweest moet ik zeggen.
En over die logica, 9 is gewoon de enige die kan kloppen als je ze nagaat, ik heb geen idee hoe ik dat moet bewijzen. Logica is nooit mijn sterkste kant geweest moet ik zeggen.
ff wachten nog


Glowmouse heeft het in feite al gezegd. Alle uitspraken sluiten elkaar uit, d.w.z. als 1 waar is, is 2 t/m 10 niet waar, als 2 waar is zijn 1 en 3 t/m 10 niet waar, enz. Ergo, er kan er hooguit één waar zijn, en er zijn er minstens 9 onwaar. En verder spreekt 10 zichzelf tegen, aangezien er maar 10 beweringen zijn. Blijft over dat alleen 9 waar kan zijn.quote:Op dinsdag 3 februari 2009 02:39 schreef Game_Error het volgende:
En over die logica, 9 is gewoon de enige die kan kloppen als je ze nagaat, ik heb geen idee hoe ik dat moet bewijzen. Logica is nooit mijn sterkste kant geweest moet ik zeggen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


De groeifactor per week is 1.5.
Hoe groot is de groeifactor per dag?
Antwoordmodel: De groeifactor per week is 1,5^0.25=1.107
Hoe komt het bij die 0.25?
Hoe groot is de groeifactor per dag?
Antwoordmodel: De groeifactor per week is 1,5^0.25=1.107
Hoe komt het bij die 0.25?


Mits exponentiële groei zou het antwoord 1.5^(1/7) moeten zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Lijkt mij ook.quote:Op dinsdag 3 februari 2009 15:51 schreef julian6 het volgende:
Dat dacht ik dus ook, misschien staat er weer een fout in dat antwoordmodelboek.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja inderdaad, als je dit fout doet ben je duidelijk slecht in wiskunde.quote:Op dinsdag 3 februari 2009 15:55 schreef julian6 het volgende:
Wat een amateurs die wiskundeboekmakers
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


xe-machts-wortel?quote:Op woensdag 4 februari 2009 17:52 schreef julian6 het volgende:
Kort heel dom vraagje: hoe noem je een √ teken met een x ervoor/erop?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


een xe machtswortel.quote:Op woensdag 4 februari 2009 17:52 schreef julian6 het volgende:
Kort heel dom vraagje: hoe noem je een √ teken met een x ervoor/erop?
Edit: Iblis was mij voor.


x√ heeft geen betekenis, zo los. x√9 is gewoon ‘x maal wortel 9’.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Gast... ik stel de vraag niet, ik probeer er juist meer duidelijkheid over te krijgen wat de vraag precies is. Maar toch bedankt voor de oplossing van mijn plaatje, ik had me bijna opgeknoopt bij het zien van deze opgave.quote:Op woensdag 4 februari 2009 17:59 schreef Superbaddd het volgende:
Het is n-de machtswortel uit a.


In het algemeen. Specifieker.
Want, 642 = 4096, 163 = 4096, en 84 = 4096.
En in het algemeen geldt dat:
Maar x√4096 is gewoon x*64.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:23:41 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


ja maar dan een x ipv die n, hoe noem je die?quote:Op woensdag 4 februari 2009 17:56 schreef TheSilverSpoon het volgende:
[..]
Je zei: ervoor/erop... wat is het nou?
[ afbeelding ]
??


Graag gedaan GASTquote:Op woensdag 4 februari 2009 18:01 schreef TheSilverSpoon het volgende:
[..]
Gast... ik stel de vraag niet, ik probeer er juist meer duidelijkheid over te krijgen wat de vraag precies is. Maar toch bedankt voor de oplossing van mijn plaatje, ik had me bijna opgeknoopt bij het zien van deze opgave.


Als je er een n zet dan is het een ne machtswortel, bij een x is het een xe machtswortel... je begrijpt het idee inmiddels wel. Dat getal geeft de macht van de wortel aan, niets meer niets minder.quote:Op woensdag 4 februari 2009 18:06 schreef julian6 het volgende:
ja maar dan een x ipv die n, hoe noem je die?
Zie de smiley boven mijn vorige post, dan zijn de caps niet nodigquote:


stomme vraag, maar nu kom ik uit iets heel simpels niet eens meer uit 
je staat op 400m van een kerk af de toren is 130 meter hoog, welke hoek kijk je nu naar de toren toe
het is toch tan= 130/400....
wat zie ik over t hoofd? het antwoord moet rond de 18 graden liggen maar ik kom er niet uit....
je staat op 400m van een kerk af de toren is 130 meter hoog, welke hoek kijk je nu naar de toren toe
het is toch tan= 130/400....
wat zie ik over t hoofd? het antwoord moet rond de 18 graden liggen maar ik kom er niet uit....
Op donderdag 22 mei 2008 10:28 schreef Spittie het volgende:
swarma spam hoer
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.


tangens(hoek) = 130/400 inderdaad, en daaruit volgt dat hoek ~= 18 graden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


arctan(130/400) = 18,0quote:Op woensdag 4 februari 2009 22:13 schreef swarmahoer het volgende:
stomme vraag, maar nu kom ik uit iets heel simpels niet eens meer uit
je staat op 400m van een kerk af de toren is 130 meter hoog, welke hoek kijk je nu naar de toren toe
het is toch tan= 130/400....
wat zie ik over t hoofd? het antwoord moet rond de 18 graden liggen maar ik kom er niet uit....
Staat je rekenmachine wel op graden, en niet op radialen?
Ten percent faster with a sturdier frame


ow kut ik heb er nog naar gekeken maar deg is het dusquote:Op woensdag 4 februari 2009 22:15 schreef TC03 het volgende:
[..]
arctan(130/400) = 18,0
Staat je rekenmachine wel op graden, en niet op radialen?
wat is arctan
Op donderdag 22 mei 2008 10:28 schreef Spittie het volgende:
swarma spam hoer
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.


ow tan -1 ik zie het al 
Op donderdag 22 mei 2008 10:28 schreef Spittie het volgende:
swarma spam hoer
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.


tan(hoek) = 130/400
Links wil je hoek hebben, dus je wilt 'tan' weghalen. Dat doe je met zijn inverse functie. Er geldt arctan(tan(hoek)) = hoek (voor hoeken tussen -90 en 90 graden).
Links wil je hoek hebben, dus je wilt 'tan' weghalen. Dat doe je met zijn inverse functie. Er geldt arctan(tan(hoek)) = hoek (voor hoeken tussen -90 en 90 graden).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De inverse van de tangens functie. Maar als je dat niet begrijpt, dan heb je de opgave dus ook niet echt begrepen (dat is iets anders dan het juiste antwoord produceren).quote:Op woensdag 4 februari 2009 22:23 schreef swarmahoer het volgende:
[..]
ow kut ik heb er nog naar gekeken maar deg is het dus
wat is arctan


dank jullie  ik heb t ooit in de 3e gehad
ik heb t ooit in de 3e gehad  allang mn examen enzo gehad dus was al weer weggezakt
allang mn examen enzo gehad dus was al weer weggezakt  en dacht dat radiaal voor graden was maar natuurlijk is dat degree
en dacht dat radiaal voor graden was maar natuurlijk is dat degree 
Op donderdag 22 mei 2008 10:28 schreef Spittie het volgende:
swarma spam hoer
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.


Even een check voor de zekerheid:
Stel je hebt een driehoek met A (1,-2), B (5,4) en C(10,5). Gevraagd is de vergelijking van de omgeschreven cirkel van de driehoek.
** mijn concept oplossing: ik stel vergelijkingen op van 2 middelloodlijnen op van zijden van de driehoek. Snijpunt van deze twee geeft met het middelpunt van de gevraagde cirkel. De straal haal ik dan uit de afstand van het middelpunt tot een van beide hoekpunten
** alternatief: vul de punten gewoon in de algemene vergelijking van cirkel. Dit kan ook wel eens een stelsel van vergelijkingen opleveren met onbekenden. Wat gefrutsel ofzo en dan moet je het ook kunnen vinden...
Stel je hebt een driehoek met A (1,-2), B (5,4) en C(10,5). Gevraagd is de vergelijking van de omgeschreven cirkel van de driehoek.
** mijn concept oplossing: ik stel vergelijkingen op van 2 middelloodlijnen op van zijden van de driehoek. Snijpunt van deze twee geeft met het middelpunt van de gevraagde cirkel. De straal haal ik dan uit de afstand van het middelpunt tot een van beide hoekpunten
** alternatief: vul de punten gewoon in de algemene vergelijking van cirkel. Dit kan ook wel eens een stelsel van vergelijkingen opleveren met onbekenden. Wat gefrutsel ofzo en dan moet je het ook kunnen vinden...
kloep kloep


LIjken me beide juiste oplossingen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Met de tweede kom je ook constructief op een antwoord.quote:Op zaterdag 7 februari 2009 08:42 schreef Smart-Einstein het volgende:
De eerste lijkt me wel beter, want die tweede is meer trial and error.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oh Iblis nog heel erg bedankt, ik las het net pas 
"Reality is an illusion created by a lack of alcohol."


Nee. Noem de coördinaten van het middelpunt van de cirkel (p;q) en de straal van de cirkel r, dan krijg je een stelsel van drie vergelijkingen met drie onbekenden p,q,r dat je op gewoon kunt lossen. Niks trial and error dus.quote:Op zaterdag 7 februari 2009 08:42 schreef Smart-Einstein het volgende:
De eerste lijkt me wel beter, want die tweede is meer trial and error.


dat zijn vergelijkingen die zijn analytisch (bijna) niet oplosbaar, alleen numeriek... gewoon trial and error dusquote:Op zaterdag 7 februari 2009 13:16 schreef Riparius het volgende:
[..]
Nee. Noem de coördinaten van het middelpunt van de cirkel (p;q) en de straal van de cirkel r, dan krijg je een stelsel van drie vergelijkingen met drie onbekenden p,q,r dat je op gewoon kunt lossen. Niks trial and error dus.


Die zijn prima oplosbaar. Ik denk zelfs dat het op papier sneller gaat dan de vergelijkingen van de middelloodlijnen opstellen.quote:Op zaterdag 7 februari 2009 15:15 schreef Smart-Einstein het volgende:
[..]
dat zijn vergelijkingen die zijn analytisch (bijna) niet oplosbaar, alleen numeriek... gewoon trial and error dus
Met de pc gaat het nog sneller: ik vul die drie vergelijkingen in en druk op solve en krijg zo de exacte oplossing. Nog voordat jij ook maar één vergelijking van een middelloodlijn gevonden hebt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De PC doet het numeriek ja, is dus ook niet exact. Schrijf het maar een uit op papier, je krijgt een ongelooflijk gore uitdrukking die zo niet op te lossen is. Het gaat om een stelsel niet lineaire vergelijkingen he..quote:Op zaterdag 7 februari 2009 15:18 schreef GlowMouse het volgende:
[..]
Die zijn prima oplosbaar. Ik denk zelfs dat het op papier sneller gaat dan de vergelijkingen van de middelloodlijnen opstellen.
Met de pc gaat het nog sneller: ik vul die drie vergelijkingen in en druk op solve en krijg zo de exacte oplossing. Nog voordat jij ook maar één vergelijking van een middelloodlijn gevonden hebt.
Daarom is (denk ik) de methode met de middelloodlijnen sneller


De pc doet het niet numeriek, de software die ik gebruik niet althans. Ik krijg netjes breuken als antwoord.quote:Op zaterdag 7 februari 2009 15:27 schreef Smart-Einstein het volgende:
[..]
De PC doet het numeriek ja, is dus ook niet exact. Schrijf het maar een uit op papier, je krijgt een ongelooflijk gore uitdrukking die zo niet op te lossen is. Het gaat om een stelsel niet lineaire vergelijkingen he..
Daarom is (denk ik) de methode met de middelloodlijnen sneller
En zo onmogelijk is de uitdrukking nou ook weer niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je krijg wel een enorm vieze substitutie met een wortel in een wortel.quote:Op zaterdag 7 februari 2009 15:34 schreef GlowMouse het volgende:
[..]
De pc doet het niet numeriek, de software die ik gebruik niet althans. Ik krijg netjes breuken als antwoord.
En zo onmogelijk is de uitdrukking nou ook weer niet.
Maar ik ben wel geintereseerd, welk programma gebruik jij dan? Dan kun je zeker ook alle tussenstappen zien als het een niet numeriek programma is?


We hebben:quote:Op zaterdag 7 februari 2009 15:38 schreef Smart-Einstein het volgende:
[..]
Je krijg wel een enorm vieze substitutie met een wortel in een wortel.
(1) (x-1)²+(y+2)² = c²
(2) (x-5)²+(y-4)² = c²
(3) (x-10)²+(y-5)² = c²
(1) en (2) levert y = 3 - 2/3 x
(2) en (3) levert y = 42 - 5x
Merk op dat dit gewoon de vergelijkingen van twee middelloodlijnen zijn. Je komt dus op hetzelfde uit, maar dan sneller.
Scientific Workplace. Tussenstapjes zie je niet, maar ik weet ook niet of je die wel wilt zien. Een computer redeneert nooit hetzelfde als een mens.quote:Op zaterdag 7 februari 2009 15:38 schreef Smart-Einstein het volgende:
Maar ik ben wel geintereseerd, welk programma gebruik jij dan? Dan kun je zeker ook alle tussenstappen zien als het een niet numeriek programma is?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nee. Je had het beter gewoon even met potlood en papier uit kunnen proberen. Heb je helemaal geen computerprogramma voor nodig. De clou is dat je twee lineaire vergelijkingen in p en q overhoudt als je de tweede vergelijking van de eerste aftrekt en de derde vergelijking van de tweede. De kwadratische termen vallen dan immers allemaal tegen elkaar weg. En een stelsel van twee lineaire vergelijkingen met twee onbekenden is heel eenvoudig op te lossen. Heb je p en q, dan is het kwadraat van r, en daarmee r, ook eenvoudig te bepalen uit één der drie oorspronkelijke vergelijkingen. Niet zo smart dus die opmerkingen van je.quote:Op zaterdag 7 februari 2009 15:38 schreef Smart-Einstein het volgende:
[..]
Je krijg wel een enorm vieze substitutie met een wortel in een wortel.
Maar ik ben wel geintereseerd, welk programma gebruik jij dan? Dan kun je zeker ook alle tussenstappen zien als het een niet numeriek programma is?


Rpiarius, bij je laatste drie posts krijg ik het idee dat je het alleen maar doet om mij te herhalen 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nee. Bij de eerste van de drie door jouw genoemde posts zou je dat inderdaad kunnen denken, maar ik wist op dat moment niet dat jij een soortgelijk antwoord postte, dat kun je zien aan het tijdsverschil van één minuut. Bij de laatste twee herhaal ik jou niet zozeer, maar geef ik een antwoord op de opmerkingen van Smart-Einstein (wat een nick in dit verband...) vanuit een iets andere invalshoek.quote:Op zaterdag 7 februari 2009 16:26 schreef GlowMouse het volgende:
Rpiarius, bij je laatste drie posts krijg ik het idee dat je het alleen maar doet om mij te herhalen


Niet zo serieus reageren  op mijn opmerking dan, verder worden je bijdragen hooglijk gewaardeerd
op mijn opmerking dan, verder worden je bijdragen hooglijk gewaardeerd
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zaterdag 7 februari 2009 15:55 schreef GlowMouse het volgende:
[..]
We hebben:
(1) (x-1)²+(y+2)² = c²
(2) (x-5)²+(y-4)² = c²
(3) (x-10)²+(y-5)² = c²
(1) en (2) levert y = 3 - 2/3 x
(2) en (3) levert y = 42 - 5x
Merk op dat dit gewoon de vergelijkingen van twee middelloodlijnen zijn. Je komt dus op hetzelfde uit, maar dan sneller.
[..]
Scientific Workplace. Tussenstapjes zie je niet, maar ik weet ook niet of je die wel wilt zien. Een computer redeneert nooit hetzelfde als een mens.
Jullie hebben beide gelijk. Ik heb het op papier uitgewerkt, voor de coordinaten [a,b] [c,d] en [e,f] waarbij [p,q] het midden is. Als je het voor zo'n algemeen geval uitschrijft ziet her er vies uit. sorryquote:Op zaterdag 7 februari 2009 16:23 schreef Riparius het volgende:
[..]
Nee. Je had het beter gewoon even met potlood en papier uit kunnen proberen. Heb je helemaal geen computerprogramma voor nodig. De clou is dat je twee lineaire vergelijkingen in p en q overhoudt als je de tweede vergelijking van de eerste aftrekt en de derde vergelijking van de tweede. De kwadratische termen vallen dan immers allemaal tegen elkaar weg. En een stelsel van twee lineaire vergelijkingen met twee onbekenden is heel eenvoudig op te lossen. Heb je p en q, dan is het kwadraat van r, en daarmee r, ook eenvoudig te bepalen uit één der drie oorspronkelijke vergelijkingen. Niet zo smart dus die opmerkingen van je.


Ik ben even wat analytische meetkunde aan het herhalen. Ik heb enkele dingen die me (nog) niet duidelijk zijn. Het eerste stukje gaat over ellipsen.
Voor ellipsen heb je een bepaalde standaardvergelijking:
(x-h)2/a2 + (y-k)2/b2 = 1
Hierbij geldt:
(h,k) is midden van de ellips
a=halve lange as
b=halve korte as
c=plaats van het brandpunt t.o.v. 'het midden
1) ik snap niet waarom geldt a2=b2+c2. Dus kwadraat lange as is altijd de som van de kwadraten van de 2 anderen.
Daarna wil ik bv deze ellips tekenen: 4y2 +9x2 -24y-72x+144 =0
Herschrijven levert mij
(x-4)2 /4 + (y-3)2 /9 =1
levert mij het midden (4,3) op.
ik heb nu in de vgl de 9 als grootste getal 9 en kleinste getal de 4. Dus a=3 en b=2.
Maar dit vind ik al niet in de haak omdat in de oorspronkelijke vergelijking de x en de a bij elkaar horen.
Maar enfin: a=3, b=2 en volgens a2=b2+c2 volgt c=sqrt(5).
Met deze info is alles te vinden (ook brandpunten en 4 toppen), en de lange as is verticaal.
Dit klopt allemaal wel, maar volgens mij zit er iets niet goed.
Bij hyperbolen (volgende stukje) heb ik nl moeite om uit te zoeken wat de lange- en korte as wordt en hoe de a, b, en c zich verhouden.
Kan iemand hier wat mee? en evt. een overzicht geven hoe dit in elkaar zit en waarom.
Bedankt!
Voor ellipsen heb je een bepaalde standaardvergelijking:
(x-h)2/a2 + (y-k)2/b2 = 1
Hierbij geldt:
(h,k) is midden van de ellips
a=halve lange as
b=halve korte as
c=plaats van het brandpunt t.o.v. 'het midden
1) ik snap niet waarom geldt a2=b2+c2. Dus kwadraat lange as is altijd de som van de kwadraten van de 2 anderen.
Daarna wil ik bv deze ellips tekenen: 4y2 +9x2 -24y-72x+144 =0
Herschrijven levert mij
(x-4)2 /4 + (y-3)2 /9 =1
levert mij het midden (4,3) op.
ik heb nu in de vgl de 9 als grootste getal 9 en kleinste getal de 4. Dus a=3 en b=2.
Maar dit vind ik al niet in de haak omdat in de oorspronkelijke vergelijking de x en de a bij elkaar horen.
Maar enfin: a=3, b=2 en volgens a2=b2+c2 volgt c=sqrt(5).
Met deze info is alles te vinden (ook brandpunten en 4 toppen), en de lange as is verticaal.
Dit klopt allemaal wel, maar volgens mij zit er iets niet goed.
Bij hyperbolen (volgende stukje) heb ik nl moeite om uit te zoeken wat de lange- en korte as wordt en hoe de a, b, en c zich verhouden.
Kan iemand hier wat mee? en evt. een overzicht geven hoe dit in elkaar zit en waarom.
Bedankt!
kloep kloep


Dan hier hyperbolen; hier is de algemene vergelijking (x-h)2/a2 - (y-k)2/b2 = 1
Ook hier de a onder de x en de b onder de y.
Als ik nu deze 3 hyperbolen wil tekenen
1) 36xa2 -64ya2 = 2304
2) 12ya2 -4xa2 +72y+16x+44=0
3) 3xa2 -4ya2 -18x-40y-85=0
Herschijven naar een standaard vorm is geen punt. Dat lukt wel. Maar ook hier: wat is de lange as en de korte as, hoe zit het met de verhouding tussen a,b en c. En hoe kom je er achter hoe de hyperbool ligt als je m tekent.
Bij 1) vind ik xa2 /64 -ya2 /36 =1
is a dan 8 en b=6 omdat 64 onder de x staat? Of omdat 64 het grootste getal is?!
Bij 2) en 3) zelfde soort onduidelijkheden.
Het moet op papier, de inzet van maple of cabri of iets dergelijks mag niet.
Ook hier de a onder de x en de b onder de y.
Als ik nu deze 3 hyperbolen wil tekenen
1) 36xa2 -64ya2 = 2304
2) 12ya2 -4xa2 +72y+16x+44=0
3) 3xa2 -4ya2 -18x-40y-85=0
Herschijven naar een standaard vorm is geen punt. Dat lukt wel. Maar ook hier: wat is de lange as en de korte as, hoe zit het met de verhouding tussen a,b en c. En hoe kom je er achter hoe de hyperbool ligt als je m tekent.
Bij 1) vind ik xa2 /64 -ya2 /36 =1
is a dan 8 en b=6 omdat 64 onder de x staat? Of omdat 64 het grootste getal is?!
Bij 2) en 3) zelfde soort onduidelijkheden.
Het moet op papier, de inzet van maple of cabri of iets dergelijks mag niet.
kloep kloep


Je vragen zijn wat lastig (bewerkelijk) om hier compleet te beantwoorden, maar ik zal je toch even op weg helpen. Zoals je (hopelijk) weet is een ellips meetkundig te definiëren als een verzameling punten (meetkundige plaats zoals men vroeger zei) waarvan de som van de afstanden tot twee gegeven punten (de brandpunten) gelijk is.quote:Op maandag 9 februari 2009 13:22 schreef Borizzz het volgende:
Ik ben even wat analytische meetkunde aan het herhalen. Ik heb enkele dingen die me (nog) niet duidelijk zijn. Het eerste stukje gaat over ellipsen.
Voor ellipsen heb je een bepaalde standaardvergelijking:
(x-h)2/a2 + (y-k)2/b2 = 1
Hierbij geldt:
(h,k) is midden van de ellips
a=halve lange as
b=halve korte as
c=plaats van het brandpunt t.o.v. 'het midden
1) ik snap niet waarom geldt a2=b2+c2. Dus kwadraat lange as is altijd de som van de kwadraten van de 2 anderen.
Welnu, beschouw voor het gemak een ellips waarvan het centrum in de oorsprong ligt en de lange as langs de x-as. De standaardvergelijking is dan
x2/a2 + y2/b2 = 1 (a > b)
Noem de brandpunten (foci) F1 en F2, de coordinaten daarvan zijn dan (-c;0) en (c;0).
Beschouw nu eerst het punt (a;0) waar de ellips de positieve x-as snijdt. De som van de afstanden van dit punt tot de brandpunten F1(-c;0) en F2(c;0) bedraagt (c+a) + (a-c) = 2a.
Dit betekent dus dat de som van de afstanden tot F1 en F2 voor elk ander punt op de ellips ook 2a zal moeten zijn. Beschouw nu het punt (0;b) waar de ellips de positieve y-as snijdt. Vanwege de symmetrie moet de afstand van dit punt tot F1 en tot F2 elk gelijk zijn aan a, de som van de afstanden moet immers 2a zijn. Maar de punten (0;b), (0;0) en (c;0) vormen een rechthoekige driehoek waarvan de rechthoekszijden een lengte b en c hebben, en de lengte van de schuine zijde is, zoals we net hebben gevonden, gelijk aan a. En dus is volgens Pythagoras:
a2 = b2 + c2
Natuurlijk moet je ook nog kunnen aantonen dat de gewone meetkundige definitie van een ellips voert tot de standaardvergelijking uit de analytische meetkunde, maar als je wil zien hoe dat wordt afgeleid moet je maar even hier kijken.
Voor de hyperbool geldt iets soortgelijks, deze is meetkundig te definiëren als een verzameling punten waarvan het verschil van de afstanden tot twee gegeven punten (de brandpunten) constant is, zie hier.
[ Bericht 0% gewijzigd door Riparius op 09-02-2009 22:18:30 ]


Wat ik hieruit begrijp is dat voor zowel hyperbool als ellips de a dus parallel aan de x-as is, b parallel aan y as, en c de plaats van de brandpunten t.o.v. het midden.
Akkoord. Duidelijk verhaal verder.
Even toepassen op een hyperbool: 36x2 - 64y2 = 2304
Omschrijven levert x2/64 - y2/36 =1
a2=64 dus a=8
b2=36 dus b=6
gevolg: c=10.
Midden hyperbool (0,0)
Lange as is de a, dus hyperbool heeft zijn brandpunten op de x-as.
F1 (10,0) F2 (-10,0)
Top (8,0) en (-8,0)
asymptoot y=+/- 3/4 x.
Je hebt ook nog 2 andere toppen die verder niet veel doen: (0,6) en (0,-6). Klopt dit?
Dan kan ik daarna een andere hyperbool bekijken.
Akkoord. Duidelijk verhaal verder.
Even toepassen op een hyperbool: 36x2 - 64y2 = 2304
Omschrijven levert x2/64 - y2/36 =1
a2=64 dus a=8
b2=36 dus b=6
gevolg: c=10.
Midden hyperbool (0,0)
Lange as is de a, dus hyperbool heeft zijn brandpunten op de x-as.
F1 (10,0) F2 (-10,0)
Top (8,0) en (-8,0)
asymptoot y=+/- 3/4 x.
Je hebt ook nog 2 andere toppen die verder niet veel doen: (0,6) en (0,-6). Klopt dit?
Dan kan ik daarna een andere hyperbool bekijken.
kloep kloep


Dat begrijp ik niet. Je hyperbool snijdt de y-as toch niet?quote:Op maandag 9 februari 2009 20:42 schreef Borizzz het volgende:
Je hebt ook nog 2 andere toppen die verder niet veel doen: (0,6) en (0,-6). Klopt dit?


Nou ja ik dacht: je rekent ook een b uit. Levert die punten op, maar je doet er niet veel mee.
kloep kloep


Maar belangrijker: hoe kom ik er achter of een hyperbool zijn brandpunten op de x-as of de y-as (of parallel hieraan) heeft liggen?
kloep kloep


Als je y=0 stelt in je vergelijking vind je de snijpunten van de hyperbool met de x-as. Maar als je x=0 stelt dan heeft de resulterende vergelijking geen reële oplossingen voor y. Dus hebben de punten (0;b) en (0;-b) hier geen speciale betekenis.quote:Op maandag 9 februari 2009 20:59 schreef Borizzz het volgende:
Nou ja ik dacht: je rekent ook een b uit. Levert die punten op, maar je doet er niet veel mee.
[ Bericht 0% gewijzigd door Riparius op 09-02-2009 23:08:37 ]


ok. dank je. Ik ga t even uitzoeken.
Ik zal nog enkele uitwerkingen posten (later vanavond). Miss wil je het dan even checken of het een beetje klopt.
bedankt voor je hulp iig.
Ik zal nog enkele uitwerkingen posten (later vanavond). Miss wil je het dan even checken of het een beetje klopt.
bedankt voor je hulp iig.
kloep kloep


De standaardvergelijking van een hyperbool met de assen langs de x-as en y-as is:quote:Op maandag 9 februari 2009 21:01 schreef Borizzz het volgende:
Maar belangrijker: hoe kom ik er achter of een hyperbool zijn brandpunten op de x-as of de y-as (of parallel hieraan) heeft liggen?
(1) x2/a2 - y2/b2 = 1
De brandpunten F1(-c;0) en F2(c;0) van deze hyperbool liggen op de x-as, en hierbij geldt:
(2) c2 = a2 + b2
Het is eenvoudig in te zien dat vergelijking (1) altijd een hyperbool voorstelt waarvan de 'lange' as (hoofdas) langs de x-as ligt. Immers, als je x=0 stelt in vergelijking (1), dan krijg je y2/b2 = -1, en deze vergelijking heeft geen reële oplossingen voor y.
Je kunt een hyperbool waarvan de brandpunten op de y-as liggen (symmetrisch t.o.v. de oorsprong) verkrijgen door een hyperbool waarvan de brandpunten op de x-as liggen (symmetrisch t.o.v. de oorprong) te spiegelen in de lijn y=x. Dat komt neer op het omwisselen van x en y in de algemene vergelijking (1).


Toch kom ik nog steeds niet uit deze: 3x2 -4y2 -18x -40y -85 =0.
Als ik m omschrijf vind ik deze: (x-3)2 /4 - (y-5)2 /3 =1
volgt dus a2 =4 en a=2
b2 =3 en b=sqrt(3), c wordt dan sqrt(7)
Volgens jouw opmerking hierboven heeft deze hyperbool geen snijpunten met de y-as. Geen oplossingen als x=0.
Maar bijv. voor deze hyperbool kom ik nog niet achter hoe de brandpunten liggen.
Als ik m omschrijf vind ik deze: (x-3)2 /4 - (y-5)2 /3 =1
volgt dus a2 =4 en a=2
b2 =3 en b=sqrt(3), c wordt dan sqrt(7)
Volgens jouw opmerking hierboven heeft deze hyperbool geen snijpunten met de y-as. Geen oplossingen als x=0.
Maar bijv. voor deze hyperbool kom ik nog niet achter hoe de brandpunten liggen.
kloep kloep


En deze dan ook niet:
12y2 -4x2 +72y +16x +44=0.
Herschreven: (y+3)2 /4 - (x-2)2 /12 =1
a=sqrt(12) en b=2, geeft c=4.
geen oplossingen voor x als y=0, snijdt de x-as dus niet.
12y2 -4x2 +72y +16x +44=0.
Herschreven: (y+3)2 /4 - (x-2)2 /12 =1
a=sqrt(12) en b=2, geeft c=4.
geen oplossingen voor x als y=0, snijdt de x-as dus niet.
kloep kloep