SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



De restricties zijn dan weer discutabel, temeer omdat de baseline sales mede-afhankelijk is van het effect van de parameters. Vicieuze cirkel zou ik denken?quote:Op dinsdag 27 januari 2009 23:07 schreef GlowMouse het volgende:
t heeft bij jouw de functie van wat je normaal als i hebt: je onderscheid er de cases mee. Echte mensen werken met vectornotatie en vermelden daarmee alle cases in 1x zodat je die t niet hoeft te noemen. Zolang t maar niet in je regressoren terugkomt is het goed.
Als prod1 dan 2x zoveel verkocht wordt als prod2 bijvoorbeeld, kun je zeggen dat de coefficient bij prod1*actie1 tweemaal zo groot moet zijn als bij prod1*actie2. Met zulke lineaire restricties is een model nog eenvoudig te schatten.
Zal m'n docent eens aanschrijven, en zal 't resultaat dan we weer posten. Je suggesties en uitleg worden meegenomen.


Je wilt het toch proportioneel aan de verkopen? Wat loop je dan met de baseline sales, die zijn daarvoor helemaal niet van belang.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat is ook zo, ik leg het als leek ook niet al te best uit (uiteindelijke interesse ligt ook meer in de implicaties vande uitkomst dan de weg er naar toe).quote:Op dinsdag 27 januari 2009 23:30 schreef GlowMouse het volgende:
Je wilt het toch proportioneel aan de verkopen? Wat loop je dan met de baseline sales, die zijn daarvoor helemaal niet van belang.
Ik noem de baseline sales steeds omdat het model daar nu op stukloopt. Als dat allemaal gelijk was geweest, en de aanname dat activiteiten gelijke impact hadden voor de verschillende producten, dan had ik het wel kunnen toepassen.


Ik heb een testmodel gemaakt met daarin gefingeerde waardes zodat ik voor mijzelf wat meer begrip kreeg over de betekenis en effect van een en ander. Op de huidige manier liep het model compleet mank op het moment dat de basisverkoop van de producten onderling sterk uiteenliep.
Door de ln toe te passen op de verkoopcijfers krijg ik een parameter die ik middels een formule terug kan rekenen naar een percentage (relatieve toename). Het testmodel laat een fit van (niet gek) R square=1 zien, en de omgerekende parameters geven exact de groei aan die ik gegeven heb tijdens actieperiodes.
Dit heb ik ook toegepast op mijn eigen model en data, en de fit is daarmee weer een stuk toegenomen, nu tot zo'n 0,85R square. Ook de significantie van de 'acties' is sterk toegenomen hierdoor.
Hiermee lijkt mijn probleem opgelost.
[ Bericht 8% gewijzigd door TheSilverSpoon op 28-01-2009 08:19:05 ]
Door de ln toe te passen op de verkoopcijfers krijg ik een parameter die ik middels een formule terug kan rekenen naar een percentage (relatieve toename). Het testmodel laat een fit van (niet gek) R square=1 zien, en de omgerekende parameters geven exact de groei aan die ik gegeven heb tijdens actieperiodes.
Dit heb ik ook toegepast op mijn eigen model en data, en de fit is daarmee weer een stuk toegenomen, nu tot zo'n 0,85R square. Ook de significantie van de 'acties' is sterk toegenomen hierdoor.
Hiermee lijkt mijn probleem opgelost.
[ Bericht 8% gewijzigd door TheSilverSpoon op 28-01-2009 08:19:05 ]


Als je een hoge R² zoekt, heb ik nog wel een programma dat alle combinaties van regressoren en kruistermen afgaat en zo naar de beste fit zoekt 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Kan iemand mij uitleggen stapgewijs hoe je dit naar echelon vorm moet vegen:
1 -3 4 -4
3 -7 7 -8
-4 6 -1 4
En hoe kan je daarna zien of er oneindig veel oplossing zijn of niet?
Alvast bedankt
1 -3 4 -4
3 -7 7 -8
-4 6 -1 4
En hoe kan je daarna zien of er oneindig veel oplossing zijn of niet?
Alvast bedankt


drie keer de eerste rij van de tweede rij aftrekken
1 -3 4 -4
0 2 -5 4
-4 5 -1 4
vier keer de eerste rij bij de derde rij optellen
1 -3 4 -4
0 2 -5 4
0 -6 15 -12
tweede rij door twee delen
1 -3 4 -4
0 1 -5/2 2
0 -6 15 -12
tweede rij 3x bij de eerste/6x bij de derde optellen
1 0 -7/2 2
0 1 -5/2 2
0 0 0 0
Nu heb je x1 - 7/2 x3 = 2 en x2 -5/2 x3 = 2. Als je x3 vrij kiest, liggen x1 en x2 vast: x1 = 2 + 7/2 x3 en x2 = 2 + 5/2 * x3.
1 -3 4 -4
0 2 -5 4
-4 5 -1 4
vier keer de eerste rij bij de derde rij optellen
1 -3 4 -4
0 2 -5 4
0 -6 15 -12
tweede rij door twee delen
1 -3 4 -4
0 1 -5/2 2
0 -6 15 -12
tweede rij 3x bij de eerste/6x bij de derde optellen
1 0 -7/2 2
0 1 -5/2 2
0 0 0 0
Nu heb je x1 - 7/2 x3 = 2 en x2 -5/2 x3 = 2. Als je x3 vrij kiest, liggen x1 en x2 vast: x1 = 2 + 7/2 x3 en x2 = 2 + 5/2 * x3.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik moet m.b.v. Six Sigma een verbeterplan maken om de uitval van studenten in jaar 1 te verbeteren. Ik heb geen idee hoe en waar ik moet beginnen. Moet ik gewoon het DMAIC schema invullen? Hiervoor heb ik niet alle gegevens en deze worden ook niet verstrekt. Wie o wie kan me hierbij helpen?? Bij voorbaat dank!


Dit is een wiskundeotopic, je kunt beter naar een ander huiswerktopic gaan.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt, volgens mij lukt het nu met de echelon vorm zoekenquote:Op woensdag 28 januari 2009 13:19 schreef GlowMouse het volgende:
drie keer de eerste rij van de tweede rij aftrekken
1 -3 4 -4
0 2 -5 4
-4 5 -1 4
vier keer de eerste rij bij de derde rij optellen
1 -3 4 -4
0 2 -5 4
0 -6 15 -12
tweede rij door twee delen
1 -3 4 -4
0 1 -5/2 2
0 -6 15 -12
tweede rij 3x bij de eerste/6x bij de derde optellen
1 0 -7/2 2
0 1 -5/2 2
0 0 0 0
Nu heb je x1 - 7/2 x3 = 2 en x2 -5/2 x3 = 2. Als je x3 vrij kiest, liggen x1 en x2 vast: x1 = 2 + 7/2 x3 en x2 = 2 + 5/2 * x3.


Zoek eens op wat vrije variabelen zijn en hoe zich dat in deze matrix laat vertalen naar oneindig veel oplossingen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Lekker cynisch... Het model dat ik gebruik is een model dat meer gebruikt wordt in het onderzoeksgebied. Dat de fit niet heilig is heb ik al eerder bevestigd, in dit geval is het model wel verbeterd door de toevoeging die ik heb gedaan.quote:Op woensdag 28 januari 2009 09:50 schreef GlowMouse het volgende:
Als je een hoge R² zoekt, heb ik nog wel een programma dat alle combinaties van regressoren en kruistermen afgaat en zo naar de beste fit zoekt


In mijn boek wordt een punt op een lijn genoemd (x,x/(1+x)) Ik snap niet precies wat er met deze notatie genoemd wordt, dit is toch geen punt?


Een coordinaat bestaat normaal uit een x- en y-coordinaat. Bv (2,3)
Nu is de x coordinaat gewoon x.
De y coordinaat is nu x/(1+x)
De formule van dit verhaal is dus y = x/(1+x) als ik je verhaal goed begrijp.
Nu is de x coordinaat gewoon x.
De y coordinaat is nu x/(1+x)
De formule van dit verhaal is dus y = x/(1+x) als ik je verhaal goed begrijp.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


En jij doet Harvard?quote:Op zaterdag 31 januari 2009 23:06 schreef nickybol het volgende:
In mijn boek wordt een punt op een lijn genoemd (x,x/(1+x)) Ik snap niet precies wat er met deze notatie genoemd wordt, dit is toch geen punt?
IL-uni's zijn ook niet meer wat het geweest is.
Ten percent faster with a sturdier frame


Ik hoop dat iemand mij even wil helpen.
Mijn neefje heeft een proeftoets meegekregen voor wiskunde en er is mij gevraagd om hem hiermee te helpen (echter kom ik niet uit onderstaande).
Kan iemand mij helpen?
Ik kan onderstaande niet vinden op zijn rekenmachine (type FX-82MS). Al reeds op google gekeken, echter niks kunnen vinden. Wellicht dat één van jullie dit weet.
Tevens bij opdracht 3 kom ik er niet uit met de uitkomst.
Bij onderstaande 3 kom ik er helemaal niet uit.
Wellicht "NEWBIE" vragen maar mij lukt het niet en uit het boek (Basis Wiskunde van Kees van den Hoek wordt ik al helemaal niks wijzer)..
Alvast bedankt voor de hulp
Mijn neefje heeft een proeftoets meegekregen voor wiskunde en er is mij gevraagd om hem hiermee te helpen (echter kom ik niet uit onderstaande).
Kan iemand mij helpen?
Ik kan onderstaande niet vinden op zijn rekenmachine (type FX-82MS). Al reeds op google gekeken, echter niks kunnen vinden. Wellicht dat één van jullie dit weet.
Tevens bij opdracht 3 kom ik er niet uit met de uitkomst.
Bij onderstaande 3 kom ik er helemaal niet uit.
Wellicht "NEWBIE" vragen maar mij lukt het niet en uit het boek (Basis Wiskunde van Kees van den Hoek wordt ik al helemaal niks wijzer)..
Alvast bedankt voor de hulp


Welke 'onderstaande 3'? Er staan er helemaal geen 3 onder waar je dat zegt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


2a: 1.06^(-20)
2b: Vlak onder on zit het knopje voor de derdemachtswortel. Vierdemachtswortel gaat via 4[shift]^170.
2c: log(89)/log(3)
2b: Vlak onder on zit het knopje voor de derdemachtswortel. Vierdemachtswortel gaat via 4[shift]^170.
2c: log(89)/log(3)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Super hier kan ik iets mee!!!quote:Op zondag 1 februari 2009 12:37 schreef GlowMouse het volgende:
2a: 1.06^(-20)
2b: Vlak onder on zit het knopje voor de derdemachtswortel. Vierdemachtswortel gaat via 4[shift]^170.
2c: log(89)/log(3)


Ah shit, gewoon een afleesfoutje. Ik ben nog steeds in de war met die punten en die komma's sinds ik hier in Amerika ben aangekomen en zit weer veel te moeilijk te denken. Gewoon een simpel coordinaat dus.. Thanks anywayquote:Op zaterdag 31 januari 2009 23:18 schreef -J-D- het volgende:
Een coordinaat bestaat normaal uit een x- en y-coordinaat. Bv (2,3)
Nu is de x coordinaat gewoon x.
De y coordinaat is nu x/(1+x)
De formule van dit verhaal is dus y = x/(1+x) als ik je verhaal goed begrijp.


Nee, eerder een interpretatiefout. Daarom kun je ook beter een puntkomma gebruiken als scheidingsteken bij coördinaten, dus bijv. (2;3) en (0,5;1,5). Bijna niemand die het doet, terwijl het toch zo'n voor de hand liggende oplossing is. Maar het lost de verwarring rond het gebruik van de punt en de komma als decimaal scheidingsteken natuurlijk niet op. In Nederland gebruikt niemand een komma als scheidingsteken voor duizendtallen maar wel een punt, en dus zou het oprukkende Angelsaksische gebruik van de punt als decimaal scheidingsteken in ieder geval in Nederland ontmoedigd moeten worden.quote:Op zondag 1 februari 2009 19:56 schreef nickybol het volgende:
[..]
Ah shit, gewoon een afleesfoutje. Ik ben nog steeds in de war met die punten en die komma's sinds ik hier in Amerika ben aangekomen en zit weer veel te moeilijk te denken. Gewoon een simpel coordinaat dus.. Thanks anyway


Is het internationaal niet meestal een punt als decimaal scheidingsteken in plaats van een komma? Hier in Amerika is het alleen maar een punt als decimaal scheidingsteken, en wordt een komma gebruikt voor duizendtallen.


Nullen kun je beter schrappen door te vermenigvuldigen met machten van 10. Zodoende blijft alleen het decimale scheidingsteken over, dat punt of komma, dat maakt zoveel niet uit. Een voordeel van deze notatie is dat je geen onterechte nauwkeurigheid aan een waarde koppelt.quote:Op maandag 2 februari 2009 04:41 schreef nickybol het volgende:
Is het internationaal niet meestal een punt als decimaal scheidingsteken in plaats van een komma? Hier in Amerika is het alleen maar een punt als decimaal scheidingsteken, en wordt een komma gebruikt voor duizendtallen.


quote:Op maandag 2 februari 2009 04:41 schreef nickybol het volgende:
Is het internationaal niet meestal een punt als decimaal scheidingsteken in plaats van een komma? Hier in Amerika is het alleen maar een punt als decimaal scheidingsteken, en wordt een komma gebruikt voor duizendtallen.
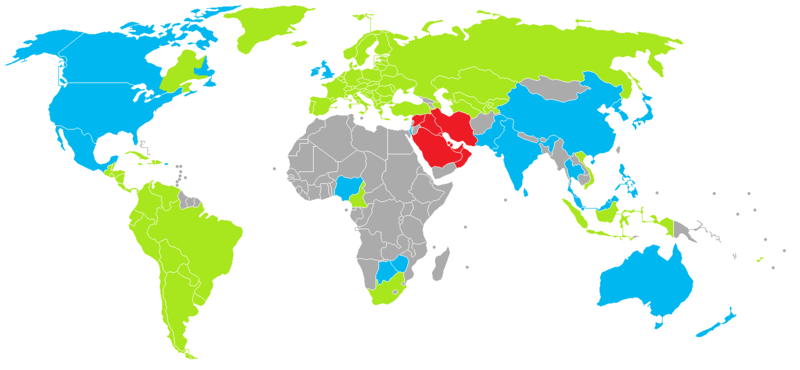
Blauw is punt, groen is komma, rood is iets Arabisch. In veel wetenschappelijke literatuur vind je wel de '.'. Let overigens op de briljante situatie in Canada.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Opgave 3a of heel opgave 3?quote:Op zondag 1 februari 2009 12:31 schreef peter070 het volgende:
Tevens bij opdracht 3 kom ik er niet uit met de uitkomst.
anyways, bij opgave 3 ga je eerst buiten haakjes werken en dan krijg je
| 1 |
Vervolgens weet ik niet meer wat de officiele stap is dat je moet doen, wiskunde is iets te lang geleden, maar mijn instinct zegt dat je eerst de vergelijking uitrekent (waarbij zijn de twee kanten gelijk), en vervolgens pak je een getal net boven en en net daaronder, waardoor je weet wanneer de vergelijking klopt..
| 1 2 3 4 5 6 7 8 | -3x - 12 = 2x +1/2 0 = x + 12 1/2 x = -12 1/2 als je dan uitrekent voor x = -13 komt er uit 27 < 26.5, en voor x = -12 24 < 24.5 -13 < -12, dus de uitkomst is x => -12 1/2 |
Mijn wiskunde is te ver weggezakt en dit kan vast veel sneller en makkelijker


quote:Op zondag 1 februari 2009 12:31 schreef peter070 het volgende:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | a) q(a) = 5 - 1 = 4000 kg b) evenwicht = q(a) = q(v) => -2 1/2p + 20 = p -1 => 0 = 3.5p - 21 => 21 = 3.5p => p = 6 evenwichtsprijs = 6 euro evenwichtshoeveelheid = 5000 kilo c) aanbodsoverschot van 3500 kg => q(a) - q(v) = 3.5 p-1 - (-2.5p + 20) = 3.5 p -1 +2.5p -20 = 3.5 3.5p -21 = 3.5 3.5p = 24.5 p = 7 euro even controleren aanbod = 7-1 = 6000 kilo vraag = -2.5 x 7 + 20 = 2500 kilo d) deze vraag begrijp ik ook niet :P |


d: q_v = -2.5 * 5.5 + 20 = 6250 kg ; q_a = 4500 kg. Het verschil, 1750 kg, zal de overheid moeten importeren voor 12250 euro.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik begreep voornamelijk de vraagstelling nietquote:Op maandag 2 februari 2009 11:30 schreef GlowMouse het volgende:
d: q_v = -2.5 * 5.5 + 20 = 6250 kg ; q_a = 4500 kg. Het verschil, 1750 kg, zal de overheid moeten importeren voor 12250 euro.


Ik begrijp hem ook niet maar het is het enige dat je kan doenquote:Op maandag 2 februari 2009 11:35 schreef Stranger het volgende:
[..]
Ik begreep voornamelijk de vraagstelling nietZe moeten wiskunde niet te praktijkgericht proberen te maken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | 6 3 96 2 6 72 1 1 18 640 560 b) W = 640x + 560y c) 6x + 3y <= 96 (constructie), wordt versimpeld tot 2x + y <= 32 2x + 6y <= 72 (bekleding), wordt versimpeld tot x + 3y <= 36 x + y <= 18 (vewerking) d) het toegestane gebied teken je in een assenstelsel. Mijn paint skillss zijn niet zo goed, maar om je een beeld te geven, het ziet er ongeveer zo uit: |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | Roze = Bekleding Rood = afwerking Groen = de niveaulijn gevraagd bij e) f) Zoals je in de grafiek ziet, zijn er 4 hoekpunten, namelijk (16,0), (0,12) en de snijpunten van rood en roze en rood en blauw, welke, als je de grafiek goed tekent, (9,9) en (14,4) zijn. Je vult dit allemaal in de formule voor W in en dan krijg je op (16,0) = 10240 (0,12) = 6720 (9,9) = 10800 (14,4) = 11200 Dus bij 14 fauteuils en 4 sofa's is de maximale winst g) Ik denk dat je hier de tabel opnieuw moet invullen maar dan verrekend met het aantal fauteuils en sofa's dat je maakt 84 uur 12 uur 96 uur 28 uur 24 uur 52 uur 14 uur 4 uur 18 uur 8960 2240 11200 h) uit de tabel af te lezen: bekleding, houdt 20 uur over. |


Even logica:
Gewoon een puzzeltje. Ben benieuwd of iemand de oplossing ziet!
Hier staan 10 genummerde beweringen. Hoeveel ervan zijn waar?
1. Precies één van deze beweringen is onwaar.
2. Precies twee van deze beweringen zijn onwaar.
3. Precies drie van deze beweringen zijn onwaar.
4. Precies vier van deze beweringen zijn onwaar.
5. Precies vijf van deze beweringen zijn onwaar.
6. Precies zes van deze beweringen zijn onwaar.
7. Precies zeven van deze beweringen zijn onwaar.
8. Precies acht van deze beweringen zijn onwaar.
9. Precies negen van deze beweringen zijn onwaar.
10. Precies tien van deze beweringen zijn onwaar.
Gewoon een puzzeltje. Ben benieuwd of iemand de oplossing ziet!
Hier staan 10 genummerde beweringen. Hoeveel ervan zijn waar?
1. Precies één van deze beweringen is onwaar.
2. Precies twee van deze beweringen zijn onwaar.
3. Precies drie van deze beweringen zijn onwaar.
4. Precies vier van deze beweringen zijn onwaar.
5. Precies vijf van deze beweringen zijn onwaar.
6. Precies zes van deze beweringen zijn onwaar.
7. Precies zeven van deze beweringen zijn onwaar.
8. Precies acht van deze beweringen zijn onwaar.
9. Precies negen van deze beweringen zijn onwaar.
10. Precies tien van deze beweringen zijn onwaar.
kloep kloep


Ik gok dat 1 bewering waar is, namelijk: 9. Precies negen van deze beweringen zijn onwaar.
ff wachten nog


Er kan er duidelijk ten hoogste één waar zijn, en dan zijn er dus tenminste negen onwaar.
Maar het antwoord van Game_Error heeft toch geen onderbouwing nodig? Of wil je dat hij nog aanwijst welke 9 er dan onwaar zijn
Maar het antwoord van Game_Error heeft toch geen onderbouwing nodig? Of wil je dat hij nog aanwijst welke 9 er dan onwaar zijn
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Game_error zijn antwoord is prima inderdaad. Ik heb nog een vraagje, ik moet met behulp van Maple op twee manieren differentiëren, namelijk met de definitie (lim h->0 van (f(x-h)-f(x))/h) en gewoon met diff. Hier komen twee voor mijn oog verschillende functies uit, maar deze horen natuurlijk hetzelfde te zijn. Dit moet ik ook aantonen, maar hoe doe ik dit? (Ben nog niet zo skilled in Maple..)
"Reality is an illusion created by a lack of alcohol."


Allebei vereenvoudigen? De verschilfunctie vereenvoudigen en op de nulfunctie uitkomen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


je kunt vlg mij niet voorkomen dat maple soms een 'rare' output geeft voor twee dezelfde uitkomsten.
kun je niet gewoon beide uitkomsten plotten en over elkaar heenleggen?
welke maple invoer heb je gebruikt?
kun je niet gewoon beide uitkomsten plotten en over elkaar heenleggen?
welke maple invoer heb je gebruikt?
kloep kloep


Om welke functie gaat het?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Het gaat om de functie:
f(x) = (sqrt(x) * ln(1+x^2)) / (2 + cos(x))
ik ga er morgen mee verder ik ben bekaf en maple even goed zat nu... ik heb al duizend wazige errors gehad.
f(x) = (sqrt(x) * ln(1+x^2)) / (2 + cos(x))
ik ga er morgen mee verder ik ben bekaf en maple even goed zat nu... ik heb al duizend wazige errors gehad.
"Reality is an illusion created by a lack of alcohol."


Mijn maple-sessie.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | |\^/| Maple 12 (X86 64 LINUX) ._|\| |/|_. Copyright (c) Maplesoft, a division of Waterloo Maple Inc. 2008 \ MAPLE / All rights reserved. Maple is a trademark of <____ ____> Waterloo Maple Inc. | Type ? for help. > f := x -> (sqrt(x) * ln(1+x^2)) / (2 + cos(x)); 2 sqrt(x) ln(1 + x ) f := x -> ------------------ 2 + cos(x) > r1 := simplify(diff(f(x), x)); 2 2 2 2 r1 := 1/2 (2 ln(1 + x ) + 2 ln(1 + x ) x + ln(1 + x ) cos(x) 2 2 2 2 2 + ln(1 + x ) cos(x) x + 8 x + 4 x cos(x) + 2 x ln(1 + x ) sin(x) 3 2 / 1/2 2 2 + 2 x ln(1 + x ) sin(x)) / (x (1 + x ) (4 + 4 cos(x) + cos(x) )) / > r2 := simplify(limit((f(x + h)-f(x))/(h), h=0)); 2 2 2 2 r2 := 1/2 (2 ln(1 + x ) + 2 ln(1 + x ) x + ln(1 + x ) cos(x) 2 2 2 2 2 + ln(1 + x ) cos(x) x + 8 x + 4 x cos(x) + 2 x ln(1 + x ) sin(x) 3 2 / 1/2 + 2 x ln(1 + x ) sin(x)) / (x / 2 2 2 2 2 (4 + 4 cos(x) + cos(x) + 4 x + 4 x cos(x) + x cos(x) )) > simplify(r1 - r2); 0 > QED |
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Maple TA, wat een ramp was dat programma zeg, ik ben blij dat we er maar 4 weken mee hebben moeten werken... 
En over die logica, 9 is gewoon de enige die kan kloppen als je ze nagaat, ik heb geen idee hoe ik dat moet bewijzen. Logica is nooit mijn sterkste kant geweest moet ik zeggen.
En over die logica, 9 is gewoon de enige die kan kloppen als je ze nagaat, ik heb geen idee hoe ik dat moet bewijzen. Logica is nooit mijn sterkste kant geweest moet ik zeggen.
ff wachten nog


Glowmouse heeft het in feite al gezegd. Alle uitspraken sluiten elkaar uit, d.w.z. als 1 waar is, is 2 t/m 10 niet waar, als 2 waar is zijn 1 en 3 t/m 10 niet waar, enz. Ergo, er kan er hooguit één waar zijn, en er zijn er minstens 9 onwaar. En verder spreekt 10 zichzelf tegen, aangezien er maar 10 beweringen zijn. Blijft over dat alleen 9 waar kan zijn.quote:Op dinsdag 3 februari 2009 02:39 schreef Game_Error het volgende:
En over die logica, 9 is gewoon de enige die kan kloppen als je ze nagaat, ik heb geen idee hoe ik dat moet bewijzen. Logica is nooit mijn sterkste kant geweest moet ik zeggen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


De groeifactor per week is 1.5.
Hoe groot is de groeifactor per dag?
Antwoordmodel: De groeifactor per week is 1,5^0.25=1.107
Hoe komt het bij die 0.25?
Hoe groot is de groeifactor per dag?
Antwoordmodel: De groeifactor per week is 1,5^0.25=1.107
Hoe komt het bij die 0.25?


Mits exponentiële groei zou het antwoord 1.5^(1/7) moeten zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Lijkt mij ook.quote:Op dinsdag 3 februari 2009 15:51 schreef julian6 het volgende:
Dat dacht ik dus ook, misschien staat er weer een fout in dat antwoordmodelboek.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.