SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



12,0 cm² = 12,0 * (m/100)² = 12,0 * m² / 100² = 12,0 * m² * 10-4 = 12,0 * 10-4 m².
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je kunt gebruik maken van het regeltjequote:Op vrijdag 16 januari 2009 14:21 schreef hupseflupse het volgende:
ik loop steeds vast op het omzetten van machten.
zo zou 12,0cm2 hetzelfde moeten zijn als 12,0 x 10^-4 m2, maar ik snap niet hoe het werkt met machten en verschillende inhoudsmaten etc.. wie kan opheldering geven??
(a*b)m = am * bm
waarbij a en b van alles kunnen zijn.
Dus ( 1 centimeter )2 = ( 0,01 meter )2 = (0,01)2 (meter)2 = 10-4m2
Of,
(1 milliliter )3 = (0,001 liter )3 = (0,001)3 (liter)3
= 10-9 L3
Hierbij kun je dan weer gebruik maken van
(am)n = am*n
Dus bijvoorbeeld
(10-2)3 = 10-6
Zo vind ik het altijd handig onthouden
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


thanks! het begint al een beetje te dagen nu 
maar begrijp je deze dan? ;
58940589 mm2 = 5,89 10^7 mm2
= 1,26 10^7 10^-6 m2
= 1,26 10^1 m
stond ergens in een voorbeeld.
(sorry voor het Noob gehalte, ben hier erg slecht in)
maar begrijp je deze dan? ;
58940589 mm2 = 5,89 10^7 mm2
= 1,26 10^7 10^-6 m2
= 1,26 10^1 m
stond ergens in een voorbeeld.
(sorry voor het Noob gehalte, ben hier erg slecht in)


Je hebt 1,26*10^7 mm2quote:Op vrijdag 16 januari 2009 15:55 schreef hupseflupse het volgende:
thanks! het begint al een beetje te dagen nu
maar begrijp je deze dan? ;
58940589 mm2 = 5,89 10^7 mm2
= 1,26 10^7 10^-6 m2
= 1,26 10^1 m
stond ergens in een voorbeeld.
(sorry voor het Noob gehalte, ben hier erg slecht in)
van mm2 naar m2 is 3 stappen (dus 10^-6)
Omdat je 10^7 vermenigvuldigt met 10^- 6 moet je de machten bij elkaar optellen (7+-6= 7-6 =1)
Het antwoord is dus 1,26*10^1


Die tweede regel is gek, je komt niet zomaar op 1,26. Het moet zijn:
58.940.589 mm² = 5,89 107 mm² = 5,89 107 (m/1000)² = 5,89 107 m² / 1000² = 5,89 107 m² *10-6 = 5,89 101 m² = 58,9 m².
58.940.589 mm² = 5,89 107 mm² = 5,89 107 (m/1000)² = 5,89 107 m² / 1000² = 5,89 107 m² *10-6 = 5,89 101 m² = 58,9 m².
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hallo, nog wat over grafentheorie.
In de Petersen-graaf zit de K5 verstopt.
Die is gemakkelijk te zien.
Maar er moet ook de K3,3 inzitten. Deze zie ik niet.
Wie kan me helpen hiermee?
In de Petersen-graaf zit de K5 verstopt.
Die is gemakkelijk te zien.
Maar er moet ook de K3,3 inzitten. Deze zie ik niet.
Wie kan me helpen hiermee?


Je definitie van verstoppen is wat vreemd, maar op wikipedia staat het antwoord.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik kom hier even niet uit. Lineaire algrabra
Laat gegeven zijn het vlak W in R3 met vergelijking x1 + 3x2 - x3 = 0.
(a) Construeer een orthogonale basis van W.
antwoord:
Ik zie wel dat w1 en w2 nulruimten zijn van (1 3 -1 | 0 )
Maar dan? Dan snap ik er niks meer van.
Laat gegeven zijn het vlak W in R3 met vergelijking x1 + 3x2 - x3 = 0.
(a) Construeer een orthogonale basis van W.
antwoord:
Ik zie wel dat w1 en w2 nulruimten zijn van (1 3 -1 | 0 )
Maar dan? Dan snap ik er niks meer van.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Ik weet wat ze bedoelen met contracting, maar dit kan ik niet volgen.quote:Op zondag 18 januari 2009 17:27 schreef GlowMouse het volgende:
Je definitie van verstoppen is wat vreemd, maar op wikipedia staat het antwoord.
Jij wel?
Want ik had wikipedia ook al gevonden, maar kwam toch niet verder.
Wat moet je precies op wat leggen?


Ze maken een vector w2' die loodrecht staat op w1. Andersom kan ook: een vector w1' maken die loodrecht staat op w2.quote:
En zij gebruiken dat de loodrechte projectie van w2 op w1 gegeven wordt door w1Tw2/(w1Tw1) * w1 = -3/2 w1. Het stuk van w2 dat loodrecht op w1 staat, wordt dus gegeven door w2 - (-3/2)w1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Sorry ik snap het antwoord nog helemaal niet, wat is nou eigenlijk het antwoord?quote:Op zondag 18 januari 2009 17:40 schreef GlowMouse het volgende:
[..]
Ze maken een vector w2' die loodrecht staat op w1. Andersom kan ook: een vector w1' maken die loodrecht staat op w2.
En zij gebruiken dat de loodrechte projectie van w2 op w1 gegeven wordt door w1Tw2/(w1Tw1) * w1 = -3/2 w1. Het stuk van w2 dat loodrecht op w1 staat, wordt dus gegeven door w2 - (-3/2)w1.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Het antwoord gaf je zelf al, maar loodrecht projecteren is dus het tussenstapje.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je definitie van 'verstoppen' vond ik nogal vreemd, maar het is een minor zoals uiteengezet op http://en.wikipedia.org/wiki/Minor_(graph_theory)quote:Op zondag 18 januari 2009 18:19 schreef Beo_beo het volgende:
GlowMouse, waarom mag dat punt zomaar verwijden?
Dat is toch geen contractie dan?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoi Allen.
Hier een vraagje over statistiek. Heb daar al jaren niet echt meer iets mee gedaan, dus dat is een beetje weggezakt. Ik heb een bepaald experiment op twee verschillende manieren uitgevoerd en heb daarmee twee datasets vergaard (een lijstje gemiddeldes). Wat ik nu wil weten is of de ene methode beter is dan de andere, oftewel, ik wel weten of er een significant verschil zit tussen de twee datasets.
Welke statistische toets kan ik hiervoor het best gebruiken? Ik heb dus gemiddelde A (gebaseerd op 10 datapunten) en gemiddelde B (ook gebaseerd op 10 datapunten) en ik wil dus weten of A en B significant van elkaar verschillen.
Wie kan mijn geheugen even opfrissen?
EDIT: Diep in mijn geheugen graven leverde de t-toets op. Is dit een goede test om te gebruiken? En zo ja, hoe gebruik je deze ook weer? Als ik in de tabel opzoek bij 9 vrijheidsgraden en 0.05 dan vind ik een t-waarde van 1.833. Als ik de t-waarde van mijn toets uitrekenen, is het verschil dan signicant als "berekende waarde > tabelwaarde" of juist andersom?
[ Bericht 20% gewijzigd door Bioman_1 op 19-01-2009 10:29:18 ]
Hier een vraagje over statistiek. Heb daar al jaren niet echt meer iets mee gedaan, dus dat is een beetje weggezakt. Ik heb een bepaald experiment op twee verschillende manieren uitgevoerd en heb daarmee twee datasets vergaard (een lijstje gemiddeldes). Wat ik nu wil weten is of de ene methode beter is dan de andere, oftewel, ik wel weten of er een significant verschil zit tussen de twee datasets.
Welke statistische toets kan ik hiervoor het best gebruiken? Ik heb dus gemiddelde A (gebaseerd op 10 datapunten) en gemiddelde B (ook gebaseerd op 10 datapunten) en ik wil dus weten of A en B significant van elkaar verschillen.
Wie kan mijn geheugen even opfrissen?
EDIT: Diep in mijn geheugen graven leverde de t-toets op. Is dit een goede test om te gebruiken? En zo ja, hoe gebruik je deze ook weer? Als ik in de tabel opzoek bij 9 vrijheidsgraden en 0.05 dan vind ik een t-waarde van 1.833. Als ik de t-waarde van mijn toets uitrekenen, is het verschil dan signicant als "berekende waarde > tabelwaarde" of juist andersom?
[ Bericht 20% gewijzigd door Bioman_1 op 19-01-2009 10:29:18 ]
Theories come and theories go. The frog remains


Je moet je eerst afvragen wat beter is. Hoger gemiddelde, grotere mediaan, kleinere variantie, etc.
De two-sample t-test is een goede test op het gemiddelde wanneer je niets over de variantie weet, maar daarvoor moeten de waarnemingen wel uit een normale verdeling komen. Omdat je maar 10 waarnemingen hebt is die aanname erg cruciaal. Wie zegt anders immers dat de verwachting bestaat? Je bent dan aangewezen op een parametervrije toets.
De two-sample t-test is een goede test op het gemiddelde wanneer je niets over de variantie weet, maar daarvoor moeten de waarnemingen wel uit een normale verdeling komen. Omdat je maar 10 waarnemingen hebt is die aanname erg cruciaal. Wie zegt anders immers dat de verwachting bestaat? Je bent dan aangewezen op een parametervrije toets.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


tnx. Ik zat ook al te denken over de "normale verdeling aanname". Ik denk dat de Wilcoxon signed-rank test het best werkt voor wat ik wil doen. Zal daar eens verder naar kijken.quote:Op maandag 19 januari 2009 11:33 schreef GlowMouse het volgende:
Je moet je eerst afvragen wat beter is. Hoger gemiddelde, grotere mediaan, kleinere variantie, etc.
De two-sample t-test is een goede test op het gemiddelde wanneer je niets over de variantie weet, maar daarvoor moeten de waarnemingen wel uit een normale verdeling komen. Omdat je maar 10 waarnemingen hebt is die aanname erg cruciaal. Wie zegt anders immers dat de verwachting bestaat? Je bent dan aangewezen op een parametervrije toets.
Theories come and theories go. The frog remains


Dat lijkt me een goede keus. Houd er alleen rekening mee dat parametervrije toetsen een onjuiste nulhypothese niet zo snel verwerpen, dus zolang je niet verwerpt heb je niet zo'n sterke uitspraak.quote:Op maandag 19 januari 2009 11:41 schreef Bioman_1 het volgende:
[..]
tnx. Ik zat ook al te denken over de "normale verdeling aanname". Ik denk dat de Wilcoxon signed-rank test het best werkt voor wat ik wil doen. Zal daar eens verder naar kijken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


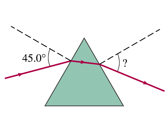
Licht valt onder een hoek van 45 graden in op een gelijkzijdig (alle hoeken 60 graden) prisma. De brekingsindex van het prisma bedraagt 1,54.
Bereken onder welke hoek het licht het prisma verlaat.
---
Mijn idee:
Je begint natuurlijk met theta = arcsin(sin[45]*1,54). theta = 27,33 graden.
Dan beredeneer ik:
Licht valt loodrecht in, dus 90 graden - 27,33 graden = 62,66 graden aan het linkerbeen in de driehoek die aan de top van de prisma wordt gevormd.
Een driehoek heeft 180 graden, dus 180 - (60+62,66) = 57,33 graden voor het rechterbeen van de driehoek. Daar valt het licht loodrecht uit (in een hoek met 90 graden dus), en 90 - 57,33 = 32,66 voor de hoek van 'inval' als ik opnieuw de wet van snellius ga toepassen.
Dit geeft voor de hoek van uitval: theta = arcsin(sin[32,33]*1,54) = 55,44 graden.
Maar het antwoord is 56,3 graden. Maak ik een fout of is dit een kwestie van afronding?
[ Bericht 1% gewijzigd door Koewam op 20-01-2009 23:19:23 ]


1. dit is het wiskunde-topic, niet voor natuurkunde dus
2. arcsin(sin[32,66]*1,54) geeft bij mij een juist antwoord
3. die hoek vind je sneller door de beide normalen te tekenen en te gebruiken dat de som van hoeken in een vierhoek 360 graden is
2. arcsin(sin[32,66]*1,54) geeft bij mij een juist antwoord
3. die hoek vind je sneller door de beide normalen te tekenen en te gebruiken dat de som van hoeken in een vierhoek 360 graden is
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


1. Wist nog niet dat dit gesplitst was, bedankt.
2. Ah gos ja, overtikfout. Bedankt.
3. Is de hoek die de twee normalen op het snijpunt maakt 90 graden? Tophoek 60, twee hoeken in de normalen 90 + 90, opgeteld is dat 240. 360 - 240 = 120. Ik snap niet hoe dat werkt.
2. Ah gos ja, overtikfout. Bedankt.
3. Is de hoek die de twee normalen op het snijpunt maakt 90 graden? Tophoek 60, twee hoeken in de normalen 90 + 90, opgeteld is dat 240. 360 - 240 = 120. Ik snap niet hoe dat werkt.


90 graden inderdaad want het is een normaal. Dan kom je op 120 graden uit voor de onderste hoek. Dan gebruik je de driehoek waarvan één zijde gegeven wordt door de lichtstraal en de andere twee door de normalen om die 32,66 graden te vinden. Scheelt 1x rekenen en is denk ik ook makkelijker uit te tekenen en begrijpbaar te maken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik ben niet van 't kansrekenen en statistiek en ik kom niet uit deze simpele vraagstelling.
"Uit een onderzoek op basis van een steekproef met omvang 25 bleek een gemiddelde van 76 met een foutmarge van 12 voor een betrouwbaarheid van 95%. Vermeld het 95% betrouwbaarheidsinterval."
Er moet 64 tot 88 uitkomen maar hoe? Geen idee, ik heb hier nooit les in gehad..
"Uit een onderzoek op basis van een steekproef met omvang 25 bleek een gemiddelde van 76 met een foutmarge van 12 voor een betrouwbaarheid van 95%. Vermeld het 95% betrouwbaarheidsinterval."
Er moet 64 tot 88 uitkomen maar hoe? Geen idee, ik heb hier nooit les in gehad..
Ik ben een superster want ik drink jupiler!


Een betrouwbaarheidsinterval is een interval dat, wanneer telkens op dezelfde wijze geconstrueerd, naar verwachting in een vast percentage van de gevallen (hier: 95%) de juiste parameter bevat. Die parameter is hier de verwachting. Het begrip foutmarge ken ik niet, maar is blijkbaar op analoge wijze gedefinieerd. Daar het gemiddelde een schatter is voor de verwachting (mits de verwachting bestaat), zijn de grenzen van het betrouwbaarheidsinterval 76 +/- 12.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Potdomme dat was wel erg simpel, maar ik snap er nu wat meer van. Dankjewel.
Ik ben een superster want ik drink jupiler!


Dilemma hiero:
TEG x sin(30) - TEC cos(45) = 0
TEG x cos(30) - TEC sin(45) - 20 = 0
*met sin(30) bedoel ik sinus 30 graden enz.
Ik moet TEC en TEG weten dmv substitueren oid
woensdag tentamen!
[ Bericht 7% gewijzigd door Marthh op 25-01-2009 12:59:31 ]
TEG x sin(30) - TEC cos(45) = 0
TEG x cos(30) - TEC sin(45) - 20 = 0
*met sin(30) bedoel ik sinus 30 graden enz.
Ik moet TEC en TEG weten dmv substitueren oid
woensdag tentamen!
[ Bericht 7% gewijzigd door Marthh op 25-01-2009 12:59:31 ]


schrijf bijvoorbeeld de eerste vergelijking als TEG = TEC cos(45) / sin(30).quote:Op zondag 25 januari 2009 12:45 schreef Marthh het volgende:
Dilemma hiero:
TEG x sin(30) - TEC cos(45) = 0
TEG x cos(30) - TEC sin(45) - 20 = 0
*met sin(30) bedoel ik sinus 30 graden enz.
Ik moet TEC en TEG weten dmv substitueren oid
woensdag tentamen!
Dit vul je dan in de 2e vergelijking in, zodat de 2e vergelijking alleen nog maar de variabele TEC bevat. Die kan je oplossen, en de gevonden waarde voor TEC vul je dan weer in de eerste vergelijking in om de oplossing voor de andere variabele te vinden.
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


quote:Op zondag 25 januari 2009 20:57 schreef Pietjuh het volgende:
[..]
schrijf bijvoorbeeld de eerste vergelijking als TEG = TEC cos(45) / sin(30).
Dit vul je dan in de 2e vergelijking in, zodat de 2e vergelijking alleen nog maar de variabele TEC bevat. Die kan je oplossen, en de gevonden waarde voor TEC vul je dan weer in de eerste vergelijking in om de oplossing voor de andere variabele te vinden.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik snap de methode, maar waarom is TEG = TEC cos(45) / sin(30)?quote:Op zondag 25 januari 2009 20:57 schreef Pietjuh het volgende:
[..]
schrijf bijvoorbeeld de eerste vergelijking als TEG = TEC cos(45) / sin(30).
Dit vul je dan in de 2e vergelijking in, zodat de 2e vergelijking alleen nog maar de variabele TEC bevat. Die kan je oplossen, en de gevonden waarde voor TEC vul je dan weer in de eerste vergelijking in om de oplossing voor de andere variabele te vinden.


Elementaire algebra, brugklas niveau. Als geldt ab - cd = 0 en b is ongelijk aan 0, dan geldt a = cd/b.quote:Op maandag 26 januari 2009 21:26 schreef Marthh het volgende:
[..]
Ik snap de methode, maar waarom is TEG = TEC cos(45) / sin(30)?
Overigens geldt sin 30° = ½ en sin 45° = cos 45° = ½√2, dus daar zou ik even mee beginnen.


Okee snapquote:Op maandag 26 januari 2009 22:20 schreef Riparius het volgende:
[..]
Elementaire algebra, brugklas niveau. Als geldt ab - cd = 0 en b is ongelijk aan 0, dan geldt a = cd/b.
Overigens geldt sin 30° = ½ en sin 45° = cos 45° = ½√2, dus daar zou ik even mee beginnen.
eindelijk


Ik heb twee vraagjes:
1)
F*cos(30)=0,2*(400+F*sin(30))
Hoe bereken ik F uit? Antwoord is 104,4N.
2)
Je hebt twee vectoren:
V1=
(x4+x2-1/2d)cos(...)
(x4+x2-1/2d)sin(...)
0
Fz=
0
-mg
0
Wat is dan V1*Fz? Hoe moet je dat doen? Het antwoord is:
V1*Fz:
0
0
-(x4+x2-1/2d)cos(...)mg
Alvast bedankt
[ Bericht 37% gewijzigd door BK89 op 27-01-2009 12:45:21 ]
1)
F*cos(30)=0,2*(400+F*sin(30))
Hoe bereken ik F uit? Antwoord is 104,4N.
2)
Je hebt twee vectoren:
V1=
(x4+x2-1/2d)cos(...)
(x4+x2-1/2d)sin(...)
0
Fz=
0
-mg
0
Wat is dan V1*Fz? Hoe moet je dat doen? Het antwoord is:
V1*Fz:
0
0
-(x4+x2-1/2d)cos(...)mg
Alvast bedankt
[ Bericht 37% gewijzigd door BK89 op 27-01-2009 12:45:21 ]


je haalt alles met een F erin naar de linker kant, dan krijg je
F*cos(30)-,2*F*sin(30)=80
F(cos(30)-,2*sin(30))=80
F=80/(cos(30)-,2*sin(30))=104,35 (niet gelet op significantie)
En van die vectoren heb ik ook geen idee, bedoel je die * als een dot-product of niet?
Ik zou zeggen dat het overigens
0
-(x4+x2-1/2d)sin(...)mg
0
zou worden
F*cos(30)-,2*F*sin(30)=80
F(cos(30)-,2*sin(30))=80
F=80/(cos(30)-,2*sin(30))=104,35 (niet gelet op significantie)
En van die vectoren heb ik ook geen idee, bedoel je die * als een dot-product of niet?
Ik zou zeggen dat het overigens
0
-(x4+x2-1/2d)sin(...)mg
0
zou worden
ff wachten nog


Bedankt voor het uitleg van vraag 1, zal zo ff proberenquote:Op dinsdag 27 januari 2009 13:32 schreef Game_Error het volgende:
je haalt alles met een F erin naar de linker kant, dan krijg je
F*cos(30)-,2*F*sin(30)=80
F(cos(30)-,2*sin(30))=80
F=80/(cos(30)-,2*sin(30))=104,35 (niet gelet op significantie)
En van die vectoren heb ik ook geen idee, bedoel je die * als een dot-product of niet?
Ik zou zeggen dat het overigens
0
-(x4+x2-1/2d)sin(...)mg
0
zou worden


Er is een andere optie voor vraag 1 die ik kan bedenken, en dat is dat ze het cross-product nemen, deze methode is bedoelt om een vector te vinden die orthogonaal staat op de originele 2 vectoren, in de geval levert dat dus:
0
0
-(x4+x2-1/2d)cos(...)mg
Precies wat jij zocht.
0
0
-(x4+x2-1/2d)cos(...)mg
Precies wat jij zocht.
ff wachten nog


Inmiddels ben ik wat stappen verder met eerdere vragen die nog onbeantwoord waren gebleven. Echter, nu doet het volgende zich voor.
Bij een normale multiple regressie bekijk ik de verkoop van verschillende producten als afhankelijke variabele en gebruik verschillende marketingacties als onafhankelijke factoren (dummyvariabelen). Aangezien de producten onderling nogal verscihllen in hun standaardverkoopvolume (sommige bijv. 100stuks/mnd en andere 500st/mnd compenseer ik daarvoor door voor ieder product een dummyvariabele aan te maken in de regressie (eigenlijk een dummy minder, omdat allemaal 0 het referentieproduct is). Het model heeft een behoorlijke fit en de parameters zijn nagenoeg allemaal significant.
Stel, de waarde voor de constante is 1000 (dus 1000 stuks per maand), en de waarde voor drie parameters die staan voor een actie zijn respectievelijk 200, 400 en 300.
Dan is mijn interpretatie dat het individueel uitvoeren van deze acties dezelfde toename aan verkoop veroorzaken. Actie 1: 1200 totaal ; Actie 2 1400 totaal; Actie 3 1300 totaal.
Nou is bijvoorbeeld de parameter voor de dummy van product X= -500 (de basisverkoop van product X ligt dus zo'n 500 producten/mnd lager), het lijkt me dan niet redelijk om aan te nemen dat de verkoop toeneemt met 200 als je actie 1 uitvoert. Mag ik wel de relatieve toename van de constante icm een actie (bijv 20% voor actie 1) gebruiken om het effect van actie 1 op product X uit te drukken? Dat zou dan betekenen dat de verwachting is dat actie 1 icm met product x een verkoop van ongeveer 600 producten zou opleveren.
Bij een normale multiple regressie bekijk ik de verkoop van verschillende producten als afhankelijke variabele en gebruik verschillende marketingacties als onafhankelijke factoren (dummyvariabelen). Aangezien de producten onderling nogal verscihllen in hun standaardverkoopvolume (sommige bijv. 100stuks/mnd en andere 500st/mnd compenseer ik daarvoor door voor ieder product een dummyvariabele aan te maken in de regressie (eigenlijk een dummy minder, omdat allemaal 0 het referentieproduct is). Het model heeft een behoorlijke fit en de parameters zijn nagenoeg allemaal significant.
Stel, de waarde voor de constante is 1000 (dus 1000 stuks per maand), en de waarde voor drie parameters die staan voor een actie zijn respectievelijk 200, 400 en 300.
Dan is mijn interpretatie dat het individueel uitvoeren van deze acties dezelfde toename aan verkoop veroorzaken. Actie 1: 1200 totaal ; Actie 2 1400 totaal; Actie 3 1300 totaal.
Nou is bijvoorbeeld de parameter voor de dummy van product X= -500 (de basisverkoop van product X ligt dus zo'n 500 producten/mnd lager), het lijkt me dan niet redelijk om aan te nemen dat de verkoop toeneemt met 200 als je actie 1 uitvoert. Mag ik wel de relatieve toename van de constante icm een actie (bijv 20% voor actie 1) gebruiken om het effect van actie 1 op product X uit te drukken? Dat zou dan betekenen dat de verwachting is dat actie 1 icm met product x een verkoop van ongeveer 600 producten zou opleveren.


Dan heb je je regressiemodel verkeerd gespecificeerd.quote:Op dinsdag 27 januari 2009 21:00 schreef TheSilverSpoon het volgende:
Nou is bijvoorbeeld de parameter voor de dummy van product X= -500 (de basisverkoop van product X ligt dus zo'n 500 producten/mnd lager), het lijkt me dan niet redelijk om aan te nemen dat de verkoop toeneemt met 200 als je actie 1 uitvoert.
Nee.quote:Mag ik wel de relatieve toename van de constante icm een actie (bijv 20% voor actie 1) gebruiken om het effect van actie 1 op product X uit te drukken? Dat zou dan betekenen dat de verwachting is dat actie 1 icm met product x een verkoop van ongeveer 600 producten zou opleveren.
[ Bericht 0% gewijzigd door GlowMouse op 27-01-2009 21:22:20 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op dinsdag 27 januari 2009 21:11 schreef GlowMouse het volgende:
Dan heb je je regressiemodel verkeerd gespecificeertd.
Door de producten als binaire variabelen mee te nemen in de regressievergelijking compenseer ik voor het verkoopvolume dat veroorzaakt wordt door het product zelf. Deze werkwijze is mij nota bene door een docent aangeraden, en we hebben het samen ook doorgelopen. Zelf had ik meer met het idee om de verschillende producten aan te duiden (nesten) in de termen van de dummies. Dus product i in week t.
Dat de parameter voor de constante (een product met baseline rond de 1000) hoger is dan een ander product is niet gek. Als de parameter voor een ander product lager is, dan is daar niets geks aan als die parameter negatief is. Dus iets meer argumentatie zou welkom zijn
De fit van het model is zoals gezegd ook hoog, R square rond de 0,8 en adjusted R square rond de 0,77.


Als jij je model specificeert als verkoop = b0 + b1*actie1 + b2*actie2 + b3*actie3 + b4*product1 + b5*product2 + b6*product 3 + b7*product4 + ... + eps, dan geef je daarmee aan dat je verwacht dat de verkopen van een willekeurig product ceteris paribus met b1 toenemen wanneer je actie1 laat lopen voor dat product. Zeg je vervolgens dat je niet denkt dat dat het geval is, is je model onjuist gespecificeerd. Dan zul je kruistermen mee moeten nemen tussen producten en acties en een grote R² dat dat gaat geven!.quote:Op dinsdag 27 januari 2009 21:20 schreef TheSilverSpoon het volgende:
[..]
Door de producten als binaire variabelen mee te nemen in de regressievergelijking compenseer ik voor het verkoopvolume dat veroorzaakt wordt door het product zelf. Deze werkwijze is mij nota bene door een docent aangeraden, en we hebben het samen ook doorgelopen. Zelf had ik meer met het idee om de verschillende producten aan te duiden (nesten) in de termen van de dummies. Dus product i in week t.
Een hoge (adjusted) R² zegt niet zoveel. Zeker hier, waar je een groot deel 'verklaart' met de juiste dummycategorie.quote:De fit van het model is zoals gezegd ook hoog, R square rond de 0,8 en adjusted R square rond de 0,77.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Op de wijze die jij schetst heb ik het inderdaad ingevoerd.quote:Op dinsdag 27 januari 2009 21:29 schreef GlowMouse het volgende:
[..]
Als jij je model specificeert als verkoop = b0 + b1*actie1 + b2*actie2 + b3*actie3 + b4*product1 + b5*product2 + b6*product 3 + b7*product4 + ... + eps, dan geef je daarmee aan dat je verwacht dat de verkopen van een willekeurig product ceteris paribus met b1 toenemen wanneer je actie1 laat lopen voor dat product. Zeg je vervolgens dat je niet denkt dat dat het geval is, is je model onjuist gespecificeerd. Dan zul je kruistermen mee moeten nemen tussen producten en acties en een grote R² dat dat gaat geven!.
Ik laat het model uiteindelijk draaien in 4 sets (productcategorieën) omdat ik verwacht dat daar wel verschillen optreden, en doe inderdaad daarmee de aanname dat het effect voor de verschillende producten gelijk is. Let wel, ik verwacht dat het relatieve effect gelijk is voor verschillende producten. Volgens jou kan ik dat nooit op deze wijze berekenen?
Stel: Product X (basisverkoop van 100) en product Y is de constante met een basisverkoop van 400.
Als ik de fomule bekijk, dan wordt inderdaad het effect van de basisverkoop opgevangen door de productdummy. Dat is vrij simpel. Maar, als ik het goed begrijp (en zie), dan levert een actie bij product X met een toename van 10%, maar een hele kleine bijdrage aan de parameter vergeleken met een actie van product Y met dezelfde relatieve toename. Respectievelijk 10 en 40. Dit is dan ook de reden dat je hier niet de toename van de verkoop uit kan halen voor verschillende producten.
Wat zou jij suggereren? Een model met 'nested' variabelen, waarbij ik het product opneem in de parameter; dus bijv: Dummy voor actie 1, voor product i in week t
Dat is ook helemaal waar, zeker aangezien het om ongeveer 27 producten gaat, en slechts 8 andere dummies.quote:Een hoge (adjusted) R² zegt niet zoveel. Zeker hier, waar je een groot deel 'verklaart' met de juiste dummycategorie.


Als je relatieve veranderingen wilt bekijken, moet je logaritmen in je model opnemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Mmm, daar heb ik al wat van gezien inderdaad. Maar de huidige specificatie van het model geeft ook niet eens de absolute verandering aan als ik het goed zie, zoals ik probeerde te verwoorden in vorige post, n´est pas?quote:Op dinsdag 27 januari 2009 22:05 schreef GlowMouse het volgende:
Als je relatieve veranderingen wilt bekijken, moet je logaritmen in je model opnemen.


Waarom je de week toe wilt voegen snap ik niet, maar afgezien daarvan is het wat ik eerder bedoelde met kruistermen. Je voegt als regressoren actie1*product1, actie1*product2, etc toe. Je verlaat daarmee wel de gedachte van de gelijke relatieve verandering voor ieder product, hoewel dat met wat lineaire restricties op de regressiecoëfficienten wel te verhelpen is.quote:Op dinsdag 27 januari 2009 22:23 schreef TheSilverSpoon het volgende:
[..]
Mmm, daar heb ik al wat van gezien inderdaad. Maar de huidige specificatie van het model geeft ook niet eens de absolute verandering aan als ik het goed zie, zoals ik probeerde te verwoorden in vorige post, n´est pas?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


(Vergeet ik nog te zeggen, maar bedankt voor je input! Zit nu in 't buitenland zonder boeken, en kan derhalve ook niet de slag maken die ik gedacht had te maken. Ik lijk redelijk op 't verkeerde been gezet door de docent, zeker omdat hij weet waar ik naar toe werk.)quote:Op dinsdag 27 januari 2009 22:25 schreef GlowMouse het volgende:
Waarom je de week toe wilt voegen snap ik niet, maar afgezien daarvan is het wat ik eerder bedoelde met kruistermen. Je voegt als regressoren actie1*product1, actie1*product2, etc toe. Je verlaat daarmee wel de gedachte van de gelijke relatieve verandering voor ieder product, hoewel dat met wat lineaire restricties op de regressiecoëfficienten wel te verhelpen is.
Week voeg ik toe omdat het belangrijk is. In het model is het dan ook eigenlijk:
Verkoop(product i, week t) = b0 + b1*actie1(product i week t) + b2*actie2(product i week t) + b3*actie3(product i week t) + b4*product1 + b5*product2(product i week t) + b6*product 3(product i week t) + b7*product4(product i week t) + ... + eps
In woorden: de aanwezigheid van de acties is afhankelijk van de week en het product. Voor alle producten heb ik tientallen weken aan data. Week is niet zozeer belangrijk voor de tijd als wel om elke 'case' de juiste dummywaarden mee te geven op basis van het weeknummer.
Mmm, gelijke relatieve verandering wil ik juist wel aanhouden, op z'n minst per productgroep (bestaande uit zo'n 5-8 producten).
Bovenstaande formule komt uit een gelijksoortig onderzoek. In dit geval wordt er gepooled over de verschillende winkels (waar ongetwijfeld ook andere baseline sales zijn), ik zou dan kunnen poolen over de productsoorten. (Later wordt nog een formule gegeven voor de omrekening van de parameter naar het percentage toename dat een actie veroorzaakt.
Overigens worden acties hier wel als combinatie gezien, en niet los behandeld.


t heeft bij jouw de functie van wat je normaal als i hebt: je onderscheid er de cases mee. Echte mensen werken met vectornotatie en vermelden daarmee alle cases in 1x zodat je die t niet hoeft te noemen. Zolang t maar niet in je regressoren terugkomt is het goed.
Als prod1 dan 2x zoveel verkocht wordt als prod2 bijvoorbeeld, kun je zeggen dat de coefficient bij prod1*actie1 tweemaal zo groot moet zijn als bij prod1*actie2. Met zulke lineaire restricties is een model nog eenvoudig te schatten.
Als prod1 dan 2x zoveel verkocht wordt als prod2 bijvoorbeeld, kun je zeggen dat de coefficient bij prod1*actie1 tweemaal zo groot moet zijn als bij prod1*actie2. Met zulke lineaire restricties is een model nog eenvoudig te schatten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0