Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Nou, niet direct; zo'n elitistische reply is nu even te kort door de bocht. Uit zijn post proef ik dat hij al vermoedt dat hij een foutieve berekening gemaakt heeft; hij twijfelt nl. zelf al aan de geldigheid v/d uitdrukking ∞ - ∞ = "iets"???. Het gaat mis doordat hij niet van te voren geprobeerd heeft de uitdrukking via de worteltruuk algebraïsch om te vormen tot een uitdrukking waar wèl een fatsoenlijk limietberekening mee gemaakt kan worden (zie post Haushofer), en om het inzichtelijk voor hem te maken, zet ik nog even wat extra stappen ertussen, gebaseerd op die andere worteltruuk.quote:Op donderdag 3 mei 2012 18:45 schreef Riparius het volgende:
Je fundamentele denkfout is dat je denkt dat je het symbool ∞ mag behandelen als een gewoon getal, maar dat is niet zo, ∞ is geen getal. Je mag dus ook niet zeggen dat een bepaalde limiet of een bepaalde grootheid 'gelijk' is aan 'oneindig', dat heeft geen betekenis. De rekenregel dat de limiet van een verschil van twee uitdrukkingen gelijk is aan het verschil van de limieten van die beide uitdrukkingen geldt ook alleen maar als de limieten van beide termen elk afzonderlijk bestaan, en dat is hier niet het geval.
vermenigvuldigd met
[ Bericht 0% gewijzigd door VanishedEntity op 04-05-2012 04:58:37 ]
Sowieso is voor fysici oneindig gelijk aan 0quote:
[..]
In wat geavanceerdere boeken kom je het wel eens tegen.
Kan iemand mij helpen met dit vraagstuk:
For iterative elimination of strictly dominated strategies, show that the sets are nested (deelvraag 1)(wat is nested?) and that the procedure terminates in finitely many rounds if the game is finite (2). Can you provide a tight upper bound on the number of iterations that might be required? (3)
Ik weet sowieso niet wat nested betekent.
Verder zou ik bij (deelvraag 2) show that the procedure terminates in finitely many rounds if the game is finite.
Antwoorden:
When there's strictly dominance, one strategy s(DOM)i always dominates s(not DOM) i, because
utility player i (s(DOM)i, s - i) > utility player i (s(not DOM)i, s-i) So the utility of player i is strictly higher when using dominant strategy s for all s - i which are in the set of S - i (s - i and S - i are the strategies of all other players except player i ) When there are only strictly dominating strategies and there is a finite game, the procedure of iteration has also to be finite.
Klopt dit? En kan iemand mij helpen met die 2 andere deelvragen? Thanks!
quote:
[..]
Sowieso is voor fysici oneindig gelijk aan 0
Wat ze bedoelen met "A is nested in B" is denk ik "A is een deelverzameling van B". Ik snap alleen niet wat ze met "the sets" bedoelen.quote:
Game Theory:
Kan iemand mij helpen met dit vraagstuk:
For iterative elimination of strictly dominated strategies, show that the sets are nested (deelvraag 1)(wat is nested?) and that the procedure terminates in finitely many rounds if the game is finite (2). Can you provide a tight upper bound on the number of iterations that might be required? (3)
Ik weet sowieso niet wat nested betekent.
Verder zou ik bij (deelvraag 2) show that the procedure terminates in finitely many rounds if the game is finite.
Antwoorden:
When there's strictly dominance, one strategy s(DOM)i always dominates s(not DOM) i, because
utility player i (s(DOM)i, s - i) > utility player i (s(not DOM)i, s-i) So the utility of player i is strictly higher when using dominant strategy s for all s - i which are in the set of S - i (s - i and S - i are the strategies of all other players except player i ) When there are only strictly dominating strategies and there is a finite game, the procedure of iteration has also to be finite.
Klopt dit? En kan iemand mij helpen met die 2 andere deelvragen? Thanks!
Ik snap je uitwerking niet omdat ik die notaties niet ken.
Als twee driehoeken twee zijden delen en een hoek. En die hoek is 90 graden, maar is ingesloten. Is er dan sprake van congruentiegeval ZZR of ZHZ ? Volgens mijn antwoorden gaat het om ZZR, maar de definitie spreekt over een niet-ingesloten hoek.
Het is een uitspraak die vaak gedaan wordt ivm "renormalizatie"; het verschijnsel dat (met name in quantumveldentheorieën) fysici uit naieve berekeningen oneindig krijgen. De renormalisatieprocedure maakt daar een eindig antwoord van.quote:Op vrijdag 4 mei 2012 11:54 schreef thenxero het volgende:
[..]Serieus? Dat is wel een erg grove benadering.
Een ander pareltje wat o.a. gebruikt wordt in snaartheorie is de "identiteit"
waarmee via analytische continuatie bepaalde divergenties in je uitdrukkingen geregulariseerd worden. De manier waarop dat in tekstboeken wordt beschreven zou de meeste wiskundigen niet bepaald fijn overkomen, denk ik
Het lijkt mij ook ZHZ.quote:
Ik heb een korte vraag over meetkunde/congruentie:
Als twee driehoeken twee zijden delen en een hoek. En die hoek is 90 graden, maar is ingesloten. Is er dan sprake van congruentiegeval ZZR of ZHZ ? Volgens mijn antwoorden gaat het om ZZR, maar de definitie spreekt over een niet-ingesloten hoek.
ZZR is eigenlijk geen afzonderlijk congruentiekenmerk, want als twee rechthoekige driehoeken de hypotenusa en een rechthoekszijde gemeen hebben, dan hebben ze ook de andere rechthoekszijde gemeen op grond van Pythagoras en zijn ze dus congruent volgens congruentiekenmerk ZHZ. Maar soms wordt ZZR toch als een afzonderlijk congruentiekenmerk gegeven (zie bijvoorbeeld hier) omdat er bij ZZH nog twee mogelijkheden kunnen zijn. Om ZZH toch als congruentiekenmerk te kunnen gebruiken moet je als extra voorwaarde stipuleren dat de zijde tegenover de gemene hoek de langste van de twee gemene zijden is.quote:
Ik heb een korte vraag over meetkunde/congruentie:
Als twee driehoeken twee zijden delen en een hoek. En die hoek is 90 graden, maar is ingesloten. Is er dan sprake van congruentiegeval ZZR of ZHZ ? Volgens mijn antwoorden gaat het om ZZR, maar de definitie spreekt over een niet-ingesloten hoek.
Nu weet ik weer waarom ik gestopt ben met natuurkundequote:
[..]
Het is een uitspraak die vaak gedaan wordt ivm "renormalizatie"; het verschijnsel dat (met name in quantumveldentheorieën) fysici uit naieve berekeningen oneindig krijgen. De renormalisatieprocedure maakt daar een eindig antwoord van.
Een ander pareltje wat o.a. gebruikt wordt in snaartheorie is de "identiteit"
waarmee via analytische continuatie bepaalde divergenties in je uitdrukkingen geregulariseerd worden. De manier waarop dat in tekstboeken wordt beschreven zou de meeste wiskundigen niet bepaald fijn overkomen, denk ik
Je hebt hier eigenlijk ζ(-1) = -1/12, dus het is minder idioot dan het er uit ziet en ook wiskundig interessant. Het idee is afkomstig van Ramanujan. Mooi voorbeeld van hoe krankzinnigheid en genialiteit dicht bij elkaar kunnen liggen.quote:Op vrijdag 4 mei 2012 19:53 schreef thenxero het volgende:
[..]
Nu weet ik weer waarom ik gestopt ben met natuurkunde
Is g'(q) + 12aq2 + 6aq
Ik twijfel hoe ik het afgeleiden krijg van 3a2q . Mijn boek heeft er geen uitleg over. Is hier iemand die weet hoe het zit?
Je wil de afgeleide naar q bepalen van je uitdrukking. Dan beschouw je a dus als een constante. Je krijgt dan:quote:
Ik heb: g(q) = 4aq3 + 3a2q - a3
Is g'(q) + 12aq2 + 6aq
Ik twijfel hoe ik de afgeleide krijg van 3a2q . Mijn boek heeft er geen uitleg over. Is hier iemand die weet hoe het zit?
g'(q) = 12aq2 + 3a2
De afgeleide van 3a2q is dus 3a2, net zoals f(x) = 3x --> f ' (x) = 3
f(a) = 0,3a3p3
Wordt het dan: f'(a) =0,9a2 ?
In een bewijs dat ik probeer te maken, zou het erg prettig zijn als ik kan bewijzen dat
ax_1^{2d}+bx_2^{2d}-2dx_1^ax_2^b met a+b=2d, a,b en d natuurlijk een som van maximaal 2 kwadraten is. Dan kan ik vervolgens met inductie bewijzen dat dergelijke polynomen van een hogere macht de som van maximaal 3n-4 kwadraten zijn. Iemand een idee hoe je die 2 kwadraten maakt?
Alvast bedankt!
Het dingetje wat je in je functie stopt, in dit geval de a, is niet je constante, maar je variabele.quote:
Hoe weet je precies of het een constante is?
f(a) = 0,3a3p3
Wordt het dan: f'(a) =0,9a2 ?
De a en b die je als coëfficiënten noemt, zijn dezelfde als de a en b die je als exponenten noemt?quote:
Hoi,
In een bewijs dat ik probeer te maken, zou het erg prettig zijn als ik kan bewijzen dat
ax_1^{2d}+bx_2^{2d}-2dx_1^ax_2^b met a+b=2d, a,b en d natuurlijk een som van maximaal 2 kwadraten is. Dan kan ik vervolgens met inductie bewijzen dat dergelijke polynomen van een hogere macht de som van maximaal 3n-4 kwadraten zijn. Iemand een idee hoe je die 2 kwadraten maakt?
Alvast bedankt!
jaquote:
[..]
De a en b die je als coëfficiënten noemt, zijn dezelfde als de a en b die je als exponenten noemt?
Dus mijn antwoord klopt?quote:
[..]
Het dingetje wat je in je functie stopt, in dit geval de a, is niet je constante, maar je variabele.
Ik ben zelf uitgegaan van de reële getallen, daar staat echter niets over in de opgave.quote:
En in welke ring moeten de coëfficiënten van de polynomen zitten die je moet kwadrateren?
Bijna, omdat de p^3 bij dezelfde term hoort, mag je hem niet zomaar weglaten. Net als de 0,3 die negeer je ook niet. Je antwoord is dan 0,9a2p3quote:
Dan is het een slechte opgave.quote:
[..]
Ik ben zelf uitgegaan van de reële getallen, daar staat echter niets over in de opgave.
Edit: laat maar, verkeerd gelezen.
Nee, want in jouw afgeleide naar a is je constante factor p3 plotseling verdwenen.quote:
Duidelijk, danku!quote:
[..]
Bijna, omdat de p^3 bij dezelfde term hoort, mag je hem niet zomaar weglaten. Net als de 0,3 die negeer je ook niet. Je antwoord is dan 0,9a2p3
Een polynoom f in R[x] met f(x) >= 0 voor alle x in R kun je schrijven als de som van 2 kwadraten van polynomen in R[x]. Ken je die stelling?quote:
Hoi,
In een bewijs dat ik probeer te maken, zou het erg prettig zijn als ik kan bewijzen dat
ax_1^{2d}+bx_2^{2d}-2dx_1^ax_2^b met a+b=2d, a,b en d natuurlijk een som van maximaal 2 kwadraten is. Dan kan ik vervolgens met inductie bewijzen dat dergelijke polynomen van een hogere macht de som van maximaal 3n-4 kwadraten zijn. Iemand een idee hoe je die 2 kwadraten maakt?
Alvast bedankt!
Ja, maar ik zie nog even niet waarom dit polynoom altijd >=0 moet zijn, maar ik zal er weer even over nadenken..quote:
[..]
Een polynoom f in R[x] met f(x) >= 0 voor alle x in R kun je schrijven als de som van 2 kwadraten van polynomen in R[x]. Ken je die stelling?
Ken je de herschikkingsongelijkheid?quote:
[..]
Ja, maar ik zie nog even niet waarom dit polynoom altijd >=0 moet zijn, maar ik zal er weer even over nadenken..
Daar ben ik mee aan het prutsen ja. Dat geeft me dat 2x_1^ax_2^b <= x_1^{2d}+x_2^{2d}. Maar dan moet ik het nu nog goed zien te krijgen met de coefficienten erbij..quote:
Dankjewel, maar hier kom ik ook nog niet echt uit. Dit is overigens de eerste keer dat ik van de regel hoor, dus ik heb even gegoogled. Hij lijkt alleen voor polynomen met één variabele te werken. Dan kun je natuurlijk die andere als een constante kiezen. Maar dan is het ook nog relevant of a en b even of oneven zijn bij het nagaan van het aantal negatieve oplossingen,terwijl je daar niks van weet? En zet je een + voor alle 0x^c met a_1<c<2d termen?quote:Op zondag 6 mei 2012 22:52 schreef thabit het volgende:
Hmm, ja, ik was misschien iets te snel daarmee. Maar het kan wel met de tekenregel van Descartes.
Voor mijn minor bedrijfseconomie heb ik namelijk een vraag en ik kom er echt niet uit!
Wie zou me kunnen helpen aan het antwoord en de berekening?
Het betreft vraag 10
Minor bedrijfseconomie? Dit lijkt meer 5VWO M&Oquote:
Ik weet niet of ik hier goed zit verbeter me maar als ik naar een ander topic moet
Voor mijn minor bedrijfseconomie heb ik namelijk een vraag en ik kom er echt niet uit!
[ afbeelding ]
Wie zou me kunnen helpen aan het antwoord en de berekening?
Het betreft vraag 10
hint: de toename van de kosten / de toename aantal producten = variabele kosten.
hieruit kun je de totale variabele kosten berekenen van bijv. 100.000 producten.
hieruit kun je de constante kosten berekenen.
Dan heb je de formule: kostprijs = c/n + v/b
winstopslag erover, klaar.
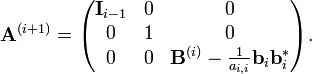
zou ik alleen nog
http://en.wikipedia.org/w(...)e_Cholesky_algorithm
Ik ben in zoverre bekend met de Cholesky-decompositie dat ik het algoritme ken om de ontbinding te vinden inquote:Op dinsdag 8 mei 2012 23:09 schreef Dale. het volgende:
Is iemand hier toevallig bekend met de Cholesky decompositie? Ik heb. Nu wordt er gevraagd op de cholesky decompositie te geven in termen van "consituent submatrices". Nu wil ik het eerst nog zelf proberen maar wat wordt precies bedoeld met "constituent submatrices"? Moet ik de cholesky decompositie dus uitdrukken in de termen
,
en
? Want dan zou ik dus
[ afbeelding ]
zou ik alleen nog
http://en.wikipedia.org/w(...)e_Cholesky_algorithm
dan geldt
-edit- geloof dat 't kan aangezien B symmetrisch is.
[ Bericht 22% gewijzigd door Dale. op 09-05-2012 01:20:32 ]
opgave 15 en 16.Zit er al anderhalf uur mee te kloten.. help
Welke manieren heb je om je GR hierbij te gebruiken?
De formule is L = 10log(I/I0)
Als ik de L en de I0 al weet, hoe kan ik dan de I uitrekenen?
Als je met die 10 het grondtal bedoelt van de logaritme, dan moet je dat wel superscripten, anders sticht je alleen maar verwarring. Dus:quote:
Ik heb een probleempje met natuurkunde waar ik maar niet uitkom. Maar aangezien het met het vervormen van een formule te maken heeft post ik het hier
De formule is L = 10log(I/I0)
Als ik de L en de I0 al weet, hoe kan ik dan de I uitrekenen?
L = 10log(I/I0)
Verder kun je gewoon gebruik maken van de definitie van de logaritme: glog a is de exponent waartoe je g moet verheffen om a te verkrijgen. Hier is L dus de macht waartoe je 10 moet verheffen om I/I0 te verkrijgen:
10L = I/I0
[ Bericht 0% gewijzigd door Riparius op 10-05-2012 21:06:58 ]
Met als voorbeeld de drie punten A(2,0,0), B(0,3,0) en C(0,0,4) in een stelsel Oxyz vind ik als volgt de vergelijking van de twee lijnen door A & B en B & C
(2-0)(y-3) = (0-3)(x-0)
2(y-3) = -3x
2y - 6 = -3x
2y + 3x = 6
(3-0)(z-4) = (0-4)(y-0)
3(z-4) = -4y
3z - 12 = -4y
3z + 4y = 12
Volgens een vriend kon je ze dan vermenigvuldigen met d, gelijkstellen en bij elkaar voegen, en dat is waar ik het kwijt raak.
2dy + 3dx = 6d
3dz + 4dy = 12d
2dy + 3dx = 6d
(3/2)dz + 2dy = 6d
3dx + 2dy + (3/2)dz = 6d
Vanaf daar begrijp ik het wel weer, d = 1
3x + 2y + (3/2)z = 6
En er fancy uit laten zien
(3/6)x + (2/6)y + (3/12)z = 1
(x/2) + (y/3) + (z/4) = 1
Ik zie in dit alles het vlak als een bundeling lijnen vanuit punt B met als 'uiterste' lijnen de twee in het begin gevonden vergelijkingen, waarin iedere lijn gelimiteerd is door de d uit ax + by + cz = d. Is dit juist, of zit ik daarin fout?
Hierbij uitgegaan van punt A met richtingsvectoren geconstrueerd uit A-B en A-C
Bepaal de normaalvector door het kruisproduct nemen
Vul een punt in om d te vinden:
Invullen en uitschrijven:
De vergelijkingen die je geeft stellen in de driedimensionale ruimte vlakken voor, geen lijnen, dus hier gaat het al fout.quote:Op vrijdag 11 mei 2012 17:53 schreef Quir het volgende:
Ik ben bezig met het doorwerken van Basisboek Wiskunde maar loop nu wat vast bij de vlakken. Er wordt gevraagd een vergelijking van een vlak op te stellen door drie gegeven punten, en die kan ik vinden, maar ik snap er een deel niet van.
Met als voorbeeld de drie punten A(2,0,0), B(0,3,0) en C(0,0,4) in een stelsel Oxyz vind ik als volgt de vergelijking van de twee lijnen door A & B en B & C
Het idee is dat je eerst een normaalvector n bepaalt van je vlak V. Dat is een vector die loodrecht op het vlak staat. Is nu v = (x,y,z) een willekeurige vector met eindpunt in je vlak V en v0 = (x0,y0,z0) een vaste vector met eindpunt in je vlak, dan is vector v - v0 evenwijdig aan je vlak en staat deze verschilvector dus loodrecht op je normaalvector n, zodat het inproduct van v- v0 en n gelijk is aan nul:
(1) n∙(v - v0) = 0
En dus geldt ook:
(2) n∙v = n∙v0
Een vaste vector v0 met eindpunt in je vlak V ken je al omdat je immers de drie punten A,B en C kent die in vlak V liggen, zodat je hier voor v0 bijvoorbeeld de vector a = (2,0,0) zou kunnen nemen zodat x0 =2, y0 = 0 en z0 = 0.
De kunst is nu om een geschikte normaalvector n = (a,b,c) te bepalen want dan kun je voor (1) schrijven:
(3) a(x - x0) + b(y - y0) + c(z - z0) = 0,
en voor (2) kun je schrijven:
(4) ax + by + cz = ax0 + by0 + cz0,
en (3) of (4) is uiteraard de gezochte cartesische vergelijking van je vlak. Om nu een geschikte normaalvector n = (a,b,c) en daarmee de waarden van a,b en c te vinden kun je bedenken dat n loodrecht staat op zowel de verschilvector b - a als de verschilvector c - a, aangezien deze beide verschilvectoren evenwijdig zijn aan vlak V. En dus moet het inproduct van n = (a,b,c) met zowel b - a = (-2,3,0) als c - a = (-2,0,4) gelijk zijn aan nul. Dit geeft:
(5a) -2a + 3b = 0
(5b) -2a + 4c = 0
Hier heb je twee lineaire vergelijkingen in drie onbekenden a, b en c, en dus lijkt het alsof je nog één lineaire vergelijking tekort komt. Maar dat is niet zo, want als we n met een scalar vermenigvuldigen, dan hebben we nog steeds een vector die loodrecht op vlak V staat, dus zijn a,b,c niet eenduidig bepaald. Dat is ook meteen duidelijk uit de cartesische vergelijking (3) want als je hier beide leden met een getal ongelijk nul vermenigvuldigt, dan heb je nog steeds een geldige cartesische vergelijking van je vlak V.
We kunnen nu met (5a) en (5b) de waarde van a en b uitdrukken in c. Uit (5b) volgt dat a = 2c en substitutie hiervan in (5a) levert b = (4/3)∙c en dus hebben we n = (2c, (4/3)∙c, c). Kiezen we nu bijvoorbeeld c = 3, dan krijgen we n = (6, 4, 3). Op grond van (3) wordt de cartesische vergelijking van je vlak V nu:
(6) 6(x - 2) + 4(y - 0) + 3(z - 0) = 0,
en uitwerken hiervan geeft:
(7) 6x + 4y + 3z = 12
Je kunt nu door invullen gemakkelijk controleren dat de coördinaten van de punten A, B en C inderdaad aan (7) voldoen. Overigens hadden we in dit speciale geval de vergelijking van het vlak direct uit het hoofd kunnen opschrijven in de vorm (1/2)∙x + (1/3)∙y + (1/4)∙z = 1 omdat van elk van de drie gegeven punten A resp. B resp. C alleen de x- resp. y- resp. z-coördinaat ongelijk is aan nul. Maar in het algemeen is dat uiteraard niet zo als je de cartesische vergelijking van een vlak door drie gegeven punten op moet stellen.
[ Bericht 1% gewijzigd door Riparius op 12-05-2012 02:21:53 ]
Het is niet het superscript van de formulequote:
[..]
Als je met die 10 het grondtal bedoelt van de logaritme, dan moet je dat wel superscripten, anders sticht je alleen maar verwarring. Dus:
L = 10log(I/I0)
Verder kun je gewoon gebruik maken van de definitie van de logaritme: glog a is de exponent waartoe je g moet verheffen om a te verkrijgen. Hier is L dus de macht waartoe je 10 moet verheffen om I/I0 te verkrijgen:
10L = I/I0
Ik begrijp niet wat je bedoelt, en in ieder geval sticht je verwarring, precies zoals ik al zei. Als je 10 een factor is dan moet je 10∙log(I/I0) schrijven en ook het grondtal van je logaritme specificeren, want het symbool log is ambigu.quote:
[..]
Het is niet het superscript van de formule
Ik schreef de formule precies over uit mijn BINAS. Ik ga er in ieder geval van uit dat het 10 * is, maar is ook niet duidelijk aangegeven. Er staat L = 10 log(I/I0)quote:
[..]
Ik begrijp niet wat je bedoelt, en in ieder geval sticht je verwarring, precies zoals ik al zei. Als je 10 een factor is dan moet je 10∙log(I/I0) schrijven en ook het grondtal van je logaritme specificeren, want het symbool log is ambigu.
Goed. Aangenomen dat Briggse logaritmen (grondtal 10) bedoeld zijn krijgen we dan:quote:
[..]
Ik schreef de formule precies over uit mijn BINAS. Ik ga er in ieder geval van uit dat het 10 * is, maar is ook niet duidelijk aangegeven. Er staat L = 10 log(I/I0)
I = I0∙10L/10
Wat is hier nu moeilijk aan?
Bedankt!
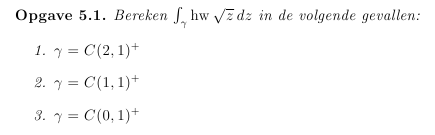
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.
Bij de tweede kun je over een deel van de cirkel integreren dat 0 niet bevat, en dan een limiet daarvan nemen zodat je pad in de limiet de hele cirkel is.quote:
Ik heb nog wat moeite met hoe complexe integralen werken.
[ afbeelding ]
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.
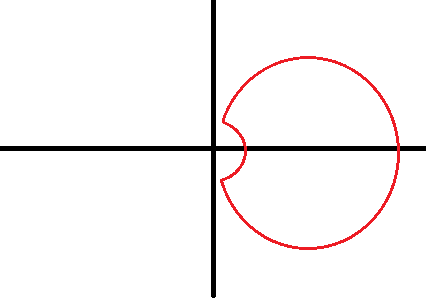
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
De hoofdwaarde van √z voor z = r∙eiφ met -π < φ ≤ π en r ≥ 0 is √r∙eiφ/2 en daarmee gedefinieerd voor elke z ∈C. Maar inderdaad is deze functie alleen holomorf op C\(-∞,0].quote:
Ik heb nog wat moeite met hoe complexe integralen werken.
[ afbeelding ]
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.
Je moet dan wel de integraal over dat kleine cirkeltje dan afschatten en laten zien dat dat in de limiet naar 0 gaat.quote:
Zoiets dus?
[ afbeelding ]
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
Bij de derde kun je het gewoon direct parametriseren.
Inderdaad, bij het tweede geval kom je door een limietbeschouwing tot de conclusie dat de integraal langs γ ook hier nul moet zijn, want de integraal langs de gesloten curve in je plaatje blijft 0, hoe klein je het boogje rond de oorsprong ook maakt.quote:
Zoiets dus?
[ afbeelding ]
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
Voor de derde opgave heb je z(φ) = eiφ als parametervoorstelling van je curve.
Die derde ga ik even proberen met parametrizeren.
De integraal over zo'n gesloten kromme is inderdaad 0, maar je moet nog wel aantonen dat alles in de limiet ook goed gaat. In dit voorbeeld is dat vrijwel triviaal, maar 't is wel goed om je daar in het algemeen bewust van te zijn.quote:
Kun je met dat bolletje niet zeggen dat de functie holomorf is op een omgeving van de afsluiting van dat gebied, en dus (stelling) dat de integraal over de rand 0 is? Omdat het dan weer gewoon een gesloten kromme is enzo.
Die derde ga ik even proberen met parametrizeren.
Ik heb 6 VWO WisB al afgerond, en iemand in het examentopic kwam aanzetten dat we Riemann sommen moeten beheersen (ofwel invoeren op de GR)
Maar hoe moest dat ookalweer!?
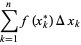
Ik gebruik Mathprint instellingen op de GR, als ik dan die somrij pak, welke waarden moet ik dan invullen? Ik ben heel die rotzooi vergeten
Gaan we even uit van de vraag dat ik de oppervlakte van x=2 tot x=24 wil weten van de functie 3^x - 9x
En ja, ik zou hier ook gewoon een integraal voor kunnen pakken, maar het gaat me nu specifiek om de Riemannsom
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
Terwijl
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt
.Ik streepte de
Klopt dit?
Wat wil je oplossen? Wat is six?quote:
Hoe los ik dit op?
Ik streepte deen de
tegen elkaar weg:
Klopt dit?
(six=6 ziet er wel logisch uit, net zoiets als two = 2?
)Numbersquote:
one
two
three
four
five
six
seven
eight
nine
ten
quote:
Hoe los ik dit op?
Ik streepte de
Klopt dit?
Bijna, de 'echte' vraag is echter
Thanks bro, je bent m'n held.quote:
Op Thabits manier krijg je een bovensom en ondersom (dus een bovengrens en ondergrens voor de integraal). Je kan ook steeds op ieder interval [xk, xk+1] de waarden in het midden nemen en daar f evalueren. Dan krijg je iets wat direct wat dichter bij de integraal zal zitten dan de ondersom of bovensom, en het is ook wat makkelijker te berekenen omdat je niet het supremum of infimum op ieder intervalletje hoeft te bepalen (dan moet je steeds nagaan of de functie daalt of stijgt op dat interval, etc).
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
Terwijl
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt
Maargoed, stel dat ik dan het als stapgrootte 1/10 wil nemen oid. Hoe moet dit dan? Ik probeerde het net, maar blijkbaar fout.
[ Bericht 3% gewijzigd door Amoeba op 13-05-2012 13:54:25 ]
hij zit grappig te doen, hij streept de n van sin(x) wegquote:
Lees je eigen post nog maar eens na, hier kan ik niks mee
Ik snap het nu pas... Beetje jammer dat hij 1/n erbij optelt in plaats van vermenigvuldigtquote:
[..]
hij zit grappig te doen, hij streept de n van sin(x) weg
aightquote:
[ Bericht 100% gewijzigd door Amoeba op 13-05-2012 13:54:18 ]
Waar ik *1 doe moet het *0.1 worden. En je evalueert f dus op 2.05, 2.15, 2.25, ..., 23.95.quote:
(ninja dat je bent)
Beetje afwijkend.
Onder Y1 staat 3^x - 9x
x=2 -> n= 23 (Y1(k+.5)*1/10)
Je krijgt
xk = 2+0.05k
Mag je zelf nadenken over welke k je precies moet sommeren.
Ik doe Wiskunde B, het enige waarvan ik die somformule ken is van die Riemannsom. Ik snap dan ook bar weinig van wat al die tekentjes betekenen. De bovenste was toch het aantal rechthoeken? En die onderste: geen idee
Dit heb je hopelijk toch ook wel eens gezien bij rekenkundige rijen en meetkundige rijen.
Om te zien wat er gebeurt kan je het beste even voor jezelf een plaatje tekenen, en dan de bijbehorende som bedenken.
En jawel, ook die rotzooi stond in m'n GR
Maargoed, dat k=2, is dat het onderste limiet?
Die 5, staat dat voor het aantal rechthoeken -1?
k=2 is de eerste term in de som, k=5 de laatste in dat geval. Niet per se aantal rechthoeken -1.quote:
Ik heb wel WisD, maar ook rijen is al een jaar terug. Ik heb dit jaar WisB gedaan (in 2 jaar) en volgend jaar WisD (dus ook in 2 jaar, omdat ik dit jaar geen WisD gedaan heb)
En jawel, ook die rotzooi stond in m'n GR
Maargoed, dat k=2, is dat het onderste limiet?
Die 5, staat dat voor het aantal rechthoeken -1?
Dan zou ik:
x=2 -> x=11 moeten nemen, en in de somnotatie:
Y1(2+0.5k)*0.5
Daarbij moeten zetten?
Ik wil gewoon een integraal uit kunnen drukken (benaderen) met een Riemannsom, op de manier van een somrij. Stel dat zo'n rotvraag komt in het examen, dan wil ik die toch graag op kunnen lossen.
Dit is nice, maar hoe moet het met een interval van 0.1?quote:
Op Thabits manier krijg je een bovensom en ondersom (dus een bovengrens en ondergrens voor de integraal). Je kan ook steeds op ieder interval [xk, xk+1] de waarden in het midden nemen en daar f evalueren. Dan krijg je iets wat direct wat dichter bij de integraal zal zitten dan de ondersom of bovensom, en het is ook wat makkelijker te berekenen omdat je niet het supremum of infimum op ieder intervalletje hoeft te bepalen (dan moet je steeds nagaan of de functie daalt of stijgt op dat interval, etc).
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
Terwijl
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt
quote:
Ik heb het net al een keer voorgedaan, dus nu mag jij.
?
Is dat niet goed danquote:
[..]
hij zit grappig te doen, hij streept de n van sin(x) weg
Nee, als je dit had gezegd was het wel goed geweest:quote:
Volgende keer beter
quote:Op zondag 13 mei 2012 14:37 schreef thenxero het volgende:
[..]
Nee, als je dit had gezegd was het wel goed geweest:
Volgende keer beter
Je moet geen { } haken gebruiken. Daardoor gaat wolframalhpa de mist in.quote:
Je begin en eindwaardes van k kloppen niet. Waarom heb je die zo gekozen?
Ohquote:
[..]
Nee, als je dit had gezegd was het wel goed geweest:
Volgende keer beter
Dit is dan ook weer niet goed zeker
Omdat ik het interval van 2 tot 24 wilde..quote:
[..]
Je moet geen { } haken gebruiken. Daardoor gaat wolframalhpa de mist in.
Je begin en eindwaardes van k kloppen niet. Waarom heb je die zo gekozen?
Xk klopt wel?
Ziet er prima uit hoor.quote:
[ afbeelding ]
Dit is dan ook weer niet goed zeker
Als je sommeert van k=2 tot k=24, dan is dus je het eerste midden van de deelintervalletjes bij 2+0.5*2 = 3, en de laatste bij 2+0.5*24 = 14. Je "integreert" dus eigenlijk van 2.75 tot 14.25 op deze manier.quote:
[tex]
[..]
Omdat ik het interval van 2 tot 24 wilde..
Xk klopt wel?
Xk = Xbeginwaarde +stapgrootte*k
a en b zou ik dan zo uit moeten drukken dat de Xk * k = a (die waarde van k dus), evenals voor b?
Zit ik zo goed?
xk = linkergrens + (de helft van de stapgrootte) + (stapgrootte * k)
En dan sommeren van k=0 tot k zodanig dat x_k = (rechtergrens - de helft van de stapgrootte).
Of anders gezegd: Als linkergrens a heet, en rechtergrens b, dan laat je k zo lopen dat je (b-a)/(stapgrootte) termen krijgt.
Stel dat ik wil gaan van x=5 tot x=10
Functie: 3x - 2x^2
Stapgrootte: 1/10
Dan is dit fout. Laat het me nogmaals proberen..
Stel dat ik wil gaan van x=5 tot x=10
Functie: 3x - 2x^2
Stapgrootte: 1/10
Zo?
.Edit: Ik heb die integraal bekeken.
Moet k van 30 tot 80 lopen?
Komt het nu wel mooi overeen met de integraal?
Maargoed, dan geldt dus dit:
. Wat komt eruit? En wat komt er uit de integraal?-470,833 bij de integraal.
Hoe lost je GR eigenlijk een integraal op, een somrij toch gewoon?
Mijn primitieve komt uit op -2025/6 Hetzelfde als de integraal dus.
Ik weet niet hoe je GR het doet. Er zijn wel methodes die nauwkeuriger en sneller werken dan Riemannsommen. Kijk eens op http://en.wikipedia.org/wiki/Numerical_integration bijvoorbeeld. In plaats van met rechthoeken kan je met trapeziumpjes werken.
Ik toch echt maar 3.0.. Maar dat heeft vast weer met staatsexamen te maken.quote:
Genoeg tijd op het centraal examen, 3.5 uur voor Wiskunde B. Harstikke bedankt.
Ik dacht het wel, want ik meen me te herinneren dat de GR soms niet het precieze antwoord gaf bij het controleren van een integraal (dus dat de GR bijvoorbeeld 1.0001 als antwoord gaf terwijl het gewoon 1 moest zijn). Daarnaast is er dacht ik ook geen analytische methode die voor elke integraal werkt (want er bestaat niet altijd een integraal).quote:
-470,825 bij de somrij
-470,833 bij de integraal.
Hoe lost je GR eigenlijk een integraal op, een somrij toch gewoon?
Mijn primitieve komt uit op -2025/6 Hetzelfde als de integraal dus.
Succes met je examen!
hebt, kan je die oplossen door f te schrijven als een matrix (met een bepaalde beginvector) en de eigenvectoren te zoeken en de beginvector in die eigenvectoren uit te drukken, of door een genererende functie te zoeken.
Maar iets in de trant van
lijkt me niet op te lossen voor een willkeurige a0.
Voor
geldt wel
Maar het lukt me ook niet echt om dit op een systematische manier aan te tonen.
(Je kan wel in het algemeen stellen dat je een functie
Speciaal onderwijs. Ieder examen een half uur langer!quote:
[..]
Ik toch echt maar 3.0.. Maar dat heeft vast weer met staatsexamen te maken.
Je bedoelt dat een primitieve niet altijd in elementaire functies is uit te drukken, dat is iets anders dan beweren dat er geen primitieve is.quote:Op zondag 13 mei 2012 15:49 schreef kutkloon7 het volgende:
[..]
Ik dacht het wel, want ik meen me te herinneren dat de GR soms niet het precieze antwoord gaf bij het controleren van een integraal (dus dat de GR bijvoorbeeld 1.0001 als antwoord gaf terwijl het gewoon 1 moest zijn). Daarnaast is er dacht ik ook geen analytische methode die voor elke integraal werkt (want er bestaat niet altijd een integraal).
Overigens denk ik dat een doodgewone GR wellicht altijd numerieke methoden gebruikt voor het evalueren van definiete integralen. Wat WolframAlpha doet is een stuk geavanceerder, want die weet ook voor sommige oneigenlijke integralen en integralen waarbij een primitieve niet in elementaire functies is uit te drukken toch het exacte antwoord te produceren. Vaak komt dat antwoord dan ietsje later pas op je scherm, namelijk nadat er al een numeriek antwoord is verschenen. Dat duidt erop dat WolframAlpha gebruik maakt van een bibliotheek met 'bekende' integralen die exact zijn te evalueren ook als een primitieve niet in elementaire functies is uit te drukken.
Probeer eens wat je GR hiervan bakt:
∫01 ln(x)/(x-1)dx
Er hoort pi²/6 uit te komen, maar de GR geeft wel wat anders: 1.644828 ipv 1.64493. Komt inderdaad doordat de GR het altijd numeriek doet.quote:
[..]
Je bedoelt dat een primitieve niet altijd in elementaire functies is uit te drukken, dat is iets anders dan beweren dat er geen primitieve is.
Overigens denk ik dat een doodgewone GR wellicht altijd numerieke methoden gebruikt voor het evalueren van definiete integralen. Wat WolframAlpha doet is een stuk geavanceerder, want die weet ook voor sommige oneigenlijke integralen en integralen waarbij een primitieve niet in elementaire functies is uit te drukken toch het exacte antwoord te produceren. Vaak komt dat antwoord dan ietsje later pas op je scherm, namelijk nadat er al een numeriek antwoord is verschenen. Dat duidt erop dat WolframAlpha gebruik maakt van een bibliotheek met 'bekende' integralen die exact zijn te evalueren ook als een primitieve niet in elementaire functies is uit te drukken.
Probeer eens wat je GR hiervan bakt:
∫01 ln(x)/(x-1)dx
Is deze met behulp van partieël integreren algebraïsch te doen?quote:
[..]
Je bedoelt dat een primitieve niet altijd in elementaire functies is uit te drukken, dat is iets anders dan beweren dat er geen primitieve is.
Overigens denk ik dat een doodgewone GR wellicht altijd numerieke methoden gebruikt voor het evalueren van definiete integralen. Wat WolframAlpha doet is een stuk geavanceerder, want die weet ook voor sommige oneigenlijke integralen en integralen waarbij een primitieve niet in elementaire functies is uit te drukken toch het exacte antwoord te produceren. Vaak komt dat antwoord dan ietsje later pas op je scherm, namelijk nadat er al een numeriek antwoord is verschenen. Dat duidt erop dat WolframAlpha gebruik maakt van een bibliotheek met 'bekende' integralen die exact zijn te evalueren ook als een primitieve niet in elementaire functies is uit te drukken.
Probeer eens wat je GR hiervan bakt:
∫01 ln(x)/(x-1)dx
Nee.quote:
[..]
Is deze met behulp van partieël integreren algebraïsch te doen?
Uhuh, dat bedoel ik inderdaad (hoewel er natuurlijk ook functies zonder primitieve zijn, maar dat is weer een ander verhaal want die zijn dan niet continu).quote:
[..]
Je bedoelt dat een primitieve niet altijd in elementaire functies is uit te drukken, dat is iets anders dan beweren dat er geen primitieve is.
Bedoel je de karakteristieke polynoom van een matrix?quote:
Heb je al de methode geprobeerd met karakteristieke polynoom, particuliere oplossing, etc? (komt op hetzelfde neer als genererende functies, maar dan sneller)
Ik zou niet weten hoe dat werkt, bij een kwadratische functie.
Je hebt gelijk, dat werkt alleen bij lineaire recurrente betrekkingen. Het enige wat ik zou kunnen bedenken is wat proberen met een genererende functie... misschien komt er wat moois uit maar misschien ook niet.quote:
[..]
Bedoel je de karakteristieke polynoom van een matrix?
Ik zou niet weten hoe dat werkt, bij een kwadratische functie.
Je hebt een beetje hetzelfde probleem als bij differentiaalvergelijkingen: vaak is er gewoon geen analytische oplossing.
De afgeleide hiervan is 32x x ln(3) x 2 (doordifferentiëren), maar uit de primitieve kom ik niet. Hier is ook een regel voor lijkt me?
Je zou kunnen beginnen met te bedenken dat:quote:
Snel vraagje: wat is de primitieve van 32x?
De afgeleide hiervan is 32x x ln(3) x 2 (door differentiëren), maar uit de primitieve kom ik niet. Hier is ook een regel voor lijkt me?
32x = (32)x = 9x
Het is dus gewoon een exponentiële functie, en aangezien 9 = eln 9 heb je dus:
32x = 9x = (eln 9)x = ex∙ln 9
Nu zou het je geen moeite meer mogen kosten hiervan een primitieve op te schrijven.
Hartstikke bedankt! Dat zou betekenen dat het 1/ln(9) x ex wordt?quote:
[..]
Je zou kunnen beginnen met te bedenken dat:
32x = (32)x = 9x
Het is dus gewoon een exponentiële functie, en aangezien 9 = eln 9 heb je dus:
32x = 9x = (eln 9)x = ex∙ln 9
Nu zou het je geen moeite meer mogen kosten hiervan een primitieve op te schrijven.
Nee, een primitieve van ex∙ln 9 is 1/ln(9)∙ex∙ln 9.quote:
[..]
Hartstikke bedankt! Dat zou betekenen dat het 1/ln(9) ∙ ex wordt?
Gebruik alleen geen letter x als teken voor vermenigvuldiging, en zeker niet als je x ook nog als variabele gebruikt.
Verder kun je natuurlijk altijd WolframAlpha gebruiken om de afgeleide te bepalen en zo te controleren of je primitieve wel juist is.
Ok, dank! Ik hoopte dat er misschien een bekende methode was om dit soort recurrente betrekkingen op te lossen, maar ik dacht al dat veel niet-lineaire recurrente betrekkingen niet echt 'op te lossen' zijn.quote:
[..]
Je hebt gelijk, dat werkt alleen bij lineaire recurrente betrekkingen. Het enige wat ik zou kunnen bedenken is wat proberen met een genererende functie... misschien komt er wat moois uit maar misschien ook niet.
Je hebt een beetje hetzelfde probleem als bij differentiaalvergelijkingen: vaak is er gewoon geen analytische oplossing.
Is in het algemeen niet te doen, alleen in speciale gevallen. Dit soort kwadratische recursies spelen zelfs een belangrijke rol in de chaostheorie. Je kunt er ook fractals mee maken, zoals de Mandelbrotverzameling.quote:
[..]
Ok, dank! Ik hoopte dat er misschien een bekende methode was om dit soort recurrente betrekkingen op te lossen, maar ik dacht al dat veel niet-lineaire recurrente betrekkingen niet echt 'op te lossen' zijn.
Een voorbeeld van eentje die nog wel te doen is (ik verklap de oplossing nog niet):
a1 = 1/3, an+1 = 2an2 - 1.
Tja, da's een leuke. Als kutkloon nu z'n goniometrische identiteiten maar goed kent ...quote:
[..]
Is in het algemeen niet te doen, alleen in speciale gevallen. Dit soort kwadratische recursies spelen zelfs een belangrijke rol in de chaostheorie. Je kunt er ook fractals mee maken, zoals de Mandelbrotverzameling.
Een voorbeeld van eentje die nog wel te doen is (ik verklap de oplossing nog niet):
a1 = 1/3, an+1 = 2an2 - 1.
op het gebied
Ik weet alleen niet wat ik kan zeggen over het punt (1,1), een hoekpunt van de driehoek T. Het is geen globaal max/min, maar is het een lokaal max/min?
Weet iemand hoe ik dit kan aanpakken?
Bedankt.
Sorry. Ik bedoelde naar links.quote:
Je krijgt 2x = pi - (pi/2 - 3x) + k*2pi, welke - gaat er naar rechts?
Dat is het natuurlijk... Wat stom dat ik dit niet zelf kon bedenken. Dank u!quote:
Je mag altijd beide leden met -1 vermenigvuldigen als je dat bedoelt
Je moet bedenken dat als je hebt:quote:
[..]
Sorry. Ik bedoelde naar links.
[..]
Dat is het natuurlijk... Wat stom dat ik dit niet zelf kon bedenken. Dank u!
sin α = sin β,
dat dan geldt:
α = β + 2kπ ∨α = (π - β) + 2kπ, k ∈ Z
Edit: ik zie dat je dat kennelijk al had bedacht.
Ik zie je post nu pas, leuke post welquote:
[..]
Is in het algemeen niet te doen, alleen in speciale gevallen. Dit soort kwadratische recursies spelen zelfs een belangrijke rol in de chaostheorie. Je kunt er ook fractals mee maken, zoals de Mandelbrotverzameling.
Een voorbeeld van eentje die nog wel te doen is (ik verklap de oplossing nog niet):
a1 = 1/3, an+1 = 2an2 - 1.
Ik moest eerlijk gezegd even op wolfram spieken voor de identiteit sin2 x - cos2 x = -2cos2 x, maar ik ben er uit geloof ik:
Zonder die hint van Riparius weet ik niet of ik het zou snappenSPOILERan = 2an-12 - 1
Als |a0| ≤ 1, dan geldt voor elke n ∈ N dat |an| ≤ 1
Dit betekent dat we elke an kunnen schrijven als een sinus.
Neem an = sin α
Dan an+1 = 2sin2(α) - 1 = 2sin2(α) - (sin2(α) + cos2(α)) = sin2(α) - cos2(α) = -cos 2α = -sin(π/2 - 2α) = sin(2α - π/2)
En als we nu niet naar an kijken, maar naar αn = arcsin an, hebben we de recursie
αn = 2αn-1 - π/2
Die een niet al te moeilijke oplossing heeft:
en als we nu weer aan beide kanten de sinus nemen:
[ Bericht 4% gewijzigd door kutkloon7 op 19-05-2012 22:47:59 ]
Het kan eenvoudiger, daarom gaf ik kutkloon ook goniometrische identiteiten als hint.quote:
Vet dat dat met zo'n goniometrische substitutie kan. Ik had zo'n substitutie denk ik nooit zelf bedacht.
SPOILERAls je hebt:
an+1 = 2an2 - 1
Dan doet dit (mij) meteen denken aan:
cos 2α = 2∙cos2α - 1
En dus hebben we kennelijk een rij cosinussen waarbij de hoek steeds verdubbelt:
cos φ, cos 2φ, cos 4φ, ...
Nemen we nu:
(1) a1 = cos φ,
dan is a2 = cos 2φ, a3 = cos 4φ enz. en dus in het algemeen:
(2) an = cos(2n-1∙φ)
Uit (1) en a1 = 1/3 volgt dat we φ zodanig moeten kiezen dat cos φ = 1/3, en dus
(3) φ = arccos(1/3)
Uiteraard kan φ = -arccos(1/3) ook, maar aangezien de cosinus een even functie is maakt dat niets uit. Substitutie van (3) in (2) geeft nu:
(4) an = cos(2n-1∙(arccos(1/3)))
Zo zie je maar, goniometrische identiteiten uit het blote hoofd kennen kan nuttig zijn.
[ Bericht 0% gewijzigd door Riparius op 19-05-2012 23:19:36 ]
Slim, ziet er een stuk minder mysterieus uitquote:
[..]
Het kan eenvoudiger, daarom gaf ik kutkloon ook goniometrische identiteiten als hint.SPOILERAls je hebt:
an+1 = 2an2 - 1
Dan doet dit (mij) meteen denken aan:
cos 2α = 2∙cos2a - 1
En dus hebben we kennelijk een rij cosinussen waarbij de hoek steeds verdubbelt:
cos φ, cos 2φ, cos 4φ, ...
Nemen we nu:
(1) a1 = cos φ,
dan is a2 = cos 2φ, a3 = cos 4φ enz. en dus in het algemeen:
(2) an = cos(2n-1∙φ)
Uit (1) en a1 = 1/3 volgt dat we φ zodanig moeten kiezen dat cos φ = 1/3, en dus
(3) φ = arccos(1/3)
Uiteraard kan φ = -arccos(1/3) ook, maar aangezien de cosinus een even functie is maakt dat niets uit. Substitutie van (3) in (2) geeft nu:
(4) an = cos(2n-1∙(arccos(1/3)))
Zo zie je maar, goniometrische identiteiten uit het blote hoofd kennen kan nuttig zijn.
(Had ik maar even de moeite genomen om het als cosinus op te schrijven, ik had er nog aan gedacht
)[ Bericht 5% gewijzigd door kutkloon7 op 19-05-2012 23:24:46 ]
Zie je post nu pas, dank!quote:
[..]
De vergelijkingen die je geeft stellen in de driedimensionale ruimte vlakken voor, geen lijnen, dus hier gaat het al fout.
Het idee is dat je eerst een normaalvector n bepaalt van je vlak V. Dat is een vector die loodrecht op het vlak staat. Is nu v = (x,y,z) een willekeurige vector met eindpunt in je vlak V en v0 = (x0,y0,z0) een vaste vector met eindpunt in je vlak, dan is vector v - v0 evenwijdig aan je vlak en staat deze verschilvector dus loodrecht op je normaalvector n, zodat het inproduct van v- v0 en n gelijk is aan nul:
(1) n∙(v - v0) = 0
En dus geldt ook:
(2) n∙v = n∙v0
Een vaste vector v0 met eindpunt in je vlak V ken je al omdat je immers de drie punten A,B en C kent die in vlak V liggen, zodat je hier voor v0 bijvoorbeeld de vector a = (2,0,0) zou kunnen nemen zodat x0 =2, y0 = 0 en z0 = 0.
De kunst is nu om een geschikte normaalvector n = (a,b,c) te bepalen want dan kun je voor (1) schrijven:
(3) a(x - x0) + b(y - y0) + c(z - z0) = 0,
en voor (2) kun je schrijven:
(4) ax + by + cz = ax0 + by0 + cz0,
en (3) of (4) is uiteraard de gezochte cartesische vergelijking van je vlak. Om nu een geschikte normaalvector n = (a,b,c) en daarmee de waarden van a,b en c te vinden kun je bedenken dat n loodrecht staat op zowel de verschilvector b - a als de verschilvector c - a, aangezien deze beide verschilvectoren evenwijdig zijn aan vlak V. En dus moet het inproduct van n = (a,b,c) met zowel b - a = (-2,3,0) als c - a = (-2,0,4) gelijk zijn aan nul. Dit geeft:
(5a) -2a + 3b = 0
(5b) -2a + 4c = 0
Hier heb je twee lineaire vergelijkingen in drie onbekenden a, b en c, en dus lijkt het alsof je nog één lineaire vergelijking tekort komt. Maar dat is niet zo, want als we n met een scalar vermenigvuldigen, dan hebben we nog steeds een vector die loodrecht op vlak V staat, dus zijn a,b,c niet eenduidig bepaald. Dat is ook meteen duidelijk uit de cartesische vergelijking (3) want als je hier beide leden met een getal ongelijk nul vermenigvuldigt, dan heb je nog steeds een geldige cartesische vergelijking van je vlak V.
We kunnen nu met (5a) en (5b) de waarde van a en b uitdrukken in c. Uit (5b) volgt dat a = 2c en substitutie hiervan in (5a) levert b = (4/3)∙c en dus hebben we n = (2c, (4/3)∙c, c). Kiezen we nu bijvoorbeeld c = 3, dan krijgen we n = (6, 4, 3). Op grond van (3) wordt de cartesische vergelijking van je vlak V nu:
(6) 6(x - 2) + 4(y - 0) + 3(z - 0) = 0,
en uitwerken hiervan geeft:
(7) 6x + 4y + 3z = 12
Je kunt nu door invullen gemakkelijk controleren dat de coördinaten van de punten A, B en C inderdaad aan (7) voldoen. Overigens hadden we in dit speciale geval de vergelijking van het vlak direct uit het hoofd kunnen opschrijven in de vorm (1/2)∙x + (1/3)∙y + (1/4)∙z = 1 omdat van elk van de drie gegeven punten A resp. B resp. C alleen de x- resp. y- resp. z-coördinaat ongelijk is aan nul. Maar in het algemeen is dat uiteraard niet zo als je de cartesische vergelijking van een vlak door drie gegeven punten op moet stellen.
Ik heb nog wel een klassieker voor je (niet door mij bedacht dus) waar je eens je tanden in kunt zetten:quote:
Vet dat dat met zo'n goniometrische substitutie kan. Ik had zo'n substitutie denk ik nooit zelf bedacht.
We hebben een halve bol, waarvan we de straal voor het gemak gelijk aan één veronderstellen. Deze halve bol verdelen we nu door een vlak evenwijdig aan het deelvlak in twee delen met gelijke inhoud. Bereken de afstand van het deelvlak tot het middelpunt van de halve bol.
Gevraagd wordt een exacte uitdrukking voor de bedoelde afstand, dus geen numerieke benadering.
Nasty, ik dacht aan een simpele benadering, maar dan blijf ik hangen op de vergelijking h3-3h+1=0quote:
[..]
Ik heb nog wel een klassieker voor je (niet door mij bedacht dus) waar je eens je tanden in kunt zetten:
We hebben een halve bol, waarvan we de straal voor het gemak gelijk aan één veronderstellen. Deze halve bol verdelen we nu door een vlak evenwijdig aan het deelvlak in twee delen met gelijke inhoud. Bereken de afstand van het deelvlak tot het middelpunt van de halve bol.
Gevraagd wordt een exacte uitdrukking voor de bedoelde afstand, dus geen numerieke benadering.
Is het antwoord sin(1/3) ?quote:
[..]
Ik heb nog wel een klassieker voor je (niet door mij bedacht dus) waar je eens je tanden in kunt zetten:
We hebben een halve bol, waarvan we de straal voor het gemak gelijk aan één veronderstellen. Deze halve bol verdelen we nu door een vlak evenwijdig aan het deelvlak in twee delen met gelijke inhoud. Bereken de afstand van het deelvlak tot het middelpunt van de halve bol.
Gevraagd wordt een exacte uitdrukking voor de bedoelde afstand, dus geen numerieke benadering.
Nee.quote:
(Wentelen om de x-as?)
De inhoud van die halve bol is 2/3pi
Dus met behulp van primiteren berekenen voor welke x coordinaat dit 1/3pi is?
Ik kom uit op a3 -3a + 3 = 0quote:
[..]
Nasty, ik dacht aan een simpele benadering, maar dan blijf ik hangen op de vergelijking h3-3h+1=0
Die heeft als enige reële oplossing iets van -2...quote:
Wat doe ik fout?quote:
[..]
Die heeft als enige reële oplossing iets van -2...
De inhoud van een bol is 4/3pi. De inhoud van de halve bol met middelpunt M op de oorsprong (0 , 0). dus 2/3pi.
Dan neem ik de formule x2 + y2 = 1, druk x uit in y.
Dus x = wortel(1-y2)
Integraal van 0 tot a = 1/3 pi
Je moet de functie kwadrateren, dus die wortel valt mooi weg. De primitieve is dan toch x-1/3x3
Nou van 0 tot a. Blijft over:
a-1/3a3 = 1/3 (pi valt weg)
vermenigvuldigen met 3 en overhevelen naar een kant?
Dit is de formule van een cilinder, niet van een bol.quote:
[..]
Wat doe ik fout?
De inhoud van een bol is 4/3pi. De inhoud van de halve bol met middelpunt M op de oorsprong (0 , 0). dus 2/3pi.
Dan neem ik de formule x2 + y2 = 1, druk x uit in y.
quote:
[..]
Dit is de formule van een cilinder, niet van een bol.
Een bol is 3-dimensionaal, en je hebt nergens een z-coordinaat in je formule gebruikt.quote:
Om exact te zijn. Dit is de formule van de eenheidscirkel, wat bij wentelen om de x-as een bol geeft.quote:
[..]
Dit is de formule van een cilinder, niet van een bol.
Nope. Ik geef de integraal. Ik ga uit van een tweedimensionale figuur die ik vervolgens om de x-as ga wentelen. Dit geeft dus de inhoud van een bol!quote:
[..]
Een bol is 3-dimensionaal, en je hebt nergens een z-coordinaat in je formule gebruikt.
Ah, ok. Dan begrijp ik gewoon niet helemaal wat je precies deedquote:
[..]
Om exact te zijn. Dit is de formule van de eenheidscirkel, wat bij wentelen om de x-as een bol geeft.
Dat kan je in principe exact oplossen (wel lelijk).quote:
Godverdomme, ik vermenigvuldig 2x met 3 bij c. Inderdaad, de vergelijking is x^3 - 3x + 1 = 0
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Met x = m+n
en 3mn = 3 ofwel mn = 1
Ik heb staan:
a3 -3a + 1 = 0
Grafisch geeft dit het juiste antwoord.
Nou goed, gaan we hier de ABCD formule op loslaten.
a = m+n
(m+n)3 -3(m+n) + 1 = 0
Dus
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Dus 3mn = 3 ergo mn = 1
n = 1/m
Dus
m3 + 1/m3 + 1 = 0
Vermeningvuldigen met m3
m6 + m3 + 1 = 0
Substitutie naar q.
q = m3
q2 + q + 1 = 0
D = b2 -4ac
D = -3
Of moet ik hiermee verder rekenen..?
Je bent zeker op de goede weg. Zoals inmiddels duidelijk is leidt het probleem tot een kubische vergelijking en die kun je in principe oplossen met de methode die aan Cardano wordt toegeschreven (maar niet van hem is), en dat is wat je hier ook doet. Maar nu loop je stuk op die negatieve discriminant ...quote:
Riparius, dan ga ik met de ABCD formule aan de gang.
Ik heb staan:
a3 -3a + 1 = 0
Grafisch geeft dit het juiste antwoord.
Nou goed, gaan we hier de ABCD formule op loslaten.
a = m+n
(m+n)3 -3(m+n) + 1 = 0
Dus
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Dus 3mn = 3 ergo mn = 1
n = 1/m
Dus
m3 + 1/m3 + 1 = 0
Vermeningvuldigen met m3
m6 + m3 + 1 = 0
Substitutie naar q.
q = m3
q2 + q + 1 = 0
D = b2 -4ac
D = -3
Of moet ik hiermee verder rekenen..?
i*wortel 3. Ik ga verder.quote:
[..]
Je bent zeker op de goede weg. Zoals inmiddels duidelijk is leidt het probleem tot een kubische vergelijking en die kun je in principe oplossen met de methode die aan Cardano wordt toegeschreven (maar niet van hem is), en dat is wat je hier ook doet. Maar nu loop je stuk op die negatieve discriminant ...
ABCD formule wist ik enkel het bestaan van trouwens.
Als ik dan alles terugreken naar a kom ik uit op in beide gevallen uit op 1,53 (zegt mijn GR)
Ik zat nu wel op wolframalpha naar het definitieve antwoord te kijken, maar nee, geen idee hoe ze daaraan komen.
Ofwel:
Waar dit het antwoord was waar ik op uitkwam:
[ Bericht 25% gewijzigd door Amoeba op 21-05-2012 00:41:22 ]
Dat moet gelijk zijn aan een kwart v/d inhoud van een bol, dus pi/3 .
Dus dan krijg je cos(p) = 1/2. Dus p=pi/3. Dat is dus de hoek t.o.v. het grondvlak. Dus sin(pi/3) = (hoogte van het snijvlak) / (straal (=1)) = hoogte van het snijvlak. Maar sin(pi/3)=0.8... veel te groot.
Tja, je GR zegt zoveel, maar de bedoeling was een exacte uitdrukking te geven, en het is toch duidelijk dat het antwoord reëel moet zijn en op het interval (0,1) moet liggen. Toch zit je best dichtbij.quote:
Nougoed, dan heb ik q = -.5 ± .5 i rt 3
Als ik dan alles terugreken naar a kom ik uit op in beide gevallen uit op 1,53 (zegt mijn GR)
Ik zat nu wel op wolframalpha naar het definitieve antwoord te kijken, maar nee, geen idee hoe ze daaraan komen.
Je hebt nu m3 = -½ + i∙½√3 en n3 = -½ - i∙½√3 (of omgekeerd),
aangezien het product van m3 en n3 gelijk moet zijn aan 1 omdat ook mn = 1, terwijl de som van m3 en n3 gelijk moet zijn aan -1 aangezien m3 + n3 + 1 = 0. Nu maar weer even zelf verder denken ...
Het lijkt erop alsof je hier het interval waarover je r neemt als constant beschouwt, maar dat is niet zo als je p varieert ...quote:
Ik snap trouwens niet waar het bij mij mis gaat. Ik probeerde bolcoördinaten toe te passen en dan bereken je dus
Je hebt de substitutie x = m + n gemaakt en onder de voorwaarde mn = 1 de waarden van m3 en n3 gevonden. Nu is het dus inderdaad zaak m en n te vinden, maar hoe ...quote:
Ik snap je redenatie, maar uiteindelijk staan alle regels waar m en n aan moeten voldoen hier op papier. Blijkbaar wil je op een andere manier van n = 1/m n en m 'ontrafelen'?
Uitgaande van de regel m3 = -½ + i∙½√3
(-½ + i∙½√3)3 = 1
Waarom heb ik totaal niet het gevoel dat mij dit verder helpt.
Je doet het goed hoor, en wat je zegt klopt, m3 en n3 zijn elkaars kwadraat ...quote:
Vooruit, verder.
Als m6 = n3 dan geldt natuurlijk ook m2 = n
Ik begrijp dat je het een fascinerend probleem vindt, en je zit ook op de goede weg, maar ik zou als ik jou was nu toch maar gaan slapen, anders is het zo half vijf en heb je geen bed gezien.quote:
Dit is werkelijk echt wazig. Leuk probleempje zadel je me mee op, en ik kan bijna niet slapen voordat ik dit heb opgelost. Om half 5 eruit, en daarna een hele dag naar school...
n√n= 1
n + √n = x
met n = 3√(-0.5 + 0.5i√3)
Waarom klopt dit niet
[ Bericht 1% gewijzigd door Amoeba op 21-05-2012 02:01:38 ]
[ Bericht 15% gewijzigd door Don_Vanelli op 21-05-2012 08:30:12 ]
Dat is correct.quote:Op maandag 21 mei 2012 08:21 schreef Don_Vanelli het volgende:
Het heeft me een uur van mn leven gekost, maar volgens mij is het antwoord dat de afstand tot de oorsprong gelijk is aan
Maar verklap nog maar niet hoe je het hebt gedaan, dan kan Amoeba nog even door puzzelen.
Ik moet toch uitkomen op een dikke gare wortel met 500x i? Of is dat te 'vereenvoudigen' tot 2cos4pi/9?quote:
[..]
Dat is correct.
Maar verklap nog maar niet hoe je het hebt gedaan, dan kan Amoeba nog even door puzzelen.
Je hebt twee complexe getallen m3 = -½ + i∙½√3 en n3 = -½ - i∙½√3 en je probleem is nu dat je van deze twee complexe getallen de derdemachtswortels moet bepalen. Maar dat is niet zuiver algebraïsch te doen en dat is precies waarop je stuk loopt.quote:
[..]
Ik moet toch uitkomen op een dikke gare wortel met 500x i? Of is dat te 'vereenvoudigen' tot 2cos4pi/9?
De kubische vergelijking x3 - 3x + 1 = 0 die je op moet lossen heeft uitsluitend reële wortels, maar opmerkelijk genoeg zijn deze wortels met de formules van Cardano toch niet zonder complexe getallen uit te drukken. Daarom noemde men dit casus irreducibilis ('het onherleidbare geval').
Je kunt nu een paar dingen doen, namelijk verder werken met complexe getallen en gebruik maken van de formule van De Moivre, of zonder complexe getallen werken door een goniometrische substitutie in je oorspronkelijke kubische vergelijking uit te voeren.
m3 = -1/2 - 1/2i√3
3*argz = 240 graden, dus arg z = 80 graden.
m = cos80 + i*sin80
n = 1/m
a = m+n
cos 80 + isin80 + 1/(cos80 + i*sin80)
Inderdaad, daar komt het wel op neer, dat heb je snel gevonden (er zijn natuurlijk drie reële wortels, maar deze moet je hebben).quote:
Meh.
m3 = -1/2 - 1/2i√3
3*argz = 240 graden, dus arg z = 80 graden.
m = cos80 + i*sin80
n = 1/m
a = m+n
cos 80 + isin80 + 1/(cos80 + i*sin80)
Als je nu nog ziet dat 1/(cos 80° + i*sin 80°) = cos 80° - i*sin80° (waarom?) dan ben je klaar.
cos-x = cosx
sin-x = -sinx
Gonio + De Moivre.
Maar even een vraagje uit nieuwsgierigheid, wat heb jij (allemaal) gestudeerd?
Ah, je zit in mijn postgeschiedenis te kijken? Sorry, maar ik beantwoord geen privé vragen.quote:
(cos80 + i sin80)-1 = cos-80 + isin-80
cos-x = cosx
sin-x = -sinx
Gonio + De Moivre.
Maar even een vraagje uit nieuwsgierigheid, wat heb jij (allemaal) gestudeerd?
Neen. Ik kwam toevallig je post tegen bij de vraag over dat gedicht van (Schrijver?), ik zie je regelmatig in DIG en hier. Sorry, ik was enkel benieuwd.quote:
[..]
Ah, je zit in mijn postgeschiedenis te kijken? Sorry, maar ik beantwoord geen privé vragen.
Ohja, het volgens mij integreer ik nu een stuk van de bol waaruit nog een kegel ontbreekt. Dat zou je er wel weer bij op kunnen tellen: 1/3 pi r² h, met r=cos(p), h=sin(p). Dan krijg jequote:
[..]
Het lijkt erop alsof je hier het interval waarover je r neemt als constant beschouwt, maar dat is niet zo als je p varieert ...
Maar dat is nog steeds wat anders geloof ik, want dan krijg ik numeriek p=0.28.
[ Bericht 1% gewijzigd door thenxero op 21-05-2012 11:19:07 ]
Je maakt het allemaal veel te moeilijk met die drievoudige integraal, want eigenlijk maak je gebruik van het feit dat de oppervlakte van een cirkel met straal r gelijk is aan:quote:
[..]
Ohja, het volgens mij integreer ik nu een stuk van de bol waaruit nog een kegel ontbreekt. Dat zou je er wel weer bij op kunnen tellen
∫02π ∫0r ρdρdθ
Je kunt veel beter een enkelvoudige integraal met ϕ als variabele opstellen.
Ik krijg een beetje een punthoofd van WolframAlpha, want die wil mijn bolcoördinaten met (r,θ,ϕ) niet herkennen, dus ik heb me even moeten behelpen met f voor ϕ, maar de integraal die je zoekt is deze.
Maar goed, dat is alleen om even te laten zien wat je dan krijgt. Voor p = π/2 krijg je het volume van de halve bol, zijnde (2/3)∙π.
Eenvoudiger gaat het als volgt. Beschouw een snijvlak op een hoogte h vanaf het grondvlak van de halve bol en zij r de straal van de snijcirkel. Dan hebben we:
r = cos ϕ,
en:
h = sin ϕ,
dus ook:
dh = cos ϕ∙dϕ
Dit geeft voor de volumedifferentiaal dV:
dV = π∙r2∙dh = π∙cos3ϕ∙dϕ
En dus krijgen we voor het volume V met ϕ = p:
∫0p π∙cos3ϕ∙dϕ
Je kunt nu gemakkelijk in WolframAlpha nagaan (weer met f voor ϕ) dat dit precies hetzelfde resultaat oplevert als die onnodig lastige drievoudige integraal.
[ Bericht 5% gewijzigd door Riparius op 21-05-2012 13:03:29 ]
Nou ja, dilemma's, het is gewoon een opgave (uit het boek Beknopte Hoogere Algebra van Fred Schuh uit 1926, p. 287 als je het precies wil weten). Maar probeer eerst eens of je die kubische vergelijking op kunt lossen met een goniometrische substitutie, dus zonder gebruik van complexe getallen. Of kijk eens of je verder komt met de aanpak van thenxero.quote:
Maargoed, heb je nog meer van zulke interessante dilemma's?
[ Bericht 0% gewijzigd door Riparius op 21-05-2012 13:20:33 ]
Post hier maar. Als ik het niet weet op te lossen dan iemand anders wellicht wel. Is altijd leerzaam, ook voor de meelezers.quote:
Ja leuk, dan kan ik weer domme opmerkingen maken enzo.quote:
[..]
Post hier maar. Als ik het niet weet op te lossen dan iemand anders wellicht wel. Is altijd leerzaam, ook voor de meelezers.
Wat had je precies ingevoerd bij WolframAlpha?quote:
Ik heb er nog wel een voor jou als je wil? Maar hoe kon ik nou uitkomen op die oplossing van Wolframalpha, ofwel dat 'wortelantwoord'? Daar wil ik nog wel mee verder. Een zetje, gaarne.
De oppervlakte O wordt gegeven door een functie:
O = sin(2a) + sin(a)√(21+4cos2(a))
Bereken exact de maximale waarde van O met behulp van differentieren. Met berekening gaarne, numeriek oplossen is te simpel.
Verder heb ik geen les gehad over bolcoördinaten en dubbele integralen, zoals gezegd: Buiten een CE Wiskunde B en 2 boeken Wiskunde D en een goede motivatie heb ik niet zo veel parate wiskundekennis.
De kubische functie. Naar de exacte antwoorden gekeken, ofwel de middelste daarvan die op het gevraagde interval ligt.quote:
[..]
Wat had je precies ingevoerd bij WolframAlpha?
Als ik even kijk dan zie ik daar op het eerste gezicht geen interessant of elegant antwoord uitkomen, dus óf je hebt de opgave verkeerd overgenomen, óf ik mis iets.quote:
Goed, het gaat over een driehoek.
De oppervlakte O wordt gegeven door een functie:
O = sin(2a) + sin(a)√(21+4cos2(a))
Bereken exact de maximale waarde van O met behulp van differentieren. Met berekening gaarne, numeriek oplossen is te simpel.
Je mist iets. Dit was een vraag op mijn proefwerk, om dit numeriek op te lossen. Maar zoals gegeven, eerst differentieren. De afgeleide moet 0 zijn.quote:
[..]
Als ik even kijk dan zie ik daar op het eerste gezicht geen interessant of elegant antwoord uitkomen, dus óf je hebt de opgave verkeerd overgenomen, óf ik mis iets.
Numeriek oplossen geeft O = 5. Dit gaf ons de drive om dit proberen exact te doen. Wat gelukt is.
OK. Dit is gewoon wat je met de formule's van Cardano krijgt. Je had:quote:
[..]
De kubische functie. Naar de exacte antwoorden gekeken, ofwel de middelste daarvan die op het gevraagde interval ligt.
m3 = -½ + i∙½√3 en n3 = -½ - i∙½√3
Elk van deze vergelijkingen heeft niet één maar drie oplossingen. Je krijgt dus 3 complexe getallen m1, m2, m3 en drie complexe getallen n1, n2, n3. Aangezien x = m + n kun je zo 9 combinaties maken, maar daarvan voldoen er maar 3, omdat je ook nog aan de voorwaarde mn = 1 moet voldoen.
Heb je één set oplossingen die voldoen, laten we zeggen m1 en n1 , dan kun je de twee andere waarden voor m en n vinden door te vermenigvuldigen met de beide primitieve derdemachts eenheidswortels, namelijk
ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3
Aangezien ε1ε2 = 1 krijg je dan:
x1 = m1 + n1
x2 = ε1m1 + ε2n1
x3 = ε2m1 + ε1n1
Ik neem aan dat het nu wel wat duidelijker wordt hoe de uitdrukkingen die WolframAlpha geeft zijn opgebouwd.
Dan kom ik inderdaad ook uit op q³-3q+1=0 met q=sin(p)quote:
[..]
Je maakt het allemaal veel te moeilijk met die drievoudige integraal, want eigenlijk maak je gebruik van het feit dat de oppervlakte van een cirkel met straal r gelijk is aan:
∫02π ∫0r ρdρdθ
Je kunt veel beter een enkelvoudige integraal met ϕ als variabele opstellen.
Ik krijg een beetje een punthoofd van WolframAlpha, want die wil mijn bolcoördinaten met (r,θ,ϕ) niet herkennen, dus ik heb me even moeten behelpen met f voor ϕ, maar de integraal die je zoekt is deze.
Maar goed, dat is alleen om even te laten zien wat je dan krijgt. Voor p = π/2 krijg je het volume van de halve bol, zijnde (2/3)∙π.
Eenvoudiger gaat het als volgt. Beschouw een snijvlak op een hoogte h vanaf het grondvlak van de halve bol en zij r de straal van de snijcirkel. Dan hebben we:
r = cos ϕ,
en:
h = sin ϕ,
dus ook:
dh = cos ϕ∙dϕ
Dit geeft voor de volumedifferentiaal dV:
dV = π∙r2∙dh = π∙cos3ϕ∙dϕ
En dus krijgen we voor het volume V met ϕ = p:
∫0p π∙cos3ϕ∙dϕ
Je kunt nu gemakkelijk in WolframAlpha nagaan (weer met f voor ϕ) dat dit precies hetzelfde resultaat oplevert als die onnodig lastige drievoudige integraal.
.Ik snap hoe je die enkele integraal bepaalt, maar ik snap niet wat er mis was met mijn redenatie en hoe jij aan de correcte drievoudige integraal bent gekomen (ik zie bijvoorbeeld de jacobiaan niet meer terug).
Ik beweer dat { (r,θ,ϕ) : 0<r<1, 0<θ<2pi, 0<ϕ<p } gelijk is aan de verzameling van de afgezaagde bovenhelft van de bol minus de kegel. Zie plaatje.
hoe vereenvoudig je het volgende?
Er valt niet zoveel te vereenvoudigen. Je kan het kwadraat loslaten op de teller en noemer... maar of het daar eenvoudiger van wordt...quote:Op maandag 21 mei 2012 17:13 schreef gogosweden het volgende:
een wss heel domme vraag van mij hier:
hoe vereenvoudig je het volgende??
hmm daar heb je wel een punt.quote:
[..]
Er valt niet zoveel te vereenvoudigen. Je kan het kwadraat loslaten op de teller en noemer... maar of het daar eenvoudiger van wordt...
Volgens het boek word het :
maar hoe ze dat gekregen hebben is mij een raadsel
ohja klopt. Best simpel eigelijk, bedankt!quote:
Dit is de frequentietabel:
inhoud in ml: 100 200 330 500
frequentie: 19 26 41 3
Alvast bedankt
edit: in de post staan de getallen niet onder elkaar, maar het is gewoon in die volgorde.
Dus hier is je mediaan het 45e getal, dus 200.
Dat de mediaan het 45e getal is begrijp ik, maar ik snap niet hoe je dan bij 200 komt. Misschien dom, ik weet hetquote:
mediaan is het middelste getal bij een onevenreeks, bij een even reeks het gemiddelde van de 2 middelste waarnemingen.
Dus hier is je mediaan het 45e getal, dus 200.
Mediaan= de middelste waarneming van de reeks.
Gemiddelde= spreekt voor zich denk ik.
Hier heb je 6 waarnemingen, de mediaan is dan waarneming (3+4)/2= 17/2 = 8,5
Vaak wordt een mediaan gebruikt om de verdeling van de getallen aan te geven, de mediaan kan 3 zijn, maar door een hele hoge uitschieter kan het gemiddelde op 11 komen te liggen. Het wordt gebruikt om de verdeling van de waarnemingen weer te geven zegmaar. Correct me if im wrong iemand.
Mij werd de brieven overhandigd / Mij werden de brieven overhandigd (werden toch ?! Maar twijfel nu inees)
Mij werden de brieven overhandigd.quote:
Is het:
Mij werd de brieven overhandigd / Mij werden de brieven overhandigd (werden toch ?! Maar twijfel nu inees)
Onderwerp is 'de brieven', dus moet pv ook in meervoud staan.
Volgens mij heb ik hem (bijna) gevonden. Je gebruikt wat gonio om alle sinussen in cosinussen te veranderen. Dan substitueer je p=cos²(a), en dat geeft een tweedegraadsvergelijking met als oplossingenquote:
[..]
Je mist iets. Dit was een vraag op mijn proefwerk, om dit numeriek op te lossen. Maar zoals gegeven, eerst differentieren. De afgeleide moet 0 zijn.
Numeriek oplossen geeft O = 5. Dit gaf ons de drive om dit proberen exact te doen. Wat gelukt is.
en
Dus
Als ik dit weer invul in wolfram krijg ik helaas 4.99 in plaats van 5
Zet de getallen op een rijtje (van klein naar groot). Wat is het 45e getal?quote:
[..]
Dat de mediaan het 45e getal is begrijp ik, maar ik snap niet hoe je dan bij 200 komt. Misschien dom, ik weet het
3+4 is geen 17quote:
je hebt een reeks waarnemingen, ik zal even een voorbeeld geven: 3 5 8 9 11 15
Mediaan= de middelste waarneming van de reeks.
Gemiddelde= spreekt voor zich denk ik.
Hier heb je 6 waarnemingen, de mediaan is dan waarneming (3+4)/2= 17/2 = 8,5
Vaak wordt een mediaan gebruikt om de verdeling van de getallen aan te geven, de mediaan kan 3 zijn, maar door een hele hoge uitschieter kan het gemiddelde op 11 komen te liggen. Het wordt gebruikt om de verdeling van de waarnemingen weer te geven zegmaar. Correct me if im wrong iemand.
Oké top bedanktquote:
[..]
Mij werden de brieven overhandigd.
Onderwerp is 'de brieven', dus moet pv ook in meervoud staan.
Excuses trouwens, had niet gelezen dat dit voor wiskunde vraagstukken was.quote:
jajajaja je weet wat ik bedoelWelke getallen? De frequentie of inhoud in ml?quote:
[..]
Zet de getallen op een rijtje (van klein naar groot). Wat is het 45e getal?
Ik ben hier echt zo slecht in
dus je hebt de frequentie, hoevaak iets voorkomt, uitgeschreven in die getallen. Het 45e getal is dus 200
Duidelijk, maar om dat nou elke keer uit te schrijven is ook niet de bedoeling denk ik. Kan je aan de frequentietabel zien wat het 45e getal is?quote:
nou ej zou dan 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 330 .......................................... 500 500 500
dus je hebt de frequentie, hoevaak iets voorkomt, uitgeschreven in die getallen. Het 45e getal is dus 200
Kijk, dát is nou wat ik zo superleuk vind aan wiskunde. Heel lang bezig met een opgave, lekker puzzelen en dan úiteindelijk er zelf uitkomen, het gevoel dat je dan krijgt
Dat is een van de redenen waarom ik graag een wiskundige studie, als TW of Econometrie wil gaan doen Helaas mis ik nu gewoon wiskundekennis om het te volgen
Tel alle frequenties bij elkaar op, dan kom je op 89, het middelste getal is het getal tussen 44 en 46, dus 45, de 45e waarneming is de laatste 200quote:
[..]
Duidelijk, maar om dat nou elke keer uit te schrijven is ook niet de bedoeling denk ik. Kan je aan de frequentietabel zien wat het 45e getal is?
Ah ja, ik zie het.quote:
[..]
Tel alle frequenties bij elkaar op, dan kom je op 89, het middelste getal is het getal tussen 44 en 46, dus 45, de 45e waarneming is de laatste 200
Hartstikke bedankt
De leukste opgaves vind ik toch eigenlijk opgaves waarbij je weinig algebra nodig hebt, maar het probleem gewoon heel handig moet aanpakken waardoor een schijnbaar onmogelijk probleem opeens heel eenvoudig wordt.quote:
@ Dat ''vraagstuk'' een paar bladzijde's geleden.
Kijk, dát is nou wat ik zo superleuk vind aan wiskunde. Heel lang bezig met een opgave, lekker puzzelen en dan úiteindelijk er zelf uitkomen, het gevoel dat je dan krijgt
Helaas mis ik nu gewoon wiskundekennis om het te volgen
Ik zie dat ik een stomme rekenfout heb gemaakt. Als ik die verbeter kom ik wel goed uit.quote:
[..]
Volgens mij heb ik hem (bijna) gevonden. Je gebruikt wat gonio om alle sinussen in cosinussen te veranderen. Dan substitueer je p=cos²(a), en dat geeft een tweedegraadsvergelijking met als oplossingen
en
Dus
Als ik dit weer invul in wolfram krijg ik helaas 4.99 in plaats van 5
Nu nog 5 eruit zien te krijgen
Waarom maar dan ook waarom zou je a eruit halen?quote:
[..]
Ik zie dat ik een stomme rekenfout heb gemaakt. Als ik die verbeter kom ik wel goed uit.
Nu nog 5 eruit zien te krijgen
Kijk eens naar de functie zelf?
sin(2a) + sin(a)(21+4cos2(a))
Ik heb zelf even het antwoord niet meer bij de hand, maar ik kan me herinneren dat je ook een oplossing voor de sinus kreeg. (dus sin a = .....)
sin2a zet je om in 2cosAsinA
cosA heb je nog wel staan volgens mij?
Hoek alfa was gegeven (de plaats dan) en de zijden 5 en 2.
Nou, als je als basis de zijde 5 nam, 2 stond daar zo ongeveer loodrecht op, dan was het makkelijk om aan te bewijzen dat de oppervlakte van de driehoek maximaal is als die zijde van 2 loodrecht op die van 5 stond. Ergo, 1/2 * basis * hoogte leverde sowieso 5 op.
De beste opgaves zijn hordes vol algebra van een schijnbaar eenvoudige opgave. Zoals die bol, ik dacht serieus: Dat wordt peanuts.quote:
[..]
De leukste opgaves vind ik toch eigenlijk opgaves waarbij je weinig algebra nodig hebt, maar het probleem gewoon heel handig moet aanpakken waardoor een schijnbaar onmogelijk probleem opeens heel eenvoudig wordt.
Zelfs beide Wiskunde docenten op het VWO hier kennen die formule niet... (Calando)
Zodat je hem kan invullen... bijvoorbeeld als volgt:quote:
[..]
Waarom maar dan ook waarom zou je a eruit halen?
(noteer even x=2/sqrt(29))
Poepoe, wat een typwerk
Ik maak dus gebruik van sin(arccos(x))=sqrt(1-x^2). Dat kan je bewijzen met sin² z + cos² z =1 en dan z=arcos(x) te nemen.
[ Bericht 3% gewijzigd door thenxero op 21-05-2012 19:47:48 ]
Cardano. En ze hebben er hopelijk wel van gehoord, maar kennen het niet uit hun hoofd. De meeste wiskundeprofessors zullen die formule ook niet uit hun hoofd kennenquote:
[..]
Zelfs beide Wiskunde docenten op het VWO hier kennen die formule niet... (Calando)
.Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.
Maar het zal ongetwijfeld kloppen! 2/r29 komt inderdaad heel bekend voor
Trouwens, de app van Wolframalpha voor Android is ook wel echt geil.
Ja die gast heet Cardano. Ook wel grappig dat vanwege die formule de imaginaire getallen "in" zijn geraakt. Want toen realiseerde men zich dat imaginaire getallen wel degelijk betekenis/nut hadden, omdat het kan gebeuren dat je met die formule negatieve getallen in de wortel kan krijgen, terwijl de oplossing toch reëel is.quote:
Oh, heet die gast Cardano.
Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.
Maar het zal ongetwijfeld kloppen! 2/r29 komt inderdaad heel bekend voor
Er zijn inderdaad meerdere manieren (zoals wel vaker met gonio). Je zou bijvoorbeeld alles als sin kunnen schrijven, en dan krijg je een kwadratische vergelijking in termen van sinus.
Meh, ik zat in de trein, maar ik heb hier op papier dezelfde berekening staanquote:
[..]
Zodat je hem kan invullen... bijvoorbeeld als volgt:
(noteer even x=2/sqrt(29))
Poepoe, wat een typwerk
Ik maak dus gebruik van sin(arccos(x))=sqrt(1-x^2). Dat kan je bewijzen met sin² z + cos² z =1 en dan z=arcos(x) te nemen.
vraag: Bereken de inhoud in cm³ van een parabolöide met een hoogte van 12 cm en een straal van 4 cm. Rond af op twee decimalen.
Hier snap ik werkelijk geen kut van, dus als iemand mij wil helpen, graag!
a=4, en invullenquote:
stukje inleiding: Van een parabolöide is de straal a en de hoogte 3a. De inhoud is te berekenen met de formule inhoud = 4,71a³ (tot de macht 3 voor degene die het niet kunnen lezen)
vraag: Bereken de inhoud in cm³ van een parabolöide met een hoogte van 12 cm en een straal van 4 cm. Rond af op twee decimalen.
Hier snap ik werkelijk geen kut van, dus als iemand mij wil helpen, graag!
Die klopt, thanks. Zou je misschien willen uitleggen waarom a=4 ?quote:
Differentieren geeft
dus
Precies wat ik ook hadquote:
Bereken de straal van de parabolöide in mm.
Deze weet ik ook niet..
een paraboloïde is een parabool die om de y-as is gewenteld?quote:
Van een parabolöide is de hoogte drie keer de straal. De inhoud is 185 cm³.
Bereken de straal van de parabolöide in mm.
Deze weet ik ook niet..
4,71a³ = 185 en dan oplossen voor a, en a is de straal (in cm).quote:
Van een parabolöide is de hoogte drie keer de straal. De inhoud is 185 cm³.
Bereken de straal van de parabolöide in mm.
Deze weet ik ook niet..
Yup.quote:
[..]
een paraboloïde is een parabool die om de y-as is gewenteld?
Ja. En ik denk dat ie bedoelt dat ie afgezaagd wordt op een hoogte 3a en dat de straal daar dan a is.quote:
[..]
een paraboloïde is een parabool die om de y-as is gewenteld?
Ergens vrees ik dan datquote:
[..]
Ja. En ik denk dat ie bedoelt dat ie afgezaagd wordt op een hoogte 3a en dat de straal daar dan a is.
Die klopt ook. Hartstikke bedanktquote:
[..]
4,71a³ = 185 en dan oplossen voor a, en a is de straal (in cm).
Behalve dan dat de inhoud van een dergelijk object wordt gegeven doorquote:
Ik zit in havo3, dit gaat me iets te verquote:
[..]
Behalve dan dat de inhoud van een dergelijk object wordt gegeven door
Kwadrateren levert
Nu het rationale deel in irrationale deel afzonderlijk links en rechts van de vgl. aan elkaar gelijk stellen:
a = d + e
en vervolgens loop ik hier vast:
Wiki zegt vervolgens:
Ik zie de gemaakte stappen to-taal niet, sorry....
[ Bericht 8% gewijzigd door VanishedEntity op 21-05-2012 22:02:00 ]
Kies wiskunde B, doe daarna het vwo, dan zie je het vanzelfquote:
[..]
Ik zit in havo3, dit gaat me iets te ver
http://en.wikipedia.org/w(...)ting_nested_radicalsquote:
Kan er iemand mij even helpen met het root denesting algoritme?
Kwadrateren levert
Nu het rationale deel in irrationale deel afzonderlijk links en rechts van de vgl. aan elkaar gelijk stellen:
a = d + e
en vervolgens loop ik hier vast:
Uhuquote:
[..]
De leukste opgaves vind ik toch eigenlijk opgaves waarbij je weinig algebra nodig hebt, maar het probleem gewoon heel handig moet aanpakken waardoor een schijnbaar onmogelijk probleem opeens heel eenvoudig wordt.
Een tijdje geleden zat ik ook wat te rekenen met formules van de vorm:
En tot mijn stomme verbazing lukte het om een recurrente formule te geven voor de coëfficienten van een polynoom in n met graad m + 1, zodat deze polynoom voor elke waarde (>= 0) dezelfde waarde heeft als de som.
Nu kan dit ook door gewoon de waardes die de som aanneemt te observeren en een polynoom van graad m + 1 te zoeken die de dezelfde waardes aanneemt, maar ik vond het toch een mooi resultaat
ja zo ver was ik al... Ik zie alleen even niet hoe ze vanquote:
[..]
http://en.wikipedia.org/w(...)ting_nested_radicals
naar
gaan.
Deze laat ik lopen.... misschien iets voor Ripariusquote:
Helemaal mee eens. Heeft iemand voor de grap zelf de afleiding voor het getal van de ossen wel eens opgeschreven? Ik ga er persoonlijk niet aan beginnen, kost me teveel inkt
quote:
[..]
ja zo ver was ik al... Ik zie alleen even niet hoe ze van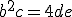
naar
gaan.
dus krijg je:
en dan is het slechts een kwestie van het oplossen van een kwadratische vergelijking
Thnx enniewee, vanaf hier is het een koud kunstje.
Pfoeh, ik ben er voor de lol aan begonnen, maar ik begin in te zien dat dit erg veel werk ik, en de kudde waarschijnlijk niet bepaald klein isquote:
Helemaal mee eens. Heeft iemand voor de grap zelf de afleiding voor het getal van de ossen wel eens opgeschreven? Ik ga er persoonlijk niet aan beginnen, kost me teveel inkt
Ik moet nog even kijken hoeveel ik er nog aan verder ga werken..
Ja. Voor Calando kun je beter bij je muziekdocent terechtquote:
.Over de manier waarop Cardano de formule te pakken kreeg en alle intriges en geheimzinnigdoenerij zou een prachtige film (à la The Name of the Rose) zijn te maken. Voor een stukje geschiedenis over hoe complexe getallen werden ontdekt door problemen met het oplossen van kubische vergelijkingen moet je dit maar eens lezen.
Een kubische vergelijking met reële coëfficienten en drie verschillende louter reële wortels kun je niet echt oplossen met Cardano omdat je de oplossingen dan alleen uit kunt drukken met behulp van derdemachtswortels uit complexe getallen die je niet algebraïsch kunt herleiden. Als de kubische vergelijking één reële en twee toegevoegd complexe wortels heeft dan lukt het wel.quote:Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.
Ja. Maar ik begrijp nog steeds niet waarom je met de hoek ϕ die een straal naar de snijcirkel maakt met het grondvlak van de halve bol wilde werken. Gevraagd werd immers naar de afstand h van het deelvlak tot het grondvlak om de halve bol in twee delen met gelijke volumes te verdelen, en dan ligt het toch wel érg voor de hand om dat als parameter te nemen. Met behulp van de bekende formule voor het volume van een omwentelingslichaam kom je dan direct op h3 - 3h + 1 = 0 uit.quote:
[..]
Dan kom ik inderdaad ook uit op q³-3q+1=0 met q=sin(p)
Dat heb ik al uitgelegd: in de correcte drievoudige integraal zit een dubbelintegraal die niets meer doet dan de oppervlakte van een cirkel met straal r uitdrukken. Heb ik geen Jacobiaan voor nodig.quote:Ik snap hoe je die enkele integraal bepaalt, maar ik snap niet wat er mis was met mijn redenatie en hoe jij aan de correcte drievoudige integraal bent gekomen (ik zie bijvoorbeeld de jacobiaan niet meer terug).
Wat er mis is, is dat je een verkeerde integrand gebruikt als gevolg van verwarring over wat θ en ϕ precies voorstellen.
Ja. Dit klopt ook en uiteraard is dit met een drievoudige integraal in bolcoördinaten uit te rekenen. Maar laten we eerst eens nagaan wat er uit zou moeten komen.quote:Ik beweer dat { (r,θ,ϕ) : 0<r<1, 0<θ<2pi, 0<ϕ<p } gelijk is aan de verzameling van de afgezaagde bovenhelft van de bol minus de kegel. Zie plaatje.
[ afbeelding ]
Voor het volume van het bolsegment hadden we (na herleiding) al gevonden dat dit gelijk is aan:
(1) π∙sin p - (1/3)∙π∙sin3p
Het volume van de kegel in je figuur is natuurlijk eenvoudig te bepalen. De oppervlakte van het grondvlak is π∙cos2p = π∙(1 - sin2p) en de hoogte is sin p, zodat het volume van de kegel dus wordt:
(2) (1/3)∙π∙sin p - (1/3)∙π∙sin3p
Het volume dat je nu wil berekenen is het verschil van (1) en (2), en dit is dus eenvoudig:
(3) (2/3)∙π∙sin p
Goed, nu we weten wat er uit moet komen hebben we een controlemogelijkheid. Ik moet bekennen dat dit mij ook wat hoofdbrekens opleverde. Voor een volume elementje dV hebben we bij gebruik van bolcoördinaten volgens Wikipedia (link):
(4) dV = r2∙sin θ∙dr∙dθ∙dϕ
Maar nu begint het grote verwarringsspel, want hier stelt niet ϕ maar θ de inclinatie voor, terwijl jij daarvoor ϕ gebruikt. Dus moeten we de rollen van θ en ϕ omwisselen en krijgen we:
(5) dV = r2∙sin ϕ∙dr∙dϕ∙dθ
Zijn we er nu? Nee, want hier stelt ϕ de inclinatie t.o.v. de normaal voor, terwijl bij jou ϕ de inclinatie t.o.v. het grondvlak voorstelt. Dus moeten we hier ϕ vervangen door ½π - ϕ en hebben we sin(½π - ϕ) = cos ϕ, zodat we voor jouw berekening krijgen:
(6) dV = r2∙cos ϕ∙dr∙dϕ∙dθ
En hiervoor mag ik ook schrijven:
(7) dV = r2∙cos ϕ∙dr∙dθ∙dϕ
De integraal voor je volume wordt nu:
(8) ∫0p ∫02π ∫01 r2∙cos ϕ∙dr∙dθ∙dϕ
Zoals je in WolframAlpha kunt nagaan (weer met f voor ϕ) levert dit inderdaad (2/3)∙π∙sin p op. Het klopt dus als een bus.
Wat nog minder bekend schijnt te zijn (maar vroeger gewoon standaard stof was) is dat je elke gereduceerde kubische vergelijking met uitsluitend reële wortels op kunt lossen zonder Cardano en zonder complexe getallen. Onder een gereduceerde kubische vergelijking verstaan we een derdegraadsvergelijking waarin de kwadratische term ontbreekt. Je kunt elke kubische vergelijking gemakkelijk herleiden tot zo'n gereduceerde vergelijking door een geschikte lineaire substitutie uit te voeren.quote:
[..]
De beste opgaves zijn hordes vol algebra van een schijnbaar eenvoudige opgave. Zoals die bol, ik dacht serieus: Dat wordt peanuts.
Zelfs beide Wiskunde docenten op het VWO hier kennen die formule niet... (Cardano)
De methode berust op de goniometrische identiteit voor de cosinus van de drievoudige hoek:
cos 3φ = 4∙cos3φ - 3∙cos φ
Ik neem als voorbeeld nog even de inmiddels bekende vergelijking:
z3 - 3z + 1 = 0
We brengen eerst de constante term naar het rechterlid:
z3 - 3z = -1
Het idee is nu dat we een substitutie z = r∙cos φ uitvoeren en dan het linkerlid omwerken tot 4∙cos3φ - 3∙cos φ, want dat is immers gelijk aan cos 3φ. Substitutie geeft:
r3∙cos3φ - 3∙r∙cos φ = -1
Nu willen we links een term 4∙cos3φ hebben, dus delen we beide leden door r3 en vermenigvuldigen we beide leden met 4. Dit geeft:
4∙cos3φ - (12/r2)∙cos φ = -4/r3
De eerste term in het linkerlid is nu in orde, maar nu moeten we nog zorgen dat de tweede term in het linkerlid gelijk wordt aan - 3∙cos φ en dat kunnen we doen door een geschikte waarde voor r te kiezen. We willen dat 12/r2 gelijk wordt aan 3, en dus kunnen we r = 2 nemen. Dit geeft:
4∙cos3φ - 3∙cos φ = -1/2
En dus:
cos 3φ = -1/2
Nu zien we dat 3φ = (2/3)∙π + 2∙k∙π en dus φ = (2/9)∙π + (2/3)∙k∙π, k ∈Z. We zouden ook de tegengestelde waarden voor φ kunnen nemen, maar dat maakt niets uit omdat de cosinus een even functie is. Aangezien z = r∙cos φ en r = 2 vinden we zo met k = 0, 1, 2 de wortels:
z1 = 2∙cos((2/9)∙π), z2 = 2∙cos((8/9)∙π), z3 = 2∙cos((14/9)∙π)
Met drie opeenvolgende waarden van k zijn we 'rond' en hebben we dus alle drie de wortels gevonden. Hiermee is de vergelijking opgelost.
Uiteraard is mij dat bekend. En er zijn nog meer varianten, bijvoorbeeld gebruik van een hyperbolische substitutie. Maar ik vond het vooral voor schoolgebruik aardig om eens te laten zien dat het met een beetje elementaire goniometrie en zonder kennis van complexe getallen ook prima gaat. Zo werd het vroeger ook meestal geleerd, toen er nog geen rekenmachines of computers bestonden en je het moest doen met goniometrische tafels.quote:
De (schijnbaar) complexe oplossing van cardano kan ook vrij gemakkelijk naar complexe e-machten worden ongeschreven. Vanuit daar kom je ook aan de correcte oplossing. Dat is wat meer op de automatische piloot ipv goniometrische identiteiten te kennen.
Ik snapte niet exact wat je deed, totdat ik het een tweede keer las. Die moet ik onthouden.quote:
[..]
Uiteraard is mij dat bekend. En er zijn nog meer varianten, bijvoorbeeld gebruik van een hyperbolische substitutie. Maar ik vond het vooral voor schoolgebruik aardig om eens te laten zien dat het met een beetje elementaire goniometrie en zonder kennis van complexe getallen ook prima gaat. Zo werd het vroeger ook meestal geleerd, toen er nog geen rekenmachines of computers bestonden en je het moest doen met goniometrische tafels.
4cos3x - 3cosx = cos3x
Je kunt de identiteit voor cos 3φ ook gewoon afleiden door uit te gaan van cos 2φ = 2∙cos2φ - 1 en sin 2φ = 2∙sinφ∙cosφ en cos 3φ = cos(2φ + φ) te herleiden met het bekende additietheorema cos(α + β) = cos α∙cos β - sin α∙sin β.quote:
[..]
Ik snapte niet exact wat je deed, totdat ik het een tweede keer las. Die moet ik onthouden.
4cos3x - 3cosx = cos3x
Of, gebruik de formule van De Moivre (cos φ + i∙sinφ)n = cos nφ + i∙sin nφ met n = 3, dan krijg je als bonus ook meteen sin 3φ = 3∙sin φ - 4∙sin3φ.
Dus x substitueren naar rcosx
(Dit had beter rcosa kunnen zijn omdat x al een variabele is ja, maar dat doet er nu even niet toe.)
dus 6r3cos3x -4rcosx = 9
Delen door 6r3
cos3x - (2/3)/r2cosx = 1,5/r 3
Vermenigvuldigen met 4, even r uitrekenen.
r = 2/3 * √2
Enfin, dan staat mijn vergelijking dus:
cos3x = 81 / 8√2
Wat doe ik fout/hoe moet ik verder?
De functie heeft één oplossing.
Ook cos3x = 81 / 8√2 heeft uiteraard geen oplossingen.
Of de functie f(x) = 15x 3+12x +7
Zelfde manier:
r = 4i/√15
cos3a= 7√15 / 16i
[ Bericht 2% gewijzigd door Amoeba op 22-05-2012 10:30:45 ]
[ Bericht 98% gewijzigd door Amoeba op 22-05-2012 09:55:53 ]
Een konijn uit denemarken sprong vorig jaar volgens het volgende model:
h = de hoogte in meters van de grond en x is de afstand in meters langs de grond vanaf het punt waar het konijn de lucht in sprong.
Hoe hoog kwam het konijn?
ik kom er maar niet uit, ik denk dat ik deze formule moet gebruiken maar hoe is me een raadsel:
Maximum vinden we wanneer
Dus het antwoord is
Thanks !quote:
Je begint gewoon met het berekenen van de eerste afgeleide:
Maximum vinden we wanneer
Dus het antwoord is
Aaaah, daar liep het dus op stuk. Bedankt!quote:
[..]
Zijn we er nu? Nee, want hier stelt ϕ de inclinatie t.o.v. de normaal voor, terwijl bij jou ϕ de inclinatie t.o.v. het grondvlak voorstelt.
Dat is simpelweg het eerste waar ik aan dacht, en het is op zich niet zoveel moeilijker dan dat wentelen, als je geen gekke fouten gaat makenquote:Ja. Maar ik begrijp nog steeds niet waarom je met de hoek ϕ die een straal naar de snijcirkel maakt met het grondvlak van de halve bol wilde werken.
.Dit is een vergelijking, geen functie. Wat je verder fout doet is dat je mijn uitleg kennelijk toch niet goed genoeg hebt gelezen. De goniometrische oplossingsmethode voor gereduceerde kubische vergelijkingen werkt alleen als de vergelijking uitsluitend reële wortels heeft, en dat is hier niet het geval.quote:
Goed, ik ging nu uit van de functie 6x3 -4x = 9
Dus x substitueren naar rcosx
(Dit had beter rcosa kunnen zijn omdat x al een variabele is ja, maar dat doet er nu even niet toe.)
dus 6r3cos3x -4rcosx = 9
Delen door 6r3
cos3x - (2/3)/r2cosx = 1,5/r 3
Vermenigvuldigen met 4, even r uitrekenen.
r = 2/3 * √2
Enfin, dan staat mijn vergelijking dus:
cos3x = 81 / 8√2
Wat doe ik fout/hoe moet ik verder?
De functie heeft één oplossing.
Om vooraf te zien of een gereduceerde kubische vergelijking met reële coëfficiënten uitsluitend reële wortels heeft of niet kun je kijken naar de discriminant van de vergelijking.
Hebben we de vergelijking:
z3 + pz + q = 0,
dan is de discriminant:
D = (p/3)3 + (q/2)2,
wat uiteraard makkelijk is te onthouden.
Je hebt nu de volgende mogelijkheden:
D > 0: Eén reële wortel en twee toegevoegd complexe wortels.
D = 0: Drie reële wortels waarvan er (tenminste) twee samenvallen.
D < 0: Drie reële wortels.
Let erop dat dit anders is dan bij vierkantsvergelijkingen, daar heb je geen reële wortels als de discriminant negatief is, hier zijn de wortels dan juist uitsluitend reëel.
Alleen als D ≤ 0 kun je de goniometrische oplossingsmethode toepassen. Je kunt dat ook nagaan door de algemene vergelijking z3 + pz + q = 0 goniometrisch op te lossen. Aangezien de cosinus functie alleen waarden aanneemt op het interval [-1,1] en dus moet gelden | cos 3φ | ≤ 1 vindt je dan een conditie voor p en q die equivalent is met D ≤ 0. Daaruit volgt dat het dus inderdaad altijd mogelijk is de vergelijking goniometrisch op te lossen als de wortels louter reëel zijn. Is dat niet het geval dan zijn er nog wel andere mogelijkheden, zoals het gebruik van een hyperbolische substitutie, maar dat zou nu wat te ver voeren.
Is D > 0, dan bereken je:
u3 = -½q + √D en v3 = -½q - √D
Nu heb je één reële waarde van u en één reële waarde van v die je kunt berekenen. De drie wortels van de vergelijking zijn dan:
z1 = u + v
z2 = ε1∙u + ε2∙v
z3 = ε2∙u + ε1∙v,
waarin ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3.
Zoals je ziet is dan z1 de reële wortel en zijn z2 en z3 de toegevoegd (geconjugeerde) complexe wortels. Het is dus helemaal niet moeilijk om kubische vergelijkingen op te lossen (en ja, ik schrijf deze hele post gewoon op uit het hoofd).
Maargoed, ik zal eens aan de gang gaan. Nog een kort vraagje:
Dit zijn altijd 'de sleutels' om tot de wortels te komen? Het is me niet helemaal duidelijk hoe je tot dit antwoord komt:
ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3.
Bonusvraagje: Hebben jullie iets handigs voor die latexcode? De link in de OP werkt niet meer, en al die symbolen zo is een beetje moeilijk om uit het hoofd te leren.
[ Bericht 24% gewijzigd door Amoeba op 22-05-2012 20:44:15 ]
Deze komt niet 'mooi' uit maar ik zal hem toch even voordoen. Rechterlid herleiden op nul geeft:quote:
Goed, ik ging nu uit van de vergelijking 6x3 - 4x = 9
6x3 - 4x - 9 = 0
Nu beide leden delen door zes om de coëfficient van x3 gelijk te maken aan één:
x3 - (2/3)∙x -(3/2) = 0
We hebben p = -2/3 en q = -3/2, en dus is D = (-2/9)3 + (-3/4)2 = -8/729 + 16/9 = 6433/11664 > 0, zodat er één reële wortel is (en twee toegevoegd complexe wortels). Merk op dat 11664 = 1082. De reële wortel is:
x = (3/4 + (1/108)∙√6433)1/3 + (3/4 - (1/108)∙√6433)1/3
Als je dit in WolframAlpha berekent, zie je dat het klopt met wat je numeriek met je GR of zo kunt vinden, maar dit is de exacte reële wortel. Wolfram heeft zelfs in de gaten dat 6x3 - 4x - 9 het minimale polynoom is voor deze wortel.
Ja, dit geldt altijd. Die ε1 en ε2 zijn de twee complexe derdemachtswortels van één. Dat kun je gemakkelijk controleren door ε13 en ε23 te berekenen. En er geldt ook ε1ε2 = 1.quote:
Nouja, de functie was f(x). Ik had hem al omgebouwd tot de 'vergelijking' die je daar zag.
Maargoed, ik zal eens aan de gang gaan. Nog een kort vraagje:
Dit zijn altijd 'de sleutels' om tot de wortels te komen? Het is me niet helemaal duidelijk hoe je tot dit antwoord komt:
ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3.
Zijn nu u en v de reële waarden die voldoen aan u∙v = -p/3, dan zal het product (ε1∙u)∙(ε2∙v) en het product (ε2∙u)∙(ε1∙v)
dus ook gelijk zijn aan -p/3 zodat deze combinaties ook voldoen en daarmee de twee andere (toegevoegd complexe) wortels opleveren.
Ah, nu weet ik weer wat er aan de hand was. Uiteindelijk kwam je uit op cos2a = 4/29quote:
Voor de volledigheid: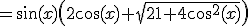
Differentieren geeft(1)
geeft:
dus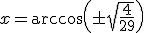
voldoet niet aan (1), dus
Nou, cosa = 2/√29
Dus kun je even een driehoek opstellen (soscastoa.. basisschool als je 't mij vraagt!)
dus de aanliggende zijde is 2, de schuine zijde √29
Een eenvoudig rekensommetje (Pythagoras) wijst dan uit dat de andere zijde uiteraard 5 is. Nu is het uiteraard alweer mogelijk om op basis van beredeneren te bewijzen dat de maximale oppervlakte 5 is. .Maargoed, wat we ook kunnen doen is nu de sinus uitdrukken. 5/√29
Nou goed, cosa = 2/√29 en sina = 5/√29
Vul dit in: komt perfect uit
Want sin2a = 2cosa*sina
[ Bericht 0% gewijzigd door Amoeba op 22-05-2012 21:04:39 (Typo) ]
Stiekem gebruikten wij ook de stelling van Pythagoras, maar dan in de vorm sin²+cos²=1. Komt dus op hetzelfde neer.quote:
[..]
Ah, nu weet ik weer wat er aan de hand was. Uiteindelijk kwam je uit op cos2a = 4/29
Nou, cosa = 2/√29
Dus kun je even een driehoek opstellen (soscastoa.. basisschool als je 't mij vraagt!)
dus de aanliggende zijde is 2, de schuine zijde √29
Een eenvoudig rekensommetje (Pythagoras) wijst dan uit dat de andere zijde uiteraard 5 is. Nu is het uiteraard alweer mogelijk om op basis van beredeneren te bewijzen dat de maximale oppervlakte 5 is. .Maargoed, wat we ook kunnen doen is nu de sinus uitdrukken. 5/√29
Nou goed, cosa = 2/√29 en sina = 5/√29
Vul dit in: komt perfect uit
Want sin2a = 2cosa*sina
Maargoed, zo kon het dus ook. Persoonlijk vond ik dit wat makkelijker. Als je maar op het antwoord komt, zullen we maar zeggen?quote:
[..]
Stiekem gebruikten wij ook de stelling van Pythagoras, maar dan in de vorm sin²+cos²=1. Komt dus op hetzelfde neer.