SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nou, niet direct; zo'n elitistische reply is nu even te kort door de bocht. Uit zijn post proef ik dat hij al vermoedt dat hij een foutieve berekening gemaakt heeft; hij twijfelt nl. zelf al aan de geldigheid v/d uitdrukking ∞ - ∞ = "iets"???. Het gaat mis doordat hij niet van te voren geprobeerd heeft de uitdrukking via de worteltruuk algebraïsch om te vormen tot een uitdrukking waar wèl een fatsoenlijk limietberekening mee gemaakt kan worden (zie post Haushofer), en om het inzichtelijk voor hem te maken, zet ik nog even wat extra stappen ertussen, gebaseerd op die andere worteltruuk.quote:Op donderdag 3 mei 2012 18:45 schreef Riparius het volgende:
Je fundamentele denkfout is dat je denkt dat je het symbool ∞ mag behandelen als een gewoon getal, maar dat is niet zo, ∞ is geen getal. Je mag dus ook niet zeggen dat een bepaalde limiet of een bepaalde grootheid 'gelijk' is aan 'oneindig', dat heeft geen betekenis. De rekenregel dat de limiet van een verschil van twee uitdrukkingen gelijk is aan het verschil van de limieten van die beide uitdrukkingen geldt ook alleen maar als de limieten van beide termen elk afzonderlijk bestaan, en dat is hier niet het geval.
vermenigvuldigd met
[ Bericht 0% gewijzigd door VanishedEntity op 04-05-2012 04:58:37 ]
Sowieso is voor fysici oneindig gelijk aan 0quote:
[..]
In wat geavanceerdere boeken kom je het wel eens tegen.
-
Game Theory:
Kan iemand mij helpen met dit vraagstuk:
For iterative elimination of strictly dominated strategies, show that the sets are nested (deelvraag 1)(wat is nested?) and that the procedure terminates in finitely many rounds if the game is finite (2). Can you provide a tight upper bound on the number of iterations that might be required? (3)
Ik weet sowieso niet wat nested betekent.
Verder zou ik bij (deelvraag 2) show that the procedure terminates in finitely many rounds if the game is finite.
Antwoorden:
When there's strictly dominance, one strategy s(DOM)i always dominates s(not DOM) i, because
utility player i (s(DOM)i, s - i) > utility player i (s(not DOM)i, s-i) So the utility of player i is strictly higher when using dominant strategy s for all s - i which are in the set of S - i (s - i and S - i are the strategies of all other players except player i ) When there are only strictly dominating strategies and there is a finite game, the procedure of iteration has also to be finite.
Klopt dit? En kan iemand mij helpen met die 2 andere deelvragen? Thanks!
Kan iemand mij helpen met dit vraagstuk:
For iterative elimination of strictly dominated strategies, show that the sets are nested (deelvraag 1)(wat is nested?) and that the procedure terminates in finitely many rounds if the game is finite (2). Can you provide a tight upper bound on the number of iterations that might be required? (3)
Ik weet sowieso niet wat nested betekent.
Verder zou ik bij (deelvraag 2) show that the procedure terminates in finitely many rounds if the game is finite.
Antwoorden:
When there's strictly dominance, one strategy s(DOM)i always dominates s(not DOM) i, because
utility player i (s(DOM)i, s - i) > utility player i (s(not DOM)i, s-i) So the utility of player i is strictly higher when using dominant strategy s for all s - i which are in the set of S - i (s - i and S - i are the strategies of all other players except player i ) When there are only strictly dominating strategies and there is a finite game, the procedure of iteration has also to be finite.
Klopt dit? En kan iemand mij helpen met die 2 andere deelvragen? Thanks!
quote:
[..]
Sowieso is voor fysici oneindig gelijk aan 0
Wat ze bedoelen met "A is nested in B" is denk ik "A is een deelverzameling van B". Ik snap alleen niet wat ze met "the sets" bedoelen.quote:
Game Theory:
Kan iemand mij helpen met dit vraagstuk:
For iterative elimination of strictly dominated strategies, show that the sets are nested (deelvraag 1)(wat is nested?) and that the procedure terminates in finitely many rounds if the game is finite (2). Can you provide a tight upper bound on the number of iterations that might be required? (3)
Ik weet sowieso niet wat nested betekent.
Verder zou ik bij (deelvraag 2) show that the procedure terminates in finitely many rounds if the game is finite.
Antwoorden:
When there's strictly dominance, one strategy s(DOM)i always dominates s(not DOM) i, because
utility player i (s(DOM)i, s - i) > utility player i (s(not DOM)i, s-i) So the utility of player i is strictly higher when using dominant strategy s for all s - i which are in the set of S - i (s - i and S - i are the strategies of all other players except player i ) When there are only strictly dominating strategies and there is a finite game, the procedure of iteration has also to be finite.
Klopt dit? En kan iemand mij helpen met die 2 andere deelvragen? Thanks!
Ik snap je uitwerking niet omdat ik die notaties niet ken.
Ik heb een korte vraag over meetkunde/congruentie:
Als twee driehoeken twee zijden delen en een hoek. En die hoek is 90 graden, maar is ingesloten. Is er dan sprake van congruentiegeval ZZR of ZHZ ? Volgens mijn antwoorden gaat het om ZZR, maar de definitie spreekt over een niet-ingesloten hoek.
Als twee driehoeken twee zijden delen en een hoek. En die hoek is 90 graden, maar is ingesloten. Is er dan sprake van congruentiegeval ZZR of ZHZ ? Volgens mijn antwoorden gaat het om ZZR, maar de definitie spreekt over een niet-ingesloten hoek.
Het is een uitspraak die vaak gedaan wordt ivm "renormalizatie"; het verschijnsel dat (met name in quantumveldentheorieën) fysici uit naieve berekeningen oneindig krijgen. De renormalisatieprocedure maakt daar een eindig antwoord van.quote:Op vrijdag 4 mei 2012 11:54 schreef thenxero het volgende:
[..]Serieus? Dat is wel een erg grove benadering.
Een ander pareltje wat o.a. gebruikt wordt in snaartheorie is de "identiteit"
waarmee via analytische continuatie bepaalde divergenties in je uitdrukkingen geregulariseerd worden. De manier waarop dat in tekstboeken wordt beschreven zou de meeste wiskundigen niet bepaald fijn overkomen, denk ik
-
Het lijkt mij ook ZHZ.quote:
Ik heb een korte vraag over meetkunde/congruentie:
Als twee driehoeken twee zijden delen en een hoek. En die hoek is 90 graden, maar is ingesloten. Is er dan sprake van congruentiegeval ZZR of ZHZ ? Volgens mijn antwoorden gaat het om ZZR, maar de definitie spreekt over een niet-ingesloten hoek.
ZZR is eigenlijk geen afzonderlijk congruentiekenmerk, want als twee rechthoekige driehoeken de hypotenusa en een rechthoekszijde gemeen hebben, dan hebben ze ook de andere rechthoekszijde gemeen op grond van Pythagoras en zijn ze dus congruent volgens congruentiekenmerk ZHZ. Maar soms wordt ZZR toch als een afzonderlijk congruentiekenmerk gegeven (zie bijvoorbeeld hier) omdat er bij ZZH nog twee mogelijkheden kunnen zijn. Om ZZH toch als congruentiekenmerk te kunnen gebruiken moet je als extra voorwaarde stipuleren dat de zijde tegenover de gemene hoek de langste van de twee gemene zijden is.quote:
Ik heb een korte vraag over meetkunde/congruentie:
Als twee driehoeken twee zijden delen en een hoek. En die hoek is 90 graden, maar is ingesloten. Is er dan sprake van congruentiegeval ZZR of ZHZ ? Volgens mijn antwoorden gaat het om ZZR, maar de definitie spreekt over een niet-ingesloten hoek.
Nu weet ik weer waarom ik gestopt ben met natuurkundequote:
[..]
Het is een uitspraak die vaak gedaan wordt ivm "renormalizatie"; het verschijnsel dat (met name in quantumveldentheorieën) fysici uit naieve berekeningen oneindig krijgen. De renormalisatieprocedure maakt daar een eindig antwoord van.
Een ander pareltje wat o.a. gebruikt wordt in snaartheorie is de "identiteit"
waarmee via analytische continuatie bepaalde divergenties in je uitdrukkingen geregulariseerd worden. De manier waarop dat in tekstboeken wordt beschreven zou de meeste wiskundigen niet bepaald fijn overkomen, denk ik
Je hebt hier eigenlijk ζ(-1) = -1/12, dus het is minder idioot dan het er uit ziet en ook wiskundig interessant. Het idee is afkomstig van Ramanujan. Mooi voorbeeld van hoe krankzinnigheid en genialiteit dicht bij elkaar kunnen liggen.quote:Op vrijdag 4 mei 2012 19:53 schreef thenxero het volgende:
[..]
Nu weet ik weer waarom ik gestopt ben met natuurkunde
Ik heb: g(q) = 4aq3 + 3a2q - a3
Is g'(q) + 12aq2 + 6aq
Ik twijfel hoe ik het afgeleiden krijg van 3a2q . Mijn boek heeft er geen uitleg over. Is hier iemand die weet hoe het zit?
Is g'(q) + 12aq2 + 6aq
Ik twijfel hoe ik het afgeleiden krijg van 3a2q . Mijn boek heeft er geen uitleg over. Is hier iemand die weet hoe het zit?
Je wil de afgeleide naar q bepalen van je uitdrukking. Dan beschouw je a dus als een constante. Je krijgt dan:quote:
Ik heb: g(q) = 4aq3 + 3a2q - a3
Is g'(q) + 12aq2 + 6aq
Ik twijfel hoe ik de afgeleide krijg van 3a2q . Mijn boek heeft er geen uitleg over. Is hier iemand die weet hoe het zit?
g'(q) = 12aq2 + 3a2
Als je 3a2q naar q afleidt dan is 3a2 gewoon een constante en q de variabele.
De afgeleide van 3a2q is dus 3a2, net zoals f(x) = 3x --> f ' (x) = 3
De afgeleide van 3a2q is dus 3a2, net zoals f(x) = 3x --> f ' (x) = 3
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Hoi,
In een bewijs dat ik probeer te maken, zou het erg prettig zijn als ik kan bewijzen dat
ax_1^{2d}+bx_2^{2d}-2dx_1^ax_2^b met a+b=2d, a,b en d natuurlijk een som van maximaal 2 kwadraten is. Dan kan ik vervolgens met inductie bewijzen dat dergelijke polynomen van een hogere macht de som van maximaal 3n-4 kwadraten zijn. Iemand een idee hoe je die 2 kwadraten maakt?
Alvast bedankt!
In een bewijs dat ik probeer te maken, zou het erg prettig zijn als ik kan bewijzen dat
ax_1^{2d}+bx_2^{2d}-2dx_1^ax_2^b met a+b=2d, a,b en d natuurlijk een som van maximaal 2 kwadraten is. Dan kan ik vervolgens met inductie bewijzen dat dergelijke polynomen van een hogere macht de som van maximaal 3n-4 kwadraten zijn. Iemand een idee hoe je die 2 kwadraten maakt?
Alvast bedankt!
Het dingetje wat je in je functie stopt, in dit geval de a, is niet je constante, maar je variabele.quote:
Hoe weet je precies of het een constante is?
f(a) = 0,3a3p3
Wordt het dan: f'(a) =0,9a2 ?
De a en b die je als coëfficiënten noemt, zijn dezelfde als de a en b die je als exponenten noemt?quote:
Hoi,
In een bewijs dat ik probeer te maken, zou het erg prettig zijn als ik kan bewijzen dat
ax_1^{2d}+bx_2^{2d}-2dx_1^ax_2^b met a+b=2d, a,b en d natuurlijk een som van maximaal 2 kwadraten is. Dan kan ik vervolgens met inductie bewijzen dat dergelijke polynomen van een hogere macht de som van maximaal 3n-4 kwadraten zijn. Iemand een idee hoe je die 2 kwadraten maakt?
Alvast bedankt!
jaquote:
[..]
De a en b die je als coëfficiënten noemt, zijn dezelfde als de a en b die je als exponenten noemt?
Dus mijn antwoord klopt?quote:
[..]
Het dingetje wat je in je functie stopt, in dit geval de a, is niet je constante, maar je variabele.
Ik ben zelf uitgegaan van de reële getallen, daar staat echter niets over in de opgave.quote:
En in welke ring moeten de coëfficiënten van de polynomen zitten die je moet kwadrateren?
Bijna, omdat de p^3 bij dezelfde term hoort, mag je hem niet zomaar weglaten. Net als de 0,3 die negeer je ook niet. Je antwoord is dan 0,9a2p3quote:
Dan is het een slechte opgave.quote:
[..]
Ik ben zelf uitgegaan van de reële getallen, daar staat echter niets over in de opgave.
Edit: laat maar, verkeerd gelezen.
Duidelijk, danku!quote:
[..]
Bijna, omdat de p^3 bij dezelfde term hoort, mag je hem niet zomaar weglaten. Net als de 0,3 die negeer je ook niet. Je antwoord is dan 0,9a2p3
Een polynoom f in R[x] met f(x) >= 0 voor alle x in R kun je schrijven als de som van 2 kwadraten van polynomen in R[x]. Ken je die stelling?quote:
Hoi,
In een bewijs dat ik probeer te maken, zou het erg prettig zijn als ik kan bewijzen dat
ax_1^{2d}+bx_2^{2d}-2dx_1^ax_2^b met a+b=2d, a,b en d natuurlijk een som van maximaal 2 kwadraten is. Dan kan ik vervolgens met inductie bewijzen dat dergelijke polynomen van een hogere macht de som van maximaal 3n-4 kwadraten zijn. Iemand een idee hoe je die 2 kwadraten maakt?
Alvast bedankt!
Ja, maar ik zie nog even niet waarom dit polynoom altijd >=0 moet zijn, maar ik zal er weer even over nadenken..quote:
[..]
Een polynoom f in R[x] met f(x) >= 0 voor alle x in R kun je schrijven als de som van 2 kwadraten van polynomen in R[x]. Ken je die stelling?
Ken je de herschikkingsongelijkheid?quote:
[..]
Ja, maar ik zie nog even niet waarom dit polynoom altijd >=0 moet zijn, maar ik zal er weer even over nadenken..
Daar ben ik mee aan het prutsen ja. Dat geeft me dat 2x_1^ax_2^b <= x_1^{2d}+x_2^{2d}. Maar dan moet ik het nu nog goed zien te krijgen met de coefficienten erbij..quote:
Dankjewel, maar hier kom ik ook nog niet echt uit. Dit is overigens de eerste keer dat ik van de regel hoor, dus ik heb even gegoogled. Hij lijkt alleen voor polynomen met één variabele te werken. Dan kun je natuurlijk die andere als een constante kiezen. Maar dan is het ook nog relevant of a en b even of oneven zijn bij het nagaan van het aantal negatieve oplossingen,terwijl je daar niks van weet? En zet je een + voor alle 0x^c met a_1<c<2d termen?quote:Op zondag 6 mei 2012 22:52 schreef thabit het volgende:
Hmm, ja, ik was misschien iets te snel daarmee. Maar het kan wel met de tekenregel van Descartes.
Je kunt x2=1 substitueren. Het is voldoende te laten zien dat het polynoom in x1 dat je dan krijgt alleen niet-negatieve waarden aanneemt. Je moet dan onderscheid maken tussen x1>0 en x1<0. Voor x1>0 kun je gebruiken dat x1=1 een dubbel nulpunt is. Voor x1<0 kun je het resultaat voor x1>0 gebruiken.
Ik weet niet of ik hier goed zit verbeter me maar als ik naar een ander topic moet 
Voor mijn minor bedrijfseconomie heb ik namelijk een vraag en ik kom er echt niet uit!
Wie zou me kunnen helpen aan het antwoord en de berekening?
Het betreft vraag 10
Voor mijn minor bedrijfseconomie heb ik namelijk een vraag en ik kom er echt niet uit!
Wie zou me kunnen helpen aan het antwoord en de berekening?
Het betreft vraag 10
Minor bedrijfseconomie? Dit lijkt meer 5VWO M&Oquote:
Ik weet niet of ik hier goed zit verbeter me maar als ik naar een ander topic moet
Voor mijn minor bedrijfseconomie heb ik namelijk een vraag en ik kom er echt niet uit!
[ afbeelding ]
Wie zou me kunnen helpen aan het antwoord en de berekening?
Het betreft vraag 10
hint: de toename van de kosten / de toename aantal producten = variabele kosten.
hieruit kun je de totale variabele kosten berekenen van bijv. 100.000 producten.
hieruit kun je de constante kosten berekenen.
Dan heb je de formule: kostprijs = c/n + v/b
winstopslag erover, klaar.
26"
Fading slowly.
Fading slowly.
Is iemand hier toevallig bekend met de Cholesky decompositie? Ik heb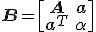 
. Nu wordt er gevraagd op de cholesky decompositie te geven in termen van "consituent submatrices". Nu wil ik het eerst nog zelf proberen maar wat wordt precies bedoeld met "constituent submatrices"? Moet ik de cholesky decompositie dus uitdrukken in de term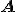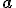en 
, 
en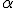 
? Want dan zou ik dus 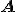kunnen schrijven in iets als
zou ik alleen nog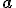 en 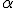erin moeten verwerken...
http://en.wikipedia.org/w(...)e_Cholesky_algorithm
zou ik alleen nog
http://en.wikipedia.org/w(...)e_Cholesky_algorithm
Ik ben in zoverre bekend met de Cholesky-decompositie dat ik het algoritme ken om de ontbinding te vinden inquote:Op dinsdag 8 mei 2012 23:09 schreef Dale. het volgende:
Is iemand hier toevallig bekend met de Cholesky decompositie? Ik heb
[ afbeelding ]
zou ik alleen nog
http://en.wikipedia.org/w(...)e_Cholesky_algorithm
Als ik 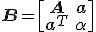nou verander naar..., horizontaal gespiegeld en verticaal gespiegeld, 
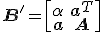blijven decomposities van 
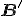dan gelijkwaardig zolang je maar dezelfde transformaties weer doet op het antwoord? Want dan kan ik schrijven
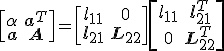
dan geldt
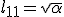
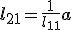
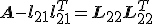
-edit- geloof dat 't kan aangezien B symmetrisch is.
[ Bericht 22% gewijzigd door Dale. op 09-05-2012 01:20:32 ]
dan geldt
-edit- geloof dat 't kan aangezien B symmetrisch is.
[ Bericht 22% gewijzigd door Dale. op 09-05-2012 01:20:32 ]
Het lijkt me wel dat dit mogelijk is ja, al heb ik een dergelijke transformatie (waarbij er zowel horizontaal als verticaal wordt gespiegeld) nog nooit eerder gezien/gebruikt. Overigens is het noodzakelijk dat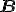 
symmetrisch is, anders kon je de cholesky decompositie niet eens gebruiken, maar moest je de minder efficiënte LU decompositie gebruiken.
opgave 15 en 16.
Wat heb je geprobeerd?
Welke manieren heb je om je GR hierbij te gebruiken?
Welke manieren heb je om je GR hierbij te gebruiken?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
In de uitwerkingen staat dat ik de normale verdelingsfunctie moet gebruiken. Ik heb zelf al verschillende dingen bij y1 en y2 lopen invullen, en dan intersecten maar dit geeft foutmeldingen.
Ben je bekend met normalcdf en de getallen die je daarbij kan invullen?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Ik heb een probleempje met natuurkunde waar ik maar niet uitkom. Maar aangezien het met het vervormen van een formule te maken heeft post ik het hier
De formule is L = 10log(I/I0)
Als ik de L en de I0 al weet, hoe kan ik dan de I uitrekenen?
De formule is L = 10log(I/I0)
Als ik de L en de I0 al weet, hoe kan ik dan de I uitrekenen?
Als je met die 10 het grondtal bedoelt van de logaritme, dan moet je dat wel superscripten, anders sticht je alleen maar verwarring. Dus:quote:
Ik heb een probleempje met natuurkunde waar ik maar niet uitkom. Maar aangezien het met het vervormen van een formule te maken heeft post ik het hier
De formule is L = 10log(I/I0)
Als ik de L en de I0 al weet, hoe kan ik dan de I uitrekenen?
L = 10log(I/I0)
Verder kun je gewoon gebruik maken van de definitie van de logaritme: glog a is de exponent waartoe je g moet verheffen om a te verkrijgen. Hier is L dus de macht waartoe je 10 moet verheffen om I/I0 te verkrijgen:
10L = I/I0
[ Bericht 0% gewijzigd door Riparius op 10-05-2012 21:06:58 ]
