SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ken je de herschikkingsongelijkheid?quote:Op zondag 6 mei 2012 22:16 schreef marleenhoofd- het volgende:
[..]
Ja, maar ik zie nog even niet waarom dit polynoom altijd >=0 moet zijn, maar ik zal er weer even over nadenken..


Daar ben ik mee aan het prutsen ja. Dat geeft me dat 2x_1^ax_2^b <= x_1^{2d}+x_2^{2d}. Maar dan moet ik het nu nog goed zien te krijgen met de coefficienten erbij..quote:


Dankjewel, maar hier kom ik ook nog niet echt uit. Dit is overigens de eerste keer dat ik van de regel hoor, dus ik heb even gegoogled. Hij lijkt alleen voor polynomen met één variabele te werken. Dan kun je natuurlijk die andere als een constante kiezen. Maar dan is het ook nog relevant of a en b even of oneven zijn bij het nagaan van het aantal negatieve oplossingen,terwijl je daar niks van weet? En zet je een + voor alle 0x^c met a_1<c<2d termen?quote:Op zondag 6 mei 2012 22:52 schreef thabit het volgende:
Hmm, ja, ik was misschien iets te snel daarmee. Maar het kan wel met de tekenregel van Descartes.


Je kunt x2=1 substitueren. Het is voldoende te laten zien dat het polynoom in x1 dat je dan krijgt alleen niet-negatieve waarden aanneemt. Je moet dan onderscheid maken tussen x1>0 en x1<0. Voor x1>0 kun je gebruiken dat x1=1 een dubbel nulpunt is. Voor x1<0 kun je het resultaat voor x1>0 gebruiken.


Ik weet niet of ik hier goed zit verbeter me maar als ik naar een ander topic moet 
Voor mijn minor bedrijfseconomie heb ik namelijk een vraag en ik kom er echt niet uit!
Wie zou me kunnen helpen aan het antwoord en de berekening?
Het betreft vraag 10
Voor mijn minor bedrijfseconomie heb ik namelijk een vraag en ik kom er echt niet uit!
Wie zou me kunnen helpen aan het antwoord en de berekening?
Het betreft vraag 10


Minor bedrijfseconomie? Dit lijkt meer 5VWO M&Oquote:Op maandag 7 mei 2012 00:34 schreef AL-CAPONE het volgende:
Ik weet niet of ik hier goed zit verbeter me maar als ik naar een ander topic moet
Voor mijn minor bedrijfseconomie heb ik namelijk een vraag en ik kom er echt niet uit!
[ afbeelding ]
Wie zou me kunnen helpen aan het antwoord en de berekening?
Het betreft vraag 10
hint: de toename van de kosten / de toename aantal producten = variabele kosten.
hieruit kun je de totale variabele kosten berekenen van bijv. 100.000 producten.
hieruit kun je de constante kosten berekenen.
Dan heb je de formule: kostprijs = c/n + v/b
winstopslag erover, klaar.
26"
Fading slowly.
Fading slowly.


Is iemand hier toevallig bekend met de Cholesky decompositie? Ik heb 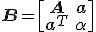 . Nu wordt er gevraagd op de cholesky decompositie te geven in termen van "consituent submatrices". Nu wil ik het eerst nog zelf proberen maar wat wordt precies bedoeld met "constituent submatrices"? Moet ik de cholesky decompositie dus uitdrukken in de termen
. Nu wordt er gevraagd op de cholesky decompositie te geven in termen van "consituent submatrices". Nu wil ik het eerst nog zelf proberen maar wat wordt precies bedoeld met "constituent submatrices"? Moet ik de cholesky decompositie dus uitdrukken in de termen 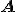 ,
, 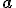 en
en 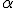 ? Want dan zou ik dus
? Want dan zou ik dus 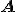 kunnen schrijven in iets als
kunnen schrijven in iets als
zou ik alleen nog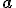 en
en 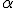 erin moeten verwerken...
erin moeten verwerken...
http://en.wikipedia.org/w(...)e_Cholesky_algorithm
zou ik alleen nog
http://en.wikipedia.org/w(...)e_Cholesky_algorithm


Ik ben in zoverre bekend met de Cholesky-decompositie dat ik het algoritme ken om de ontbinding te vinden inquote:Op dinsdag 8 mei 2012 23:09 schreef Dale. het volgende:
Is iemand hier toevallig bekend met de Cholesky decompositie? Ik heb. Nu wordt er gevraagd op de cholesky decompositie te geven in termen van "consituent submatrices". Nu wil ik het eerst nog zelf proberen maar wat wordt precies bedoeld met "constituent submatrices"? Moet ik de cholesky decompositie dus uitdrukken in de termen
,
en
? Want dan zou ik dus
kunnen schrijven in iets als
[ afbeelding ]
zou ik alleen nogen
erin moeten verwerken...
http://en.wikipedia.org/w(...)e_Cholesky_algorithm


Als ik 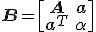 nou verander naar..., horizontaal gespiegeld en verticaal gespiegeld,
nou verander naar..., horizontaal gespiegeld en verticaal gespiegeld, 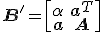 blijven decomposities van
blijven decomposities van 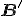 dan gelijkwaardig zolang je maar dezelfde transformaties weer doet op het antwoord? Want dan kan ik schrijven
dan gelijkwaardig zolang je maar dezelfde transformaties weer doet op het antwoord? Want dan kan ik schrijven
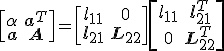
dan geldt
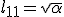
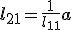
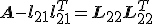
-edit- geloof dat 't kan aangezien B symmetrisch is.
[ Bericht 22% gewijzigd door Dale. op 09-05-2012 01:20:32 ]
dan geldt
-edit- geloof dat 't kan aangezien B symmetrisch is.
[ Bericht 22% gewijzigd door Dale. op 09-05-2012 01:20:32 ]


Het lijkt me wel dat dit mogelijk is ja, al heb ik een dergelijke transformatie (waarbij er zowel horizontaal als verticaal wordt gespiegeld) nog nooit eerder gezien/gebruikt. Overigens is het noodzakelijk dat 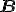 symmetrisch is, anders kon je de cholesky decompositie niet eens gebruiken, maar moest je de minder efficiënte LU decompositie gebruiken.
symmetrisch is, anders kon je de cholesky decompositie niet eens gebruiken, maar moest je de minder efficiënte LU decompositie gebruiken.


Wat heb je geprobeerd?
Welke manieren heb je om je GR hierbij te gebruiken?
Welke manieren heb je om je GR hierbij te gebruiken?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


In de uitwerkingen staat dat ik de normale verdelingsfunctie moet gebruiken. Ik heb zelf al verschillende dingen bij y1 en y2 lopen invullen, en dan intersecten maar dit geeft foutmeldingen.


Ben je bekend met normalcdf en de getallen die je daarbij kan invullen?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Ik heb een probleempje met natuurkunde waar ik maar niet uitkom. Maar aangezien het met het vervormen van een formule te maken heeft post ik het hier 
De formule is L = 10log(I/I0)
Als ik de L en de I0 al weet, hoe kan ik dan de I uitrekenen?
De formule is L = 10log(I/I0)
Als ik de L en de I0 al weet, hoe kan ik dan de I uitrekenen?


Als je met die 10 het grondtal bedoelt van de logaritme, dan moet je dat wel superscripten, anders sticht je alleen maar verwarring. Dus:quote:Op donderdag 10 mei 2012 13:24 schreef TheDutchguy het volgende:
Ik heb een probleempje met natuurkunde waar ik maar niet uitkom. Maar aangezien het met het vervormen van een formule te maken heeft post ik het hier
De formule is L = 10log(I/I0)
Als ik de L en de I0 al weet, hoe kan ik dan de I uitrekenen?
L = 10log(I/I0)
Verder kun je gewoon gebruik maken van de definitie van de logaritme: glog a is de exponent waartoe je g moet verheffen om a te verkrijgen. Hier is L dus de macht waartoe je 10 moet verheffen om I/I0 te verkrijgen:
10L = I/I0
[ Bericht 0% gewijzigd door Riparius op 10-05-2012 21:06:58 ]


Ik ben bezig met het doorwerken van Basisboek Wiskunde maar loop nu wat vast bij de vlakken. Er wordt gevraagd een vergelijking van een vlak op te stellen door drie gegeven punten, en die kan ik vinden, maar ik snap er een deel niet van.
Met als voorbeeld de drie punten A(2,0,0), B(0,3,0) en C(0,0,4) in een stelsel Oxyz vind ik als volgt de vergelijking van de twee lijnen door A & B en B & C
(2-0)(y-3) = (0-3)(x-0)
2(y-3) = -3x
2y - 6 = -3x
2y + 3x = 6
(3-0)(z-4) = (0-4)(y-0)
3(z-4) = -4y
3z - 12 = -4y
3z + 4y = 12
Volgens een vriend kon je ze dan vermenigvuldigen met d, gelijkstellen en bij elkaar voegen, en dat is waar ik het kwijt raak.
2dy + 3dx = 6d
3dz + 4dy = 12d
2dy + 3dx = 6d
(3/2)dz + 2dy = 6d
3dx + 2dy + (3/2)dz = 6d
Vanaf daar begrijp ik het wel weer, d = 1
3x + 2y + (3/2)z = 6
En er fancy uit laten zien
(3/6)x + (2/6)y + (3/12)z = 1
(x/2) + (y/3) + (z/4) = 1
Ik zie in dit alles het vlak als een bundeling lijnen vanuit punt B met als 'uiterste' lijnen de twee in het begin gevonden vergelijkingen, waarin iedere lijn gelimiteerd is door de d uit ax + by + cz = d. Is dit juist, of zit ik daarin fout?
Met als voorbeeld de drie punten A(2,0,0), B(0,3,0) en C(0,0,4) in een stelsel Oxyz vind ik als volgt de vergelijking van de twee lijnen door A & B en B & C
(2-0)(y-3) = (0-3)(x-0)
2(y-3) = -3x
2y - 6 = -3x
2y + 3x = 6
(3-0)(z-4) = (0-4)(y-0)
3(z-4) = -4y
3z - 12 = -4y
3z + 4y = 12
Volgens een vriend kon je ze dan vermenigvuldigen met d, gelijkstellen en bij elkaar voegen, en dat is waar ik het kwijt raak.
2dy + 3dx = 6d
3dz + 4dy = 12d
2dy + 3dx = 6d
(3/2)dz + 2dy = 6d
3dx + 2dy + (3/2)dz = 6d
Vanaf daar begrijp ik het wel weer, d = 1
3x + 2y + (3/2)z = 6
En er fancy uit laten zien
(3/6)x + (2/6)y + (3/12)z = 1
(x/2) + (y/3) + (z/4) = 1
Ik zie in dit alles het vlak als een bundeling lijnen vanuit punt B met als 'uiterste' lijnen de twee in het begin gevonden vergelijkingen, waarin iedere lijn gelimiteerd is door de d uit ax + by + cz = d. Is dit juist, of zit ik daarin fout?
"Social order at the expense of liberty is hardly a bargain."


Parametervergelijking:
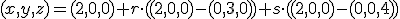
Hierbij uitgegaan van punt A met richtingsvectoren geconstrueerd uit A-B en A-C
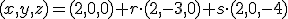
Bepaal de normaalvector door het kruisproduct nemen
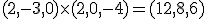
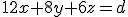
Vul een punt in om d te vinden:
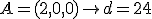
Invullen en uitschrijven:
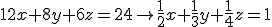
Hierbij uitgegaan van punt A met richtingsvectoren geconstrueerd uit A-B en A-C
Bepaal de normaalvector door het kruisproduct nemen
Vul een punt in om d te vinden:
Invullen en uitschrijven:


Daar ga ik zo mee aan de gang, bedankt.
"Social order at the expense of liberty is hardly a bargain."


De vergelijkingen die je geeft stellen in de driedimensionale ruimte vlakken voor, geen lijnen, dus hier gaat het al fout.quote:Op vrijdag 11 mei 2012 17:53 schreef Quir het volgende:
Ik ben bezig met het doorwerken van Basisboek Wiskunde maar loop nu wat vast bij de vlakken. Er wordt gevraagd een vergelijking van een vlak op te stellen door drie gegeven punten, en die kan ik vinden, maar ik snap er een deel niet van.
Met als voorbeeld de drie punten A(2,0,0), B(0,3,0) en C(0,0,4) in een stelsel Oxyz vind ik als volgt de vergelijking van de twee lijnen door A & B en B & C
Het idee is dat je eerst een normaalvector n bepaalt van je vlak V. Dat is een vector die loodrecht op het vlak staat. Is nu v = (x,y,z) een willekeurige vector met eindpunt in je vlak V en v0 = (x0,y0,z0) een vaste vector met eindpunt in je vlak, dan is vector v - v0 evenwijdig aan je vlak en staat deze verschilvector dus loodrecht op je normaalvector n, zodat het inproduct van v- v0 en n gelijk is aan nul:
(1) n∙(v - v0) = 0
En dus geldt ook:
(2) n∙v = n∙v0
Een vaste vector v0 met eindpunt in je vlak V ken je al omdat je immers de drie punten A,B en C kent die in vlak V liggen, zodat je hier voor v0 bijvoorbeeld de vector a = (2,0,0) zou kunnen nemen zodat x0 =2, y0 = 0 en z0 = 0.
De kunst is nu om een geschikte normaalvector n = (a,b,c) te bepalen want dan kun je voor (1) schrijven:
(3) a(x - x0) + b(y - y0) + c(z - z0) = 0,
en voor (2) kun je schrijven:
(4) ax + by + cz = ax0 + by0 + cz0,
en (3) of (4) is uiteraard de gezochte cartesische vergelijking van je vlak. Om nu een geschikte normaalvector n = (a,b,c) en daarmee de waarden van a,b en c te vinden kun je bedenken dat n loodrecht staat op zowel de verschilvector b - a als de verschilvector c - a, aangezien deze beide verschilvectoren evenwijdig zijn aan vlak V. En dus moet het inproduct van n = (a,b,c) met zowel b - a = (-2,3,0) als c - a = (-2,0,4) gelijk zijn aan nul. Dit geeft:
(5a) -2a + 3b = 0
(5b) -2a + 4c = 0
Hier heb je twee lineaire vergelijkingen in drie onbekenden a, b en c, en dus lijkt het alsof je nog één lineaire vergelijking tekort komt. Maar dat is niet zo, want als we n met een scalar vermenigvuldigen, dan hebben we nog steeds een vector die loodrecht op vlak V staat, dus zijn a,b,c niet eenduidig bepaald. Dat is ook meteen duidelijk uit de cartesische vergelijking (3) want als je hier beide leden met een getal ongelijk nul vermenigvuldigt, dan heb je nog steeds een geldige cartesische vergelijking van je vlak V.
We kunnen nu met (5a) en (5b) de waarde van a en b uitdrukken in c. Uit (5b) volgt dat a = 2c en substitutie hiervan in (5a) levert b = (4/3)∙c en dus hebben we n = (2c, (4/3)∙c, c). Kiezen we nu bijvoorbeeld c = 3, dan krijgen we n = (6, 4, 3). Op grond van (3) wordt de cartesische vergelijking van je vlak V nu:
(6) 6(x - 2) + 4(y - 0) + 3(z - 0) = 0,
en uitwerken hiervan geeft:
(7) 6x + 4y + 3z = 12
Je kunt nu door invullen gemakkelijk controleren dat de coördinaten van de punten A, B en C inderdaad aan (7) voldoen. Overigens hadden we in dit speciale geval de vergelijking van het vlak direct uit het hoofd kunnen opschrijven in de vorm (1/2)∙x + (1/3)∙y + (1/4)∙z = 1 omdat van elk van de drie gegeven punten A resp. B resp. C alleen de x- resp. y- resp. z-coördinaat ongelijk is aan nul. Maar in het algemeen is dat uiteraard niet zo als je de cartesische vergelijking van een vlak door drie gegeven punten op moet stellen.
[ Bericht 1% gewijzigd door Riparius op 12-05-2012 02:21:53 ]


Het is niet het superscript van de formulequote:Op donderdag 10 mei 2012 18:39 schreef Riparius het volgende:
[..]
Als je met die 10 het grondtal bedoelt van de logaritme, dan moet je dat wel superscripten, anders sticht je alleen maar verwarring. Dus:
L = 10log(I/I0)
Verder kun je gewoon gebruik maken van de definitie van de logaritme: glog a is de exponent waartoe je g moet verheffen om a te verkrijgen. Hier is L dus de macht waartoe je 10 moet verheffen om I/I0 te verkrijgen:
10L = I/I0


Ik begrijp niet wat je bedoelt, en in ieder geval sticht je verwarring, precies zoals ik al zei. Als je 10 een factor is dan moet je 10∙log(I/I0) schrijven en ook het grondtal van je logaritme specificeren, want het symbool log is ambigu.quote:Op vrijdag 11 mei 2012 22:11 schreef TheDutchguy het volgende:
[..]
Het is niet het superscript van de formule


Ik schreef de formule precies over uit mijn BINAS. Ik ga er in ieder geval van uit dat het 10 * is, maar is ook niet duidelijk aangegeven. Er staat L = 10 log(I/I0)quote:Op vrijdag 11 mei 2012 22:19 schreef Riparius het volgende:
[..]
Ik begrijp niet wat je bedoelt, en in ieder geval sticht je verwarring, precies zoals ik al zei. Als je 10 een factor is dan moet je 10∙log(I/I0) schrijven en ook het grondtal van je logaritme specificeren, want het symbool log is ambigu.


Je moet inderdaad met 10 vermenigvuldigen (en 10 is ook het grondtal geloof ik) om het geluidsniveau in dB (deciBell) te krijgen. Als je die 10 weglaat krijg je het in B (Bell).


Goed. Aangenomen dat Briggse logaritmen (grondtal 10) bedoeld zijn krijgen we dan:quote:Op vrijdag 11 mei 2012 22:50 schreef TheDutchguy het volgende:
[..]
Ik schreef de formule precies over uit mijn BINAS. Ik ga er in ieder geval van uit dat het 10 * is, maar is ook niet duidelijk aangegeven. Er staat L = 10 log(I/I0)
I = I0∙10L/10
Wat is hier nu moeilijk aan?




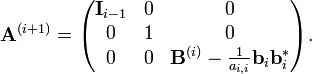
 opgave 15 en 16.
opgave 15 en 16.