SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



De beste opgaves zijn hordes vol algebra van een schijnbaar eenvoudige opgave. Zoals die bol, ik dacht serieus: Dat wordt peanuts.quote:Op maandag 21 mei 2012 18:43 schreef thenxero het volgende:
[..]
De leukste opgaves vind ik toch eigenlijk opgaves waarbij je weinig algebra nodig hebt, maar het probleem gewoon heel handig moet aanpakken waardoor een schijnbaar onmogelijk probleem opeens heel eenvoudig wordt.
Zelfs beide Wiskunde docenten op het VWO hier kennen die formule niet... (Calando)


Zodat je hem kan invullen... bijvoorbeeld als volgt:quote:Op maandag 21 mei 2012 19:26 schreef Amoeba het volgende:
[..]
Waarom maar dan ook waarom zou je a eruit halen?
(noteer even x=2/sqrt(29))
Poepoe, wat een typwerk
Ik maak dus gebruik van sin(arccos(x))=sqrt(1-x^2). Dat kan je bewijzen met sin≤ z + cos≤ z =1 en dan z=arcos(x) te nemen.
[ Bericht 3% gewijzigd door thenxero op 21-05-2012 19:47:48 ]


Cardano. En ze hebben er hopelijk wel van gehoord, maar kennen het niet uit hun hoofd. De meeste wiskundeprofessors zullen die formule ook niet uit hun hoofd kennenquote:Op maandag 21 mei 2012 19:38 schreef Amoeba het volgende:
[..]
Zelfs beide Wiskunde docenten op het VWO hier kennen die formule niet... (Calando)


Oh, heet die gast Cardano.
Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.
Maar het zal ongetwijfeld kloppen! 2/r29 komt inderdaad heel bekend voor
Trouwens, de app van Wolframalpha voor Android is ook wel echt geil.
[ Bericht 13% gewijzigd door #ANONIEM op 21-05-2012 19:55:11 ]
Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.
Maar het zal ongetwijfeld kloppen! 2/r29 komt inderdaad heel bekend voor
Trouwens, de app van Wolframalpha voor Android is ook wel echt geil.
[ Bericht 13% gewijzigd door #ANONIEM op 21-05-2012 19:55:11 ]


Ja die gast heet Cardano. Ook wel grappig dat vanwege die formule de imaginaire getallen "in" zijn geraakt. Want toen realiseerde men zich dat imaginaire getallen wel degelijk betekenis/nut hadden, omdat het kan gebeuren dat je met die formule negatieve getallen in de wortel kan krijgen, terwijl de oplossing toch reŽel is.quote:Op maandag 21 mei 2012 19:51 schreef Amoeba het volgende:
Oh, heet die gast Cardano.
Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.
Maar het zal ongetwijfeld kloppen! 2/r29 komt inderdaad heel bekend voor
Er zijn inderdaad meerdere manieren (zoals wel vaker met gonio). Je zou bijvoorbeeld alles als sin kunnen schrijven, en dan krijg je een kwadratische vergelijking in termen van sinus.


Meh, ik zat in de trein, maar ik heb hier op papier dezelfde berekening staanquote:Op maandag 21 mei 2012 19:42 schreef thenxero het volgende:
[..]
Zodat je hem kan invullen... bijvoorbeeld als volgt:
(noteer even x=2/sqrt(29))
Poepoe, wat een typwerk
Ik maak dus gebruik van sin(arccos(x))=sqrt(1-x^2). Dat kan je bewijzen met sin≤ z + cos≤ z =1 en dan z=arcos(x) te nemen.


stukje inleiding: Van een parabolŲide is de straal a en de hoogte 3a. De inhoud is te berekenen met de formule inhoud = 4,71a≥ (tot de macht 3 voor degene die het niet kunnen lezen)
vraag: Bereken de inhoud in cm≥ van een parabolŲide met een hoogte van 12 cm en een straal van 4 cm. Rond af op twee decimalen.
Hier snap ik werkelijk geen kut van, dus als iemand mij wil helpen, graag!
vraag: Bereken de inhoud in cm≥ van een parabolŲide met een hoogte van 12 cm en een straal van 4 cm. Rond af op twee decimalen.
Hier snap ik werkelijk geen kut van, dus als iemand mij wil helpen, graag!


a=4, en invullenquote:Op maandag 21 mei 2012 21:17 schreef Wicky15 het volgende:
stukje inleiding: Van een parabolŲide is de straal a en de hoogte 3a. De inhoud is te berekenen met de formule inhoud = 4,71a≥ (tot de macht 3 voor degene die het niet kunnen lezen)
vraag: Bereken de inhoud in cm≥ van een parabolŲide met een hoogte van 12 cm en een straal van 4 cm. Rond af op twee decimalen.
Hier snap ik werkelijk geen kut van, dus als iemand mij wil helpen, graag!


Van een parabolŲide is de hoogte drie keer de straal. De inhoud is 185 cm≥.
Bereken de straal van de parabolŲide in mm.
Deze weet ik ook niet..
Bereken de straal van de parabolŲide in mm.
Deze weet ik ook niet..


een paraboloÔde is een parabool die om de y-as is gewenteld?quote:Op maandag 21 mei 2012 21:26 schreef Wicky15 het volgende:
Van een parabolŲide is de hoogte drie keer de straal. De inhoud is 185 cm≥.
Bereken de straal van de parabolŲide in mm.
Deze weet ik ook niet..


4,71a≥ = 185 en dan oplossen voor a, en a is de straal (in cm).quote:Op maandag 21 mei 2012 21:26 schreef Wicky15 het volgende:
Van een parabolŲide is de hoogte drie keer de straal. De inhoud is 185 cm≥.
Bereken de straal van de parabolŲide in mm.
Deze weet ik ook niet..


Yup.quote:Op maandag 21 mei 2012 21:27 schreef Don_Vanelli het volgende:
[..]
een paraboloÔde is een parabool die om de y-as is gewenteld?


Ja. En ik denk dat ie bedoelt dat ie afgezaagd wordt op een hoogte 3a en dat de straal daar dan a is.quote:Op maandag 21 mei 2012 21:27 schreef Don_Vanelli het volgende:
[..]
een paraboloÔde is een parabool die om de y-as is gewenteld?


Ergens vrees ik dan datquote:Op maandag 21 mei 2012 21:30 schreef thenxero het volgende:
[..]
Ja. En ik denk dat ie bedoelt dat ie afgezaagd wordt op een hoogte 3a en dat de straal daar dan a is.


Die klopt ook. Hartstikke bedanktquote:Op maandag 21 mei 2012 21:28 schreef thenxero het volgende:
[..]
4,71a≥ = 185 en dan oplossen voor a, en a is de straal (in cm).


Ik zit in havo3, dit gaat me iets te verquote:Op maandag 21 mei 2012 21:40 schreef Don_Vanelli het volgende:
[..]
Behalve dan dat de inhoud van een dergelijk object wordt gegeven door


Kan er iemand mij even helpen met het root denesting algoritme?
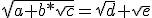
Kwadrateren levert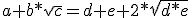
Nu het rationale deel in irrationale deel afzonderlijk links en rechts van de vgl. aan elkaar gelijk stellen:
a = d + e
en vervolgens loop ik hier vast:
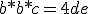
Wiki zegt vervolgens: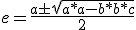
Ik zie de gemaakte stappen to-taal niet, sorry....
[ Bericht 8% gewijzigd door VanishedEntity op 21-05-2012 22:02:00 ]
Kwadrateren levert
Nu het rationale deel in irrationale deel afzonderlijk links en rechts van de vgl. aan elkaar gelijk stellen:
a = d + e
en vervolgens loop ik hier vast:
Wiki zegt vervolgens:
Ik zie de gemaakte stappen to-taal niet, sorry....
[ Bericht 8% gewijzigd door VanishedEntity op 21-05-2012 22:02:00 ]


Kies wiskunde B, doe daarna het vwo, dan zie je het vanzelfquote:Op maandag 21 mei 2012 21:46 schreef Wicky15 het volgende:
[..]
Ik zit in havo3, dit gaat me iets te ver


http://en.wikipedia.org/w(...)ting_nested_radicalsquote:Op maandag 21 mei 2012 21:48 schreef VanishedEntity het volgende:
Kan er iemand mij even helpen met het root denesting algoritme?
Kwadrateren levert
Nu het rationale deel in irrationale deel afzonderlijk links en rechts van de vgl. aan elkaar gelijk stellen:
a = d + e
en vervolgens loop ik hier vast:


Uhuquote:Op maandag 21 mei 2012 18:43 schreef thenxero het volgende:
[..]
De leukste opgaves vind ik toch eigenlijk opgaves waarbij je weinig algebra nodig hebt, maar het probleem gewoon heel handig moet aanpakken waardoor een schijnbaar onmogelijk probleem opeens heel eenvoudig wordt.
Een tijdje geleden zat ik ook wat te rekenen met formules van de vorm:
En tot mijn stomme verbazing lukte het om een recurrente formule te geven voor de coŽfficienten van een polynoom in n met graad m + 1, zodat deze polynoom voor elke waarde (>= 0) dezelfde waarde heeft als de som.
Nu kan dit ook door gewoon de waardes die de som aanneemt te observeren en een polynoom van graad m + 1 te zoeken die de dezelfde waardes aanneemt, maar ik vond het toch een mooi resultaat


Helemaal mee eens. Heeft iemand voor de grap zelf de afleiding voor het getal van de ossen wel eens opgeschreven? Ik ga er persoonlijk niet aan beginnen, kost me teveel inkt 


ja zo ver was ik al... Ik zie alleen even niet hoe ze vanquote:Op maandag 21 mei 2012 21:53 schreef Don_Vanelli het volgende:
[..]
http://en.wikipedia.org/w(...)ting_nested_radicals
naar
gaan.


Deze laat ik lopen.... misschien iets voor Ripariusquote:Op maandag 21 mei 2012 22:02 schreef Don_Vanelli het volgende:
Helemaal mee eens. Heeft iemand voor de grap zelf de afleiding voor het getal van de ossen wel eens opgeschreven? Ik ga er persoonlijk niet aan beginnen, kost me teveel inkt


quote:Op maandag 21 mei 2012 22:05 schreef VanishedEntity het volgende:
[..]
ja zo ver was ik al... Ik zie alleen even niet hoe ze van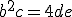
naar
gaan.
dus krijg je:
en dan is het slechts een kwestie van het oplossen van een kwadratische vergelijking


damn, you beat me to it; had net al d=a-e en e=a-d op papier gezet...
Thnx enniewee, vanaf hier is het een koud kunstje.
Thnx enniewee, vanaf hier is het een koud kunstje.


Pfoeh, ik ben er voor de lol aan begonnen, maar ik begin in te zien dat dit erg veel werk ik, en de kudde waarschijnlijk niet bepaald klein isquote:Op maandag 21 mei 2012 22:02 schreef Don_Vanelli het volgende:
Helemaal mee eens. Heeft iemand voor de grap zelf de afleiding voor het getal van de ossen wel eens opgeschreven? Ik ga er persoonlijk niet aan beginnen, kost me teveel inkt
Ik moet nog even kijken hoeveel ik er nog aan verder ga werken..
26"
Fading slowly.
Fading slowly.


Ja. Voor Calando kun je beter bij je muziekdocent terechtquote:
Over de manier waarop Cardano de formule te pakken kreeg en alle intriges en geheimzinnigdoenerij zou een prachtige film (ŗ la The Name of the Rose) zijn te maken. Voor een stukje geschiedenis over hoe complexe getallen werden ontdekt door problemen met het oplossen van kubische vergelijkingen moet je dit maar eens lezen.
Een kubische vergelijking met reŽle coŽfficienten en drie verschillende louter reŽle wortels kun je niet echt oplossen met Cardano omdat je de oplossingen dan alleen uit kunt drukken met behulp van derdemachtswortels uit complexe getallen die je niet algebraÔsch kunt herleiden. Als de kubische vergelijking ťťn reŽle en twee toegevoegd complexe wortels heeft dan lukt het wel.quote:Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.


Ja. Maar ik begrijp nog steeds niet waarom je met de hoek ϕ die een straal naar de snijcirkel maakt met het grondvlak van de halve bol wilde werken. Gevraagd werd immers naar de afstand h van het deelvlak tot het grondvlak om de halve bol in twee delen met gelijke volumes te verdelen, en dan ligt het toch wel ťrg voor de hand om dat als parameter te nemen. Met behulp van de bekende formule voor het volume van een omwentelingslichaam kom je dan direct op h3 - 3h + 1 = 0 uit.quote:Op maandag 21 mei 2012 17:05 schreef thenxero het volgende:
[..]
Dan kom ik inderdaad ook uit op q≥-3q+1=0 met q=sin(p).
Dat heb ik al uitgelegd: in de correcte drievoudige integraal zit een dubbelintegraal die niets meer doet dan de oppervlakte van een cirkel met straal r uitdrukken. Heb ik geen Jacobiaan voor nodig.quote:Ik snap hoe je die enkele integraal bepaalt, maar ik snap niet wat er mis was met mijn redenatie en hoe jij aan de correcte drievoudige integraal bent gekomen (ik zie bijvoorbeeld de jacobiaan niet meer terug).
Wat er mis is, is dat je een verkeerde integrand gebruikt als gevolg van verwarring over wat θ en ϕ precies voorstellen.
Ja. Dit klopt ook en uiteraard is dit met een drievoudige integraal in bolcoŲrdinaten uit te rekenen. Maar laten we eerst eens nagaan wat er uit zou moeten komen.quote:Ik beweer dat { (r,θ,ϕ) : 0<r<1, 0<θ<2pi, 0<ϕ<p } gelijk is aan de verzameling van de afgezaagde bovenhelft van de bol minus de kegel. Zie plaatje.
[ afbeelding ]
Voor het volume van het bolsegment hadden we (na herleiding) al gevonden dat dit gelijk is aan:
(1) π∙sin p - (1/3)∙π∙sin3p
Het volume van de kegel in je figuur is natuurlijk eenvoudig te bepalen. De oppervlakte van het grondvlak is π∙cos2p = π∙(1 - sin2p) en de hoogte is sin p, zodat het volume van de kegel dus wordt:
(2) (1/3)∙π∙sin p - (1/3)∙π∙sin3p
Het volume dat je nu wil berekenen is het verschil van (1) en (2), en dit is dus eenvoudig:
(3) (2/3)∙π∙sin p
Goed, nu we weten wat er uit moet komen hebben we een controlemogelijkheid. Ik moet bekennen dat dit mij ook wat hoofdbrekens opleverde. Voor een volume elementje dV hebben we bij gebruik van bolcoŲrdinaten volgens Wikipedia (link):
(4) dV = r2∙sin θ∙dr∙dθ∙dϕ
Maar nu begint het grote verwarringsspel, want hier stelt niet ϕ maar θ de inclinatie voor, terwijl jij daarvoor ϕ gebruikt. Dus moeten we de rollen van θ en ϕ omwisselen en krijgen we:
(5) dV = r2∙sin ϕ∙dr∙dϕ∙dθ
Zijn we er nu? Nee, want hier stelt ϕ de inclinatie t.o.v. de normaal voor, terwijl bij jou ϕ de inclinatie t.o.v. het grondvlak voorstelt. Dus moeten we hier ϕ vervangen door ½π - ϕ en hebben we sin(½π - ϕ) = cos ϕ, zodat we voor jouw berekening krijgen:
(6) dV = r2∙cos ϕ∙dr∙dϕ∙dθ
En hiervoor mag ik ook schrijven:
(7) dV = r2∙cos ϕ∙dr∙dθ∙dϕ
De integraal voor je volume wordt nu:
(8) ∫0p ∫02π ∫01 r2∙cos ϕ∙dr∙dθ∙dϕ
Zoals je in WolframAlpha kunt nagaan (weer met f voor ϕ) levert dit inderdaad (2/3)∙π∙sin p op. Het klopt dus als een bus.


Wat nog minder bekend schijnt te zijn (maar vroeger gewoon standaard stof was) is dat je elke gereduceerde kubische vergelijking met uitsluitend reŽle wortels op kunt lossen zonder Cardano en zonder complexe getallen. Onder een gereduceerde kubische vergelijking verstaan we een derdegraadsvergelijking waarin de kwadratische term ontbreekt. Je kunt elke kubische vergelijking gemakkelijk herleiden tot zo'n gereduceerde vergelijking door een geschikte lineaire substitutie uit te voeren.quote:Op maandag 21 mei 2012 19:38 schreef Amoeba het volgende:
[..]
De beste opgaves zijn hordes vol algebra van een schijnbaar eenvoudige opgave. Zoals die bol, ik dacht serieus: Dat wordt peanuts.
Zelfs beide Wiskunde docenten op het VWO hier kennen die formule niet... (Cardano)
De methode berust op de goniometrische identiteit voor de cosinus van de drievoudige hoek:
cos 3φ = 4∙cos3φ - 3∙cos φ
Ik neem als voorbeeld nog even de inmiddels bekende vergelijking:
z3 - 3z + 1 = 0
We brengen eerst de constante term naar het rechterlid:
z3 - 3z = -1
Het idee is nu dat we een substitutie z = r∙cos φ uitvoeren en dan het linkerlid omwerken tot 4∙cos3φ - 3∙cos φ, want dat is immers gelijk aan cos 3φ. Substitutie geeft:
r3∙cos3φ - 3∙r∙cos φ = -1
Nu willen we links een term 4∙cos3φ hebben, dus delen we beide leden door r3 en vermenigvuldigen we beide leden met 4. Dit geeft:
4∙cos3φ - (12/r2)∙cos φ = -4/r3
De eerste term in het linkerlid is nu in orde, maar nu moeten we nog zorgen dat de tweede term in het linkerlid gelijk wordt aan - 3∙cos φ en dat kunnen we doen door een geschikte waarde voor r te kiezen. We willen dat 12/r2 gelijk wordt aan 3, en dus kunnen we r = 2 nemen. Dit geeft:
4∙cos3φ - 3∙cos φ = -1/2
En dus:
cos 3φ = -1/2
Nu zien we dat 3φ = (2/3)∙π + 2∙k∙π en dus φ = (2/9)∙π + (2/3)∙k∙π, k ∈Z. We zouden ook de tegengestelde waarden voor φ kunnen nemen, maar dat maakt niets uit omdat de cosinus een even functie is. Aangezien z = r∙cos φ en r = 2 vinden we zo met k = 0, 1, 2 de wortels:
z1 = 2∙cos((2/9)∙π), z2 = 2∙cos((8/9)∙π), z3 = 2∙cos((14/9)∙π)
Met drie opeenvolgende waarden van k zijn we 'rond' en hebben we dus alle drie de wortels gevonden. Hiermee is de vergelijking opgelost.


De (schijnbaar) complexe oplossing van cardano kan ook vrij gemakkelijk naar complexe e-machten worden ongeschreven. Vanuit daar kom je ook aan de correcte oplossing. Dat is wat meer op de automatische piloot ipv goniometrische entiteiten te kennen.


Uiteraard is mij dat bekend. En er zijn nog meer varianten, bijvoorbeeld gebruik van een hyperbolische substitutie. Maar ik vond het vooral voor schoolgebruik aardig om eens te laten zien dat het met een beetje elementaire goniometrie en zonder kennis van complexe getallen ook prima gaat. Zo werd het vroeger ook meestal geleerd, toen er nog geen rekenmachines of computers bestonden en je het moest doen met goniometrische tafels.quote:Op dinsdag 22 mei 2012 07:34 schreef Don_Vanelli het volgende:
De (schijnbaar) complexe oplossing van cardano kan ook vrij gemakkelijk naar complexe e-machten worden ongeschreven. Vanuit daar kom je ook aan de correcte oplossing. Dat is wat meer op de automatische piloot ipv goniometrische identiteiten te kennen.


Ik snapte niet exact wat je deed, totdat ik het een tweede keer las. Die moet ik onthouden.quote:Op dinsdag 22 mei 2012 07:49 schreef Riparius het volgende:
[..]
Uiteraard is mij dat bekend. En er zijn nog meer varianten, bijvoorbeeld gebruik van een hyperbolische substitutie. Maar ik vond het vooral voor schoolgebruik aardig om eens te laten zien dat het met een beetje elementaire goniometrie en zonder kennis van complexe getallen ook prima gaat. Zo werd het vroeger ook meestal geleerd, toen er nog geen rekenmachines of computers bestonden en je het moest doen met goniometrische tafels.
4cos3x - 3cosx = cos3x


Je kunt de identiteit voor cos 3φ ook gewoon afleiden door uit te gaan van cos 2φ = 2∙cos2φ - 1 en sin 2φ = 2∙sinφ∙cosφ en cos 3φ = cos(2φ + φ) te herleiden met het bekende additietheorema cos(α + β) = cos α∙cos β - sin α∙sin β.quote:Op dinsdag 22 mei 2012 08:12 schreef Amoeba het volgende:
[..]
Ik snapte niet exact wat je deed, totdat ik het een tweede keer las. Die moet ik onthouden.
4cos3x - 3cosx = cos3x
Of, gebruik de formule van De Moivre (cos φ + i∙sinφ)n = cos nφ + i∙sin nφ met n = 3, dan krijg je als bonus ook meteen sin 3φ = 3∙sin φ - 4∙sin3φ.


Goed, ik ging nu uit van de functie 6x3 -4x = 9
Dus x substitueren naar rcosx
(Dit had beter rcosa kunnen zijn omdat x al een variabele is ja, maar dat doet er nu even niet toe.)
dus 6r3cos3x -4rcosx = 9
Delen door 6r3
cos3x - (2/3)/r2cosx = 1,5/r 3
Vermenigvuldigen met 4, even r uitrekenen.
r = 2/3 * √2
Enfin, dan staat mijn vergelijking dus:
cos3x = 81 / 8√2
Wat doe ik fout/hoe moet ik verder?
De functie heeft ťťn oplossing.
Ook cos3x = 81 / 8√2 heeft uiteraard geen oplossingen.
Of de functie f(x) = 15x 3+12x +7
Zelfde manier:
r = 4i/√15
cos3a= 7√15 / 16i
[ Bericht 2% gewijzigd door #ANONIEM op 22-05-2012 10:30:45 ]
Dus x substitueren naar rcosx
(Dit had beter rcosa kunnen zijn omdat x al een variabele is ja, maar dat doet er nu even niet toe.)
dus 6r3cos3x -4rcosx = 9
Delen door 6r3
cos3x - (2/3)/r2cosx = 1,5/r 3
Vermenigvuldigen met 4, even r uitrekenen.
r = 2/3 * √2
Enfin, dan staat mijn vergelijking dus:
cos3x = 81 / 8√2
Wat doe ik fout/hoe moet ik verder?
De functie heeft ťťn oplossing.
Ook cos3x = 81 / 8√2 heeft uiteraard geen oplossingen.
Of de functie f(x) = 15x 3+12x +7
Zelfde manier:
r = 4i/√15
cos3a= 7√15 / 16i
[ Bericht 2% gewijzigd door #ANONIEM op 22-05-2012 10:30:45 ]


even een vraag hier.
Een konijn uit denemarken sprong vorig jaar volgens het volgende model:
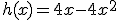
h = de hoogte in meters van de grond en x is de afstand in meters langs de grond vanaf het punt waar het konijn de lucht in sprong.
Hoe hoog kwam het konijn?
ik kom er maar niet uit, ik denk dat ik deze formule moet gebruiken maar hoe is me een raadsel:
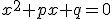
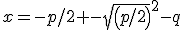
Een konijn uit denemarken sprong vorig jaar volgens het volgende model:
h = de hoogte in meters van de grond en x is de afstand in meters langs de grond vanaf het punt waar het konijn de lucht in sprong.
Hoe hoog kwam het konijn?
ik kom er maar niet uit, ik denk dat ik deze formule moet gebruiken maar hoe is me een raadsel:
Winnaar KLB verkiezingen 2012.


Je begint gewoon met het berekenen van de eerste afgeleide:
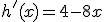
Maximum vinden we wanneer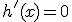
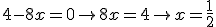
Dus het antwoord is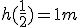
Maximum vinden we wanneer
Dus het antwoord is


Thanks !quote:Op dinsdag 22 mei 2012 15:50 schreef zoem het volgende:
Je begint gewoon met het berekenen van de eerste afgeleide:
Maximum vinden we wanneer
Dus het antwoord is
Winnaar KLB verkiezingen 2012.


Aaaah, daar liep het dus op stuk. Bedankt!quote:Op dinsdag 22 mei 2012 03:09 schreef Riparius het volgende:
[..]
Zijn we er nu? Nee, want hier stelt ϕ de inclinatie t.o.v. de normaal voor, terwijl bij jou ϕ de inclinatie t.o.v. het grondvlak voorstelt.
Dat is simpelweg het eerste waar ik aan dacht, en het is op zich niet zoveel moeilijker dan dat wentelen, als je geen gekke fouten gaat makenquote:Ja. Maar ik begrijp nog steeds niet waarom je met de hoek ϕ die een straal naar de snijcirkel maakt met het grondvlak van de halve bol wilde werken.


Dit is een vergelijking, geen functie. Wat je verder fout doet is dat je mijn uitleg kennelijk toch niet goed genoeg hebt gelezen. De goniometrische oplossingsmethode voor gereduceerde kubische vergelijkingen werkt alleen als de vergelijking uitsluitend reŽle wortels heeft, en dat is hier niet het geval.quote:Op dinsdag 22 mei 2012 09:32 schreef Amoeba het volgende:
Goed, ik ging nu uit van de functie 6x3 -4x = 9
Dus x substitueren naar rcosx
(Dit had beter rcosa kunnen zijn omdat x al een variabele is ja, maar dat doet er nu even niet toe.)
dus 6r3cos3x -4rcosx = 9
Delen door 6r3
cos3x - (2/3)/r2cosx = 1,5/r 3
Vermenigvuldigen met 4, even r uitrekenen.
r = 2/3 * √2
Enfin, dan staat mijn vergelijking dus:
cos3x = 81 / 8√2
Wat doe ik fout/hoe moet ik verder?
De functie heeft ťťn oplossing.
Om vooraf te zien of een gereduceerde kubische vergelijking met reŽle coŽfficiŽnten uitsluitend reŽle wortels heeft of niet kun je kijken naar de discriminant van de vergelijking.
Hebben we de vergelijking:
z3 + pz + q = 0,
dan is de discriminant:
D = (p/3)3 + (q/2)2,
wat uiteraard makkelijk is te onthouden.
Je hebt nu de volgende mogelijkheden:
D > 0: Eťn reŽle wortel en twee toegevoegd complexe wortels.
D = 0: Drie reŽle wortels waarvan er (tenminste) twee samenvallen.
D < 0: Drie reŽle wortels.
Let erop dat dit anders is dan bij vierkantsvergelijkingen, daar heb je geen reŽle wortels als de discriminant negatief is, hier zijn de wortels dan juist uitsluitend reŽel.
Alleen als D ≤ 0 kun je de goniometrische oplossingsmethode toepassen. Je kunt dat ook nagaan door de algemene vergelijking z3 + pz + q = 0 goniometrisch op te lossen. Aangezien de cosinus functie alleen waarden aanneemt op het interval [-1,1] en dus moet gelden | cos 3φ | ≤ 1 vindt je dan een conditie voor p en q die equivalent is met D ≤ 0. Daaruit volgt dat het dus inderdaad altijd mogelijk is de vergelijking goniometrisch op te lossen als de wortels louter reŽel zijn. Is dat niet het geval dan zijn er nog wel andere mogelijkheden, zoals het gebruik van een hyperbolische substitutie, maar dat zou nu wat te ver voeren.
Is D > 0, dan bereken je:
u3 = -½q + √D en v3 = -½q - √D
Nu heb je ťťn reŽle waarde van u en ťťn reŽle waarde van v die je kunt berekenen. De drie wortels van de vergelijking zijn dan:
z1 = u + v
z2 = ε1∙u + ε2∙v
z3 = ε2∙u + ε1∙v,
waarin ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3.
Zoals je ziet is dan z1 de reŽle wortel en zijn z2 en z3 de toegevoegd (geconjugeerde) complexe wortels. Het is dus helemaal niet moeilijk om kubische vergelijkingen op te lossen (en ja, ik schrijf deze hele post gewoon op uit het hoofd).


Nouja, de functie was f(x). Ik had hem al omgebouwd tot de 'vergelijking' die je daar zag.
Maargoed, ik zal eens aan de gang gaan. Nog een kort vraagje:
Dit zijn altijd 'de sleutels' om tot de wortels te komen? Het is me niet helemaal duidelijk hoe je tot dit antwoord komt:
ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3.
Bonusvraagje: Hebben jullie iets handigs voor die latexcode? De link in de OP werkt niet meer, en al die symbolen zo is een beetje moeilijk om uit het hoofd te leren.
[ Bericht 24% gewijzigd door #ANONIEM op 22-05-2012 20:44:15 ]
Maargoed, ik zal eens aan de gang gaan. Nog een kort vraagje:
Dit zijn altijd 'de sleutels' om tot de wortels te komen? Het is me niet helemaal duidelijk hoe je tot dit antwoord komt:
ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3.
Bonusvraagje: Hebben jullie iets handigs voor die latexcode? De link in de OP werkt niet meer, en al die symbolen zo is een beetje moeilijk om uit het hoofd te leren.
[ Bericht 24% gewijzigd door #ANONIEM op 22-05-2012 20:44:15 ]


Deze komt niet 'mooi' uit maar ik zal hem toch even voordoen. Rechterlid herleiden op nul geeft:quote:Op dinsdag 22 mei 2012 09:32 schreef Amoeba het volgende:
Goed, ik ging nu uit van de vergelijking 6x3 - 4x = 9
6x3 - 4x - 9 = 0
Nu beide leden delen door zes om de coŽfficient van x3 gelijk te maken aan ťťn:
x3 - (2/3)∙x -(3/2) = 0
We hebben p = -2/3 en q = -3/2, en dus is D = (-2/9)3 + (-3/4)2 = -8/729 + 16/9 = 6433/11664 > 0, zodat er ťťn reŽle wortel is (en twee toegevoegd complexe wortels). Merk op dat 11664 = 1082. De reŽle wortel is:
x = (3/4 + (1/108)∙√6433)1/3 + (3/4 - (1/108)∙√6433)1/3
Als je dit in WolframAlpha berekent, zie je dat het klopt met wat je numeriek met je GR of zo kunt vinden, maar dit is de exacte reŽle wortel. Wolfram heeft zelfs in de gaten dat 6x3 - 4x - 9 het minimale polynoom is voor deze wortel.


Ja, dit geldt altijd. Die ε1 en ε2 zijn de twee complexe derdemachtswortels van ťťn. Dat kun je gemakkelijk controleren door ε13 en ε23 te berekenen. En er geldt ook ε1ε2 = 1.quote:Op dinsdag 22 mei 2012 20:37 schreef Amoeba het volgende:
Nouja, de functie was f(x). Ik had hem al omgebouwd tot de 'vergelijking' die je daar zag.
Maargoed, ik zal eens aan de gang gaan. Nog een kort vraagje:
Dit zijn altijd 'de sleutels' om tot de wortels te komen? Het is me niet helemaal duidelijk hoe je tot dit antwoord komt:
ε1 = -½ + i∙½√3 en ε2 = -½ - i∙½√3.
Zijn nu u en v de reŽle waarden die voldoen aan u∙v = -p/3, dan zal het product (ε1∙u)∙(ε2∙v) en het product (ε2∙u)∙(ε1∙v)
dus ook gelijk zijn aan -p/3 zodat deze combinaties ook voldoen en daarmee de twee andere (toegevoegd complexe) wortels opleveren.


Ah, nu weet ik weer wat er aan de hand was. Uiteindelijk kwam je uit op cos2a = 4/29quote:Op maandag 21 mei 2012 21:24 schreef Don_Vanelli het volgende:
Voor de volledigheid: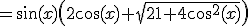
Differentieren geeft(1)
geeft:
dus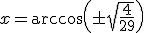
voldoet niet aan (1), dus
Nou, cosa = 2/√29
Dus kun je even een driehoek opstellen (soscastoa.. basisschool als je 't mij vraagt!)
dus de aanliggende zijde is 2, de schuine zijde √29
Een eenvoudig rekensommetje (Pythagoras) wijst dan uit dat de andere zijde uiteraard 5 is. Nu is het uiteraard alweer mogelijk om op basis van beredeneren te bewijzen dat de maximale oppervlakte 5 is. .Maargoed, wat we ook kunnen doen is nu de sinus uitdrukken. 5/√29
Nou goed, cosa = 2/√29 en sina = 5/√29
Vul dit in: komt perfect uit
Want sin2a = 2cosa*sina
[ Bericht 0% gewijzigd door #ANONIEM op 22-05-2012 21:04:39 (Typo) ]


Stiekem gebruikten wij ook de stelling van Pythagoras, maar dan in de vorm sin≤+cos≤=1. Komt dus op hetzelfde neer.quote:Op dinsdag 22 mei 2012 21:03 schreef Amoeba het volgende:
[..]
Ah, nu weet ik weer wat er aan de hand was. Uiteindelijk kwam je uit op cos2a = 4/29
Nou, cosa = 2/√29
Dus kun je even een driehoek opstellen (soscastoa.. basisschool als je 't mij vraagt!)
dus de aanliggende zijde is 2, de schuine zijde √29
Een eenvoudig rekensommetje (Pythagoras) wijst dan uit dat de andere zijde uiteraard 5 is. Nu is het uiteraard alweer mogelijk om op basis van beredeneren te bewijzen dat de maximale oppervlakte 5 is. .Maargoed, wat we ook kunnen doen is nu de sinus uitdrukken. 5/√29
Nou goed, cosa = 2/√29 en sina = 5/√29
Vul dit in: komt perfect uit
Want sin2a = 2cosa*sina

