Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
[ Bericht 95% gewijzigd door GlowMouse op 09-03-2010 09:38:26 ]
quote:Inderdaad, maar als jij een driehoek hebt met een cirkel eromheen dan ligt het voor de hand om het eindpunt van een straal samen te laten vallen met een hoekpunt van je driehoek. En dan heb je maar drie mogelijkheden om twee stralen weer te geven.Op vrijdag 5 februari 2010 22:46 schreef gaussie het volgende:
Maar het hangt toch af waar je die twee stralen tekent? Je hoeft toch geen gelijkzijdige te krijgen?
quote:
quote:Dat is mijn conclusie niet. Maak eens een paint.Op vrijdag 5 februari 2010 22:53 schreef gaussie het volgende:
Het blijft onduidelijk voor mij. Van welke axioma, definitie of stelling maak je gebruik om te beweren dat hoek c 60 graden is?
quote:Je praat makkelijker over een hoek als je hem ook kunt zien, zeker als de betreffende hoek niet in het verhaal genoemd wordt.
quote:Ik heb niet het idee dat je nou erg je best doet om het antwoord logisch te beredeneren aan de hand van een figuur. En zo doe je je nick geen eer aan ...Op vrijdag 5 februari 2010 23:11 schreef gaussie het volgende:
Ik heb het geprobeerd te tekenen, schijnbaar doe ik iets fout. Kun je gewoon het antwoord geven en de intuitie daarachter? Zoniet dan wacht ik wel tot iemand anders het juiste antwoord kan geven....
Maar vooruit, ik ga je even op weg helpen.
Gegeven is een driehoek ABC. Noem het snijpunt van de middelloodlijnen O, dit is dan het middelpunt van de omgeschreven cirkel, en dus geldt:
OA = OB = OC = r,
waarbij r de straal is van de omgeschreven cirkel. Nu is echter ook gegeven AB = r, en dus is
OA = OB = AB,
zodat driehoek OAB gelijkzijdig is.
De som van de hoeken van een driehoek is 180 graden, en dus geldt voor driehoek ABC:
∠CAB + ∠ABC + ∠BCA = 180°
Maar nu wordt elk van de drie hoeken door de lijnstukken vanaf de hoekpunten A,B,C naar O in twee delen verdeeld. Kijk nu eens naar deze zes hoeken en wat je daar over kunt zeggen.
quote:Omdat we de indruk hebben dat je niet erg veel moeite doet om zelf na te denken. Maar je wil een kant en klaar antwoord, nou dat kan.Op vrijdag 5 februari 2010 23:39 schreef gaussie het volgende:
Prima dat jullie me dwingen om zelf over de oplossing na te denken, maar andere mensen hier krijgen gewoon een kant en klaar antwoord. Snap niet waarom dit niet in mijn geval gebeurt....
Als je het goed doet, moet je kunnen beredeneren dat hoek γ = 30°.
quote:Er wordt een driehoek met drie gelijke zijden geconstrueerd zonder enige stelling te gebruiken.Op zaterdag 6 februari 2010 00:02 schreef gaussie het volgende:
Nee, dat heb je verkeerd geinterpreteerd. Mn meetkundig inzicht liet me in de steek. Soms zie je het gewoon niet. En niet iedereen zit op hetzelfde wiskunde niveau... Ik ga ervan uit dat je gebruik gemaakt heb van hoek c= 0.5*boog ab. Maar dan moet gelden dat boog ab 60 graden is. Wat ik nog steeds niet zie is, waarom de gebruikte assumptie tot een gelijkzijdige driehoek leidt? Maak je gebruik van een definitie, stelling etc... En zo ja welke.
quote:Nee, ik heb niet gebruik gemaakt van cirkelbogen. Bovendien is de veronderstelling dat driehoek ABC gelijkzijdig zou zijn onjuist. Maar dat wist je al, want anders kon hoek γ niet 30 graden zijn. Sterker nog, er volgt uit de gegevens ook niet dat driehoek ABC gelijkbenig zou zijn, dat hoeft helemaal niet. Wat wél geldt, is dat driehoek OAB gelijkzijdig is, dat is immers gegeven door AB = OA = OB.Op zaterdag 6 februari 2010 00:02 schreef gaussie het volgende:
Nee, dat heb je verkeerd geinterpreteerd. Mn meetkundig inzicht liet me in de steek. Soms zie je het gewoon niet. En niet iedereen zit op hetzelfde wiskunde niveau... Ik ga ervan uit dat je gebruik gemaakt heb van hoek c= 0.5*boog ab. Maar dan moet gelden dat boog ab 60 graden is. Wat ik nog steeds niet zie is, waarom de gebruikte assumptie tot een gelijkzijdige driehoek leidt? Maak je gebruik van een definitie, stelling etc... En zo ja welke.
quote:Ja, het omgekeerde geldt ook, en dat kun je inderdaad het eenvoudigst inzien met cirkelbogen. Als ∠ACB = 30°, dan is bg(AB) = ∠AOB = 60°, en aangezien OA = OB geldt ∠OAB = ∠ABO. Aangezien de som van de hoeken van driehoek OAB 180 graden is, volgt dus ∠OAB = ∠ABO = 60°, waaruit weer volgt dat OAB gelijkzijdig is, zodat AB = OA = OB en AB dus gelijk is aan de straal van de omgeschreven cirkel van driehoek ABC.Op zaterdag 6 februari 2010 00:14 schreef gaussie het volgende:
Ok, maar geldt de converse dan ook of niet? Met converse bedoel ik; als driehoek abc 1 hoek van 30 graden heeft, dat dan een zijde even lang is als de straal van de omgeschreven cirkel? Zo ja uit welk argument volgt dat dan?
[ Bericht 0% gewijzigd door Riparius op 06-02-2010 02:49:47 ]
tvp.
Ik heb nu:
Stel |b| ≤ a
0 ≤ |b| ≤ a, dus 0 ≤ a
|b| ≤ a, dus b ≤ a (omdat |b|=b, of -|b|=b, en -|b|≤|b|)
|b|≤a dus -a≤-|b|
Kan ik hier al concluderen dat dan -a ≤ b?
[ Bericht 0% gewijzigd door Hanneke12345 op 07-02-2010 15:59:38 ]
quote:Deze stap volg ik al niet, want b kan ook negatief zijn. Ik zou beginnen om twee gevallen te onderscheiden. Je hebt zoals je zelf al opmerkt |b| = b of |b| = -b, aangenomen dat b reëel is uiteraard.Op zondag 7 februari 2010 15:46 schreef Hanneke12345 het volgende:
Ik moet bewijzen dat |b|≤a dan en slechts dan als -a ≤ b ≤ a,
Ik heb nu:
Stel |b| ≤ a
0 ≤ b ≤ a, dus 0 ≤ a
[ Bericht 2% gewijzigd door Riparius op 07-02-2010 16:00:50 ]
quote:Oh, ik ben daar absoluutstrepen vergeten. Maar de andere kant op bewijzen is net gelukt, dus ik ga een nieuwe poging wagen!Op zondag 7 februari 2010 15:55 schreef Riparius het volgende:
[..]
Deze stap volg ik al niet, want b kan ook negatief zijn. Ik zou beginnen om twee gevallen te onderscheiden. Je hebt zoals je zelf al opmerkt |b| = b of |b| = -b, aangenomen dat b reëel is uiteraard.
Stel |b| ≤ a
0 ≤ |b| ≤ a, dus 0 ≤ a
|b| = b of |b| = -b
Als |b| = b, dan b ≤ a, en omdat 0 ≤ a en 0 ≤ b is -a ≤ b
Als |b| = -b, dan -b ≤ a dus -a ≤ b, en b ≤ 0, 0 ≤ a, dus b ≤ a
Dus in beide gevallen geldt -a ≤ b ≤ a.
Toch? Of ben ik toch noge rgens te overhaast?
quote:volgt niet direct uit de axioma's.
quote:Als 0 ≤ b, dan |b| = b, als b ≤ 0, dan |b| = -b, b ≤ 0 of 0 ≤ b, dus ..Op zondag 7 februari 2010 16:19 schreef GlowMouse het volgende:
Het klopt allemaal wel, maar
[..]
volgt niet direct uit de axioma's.
Dat moet ik echt zo uitschrijven, ja?
Te bewijzen: ||a|-|b|| ≤ |a-b|
Het antwoordenmodel zegt dat ik gebruik kan maken van dat wat ik eerder aangetoond heb, |b|≤a desda -a ≤ b ≤ a.
Aan te tonen: -|a-b| ≤ |a|-|b|≤|a-b|, oké zover snap ik het.
Vervolgens doen ze:
|b|=|(b-a)+a|≤|b-a|+|a|=|a-b|+|a|. which implies the first inequality. Ik heb echt geen idee waarom.
quote:Op zondag 7 februari 2010 16:23 schreef Hanneke12345 het volgende:
[..]
Als 0 ≤ b, dan |b| = b, als b ≤ 0, dan |b| = -b, b ≤ 0 of 0 ≤ b, dus ..
Dat moet ik echt zo uitschrijven, ja?
quote:Daar staat |b| <= |a-b| + |a| ofwel |a|-|b| >= -|a-b|.Op zondag 7 februari 2010 19:58 schreef Hanneke12345 het volgende:
Ik kom deze echt niet uit.
Te bewijzen: ||a|-|b|| ≤ |a-b|
Het antwoordenmodel zegt dat ik gebruik kan maken van dat wat ik eerder aangetoond heb, |b|≤a desda -a ≤ b ≤ a.
Aan te tonen: -|a-b| ≤ |a|-|b|≤|a-b|, oké zover snap ik het.
Vervolgens doen ze:
|b|=|(b-a)+a|≤|b-a|+|a|=|a-b|+|a|. which implies the first inequality. Ik heb echt geen idee waarom.
' De grafiek ontstaat door de vermenigvuldiging t.o.v. de x-as met factor -2 gevolgd door de verschuiving 2 omhoog '
Waarom is het 2 omhoog en niet 1 ?
quote:Dat hangt ervan af wat je oorspronkelijke functie is, dat vertel je er niet bij.Op dinsdag 9 februari 2010 21:02 schreef Joewy het volgende:
n(x) = 1 - 2 cos x
' De grafiek ontstaat door de vermenigvuldiging t.o.v. de x-as met factor -2 gevolgd door de verschuiving 2 omhoog '
Waarom is het 2 omhoog en niet 1 ?
quote:Dan moet het een fout zijn in je boek.Op dinsdag 9 februari 2010 21:30 schreef Joewy het volgende:
De standaard f(x) = cos x, sorry.
Ik heb een vraagje:
als ik een berekening laat uitvoeren met Matlab, dan geeft hij het antwoord exact weer, dus in "som-vorm"
,maar wat ik wil is dat hij er gelijk één getal uit braakt.
Dus eigenlijk van een exact antwoord wil ik direct de benadering in 3 cijfers achter de komma.
Maar hoe laat ik hem dat weten...
vb: stel je hebt iets van (5*10)/2, dan drukt hij het uit als 50/2, maar ik wil dan dat ie direct 25 geeft.
(maar dan gaat het over getallen als -1529507700186385500251/33351231400106740678656+63595717592748263604825/68078519651958026928128*cos(3/10*pi)+158291783209258431323833/2668098512008539254292480*sin(3/10*pi)-4851982502419173/360287970189639680*cos(1/5*pi))
Ik krijg wel een antwoord als ik hetzelfde nog's laat uitvoeren, maar dan moet ik dus weer een extra opdracht geven.
Docent weet het ook niet.
(kom er even niet uit met die macht en haakjes
150 = 100(1+r)5
quote:http://forum.allaboutcircuits.com/showthread.php?t=8234Op donderdag 11 februari 2010 11:27 schreef gias het volgende:
Staat ie standaard op.
Docent weet het ook niet.
ik heb het nog nooit gezien

Dit heb ik gister van het bord overgenomen op school, maar iets zegt me dat dit niet klopt. Als ik namelijk in de primitieve functie 1 invul, komt er 17/15e uit, en dit moet nog met 2pi vermenigvuldigd worden. Dan kan het antwoord toch nooit 16/15 pi zijn? Ik kom in dit geval uit op 34/15 pi. Hoe zit de vork nou in de steel hier?
quote:Ik denk dat je die kwadraat dan verkeerd hebt uitgewerkt. Als je als primitieve 1/5*x^5-2/3*x^3+x neemt komt er wel 16/15 pi uitOp vrijdag 12 februari 2010 16:01 schreef beertenderrr het volgende:
Die hoorde daar niet, fout opgeschrevenDie kwadraat wordt die stap erboven al weggewerkt.
trouwens hoe kan je nou weer de inhoud van een vlakdeel berekenen, stomme vraag zeg
quote:Als dat zo op het bord heeft gestaan als je het hier hebt gepost dan begrijpt je docent kennelijk ook niet hoe je het volume van een omwentelingslichaam berekent. Die factor 2π klopt dan niet en het antwoord 16/15 π dus ook niet. Het omwentelingslichaam past in een cilinder met straal 1 en lengte 1, en het volume daarvan is π. Je uitkomst kan dus niet kloppen.Op vrijdag 12 februari 2010 20:09 schreef beertenderrr het volgende:
holy shit, wat domhet klopt idd ja. Bedankt voor de hulp
en ja, de vraagstelling is idd wat krom.
Bewijs:
Zij
Moet ik die |x| uit de noemer zien te krijgen? Hoe kan ik dat doen?
[ Bericht 3% gewijzigd door motorbloempje op 01-09-2013 21:36:49 ]
quote:Dan geldt:Op zaterdag 13 februari 2010 15:24 schreef GlowMouse het volgende:
Relateer hem niet aan epsilon, maar schat hem af. Zorg dat 1/|x| niet te groot wordt door delta altijd kleiner dan 0.25 te kiezen.
Dus volgt dat:
Dus:
En daarmee is het bewezen?
[ Bericht 1% gewijzigd door motorbloempje op 01-09-2013 21:36:54 ]
quote:wat denk je zelf?Op zaterdag 13 februari 2010 15:28 schreef BasementDweller het volgende:
[..]
En daarmee is het bewezen?
quote:Dit gaat al niet goed. De uitspraak lim x→½ 1/x = 2 betekent dat er voor elke ε > 0 een δ > 0 bestaat zodanig dat | 1/x - 2 | < ε voor elke x waarvoor geldt 0 < | x - ½ | < δ. Je moet dus een existentiebewijs geven en laten zien dat er voor elke ε > 0 zo'n δ > 0 bestaat. Dit doe je door uit te gaan van | 1/x - 2 | < ε en daaruit te herleiden waaraan x moet voldoen. Dan kun je δ in ε uitdrukken, waarmee het gestelde is aangetoond.Op zaterdag 13 februari 2010 15:22 schreef BasementDweller het volgende:
Bewijs met de epsilon-delta definitie van een limiet dat:
[ afbeelding ]
Bewijs:
Zij [ afbeelding ]willekeurig. Neem [ afbeelding ] en laat[ afbeelding ] voldoen aan[ afbeelding ]. Dan geldt:[ afbeelding ].
Moet ik die |x| uit de noemer zien te krijgen? Hoe kan ik dat doen?
quote:Ja, want voor elke epsilon>0 is er een delta>0 zodanig dat als |x-1/2| < delta dat dan |1/x -2| < epsilon .
quote:Dat is toch precies wat ik nu gedaan heb?Op zaterdag 13 februari 2010 15:32 schreef Riparius het volgende:
[..]
Dit gaat al niet goed. De uitspraak lim x→½ 1/x = 2 betekent dat er voor elke ε > 0 een δ > 0 bestaat zodanig dat | 1/x - 2 | < ε voor elke x waarvoor geldt 0 < | x - ½ | < δ. Je moet dus een existentiebewijs geven en laten zien dat er voor elke ε > 0 zo'n δ > 0 bestaat. Dit doe je door uit te gaan van | 1/x - 2 | < ε en daaruit te herleiden waaraan x moet voldoen. Dan kun je δ in ε uitdrukken, waarmee het gestelde is aangetoond.
Waarneer refereerde je precies met "dit gaat niet altijd goed"?
quote:Het staat er nu alleen meer als een kladje zoals Riparius opmerkt. Je begint met zij eps>0, neem delta = min{1/4, eps/8}, zij x in Df, |x-2|<delta, dan .... < eps, klaar. Delta>0 komt bv. ook nooit voor als aparte regel in je bewijs.Op zaterdag 13 februari 2010 15:35 schreef BasementDweller het volgende:
[..]
Ja, want voor elke epsilon>0 is er een delta>0 zodanig dat als |x-1/2| < delta dat dan |1/x -2| < epsilon .
quote:Beter lezen, dit schrijf ik niet. Verder bedoel ik dat je een existentiebewijs moet geven en dat je dat kunt doen door te laten zien dat je bij elke gegeven ε > 0 een δ > 0 kunt construeren die aan het gestelde voldoet.Op zaterdag 13 februari 2010 15:36 schreef BasementDweller het volgende:
[..]
Dat is toch precies wat ik nu gedaan heb?
Waarneer refereerde je precies met "dit gaat niet altijd goed"?
quote:Je bedoelt zeker: delta < min(1/4,epsilon/8.Op zaterdag 13 februari 2010 15:38 schreef GlowMouse het volgende:
[..]
Het staat er nu alleen meer als een kladje zoals Riparius opmerkt. Je begint met zij eps>0, neem delta = min{1/4, eps/8}, zij x in Df, |x-2|<delta, dan .... < eps, klaar. Delta>0 komt bv. ook nooit voor als aparte regel in je bewijs.
Delta>0 vind ik wel ergens terug in een bewijsje in mijn diktaat, maar is inderdaad overbodig omdat delta groter is dan de absolute waarde van iets.
Is inderdaad wel netjes om het op die manier op te schrijven, maar ik wilde hier meer laten zien wat ik aan het doen was. Bedankt!
Te bewijzen:
Bewijs:
Zij
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:37:00 ]
quote:Delta kan anders natuurlijk ook nul zijn, dus het moet wel genoemd worden.Op zaterdag 13 februari 2010 15:42 schreef BasementDweller het volgende:
[..]
Je bedoelt zeker: delta < min(1/4,epsilon/8.Delta>0 vind ik wel ergens terug in een bewijsje in mijn diktaat, maar is inderdaad overbodig omdat delta groter is dan de absolute waarde van iets.
Is inderdaad wel netjes om het op die manier op te schrijven, maar ik wilde hier meer laten zien wat ik aan het doen was. Bedankt!
http://mathworld.wolfram.com/Epsilon-DeltaProof.html
quote:Nee. Je omwerking van 1/(1+x2) - 1/2 klopt al niet.Op zaterdag 13 februari 2010 16:16 schreef BasementDweller het volgende:
Even om te checken of ik het nu goed doe, een ander voorbeeld van een delta-epsilon limiet.
Te bewijzen: [ afbeelding ]
Bewijs:
Zij [ afbeelding ]. Neem [ afbeelding ]. Laat [ afbeelding ] voldoen aan [ afbeelding ]. Dan geldt: [ afbeelding ].[ afbeelding ]
quote:oepsOp zaterdag 13 februari 2010 16:26 schreef Riparius het volgende:
[..]
Nee. Je omwerking van 1/(1+x2) - 1/2 klopt al niet.
quote:Nee, bij het bewijs van een limiet voor x → a aan de hand van de ε,δ definitie gaat het om waarden van x zodanig dat 0 < | x - a | < δ, en dan kan δ niet nul zijn.Op zaterdag 13 februari 2010 16:25 schreef BasementDweller het volgende:
[..]
Delta kan anders natuurlijk ook nul zijn, dus het moet wel genoemd worden.
http://mathworld.wolfram.com/Epsilon-DeltaProof.html
quote:Ik krijg met mathematica hetzelfde, dus wat zou het volgens jou wel moeten zijn dan?Op zaterdag 13 februari 2010 16:26 schreef Riparius het volgende:
[..]
Nee. Je omwerking van 1/(1+x2) - 1/2 klopt al niet.
quote:Dat is wat ik bedoel, je noemt dus dat delta groter is dan nul door te zeggen dat 0 < | x - a | < δ .Op zaterdag 13 februari 2010 16:31 schreef Riparius het volgende:
[..]
Nee, bij het bewijs van een limiet voor x → a aan de hand van de ε,δ definitie gaat het om waarden van x zodanig dat 0 < | x - a | < δ, en dan kan δ niet nul zijn.
quote:Minnetjes en plusjes gaan fout. Dat zie je ook als je gewoon x=1 invult.Op zaterdag 13 februari 2010 16:34 schreef BasementDweller het volgende:
[..]
Ik krijg met mathematica hetzelfde, dus wat zou het volgens jou wel moeten zijn dan?
quote:Als ik x=1 invul krijg ik voor beide 0.. volgens mij klopt ie toch echt.Op zaterdag 13 februari 2010 16:37 schreef GlowMouse het volgende:
[..]
Minnetjes en plusjes gaan fout. Dat zie je ook als je gewoon x=1 invult.
quote:Nee, het ligt anders (en subtieler). Er is een verschil tussen de ε,δ definities bij een limiet voor x → a en bij continuïteit in x = a.Op zaterdag 13 februari 2010 16:36 schreef BasementDweller het volgende:
[..]
Dat is wat ik bedoel, je noemt dus dat delta groter is dan nul door te zeggen dat 0 < | x - a | < δ .
[ Bericht 0% gewijzigd door Riparius op 13-02-2010 16:59:18 ]
quote:Continuiteit heb ik nog niet zo 'rigoreus' gekregen, maar hier lees ik hetzelfde:Op zaterdag 13 februari 2010 16:43 schreef Riparius het volgende:
[..]
Nee, het ligt anders (en subtieler). Er is een verschil tussen de ε,δ definities bij een limiet voor x → a en bij continuiteit in x = a.
quote:http://mathworld.wolfram.com/Epsilon-DeltaDefinition.htmlfor all epsilon>0 there is delta>0 such that, whenever 0<|x-x_0|<delta, then |f(x)-y_0|<epsilon
Je begint dus met 0<|x-x_0|<delta en laat zien dat daaruit volgt dat |f(x)-y_0|<epsilon. Je neem dus aan dat 0<delta.
quote:Het enige verschil is toch dat je de limietwaarde neemt ipv f(c)?Op zaterdag 13 februari 2010 16:43 schreef Riparius het volgende:
[..]
Nee, het ligt anders (en subtieler). Er is een verschil tussen de ε,δ definities bij een limiet voor x → a en bij continuiteit in x = a.
quote:In de noemer krijg je 1-x², wat overigens hetzelfde is door de absoluutstrepen.Op zaterdag 13 februari 2010 16:41 schreef BasementDweller het volgende:
[..]
Als ik x=1 invul krijg ik voor beide 0.. volgens mij klopt ie toch echt.
quote:Ja, het klopt dus wel gewoonOp zaterdag 13 februari 2010 16:49 schreef GlowMouse het volgende:
In de noemer krijg je 1-x², wat overigens hetzelfde is door de absoluutstrepen. Je eerste ongelijkheidsteken vind ik een onlogische stap.
Wat ik eigenlijk doe bij het eerste ongelijkheidsteken, is die |(x-1)| vervangen door delta.
edit: oja, kwadraatje vergeten over te typen verderop.
Anyway, is het inhoudelijk correct?
quote:Ja, maar δ=0 komt in dat hele verhaal niet te pas. Bovendien klopt de definitie van continuiteit die in je linkje wordt gegeven niet, want hier wordt x = x0 ten onrechte uitgesloten door 0 < | x - x0 | < δ te nemen. Kijk maar eens naar de functie f(x) = (sin x) /x. Die zou continu zijn in x = 0 als we het verhaal uit je linkje mogen geloven, maar dit is niet zo, want de functie is niet gedefinieerd voor x = 0. Je kunt de discontinuïteit in x = 0 wel opheffen door f(0) = 1 te definiëren, want lim x→0 (sin x)/x = 1, maar dat is een ander verhaal.Op zaterdag 13 februari 2010 16:46 schreef BasementDweller het volgende:
[..]
Continuiteit heb ik nog niet zo 'rigoreus' gekregen, maar hier lees ik hetzelfde:
[..]
http://mathworld.wolfram.com/Epsilon-DeltaDefinition.html
Je begint dus met 0<|x-x_0|<delta en laat zien dat daaruit volgt dat |f(x)-y_0|<epsilon. Je neem dus aan dat 0<delta.
quote:Nee, 14/9de komt uit de lucht vallen.Op zaterdag 13 februari 2010 16:53 schreef BasementDweller het volgende:
[..]
Anyway, is het inhoudelijk correct?
quote:Omdat delta < 1/4 en |x-1|<delta, volgt |x-1|<1/4 dusOp zaterdag 13 februari 2010 16:59 schreef GlowMouse het volgende:
[..]
Nee, 14/9de komt uit de lucht vallen.
Verder heb ik een rekenfout gemaakt en moet het 14/25 zijn ipv 14/9.
[ Bericht 22% gewijzigd door motorbloempje op 01-09-2013 21:37:08 ]
quote:Dit gaat helemaal niet goed, dus laat ik het maar even voor je uitwerken.Op zaterdag 13 februari 2010 17:02 schreef BasementDweller het volgende:
[..]
Omdat delta < 1/4 en |x-1|<delta, volgt |x-1|<1/4 dus [ afbeelding ]. Als ik 3/4 invul is de breuk het grootst (is eigenlijk niet triviaal, hoe kan ik dit meenemen in het bewijs?) dus dat heb ik gedaan.
Verder heb ik een rekenfout gemaakt en moet het 14/25 zijn ipv 14/9.
De opgave: bewijs aan de hand van de ε,δ definitie dat lim x→1 1/(1+x2) = 1/2.
We bekijken eerst eens de uitdrukking 1/(1 + x2). Er geldt x2 ≥ 0, dus 1 + x2 ≥ 1, dus 1/(1 + x2) ≤ 1, en aangezien ook geldt 1/(1 + x2) > 0 hebben we dus:
(1) 0 < 1/(1 + x2) ≤ 1,
en dus ook:
(2) -½ < 1/(1 + x2) - ½ ≤ ½,
en dus:
(3) | 1/(1 + x2) - ½ | ≤ ½
Dit betekent dat voor ε > ½ elke waarde van δ > 0 voldoet, aangezien (3) geldt voor elke x en daarmee ook voor elke x die voldoet aan 0 < | x - 1 | < δ, ongeacht de keuze van δ. We hoeven nu dus alleen nog waarden van ε ≤ ½ te onderzoeken.
Sluiten we x = 0 uit, dan is | 1/(1 + x2) | < 1 en dus ook | 1/(1 + x2) - ½ | < ½, zodat we kunnen concluderen dat voor ε = ½ de waarde δ = 1 voldoet, we hebben immers:
(4) | 1/(1 + x2) - ½ | < ½ voor elke x zodanig dat 0 < | x - 1 | < 1
In zijn algemeenheid kun je voor lim x→a f(x) = L opmerken dat een gegeven δ0 die voldoet voor een gegeven ε0 ook zal voldoen voor elke andere ε > ε0, daar immers uit | f(x) - L | < ε0 en ε0 < ε ook volgt dat | f(x) - L | < ε indien 0 < | x - a | < δ0. Het is dus irrelevant om willekeurig grote waarden van ε te onderzoeken zodra we een bovengrens voor ε hebben gevonden, het is dan nog uitsluitend van belang aan te tonen dat voor elke willekeurig kleine ε > 0 een δ > 0 bestaat waarmee aan de voorwaarden uit de definitie wordt voldaan. Voor deze opgave hebben we al gevonden dat we alleen nog waarden van ε < ½ hoeven te onderzoeken.
We willen nu aantonen dat voor elke positieve ε < ½ een δ > 0 bestaat zodanig dat
(5) | 1/(1 + x2) - ½ | < ε
indien
(6) 0 < | x - 1 | < δ
Voor (5) kunnen we schrijven:
(7) | (1 - x)(1 + x)/(2∙(1 + x2)) | < ε
En aangezien we voor ε < ½ mogen veronderstellen dat δ < 1 en dus blijkens (6) | x + 1| niet 0 kan zijn kunnen we (7) herschrijven als:
(8) | x - 1 | < 2ε ∙| (1 + x2)/(1 + x) |
Nu moeten we de factor | (1 + x2)/(1 + x) | onderzoeken, en aangezien we δ < 1 mogen veronderstellen, en dus | x - 1 | < 1, kunnen we ons beperken tot het interval (0,2).
Het is direct te zien dat (1 + x2)/(1 + x) gelijk is aan 1 voor x = 0 en x = 1. Ook is duidelijk dat deze uitdrukking positief is op het interval (0,2) en dat de waarde in ieder geval stijgend is voor x > 1 aangezien x2 sneller in grootte toeneemt dan x voor x > 1. Maar nu zijn we geïnteresseerd in een minimum van deze uitdrukking op het interval (0,2). Als we namelijk een ondergrens m > 0 kunnen bepalen zodanig dat:
(9) m < | (1 + x2)/(1 + x) |
Dan is ook:
(10) 2ε∙m < 2ε∙| (1 + x2)/(1 + x) |
In dit geval volgt uit (8) en (10) dat voor elke positieve ε < ½ de keuze δ = 2ε∙m impliceert dat voor elke x zodanig dat 0 < | x - 1 | < δ wordt voldaan aan (8) en daarmee dus ook aan (7) en dus ook aan (5), zoals gewenst.
Nu is eenvoudig te bepalen dat (1 + x2)/(1 + x) op het interval (0,2) een minimum aanneemt bij x = -1+√2 en dat dit minimum 2√2 - 2 bedraagt. Ook is 2√2 - 2 > ½, dus kunnen we bijvoorbeeld m = ½ nemen, er geldt immers op het interval (0,2):
(11) ½ < | (1 + x2)/(1 + x) |
Kiezen we dus bij een willekeurig kleine ε < ½ voor δ = 2ε∙½ = ε, dan wordt voor elke x die voldoet aan (6) voldaan aan (8) en daarmee ook aan (5). Hiermee is aangetoond dat er inderdaad voor voor elke ε > 0 een δ > 0 bestaat zodanig dat voor elke x die voldoet aan (6) wordt voldaan aan (5), QED.
[ Bericht 0% gewijzigd door Riparius op 14-02-2010 17:30:17 ]
Stel dat het niet zo is. Dus b<a. Dan is a > b, maar dat is nog geen tegenspraak. Ik weet wel dat er oneindig veel getallen nog tussen a en b liggen, waarvoor dus geldt dat a>b1>b, maar ik weet niet hoe ik dat wiskundig moet gaan opschrijven of ik dat uberhaupt zomaar aan kan nemen.
Neem aan a <= b1 voor alle b1 > b, maar a > b.
Je moet dan op een tegenspraak uitkomen, en dat kan hier door een b1>b te vinden zodanig dat a > b1.
quote:Wauw dat is een hoop werk, dank je wel!!Op zondag 14 februari 2010 16:07 schreef Riparius het volgende:
[..]
Dit gaat helemaal niet goed, dus laat ik het maar even voor je uitwerken.
De opgave: bewijs aan de hand van de ε,δ definitie dat lim x→1 1/(1+x2) = 1/2.
We bekijken eerst eens de uitdrukking 1/(1 + x2). Er geldt x2 ≥ 0, dus 1 + x2 ≥ 1, dus 1/(1 + x2) ≤ 1, en aangezien ook geldt 1/(1 + x2) > 0 hebben we dus:
(1) 0 < 1/(1 + x2) ≤ 1,
en dus ook:
(2) -½ < 1/(1 + x2) - ½ ≤ ½,
en dus:
(3) | 1/(1 + x2) - ½ | ≤ ½
Dit betekent dat voor ε > ½ elke waarde van δ > 0 voldoet, aangezien (3) geldt voor elke x en daarmee ook voor elke x die voldoet aan 0 < | x - 1 | < δ, ongeacht de keuze van δ. We hoeven nu dus alleen nog waarden van ε ≤ ½ te onderzoeken.
Sluiten we x = 0 uit, dan is | 1/(1 + x2) | < 1 en dus ook | 1/(1 + x2) - ½ | < ½, zodat we kunnen concluderen dat voor ε = ½ de waarde δ = 1 voldoet, we hebben immers:
(4) | 1/(1 + x2) - ½ | < ½ voor elke x zodanig dat 0 < | x - 1 | < 1
In zijn algemeenheid kun je voor lim x→a f(x) = L opmerken dat een gegeven δ0 die voldoet voor een gegeven ε0 ook zal voldoen voor elke andere ε > ε0, daar immers uit | f(x) - L | < ε0 en ε0 < ε ook volgt dat | f(x) - L | < ε indien 0 < | x - a | < δ0. Het is dus irrelevant om willekeurig grote waarden van ε te onderzoeken zodra we een bovengrens voor ε hebben gevonden, het is dan nog uitsluitend van belang aan te tonen dat voor elke willekeurig kleine ε > 0 een δ > 0 bestaat waarmee aan de voorwaarden uit de definitie wordt voldaan. Voor deze opgave hebben we al gevonden dat we alleen nog waarden van ε < ½ hoeven te onderzoeken.
We willen nu aantonen dat voor elke positieve ε < ½ een δ > 0 bestaat zodanig dat
(5) | 1/(1 + x2) - ½ | < ε
indien
(6) 0 < | x - 1 | < δ
Voor (5) kunnen we schrijven:
(7) | (1 - x)(1 + x)/(2∙(1 + x2)) | < ε
En aangezien we voor ε < ½ mogen veronderstellen dat δ < 1 en dus blijkens (6) | x + 1| niet 0 kan zijn kunnen we (7) herschrijven als:
(8) | x - 1 | < 2ε ∙| (1 + x2)/(1 + x) |
Nu moeten we de factor | (1 + x2)/(1 + x) | onderzoeken, en aangezien we δ < 1 mogen veronderstellen, en dus | x - 1 | < 1, kunnen we ons beperken tot het interval (0,2).
Het is direct te zien dat (1 + x2)/(1 + x) gelijk is aan 1 voor x = 0 en x = 1. Ook is duidelijk dat deze uitdrukking positief is op het interval (0,2) en dat de waarde in ieder geval stijgend is voor x > 1 aangezien x2 sneller in grootte toeneemt dan x voor x > 1. Maar nu zijn we geïnteresseerd in een minimum van deze uitdrukking op het interval (0,2). Als we namelijk een ondergrens m > 0 kunnen bepalen zodanig dat:
(9) m < | (1 + x2)/(1 + x) |
Dan is ook:
(10) 2ε∙m < 2ε∙| (1 + x2)/(1 + x) |
In dit geval volgt uit (8) en (10) dat voor elke positieve ε < ½ de keuze δ = 2ε∙m impliceert dat voor elke x zodanig dat 0 < | x - 1 | < δ wordt voldaan aan (8) en daarmee dus ook aan (7) en dus ook aan (5), zoals gewenst.
Nu is eenvoudig te bepalen dat (1 + x2)/(1 + x) op het interval (0,2) een minimum aanneemt bij x = -1+√2 en dat dit minimum 2√2 - 2 bedraagt. Ook is 2√2 - 2 > ½, dus kunnen we bijvoorbeeld m = ½ nemen, er geldt immers op het interval (0,2):
(11) ½ < | (1 + x2)/(1 + x) |
Kiezen we dus bij een willekeurig kleine ε < ½ voor δ = 2ε∙½ = ε, dan wordt voor elke x die voldoet aan (6) voldaan aan (8) en daarmee ook aan (5). Hiermee is aangetoond dat er inderdaad voor voor elke ε > 0 een δ > 0 bestaat zodanig dat voor elke x die voldoet aan (6) wordt voldaan aan (5), QED.
(heb nu even geen tijd maar ga het binnenkort zeker doornemen! Als ik dan nog vragen heb horen jullie het wel
a < n is makkelijk. Round(a)+1 (mag dat gewoon?).
1/n < a kom ik niet uit. Ik dacht eerst 't zelfde te doen als net. a/2. Maar als a irrationaal is kan dat niet omgevormd anar 1/n. round(a)/2 gaat ook alleen maar goed als a groter is dan een half.
quote:Kies een n zodanig dat n > 1/a en tevens n > a. Dan is 1/n < a en a < n, waaruit het gestelde volgt.Op zondag 14 februari 2010 21:10 schreef Hanneke12345 het volgende:
Oké ik kom er weer niet uit. Prove that if a>0, then there exists n in N such that 1/n < a < n.
a < n is makkelijk. Round(a)+1 (mag dat gewoon?).
1/n < a kom ik niet uit. Ik dacht eerst 't zelfde te doen als net. a/2. Maar als a irrationaal is kan dat niet omgevormd anar 1/n. round(a)/2 gaat ook alleen maar goed als a groter is dan een half.
ik heb 2 vectoren die een plane opspannen laten we zeggen:
P(50,0,0) en Q(0,0,50) (x,y,z)
met een normaal van de plane N(0,1,0)
Nu moet ik een vector R bepalen die +30 graden is tov vector P die ook in de plane ligt. Hoe doe ik dit?
Kom niet verder dan in het invullen van deze formule:
P*R = |P| |R| * cos( hoek )
P weet ik hier, lengte van R ook moet hoe reken ik nou die vector R uit? want als ik het oplos deel ik het rechter stuk door vector P maar dan ligt vector R nog steeds op dezelfde richting als P
die kun je niet oplossen door rechts door P te delen, want er staat geen P maar |P|. Bovendien kun je niet delen door een vector.
Je kunt R schrijven als lineaire combinatie van P en Q omdat hij in het vlak ligt.
quote:Ik begrijp niet zo goed waarom je hier met een inproduct wil werken. Als R in hetzelfde vlak ligt als P en Q en dezelfde lengte heeft als P omdat je P over een hoek van 30 graden in positieve richting roteert om R te verkrijgen, dan heb je R(50*cos(-30°),0,50*sin(-30°)). Het minteken is vanwege de ligging van je normaal (kurketrekkerregel).Op dinsdag 16 februari 2010 10:28 schreef greatchampion het volgende:
een probleem met het inproduct waar ik niet helemaal uit kom:
ik heb 2 vectoren die een plane opspannen laten we zeggen:
P(50,0,0) en Q(0,0,50) (x,y,z)
met een normaal van de plane N(0,1,0)
Nu moet ik een vector R bepalen die +30 graden is tov vector P die ook in de plane ligt. Hoe doe ik dit?
Kom niet verder dan in het invullen van deze formule:
P*R = |P| |R| * cos( hoek )
P weet ik hier, lengte van R ook moet hoe reken ik nou die vector R uit? want als ik het oplos deel ik het rechter stuk door vector P maar dan ligt vector R nog steeds op dezelfde richting als P. Ik zie volgens mij iets over het hoofd
quote:Ja, ik dacht dat ik de vector Q kon uitrekenen door de vergelijking op te lossen aangezien ik de rest van de gegevens had. Maar het kon dus simpelerOp dinsdag 16 februari 2010 11:42 schreef Riparius het volgende:
[..]
Ik begrijp niet zo goed waarom je hier met een inproduct wil werken. Als R in hetzelfde vlak ligt als P en Q en dezelfde lengte heeft als P omdat je P over een hoek van 30 graden in positieve richting roteert om R te verkrijgen, dan heb je R(50*cos(-30°),0,50*sin(-30°)). Het minteken is vanwege de ligging van je normaal (kurketrekkerregel).
heb nu: R = P * cos( hoek in radialen ) + Q * sin( hoek in radialen )
thx
Voor n=2 is het duidelijk:
Als je nu kijkt naar n=3, dan:
Mag je nu zeggen:
dus voor n=3 is hij Abels, op dezelfde manier voor n+1
[ Bericht 0% gewijzigd door motorbloempje op 01-09-2013 21:37:15 ]
quote:Op zondag 14 februari 2010 21:10 schreef Hanneke12345 het volgende:
Oké ik kom er weer niet uit. Prove that if a>0, then there exists n in N such that 1/n < a < n.
a < n is makkelijk. Round(a)+1 (mag dat gewoon?).
1/n < a kom ik niet uit. Ik dacht eerst 't zelfde te doen als net. a/2. Maar als a irrationaal is kan dat niet omgevormd anar 1/n. round(a)/2 gaat ook alleen maar goed als a groter is dan een half.

Is dit een goed genoeg antwoord? Nja, behalve dan dat 1 a>=1 moet zijn en 2 a<1.
de laatste dus bij 2 gaat ook wel heel snel.
quote:ik wil het aantonen voor n>1, voor n=2 klopt het, maar nu voor n>2Op dinsdag 16 februari 2010 13:55 schreef GlowMouse het volgende:
Waarom zou je n=3 nodig hebben om het gevraagde aan te tonen?
daarom keek ik naar 3 en zag dat ik terug uit kom op n=2
quote:Je wilt aantonen dat de groep Abels is. Je hebt aangetoond ab=ba. Wat wil je nog meer aantonen?Op dinsdag 16 februari 2010 14:18 schreef JoPiDo het volgende:
[..]
ik wil het aantonen voor n>1, voor n=2 klopt het, maar nu voor n>2
daarom keek ik naar 3 en zag dat ik terug uit kom op n=2
quote:ik heb aangetoond dat het voor n=2 geldt, maar niet voor n>2, dat moet ik ook aantonenOp dinsdag 16 februari 2010 14:20 schreef GlowMouse het volgende:
[..]
Je wilt aantonen dat de groep Abels is. Je hebt aangetoond ab=ba. Wat wil je nog meer aantonen?
quote:??Op dinsdag 16 februari 2010 14:29 schreef GlowMouse het volgende:
Wat heeft commutativiteit met n te maken?
hoe laat ik zien dat het geldt voor n>2? dat is niet zo'n heel rare vraag...?
quote:Dat hoef je niet te bewijzen, er is alleen gegeven dat het voor alle n geldt. Er staat niet dat je voor alle n moet bewijzen dat G abels is.Op dinsdag 16 februari 2010 14:34 schreef JoPiDo het volgende:
[..]
??
hoe laat ik zien dat het geldt voor n>2? dat is niet zo'n heel rare vraag...?
Bereken de oppervlakte van V.
Om de een of andere reden zie ik niet wat ik fout doe/anders moet doen?
Ik bereken totale oppervlakte onder lijn x en y ( dus 7 x 8 = 56)
Primitiveer f(x), F(x) = -8x^-1.
Dan is het dus 56 - [F(x)]1tm8 = 56 - 7 = 49
|Maar dat klopt niet..
quote:Op dinsdag 16 februari 2010 15:23 schreef GlowMouse het volgende:
Als je een figuur tekent, zie je dat je nu de oppervlakte bepaalt van het stuk begrensd door de grafiek, de lijn y=8 en de lijn x=8.
Ah ik zie het al, ik heb de vraag verkeerd begrepen!
Bedankt, nu klopt het!
quote:Ik zit nog eens te kijken, maar kan ik egienlijk niet net als ik bij 2 doe bij 1 gelijk zeggen dat voor elke n>1 1/n<a, omdat a >=1 ?Op dinsdag 16 februari 2010 14:11 schreef GlowMouse het volgende:
bij 1 zou ik 1/n<a iets uitgebreider motiveren: 1<a dus n < na dus 1 < na en vermenigvuldigen met het positief getal 1/n (waarom positief?) levert 1/n < a.
de laatste dus bij 2 gaat ook wel heel snel.
quote:de stap van n>1 naar 1/n < 1 moet uiteraard gemotiveerd worden; het is allemaal evenveel werk.Op dinsdag 16 februari 2010 16:09 schreef Hanneke12345 het volgende:
[..]
Ik zit nog eens te kijken, maar kan ik egienlijk niet net als ik bij 2 doe bij 1 gelijk zeggen dat voor elke n>1 1/n<a, omdat a >=1 ?
Een andere vraag dan: Ik moet bewijzen dat een ondergroep in een abelse groep ook abels is. Maar een ondergroep heeft toch altijd dezelfde bewerking als de normale groep, en is dus automatisch abels? Valt daar nog iets in te bewijzen?
Daarna "geef een niet-triviaal voorbeeld van een abelse ondergroep van een niet-abelse groep", een groep met drie elementen {e, a, a-1} met orde van a is 2 is zeker triviaal?
{e} lijkt me zeker triviaal, die van jou weet ik niet.
[ Bericht 80% gewijzigd door Zuivelkoe op 16-02-2010 19:58:17 ]
Ik heb verzameling A = {a,b,c} . Eenvoudig. Van A* zijn bv woorden als aa,bb en cc te maken
Wat als een element een verzameling opzich is? Dus B = {a,b,{c,d}} . Wat zijn van B* woorden die ik kan maken op aa en bb na?
quote:Wel, bijvoorbeeld iets als ab{c,d}bba.Op dinsdag 16 februari 2010 21:12 schreef Keiichi het volgende:
Ik ben bezig met verzamelingsleer. Waar ik niet helemaal aan uit kom met de informatie die ik heb.
Ik heb verzameling A = {a,b,c} . Eenvoudig. Van A* zijn bv woorden als aa,bb en cc te maken
Wat als een element een verzameling opzich is? Dus B = {a,b,{c,d}} . Wat zijn van B* woorden die ik kan maken op aa en bb na?
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
quote:Nee, met triviaal wordt {e} bedoeld.Op dinsdag 16 februari 2010 16:39 schreef Hanneke12345 het volgende:
Ah, oké.
Een andere vraag dan: Ik moet bewijzen dat een ondergroep in een abelse groep ook abels is. Maar een ondergroep heeft toch altijd dezelfde bewerking als de normale groep, en is dus automatisch abels? Valt daar nog iets in te bewijzen?
Daarna "geef een niet-triviaal voorbeeld van een abelse ondergroep van een niet-abelse groep", een groep met drie elementen {e, a, a-1} met orde van a is 2 is zeker triviaal?
quote:Dat lijkt me gewoon machtsverheffen:Op dinsdag 16 februari 2010 21:37 schreef poesemuis het volgende:
als
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
heb je een plaatje van de opgave, want ik snap je notatie niet.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:38:24 ]
quote:Je kunt een superscript met [sup] en [ /sup] en een subscript tussen [sub] en [ /sub] (maar dan zonder spaties). Misschien maakt dat je opgave wat leesbaarder.Op dinsdag 16 februari 2010 21:37 schreef poesemuis het volgende:
als
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
quote:het is een t, en direct daarna twee cijfers, eentje boven en eentje onder, de 2 boven en de 0 daaronder, geen machtnotatieOp dinsdag 16 februari 2010 21:47 schreef thabit het volgende:
[..]
Je kunt een superscript met [sup] en [ /sup] en een subscript tussen [sub] en [ /sub] (maar dan zonder spaties). Misschien maakt dat je opgave wat leesbaarder.
want zo klopt het toch:
2log(1+t0) = log(1+t0+T)
log((1+t0)^2) = log(1+t0+T)
(1+t0)^2 = 1+t0+T
1 + 2t0 + t0^2 = 1+t0+T
T = t0 + t0^2
quote:Om te beginnen: gebruik alsjeblieft een duidelijke notatie, subscript en superscript zijn er niet voor niks. Nu is het zo dat iemand eerst je opgave moet ontcijferen om überhaupt te kunnen snappen wat de vraag is. En dat geldt helaas niet alleen voor jou.Op dinsdag 16 februari 2010 21:37 schreef poesemuis het volgende:
als
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
Wat ik eruit opmaak is dat je hebt:
2∙log(1 + t0) = log(1 + t0 + T)
Dan hebben we dus:
(1 + t0)2 = 1 + t0 + T
En dus:
T = (1 + t0)2 - t0 - 1
En uitwerken geeft dan:
T = t0 + t02
De nul in t0 is een index en de twee in t02 een kwadraat, niks bijzonders dus.
quote:Ik weet niet wat dat sub en sub is.. maar ik zal eens uitzoekenOp dinsdag 16 februari 2010 22:34 schreef Riparius het volgende:
[..]
Om te beginnen: gebruik alsjeblieft een duidelijke notatie, subscript en superscript zijn er niet voor niks. Nu is het zo dat iemand eerst je opgave moet ontcijferen om überhaupt te kunnen snappen wat de vraag is. En dat geldt helaas niet alleen voor jou.
Wat ik eruit opmaak is dat je hebt:
2∙log(1 + t0) = log(1 + t0 + T)
Dan hebben we dus:
(1 + t0)2 = 1 + t0 + T
En dus:
T = (1 + t0)2 - t0 - 1
En uitwerken geeft dan:
T = t0 + t02
De nul in t0 is een index en de twee in t02 een kwadraat, niks bijzonders dus.
De verdubbelingstijd van 1+bt ,met t=tijd en b=positieve constante, verdubbelingstijd in T
het antwoord moet zijn T = (1/b) + t0 (t-nul staat daar)
ik begrijp niet hoe je daaraan komt, iemand?
hoe ik begonnen was:
2(1+bt0) = 1 + bt0 + T
2 + 2bt0 = 1 + bt0 + T
T = 1 + bt0
2+ 2bt0 = 1 + bt0 + bT
ja, zo klopt het
quote:Op dinsdag 16 februari 2010 14:44 schreef -jos- het volgende:
[..]
Dat hoef je niet te bewijzen, er is alleen gegeven dat het voor alle n geldt. Er staat niet dat je voor alle n moet bewijzen dat G abels is.
sorry, jullie hebben helemaal gelijk!
ik was in de war, er wordt natuurlijk maar 1 groep bedoeld waarop deze bewerking geldt en ik had in mijn hoofd verschillende groepen waarin voor elke groep de n anders is
xn+1 = a(1-xn) = xn (omdat we te maken hebben met een evenwichtspunt)
waarom is dan xn = a / (1+a)?
quote:Elementaire algebra. Als:Op woensdag 17 februari 2010 16:23 schreef poesemuis het volgende:
Als
xn+1 = a(1-xn) = xn (omdat we te maken hebben met een evenwichtspunt)
waarom is dan xn = a / (1+a)?
xn = a∙(1 - xn),
Dan is:
xn = a - a∙xn,
En dus:
xn + a∙xn = a,
Dus:
xn∙(1 + a) = a,
Dus:
xn = a/(1 + a)
Welke vooropleiding heb je eigenlijk? Dit zou toch geen probleem mogen zijn ...
Voor de drie zijden a, b en c van een driehoek als ook voor de tegenover de zijde c liggende hoek, dat wil zeggen de door de twee zijden, a en b ingesloten hoek, γ geldt:
c^2 = a^2 + b^2 - 2 a b cos©
Als je het bewijs van de cosinus regel bekijkt dan zie je in dat dit een implicatie is in de vorm A impliceert B. Dus een Als..., dan.... stelling. A is de hypothese en B is dan de conclusie. In dit geval is de conclusie duidelijk c^2 = a^2 + b^2 - 2 a b cos©.
Nu lees ik in een boek dat de converse van de cosinus regel niet waar is. Met converse bedoel ik het verwisselen van de hypothese met de conclusie. Dus B impliceert A. Volgens het boek komt dit omdat in het bewijs van de cosinus regel gebruik wordt gemaakt van de stelling van Pythagoras. Dit klopt maar wat is de samenhang met de converse? Dit ontgaat mij. kan iemand me uitleggen waarom de converse niet waar is? Hetzij met een tegenvoorbeeld of logisch argument.
quote:De cosinusfunctie is injectief op [0, pi] dus het enige dat fout zou kunnen gaan is de driehoeksongelijkheid: misschien is het mogelijk om een viertal (a,b,c,gamma) te vinden dat aan de cosinusregel voldoet maar bijvoorbeeld niet a <= b + c. Als inderdaad a > b + c geldt dan hebben we c < a - b en dus c2 < a2 + b2 - 2ab. Ofwel 2ab*cos(gamma) > 2ab. Maar de cosinus zit altijd op het interval [-1,1] dus die driehoeksongelijkheid moet gewoon gelden. Evenzo voor de andere driehoeksongelijkheden.Op woensdag 17 februari 2010 22:03 schreef gaussie het volgende:
Ik heb een vraag over de cosinus regel. Ik neem aan dat hij bekend is. Maar ik zal hem voor de duidelijkheid herhalen:
Voor de drie zijden a, b en c van een driehoek als ook voor de tegenover de zijde c liggende hoek, dat wil zeggen de door de twee zijden, a en b ingesloten hoek, γ geldt:
c^2 = a^2 + b^2 - 2 a b cos©
Als je het bewijs van de cosinus regel bekijkt dan zie je in dat dit een implicatie is in de vorm A impliceert B. Dus een Als..., dan.... stelling. A is de hypothese en B is dan de conclusie. In dit geval is de conclusie duidelijk c^2 = a^2 + b^2 - 2 a b cos©.
Nu lees ik in een boek dat de converse van de cosinus regel niet waar is. Met converse bedoel ik het verwisselen van de hypothese met de conclusie. Dus B impliceert A. Volgens het boek komt dit omdat in het bewijs van de cosinus regel gebruik wordt gemaakt van de stelling van Pythagoras. Dit klopt maar wat is de samenhang met de converse? Dit ontgaat mij. kan iemand me uitleggen waarom de converse niet waar is? Hetzij met een tegenvoorbeeld of logisch argument.
De 'converse' geldt dus gewoon.
quote:Kun je even vertellen in welk boek dat staat? Of letterlijk citeren wat het boek hierover zegt?Op woensdag 17 februari 2010 22:03 schreef gaussie het volgende:
Nu lees ik in een boek dat de converse van de cosinus regel niet waar is. Met converse bedoel ik het verwisselen van de hypothese met de conclusie. Dus B impliceert A. Volgens het boek komt dit omdat in het bewijs van de cosinus regel gebruik wordt gemaakt van de stelling van Pythagoras. Dit klopt maar wat is de samenhang met de converse? Dit ontgaat mij. kan iemand me uitleggen waarom de converse niet waar is? Hetzij met een tegenvoorbeeld of logisch argument.
quote:Mijn post was een bewijs, ik zal het argument even verduidelijken:Op woensdag 17 februari 2010 22:35 schreef gaussie het volgende:
Het is nu veel duidelijker. Dit is gewoon een fout in het boek. Heb je misschien een bewijs van de converse? Ik kan hem namelijk nergens vinden....
Neem een viertal (a, b, c, gamma), met a,b,c > 0 en gamma in [0, pi] dat aan de vergelijking in de cosinusregel voldoet. Dan geldt voor a, b, c de driehoeksongelijkheid (omdat cos(gamma) in [-1, 1] zit, probeer maar uit te werken). Er is dus een driehoek met zijden a, b, c. De driehoek zal ook een hoek tegenover c hebben, noem deze hoek gamma'. Voor gamma' geldt dat het in [0, pi] zit en aan de cosinusregel voldoet. Omdat gamma daar ook aan voldoet, geldt cos(gamma) = cos(gamma'). Maar dan ook gamma = gamma' want op [0,pi] is de cosinusfunctie strikt dalend van 1 naar -1 en kan dus twee verschillende gammas dezelfde waarde aannemen.
ik kan echt niets bedenken!
quote:Q/ZOp donderdag 18 februari 2010 23:36 schreef JoPiDo het volgende:
weet iemand een groep met oneindige orde, waarin elk element eindige orde heeft?
ik kan echt niets bedenken!
[ Bericht 39% gewijzigd door Mike544 op 19-02-2010 11:43:45 ]
Intro:
Two games (N; v) and (N;w) are strategically equivalent if there exists Alfa > 0 and Beta in |R^n such
that for all C SUB N w(C) = Alfa *v(C) + Beta* (C) = Alfa*v(C) + sum(i in C) Beta i
(SUB bedoel ik dus C is een subset van N, i in C is i is a member of C)
De vraag is nu:
Prove that strategic equivalence is an equivalence relation (i.e., it is reflexive, symmetric and
transitive).
Ik snap onder het mom van dat er een logische relatie is onderling, dat w(C) -> w(C), en als symmetrisch is dat daaruit transitiviteit volgt, maar hoe ik dit in duidelijke taal neerknal is een ander verhaal. Met mijn beknopte en half vergeten logica kennis weet ik enkel enigszins iets over p-morfismes en dat ze dezelfde eigenschappen hebben in zo'n geval. Maar of dit vergelijkbaar is?
Iemand die me in een richting kan wijzen? Alvast bedankt (weer verder gaat huiswerken)
Ik zal een eigenschap voordoen, dan kun je de andere twee zelf.
Reflexive: (N,v) is strategisch equivalent met (N,v) omdat dit direct volgt uit de definitie met alpha=1 en beta=0.
Symmetric: Als (N,v) equivalent is aan (N,w) dan geldt ...., nu geldt ook dat (N,w) equivalent is aan (N,v) omdat ....
Hartstikke bedankt, dat is een goeie ogenopener.
Me bedenksel voortgebouwd op je eye opener:
Symmetrie met dezelfde waarden voor alfa/beta. Uit reflexiviteit en symmetrie volgt transiviteit. Wat weer op neer komt dat de relatie equivalent is.
[ Bericht 27% gewijzigd door koffiegast op 21-02-2010 02:37:59 ]
De limiet van f in a bestaat niet als er voor een zekere
Klopt dit?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:38:46 ]
quote:Zeker weten? Het klinkt namelijk als een soort van instinker.Op dinsdag 16 februari 2010 21:33 schreef thabit het volgende:
[..]
Wel, bijvoorbeeld iets als ab{c,d}bba.
quote:Nee.Op zondag 21 februari 2010 02:23 schreef koffiegast het volgende:
Symmetrie met dezelfde waarden voor alfa/beta.
quote:Nee.Uit reflexiviteit en symmetrie volgt transiviteit.
quote:Nee, er moet een eps>0 bestaan zodanig dat er geen delta>0 bestaat zodanig dat de implicatie waar is.Op zondag 21 februari 2010 16:30 schreef BasementDweller het volgende:
Ik moet aan de hand van de delta-epsilon definitie van een limiet bewijzen dat een limiet niet bestaat. Daarvoor wil ik de negatie van de eps-delta definitie gebruiken. Als ik het goed heb luidt deze als volgt:
De limiet van f in a bestaat niet als er voor een zekere [ afbeelding ] een positief reëel getal [ afbeelding ]bestaat zodat de volgende implicatie niet waar is: [ afbeelding ] en[ afbeelding ] [ afbeelding ] [ afbeelding ].
Klopt dit?
[ Bericht 3% gewijzigd door GlowMouse op 21-02-2010 16:51:47 ]
quote:Ja.Op zondag 21 februari 2010 16:33 schreef Keiichi het volgende:
[..]
Zeker weten? Het klinkt namelijk als een soort van instinker.
[ Bericht 49% gewijzigd door BasementDweller op 21-02-2010 16:50:37 ]
quote:Blijkbaar mag ik dan weer gaan opzoeken hoe relaties in domeinen in zijn werk gaat
Ik kom niet van een wiskundige achtergrond. Waar ik nu op zoek zijn lineaire functies, mapping, morfismes en relaties tussen functies, is dit wel waar ik naar moet zoeken?
[ Bericht 13% gewijzigd door koffiegast op 21-02-2010 18:00:46 ]
quote:Wat ik snap van reflexief/symmetrie/transitief is dat je dingen als het volgende moet hebben:Op zondag 21 februari 2010 18:07 schreef GlowMouse het volgende:
Nee, dit kun je gewoon beredeneren vanuit de definities.
for all a in N, Raa
for all a,b in N, Rab -> Rba
for all a,b,c in N, Rab ^ Rbc -> Rac
Ik heb alleen nooit iets geleerd over hoe ik dit kan koppelen bij zoiets als die functies.
Ik zie wel in dat als je alfa = 1, beta = 0 doet dat je dan v(N) = w(N) krijgt, maar of dat reflexief is.. dat weet ik eigenlijk niet eens zeker. Wat ik maar dus aannam was dat in dit geval reflexief was en dat je dus Rv(N),w(N) hebt en dus ook Rw(N),v(N) en dus symmetrie hebt en dat je hieruit ook transitief hebt. Maar dat was meer een hersenscheet, ik heb eerlijk gezegd geen flauw idee hoe ik die functie moet koppelen aan iets als een relatie, want ik heb zoiets nooit gehad.
Kan bij symmetrie het zo zijn dat je bij de definitie bv zoiets kan hebben:
w(C) = Alfa*v(C) + sum(i in C) Beta i
v(C) = 1/alfa*w(C) + sum(i in C) -(Beta i / alfa)
Ik was onder de impressie dat bij symmetrie dezelfde soort handelingen moeten worden gedaan, maar blijkbaar komt symmetrie enkel er op neer dat je van het ene naar het andere kant met de bepaalde waardens?
[ Bericht 7% gewijzigd door koffiegast op 21-02-2010 18:35:18 ]
"Reflexive: (N,v) is strategisch equivalent met (N,v) omdat dit direct volgt uit de definitie met alpha=1 en beta=0.
Symmetric: Als (N,v) equivalent is aan (N,w) dan geldt ...., nu geldt ook dat (N,w) equivalent is aan (N,v) omdat ...."
Ik moet toch juist aantonen dat het equivalent op basis van dat het strategical equivalent is i.p.v. dat ik aanneem dat het equivalent is?
for all a,b in N, Rab -> Rba
Voor het bewijs hiervan neem je Rab aan en kom je van daaruit op Rba.
Ik raak in de war van het stukje ''may be true of something". Wat is dat "something"? Een wiskundig object? Kan iemand dit verduidelijken met een voorbeeld?
Axioma's zijn altijd uitgangspunten van waaruit je verder redeneert. Zo bestaan er ook axioma's voor de verzamelingenleer. Een van de eerste voorbeelden die mensen vaak geven als verzamelingen worden uitgelegd is een verzameling van koeien. Dit is echter een slecht voorbeeld want uit de axioma's voor de verzamelingenleer kan niet afgeleid worden dat er zoiets als een verzameling van koeien bestaat.
quote:Wat ze met "they may be true of something" bedoelen snap ik ook niet echt. Met "Axioms are not true in any absolute sense" bedoelen ze denk ik dat je niet kan afleiden/bewijzen dat ze waar zijn. Axioma's zijn eigenlijk aannames die je moet maken waaruit alle andere stellingen in een systeem uit volgen. Als je dat idee snapt voegt het zinnetje "but they may be true of something" denk ik niet zoveel toeOp maandag 22 februari 2010 14:13 schreef gaussie het volgende:
Ik ben nu het boek concepts of modern mathematics aan het lezen. Een aanrader voor iedereen die geinteresseerd is in wiskunde, maar dat terzijde. In het hoofstuk over axiomatische systemen ben ik een beetje vastgelopen. Vooral op 1 bepaalde passage. Die luidt als volgt: 'Are the group axioms true?', is a nonsense question. Axioms are not true in any absolute sense; but they may be true of something.
Ik raak in de war van het stukje ''may be true of something". Wat is dat "something"? Een wiskundig object? Kan iemand dit verduidelijken met een voorbeeld?
Als je de functie x/(x+3) integreer kom je uit op:
x-3ln(x+3)+C
Maar als ik dat vervolgens afleidt kom ik uit op:
1-3/(x+3). En dus niet x/(x+3). Dit is dezelfde functie, maar hoe schrijf je 1-3(x+3) om naar x/(x+3) of moet je dat gewoon beredeneren oid?
quote:van 1-3/(x+3) naar x/x+3 is makkelijk, je schrijft gewoon 1 om naar x+3/x+3Op dinsdag 23 februari 2010 14:49 schreef Conversatie het volgende:
Ik vroeg me het volgende af:
Als je de functie x/(x+3) integreer kom je uit op:
x-3ln(x+3)+C
Maar als ik dat vervolgens afleidt kom ik uit op:
1-3/(x+3). En dus niet x/(x+3). Dit is dezelfde functie, maar hoe schrijf je 1-3(x+3) om naar x/(x+3) of moet je dat gewoon beredeneren oid?
andersom gebruik je staartdelen
quote:Ah verrek, dat ik daar niet zelf op kwam.Op dinsdag 23 februari 2010 15:11 schreef -jos- het volgende:
[..]
van 1-3(x+3) naar x/x+3 is makkelijk, je schrijft gewoon 1 om naar x+3/x+3
andersom gebruik je staartdelen
Ik dacht: t/n
t = x
t'= 1
n= (3x^2+1)^2
n'= 12x(3x^2+1)
Dus:
f'(x) =
En dat valt te herleiden tot:
Maar volgens het antwoordboekje moet ik niet 12x^2 krijgen, maar 9x^2 ?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:40:00 ]
Bedankt
f(x) = x e^x
Dus:
f'(x) = e^x + xe^x
f ''(x)= 2e^x + xe^x
F '' (x) = 0 levert op x = -2
Maar wat moet ik dan doen?
quote:Bepaal de richtingscoëfficiënt van de buigraaklijn en de coördinaten van het buigpunt. Met die twee gegevens kun je de vergelijking van de buigraaklijn opstellen.Op donderdag 25 februari 2010 15:27 schreef Siddartha het volgende:
Stel een vergelijking op van de buigraaklijn k van de grafiek van
f(x) = x e^x
Dus:
f'(x) = e^x + xe^x
f''(x)= 2e^x + xe^x
f'' (x) = 0 levert op x = -2
Maar wat moet ik dan doen?
quote:Ah, x=-2 invullen in f'(x) geeft de rc !Op donderdag 25 februari 2010 16:22 schreef Riparius het volgende:
[..]
Bepaal de richtingscoëfficiënt van de buigraaklijn en de coördinaten van het buigpunt. Met die twee gegevens kun je de vergelijking van de buigraaklijn opstellen.
Bedankt, nu klopt het.
Nu ik toch aan het vragen ben, hoe kan ik dit (algebraisch) oplossen:
( Er moet staan, e tot de macht -0.01x^2)
[ Bericht 19% gewijzigd door motorbloempje op 01-09-2013 21:40:07 ]
quote:Nee, zou je me die uit kunnen leggen?
(Wiki/mathworld/google bieden ook geen uitleg)
f(x) = 1 + 2sin(x-1/3Pi) Met domein [0, 2Pi ]
Bereken de oppervlakte van het vlakdeel dat ingesloten wordt door de grafiek van f en de x-as.
Ik kom er niet uit... Snijpunten berekenen, dan primitiveren.
Snijpunten zijn (volgens mij) x= 1/2 Pi V x= 1/1/6Pi
F(x) = x-2cos(x-1/3Pi)
Als ik dan F(1/1/6Pi) - F(1/2Pi) doe krijg ik
1/1/6Pi + Wortel3 - 1/2Pi +wortel3 = 2wortel3 + 5/6Pi
Maar volgens het antwoordboekje moet het 2wortel 3 + 1/1/3Pi zijn ?
quote:De vergelijking die je geeft is niet algebraïsch op te lossen, en Lambert W verandert daar niets aan. Weet je wel zeker dat je de juiste vergelijking hebt opgesteld als het expliciet de bedoeling is deze algebraïsch op te lossen?Op donderdag 25 februari 2010 19:30 schreef Siddartha het volgende:
[..]
Nee, zou je me die uit kunnen leggen?
(Wiki/mathworld/google bieden ook geen uitleg)
quote:Je snijpunten met de x-as zijn fout. Bereken die nog eens of laat zien wat je gedaan hebt.Op vrijdag 26 februari 2010 12:05 schreef Siddartha het volgende:
Gegeven is de functie :
f(x) = 1 + 2sin(x-1/3Pi) Met domein [0, 2Pi ]
Bereken de oppervlakte van het vlakdeel dat ingesloten wordt door de grafiek van f en de x-as.
Ik kom er niet uit... Snijpunten berekenen, dan primitiveren.
Snijpunten zijn (volgens mij) x= 1/2 Pi V x= 1/1/6Pi
F(x) = x-2cos(x-1/3Pi)
Als ik dan F(1/1/6Pi) - F(1/2Pi) doe krijg ik
1/1/6Pi + Wortel3 - 1/2Pi +wortel3 = 2wortel3 + 5/6Pi
Maar volgens het antwoordboekje moet het 2wortel 3 + 1/1/3Pi zijn ?
quote:Daar moet inderdaad wel de fout zitten.Op vrijdag 26 februari 2010 12:12 schreef Riparius het volgende:
[..]
Je snijpunten met de x-as zijn fout. Bereken die nog eens of laat zien wat je gedaan hebt.
Even kijken,
1+2sin(x-1/3Pi) = 0
sin(x-1/3Pi) = -0.5
Sin p = -0.5
p = 1/1/6Pi v p = 1/5/6Pi
Dus
x= 1/1/6Pi + 1/3Pi = 1/1/2Pi
v
x= 2/1/6Pi
Hmm, dan komt het nog steeds niet uit?
quote:Hier gaat het verkeerd.Op vrijdag 26 februari 2010 12:24 schreef Siddartha het volgende:
[..]
Daar moet inderdaad wel de fout zitten.
Even kijken,
1+2sin(x-1/3Pi) = 0
sin(x-1/3Pi) = -0.5
Sin p = -0.5
p = 1/1/6Pi v p = 1/5/6Pi
sin(x-π/3) = -½
x - π/3 = -1/6∙π + 2kπ of x - π/3 = 7/6∙π + 2kπ.
Nu mag je zelf weer even verder.
quote:Ah, dat anders opschrijven geeftOp vrijdag 26 februari 2010 12:30 schreef Riparius het volgende:
[..]
Hier gaat het verkeerd.
sin(x-π/3) = -½
x - π/3 = -1/6∙π + 2kπ of x - π/3 = 7/6∙π + 2kπ.
Nu mag je zelf weer even verder.
x= 1/6Pi v x= 1/1/2Pi
En dan klopt de rest ook!
Bedankt!
Let T: V-> V be an invertible transformation. Show that if v in Vis an eigenvector of T, then [v] in P(V) is a fixed point of the projective transformation 'tau' defined by T. Prove that any projective transformation of P2(R) has a fixed point.
Eerste deel van de vraag lukte nog wel. Met een plaatje erbij wat het in de R2 betekent enzo. Dat snap ik wel redelijk. Denk ik.
Tweede deel "bewijs dat elke projectieve transformatie van P2(R) een fixed point heeft" is lastiger. Ik moet mezelf afvragen, denk ik, of er altijd een (reële) eigenwaarde (dus bijbehorende eigenvector ook reëel, toch?) is. Een trasnformatie met P2(R), dus in de R3. De representatieve matrix is dus 3x3. Voor de eigenwaarden te berekenen krijg je een derdegraadspolynoom dus in principe drie antwoorden. Als er een complexe waarde bij zit, dan ook de complex geconjugeerde. Dus zou er minstens één reële oplossing moeten zijn.
Ik twijfel alleen nog of het niet ook kan dat stel je hebt λ1, λ2, λ3. Dat dan λ1 = λ2 en λ3 is de complex geconjugeerde van deze. Dus twee dezelfde complexe waarden.
En daarbij kan een eigenwaarde ook altijd 0 zijn, toch? Of zelfs alledrie nul. Als de enige eigenwaarde nul is, gaat het dan allemaal nog wel zoals ik wil gaan?
Bovendien, als een polynoom f in R[x] een complex nulpunt a van een bepaalde multipliciteit heeft, dan heeft de complex geconjugeerde a' dezelfde multipliciteit als nulpunt: g := (x-a)(x-a') heeft reele coefficienten en dus f/g ook.
Als f(x) een polynoom is en a een nulpunt, dan kun je f(x) factoriseren: f(x) = (x-a)m * g(x), waarbij m een positief geheel getal is en g(x) een polynoom dat a niet als nulpunt heeft. De multipliciteit van a is dan m.
rank(A) = rank(A*A)
(waarbij A* de getransponeerde van de complex geconjugeerde van A is).
De hint is om te gebruiken dat ker(A) = ker(A*A). Verder weet ik dat Ran(A) + dim(ker(A)) = n (misschien dat ik dat nodig heb).
Kan iemand een hint geven, want ik zie niet hoe ik dit kan aanpakken
rank(A) + dim(ker(A)) = n
rank(A*A) + dim(ker(A*A)) = n
meer heb je niet nodig.
Klein hintje nodig hoe te beginnen
Ik heb al bedacht: Als Ax=0 => x=0, dan IAx=I0=0 => x=0. Ook geldt: Ix=0 => x=0.
quote:Bedoel je met Col A de range van A?Op zondag 28 februari 2010 19:43 schreef GlowMouse het volgende:
A is links-inverteerbaar desda Ax=b slechts één oplossing heeft voor iedere b in ColA.
Klopt dit?
Het is waarschijnlijk iets heel simpels, maar ik zie het gewoon niet
Ik weet ook niet wat je kan zeggen over AT als Ax=0 =>x=0. Misschien dat ATx=0 => x=0 ?
dus kolommen A lin.onafh.
dus rank(AT) =n en m>=n.
dus AT x = b heeft een oplossing voor elke x.
quote:Oké. Dus alleen maar nullen is in ieder geval niet mogelijk, en alleen maar complexe getallen ook niet. Wat je nu zegt over multipliciteit herinner ik me inderdaad van lineaire algebra.Op zondag 28 februari 2010 14:44 schreef thabit het volgende:
Een projectieve transformatie is altijd inverteerbaar. Als ze dat niet is, dan moet ze een punt in V naar 0 sturen, maar daar is dan de afbeelding niet gedefinieerd.
Als f(x) een polynoom is en a een nulpunt, dan kun je f(x) factoriseren: f(x) = (x-a)m * g(x), waarbij m een positief geheel getal is en g(x) een polynoom dat a niet als nulpunt heeft. De multipliciteit van a is dan m.
Maar is 't niet alsnog mogelijk om twee complexe eigenwaarden te hebben en één eigenwaarde 0?
quote:Nee, want dan zou de matrix een niet-triviale kern hebben en er dus punten naar (0:0:0) gestuurd moeten worden.Op zondag 28 februari 2010 21:35 schreef Hanneke12345 het volgende:
[..]
Oké. Dus alleen maar nullen is in ieder geval niet mogelijk, en alleen maar complexe getallen ook niet. Wat je nu zegt over multipliciteit herinner ik me inderdaad van lineaire algebra.
Maar is 't niet alsnog mogelijk om twee complexe eigenwaarden te hebben en één eigenwaarde 0?
Bedankt, dan snap ik het geloof ik wel
quote:Je bedoelt een oplossing voor elke b?Op zondag 28 februari 2010 20:45 schreef GlowMouse het volgende:
Ax=0 =>x=0
dus kolommen A lin.onafh.
dus rank(AT) =n en m>=n.
dus AT x = b heeft een oplossing voor elke x.
f(x) = 2sin^2 x + sin x - 1
Punt A ligt op de grafiek met Xa = 1/3Pi
Stel de lijn k op die de grafiek raakt in A.
Eerst f(x) anders opschrijven:
f(x) = -cos2x +sinx
Die differentieren: f'(x) = sin2x + cosx
Invullen voor f'(1/3Pi) geeft de rc, dus:
f'(1/3Pi) =Wortel3 + 1/2
Dan k = (wortel3+1/2)x + b gelijkstellen aan f(1/3Pi)
(wortel3 +1/2)(1/3Pi)+ b = -1 + 1/2Wortel3
b= -1 + 1/2wortel3 -1/3Piwortel3 - 1/6Pi
Maar dit klopt niet( -1 moet +1/2 zijn?).
Heeft iemand nog tips voor goniometrie, met name het omzetten van sinussen in cosinussen en andersom? Ik heb de standaard omzettingen ( sin^2 x + cos^2 x = 1 bijv.), maar ik snap niet precies wat ik moet doen als de gegeven functie niet helemaal volgens zo'n omzetting is (zoals hierboven).
(Wijziging: andere vraag gepakt)
[ Bericht 42% gewijzigd door Siddartha op 01-03-2010 11:12:13 ]
quote:Nee, hier gaat het fout. Je gebruikt de kettingregel niet correct. De afgeleide van -cos 2x is 2∙sin 2x.Op maandag 1 maart 2010 08:46 schreef Siddartha het volgende:
Gegeven is de formule :
f(x) = 2sin^2 x + sin x - 1
Punt A ligt op de grafiek met Xa = 1/3Pi
Stel de lijn k op die de grafiek raakt in A.
Eerst f(x) anders opschrijven:
f(x) = -cos2x +sinx
Die differentiëren: f'(x) = sin2x + cosx
quote:Leg eens uit waarom je de functie hierboven überhaupt wil omschrijven. Kennelijk om het jezelf wat makkelijker te maken bij het differentiëren, maar dat doe je dan alsnog fout. Het is niet nodig deze functie om te schrijven om de afgeleide ervan te bepalen. Bij integreren daarentegen kunnen goniometrische identiteiten goede diensten bewijzen, bijvoorbeeld om een integrand die een rationale functie is van sin x, cos x en tan x om te zetten in een rationale functie van t via de substitutie t = tan ½x.Op maandag 1 maart 2010 08:46 schreef Siddartha het volgende:
Heeft iemand nog tips voor goniometrie, met name het omzetten van sinussen in cosinussen en andersom? Ik heb de standaard omzettingen ( sin^2 x + cos^2 x = 1 bijv.), maar ik snap niet precies wat ik moet doen als de gegeven functie niet helemaal volgens zo'n omzetting is (zoals hierboven).
[ Bericht 0% gewijzigd door Riparius op 01-03-2010 16:03:06 ]
quote:Volgens mij is het ook niet noodzakelijk, maar meer om vertrouwd te raken met goniometrische functies. Maar ik zou dus ook een functie als f(x)= sin^2 (3x) gewoon volgens de productregel kunnen integreren/differntieren ?Op maandag 1 maart 2010 15:01 schreef Riparius het volgende:
[..]
Leg eens uit waarom je de functie hierboven überhaupt wil omschrijven. Kennelijk om het jezelf wat makkelijker te maken bij het differentiëren, maar dat doe je dan alsnog fout. Het is niet nodig deze functie om te schrijven om de afgeleide ervan te bepalen. Bij integreren daarentegen kunnen goniometrische identiteiten goede diensten bewijzen, bijvoorbeeld om een integrand die een rationale functie is van sin x, cos x en tan x om te zetten in een rationale functie van t via de substitutie t = tan ½x.
quote:Differentiëren is eenvoudig m.b.v. (tweemaal!) de kettingregel, maar integreren van iets als f(x) = sin2(3x) is (uit het blote hoofd) niet zo eenvoudig. Maar het kwadraat van een sinus of cosinus kun je eenvoudig omzetten in de cosinus van de dubbele hoek en dan kun je het wel weer eenvoudig integreren.Op maandag 1 maart 2010 16:55 schreef Siddartha het volgende:
[..]
Volgens mij is het ook niet noodzakelijk, maar meer om vertrouwd te raken met goniometrische functies. Maar ik zou dus ook een functie als f(x)= sin^2 (3x) gewoon volgens de productregel kunnen integreren/differntieren ?
quote:Dus bij primitiveren wel gebruik maken van de identiteiten?Op maandag 1 maart 2010 17:04 schreef Riparius het volgende:
[..]
Differentiëren is eenvoudig m.b.v. (tweemaal!) de kettingregel, maar integreren van iets als f(x) = sin2(3x) is (uit het blote hoofd) niet zo eenvoudig. Maar het kwadraat van een sinus of cosinus kun je eenvoudig omzetten in de cosinus van de dubbele hoek en dan kun je het wel weer eenvoudig integreren.
Dan zit er niks anders op dan meer oefenen.
quote:Tja, ach, de voornaamste goniometrische identiteiten zou je gewoon uit het hoofd moeten kennen. Als je dat niet lukt, zorg ervoor dat je dan in ieder geval de somformules voor cos(α+β) en sin(α+β) wel uit het blote hoofd kent, aangezien je de meeste andere identiteiten daar gemakkelijk uit af kunt leiden. Voor de cosinus van de dubbele hoek zijn er drie formules die vaak van pas komen, als volgt:Op maandag 1 maart 2010 17:18 schreef Siddartha het volgende:
[..]
Dus bij primitiveren wel gebruik maken van de identiteiten?
Dan zit er niks anders op dan meer oefenen.
cos 2α = cos2α - sin2α
cos 2α = 2cos2α - 1
cos 2α = 1 - 2sin2α
Uit de tweede en derde van deze formules volgt direct hoe je een kwadraat van een cosinus of sinus om kunt zetten in de cosinus van de dubbele hoek:
cos2α = ½(1 + cos 2α)
sin2α = ½(1 - cos 2α)
Zo kan ik direct zeggen dat f(x) = sin23x = ½(1 - cos 6x), zodat een primitieve van deze functie is: F(x) = ½x - (1/12)∙sin 6x.
verkapte tvp overigens.
quote:Ik zal het zo proberen te onthouden en er nog wat mee oefenen.Op maandag 1 maart 2010 17:34 schreef Riparius het volgende:
[..]
Tja, ach, de voornaamste goniometrische identiteiten zou je gewoon uit het hoofd moeten kennen. Als je dat niet lukt, zorg ervoor dat je dan in ieder geval de somformules voor cos(α+β) en sin(α+β) wel uit het blote hoofd kent, aangezien je de meeste andere identiteiten daar gemakkelijk uit af kunt leiden. Voor de cosinus van de dubbele hoek zijn er drie formules die vaak van pas komen, als volgt:
cos 2α = cos2α - sin2α
cos 2α = 2cos2α - 1
cos 2α = 1 - 2sin2α
Uit de tweede en derde van deze formules volgt direct hoe je een kwadraat van een cosinus of sinus om kunt zetten in de cosinus van de dubbele hoek:
cos2α = ½(1 + cos 2α)
sin2α = ½(1 - cos 2α)
Zo kan ik direct zeggen dat f(x) = sin23x = ½(1 - cos 6x), zodat een primitieve van deze functie is: F(x) = ½x - (1/12)∙sin 6x.
In ieder geval bedankt voor je hulp
quote:Dat is waar. Als je begrijpt dat:Op maandag 1 maart 2010 17:55 schreef Borizzz het volgende:
Complexe functies kun je ook gebruiken bij het vinden van goniometrische relaties.
verkapte tvp overigens.
cos(α+β) + i∙sin(α+β) = (cos α + i∙sin α)(cos β + i∙sin β)
dan hoef je zelfs de somformules voor cos(α+β) en sin(α+β) niet uit het blote hoofd te weten. Maar ik heb het idee dat Siddartha daar nog niet aan toe is.
quote:Klopt, ik heb geen idee waar het over gaat.Op maandag 1 maart 2010 18:10 schreef Riparius het volgende:
[..]
Dat is waar. Als je begrijpt dat:
cos(α+β) + i∙sin(α+β) = (cos α + i∙sin α)(cos β + i∙sin β)
dan hoef je zelfs de somformules voor cos(α+β) en sin(α+β) niet uit het blote hoofd te weten. Maar ik heb het idee dat Siddartha daar nog niet aan toe is.
Om mijn 'niveau' aan te geven, ik heb wiskunde a12 afgesloten met een 8+. Daarna ben ik een verkeerde studie gaan doen, waarna ik erachter kwam dat ik wat met wiskunde wil gaan doen. Dus probeer ik nu in april mijn voortentamen wiskunde B (nieuwe nieuwe nieuwe fase) met zelfstudie te halen. Wat nog best pittig is, in die korte tijd.
quote:De identiteit die ik gaf laat zien dat bij vermenigvuldiging van twee complexe getallen de argumenten worden opgeteld. In Nederland is het nog steeds zo dat complexe getallen niet in de normale schoolstof zitten, terwijl dat in veel andere landen wel zo is. Ik kwam pas nog wat aardige PDFjes tegen van een Vlaamse zomercursus, hier. Daar zit een ook PDF bij met een inleiding in de complexe getallen. Misschien heb je daar wat aan.Op maandag 1 maart 2010 18:19 schreef Siddartha het volgende:
[..]
Klopt, ik heb geen idee waar het over gaat.
quote:Ah, zo. Wat moet je (ongeveer) weten voor dat tentamen in april? Wellicht heb ik nog wat linkjes of tips voor je.Om mijn 'niveau' aan te geven, ik heb wiskunde a12 afgesloten met een 8+. Daarna ben ik een verkeerde studie gaan doen, waarna ik erachter kwam dat ik wat met wiskunde wil gaan doen. Dus probeer ik nu in april mijn voortentamen wiskunde B (nieuwe nieuwe nieuwe fase) met zelfstudie te halen. Wat nog best pittig is, in die korte tijd.
quote:Ik heb het bij mijn favorieten gezet, ik ga het zeker doorbladeren. Er staat ook goniometrie bij, met een beetje uitleg! Geweldig, dat is al een stuk beter dan puur wat formules en opdrachten.Op maandag 1 maart 2010 18:45 schreef Riparius het volgende:
[..]
De identiteit die ik gaf laat zien dat bij vermenigvuldiging van twee complexe getallen de argumenten worden opgeteld. In Nederland is het nog steeds zo dat complexe getallen niet in de normale schoolstof zitten, terwijl dat in veel andere landen wel zo is. Ik kwam pas nog wat aardige PDFjes tegen van een Vlaamse zomercursus, hier. Daar zit een ook PDF bij met een inleiding in de complexe getallen. Misschien heb je daar wat aan.
[..]
Ah, zo. Wat moet je (ongeveer) weten voor dat tentamen in april? Wellicht heb ik nog wat linkjes of tips voor je.
Mijn grootste deficiënt is meetkunde/goniometrie. Primitiver en de afgeleide vinden lukt aardig, maar die gebieden blijven nog onduidelijk voor me. Hoe zo'n functie om te schrijven en wat wel/niet geoorloofd is, is me nog niet helemaal duidelijk.
Inhoud van Wiskunde B:
In het centraal examen zal meer dan in de vorige situatie het geval was aandacht
worden besteed aan formele wiskunde, wiskunde zonder context, en het abstracte
denken. Subdomein A5 is hierdoor aan het examenprogramma toegevoegd. Het geeft
aan dat de bij het examenprogramma passende algebraïsche vaardigheden ook zonder
gebruik van een grafische rekenmachine moeten worden beheerst.
Domeinen Subdomeinen
A: Vaardigheden A1: Informatievaardigheden
A2: Onderzoeksvaardigheden
A3: Technisch-instrumentele vaardigheden
A4: Oriëntatie op studie en beroep
A5: Algebraïsche vaardigheden
Bg: Functies en grafieken Bg1: Standaardfuncties
Bg2: Functies, grafieken, vergelijkingen en ongelijkheden
Cg: Discrete analyse Cg1: Veranderingen
Bb: Differentiaal- en
integraalrekening
Bb1: Afgeleide functies
Bb2: Algebraïsche technieken
Bb3: Integraalrekening
Db: Goniometrische functies Db1: Goniometrische functies
Gb: Voortgezette meetkunde Gb1: Oriëntatie op bewijzen
Gb2: Constructie en bewijzen in de vlakke meetkunde
F: Keuzeonderwerpen
Bron: http://www.digischool.nl/(...)B_vwo_DEFINITIEF.pdf
Gaat daar jouw tentamen over?
Op zich wel pittige onderdelen, maar wel te doen als je er de tijd voor hebt en er energie in wil steken.
En hier op dit forum kunnen we jou wel een handje helpen.
quote:OK. Die PDF vind ik nogal een 'ambtelijk' stuk, waar ik niet zoveel wijzer van word. Vaak wordt het Basisboek Wiskunde van Van de Craats aangeraden. Ik kende dat boek inhoudelijk niet zo, maar het blijkt integraal op een legale (!) webserver te staan, zodat ik het eens door heb kunnen nemen, en ik ben er niet enthousiast over. Ik vind het niet erg geschikt voor zelfstudie als je niet op een docent terug kunt vallen, al was het maar door het ontbreken van uitwerkingen.Op maandag 1 maart 2010 18:58 schreef Siddartha het volgende:
[..]
Ik heb het bij mijn favorieten gezet, ik ga het zeker doorbladeren. Er staat ook goniometrie bij, met een beetje uitleg! Geweldig, dat is al een stuk beter dan puur wat formules en opdrachten.
Mijn grootste deficiënt is meetkunde/goniometrie. Primitiver en de afgeleide vinden lukt aardig, maar die gebieden blijven nog onduidelijk voor me. Hoe zo'n functie om te schrijven en wat wel/niet geoorloofd is, is me nog niet helemaal duidelijk.
[snip]
Db: Goniometrische functies Db1: Goniometrische functies
Gb: Voortgezette meetkunde Gb1: Oriëntatie op bewijzen
Gb2: Constructie en bewijzen in de vlakke meetkunde
F: Keuzeonderwerpen[/i]
Bron: http://www.digischool.nl/(...)B_vwo_DEFINITIEF.pdf
Veel beter geschikt voor zelfstudie vind ik dan een aantal publicaties van de Open Universiteit die je terug kunt vinden op hun website als je even slim zoekt. Die geven meer dan je waarschijnlijk nodig hebt, maar ik zou ze zeker eens doorkijken, je kunt er veel uit leren.
Voor de vlakke meetkunde, tenslotte, kun je hier goed terecht. Mooi overzicht van alle belangrijke stellingen, met bewijzen.
quote:Het is een keuze onderdeel binnen wiskunde D.Op maandag 1 maart 2010 18:45 schreef Riparius het volgende:
[..]
In Nederland is het nog steeds zo dat complexe getallen niet in de normale schoolstof zitten, terwijl dat in veel andere landen wel zo is. Ik kwam pas nog wat aardige PDFjes tegen van een Vlaamse zomercursus,
bron: http://www.nvvw.nl/media/downloads/examens/examenprogramma_wiskunde_d_vwo_definitief.pdf
Het is alleen jammer dat niet alle middelbare scholen wiskunde D ook daadwerkelijk aanbieden.
quote:Vd Craats heeft ook een "inleiding" geschreven over complexe getallen:Ah, zo. Wat moet je (ongeveer) weten voor dat tentamen in april? Wellicht heb ik nog wat linkjes of tips voor je.
http://staff.science.uva.nl/~craats/CGnieuw.pdf
quote:Ja, dat weet ik. Maar daarmee is het nog geen standaard onderdeel van de stof, terwijl dat in veel andere (Europese) landen wel zo is.Op maandag 1 maart 2010 21:16 schreef Borizzz het volgende:
[..]
Het is een keuze onderdeel binnen wiskunde D.
bron: http://www.nvvw.nl/media/downloads/examens/examenprogramma_wiskunde_d_vwo_definitief.pdf
[..]
quote:Ja, weet ik. Hoewel ik zijn oude versie wat aardiger vind.Vd Craats heeft ook een "inleiding" geschreven over complexe getallen:
http://staff.science.uva.nl/~craats/CGnieuw.pdf
quote:Bedankt! Daar kom ik al een stuk verder mee.Op maandag 1 maart 2010 20:12 schreef Riparius het volgende:
[..]
OK. Die PDF vind ik nogal een 'ambtelijk' stuk, waar ik niet zoveel wijzer van word. Vaak wordt het Basisboek Wiskunde van Van de Craats aangeraden. Ik kende dat boek inhoudelijk niet zo, maar het blijkt integraal op een legale (!) webserver te staan, zodat ik het eens door heb kunnen nemen, en ik ben er niet enthousiast over. Ik vind het niet erg geschikt voor zelfstudie als je niet op een docent terug kunt vallen, al was het maar door het ontbreken van uitwerkingen.
Veel beter geschikt voor zelfstudie vind ik dan een aantal publicaties van de Open Universiteit die je terug kunt vinden op hun website als je even slim zoekt. Die geven meer dan je waarschijnlijk nodig hebt, maar ik zou ze zeker eens doorkijken, je kunt er veel uit leren.
Voor de vlakke meetkunde, tenslotte, kun je hier goed terecht. Mooi overzicht van alle belangrijke stellingen, met bewijzen.
Verder zal ik gewoon moeten doorbijten en veel oefenen.
Weet je toevallig ook (Wat een vragen!) hoe het niveau van een voortentamen is? (http://www.ccvx.nl/)
Ik zie net dat zo'n examen iets afwijkt van een normaal eindexamen,
"Het programma van het voortentamen wiskunde B is gebaseerd op het examenprogramma Wiskunde B van
het vwo en omvat de volgende domeinen uit dit programma:
- A5: Algebraïsche vaardigheden
- Bg: Functies en Grafieken
- Bb: Differentiaal- en integraalrekening
- Cg: Discrete analyse
- Db: Goniometrische functies
- Gb: Voortgezette Meetkunde
Bij het voortentamen ligt de nadruk op domeinen Bg en Bb en Db. De algebraïsche vaardigheden komen in de
opgaven over deze drie domeinen met nadruk aan de orde. In bijlage 1 vindt u een overzicht van de inhoud
van de domeinen."
quote:Probeer een goede balans te bewaren tussen het krijgen van inzicht en het krijgen van routine in het oplossen van opgaven of het gebruik van standaardtechnieken (zoals algebraïsche herleidingen, werken met goniometrische formules of differentiëren). Wiskunde gaat niet (alleen) over het maken van sommetjes. En wees niet bang dat je te veel doet, dat is nooit weg als je later verder gaat met iets waar wiskunde aan te pas komt.Op dinsdag 2 maart 2010 10:08 schreef Siddartha het volgende:
[..]
Bedankt! Daar kom ik al een stuk verder mee.
Verder zal ik gewoon moeten doorbijten en veel oefenen.
quote:Geen idee, eerlijk gezegd. Maar pin jezelf niet vast op allerlei opsommingen over wat je wel of niet moet weten. Je kunt beter te veel weten dan te weinig.Weet je toevallig ook (Wat een vragen!) hoe het niveau van een voortentamen is? (http://www.ccvx.nl/)
Ik zie net dat zo'n examen iets afwijkt van een normaal eindexamen,
Stel r+sqrt{2}=a/b
dan (r+sqrt{2})^2=a^2/b^2
Dus r^2+2sqrt{2}+2=a^2/b^2
Kan ik dan nu gewoon 2(1/2r^2+sqrt{2}+1)=a^2/b^2, en dan concluderen dat ggd(a,b) minstens 2 moet zijn dus tegenspraak?
[ Bericht 0% gewijzigd door Hanneke12345 op 02-03-2010 12:54:33 ]
quote:Ik begrijp je aanpak niet zo, althans niet als je gebruik mag maken van het feit dat √2 irrationaal is. Als r + √2 = a/b (met a,b ∈ ℤ, b ≠ 0) en r ∈ ℚ, dan zijn er twee getallen p,q ∈ ℤ, q ≠ 0 zodanig dat r = p/q en heb je dus √2 = a/b - p/q = (aq - bp)/bq, waarmee √2 rationaal zou zijn: een tegenspraak. Ergo, r + √2 is niet rationaal voor r ∈ ℚ.Op dinsdag 2 maart 2010 12:39 schreef Hanneke12345 het volgende:
Ik wil laten zien dat {r+sqrt{2} : r in Q} irrationaal is.
Stel r+sqrt{2}=a/b
dan (r+sqrt{2})^2=a^2/b^2
Dus r^2+2sqrt{2}+2=a^2/b^2
Kan ik dan nu gewoon 2(1/2r^2+sqrt{2}+1)=a^2/b^2, en dan concluderen dat ggd(a,b) minstens 2 moet zijn dus tegenspraak?
f(x) = sin 2x
V is het vlakdeel dat word ingesloten door f(x), de x-as, x= 1/3Pi, en x= 1/6Pi.
Bereken het omwentelingslichaam dat ontstaat als V wentelt om de x-as.
Ah, ik moet f(x) eerst kwadrateren en dan pas integreren!
[ Bericht 31% gewijzigd door Siddartha op 02-03-2010 13:56:04 ]
quote:Je bedoelt neem ik aan het volume van het omwentelingslichaam? En wat is je uitkomst?Op dinsdag 2 maart 2010 13:50 schreef Siddartha het volgende:
Dit is zo frustrerend!
f(x) = sin 2x
V is het vlakdeel dat wordt ingesloten door f(x), de x-as, x= 1/3Pi, en x= 1/6Pi.
Bereken het omwentelingslichaam dat ontstaat als V wentelt om de x-as.
Ah, ik moet f(x) eerst kwadrateren en dan pas integreren!
quote:In het boek staat gewoon 'het vlakdeel', wat in dit geval gelijk is aan het volume (toch?).Op dinsdag 2 maart 2010 14:22 schreef Riparius het volgende:
[..]
Je bedoelt neem ik aan het volume van het omwentelingslichaam? En wat is je uitkomst?
Uitkomst had ik 1/12Pi^2 + 1/8Pi Wortel3
(als primitive functie had ik F(x) = 1/2x -1/8sin4x , invullen voor b=1/3pi en a = 1/6 pi, etc geeft de inhoud. Dat keer Pi en ik heb de uitkomst.)
Maar ik vind het vreemd dat je de originele functie moet kwadrateren en niet de uitkomsten van de integrale functie.
quote:Nee, want een vlakdeel heeft geen volume. En bij een omwentelingslichaam kan het ook nog zijn dat wordt gevraagd de oppervlakte van dat omwentelingslichaam te berekenen. In de opgave moet duidelijk staan wat de bedoeling is.Op dinsdag 2 maart 2010 15:40 schreef Siddartha het volgende:
[..]
In het boek staat gewoon 'het vlakdeel', wat in dit geval gelijk is aan het volume (toch?).
quote:Dit is correct.Uitkomst had ik 1/12Pi^2 + 1/8Pi Wortel3
(als primitive functie had ik F(x) = 1/2x -1/8sin4x , invullen voor b=1/3pi en a = 1/6 pi, etc geeft de inhoud. Dat keer Pi en ik heb de uitkomst.)
quote:Snijd het omwentelingslichaam in gedachten eens in n hele dunne plakjes met een dikte Δx, waarbij het snijvlak loodrecht op de as van de rotatie staat. Elk van die dunne plakjes kun je bij benadering als een cilinder met straal f(xk) en lengte Δx beschouwen. Het volume van één zo'n cilinder is dan π∙{f(xk)}2∙Δx. Het volume van al die plakjes (met k = 1,2 ... n) moet je sommeren om een benadering te krijgen van het volume van het omwentelingslichaam. Deze benadering wordt beter naarmate je de plakjes dunner maakt. Zo krijg je de limiet van wat ze wel een Riemann som noemen, en deze limiet is de integraal die je hebt uitgerekend.Maar ik vind het vreemd dat je de originele functie moet kwadrateren en niet de uitkomsten van de integrale functie.
Wat jij wilde is de oppervlakte van het vlakdeel kwadrateren, maar daarmee bereken je geen inhoud (waarom niet?). Probeer het maar eens met wat eenvoudige figuren als een cirkel of een vierkant die je om hun symmetrie-as roteert, dan zie je dat jouw idee over het volume van een omwentelingslichaam niet klopt.
[ Bericht 0% gewijzigd door Riparius op 02-03-2010 18:57:45 ]
Plaatsvervangend probleempje voor wie het leuk vind om over na te denken.
Construeer vierkant met alleen een passer en een lineaal.
(dus GEEN geo ofzo).
[ Bericht 77% gewijzigd door Borizzz op 02-03-2010 21:19:07 ]
quote:GGB: 6/14 * 5/13 * 8/12 =10/91Op dinsdag 2 maart 2010 21:12 schreef GlowMouse het volgende:
Reken die kansen eens afzonderlijk voor mij uit dan
GBG: 6/14 * 8/13 * 5/12 =10/91
BGG: 8/14 * 6/13 * 5/12 = 10/91
Samen 30/91ong 0.3296
Oke laat maar, kleine misvatting
Maar ik vind het didactisch niet echt verantwoord om het zo kort neer te zetten.
Beter is het om het geheel uit te werken en het te laten zien.
quote:Dus een integraal is de somfunctie van alle 'y' op gebied delta x (waar x zo klein mogelijk is) en is dus voor elke delta x eigenlijk (een benadering van) de straal?Op dinsdag 2 maart 2010 16:39 schreef Riparius het volgende:
[..]
Snijd het omwentelingslichaam in gedachten eens in n hele dunne plakjes met een dikte Δx, waarbij het snijvlak loodrecht op de as van de rotatie staat. Elk van die dunne plakjes kun je bij benadering als een cilinder met straal f(xk) en lengte Δx beschouwen. Het volume van één zo'n cilinder is dan π∙{f(xk)}2∙Δx. Het volume van al die plakjes (met k = 1,2 ... n) moet je sommeren om een benadering te krijgen van het volume van het omwentelingslichaam. Deze benadering wordt beter naarmate je de plakjes dunner maakt. Zo krijg je de limiet van wat ze wel een Riemann som noemen, en deze limiet is de integraal die je hebt uitgerekend.
Wat jij wilde is de oppervlakte van het vlakdeel kwadrateren, maar daarmee bereken je geen inhoud (waarom niet?). Probeer het maar eens met wat eenvoudige figuren als een cirkel of een vierkant die je om hun symmetrie-as roteert, dan zie je dat jouw idee over het volume van een omwentelingslichaam niet klopt.
Hmm, wat ik dus deed was puur de oppervlakte kwadrateren, terwijl oppervlakte niet gelijk is aan straal. Wat ik deed was de stralen/lijnen onder het gegeven gebied uitrekenen, bij elkaar optellen en dan kwadrateren. Door de formule van de integraal te kwadrateren, kwadrateer ik elke straal en ( x Pi) krijg ik wel de inhoud.
Klopt dit een beetje?
quote:Ik volg het niet helemaal waarom je de stappen neemt die je neemt, maar volgens mij klopt het niet.Op dinsdag 2 maart 2010 23:40 schreef Siddartha het volgende:
[..]
Dus een integraal is de somfunctie van alle 'y' op gebied delta x (waar x zo klein mogelijk is) en is dus voor elke delta x eigenlijk (een benadering van) de straal?
Hmm, wat ik dus deed was puur de oppervlakte kwadrateren, terwijl oppervlakte niet gelijk is aan straal. Wat ik deed was de stralen/lijnen onder het gegeven gebied uitrekenen, bij elkaar optellen en dan kwadrateren. Door de formule van de integraal te kwadrateren, kwadrateer ik elke straal en ( x Pi) krijg ik wel de inhoud.
Klopt dit een beetje?
Een voorbeeld:
De straal van het cilindertje is de functiewaarde en de "hoogte" van de cilinder is de dx. Je kan het zien als een worst die je in infinitesimaal dunne plakjes snijdt. Als je de volumes van de kleine plakjes bij elkaar optelt heb je het formule van de hele worst. Een worst die in dikte varieert kan je zien als een niet-constante functie. Stel dat je worst wel kaarsrecht is met constante straal f(x)=c en lengte L. Dan kun je de inhoud uitrekenen met de "standaardformule" voor een cilinder: pi × c² × L (dat is dus gewoon de "oppervlakte maal hoogte". Je kan ook de volgende integraal uitrekenen:
Voor een gewone cilinder is dit eigenlijk overbodig werk, maar het geeft je misschien wel een idee dat het voor niet-constante formules ook de inhoud geeft.
Misschien is het wel een leuke oefening om mbv een omwentelingslichaam de inhoud van een kegel met hoogte L te bepalen
[ Bericht 2% gewijzigd door motorbloempje op 01-09-2013 21:40:28 ]
quote:Ik had in een opgave de uitkomst van de integraal gekwadrateerd en vroeg me af waarom je de hele formule moest kwadrateren. Maar dat is dus omdat de integraal een verzameling is van stralen (of benaderingen ervan) voor elk stapje delta x binnen het aangegeven gebied?Op woensdag 3 maart 2010 00:29 schreef BasementDweller het volgende:
[..]
Ik volg het niet helemaal waarom je de stappen neemt die je neemt, maar volgens mij klopt het niet.
Een voorbeeld:
De straal van het cilindertje is de functiewaarde en de "hoogte" van de cilinder is de dx. Je kan het zien als een worst die je in infinitesimaal dunne plakjes snijdt. Als je de volumes van de kleine plakjes bij elkaar optelt heb je het formule van de hele worst. Een worst die in dikte varieert kan je zien als een niet-constante functie. Stel dat je worst wel kaarsrecht is met constante straal f(x)=c en lengte L. Dan kun je de inhoud uitrekenen met de "standaardformule" voor een cilinder: pi × c² × L (dat is dus gewoon de "oppervlakte maal hoogte". Je kan ook de volgende integraal uitrekenen:
[ afbeelding ]
Voor een gewone cilinder is dit eigenlijk overbodig werk, maar het geeft je misschien wel een idee dat het voor niet-constante formules ook de inhoud geeft.
Misschien is het wel een leuke oefening om mbv een omwentelingslichaam de inhoud van een kegel met hoogte L te bepalen. Je zou een kegel kunnen kiezen met als tophoek 90 graden. Dan kan je de functie f(x)=x gebruiken. Welke integraal bereken je dan?
Hmm, een kegel. De f(x) lijn is in dit geval de schuine zijde, de x-lijn de hoogte(L) en x=b is de straal. Als ik f(x) primitiveer en voor 2 getallen invul (waarvan a = 0), krijg ik de oppervlakte onder de lijn. Zonder de primitive had ik gewoon uitgerekent: Pi x straal^2 x L x 1/3
Maar omdat F(x) = 1/2x^2 voor (b=x en a=0) al de oppervlakte geeft, hoef ik toch alleen maar:
Pi x F(x)^2 uit te rekenen?
quote:Nee, je vervalt weer in dezelfde denkfout door de primitieve te kwadrateren, en daarmee in feite de oppervlakte van het vlakdeel omder de curve te kwadrateren.Op woensdag 3 maart 2010 08:19 schreef Siddartha het volgende:
[..]
Ik had in een opgave de uitkomst van de integraal gekwadrateerd en vroeg me af waarom je de hele formule moest kwadrateren. Maar dat is dus omdat de integraal een verzameling is van stralen (of benaderingen ervan) voor elk stapje delta x binnen het aangegeven gebied?
Hmm, een kegel. De f(x) lijn is in dit geval de schuine zijde, de x-lijn de hoogte(L) en x=b is de straal. Als ik f(x) primitiveer en voor 2 getallen invul (waarvan a = 0), krijg ik de oppervlakte onder de lijn. Zonder de primitive had ik gewoon uitgerekent: Pi x straal^2 x L x 1/3
Maar omdat F(x) = 1/2x^2 voor (b=x en a=0) al de oppervlakte geeft, hoef ik toch alleen maar:
Pi x F(x)^2 uit te rekenen?
quote:In de laatste regel bedoel ik F(x) als gehele functie te kwadrateren, dusOp woensdag 3 maart 2010 08:44 schreef Riparius het volgende:
[..]
Nee, je vervalt weer in dezelfde denkfout door de primitieve te kwadrateren, en daarmee in feite de oppervlakte van het vlakdeel omder de curve te kwadrateren.
F(x) = 1/2x^2
F(x)^2 = 1/4x^4 (En daarvoor invullen, x Pi geeft het volume, toch?)
quote:Ik begrijp wat je bedoelt, maar het is gewoon fout. Het volume van een omwentelingslichaam verkregen door de curve van y = f(x) tussen x=a en x= b rond de x-as te wentelen wordt gegeven door:Op woensdag 3 maart 2010 09:05 schreef Siddartha het volgende:
[..]
In de laatste regel bedoel ik F(x) als gehele functie te kwadrateren, dus
F(x) = 1/2x^2
F(x)^2 = 1/4x^4 (En daarvoor invullen, x Pi geeft het volume, toch?)
(1) π∙∫ab (f(x))2dx
Maar wat jij schijnt te denken is dat dit hetzelfde is als:
(2) π∙[∫ab f(x)dx]2
Maar (2) is niet hetzelfde als (1), en bovendien kan (2) onmogelijk het volume van het omwentelingslichaam voorstellen. Zie je ook waarom?
Ik heb wat vragen over ontbinden in factoren:
1. Ik begrijp deze stappen niet:
2. Ik moet de determinant van een matrix bepalen. Ik kom op de hieronderstaande waarde uit:
( de vergelijking moet als uitkomst 0 hebben).
Als antwoord is alleen het eindantwoord gegeven: a = 0 a = 1 of a = 2.
Ik kom hier niet op uit heb ik iets fout gedaan of zien jullie deze antwoorden zo?
Alvast bedankt
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:40:33 ]
quote:1. Een derdegraads polynoom is wat lastig te ontbinden in factoren tenzij je tenminste één van de nulpunten zo al ziet (of echt een kubische vergelijking wilt gaan oplossen), maar in dit geval is het betrekkelijk eenvoudig. Het product van de wortels van a3 - 3a + 2 = 0 is -2, dus ligt het voor de hand plus of min 1 en plus of min 2 te proberen, en dan kom je er snel achter dat a = 1 en a = -2 voldoen. Door het uitvoeren van een polynoomstaartdeling vind je dan (a3 - 3a + 2)/(a + 2) = a2 - 2a + 1, en dus a3 - 3a + 2 = (a + 2)(a2 - 2a + 1). Verder is a2 - 2a + 1 = (a - 1)2, maar dat is gewoon een kwestie van het merkwaardig product (a - b)2 = a2 -2ab + b2 gebruiken.Op woensdag 3 maart 2010 13:35 schreef Matr het volgende:
Hallo,
Ik heb wat vragen over ontbinden in factoren:
1. Ik begrijp deze stappen niet:
[ afbeelding ]
2. Ik moet de determinant van een matrix bepalen. Ik kom op de hieronderstaande waarde uit:
( de vergelijking moet als uitkomst 0 hebben).
[ afbeelding ]
Als antwoord is alleen het eindantwoord gegeven: a = 0 a = 1 of a = 2.
Ik kom hier niet op uit heb ik iets fout gedaan of zien jullie deze antwoorden zo?
Alvast bedankt
2. Hier ben je kennelijk haakjes vergeten. Als je hebt (a - 1)(a2 - 2a) = 0 dan kun je uit de tweede factor van dit product nog een factor a buiten haakjes halen en krijg je dus a(a - 1)(a - 2) = 0, waaruit volgt a = 0 of a = 1 of a = 2.
Modale logica dus. Modale logica is strikt gezien de studie naar het deductieve gedrag van de expressies 'het is noodzakelijk dat' (□) en 'het is mogelijk dat' (◊). Nu heeft de docent syntaxis (wat welgevormde zinnen zijn) en axiomatiek beschreven (de drie axioma's van de propositielogica, de Neccissitatie-regel (N) en het K(ripke)-, D-, U, en T-axioma). Deze axiomatiek wordt dus gebruikt om verdere welgevormde proposities te bewijzen (kijken of ze dus afleidbaar zijn uit die axioma's).
Ik heb de volgende opgaven:
1. Bewijs zelf het omgekeerde ⊨ ¬□(φ ∧¬φ) ⇒ C! D
2. Toon aan dat T sterker is dan D.
3. Bewijs dat T inderdaad U impliceert, als ook N geldt.
4. Toon de volgende beweringen aan:
Axioma's:
N: ⊨ If φ is a theorem of K, then so is □φ (Neccissitatie regel)
K: ⊨ □(φ →ψ) → (□φ →□ψ). (Distribution Axiom)
T: ⊨ □φ→φ
U: ⊨ □(□φ→φ)
D: ⊨ □φ→◊φ
Axioma's voor de propositielogica (die we gebruiken voor de modale logica)
A1:
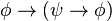
A2:

A3:

Ik moet dus een aantal zaken bewijzen. Hierbij ga ik er vanuit dat ik vanaf de conclusie (het bewijs) mezelf terug moet werken naar de axioma's toe. Maar hoe werkt zoiets precies? Hoe begin ik daarmee?
Alvast bedankt!
[ Bericht 0% gewijzigd door #ANONIEM op 03-03-2010 21:53:58 ]
quote:Hmm, wat ik deed was dus weer dezelfde fout: De oppervlakte kwadrateren.Op woensdag 3 maart 2010 09:18 schreef Riparius het volgende:
[..]
Ik begrijp wat je bedoelt, maar het is gewoon fout. Het volume van een omwentelingslichaam verkregen door de curve van y = f(x) tussen x=a en x= b rond de x-as te wentelen wordt gegeven door:
(1) π∙∫ab (f(x))2dx
Maar wat jij schijnt te denken is dat dit hetzelfde is als:
(2) π∙[∫ab f(x)dx]2
Maar (2) is niet hetzelfde als (1), en bovendien kan (2) onmogelijk het volume van het omwentelingslichaam voorstellen. Zie je ook waarom?
Door f(x) te kwadrateren, kwadrateer je alleen de straal voor elke x, en met integreren tel je dan alle gekwadrateerde stralen in een gebied(=lengte) bij elkaar op. En dus heb je de straal^2 x lengte zo berekent.( Dan volgt vanzelf keer Pi)
Terwijl je door F(x) te kwadrateren, tel je alle stralen bij elkaar op in een gebied en dat kwadrateer je. Wat dus fout is.
Ik denk dat ik het nu snap!
quote:Je kunt het beste denken aan het verdelen van een omwentelingslichaam in hele dunne plakjes die elk bij benadering een cilinder zijn. Door de volumina van die cilinders bij elkaar op te tellen krijg je een benadering voor het volume van het omwentelingslichaam die beter wordt naarmate de plakjes dunner worden. Een integraal is in principe te definiëren als de limiet van een dergelijke Riemann som. Dat suggereert het integraalteken ook. De ∫ is oorspronkelijk een langgerekte s van summa. Probeer om het principe beter te begrijpen eens of je ook een formule kunt opstellen voor de manteloppervlakte van een omwentelingslichaam (hint: stel eerst een formule op voor de lengte van de curve van y = f(x) tussen x=a en x=b).Op woensdag 3 maart 2010 15:41 schreef Siddartha het volgende:
[..]
Hmm, wat ik deed was dus weer dezelfde fout: De oppervlakte kwadrateren.
Door f(x) te kwadrateren, kwadrateer je alleen de straal voor elke x, en met integreren tel je dan alle gekwadrateerde stralen in een gebied(=lengte) bij elkaar op. En dus heb je de straal^2 x lengte zo berekend.( Dan volgt vanzelf keer Pi)
Terwijl je door F(x) te kwadrateren, tel je alle stralen bij elkaar op in een gebied en dat kwadrateer je. Wat dus fout is.
Ik denk dat ik het nu snap!
quote:Nou, de lengte is y voor f(delta x) maal 2 omdat je met y alleen maar de straal van het midden naar de 'cirkel' hebt, terwijl je aan de andere kant nog eens die lengte hebt.Op woensdag 3 maart 2010 15:56 schreef Riparius het volgende:
[..]
Probeer om het principe beter te begrijpen eens of je ook een formule kunt opstellen voor de manteloppervlakte van een omwentelingslichaam (hint: stel eerst een formule op voor de lengte van de curve van y = f(x) tussen x=a en x=b).
dus lengte is 2y: 2f(x)
Omtrek van een figuur is Pi x lengte.
Om de lengte van elke delta x bij elkaar op te tellen kan ik de integraal gebruiken. Door (2f(x)) te primitiveren tel ik al die lengtes bij elkaar op en door dan met Pi te vermenigvuldigen krijg ik de omtrek/mantel. Toch?
quote:Nee, dat gaat niet goed. Eerst de booglengte s van de curve van y = f(x) tussen x=a en x=b. Die wordt gegeven door:Op woensdag 3 maart 2010 16:23 schreef Siddartha het volgende:
[..]
Nou, de lengte is y voor f(delta x) maal 2 omdat je met y alleen maar de straal van het midden naar de 'cirkel' hebt, terwijl je aan de andere kant nog eens die lengte hebt.
dus lengte is 2y: 2f(x)
Omtrek van een figuur is Pi x lengte.
Om de lengte van elke delta x bij elkaar op te tellen kan ik de integraal gebruiken. Door (2f(x)) te primitiveren tel ik al die lengtes bij elkaar op en door dan met Pi te vermenigvuldigen krijg ik de omtrek/mantel. Toch?
(1) s = ∫ab √(1 + (f'(x))2)dx
Voor de afleiding van deze formule moet je hier maar even kijken.
Nu de manteloppervlakte. Hierbij neem ik aan dat f(x) op het interval [a,b] niet negatief wordt. Verdeel het omwentelingslichaam weer in heel dunne plakjes met een dikte Δx, dan kun je de manteloppervlakte van één zo'n plakje (ring) benaderen door de booglengte van de curve van y = f(x) over het betreffende interval te vermenigvuldigen met de omtrek 2πr van zo'n ring. Dit geeft als benadering voor de manteloppervlakte van één zo'n ring
2π∙f(xk)√(1 + (f'(xk))2)Δx,
waarbij xk een waarde van x is op het betreffende intervalletje. Om de manteloppervlakte van x=a tot x=b te benaderen moet je al deze stukjes (met k = 1 ... n) optellen, waarbij de benadering weer beter wordt naarmate we de dikte Δx van de plakjes tot nul laten naderen. Voor de manteloppervlakte A van het omwentelingslichaam dat ontstaat door de curve van y = f(x) tusen x=a en x=b om de x-as te wentelen vinden we zo:
(2) A = 2π∙∫ab f(x)∙√(1 + (f'(x))2)dx
Probeer eens of je nu formules voor de inhoud en de oppervlakte van een bol met straal r kunt afleiden. Neem f(x) = √(r2 - x2) (r > 0). De grafiek hiervan is een halve cirkel met als middelpunt de oorsprong en als straal r, zodat bij wenteling om de x-as een bol met straal r ontstaat.
quote:Wat ik dus deed gaf niet de oppervlakte van een willekeurig figuur (met f(x) ongedifineerd)?
Ik heb gewoon de formule gepakt van de omtrek van een cirkel (dat gebeurt er namelijk ook op delta x)
2Pi r = Pi maal lengte. En de rest staat in mijn vorige post.
Ik snap niet goed waarvoor ik een booglengte nodig heb?
Waarom moet je nu niet als eerste stap f(x) keer 2 doen? Dan heb je namelijk de 2 x straal op vlakdeel delta x, waarna je kan gaan integreren (en uiteindelijk nog keer Pi).
quote:Nee.Op woensdag 3 maart 2010 17:41 schreef Siddartha het volgende:
[..]
Wat ik dus deed gaf niet de oppervlakte van een willekeurig figuur (met f(x) ongedefineerd)?
quote:Nee, om de lengte van één zo'n dunne ring te bepalen moet je de omtrek 2πr = 2πf(xk) vermenigvuldigen met de breedte van de ring, en die breedte is gelijk aan de booglengte van de curve y = f(x) over dat intervalletje. De breedte van de ring is niet Δx, dat zou alleen zo zijn als de curve horizontaal loopt (en dus f'(x) = 0).Ik heb gewoon de formule gepakt van de omtrek van een cirkel (dat gebeurt er namelijk ook op delta x)
2Pi r = Pi maal lengte. En de rest staat in mijn vorige post.
quote:Omdat de breedte van elke ring afhangt van de steilheid van de curve op het betreffende intervalletje.Ik snap niet goed waarvoor ik een booglengte nodig heb?
quote:Op jouw manier bereken je gewoon de oppervlakte van het vlakdeel onder de curve vermenigvuldigd met 2π. Dan krijg je niet de manteloppervlakte van het omwentelingslichaam. Probeer het maar eens met een halve cirkel als curve.
Waarom moet je nu niet als eerste stap f(x) keer 2 doen? Dan heb je namelijk de 2 x straal op vlakdeel delta x, waarna je kan gaan integreren (en uiteindelijk nog keer Pi).
quote:Kun je even specificeren wat je me wilt laten doen?Op woensdag 3 maart 2010 18:09 schreef Riparius het volgende:
[..]
Nee.
[..]
Nee, om de lengte van één zo'n dunne ring te bepalen moet je de omtrek 2πr = 2πf(xk) vermenigvuldigen met de breedte van de ring, en die breedte is gelijk aan de booglengte van de curve y = f(x) over dat intervalletje. De breedte van de ring is niet Δx, dat zou alleen zo zijn als de curve horizontaal loopt (en dus f'(x) = 0).
[..]
Omdat de breedte van elke ring afhangt van de steilheid van de curve op het betreffende intervalletje.
[..]
Op jouw manier bereken je gewoon de oppervlakte van het vlakdeel onder de curve vermenigvuldigd met 2π. Dan krijg je niet de manteloppervlakte van het omwentelingslichaam. Probeer het maar eens met een halve cirkel als curve.
Dus, wat voor figuur en wat ik moet berekenen ( oppervlakte/omtrek/beide)?
En ik neem aan dat lengte is de x-as en y geeft de breedte? (die heb ik in eerdere berichten een paar keer door elkaar gebruikt.)
Trouwens, heel erg bedankt hiervoor. Dit zal meer voor mijn inzicht doen dan puur wat sommetjes maken.
quote:Probeer gewoon eens de oppervlakte en het volume te berekenen van een bol met straal r door een halve cirkel met straal r om de x-as te laten wentelen, zoals ik hierboven al had voorgesteld. Begin maar met het volume, dat is het eenvoudigst.Op woensdag 3 maart 2010 18:17 schreef Siddartha het volgende:
[..]
Kun je even specificeren wat je me wilt laten doen?
Dus, wat voor figuur en wat ik moet berekenen ( oppervlakte/omtrek/beide)?
En ik neem aan dat lengte is de x-as en y geeft de breedte? (die heb ik in eerdere berichten een paar keer door elkaar gebruikt.)
Trouwens, heel erg bedankt hiervoor. Dit zal meer voor mijn inzicht doen dan puur wat sommetjes maken.
quote:En als je eenmaal het volume hebt is de oppervlakte ook nog maar één stap(je)Op woensdag 3 maart 2010 18:26 schreef Riparius het volgende:
[..]
Probeer gewoon eens de oppervlakte en het volume te berekenen van een bol met straal r door een halve cirkel met straal r om de x-as te laten wentelen, zoals ik hierboven al had voorgesteld. Begin maar met het volume, dat is het eenvoudigst.
quote:Volume is:Op woensdag 3 maart 2010 18:26 schreef Riparius het volgende:
[..]
Probeer gewoon eens de oppervlakte en het volume te berekenen van een bol met straal r door een halve cirkel met straal r om de x-as te laten wentelen, zoals ik hierboven al had voorgesteld. Begin maar met het volume, dat is het eenvoudigst.
Eerst de gewone formule: f(x) = Wortel(r^2 - x^2)
Dat kwadrateren, dan primitiveren geeft als volume:
V = Pi x [(r^2)x - 1/3x^3]a,b met a=-r en b=r
quote:Ja, en als je dat uitwerkt, wat krijg je dan uiteindelijk?Op woensdag 3 maart 2010 19:12 schreef Siddartha het volgende:
[..]
Volume is:
Eerst de gewone formule: f(x) = Wortel(r^2 - x^2)
Dat kwadrateren, dan primitiveren geeft als volume:
V = Pi x [(r^2)x - 1/3x^3]a,b met a=-r en b=r
quote:Dan krijg je Pi maal 2r^3 - 2/3r^3 = Pi maal 1/1/3r^3Op woensdag 3 maart 2010 19:26 schreef Riparius het volgende:
[..]
Ja, en als je dat uitwerkt, wat krijg je dan uiteindelijk?
Ok, dat is wel erg handig!
quote:Juist. Het volume van een bol met straal r is dus 4/3∙π∙r3.Op woensdag 3 maart 2010 19:33 schreef Siddartha het volgende:
[..]
Dan krijg je Pi maal 2r^3 - 2/3r^3 = Pi maal 1/1/3r^3
Ok, dat is wel erg handig!
Maar nu de oppervlakte ...
quote:Dat is dus 2Pi maal lengte ( en niet breedte, zoals ik de vorige keer deed!).Op woensdag 3 maart 2010 19:38 schreef Riparius het volgende:
[..]
Juist. Het volume van een bol met straal r is dus 4/3∙π∙r3.
Maar nu de oppervlakte ...
Lengte is

Waarbij dy/dx = - 1/(Wortel(r^2- x^2))
Kwadrateren geeft = 1/(r^2 -x^2)
Klopt het tot nu toe nog? Waarschijnlijk zal ik de functie moeten primitiveren, want anders kan ik ook niet x=r invullen.
quote:Het lijkt me toch echt dat dat andersom moet: met de axioma's beginnen en vanaf daar naar de conclusie werken.Op woensdag 3 maart 2010 14:26 schreef Friek_ het volgende:
[..]
Ik moet dus een aantal zaken bewijzen. Hierbij ga ik er vanuit dat ik vanaf de conclusie (het bewijs) mezelf terug moet werken naar de axioma's toe. Maar hoe werkt zoiets precies? Hoe begin ik daarmee?
Het lijkt me dat (1) makkelijk is op te lossen door □(φ ∧¬φ) aan te nemen, D toe te passen en dan vervolgens φ ∧¬φ te concluderen, waaruit je met propositielogica weer een falsum kan afleiden.
Je hebt T niet gegeven, dus (2) en (3) kan ik niet oplossen. En U begrijp ik niet, zit daar een tikfout in?
Bij (4) volgt de tweede regel uit (D) door □φ voor φ te substitueren. Voor de eerste regel heb je misschien U nodig, maar dan moet ik wel de juiste formulering weten.
quote:Ik heb de post aangepast. Bedankt voor je reactie tot zover.Op woensdag 3 maart 2010 20:32 schreef thabit het volgende:
[..]
Het lijkt me toch echt dat dat andersom moet: met de axioma's beginnen en vanaf daar naar de conclusie werken.
Het lijkt me dat (1) makkelijk is op te lossen door □(φ ∧¬φ) aan te nemen, D toe te passen en dan vervolgens φ ∧¬φ te concluderen, waaruit je met propositielogica weer een falsum kan afleiden.
Je hebt T niet gegeven, dus (2) en (3) kan ik niet oplossen. En U begrijp ik niet, zit daar een tikfout in?
Bij (4) volgt de tweede regel uit (D) door □φ voor φ te substitueren. Voor de eerste regel heb je misschien U nodig, maar dan moet ik wel de juiste formulering weten..
quote:Nee, dit gaat al niet goed, je vergeet de kettingregel bij het differentiëren. De formule voor de manteloppervlakte (area) van het omwentelingslichaam verkregen door de curve van y = f(x) (≥ 0) tussen x=a en x=b om de x-as te wentelen isOp woensdag 3 maart 2010 20:04 schreef Siddartha het volgende:
[..]
Dat is dus 2Pi maal lengte ( en niet breedte, zoals ik de vorige keer deed!).
Lengte is
[ afbeelding ]
Waarbij dy/dx = - 1/(Wortel(r^2- x^2))
Kwadrateren geeft = 1/(r^2 -x^2)
Klopt het tot nu toe nog? Waarschijnlijk zal ik de functie moeten primitiveren, want anders kan ik ook niet x=r invullen.
A = 2π∙∫ab f(x)∙√(1 + (f'(x))2)dx
We moeten nu eerst de integrand f(x)∙√(1 + (f'(x))2) berekenen met f(x) = √(r2 - x2). Daarvoor moeten we dus de afgeleide f'(x) bepalen. Ik vind het zelf vaak handig om een wortel even om te schrijven naar een macht, dus:
f(x) = (r2 - x2)1/2
Dan is (let op de kettingregel):
f'(x) = 1/2∙(r2 - x2)-1/2∙(-2x) = -x∙(r2 - x2)-1/2
Voor het kwadraat van f'(x) krijgen we dan:
(f'(x))2 = x2∙(r2 - x2)-1 = x2/(r2 - x2)
En dus hebben we dan ook:
1 + (f'(x))2 = 1 + x2/(r2 - x2) = (r2 - x2)/(r2 - x2) + x2/(r2 - x2) = r2/(r2 - x2).
Nu kun je de berekening van de integrand f(x)∙√(1 + (f'(x))2) zelf wel afmaken en dan integreren over het interval [-r,r] en vermenigvuldigen met 2π om de oppervlakte van een bol met straal r te vinden.
quote:Voor (2) moet je aantonen dat als T geldt, dat dan ook D geldt. ◊φ interpreteer ik als ¬□¬φ. Je hebt dus de implicatie □φ → φ en je wilt daaruit afleiden □φ → ¬□¬φ. Je kunt nu A3 toepassen en ¬φ → ¬□φ afleiden. Substitueer nu ¬φ voor φ en er staat ¬¬φ → ¬□¬φ. De implicaties □φ → φ, φ → ¬¬φ en ¬¬φ → ¬□¬φ tezamen geven □φ → ¬□¬φ.Op woensdag 3 maart 2010 14:26 schreef Friek_ het volgende:
Kan iemand (Iblis, GlowMouse?) me helpen bij het vak 'modale logica'? Ik zit alweer met problemen rondom de wat meer wiskundige kant van mijn studie.
Modale logica dus. Modale logica is strikt gezien de studie naar het deductieve gedrag van de expressies 'het is noodzakelijk dat' (□) en 'het is mogelijk dat' (◊). Nu heeft de docent syntaxis (wat welgevormde zinnen zijn) en axiomatiek beschreven (de drie axioma's van de propositielogica, de Neccissitatie-regel (N) en het K(ripke)-, D-, U, en T-axioma). Deze axiomatiek wordt dus gebruikt om verdere welgevormde proposities te bewijzen (kijken of ze dus afleidbaar zijn uit die axioma's).
Ik heb de volgende opgaven:
1. Bewijs zelf het omgekeerde ⊨ ¬□(φ ∧¬φ) ⇒ C! D
2. Toon aan dat T sterker is dan D.
3. Bewijs dat T inderdaad U impliceert, als ook N geldt.
4. Toon de volgende beweringen aan:⊨ □φ → □□φ ⊨ □□φ → □φ
Axioma's:
N: ⊨ If φ is a theorem of K, then so is □φ (Neccissitatie regel)
K: ⊨ □(φ →ψ) → (□φ →□ψ). (Distribution Axiom)
T: ⊨ □φ→φ
U: ⊨ □(□φ→φ)
D: ⊨ □φ→◊φ
Bij (4) neem je voor alle φ, □φ→φ als axioma aan. Een axioma is per definitie een theorema dus passen we N toe met □φ→φ gesubstitueerd voor φ. Dan krijg je □(□φ→φ).
PS: Mijn uitwerkingen zijn uiteraard wel wat informeel, je zult ze zelf moeten formaliseren.
Ik moet de bezettingsgraad van een AGV (Automatic Guided Vehicle) uitrekenen.
Het zit zo.
Je hebt een haven met kranen, 5 stuks totaal. Per kraan 2 AGV's. De kranen pikken een container op en zetten die op de AGV, die rijdt er vervolgens mee naar de loods en weer terug.
Tijd die nodig is om container vanaf schip te laden = 6 minuten
Tijd die nodig is om container van kraan op AGV te zetten = 2 minuten.
Gemiddelde rijtijd naar en van loods = 6 minuten.
De kranen zijn 0.8 bezet, die loodsen dus gemiddeld 6 containers per uur. (0,8 * (60/6+2).
De AGV's doen gemiddeld 14 minuten over 1 container( 6+6+2).
De 2 AGV's kunnen dus in 1 uur 2*(60/14) = 8.57 containers aan.
Bezettingsgraad = 6/8.57 = 0.7
Klinkt in mijn ogen allemaal goed. Alleen als ik de simualtie run (met Delphi/Tomas) krijg ik toch wel een stuk hogere bezettingsgraad uit, namelijk 0.91
Hou ik ergens geen rekening mee? Je zou verwachten dat mijn bezettingsgraad alleen geld in het meest efficiënte geval en dat de werkelijke zelfs lager zou moeten liggen.....
Net hele verhaal getypt. Zie ik dat er toch al gesimuleerd is met een extra 4 minuten lostijd per AGV bij de loods. Tja dan komt het wel goed uit
Ik ga zelf weer verder
Los op: 10 log(x²-4x+5)=0
bvd
Ik heb geleerd dat een eigenshap van een genormaliseerde vector is dat het (standaard) inproduct met zichzelf gelijk aan 1 is. Als ik aan mathematica vraag of ie (1,i,0) voor me wil normaliseren, geeft ie 1/sqrt2 (1,i,0). Maar als ik dan het inproduct met dezelfde vector neem krijg ik 0, en dus niet 1. Hoe zit dat nou?
quote:Ah, logisch. Bedankt!Op zondag 7 maart 2010 14:54 schreef GlowMouse het volgende:
Bij een complexe vector neem je het inproduct met zijn complex geadjugeerde.
Om te laten zien dat de afbeelding abels is, moet ik dan laten zien dat geldt: f(xy)=f(yx) of moet ik verder gaan en laten zien dat xy=yx?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:41:37 ]
quote:Bedoel je dit?Op maandag 8 maart 2010 18:26 schreef julian6 het volgende:
Wie weet hoe je 4√x-x in je GR moet intikken?
Dan lijkt het me straightforward intypen met haakjes om de x-x.
Als je dit bedoelt:
Tja... je kan het gewoon intikken in je GR, alleen wat verwacht je voor een antwoord?
[ Bericht 2% gewijzigd door motorbloempje op 01-09-2013 21:41:41 ]
quote:Welke tabel en welke waardes? Je moet echt meer info geven als je wil dat mensen je kunnen helpen.Op maandag 8 maart 2010 20:59 schreef julian6 het volgende:
De bijbehorende tabel staat in mijn boek, maar de waardes komen niet overeen als ik het vergelijk met die in mijn GR
quote:Abels betekent xy = yx voor elke x en y in G. Als jij f(xy)=f(yx) aantoont, toon je aan dat (xy)² = (yx)², ofwel xyxy = yxyx. Hiermee toon je niet aan dat xy=yx.Op maandag 8 maart 2010 15:38 schreef JoPiDo het volgende:
[ afbeelding ]
Om te laten zien dat de afbeelding abels is, moet ik dan laten zien dat geldt: f(xy)=f(yx) of moet ik verder gaan en laten zien dat xy=yx?
quote:Op maandag 8 maart 2010 21:08 schreef GlowMouse het volgende:
[..]
Abels betekent xy = yx voor elke x en y in G. Als jij f(xy)=f(yx) aantoont, toon je aan dat (xy)² = (yx)², ofwel xyxy = yxyx. Hiermee toon je niet aan dat xy=yx.
Ik heb hem al uitgewerkt naar xy=yx, bedankt voor je reactie!
quote:Het hoofdstuk gaat over toenamediagrammen en ik ben nu bij een vraag aan beland waarbij ik tijdsintervallen moet berekenen. De waardes die bij de formule 4√x-x horen volgens mij boek zijn:Op maandag 8 maart 2010 21:00 schreef BasementDweller het volgende:
[..]
Welke tabel en welke waardes? Je moet echt meer info geven als je wil dat mensen je kunnen helpen.
X y1
0 0
1 3
2 3.6569
3 3.9282
4 4
5 3.9443
6 3.798
en als ik het in mijn GR plot en de tabel bekijk dan staat er of overal 0, of ERROR of allemaal negatieve waardes
quote:Dus in menu TABLE vul je in:Op dinsdag 9 maart 2010 10:26 schreef julian6 het volgende:
[..]
Het hoofdstuk gaat over toenamediagrammen en ik ben nu bij een vraag aan beland waarbij ik tijdsintervallen moet berekenen. De waardes die bij de formule 4√x-x horen volgens mij boek zijn:
X y1
0 0
1 3
2 3.6569
3 3.9282
4 4
5 3.9443
6 3.798
en als ik het in mijn GR plot en de tabel bekijk dan staat er of overal 0, of ERROR of allemaal negatieve waardes
4Wortelx - x (zonder haakjes!)
En dan klopt het gewoon.
(Weet je zeker dat je het goed ingevoerd hebt/er ook y=... staat en niet x=.. ? )
4√(x)-x
Ben student werktuigbouwkunde (hbo) en ben bezig een machine te ontwikkelen. Om alle krachten en spanningen goed in beeld te brengen komt er helaas wat wiskunde bij kijken. Dit is helaas niet mijn allersterkste punt.
De opdracht is om een functie te maken van hoek alpha.

Hopelijk kan iemand me helpen want ik kom er niet uit.
quote:nee die hoek is niet 90 graden.Op dinsdag 9 maart 2010 16:27 schreef Mindstream het volgende:
is die hoek helemaal rechts ook 90 graden? Dan is het makkelijk want de som van de hoeken van een vierhoek is altijd 360 graden.
quote:Je geeft niet voldoende informatie, maar uitgaande van de veronderstelling dat de linker driehoek in je figuur gelijkbenig is krijg ik:Op dinsdag 9 maart 2010 16:23 schreef toma het volgende:
Hopelijk zit ik hier in het goede topic.
Ben student werktuigbouwkunde (hbo) en ben bezig een machine te ontwikkelen. Om alle krachten en spanningen goed in beeld te brengen komt er helaas wat wiskunde bij kijken. Dit is helaas niet mijn allersterkste punt.
De opdracht is om een functie te maken van hoek alpha.
[ afbeelding ]
Hopelijk kan iemand me helpen want ik kom er niet uit.
α = arcsin (2∙(L3 - ½√2∙L2 + L4∙cos β)/L1)
Was dat wat je bedoelde?
quote:Hoe bedoel je gelijkbenig? Hoek alpha is in de top van de vierhoek iig links en rechts niet gelijk aan elkaar. En welke informatie moet je nog meer weten? De verticale zijde tussen L2 en (1/2)L1 staat loodrecht op L3. Verder is geen één hoek 90 graden.Op dinsdag 9 maart 2010 17:23 schreef Riparius het volgende:
[..]
Je geeft niet voldoende informatie, maar uitgaande van de veronderstelling dat de linker driehoek in je figuur gelijkbenig is krijg ik:
α = arcsin (2∙(L3 - ½√2∙L2 + L4∙cos β)/L1)
Was dat wat je bedoelde?
Heel erg bedankt alvast
En zou je misschien kunnen beargumenteren hoe je aan het antwoord komt?
quote:Nee, maar dat heb ik ook niet beweerd of aangenomen. Weet je eigenlijk wel wat een gelijkbenige driehoek is? Zoals gezegd heb ik aangenomen dat de linker driehoek in je figuur gelijkbenig is. Dat betekent dus dat de lengte van de hoogtelijn in je figuur gelijk is aan de lengte van het lijnstuk vanaf het hoekpunt linksonder in je figuur totaan het voetpunt van je hoogtelijn.Op dinsdag 9 maart 2010 17:31 schreef toma het volgende:
[..]
Hoe bedoel je gelijkbenig? Hoek alpha is in de top van de vierhoek iig links en rechts niet gelijk aan elkaar.
quote:Dat was me natuurlijk al duidelijk. Maar als jij meent dat de linker driehoek in je figuur niet gelijkbenig is, dan geef je te weinig informatie.En welke informatie moet je nog meer weten? De verticale zijde tussen L2 en (1/2)L1 staat loodrecht op L3. Verder is geen één hoek 90 graden.
quote:Het gaat erom dat je de (horizontale) afstand van het meest rechtse hoekpunt in je figuur totaan de hoogtelijn bepaalt. Laten we die afstand d noemen, dan is het duidelijk dat sin α = d/(½L1). Probeer nu zelf eens een uitdrukking voor d te vinden, dan zie je hoe het zit.Heel erg bedankt alvast
En zou je misschien kunnen beargumenteren hoe je aan het antwoord komt?
quote:Sorry, ik begreep niet goed wat je bedoelde met die gelijkbenige driehoek.Op dinsdag 9 maart 2010 17:43 schreef Riparius het volgende:
[..]
Nee, maar dat heb ik ook niet beweerd of aangenomen. Weet je eigenlijk wel wat een gelijkbenige driehoek is? Zoals gezegd heb ik aangenomen dat de linker driehoek in je figuur gelijkbenig is. Dat betekent dus dat de lengte van de hoogtelijn in je figuur gelijk is aan de lengte van het lijnstuk vanaf het hoekpunt linksonder in je figuur totaan het voetpunt van je hoogtelijn.
[..]
Dat was me natuurlijk al duidelijk. Maar als jij meent dat de linker driehoek in je figuur niet gelijkbenig is, dan geef je te weinig informatie.
[..]
Het gaat erom dat je de (horizontale) afstand van het meest rechtse hoekpunt in je figuur totaan de hoogtelijn bepaalt. Laten we die afstand d noemen, dan is het duidelijk dat sin α = d/(½L1). Probeer nu zelf eens een uitdrukking voor d te vinden, dan zie je hoe het zit.

Maar dit oranje gekleurde gedeelte is niet gelijkbenig. Dus ik ben bang dat jouw oplossing niet klopt.
quote:Mijn oplossing klopt, onder de voorwaarde dat de oranje driehoek gelijkbenig zou zijn. Nu zeg je dat dat niet zo is, en dan wordt het een stuk ingewikkelder. Laten we de hoogte van de oranje driehoek h noemen, en de basis b. Dan geldt volgens Pythagoras:Op dinsdag 9 maart 2010 17:51 schreef toma het volgende:
[..]
Sorry, ik begreep niet goed wat je bedoelde met die gelijkbenige driehoek.
[ afbeelding ]
Maar dit oranje gekleurde gedeelte is niet gelijkbenig. Dus ik ben bang dat jouw oplossing niet klopt.
(1) b = √(L22 - h2)
En voor de hoogte h hebben we:
(2) h = ½L1∙cos α + L4∙sin β
Door substitutie van (2) in (1) krijg je dan een uitdrukking voor b, waarna we de afstand d van het meest rechtse hoekpunt in de figuur tot de hoogtelijn kunnen geven als:
(3) d = (L3 - b) + L4∙cos β
Tot slot is dan:
(4) sin α = 2d/L1
Door nu de gevonden uitdrukking voor b in (3) te substituren en de aldus gevonden uitdrukking voor d weer in (4) krijg je een betrekking waaruit je sin α kunt oplossen, en dus ook een uitdrukking voor α kunt geven.
quote:Duizend maal dankOp dinsdag 9 maart 2010 19:04 schreef Riparius het volgende:
[..]
Mijn oplossing klopt, onder de voorwaarde dat de oranje driehoek gelijkbenig zou zijn. Nu zeg je dat dat niet zo is, en dan wordt het een stuk ingewikkelder. Laten we de hoogte van de oranje driehoek h noemen, en de basis b. Dan geldt volgens Pythagoras:
(1) b = √(L22 - h2)
En voor de hoogte h hebben we:
(2) h = ½L1∙cos α + L4∙sin β
Door substitutie van (2) in (1) krijg je dan een uitdrukking voor b, waarna we de afstand d van het meest rechtse hoekpunt in de figuur tot de hoogtelijn kunnen geven als:
(3) d = (L3 - b) + L4∙cos β
Tot slot is dan:
(4) sin α = 2d/L1
Door nu de gevonden uitdrukking voor b in (3) te substituren en de aldus gevonden uitdrukking voor d weer in (4) krijg je een betrekking waaruit je sin α kunt oplossen, en dus ook een uitdrukking voor α kunt geven.
Ik heb alles ingevuld. Uiteindelijk krijg ik dit.
sin α = ( 2∙(L3 - √( L22 - ( ½L1∙cos α+ L4∙sin β )2 ) + L4 ∙ cos β ) / L1
Nu heb ik nog steeds aan beide zeiden α staan. Maar dat moet ik nog even oplossen
Ik heb in L1 1990t/m 2000 staan
in L2 aantal mannen
in L3 aantal vrouwen
In L4 moet ik het totaal hebben.
Ik heb al geprobeerd om dan L4>Enter>Sum(L2+L3) maar dan krijg ik een dismatch error.
Hoe werkt dit?
32 * q^2/16 + 16000
wat moet ik hiermee?
quote:Eronder staat wel: 2 * q^2 + 16000Op woensdag 10 maart 2010 20:21 schreef GlowMouse het volgende:
geen idee, dat is gewoon een uitdrukking.
hoe zou ik daar dan bij moeten komen?
quote:ok.Op woensdag 10 maart 2010 20:33 schreef GlowMouse het volgende:
je kunt gebruiken dat a*b = b*a. Hier kun je q² en 1/16 omwisselen, en dan is het niet zo lastig meer.
quote:Nee, met deze uitleg niet. Misschien herken ik het niet ofzo, maar m'n leraar zei dat het tweede klas stof is.
= 32 * 1/16 * q² + 16000
quote:Is dit het antwoord ofzo.. sorry snap er niets van. In mijn boek staat dat het antwoord: 2 * q^2 + 16000 is.Op woensdag 10 maart 2010 20:41 schreef GlowMouse het volgende:
32 * q^2 * 1/16 + 16000
= 32 * 1/16 * q² + 16000
quote:Geen tijd meer voor. Wat ik ook niet snap.. wat moet ik met dit? Het ging eerst namelijk de hele tijd over MK=TK', dacht daarom dat ik die 16000 ook moest weglaten.Op woensdag 10 maart 2010 20:45 schreef GlowMouse het volgende:
Als je dit niet ziet, zou ik toch wat onderbouwliteratuur openslaan.
ik ben bezig met een probleempje voor een vriend. Het gaat erom om de gewichten van een formule te vinden waarmee een eindcijfer berekend is. Er is gegeven dat de formule uit 5 onderdelen met 5 gewichten bestaat, de cijfers waarmee de gewichten worden vermenigvuldigd en dan bij elkaar worden opgeteld zijn bekend. Er is een dataset van 60 mensen, dus in principe meer dan genoeg om gewoon een stelsel van 5 vergelijkingen met 5 onbekenden op te lossen, alleen is het probleem dat de cijfers afgerond zijn in de dataset. De bedoeling is om de gewichten zo dicht mogelijk te benaderen, hoe dat staat vrij maar het lijkt me waarschijnlijk dat dit met een wiskundig programma moet, of zijn er suggesties om dit mooi met de hand zelf te doen? De cijfers worden op halven afgerond. Iemand een idee hoe dit aan te pakken? Thanks!
Dit is de formule trouwens:
f(x) = g1 * D + g2 * S1 + g3 * S2 + g4 * e^(-3(D-S1)2 + g5 * e^(-3(D-S2)2
Waarbij D het cijfer is dat gegeven is door de docent, S1 is het cijfer gegeven door de eerste student en S2 is het cijfer gegeven door de tweede student. g1 tot en met g5 zijn de gewichten. D, S1 en S2 zijn dus gewoon bekend, net als de e-machten die erin voorkomen.
quote:Toevallig data mining techniques bij de VU?Op woensdag 10 maart 2010 22:10 schreef Dzy het volgende:
Hey hey,
ik ben bezig met een probleempje voor een vriend. Het gaat erom om de gewichten van een formule te vinden waarmee een eindcijfer berekend is. Er is gegeven dat de formule uit 5 onderdelen met 5 gewichten bestaat, de cijfers waarmee de gewichten worden vermenigvuldigd en dan bij elkaar worden opgeteld zijn bekend. Er is een dataset van 60 mensen, dus in principe meer dan genoeg om gewoon een stelsel van 5 vergelijkingen met 5 onbekenden op te lossen, alleen is het probleem dat de cijfers afgerond zijn in de dataset. De bedoeling is om de gewichten zo dicht mogelijk te benaderen, hoe dat staat vrij maar het lijkt me waarschijnlijk dat dit met een wiskundig programma moet, of zijn er suggesties om dit mooi met de hand zelf te doen? De cijfers worden op halven afgerond. Iemand een idee hoe dit aan te pakken? Thanks!
Dit is de formule trouwens:
f(x) = g1 * D + g2 * S1 + g3 * S2 + g4 * e^(-3(D-S1)2 + g5 * e^(-3(D-S2)2
Waarbij D het cijfer is dat gegeven is door de docent, S1 is het cijfer gegeven door de eerste student en S2 is het cijfer gegeven door de tweede student. g1 tot en met g5 zijn de gewichten. D, S1 en S2 zijn dus gewoon bekend, net als de e-machten die erin voorkomen.
Ik heb zelf geprobeerd met weka iets te vinden, maar nog niet veel succes daarmee geboekt (vanwege dat afronden en linear regression altijd een E toevoegt
Ik heb wel succes geboekt met evolutionary algorithm (simpele GA met real values, gaussian perturbation mutation, scattered crossover, etcetera met een eigen fitness functie die voor alle instanties kijkt wat de uitkomst is met de waardens en vervolgens afrondt naar halve getallen (kun je simpel doen door je uitkomst *2 te doen en vervolgens afronden op een geheel getal om weer te delen door 2 om afrondingen te krijgen op halve (dus 5, 5.5, 6, 6.5, etc)). Ik heb zelf Matlab gebruikt hiervoor, maar je kunt ook Mobat gebruiken (moet je even eigen functie uitschrijven) of je kunt het helemaal zelf programmeren. Ik wou zelf nog een andere methode proberen omdat ik issues heb met missing values (heb nog niet achterhaald wat zijn methode daarvoor is, ik heb wel al een oplossing met 0 fouten gevonden als ik enkel de data gebruik die geen missing values bevatten).
[Bèta wiskunde] Huiswerk- en vragentopic 2