Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
quote:
quote:Erm...
tvp6
Uiteindelijke kwam hij tot de conclusie dat twee formules essentieel voor ons zijn... mijn vraag was of er een bepaalde naam voor deze formules is en of er meer informatie over te vinden is zodat ik de precieze definitie van al die leuke tekentjes wat beter kan begrijpen.
De twee formules waren de volgende: (Op die tweede X moet nog een streepje maar die krijg ik er niet op)
_
Xιn - 1,96 σ / √n < μ < Xιn + 1,96 σ / √n
en (op deze X hoort uiteraard ook nog een streepje)
μ = Xn ± t (n - 1) S / √n
quote:Maar hoe moet ik S bepalen dan ?Op dinsdag 15 december 2009 23:27 schreef GlowMouse het volgende:
Het zijn betrouwbaarheidsintervallen, de eerste gebaseerd op een steekproef uit de normale verdeling waarvan de standaardafwijking bekend is (sigma), de tweede gebaseerd op een steekproef uit de normale verdeling waarvan de standaardafwijking onbekend is (en geschat wordt met S).
quote:Je bent een topperOp dinsdag 15 december 2009 23:36 schreef GlowMouse het volgende:
http://www.wetenschapsforum.nl/index.php?showtopic=64168
dankje !
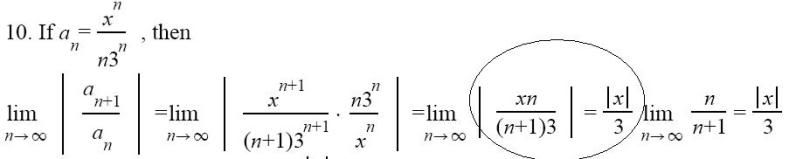
Zie het omkringelde. Hoe kunnen ze nou heel droog die twee n'en wegstrpen. Ik heb getracht het uit te werken door die 3(n+1) uit te werken tot : 3n + 3 en dan dingen wegstrepen, maar dan nog kom ik er niet op. Help please.
p.s.
Dit is trouwens een ratio test (Quotiëntentest)
quote:je maakt je cirkeltje te kleinOp woensdag 16 december 2009 16:50 schreef Burakius het volgende:
[ afbeelding ]
Zie het omkringelde. Hoe kunnen ze nou heel droog die twee n'en wegstrpen. Ik heb getracht het uit te werken door die 3(n+1) uit te werken tot : 3n + 3 en dan dingen wegstrepen, maar dan nog kom ik er niet op. Help please.
p.s.
Dit is trouwens een ratio test (Quotiëntentest)
.|x/3+3/n| ---> daarna de limiet bepalen geeft: x/3+0
En dan om de convergentiestraal te bepalen: x/3 = +- 1 dus x = +/- 3 R= 3 En dan moet je die weer invullen in de originele etc. etc.
quote:Er wordt helemaal niks 'weggestreept'. Die factor |x|/3 is onafhankelijk van n en dus een constante factor wanneer n je variabele is. Zodoende is de limiet van |xn/3(n+1)| voor n →∞ gelijk aan |x|/3 maal de limiet van n/(n+1) voor n →∞.Op woensdag 16 december 2009 16:50 schreef Burakius het volgende:
[ afbeelding ]
Zie het omkringelde. Hoe kunnen ze nou heel droog die twee n'en wegstrpen. Ik heb getracht het uit te werken door die 3(n+1) uit te werken tot : 3n + 3 en dan dingen wegstrepen, maar dan nog kom ik er niet op. Help please.
p.s.
Dit is trouwens een ratio test (Quotiëntentest)
Dit is dus een Bessel-functie van de 1ste orde. Heel leuk en aardig dat ze hier een Ratio test gebruiken. Nu kom ik zelf op :
(x/2)2 lim 1/n+2
Zoals jullie zien mis ik die n+1 die ook bij de noemer hoort. Nu zal het vast liggen aan iets met die faculteiten. [b]Ik weet dat (blijkbaar) ((n+1)+1)! = (n+2)! [b/] En ik weet ook dat (n+2)! = (n+2)n!
Als ik dit toepas kan ik wegstrepen etc. , maar dan houd ik die n+1 niet over iig.
Wat doe ik fout? (graag het dikgedrukte ook verifiëren)
quote:dat klopt niet.En ik weet ook dat (n+2)! = (n+2)n!
quote:Oke dat zou goed kunnen. Voor (n+1)! = (n+1)n! wel geldig.
Dus dan is het voor (n+2)! = (n+1)(n+2) n! of iets in die richting?
quote:Tja, je kent de definitie van ! toch hoop ik?Op woensdag 16 december 2009 21:31 schreef Burakius het volgende:
[..]
Oke dat zou goed kunnen. Voor (n+1)! = (n+1)n! wel geldig.
Dus dan is het voor (n+2)! = (n+1)(n+2) n! of iets in die richting?
quote:tja ik weet dat (n+2)! = (n+1) * (n+2) * ....... etc. dus = (n+1) * (n+2) * n! (hoop dat dit correct is).Op woensdag 16 december 2009 21:34 schreef Iblis het volgende:
[..]
Tja, je kent de definitie van ! toch hoop ik?
Het is faculteit. Dus 3! = 1 * 2 * 3
quote:Ik zou het wel andersom schrijven, nu lijkt het net of de termen steeds hoger gaat, maar dus:Op woensdag 16 december 2009 21:42 schreef Burakius het volgende:
[..]
tja ik weet dat (n+2)! = (n+1) * (n+2) * ....... etc. dus = (n+1) * (n+2) * n! (hoop dat dit correct is).
Het is faculteit. Dus 3! = 1 * 2 * 3
(n+2)! = (n+2) * (n+1)! = (n+2) * (n+1) * n!
quote:Thx duidelijk!Op woensdag 16 december 2009 21:53 schreef Dzy het volgende:
[..]
Ik zou het wel andersom schrijven, nu lijkt het net of de termen steeds hoger gaat, maar dus:
(n+2)! = (n+2) * (n+1)! = (n+2) * (n+1) * n!
Technisch verhaal:
Ik doe een onderzoek naar de effectiviteit van een interventie. Werkt onze beinvloeding ja/nee?
Idee: we hebben 3 plekken in Nederland gepakt. Op twee plekken hebben we een bord neergezet, namelijk bord1 of bord2. Op de derde plek staat niets (controleconditie).
Bij deze plekken hebben wij op drie dagen, voor twee weken, geobserveerd. Eerste voordat de borden er stonden (voor-/nulmeting) en daarna terwijl de borden er staan.
Mijn variabelen in mijn databestand ziet er ongeveer zo uit:
T0-1 T0-2 T0-3 T0-4 T0-5 T0-6 T1-1 T1-2 T1-3 T1-4 T1-5 T1-6 Conditie
T0-1 is de eerste dag van de nulmeting, T0-3 is de derde dag van de nulmeting enz.
T1-1 is de eerste dag van de nameting, T1-5 is de vijfde dag van de nameting enz.
Conditie is het bord dat er staat, 1,2 of 3 (waarbij 3 geen bord is).
Daaronder staan dus 3 rijen met cijfers, voor elk geobserveerde plaats 1.
Mijn vraag is deze: Hoe kan ik de effectiviteit van onze interventie berekenen? Doordat we maar drie plaatsen hebben, is er een n van 3 (erg weinig dus). Is er een mogelijkheid de data van de verschillende meetmomenten als 'within' info mee te nemen of nog iets anders ermee te doen?
Als ik een repeated measures anova doe kan ik wel contrasten bekijken tussen alle verschillende meetmomenten, maar ik wil eigenlijk een duidelijk contrast tussen nulmeting en nameting.
Als ik een gemiddelde pak van de nulmeting en de nameting heb ik het gevoel dat ik veel informatie weggooi door simpelweg een gemiddelde te pakken, terwijl ik in feite 6 observaties heb.
Kan iemand mij helpen?
Alvast bedankt!
daar verder
[ Bericht 91% gewijzigd door GlowMouse op 17-12-2009 21:56:39 ]
Ik hoef niet perse met a1 en a2 zelf te werken dus ik dacht het volgende: ik maak tien kleine lijsten (de lengte/geheugen is even niet zo belangrijk) A0, A1,...,A9 waarbij ik in lijst Ai alle getallen uit A stop die eindigen op i in hun decimale representatie (dus bijv 101 gaat naar A1, 1004404 gaat naar A4). Daarna maak ik een forloop die een b getal uit B neemt en dan i=b%10 uitrekent, dan zoek ik alleen in lijst Ai naar het getal b.
Dit algortime heeft toch hoogstens orde n? Is er nog een slimmer/sneller algoritme?
Alvast bedankt!
quote:Het opzoeken kost ook nog O(n) zodat je voor het totaal op O(n²) komt. Door sorteren van beide lijsten kun je tot O(n logn) komen, maar de vraag is of dat bij n=100 veel uitmaakt.Daarna maak ik een forloop die een b getal uit B neemt en dan i=b%10 uitrekent, dan zoek ik alleen in lijst Ai naar het getal b.
Als de lijsten van getallen niet bounded zijn dan is m'n eerste indruk dat je ze het beste individueel kunt sorteren (n log n), en dan mergen wat met gesorteerde lijsten lineair kan. Tijdens de merge kun je dan op duplicaten checken.
Is de boel wel gebound of weet je meer over de input, dan kun je een lineaire oplossing nadenken.
quote:Die bound heb je ook, want je weet dat het natuurlijke getallen zijn. Je kan dan het maximum zoeken in O(n), een array maken vol booleans met de maximumgrootte van het gevonden maximum + 1, en alle startwaarden in die array op false zetten.Op zaterdag 19 december 2009 13:06 schreef Iblis het volgende:
Is de boel wel gebound of weet je meer over de input, dan kun je een lineaire oplossing nadenken.
Tijdens de eerste for-loop zet je indices in je array die corresponderen met de getallen die in je eerste lijst staan op true (O(n)). Tijdens de tweede for-loop kijk je of de indices in je array die corresponderen met de getallen in je tweede lijst al op true staan (O(n)), zo ja, dan zit ie in beide. Kan een heleboel geheugen kosten als het maximum heel groot is enzo, maargoed, de orde is lager -.-
Jouw 'oplossing' is niet goed, je ziet zelf dat het al fout gaat bij een groot getal.
quote:Er zullen vast wel meer bounds zijn waardoor het makkelijk wordt om een lineaire oplossing te bedenken. Als je weet dat de getallen natuurlijke getallen zijn (zoals in dit geval) ook, dus ksnap niet precies wat je bedoelt.Op zaterdag 19 december 2009 14:12 schreef GlowMouse het volgende:
Iblis heeft het over een a priori bekende bound, bedenk maar eens waarom het dan makkelijk wordt
Jouw 'oplossing' is niet goed, je ziet zelf dat het al fout gaat bij een groot getal.
Het kan veel geheugen kosten maar in theorie gaat dit goed hoor, en er werd volgens mij niet gevraagd om rekening te houden met het geheugen. Kan je iets concreter vertellen wat er volgens jou dan mis gaat -.-
Overigens, wat Optimistic1 doet, is simpelweg de input hashen. En in feite kan dat algemener. En dan kun je – met random data – wel een in de praktijk lineaire oplossing krijgen. Maar de vraag is dus even of je worst-case wilt gaan zitten analyseren of niet.
quote:In de praktijk kan je hierop letten, maar om de orde van n te bepalen hoef je niet te letten op maximumgetal K en kdenk dat Optimistic bedoelde dat hij de laagste orde n wou. De oplossing die ik in mn post noemde is overigens ook geaccepteerd als oplossing (als n dichtbij K zit), alleen wordt hij nauwelijks gebruikt -.-Op zaterdag 19 december 2009 14:22 schreef GlowMouse het volgende:
Je moet kijken naar de verwerkingstijd als functie van je input. In jouw functie is die exponentieel, want om een groot getal K in te voeren kost dat mij log(K) stapjes terwijl de geheugenallokatie K stapjes kost.
Wat Iblis zegt kan mis gaan (ook al kom je in de praktijk niet altijd tegen dat je getallen groter dan 2^64 moet verwerken) waar ingewikkelde oplossingen voor zijn (met nog meer trees en arrays), dus daar gaan we niet aan beginnen -.- Daarom kan Optimistic maar beter zoiets zeggen (wat in de vorige posts al beetje gezegd is, maar het algoritme is nog niet echt gegeven):
- Beide lijsten sorteren (via merge-sort heb je uiteindelijk de laagste orde, namelijk O(n log(n)), maar quick-sort is in de praktijk sneller maar heeft worst-case O(n^2)).
- Neem telkens het minimum van de twee gesorteerde lijsten en kijk of hij overeenkomt met het minimum van de andere lijst. Zo niet, streep die weg en herhaal.
*Kies een random punt P op de kromme E.
*Bereken de eerste s veelvouden van P, namelijk P, 2P, 3P,...,sP, waarbij s=p^(1/4) (bij mij is s ongeveer 100) en sla deze op in een lijst.
*Bereken Q:=(2*s+1)P en R=(p+1)P door binaire expansie van p+1 te gebruiken.
*Schrijf t=[sqrt(p)/(2*s+1)] (dit is een getal ongeveer gelijk aan s) en bereken
R +/-P, R+/- 2P,R+/-3P,....,R+/-tP en dit zijn 2s+1 punten. Deze sla ik weer op in een lijst.
Er is een stelling die zegt dat er een i en j bestaan met R+iQ=jP, dus er is een punt zowel in de 1e als in de 2e lijst en dat punt wil ik vinden... want als ik die vind en dus ook i en j weet..
dan kan ik weten wat het aantal punten is op mijn kromme E. Over het vinden van dit punt staat;
"It is important that one can efficiently search among the points in the
list of baby steps; one should sort this list or use some kind of hash coding.
It is not difficult to see that the running time of this algorithm is O(p1/4+e)"
http://www.mat.uniroma2.it/~schoof/ctg.pdf
Mijn idee was om dus om gebruik te maken van de x-coordinaat van de punten en die gaan onthouden.
a= 0,5(0,84a+0,4c) + 0,8c
a = 1,72
waarom wordt dit 1,72c ?
quote:Als je a invult krijg je:
ok, ik heb alleen mn telefoont en moment tot mijn beschikkng, dus alle informatie kan ik niet geven, maar het schijnt dat je hieraan genoeg hebt:
a= 0,5(0,84a+0,4c) + 0,8c
a = 1,72
waarom wordt dit 1,72c ?
1,72 = 0,5(0,84·1,72 + 0,4·c) + 0,8c
Vermenigvuldig met 2:
3,44 = 0,84·1,72 + 0,4c + 1,6c
3,44 = 1,44 + 2,0c
2,00 = 2,0c
c = 1,00
Excuus, maar ik gaf het niet goed aan.
Uit de berekening achter A, moet 1,72C uitkomen.
Dus A=0,5(0,84a+0,4c)+0,8c
Ik hoop dat ik het zo duidelijk heb kunnen maken, zag dat ik net de c vergeten was, nog al een belangrijk verschil he :p
a= 0,5(0,84a+0,4c) + 0,8c
oplossen naar c. Om dat de doen, begin met vermenigvuldigen met 2:
2a= 0,84a + 0,4c + 1,6c
0,84a naar de andere kant, termen met c samenvoegen:
1,16a = 2,0c
Deel links en rechts door 1,16:
a = 1,72c
quote:Haha yeah! Mijn dank is groot, ik snap 'm! Dit brengt mij weer een stuk verder.Op maandag 21 december 2009 21:16 schreef Iblis het volgende:
Ah, ik snap wat je wilt, maar je schrijft het raar op. Wat je wilt is:
a= 0,5(0,84a+0,4c) + 0,8c
oplossen naar c. Om dat de doen, begin met vermenigvuldigen met 2:
2a= 0,84a + 0,4c + 1,6c
0,84a naar de andere kant, termen met c samenvoegen:
1,16a = 2,0c
Deel links en rechts door 1,16:
a = 1,72c
Super!
.Oh nevermind, heb het al
quote:Inderdaad, zag het direct nadat ik het postteOp dinsdag 22 december 2009 00:09 schreef GlowMouse het volgende:
gebruik det(AB)=det(A)det(B) en I=A*A^-1.
Zij T: R2 ->R2 een lineaire afbeelding met als eigenschap |Tx|=|x| voor alle x in R2. Laat zien dat T ofwel een rotatie is, of een loodrechte spiegeling.
Het lijkt zo triviaal, maar ik heb geen idee hoe ik dit zou kunnen laten zien.
[ Bericht 80% gewijzigd door GlowMouse op 22-12-2009 00:28:46 ]
Maar stel dat bedoeld word dat de absolute waarde van x behouden blijft, dan impliceert dat dat T ofwel de identiteitsmatrix is, of minus de identiteitsmatrix. In het geval dat T de identiteitsmatrix is kan je het opvatten als een rotatie van 2pi, en als het minus de identiteitsmatrix is als spiegeling of rotatie van pi (is dat hetzelfde?).
Kan me haast niet voorstellen dat dit bedoeld wordt
quote:Bij lineaire algebra wordt |x| opgevat als 'de lengte van x' . ||x|| wordt daar nooit gebruikt...Op dinsdag 22 december 2009 00:29 schreef GlowMouse het volgende:
Hebben we het over ||Tx|| of over |Tx| (component-wise absolute waarde)?
Het is me nooit uitgelegd wat het verschil is tussen die twee. Ik dacht dat het een kwestie van verschillende notatie maar zelfde betekenis was.
[ Bericht 8% gewijzigd door BasementDweller op 22-12-2009 00:40:17 ]
quote:Ik vermoed van niet.Op dinsdag 22 december 2009 00:38 schreef GlowMouse het volgende:
heb je algebraïsche eigenschappen geleerd van rotatiematrices/spiegelmatrices?
Er is trouwens een hint:
Laat zien dat Te2 loodrecht staat op Te1
(was misschien handig geweest als ik die er direct had bij gezet, maar ik dacht misschien weet jij een andere manier, want hiermee kwam ik niet verder)
hier heb je al dat T tranpose zijn inverse is, een van de eigenschappen van een rotatiematrix (zie http://en.wikipedia.org/wiki/Rotation_matrix ).
quote:Dat aantonen gaat op dezelfde manier als wat ik juist deed. Hiermee ben je klaar
[..]
Ik vermoed van niet.
Er is trouwens een hint:
Laat zien dat Te2 loodrecht staat op Te1
[ Bericht 50% gewijzigd door motorbloempje op 01-09-2013 21:33:59 ]
|Ax|=|x| => A(x) dot A(y)= x dot y
Dus omdat e1 dot e2 =0, Te1 dot Te2 = 0. Met behulp van die stelling is het dus erg eenvoudig om te laten zien dat Te2 loodrecht staat op Te1, maar heb ik daarmee dan aangetoond dat T een rotatie of een loodrechte spiegeling is? Zo ja, waarom?
[ Bericht 1% gewijzigd door BasementDweller op 22-12-2009 01:25:12 ]
Je kunt ook zeggen x=x(1)e1 + x(2)e2, dus Tx = x(1) Te1 + x(2) Te2, dus je hebt dezelfde vector maar dan tov een andere orthogonale basis.
quote:Ja, intuïtief snap ik het wel.Op dinsdag 22 december 2009 01:19 schreef GlowMouse het volgende:
intuïtief: alles blijft even lang en er vervormt niks
Je kunt ook zeggen x=x(1)e1 + x(2)e2, dus Tx = x(1) Te1 + x(2) Te2, dus je hebt dezelfde vector maar dan tov een andere orthogonale basis.
Ah, ik snap het al. Als de basis loodrecht blijft na afbeelden, betekent dat dat er geen vervorming is en dan kan je alleen maar roteren of spiegelen. Niet echt een prachtig bewijs, maar ze vragen eigenlijk ook alleen maar 'laat zien' .
Oke bedankt, ik ben eruit
!(Wat ik wel slecht vind aan die opgave is dat het met die hint niet hard bewezen is, maar eigenlijk nog steeds vrij intuïtief. En dat terwijl ik het zonder die hint intuïtief ook al prima begrijp. Bovendien had ik er een stelling uit een ander hoofdstuk bij nodig...
)[ Bericht 8% gewijzigd door BasementDweller op 22-12-2009 01:36:36 ]
Zij A: R² -> R² een lineaire afbeelding ongelijk aan O, de nul-afbeelding. Stel M²=O.
(a) Bewijs dat dim(ker(M))=1 (dus de dimensie van de kern van M is gelijk aan 1)
Om dit te bewijzen wou ik gebruik maken van twee matrices. Matrix A heeft één getal in de rechterbovenhoek. Matrix B heeft één getal in de linkerbenedenhoek. Voor die matrices geldt A²=B²=0. Dan is het makkelijk om te te laten zien dat ker(A)= { x¤R² | x =t(1,0), voor alle t¤R} en ker(B)= { x¤R² | x= t (0,1), voor alle t¤R}. Omdat ker(A) en ker(B) één vrijheidsgraad hebben geldt: dim(ker(A))=dim(ker(B))=1.
Echter, bij vraag (c) wordt pas een voorbeeld gevraagd van een dergelijke afbeelding M. Mijn conclusie is dus dat (a) ook in het algemeen bewezen kan worden zonder gebruik te maken van Matrix A en B.
Heeft iemand enig idee hoe?
Maar het is ook makkelijk in te zien dat M een lineaire combinatie moet zijn van A en B, en vervolgens dat niet beide gewichten ongelijk aan 0 kunnen zijn.
quote:Wat bedoel je er precies mee dat de kolommen van M in de nulruimte zitten?Op donderdag 24 december 2009 00:42 schreef GlowMouse het volgende:
Je weet dat dim(ker(M)) 0,1 of 2 kan zijn, en 0 en 2 kun je vrij makkelijk wegstrepen (0 omdat de kolommen van m in de nulruimte zitten, 2 omdat het niet de nulmatrix is).
Maar het is ook makkelijk in te zien dat M een lineaire combinatie moet zijn van A en B, en vervolgens dat niet beide gewichten ongelijk aan 0 kunnen zijn.
Gegeven: Zij A: Rn -> Rn een lineaire afbeelding met de eigenschap A² = A.
Te bewijzen: Zij V een lineaire deelruimte van Rn. De doorsnede van ker(A) en A(V) is de verzameling bestaande uit slechts de nulvector.
Heb een hint nodig.. ik blijf dit soort opgaves lastig vinden
[ Bericht 100% gewijzigd door GlowMouse op 24-12-2009 16:30:18 ]
quote:Waarom weet ik dat Av=0 ?Op donderdag 24 december 2009 16:27 schreef thabit het volgende:
Neem een element v van Rn dat zowel in ker(A) als A(V) zit. Te bewijzen: v=0. Je weet: Av = 0 en er is een w met v = Aw. Nu jij weer.
Bedoel je dat je Av gelijk kan stellen aan nul omdat A een lineaire afb is?
quote:je neemt aan dat hij zit in de doorsnede van ker(A) en A(V).Waarom weet ik dat Av=0 ?
quote:Lineaire afbeeldingen zijn niet vierkant. Maar als je n=2 neemt en A de lineaire afbeelding (x,y) -> (y,0) dan heb je een tegenvoorbeeld want (1,0) zit in zowel kern als beeld.Op donderdag 24 december 2009 16:38 schreef GlowMouse het volgende:
Ligt het aan mij of heb je ook genoeg aan 'A is vierkant'?
Is het omdat W een deelruimte is van Rn, dat je daardoor Aw gelijk kan stellen aan v omdat v in Rn zit?
Maar als dat zo is. Dan is Av=AAw=Aw=v=0 en ben je klaar
. Het is me nu duidelijk !f(x) = 1/ (1+x)2
Ik heb totaal geen idee hoe het nou wordt omgezet tot een power series. In het boek (blz. 732) staat er wel wat theorie, maar ik kom er niet uit. Zelf aerostudents (handige site), waar de uitwerkingen op staan laten mij in de steek. Wat wordt er precies gebruikt? iets met a/1-r = ar^n-1 iig.
Maar, denk ook aan de afgeleide.
quote:Een mooie kerstgedachte.Op donderdag 24 december 2009 23:12 schreef Iblis het volgende:
Maar, denk ook aan de afgeleide.
.quote:Op donderdag 24 december 2009 23:09 schreef thabit het volgende:
Ik zou beginnen met 1/(1+x), weet je daar de machtreeksrepresentatie van?
sommatieteken: (-1)^n * x^n lijkt mij ???
quote:Idd een Christen hahaha. Laat ik dat nou net niet zijnOp donderdag 24 december 2009 23:12 schreef Iblis het volgende:
Goddeloze mathematici ook altijd. Augustinus zei het al: De goede Christen moet bevreesd zijn voor de mathematici. Op kerstavond!
Maar, denk ook aan de afgeleide.
. Wat doe jij trouwens hier op dit tijdstip op deze dag ?quote:Goed, nu de kerstgedachte toepassen.Op donderdag 24 december 2009 23:14 schreef Burakius het volgende:
[..]
sommatieteken: (-1)^n * x^n lijkt mij ???
quote:Jou helpen.
[..]
Idd een Christen hahaha. Laat ik dat nou net niet zijn
quote:Iemand met de naam van de duivel die een Moslim helpt
.. Nederland is té multicultureel hahaha. Je was natuurlijk de hele dag op mij aan het wachten hahaha
.hmmm heb jij toevallig een boek van Dostojevski gelezen?
quote:Zeker. Maar dat is denk ik meer voor de alfa-topic.
[..]
Iemand met de naam van de duivel die een Moslim helpt
Nederland is té multicultureel hahaha. Je was natuurlijk de hele dag op mij aan het wachten hahaha
hmmm heb jij toevallig een boek van Dostojevski gelezen?
quote:Kijk zonder differntiatie of whatever dat ook moge zijn wat je hier moet doen kom ik tot:Op donderdag 24 december 2009 23:20 schreef thabit het volgende:
[..]
Goed, nu de kerstgedachte toepassen.
f(x) = 1/(1+x)2 --> 1/1+x sommatieteken: 1/1+x ----> 1/1+x sommatieteken: 1/1-(-x)
--> 1/1+x sommatieteken: (-x)n --> 1/1+x sommatieteken: (-1)n * xn
Maar ja..
Voor 1/(1+x) weet je nu al een reeks, en als je die differentieert… dan moet het (bijna) uitkomen.
f(x) = 1/ (1+x)²
f'(x) = -2/(1+x)³
f''(x) = 6/(1+x)^4
en dan zie je het patroontje:
dus
vul je in in de formule voor de taylorreeks rond x=0 en je bent klaar.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:06 ]
Stel v=(v1, v2, ... , vn)t. We definiëren v* als de complex geconjugeerde van v. Dan geldt v*tv= (v1² + ... + vn²).
Ik zie niet in waarom dit waar is. Ik krijg: v*tv=(v1*v1 + v2*v2 + ... + vn*vn)
(let op: * betekent de geconjugeerde, niet vermenigvuldiging)
Als tegenvoorbeeld:
Stel dat v1= 1+i, dan is v1*=1-i. Dus v1*v1=(1-i)(1+i)!=(1+i)²=v12
[ Bericht 3% gewijzigd door BasementDweller op 25-12-2009 16:19:46 ]
quote:Gewoon de afgeleide dus? Sorry als dit geen nut heeft, maar ik heb binnenkort toch een toets over differentieren en integreeren.Op donderdag 24 december 2009 23:05 schreef Burakius het volgende:
Oke guys. Calculus 11.9. Ik moet nu "use differentation to find a power series representation for:
f(x) = 1/ (1+x)2
Ik doe het altijd zo:
f(x) = 1/ (1+x)2 = (1 + x)-2
Deze regel geldt:
f(x) = xa
f'(x) = axa-1
Dus hier:
f(x) = (1 + x)-2
f'(x) = -2 * (1 + x)-3 = -2 * 1 / (1 + x)3 = -2 / (1 + x)3
quote:Een fouriertransformatie is een integraaltransformatie, maar er zijn er meerdere. http://nl.wikipedia.org/wiki/Integraaltransformatie is vrij duidelijk wat dat betreft.
Zou iemand me kort uit kunnen leggen wat een integraaltransformatie is, ik weet dit niet precies en van wikipedia en google werd ik ook niet veel wijzer. Ik weet wel wat bijvoorbeeld de fourieranalyse is, hoe hij werkt en wat hij doet.
quote:Nee, ze bedoelen een taylorreeks met oneindig veel termen.
[..]
Gewoon de afgeleide dus? Sorry als dit geen nut heeft, maar ik heb binnenkort toch een toets over differentieren en integreeren.
quote:vreemd
In mijn lial diktaat staat het volgende:
Stel v=(v1, v2, ... , vn)t. We definiëren v* als de complex geconjugeerde van v. Dan geldt v*tv= (v1² + ... + vn²).
quote:Ik begrijp het niet helemaal. Bedoelen ze dat een integraaltransformatie de afgeleide van de integraal van <een functie maal nog iets> is? Dan is het me namelijk wel geheel duidelijk.Op vrijdag 25 december 2009 17:14 schreef GlowMouse het volgende:
Een fouriertransformatie is een integraaltransformatie, maar er zijn er meerdere. http://nl.wikipedia.org/wiki/Integraaltransformatie is vrij duidelijk wat dat betreft.
quote:Sorry :SOp vrijdag 25 december 2009 17:14 schreef GlowMouse het volgende:
Nee, ze bedoelen een taylorreeks met oneindig veel termen.
quote:Ik denk dat het gewoon een fout is. Als er |v1²| + ... had gestaan dan klopt het.
Ik heb het nog nooit gehad, en kom het nu opeens tegen in mijn wiskundeboek.
[ Bericht 1% gewijzigd door AE86_Trueno op 27-12-2009 13:00:17 ]
quote:http://nl.wikipedia.org/wiki/Combinatie_%28wiskunde%29Op zondag 27 december 2009 12:54 schreef AE86_Trueno het volgende:
Ik voel me echt dom, maar wat moet er gebeuren wanneer er dit staat:
[ afbeelding ]
Ik heb het nog nooit gehad, en kom het nu opeens tegen in mijn wiskundeboek.
quote:Dankjewel, ik had het al wel ooit gehad. Was het alleen vergetenOp zondag 27 december 2009 13:00 schreef BasementDweller het volgende:
[..]
http://nl.wikipedia.org/wiki/Combinatie_%28wiskunde%29
Zelf heb ik ook een vraagje.
De opgave is: bereken de limiet als (x,y,z)->(0,0,0) van sin(xyz)/xyz.
Ik dacht dat je dan gewoon xyz kon substitueren door t. Dan krijg je lim van t->0 sin(t)/t. Met de regel van L'Hôpital blijkt dat 1 te zijn. Het antwoord is echter 0... dus waarom is mijn antwoord fout en hoe kan je het wel doen?
quote:Inderdaad.... is het antwoord in het boek weer eens fout
.Is mijn argumentatie correct? Mag je dat xyz=t gebruiken?
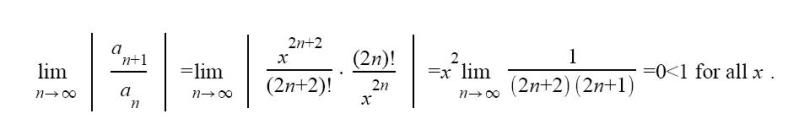
Ik zit weer in de problemen met die faculteiten. Ik irriteer me er mateloos aan. Dus kan iemand me zeggen wat ik fout doe als ik zeg dat:
Ik (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n!
Ik (2n)! ook zou kunnen shrijven als: (2n)n!
Daar ergens moet mijn fout zitten.
pak n=3, links staat 6!, ofwel 6*5*4*3*2*1
rechts staat 6*3!, ofwel 6*3*2*1.
Bij (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n! kun je zo ook laten zien dat het fout is.
Neem anders een paar concrete gevallen om het idee te krijgen. n = 3, dan (2n + 2)! = 8! = 8·7·6·5·4·3·2·1 = 8·7·6! bijvoorbeeld, maar natuurlijk niet 8·7·3! wat jij zegt.
Faculteiten .. mijn nachtmerrie.
quote:Jup, die (2n)! in teller en noemer vallen tegen elkaar weg.
Ja dus het wordt eigenlijk - (2n+2)(2n+1)(2n)! waardoor ik die (2n)! kan wegstrepen . Toch..
Faculteiten .. mijn nachtmerrie.
quote:Als dank mag jij mijn nieuwe avatar uitkiezen. (keep it pro-MuslimOp zondag 27 december 2009 23:58 schreef Iblis het volgende:
[..]
Jup, die (2n)! in teller en noemer vallen tegen elkaar weg.
).
quote:Zonder kerstmuts had ik het misschien gedaan. Maar het is Ibo zijn call aahahaa. Wil je me onder je Glowmouse apprentice gang scharen ofzo?
quote:Dan lijkt me, omdat het toch in de β-sfeer te houden een crop / verkleining uit:
[..]
Als dank mag jij mijn nieuwe avatar uitkiezen. (keep it pro-Muslim
Bron: Wikimedia Commons. Maker: Dmharvey. Licentie: CC-BY-SA.
Wel prima. De behangpatroongroep p3 uit het Alhambra.
quote:Gedaan. Best wel vet, meteen ff het wikipaginaatje lezen! Wat is precies het verhaal er achter?Op maandag 28 december 2009 00:07 schreef Iblis het volgende:
[..]
Dan lijkt me, omdat het toch in de β-sfeer te houden een crop / verkleining uit:
[ link | afbeelding ]
Bron: Wikimedia Commons. Maker: Dmharvey. Licentie: CC-BY-SA.
Wel prima. De behangpatroongroep p3 uit het Alhambra.
Maar, los daarvan, het is een typisch voorbeeld van Islamitische ornamentiek om een vlak te versieren met regelmatige patronen (die na rotatie of spiegeling hetzelfde blijven). De indeling ‘p3’ is wiskundig, in het Alhambra vind je alle 17 indelingen al.
Ook de Nederlandse artiest Escher die bekend is om z’n patronen en indelingen heeft in het Alhambra veel inspiratie opgedaan.
Ze gebruikten uiteraard zulke geometrische versieringen i.v.m. met het taboe op afbeeldingen van levende wezens, maar dat hoef ik jou denk ik niet te vertellen.
Edit: nu niet meer
Ik ben bezig met de afgeleide bepalen, differentiëren, maar het lukt niet helemaal.
Kan iemand mij uitleggen welke stappen je neemt om bijvoorbeeld: f(x)= (x^2 + 2x)(3x + 5) op te lossen?
Alvast bedankt!
quote:Heb je de productregel al gehad?
Hoi,
Ik ben bezig met de afgeleide bepalen, differentiëren, maar het lukt niet helemaal.
Kan iemand mij uitleggen welke stappen je neemt om bijvoorbeeld: f(x)= (x^2 + 2x)(3x + 5) op te lossen?
Alvast bedankt!
en dat afleiden gaat vanzelf.
Je kan het met de productformule, maar ik denk dat dit eenvoudiger is.
quote:
nee, zegt me weinig.
quote:Dan zou ik gewoon, wat Beregd ook zegt, de haakjes wegwerken (dan kom je op wat hij zegt als het goed is) en dan afleiden. Lukt dat?
quote:Op maandag 28 december 2009 14:23 schreef Beregd het volgende:
=3x³+11x²+10x
en dat afleiden gaat vanzelf.
Je kan het met de productformule, maar ik denk dat dit eenvoudiger is.
hoe kom je bij 11x^2, ik kwam uit op 11x^4?
quote:hoe dat?Op maandag 28 december 2009 14:36 schreef evelien89 het volgende:
[..]
hoe kom je bij 11x^2, ik kwam uit op 11x^4?
quote:5x^2 + 6^2 ?
quote:de exponenten mag je niet optellen!
als je niet inziet waarom, moet je x maar eens vervangen door 2 of 3 bvb.
Stel dat a=x². Dan zie je dat 5x² + 6x² = 11x²
Nog eentje: y = 5x2 + 2x + 1 → y' = 10x + 2
Dat eerste deel is helder, ik snap alleen niet waarom het '+2' op het eind is.
Zo ja, wat kreeg je eruit?
quote:Dat komt van 2x, als je dat afleidt krijg je 2.
owja, ik zie het nu ook.
Nog eentje: y = 5x2 + 2x + 1 → y' = 10x + 2
Dat eerste deel is helder, ik snap alleen niet waarom het '+2' op het eind is.
quote:en die +1 dan? Moet je die dan weglaten?Op maandag 28 december 2009 15:15 schreef Iblis het volgende:
[..]
Dat komt van 2x, als je dat afleidt krijg je 2.
quote:De afgeleide van een constante is 0.Op maandag 28 december 2009 15:35 schreef evelien89 het volgende:
[..]
en die +1 dan? Moet je die dan weglaten?
De afgeleide kan je zien als de helling. Als je de grafiek van bijvoorbeeld y=3 tekent, dan heeft ie een helling van 0. Daarom is het ook in te zien dat y'=0 .
(5x + 3) (x^2 + 3). Ik kwam uit op: 16x + 15. Wat doe ik fout?
opletten, evelien!
: (1-x)2/3
Aangezien ik hier geen uitwerkingen van heb, en er in Calculus geen antwoord staat en ik er niet uitkom graag hulp. Tot zover heb ik dit al gedaan:
f(x) = (1-x)2/3
f (0) = 1
f '(x) = -2/3 (1-x)-1/3
f ' (0) = 2/3
f '' (x) = -2/9(1-x)-4/3
f '' (0) = 2/9
f ''' (x) = 8/27(1-x)-7/3
f ''' (0) = 8/27
f '''' (x) = 56/81(1-x)-10/3
f ''''(0) = 58/81
Daarmee ga ik nu f (n)(0) bepalen:
= ...... / 3n
Waar de puntjes staan heb ik nog niets kunnen bedenken. Verder zou het kunnen dat ik geen altererende iets heb, en dat dat wel hoort etc.
Ik wil die f^n(0) weten om dit in te vullen:
sommatieteken: (f^n(0)/ n!) * x^n
Daarna kan ik dit weer gebruiken om het in een taylorreeks te gieten. Mar goed wie helpt me uit de brand. Ik vind dit hoofdstuk sowieso een en al vaagheid. Elke keer gebruiken ze opeens een andere methode en manier.
http://www.ucl.ac.uk/Mathematics/geomath/level2/series/ser8.html
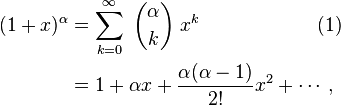
Daarna moet ik op een of andere manier van die reeks een powerreeks maken?
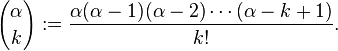
quote:Op zich, maar als de vraag expliciet zo gesteld wordt.
waarbij je gelijk ziet dat het hele gedoe met binomiaalcoefficienten zinloos is omdat je er met differentieren ook al op uitkwam
quote:Kijk deze heb ik ook gewoon normaal op mijn formuleblad staan. Ik moet het nu specifiek doen met binominale etc. Maar het is zo vaag. Bijvoorbeeld deze som:Op maandag 28 december 2009 19:47 schreef GlowMouse het volgende:
waarbij je gelijk ziet dat het hele gedoe met binomiaalcoefficienten zinloos is omdat je er met differentieren ook al op uitkwam
wortel (1+x) ==> (1+x)1/2
Die kun je dan ook zo invullen zou je zeggen in dat formaatje, maar daar komt toch echt iets anders uit bij de antwoorden. In de uitwerkingen doen ze dit:
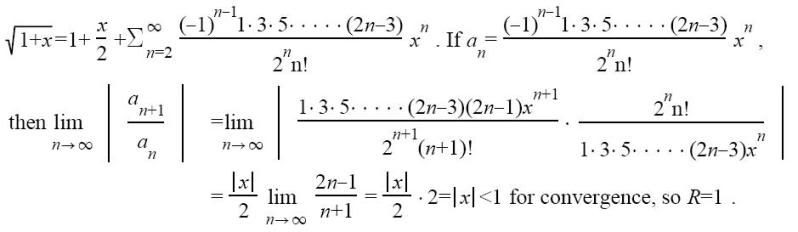
quote:Wel. Je krijgt in de teller 1/2·-1/2·-3/2·-5/2··· in de teller, als je die samenvoegt krijg je 2n, die dan naar de noemer verhuist.
Die 2n n! krijg je dus niet bij het "gewoon" invullen van die standaard vorm gegeven door Ibo.
quote:Ja en die moet je weer omschrijven tot een sommatieteken toch?Op maandag 28 december 2009 19:45 schreef Iblis het volgende:
Zoals er staat, geldt het voor elke α, of het nou geheel of reëel (of zelfs complex) is, dat zegt GlowMouse’ link ook. Dus in jouw geval krijg je:
[ afbeelding ]
quote:Ik vermoed dat je wat anders bedoelt en dat dat niet juist is.
[..]
Ja en die moet je weer omschrijven tot een sommatieteken toch?
quote:Neem nou als voorbeeld 1/(2+3)3 ...Op maandag 28 december 2009 19:45 schreef Iblis het volgende:
Zoals er staat, geldt het voor elke α, of het nou geheel of reëel (of zelfs complex) is, dat zegt GlowMouse’ link ook. Dus in jouw geval krijg je:
[ afbeelding ]
In standaardvorm met jouw dingetje, krijg je dan:
k = -3
Dus 1+3x + (12/2!)*x2 +( -60/3!)*x3 etc. etc. , maar hierna moet er nog iets zijn, omdat ! het boek dan opeens komt met (ja het is paint sorry):
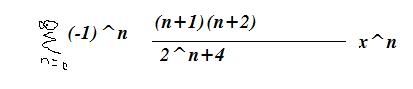
Goed ik kan begrijpen waarom er (n+1) (n+2) staat, (alhoewel ik daar zelf echt niet op zou komen), maar waarom die 2^n+4 in de noemer... en er is zelfs geen faculteit meer!
quote:Het het precies zo ingevuld als hier (op dezer maniier):Op maandag 28 december 2009 22:32 schreef Iblis het volgende:
Die k loopt van 0 t/m ∞.
Je schreef 1/(2 + 3)3, dat lijkt me niet correct vanwege missende x. Wat is de juist formule?
quote:1/ (2+x)3Op maandag 28 december 2009 22:45 schreef Iblis het volgende:
Sorry, ik volg echt niet wat je doet.
Je schreef 1/(2 + 3)3, dat lijkt me niet correct vanwege missende x. Wat is de juist formule?
Oke werk die maar zo uit met binominale dat je tot het antwoord komt die ik heb gepaint. Stap voor stap als het kan. Ik ben echt aan het einde van mijn latijn. Ik zie het gewoon niet meer.
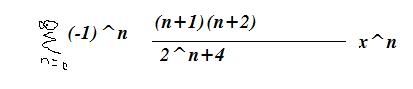(dit is het antwoord van het boek. )quote:Dat dacht ik niet.
Die twee er uit halen waardoor je : 2* (1 + x/2) -3 krijgt toch?
quote:1/2 (1+x/2)-3
???
Excuses, ik had me door jou op het verkeerde been laten zetten (maar mijn schuld, want ik lette niet op en typte stom over, sorry!)
Uiteraard geldt (2 + x) = 2(1 + x/2), niet 1/2(1 + x/2), dus je krijgt:
[ Bericht 77% gewijzigd door Iblis op 28-12-2009 23:47:09 ]
quote:Oke, en dan zo invullen ff kijken . ik edit het hier wel.Op maandag 28 december 2009 23:05 schreef Iblis het volgende:
Nee, je haakjes staan hier echt verkeerd. (1/2(1 + x/2))-3 wil je.
Probeer dus eerst die formule in de goede vorm te krijgen, nogmaals:
Nu naar jouw Wikipedia-vorm:
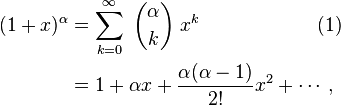
Merk dus op dat we niet x maar x/2 hebben, en dat we verder α = -3 hebben. Dan krijg je dus deze sommatie (ik gebruik k ook, net als hierboven, niet n zoals je boek):
Dat gaan we dan uitschrijven, en dan krijgen we:
Nu zullen we de algemene uitdrukking voor elke term bepalen. Het lastigste is (denk ik) even die -3·(-3 - 1)·(-3 - 2), enz, je ziet dat dit wordt:
-3
-3·-4
-3·-4·-5
-3·-4·-5·-6
Enz.
Dus het teken klapt telkens om, dus dat geeft (-1)k. Verder zie je je een soort van faculteitsontwikkeling onstaan, behalve dat de 1·2 telkens ontbreekt, en het in de k-e term t/m (k + 2) gaat, m.a.w.:
-3 = (-1)1 · 3!/(1·2)
-3·-4 = (-1)2 · 4!/(1·2)
-3·-4·-5 = (-1)3 · 5!/(1·2)
-3·-4·-5·-6 = (-1)4 · 6!/(1·2)
Dus dat geeft in feite als algemene uitdrukking (-1)^(k!)/2, als je dat invult krijg je:
Nu komen we weer bij jouw favoriet: faculteiten. In de teller heb je (k + 2)! staan, in de noemer k!, bedenk (k + 2)! = (k + 2)(k + 1)k!, en dan kun je k! dus wegdelen:
En als laatste, merk op 8 = 23, dus:
Waar jouw sommatie zo uit volgt:
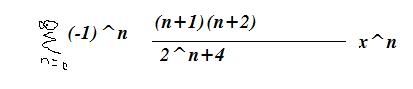
Ik wou graag even controleren of ik dit een beetje correct heb gedaan. Ik moet hier een power series van maken m.b.v. binominale. (11.10 som 28 , deel 6 Calculus).
(1-x)2/3
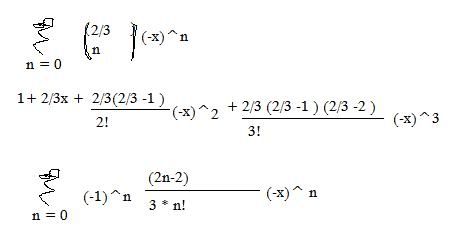
edit: hij klopt volgens mij niet. Ik ga vast en zeker de fout in door de teller in de taylorreeks verkeerd te definiëren bij het laatste sommatieteken. Ik heb er echt moeite mee.
Ik zie zeg maar: dat het gaat van 2/3 * -1/3 , 2/3 * -4/3 , 2/3 * -7/3 etc.
Ik kom er namelijk niet helemaal uit. Even een introductie: Ik heb voor een PO wiskunde een Chinees Postbode Probleem ontwikkeld die ik moet oplossen. Omdat ik ooit zelf postbode ben geweest, vond ik dat leuk, maar dat terzijde
. Ik ben dus nu op zoek naar de optimale route, waar dus de minste afstand wordt afgelegd. Een probleem is alleen dat de postbode een maximaal gewicht met zich mee mag nemen. Voor de duidelijkheid zal ik het hieronder even in plaatjes demonstreren:
De wijk schematisch weergegeven. Waar de huizen aan de weg vastzitten kan de post besteld worden. Het startpunt staat op dit plaatje als vaste waarde. Echter ben ik dus op zoek naar het ideale startpunt, dus deze zit daar niet vast.
De wijk in een graaf weergegeven. Zoals jullie zien is de flat en de route onder dijkwater verdwenen. Deze flat wordt altijd apart besteld, dus die onderste route heeft ook geen enkele meerwaarde en is dus per definitie inefficiënt.
De bundels die per straat (even en oneven) als standaard gelden.
Voor de postbode gelden Euler cirkels, oftewel, de postbode moet altijd weer uitkomen bij zijn fiets. Deze blijft de hele periode van het post bezorgen op 1 plaats staan (het startpunt).
Ik vroeg me dus af wat het beste startpunt is en hoe ik dit bereken. Ik ben pas sinds gister bekend met topologie en heb op een ander voorbeeld gebruik gemaakt van het algoritme van Fleury. Ik vroeg me echter af of er een formule was om dit probleem op te lossen en wat deze dan zou moeten zijn. Als jullie geen zin hebben om te puzzelen/rekenen, maar wel weten welk algoritme ik het best kan toepassen, laat het me dan ook weten. Dan kan ik me daar ook weer verder in verdiepen.
Ow en mocht het handig zijn, ik heb een applet gevonden waarbij je met verschillende algoritmen dergelijke topologische problemen op kan lossen. Klikkerdeklik.
Mocht het niet duidelijk zijn, of meer info nodig, let me know!
Maar in dezelfde regressieanalyse staat ook een correlatieschema wat andere correlaties laat zien dan het correlatieschema uit analyze->correlate en dus ook anders dan die uit mijn model summary. Wat laat het correlatieschema uit de regressieanalyse dan zien?
De bovenste is de Corruptie coefficient zonder de andere variabelen en de onderste is met de andere variabelen erbij. Ook bij de sociale uitgaven en pc per unit komt ik zelfs op een -getal uit!
quote:zie handleiding
Ik heb 4 onafhankelijke variabelen en 1 afhankelijke. Als ik gewoon een correlatieschema laat maken met analyze->correlate krijg ik dezelfde uitkomsten als de R in de model summary van de regressieanalyse.
Maar in dezelfde regressieanalyse staat ook een correlatieschema wat andere correlaties laat zien dan het correlatieschema uit analyze->correlate en dus ook anders dan die uit mijn model summary. Wat laat het correlatieschema uit de regressieanalyse dan zien?
quote:Dit is heel normaal: voeg je regressoren toe dan verandert de coëfficient van de oorspronkelijke regressoren vaak. Hij kan ook opeens wel significant worden.
En weet iemand hoe dit kan:
[ afbeelding ]
De bovenste is de Corruptie coefficient zonder de andere variabelen en de onderste is met de andere variabelen erbij. Ook bij de sociale uitgaven en pc per unit komt ik zelfs op een -getal uit!
.Het chinese postbode probleem is op zich zelf wel makkelijk, maar er zijn een aantal belangrijke verschillen met jouw versie:
* je beperkt het maximale gewicht dat een postbode kan dragen, waardoor meerdere rondes gelopen moeten worden.
* de chinese postbode bezorgt de post aan beide kanten van een straat.
Deze wiki pagina vermeldt summier wat over het chinese postbode probleem en daar staan ook enkele varianten waarvan bekend is dat ze erg lastig zijn (NP-complete). Deze varianten lijken sterk op jouw probleem, dus vandaar dat ik vermoed dat er geen efficient algoritme is.
Wat is het precieze doel van je werkstuk? Wil je alleen de optimale oplossing voor dit probleem hebben, of wil je een wat algemener verhaal houden?
Ja dat het niet heel eenvoudig zou zijn, had ik al verwacht. Ook die wiki pagina heb ik gezien, maar daar kwam ik niet veel verder mee helaas.
Het doel is overigens om een algemener verhaal te houden, dus een oplossing is niet per sé nodig. Ik heb overigens met beredeneren een optimum gevonden van 23, het is alleen jammer dat ik hier geen formule bij kan bedenken en dit kan controleren en bewijzen. Maar ja, ik denk niet dat zoiets gevraagd wordt van een VWO wiksunde leerling, maar eerder voor een eindscriptie van een wiskunde student.
Ik denk dat ik dus een redelijk antwoord heb op het vraagstuk door middel van redenatie, en dat dit wel als goed geaccepteerd word
Ik moet (Ik weet echt niet hoe je deze in het Neerlands moet neerzetten):
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point.
(som 25, 13.2 , Calculus deel 6): x = e-tcos t, y= e-tsin t, z = e-t ; (1,0,1)
Nu is het niet moeilijk om tot hier te komen:
r(t) = < e-tcos t i, e-tsin t j, e-t k >
r ' (t) = < -e-t(cost+sint) i, -e-t (sint -cost) j, -e-t k >
Wat ik nu niet snap is dat er van (1,0,1) opeens t = 0 omdat die correspondeerd tot (1,0,1).
Wat er daarna gebeurt is natuurlijk weer een eitje.
quote:Dus eigenlijk dit:Op woensdag 30 december 2009 17:30 schreef GlowMouse het volgende:
Je moet t vinden zdd r(t)=0. Z beperkt de enige mogelijkheid tot t=0, en die blijkt ook te voldoen voor x en y..
r(t) = < e-tcos t i, e-tsin t j, e-t k >
Ik vul voor i 1 in, dat wordt niet 0. , ik vul voor j 0 in, dat wordt wél 0 , ik vul voor k 1 in en dat wordt niet 0.
Dus daarom t = 0 is de enige mogelijkheid???
k³-1 is alleen priem als k=2.
Bewijs:
Als k oneven is, dan k=2n+1 met n in Z. Dan is k³-1=(2n+1)³=8n³+12n²+6n en dus deelbaar door 2 en is k³-1 dus niet priem. Dus k moet even zijn. We weten dat k>1 want een priemgetal p>1. Voor k=2 is k³-1=7 dus inderdaad priem.
Hoe laat ik nu zien dat voor geen enkele andere even k, k³-1 priem is?
quote:Mag je i, j en k invullen? Wat stellen ze voor?
[..]
Dus eigenlijk dit:
r(t) = < e-tcos t i, e-tsin t j, e-t k >
Ik vul voor i 1 in, dat wordt niet 0. , ik vul voor j 0 in, dat wordt wél 0 , ik vul voor k 1 in en dat wordt niet 0.
Dus daarom t = 0 is de enige mogelijkheid???
quote:Met k=4 krijg ik 63, geen priem
Te bewijzen:
k³-1 is alleen priem als k=2.
Bewijs:
Als k oneven is, dan k=2n+1 met n in Z. Dan is k³-1=(2n+1)³=8n³+12n²+6n en dus deelbaar door 2 en is k³-1 dus niet priem. Dus k moet even zijn. We weten dat k>1 want een priemgetal p>1. Voor k=2 is k³-1=7 dus inderdaad priem.
Hoe laat ik nu zien dat voor geen enkele andere even k, k³-1 priem is?
quote:Dat klopt, want ik moet dan ook aantonen dat voor k=4,6,8,10,12,... k³-1 niet priem is.
quote:Oh, faal. Maar nu zie ik wel een patroontje.
[..]
Dat klopt, want ik moet dan ook aantonen dat voor k=4,6,8,10,12,... k³-1 niet priem is.
Bij k=4 heb je deelbaarheid door 3
bij k=6 deelbaarheid door 5
bij k=8 deelbaarheid door 7
bij k=10 deelbaarheid door 9
bij k=11 deelbaarheid door 11
daarmee kom je eruit
[ Bericht 6% gewijzigd door GlowMouse op 03-01-2010 20:40:10 ]
Dus wat je dan eigenlijk moet bewijzen is dat k-1 | k³-1 . Als k=2, dan 1 | k³-1 (niet erg want een priemgetal heeft als deler 1). Maar als k>2 dan is er een getal >1 dat k³-1 deelt, en is het dus niet priem.
k³-1=(k-1)(k+1)k + (k-1) en is dus inderdaad deelbaar door k-1.
QED
quote:Maak het niet zo moeilijk. Je hebt:Op zondag 3 januari 2010 20:57 schreef BasementDweller het volgende:
Ohja, bedankt
Dus wat je dan eigenlijk moet bewijzen is dat k-1 | k³-1 . Als k=2, dan 1 | k³-1 (niet erg want een priemgetal heeft als deler 1). Maar als k>2 dan is er een getal >1 dat k³-1 deelt, en is het dus niet priem.
k³-1=(k - 1)(k + 1)k + (k - 1) en is dus inderdaad deelbaar door k-1.
QED
k3 - 1 = (k - 1)(k2 + k + 1)
Voor elk natuurlijk getal k > 1 is k3 - 1 deelbaar door k - 1, en dus kan k3 - 1 niet priem zijn voor enig natuurlijk getal k > 2.
quote:Dat is precies wat ik zeg.Op maandag 4 januari 2010 15:39 schreef Riparius het volgende:
[..]
Maak het niet zo moeilijk. Je hebt:
k3 - 1 = (k - 1)(k2 + k + 1)
Voor elk natuurlijk getal k > 1 is k3 - 1 deelbaar door k - 1, en dus kan k3 - 1 niet priem zijn voor enig natuurlijk getal k > 2.
quote:Hier kom ik niet uit..Bij het overseinen van morsetekens is de kans dat een letter goed ontvangen wordt 0.90. Noem m : aantal goed overgeseinde letters.
a) Hoe groot is de kans dat een woord van 4 letters goed ontvangen wordt? P(m=...)=...
b) Hoe groot is de kans dat een zin van 100 letters meer dan 6 fouten bevat? Noem k : aantal fout overgeseinde letters.
De verdeling bij a) is volgens mij binominaal P(m=4) = m ~ Bin (4 ; 0.90).. maar dan?
quote:Te weinig gegevens: je kent de afhankelijkheden tussen de kansen niet.Op woensdag 6 januari 2010 11:05 schreef Booomer het volgende:
[..]
Hier kom ik niet uit..
De verdeling bij a) is volgens mij binominaal P(m=4) = m ~ Bin (4 ; 0.90).. maar dan?
quote:Meer gegevens worden niet gegeven...Op woensdag 6 januari 2010 11:47 schreef thabit het volgende:
[..]
Te weinig gegevens: je kent de afhankelijkheden tussen de kansen niet.
quote:Dan kun je dus ook geen antwoord geven.
[..]
Meer gegevens worden niet gegeven...
ey = x2 +x - 6
x2 +x - 6 - ey =0
x = (-1 ± sqrt(-4*(6- ey)))/2
x = -1/2 - sqrt(6-ey )
Klopt?
quote:x = (-1 ± sqrt(1 -4*(6- ey)))/2Op woensdag 6 januari 2010 13:03 schreef GlowMouse het volgende:
Nee, de b^2 uit de abc-formule zie ik niet terug, en er verdwijnt een minteken binnen de wortel. En waarom kies je voor - en niet voor +, voor de wortel?
x = -1/2 - sqrt(-5+ey)
zoiets?
die klopt, die daarna niet. En waarom kies je voor - en niet voor +, voor de wortel?
quote:-1/2 + 1/2sqrt(23+4ey)Op woensdag 6 januari 2010 13:24 schreef GlowMouse het volgende:
x = (-1 ± sqrt(1 -4*(6- e^y)))/2
die klopt, die daarna niet. En waarom kies je voor - en niet voor +, voor de wortel?
En waarom voor - en niet +? ja dat is dus fout
Dy = By-1
Df= (2,oneindig)
Dus het moet + zijn omdat hij anders buiten het bereik valt ofzo?
wiskundig gezien hoort het domein gewoon bij het functievoorschrift gegeven te zijn
quote:Alleen daar doen ze niet aan op de middelbare schoolOp woensdag 6 januari 2010 13:50 schreef GlowMouse het volgende:
wiskundig gezien hoort het domein gewoon bij het functievoorschrift gegeven te zijn
quote:By-1 is bereik van de inverseOp woensdag 6 januari 2010 13:50 schreef GlowMouse het volgende:
De notatie By-1 ken ik niet, maar het heeft wel te maken met domein en bereik. Kijk je naar y = ln(x-2) + ln(x+3), voor welke x kun je die uitrekenen? En welke waarden kan y dus aannemen?
wiskundig gezien hoort het domein gewoon bij het functievoorschrift gegeven te zijn
En kan je uitrekenen voor x > 2
En y kan volgens mij gewoon elke waarde aannemen?
quote:Nee, dit klopt ook al niet. Het moet zijn:Op woensdag 6 januari 2010 13:24 schreef GlowMouse het volgende:
x = (-1 ± sqrt(1 -4*(6- e^y)))/2
die klopt, die daarna niet.
x = -½ ± ½√(1 + 4(6+ey))
En aangezien x > 2 moet zijn voldoet dus alleen:
x = -½ + ½√(1 + 4(6+ey))
-1/2 ± sqrt(4ey-23)/2
voor y kun je dus alles invullen, en hoe zorg je nou dat altijd geldt x>2?
f= alfa voor x=0
a) Geef een alfa waarvoor geldt dat f continu is:
Hiervoor had ik alfa = pi gegeven, aangezien de limiet van (sin (pi*x))/x wanneer x-->0 , pi is.
b) geef aan of f differentieerbaar is in f(0). Zo ja, geef f ' (0). Zo nee, leg uit waarom niet.
Ik had van niet omdat je hij daar een hoek hebt, hetzelfde principe als de afgeleide van f(x)=|x| in 0, die bestaat ook niet. Klopt dit?
quote:Mijn aanpak was:Find the sum of the following geometric serie:
a + a(1+ a)-1 + a(1+ a)-2 + a(1+ a)-3 + a(1+ a)-4 + ..., (a > 0)
Sn = a / 1-(1-a)-1 = a / 1-1+a-1 = a1 / a-1 = a2
> Het antwoord moet echter "1 + a" zijn.
-----------------------
De tweede vraag is:
quote:Eerst probeerde ik de somformule (met t=tijd ongedefenieerd) gelijkstellen aan de huidige reserve, maar dat werkte niet. Ik zie eigenlijk ook niet hoe een oneindige (het einde is immers onbekend) reeks een factor van |k|>1 (1,02) kan hebben.The world's total consumption of natural gas was 1824 million tons oil equivalent (mtoe) in 1994. The reserves at the end of that year were estimated to be 128 300 mtoe. If consumption had increased by 2% in each of the coming years, and no new sources were ever discovered, how much longer would these reserves have lasted?
Kan iemand hulp bieden?
quote:(1-a)-1 is natuurlijk niet hetzelfde als 1-a-1 en buiten dat haal je een + en een - doorelkaar.Op woensdag 6 januari 2010 18:54 schreef Matthijs- het volgende:
Ik ben tegen twee vragen aangelopen over meetkundige rijen waar ik niet uitkom. De eerste vraag is:
[..]
Mijn aanpak was:
Sn = a / 1-(1-a)-1 = a / 1-1+a-1 = a1 / a-1 = a2
> Het antwoord moet echter "1 + a" zijn.
quote:Als het einde onbekend is, dan is de reeks natuurlijk niet per se oneindig. Voer de lengte van de reeks in als variabele.Op woensdag 6 januari 2010 18:54 schreef Matthijs- het volgende:
De tweede vraag is:
[..]
Eerst probeerde ik de somformule (met t=tijd ongedefenieerd) gelijkstellen aan de huidige reserve, maar dat werkte niet. Ik zie eigenlijk ook niet hoe een oneindige (het einde is immers onbekend) reeks een factor van |k|>1 (1,02) kan hebben.
Kan iemand hulp bieden?
quote:Probeer de limiet maar uit te werken die de afgeleide definieert.Op woensdag 6 januari 2010 18:53 schreef martijnnum1 het volgende:
wat moet het dan zijn?
quote:pak de definitie van de afgeleide erbij
= lim h->0 van (sin(pi*(h)/(h)) - 0 / h
= lim h->0 van (sin(pi*(h)/(h)) * 1/h = lim h->0 van (sin(pi*(h))/(h^2)
maar dan kom je er toch nog op uit dat die limiet niet bestaat, en dus de afgeleide niet bestaat?
oke f'(o) = lim h->0 f(0+h)-f(0) / h
=lim h->0 (pi+h-pi)/h
lim h-> h/h=1
klopt dit dan wel?
weet alleen niet of die f(0+h) nu klopt..
=lim h->0 (sin(pi*h)-pi)/h
verder kom ik wederom niet..
f(0+h) = ...
Dus ik moet een functie h(x,y) en g(x,y) vinden zó dat g(x,y) =< f(x,y) =< h(x,y). Als h(x,y) heb ik genomen 2x²y/x² =2y waarvan makkelijk na te gaan is dat de limiet nul is.
Ik kan alleen geen g(x,y) bedenken waarvan de limiet makkelijk te bepalen is.
quote:Jouw h(x,y) werkt niet als y negatief is (en dit is meteen een hint voor het vinden van g(x,y)Op woensdag 6 januari 2010 19:59 schreef BasementDweller het volgende:
Ik wil met behulp van de insluitstelling laten zien dat de limiet van f(x,y)= 2 x²y / (x² + y²) nul is als (x,y)->(0,0).
Dus ik moet een functie h(x,y) en g(x,y) vinden zó dat g(x,y) =< f(x,y) =< h(x,y). Als h(x,y) heb ik genomen 2x²y/x² =2y waarvan makkelijk na te gaan is dat de limiet nul is.
Ik kan alleen geen g(x,y) bedenken waarvan de limiet makkelijk te bepalen is.
).kom er alleen nog steeds niet uit, door de noemer van 0.
Of moet je hier l'hopital gebruiken?
quote:Klopt h(x,y)= 2|y| en g(x,y)=-2|y| wel ?Op woensdag 6 januari 2010 20:09 schreef thabit het volgende:
[..]
Jouw h(x,y) werkt niet als y negatief is (en dit is meteen een hint voor het vinden van g(x,y)
quote:Ik zou L'Hopital gebruiken, als ik jou was.Op woensdag 6 januari 2010 20:11 schreef martijnnum1 het volgende:
lim h->0 ((sin (pi*h))/h - pi)/ h = lim h->0 ((sin( p*h ))/ h) / (h) - pi/ h
kom er alleen nog steeds niet uit, door de noemer van 0.
Of moet je hier l'hopital gebruiken?
quote:Ja.Op woensdag 6 januari 2010 20:14 schreef BasementDweller het volgende:
[..]
Klopt h(x,y)= 2|y| en g(x,y)=-2|y| wel ?
quote:Merci
. Ik zal nooit meer absoluutstrepen vergeten 
Gegeven: aan het begin zijn 100 mensen, de voorplantingsquote is 0,8. Dit houdt in, dat die 100 mensen, het doorvertellen aan 80 mensen, die 80 weer aan 64 anderen, etc.
Die 100 mensen ''besmetten'' er dus 80, die 80 weer 64, die 64 weer 51,2, etc.
Dus 100+80+64+51,2+.....
Kan ik dan met een formule berekenen hoeveel mensen er uiteindelijk ''geinfecteerd'' zijn?
De opgave luidt:
Show that each of the following functions is differentiable at each point in its domain. Decide which of the functions are C1.
Vervolgens staan er een aantal functies. Eén daarvan is de volgende: f(x,y)=xy/sqrt(x²+y²). (ik neem aan dat als domein bedoeld wordt: heel R² behalve (0,0)). Daarvan heb ik de partiële afgeleiden bepaald. df/dy=x³/(x²+y²)^3/2 en hetzelfde voor df/dx maar dan de x en y omgewisseld. De partiële afgeleiden bestaan dus en zijn continu in alle punten behalve (0,0). Als ik het goed begrijp is volgens de theorie functie f dan differentieerbaar en ook van klasse C1.
Wat ik niet snap:
- In de theorie staat ergens dezelfde functie f(x,y) met als extra definitie f(0,0)=(0,0) wel continu is, partiële afgeleiden heeft in het punt (0,0) maar toch niet differentieerbaar is, terwijl er een stelling is die zegt dat als de partiële afgeleiden bestaan en continu zijn in de 'neighborhood' van x in het domein, dan is f differentieerbaar in het punt x.
- Als een functie differentieerbaar is, is het toch automatisch C1? Als dit zo is vind ik de vraagstelling erg onlogisch.
- Dan zal het wel fout gaan met continuïteit
-Is C1 niet continu differtieerbaar? Pak de functie x²sin(1/x) als x<>0, en 0 als x=0. Die is wel diffbaar maar niet cont.diffbaar, en zit dus niet in C1.
quote:Wat moet de df/dy dan wel zijn?Op donderdag 7 januari 2010 15:56 schreef GlowMouse het volgende:
Je df/dy is fout.
- Dan zal het wel fout gaan met continuïteit
-Is C1 niet continu differtieerbaar? Pak de functie x²sin(1/x) als x<>0, en 0 als x=0. Die is wel diffbaar maar niet cont.diffbaar, en zit dus niet in C1.
Als ik 'm integreer krijg ik toch echt weer f(x,y) terug...De afgeleide van jouw functie is -Cos[1/x] + 2 x Sin[1/x]. Is die niet continu differentieerbaar omdat ie niet in het hele domein van de originele functie gedefinieerd is? (namelijk als x=0)
quote:de kettingregelterm is geen x².
[..]
Wat moet de df/dy dan wel zijn?
quote:Jouw afgeleidefunctie geldt voor x<>0. De afgeleide in 0 is lim(x->0) (f(x)-f(0)/(x-0) = lim(x->0) xsin(1/x) = 0. Je ziet dat de functie overal diffbaar is, maar de afgeleide is niet continu.
De afgeleide van jouw functie is -Cos[1/x] + 2 x Sin[1/x]. Is die niet continu differentieerbaar omdat ie niet in het hele domein van de originele functie gedefinieerd is? (namelijk als x=0)
quote:Klopt, dat is gewoon x. Maar je hebt nog een x uit de teller...Op donderdag 7 januari 2010 17:42 schreef GlowMouse het volgende:
[..]
de kettingregelterm is geen x².
maak teveel foutjes de laatste tijdquote:Oke, bedankt. Volgens mij begin ik het wel te snappen. Misschien kom ik er later nog op terug.Op donderdag 7 januari 2010 17:42 schreef GlowMouse het volgende:
Jouw afgeleidefunctie geldt voor x<>0. De afgeleide in 0 is lim(x->0) (f(x)-f(0)/(x-0) = lim(x->0) xsin(1/x) = 0. Je ziet dat de functie overal diffbaar is, maar de afgeleide is niet continu.
quote:Ik vergeef het jeOp donderdag 7 januari 2010 17:56 schreef GlowMouse het volgende:
quote:Ik heb het gehad vorig jaar met wiskunde, dat weet ik wel, maar hoe het moet
Op de GR, eerst 100 invoeren, dan met de ANS toets en weet ik veel wat er iets van maken toch
quote:De partiele afgeleiden zijn niet continu in 0: voor x != 0 geldt df/dy(x,0) = 1 en voor y != 0 geldt df/dy(0,y) = 0.Op donderdag 7 januari 2010 14:41 schreef BasementDweller het volgende:
- In de theorie staat ergens dezelfde functie f(x,y) met als extra definitie f(0,0)=(0,0) wel continu is, partiële afgeleiden heeft in het punt (0,0) maar toch niet differentieerbaar is, terwijl er een stelling is die zegt dat als de partiële afgeleiden bestaan en continu zijn in de 'neighborhood' van x in het domein, dan is f differentieerbaar in het punt x.
Bijvoorbeeld bij deze figuur?Alvast bedankt!
quote:Ja x-coordinaat is eerst positief, daarna negatief. Dus houdt dat in dat hij 2 periodes op de x-richting aflegt. En op de y-richting? Lijkt me niet dat je dat ook zo kunt doen.Op donderdag 7 januari 2010 21:54 schreef GlowMouse het volgende:
Pak een punt, kies een richting, en volg de figuur tot je bij je startpunt terug bent. En kijk tijdens dat wandelen wat er met de x-coordinaat gebeurt.
Ik ben een beetje met Excel aan het kloten, want ik probeer via Excel normale verdeling en de betrouwbaarheid van een X-aantal metingen uit te rekenen.
Excel schijnt dit allemaal feilloos voor je te kunnen doen...
quote:y kan ook zo, maar dan moet je het wel eerst goed kunnen. De sinus is op [0, 2pi] ook zowel positief als negatief, en toch maar één periode.
[..]
Ja x-coordinaat is eerst positief, daarna negatief. Dus houdt dat in dat hij 2 periodes op de x-richting aflegt. En op de y-richting? Lijkt me niet dat je dat ook zo kunt doen.
quote:ik snap niet wat je wilt, maar probeer de helpfunctie eens
Even een snelle vraag... misschien dat GlowMouse het weet.
Ik ben een beetje met Excel aan het kloten, want ik probeer via Excel normale verdeling en de betrouwbaarheid van een X-aantal metingen uit te rekenen.
Excel schijnt dit allemaal feilloos voor je te kunnen doen...
quote:Ik bedoelde eigenlijk dit:Op donderdag 7 januari 2010 22:00 schreef GlowMouse het volgende:
[..]
ik snap niet wat je wilt, maar probeer de helpfunctie eens
Het betrouwbaarheidsinterval voor een grote steekproef (of populatie) wordt berekend met de
werkbladfunctie ‘BETROUWBAARHEID’.
Normaal reken ik dat hele statistiek gedoe op de ouderwetse manier uit...
Maar blijkbaar kun je met werkbladfunctie's alles voor je uit laten rekenen door Excel... alleen ik ben zo vreselijk slecht met dit soort programma's.
Ik kan nergens goed vinden hoe je het nu precies moet uitrekenen... wat en hoe en waar ik mijn resultaten nu precies moet invullen... etc.
quote:http://www.bloggpro.com/a(...)-intervals-in-excel/
[..]
Ik bedoelde eigenlijk dit:
Het betrouwbaarheidsinterval voor een grote steekproef (of populatie) wordt berekend met de
werkbladfunctie ‘BETROUWBAARHEID’.
Normaal reken ik dat hele statistiek gedoe op de ouderwetse manier uit...
Maar blijkbaar kun je met werkbladfunctie's alles voor je uit laten rekenen door Excel... alleen ik ben zo vreselijk slecht met dit soort programma's.
Ik kan nergens goed vinden hoe je het nu precies moet uitrekenen... wat en hoe en waar ik mijn resultaten nu precies moet invullen... etc.
quote:Zie je wel... ik kan gewoon niet met google zoekenOp donderdag 7 januari 2010 22:16 schreef GlowMouse het volgende:
[..]
http://www.bloggpro.com/a(...)-intervals-in-excel/
Thnx !
1 balletje: b ~ N(2 ; 0,5)
vloeibare substantie: v ~ N(185 ; 10)
soep: s = 4*b + v
a) Bepaal de verdeling van s.
Ik kom tot:
μs = 4 * μb + μv = 4 * 2 + 185 = 193
σs = √(4 * 0,52 + 102) = 10,1
s ~ N(μ=193 ; σ=10,1)
b. Bereken de kans op overstromen van het bekertje.
s = (x - μ) / σ =
(200 - 193) / 10,1 = 0,69
P(z > 0,69) = 0,0455 (opgezocht in z-waarden tabel)
Gaat dit goed?
[ Bericht 6% gewijzigd door Booomer op 08-01-2010 12:11:58 ]
quote:Alle informatie die gegeven wordt, heb ik gepost. Het zou kunnen dat ik bij (a) niet voldoende berekend heb, maar ik weet niet wat ik nog moet doen..Op vrijdag 8 januari 2010 12:15 schreef thabit het volgende:
Wederom te weinig gegevens want er wordt niets over de covariantie tussen b en v verondersteld.
quote:De vraagsteller schoppen, aangezien hij/zij duidelijk geen idee heeft wat hij/zij opschrijft.Op vrijdag 8 januari 2010 12:18 schreef Booomer het volgende:
[..]
Alle informatie die gegeven wordt, heb ik gepost. Het zou kunnen dat ik bij (a) niet voldoende berekend heb, maar ik weet niet wat ik nog moet doen..
quote:En als ik nu naar de docent stap, weet ie het zo voor me op te lossen met de gegevens die er zijn. Vergeet ik gewoon niet iets te berekenen?Op vrijdag 8 januari 2010 12:25 schreef thabit het volgende:
[..]
De vraagsteller schoppen, aangezien hij/zij duidelijk geen idee heeft wat hij/zij opschrijft.
quote:Als je docent denkt dat-ie het met deze gegevens kan oplossen, dan heeft-ie het zelf ook niet begrepen.Op vrijdag 8 januari 2010 12:31 schreef Booomer het volgende:
[..]
En als ik nu naar de docent stap, weet ie het zo voor me op te lossen met de gegevens die er zijn. Vergeet ik gewoon niet iets te berekenen?
quote:Op vrijdag 8 januari 2010 12:39 schreef thabit het volgende:
[..]
Als je docent denkt dat-ie het met deze gegevens kan oplossen, dan heeft-ie het zelf ook niet begrepen.
Kijk nou gewoon even naar wat ik gedaan heb. Wat mist er dan? Je weet toch hoeveel balletjes en hoeveel vloeibare substantie in de soep gaat? De variantie staat er ook..Hoe kan ik deze kettingbreuk afleiden, of bewijzen dat dit patroon 'oneindig lang doorgaat'?
[ Bericht 12% gewijzigd door motorbloempje op 01-09-2013 21:34:23 ]
http://en.wikipedia.org/wiki/Generalized_continued_fraction
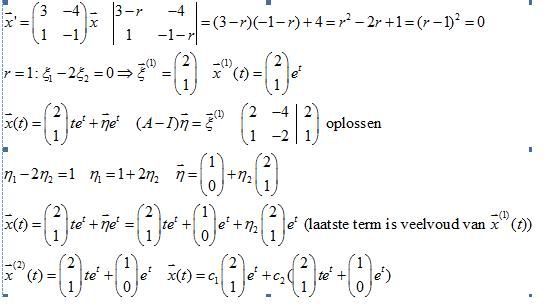
Waarom staat onder de deelstreep, eerste lid aan de rechterkant van de onderste formule, ineens S-B , terwijl in de e macht van de integraal B-S staat? Ik heb hem al 3x uitgewerkt maar kom toch steeds op een andere uitkomst...
quote:de volgorde in de teller is ook omgedraaid; (a-b)/(c-d) = (b-a)/(d-c). Bij de tweede breuk gebeurt iets vergelijkbaars, heb je dat wel gezien?
Laplace transformatie > klein vraagje over een minteken dat ineens verschijnt bij het integreren.
[ afbeelding ]
Waarom staat onder de deelstreep, eerste lid aan de rechterkant van de onderste formule, ineens S-B , terwijl in de e macht van de integraal B-S staat? Ik heb hem al 3x uitgewerkt maar kom toch steeds op een andere uitkomst...
quote:http://www.math.utah.edu/~gustafso/2250directionfields.pdf
Heey ik kan het onderste volledig doen, maar er staat ook : draw a direction field and sketch a few trajectories. Zou iemand mij kunnen helpen hoe ik dit stapsgewijs kan doen?
[ afbeelding ]
quote:Maarem, als ik het in 'mijn vorm' op zou schrijven zou het dus uiteraard ook goed zijn. Wat is het praktisch nut dan van het omdraaien? Er gebeuren erg vaak dingen in uitwerkingen waarvan ik denk: jemig wil je het echt zo moeilijk mogelijk maken om het te begrijpen?
de volgorde in de teller is ook omgedraaid; (a-b)/(c-d) = (b-a)/(d-c). Bij de tweede breuk gebeurt iets vergelijkbaars, heb je dat wel gezien?
quote:Het is deels esthetisch, om de symmetrie te benadrukken, soms is het om het aantal mintekens in de formule wat kleiner te krijgen, soms is het simpelweg conventie om een bepaalde vorm aan te houden.
[..]
Maarem, als ik het in 'mijn vorm' op zou schrijven zou het dus uiteraard ook goed zijn. Wat is het praktisch nut dan van het omdraaien? Er gebeuren erg vaak dingen in uitwerkingen waarvan ik denk: jemig wil je het echt zo moeilijk mogelijk maken om het te begrijpen?
Nog een dingetje waar ik mee zit: partial fractions. Dat lukt eigenlijk meestal prima, maar bij deze kom ik er niet uit. Wat is daarbij de methode?
ik doel uiteraard niet op de algehele partfrac methode, die staat hier ook wel in mijn boek. Maar geen idee hoe ik het hierbij aanpak.
weet het al Jemig moet ik vaker doen. Eerst een uur prutsen zonder results. Even op fok zetten, en 30 sec na posten de methode ineens weten
wazig.Even wel de uitwerking:
maak er van: (AS+B)/S + (CS+D)/(S^2+4) --> weer gelijknamig maken en de functie aan bovenkant gelijkstellen aan de teller van eerste functie. Dan a,b,c,d oplossen.
) maar vanaf hoofdstuk 4 is het onbekend en is de syllabus erg vaag en beknopt. Ik vind op internet deze uitleg over wat een stochast nou precies is. Betekent dat dat je voor de stochast apart een kansruimte (Omega, A en p) moet definieren? Wikipedia geeft als voorbeeld het gooien met een dobbelsteen. Eerst is Omega {1,2,3,4,5,6} x {1,2,3,4,5,6}, is de omega voor de stochast dan {2,3,4,5,6,7,8,9,10,11,12}?
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | f(x) = 1 + x + x^2 = 7\\ f'(x) = 1 + 2x = 5\\ f''(x) = 2 \\ f^{(n)}(x) = 0 \text{ met } n >= 3 \end{eqnarray} De Taylorserie met a = 2\\ \begin{eqnarray} \Sum_{n=0}^{\infty} f^{(n)}(2) (x - 2)^n / n! \\ = 7*1/1 + 5(x-2)/1 + 2(x - 2)^2/2 + 0(x - 2)^3/3! + 0(x - 4)^4/4! + ... \\ = 7 + (5x-10) + (x - 2)^2 \\ = 1 + 3x + x^2 \end{eqnarray} |
Maar hoe kan 1 + x + x^2 = 1 + 3x + x^2?
Ik heb het meermalen nagerekend, maar ik krijg steeds hetzelfde resultaat.
| 1 2 3 4 | = (7 - 10) + 5x + x^2 - 4x + 4 = (7 - 10 + 4) + (5-4)x + x^2 = 1 + x + x^2 |
Ik zal wel per ongeluk 2x in plaats van 4x genomen hebben.
Maar zo klopt die inderdaad.
quote:Hm, oké. Maar wat bedoelen ze dan precies metOp maandag 11 januari 2010 21:12 schreef thabit het volgende:
De stochast is in dit geval de som van de twee waarden van de dobbelstenen. Omega is dan nog steeds gewoon {1,2,3,4,5,6} x {1,2,3,4,5,6}. En de stochast is de functie X: Omega -> R die (s, t) naar s + t stuurt.
quote:Waar haal je dit vandaan? Ik kan hieraan namelijk niet ruiken wat er met A bedoeld wordt.Op maandag 11 januari 2010 23:38 schreef Hanneke12345 het volgende:
[..]
Hm, oké. Maar wat bedoelen ze dan precies met [ afbeelding ] (ik moet nog even opzoeken hoe ik zo'n gave A maak in latex ;x)? Stel dat het gaat om lager te gooien dan 5, dan is X(omega) kleiner of gelijk aan 5, dan is die verzameling van omega's dus {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (3,1), (3,2), (4,1)}? en dus in A, want elke deelverzameling is in A.
| 1 |
Geeft:
En:
| 1 |
Geeft:
quote:Bedoel je niet dat
Als sier-A gelijk is aan hoofdletter omega dan zit jouw set erin ja, maar A kan ook een andere verzameling zijn.
quote:ja sorry, de powerset van omegaOp maandag 11 januari 2010 23:49 schreef Iblis het volgende:
[..]
Bedoel je niet dat [ afbeelding ] hier?
?a) Zij T een lineaire transformatie van R3 in R3 zodanig dat:
Tv1=v2 ; Tv2 = v2-v1 ; Tv3 = v3
Vind eerst de matrix B van T ten opzichte van B en dan de standaardmatrix van T .
Hoe moet ik matrix B in godsnaam vinden? Volgens de uitwerkingen moet het zo:
B= [T]B = [[Tv1]B [Tv2]B [Tv3]B =
Alleen ik heb geen flauw idee hoe ze daar aan komen?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:30 ]
quote:Een beetje te uitgebreid. Ik ben meer in tijdnood. Is het niet mogelijk dat je alleen deze even voordoet? Al is het niet teveel gevraagd.Op maandag 11 januari 2010 12:18 schreef GlowMouse het volgende:
[..]
de volgorde in de teller is ook omgedraaid; (a-b)/(c-d) = (b-a)/(d-c). Bij de tweede breuk gebeurt iets vergelijkbaars, heb je dat wel gezien?
[..]
http://www.math.utah.edu/~gustafso/2250directionfields.pdf
Ik doe een research master in neuroscience, en voor een stage waar nogal veel signaalanalyse bij komt kijken moet ik wat meer weten van lineaire algebra. Alleen heb ik sinds Natuur en Techniek op de middelbare school niks meer met wiskunde gedaan.
Weet iemand misschien een goed inleidend boek?Als iemand een cursus weet die gegeven wordt tussen nu en eind mei zou dat ook welkom zijn.
Oja, hetzelfde geldt trouwens voor Fourieranalyse.
[ Bericht 4% gewijzigd door Mini_rulez op 12-01-2010 13:37:43 ]
Best wel veel lessen en hij bouwt het geleidelijk op. Dit is echt super!
quote:Ik ga meteen kijken of de bieb het heeft, dankjewel voor je uitgebreide reactie!Op dinsdag 12 januari 2010 14:35 schreef Burakius het volgende:
Linear Algebra and Its applications van David C. Lay (voor uitwerkingen van dit boek verwijs ik je naar www.aerostudents.com) . Verder heb ik ook een youtube link voor je.
Best wel veel lessen en hij bouwt het geleidelijk op. Dit is echt super!
(matrix A) (v1) (matrix A) (v2)
=
Ik hoop dat het duidelijk is. Rond elke matrix en vector moet nog [A]B maar ik weet niet hoe dat moet.
Maar het probleem is dat ik de laatste stap gewoon totaal niet snap. Hoe komen ze van die 2 Basis vectoren bij die 2x2 matrix?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:34 ]
quote:Find the matrix B of the linear transformation T(x) = Ax with respect to the basis B=(v1,v2). Construct B "Column by column".Op dinsdag 12 januari 2010 23:19 schreef GlowMouse het volgende:
waar staat de vraag?
Definieer M = [v1 v2];
Je krijgt dus een x tov basis B. Die moet je eerst omzetten naar een standaardbasis en dan heb je Mx. Dan kun je T toepassen: AMx. En dan moet je weer terug naar de basis B (de laatste stap die jij niet snapt): inv(M)AMx.
De matrix bij de hele transformatie wordt dus gegeven door inv(M)AM.
UA = (XA)1/3 (YA) 2/3 (XB)-2/3
UB = (XB)2/3 (YB) 1/3
Stel X0=100, Y0=100.
Stel dat de volgende allocatie geldt: XA = 33⅓, YA = 66⅔, XB = 66⅔, YB = 33⅓.
c) Bereken hoeveel consument A maximaal zou willen opgeven van goed Y (WTP) als hij/zij één eenheid meer van goed X zou ontvangen. Met andere woorden, bereken de marginale substitutieverhouding van consument A.
Meer wiskunde dan economie dacht ik, dus vandaar in dit topic.
Ik kom uit op 0,064 / 0,032 = 2, terwijl de uitwerking een uitkomst geeft van 5,0625
hoe verkrijg ik de inverse laplace transformatie van 1 / ( s^4 + 1) ?
Is dit met breuksplitsen mogelijk?
quote:Je kunt breuksplitsing gebruiken ja, maar niet zonder complexe getallen. Om je uitkomst te controleren kun je even hier kijken en dan InverseLaplaceTransform[1/(1+s^4),s,t] invoeren.Op woensdag 13 januari 2010 20:39 schreef Holy_Goat het volgende:
hoioi,
hoe verkrijg ik de inverse laplace transformatie van 1 / ( s^4 + 1) ?
Is dit met breuksplitsen mogelijk?
quote:Eerst moet je het decimale stelsel goed snappen. Een getal als:
wie kan mij uitleggen hoe Binair stelsel werkt. ik snap er niks vannnnnnnnnnnnnnnnnnnnnnnn
123 zegt:
3 eenheden
+ 2 tientallen
+ 1 honderdtal
Het is een tientalligstelsel, omdat we na tien cijfers weer opnieuw beginnen en de volgende positie eentje hoger maken:
1 2 3 4 5 6 7 8 9 (cijfers op) 10 11 12 13 14 15 16 17 18 19 20 enz.
Bij het binaire stelsel gebruikt men maar twee cijfers, 0 en 1. Je cijfers zijn dus sneller op, maar het opnoemen gaat in principe hetzelfde:
| 1 2 | Decimaal: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Is het duidelijk hoe men telt in binair?
quote:Ja maar dat is een andere manier lijkt mij. Ze vragen om matrix B op drie verschillene manieren te vinden:Op woensdag 13 januari 2010 13:13 schreef GlowMouse het volgende:
Die 9 in A, is dat geen -9?
Definieer M = [v1 v2];
Je krijgt dus een x tov basis B. Die moet je eerst omzetten naar een standaardbasis en dan heb je Mx. Dan kun je T toepassen: AMx. En dan moet je weer terug naar de basis B (de laatste stap die jij niet snapt): inv(M)AMx.
De matrix bij de hele transformatie wordt dus gegeven door inv(M)AM.
1) Use the formula inv(S)AS;
2) Use a commutative diagram;
3) Construct B "column by column".
Maar ik snap het denk ik al. Je moet met die twee vectoren die je als antwoord krijgt van A*v1 en A*v2 zoeken naar een lineaire combinatie met A.
Dan krijg je dus vier getallen en die moeten dan matrix B voorstellen. Weet niet waarom het zo moet, maar wel hoe.
Ik krijg als vergelijking voor het vlak: 3x-4y+5=0. Maar als ik een 3D-plot maak dan zie ik dat vlak niet de functie raken. Dus, is mijn antwoord fout? Ik kan geen fout vinden