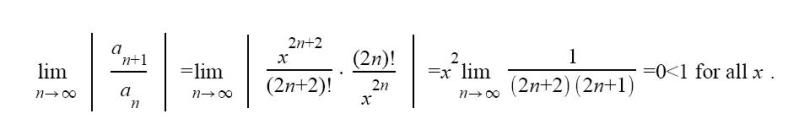SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Kijk zonder differntiatie of whatever dat ook moge zijn wat je hier moet doen kom ik tot:quote:Op donderdag 24 december 2009 23:20 schreef thabit het volgende:
[..]
Goed, nu de kerstgedachte toepassen.
f(x) = 1/(1+x)2 --> 1/1+x sommatieteken: 1/1+x ----> 1/1+x sommatieteken: 1/1-(-x)
--> 1/1+x sommatieteken: (-x)n --> 1/1+x sommatieteken: (-1)n * xn
Maar ja..
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik snap niet helemaal wat je doet, maar in concreto, merk op:
Voor 1/(1+x) weet je nu al een reeks, en als je die differentieert… dan moet het (bijna) uitkomen.
Voor 1/(1+x) weet je nu al een reeks, en als je die differentieert… dan moet het (bijna) uitkomen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
is dat nou handig, standaardreeksen leren?
f(x) = 1/ (1+x)²
f'(x) = -2/(1+x)³
f''(x) = 6/(1+x)^4
en dan zie je het patroontje:
dus
vul je in in de formule voor de taylorreeks rond x=0 en je bent klaar.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:06 ]
f(x) = 1/ (1+x)²
f'(x) = -2/(1+x)³
f''(x) = 6/(1+x)^4
en dan zie je het patroontje:
dus
vul je in in de formule voor de taylorreeks rond x=0 en je bent klaar.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:06 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
In mijn lial diktaat staat het volgende:
Stel v=(v1, v2, ... , vn)t. We definiëren v* als de complex geconjugeerde van v. Dan geldt v*tv= (v1² + ... + vn²).
Ik zie niet in waarom dit waar is. Ik krijg: v*tv=(v1*v1 + v2*v2 + ... + vn*vn)
(let op: * betekent de geconjugeerde, niet vermenigvuldiging)
Als tegenvoorbeeld:
Stel dat v1= 1+i, dan is v1*=1-i. Dus v1*v1=(1-i)(1+i)!=(1+i)²=v12
[ Bericht 3% gewijzigd door BasementDweller op 25-12-2009 16:19:46 ]
Stel v=(v1, v2, ... , vn)t. We definiëren v* als de complex geconjugeerde van v. Dan geldt v*tv= (v1² + ... + vn²).
Ik zie niet in waarom dit waar is. Ik krijg: v*tv=(v1*v1 + v2*v2 + ... + vn*vn)
(let op: * betekent de geconjugeerde, niet vermenigvuldiging)
Als tegenvoorbeeld:
Stel dat v1= 1+i, dan is v1*=1-i. Dus v1*v1=(1-i)(1+i)!=(1+i)²=v12
[ Bericht 3% gewijzigd door BasementDweller op 25-12-2009 16:19:46 ]
Zou iemand me kort uit kunnen leggen wat een integraaltransformatie is, ik weet dit niet precies en van wikipedia en google werd ik ook niet veel wijzer. Ik weet wel wat bijvoorbeeld de fourieranalyse is, hoe hij werkt en wat hij doet.
Finally, someone let me out of my cage
Gewoon de afgeleide dus? Sorry als dit geen nut heeft, maar ik heb binnenkort toch een toets over differentieren en integreeren.quote:Op donderdag 24 december 2009 23:05 schreef Burakius het volgende:
Oke guys. Calculus 11.9. Ik moet nu "use differentation to find a power series representation for:
f(x) = 1/ (1+x)2
Ik doe het altijd zo:
f(x) = 1/ (1+x)2 = (1 + x)-2
Deze regel geldt:
f(x) = xa
f'(x) = axa-1
Dus hier:
f(x) = (1 + x)-2
f'(x) = -2 * (1 + x)-3 = -2 * 1 / (1 + x)3 = -2 / (1 + x)3
Finally, someone let me out of my cage
Een fouriertransformatie is een integraaltransformatie, maar er zijn er meerdere. http://nl.wikipedia.org/wiki/Integraaltransformatie is vrij duidelijk wat dat betreft.quote:Op vrijdag 25 december 2009 16:45 schreef minibeer het volgende:
Zou iemand me kort uit kunnen leggen wat een integraaltransformatie is, ik weet dit niet precies en van wikipedia en google werd ik ook niet veel wijzer. Ik weet wel wat bijvoorbeeld de fourieranalyse is, hoe hij werkt en wat hij doet.
Nee, ze bedoelen een taylorreeks met oneindig veel termen.quote:
[..]
Gewoon de afgeleide dus? Sorry als dit geen nut heeft, maar ik heb binnenkort toch een toets over differentieren en integreeren.
vreemdquote:
In mijn lial diktaat staat het volgende:
Stel v=(v1, v2, ... , vn)t. We definiëren v* als de complex geconjugeerde van v. Dan geldt v*tv= (v1² + ... + vn²).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik begrijp het niet helemaal. Bedoelen ze dat een integraaltransformatie de afgeleide van de integraal van <een functie maal nog iets> is? Dan is het me namelijk wel geheel duidelijk.quote:Op vrijdag 25 december 2009 17:14 schreef GlowMouse het volgende:
Een fouriertransformatie is een integraaltransformatie, maar er zijn er meerdere. http://nl.wikipedia.org/wiki/Integraaltransformatie is vrij duidelijk wat dat betreft.
Sorry :Squote:Op vrijdag 25 december 2009 17:14 schreef GlowMouse het volgende:
Nee, ze bedoelen een taylorreeks met oneindig veel termen.
Finally, someone let me out of my cage
Ik voel me echt dom, maar wat moet er gebeuren wanneer er dit staat (factor):
Ik heb het nog nooit gehad, en kom het nu opeens tegen in mijn wiskundeboek.
[ Bericht 1% gewijzigd door AE86_Trueno op 27-12-2009 13:00:17 ]
Ik heb het nog nooit gehad, en kom het nu opeens tegen in mijn wiskundeboek.
[ Bericht 1% gewijzigd door AE86_Trueno op 27-12-2009 13:00:17 ]
http://nl.wikipedia.org/wiki/Combinatie_%28wiskunde%29quote:Op zondag 27 december 2009 12:54 schreef AE86_Trueno het volgende:
Ik voel me echt dom, maar wat moet er gebeuren wanneer er dit staat:
[ afbeelding ]
Ik heb het nog nooit gehad, en kom het nu opeens tegen in mijn wiskundeboek.
Dankjewel, ik had het al wel ooit gehad. Was het alleen vergetenquote:Op zondag 27 december 2009 13:00 schreef BasementDweller het volgende:
[..]
http://nl.wikipedia.org/wiki/Combinatie_%28wiskunde%29
Geen probleem.
Zelf heb ik ook een vraagje.
De opgave is: bereken de limiet als (x,y,z)->(0,0,0) van sin(xyz)/xyz.
Ik dacht dat je dan gewoon xyz kon substitueren door t. Dan krijg je lim van t->0 sin(t)/t. Met de regel van L'Hôpital blijkt dat 1 te zijn. Het antwoord is echter 0... dus waarom is mijn antwoord fout en hoe kan je het wel doen?
Zelf heb ik ook een vraagje.
De opgave is: bereken de limiet als (x,y,z)->(0,0,0) van sin(xyz)/xyz.
Ik dacht dat je dan gewoon xyz kon substitueren door t. Dan krijg je lim van t->0 sin(t)/t. Met de regel van L'Hôpital blijkt dat 1 te zijn. Het antwoord is echter 0... dus waarom is mijn antwoord fout en hoe kan je het wel doen?
Inderdaad.... is het antwoord in het boek weer eens foutquote:
.Is mijn argumentatie correct? Mag je dat xyz=t gebruiken?
de regel van L'Hôpital heb je trouwens niet nodig, je kunt ook de definitie van de afgeleide pakken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nog een vraagje jonges.
Ik zit weer in de problemen met die faculteiten. Ik irriteer me er mateloos aan. Dus kan iemand me zeggen wat ik fout doe als ik zeg dat:
Ik (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n!
Ik (2n)! ook zou kunnen shrijven als: (2n)n!
Daar ergens moet mijn fout zitten.
Ik zit weer in de problemen met die faculteiten. Ik irriteer me er mateloos aan. Dus kan iemand me zeggen wat ik fout doe als ik zeg dat:
Ik (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n!
Ik (2n)! ook zou kunnen shrijven als: (2n)n!
Daar ergens moet mijn fout zitten.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik (2n)! ook zou kunnen shrijven als: (2n)n!
pak n=3, links staat 6!, ofwel 6*5*4*3*2*1
rechts staat 6*3!, ofwel 6*3*2*1.
Bij (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n! kun je zo ook laten zien dat het fout is.
pak n=3, links staat 6!, ofwel 6*5*4*3*2*1
rechts staat 6*3!, ofwel 6*3*2*1.
Bij (2n+2)! ook zou kunnen schrijven als: (2n+2)(2n+1)n! kun je zo ook laten zien dat het fout is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, (2n + 2)! = (2n + 2)·(2n + 1)·(2n)!.
Neem anders een paar concrete gevallen om het idee te krijgen. n = 3, dan (2n + 2)! = 8! = 8·7·6·5·4·3·2·1 = 8·7·6! bijvoorbeeld, maar natuurlijk niet 8·7·3! wat jij zegt.
Neem anders een paar concrete gevallen om het idee te krijgen. n = 3, dan (2n + 2)! = 8! = 8·7·6·5·4·3·2·1 = 8·7·6! bijvoorbeeld, maar natuurlijk niet 8·7·3! wat jij zegt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Damn, is er geen manier om dit makkelijk te kunnen bepalen ?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik snap eerlijk gezegd niet wat de moeilijkheid is. Het is gewoon de faculteit-definitie uitschrijven. (2n + 2)! = (2n + 2)·(2n + 2 - 1)·(2n + 2 - 2)·(2n + 2 - 3)···3·2·1 = (2n + 2)(2n + 1)(2n)···3·2·1.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja dus het wordt eigenlijk - (2n+2)(2n+1)(2n)! waardoor ik die (2n)! kan wegstrepen . Toch..
Faculteiten .. mijn nachtmerrie.
Faculteiten .. mijn nachtmerrie.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Jup, die (2n)! in teller en noemer vallen tegen elkaar weg.quote:
Ja dus het wordt eigenlijk - (2n+2)(2n+1)(2n)! waardoor ik die (2n)! kan wegstrepen . Toch..
Faculteiten .. mijn nachtmerrie.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Als dank mag jij mijn nieuwe avatar uitkiezen. (keep it pro-Muslimquote:Op zondag 27 december 2009 23:58 schreef Iblis het volgende:
[..]
Jup, die (2n)! in teller en noemer vallen tegen elkaar weg.
).
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
