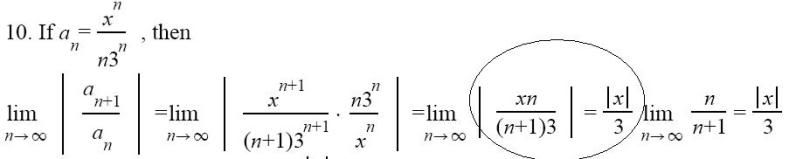SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


tvp
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Mijn statistiek docent ging vandaag weer even helemaal uit z'n dak in de les, en aangezien ik meer een bioloog ben dan iemand van de Wiskunde A volgde ik het niet helemaal.
Uiteindelijke kwam hij tot de conclusie dat twee formules essentieel voor ons zijn... mijn vraag was of er een bepaalde naam voor deze formules is en of er meer informatie over te vinden is zodat ik de precieze definitie van al die leuke tekentjes wat beter kan begrijpen.
De twee formules waren de volgende: (Op die tweede X moet nog een streepje maar die krijg ik er niet op)
_
Xιn - 1,96 σ / √n < μ < Xιn + 1,96 σ / √n
en (op deze X hoort uiteraard ook nog een streepje)
μ = Xn ± t (n - 1) S / √n
Uiteindelijke kwam hij tot de conclusie dat twee formules essentieel voor ons zijn... mijn vraag was of er een bepaalde naam voor deze formules is en of er meer informatie over te vinden is zodat ik de precieze definitie van al die leuke tekentjes wat beter kan begrijpen.
De twee formules waren de volgende: (Op die tweede X moet nog een streepje maar die krijg ik er niet op)
_
Xιn - 1,96 σ / √n < μ < Xιn + 1,96 σ / √n
en (op deze X hoort uiteraard ook nog een streepje)
μ = Xn ± t (n - 1) S / √n


Het zijn betrouwbaarheidsintervallen, de eerste gebaseerd op een steekproef uit de normale verdeling waarvan de standaardafwijking bekend is (sigma), de tweede gebaseerd op een steekproef uit de normale verdeling waarvan de standaardafwijking onbekend is (en geschat wordt met S).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Maar hoe moet ik S bepalen dan ?quote:Op dinsdag 15 december 2009 23:27 schreef GlowMouse het volgende:
Het zijn betrouwbaarheidsintervallen, de eerste gebaseerd op een steekproef uit de normale verdeling waarvan de standaardafwijking bekend is (sigma), de tweede gebaseerd op een steekproef uit de normale verdeling waarvan de standaardafwijking onbekend is (en geschat wordt met S).


Je bent een topperquote:Op dinsdag 15 december 2009 23:36 schreef GlowMouse het volgende:
http://www.wetenschapsforum.nl/index.php?showtopic=64168


Hij moet wel gedeeld worden door n-1 hier trouwens.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


TVP2 / TVP3 = TVP-1 
★5731U★ Death from above '79★You're a woman, i'm a machinielsie ★ ✠ ★ Telkens weer een beetje sterven★ I was born in a winterstorm, i live there still★


Zie het omkringelde. Hoe kunnen ze nou heel droog die twee n'en wegstrpen. Ik heb getracht het uit te werken door die 3(n+1) uit te werken tot : 3n + 3 en dan dingen wegstrepen, maar dan nog kom ik er niet op. Help please.
p.s.
Dit is trouwens een ratio test (Quotiëntentest)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Deel de teller en de noemer eens door de hoogste macht van de variabele waarvoor je de limiet neemt (n^1 dus). Dan krijg je dus lim n->inf van x / (3+3/n), dit is dus x/(3+0) = x/3
"Reality is an illusion created by a lack of alcohol."


je maakt je cirkeltje te kleinquote:Op woensdag 16 december 2009 16:50 schreef Burakius het volgende:
[ afbeelding ]
Zie het omkringelde. Hoe kunnen ze nou heel droog die twee n'en wegstrpen. Ik heb getracht het uit te werken door die 3(n+1) uit te werken tot : 3n + 3 en dan dingen wegstrepen, maar dan nog kom ik er niet op. Help please.
p.s.
Dit is trouwens een ratio test (Quotiëntentest)


Limietwaarde. Vul voor n een groot getal in (10.000 oid), dan krijg je dus: (xn)/(3n + 3). Dan zie je dat hoe groter n wordt, hoe minder die drie uitmaakt. Dus in feite houdt je voor n -> oneindig xn/3n = x/3 over  .
.


Ja maar ze hebben nog niet eens iets met de limiet gedaan wtf. Ze zijn nog bezig met het proces te vereenvoudigen, maar toch hebben ze opeens zomaar wel ff snel de limiet berekend van 3/n wat natuurlijk 0 is. Wat een josti's. Ga het mooi op eigen manier doen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Edit, laat maar. Ik zie dat ze het idd hebben uitgewerkt na het = teken. Sjonge jonge jonge. Wat een bal gehakten zijn het ook.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Oh ik had niet goed gekeken, ze hebben inderdaad gewoon een gedeelte buiten de limiet gehaald, en daarmee gedaan wat ik zei.
"Reality is an illusion created by a lack of alcohol."


Ja en de absolute waarde zetten ze alleen om de x omdat alle andere delen (de drie, en de n/(n+1) toch sowieso positief zijn)
"Reality is an illusion created by a lack of alcohol."


Mwah ze doen : lim n-> oneindig |xn/3n+3| ---> delen door hoogste macht noemer door n --->
|x/3+3/n| ---> daarna de limiet bepalen geeft: x/3+0
En dan om de convergentiestraal te bepalen: x/3 = +- 1 dus x = +/- 3 R= 3 En dan moet je die weer invullen in de originele etc. etc.
|x/3+3/n| ---> daarna de limiet bepalen geeft: x/3+0
En dan om de convergentiestraal te bepalen: x/3 = +- 1 dus x = +/- 3 R= 3 En dan moet je die weer invullen in de originele etc. etc.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Nee eens goed kijken, ze zetten alleen de |x|/3 voor de limiet aangezien die toch niet beinvloed worden door de limiet, daarna doen ze pas de limiet uitwerken.
"Reality is an illusion created by a lack of alcohol."


mja, maar het maakt niet veel uit an sich. Op mijn manier kom je er ook op uit.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Er wordt helemaal niks 'weggestreept'. Die factor |x|/3 is onafhankelijk van n en dus een constante factor wanneer n je variabele is. Zodoende is de limiet van |xn/3(n+1)| voor n →∞ gelijk aan |x|/3 maal de limiet van n/(n+1) voor n →∞.quote:Op woensdag 16 december 2009 16:50 schreef Burakius het volgende:
[ afbeelding ]
Zie het omkringelde. Hoe kunnen ze nou heel droog die twee n'en wegstrpen. Ik heb getracht het uit te werken door die 3(n+1) uit te werken tot : 3n + 3 en dan dingen wegstrepen, maar dan nog kom ik er niet op. Help please.
p.s.
Dit is trouwens een ratio test (Quotiëntentest)


Ik heb er nog één meesterlijke meesters der Brontosaurussen.
Dit is dus een Bessel-functie van de 1ste orde. Heel leuk en aardig dat ze hier een Ratio test gebruiken. Nu kom ik zelf op :
(x/2)2 lim 1/n+2
Zoals jullie zien mis ik die n+1 die ook bij de noemer hoort. Nu zal het vast liggen aan iets met die faculteiten. [b]Ik weet dat (blijkbaar) ((n+1)+1)! = (n+2)! [b/] En ik weet ook dat (n+2)! = (n+2)n!
Als ik dit toepas kan ik wegstrepen etc. , maar dan houd ik die n+1 niet over iig.
Wat doe ik fout? (graag het dikgedrukte ook verifiëren)
Dit is dus een Bessel-functie van de 1ste orde. Heel leuk en aardig dat ze hier een Ratio test gebruiken. Nu kom ik zelf op :
(x/2)2 lim 1/n+2
Zoals jullie zien mis ik die n+1 die ook bij de noemer hoort. Nu zal het vast liggen aan iets met die faculteiten. [b]Ik weet dat (blijkbaar) ((n+1)+1)! = (n+2)! [b/] En ik weet ook dat (n+2)! = (n+2)n!
Als ik dit toepas kan ik wegstrepen etc. , maar dan houd ik die n+1 niet over iig.
Wat doe ik fout? (graag het dikgedrukte ook verifiëren)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


dat klopt niet.quote:En ik weet ook dat (n+2)! = (n+2)n!
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oke dat zou goed kunnen. Voor (n+1)! = (n+1)n! wel geldig.quote:
Dus dan is het voor (n+2)! = (n+1)(n+2) n! of iets in die richting?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Tja, je kent de definitie van ! toch hoop ik?quote:Op woensdag 16 december 2009 21:31 schreef Burakius het volgende:
[..]
Oke dat zou goed kunnen. Voor (n+1)! = (n+1)n! wel geldig.
Dus dan is het voor (n+2)! = (n+1)(n+2) n! of iets in die richting?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


tja ik weet dat (n+2)! = (n+1) * (n+2) * ....... etc. dus = (n+1) * (n+2) * n! (hoop dat dit correct is).quote:Op woensdag 16 december 2009 21:34 schreef Iblis het volgende:
[..]
Tja, je kent de definitie van ! toch hoop ik?
Het is faculteit. Dus 3! = 1 * 2 * 3
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ik zou het wel andersom schrijven, nu lijkt het net of de termen steeds hoger gaat, maar dus:quote:Op woensdag 16 december 2009 21:42 schreef Burakius het volgende:
[..]
tja ik weet dat (n+2)! = (n+1) * (n+2) * ....... etc. dus = (n+1) * (n+2) * n! (hoop dat dit correct is).
Het is faculteit. Dus 3! = 1 * 2 * 3
(n+2)! = (n+2) * (n+1)! = (n+2) * (n+1) * n!
"Reality is an illusion created by a lack of alcohol."


Thx duidelijk!quote:Op woensdag 16 december 2009 21:53 schreef Dzy het volgende:
[..]
Ik zou het wel andersom schrijven, nu lijkt het net of de termen steeds hoger gaat, maar dus:
(n+2)! = (n+2) * (n+1)! = (n+2) * (n+1) * n!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Beste mensen, ik heb een statistisch probleem:
Technisch verhaal:
Ik doe een onderzoek naar de effectiviteit van een interventie. Werkt onze beinvloeding ja/nee?
Idee: we hebben 3 plekken in Nederland gepakt. Op twee plekken hebben we een bord neergezet, namelijk bord1 of bord2. Op de derde plek staat niets (controleconditie).
Bij deze plekken hebben wij op drie dagen, voor twee weken, geobserveerd. Eerste voordat de borden er stonden (voor-/nulmeting) en daarna terwijl de borden er staan.
Mijn variabelen in mijn databestand ziet er ongeveer zo uit:
T0-1 T0-2 T0-3 T0-4 T0-5 T0-6 T1-1 T1-2 T1-3 T1-4 T1-5 T1-6 Conditie
T0-1 is de eerste dag van de nulmeting, T0-3 is de derde dag van de nulmeting enz.
T1-1 is de eerste dag van de nameting, T1-5 is de vijfde dag van de nameting enz.
Conditie is het bord dat er staat, 1,2 of 3 (waarbij 3 geen bord is).
Daaronder staan dus 3 rijen met cijfers, voor elk geobserveerde plaats 1.
Mijn vraag is deze: Hoe kan ik de effectiviteit van onze interventie berekenen? Doordat we maar drie plaatsen hebben, is er een n van 3 (erg weinig dus). Is er een mogelijkheid de data van de verschillende meetmomenten als 'within' info mee te nemen of nog iets anders ermee te doen?
Als ik een repeated measures anova doe kan ik wel contrasten bekijken tussen alle verschillende meetmomenten, maar ik wil eigenlijk een duidelijk contrast tussen nulmeting en nameting.
Als ik een gemiddelde pak van de nulmeting en de nameting heb ik het gevoel dat ik veel informatie weggooi door simpelweg een gemiddelde te pakken, terwijl ik in feite 6 observaties heb.
Kan iemand mij helpen?
Alvast bedankt!
Technisch verhaal:
Ik doe een onderzoek naar de effectiviteit van een interventie. Werkt onze beinvloeding ja/nee?
Idee: we hebben 3 plekken in Nederland gepakt. Op twee plekken hebben we een bord neergezet, namelijk bord1 of bord2. Op de derde plek staat niets (controleconditie).
Bij deze plekken hebben wij op drie dagen, voor twee weken, geobserveerd. Eerste voordat de borden er stonden (voor-/nulmeting) en daarna terwijl de borden er staan.
Mijn variabelen in mijn databestand ziet er ongeveer zo uit:
T0-1 T0-2 T0-3 T0-4 T0-5 T0-6 T1-1 T1-2 T1-3 T1-4 T1-5 T1-6 Conditie
T0-1 is de eerste dag van de nulmeting, T0-3 is de derde dag van de nulmeting enz.
T1-1 is de eerste dag van de nameting, T1-5 is de vijfde dag van de nameting enz.
Conditie is het bord dat er staat, 1,2 of 3 (waarbij 3 geen bord is).
Daaronder staan dus 3 rijen met cijfers, voor elk geobserveerde plaats 1.
Mijn vraag is deze: Hoe kan ik de effectiviteit van onze interventie berekenen? Doordat we maar drie plaatsen hebben, is er een n van 3 (erg weinig dus). Is er een mogelijkheid de data van de verschillende meetmomenten als 'within' info mee te nemen of nog iets anders ermee te doen?
Als ik een repeated measures anova doe kan ik wel contrasten bekijken tussen alle verschillende meetmomenten, maar ik wil eigenlijk een duidelijk contrast tussen nulmeting en nameting.
Als ik een gemiddelde pak van de nulmeting en de nameting heb ik het gevoel dat ik veel informatie weggooi door simpelweg een gemiddelde te pakken, terwijl ik in feite 6 observaties heb.
Kan iemand mij helpen?
Alvast bedankt!


Stel ik heb twee lijsten A en B van ongeveer 100 natuurlijke getallen. Ik weet dat er een getal bestaat in beide lijsten. Maar ik wil een algoritme schrijven dat voor mij op een snelle manier uitzoekt welk getal dat is (ik vergeet even over de posities van dat getal in a1 en a2).
Ik hoef niet perse met a1 en a2 zelf te werken dus ik dacht het volgende: ik maak tien kleine lijsten (de lengte/geheugen is even niet zo belangrijk) A0, A1,...,A9 waarbij ik in lijst Ai alle getallen uit A stop die eindigen op i in hun decimale representatie (dus bijv 101 gaat naar A1, 1004404 gaat naar A4). Daarna maak ik een forloop die een b getal uit B neemt en dan i=b%10 uitrekent, dan zoek ik alleen in lijst Ai naar het getal b.
Dit algortime heeft toch hoogstens orde n? Is er nog een slimmer/sneller algoritme?
Alvast bedankt!
Ik hoef niet perse met a1 en a2 zelf te werken dus ik dacht het volgende: ik maak tien kleine lijsten (de lengte/geheugen is even niet zo belangrijk) A0, A1,...,A9 waarbij ik in lijst Ai alle getallen uit A stop die eindigen op i in hun decimale representatie (dus bijv 101 gaat naar A1, 1004404 gaat naar A4). Daarna maak ik een forloop die een b getal uit B neemt en dan i=b%10 uitrekent, dan zoek ik alleen in lijst Ai naar het getal b.
Dit algortime heeft toch hoogstens orde n? Is er nog een slimmer/sneller algoritme?
Alvast bedankt!


Het opzoeken kost ook nog O(n) zodat je voor het totaal op O(n²) komt. Door sorteren van beide lijsten kun je tot O(n logn) komen, maar de vraag is of dat bij n=100 veel uitmaakt.quote:Daarna maak ik een forloop die een b getal uit B neemt en dan i=b%10 uitrekent, dan zoek ik alleen in lijst Ai naar het getal b.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Worst case is natuurlijk als alle getallen in A op hetzelfde eindigen, en dat dus, zeg |A0| = |A|, en idem voor B, waardoor je nog steeds n keer een lijst van n getallen lineair doorzoekt.
Als de lijsten van getallen niet bounded zijn dan is m'n eerste indruk dat je ze het beste individueel kunt sorteren (n log n), en dan mergen wat met gesorteerde lijsten lineair kan. Tijdens de merge kun je dan op duplicaten checken.
Is de boel wel gebound of weet je meer over de input, dan kun je een lineaire oplossing nadenken.
Als de lijsten van getallen niet bounded zijn dan is m'n eerste indruk dat je ze het beste individueel kunt sorteren (n log n), en dan mergen wat met gesorteerde lijsten lineair kan. Tijdens de merge kun je dan op duplicaten checken.
Is de boel wel gebound of weet je meer over de input, dan kun je een lineaire oplossing nadenken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Die bound heb je ook, want je weet dat het natuurlijke getallen zijn. Je kan dan het maximum zoeken in O(n), een array maken vol booleans met de maximumgrootte van het gevonden maximum + 1, en alle startwaarden in die array op false zetten.quote:Op zaterdag 19 december 2009 13:06 schreef Iblis het volgende:
Is de boel wel gebound of weet je meer over de input, dan kun je een lineaire oplossing nadenken.
Tijdens de eerste for-loop zet je indices in je array die corresponderen met de getallen die in je eerste lijst staan op true (O(n)). Tijdens de tweede for-loop kijk je of de indices in je array die corresponderen met de getallen in je tweede lijst al op true staan (O(n)), zo ja, dan zit ie in beide. Kan een heleboel geheugen kosten als het maximum heel groot is enzo, maargoed, de orde is lager -.-


Iblis heeft het over een a priori bekende bound, bedenk maar eens waarom het dan makkelijk wordt 
Jouw 'oplossing' is niet goed, je ziet zelf dat het al fout gaat bij een groot getal.
Jouw 'oplossing' is niet goed, je ziet zelf dat het al fout gaat bij een groot getal.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Er zullen vast wel meer bounds zijn waardoor het makkelijk wordt om een lineaire oplossing te bedenken. Als je weet dat de getallen natuurlijke getallen zijn (zoals in dit geval) ook, dus ksnap niet precies wat je bedoelt.quote:Op zaterdag 19 december 2009 14:12 schreef GlowMouse het volgende:
Iblis heeft het over een a priori bekende bound, bedenk maar eens waarom het dan makkelijk wordt
Jouw 'oplossing' is niet goed, je ziet zelf dat het al fout gaat bij een groot getal.
Het kan veel geheugen kosten maar in theorie gaat dit goed hoor, en er werd volgens mij niet gevraagd om rekening te houden met het geheugen. Kan je iets concreter vertellen wat er volgens jou dan mis gaat -.-


Je moet kijken naar de verwerkingstijd als functie van je input. In jouw functie is die exponentieel, want om een groot getal K in te voeren kost dat mij log(K) stapjes terwijl de geheugenallokatie K stapjes kost.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De bound komt dan sowieso niet te liggen bij de lengte van de input maar bij de maximale waarde van de getallen in de input. Of je nu rijen van 2 of rijen van 10.000 wil vergelijken, je hoofdprobleem zal waarschijnlijk zijn – op een 64-bits machine b.v. – een array van 264 booleans te alloceren.
Overigens, wat Optimistic1 doet, is simpelweg de input hashen. En in feite kan dat algemener. En dan kun je – met random data – wel een in de praktijk lineaire oplossing krijgen. Maar de vraag is dus even of je worst-case wilt gaan zitten analyseren of niet.
Overigens, wat Optimistic1 doet, is simpelweg de input hashen. En in feite kan dat algemener. En dan kun je – met random data – wel een in de praktijk lineaire oplossing krijgen. Maar de vraag is dus even of je worst-case wilt gaan zitten analyseren of niet.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


In de praktijk kan je hierop letten, maar om de orde van n te bepalen hoef je niet te letten op maximumgetal K en kdenk dat Optimistic bedoelde dat hij de laagste orde n wou. De oplossing die ik in mn post noemde is overigens ook geaccepteerd als oplossing (als n dichtbij K zit), alleen wordt hij nauwelijks gebruikt -.-quote:Op zaterdag 19 december 2009 14:22 schreef GlowMouse het volgende:
Je moet kijken naar de verwerkingstijd als functie van je input. In jouw functie is die exponentieel, want om een groot getal K in te voeren kost dat mij log(K) stapjes terwijl de geheugenallokatie K stapjes kost.
Wat Iblis zegt kan mis gaan (ook al kom je in de praktijk niet altijd tegen dat je getallen groter dan 2^64 moet verwerken) waar ingewikkelde oplossingen voor zijn (met nog meer trees en arrays), dus daar gaan we niet aan beginnen -.- Daarom kan Optimistic maar beter zoiets zeggen (wat in de vorige posts al beetje gezegd is, maar het algoritme is nog niet echt gegeven):
- Beide lijsten sorteren (via merge-sort heb je uiteindelijk de laagste orde, namelijk O(n log(n)), maar quick-sort is in de praktijk sneller maar heeft worst-case O(n^2)).
- Neem telkens het minimum van de twee gesorteerde lijsten en kijk of hij overeenkomt met het minimum van de andere lijst. Zo niet, streep die weg en herhaal.


De getallen die ik heb komen doordat ik een algoritme gebruik om het aantal punten op een elliptische kromme E gedefinieerd over een lichaam Fp uit te rekenen. Het algortime heeft complexiteit O(p1/4+e) en gaat als volgt:
*Kies een random punt P op de kromme E.
*Bereken de eerste s veelvouden van P, namelijk P, 2P, 3P,...,sP, waarbij s=p^(1/4) (bij mij is s ongeveer 100) en sla deze op in een lijst.
*Bereken Q:=(2*s+1)P en R=(p+1)P door binaire expansie van p+1 te gebruiken.
*Schrijf t=[sqrt(p)/(2*s+1)] (dit is een getal ongeveer gelijk aan s) en bereken
R +/-P, R+/- 2P,R+/-3P,....,R+/-tP en dit zijn 2s+1 punten. Deze sla ik weer op in een lijst.
Er is een stelling die zegt dat er een i en j bestaan met R+iQ=jP, dus er is een punt zowel in de 1e als in de 2e lijst en dat punt wil ik vinden... want als ik die vind en dus ook i en j weet..
dan kan ik weten wat het aantal punten is op mijn kromme E. Over het vinden van dit punt staat;
"It is important that one can efficiently search among the points in the
list of baby steps; one should sort this list or use some kind of hash coding.
It is not difficult to see that the running time of this algorithm is O(p1/4+e)"
http://www.mat.uniroma2.it/~schoof/ctg.pdf
Mijn idee was om dus om gebruik te maken van de x-coordinaat van de punten en die gaan onthouden.
*Kies een random punt P op de kromme E.
*Bereken de eerste s veelvouden van P, namelijk P, 2P, 3P,...,sP, waarbij s=p^(1/4) (bij mij is s ongeveer 100) en sla deze op in een lijst.
*Bereken Q:=(2*s+1)P en R=(p+1)P door binaire expansie van p+1 te gebruiken.
*Schrijf t=[sqrt(p)/(2*s+1)] (dit is een getal ongeveer gelijk aan s) en bereken
R +/-P, R+/- 2P,R+/-3P,....,R+/-tP en dit zijn 2s+1 punten. Deze sla ik weer op in een lijst.
Er is een stelling die zegt dat er een i en j bestaan met R+iQ=jP, dus er is een punt zowel in de 1e als in de 2e lijst en dat punt wil ik vinden... want als ik die vind en dus ook i en j weet..
dan kan ik weten wat het aantal punten is op mijn kromme E. Over het vinden van dit punt staat;
"It is important that one can efficiently search among the points in the
list of baby steps; one should sort this list or use some kind of hash coding.
It is not difficult to see that the running time of this algorithm is O(p1/4+e)"
http://www.mat.uniroma2.it/~schoof/ctg.pdf
Mijn idee was om dus om gebruik te maken van de x-coordinaat van de punten en die gaan onthouden.