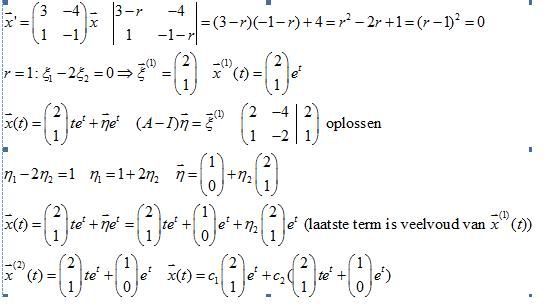SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
maak teveel foutjes de laatste tijd
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oke, bedankt. Volgens mij begin ik het wel te snappen. Misschien kom ik er later nog op terug.quote:Op donderdag 7 januari 2010 17:42 schreef GlowMouse het volgende:
Jouw afgeleidefunctie geldt voor x<>0. De afgeleide in 0 is lim(x->0) (f(x)-f(0)/(x-0) = lim(x->0) xsin(1/x) = 0. Je ziet dat de functie overal diffbaar is, maar de afgeleide is niet continu.
Ik vergeef het jequote:Op donderdag 7 januari 2010 17:56 schreef GlowMouse het volgende:
Ik heb het gehad vorig jaar met wiskunde, dat weet ik wel, maar hoe het moetquote:
Op de GR, eerst 100 invoeren, dan met de ANS toets en weet ik veel wat er iets van maken toch
100+80+64+51,2+..... = 100/(1-0,8).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De partiele afgeleiden zijn niet continu in 0: voor x != 0 geldt df/dy(x,0) = 1 en voor y != 0 geldt df/dy(0,y) = 0.quote:Op donderdag 7 januari 2010 14:41 schreef BasementDweller het volgende:
- In de theorie staat ergens dezelfde functie f(x,y) met als extra definitie f(0,0)=(0,0) wel continu is, partiële afgeleiden heeft in het punt (0,0) maar toch niet differentieerbaar is, terwijl er een stelling is die zegt dat als de partiële afgeleiden bestaan en continu zijn in de 'neighborhood' van x in het domein, dan is f differentieerbaar in het punt x.
Ik vraag mij af hoe je aan een Lissajous figuur kunt zien hoeveel periodes hij aflegt.
Bijvoorbeeld bij deze figuur?
Alvast bedankt!
Bijvoorbeeld bij deze figuur?
Bijvoorbeeld bij deze figuur?Alvast bedankt!
Pak een punt, kies een richting, en volg de figuur tot je bij je startpunt terug bent. En kijk tijdens dat wandelen wat er met de x-coordinaat gebeurt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja x-coordinaat is eerst positief, daarna negatief. Dus houdt dat in dat hij 2 periodes op de x-richting aflegt. En op de y-richting? Lijkt me niet dat je dat ook zo kunt doen.quote:Op donderdag 7 januari 2010 21:54 schreef GlowMouse het volgende:
Pak een punt, kies een richting, en volg de figuur tot je bij je startpunt terug bent. En kijk tijdens dat wandelen wat er met de x-coordinaat gebeurt.
Even een snelle vraag... misschien dat GlowMouse het weet.
Ik ben een beetje met Excel aan het kloten, want ik probeer via Excel normale verdeling en de betrouwbaarheid van een X-aantal metingen uit te rekenen.
Excel schijnt dit allemaal feilloos voor je te kunnen doen...
Ik ben een beetje met Excel aan het kloten, want ik probeer via Excel normale verdeling en de betrouwbaarheid van een X-aantal metingen uit te rekenen.
Excel schijnt dit allemaal feilloos voor je te kunnen doen...
y kan ook zo, maar dan moet je het wel eerst goed kunnen. De sinus is op [0, 2pi] ook zowel positief als negatief, en toch maar één periode.quote:Op donderdag 7 januari 2010 21:57 schreef Pimmeltje het volgende:
[..]
Ja x-coordinaat is eerst positief, daarna negatief. Dus houdt dat in dat hij 2 periodes op de x-richting aflegt. En op de y-richting? Lijkt me niet dat je dat ook zo kunt doen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ik snap niet wat je wilt, maar probeer de helpfunctie eensquote:
Even een snelle vraag... misschien dat GlowMouse het weet.
Ik ben een beetje met Excel aan het kloten, want ik probeer via Excel normale verdeling en de betrouwbaarheid van een X-aantal metingen uit te rekenen.
Excel schijnt dit allemaal feilloos voor je te kunnen doen...
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hmm, maar het klopt dus dat van negatief en positief? Ik begrijp met die y niet, want dat houdt in dat er in d y-richting 6 periodes zijn?
Ik bedoelde eigenlijk dit:quote:Op donderdag 7 januari 2010 22:00 schreef GlowMouse het volgende:
[..]
ik snap niet wat je wilt, maar probeer de helpfunctie eens
Het betrouwbaarheidsinterval voor een grote steekproef (of populatie) wordt berekend met de
werkbladfunctie ‘BETROUWBAARHEID’.
Normaal reken ik dat hele statistiek gedoe op de ouderwetse manier uit...
Maar blijkbaar kun je met werkbladfunctie's alles voor je uit laten rekenen door Excel... alleen ik ben zo vreselijk slecht met dit soort programma's.
Ik kan nergens goed vinden hoe je het nu precies moet uitrekenen... wat en hoe en waar ik mijn resultaten nu precies moet invullen... etc.
Nee dat klopt niet, je moet goed nadenken wanneer je één periode hebt: dat is als x op een punt is waar hij precies dezelfde beweging nog een keer gaat maken. Dat heeft niets met positief/negatief te maken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
http://www.bloggpro.com/a(...)-intervals-in-excel/quote:
[..]
Ik bedoelde eigenlijk dit:
Het betrouwbaarheidsinterval voor een grote steekproef (of populatie) wordt berekend met de
werkbladfunctie ‘BETROUWBAARHEID’.
Normaal reken ik dat hele statistiek gedoe op de ouderwetse manier uit...
Maar blijkbaar kun je met werkbladfunctie's alles voor je uit laten rekenen door Excel... alleen ik ben zo vreselijk slecht met dit soort programma's.
Ik kan nergens goed vinden hoe je het nu precies moet uitrekenen... wat en hoe en waar ik mijn resultaten nu precies moet invullen... etc.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Zie je wel... ik kan gewoon niet met google zoekenquote:Op donderdag 7 januari 2010 22:16 schreef GlowMouse het volgende:
[..]
http://www.bloggpro.com/a(...)-intervals-in-excel/
Thnx !
Een soepautomaat bevat bekertjes waar maximaal 200 cc in kan. Allereerst dropt de automaat 4 balletjes in het bekertje en vervolgens wordt een vloeibare substantie toegevoegd. Neem aan:
1 balletje: b ~ N(2 ; 0,5)
vloeibare substantie: v ~ N(185 ; 10)
soep: s = 4*b + v
a) Bepaal de verdeling van s.
Ik kom tot:
μs = 4 * μb + μv = 4 * 2 + 185 = 193
σs = √(4 * 0,52 + 102) = 10,1
s ~ N(μ=193 ; σ=10,1)
b. Bereken de kans op overstromen van het bekertje.
s = (x - μ) / σ =
(200 - 193) / 10,1 = 0,69
P(z > 0,69) = 0,0455 (opgezocht in z-waarden tabel)
Gaat dit goed?
[ Bericht 6% gewijzigd door Booomer op 08-01-2010 12:11:58 ]
1 balletje: b ~ N(2 ; 0,5)
vloeibare substantie: v ~ N(185 ; 10)
soep: s = 4*b + v
a) Bepaal de verdeling van s.
Ik kom tot:
μs = 4 * μb + μv = 4 * 2 + 185 = 193
σs = √(4 * 0,52 + 102) = 10,1
s ~ N(μ=193 ; σ=10,1)
b. Bereken de kans op overstromen van het bekertje.
s = (x - μ) / σ =
(200 - 193) / 10,1 = 0,69
P(z > 0,69) = 0,0455 (opgezocht in z-waarden tabel)
Gaat dit goed?
[ Bericht 6% gewijzigd door Booomer op 08-01-2010 12:11:58 ]
Alle informatie die gegeven wordt, heb ik gepost. Het zou kunnen dat ik bij (a) niet voldoende berekend heb, maar ik weet niet wat ik nog moet doen..quote:Op vrijdag 8 januari 2010 12:15 schreef thabit het volgende:
Wederom te weinig gegevens want er wordt niets over de covariantie tussen b en v verondersteld.
De vraagsteller schoppen, aangezien hij/zij duidelijk geen idee heeft wat hij/zij opschrijft.quote:Op vrijdag 8 januari 2010 12:18 schreef Booomer het volgende:
[..]
Alle informatie die gegeven wordt, heb ik gepost. Het zou kunnen dat ik bij (a) niet voldoende berekend heb, maar ik weet niet wat ik nog moet doen..
En als ik nu naar de docent stap, weet ie het zo voor me op te lossen met de gegevens die er zijn. Vergeet ik gewoon niet iets te berekenen?quote:Op vrijdag 8 januari 2010 12:25 schreef thabit het volgende:
[..]
De vraagsteller schoppen, aangezien hij/zij duidelijk geen idee heeft wat hij/zij opschrijft.
Als je docent denkt dat-ie het met deze gegevens kan oplossen, dan heeft-ie het zelf ook niet begrepen.quote:Op vrijdag 8 januari 2010 12:31 schreef Booomer het volgende:
[..]
En als ik nu naar de docent stap, weet ie het zo voor me op te lossen met de gegevens die er zijn. Vergeet ik gewoon niet iets te berekenen?
quote:Op vrijdag 8 januari 2010 12:39 schreef thabit het volgende:
[..]
Als je docent denkt dat-ie het met deze gegevens kan oplossen, dan heeft-ie het zelf ook niet begrepen.
Kijk nou gewoon even naar wat ik gedaan heb. Wat mist er dan? Je weet toch hoeveel balletjes en hoeveel vloeibare substantie in de soep gaat? De variantie staat er ook..
Ik ben altijd in de veronderstelling geweest dat de er geen 'patroon' zat in het getal pi. Nu vind ik op wikipedia echter het volgende: 
Hoe kan ik deze kettingbreuk afleiden, of bewijzen dat dit patroon 'oneindig lang doorgaat'?
[ Bericht 12% gewijzigd door motorbloempje op 01-09-2013 21:34:23 ]
Hoe kan ik deze kettingbreuk afleiden, of bewijzen dat dit patroon 'oneindig lang doorgaat'?
[ Bericht 12% gewijzigd door motorbloempje op 01-09-2013 21:34:23 ]
Ah, ik denk dat ik het antwoord al gevonden heb:
http://en.wikipedia.org/wiki/Generalized_continued_fraction
http://en.wikipedia.org/wiki/Generalized_continued_fraction
Heey ik kan het onderste volledig doen, maar er staat ook : draw a direction field and sketch a few trajectories. Zou iemand mij kunnen helpen hoe ik dit stapsgewijs kan doen?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Laplace transformatie > klein vraagje over een minteken dat ineens verschijnt bij het integreren.
Waarom staat onder de deelstreep, eerste lid aan de rechterkant van de onderste formule, ineens S-B , terwijl in de e macht van de integraal B-S staat? Ik heb hem al 3x uitgewerkt maar kom toch steeds op een andere uitkomst...
Waarom staat onder de deelstreep, eerste lid aan de rechterkant van de onderste formule, ineens S-B , terwijl in de e macht van de integraal B-S staat? Ik heb hem al 3x uitgewerkt maar kom toch steeds op een andere uitkomst...
de volgorde in de teller is ook omgedraaid; (a-b)/(c-d) = (b-a)/(d-c). Bij de tweede breuk gebeurt iets vergelijkbaars, heb je dat wel gezien?quote:
Laplace transformatie > klein vraagje over een minteken dat ineens verschijnt bij het integreren.
[ afbeelding ]
Waarom staat onder de deelstreep, eerste lid aan de rechterkant van de onderste formule, ineens S-B , terwijl in de e macht van de integraal B-S staat? Ik heb hem al 3x uitgewerkt maar kom toch steeds op een andere uitkomst...
http://www.math.utah.edu/~gustafso/2250directionfields.pdfquote:
Heey ik kan het onderste volledig doen, maar er staat ook : draw a direction field and sketch a few trajectories. Zou iemand mij kunnen helpen hoe ik dit stapsgewijs kan doen?
[ afbeelding ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Maarem, als ik het in 'mijn vorm' op zou schrijven zou het dus uiteraard ook goed zijn. Wat is het praktisch nut dan van het omdraaien? Er gebeuren erg vaak dingen in uitwerkingen waarvan ik denk: jemig wil je het echt zo moeilijk mogelijk maken om het te begrijpen?quote:
de volgorde in de teller is ook omgedraaid; (a-b)/(c-d) = (b-a)/(d-c). Bij de tweede breuk gebeurt iets vergelijkbaars, heb je dat wel gezien?
Het is deels esthetisch, om de symmetrie te benadrukken, soms is het om het aantal mintekens in de formule wat kleiner te krijgen, soms is het simpelweg conventie om een bepaalde vorm aan te houden.quote:
[..]
Maarem, als ik het in 'mijn vorm' op zou schrijven zou het dus uiteraard ook goed zijn. Wat is het praktisch nut dan van het omdraaien? Er gebeuren erg vaak dingen in uitwerkingen waarvan ik denk: jemig wil je het echt zo moeilijk mogelijk maken om het te begrijpen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
sja... estetische regels doen we eigenlijk niet zo veel normaal gesproken tijdens college
Nog een dingetje waar ik mee zit: partial fractions. Dat lukt eigenlijk meestal prima, maar bij deze kom ik er niet uit. Wat is daarbij de methode?
ik doel uiteraard niet op de algehele partfrac methode, die staat hier ook wel in mijn boek. Maar geen idee hoe ik het hierbij aanpak.
Nog een dingetje waar ik mee zit: partial fractions. Dat lukt eigenlijk meestal prima, maar bij deze kom ik er niet uit. Wat is daarbij de methode?
ik doel uiteraard niet op de algehele partfrac methode, die staat hier ook wel in mijn boek. Maar geen idee hoe ik het hierbij aanpak.
Oe! Laat maar 
weet het al
Jemig moet ik vaker doen. Eerst een uur prutsen zonder results. Even op fok zetten, en 30 sec na posten de methode ineens weten wazig.
Even wel de uitwerking:
maak er van: (AS+B)/S + (CS+D)/(S^2+4) --> weer gelijknamig maken en de functie aan bovenkant gelijkstellen aan de teller van eerste functie. Dan a,b,c,d oplossen.
weet het al Jemig moet ik vaker doen. Eerst een uur prutsen zonder results. Even op fok zetten, en 30 sec na posten de methode ineens weten
wazig.Even wel de uitwerking:
maak er van: (AS+B)/S + (CS+D)/(S^2+4) --> weer gelijknamig maken en de functie aan bovenkant gelijkstellen aan de teller van eerste functie. Dan a,b,c,d oplossen.
Ik snap echt heel weinig van stochastiek. De eerste drie hoofdstukken gingen nog wel (die gaan dan ook niet verder dan middelbareschoolwiskunde ) maar vanaf hoofdstuk 4 is het onbekend en is de syllabus erg vaag en beknopt.
Ik vind op internet deze uitleg over wat een stochast nou precies is. Betekent dat dat je voor de stochast apart een kansruimte (Omega, A en p) moet definieren? Wikipedia geeft als voorbeeld het gooien met een dobbelsteen. Eerst is Omega {1,2,3,4,5,6} x {1,2,3,4,5,6}, is de omega voor de stochast dan {2,3,4,5,6,7,8,9,10,11,12}?
) maar vanaf hoofdstuk 4 is het onbekend en is de syllabus erg vaag en beknopt. Ik vind op internet deze uitleg over wat een stochast nou precies is. Betekent dat dat je voor de stochast apart een kansruimte (Omega, A en p) moet definieren? Wikipedia geeft als voorbeeld het gooien met een dobbelsteen. Eerst is Omega {1,2,3,4,5,6} x {1,2,3,4,5,6}, is de omega voor de stochast dan {2,3,4,5,6,7,8,9,10,11,12}?
De stochast is in dit geval de som van de twee waarden van de dobbelstenen. Omega is dan nog steeds gewoon {1,2,3,4,5,6} x {1,2,3,4,5,6}. En de stochast is de functie X: Omega -> R die (s, t) naar s + t stuurt.
Van een functie f(x) moet ik de tailor serie berekenen als a = 2. Ik krijg alleen een heel vreemd resultaat.
Maar hoe kan 1 + x + x^2 = 1 + 3x + x^2?
Ik heb het meermalen nagerekend, maar ik krijg steeds hetzelfde resultaat.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | f(x) = 1 + x + x^2 = 7\\ f'(x) = 1 + 2x = 5\\ f''(x) = 2 \\ f^{(n)}(x) = 0 \text{ met } n >= 3 \end{eqnarray} De Taylorserie met a = 2\\ \begin{eqnarray} \Sum_{n=0}^{\infty} f^{(n)}(2) (x - 2)^n / n! \\ = 7*1/1 + 5(x-2)/1 + 2(x - 2)^2/2 + 0(x - 2)^3/3! + 0(x - 4)^4/4! + ... \\ = 7 + (5x-10) + (x - 2)^2 \\ = 1 + 3x + x^2 \end{eqnarray} |
Maar hoe kan 1 + x + x^2 = 1 + 3x + x^2?
Ik heb het meermalen nagerekend, maar ik krijg steeds hetzelfde resultaat.
Jesus hates you.
| 1 2 3 4 | = (7 - 10) + 5x + x^2 - 4x + 4 = (7 - 10 + 4) + (5-4)x + x^2 = 1 + x + x^2 |
Ik zal wel per ongeluk 2x in plaats van 4x genomen hebben.
Maar zo klopt die inderdaad.
Jesus hates you.
Hm, oké. Maar wat bedoelen ze dan precies met (ik moet nog even opzoeken hoe ik zo'n gave A maak in latex ;x)? Stel dat het gaat om lager te gooien dan 5, dan is X(omega) kleiner of gelijk aan 5, dan is die verzameling van omega's dus {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (3,1), (3,2), (4,1)}? en dus in A, want elke deelverzameling is in A.quote:Op maandag 11 januari 2010 21:12 schreef thabit het volgende:
De stochast is in dit geval de som van de twee waarden van de dobbelstenen. Omega is dan nog steeds gewoon {1,2,3,4,5,6} x {1,2,3,4,5,6}. En de stochast is de functie X: Omega -> R die (s, t) naar s + t stuurt.
Als sier-A gelijk is aan hoofdletter omega dan zit jouw set erin ja, maar A kan ook een andere verzameling zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Waar haal je dit vandaan? Ik kan hieraan namelijk niet ruiken wat er met A bedoeld wordt.quote:Op maandag 11 januari 2010 23:38 schreef Hanneke12345 het volgende:
[..]
Hm, oké. Maar wat bedoelen ze dan precies met [ afbeelding ] (ik moet nog even opzoeken hoe ik zo'n gave A maak in latex ;x)? Stel dat het gaat om lager te gooien dan 5, dan is X(omega) kleiner of gelijk aan 5, dan is die verzameling van omega's dus {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (3,1), (3,2), (4,1)}? en dus in A, want elke deelverzameling is in A.
volgens mij mist Hanneke12345 wat maattheorie
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
| 1 |
Geeft:
En:
| 1 |
Geeft:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Bedoel je niet dat hier?quote:
Als sier-A gelijk is aan hoofdletter omega dan zit jouw set erin ja, maar A kan ook een andere verzameling zijn.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
ja sorry, de powerset van omegaquote:Op maandag 11 januari 2010 23:49 schreef Iblis het volgende:
[..]
Bedoel je niet dat [ afbeelding ] hier?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Is er een ezelsbruggetje om te leren hoe je de OLS estimators moet differentiëren? Dus de gehele rekensom dat je de beta's als laatste overhoudt? Ik vergeet continu stappen. Zeg maar een uitleg in 3 regels ?
?
Ik weet het wel
In R3 zijn vectoren v1 = 
, v2 = 
en de deelruimte V = {v1, v2}
a) Zij T een lineaire transformatie van R3 in R3 zodanig dat:
Tv1=v2 ; Tv2 = v2-v1 ; Tv3 = v3
Vind eerst de matrix B van T ten opzichte van B en dan de standaardmatrix van T .
Hoe moet ik matrix B in godsnaam vinden? Volgens de uitwerkingen moet het zo:
B= [T]B = [[Tv1]B [Tv2]B [Tv3]B =
Alleen ik heb geen flauw idee hoe ze daar aan komen?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:30 ]
a) Zij T een lineaire transformatie van R3 in R3 zodanig dat:
Tv1=v2 ; Tv2 = v2-v1 ; Tv3 = v3
Vind eerst de matrix B van T ten opzichte van B en dan de standaardmatrix van T .
Hoe moet ik matrix B in godsnaam vinden? Volgens de uitwerkingen moet het zo:
B= [T]B = [[Tv1]B [Tv2]B [Tv3]B =
Alleen ik heb geen flauw idee hoe ze daar aan komen?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:30 ]
Een beetje te uitgebreid. Ik ben meer in tijdnood. Is het niet mogelijk dat je alleen deze even voordoet? Al is het niet teveel gevraagd.quote:Op maandag 11 januari 2010 12:18 schreef GlowMouse het volgende:
[..]
de volgorde in de teller is ook omgedraaid; (a-b)/(c-d) = (b-a)/(d-c). Bij de tweede breuk gebeurt iets vergelijkbaars, heb je dat wel gezien?
[..]
http://www.math.utah.edu/~gustafso/2250directionfields.pdf
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ok, het is geen huiswerkvraag maar ik heb wel even wiskunde-advies nodig.
Ik doe een research master in neuroscience, en voor een stage waar nogal veel signaalanalyse bij komt kijken moet ik wat meer weten van lineaire algebra. Alleen heb ik sinds Natuur en Techniek op de middelbare school niks meer met wiskunde gedaan.
Weet iemand misschien een goed inleidend boek?
Als iemand een cursus weet die gegeven wordt tussen nu en eind mei zou dat ook welkom zijn.
Oja, hetzelfde geldt trouwens voor Fourieranalyse.
[ Bericht 4% gewijzigd door Mini_rulez op 12-01-2010 13:37:43 ]
Ik doe een research master in neuroscience, en voor een stage waar nogal veel signaalanalyse bij komt kijken moet ik wat meer weten van lineaire algebra. Alleen heb ik sinds Natuur en Techniek op de middelbare school niks meer met wiskunde gedaan.
Weet iemand misschien een goed inleidend boek?Als iemand een cursus weet die gegeven wordt tussen nu en eind mei zou dat ook welkom zijn.
Oja, hetzelfde geldt trouwens voor Fourieranalyse.
[ Bericht 4% gewijzigd door Mini_rulez op 12-01-2010 13:37:43 ]
Are you pondering what I'm pondering?
Linear Algebra and Its applications van David C. Lay (voor uitwerkingen van dit boek verwijs ik je naar www.aerostudents.com) . Verder heb ik ook een youtube link voor je.
Best wel veel lessen en hij bouwt het geleidelijk op. Dit is echt super!
Best wel veel lessen en hij bouwt het geleidelijk op. Dit is echt super!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik ga meteen kijken of de bieb het heeft, dankjewel voor je uitgebreide reactie!quote:Op dinsdag 12 januari 2010 14:35 schreef Burakius het volgende:
Linear Algebra and Its applications van David C. Lay (voor uitwerkingen van dit boek verwijs ik je naar www.aerostudents.com) . Verder heb ik ook een youtube link voor je.
Best wel veel lessen en hij bouwt het geleidelijk op. Dit is echt super!
Are you pondering what I'm pondering?
B = [[T(v1)]B[T(v2)]B] =
(matrix A) (v1) (matrix A) (v2)
* 
, * 
=
, = 
Ik hoop dat het duidelijk is. Rond elke matrix en vector moet nog [A]B maar ik weet niet hoe dat moet.
Maar het probleem is dat ik de laatste stap gewoon totaal niet snap. Hoe komen ze van die 2 Basis vectoren bij die 2x2 matrix?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:34 ]
(matrix A) (v1) (matrix A) (v2)
=
Ik hoop dat het duidelijk is. Rond elke matrix en vector moet nog [A]B maar ik weet niet hoe dat moet.
Maar het probleem is dat ik de laatste stap gewoon totaal niet snap. Hoe komen ze van die 2 Basis vectoren bij die 2x2 matrix?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:34:34 ]
Find the matrix B of the linear transformation T(x) = Ax with respect to the basis B=(v1,v2). Construct B "Column by column".quote:Op dinsdag 12 januari 2010 23:19 schreef GlowMouse het volgende:
waar staat de vraag?
Die 9 in A, is dat geen -9?
Definieer M = [v1 v2];
Je krijgt dus een x tov basis B. Die moet je eerst omzetten naar een standaardbasis en dan heb je Mx. Dan kun je T toepassen: AMx. En dan moet je weer terug naar de basis B (de laatste stap die jij niet snapt): inv(M)AMx.
De matrix bij de hele transformatie wordt dus gegeven door inv(M)AM.
Definieer M = [v1 v2];
Je krijgt dus een x tov basis B. Die moet je eerst omzetten naar een standaardbasis en dan heb je Mx. Dan kun je T toepassen: AMx. En dan moet je weer terug naar de basis B (de laatste stap die jij niet snapt): inv(M)AMx.
De matrix bij de hele transformatie wordt dus gegeven door inv(M)AM.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
2. Beschouw de volgende nutsfuncties van consumenten A en B:
UA = (XA)1/3 (YA) 2/3 (XB)-2/3
UB = (XB)2/3 (YB) 1/3
Stel X0=100, Y0=100.
Stel dat de volgende allocatie geldt: XA = 33⅓, YA = 66⅔, XB = 66⅔, YB = 33⅓.
c) Bereken hoeveel consument A maximaal zou willen opgeven van goed Y (WTP) als hij/zij één eenheid meer van goed X zou ontvangen. Met andere woorden, bereken de marginale substitutieverhouding van consument A.
Meer wiskunde dan economie dacht ik, dus vandaar in dit topic.
Ik kom uit op 0,064 / 0,032 = 2, terwijl de uitwerking een uitkomst geeft van 5,0625
UA = (XA)1/3 (YA) 2/3 (XB)-2/3
UB = (XB)2/3 (YB) 1/3
Stel X0=100, Y0=100.
Stel dat de volgende allocatie geldt: XA = 33⅓, YA = 66⅔, XB = 66⅔, YB = 33⅓.
c) Bereken hoeveel consument A maximaal zou willen opgeven van goed Y (WTP) als hij/zij één eenheid meer van goed X zou ontvangen. Met andere woorden, bereken de marginale substitutieverhouding van consument A.
Meer wiskunde dan economie dacht ik, dus vandaar in dit topic.
Ik kom uit op 0,064 / 0,032 = 2, terwijl de uitwerking een uitkomst geeft van 5,0625
"More than an end to war, we want an end to the beginning of all wars"
hoioi,
hoe verkrijg ik de inverse laplace transformatie van 1 / ( s^4 + 1) ?
Is dit met breuksplitsen mogelijk?
hoe verkrijg ik de inverse laplace transformatie van 1 / ( s^4 + 1) ?
Is dit met breuksplitsen mogelijk?
Je kunt breuksplitsing gebruiken ja, maar niet zonder complexe getallen. Om je uitkomst te controleren kun je even hier kijken en dan InverseLaplaceTransform[1/(1+s^4),s,t] invoeren.quote:Op woensdag 13 januari 2010 20:39 schreef Holy_Goat het volgende:
hoioi,
hoe verkrijg ik de inverse laplace transformatie van 1 / ( s^4 + 1) ?
Is dit met breuksplitsen mogelijk?
