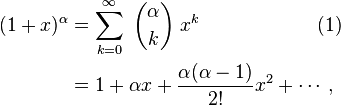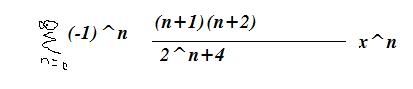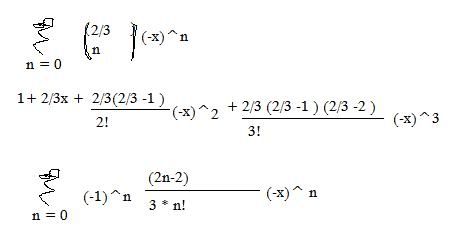SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Nee, je haakjes staan hier echt verkeerd. (1/2(1 + x/2))-3 wil je.
Excuses, ik had me door jou op het verkeerde been laten zetten (maar mijn schuld, want ik lette niet op en typte stom over, sorry!)
Uiteraard geldt (2 + x) = 2(1 + x/2), niet 1/2(1 + x/2), dus je krijgt:
[ Bericht 77% gewijzigd door Iblis op 28-12-2009 23:47:09 ]
Excuses, ik had me door jou op het verkeerde been laten zetten (maar mijn schuld, want ik lette niet op en typte stom over, sorry!)
Uiteraard geldt (2 + x) = 2(1 + x/2), niet 1/2(1 + x/2), dus je krijgt:
[ Bericht 77% gewijzigd door Iblis op 28-12-2009 23:47:09 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Oke, en dan zo invullen ff kijken . ik edit het hier wel.quote:Op maandag 28 december 2009 23:05 schreef Iblis het volgende:
Nee, je haakjes staan hier echt verkeerd. (1/2(1 + x/2))-3 wil je.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Mijn uitwerking. Nu met de goede omschrijving. 
Probeer dus eerst die formule in de goede vorm te krijgen, nogmaals:
Nu naar jouw Wikipedia-vorm:
Merk dus op dat we niet x maar x/2 hebben, en dat we verder α = -3 hebben. Dan krijg je dus deze sommatie (ik gebruik k ook, net als hierboven, niet n zoals je boek):
Dat gaan we dan uitschrijven, en dan krijgen we:
Nu zullen we de algemene uitdrukking voor elke term bepalen. Het lastigste is (denk ik) even die -3·(-3 - 1)·(-3 - 2), enz, je ziet dat dit wordt:
-3
-3·-4
-3·-4·-5
-3·-4·-5·-6
Enz.
Dus het teken klapt telkens om, dus dat geeft (-1)k. Verder zie je je een soort van faculteitsontwikkeling onstaan, behalve dat de 1·2 telkens ontbreekt, en het in de k-e term t/m (k + 2) gaat, m.a.w.:
-3 = (-1)1 · 3!/(1·2)
-3·-4 = (-1)2 · 4!/(1·2)
-3·-4·-5 = (-1)3 · 5!/(1·2)
-3·-4·-5·-6 = (-1)4 · 6!/(1·2)
Dus dat geeft in feite als algemene uitdrukking (-1)^(k!)/2, als je dat invult krijg je:
Nu komen we weer bij jouw favoriet: faculteiten. In de teller heb je (k + 2)! staan, in de noemer k!, bedenk (k + 2)! = (k + 2)(k + 1)k!, en dan kun je k! dus wegdelen:
En als laatste, merk op 8 = 23, dus:
Waar jouw sommatie zo uit volgt:
Probeer dus eerst die formule in de goede vorm te krijgen, nogmaals:
Nu naar jouw Wikipedia-vorm:
Merk dus op dat we niet x maar x/2 hebben, en dat we verder α = -3 hebben. Dan krijg je dus deze sommatie (ik gebruik k ook, net als hierboven, niet n zoals je boek):
Dat gaan we dan uitschrijven, en dan krijgen we:
Nu zullen we de algemene uitdrukking voor elke term bepalen. Het lastigste is (denk ik) even die -3·(-3 - 1)·(-3 - 2), enz, je ziet dat dit wordt:
-3
-3·-4
-3·-4·-5
-3·-4·-5·-6
Enz.
Dus het teken klapt telkens om, dus dat geeft (-1)k. Verder zie je je een soort van faculteitsontwikkeling onstaan, behalve dat de 1·2 telkens ontbreekt, en het in de k-e term t/m (k + 2) gaat, m.a.w.:
-3 = (-1)1 · 3!/(1·2)
-3·-4 = (-1)2 · 4!/(1·2)
-3·-4·-5 = (-1)3 · 5!/(1·2)
-3·-4·-5·-6 = (-1)4 · 6!/(1·2)
Dus dat geeft in feite als algemene uitdrukking (-1)^(k!)/2, als je dat invult krijg je:
Nu komen we weer bij jouw favoriet: faculteiten. In de teller heb je (k + 2)! staan, in de noemer k!, bedenk (k + 2)! = (k + 2)(k + 1)k!, en dan kun je k! dus wegdelen:
En als laatste, merk op 8 = 23, dus:
Waar jouw sommatie zo uit volgt:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
DUDE NICE! SUPER ERG MUCHO VEEL BEDANKT!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Yo brontosaurussen,
Ik wou graag even controleren of ik dit een beetje correct heb gedaan. Ik moet hier een power series van maken m.b.v. binominale. (11.10 som 28 , deel 6 Calculus).
(1-x)2/3
edit: hij klopt volgens mij niet. Ik ga vast en zeker de fout in door de teller in de taylorreeks verkeerd te definiëren bij het laatste sommatieteken. Ik heb er echt moeite mee.
Ik zie zeg maar: dat het gaat van 2/3 * -1/3 , 2/3 * -4/3 , 2/3 * -7/3 etc.
Ik wou graag even controleren of ik dit een beetje correct heb gedaan. Ik moet hier een power series van maken m.b.v. binominale. (11.10 som 28 , deel 6 Calculus).
(1-x)2/3
edit: hij klopt volgens mij niet. Ik ga vast en zeker de fout in door de teller in de taylorreeks verkeerd te definiëren bij het laatste sommatieteken. Ik heb er echt moeite mee.
Ik zie zeg maar: dat het gaat van 2/3 * -1/3 , 2/3 * -4/3 , 2/3 * -7/3 etc.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Iemand goed met algoritmes en zin om te puzzelen? 
Ik kom er namelijk niet helemaal uit.
Even een introductie: Ik heb voor een PO wiskunde een Chinees Postbode Probleem ontwikkeld die ik moet oplossen. Omdat ik ooit zelf postbode ben geweest, vond ik dat leuk, maar dat terzijde
. Ik ben dus nu op zoek naar de optimale route, waar dus de minste afstand wordt afgelegd. Een probleem is alleen dat de postbode een maximaal gewicht met zich mee mag nemen. Voor de duidelijkheid zal ik het hieronder even in plaatjes demonstreren:
De wijk schematisch weergegeven. Waar de huizen aan de weg vastzitten kan de post besteld worden. Het startpunt staat op dit plaatje als vaste waarde. Echter ben ik dus op zoek naar het ideale startpunt, dus deze zit daar niet vast.
De wijk in een graaf weergegeven. Zoals jullie zien is de flat en de route onder dijkwater verdwenen. Deze flat wordt altijd apart besteld, dus die onderste route heeft ook geen enkele meerwaarde en is dus per definitie inefficiënt.
De bundels die per straat (even en oneven) als standaard gelden.
Voor de postbode gelden Euler cirkels, oftewel, de postbode moet altijd weer uitkomen bij zijn fiets. Deze blijft de hele periode van het post bezorgen op 1 plaats staan (het startpunt).
Ik vroeg me dus af wat het beste startpunt is en hoe ik dit bereken. Ik ben pas sinds gister bekend met topologie en heb op een ander voorbeeld gebruik gemaakt van het algoritme van Fleury. Ik vroeg me echter af of er een formule was om dit probleem op te lossen en wat deze dan zou moeten zijn. Als jullie geen zin hebben om te puzzelen/rekenen, maar wel weten welk algoritme ik het best kan toepassen, laat het me dan ook weten. Dan kan ik me daar ook weer verder in verdiepen.
Ow en mocht het handig zijn, ik heb een applet gevonden waarbij je met verschillende algoritmen dergelijke topologische problemen op kan lossen. Klikkerdeklik.
Mocht het niet duidelijk zijn, of meer info nodig, let me know!
Ik kom er namelijk niet helemaal uit. Even een introductie: Ik heb voor een PO wiskunde een Chinees Postbode Probleem ontwikkeld die ik moet oplossen. Omdat ik ooit zelf postbode ben geweest, vond ik dat leuk, maar dat terzijde
. Ik ben dus nu op zoek naar de optimale route, waar dus de minste afstand wordt afgelegd. Een probleem is alleen dat de postbode een maximaal gewicht met zich mee mag nemen. Voor de duidelijkheid zal ik het hieronder even in plaatjes demonstreren:
De wijk schematisch weergegeven. Waar de huizen aan de weg vastzitten kan de post besteld worden. Het startpunt staat op dit plaatje als vaste waarde. Echter ben ik dus op zoek naar het ideale startpunt, dus deze zit daar niet vast.
De wijk in een graaf weergegeven. Zoals jullie zien is de flat en de route onder dijkwater verdwenen. Deze flat wordt altijd apart besteld, dus die onderste route heeft ook geen enkele meerwaarde en is dus per definitie inefficiënt.
De bundels die per straat (even en oneven) als standaard gelden.
Voor de postbode gelden Euler cirkels, oftewel, de postbode moet altijd weer uitkomen bij zijn fiets. Deze blijft de hele periode van het post bezorgen op 1 plaats staan (het startpunt).
Ik vroeg me dus af wat het beste startpunt is en hoe ik dit bereken. Ik ben pas sinds gister bekend met topologie en heb op een ander voorbeeld gebruik gemaakt van het algoritme van Fleury. Ik vroeg me echter af of er een formule was om dit probleem op te lossen en wat deze dan zou moeten zijn. Als jullie geen zin hebben om te puzzelen/rekenen, maar wel weten welk algoritme ik het best kan toepassen, laat het me dan ook weten. Dan kan ik me daar ook weer verder in verdiepen.
Ow en mocht het handig zijn, ik heb een applet gevonden waarbij je met verschillende algoritmen dergelijke topologische problemen op kan lossen. Klikkerdeklik.
Mocht het niet duidelijk zijn, of meer info nodig, let me know!
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
Inmiddels zelf een beetje aan het puzzelen geweest. Alleen de punten A, J, N, C, E, F, K, I zijn mogelijk optimaal. Bij elk van deze ben ik routes wezen tekenen, en elke keer kom ik op 23 uit. Nu alleen nog de formule zoeken die dat ook als oplossing kan geven 
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
Ik heb 4 onafhankelijke variabelen en 1 afhankelijke. Als ik gewoon een correlatieschema laat maken met analyze->correlate krijg ik dezelfde uitkomsten als de R in de model summary van de regressieanalyse.
Maar in dezelfde regressieanalyse staat ook een correlatieschema wat andere correlaties laat zien dan het correlatieschema uit analyze->correlate en dus ook anders dan die uit mijn model summary. Wat laat het correlatieschema uit de regressieanalyse dan zien?
Maar in dezelfde regressieanalyse staat ook een correlatieschema wat andere correlaties laat zien dan het correlatieschema uit analyze->correlate en dus ook anders dan die uit mijn model summary. Wat laat het correlatieschema uit de regressieanalyse dan zien?
En weet iemand hoe dit kan:
De bovenste is de Corruptie coefficient zonder de andere variabelen en de onderste is met de andere variabelen erbij. Ook bij de sociale uitgaven en pc per unit komt ik zelfs op een -getal uit!
De bovenste is de Corruptie coefficient zonder de andere variabelen en de onderste is met de andere variabelen erbij. Ook bij de sociale uitgaven en pc per unit komt ik zelfs op een -getal uit!
zie handleidingquote:Op woensdag 30 december 2009 14:27 schreef thijsltc het volgende:
Ik heb 4 onafhankelijke variabelen en 1 afhankelijke. Als ik gewoon een correlatieschema laat maken met analyze->correlate krijg ik dezelfde uitkomsten als de R in de model summary van de regressieanalyse.
Maar in dezelfde regressieanalyse staat ook een correlatieschema wat andere correlaties laat zien dan het correlatieschema uit analyze->correlate en dus ook anders dan die uit mijn model summary. Wat laat het correlatieschema uit de regressieanalyse dan zien?
Dit is heel normaal: voeg je regressoren toe dan verandert de coëfficient van de oorspronkelijke regressoren vaak. Hij kan ook opeens wel significant worden.quote:
En weet iemand hoe dit kan:
[ afbeelding ]
De bovenste is de Corruptie coefficient zonder de andere variabelen en de onderste is met de andere variabelen erbij. Ook bij de sociale uitgaven en pc per unit komt ik zelfs op een -getal uit!
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
beertenderrr: je hebt een leuk probleem bedacht, alleen vrees ik dat er geen efficient algoritme voor bestaat 
.
Het chinese postbode probleem is op zich zelf wel makkelijk, maar er zijn een aantal belangrijke verschillen met jouw versie:
* je beperkt het maximale gewicht dat een postbode kan dragen, waardoor meerdere rondes gelopen moeten worden.
* de chinese postbode bezorgt de post aan beide kanten van een straat.
Deze wiki pagina vermeldt summier wat over het chinese postbode probleem en daar staan ook enkele varianten waarvan bekend is dat ze erg lastig zijn (NP-complete). Deze varianten lijken sterk op jouw probleem, dus vandaar dat ik vermoed dat er geen efficient algoritme is.
Wat is het precieze doel van je werkstuk? Wil je alleen de optimale oplossing voor dit probleem hebben, of wil je een wat algemener verhaal houden?
.Het chinese postbode probleem is op zich zelf wel makkelijk, maar er zijn een aantal belangrijke verschillen met jouw versie:
* je beperkt het maximale gewicht dat een postbode kan dragen, waardoor meerdere rondes gelopen moeten worden.
* de chinese postbode bezorgt de post aan beide kanten van een straat.
Deze wiki pagina vermeldt summier wat over het chinese postbode probleem en daar staan ook enkele varianten waarvan bekend is dat ze erg lastig zijn (NP-complete). Deze varianten lijken sterk op jouw probleem, dus vandaar dat ik vermoed dat er geen efficient algoritme is.
Wat is het precieze doel van je werkstuk? Wil je alleen de optimale oplossing voor dit probleem hebben, of wil je een wat algemener verhaal houden?
thnx voor je antwoord
Ja dat het niet heel eenvoudig zou zijn, had ik al verwacht. Ook die wiki pagina heb ik gezien, maar daar kwam ik niet veel verder mee helaas.
Het doel is overigens om een algemener verhaal te houden, dus een oplossing is niet per sé nodig. Ik heb overigens met beredeneren een optimum gevonden van 23, het is alleen jammer dat ik hier geen formule bij kan bedenken en dit kan controleren en bewijzen. Maar ja, ik denk niet dat zoiets gevraagd wordt van een VWO wiksunde leerling, maar eerder voor een eindscriptie van een wiskunde student.
Ik denk dat ik dus een redelijk antwoord heb op het vraagstuk door middel van redenatie, en dat dit wel als goed geaccepteerd word
Ja dat het niet heel eenvoudig zou zijn, had ik al verwacht. Ook die wiki pagina heb ik gezien, maar daar kwam ik niet veel verder mee helaas.
Het doel is overigens om een algemener verhaal te houden, dus een oplossing is niet per sé nodig. Ik heb overigens met beredeneren een optimum gevonden van 23, het is alleen jammer dat ik hier geen formule bij kan bedenken en dit kan controleren en bewijzen. Maar ja, ik denk niet dat zoiets gevraagd wordt van een VWO wiksunde leerling, maar eerder voor een eindscriptie van een wiskunde student.
Ik denk dat ik dus een redelijk antwoord heb op het vraagstuk door middel van redenatie, en dat dit wel als goed geaccepteerd word
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me
Oke wiskundegeleerden,
Ik moet (Ik weet echt niet hoe je deze in het Neerlands moet neerzetten):
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point.
(som 25, 13.2 , Calculus deel 6): x = e-tcos t, y= e-tsin t, z = e-t ; (1,0,1)
Nu is het niet moeilijk om tot hier te komen:
r(t) = < e-tcos t i, e-tsin t j, e-t k >
r ' (t) = < -e-t(cost+sint) i, -e-t (sint -cost) j, -e-t k >
Wat ik nu niet snap is dat er van (1,0,1) opeens t = 0 omdat die correspondeerd tot (1,0,1).
Wat er daarna gebeurt is natuurlijk weer een eitje.
Ik moet (Ik weet echt niet hoe je deze in het Neerlands moet neerzetten):
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point.
(som 25, 13.2 , Calculus deel 6): x = e-tcos t, y= e-tsin t, z = e-t ; (1,0,1)
Nu is het niet moeilijk om tot hier te komen:
r(t) = < e-tcos t i, e-tsin t j, e-t k >
r ' (t) = < -e-t(cost+sint) i, -e-t (sint -cost) j, -e-t k >
Wat ik nu niet snap is dat er van (1,0,1) opeens t = 0 omdat die correspondeerd tot (1,0,1).
Wat er daarna gebeurt is natuurlijk weer een eitje.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Je moet t vinden zdd r(t)=0. Z beperkt de enige mogelijkheid tot t=0, en die blijkt ook te voldoen voor x en y..
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus eigenlijk dit:quote:Op woensdag 30 december 2009 17:30 schreef GlowMouse het volgende:
Je moet t vinden zdd r(t)=0. Z beperkt de enige mogelijkheid tot t=0, en die blijkt ook te voldoen voor x en y..
r(t) = < e-tcos t i, e-tsin t j, e-t k >
Ik vul voor i 1 in, dat wordt niet 0. , ik vul voor j 0 in, dat wordt wél 0 , ik vul voor k 1 in en dat wordt niet 0.
Dus daarom t = 0 is de enige mogelijkheid???
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Te bewijzen:
k³-1 is alleen priem als k=2.
Bewijs:
Als k oneven is, dan k=2n+1 met n in Z. Dan is k³-1=(2n+1)³=8n³+12n²+6n en dus deelbaar door 2 en is k³-1 dus niet priem. Dus k moet even zijn. We weten dat k>1 want een priemgetal p>1. Voor k=2 is k³-1=7 dus inderdaad priem.
Hoe laat ik nu zien dat voor geen enkele andere even k, k³-1 priem is?
k³-1 is alleen priem als k=2.
Bewijs:
Als k oneven is, dan k=2n+1 met n in Z. Dan is k³-1=(2n+1)³=8n³+12n²+6n en dus deelbaar door 2 en is k³-1 dus niet priem. Dus k moet even zijn. We weten dat k>1 want een priemgetal p>1. Voor k=2 is k³-1=7 dus inderdaad priem.
Hoe laat ik nu zien dat voor geen enkele andere even k, k³-1 priem is?
Mag je i, j en k invullen? Wat stellen ze voor?quote:
[..]
Dus eigenlijk dit:
r(t) = < e-tcos t i, e-tsin t j, e-t k >
Ik vul voor i 1 in, dat wordt niet 0. , ik vul voor j 0 in, dat wordt wél 0 , ik vul voor k 1 in en dat wordt niet 0.
Dus daarom t = 0 is de enige mogelijkheid???
Met k=4 krijg ik 63, geen priemquote:
Te bewijzen:
k³-1 is alleen priem als k=2.
Bewijs:
Als k oneven is, dan k=2n+1 met n in Z. Dan is k³-1=(2n+1)³=8n³+12n²+6n en dus deelbaar door 2 en is k³-1 dus niet priem. Dus k moet even zijn. We weten dat k>1 want een priemgetal p>1. Voor k=2 is k³-1=7 dus inderdaad priem.
Hoe laat ik nu zien dat voor geen enkele andere even k, k³-1 priem is?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh, faal. Maar nu zie ik wel een patroontje.quote:
[..]
Dat klopt, want ik moet dan ook aantonen dat voor k=4,6,8,10,12,... k³-1 niet priem is.
Bij k=4 heb je deelbaarheid door 3
bij k=6 deelbaarheid door 5
bij k=8 deelbaarheid door 7
bij k=10 deelbaarheid door 9
bij k=11 deelbaarheid door 11
daarmee kom je eruit
[ Bericht 6% gewijzigd door GlowMouse op 03-01-2010 20:40:10 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ohja, bedankt
Dus wat je dan eigenlijk moet bewijzen is dat k-1 | k³-1 . Als k=2, dan 1 | k³-1 (niet erg want een priemgetal heeft als deler 1). Maar als k>2 dan is er een getal >1 dat k³-1 deelt, en is het dus niet priem.
k³-1=(k-1)(k+1)k + (k-1) en is dus inderdaad deelbaar door k-1.
QED
Dus wat je dan eigenlijk moet bewijzen is dat k-1 | k³-1 . Als k=2, dan 1 | k³-1 (niet erg want een priemgetal heeft als deler 1). Maar als k>2 dan is er een getal >1 dat k³-1 deelt, en is het dus niet priem.
k³-1=(k-1)(k+1)k + (k-1) en is dus inderdaad deelbaar door k-1.
QED
Maak het niet zo moeilijk. Je hebt:quote:Op zondag 3 januari 2010 20:57 schreef BasementDweller het volgende:
Ohja, bedankt
Dus wat je dan eigenlijk moet bewijzen is dat k-1 | k³-1 . Als k=2, dan 1 | k³-1 (niet erg want een priemgetal heeft als deler 1). Maar als k>2 dan is er een getal >1 dat k³-1 deelt, en is het dus niet priem.
k³-1=(k - 1)(k + 1)k + (k - 1) en is dus inderdaad deelbaar door k-1.
QED
k3 - 1 = (k - 1)(k2 + k + 1)
Voor elk natuurlijk getal k > 1 is k3 - 1 deelbaar door k - 1, en dus kan k3 - 1 niet priem zijn voor enig natuurlijk getal k > 2.
Dat is precies wat ik zeg.quote:Op maandag 4 januari 2010 15:39 schreef Riparius het volgende:
[..]
Maak het niet zo moeilijk. Je hebt:
k3 - 1 = (k - 1)(k2 + k + 1)
Voor elk natuurlijk getal k > 1 is k3 - 1 deelbaar door k - 1, en dus kan k3 - 1 niet priem zijn voor enig natuurlijk getal k > 2.
Hier kom ik niet uit..quote:Bij het overseinen van morsetekens is de kans dat een letter goed ontvangen wordt 0.90. Noem m : aantal goed overgeseinde letters.
a) Hoe groot is de kans dat een woord van 4 letters goed ontvangen wordt? P(m=...)=...
b) Hoe groot is de kans dat een zin van 100 letters meer dan 6 fouten bevat? Noem k : aantal fout overgeseinde letters.
De verdeling bij a) is volgens mij binominaal P(m=4) = m ~ Bin (4 ; 0.90).. maar dan?
Te weinig gegevens: je kent de afhankelijkheden tussen de kansen niet.quote:Op woensdag 6 januari 2010 11:05 schreef Booomer het volgende:
[..]
Hier kom ik niet uit..
De verdeling bij a) is volgens mij binominaal P(m=4) = m ~ Bin (4 ; 0.90).. maar dan?
Meer gegevens worden niet gegeven...quote:Op woensdag 6 januari 2010 11:47 schreef thabit het volgende:
[..]
Te weinig gegevens: je kent de afhankelijkheden tussen de kansen niet.
Dan kun je dus ook geen antwoord geven.quote:
[..]
Meer gegevens worden niet gegeven...
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ik moet de inverse bepalen van y = ln(x-2) + ln(x+3)
ey = x2 +x - 6
x2 +x - 6 - ey =0
x = (-1 ± sqrt(-4*(6- ey)))/2
x = -1/2 - sqrt(6-ey )
Klopt?
ey = x2 +x - 6
x2 +x - 6 - ey =0
x = (-1 ± sqrt(-4*(6- ey)))/2
x = -1/2 - sqrt(6-ey )
Klopt?
Nee, de b^2 uit de abc-formule zie ik niet terug, en er verdwijnt een minteken binnen de wortel. En waarom kies je voor - en niet voor +, voor de wortel?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
x = (-1 ± sqrt(1 -4*(6- ey)))/2quote:Op woensdag 6 januari 2010 13:03 schreef GlowMouse het volgende:
Nee, de b^2 uit de abc-formule zie ik niet terug, en er verdwijnt een minteken binnen de wortel. En waarom kies je voor - en niet voor +, voor de wortel?
x = -1/2 - sqrt(-5+ey)
zoiets?
x = (-1 ± sqrt(1 -4*(6- e^y)))/2
die klopt, die daarna niet. En waarom kies je voor - en niet voor +, voor de wortel?
die klopt, die daarna niet. En waarom kies je voor - en niet voor +, voor de wortel?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
-1/2 + 1/2sqrt(23+4ey)quote:Op woensdag 6 januari 2010 13:24 schreef GlowMouse het volgende:
x = (-1 ± sqrt(1 -4*(6- e^y)))/2
die klopt, die daarna niet. En waarom kies je voor - en niet voor +, voor de wortel?
En waarom voor - en niet +? ja dat is dus fout
Dy = By-1
Df= (2,oneindig)
Dus het moet + zijn omdat hij anders buiten het bereik valt ofzo?
De notatie By-1 ken ik niet, maar het heeft wel te maken met domein en bereik. Kijk je naar y = ln(x-2) + ln(x+3), voor welke x kun je die uitrekenen? En welke waarden kan y dus aannemen?
wiskundig gezien hoort het domein gewoon bij het functievoorschrift gegeven te zijn
wiskundig gezien hoort het domein gewoon bij het functievoorschrift gegeven te zijn
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Alleen daar doen ze niet aan op de middelbare schoolquote:Op woensdag 6 januari 2010 13:50 schreef GlowMouse het volgende:
wiskundig gezien hoort het domein gewoon bij het functievoorschrift gegeven te zijn
By-1 is bereik van de inversequote:Op woensdag 6 januari 2010 13:50 schreef GlowMouse het volgende:
De notatie By-1 ken ik niet, maar het heeft wel te maken met domein en bereik. Kijk je naar y = ln(x-2) + ln(x+3), voor welke x kun je die uitrekenen? En welke waarden kan y dus aannemen?
wiskundig gezien hoort het domein gewoon bij het functievoorschrift gegeven te zijn
En kan je uitrekenen voor x > 2
En y kan volgens mij gewoon elke waarde aannemen?
Nee, dit klopt ook al niet. Het moet zijn:quote:Op woensdag 6 januari 2010 13:24 schreef GlowMouse het volgende:
x = (-1 ± sqrt(1 -4*(6- e^y)))/2
die klopt, die daarna niet.
x = -½ ± ½√(1 + 4(6+ey))
En aangezien x > 2 moet zijn voldoet dus alleen:
x = -½ + ½√(1 + 4(6+ey))
Klopt, dan pakken we de inverse erbij (waarbij gebruikt dat 1 -4*(6- e^y) = 1-24+4e^y)
-1/2 ± sqrt(4ey-23)/2
voor y kun je dus alles invullen, en hoe zorg je nou dat altijd geldt x>2?
-1/2 ± sqrt(4ey-23)/2
voor y kun je dus alles invullen, en hoe zorg je nou dat altijd geldt x>2?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ik zat al te zoeken wat die -23 onder de wortel deed
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Gegeven is f= (sin (pi*x))/x voor x = alles behalve 0
f= alfa voor x=0
a) Geef een alfa waarvoor geldt dat f continu is:
Hiervoor had ik alfa = pi gegeven, aangezien de limiet van (sin (pi*x))/x wanneer x-->0 , pi is.
b) geef aan of f differentieerbaar is in f(0). Zo ja, geef f ' (0). Zo nee, leg uit waarom niet.
Ik had van niet omdat je hij daar een hoek hebt, hetzelfde principe als de afgeleide van f(x)=|x| in 0, die bestaat ook niet. Klopt dit?
f= alfa voor x=0
a) Geef een alfa waarvoor geldt dat f continu is:
Hiervoor had ik alfa = pi gegeven, aangezien de limiet van (sin (pi*x))/x wanneer x-->0 , pi is.
b) geef aan of f differentieerbaar is in f(0). Zo ja, geef f ' (0). Zo nee, leg uit waarom niet.
Ik had van niet omdat je hij daar een hoek hebt, hetzelfde principe als de afgeleide van f(x)=|x| in 0, die bestaat ook niet. Klopt dit?
Ik ben tegen twee vragen aangelopen over meetkundige rijen waar ik niet uitkom. De eerste vraag is:
Sn = a / 1-(1-a)-1 = a / 1-1+a-1 = a1 / a-1 = a2
> Het antwoord moet echter "1 + a" zijn.
-----------------------
De tweede vraag is:
Kan iemand hulp bieden?
Mijn aanpak was:quote:Find the sum of the following geometric serie:
a + a(1+ a)-1 + a(1+ a)-2 + a(1+ a)-3 + a(1+ a)-4 + ..., (a > 0)
Sn = a / 1-(1-a)-1 = a / 1-1+a-1 = a1 / a-1 = a2
> Het antwoord moet echter "1 + a" zijn.
-----------------------
De tweede vraag is:
Eerst probeerde ik de somformule (met t=tijd ongedefenieerd) gelijkstellen aan de huidige reserve, maar dat werkte niet. Ik zie eigenlijk ook niet hoe een oneindige (het einde is immers onbekend) reeks een factor van |k|>1 (1,02) kan hebben.quote:The world's total consumption of natural gas was 1824 million tons oil equivalent (mtoe) in 1994. The reserves at the end of that year were estimated to be 128 300 mtoe. If consumption had increased by 2% in each of the coming years, and no new sources were ever discovered, how much longer would these reserves have lasted?
Kan iemand hulp bieden?
Oh really?
(1-a)-1 is natuurlijk niet hetzelfde als 1-a-1 en buiten dat haal je een + en een - doorelkaar.quote:Op woensdag 6 januari 2010 18:54 schreef Matthijs- het volgende:
Ik ben tegen twee vragen aangelopen over meetkundige rijen waar ik niet uitkom. De eerste vraag is:
[..]
Mijn aanpak was:
Sn = a / 1-(1-a)-1 = a / 1-1+a-1 = a1 / a-1 = a2
> Het antwoord moet echter "1 + a" zijn.
Als het einde onbekend is, dan is de reeks natuurlijk niet per se oneindig. Voer de lengte van de reeks in als variabele.quote:Op woensdag 6 januari 2010 18:54 schreef Matthijs- het volgende:
De tweede vraag is:
[..]
Eerst probeerde ik de somformule (met t=tijd ongedefenieerd) gelijkstellen aan de huidige reserve, maar dat werkte niet. Ik zie eigenlijk ook niet hoe een oneindige (het einde is immers onbekend) reeks een factor van |k|>1 (1,02) kan hebben.
Kan iemand hulp bieden?
