Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Wiskundig inhoudelijk:
OP
ik moet voor mijn examen limieten kunnen vast stellen en volgens mijn leraar moest ik dan naar de standaard vormen toe werken.
nou is mijn vraag:
(4 + a/x )^x met x --> oneindig, wat is het limiet en hoe kom ik daar op?
de standaard vorm is
(1 + a/x)^x met limiet e^a
alvast bedankt!
(had de andere topic vol gemaakt)
quote:Op maandag 11 mei 2009 14:54 schreef GlowMouse het volgende:
Daar valt weinig aan om te schrijven, je ziet zo dat die naar oneindig gaat.
maar hoezo komen ze dan bij de standaard limiet op e^a?
het lijkt mij persoonlijk logisch dat het limiet dan 1^x --> 1 zou zijn.
nog een vraag los van limieten.
zou je de 4 bij (4 + a/x)^x uberhaupt buiten haakjes kunnen halen? me leraar was daar namelijk nogal vaag over en wist het zelf niet.
quote:Nee. (1 + 1/n) blijft namelijk groter dan 1 hoewel het wel naar 1 toegaat, maar je krijgt in (1 + 1/n)n wel steeds meer factoren als n groter wordt. Verder is (1 + 1/n)n monotoon stijgend, zodat de limiet nooit 1 kan zijn. Kijk maar eens even hier, hopelijk begrijp je het dan beter.Op maandag 11 mei 2009 15:07 schreef Krediax het volgende:
Kan je nog wat meer uitleggen daarbij? (ik vind het ook logisch lijken dat het naar oneindig gaat a/x --> verwaardeloosbaar)
maar hoezo komen ze dan bij de standaard limiet op e^a?
het lijkt mij persoonlijk logisch dat het limiet dan 1^x --> 1 zou zijn.
quote:Bedenkelijke leraar heb jij dan. Je kunt schrijven:nog een vraag los van limieten.
zou je de 4 bij (4 + a/x)^x uberhaupt buiten haakjes kunnen halen? me leraar was daar namelijk nogal vaag over en wist het zelf niet.
(4 + a/x) = 4(1 + ¼a/x),
zodat we krijgen:
(4 + a/x)x = 4x(1 + ¼a/x)x
Nu convergeert (1 + ¼a/x)x uiteraard naar e¼a voor x → ∞, maar 4x divergeert voor x → ∞ zodat het product ook divergeert.
Me leraar is nogal verstrooid van tijd tot tijd... eigenlijk altijd.
op zicht niet erg want ik snap meestal wel wat hij bedoeld maar hier kwam ik niet uit en hij was helemaal van de slag door de vraag (had hij niet verwacht).
maja nogmaals tnx, weet ik ook weer hoe je buiten haakjes kan schrijven als het tot de macht x is
quote:Gauw terugsturen die leraar als je hem op zicht hebt. Is echt geen knip voor de neus waard als hij bij zoiets simpels al met zijn mond vol tanden staat.Op maandag 11 mei 2009 15:59 schreef Krediax het volgende:
Tnx!
M'n leraar is nogal verstrooid van tijd tot tijd... eigenlijk altijd.
op zicht niet erg want ik snap meestal wel wat hij bedoelt maar hier kwam ik niet uit en hij was helemaal van de slag door de vraag (had hij niet verwacht).
maja nogmaals tnx, weet ik ook weer hoe je buiten haakjes kan schrijven als het tot de macht x is
P.S. Je leraar Nederlands stelt ook niet veel voor zo te zien ...
quote:Haha, tvp.Op maandag 11 mei 2009 16:02 schreef Riparius het volgende:
[..]
P.S. Je leraar Nederlands stelt ook niet veel voor zo te zien ...
quote:
1-2+3-4...-1000 = ?
quote:1+3+...+999 - (2+4+...+1000) = 500*500 - 500*501 = 500(500-501) = -500.
f('x) = 3(3+x2y)2 * 2yx
f('y) = 3(3+x2y)2 * x^2
Wat is in dit geval de 2nd order ? Dus F'(xx) F'(yy) en f'(xy)
=>
h = 1000 / x(x+4)
Kan iemand mij deze stap uitleggen.
quote:Je deelt beide leden van je vergelijking door het product x(x+4) en dan krijg je het resultaat dat je geeft. Ofwel: als abc = p en ab is ongelijk aan 0, dan is c = p/ab.Op vrijdag 15 mei 2009 15:46 schreef TBY het volgende:
I = x * (x+4) * h = 1000
=>
h = 1000 / x(x+4)
Kan iemand mij deze stap uitleggen.
quote:Wat is nu precies je probleem? Je kunt de uitdrukkingen die je hebt gevonden toch gewoon opnieuw differentiëren naar x of naar y? En doe eens wat aan je notatie, dit lijkt nergens op.Op vrijdag 15 mei 2009 14:26 schreef sitting_elfling het volgende:
Bij f(x,y) (3+x2y)3
f('x) = 3(3+x2y)2 * 2yx
f('y) = 3(3+x2y)2 * x^2
Wat is in dit geval de 2nd order ? Dus F'(xx) F'(yy) en f'(xy)
Stom dat ik dat niet zagHoe differentieer je de volgende functies?
l(x) = 4logx
k(x) = 8 * 3^x
quote:Voor log(x) moet je gewoon de standaard-afgeleide zoeken. Die is gewoon 1/x (tenzij je met log(x) de 10-log bedoelt). En die eerste is ook een standaardvorm, namelijk: nx, en dat is gelijk aan log(n)*nx.Op vrijdag 15 mei 2009 17:45 schreef TBY het volgende:
Nog een vraag:
Hoe differentieer je de volgende functies?
l(x) = 4logx
k(x) = 8 * 3^x
Al die vormen moeten wel ergens in je boek staan.
quote:zo ver ik uit jouw post kan herleiden:Op vrijdag 15 mei 2009 15:46 schreef TBY het volgende:
I = x * (x+4) * h = 1000
=>
h = 1000 / x(x+4)
Kan iemand mij deze stap uitleggen.
x*(x+4) * h=1000.
Nu wil je h vrijschrijven, dus beide zijden van de vergelijking delen door x*(x+4):
levert
h= 1000 / (x*(x+4)).
Je kunt dit overigens nog mooier schrijven met behulp van "delen door een breuk is vermenigvuldigen met het omgekeerde".
quote:alog(x) = log(x)/log(a) natuurlijk, dus dan krijg je gewoon een constante 1/log(a) ervoor.
Uit mijn hoofd is de afgeleide van f(x) = alog (x) gelijk aan 1/(x*ln(a)).
quote:Laat maar, biertje te veel op. GlupOp vrijdag 15 mei 2009 20:41 schreef Iblis het volgende:
[..]
alog(x) = log(x)/log(a) natuurlijk, dus dan krijg je gewoon een constante 1/log(a) ervoor.
[ Bericht 5% gewijzigd door Borizzz op 15-05-2009 22:20:14 ]
quote:
twee vaten staan boven elkaar. Op t=0 bevat het bovenste vat 10 l water waarin 2 kg zout is opgelost en het onderste vat bevat 5 l zuiver water. In het bovenste vt stroomt zuiver water met een debiet van 2 l/min en de vloeistof uit het bovenste vat stroomt in het onderse vat m, eveneens met een debiet van 2 l/min. De vloeistof uit het onderste vat stroomt weg met een debiet van 1 l/min.
Na hoeveel tijd bevatten beide vaten evenveel zout en hoeveel bedraagt deze hoeveelheid?
We zitten in het hoofdstuk over differentiaalvergelijkingen.
paint:
kan iemand me op weg helpen?
quote:Vertel eens wat je zelf al geprobeerd hebt. Ik kom uit op twee differentiaalvergelijkingen (één voor elk vat) en deze differentiaalvergelijkingen zijn ook gewoon op te lossen, zodat de hoeveelheid zout (in kg) in elk vat is uit te drukken als functie van t (in minuten). Maar gelijkstelling levert dan een vergelijking op die ik alleen numeriek op kan lossen. Ik kom uit op t = 4,28838336973... minuten, en de hoeveelheid zout in elk van beide vaten bedraagt dan 0,848... kg.Op zaterdag 16 mei 2009 15:19 schreef rontvierkand het volgende:
de vraag:
twee vaten staan boven elkaar. Op t=0 bevat het bovenste vat 10 l water waarin 2 kg zout is opgelost en het onderste vat bevat 5 l zuiver water. In het bovenste vt stroomt zuiver water met een debiet van 2 l/min en de vloeistof uit het bovenste vat stroomt in het onderse vat m, eveneens met een debiet van 2 l/min. De vloeistof uit het onderste vat stroomt weg met een debiet van 1 l/min.
Na hoeveel tijd bevatten beide vaten evenveel zout en hoeveel bedraagt deze hoeveelheid?
We zitten in het hoofdstuk over differentiaalvergelijkingen.
paint:[ afbeelding ]
kan iemand me op weg helpen?
Ik moet b oplossen uit een mechanica vraagstuk.
8*(10^6)= 2400*b / 0,6667*b^4
Waarbij de term 0,6667*b^4 onder de deelstreep staat!
Met b in m [meter]
De oplossing voor b moet zijn b = 0,0766meter
Graag een antwoord in stappen zodat ik zie wat er gebeurt,
ik snap dat ik dit met de solver zo kan oplossen,
maar ik wil graag weten hoe het ook alweer zat.
Met vriendelijke groet,
en alvast Bedankt
H
[ Bericht 0% gewijzigd door Hildir op 16-05-2009 21:43:30 ]
quote:Vermenigvuldig beide leden van je vergelijking met de noemer van de breuk in het rechterlid, oftewel 0,6667*b^4, zodat je de breuk in het rechterlid kwijt raakt. Herleid het rechterlid van de vergelijking dan op 0 en haal vervolgens in het linkerlid b buiten haakjes. Nu zou het oplossen verder geen probleem mogen geven. Houd er wel rekening mee dat b = 0 geen valide oplossing is van je oorspronkelijke vergelijking.Op zaterdag 16 mei 2009 21:37 schreef Hildir het volgende:
Hallo ik heb een vraagje,
Ik moet b oplossen uit een mechanica vraagstuk.
8*(10^6)= 2400N*b / 0,6667*b^4
Waarbij de term 0,6667*b^4 onder de deelstreep staat!
Met b in m [meter]
De oplossing voor b moet zijn b = 0,0766meter
Graag een antwoord in stappen zodat ik zie wat er gebeurt,
ik snap dat ik dit met de solver zo kan oplossen,
maar ik wil graag weten hoe het ook alweer zat.
Met vriendelijke groet,
en alvast Bedankt
H
ik kom tot zover:
(8*10^6)* 0,6667*b^4 = 2400*b
uitwerken
53336000*b^4 = 2400*b
Nu kom ik niet verder, kun je het voordoen met cijfers in stappen?
mvg, H
quote:Je kunt beter eerst nog even beide leden vermenigvuldigen met 3/2, want ik heb zo'n idee dat die 0,6667 een afronding is van 2/3. Dus:Op zaterdag 16 mei 2009 21:47 schreef Hildir het volgende:
Ik volg je niet helemaal,
ik kom tot zover:
(8*10^6)* 0,6667*b^4 = 2400*b
uitwerken
53336000*b^4 = 2400*b
Nu kom ik niet verder, kun je het voordoen met cijfers in stappen?
mvg, H
(8*10^6)* 0,6667*b^4 = 2400*b
Beide leden vermenigvuldigen met 3/2:
(8*10^6)*b^4 = 3600*b
Beide leden delen door 1000:
(8*10^3)*b^4 = 3,6*b
Rechterlid herleiden op 0:
(8*10^3)*b^4 - 3,6*b = 0
b buiten haakjes halen:
b*((8*10^3)*b^3 - 3,6) = 0
Kun je nu verder?
[ Bericht 0% gewijzigd door Riparius op 16-05-2009 22:09:04 ]
het is een tijd geleden dat ik hier actief mee bezig ben geweest,
bedankt voor je snelle reacties!
mvg, Hildir
quote:Ok. We waren gekomen tot:Op zaterdag 16 mei 2009 21:57 schreef Hildir het volgende:
Nou ik wil niet vervelend zijn, maar zou je het helemaal kunnen uitwerken,
het is een tijd geleden dat ik hier actief mee bezig ben geweest,
bedankt voor je snelle reacties!
mvg, Hildir
b*((8*10^3)*b^3 - 3,6) = 0
Nu kan een product van twee factoren alleen maar 0 zijn als één van beide factoren 0 is, dus:
b = 0 of (8*10^3)*b^3 - 3,6 = 0.
Zoals gezegd is b = 0 geen geldige oplossing van je oorspronkelijke vergelijking (delen door 0 heeft geen betekenis), dus gaan we alleen verder met:
(8*10^3)*b^3 - 3,6 = 0
Dit geeft:
(8*10^3)*b^3 = 3,6
Beide leden delen door 8*10^3 geeft:
b^3 = 3,6/(8*10^3)
Hiervoor kunnen we schrijven:
b^3 = (3,6/8)*10-3
Of:
b3 = 0,45*10-3
Nu nog de derdemachtswortel nemen (daarvoor heb je wel een calculator nodig) en je krijgt:
b ≈ 0,766*10-1.
erg gewaardeerd, Respect!
Met vriendelijke groet,
Melle de Boer
quote:x1=2*e^(-0.2*t)Op zaterdag 16 mei 2009 20:41 schreef Riparius het volgende:
[..]
Vertel eens wat je zelf al geprobeerd hebt. Ik kom uit op twee differentiaalvergelijkingen (één voor elk vat) en deze differentiaalvergelijkingen zijn ook gewoon op te lossen, zodat de hoeveelheid zout (in kg) in elk vat is uit te drukken als functie van t (in minuten). Maar gelijkstelling levert dan een vergelijking op die ik alleen numeriek op kan lossen. Ik kom uit op t = 4,28838336973... minuten, en de hoeveelheid zout in elk van beide vaten bedraagt dan 0,848... kg.
x2=20*ln(t)+C
maar ik denk dat mijn vergelijkingen fout zijn want ik kan de voorwaarde van t=0 niet invullen in de tweede vergelijking (ln(0)bestaat niet).
quote:Ik had zelf de hoeveelheid zout in het eerste vat x genoemd en de hoeveelheid zout in het tweede vat y (om niet met indices te hoeven werken). Voor de hoeveelheid zout x (in kg) in het bovenste vat als functie van de tijd t (in minuten) heb ik dan de volgende differentiaalvergelijking:Op zondag 17 mei 2009 11:10 schreef rontvierkand het volgende:
[..]
x1=2*e^(-0.2*t)
x2=20*ln(t)+C
maar ik denk dat mijn vergelijkingen fout zijn want ik kan de voorwaarde van t=0 niet invullen in de tweede vergelijking (ln(0)bestaat niet).
dx = -(1/5)∙x∙dt
Oplossing van deze differentiaalvergelijking onder de randvoorwaarde x(0) = 2 levert dan inderdaad:
x = 2∙e-t/5
Je eerste vergelijking is dus in orde, maar je tweede vergelijking niet. Maar laat nu eerst eens zien welke differentiaalvergelijking je voor het onderste vat hebt opgesteld en hoe je die dacht op te lossen.
quote:ik had dy=(2/5)∙e-t/5dt+y*dtOp zondag 17 mei 2009 13:31 schreef Riparius het volgende:
[..]
Ik had zelf de hoeveelheid zout in het eerste vat x genoemd en de hoeveelheid zout in het tweede vat y (om niet met indices te hoeven werken). Voor de hoeveelheid zout x (in kg) in het bovenste vat als functie van de tijd t (in minuten) heb ik dan de volgende differentiaalvergelijking:
dx = -(1/5)∙x∙dt
Oplossing van deze differentiaalvergelijking onder de randvoorwaarde x(0) = 2 levert dan inderdaad:
x = 2∙e-t/5
Je eerste vergelijking is dus in orde, maar je tweede vergelijking niet. Maar laat nu eerst eens zien welke differentiaalvergelijking je voor het onderste vat hebt opgesteld en hoe je die dacht op te lossen.
dan wordt y(t) = -e(-(1/5)*t)/3-e^(t)
quote:Nee. De differentiaalvergelijking die je hebt opgesteld klopt niet en de oplossing die je daarvan geeft ook niet.Op zondag 17 mei 2009 15:12 schreef rontvierkand het volgende:
[..]
ik had dy=(2/5)∙e-t/5dt+y*dt
dan wordt y(t) = -e(-(1/5)*t)/3-e^(t)
In het onderste vat stroomt zout water uit het bovenste vat maar er stroomt ook zilt water weg uit het onderste vat. Verder is het zo dat er per minuut 2 liter zout water in het onderste vat stroomt maar dat er per minuut maar 1 liter water wegloopt uit het onderste vat. Dit betekent dat de hoeveelheid water in het onderste vat met 1 liter per minuut toeneemt. Op tijdstip t=0 zit er 5 liter water in het onderste vat en op tijdstip t (in minuten) dus (t + 5) liter.
We bekijken nu eerst hoeveel zout er uit het bovenste vat in het onderste vat komt gedurende een heel klein tijdsinterval [t, t+Δt]. Die hoeveelheid is gelijk aan de hoeveelheid zout die uit het bovenste vat verdwijnt gedurende datzelfde tijdsinterval, en deze hoeveelheid hadden we al berekend, die is bij benadering
(2Δt/10)∙x,
waarbij x de hoeveelheid zout in het bovenste vat op tijdstip t voorstelt.
Maar nu verdwijnt er ook zout uit het onderste vat. De hoeveelheid water in het onderste vat op tijdstip t is (t+5) liter en het water stroomt er uit met een debiet van 1 liter per seconde. Over een heel klein tijdsinterval Δt verdwijnt dus bij benadering een deel 1∙Δt/(t+5) van de op dat moment aanwezige hoeveelheid zout y uit het onderste vat, ofwel een hoeveelheid
(Δt/(t+5))∙y
De verandering Δy van de hoeveelheid zout in het onderste vat gedurende het kleine tijdsinterval Δt is gelijk aan de toename ten gevolge van de instroom verminderd met de afname als gevolg van de uitstroom, dus:
Δy ≈ (2Δt/10)∙x - (Δt/(t+5))∙y
De benadering is een gevolg van het feit dat we hebben aangenomen dat de hoeveelheden zout in de beide vaten gedurende een heel klein tijdsinterval niet noemenswaardig veranderen. Deze benadering wordt beter naarmate we het tijdsinterval kleiner maken, zodat we bij de overgang naar een infinitesimaal tijdsinterval dt krijgen:
dy = (1/5)∙x∙dt - (1/(t+5))∙y∙dt
Maar nu hadden we al gevonden dat geldt:
x = 2∙e-t/5,
Zodat we krijgen:
dy = (2/5)∙e-t/5∙dt - (1/(t+5))∙y∙dt
Dit is een lineaire differentiaalvergelijking van de eerste orde met niet-scheidbare variabelen, die we in de volgende standaardvorm kunnen brengen:
dy/dt + (1/(t+5))∙y = (2/5)∙e-t/5
Nu mag je het zelf weer even proberen.
[ Bericht 0% gewijzigd door Riparius op 17-05-2009 16:36:33 ]
quote:Ik had die 5 liter in het onderste vat er niet bij geteld, ik kan geloven dat het niet werkte.Op zondag 17 mei 2009 16:01 schreef Riparius het volgende:
[..]
Nee. De differentiaalvergelijking die je hebt opgesteld klopt niet en de oplossing die je daarvan geeft ook niet.
In het onderste vat stroomt zout water uit het bovenste vat maar er stroomt ook zilt water weg uit het onderste vat. Verder is het zo dat er per minuut 2 liter zout water in het onderste vat stroomt maar dat er per minuut maar 1 liter water wegloopt uit het onderste vat. Dit betekent dat de hoeveelheid water in het onderste vat met 1 liter per minuut toeneemt. Op tijdstip t=0 zit er 5 liter water in het onderste vat en op tijdstip t (in minuten) dus (t + 5) liter.
We bekijken nu eerst hoeveel zout er uit het bovenste vat in het onderste vat komt gedurende een heel klein tijdsinterval [t, t+Δt]. Die hoeveelheid is gelijk aan de hoeveelheid zout die uit het bovenste vat verdwijnt gedurende datzelfde tijdsinterval, en deze hoeveelheid hadden we al berekend, die is bij benadering
(2Δt/10)∙x,
waarbij x de hoeveelheid zout in het bovenste vat op tijdstip t voorstelt.
Maar nu verdwijnt er ook zout uit het onderste vat. De hoeveelheid water in het onderste vat op tijdstip t is (t+5) liter en het water stroomt er uit met een debit van 1 liter per seconde. Over een heel klein tijdsinterval Δt verdwijnt dus bij benadering een deel 1∙Δt/(t+5) van de op dat moment aanwezige hoeveelheid zout y uit het onderste vat, ofwel een hoeveelheid
(Δt/(t+5))∙y
De verandering Δy van de hoeveelheid zout in het onderste vat gedurende het kleine tijdsinterval Δt is gelijk aan de toename ten gevolge van de instroom verminderd met de afname als gevolg van de uitstroom, dus:
Δy ≈ (2Δt/10)∙x - (Δt/(t+5))∙y
De benadering is een gevolg van het feit dat we hebben aangenomen dat de hoeveelheden zout in de beide vaten gedurende een heel klein tijdsinterval niet noemenswaardig veranderen. Deze benadering wordt beter naarmate we het tijdsinterval kleiner maken, zodat we bij de overgang naar een infinitesimaal tijdsinterval dt krijgen:
dy = (1/5)∙x∙dt - (1/(t+5))∙y∙dt
Maar nu hadden we al gevonden dat geldt:
x = 2∙e-t/5,
Zodat we krijgen:
dy = (2/5)∙e-t/5∙dt - (1/(t+5))∙y∙dt
Dit is een lineaire differentiaalvergelijking van de eerste orde met niet-scheidbare variabelen, die we in de volgende standaardvorm kunnen brengen:
dy/dt + (1/(t+5))∙y = (2/5)∙e-t/5
Nu mag je het zelf weer even proberen.
bedankt
nu komt het wel uit dus het is in orde
quote:OK. Maar begrijp je nu ook hoe je de gevonden differentiaalvergelijking voor het onderste vat op moet lossen? En kom je dan uiteindelijk ook op dezelfde uitkomst voor het tijdstip waarop de hoeveelheden zout in beide vaten even groot zijn?Op zondag 17 mei 2009 16:39 schreef rontvierkand het volgende:
[..]
Ik had die 5 liter in het onderste vat er niet bij geteld, ik kan geloven dat het niet werkte.
bedankt
nu komt het wel uit dus het is in orde
quote:niets moeilijk aan, gewoon intikken in maple en klaar.Op zondag 17 mei 2009 16:43 schreef Riparius het volgende:
[..]
OK. Maar begrijp je nu ook hoe je de gevonden differentiaalvergelijking voor het onderste vat op moet lossen? En kom je dan uiteindelijk ook op dezelfde uitkomst voor het tijdstip waarop de hoeveelheden zout in beide vaten even groot zijn?
quote:Ja, maar dan weet je dus in feite helemaal niet hoe zo'n differentiaalvergelijking wordt opgelost. Iets intypen in een calculator of een programma is iets heel anders dan begrijpen hoe het zit.Op zondag 17 mei 2009 20:26 schreef rontvierkand het volgende:
[..]
Niets moeilijk aan, gewoon intikken in maple en klaar.
quote:dat heb ik zonet gedaan, eerst de gereduceerde oplossing zoeken, dan via variatie van de constante de particuliere oplossing zoeken, dan deze twee optellen tot een walgelijk lange vergelijking.Op zondag 17 mei 2009 20:44 schreef Riparius het volgende:
[..]
Ja, maar dan weet je dus in feite helemaal niet hoe zo'n differentiaalvergelijking wordt opgelost. Iets intypen in een calculator of een programma is iets heel anders dan begrijpen hoe het zit.
Dan gelijkstellen aan de gevonden x-waarde om zo tot een t-waarde te komen van iets rond 4,29.
Het oplossen van DV's was niet het probleem, vandaar dat ik vroeg om me op weg te helpen.
quote:Vind ik erg meevallen hoor. Niks 'walgelijk lang'. Ik kom tot:Op zondag 17 mei 2009 22:05 schreef rontvierkand het volgende:
[..]
dat heb ik zonet gedaan, eerst de gereduceerde oplossing zoeken, dan via variatie van de constante de particuliere oplossing zoeken, dan deze twee optellen tot een walgelijk lange vergelijking.
y = (-2∙t∙e-t/5 - 20∙e-t/5 + 20)/(t+5)
En gelijkstellen van x en y levert dan na herleiding de volgende vergelijking:
2∙t∙e-t/5 + 15∙e-t/5 - 10 = 0
Bij een onderzoek met 29 personen, waarvan 17 vrouw en 12 man.
8 vd 17 vrouwen antwoord positief (47%)
4 vd 12 mannnen antwoord positief (33,33%)
Heeft geslacht effect op een positief antwoord?
Chi-kwadraat toets = .546
p= .46
De vraag:
Hoe kom je op die .546?
en op de p=.46
Mijn dank is groot indien iemand mij hiermee kan helpen!
Tnx! Ik kan weer ff verder 
de gewone formule is :
y = 0,0443 ln (x) - 0,0105
help?
ln(x) = (y+0.0105) / 0.0443
Dus x = e^( (y+0.0105) / 0.0443 ).
[ Bericht 2% gewijzigd door GlowMouse op 19-05-2009 14:09:27 ]
quote:y = 0,0443 ln (x) - 0,0105Op dinsdag 19 mei 2009 13:54 schreef Lianne__ het volgende:
hoe schrijf je formules met een natuurlijk logaritme om? (dus met X vooraan ipv Y )
de gewone formule is :
y = 0,0443 ln (x) - 0,0105
help?
y + 0,0105 = 0,0443 ln (x)
ln(x) = (y + 0,0105)/0,0443
x = e(y + 0,0105)/0,0443
dank u zeer!
quote:misschien nog een domme vraag hoor...
maar hoe krijg ik e in excel?
er zijn nogal wat gegevens.. en om dat allemaal met de rekenmachine te doen.....
quote:Ik weet niets van Excel, maar ik zie op het net wel dat je EXP(x) moet kunnen gebruiken voor ex. Helpt dat?Op dinsdag 19 mei 2009 14:26 schreef Lianne__ het volgende:
[..]
misschien nog een domme vraag hoor...
maar hoe krijg ik e in excel?
er zijn nogal wat gegevens.. en om dat allemaal met de rekenmachine te doen.....
dankjulliewel...
alleen komen docenten er nu ál mee dat we de uitwerking toch anders moeten doen dan voorgeschreven..
morgen voor 12 uur moet ik het inleveren.. nu ben ik ook niet op tijd. maar docenten moeten het goede voorbeeld geven geloof ik......
en dat op het HBO
quote:Vertel eerst eens per opgave wat je zelf hebt geprobeerd en waarom dat niet lukte. Zomaar een scan neerkwakken uit je opgavenboekje en dan hopen dat een ander je huiswerk gaat doen geeft niet direct de indruk dat je er ook iets van op wil steken.Op dinsdag 19 mei 2009 18:43 schreef Gitaartovenaar het volgende:
kan iemand deze sommen aub voor me oplossen?
[ afbeelding ]
1a 4^x = 128
x = 4 log 128
b
c
d
2a
100% rente is een verdubbeling, dus bij de eerste aanbieding is het bedrag na 10 jaar verdubbeld, de verdubbelingstijd is dus 10 jaar
1000*1,1^t
1000*1,1^7=1948,71
1000*1,1^8=2143,59 dus de verdubbelingstijd is 8 jaar bij de tweede aanbieding
Voornamelijk 2b kan ik niet uitkomen, kan iemand me dan in ieder geval daar mee helpen?
[ Bericht 1% gewijzigd door GlowMouse op 19-05-2009 19:24:12 ]
quote:Dit is niet echt de bedoeling, omdat het antwoord eenvoudiger is te schrijven. Je hebt:Op dinsdag 19 mei 2009 19:10 schreef Gitaartovenaar het volgende:
Ik heb dit:
1a 4^x = 128
x = 4 log 128
4x = 128
4x = 27
22x = 27
2x = 7
x = 3½
quote:Kom op, eerst per onderdeel laten zien wat je hebt gedaan!b
c
d
quote:Ja.2a
100% rente is een verdubbeling, dus bij de eerste aanbieding is het bedrag na 10 jaar verdubbeld, de verdubbelingstijd is dus 10 jaar
quote:Dit is denk ik niet helemaal de bedoeling. Het is wel zo dat de rente eenmaal per jaar wordt uitgekeerd, maar je moet een exacter antwoord geven. Dit antwoord heb je verkregen door trial and error, en dat is niet de bedoeling.
1000*1,1^t
1000*1,1^7=1948,71
1000*1,1^8=2143,59 dus de verdubbelingstijd is 8 jaar bij de tweede aanbieding
quote:Nee, nu eerst laten zien wat je met 1b t/m 1d hebt gedaan.Voornamelijk 2b kan ik niet uitkomen, kan iemand me dan in ieder geval daar mee helpen?
quote:Dat snap ik wel, maar niet hoe je op die manier aan het begingetal komt.Op dinsdag 19 mei 2009 19:12 schreef GlowMouse het volgende:
Na 2 jaar staat er 1000 euro op de bank. Dat is het beginbedrag maal (10/12)t met t het aantal maanden dat er rente is ontvangen. Lukt het zo?
quote:Stel de vergelijking eerst maar op,
[..]
Dat snap ik wel, maar niet hoe je op die manier aan het begingetal komt.
quote:ik zou persoonlijk nooit m'n geld op die bank zetten Glowmouse ...Op dinsdag 19 mei 2009 19:12 schreef GlowMouse het volgende:
Na 2 jaar staat er 1000 euro op de bank. Dat is het beginbedrag maal (10/12)t met t het aantal maanden dat er rente is ontvangen. Lukt het zo?
quote:
[..]
ik zou persoonlijk nooit m'n geld op die bank zetten Glowmouse ...
ik was al blij dat ik die 10/12 kon lezen.quote:1b is een vergelijking waaruit je t moet oplossen. Het eindresultaat moet dus iets zijn als:Op dinsdag 19 mei 2009 19:30 schreef Gitaartovenaar het volgende:
Wat wordt bedoeld met: Druk t uit in N ?
t = ...
Maar aangezien je N niet kent zal dus N blijven staan in je antwoord.
Een random sample is representatief, al het andere niet meer.quote:Je neemt het in feite aan. En als je het aanneemt, dan mag je veel wiskunde toepassen. De basis waarop je dat rechtvaardigt is echter het zwakke punt natuurlijk. Als je naar 400 mensen een enquête stuurt over vrijetijdsbesteding, die flink wat tijd kost om in te vullen, en dat blijkt dat alleen de werklozen die terugsturen, dan is het waarschijnlijk niet representatief.
Hoe bereken je precies de representativiteit van een enquete? Ik heb een vragenlijst verstuurd naar ~400 mensen (dat is de gehele doelgroep), waarvan 89 mensen de enquete hebben ingevuld. In hoeverre kun je dit dan precies representatief noemen? Er zijn verschillende berekeningen te vinden, en ik kom er niet echt uit.
Je moet ook oppassen dat je niet de resultaten zelf gaat gebruiken om te argumenteren of de enquête representatief was. Je kunt wel zien aan heel scheve zaken, zeg dat je weet dat de verdeling man-vrouw 50/50 is en je krijgt de enquêtes in de verhouding 80/20 terug, dat er iets mogelijk niet klopt, maar omgekeerd kun je niet concluderen dat als je 50/50 terugkrijgt dat het dan wél klopt.
Ik heb dus eigenlijk een berekening (of iets in die trant) nodig zodat ik in mijn onderzoek kan aantonen in hoeverre de enquete een betrouwbaar beeld geeft. Ik ben verder niet echt thuis in statistiek e.d, dus ik heb geen idee hoe dit normaliter precies in zijn werk gaat.
De lijn l snijdt de x-as in P(a,0) en de y-as in Q(0,b).
a: geef een vergelijking van l.
b: toon aan dat x/a + y/b = 1 een vergelijking is van l
c: bereken de afstand van het punt C(1,5) tot de lijn door de punten A(0,-3) en B(6,0)
quote:Je berekent eerst de richtingscoëfficiënt van een lijn door de punten P en Q. Die richtingscoëfficiënt is:Op woensdag 20 mei 2009 21:24 schreef Burakius het volgende:
Vraag;
De lijn l snijdt de x-as in P(a,0) en de y-as in Q(0,b).
a: geef een vergelijking van l.
m = Δy/Δx = (b-0)/(0-a) = -b/a.
De vergelijking van een lijn door een punt (x0;y0) met richtingscoëfficiënt m is:
y - y0 = m(x - x0)
Invullen van x0 = a, y0 = 0 en m = -b/a geeft dan:
y = -b/a(x - a)
quote:Controleer dat de coördinaten van punt A en punt B voldoen aan de vergelijking, óf werk de vergelijking die we bij a) hebben gevonden om naar deze vorm.b: toon aan dat x/a + y/b = 1 een vergelijking is van l
quote:Stel via de hierboven gegeven manier eerst een vergelijking op van de lijn door de punten A en B. Stel dan een vergelijking op van de lijn door punt C die loodrecht staat op de lijn door A en B. Bereken het snijpunt D van deze twee lijnen. De gevraagde afstand is dan de lengte van het lijnstuk CD.c: bereken de afstand van het punt C(1,5) tot de lijn door de punten A(0,-3) en B(6,0)
Hint: het product van de richtingscoëfficiënten van twee lijnen die loodrecht op elkaar staan en niet evenwijdig lopen aan de coördinaatassen is -1.
http://www.examenblad.nl/(...)4x2yh/f=/bestand.pdf
loop vast bij vraag 6.Ik snap niet waarom ze bij de uitwerkingen ( http://www.examenblad.nl/(...)3nq00/f=/bestand.pdf ) die 5/10 x 5/9 nog x 2 doen?
Heeft iets met NCR te maken vast en zeker, maar ik snap echt niet wanneer je NCR wel moet gebruiken, en wanneer niet?
f(x)=2*x als x kleiner dan 0.5 en 2-2*x als x groter of gelijk aan 0.5.
Mijn vragen zijn als volgt; zijn er periode 2 oplossingen? Zo ja zijn ze stabiel? Geef argumenten waarom er geen stabiele oplossingen zijn met periode hoger dan 2. En is deze map chaotisch?
Wat ik tot nu toe weet is het volgende een periodiek punt is een punt waarvoor geldt: f^p(x)=x, in dit geval zijn we op zoek naar punten waarvoor geldt f^2(x)=f(f(x)=x. Maar ik weet geen criterium te vinden om de stabilteit er van te bepalen. En ik weet ook niet wanneer een map chaotisch is. Alle hulp is welkom.
quote:Je kunt eerst een zwarte en dan een witte knikker pakken, maar ook andersom. Het aantal mogelijke volgorden waarop je 2 knikkers kunt ordenen is 2!.
vraagje wat betreft examens. Ik zit oefenexamen vwo wis a.12 te maken, deze
http://www.examenblad.nl/(...)4x2yh/f=/bestand.pdf
loop vast bij vraag 6.Ik snap niet waarom ze bij de uitwerkingen ( http://www.examenblad.nl/(...)3nq00/f=/bestand.pdf ) die 5/10 x 5/9 nog x 2 doen?
quote:Die NCR knop moet je pas gaan gebruiken als je dit kent: http://nl.wikipedia.org/wiki/Binomiaalco%C3%ABffici%C3%ABntOp donderdag 21 mei 2009 22:08 schreef Jolien1989 het volgende:
vraagje wat betreft examens. Ik zit oefenexamen vwo wis a.12 te maken, deze
http://www.examenblad.nl/(...)4x2yh/f=/bestand.pdf
loop vast bij vraag 6.Ik snap niet waarom ze bij de uitwerkingen ( http://www.examenblad.nl/(...)3nq00/f=/bestand.pdf ) die 5/10 x 5/9 nog x 2 doen?
Heeft iets met NCR te maken vast en zeker, maar ik snap echt niet wanneer je NCR wel moet gebruiken, en wanneer niet?
quote:Eerst eens kijken naar g(x) = f(f(x)).
De tent map is de volgende piece wise functie;
f(x)=2*x als x kleiner dan 0.5 en 2-2*x als x groter of gelijk aan 0.5.
Mijn vragen zijn als volgt; zijn er periode 2 oplossingen? Zo ja zijn ze stabiel? Geef argumenten waarom er geen stabiele oplossingen zijn met periode hoger dan 2. En is deze map chaotisch?
Wat ik tot nu toe weet is het volgende een periodiek punt is een punt waarvoor geldt: f^p(x)=x, in dit geval zijn we op zoek naar punten waarvoor geldt f^2(x)=f(f(x)=x. Maar ik weet geen criterium te vinden om de stabilteit er van te bepalen. En ik weet ook niet wanneer een map chaotisch is. Alle hulp is welkom.
g(x) = 4x als x<0.25
g(x) = 2-4x als 0.25 <=x<0.50
g(x) = 4x-2 als 0.50<=x<=0.75
g(x) = 4-4x als 0.75 < x
Vaste punten van g zijn dus 0.4, 2/3 en 0.8. Als ik deze definitie aanhoud zijn ze allen stabel omdat g continu is in de genoemde functie (de definitie voor stabiel komt overeen met de definitie van continu
). Wat de rest betreft: geen idee.Ik heb lang naar deze matrix vemenigvuldiging gekeken; maar ik snap m niet.
R * RT =I
Er staat een matrix met maar 1 kolom gevuld (rest is weggelaten) maal een matrix met alleen een rij gevuld.
Dit komt neer op bijv. e * et als een van de vermenigvuldigingen; maar dit is toch niet zomaar 1, en de rest nullen?
Kan iemand mij dit wat inzichtelijker te maken?
quote:Wat heeft dit te maken met je verhaaltje over orthogonale matrices, wat is die R precies, en bedoel je met e de all-one vector?
Ik heb lang naar deze matrix vemenigvuldiging gekeken; maar ik snap m niet.
R * RT =I
Er staat een matrix met maar 1 kolom gevuld (rest is weggelaten) maal een matrix met alleen een rij gevuld.
Dit komt neer op bijv. e * et als een van de vermenigvuldigingen; maar dit is toch niet zomaar 1, en de rest nullen?
[ Bericht 3% gewijzigd door GlowMouse op 22-05-2009 22:23:42 ]
Het dictaat laat zien dat doordat R * RT = I (eenheidsmatrix) dat je dan mag stellen RT = R-1.
Het gaat dan om de vermenigvuldigiging R * RT = I (eenheidsmatrix) die ik niet zie.
Ik begrijp niet hoe ze hier de eenheidsmatrix uitkrijgen.
quote:Hij heeft maar 1 rij en 1 kolom gevuld (die wel bij elkaar horen) en de rest weggelaten. Schijnbaar onbelangrijk ofzo....Op vrijdag 22 mei 2009 22:20 schreef GlowMouse het volgende:
En als R inderdaad maar 1 kolom gevuld heeft, gaat R * RT nooit volle rang hebben.
quote:Dat is geen orthogonale matrix he?
[..]
Hij heeft maar 1 rij en 1 kolom gevuld (die wel bij elkaar horen) en de rest weggelaten. Schijnbaar onbelangrijk ofzo....
Hij heeft wel een hele nxn matrix met daarin maar enkele berekeningen:
Ik zal t in het kort noteren RT * R = I
- R1T - -------------- 1 0 0 ... 0
- R2T - -------------- 0 1 0 ... 0
- R3T - * R1 R2 R3 ...RN = 0 0 1 ...0
- ... - ----------------
- RnT - ----------------- 0 0 0 ....1
zoiets staat er met het gegeven dat R orthogonaal is.
quote:Wat je hier probeert te zeggen is me niet duidelijk.
- R1T - -------------- 1 0 0 ... 0
- R2T - -------------- 0 1 0 ... 0
- R3T - * R1 R2 R3 ...RN = 0 0 1 ...0
- ... - ----------------
- RnT - ----------------- 0 0 0 ....1
quote:Ik probeerde de matrix vermenigvuldigiging over te typen zoals die in het dictaat staat:Op vrijdag 22 mei 2009 22:33 schreef GlowMouse het volgende:
[..]
Wat je hier probeert te zeggen is me niet duidelijk.
RT * R = I.
Eerst de getransponeerde matrix, met alleen een focus op een rij genummerd R1T tot RNT.
Dit keer de gewone orthogonale matrix met in de kolom R1 tot en met RN.
Als derde de uitkomst; de eenheidsmatrix.
Er staat gewoon de definitie van orthogonaal: Ri staat loodrecht op Rj voor i<>j en Ri heeft norm 1.Maar dat lukte me dus niet.
Kan ik dit beter met een concreet voorbeeld eens uitwerken dan?
Maar voor mij is het op deze manier nog niet echt inzichtelijk of een bewijs.
Ri heeft norm 1 <=> (R*RT)_{ii} = 1
Dat is alles
quote:Dát snap ik dus nog niet; kun je dit nog wat meer uitleggen? Hoe kom je aan die nullen en enen?Op vrijdag 22 mei 2009 22:44 schreef GlowMouse het volgende:
Ri staat loodrecht op Rj voor i<>j <> (R*RT)_{ij} = 0
Ri heeft norm 1. (R*RT)_{ii} = 1
Dat is alles
Wat bedoel je met i<>j <> (R*RT)_{ij} = 0 en (R*RT)_{ii} = 1. Dat zegt met nog niet zoveel.
En hoe dit eruit ziet is verder niet gegeven, maar wel is de modulus 1.
Maar ik kan hier nietzomaar een matrix vermenigvuldiging mee uitvoeren.
quote:Wat bedoel je met loodrecht staan? Volgens mij staan rijen en kolommen altijd loodrecht. En i ongelijk aan j? Waarom is dit 0? Bedoel je dat dat niet overeenkomstige getallen worden vermenigvuldigd?Ri staat loodrecht op Rj voor i ongelijk aan j <=> (R*RT)_{ij} = 0.
quote:Idem...Ri heeft norm 1 <=> (R*RT)_{ii} = 1
quote:Jawel je hebt voldoende gegevens.
Maar ik kan hier nietzomaar een matrix vermenigvuldiging mee uitvoeren.
quote:Vectoren staan loodrecht op elkaar wanneer hun inproduct 0 is.Wat bedoel je met loodrecht staan? Volgens mij staan rijen en kolommen altijd loodrecht.
quote:Ik zie dat loodrecht staan niet echt terug in de matrix.Op vrijdag 22 mei 2009 23:00 schreef GlowMouse het volgende:
[..]
Jawel je hebt voldoende gegevens.
[..]
Vectoren staan loodrecht op elkaar wanneer hun inproduct 0 is.
Rn en RnT staan loodrecht, en dus zou die uitkomst 1 moeten zijn
quote:i ongelijk aan j => vectoren loodrecht dus inproduct 0.Ri staat loodrecht op Rj voor i<>j <> (R*RT)_{ij} = 0
Ri heeft norm 1. (R*RT)_{ii} = 1
i gelijk aan j, dus i*i en | i |=1, dus uitkomst is 1.
Maar deze twee staan toch ook loodracht? Is dat inproduct dan niet ook gelijk aan 0?
quote:Een vector staat toch niet loodrecht op zichzelf? Kolom i is gelijk aan Rij i van de getransponeerde matrix. Dus de diagonaalelementen in het product worden altijd 1 natuurlijk.
Maar deze twee staan toch ook loodracht? Is dat inproduct dan niet ook gelijk aan 0?
Ik zal het nog eens zelf nagaan. Bedankt!
Ik heb in mijn game theory boek de opdracht om in een 2 keer herhaald spel te bepalen wat de maximale payoff van speler een is in een deelspel perfect evenwicht als functie van a. Ik heb alleen geen idee hoe dit aan te pakken omdat er ook geen techniek voor genoemd is, ook google helpt me niet.
het spel is
| 1 2 3 | 0,4 4,3 0,0 0,0 0,0 a,a |
met als eerste natuurlijk de payoffs van speler 1 genoemd
ik ben al een poosje niet meer bezig geweest met wiskunde en kom er even niet meer uit
het is niet voor school/studie, maar dit leek mij de beste plek om de vraag te stellen.
alvast bedankt voor de hulp.
een voorbeeld van de berekening zou ook erg prettig zijn.
quote:ik ben al een dik uur aan het zoeken, maar kom er niet meer uit.Op donderdag 28 mei 2009 16:48 schreef GlowMouse het volgende:
Gebruik de tangens, is wel veel over te vinden op internet
is te lang geleden dat ik er mee bezig was.
aan de hand van een duidelijk voorbeeld kan ik misschien verder.
help?
quote:Je hebt:Op donderdag 28 mei 2009 16:48 schreef soulfly1983 het volgende:
kan iemand mij vertellen wat de lengte is van B op het moment dat A 1m 2m 3m 4m 5m en 6m is?
ik ben al een poosje niet meer bezig geweest met wiskunde en kom er even niet meer uit
het is niet voor school/studie, maar dit leek mij de beste plek om de vraag te stellen.
alvast bedankt voor de hulp.
een voorbeeld van de berekening zou ook erg prettig zijn.
[ afbeelding ]
(1) tan β = b/a
En dus:
(2) b = a∙tan β
Hier is β = 22,5°. We weten ook dat tan 45° = 1, en via de formules voor de halve hoek kunnen we dan vinden dat geldt:
(3) tan 22,5° = √2 - 1
Uit (2) en (3) volgt dan:
(4) b = (√2 - 1)∙a
Met (4) kun je nu eenvoudig b berekenen voor elke gegeven waarde van a.
bedankt, ik ga ermee aan de slag!
quote:Blijven de hoeken dan gelijk?Op donderdag 28 mei 2009 16:48 schreef soulfly1983 het volgende:
kan iemand mij vertellen wat de lengte is van B op het moment dat A 1m 2m 3m 4m 5m en 6m is?
ik ben al een poosje niet meer bezig geweest met wiskunde en kom er even niet meer uit
het is niet voor school/studie, maar dit leek mij de beste plek om de vraag te stellen.
alvast bedankt voor de hulp.
een voorbeeld van de berekening zou ook erg prettig zijn.
[ afbeelding ]
Of is C ook een constante en veranderen de hoeken met B?
ik zoek een boek/PDF/whatever wat mij iets meer kan vertellen over de wiskunde en de implicaties van de onvolledigheidsstellingen van Gödel. Heb een aardig wiskundige achtergrond dus het mag best technisch zijn
Heeft iemand een goede link/boekentip? Thabit of Iblis misschien?Er zijn nog wel wat boeken van die Wikipediabibliografie die ik t.z.t. wil lezen, (b.v. Gödel's Theorem: An Incomplete Guide to its Use and Abuse), maar daar ben ik nog niet aan toegekomen.
Er staat alleen geen bewijs bij en ik kan het bewijs ook nergens op het internet vinden.
Ik kwam zelf hierop uit:
Var(XY) = E(X2 Y2) - E2(XY) = EX2 EY2 + Cov(X2,Y2) - (EX EY + Cov(X,Y))2
= EX2 EY2 + Cov(X2,Y2) - E2X E2Y -2EX EY Cov(X,Y) - Cov(X,Y)2
=(Var X + E2X) (Var Y + E2Y) + Cov(X2,Y2) - E2X E2Y -2EX EY Cov(X,Y) - Cov(X,Y)2
=Var X Var Y + Var X E2Y + Var Y E2X + Cov(X2,Y2) -2EX EY Cov(X,Y) - Cov(X,Y)2
Als ik geen fout heb gemaakt, en de formule in het paper klopt dan moet gelden:
Cov(X2, Y2) = 4E(X)E(Y)Cov(X,Y) + 2Cov(X,Y)2
[ Bericht 6% gewijzigd door mrbombastic op 29-05-2009 18:38:46 ]
Integraal uitwerken om E((XY)²) te bepalen zal ook wel niet zo makkelijk zijn.
Ik was zelf alleen de truc tegengekomen om met Xslang = X - rho*sigmax/sigmay * Y te werken (Xslang en Y zijn dan onafhankelijk), maar daarmee was het niet te doen.Maar ik snap dr nog geen *** van.
Bijv. deze som:
Bepaal A bij de lineaire afbeelding tov standaardbasis A<1.0>=<5,2> en A<1,1>=<1,-1>
Dus volgens mij is het dan zo:
een matrix A werkt in op <1,0> en verandert deze in <5,2> .
Dus:
A * 1 1 = 5 1
0 1 2 -1
dan volgt
1 1 5 1
0 1 = 2 -1 * A-1
en dat levert mij A=4 1
3 -1
Ik heb wel iets gelezen over A'=B-1AB; maar dan reken ik A' uit; dus zo'n regel kan ik dan niet meer gebruiken. Kan iemand wat verduidelijking geven hoe dit soort dingen werken?
[ Bericht 1% gewijzigd door Borizzz op 30-05-2009 23:19:46 ]
5 -4
2 -3
Dat is ten opzichte van de basis [1 0; 0 1]. Maar tov welke basis wil je hem nou? Want dan is het gewoon navermenigvuldigen met de inverse van de matrix met in de kolommen de vectoren van de basis.
Het is toch zo dat in dit voorbeeld door een matrix A <1,0> overgaat in <5,2> en <1,1> in <1,-1>.
dus ik dacht dat
5 2 maal 11 tot de macht -1 ofzo.
1 -1 1 -1
Gewoon een beetje standaard vergelijkingen oplossen.
Maar wat heeft dat te maken met A'=B-1 AB
Maar in mijn boek (vd Craats) staat ook de vermenigvuldiging A'= B-1 AB.
Wat heeft dat er nu eigenlijk mee te maken? Want zo bereken je toch de transformatie?
Ik heb t idee dat ik het nog niet helemaal vat.
En: op welke manier kun je de inverse van een 3x3 matrix berekenen? Bij R3 ->R3 transformaties is dat wel noodzakelijk.
quote:Vegen.Op zondag 31 mei 2009 00:24 schreef Borizzz het volgende:
En: op welke manier kun je de inverse van een 3x3 matrix berekenen? Bij R3 ->R3 transformaties is dat wel noodzakelijk.
dan moet je toch
3x^6 = 6
x6 = 2
x = ...?
en moet je dan
x = 6/2
x = 2/6
of
x = 6 wortel 2 ?
ik ben mn antwoordenboek kwijt vandaar dat ik het hier vraag
en ja dit is brugklasstof maar ik weet het gewoon echt niet meer
Bepaal A bij de lineaire afbeelding tov standaardbasis A<1.0>=<5,2> en A<1,1>=<1,-1>
Uitkomst is 2x2 matrix met <5,2> en <-4,-3> als kolomvectoren.
Nu een aanvullende opmerking over de theorie hierbij. Is het nu zo dat deze matrix lineair afbeeldt tussen twee standaard bases? Kan ik in dit geval A ook berekenen met de formule B-1*A*B ? Of heb ik dan een matrix A' gevonden die de afbeelding 'terugzet'?
quote:Dank, die neem ik binnenkort es even doorOp vrijdag 29 mei 2009 11:01 schreef Iblis het volgende:
Ik heb Gödels onvolledigheidsstellingen uit een dictaat gekregen, met uitleg van de docent erbij, dus daar kan ik niet direct een boek voor aanwijzen. Het Wikipedia-artikel heeft een veelvoud aan verwijzingen, waaronder een Engelse vertaling van het oorspronkelijke artikel.
Er zijn nog wel wat boeken van die Wikipediabibliografie die ik t.z.t. wil lezen, (b.v. Gödel's Theorem: An Incomplete Guide to its Use and Abuse), maar daar ben ik nog niet aan toegekomen.
Is de (volledige) strekking van zijn stellingen door iemand met een redelijke wiskunde-achtegrond goed te begrijpen, of zijn ze ontzettend technisch?quote:Doe het zelf altijd via de cofactoren, da's vrij rechttoe rechtaan
quote:Ik weet niet wat je logica-achtergrond is. In principe is het goed te begrijpen als je goed in wiskunde bent (en als Natuurkundige ben je dat wel), maar anderzijds is het een tak van wiskunde die veelal niet onderwezen wordt. Maar als je een beetje bekend bent me Peano-rekenkunde, en wel wat van logica hebt gehad, dan moet het, denk ik, uiteindelijk wel te bevatten zijn.
Dank, die neem ik binnenkort es even door
Wat echter essentieel is, is dat er een (subtiel) verschil is tussen zaken die waar zijn, en zaken die je kunt bewijzen. Idealiter wil je dat wat waar is, dat dat bewijsbaar is, en dat wat bewijsbaar is, dat dat waar is. Neem een stelling als p -> p. (Als p, dan p). Je kunt kijken of deze waar is door verschillende waarden van p in te vullen (0 en 1), voor 0 krijg je: 0 -> 0, en dat is waar, en voor 1 krijg je 1 - 1, dat is ook waar. Dit is dus in feite een tautologie (altijd waar). De vraag is echter: kun je deze stelling ook afleiden? In de propositielogica kan dat, je doet het als volgt: Neem aan dat p geldt, dan krijg je: 'p' onder aanname van 'p'. Trek daarna je aanname, en je krijgt p -> p.
Dit lijkt wat flauw, maar dat is het idee. Je kunt je wel voorstellen dat als je niet met genoeg axiomata begint, b.v. de regel ‘je mag een aanname intrekken’ niet geeft, dat je het bewijs voor p -> p nooit rondkrijgt. Als je semantiek, d.w.z. je interpretatie gelijk blijft, dan heb je nog steeds dat p -> p waar is, maar je het niet formeel kunt afleiden, je kunt er geen bewijs voor rond krijgen.
Anderzijds, als je regels te algemeen zijn, b.v. je hebt als regel uit 'a \/ b' volgt 'a', dan krijg je dat je dingen kunt afleiden die niet waar zijn. Dat levert een inconsistent systeem. Een systeem waarbij alles wat je kunt afleiden waar is noemt men ‘sound’, en waarbij alles wat waar is ook af te leiden is, noemt men complete (of volledig).
Gödel heeft voor de gewone propositielogica twee volledigheidsstellingen bewezen. Dat geeft de basis denk ik om zijn onvolledigheidsstellingen goed te begrijpen. Die propositielogica heb ik uit logica voor informatica (of toen nog ‘voor informatici’) geleerd, en dat is een duidelijk en goed boek. (Van Benthem is een grootheid in de logica-wereld.) Bovendien wordt dat boek veel in het onderwijs gebruikt, dus je kunt het vast ergens in een de Slegte of Marktplaats 2e-hands vinden.
Dat echter zou ik wel als basiskennis willen aanraden om door te hebben hoe bewijsbaarheid en geldigheid precies van elkaar verschillen. Want dat is de crux van Gödels bewijs.
Heel erg bedankt in ieder geval!quote:Cofactoren gebruik ik alleen voor 2x2 matrices. Grotere matrices inverteer ik sowieso niet met de hand.Op dinsdag 2 juni 2009 09:38 schreef Haushofer het volgende:
[..]
Doe het zelf altijd via de cofactoren, da's vrij rechttoe rechtaan
.quote:Ik snap er eerlijk gezegd geen zak van wat je hier bedoelt. Hoe kun je lineair tussen twee bases afbeelden?Op maandag 1 juni 2009 20:21 schreef Borizzz het volgende:
Ik stelde eerder deze vraag (is nu inmiddels gelukt):
Bepaal A bij de lineaire afbeelding tov standaardbasis A<1.0>=<5,2> en A<1,1>=<1,-1>
Uitkomst is 2x2 matrix met <5,2> en <-4,-3> als kolomvectoren.
Nu een aanvullende opmerking over de theorie hierbij. Is het nu zo dat deze matrix lineair afbeeldt tussen twee standaard bases? Kan ik in dit geval A ook berekenen met de formule B-1*A*B ? Of heb ik dan een matrix A' gevonden die de afbeelding 'terugzet'?
quote:Nou ja eerst maar even bij het begin.Op dinsdag 2 juni 2009 14:23 schreef thabit het volgende:
[..]
Ik snap er eerlijk gezegd geen zak van wat je hier bedoelt. Hoe kun je lineair tussen twee bases afbeelden?
Wanneer kun je iets als een basis nemen.
i <1,0> en j <0,1> is een basis en ook a<1,1> en b<-1,1>.
Moeten vecoren die je als basis neemt altijd lineair afhankelijk zijn?
quote:Ja, per definitie.
Moeten vecoren die je als basis neemt altijd lineair onafhankelijk zijn?
quote:Zoals Iblis inderdaad zei, is dat de definitie van een basis.Op dinsdag 2 juni 2009 15:33 schreef Borizzz het volgende:
[..]
Nou ja eerst maar even bij het begin.
Wanneer kun je iets als een basis nemen.
i <1,0> en j <0,1> is een basis en ook a<1,1> en b<-1,1>.
Moeten vecoren die je als basis neemt altijd lineair afhankelijk zijn?
Probeer je maar es voor te stellen wat er zou gebeuren als je die eis niet zou stellen; dus dat je zou zeggen "een basis mag ook best lineair AFhankelijke vectoren bevatten".
En transformaties (lineaire afbeeldingen) kun je in een matrix zetten als je kijkt hoe de standaardbasis verandert.
Als A een lineaire afbeelding is van standaardbasis a naar b, dan geeft A' (=B-1*A*B) dezelfde afbeelding weer alleen gebruikmakend van de nieuwe standaardbasis. Klopt dit?
Dan is er toch ook een mogelijkheid voor de weg terug?
quote:Er is maar één standaardbasis, http://en.wikipedia.org/wiki/Standard_basis
Dan is het dus ook zo dat je in R3 drie vectoren en in R2 twee vectoren als standaardbasis hebt.
En transformaties (lineaire afbeeldingen) kun je in een matrix zetten als je kijkt hoe de standaardbasis verandert.
Als A een lineaire afbeelding is van standaardbasis a naar b
quote:Wat is B? Als je A' met een vector x vermenigvuldigt, zie je dat x eerst met B wordt vermenigvuldigd en het idee is dat Bx de vector is tov de andere basis. Die vermenigvuldig je daar met A, en dan transformeer je hem weer terug naar je standaardbasis via B-1.dan geeft A' (=B-1*A*B) dezelfde afbeelding weer alleen gebruikmakend van de nieuwe standaardbasis. Klopt dit?
quote:Alleen als je matrix dus inverteerbaar is. Neem de 0-matrix eens. Die voldoet prima aan de eisen die voor een lineaire afbeelding worden gesteld. Een voor een vector v en w geldt: f(v) = f(w) = 0. En dus f(v + w) = f(v) + f(w) = 0 en f(c*v) = c*f(v) = c*0 = 0.
Dan is er toch ook een mogelijkheid voor de weg terug?
Maar inverteerbaar, uiteraard niet. Hier blijf je natuurlijk niet in de R3, dus ik weet niet precies wat je bedoelt ,maar in z'n algemeenheid kun je niet zeggen dat lineaire afbeeldingen altijd inverteerbaar zijn. Maar zoals gezegd, als de matrix die de lineaire afbeelding voorstelt echter inverteerbaar is (desda conditie), dan is de afbeelding het ook.
[Bèta overig] huiswerk- en vragentopic
quote:Vraagje, na 8 jaar kan ik het niet meer:
Er zijn 100 balletjes, 68 rode en 32 witte.
Je mag 13 keer pakken met terugleggen.
Wat is de kans dat je nooit een witte pakt?
(Met beetje uitleg graag)
Kans 2de rood: 0.68
..
Kans 13de rood: 0.68
en omdat trekkingen onafhankelijk zijn moet je al die kansen vermenigvuldigen
Heerlijk
Het gaat om de integraal van 0 tot a van "dx/(a^2 - x^2)". Hierna pakken we een limiet die a vanaf links benadert zodat we niet door 0 delen. Dat snap ik allemaal alleen gaan ze daarna in 1 stap naar:
lim c->a- 1/2a*ln|(a+x)/(a-x)| over 0 tot c.
Hoe de fuck komen ze daarop?
Waarschijnlijk is er een heel simpel antwoord, maar ik kom er niet meer uit.
Ik wil graag de minimale marge uitrekenen. Ik zit in de volgende situatie: ik loop stage bij een bedrijf dat Google Adwords gebruikt. Ik de statistieken zie ik de volgende gegevens:
Kosten Adwords: 10.000
Opbrengst Adwords: 60.000
Nu wil ik uitrekenen wat de minimale marge moet zijn om die 10.000 terug te verdienen en break-even te draaien. Echter, ik weet de gemiddelde inkoopwaarde van de producten niet. Daarom wil ik dit eventjes uitrekenen, zodat ik kan zeggen: "op de producten moet nog ruimte zijn voor minimaal zoveel marge..."
Stel, ik heb een auto die slechts met 2 verschillende snelheden kan rijden: v+ en v-. De overgang van v+ naar v- gaat met een bepaalde rate R, die gelijk is voor v+ --> v- en v- --> v+. De eerste vraag is nu: wat is de gemiddelde verplaatsing? De aanname hierbij is dat de tijd T veel groter is dan R-1:
T >> R-1.
We kwamen al op het volgende: de gemiddelde verplaatsing is niks anders de gemiddelde snelheid maal de tijd die je meet:
<x> = 1\2*(v+ + v-)*T.
Hierin komt de rate R niet voor.
Nou is de volgende vraag: wat is <x2>? Hier lopen we beide op vast. Is er een simpele redenatie waarop je de distributie kunt verkrijgen voor dit proces onder de aanname T >> R-1 zodat je <x2> kunt uitrekenen?
Dank voor elke bijdrage
quote:Het gemiddelde van x2, net zoals <x> het gemiddelde van x isOp donderdag 4 juni 2009 12:20 schreef GlowMouse het volgende:
Wat versta jij onder <x²>?
quote:De frequentie waarmee er wordt gewisseld tussen de 2 snelheden. Die is dus constant (hangt niet van x of T af).Op donderdag 4 juni 2009 12:23 schreef thabit het volgende:
Wat is rate?
quote:Ja ik zag het al
[..]
Het gemiddelde van x2, net zoals <x> het gemiddelde van x is
Het antwoord zie ik zo niet.quote:Parameter van de exponentieel verdeelde stochasten X1,X2,... die de tijd aangeven tussen het wisselen van snelheid. Dus op t in [0,X1] rijd je snelheid v+, (X1,X1+X2] v-, etc
quote:Tsja, ik ben zelf niet zo onderlegd in statistiek en random processen, en volgens mij is het subtieler dan ik met m'n boerenverstand aankanOp donderdag 4 juni 2009 12:29 schreef GlowMouse het volgende:
[..]
Ja ik zag het al
[..]
Ik heb een data set (201 punten) waar ik een fourier benadering van nodig hebt en dan moet ik de coefficienten daarvan weten. Ik heb de volgende vergelijkingen:
A1,CL, V, S, Gamma(y), b zijn bekend. De data set is dus Gamma(y).
Ik moet uiteindelijk e berekenen. Heeft iemand enig idee hoe ik dit aanpak, bij voorkeur in MATLAB. We hebben er al uren aangezeten met nog twee mensen uit onze projectgroep, maar lukken doet het niet.
Voor de geinteresseerden: Het is om een bepaalde factor uit te rekenen, waarmee je de geinduceerde weerstand van een vliegtuig uitrekent door de liftverdeling op de vleugel (=Gamma).
quote:Ik moet zeggen dat ik me er niet heel diep in verdiept heb, maar het is mogelijk om een fourier benadering te maken van de Gamma, daar komen dan coefficienten uit. Het probleem is dat er in de fourierbenadering sin en cos termen zitten, welke coefficienten precies nodig zijn is ons niet echt duidelijk meer.Op vrijdag 5 juni 2009 08:45 schreef thabit het volgende:
1 vergelijking in N onbekenden, knappe jongen die dat kan oplossen.
b is de wing span van de vleugel
V is vliegsnelheid
S is wing oppervlak
CL is de lift coefficient, die staat ook vast
A1 is een bepaalde coefficient waaraan je de andere coefficienten weegt als het ware.
An stelt niet echt een bepaald iets voor, het zijn de coefficienten van de fourier benadering.
Werken met e machten vind ik zelf altijd een stuk lastiger, omdat ik het minder voor me zie wat er gebeurt. Ik hoop dat het probleem zo wat duidelijker is. Ik weet niet echt wat ik er meer over kan uitleggen.
quote:Op grond van de renewal reward theorem geldt dat de LRA (long run average) snelheid (v+ + v-)/2 is. Jij zegt dan: de LRA verplaatsing is dan T*(v+ + v-)/2. Hiermee gebruik je dat als lim(x->oneindig) f(x)/x = c, dat dan voor grote x ongeveer geldt dat f(x) = cx.
[..]
Tsja, ik ben zelf niet zo onderlegd in statistiek en random processen, en volgens mij is het subtieler dan ik met m'n boerenverstand aankan
Met dezelfde stelling kun je laten zien dat de LRA snelheid² gelijk is aan (v+² + v-²)/2. Analoog zou dan gelden <x²> T(v+² + v-²)/2. Maar deze is al trickier: als lim(x->oneindig) f(x)/x = c, geldt dan voor grote x ongeveer dat f(x)x = cx²?
Hier lijkt inderdaad iets fout te gaan: VarX = <x²> - <x>² = T²(a+b)²/2 en dat gaat naar oneindig. En dat strookt niet met de intuïtie die zegt dat de variantie naar 0 moet gaan. Dus ik zou zeggen <x²> = <x>²
[ Bericht 4% gewijzigd door GlowMouse op 05-06-2009 15:21:26 ]
quote:Ik zal het maandag even aan em voorleggen en dan gaan we er nog even voor zittenOp vrijdag 5 juni 2009 14:21 schreef GlowMouse het volgende:
[..]
Op grond van de renewal reward theorem geldt dat de LRA (long run average) snelheid (v+ + v-)/2 is. Jij zegt dan: de LRA verplaatsing is dan T*(v+ + v-)/2. Hiermee gebruik je dat als lim(x->oneindig) f(x)/x = c, dat dan voor grote x ongeveer geldt dat f(x) = cx.
Met dezelfde stelling kun je laten zien dat de LRA snelheid² gelijk is aan (v+² + v-²)/2. Analoog zou dan gelden <x²> T(v+² + v-²)/2. Maar deze is al trickier: als lim(x->oneindig) f(x)/x = c, geldt dan voor grote x ongeveer dat f(x)x = cx²?
Hier lijkt inderdaad iets fout te gaan: VarX = <x²> - <x>² = T²(a+b)²/2 en dat gaat naar oneindig. En dat strookt niet met de intuïtie die zegt dat de variantie naar 0 moet gaan. Dus ik zou zeggen <x²> = <x>²
In ieder geval erg bedankt. Ik ken het Renewal Reward Theorem niet, dus dat zal ik even opzoeken. Als er nog verdere inzichten zijn houd ik jullie op de hoogte 
Ik snap de numerieke methode niet echt hier. De dGamma/dy weet ik voor alle yn posities, Voneindig en delta y zijn uiteraard ook bekend. Maar de sommatie snap ik niet, wat bedoelen ze er precies mee? Kan iemand het me uitleggen?
Ik moet het in Excel kunnen verwerken.
quote:b is de spanwijdte van een vliegtuig, y is de spanwise positie (sorry weet even geen Nederlands woord daarvoor). In het midden van het vliegtuig is y gelijk aan nul en aan de vleugeltips is het b/2 en -b/2. Ik vind die omschrijving naar die som heel vreemd, wat moet ik bijvoorbeeld met die j's?Op zaterdag 6 juni 2009 22:55 schreef GlowMouse het volgende:
Ik snap het ook niet. Maar als er een b zomaar verdwijnt, dan kan ik dat ook nooit verklaren zonder te weten wat die b is.
yn is een bepaalde positie als de vleugel in een eindig aantal stukken wordt verdeeld, zoals ik het begrijp. Maar wat die y daarin dan weer doet?
quote:Ze passen steeds de Regel van Simpson toe op een interval [yj-1, yj+1] met een lengte van 2Δy. Door de benaderingen voor de integraal over al die deelintervallen te sommeren wordt een benadering verkregen voor de integraal over het gehele interval [-½b, ½b].Op zaterdag 6 juni 2009 22:51 schreef Schuifpui het volgende:
[ afbeelding ]
Ik snap de numerieke methode niet echt hier. De dGamma/dy weet ik voor alle yn posities, Voneindig en delta y zijn uiteraard ook bekend. Maar de sommatie snap ik niet, wat bedoelen ze er precies mee? Kan iemand het me uitleggen?
Ik moet het in Excel kunnen verwerken.
quote:Het idee van de simpsons rule snap ik, alleen wat ze precies integeren is me niet duidelijk. Al die verschillende y's bijvoorbeeld.Op zaterdag 6 juni 2009 23:25 schreef Riparius het volgende:
[..]
Ze passen steeds de Regel van Simpson toe op een interval [yj-1, yj+1] met een lengte van 2Δy. Door de benaderingen voor de integraal over al die deelintervallen te sommeren wordt een benadering verkregen voor de integraal over het gehele interval [-½b, ½b].
quote:In 5.75 is er maar één onafhankelijke variabele, en dat is y. Voor wat de integratie betreft kun je hier yn als een constante beschouwen. Hoe ze aan deze integraal komen en wat het (fysisch) precies voorstelt weet ik ook niet, maar dat zal ongetwijfeld op de voorafgaande bladzijden staan uitgelegd.Op zaterdag 6 juni 2009 23:35 schreef Schuifpui het volgende:
[..]
Het idee van de simpsons rule snap ik, alleen wat ze precies integeren is me niet duidelijk. Al die verschillende y's bijvoorbeeld.
quote:Ik denk dat ik hem snap, alleen het resultaat klopt nog niet echt, maar ik ga morgen maar eens verder. Nu ben ik echt te moe er voor.Op zaterdag 6 juni 2009 23:43 schreef Riparius het volgende:
[..]
In 5.75 is er maar één onafhankelijke variabele, en dat is y. Voor wat de integratie betreft kun je hier yn als een constante beschouwen. Hoe ze aan deze integraal komen en wat het (fysisch) precies voorstelt weet ik ook niet, maar dat zal ongetwijfeld op de voorafgaande bladzijden staan uitgelegd.
Het fysisch snap ik wel, maar das vrij lastig uit te leggen. Toch een poging: Als een vliegtuig vliegt, krijg je zakkende lucht achter je vliegtuig, hierdoor verandert de snelheidsvector en ook de invalshoek van het vliegtuig. Verder wordt de liftvector iets naar achter gekanteld, maar door deze ook een component tegen de stroming in heeft, dat is geinduceerde weerstand. Weerstand ten gevolge van lift. Ik wil nu de verandering van de invalshoek weten op elk plekje van de vleugel. Dat is nodig om de precieze lift verdeling vast te stellen en daarmee de precieze geinduceerde weerstand en oa.ook de overtrekhoek.
Zij V een verzameling met n natuurlijke getallen, tussen 1 en 2n (inbegrepen).
Bewijs dat er een deelverzameling is zodat de som van de elementen deelbaar is door n.
quote:Noem de elementen a1, a2, ..., an. Bekijk de deelsommen, Sk, gedefinieerd als Sk = a1 + ... + ak. Er zijn dus n van die deelsommen. Als een van die deelsommen deelbaar is door n dan ben je klaar.Op zondag 7 juni 2009 14:45 schreef mathematicus het volgende:
Zou iemand me met de volgende opgave op weg kunnen helpen?
Zij V een verzameling met n natuurlijke getallen, tussen 1 en 2n (inbegrepen).
Bewijs dat er een deelverzameling is zodat de som van de elementen deelbaar is door n.
Zo niet: duiventilprincipe (pigeon hole principle).
SPOILERBekijk Sk mod n. We weten dat er geen k is zodat Sk mod n = 0, immers, dat zou betekenen dat die deelsom deelbaar is door n. De mogelijke waarden zijn dus 1 t/m (n - 1), aangezien er echter n deelsommen zijn, moeten er twee zijn die hetzelfde zijn (duiventilprincipe). Zeg Si (mod n) = Sj (mod n). Dan is (Sj - Si) (mod n) = 0, dus ai + 1 + ... + aj is deelbaar door n.
[ Bericht 0% gewijzigd door Iblis op 07-06-2009 23:23:18 (Een k moest n zijn) ]
Bedankt!
quote:
We weten dat er geen k is zodat Sk mod n = 0, immers, dat zou betekenen dat die deelsom deelbaar is doorkn.
Bedankt!
Ik moet de spoiler lezen.
[ Bericht 2% gewijzigd door GlowMouse op 07-06-2009 16:53:19 ]
quote:Op zondag 7 juni 2009 14:45 schreef mathematicus het volgende:
Zou iemand me met de volgende opgave op weg kunnen helpen?
Zij V een verzameling met n natuurlijke getallen, tussen 1 en 2n (inbegrepen).
Bewijs dat er een deelverzameling is zodat de som van de elementen deelbaar is door n.
quote:Op zondag 7 juni 2009 15:15 schreef nectje1 het volgende:
Ik heb een vraag, weet iemand een site waar LMC (litlle man computer) wordt uitgelegd. Ik snap de branches namelijk niet helemaal goed. Hoe zit het daarmee? Wanneer moet je ook alweer voor iets branch zetten en of een naam?????
quote:Inderdaad, dat was ook waar ik even op stuk liep (vandaar de lege post). Maar bij de spoiler van Iblis werd ik toch ook nog even op het verkeerde been gezet door een typo. Zie jij die ook?Op zondag 7 juni 2009 16:55 schreef GlowMouse het volgende:
Met dat verhaal in de spoiler begrijp ik de post van mathematicus opeens wel
quote:Heeft niets met wiskunde te maken, en je hebt je eigen topic al vraag LMC (little man computer)
quote:mathematicus zag hem al
[..]
Inderdaad, dat was ook waar ik even op stuk liep (vandaar de lege post). Maar bij de spoiler van Iblis werd ik toch ook nog even op het verkeerde been gezet door een typo. Zie jij die ook?
x'(t)=F(x(t)), voor t >=0
x(0)=x0 in Rm
voor iedere x0 in R een globale unieke globale oplossing.
Dit moet ik bewijzen. Ik heb tot nu toe het volgende gevonden:
F is Lipschitz continu en ihb is F lokaal Lipschitz continu. Volgens een stelling bestaat er voor iedere
x0 in Rm een unieke maximale oplossing x(,;x0):[0,Tx0]-->Rm. Bovendien geldt OF Tx0= oo OF
lim ||x(t;xx0)|| = oo.
t-->Tx0-
Dus ik kan laten zien dat als F Lipschitz continu dat
lim ||x(t;xx0)|| = oo.
t-->Tx0-
tot een tegenspraak gaat leiden indien Tx0< oo.
Ik zit bij dit vast!!
Zou iemand mij willen helpen? Alvast bedankt.
't Is lang geleden dat ik dit soort dingen deed, maar gaat het standaardbewijs niet met een iteratief proces dat functies produceert?
xi+1(t) = x0 + integraal_0^t F(xi(s)) ds
De vraag is dan nu in hoeverre dit convergeert. Zo op het eerste gezicht zou je zeggen dat dat moet werken voor
alle t op [0, 1/L-epsilon]. Maar als dat zo is verschuif je de functie gewoon 'naar rechts' en kun je altijd 1/L - epsilon optellen bij de rechterkant van het interval waarop het gedefinieerd is.
[ Bericht 36% gewijzigd door thabit op 08-06-2009 15:48:55 ]
Het gaat over de volgende differentiaalvergelijkingen:
| 1 2 3 4 | dx = zeros(2,1); dx(1)=0.1*F-(1/10)*(pi/4)*(0.6)^2*x(2); dx(2)=(9.8/500)*x(1)-(0.02/1.2)*abs(x(2))*x(2); |
met x(1)(0)=1 & x(2)(0)=0
De vraag is:
Voor welke waarde van F is het maximum van x(1) = 1.6?
Het invullen van x(1)=1.6 en het maximum van x(2) in dx(1) invullen gaf een verkeerd antwoord.
Vind een formule voor de som van 1 - b + b² - b^3 + b^4 - b^5 ... - b^21. En geldt dit voor alle b?
Met formule bedoelen we geen sigma-notatie geval, maar een 'gewone' formule.
Waarschijnlijk zie ik iets simpels over het hoofd, want het lukt me niet...
quote:De termen van de som die je geeft vormen een meetkundige rij met als eerste term 1 en als reden -b (let op het minteken). Je kunt dus de somformule voor een aantal termen van een meetkundige rij gebruiken. Lukt het nu?Op maandag 8 juni 2009 22:07 schreef Operations1984 het volgende:
Kan iemand me helpen met de volgende twee vragen?
Vind een formule voor de som van 1 - b + b² - b^3 + b^4 - b^5 ... - b^21. En geldt dit voor alle b?
Met formule bedoelen we geen sigma-notatie geval, maar een 'gewone' formule.
Waarschijnlijk zie ik iets simpels over het hoofd, want het lukt me niet...
quote:Ok ik zal het nog eens uitschrijven.Op maandag 8 juni 2009 22:10 schreef Riparius het volgende:
[..]
De termen van de som die je geeft vormen een meetkundige rij met als eerste term 1 en als reden -b (let op het minteken). Je kunt dus de somformule voor een aantal termen van een meetkundige rij gebruiken. Lukt het nu?
Zij I=[a,b] een interval met a<b, en f: I-> R een diff.bare functie met f' begrensd. ( Staat in een opgave).
Hmm, is f' niet automatisch begrend als f diff baar is, en I is gesloten?, dus dat |f'(x)|<M, voor een M>0, en x element van I
[ Bericht 1% gewijzigd door mathematicus op 08-06-2009 23:02:56 ]
quote:Als ze bedoelen dat f weliswaar gedefinieerd is op het gesloten interval [a,b] maar differentieerbaar op het open interval (a,b) dan hoeft f' niet begrensd te zijn.Op maandag 8 juni 2009 22:46 schreef mathematicus het volgende:
Een korte vraag:
Zij I=[a,b] een interval met a<b, en f: I-> R een diff.bare functie met f' begrensd. ( Staat in een opgave).
Hmm, is f' niet automatisch begrend als f diff baar is, en I is gesloten?, dus dat |f'(x)|<M, voor een M>0, en x element van I
quote:fmax werkt niet in Matlab geloof ik?
Iemand enig idee hoe ik die variabele F in de function file moet toepassen?
En wat dacht je van function dx=func1(t,x,F)
ik heb een matlab vraag. Het gaat over een gewichtje wat aan een veerhangt, het gewichtje gaat horizontaal heen en weer (dit is x1). De snelheid van het op en neer gaan van het gewichtje is x2. T is gewoon de tijd
Twee differentiaalvergelijkingen krijg je:
dx1/dt = x2
dx2/dt = -20x1-0.5x2
x1 op t=0 = -1
x2 op t=0 = 0
Nu moet je in matlab een filmpje maken van het bewegen van het gewichtje tussen t=0 en t=7
maar het lukt echt niet....
kan iemand me helpen?
(ik heb de differentiaalvergelijkingen alwel moeten oplossen voor bepaalde t's dat is wel gelukt met ode45)
quote:Ik heb vandaag "De stelling van Gödel" van Nagel en Newman gekregen van een vriend van me, dus als ik het uit heb zal ik es laten weten of het de moeite waard is; misschien ken je het alOp vrijdag 29 mei 2009 11:01 schreef Iblis het volgende:
Ik heb Gödels onvolledigheidsstellingen uit een dictaat gekregen, met uitleg van de docent erbij, dus daar kan ik niet direct een boek voor aanwijzen. Het Wikipedia-artikel heeft een veelvoud aan verwijzingen, waaronder een Engelse vertaling van het oorspronkelijke artikel.
Er zijn nog wel wat boeken van die Wikipediabibliografie die ik t.z.t. wil lezen, (b.v. Gödel's Theorem: An Incomplete Guide to its Use and Abuse), maar daar ben ik nog niet aan toegekomen.
[ Bericht 3% gewijzigd door James.Bond op 11-06-2009 00:16:21 ]
quote:Ik heb de stationaire punten al gevonden: (0,0), (1,1), (1,-1), (-1,1), (-1,-1). Wat moet ik hierna doen?Op woensdag 10 juni 2009 20:20 schreef GlowMouse het volgende:
Heb je al wat matrices en een idee wat daarmee moet gebeuren?
Ik heb ook even een vraagje. Kan iemand mij uitleggen hoe ik deze moet opgaven moet maken?
Opgave 7 had ik wel "serieus" gedaan en toen kwam ik aan -46, maar blijkbaar moet je iets anders doen dan ik had gedaan.
Opgave 8 snap ik gewoon helemaal niet (vorige keer had ik die ook fout gedaan en daarbij snapte ik de uitwerking ook niet).
Alvast bedankt!
9 is ook een onzinvraag want -5 <= x < 3 is een conditie op de variabele x, en geen interval.
Bij 8 word je geacht te gebruiken dat wortel(a2) gelijk is aan a, dus als je een a2 buiten de wortel wilt halen, dan blijft er voor de wortel alleen een a over. Overigens is ook dit dubieus want voor a=-1 is wortel(a2) helemaal niet gelijk aan a, iets waarvan ik vermoed dat de auteur van deze opgaven het zelf niet gezien heeft.
Ik heb in ieder geval nog een voorbeeld zoals 8, dus ik zal straks eens kijken of ik die zelf kan oplossen
Bedankt in ieder geval! Met deze uitleg snap ik het al iets meer, haha.
quote:Ach, het is ook maar een cursus wiskunde om havo scholieren "richting" vwo te krijgen voor de statistiekvakken, dus misschien dat het daarom niet zo nauwkeurig komt qua afrondingen
Bij 7 is geen van de gegeven antwoorden goed: de uitdrukking is weliswaar gelijk aan de uitdrukking bij a, maar die is niet op 2 decimalen afgerond.
quote:Super, bedankt voor de goede stapsgewijze uitlegOp donderdag 11 juni 2009 00:03 schreef Iblis het volgende:
[..]
Dat wegstrepen kan niet zo maar, je hebt in de teller namelijk meerdere termen staan, en maar eentje bevat σ/√n. Als je wegstreept moet je uit elke term wegstrepen.
Je hebt...
De stap onder "and so"
Hoe werken ze zo snel die verhouding uit? De rest van de opgave wordt heel stapsgewijs uitgelegd maar nu knallen ze hier even iets te snel doorheen.
De stap daaronder natuurlijk wel weer duidelijk, het gaat om het middelste hier.
Iemand?
quote:Ik ga dit zo even proberen, bedankt
Wel, je kunt in de bovenste vergelijking de term k2X2(s) naar links gooien en dan X2(s) buiten haakjes zetten.
Mijn aanpak is alvolgt:
de lijn l is ax+by+c=0.
en dan een lijn m door de oorsprong loodrecht hierop. Snijpunt l en m is S.
Vergelijking lijn m is dan bx-ay=0.
Dan los je dit stelsel op geeft
ys=-bc/(a2+b2)
xs=-ac/(a2+b2)
Dat lukt me nog. Maar dan zeggen ze OS=|c|/sqrt(a2+b2).
Ik vermoed dat Pythagroas hier een rol speelt vanwege de afstand maar ik krijg dit niet uitgerekend.
Iemand een zet in de goede richting?
y = -(a/b)x - c/b
de lijn loodrecht hierop heeft helling h zdd. h*(-a/b) = -1.
quote:Oh, daaruit volgen die y_s en die x_s dus dat had je al.
ax+by+c=0
y = -(a/b)x - c/b
de lijn loodrecht hierop heeft helling h zdd. h*(-a/b) = -1.
Pythagoras inderdaad, die uitdrukking is sqrt(y_s² + x_s²). Je kunt dan c buiten haakjes halen.
quote:Kun je hier wat stappen bij noemen? Dat is waarschijnlijk juist datgene wat niet lukt.Op vrijdag 12 juni 2009 14:33 schreef GlowMouse het volgende:
[..]
Oh, daaruit volgen die y_s en die x_s dus dat had je al.
Pythagoras inderdaad, die uitdrukking is sqrt(y_s² + x_s²). Je kunt dan c buiten haakjes halen.
terwijl het zo simpel is....
Kan ik mezelf kwalijk nemen.
De volgende opgave krijg ik niet vereenvoudigd
(2wortel3 / wortel 2 )3
Is er toevallig iemand die mij voor deze met tussenstappen zou willen vereenvoudigen?
Sorry overigens voor de onduidelijk notatie maar kon zo gauw even geen alternatief vinden.
[ Bericht 0% gewijzigd door Kesum op 12-06-2009 18:57:23 ]
Wortel 2 keer wortel 3 is hetzelfde als wortel (2*3) dus wortel 6. Als je dit tot de macht drie doet kom je op:
Wortel 6 * Wortel 6 * Wortel 6 = 6 * Wortel 6
quote:(2∙√3/√2)3 = (√4∙√3/√2)3 = (√12/√2)3 = (√6)3 = 6∙√6.Op vrijdag 12 juni 2009 17:58 schreef Kesum het volgende:
Beste mensen,
De volgende opgave krijg ik niet vereenvoudigd
(2wortel3 / wortel 2 )3
Is er toevallig iemand die mij voor deze met tussenstappen zou willen vereenvoudigen?
Sorry overigens voor de onduidelijk notatie maar kon zo gauw even geen alternatief vinden.
Ik begrijp alleen niet goed waarom zoals in de uitleg van Dzy staat dat 2/√2 gelijk is aan √2.
Zou je dat nog eens kunnen toelichten
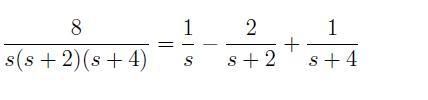
Hoe maak je deze herschrijving?
Ik zie het weer eens niet A*(s + 2)*(s + 4) + B*s*(s + 4) + C*s*(s + 2) = 8
Als je dat eens uitwerkt krijgt je dat:
A s2 + 6 A s + 8 A + B s2 + 4 B s + C s2 + 2 C s
Moet gelden.
Als je nu de termen met s2 en s en de constanten verzamelt, dan zie je dat moet gelden:
s2(A + B + C) = 0, dus (A + B + C) = 0
s(6A + 4B + 2C) = 0, dus (6A + 4B + 2C) = 0
8A = 8
Uit 8A = 8 volgt direct A = 1. Dat substitueer je, en je krijgt:
(1 + B + C) = 0
(6 + 4B + 2C) = 0
Los die twee op en je krijgt B = -2, C = 1 als oplossing.
En zo kom je op die splitsing. Dit is een standaardtechniek voor breuksplitsen overigens.
s2(A + B + C) = 0
quote:Welnu. Je wilt de breuk splitsen, en je krijgt drie breuken met in de teller respectievelijk A, B en C. Als je die gesplitste breuken weer onder een noemer brengt krijg je dus (in dit geval) A*(s + 2)*(s + 4) + B*s*(s + 4) + C*s*(s + 2) als teller, die moet natuurlijk gelijk zijn aan '8'.
Ik begrijp je uitleg, ik begrijp alleen niet hoe je komt op
s2(A + B + C) = 0
Je ziet echter dat als je die vergelijking uitschrijft dat je termen met s2, met s en constanten krijgt:
A s2 + 6 A s + 8 A + B s2 + 4 B s + C s2 + 2 C s
Dit moet natuurlijk nog steeds gelijk zijn aan 8, of wel: 0s2 + 0s + 8.
Je zou het ook zo kunnen opschrijven:
s2(A + B + C) + s(6A + 4B + 2C)s + 8A = s2*0 + s*0 + 8
Daaruit volgen dan direct de drie vergelijkingen.
quote:Oke zo, ja dat snap ik wel, en ik zag dat ook zodra ik het opscheef.Op maandag 15 juni 2009 12:57 schreef Iblis het volgende:
[..]
Welnu. Je wilt de breuk splitsen, en je krijgt drie breuken met in de teller respectievelijk A, B en C. Als je die gesplitste breuken weer onder een noemer brengt krijg je dus (in dit geval) A*(s + 2)*(s + 4) + B*s*(s + 4) + C*s*(s + 2) als teller, die moet natuurlijk gelijk zijn aan '8'.
Je ziet echter dat als je die vergelijking uitschrijft dat je termen met s2, met s en constanten krijgt:
A s2 + 6 A s + 8 A + B s2 + 4 B s + C s2 + 2 C s
Dit moet natuurlijk nog steeds gelijk zijn aan 8, of wel: 0s2 + 0s + 8.
Je zou het ook zo kunnen opschrijven:
s2(A + B + C) + s(6A + 4B + 2C)s + 8A = s2*0 + s*0 + 8
Daaruit volgen dan direct de drie vergelijkingen.
Oke top, ik snap het nu, bedankt
(X is in dit geval GDP en Y een "geluks"-indicator)
Vereenvoudig de volgende uitdrukking zo ver mogelijk:
81a³b : 27ab³
( : is dan gewoon de breukstreep)
Ik kom dan aan 3.(a/b)² Klopt dat?
De andere antwoorden zijn:
a) 81a2 : 27b²
b) 54a^4b^4
c) 3.(a/b)²
d) 3a³b : ab³
a en d zijn ook gelijk, maar die kunnen verder vereenvoudigd.
quote:Dat is niet te interpreteren zonder meer te weten. Waarom geen regressie met x en x^2?
Stel dat we een lineaire regressie uitvoeren waaruit blijkt dat X een positief effect heeft op Y en dat dit effect significant is. Vervolgens kwadrateren we X en voeren we nog een regressie uit en nu heeft X^2 een negatief effect op Y (ook significant). Hoe is dat te interpreteren?
(X is in dit geval GDP en Y een "geluks"-indicator)
quote:Whoei
Dat klopt.
a en d zijn ook gelijk, maar die kunnen verder vereenvoudigd.
√81d^3 - √24d² is ook te schrijven als: [de wortel loopt helemaal door]
a. 9d√d - d √24
b. 9d√d - 2d√6
c. d√57
d. √57d
Ik zou voor c gaan...
Dat ga ik even opschrijven in mijn grm
quote:Ik moet nog om nieuwe duracell batterijen...
Ik hoop dat de batterijen net op zijn bij die toets
Ik heb ook nog een paar vergelijkingen...
quote:Oja, dom
[..]
[ afbeelding ]
is die toets morgen ofzo?
Wortel 4 is natuurlijk 2.
Nee, die toets is donderdag, maar blegh... ik moet hem halen & ik zit stiekem te stressen
Hij heeft nu deze sommen op BB gezet, maar dan ga ik van alles proberen, terwijl ik het toch niet snap....Ik moet sowieso nog even op de vergelijkingen gaan zitten, maar dat gaat beter als ik een goede uitleg/uitwerking heb i.p.v. alleen de antwoorden - maar die pipo zet geen uitwerkingen online
Jullie lachen mij vast allemaal uit, maar ik ben gewoon een wiskunde-ramp
En die eerste is sowieso goed, volgens mij...
quote:dat ik je uitlach heeft een andere oorzaak
Jullie lachen mij vast allemaal uit, maar ik ben gewoon een wiskunde-ramp
En die eerste is sowieso goed, volgens mij...
18: = 5log(1/8 * 16) = 5log(2) = log(2) / log(5), rekenmachinewerk
19: 10log is een stijgende functie, dus je krijgt x-2 < 12 (anders klapt het teken om). Dit levert x < 14. Log uit 0 of een negatief getal kan niet, dus x-2 > 0, dus tevens x>2.
15: schrijf om naar x² - 2x + 1 = ax ofwel x² -(2+a)x + 1 = 0. Gebruik de discriminant
7: x-3 = 2(x²-9) ofwel x-3 = 2x² - 18 ofwel 2x² -x - 15 = 0, abc-formule
3: alles keer x: 3x² - 24x = 3 + 24x ofwel 3x² - 48x - 3 = 0, abc-formule.
[ Bericht 0% gewijzigd door GlowMouse op 15-06-2009 21:23:09 ]
quote:Op maandag 15 juni 2009 21:13 schreef GlowMouse het volgende:
[..]
dat ik je uitlach heeft een andere oorzaak
18: = 5log(1/8 * 16) = 5log(1/2) = log(1/2) / log(5), rekenmachinewerk
Laat die rekenmachine nou maar met rust ...
quote:De laatste keer dat ik zo'n ding heb aangeraakt kan ik mij niet herinneren. Maar ik heb discalculie dus ik maak veel fouten en ik kan daar niks aan doenOp maandag 15 juni 2009 21:20 schreef Riparius het volgende:
[..]
Laat die rekenmachine nou maar met rust ...
quote:Ik ga dit morgen lezen, want er vallen nu geen euro's
[..]
dat ik je uitlach heeft een andere oorzaak
18: = 5log(1/8 * 16) = 5log(2) = log(2) / log(5), rekenmachinewerk
19: 10log is een stijgende functie, dus je krijgt x-2 < 12 (anders klapt het teken om). Dit levert x < 14. Log uit 0 of een negatief getal kan niet, dus x-2 > 0, dus tevens x>2.
15: schrijf om naar x² - 2x + 1 = ax ofwel x² -(2+a)x + 1 = 0. Gebruik de discriminant
7: x-3 = 2(x²-9) ofwel x-3 = 2x² - 18 ofwel 2x² -x - 15 = 0, abc-formule
3: alles keer x: 3x² - 24x = 3 + 24x ofwel 3x² - 48x - 3 = 0, abc-formule.
Ja.. omdat ik verstoppertje deed? Haha. Ik ga gewoon donderdag heel de dag op de UvT sommetjes maken
quote:Komop, ik zie dat je je VWO hebt afgemaakt, dan doe je dit toch in 10 minuten? Bij 7. moet je trouwens even opletten, de oplossing die GlowMouse geeft gaat niet helemaal goed als je blind op de abc-formule afgaat. Hier kun je gebruik maken van het feit dat x2 - 9 = (x + 3)(x - 3).Op maandag 15 juni 2009 21:24 schreef automatic_ het volgende:
[..]
Ik ga dit morgen lezen, want er vallen nu geen euro's
Ja.. omdat ik verstoppertje deed? Haha. Ik ga gewoon donderdag heel de dag op de UvT sommetjes maken
quote:VWO? Ik zie het niet.
[..]
Komop, ik zie dat je je VWO hebt afgemaakt, dan doe je dit toch in 10 minuten? Bij 7. moet je trouwens even opletten, de oplossing die GlowMouse geeft gaat niet helemaal goed als je blind op de abc-formule afgaat. Hier kun je gebruik maken van het feit dat x2 - 9 = (x + 3)(x - 3).
Oplossing altijd controleren als je met breuken werkt
Merkwaardige producten lijkt me trouwens teveel gevraagd, als ik de overige vragen zie.quote:De dame doet psychologie aan de UvT, dus ik ging ervan uit dat ze wel een VWO (of equivalent) diploma heeft. Maar dat hoeft inderdaad niet persé.Op maandag 15 juni 2009 21:45 schreef GlowMouse het volgende:
[..]
VWO? Ik zie het niet.
Oplossing altijd controleren als je met breuken werkt
En waarom zouden merkwaardige producten teveel gevraagd zijn als je wel wordt geacht de abc-formule te begrijpen?
quote:Mag je die dan tegelijk gebruiken?Op maandag 15 juni 2009 20:43 schreef GlowMouse het volgende:
[..]
Dat is niet te interpreteren zonder meer te weten. Waarom geen regressie met x en x^2?
quote:tuurlijk
je moet alleen even opletten met de interpretatie.[ Bericht 4% gewijzigd door GlowMouse op 15-06-2009 22:59:04 ]
quote:Op maandag 15 juni 2009 21:36 schreef Riparius het volgende:
[..]
Komop, ik zie dat je je VWO hebt afgemaakt, dan doe je dit toch in 10 minuten?
quote:De één heeft moeite met wiskunde, de ander kennelijk met lezen.Op maandag 15 juni 2009 21:03 schreef automatic_ het volgende:
Jullie lachen mij vast allemaal uit, maar ik ben gewoon een wiskunde-ramp
quote:Nee, is gewoon een gebrek aan zelfvertrouwen.Op maandag 15 juni 2009 23:04 schreef Haushofer het volgende:
[..]
[..]
De één heeft moeite met wiskunde, de ander kennelijk met lezen.
quote:Ik heb geen VWO gedaan en dat is het hele probleem.
[..]
Komop, ik zie dat je je VWO hebt afgemaakt, dan doe je dit toch in 10 minuten? Bij 7. moet je trouwens even opletten, de oplossing die GlowMouse geeft gaat niet helemaal goed als je blind op de abc-formule afgaat. Hier kun je gebruik maken van het feit dat x2 - 9 = (x + 3)(x - 3).
Ik heb havo gedaan, HBO afgemaakt en doe nu WO & daarom moet ik zo'n debiele wiskunde-toets maken
quote:Een beetje het Idols-idee bedoel je, dat als je echt heel graag wilt dat je dan ook echt kunt.Op dinsdag 16 juni 2009 01:21 schreef Riparius het volgende:
[..]
Nee, is gewoon een gebrek aan zelfvertrouwen.
quote:Dat klinkt dan weer een beetje te 'amerikaans' als ik het zo mag zeggen. Het is helaas niet zo dat iedereen alles kan bereiken wat hij of zij zou willen. Maar een beetje VWO wiskunde is voor een redelijk intelligent persoon echt niet te hoog gegrepen. Ik heb vaker mensen bijles gegeven op VWO niveau die er in het begin werkelijk niks van bakten en door zichzelf en hun docenten allang waren afgeschreven.Op dinsdag 16 juni 2009 17:40 schreef Haushofer het volgende:
[..]
Een beetje het Idols-idee bedoel je, dat als je echt heel graag wilt dat je dan ook echt kunt.
Grappig dat je Idols noemt in dit verband, daar moet ik even iets over kwijt. Jaren geleden, in een periode dat ik een jongen intensief bijlas gaf, had ik een rare droom. Ik zat bij Idols samen met Jerney Kaagman en Henkjan Smits achter de jurytafel en er waren audities. Alleen moesten de kandidaten niet zingen maar op de stip op zo'n flip-over sheet een stelling bewijzen (!). Op een gegeven moment kwam ook de jongen die ik bijles gaf binnen, maar vreemd genoeg droeg hij nu wel zo'n typisch Jamai-brilletje. Hij moest de cosinusregel bewijzen, maar bracht er niks van terecht. Jerney, Henkjan en ikzelf keken elkaar aan en concludeerden hoofdschuddend dat hij 'niet door' was. Een week of zo later kwam ik weer bij de jongen thuis om hem bijles te geven. Toen hij de deur opendeed, zag ik het meteen. Het bleek dat hij een bril had aangeschaft. Inderdaad, precies dat Jamai-model dat ik in mijn droom had gezien! Hij is later overigens met een 8 voor wiskunde geslaagd voor zijn VWO. Het kan dus echt.
Ik snap dit niet & ik kan het zo 1,2,3 ook niet vinden hoe ze aan het antwoord komen.
Het zijn trouwens twee aparte sommen.
Bij de bovenste:
Los de vergelijking op en kies het juiste interval:
a) [-1,0]
b) [1,2]
c <-1, 1>
d <-1,0>
De onderste: dat is dus e^(x-a)
a) a = 1
b) a = x-1
c) a = x
d) a = 0
2. ik zie geen vergelijking
quote:Dan snap ik de opgave nog niet.
Sorry, je moet dan A oplossen bij de tweede...
Komt ie:
a) a = 1
b) a = x-1
c) a = x
d) a = 0
Ik dacht dat het dan abwortelc was, maar bij de antwoorden staat ab+awortelc als goede
Het functieverband tussen twee variabelen y en x is y(x)=In(x)²
Voor welk interval geldt y(x)>4
a) x > e²
b) x > (met streepje eronder) e²
c) x < e²
d) x < (met streepje eronder) e²
Ik typte hem goed over
Vreemd... Maar goed; er zitten wel meer fouten in zijn tentamens
Dat e en In gedoe snap ik echt niet... Misschien toch maar even mijn boek zoeken.
quote:De clou is hier dat je ziet dat de nulde macht van elk getal gelijk is aan 1. Dus geldt ook e0 = 1. Daarom kunnen we de vergelijking ook schrijven als:Op dinsdag 16 juni 2009 19:01 schreef automatic_ het volgende:
Ik zie het nu pas, haha.
Komt ie:Los a uit de vergelijking e^(x-a) = 1 op
a) a = 1
b) a = x-1
c) a = x
d) a = 0
ex-a = e0
En dus hebben we:
x - a = 0
En dus:
a = x.
Ik begrijp niet hoe je antwoordenboekje uitkomt op a = 0. Dat zou alleen kloppen als je al weet dat x gelijk is aan 0, maar dat is niet gegeven.
quote:Als je bedoelt √(a2(b2 + c)), dan kun je dit schrijven alsDoorlopende wortel a²(b²+c) - vereenvoudig zo ver als mogelijk:
Ik dacht dat het dan abwortelc was, maar bij de antwoorden staat ab+awortelc als goede
a√(b2 + c),
maar dan moet a wel een niet-negatief reëel getal zijn.
quote:Kun je niet even een scan van deze opgave plaatsen? Is mij een beetje te onduidelijk zo.En tenslotte (dan stop ik):
Het functieverband tussen twee variabelen y en x is y(x)=In(x)²
Voor welk interval geldt y(x)>4
a) x > e²
b) x > (met streepje eronder) e²
c) x < e²
d) x < (met streepje eronder) e²
quote:Ik heb hem even duidelijker gemaakt (zo staat hij precies op papier)
Kun je niet even een scan van deze opgave plaatsen? Is mij een beetje te onduidelijk zo.
Het functieverband tussen twee variabelen y en x is y(x)=In(x)²
Voor welk interval geldt y(x)>4
a) x > e²
b) x > e²
c) x < e²
d) x < e²
quote:Ik ben nogal van de precieze stapjes
quote:"de e-macht pakken" snap ik al nietln(x)² > 4
dus ln(x) < -2 of ln(x) > 2.
de e-macht pakken:
x < e^(-2) of x > e².
In mijn beleving sla je een stapje over ofzo, want je bent al meteen bij het juiste antwoord.
Ik ga het hoofdstuk over e en In nog wel even lezen, misschien dat het dan duidelijker is voor mij.
quote:Ah, dank je. Je bedoelde dus de tekens ≥ (groter dan of gelijk aan) en ≤ (kleiner dan of gelijk aan).Op dinsdag 16 juni 2009 19:24 schreef automatic_ het volgende:
Oke... Ik moet nog echt even op die sommen gaan zitten vrees ik.
[..]
Ik heb hem even duidelijker gemaakt (zo staat hij precies op papier)
Het functieverband tussen twee variabelen y en x is y(x)=In(x)²
Voor welk interval geldt y(x)>4
a) x > e²
b) x > e²
c) x < e²
d) x < e²
Weet je trouwens zeker dat in je opgave staat ln(x)2 en niet ln(x2) ? Het probleem is namelijk dat je
ln(x)2
zou moeten opvatten als:
{ln(x)}2,
en dan is geen van de gegeven antwoorden (geheel) juist. Ik begin nu wel grote twijfels te krijgen aan de competentie van degene die de opgaven heeft gemaakt ...
[ Bericht 0% gewijzigd door Riparius op 16-06-2009 19:48:38 ]
morgen tentamen wiskunde maar ik kwam niet uit een vraag waarvan ik vrijwel zeker weet dat die morgen gevraagd wordt.
hier komt hij dan:
Gegeven formule f(x)=x*wortel(x)
De grafiek wordt ingesloten door de y-as en de lijn x=4. Zo ontstaat vlakdeel V. D Inhoud van het lichaam M ontstaat als je vlakdeel V wentelt om de Y-as.
Ik weet dat de formule voor de inhoud van een wenteling om de y-as de integraal van 0-4 van pi x^2 dy is.
En dat ik y=x*wortel(x) moet schrijven als x=....
Nu komt het probleem, als ik dat probeer kom ik steeds uit op x=(y^2)/(x^2).
En shit wat is het irritant om formules te typen op de computer...
Iemand die verstandiger is dan ik en me kan helpen?
quote:Ja, maar zoals je zelf al had gevonden geldt y(x) > 4 ook voor x < e-2. De bij c en d genoemde 'intervallen' (die helemaal geen intervallen zijn, maar ongelijkheden) omvatten dus ook waarden van x waarvoor geldt y(x) > 4. Ik vermoed dan ook dat de maker van de opgave ln(x2) bedoelde, ook al omdat logaritmen van negatieve getallen niet reëel zijn en de logaritme van 0 niet is gedefinieerd.
[ Bericht 3% gewijzigd door Riparius op 16-06-2009 20:06:03 ]
quote:Nee toch? Wat is je waarde van y voor x = 4?Op dinsdag 16 juni 2009 19:37 schreef mcbacon0 het volgende:
Ok, eerste post op dit forum, gelijk een vraag.
morgen tentamen wiskunde maar ik kwam niet uit een vraag waarvan ik vrijwel zeker weet dat die morgen gevraagd wordt.
hier komt hij dan:
Gegeven formule f(x)=x*wortel(x)
De grafiek wordt ingesloten door de y-as en de lijn x=4. Zo ontstaat vlakdeel V. D Inhoud van het lichaam M ontstaat als je vlakdeel V wentelt om de Y-as.
Ik weet dat de formule voor de inhoud van een wenteling om de y-as de integraal van 0-4 van pi x^2 dy is.
quote:Je kunt gewoon wortels typen hoor.En dat ik y=x*wortel(x) moet schrijven als x=....
Nu komt het probleem, als ik dat probeer kom ik steeds uit op x=(y^2)/(x^2).
En shit wat is het irritant om formules te typen op de computer...
Iemand die verstandiger is dan ik en me kan helpen?
Je hebt:
y = x√x = x3/2,
En dus:
x = y2/3
Lukt het nu?
[ Bericht 0% gewijzigd door Riparius op 16-06-2009 23:50:00 ]
Dank voor het antwoord, kwam er echt even niet uit. Het lukt zo wel verder.
Op zich lukt de matrix rekenarij er omheen heel aardig.
Maar ik zit vast op een soort theorievraag.
Op een bepaald moment in de berekening bij het rechtzetten van kegelsnedes wordt een 'diagonaal matrix' gebruikt. Hieruit staan de eigenwaarden van de betreffende eigenvectoren op de hoofddiagonaal.
Nu is het zo dat als de kleinste eigenwaarde in de linkerbovenhoek van de matrix (dus plek a1,1) wordt geplaatst, dat dit tot gevolg heeft dat de kegelsnede zodanig kantelt dat de brandpunten precies op de x-as terechtkomen.
Maar dit kan ik niet verklaren waarom dit zo is. Wie wel?!
quote:Ja. (Was even denken, maar wat bij zegt klopt omdat het de diagonaalmatrix is).Op woensdag 17 juni 2009 21:46 schreef thabit het volgende:
De vergelijking voor de kegelsnede wordt dan ax2 + by2 = c met a en b de eigenwaarden, neem ik aan?
quote:Hoewel, in het algemeen komen er nog termen ex + dy bij natuurlijk, maar die kun je meestal wegwerken met kwadraat afsplitsen (alleen als a=0 blijft ex staan).Op woensdag 17 juni 2009 21:46 schreef thabit het volgende:
De vergelijking voor de kegelsnede wordt dan ax2 + by2 = c met a en b de eigenwaarden, neem ik aan?
Dus enkel y2 en x2.
quote:Okee, maar dan kun je geen parabool meer krijgen.Op woensdag 17 juni 2009 22:03 schreef Borizzz het volgende:
dx en ey werk je al weg, je hebt de diagonaalmatrix al. Op de xy plaatsen in de matrix staat al een 0.
Dus enkel y2 en x2.
quote:Een draaiing van het vlak om de oorsprong kun je altijd weergeven aan de hand van een orthogonale matrix O. Als je je kegelsnede aan de hand van een symmetrische matrix S opschrijft, dan zal de matrix van de geroteerde kegelsnede verkregen worden door S met O te conjugeren.Op woensdag 17 juni 2009 21:57 schreef Borizzz het volgende:
Ik heb al 3 van dit soort sommen geroteerd en dingetjes uitgerekend. Maar ik zie niet wat de draairichting veroorzaakt en waarom het nu ook precies op de x-as komt te liggen.
Hierin staan eigenwaarden op de hoofdiagonaal.
Maar de vraag is: als ik de kleinste eigenwaarde in D linksboven in zet, waarom levert dit een draaiing op zó dat het brandpunt op de x-as komt te liggen.
Maar ik dacht zelf dat t 'm ook kan zitten in de eigenvectoren.
Vanuit de eigenvector kun je de draaihoek berekenen.
De eignwaarde heeft daar een band mee.
quote:Dan vertellen ze toch iets over de draaihoek x?Op woensdag 17 juni 2009 22:33 schreef thabit het volgende:
De eigenvectoren zijn de assen van de kegelsnede.
quote:Daar gebruik je dus ook die orthogonale matrix voor: die verplaatst de eigenvectoren naar vectoren langs de x- en y- as.Op woensdag 17 juni 2009 22:36 schreef Borizzz het volgende:
[..]
Dan vertellen ze toch iets over de draaihoek x?
Nog ns over nadenken. Bedankt ieg.
quote:Meen je dat? Dat lijkt me iemand die een rekenmachine met 9 cijfers had en de rest maar met 0'en heeft aangevuld. Wat ontstellend knullig. Machten van twee moeten natuurlijk altijd op 2, 4, 8 of 6 eindigen. (En in die volgorde, dus 264 eindigt in ieder geval op een 6.)
Ik zag vandaag wat lesmateriaal van die docent van automatic_. Stond in dat 264 = 18446744070000000000 (of in ieder geval iets met veel nullen op het eind). Vreemde docent, er staat helemaal geen vijf in de factorisatie links
.