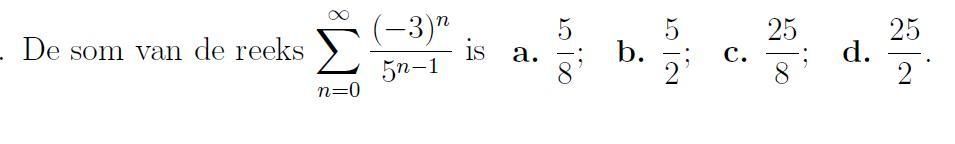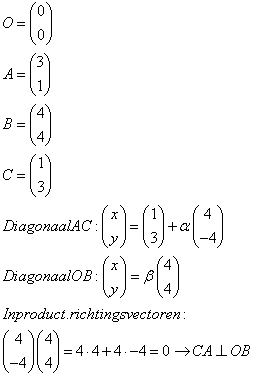SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vorige deel: [Bèta wiskunde] 'Huiswerk- en vragentopic'.
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Wiskundig inhoudelijk:
http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
OP
[ Bericht 2% gewijzigd door GlowMouse op 31-03-2009 21:38:11 ]
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Wiskundig inhoudelijk:
OP
[ Bericht 2% gewijzigd door GlowMouse op 31-03-2009 21:38:11 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


tvp
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***


Ben ik weer 
Ja weer reeksen/rijen, kheb de stof al aardig onder de knie, alleen deze nog niet, terwijl het altijd de eerste vragen van het tentamen zijn

Ik doe het zo.
Dit "moet" kloppen, want als ik beide rijen in mijn gr invoer komen er dezelfde antwoorden uit.
Dus zou de som deze meetkundige rij -3/(1+(3/5)) zijn toch? Maar dat geeft -15/8 als antwoord. wat er niet tussen staat.
Wat doe ik fout?
alvast bedankt
[ Bericht 5% gewijzigd door motorbloempje op 01-09-2013 20:47:37 ]
Ja weer reeksen/rijen, kheb de stof al aardig onder de knie, alleen deze nog niet, terwijl het altijd de eerste vragen van het tentamen zijn
Ik doe het zo.
Dit "moet" kloppen, want als ik beide rijen in mijn gr invoer komen er dezelfde antwoorden uit.
Dus zou de som deze meetkundige rij -3/(1+(3/5)) zijn toch? Maar dat geeft -15/8 als antwoord. wat er niet tussen staat.
Wat doe ik fout?
alvast bedankt
[ Bericht 5% gewijzigd door motorbloempje op 01-09-2013 20:47:37 ]
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Je reeks is met termen tot de macht n-1, maar de somformule die je toepast is voor termen tot de macht n. In plaats van een factor 3 naar voren te halen had je dus beter een factor 5 naar voren kunnen halen.


Ik begrijp niet precies wat je bedoelt. Maar ik zie wel in dat de eerste term 5 = en niet 3 zoals ik al dacht. Omdat de reeks met n=0 begint --> Ao = 5. (Dat bedoel je zeker ookquote:Op woensdag 25 maart 2009 22:32 schreef thabit het volgende:
Je reeks is met termen tot de macht n-1, maar de somformule die je toepast is voor termen tot de macht n. In plaats van een factor 3 naar voren te halen had je dus beter een factor 5 naar voren kunnen halen.
Dan klopt die rijverhouding ook niet. Dan is het wel 5/(1+(3/5)) = 25/8 (en dat is het goede antwoord)
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


quote:Op dinsdag 24 maart 2009 13:24 schreef GlowMouse het volgende:
Gebruik \frac{teller}{noemer} voor breuken, anders kun je net zo goed geen tex gebruiken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


-
[ Bericht 99% gewijzigd door motorbloempje op 01-09-2013 20:47:56 ]
[ Bericht 99% gewijzigd door motorbloempje op 01-09-2013 20:47:56 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het kan uiteraard op verschillende manieren, maar je hoeft niet eens een factor voor het somteken te halen. Kijk eerst wat de eerste term a van je reeks is, die krijg je hier door n=0 te nemen. Kijk dan wat de reden r is. De som van je (convergente) reeks is dan a/(1-r).quote:Op woensdag 25 maart 2009 22:38 schreef Agiath het volgende:
[..]
Ik begrijp niet precies wat je bedoelt. Maar ik zie wel in dat de eerste term 5 = en niet 3 zoals ik al dacht. Omdat de reeks met n=0 begint --> Ao = 5. (Dat bedoel je zeker ook)
Dan klopt die rijverhouding ook niet. Dan is het wel 5/(1+(3/5)) = 25/8 (en dat is het goede antwoord)


Zo kan het natuurlijk ook, bedanktquote:
Ik snap het, bedankt.quote:Op woensdag 25 maart 2009 22:42 schreef Riparius het volgende:
[..]
Het kan uiteraard op verschillende manieren, maar je hoeft niet eens een factor voor het somteken te halen. Kijk eerst wat de eerste term a van je reeks is, die krijg je hier door n=0 te nemen. Kijk dan wat de reden r is. De som van je (convergente) reeks is dan a/(1-r).
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


OK. Uitwerking van je opgave van gisteren ook gesnapt? Want die was toch iets lastiger dan een simpele meetkundige reeks sommeren.quote:Op woensdag 25 maart 2009 22:47 schreef Agiath het volgende:
[..]
Zo kan het natuurlijk ook, bedankt
[..]
Ik snap het, bedankt.


Ja, net nog even grondig doorgelezen en ik snap het helemaal. Bedanktquote:Op woensdag 25 maart 2009 22:49 schreef Riparius het volgende:
[..]
OK. Uitwerking van je opgave van gisteren ook gesnapt? Want die was toch iets lastiger dan een simpele meetkundige reeks sommeren.
En ik blijf zeggen dat ik die dingen (limit comparison test) nog steeds makkelijker vind dan die sommen.
Maargoed het is 11 uur geweest en het is mooi geweest voor vandaag.
Ik denk dat ik morgen misschien nog wel terug kom met wat vraagjes
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Even een vraagje over gegevens in mijn Casio TI-83.
Ik heb zojuist een normale functie ingevuld bij Y1 en nu wil ik daar een grafiek bij hebben. Ik heb de juiste window-waarden genomen, maar hij geeft een soort puntgrafiek weer. Ik wil helemaal geen puntgrafiek, ik wil een normale lijngrafiek!
Kan iemand mij helpen de grafiek te veranderen?
Ik heb zojuist een normale functie ingevuld bij Y1 en nu wil ik daar een grafiek bij hebben. Ik heb de juiste window-waarden genomen, maar hij geeft een soort puntgrafiek weer. Ik wil helemaal geen puntgrafiek, ik wil een normale lijngrafiek!
Kan iemand mij helpen de grafiek te veranderen?
hier kommt die Sonne!
alias Idril-2, alias anneVi
alias Idril-2, alias anneVi


Ja ik weet hoe dit moet.quote:Op donderdag 26 maart 2009 19:21 schreef anne_Chris het volgende:
Even een vraagje over gegevens in mijn Casio TI-83.
Ik heb zojuist een normale functie ingevuld bij Y1 en nu wil ik daar een grafiek bij hebben. Ik heb de juiste window-waarden genomen, maar hij geeft een soort puntgrafiek weer. Ik wil helemaal geen puntgrafiek, ik wil een normale lijngrafiek!
Kan iemand mij helpen de grafiek te veranderen?
Ga met je 'cursor' helemaal links van Y1 staan en daar kan je kiezen wat voor grafiek je wilt hebben. (dik dun, lijntjes etc.)
Gewoon weer op dun lijntje zetten daar
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Vector rekenen. Het zal wel heel simpel zijn maar ik weet dus niet wat ik moet doen:
Met hoofdletters bedoel ik punten, met kleine letters vectoeren.
De vragen:
a) Als hoekpunten A,B,C van driehoek ABC in het platte vlak worden geïdentificeerd met de positievectoren a,b,c, dan blijkt het punt (a+b+c)/3 op de zwaartelijn vanuit A te liggen. Reken na.Conclusie?
Mijn antwoord: in principe gaat het er om om dmv van vectoren aan te tonen dat het zwaartepunt van de driehoek op de zwaartelijn vanuit A ligt.
Positievector begint vanuit O. Ik heb a/3+b/3+c/3 getrokken. De genoemde zwaartelijn zal moeten zijn a+labda*(0,5b+0,5c-a). a is de steunvector en 0,5b-0,5c - a is de richtinsvector van de lijn. Dan heb ik een vergelijking van een lijn in vectoren en een punt. Hoe verder of heb ik de verkeerde aanpak. Ik zie niet wat ik doen moet.
b) Als hoekpunten punten A,B,C,D in de ruimte worden geïdentificeerd met de positievectoren a,b,c,d dan blijkt het punt (a+b+c+d)/4 te liggen op de lijn vanuit A naar het zwaartepunt van driehoek BCD. Reken na! Conclusie?
Ook hier. Zwaartepunt van een driehoek is a/3+b/3+c/3. Lijn van a naar het zwaartepunt heeft dan ri. vector a/3+b/3-c/3 - a. En dus is de vlg van de lijn a (steunvector+ richtingsvector) a+labda*( a/3+b/3-c/3 - a).....
Hoe zit dit?!
[ Bericht 11% gewijzigd door Borizzz op 26-03-2009 21:04:55 ]
Met hoofdletters bedoel ik punten, met kleine letters vectoeren.
De vragen:
a) Als hoekpunten A,B,C van driehoek ABC in het platte vlak worden geïdentificeerd met de positievectoren a,b,c, dan blijkt het punt (a+b+c)/3 op de zwaartelijn vanuit A te liggen. Reken na.Conclusie?
Mijn antwoord: in principe gaat het er om om dmv van vectoren aan te tonen dat het zwaartepunt van de driehoek op de zwaartelijn vanuit A ligt.
Positievector begint vanuit O. Ik heb a/3+b/3+c/3 getrokken. De genoemde zwaartelijn zal moeten zijn a+labda*(0,5b+0,5c-a). a is de steunvector en 0,5b-0,5c - a is de richtinsvector van de lijn. Dan heb ik een vergelijking van een lijn in vectoren en een punt. Hoe verder of heb ik de verkeerde aanpak. Ik zie niet wat ik doen moet.
b) Als hoekpunten punten A,B,C,D in de ruimte worden geïdentificeerd met de positievectoren a,b,c,d dan blijkt het punt (a+b+c+d)/4 te liggen op de lijn vanuit A naar het zwaartepunt van driehoek BCD. Reken na! Conclusie?
Ook hier. Zwaartepunt van een driehoek is a/3+b/3+c/3. Lijn van a naar het zwaartepunt heeft dan ri. vector a/3+b/3-c/3 - a. En dus is de vlg van de lijn a (steunvector+ richtingsvector) a+labda*( a/3+b/3-c/3 - a).....
Hoe zit dit?!
[ Bericht 11% gewijzigd door Borizzz op 26-03-2009 21:04:55 ]
kloep kloep


Het is b/2 + c/2 - a, niet b/2 - c/2 - a. Vervolgens vul je lambda=2/3 in.quote:Op donderdag 26 maart 2009 20:21 schreef Borizzz het volgende:
Vector rekenen. Het zal wel heel simpel zijn maar ik weet dus niet wat ik moet doen:
Met hoofdletters bedoel ik punten, met kleine letters vectoeren.
De vragen:
a) Als hoekpunten A,B,C van driehoek ABC in het platte vlak worden geïdentificeerd met de positievectoren a,b,c, dan blijkt het punt (a+b+c)/3 op de zwaartelijn vanuit A te liggen. Reken na.Conclusie?
Mijn antwoord: in principe gaat het er om om dmv van vectoren aan te tonen dat het zwaartepunt van de driehoek op de zwaartelijn vanuit A ligt.
Positievector begint vanuit O. Ik heb a/3+b/3+c/3 getrokken. De genoemde zwaartelijn zal moeten zijn a+labda*(0,5b+0,5c-a). a is de steunvector en 0,5b-0,5c - a is de richtinsvector van de lijn. Dan heb ik een vergelijking van een lijn in vectoren en een punt. Hoe verder of heb ik de verkeerde aanpak. Ik zie niet wat ik doen moet.


Waarom dan labda=2/3? Dit komt voor mij uit de lucht vallen... Kun je die uitrekenen.quote:Op donderdag 26 maart 2009 21:35 schreef thabit het volgende:
[..]
Het is b/2 + c/2 - a, niet b/2 - c/2 - a. Vervolgens vul je lambda=2/3 in.
Of heeft dit de maken met het feit dat labda willekeurig is en dat verschillende waarden van labda verschillende punten op de lijn aanwijzen. En dan labda=2/3 dan ingevuld in de vergelijking het punt a/3 + b/3 + c/3 aanwijst?
kloep kloep


Wel, de coefficienten van a, b en c moeten alle drie gelijk worden gemaakt aan 1/3. Er staat a - lambda*a + ... . Dus moet lambda = 2/3 gelden en dan zijn na inspectie ook de coefficienten van b en c correct.quote:Op donderdag 26 maart 2009 21:37 schreef Borizzz het volgende:
[..]
Waarom dan labda=2/3? Dit komt voor mij uit de lucht vallen... Kun je die uitrekenen.
Of heeft dit de maken met het feit dat labda willekeurig is en dat verschillende waarden van labda verschillende punten op de lijn aanwijzen. En dan labda=2/3 dan ingevuld in de vergelijking het punt a/3 + b/3 + c/3 aanwijst?


Ok dank je. De b) vraag zal dan wel op een vergelijkbare manier gaan.quote:Op donderdag 26 maart 2009 21:41 schreef thabit het volgende:
[..]
Wel, de coefficienten van a, b en c moeten alle drie gelijk worden gemaakt aan 1/3. Er staat a - lambda*a + ... . Dus moet lambda = 2/3 gelden en dan zijn na inspectie ook de coefficienten van b en c correct.
kloep kloep


Ik denk niet dat dit de bedoeling is, want concluderen dat het zwaartepunt op de zwaartelijn vanuit A ligt is een dooddoener. Het zwaartepunt in een driehoek is het snijpunt van de zwaartelijnen, en natuurlijk ligt het zwaartepunt dan op elk van de zwaartelijnen. Volgens mij is het eerder de bedoeling dat je op grond van symmetrie-overwegingen hieruit concludeert dat het bedoelde punt op elk van de drie zwaartelijnen vanuit A, B en C ligt, en dat de drie zwaartelijnen dus door één punt gaan. Een soort vectorbewijs dus voor de stelling uit de elementaire meetkunde dat de drie zwaartelijnen van een driehoek door één punt gaan.quote:Op donderdag 26 maart 2009 20:21 schreef Borizzz het volgende:
Vector rekenen. Het zal wel heel simpel zijn maar ik weet dus niet wat ik moet doen:
Met hoofdletters bedoel ik punten, met kleine letters vectoeren.
De vragen:
a) Als hoekpunten A,B,C van driehoek ABC in het platte vlak worden geïdentificeerd met de positievectoren a,b,c, dan blijkt het punt (a+b+c)/3 op de zwaartelijn vanuit A te liggen. Reken na.Conclusie?
Mijn antwoord: in principe gaat het er om om dmv van vectoren aan te tonen dat het zwaartepunt van de driehoek op de zwaartelijn vanuit A ligt.
Een vectorvoorstelling van de zwaartelijn door A is inderdaad za = a + λ∙(½∙b + ½∙c - a). Voor λ = 0 zit je in punt A en voor λ = 1 in het midden van lijnstuk BC.quote:Positievector begint vanuit O. Ik heb a/3+b/3+c/3 getrokken. De genoemde zwaartelijn zal moeten zijn a+labda*(0,5b+0,5c-a). a is de steunvector en 0,5b+0,5c - a is de richtingsvector van de lijn. Dan heb ik een vergelijking van een lijn in vectoren en een punt. Hoe verder of heb ik de verkeerde aanpak. Ik zie niet wat ik doen moet.
Je weet ook uit de elementaire meetkunde dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1met het langste stuk aan de kant van het hoekpunt, dus voor λ = 2/3 zit je in het zwaartepunt. En inderdaad is a + 2/3∙(½∙b + ½∙c - a) = 1/3∙a + 1/3∙ b + 1/3∙c. Zo, nu mag je zelf weer even verder puzzelen ...
[ Bericht 0% gewijzigd door Riparius op 26-03-2009 22:00:05 ]


ff checken
If A is the area of a circle with radius r and the circle expands as time passes, find dA/dt in terms of dr/dt.
dA/dt = pi * (dr/dt)^2
Is dit het goede antwoord?
If A is the area of a circle with radius r and the circle expands as time passes, find dA/dt in terms of dr/dt.
dA/dt = pi * (dr/dt)^2
Is dit het goede antwoord?


hoi,
ik moet voor een wiskunde po de naam geven van een ruimtelijk figuur, eentje heb ik al gevonden maar de andere zou ik echt niet weten.
even een korte beschrijving van het figuur:
het gaat om een afgeknotte piramide (4 hoeken) met daarop nog een piramide.
dat is de afgeknotte piramide
en deze zit er dan bovenop:
alvast bedankt!
ik moet voor een wiskunde po de naam geven van een ruimtelijk figuur, eentje heb ik al gevonden maar de andere zou ik echt niet weten.
even een korte beschrijving van het figuur:
het gaat om een afgeknotte piramide (4 hoeken) met daarop nog een piramide.
dat is de afgeknotte piramide
en deze zit er dan bovenop:
alvast bedankt!
no time to waste


Deze deelvraag is hiermee toch klaar? Want je toont aan door labmda=2/3 te kiezen dat het bewuste punt op de lijn ligt en dat was de vraag. Of doel je hiermee op de tweede vraag? Die is overigens nu wel gelukt.quote:Op donderdag 26 maart 2009 21:52 schreef Riparius het volgende:
Je weet ook uit de elementaire meetkunde dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1met het langste stuk aan de kant van het hoekpunt, dus voor λ = 2/3 zit je in het zwaartepunt. En inderdaad is a + 2/3∙(½∙b + ½∙c - a) = 1/3∙a + 1/3∙ b + 1/3∙c. Zo, nu mag je zelf weer even verder puzzelen ...
kloep kloep


Ja, de eerste deelvraag was in feite klaar en ik bedoelde inderdaad dat je nu zelf wel verder kon met de tweede deelvraag. Maar je zei hierboven ook dat λ = 2/3 voor jou uit de lucht kwam vallen terwijl dat natuurlijk niet zo is. Ik wilde even laten zien dat die waarde voor λ de bekende stelling weerspiegelt dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1.quote:Op vrijdag 27 maart 2009 17:53 schreef Borizzz het volgende:
[..]
Deze deelvraag is hiermee toch klaar? Want je toont aan door labmda=2/3 te kiezen dat het bewuste punt op de lijn ligt en dat was de vraag. Of doel je hiermee op de tweede vraag? Die is overigens nu wel gelukt.


Ja prima. Maar het is nu duidelijk. Maar het meetkundige verband had ik inderdaad al door. Ik heb nu wel even iets geleerd over het gebruik van lijnen die in vectornotatie staan.quote:Op vrijdag 27 maart 2009 18:08 schreef Riparius het volgende:
[..]
Ja, de eerste deelvraag was in feite klaar en ik bedoelde inderdaad dat je nu zelf wel verder kon met de tweede deelvraag. Maar je zei hierboven ook dat λ = 2/3 voor jou uit de lucht kwam vallen terwijl dat natuurlijk niet zo is. Ik wilde even laten zien dat die waarde voor λ de bekende stelling weerspiegelt dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1.
kloep kloep


Nog zoiets: een ruit en dan met vectoren laten zien dat diagonalen loodreacht staan.
Ik heb de ruit gedefinieerd met positievectoren a b c en d.
de beide diagonalen hebben dan richtingsvectoren c-a en d-b.
volgens mij gaat het er dan om dat je laat zien dat het inproduct van deze 2 richtingsvectoren 0 is.
dus (c-a)(d-b) =0 aantonen
levert mij (c-a)(d-b) = cd-cb-ad+ab = c(d-b) -a(d-b).
Maar dan ben ik er nog niet..
Ik heb de ruit gedefinieerd met positievectoren a b c en d.
de beide diagonalen hebben dan richtingsvectoren c-a en d-b.
volgens mij gaat het er dan om dat je laat zien dat het inproduct van deze 2 richtingsvectoren 0 is.
dus (c-a)(d-b) =0 aantonen
levert mij (c-a)(d-b) = cd-cb-ad+ab = c(d-b) -a(d-b).
Maar dan ben ik er nog niet..
kloep kloep


Een inproduct noteer ik als <x,y>. Bij een ruit zijn alle zijden even lang. Dus
<a-b, a-b> = <a-d, a-d> = <c-b, c-b> = <c-d, c-d>.
Als we de eerste gelijkheid uitwerken krijgen we
<a,a> - 2<a,b> + <b,b> = <a,a> - 2<a,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<a,b> - 2<a,d> = 2<a,b-d>
En bij de laatste gelijkheid krijgen we
<c,c> - 2<c,b> + <b,b> = <c,c> - 2<c,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<c,b-d>.
We zien dus <a,b-d> = <c,b-d> en als we dit naar 1 kant gooien staat er
<a-c, b-d> = <a, b-d> - <c,b-d> = 0.
<a-b, a-b> = <a-d, a-d> = <c-b, c-b> = <c-d, c-d>.
Als we de eerste gelijkheid uitwerken krijgen we
<a,a> - 2<a,b> + <b,b> = <a,a> - 2<a,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<a,b> - 2<a,d> = 2<a,b-d>
En bij de laatste gelijkheid krijgen we
<c,c> - 2<c,b> + <b,b> = <c,c> - 2<c,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<c,b-d>.
We zien dus <a,b-d> = <c,b-d> en als we dit naar 1 kant gooien staat er
<a-c, b-d> = <a, b-d> - <c,b-d> = 0.


Op die manier had ik het nog niet bekeken.
Maar ik had al een andere oplossing. Kan deze ook?
Een vierhoek heeft 4 gelijke zijden. stel vector a als een zijde en ook vector b als een zijde.
De diagonalen van deze vierhoek zijn dan (a+b) en (a-b).
Het inproduct van deze 2 is dan (a+b)(a-b) = a2 - b2.
Een eigenschap van vectoren is dat x2 = | x| 2.
dus er geldt dat (a+b)(a-b) = |a|2 - |b|2.
aangezien a en b dezelfde lengte voorstellen geldt (a+b)(a-b) = 0.
Maar ik had al een andere oplossing. Kan deze ook?
Een vierhoek heeft 4 gelijke zijden. stel vector a als een zijde en ook vector b als een zijde.
De diagonalen van deze vierhoek zijn dan (a+b) en (a-b).
Het inproduct van deze 2 is dan (a+b)(a-b) = a2 - b2.
Een eigenschap van vectoren is dat x2 = | x| 2.
dus er geldt dat (a+b)(a-b) = |a|2 - |b|2.
aangezien a en b dezelfde lengte voorstellen geldt (a+b)(a-b) = 0.
kloep kloep


Je gebruikt daar wel dat tegenover elkaar liggende diagonalen evenwijdig zijn. Ik neem aan dat dat niet in de definitie van een ruit zit?


Naja even de vraag goed herlezend: het ging om een vierhoek met evenlange zijden en tegenoverliggende zijden parallel.quote:Op vrijdag 27 maart 2009 21:19 schreef thabit het volgende:
Je gebruikt daar wel dat tegenover elkaar liggende diagonalen evenwijdig zijn. Ik neem aan dat dat niet in de definitie van een ruit zit?
kloep kloep


A street light is mounted at the top of a 15-ft-tall pole. A man 6ft tall walks away from the pole with a speed of 5 ft/s along a straight path. How fast is the tip of his shadow moving when he is 40ft from the pole?
Hoe bereken ik ook alweer waar de tip van his schaduw precies is? Dus niet het antwoord op de vraag, maar gewoon waar de tip van de schaduw is met betrekking tot de lantaarnpaal.
Hoe bereken ik ook alweer waar de tip van his schaduw precies is? Dus niet het antwoord op de vraag, maar gewoon waar de tip van de schaduw is met betrekking tot de lantaarnpaal.


Levensverzekeringswiskunde is een stom vak }:|
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen :o
Het antwoordenboek zegt dit:
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43 :N Wie heeft het verlossende antwoord?
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen :o
Het antwoordenboek zegt dit:
| 1 2 3 | 10.000 + p x ((503.387 – 167.324)/25.048) = 50.000 x (8.803,3/ 25.048) p = 564,43 |
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43 :N Wie heeft het verlossende antwoord?
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


Dit is niet goed voor mijn zelfvertrouwen, maar bedanktquote:Op zondag 29 maart 2009 19:05 schreef GlowMouse het volgende:
http://www.fi.uu.nl/toepassingen/02017/toepassing_wisweb.html
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


Ik vind het wel een mooie appletquote:Op zondag 29 maart 2009 19:06 schreef Maraca het volgende:
[..]
Dit is niet goed voor mijn zelfvertrouwen, maar bedankt
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


is het ookquote:
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


ik ben bezig met vergelijkingen oefenen voor statica, maar deze snap ik echt niet;
12/13A -A is gelijk aan 25/13 A
het zal vast heel makkelijk zijn maar...
12/13A -A is gelijk aan 25/13 A
het zal vast heel makkelijk zijn maar...


Moet dat geen 12/13A + A zijn?
12/13A + A = (12/13 + 1)A
En dan http://proto.thinkquest.nl/~klb045/h2-broptellen.html
12/13A + A = (12/13 + 1)A
En dan http://proto.thinkquest.nl/~klb045/h2-broptellen.html
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zondag 29 maart 2009 18:51 schreef Maraca het volgende:
Levensverzekeringswiskunde is een stom vak
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen
Het antwoordenboek zegt dit:
[ code verwijderd ]
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43Wie heeft het verlossende antwoord?
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
wordt
¤ 10.000 + p * 13,41675982 = 17572,....
wordt
p * 13,41675982 = 7572,....
en nu bijde kanten delen door 13,41.....
begrijpelijk ?
(vat dit niet persoonlijk op maar kon je dit nou echt niet


Wow, zo'n applet zoek ik al een tijdje. Thx.quote:
Zijn er ook applets waarmee je leert ingewikkelde stellingen te bewijzen?
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***


Het ging om een algemeen bewijs, niet om een specifieke situatie.quote:Op maandag 30 maart 2009 16:56 schreef Yannick3211 het volgende:
Met die ruit en de diagonalen, heb ik gewoon zo:
[ afbeelding ]
Maar toch bedankt
kloep kloep


Ik ken ze niet, maar als je de naam van de stelling kent, kun je natuurlijk altijd googlen op applet en de naam van de stelling. Zo'n applet lijkt me namelijk alleen werken voor die specifieke stelling.quote:Op maandag 30 maart 2009 17:38 schreef Atlanticus het volgende:
[..]
Wow, zo'n applet zoek ik al een tijdje. Thx.
Zijn er ook applets waarmee je leert ingewikkelde stellingen te bewijzen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Beste fokkers,
Heb morgen een proefwerk wiskunde over Kwadratische verbanden. En heb even een vraagje;
Hoe kun je de as van symetrie en de top uit deze formule halen;
Y= -x² + x + 6
Ik ben geen topper dus het liefst in simpele stappen uitgelegd!
Heb morgen een proefwerk wiskunde over Kwadratische verbanden. En heb even een vraagje;
Hoe kun je de as van symetrie en de top uit deze formule halen;
Y= -x² + x + 6
Ik ben geen topper dus het liefst in simpele stappen uitgelegd!


Ik heb dit nooit gehad dus voor mij is het gewoon nieuwquote:Op maandag 30 maart 2009 00:41 schreef TubewayDigital het volgende:
[..]
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
wordt
¤ 10.000 + p * 13,41675982 = 17572,....
wordt
p * 13,41675982 = 7572,....
en nu bijde kanten delen door 13,41.....
begrijpelijk ?
(vat dit niet persoonlijk op maar kon je dit nou echt niet, dit is zo elementair)
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


je zoekt voor de top de twee 0puntenquote:Op maandag 30 maart 2009 20:40 schreef Jelmer1994 het volgende:
Beste fokkers,
Heb morgen een proefwerk wiskunde over Kwadratische verbanden. En heb even een vraagje;
Hoe kun je de as van symetrie en de top uit deze formule halen;
Y= -x² + x + 6
Ik ben geen topper dus het liefst in simpele stappen uitgelegd!
-x^2+x+6=0
x^2-x-6=0
productsom:
b=-1
c=-6
pq=-6
p+q=-1
p=2
q=-3
(x+2)(x-3)=0
x=-2 v x=3
het gemiddelde van deze 2:
(-2+3)/2=1/2
dus de x-coordinaat is 1/2
invullen geeft ycoordinaat:
y=-x^2+x+6 --> y=-(1/2)^2+1/2+6=6,25
dus de coordinaten van de top zijn (1/2;6,25)
en de symmetrieas is dus de xcoordinaat van de top, dus x=1/2


kon je de top niet gewoon uitrekenen met een klein gedeelte van de abc-formule: -b/4ac?? (tis voor mij ook weer lang geleden)
I never think of the future - it comes soon enough. - Albert Einstein


-b/(2a) inderdaad, staat ook op de pagina die ik gaf.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


nou... ik doe bewegingswetenschappen maar van jou verhaal snapte ik geen moer van....
I never think of the future - it comes soon enough. - Albert Einstein


Je kunt jouw formule Y= -x² + x + 6
ook algemeen schrijven als y=ax2 +bx +c
a altijd voor het kwadraat, b voor de x en de c een getal.
in jouw formule geldt dan a=-1 b=1 en c=6.
De top van een parabool ligt altijd op de symmetrie as. Die is gelijk aan -b/2a.
dus bij jouw parabool 1/2=0,5.
nu x=0.5 in de formule invullen geeft y=6,25.
dan top (0,5 ; 6,25).
ook algemeen schrijven als y=ax2 +bx +c
a altijd voor het kwadraat, b voor de x en de c een getal.
in jouw formule geldt dan a=-1 b=1 en c=6.
De top van een parabool ligt altijd op de symmetrie as. Die is gelijk aan -b/2a.
dus bij jouw parabool 1/2=0,5.
nu x=0.5 in de formule invullen geeft y=6,25.
dan top (0,5 ; 6,25).
kloep kloep


x2ex + ex2x = xex(x + 2).quote:Op woensdag 1 april 2009 03:59 schreef nickybol het volgende:
Hoe ontbind je x^2e^x + e^x2x in factoren?


Weer een vraagje van mij
Het gaat hier om vraag b
Nu weet ik dat het antwoord moet zijn ||b-Ax|| (x= x met dakje)
Ax kan ik berekenen en Ax(dakje) = b(dakje)
Maar dan zou b-Ax toch gewoon (1/6)*[-3-,6,-1]T moeten zijn? (1-4,1-7,0-1)
Wat doe ik fout?
Het gaat hier om vraag b
Nu weet ik dat het antwoord moet zijn ||b-Ax|| (x= x met dakje)
Ax kan ik berekenen en Ax(dakje) = b(dakje)
Maar dan zou b-Ax toch gewoon (1/6)*[-3-,6,-1]T moeten zijn? (1-4,1-7,0-1)
Wat doe ik fout?
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Geen wiskundegoeroes aanwezig vandaag? 
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


(1-4,1-7,0-1) is fout. Je rekent met helen en zesden door elkaar. De eerste coordinaat is bv. 1-4/6.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op woensdag 1 april 2009 17:32 schreef GlowMouse het volgende:
(1-4,1-7,0-1) is fout. Je rekent met helen en zesden door elkaar. De eerste coordinaat is bv. 1-4/6.
Bedankt
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Nog iets wat ik niet begrijp
Nu snap ik wel dat w1*x = 0 en dat w2*x = 0
Maar waarom is w1 w1 en w2 w2?
Hoe bepaal je dat?
Wat daarna komt snap ik wel, maar hoe bepaal je die basis?
Nu snap ik wel dat w1*x = 0 en dat w2*x = 0
Maar waarom is w1 w1 en w2 w2?
Hoe bepaal je dat?
Wat daarna komt snap ik wel, maar hoe bepaal je die basis?
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


De initiële w1 en w2 kun je gewoon twee willekeurige vectoren voor pakken. Kies twee plekken vast en de derde volgt uit x1+3x2-x3=0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ja maar stel ik had w2 als w1 genomen. Had ik dan hetzelfde antwoord gekregen? Al dan niet in meervoud natuurlijkquote:Op woensdag 1 april 2009 21:43 schreef GlowMouse het volgende:
De initiële w1 en w2 kun je gewoon twee willekeurige vectoren voor pakken. Kies twee plekken vast en de derde volgt uit x1+3x2-x3=0.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Nee, een orthogonale basis is niet uniek. Maar je ziet dat je een tweedimensionale ruimte moet krijgen (driedimensionale ruimte met één lineaire restrictie), dus als jij twee orthogonale vectoren hebt die in de ruimte zitten dan ben je klaar.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb een kansberekeningsvraagstuk, ik ben zelf niet zo'n wiskunde expert, en kom er niet uit.
Stel je hebt een zak met 100 knikkers, er zitten 5 verschillende kleuren in de zak en van iedere kleur 20. Hoeveel keer moet je trekken om minstens 4 verschillend gekleurde knikkers te verkrijgen? (je trekt zonder terugleggen)
Het zou helemaal geweldig zijn als iemand kan uitleggen hoe je dit met de hand en met een GR uitrekent!
alvast superbedankt!
Stel je hebt een zak met 100 knikkers, er zitten 5 verschillende kleuren in de zak en van iedere kleur 20. Hoeveel keer moet je trekken om minstens 4 verschillend gekleurde knikkers te verkrijgen? (je trekt zonder terugleggen)
Het zou helemaal geweldig zijn als iemand kan uitleggen hoe je dit met de hand en met een GR uitrekent!
alvast superbedankt!
`either you or your head must be off, and that in about half no time! Take your choice!'


om te beginnen heeft het niks met kansberekening te maken.quote:Op donderdag 2 april 2009 12:17 schreef ALICENOR het volgende:
Ik heb een kansberekeningsvraagstuk, ik ben zelf niet zo'n wiskunde expert, en kom er niet uit.
Stel je hebt een zak met 100 knikkers, er zitten 5 verschillende kleuren in de zak en van iedere kleur 20. Hoeveel keer moet je trekken om minstens 4 verschillend gekleurde knikkers te verkrijgen? (je trekt zonder terugleggen)
Het zou helemaal geweldig zijn als iemand kan uitleggen hoe je dit met de hand en met een GR uitrekent!
alvast superbedankt!
Je moet 61 keer trekken wil je er zeker van zijn dat je minstens 4 verschillende kleuren hebt. Worst case scenario: 20 keer rood trekken, daarna 20 keer blauw trekken, daarna 20 keer groen trekken. Dan zijn rood, blauw groen op en elke volgende knikker die je trekt geeft je 4e gezochte kleur. Je kan dus maximaal 60 keer trekken waarbij je 3 kleuren trekt. De 61 keer geeft die 4e kleur.
hoe je dit met de GR doet weet ik niet


En als ik het nou zou stellen: wat is de kans dat je in 10 keer trekken minstens vier verschillende kleuren eruit haalt?
`either you or your head must be off, and that in about half no time! Take your choice!'


Dan zoek je alle mogelijke trekkingen die daaraan voldoen, en tel je de kansen op die trekkingen op. Dat opsommen is hier een monnikenwerk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Das waar, ik dacht dat met de nCr functie van de GR mss wel iets mogelijk is. Die functie kan toch al de mogelijke combinaties aangeven? Of is dat alleen bij een binomiale verdeling?
`either you or your head must be off, and that in about half no time! Take your choice!'


Dat is inderdaad alleen bij terugleggen en waarbij je bij elke trekking dezelfde kans op succes hebt. Hier kun je niet van een succes spreken.quote:Op donderdag 2 april 2009 14:20 schreef ALICENOR het volgende:
Das waar, ik dacht dat met de nCr functie van de GR mss wel iets mogelijk is. Die functie kan toch al de mogelijke combinaties aangeven? Of is dat alleen bij een binomiale verdeling?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


onder voorbehoud zeg ik 34.1%.
Wat ik zou doen is de kans uitrekenen dat je met 10 keer trekken hoogstens 3 verschillende kleuren trekt.
je hebt namelijk
P(hoogstens 3 verschillende kleuren) + P(minstens 4 verschillende kleuren) = 1
Hoe kom je aan deze opgave? Dit is geen VWO stuff, iig niet met mijn oplossingsmethode
[ Bericht 42% gewijzigd door TubewayDigital op 02-04-2009 20:07:11 ]
Wat ik zou doen is de kans uitrekenen dat je met 10 keer trekken hoogstens 3 verschillende kleuren trekt.
je hebt namelijk
P(hoogstens 3 verschillende kleuren) + P(minstens 4 verschillende kleuren) = 1
Hoe kom je aan deze opgave? Dit is geen VWO stuff, iig niet met mijn oplossingsmethode
[ Bericht 42% gewijzigd door TubewayDigital op 02-04-2009 20:07:11 ]


Ik kom hierop:
- is fout -
[ Bericht 68% gewijzigd door GlowMouse op 02-04-2009 21:31:44 ]
- is fout -
[ Bericht 68% gewijzigd door GlowMouse op 02-04-2009 21:31:44 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoe ik kom aan deze opgave, haha...
Eigenlijk gaat het om cellen in een fles. Ik loop stage op een lab, en ben bezig met celkweek. Ik heb nu een fles met ongeveer 90 verschillende celsoorten (microscopisch niet te onderscheiden maar genetisch anders) per celsoort heb ik ongeveer 65000 cellen, en dus in totaal ongeveer 6 miljoen. Nou wil mijn begeleider graag weten hoeveel kans je hebt om 10 verschillende soorten cellen te verkrijgen als je ongeveer 500 cellen eruit haalt. Dus ik heb geprobeerd het vraagstuk wat te versimpelen, aangezien het hier om erg grote aantallen gaat. Maar zelf weet ik het ook niet meer....
Vandaar...
Eigenlijk gaat het om cellen in een fles. Ik loop stage op een lab, en ben bezig met celkweek. Ik heb nu een fles met ongeveer 90 verschillende celsoorten (microscopisch niet te onderscheiden maar genetisch anders) per celsoort heb ik ongeveer 65000 cellen, en dus in totaal ongeveer 6 miljoen. Nou wil mijn begeleider graag weten hoeveel kans je hebt om 10 verschillende soorten cellen te verkrijgen als je ongeveer 500 cellen eruit haalt. Dus ik heb geprobeerd het vraagstuk wat te versimpelen, aangezien het hier om erg grote aantallen gaat. Maar zelf weet ik het ook niet meer....
Vandaar...
`either you or your head must be off, and that in about half no time! Take your choice!'


Dat zijn enorme getallen, dat zul je niet zomaar kunnen berekenen. Ik kan je wel een kans geven die ik heb bepaald mbv simulatie, dat geeft een aardige schatting.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 10 is al 0.6.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 11 is al 0.9.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 20 is al nagenoeg 1 (minder dan 10 soorten zal bij minder dan 1 op de miljoen steekproeven voorkomen)
Dus met steekproefgrootte 500 zit je wel veilig.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 10 is al 0.6.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 11 is al 0.9.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 20 is al nagenoeg 1 (minder dan 10 soorten zal bij minder dan 1 op de miljoen steekproeven voorkomen)
Dus met steekproefgrootte 500 zit je wel veilig.
| 1 2 3 4 5 6 7 8 9 10 11 12 | x=0; for i = 1:1000000 r = randint(11,1,[1 90*65000]); r = ceil(r/65000); r = unique(r); if(size(r,1) >= 10) x=x+1; end n=n+1; end x/n |
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Glowmouse, ik weet dat jij ook econometrie studeert dus ik hoop dat je mij verder kan helpen met het uitrekenen van de core van een economie, ik kom er namelijk niet uit, het is tijdens de hoorcolleges een week of drie terug behandeld, maar het staat niet tussen mijn aantekeningen dus kan jij het me misschien uitleggen? Want in het boek kan ik het niet terugvinden.
ff wachten nog


Ik wil er wel even over nadenken, u is de nutsfunctie en e is een nash evenwicht?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


is een endowment, de startsituatie waarmee de 2 handelaren in deze ruileconomie beginnen, de definitie van de core is het punt waarbij er minimaal 1 beter af is, zonder dat de andere erop achteruit gaat
ff wachten nog


Ik zit ernaar te kijken, maar is het niet vreemd dat de startsituatie niet in de core zit?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Met jouw definitie, en x1 x en x2 y noemend (wie verzint dat met zowel super- als subscript), moet je gewoon vergelijkingen oplossen.
Ik kom dan op x2 >= 3/x1 (vanwege speler 1)
en x2 <= 4-3/(4-x1)³ (vanwege speler 2)
Ik kom dan op x2 >= 3/x1 (vanwege speler 1)
en x2 <= 4-3/(4-x1)³ (vanwege speler 2)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zo zat ik ook te denken ja, maar dan heb je niet de oplossing van de slide te pakken...quote:Op donderdag 2 april 2009 23:13 schreef GlowMouse het volgende:
Met jouw definitie, en x1 x en x2 y noemend (wie verzint dat met zowel super- als subscript), moet je gewoon vergelijkingen oplossen.
Ik kom dan op x2 >= 3/x1 (vanwege speler 1)
en x2 <= 4-3/(4-x1)³ (vanwege speler 2)
En die scripts zijn absurd ja, ik ben blij als ik van dit vak af ben.
Helaas volgt ook nog wiskundige economie B
ff wachten nog


Nee, toen ik erover nadacht al en toen pas ben ik de simulatie gaan doen. Wat er gebeurde in mijn berekening is dat er heel veel dubbel werd geteld (in het stukje achter de 1-), zodat de kans nog groter zou zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Weet iemand hoe ik in standaardvorm moet opschrijven?
alvast bedankt!
[ Bericht 45% gewijzigd door motorbloempje op 01-09-2013 20:48:18 ]
alvast bedankt!
[ Bericht 45% gewijzigd door motorbloempje op 01-09-2013 20:48:18 ]


Wortel 3/wortel 6 * wortel 3 /wortel 6 * wortel 3/wortel 6 = 3wortel3 / 6wortel6?
Volgens mij is het (1/4)*wortel2, maar hoe ik daar op kom weet ik ook niet
(wortel 3/wortel6)^3 = ((wortel3/wortel6)*(wortel3/wortel3))^3=(3/wortel18)^3=(3/wortel18)*(3/wortel18)*(3/wortel18)=??
[ Bericht 26% gewijzigd door hello_moto1992 op 03-04-2009 15:28:16 ]
Volgens mij is het (1/4)*wortel2, maar hoe ik daar op kom weet ik ook niet
(wortel 3/wortel6)^3 = ((wortel3/wortel6)*(wortel3/wortel3))^3=(3/wortel18)^3=(3/wortel18)*(3/wortel18)*(3/wortel18)=??
[ Bericht 26% gewijzigd door hello_moto1992 op 03-04-2009 15:28:16 ]


-
[ Bericht 100% gewijzigd door motorbloempje op 01-09-2013 20:48:33 ]
[ Bericht 100% gewijzigd door motorbloempje op 01-09-2013 20:48:33 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


maar zowel boven de streep als onder de streep wordt dubbel geteld. Heft dat elkaar niet op?quote:Op vrijdag 3 april 2009 14:20 schreef GlowMouse het volgende:
Nee, toen ik erover nadacht al en toen pas ben ik de simulatie gaan doen. Wat er gebeurde in mijn berekening is dat er heel veel dubbel werd geteld (in het stukje achter de 1-), zodat de kans nog groter zou zijn.


Ik had nchoosek(5,3)*nchoosek(60,10) in de teller en nchoosek(100,10) in de noemer. In de noemer staat het aantal verzamelingen van 10 elementen die je kunt trekken uit een populatie van 100, daar is niets dubbel geteld. In de teller staat het aantal verzamelingen van 10 elementen die je kunt trekken uit een populatie van 60 maal het aantal manieren om zo'n populatie van 60 te vormen. De deelverzameling waarbij alles van soort 1 is tel je dan 5x.quote:Op vrijdag 3 april 2009 16:18 schreef TubewayDigital het volgende:
[..]
maar zowel boven de streep als onder de streep wordt dubbel geteld. Heft dat elkaar niet op.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


b. Stel p > q, kijk eens naar f(q + (p-q)/2)
c. Kijk eens naar f(p + (q-p)/2)
d. Geen nulpunt, dus p=q (volgt uit c). Stel nu dat f wel continu is in p, dan geldt f(p) = lim(x->p) f(x). We weten dus dat de limiet bestaat, en gelijk is aan lim(x->p-) f(x) (limiet met x komt van links). Wat kunnen we zeggen over die limiet en dus over f(p)? Doe nu hetzelfde voor x van rechts (gebruik dat p=q), en kijk wat je dan kunt zeggen over f(p).
[ Bericht 18% gewijzigd door GlowMouse op 04-04-2009 19:00:15 ]
c. Kijk eens naar f(p + (q-p)/2)
d. Geen nulpunt, dus p=q (volgt uit c). Stel nu dat f wel continu is in p, dan geldt f(p) = lim(x->p) f(x). We weten dus dat de limiet bestaat, en gelijk is aan lim(x->p-) f(x) (limiet met x komt van links). Wat kunnen we zeggen over die limiet en dus over f(p)? Doe nu hetzelfde voor x van rechts (gebruik dat p=q), en kijk wat je dan kunt zeggen over f(p).
[ Bericht 18% gewijzigd door GlowMouse op 04-04-2009 19:00:15 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


John heeft van zijn moeder 3800 dollar geleend. Hij spreekt met haar af dat hij elke maand iets zal terugbetalen. De eerste maand betaalt hij 10 dollar terug en daarna elke maand 8 dollar meer dan de vorige maand.
1) Na hoeveel maanden heeft Maurits het bedrag van 3800 dollar afgelost?
Un = 2 + 8n (want Un = U1 + (n-1) . v)
Sn = 0,5 . n . (10 + 2 + 8n)
y1 = Sn
y2 = 3800
calc > intersect geeft (30,08 ; 3800)
Dus: antwoord is na 31 maanden.
Tot zover lukte het wel, maar nu komt de volgende:
2) Hoeveel dollar had John elke maand meer moeten betalen dan de voorgaande maand opdat hij al in 22 weken het bedrag van 3800 dollar had afgelost?
Kan iemand me helpen met vraag 2? Ik zie ff niet hoe ik verder moet. Alvast bedankt!
1) Na hoeveel maanden heeft Maurits het bedrag van 3800 dollar afgelost?
Un = 2 + 8n (want Un = U1 + (n-1) . v)
Sn = 0,5 . n . (10 + 2 + 8n)
y1 = Sn
y2 = 3800
calc > intersect geeft (30,08 ; 3800)
Dus: antwoord is na 31 maanden.
Tot zover lukte het wel, maar nu komt de volgende:
2) Hoeveel dollar had John elke maand meer moeten betalen dan de voorgaande maand opdat hij al in 22 weken het bedrag van 3800 dollar had afgelost?
Kan iemand me helpen met vraag 2? Ik zie ff niet hoe ik verder moet. Alvast bedankt!
Oh really?


Eerst losten we op 0,5*n*(10 + 2 + 8n) = 3800.
Nu wordt die n 5, en die 8 wordt variabel: 0,5*22*(10 + 2 + x*22) = 3800
Nu wordt die n 5, en die 8 wordt variabel: 0,5*22*(10 + 2 + x*22) = 3800
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt, nog eentje:
( b lukt me niet, kan je me please ff op weg helpen? )
)
Ik probeer een punt p element van Bw(a;epsilon) te nemen, en hieromheen een m-bol te nemen, zodat iedere punt x van die m-bol ook in Bw(a;epsilon) zit. Hiermee heb ik dan aangetoont dat p een inwendig punt is, en omdat p willekeurig was, is dus Bw(a;epsilon) open in dm.
Maar het lukt me maar niet om mbv. de ongelijkheid van opgave a deze opgave te maken..
( b lukt me niet, kan je me please ff op weg helpen?
Ik probeer een punt p element van Bw(a;epsilon) te nemen, en hieromheen een m-bol te nemen, zodat iedere punt x van die m-bol ook in Bw(a;epsilon) zit. Hiermee heb ik dan aangetoont dat p een inwendig punt is, en omdat p willekeurig was, is dus Bw(a;epsilon) open in dm.
Maar het lukt me maar niet om mbv. de ongelijkheid van opgave a deze opgave te maken..


Dus:
Sn = 0,5 . 5 (10 + 2 + 5x)
Sn = 2,5 (12 + 5x)
Sn = 12,5x + 30
12,5x + 30 = 3800
x = $304
edit: dit is nog een reactie op de post van glowmouse
Sn = 0,5 . 5 (10 + 2 + 5x)
Sn = 2,5 (12 + 5x)
Sn = 12,5x + 30
12,5x + 30 = 3800
x = $304
edit: dit is nog een reactie op de post van glowmouse
Oh really?


Ja ziet er goed uit.quote:Op zondag 5 april 2009 20:05 schreef Matthijs- het volgende:
Dus:
Sn = 0,5 . 5 (10 + 2 + 5x)
Sn = 2,5 (12 + 5x)
Sn = 12,5x + 30
12,5x + 30 = 3800
x = $304
edit: dit is nog een reactie op de post van glowmouse
Fysicus: ik neem aan dat de bol open is tav d_w. Kun je dan opschrijven wat voor jouw punt p geldt in termen van d_w? Daarna kun je je antwoord van a gebruiken namelijk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Inderdaad.quote:Op zondag 5 april 2009 20:21 schreef GlowMouse het volgende:
[..]
Ja ziet er goed uit.
Fysicus: ik neem aan dat de bol open is tav d_w. Kun je dan opschrijven wat voor jouw punt p geldt in termen van d_w? Daarna kun je je antwoord van a gebruiken namelijk.
Dus voor p geldt: Voor elke p die in B_w(a;epsilon) zit , is er een delta>0 zodat B_w(p;delta) een deelverzameling is van B_w(a;epsilon)...
Ok, hoe gebruik ik nou a)..?


Als je nu die B_w(p;delta) hebt, kun je dan een B_m(p;f(delta)) die daar helemaal in zit?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Werkt het als we nemen f(delta)=delta/q ?quote:Op zondag 5 april 2009 20:37 schreef GlowMouse het volgende:
Als je nu die B_w(p;delta) hebt, kun je dan een B_m(p;f(delta)) die daar helemaal in zit?
Stel : x is een element van B_m(p;f(delta))
Dus d_m(x,p)<delta/q
Dus q d_m(x,p)<delta
Maar q d_m(x,p)>=d_w(x,p)
Dus d_w(x,p)<delta, endus is de tweede bol bevat in de eerste.
?


Ja ik zat al te kijken, staat die ongelijkheid bij a niet verkeerd om, maar je moet inderdaad van m-bol naar w-bol. Je hebt nu een m-bol die in een w-bol zit. Zo'n w-bol kun je altijd vinden, ofwel voor iedere p bestaat er een delta z.d.d. B_m(p;f(delta)) binnen B_w(a,r) valt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ok bedankt, blijkt dus eigelijk vrij triviaal te zijn..
Nog wat over vraag c) :
Kunnen we daar gewoon zeggen dat als een verzameling A open is tav. van d_w, er dus voor iedere x element van A een bol B_w(a,epsilon) is zodat ie in A ligt. En vanwege onderdeel b) kan je altijd een M-bol vinden die weer in deze W-bol ligt..?
Nog wat over vraag c) :
Kunnen we daar gewoon zeggen dat als een verzameling A open is tav. van d_w, er dus voor iedere x element van A een bol B_w(a,epsilon) is zodat ie in A ligt. En vanwege onderdeel b) kan je altijd een M-bol vinden die weer in deze W-bol ligt..?


Ja, of ik vergeet wat of c is triviaal.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Een vraagje over een opgave:
Voor een orthogonale mxm matrix U bewijs dat:
||Uv||22=||v||22 voor alle vectoren v uit Rm
||v||22 is de l2 norm, gedefinieerd als de som van de kwadraten van de componenten van vector v.
Ik heb het geprobeerd om het uit te schrijven, maar hier kom ik niet echt op iets nuttigs uit. Kan iemand mij een hint geven?
Voor een orthogonale mxm matrix U bewijs dat:
||Uv||22=||v||22 voor alle vectoren v uit Rm
||v||22 is de l2 norm, gedefinieerd als de som van de kwadraten van de componenten van vector v.
Ik heb het geprobeerd om het uit te schrijven, maar hier kom ik niet echt op iets nuttigs uit. Kan iemand mij een hint geven?
You don't need a weatherman to know which way the wind blows.
---------------------------------------------------------------------------------------------------------------------------------------------
Album top 100 2024
---------------------------------------------------------------------------------------------------------------------------------------------
Album top 100 2024


Schrijf ||v||2² eens als inproduct.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt, nu heb ik hem meteen. Ik wist dat ik te moeilijk zat te denken.quote:
You don't need a weatherman to know which way the wind blows.
---------------------------------------------------------------------------------------------------------------------------------------------
Album top 100 2024
---------------------------------------------------------------------------------------------------------------------------------------------
Album top 100 2024


heeft iemand de wiskunde a-lympiade opdracht evacuatie gemaakt en heeft de antwoorden nog
of kan mij helpen hier staat de opdracht ik blijf al haken bij opdracht 3
aub help het is een belangrijke opdracht
http://forums.marokko.nl/showthread.php?t=2519285
of kan mij helpen hier staat de opdracht ik blijf al haken bij opdracht 3
aub help het is een belangrijke opdracht
http://forums.marokko.nl/showthread.php?t=2519285


het gebouw heeft 22 verdiepingen
op iedere verdieping zitten 60 mensen
per persoon duurt het 1 seconde om door de deur van hun verdieping te lopen
per persoon duurt het 15 seconde om van de een naar de andere verdieping te lopen
op de trap kunnen max 2 personnen naast elkaar lopen
als je eenmaal op de trap loopt blijf je doorlopen
en het als je op de begane grond staat duurt het 5 seconde om buiten te komen
nou kijk bij opdracht d3 moet je kijken hoelang het duurt voordat 5 verdiepingen zijn geevacueerd, je moet dat berekenen met beperkingen dus dat er max 2 naast elkaar mogen lopen.....maar ik begrijp niet hoe je dat kun uitrekenen....iemand...
op iedere verdieping zitten 60 mensen
per persoon duurt het 1 seconde om door de deur van hun verdieping te lopen
per persoon duurt het 15 seconde om van de een naar de andere verdieping te lopen
op de trap kunnen max 2 personnen naast elkaar lopen
als je eenmaal op de trap loopt blijf je doorlopen
en het als je op de begane grond staat duurt het 5 seconde om buiten te komen
nou kijk bij opdracht d3 moet je kijken hoelang het duurt voordat 5 verdiepingen zijn geevacueerd, je moet dat berekenen met beperkingen dus dat er max 2 naast elkaar mogen lopen.....maar ik begrijp niet hoe je dat kun uitrekenen....iemand...


Bij die vraag heb je de methode van opdracht 2 nodig. En welke is dat?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


opdracht 2 is het zelfde alleen zijn er dan geen beperkingen,dus er kunnen zoveel mensen op de trap als je wilt geen 2 naast elkaar
hier staat de gehele opdracht
http://forums.marokko.nl/showthread.php?t=2519285
hier staat de gehele opdracht
http://forums.marokko.nl/showthread.php?t=2519285


Je methode had ik het over, niet de opdracht.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ik had bij opdracht 2
dat het 140 seconden zou zijn omdat er geen beperkingen zijn....
want 15x5=75 seconde
75+1(is van de deur op de 5e verdieping)=76 76+5(van de deur op begande grond)=81
81+59(van de overige 59 mensen)
en dit is een berekening dat de laatste van verdieping 5 beneden is
dat het 140 seconden zou zijn omdat er geen beperkingen zijn....
want 15x5=75 seconde
75+1(is van de deur op de 5e verdieping)=76 76+5(van de deur op begande grond)=81
81+59(van de overige 59 mensen)
en dit is een berekening dat de laatste van verdieping 5 beneden is


Dat ziet er goed uit. Bij de trap ontbreekt informatie, want als je heel veel treden zou hebben (die ver genoeg uit elkaar staan) dan kunnen er alsnog heel veel mensen op. Neem bv. aan dat er 20 treden per verdieping zijn en er één tree tussen twee mensen moet zitten, zodat er 20 mensen op het stuk trap tussen twee verdiepingen passen.
Stel nu dat iedereen tegelijk naar beneden wil. Hoelang duurt het dan voordat er problemen ontstaan?
Stel nu dat iedereen tegelijk naar beneden wil. Hoelang duurt het dan voordat er problemen ontstaan?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je hoeft de opdracht niet te herhalen, die heb ik gelezen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hey,
Ik heb een vraagje over het bewijs deze stelling over de Krull dimensie:
Zij X een topologische ruimte en laat Y <= X een deelverzameling zijn. Dan geldt dim Y <= dim X.
In meerdere boeken kom ik dit bewijs tegen:
Neem Y1 <!= Y2 twee irreducibele gesloten deelverzamelingen van Y. Neem hun afsluitingen X1 en X2 in X. Dan is Xi ook irreducibel en gesloten voor i=1,2. Er volgt dan dat dim Y <= dim X.
Mijn vraag is nu: waarom is XI irreducibel ? Het zou wel irreducibel zijn als i gesloten was in X maar dit is even niet het geval hier!
Waarom is het genoeg om te bewijzen voor twee irreducibele gesloten deelverzamelingen in?
Ik wou de stelling bewijzen door idd zo'n Y1 <!= Y2 in Y te nemen en vervolgens te schrijven Yi=Y doorsnijding Wi met Wi een gesloten verzameling in X voor i=1,2. Deze Wi is gesloten en ik hoef alleen nog te laten zien dat ook irreducibel is (wat mij nog niet lukt).
Ik heb een vraagje over het bewijs deze stelling over de Krull dimensie:
Zij X een topologische ruimte en laat Y <= X een deelverzameling zijn. Dan geldt dim Y <= dim X.
In meerdere boeken kom ik dit bewijs tegen:
Neem Y1 <!= Y2 twee irreducibele gesloten deelverzamelingen van Y. Neem hun afsluitingen X1 en X2 in X. Dan is Xi ook irreducibel en gesloten voor i=1,2. Er volgt dan dat dim Y <= dim X.
Mijn vraag is nu: waarom is XI irreducibel ? Het zou wel irreducibel zijn als i gesloten was in X maar dit is even niet het geval hier!
Waarom is het genoeg om te bewijzen voor twee irreducibele gesloten deelverzamelingen in?
Ik wou de stelling bewijzen door idd zo'n Y1 <!= Y2 in Y te nemen en vervolgens te schrijven Yi=Y doorsnijding Wi met Wi een gesloten verzameling in X voor i=1,2. Deze Wi is gesloten en ik hoef alleen nog te laten zien dat ook irreducibel is (wat mij nog niet lukt).
verlegen :)


Stel Xi = Z1 U Z2 met Zj != Xi gesloten in Xi en dus ook gesloten in X.
Dan zijn de doorsneden van Z1 en Z2 met Yi gesloten in Yi dus leeg of gelijk aan Yi (want Yi is irreducibel). De vereniging van Z1 en Z2 bevat Yi, dus zbda onderstellen we dat de doorsnede van Z1 met Yi gelijk is aan Yi. Dus Yi is deelverzameling van Z1. Omdat Xi de afsluiting van Yi volgt dus dat Xi bevat is Z1, dus Xi=Z1, tegenspraak.
Dan zijn de doorsneden van Z1 en Z2 met Yi gesloten in Yi dus leeg of gelijk aan Yi (want Yi is irreducibel). De vereniging van Z1 en Z2 bevat Yi, dus zbda onderstellen we dat de doorsnede van Z1 met Yi gelijk is aan Yi. Dus Yi is deelverzameling van Z1. Omdat Xi de afsluiting van Yi volgt dus dat Xi bevat is Z1, dus Xi=Z1, tegenspraak.


Twee 'puzzeltjes' waar ik niet uitkom:
1) Een rechthoekige driehoek heeft een schuine zijde van 25. De straal van de ingeschreven cirkel is 3.
Bereken de twee rechtehoekszijden.
- Dit is dus pythagoras en dus wil ik een vergelijking in x maken. Maar dit lukt me niet. Iemand een idee?
2) Binnen een vierkant ABCD is een kwartcirkel beschreven met B als middelpunt en de zijde als straal.
Een punt P op de kwartcirkel heeft een afstand 1 tot CD
en afstand 8 tot AD. Bereken de oppervlakte van vierkant ABCD.
EDIT: deze heb ik: (r-1)^2 + (r-8)^2 = r^2 oplossen geeft r.
[ Bericht 6% gewijzigd door Borizzz op 09-04-2009 08:40:40 ]
1) Een rechthoekige driehoek heeft een schuine zijde van 25. De straal van de ingeschreven cirkel is 3.
Bereken de twee rechtehoekszijden.
- Dit is dus pythagoras en dus wil ik een vergelijking in x maken. Maar dit lukt me niet. Iemand een idee?
2) Binnen een vierkant ABCD is een kwartcirkel beschreven met B als middelpunt en de zijde als straal.
Een punt P op de kwartcirkel heeft een afstand 1 tot CD
en afstand 8 tot AD. Bereken de oppervlakte van vierkant ABCD.
EDIT: deze heb ik: (r-1)^2 + (r-8)^2 = r^2 oplossen geeft r.
[ Bericht 6% gewijzigd door Borizzz op 09-04-2009 08:40:40 ]
kloep kloep


Vanuit het middelpunt van de ingeschreven cirkel kun je hulplijnen trekken naar de twee niet-rechte hoeken. Je ziet dan dat x-3 + y-3 = 25.quote:Op donderdag 9 april 2009 08:28 schreef Borizzz het volgende:
Twee 'puzzeltjes' waar ik niet uitkom:
1) Een rechthoekige driehoek heeft een schuine zijde van 25. De straal van de ingeschreven cirkel is 3.
Bereken de twee rechtehoekszijden.
- Dit is dus pythagoras en dus wil ik een vergelijking in x maken. Maar dit lukt me niet. Iemand een idee?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


oh ja ik zie het nu! Ik dacht al.. er moest echt iets bewezen worden en de strikte ongelijkheid is ook niet helemaal vanzelfsprekend. Dank je.quote:Op donderdag 9 april 2009 08:05 schreef thabit het volgende:
Stel Xi = Z1 U Z2 met Zj != Xi gesloten in Xi en dus ook gesloten in X.
Dan zijn de doorsneden van Z1 en Z2 met Yi gesloten in Yi dus leeg of gelijk aan Yi (want Yi is irreducibel). De vereniging van Z1 en Z2 bevat Yi, dus zbda onderstellen we dat de doorsnede van Z1 met Yi gelijk is aan Yi. Dus Yi is deelverzameling van Z1. Omdat Xi de afsluiting van Yi volgt dus dat Xi bevat is Z1, dus Xi=Z1, tegenspraak.
verlegen :)


Ik zie dat ik daar een klein foutje maakte. Ik zei Zj\cap Yi is leeg of gelijk aan Yi, dat moet uiteraard zijn: tenminste een Zj\cap Yi is gelijk aan Yi. Maakt voor de rest van het argument natuurlijk niet uit.


Zou iemand mij kunnen helpen met de volgende machtsvergelijking?
Het is de bedoeling dat ik de nulpunten bepaal. Het liefst in stapjes uitleggen, zodat ik het in het vervolg zelf ook kan toepassen.
f(x)= x^4 - 2x^2
f'(x) = 4x^3 - 4x
Alvast bedankt
Het is de bedoeling dat ik de nulpunten bepaal. Het liefst in stapjes uitleggen, zodat ik het in het vervolg zelf ook kan toepassen.
f(x)= x^4 - 2x^2
f'(x) = 4x^3 - 4x
Alvast bedankt
ik doe wat ik wil dus als het je niet aanstaat heb je lekker dikke pech pipoo


Nulpunten van f of van f'? Voor beide geldt: het functievoorschrift bestaat uit twee termen die allebei een factor gemeenschappelijk hebben. Die kun je dus ontbinden. Er zijn 3 manieren om nulpunten exact te bepalen: de balansmethode (werkt hier niet zo heel makkelijk, probeer maar), de abc-formule (alleen voor kwadratische vergelijkingen), of ontbinden in factoren en gebruiken dat als a*b=0 dan a=0 of b=0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De nulpunten van f'. Maar ik dacht juist dat ontbinden etc. niet mogelijk was omdat het geen vierkantsvergelijking is.
ik doe wat ik wil dus als het je niet aanstaat heb je lekker dikke pech pipoo


Zou dit kunnen kloppen?
4x^3 - 1
4x(x^2 - 1)
--> x^2 - 1 = 0
x^2 = 1
wortel uit 1 levert op x= 1 of x = -1
2x = 0
x = - 2
4x^3 - 1
4x(x^2 - 1)
--> x^2 - 1 = 0
x^2 = 1
wortel uit 1 levert op x= 1 of x = -1
2x = 0
x = - 2
ik doe wat ik wil dus als het je niet aanstaat heb je lekker dikke pech pipoo


Die '4x^3 - 1' hoort er niet. Het is misschien een denkstap, maar het is ongelijk aan 4x(x^2 - 1) en het wekt dus alleen verwarring.quote:Op vrijdag 10 april 2009 22:03 schreef miracle. het volgende:
Zou dit kunnen kloppen?
4x^3 - 1
4x(x^2 - 1)
De oplossingen zijn correct. De redenering moet alleen zijn "wortel uit 1 levert op x= 1 en minus wortel uit 1 levert op x = -1". De wortel is namelijk alleen het positieve getal.quote:--> x^2 - 1 = 0
x^2 = 1
wortel uit 1 levert op x= 1 of x = -1
Aan de rechterkant doe je min 2, en aan de linkerkant doe je gedeeld door 2, en je moet juist altijd links en rechts hetzelfde doen. Dat -2 niet goed is, zie je ook door hem weer in te vullen in 4x^3 - 4x.quote:2x = 0
x = - 2
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bij die eerste x**2 buiten haakjes halen.quote:Op vrijdag 10 april 2009 21:38 schreef miracle. het volgende:
Zou iemand mij kunnen helpen met de volgende machtsvergelijking?
Het is de bedoeling dat ik de nulpunten bepaal. Het liefst in stapjes uitleggen, zodat ik het in het vervolg zelf ook kan toepassen.
f(x)= x^4 - 2x^2
f'(x) = 4x^3 - 4x
Alvast bedankt
Dan krijg je een vergelijking in de trand van:
A * B = 0
Dan geldt:
A = 0 of B = 0
Deze zijn beide makkelijk op te lossen.
Bij de tweede moet je x buiten haakjes halen (of 4x mag ook)
En dan hetzelfde als de eerste, is echt niet moeilijk.
In het algemeen geldt dat je een zo'n groot mogelijke gemeenschappelijke deler buiten haakjes moet zien te halen bij dit soort sommen.
Jesus hates you.


Ik heb een vraagje over het berekenen van de variantie, eigenlijk alleen over de 1 en 2e kolom.
Wanneer doe je nou wel N maal X en wanneer nou niet? Want op school hebben we opdrachten op papier gekregen, maar daar hoeven we dus niet die som te maken (te zien in de links)
De rest van de berekeningen snap ik wel, zit alleen in de knoop met de 1e 2 kolommen.
school
http://nl.tinypic.com/view.php?pic=263zpd3&s=5
boek
http://nl.tinypic.com/view.php?pic=k4vvom&s=5
Wanneer doe je nou wel N maal X en wanneer nou niet? Want op school hebben we opdrachten op papier gekregen, maar daar hoeven we dus niet die som te maken (te zien in de links)
De rest van de berekeningen snap ik wel, zit alleen in de knoop met de 1e 2 kolommen.
school
http://nl.tinypic.com/view.php?pic=263zpd3&s=5
boek
http://nl.tinypic.com/view.php?pic=k4vvom&s=5
Op ut Vriethof, op un baank.
Gruuts op de Mestreechter Geis!
Hendig sjiek!
Vuilak!
Gruuts op de Mestreechter Geis!
Hendig sjiek!
Vuilak!


Dat handgeschreven spul is compleet fout. Dat zie je al omdat je bij de berekening de cijfers zelf nergens meeneemt. Dat spul uit je boek is ook fout omdat je variantie niet uit zo'n tabel kunt berekenen. Helaas is het wel de manier waarvan je verwacht wordt hem te kennen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Vreemd, want dat hand geschreven spul is wel goed beoordeeld door de leraar, alleen was het mij niet opgevallen dat in het boek die extra kolom van N maal X stond...quote:Op maandag 13 april 2009 17:43 schreef GlowMouse het volgende:
Dat handgeschreven spul is compleet fout. Dat zie je al omdat je bij de berekening de cijfers zelf nergens meeneemt. Dat spul uit je boek is ook fout omdat je variantie niet uit zo'n tabel kunt berekenen. Helaas is het wel de manier waarvan je verwacht wordt hem te kennen.
Dus jij zegt eigenlijk dat ik het gewoon verkeerd aan het leren ben?
Op ut Vriethof, op un baank.
Gruuts op de Mestreechter Geis!
Hendig sjiek!
Vuilak!
Gruuts op de Mestreechter Geis!
Hendig sjiek!
Vuilak!


Beide dingen zijn fout ja, maar het boek het minst fout. Variantie is een eigenschap van een kansverdeling. Je doet een steekproef en verkrijgt daarmee waarnemingen. Uit die waarnemingen kun je het getal berekenen dat jij hebt berekend, sommigen noemen het de steekproefvariantie maar die naam is erg misleidend, en dat getal zal gemiddeld genomen (als je heel veel steekproeven doet en telkens dat getal berekent) in de buurt liggen van de variantie van de onderliggende kansverdeling. Je kunt het dus zien als schatter van de variantie. Maar de variantie zelf laat zich zo niet berekenen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oké, bedankt voor de info. Ik zal morgen op het tentamen het zo doen zoals mij is aangeleerd, wordt het dan alsnog fout geteld dan val ik terug op de aantekeningen.quote:Op maandag 13 april 2009 18:14 schreef GlowMouse het volgende:
Beide dingen zijn fout ja, maar het boek het minst fout. Variantie is een eigenschap van een kansverdeling. Je doet een steekproef en verkrijgt daarmee waarnemingen. Uit die waarnemingen kun je het getal berekenen dat jij hebt berekend, sommigen noemen het de steekproefvariantie maar die naam is erg misleidend, en dat getal zal gemiddeld genomen (als je heel veel steekproeven doet en telkens dat getal berekent) in de buurt liggen van de variantie van de onderliggende kansverdeling. Je kunt het dus zien als schatter van de variantie. Maar de variantie zelf laat zich zo niet berekenen.
Maar het lijkt mij sterk dat de leraar het fout telt als hij het wel zo heeft uitgelegd aan de leerlingen...
Op ut Vriethof, op un baank.
Gruuts op de Mestreechter Geis!
Hendig sjiek!
Vuilak!
Gruuts op de Mestreechter Geis!
Hendig sjiek!
Vuilak!


Ik zou het maar doen zoals in het boek.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb hier een linkje gevonden, op deze manier doe ik het dus ook berekenen, alleen stap4 snap ik niet waarom ze dat op die manier opschrijven...quote:Op maandag 13 april 2009 18:30 schreef GlowMouse het volgende:
Ik zou het maar doen zoals in het boek.
http://www.phys.tue.nl/TU(...)oorbeeldstandev.html
Op ut Vriethof, op un baank.
Gruuts op de Mestreechter Geis!
Hendig sjiek!
Vuilak!
Gruuts op de Mestreechter Geis!
Hendig sjiek!
Vuilak!


Daar komt geen n bij kijken, dus dat is makkelijker dan in je boek. Die Σ betekent: tel op over alle mogelijke waarden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat handgeschreven klopt wel redelijk. Het gemiddelde zou alleen volgens de berekening 5 zijn, maar ik zie zo zonder berekening dat het gemiddelde ergens net onder de 7 zou moeten liggen. Die afwijkingen kloppen dan(doorgerend met die 5) weer wel.quote:Op maandag 13 april 2009 17:34 schreef Sjengdanny het volgende:
Ik heb een vraagje over het berekenen van de variantie, eigenlijk alleen over de 1 en 2e kolom.
Wanneer doe je nou wel N maal X en wanneer nou niet? Want op school hebben we opdrachten op papier gekregen, maar daar hoeven we dus niet die som te maken (te zien in de links)
De rest van de berekeningen snap ik wel, zit alleen in de knoop met de 1e 2 kolommen.
school
http://nl.tinypic.com/view.php?pic=263zpd3&s=5
boek
http://nl.tinypic.com/view.php?pic=k4vvom&s=5
Het kwadraat van -1 is helaas +1 (slordig)
Verder klopt het denk ik wel, maar ik kan het niet helemaal lezen.
Het enige verschil lijkt mij dat het boek een n * x kolom erbij heeft die gebruikt wordt om het gemiddelde te berekenen, terwijl je leraar zomaar een gemiddelde uit zijn duim heeft gezogen.
Jesus hates you.


Niet, daar moet je ook weer met n vermenigvuldigen. Het is gewoon compleet fout wat er gebeurt, hij werkt met de getallen uit de n-kolom alsof dat zijn waarnemingen zijn.quote:Op maandag 13 april 2009 21:09 schreef Hondenbrokken het volgende:
[..]
Die afwijkingen kloppen dan(doorgerend met die 5) weer wel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Vraagje over kansberekeningen.
Prijsveranderingen zijn per dag normaal verdeeld.
Harrie koopt aandelen van KPN van 30 euro per aandeel. Standaartafwijking is ¤0.119.
Bereken nauwkeurig (4 decimalen) de kans dat het aandeel een dag later na afronding op centen niet veranderd is.
Ik weet dat ik met normalcdf moet werken, maar wat voor getallen als linkergrens en rechtergrens? En qua gemiddelde? En moet je de continuiteitscorrectie toepassen?
Vriendin van me heeft normalcdf(-0.005,0.004,0,0.119) maar ik snap megod niet waar ze die getallen vandaan tovert? Ja ze gebruikt dus als uitgangspunt de 0, en dan de continuiteitscorrectie. Maar waarom 0.004, en niet 0.005?
Prijsveranderingen zijn per dag normaal verdeeld.
Harrie koopt aandelen van KPN van 30 euro per aandeel. Standaartafwijking is ¤0.119.
Bereken nauwkeurig (4 decimalen) de kans dat het aandeel een dag later na afronding op centen niet veranderd is.
Ik weet dat ik met normalcdf moet werken, maar wat voor getallen als linkergrens en rechtergrens? En qua gemiddelde? En moet je de continuiteitscorrectie toepassen?
Vriendin van me heeft normalcdf(-0.005,0.004,0,0.119) maar ik snap megod niet waar ze die getallen vandaan tovert? Ja ze gebruikt dus als uitgangspunt de 0, en dan de continuiteitscorrectie. Maar waarom 0.004, en niet 0.005?


Het is standaardafwijking.
Je zoekt P(29.995 <= X < 30.005) met X~N(30, 0.119²).
Continuïteitscorrectie is niet aan de orde omdat je die pas gebruikt wanneer je een discrete verdeling met een continue benadert.
Je zoekt P(29.995 <= X < 30.005) met X~N(30, 0.119²).
Continuïteitscorrectie is niet aan de orde omdat je die pas gebruikt wanneer je een discrete verdeling met een continue benadert.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat gebeurt in de laatste kolom.quote:Op maandag 13 april 2009 21:14 schreef GlowMouse het volgende:
[..]
Niet, daar moet je ook weer met n vermenigvuldigen. Het is gewoon compleet fout wat er gebeurt, hij werkt met de getallen uit de n-kolom alsof dat zijn waarnemingen zijn.
Als je daarvan de som neemt, deze door de som van de frequenties deelt en daarvan de wortel neemt klopt het wel weer.
Jesus hates you.


Er klopt niks van. De waarde geeft nu zijn eigen frequentie aan.quote:Op maandag 13 april 2009 22:25 schreef Hondenbrokken het volgende:
[..]
Dat gebeurt in de laatste kolom.
Als je daarvan de som neemt, deze door de som van de frequenties deelt en daarvan de wortel neemt klopt het wel weer.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Maar waarom dan 29.995 en 30.005 gebruiken? zodat je zo dicht mogelijk de 30 kunt benaderen? Dus als ik het goed heb wordt het dan normalcdf(29.995,30.005,30,0.119) = 0.0335quote:Op maandag 13 april 2009 22:22 schreef GlowMouse het volgende:
Het is standaardafwijking.
Je zoekt P(29.995 <= X < 30.005) met X~N(30, 0.119²).
Continuïteitscorrectie is niet aan de orde omdat je die pas gebruikt wanneer je een discrete verdeling met een continue benadert.


Zodat je bij afronding op centen op 30.00 uitkomt, zoals de opgave verlangt. Alles onder de 29.995 wordt bijvoorbeeld niet meer op 30.00 afgerond.quote:Op maandag 13 april 2009 22:33 schreef Jolien1989 het volgende:
[..]
Maar waarom dan 29.995 en 30.005 gebruiken? zodat je zo dicht mogelijk de 30 kunt benaderen? Dus als ik het goed heb wordt het dan normalcdf(29.995,30.005,30,0.119) = 0.0335
Je antwoord klopt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Geld is een discrete stochast.quote:Op maandag 13 april 2009 22:33 schreef Jolien1989 het volgende:
[..]
Maar waarom dan 29.995 en 30.005 gebruiken? zodat je zo dicht mogelijk de 30 kunt benaderen? Dus als ik het goed heb wordt het dan normalcdf(29.995,30.005,30,0.119) = 0.0335
Je kan 30,00 hebben of 30,01, maar niks daartussenin. Omdat een normale verdeling met continuewaarden moet werken neem je 30,005 omdat alles tussen de 30,00 en 30,005 naar 30,00 wordt afgerond.
In geval je niet bekend bent met de woorden discreet en continue.
discreet - stochast kan slechts een aantal waarden aannemen, geld, aantal bedden
continue - stochast kan elke tussenliggende waarde aannemen: lengte, gewicht, tijd
Jesus hates you.


Super, dankje. Had gehoopt dat ik verder en dan wel uit kwam, maar dat valt beetje tegen.quote:Op maandag 13 april 2009 22:34 schreef GlowMouse het volgende:
[..]
Zodat je bij afronding op centen op 30.00 uitkomt, zoals de opgave verlangt. Alles onder de 29.995 wordt bijvoorbeeld niet meer op 30.00 afgerond.
Je antwoord klopt.
na 7 dagen is de standaardafwijking 0.315 is, en bereken daar de kans mee dat een aandeel na 7 dagen afgerond meer dan 0.20 cent in waarde is gedaald.
Ik gebruik hierbij de N wet, dus dan wordt de standaardafwijking per 7 dagen 0.315.
Maar dan loop ik (wederom) vast. Ik gebruik nu op mn GR normalcdf(-10^99,0.205,0.20,0.315). Zit ik dan in de goede richting?
meneer koopt aandelen van 12.36 per stuk. Een adviseur vertelt dat de kans dat de KPN aandelen de komende 180 dagen, minimaal 3 euro aan waarde stijgen, gelijk is aan 0.10. Bereken de standaardafwijking van zo'n aandeel.
Als ik op miin GR (ti-83) bij y1 invoer normalcdf(3,10^99,12.36,x) en bij y2 0.10. Om vervolgens in een grafiek het snijpunt te vinden, komen die 2 lijnen nooit bij elkaar.
Ik zit ergens fout bij die 180 dagen, daar moet ik iets mee doen. Maar ik snap niet goed wat...


De bank houdt anders voor jou flink wat meer decimalen bij dan dat jij ziet hoor. En de echte wereld is bij deze vraag niet van belang: de waarde van het aandeel wordt continu verdeeld verondersteld, en is daarmee continu.quote:Op maandag 13 april 2009 22:40 schreef Hondenbrokken het volgende:
[..]
Geld is een discrete stochast.
Staat er echt 0.20 cent? Dat is wat anders dan 20 cent. Meer dan 0.20 cent is dus minder dan 30-0.0020. Je krijgt normalcdf(-1E99, 30-0.002, 30, 0.315).quote:Op maandag 13 april 2009 23:04 schreef Jolien1989 het volgende:
na 7 dagen is de standaardafwijking 0.315 is, en bereken daar de kans mee dat een aandeel na 7 dagen afgerond meer dan 0.20 cent in waarde is gedaald.
Ik gebruik hierbij de N wet, dus dan wordt de standaardafwijking per 7 dagen 0.315.
Maar dan loop ik (wederom) vast. Ik gebruik nu op mn GR normalcdf(-10^99,0.205,0.20,0.315). Zit ik dan in de goede richting?
Minimaal 3 euro stijgen is dus een waarde van meer dan 15.36, en niet een waarde van meer dan 3.quote:meneer koopt aandelen van 12.36 per stuk. Een adviseur vertelt dat de kans dat de KPN aandelen de komende 180 dagen, minimaal 3 euro aan waarde stijgen, gelijk is aan 0.10. Bereken de standaardafwijking van zo'n aandeel.
Als ik op miin GR (ti-83) bij y1 invoer normalcdf(3,10^99,12.36,x) en bij y2 0.10. Om vervolgens in een grafiek het snijpunt te vinden, komen die 2 lijnen nooit bij elkaar.
Ik zit ergens fout bij die 180 dagen, daar moet ik iets mee doen. Maar ik snap niet goed wat...
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Mijn fout idd, ik bedoelde ¤0.20, oftewel 20 cent.quote:Op maandag 13 april 2009 23:14 schreef GlowMouse het volgende:
[..]
De bank houdt anders voor jou flink wat meer decimalen bij dan dat jij ziet hoor. En de echte wereld is bij deze vraag niet van belang: de waarde van het aandeel wordt continu verdeeld verondersteld, en is daarmee continu.
[..]
Staat er echt 0.20 cent? Dat is wat anders dan 20 cent. Meer dan 0.20 cent is dus minder dan 30-0.0020. Je krijgt normalcdf(-1E99, 30-0.002, 30, 0.315).
[..]
Minimaal 3 euro stijgen is dus een waarde van meer dan 15.36, en niet een waarde van meer dan 3.
En die 2de, idd, je hebt gelijk, dankjewel!


Staat die x² onder de deelstreep?quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik gok van wel, anders staat er 5x² en dat moet een Harvard-student wel kunnen oplossen.quote:
Nickybol, zie de quotientregel of bedenk je dat 10/(2x²) = 5/x² = 5*1/x² = 5*x-2. De afgeleide daarvan is dus -10x-3 = -10/x3.
Ten percent faster with a sturdier frame


Door het te schrijven als 5 * x-2 krijg je als afgeleide -10/x³.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Niet zo handig voor een constante teller.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja, ik ben een Harvard student, maar ik zit niet in de hoek van de exacte wetenschappen... Op de middelbare school nooit meer dan wiskunde A1 gehad, en dat merk ik nu...


Klopt, maar dan weet hij ook meteen hoe het voor breuken in het algemeen gaat.quote:Op maandag 13 april 2009 23:59 schreef GlowMouse het volgende:
[..]
Niet zo handig voor een constante teller.
Ten percent faster with a sturdier frame


Op het moment ben ik mij aan het voorbereiden op mijn Wiskunde tentamen morgen (International Business And Management Studies), naast de fractionele exponenten kom ik klem te zitten in een supply/demand berekening.
Het gaat om het volgende:
Het gaat om d. (dus: Suppose the demand changes...) Zoals ik zei heb ik het dus nog niet zo te pakken met de algebra die ik voor mn kiezen krijg, en dit zou mij al aardig op weg kunnen helpen.
Het gaat om het volgende:
Het gaat om d. (dus: Suppose the demand changes...) Zoals ik zei heb ik het dus nog niet zo te pakken met de algebra die ik voor mn kiezen krijg, en dit zou mij al aardig op weg kunnen helpen.
niets


Staat daar dit?
q = 1000p - 200*sqrt(p2)
Zo ja, de wortel van een gekwadrateerd getal is gewoon het getal. Er staat dan dus: q = 1000 - 200p. Dan kan je het verder wel zelf toch lijkt me?
Overigens, is dit universiteit? Het lijkt meer op economie/wiskunde uit de onderbouw.
q = 1000p - 200*sqrt(p2)
Zo ja, de wortel van een gekwadrateerd getal is gewoon het getal. Er staat dan dus: q = 1000 - 200p. Dan kan je het verder wel zelf toch lijkt me?
Overigens, is dit universiteit? Het lijkt meer op economie/wiskunde uit de onderbouw.
Ten percent faster with a sturdier frame


nee geen sqrt. cube root.
Het inversen is voor mij nog een struikelblok, vandaar. Ik kan nog wel op iets komen als
q=1000+200(p2/3) maar omdat ik vreemdgenoeg dicht klap bij het oplossen van fractionele exponenten kom ik niet heel veel verder
Overigens HBO. Ik ben het wel met de rest van de vragen met je eens dat het redelijk dicht bij het middelbare school niveau ligt.
Het inversen is voor mij nog een struikelblok, vandaar. Ik kan nog wel op iets komen als
q=1000+200(p2/3) maar omdat ik vreemdgenoeg dicht klap bij het oplossen van fractionele exponenten kom ik niet heel veel verder
Overigens HBO. Ik ben het wel met de rest van de vragen met je eens dat het redelijk dicht bij het middelbare school niveau ligt.
niets


Wat dan wel?quote:
Ten percent faster with a sturdier frame


Cube root? Derdemachtswortel dus? Ik zie gewoon een wortel staan. Overigens is de wortel van p^2 geen p maar |p| natuurlijk 
"Reality is an illusion created by a lack of alcohol."


Natuurlijk.quote:Op dinsdag 14 april 2009 17:36 schreef Dzy het volgende:
Cube root? Derdemachtswortel dus? Ik zie gewoon een wortel staan. Overigens is de wortel van p^2 geen p maar |p| natuurlijk
Ten percent faster with a sturdier frame


Misschien is het basisboek wiskunde van Jan van de Craats iets voor jou. Maar je moet natuurlijk niet één dag voor je tentamen aan komen zetten met elementaire algebra vraagjes als je al lang weet dat je dat niet beheerst.quote:


Duidelijk.
De derdemachtswortel is hetzelfde als machtsverheffen tot de macht (1/3). Er staat dus:
q = 1000 + 200(p2)1/3
q-1000 = 200(p2)1/3
Er geldt: (xa)b = xa*b (basisregel!)
q-1000 = 200*p2/3
(q-1000)/200 = p2/3
Nu staat er p2/3, maar we willen p=p1 hebben. Dit doen we door te machtsverheffen met de macht 'a' aan beide kanten van de vergelijking, omdat je machten met elkaar mag vermenigvuldigen als je meerdere keren machtsverheft (zie de basisregel).
((q-1000)/200)a = (p2/3)a
((q-1000)/200)a = pa*2/3
a*2/3 = 1 --> a = 1/(2/3) = 3/2
Dus:
((q-1000)/200)3/2 = p1 = p
[ Bericht 3% gewijzigd door TC03 op 14-04-2009 18:08:37 ]
De derdemachtswortel is hetzelfde als machtsverheffen tot de macht (1/3). Er staat dus:
q = 1000 + 200(p2)1/3
q-1000 = 200(p2)1/3
Er geldt: (xa)b = xa*b (basisregel!)
q-1000 = 200*p2/3
(q-1000)/200 = p2/3
Nu staat er p2/3, maar we willen p=p1 hebben. Dit doen we door te machtsverheffen met de macht 'a' aan beide kanten van de vergelijking, omdat je machten met elkaar mag vermenigvuldigen als je meerdere keren machtsverheft (zie de basisregel).
((q-1000)/200)a = (p2/3)a
((q-1000)/200)a = pa*2/3
a*2/3 = 1 --> a = 1/(2/3) = 3/2
Dus:
((q-1000)/200)3/2 = p1 = p
[ Bericht 3% gewijzigd door TC03 op 14-04-2009 18:08:37 ]
Ten percent faster with a sturdier frame


Geweldig! Dank je wel voor de duidelijke uitleg, helpt mij een stuk verder.quote:Op dinsdag 14 april 2009 18:00 schreef TC03 het volgende:
Duidelijk.
De derdemachtswortel is hetzelfde als machtsverheffen tot de macht (1/3). Er staat dus:
q = 1000 + 200(p2)1/3
q-1000 = 200(p2)1/3
Er geldt: (xa)b = xa*b (basisregel!)
q-1000 = 200*p2/3
(q-1000)/200 = p2/3
Nu staat er p2/3, maar we willen p=p1 hebben. Dit doen we de met de macht 'a', aan beide kanten van de vergelijking natuurlijk.
((q-1000)/200)a = (p2/3)a
((q-1000)/200)a = pa*2/3
a*2/3 = 1 --> a = 1/(2/3) = 3/2
Dus:
((q-1000)/200)3/2 = p1 = p
niets


Iemand die het volgende weet? heb er morgen tentamen van maar kom er totaal niet uit:
b. Als je een α (alpha-fout) van 0,10 accepteert, vanaf welk aantal proefpersonen ben je dan overtuigd van een verschil in smaak? (40 proefpersonen)
c. Neem aan dat in werkelijkheid de helft van al zijn klanten het verschil kan proeven, hoe groot is dan β (beta-fout) bij het in onderdeel b berekende aantal? (10)
Iemand please?
Kom er zelf niet wijs uit want de uitleg is zwaar ontoereikend.
b. Als je een α (alpha-fout) van 0,10 accepteert, vanaf welk aantal proefpersonen ben je dan overtuigd van een verschil in smaak? (40 proefpersonen)
c. Neem aan dat in werkelijkheid de helft van al zijn klanten het verschil kan proeven, hoe groot is dan β (beta-fout) bij het in onderdeel b berekende aantal? (10)
Iemand please?
Kom er zelf niet wijs uit want de uitleg is zwaar ontoereikend.


Iets meer uitleg over de vraag zou wel handig zijn, kan je er wel mee helpen maar staat er nu wat onduidelijk. De gehele vraag posten ipv een halve en een half antwoord?
"Reality is an illusion created by a lack of alcohol."


Nu heb ik een vraagje:
Er is een familie van derdemachtsfuncties gegeven, bijvoorbeeld x^3 +4x^2 - px + 3, nu willen wij een functie vinden die door alle extreme waarden van deze familie heen gaat. Een algemeen algoritme om dit aan te pakken. We hebben zelf al naar de afgeleide gekeken maar wat we daar verder precies mee moesten kwamen we ook niet uit.
Er is een familie van derdemachtsfuncties gegeven, bijvoorbeeld x^3 +4x^2 - px + 3, nu willen wij een functie vinden die door alle extreme waarden van deze familie heen gaat. Een algemeen algoritme om dit aan te pakken. We hebben zelf al naar de afgeleide gekeken maar wat we daar verder precies mee moesten kwamen we ook niet uit.
"Reality is an illusion created by a lack of alcohol."


4. Driehoekstest (40 punten)quote:Op dinsdag 14 april 2009 23:39 schreef Dzy het volgende:
Iets meer uitleg over de vraag zou wel handig zijn, kan je er wel mee helpen maar staat er nu wat onduidelijk. De gehele vraag posten ipv een halve en een half antwoord?
De plaatselijke bakker bij ons in het dorp verkoopt elk jaar rond de Paasdagen zijn beroemde zelfgemaakte chocolade Paaseieren. Vanwege de gestegen grondstofprijzen heeft hij dit jaar zijn recept voor de vulling aangepast.
De grote vraag is natuurlijk of de consument dat proeft.
Om dat te onderzoeken biedt hij aan een 40-tal klanten de oude én de nieuwe variant aan in de vorm van een driehoekstest.
a. Aannemende dat er geen verschil te proeven is tussen de oude en de nieuwe vullingen, hoe groot is dan de kans dat minstens 40% van het aantal proefpersonen het juiste ei als afwijkend aanwijst? (5)
b. Als je een α (alpha-fout) van 0,10 accepteert, vanaf welk aantal proefpersonen ben je dan overtuigd van een verschil in smaak? (10)
c. Neem aan dat in werkelijkheid de helft van al zijn klanten het verschil kan proeven, hoe groot is dan β (beta-fout) bij het in onderdeel b berekende aantal? (10)
Als je onderdeel b niet hebt kunnen beantwoorden, ga dan uit van 20
Please help


Stel eerst je hypotheses eens op en kijk welke kansverdeling je kunt gebruiken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Afgeleide op 0 stellen en kijken of de tweede afgeleide niet 0 is. Ofwel 3x² + 8x - p = 0 en 6x+8 <> 0. Abc-formule toepassen, dan de coordinaten (x,y) vinden. Dat levert x=-4/3+(1/3)√(3p+16) V x = -4/3-(1/3)√(3p+16).quote:Op dinsdag 14 april 2009 23:42 schreef Dzy het volgende:
Er is een familie van derdemachtsfuncties gegeven, bijvoorbeeld x^3 +4x^2 - px + 3, nu willen wij een functie vinden die door alle extreme waarden van deze familie heen gaat. Een algemeen algoritme om dit aan te pakken. We hebben zelf al naar de afgeleide gekeken maar wat we daar verder precies mee moesten kwamen we ook niet uit.
Voor het gemak kijk ik alleen even naar het rechterdeel. Dus gegeven p weet je een extremum de x-coordinaat -4/3+(1/3)√(3p+16) heeft. We willen eigenlijk weten welke p een extremum geeft, gegeven x. Omschrijven van x = -4/3+(1/3)√(3p+16) levert p = (3x+4)²/3-16/3. Vul deze p in in x^3 +4x^2 - px + 3 en ik denk dat je klaar bent
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja de hypothese is bij een aantal rond de 15-20, en ik zou een binomcdf kansverdeling moeten gebruiken maar verder kom ik niet (bij b).
en bij c weet ik het ook echt niet. heb vanalles geprobeerd maar de antwoorden komen totaal niet overeen.
en bij c weet ik het ook echt niet. heb vanalles geprobeerd maar de antwoorden komen totaal niet overeen.


Zo werkt dat niet he? Kijk eens naar http://nl.wikipedia.org/wiki/Statistische_toets#Procedure voor de volledige procedure.quote:Op dinsdag 14 april 2009 23:58 schreef Platina het volgende:
Ja de hypothese is bij een aantal rond de 15-20, en ik zou een binomcdf kansverdeling moeten gebruiken maar verder kom ik niet (bij b).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja daar kom ik dus ook niet wijs uit nu, ben niet meer 100% en het huilen staat me nader dan het lachen dus dat gaat hem ook niet worden.


Ja, of een fatsoenlijk diktaat krijgen 
dit krijg ik iig nog eruit gebreid bij b:
p = 1/3 dat ze het goed hebben, n = 40 en alpha is 0,10. Dus er moet uit de binomiale verdeling komen dat er minimaal 0,900000001 kans is. Ik weet alleen niet hoe ik dit terugom moet rekenen.
(antwoord uitwerking: vanaf 18)
bij c (uitgaande van 20):
40 mensen is dus n, p is nu 0,5 want de helft kan verschil proeven. werken met 20 testpersonen.
ik kom uit op 0,563 maar dit is teveel.
(antwoord uitwerking: 0,437)
Iemand die het weet?
ik ga me hersenen wat rust gunnen
dit krijg ik iig nog eruit gebreid bij b:
p = 1/3 dat ze het goed hebben, n = 40 en alpha is 0,10. Dus er moet uit de binomiale verdeling komen dat er minimaal 0,900000001 kans is. Ik weet alleen niet hoe ik dit terugom moet rekenen.
(antwoord uitwerking: vanaf 18)
bij c (uitgaande van 20):
40 mensen is dus n, p is nu 0,5 want de helft kan verschil proeven. werken met 20 testpersonen.
ik kom uit op 0,563 maar dit is teveel.
(antwoord uitwerking: 0,437)
Iemand die het weet?
ik ga me hersenen wat rust gunnen


P(X>=16 | BV; n=40; p=1/3) = 1-P(X<=15 | BV; n=40; p=1/3) = 0.8890.quote:Op dinsdag 14 april 2009 23:51 schreef Platina het volgende:
[..]
4. Driehoekstest (40 punten)
De plaatselijke bakker bij ons in het dorp verkoopt elk jaar rond de Paasdagen zijn beroemde zelfgemaakte chocolade Paaseieren. Vanwege de gestegen grondstofprijzen heeft hij dit jaar zijn recept voor de vulling aangepast.
De grote vraag is natuurlijk of de consument dat proeft.
Om dat te onderzoeken biedt hij aan een 40-tal klanten de oude én de nieuwe variant aan in de vorm van een driehoekstest.
a. Aannemende dat er geen verschil te proeven is tussen de oude en de nieuwe vullingen, hoe groot is dan de kans dat minstens 40% van het aantal proefpersonen het juiste ei als afwijkend aanwijst? (5)
H0: geen verschil, p=1/3quote:b. Als je een α (alpha-fout) van 0,10 accepteert, vanaf welk aantal proefpersonen ben je dan overtuigd van een verschil in smaak? (10)
H1: wel veschil, p=1.
We zoeken de kleinste m waarvoor geldt P(X>=m | BV; n=40; p=1/3) <= 0.10. Uitproberen levert m=18.
'Kan proeven', 20 proeven het verschil dus sowieso niet en geven met kans 1/3 de juiste aan. De overige 20 kunnen het wel proeven, en geven het zeker juist aan. Je maakt alleen een type II fout wanneer je H0 onwaar is, ofwel wanneer er verschil is. Maar dat verschil wordt met zekerheid gedetecteerd door die groep van 20. Ik kom dus op een kans van 0.quote:c. Neem aan dat in werkelijkheid de helft van al zijn klanten het verschil kan proeven, hoe groot is dan β (beta-fout) bij het in onderdeel b berekende aantal? (10)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Danku voor de antwoorden, maar wat heb je precies bij B gedaan?
Want als ik doe: binomcdf (40,1/3,18) komt daar 0,96 uit :S
en bij C is er volgens de uitwerkingen wel een beta-fout?
naja, iig bedankt!
Want als ik doe: binomcdf (40,1/3,18) komt daar 0,96 uit :S
en bij C is er volgens de uitwerkingen wel een beta-fout?
naja, iig bedankt!


binocdf geeft P(X<=m). Je wilt 1-P(X<=m-1).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Lijkt me een fout van de uitwerkingen.quote:Op woensdag 15 april 2009 00:25 schreef Platina het volgende:
en bij C is er volgens de uitwerkingen wel een beta-fout?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Waarschijnlijk een makkelijke vraag maar ik kom er even niet uit (denk ik):
Je doet mee aan een lotto die bestaat uit 10 trekkingsgetallen waar je 2 willekeurige getallen uit mag kiezen, wat is de kans dat je wint?
Ik dacht dus: Beschouw de 2 willekeurige gekozen getallen als 'winnaars' en de 8 ongekozen als 'verliezers' dus:
P(winst; 2 winnaars en 8 verliezers) = 2 NcR 2 / 10 Ncr 2 = 0,022
Klopt?
Je doet mee aan een lotto die bestaat uit 10 trekkingsgetallen waar je 2 willekeurige getallen uit mag kiezen, wat is de kans dat je wint?
Ik dacht dus: Beschouw de 2 willekeurige gekozen getallen als 'winnaars' en de 8 ongekozen als 'verliezers' dus:
P(winst; 2 winnaars en 8 verliezers) = 2 NcR 2 / 10 Ncr 2 = 0,022
Klopt?


Als er maar één combinatie van twee getallen winst kan opleveren en de volgorde niet van belang is, dan juist.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Naja, het is me soort van gelukt met proefwerk van de kansberekening. Op school nog ff aan me medestudenten gevraagd 
GlowMouse iig ook bedankt.
GlowMouse iig ook bedankt.


Ben ik wel benieuwd wat voor redenering zij voor c hadden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb een vraag m.b.t. expliciete substitutie.
Heb ik het zo goed uitgewerkt? Zo nee kunnen jullie me dan op weg helpen?
[ Bericht 10% gewijzigd door Butterfly91 op 16-04-2009 14:24:56 ]
Heb ik het zo goed uitgewerkt? Zo nee kunnen jullie me dan op weg helpen?
[ Bericht 10% gewijzigd door Butterfly91 op 16-04-2009 14:24:56 ]


Helaas, het klopt niet. Als ik jou was, zou ik 1+ sqrt(x) vervangen door y ipv alleen sqrt(x) te vervangen door y.
Zo kwam ik er iig wel uit (het antwoord moet 0,386 zijn)
Zo kwam ik er iig wel uit (het antwoord moet 0,386 zijn)


Ik heb hem nu zo
Maar ik kom op een ander antwoord uit. Ik heb vast ergens een fout gemaakt, maar ik kan hem niet vinden.
Maar ik kom op een ander antwoord uit. Ik heb vast ergens een fout gemaakt, maar ik kan hem niet vinden.


Je vergeet in de tweede regel de haakjes om (1-1/y). Vervolgens ga je wel goed verder, alleen 2y/y = 2 en niet 2/y.quote:Op donderdag 16 april 2009 15:31 schreef Butterfly91 het volgende:
Ik heb hem nu zo
[ afbeelding ]
Maar ik kom op een ander antwoord uit. Ik heb vast ergens een fout gemaakt, maar ik kan hem niet vinden.
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!


Ah vandaar, stomme fout  . Maar dan kom ik alsnog op 1 uit en niet op 0,386. (heb ik vast weer een fout gemaakt
. Maar dan kom ik alsnog op 1 uit en niet op 0,386. (heb ik vast weer een fout gemaakt  )
)


Je bent goed op weg, alleen de vergelijking voor dx klopt niet.. y^2 = 1+ x ?? pijnlukquote:Op donderdag 16 april 2009 15:42 schreef Butterfly91 het volgende:
Ah vandaar, stomme fout. Maar dan kom ik alsnog op 1 uit en niet op 0,386. (heb ik vast weer een fout gemaakt
)
[ afbeelding ]


A physicist, a biologist and a mathematician are sitting in a street café watching people entering and leaving the house on the other side of the street. First they see two people entering the house. Time passes. After a while they notice three people leaving the house. The physicist says, "The measurement wasn't accurate." The biologist says, "They must have reproduced." The mathematician says, "If one more person enters the house then it will be empty."
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***


Ik zie niet waarom dat fout is aangezien ik x gedefinieerd heb als y2-1. Dat differentiëren en je krijgt 2yquote:Op donderdag 16 april 2009 15:47 schreef ramaap het volgende:
[..]
Je bent goed op weg, alleen de vergelijking voor dx klopt niet.. y^2 = 1+ x ?? pijnluk
Over y2: beide kanten tot de macht 2 zodat je geen SQRT(x) meer hebt maar gewoon x
Haakjes
y2=1+2SQRT(x)+x
toch


y= 1+ sqrt(x)
sqrt(x)= y-1
x = (y-1)(y-1)=y^2-2y+1
dx = (2y-2) dy
Dat zou ik zeggen
Klopt! Nu alleen ff dx hieruit berekenen (het is een omweg, want het kan makkelijker, kijk naar mijn berekening hierboven)quote:Op donderdag 16 april 2009 15:58 schreef Butterfly91 het volgende:
[..]
Ik zie niet waarom dat fout is aangezien ik x gedefinieerd heb als y2-1. Dat differentiëren en je krijgt 2y
Over y2: beide kanten tot de macht 2 zodat je geen SQRT(x) meer hebt maar gewoon x
Haakjes
y2=1+2SQRT(x)+x
toch
Ik geloof van wel jaquote:Op donderdag 16 april 2009 15:54 schreef defibrillator het volgende:
Moet je de continuïteitscorrectie alleen toepassen op normale (discrete) verdelingen?
[ Bericht 36% gewijzigd door ramaap op 16-04-2009 16:10:10 ]


Alleen als je een discrete verdeling benadert met een continue.quote:Op donderdag 16 april 2009 15:54 schreef defibrillator het volgende:
Moet je de continuïteitscorrectie alleen toepassen op normale (discrete) verdelingen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Er klopt geen hout van de manier waarop je met substituties omgaat. De integraal die je moet uitrekenen is:quote:Op donderdag 16 april 2009 15:31 schreef Butterfly91 het volgende:
Ik heb hem nu zo
[ afbeelding ]
Maar ik kom op een ander antwoord uit. Ik heb vast ergens een fout gemaakt, maar ik kan hem niet vinden.
(1) ∫01 √x / (1 + √x)∙dx
Een eerste tip: gebruik niet de letter y als substitutievariabele, deze wordt namelijk gewoonlijk al gebruikt om de afhankelijke variabele aan te geven bij een functie waarvan x de onafhankelijke variabele is. Ik zal hier daarom z gebruiken.
De substitutie die je hier kunt toepassen is:
(2) z = 1 + √x
Dan is dus:
(3) x = (z - 1)2
En dus ook:
(4) dx/dz = 2∙(z -1)
En dus:
(5) dx = 2∙(z - 1)∙dz
Uit (2) halen we dat voor x = 0 geldt z = 1 en voor x = 1 geldt z = 2. Dat zijn dus de nieuwe grenzen van het interval waarover we moeten integreren met de gesubstitueerde variable. De integraal wordt nu:
(6) ∫12 (z - 1)∙z-1∙2∙(z -1)∙dz
Dit is te schrijven als:
(7) ∫12 (2z - 4 + 2z-1)∙dz
Een primitieve van 2z - 4 + 2z-1 is z2 - 4z + 2∙ln z, en dus vinden we voor de waarde van de integraal:
(8) [z2 - 4z + 2∙ln z]12 = (4 - 8 + 2∙ln 2) - (1 - 4 + 0) = 2∙ln 2 - 1.
[ Bericht 0% gewijzigd door Riparius op 16-04-2009 20:27:57 ]


Sorry Riparius, ik heb hem op dezelfde manier staan als hierboven, maar alleen niet meer hier gepost. Die eerste twee die ik postte, daar klopte idd geen hout van. Domme fouten gemaakt.
Dat van die y wist ik niet trouwens, maar zo heb ik het geleerd.
Dat van die y wist ik niet trouwens, maar zo heb ik het geleerd.


Ja, zo klopt je uitwerking, afgezien van wat schoonheidsfoutjes in je notatie. Als je x = y2 - 2y + 1 hebt dan is dx/dy = 2y - 2 en dus dx = (2y - 2)∙dy. Verder ben je haakjes vergeten in je laatste paar integralen.quote:Op donderdag 16 april 2009 20:33 schreef Butterfly91 het volgende:
Sorry Riparius, ik heb hem op dezelfde manier staan als hierboven, maar alleen niet meer hier gepost. Die eerste twee die ik postte, daar klopte idd geen hout van. Domme fouten gemaakt.
Dat van die y wist ik niet trouwens, maar zo heb ik het geleerd.
[ afbeelding ]


Excentriciteit en kegelsneden in poolnotatie.
als e=1 een parabool en een ellips en hyperbool als e groter of kleiner dan 1. Akkoord.
Maar kan iemand mij inzichtelijk maken waarom een cirkel hoort bij e=0? Staat niet echt in mijn leerstof, maar toch schijnt het zo te zijn.
Excentriciteit is gedefinieerd als | PF | / | Pl | .
als e=1 een parabool en een ellips en hyperbool als e groter of kleiner dan 1. Akkoord.
Maar kan iemand mij inzichtelijk maken waarom een cirkel hoort bij e=0? Staat niet echt in mijn leerstof, maar toch schijnt het zo te zijn.
Excentriciteit is gedefinieerd als | PF | / | Pl | .
kloep kloep


Niet helemaal, tenzij je dit bedoelt als een chiasmequote:Op vrijdag 17 april 2009 19:39 schreef Borizzz het volgende:
Excentriciteit en kegelsneden in poolnotatie.
als e=1 een parabool en een ellips en hyperbool als e groter of kleiner dan 1. Akkoord.
Bij een ellips is de eccentriciteit op te vatten als de verhouding tussen de afstand van elk van de brandpunten tot het centrum en de lengte van de halve lange as. Een cirkel is een ellips waarvan de brandpunten in het centrum (middelpunt) liggen, zodat deze verhouding, en dus de eccentriciteit, gelijk is aan 0.quote:Maar kan iemand mij inzichtelijk maken waarom een cirkel hoort bij e=0? Staat niet echt in mijn leerstof, maar toch schijnt het zo te zijn.
Excentriciteit is gedefinieerd als | PF | / | Pl | .
[ Bericht 0% gewijzigd door Riparius op 19-04-2009 18:06:39 ]


Ik heb hulp nodig met het bewijzen van dit.
Gegeven:
Lijn m, n met middenparallel l
Punt P op m, punt Q op n
Te bewijzen:
Het snijpunt van de deellijnen van P en Q ligt op l.
Bewijs (begin):
Gegeven:
Lijn m, n met middenparallel l
Punt P op m, punt Q op n
Te bewijzen:
Het snijpunt van de deellijnen van P en Q ligt op l.
Bewijs (begin):
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Weet iemand hoe ik verder kom?Jesus hates you.


Ik zou het zo doen:
Je merkt het snijpunt van de deellijnen aan als punt T.
Uit het feit dat T op de deellijn van P ligt concludeer je dat d(T,m) = d(T,PQ). Oftewel de afstand van T naar beide lijnen is even groot.
Maar T ligt ook op de deellijn van punt Q. Dus d(T,n) = d(T,PQ).
Kun je nu het laatste stukje?
Je merkt het snijpunt van de deellijnen aan als punt T.
Uit het feit dat T op de deellijn van P ligt concludeer je dat d(T,m) = d(T,PQ). Oftewel de afstand van T naar beide lijnen is even groot.
Maar T ligt ook op de deellijn van punt Q. Dus d(T,n) = d(T,PQ).
Kun je nu het laatste stukje?
kloep kloep


Ik ken die regel niet, maar ben wel in staat met congruente driehoeken aan te tonen dat beide afstanden even groot zijn.quote:Op zondag 19 april 2009 16:55 schreef Borizzz het volgende:
Ik zou het zo doen:
Je merkt het snijpunt van de deellijnen aan als punt T.
Uit het feit dat T op de deellijn van P ligt concludeer je dat d(T,m) = d(T,PQ). Oftewel de afstand van T naar beide lijnen is even groot.
En dan dus de conclusie:quote:Maar T ligt ook op de deellijn van punt Q. Dus d(T,n) = d(T,PQ).
Kun je nu het laatste stukje?
d(T,n) = d(T,m) , dus T ligt op de middenparallel van m en n.
Bedankt voor je hulp, ik snap hem nu.
Jesus hates you.


Alle punten op de bissectrice van een hoek liggen op gelijke afstanden van de beide benen van die hoek. Daarom is het snijpunt van de bissectrices van een driehoek ook het middelpunt van de ingeschreven cirkel van die driehoek.quote:Op zondag 19 april 2009 19:04 schreef Hondenbrokken het volgende:
[..]
Ik ken die regel niet, maar ben wel in staat met congruente driehoeken aan te tonen dat beide afstanden even groot zijn.
[..]


Ik snap het, maar toch zag ik dat over het hoofd.quote:Op zondag 19 april 2009 19:16 schreef Riparius het volgende:
[..]
Alle punten op de bissectrice van een hoek liggen op gelijke afstanden van de beide benen van die hoek. Daarom is het snijpunt van de bissectrices van een driehoek ook het middelpunt van de ingeschreven cirkel van die driehoek.
Jesus hates you.


Een klein vraagje over statistiek:
'Zijn volgende onderzochte variabelen nominaal, ordinaal, continu of discontinu?
Wat wordt momenteel het meest verkocht: huizen of appartementen?
Dat zou nominaal moeten zijn en 'het meest verkocht' zou in dat opzicht slechts misleidend de indruk geven dat het ordinaal is, maar ik vrees dat ik niet helemaal kan volgen. Iemand? Alvast bedankt!
'Zijn volgende onderzochte variabelen nominaal, ordinaal, continu of discontinu?
Wat wordt momenteel het meest verkocht: huizen of appartementen?
Dat zou nominaal moeten zijn en 'het meest verkocht' zou in dat opzicht slechts misleidend de indruk geven dat het ordinaal is, maar ik vrees dat ik niet helemaal kan volgen. Iemand? Alvast bedankt!
When all things seem to end, the future still remains..


Het verschil tussen ordinaal en nominaal is niet van belang zolang je maar twee niveau's hebt. Ook zou een (discontinue) 0/1-variabele hier voldoen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Even tussendoor:
Waarom geeft (bij een priemfactorontbinding) het aantal vijfen het aantal nullen aan waarop het getal eindigt?
Dit staat in mijn boek; en hier wordt zomaar overheen gestapt alsof het een uitgemaakte zaak is....
Waarom geeft (bij een priemfactorontbinding) het aantal vijfen het aantal nullen aan waarop het getal eindigt?
Dit staat in mijn boek; en hier wordt zomaar overheen gestapt alsof het een uitgemaakte zaak is....
kloep kloep


Dus 5² zou op twee nullen eindigen?  Je moet juist zoeken naar het aantal factoren 10 (ofwel het minimum van het aantal factoren 2 en het aantal factoen 5). Bijvoorbeeld 1100 = 2³*5²*11 = 10² * 2*11. Al die andere factoren kunnen nooit voor een 0 op het eind zorgen.
Je moet juist zoeken naar het aantal factoren 10 (ofwel het minimum van het aantal factoren 2 en het aantal factoen 5). Bijvoorbeeld 1100 = 2³*5²*11 = 10² * 2*11. Al die andere factoren kunnen nooit voor een 0 op het eind zorgen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


tvp. Wiskunde opvijzelen 
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Hoi!
Over 2 maanden heb ik een toelatingstoets op het Saxion.
Hiervoor moet ik dus Wiskunde A afleggen. (ben ook pas onlangs thuis van vakantie, en heb kort geleden een opleiding gekozen, misschien beetje laat, maar het kan nog wel)
Alleen een beetje het probleem is dat ik dus:
-eerste en 2de graads functies
-het oplossen van eerste en tweede graads vergelijkingen
en -machtfuncties en logaritmen
moet leren kennen. Kan iemand mij adviseren waar eerst mee, mee te beginnen en te eindigen? Wat het beste manier is om het te leren? Heb HTO basisvaardigheden boekje ter beschikking.
Bedankt!
Over 2 maanden heb ik een toelatingstoets op het Saxion.
Hiervoor moet ik dus Wiskunde A afleggen. (ben ook pas onlangs thuis van vakantie, en heb kort geleden een opleiding gekozen, misschien beetje laat, maar het kan nog wel)
Alleen een beetje het probleem is dat ik dus:
-eerste en 2de graads functies
-het oplossen van eerste en tweede graads vergelijkingen
en -machtfuncties en logaritmen
moet leren kennen. Kan iemand mij adviseren waar eerst mee, mee te beginnen en te eindigen? Wat het beste manier is om het te leren? Heb HTO basisvaardigheden boekje ter beschikking.
Bedankt!
I pwn u!


De eerste is simpel. Gebruik de stelling van Thales, dan weet je dat de (denkbeeldige) lijn CB loodrecht staat op AC. Tevens weet je al dat AC = CD. Driehoek ABC en CBD zijn dus gelijkvormig omdat ze twee gelijke zijdes hebben. Dat betekent automatisch ook dat hoek ACB = hoek ADB.quote:Op donderdag 23 april 2009 21:57 schreef Hondenbrokken het volgende:
Nog een meetkunde-probleem:
[ link | afbeelding ]
Of hier in het groot:
http://img14.imageshack.us/img14/9529/opgave7.jpg
De tweede is wat lastiger, die weet ik even niet.
Ten percent faster with a sturdier frame


A is inderdaad congruentiegeval ZHZ.
B volgt uit hoek BEC = hoek BAC en door te kijken naar driehoek AES. We zien hoek CAE = hoek AEC omdat ze op bogen met dezelfde lengte staan, noem die hoek even x. Vanwege Thales op driehoek ABE geldt x + hoek BAC = 90. We krijgen dus 180 = hoek EAS + hoek AES + hoek ASE = (x-hoek BAC) + x + hoek ASE = 2*(x+hoek BAC) - 3*hoek BAC + hoek ASE = 0. Hieruit volgt direct hetgeen te bewijzen viel. Geen idee of het simpeler kan.
B volgt uit hoek BEC = hoek BAC en door te kijken naar driehoek AES. We zien hoek CAE = hoek AEC omdat ze op bogen met dezelfde lengte staan, noem die hoek even x. Vanwege Thales op driehoek ABE geldt x + hoek BAC = 90. We krijgen dus 180 = hoek EAS + hoek AES + hoek ASE = (x-hoek BAC) + x + hoek ASE = 2*(x+hoek BAC) - 3*hoek BAC + hoek ASE = 0. Hieruit volgt direct hetgeen te bewijzen viel. Geen idee of het simpeler kan.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Trek hulplijn BC. Dan is ∠ACB recht, aangezien deze op de halve cirkelboog AB staat (stelling van Thales). Maar dan is ∠ACB = ∠DCB. Aangezien ook AC = CD zijn driehoeken ACB en DCB congruent, waaruit volgt dat ∠BAC = ∠BDC.quote:Op donderdag 23 april 2009 21:57 schreef Hondenbrokken het volgende:
Nog een meetkunde-probleem:
[ link | afbeelding ]
Of hier in het groot:
http://img14.imageshack.us/img14/9529/opgave7.jpg
Hoek ASE is supplementair met hoek ESB, dus ∠ASE = 180° - ∠ESB. En aangezien de som van de hoeken van driehoek ESB 180 graden is, is ∠ASE gelijk aan de som van de beide andere hoeken van driehoek ESB, dus:
∠ASE = ∠SEB + ∠SBE
Nu zijn ∠SBE en ∠ABD supplementair, zodat:
∠ASE = ∠SEB + (180° - ∠ABD)
Aangezien de som van de hoeken van driehoek ABD 180 graden is hebben we dus ook:
∠ASE = ∠SEB + ∠BAC + ∠BDC
Nu hadden we al aangetoond dat ∠BDC = ∠BAC, en verder is ook ∠SEB = ∠BAC, aangezien deze beide gelijk zijn aan de helft van cirkelboog BC. Dus hebben we inderdaad:
∠ASE = ∠BAC + ∠BAC + ∠BAC = 3∙∠BAC
QED


@TC03
Het ging me vooral om die 2e. Maar toch bedankt, ik waardeer je post.
Glowmouse:
@ Riparius
Bedankt. Ik snap hem helemaal.
[ Bericht 3% gewijzigd door Hondenbrokken op 24-04-2009 08:53:16 ]
Het ging me vooral om die 2e. Maar toch bedankt, ik waardeer je post.
Glowmouse:
Waarom hebben die bogen dan een gelijke lengte? Ze lijken me juist verschillend. Maar bedankt voor je poging.quote:We zien hoek CAE = hoek AEC omdat ze op bogen met dezelfde lengte staan, noem die hoek even x
@ Riparius
Bedankt. Ik snap hem helemaal.
[ Bericht 3% gewijzigd door Hondenbrokken op 24-04-2009 08:53:16 ]
Jesus hates you.


Omdat de koorden gelijke lengte hebben (ABD en ECD zijn congruente en gelijkbenige driehoeken).quote:Op vrijdag 24 april 2009 08:39 schreef Hondenbrokken het volgende:
@TC03
Het ging me vooral om die 2e. Maar toch bedankt, ik waardeer je post.
Glowmouse:
[..]
Waarom hebben die bogen dan een gelijke lengte?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Neequote:Op vrijdag 24 april 2009 11:15 schreef GlowMouse het volgende:
[..]
Omdat de koorden gelijke lengte hebben (ABD en ECD zijn congruente en gelijkbenige driehoeken).
Driehoeken ABD en ECD zijn wel gelijkvormig, maar niet congruent. De gelijkbenige zijden van driehoek ECD zijn gelijk aan de helft van de basis van driehoek ABD. Aangezien de som van de lengten van twee zijden van een driehoek groter is dan de lengte van de derde zijde kunnen ze dus niet congruent zijn.


De wet van Murphy bij Glowmouse.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Hey,
Ik heb een vraag over de zeta-functie.
Ik zoek een "holomorfe uitbreiding" van de functie f(s):= zeta(s)/zeta(ks) waarbij k>=2 een geheel getal is. Deze uitbreiding heeft dan als domain een open deelverzameling van C die {s \in C| Re s >=1}\{1} bevat.
Voor zeta(s) heb ik al de holomorfe uitbreiding:
zeta(s)= 1/(s-1)+1/2 -s*int((x-[x]-1/2)x-1-s ), x=0..oo).
Deze geldt voor alle s in C met Re s >0, s != 1.
Ik zit nu vast met zeta(s)/zeta(ks).
Enig idee hoe het moet?
Alvast bedankt
Ik heb een vraag over de zeta-functie.
Ik zoek een "holomorfe uitbreiding" van de functie f(s):= zeta(s)/zeta(ks) waarbij k>=2 een geheel getal is. Deze uitbreiding heeft dan als domain een open deelverzameling van C die {s \in C| Re s >=1}\{1} bevat.
Voor zeta(s) heb ik al de holomorfe uitbreiding:
zeta(s)= 1/(s-1)+1/2 -s*int((x-[x]-1/2)x-1-s ), x=0..oo).
Deze geldt voor alle s in C met Re s >0, s != 1.
Ik zit nu vast met zeta(s)/zeta(ks).
Enig idee hoe het moet?
Alvast bedankt
verlegen :)


Waarschijnlijk is het enorm simpel maar ik kom er even niet op:
e^x/n = 3
e^x = 3^n
waarom?
e^x/n = 3
e^x = 3^n
waarom?
The whole problem with the world is that fools and fanatics are always so certain of themselves, and wiser people so full of doubt


http://www.wisfaq.nl/showfaq3.asp?Id=3107
Links en rechts ^n doen en dan links rekenregel M5 toepassen.
[ Bericht 0% gewijzigd door GlowMouse op 27-04-2009 13:32:02 ]
Links en rechts ^n doen en dan links rekenregel M5 toepassen.
[ Bericht 0% gewijzigd door GlowMouse op 27-04-2009 13:32:02 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


je bedoelt links en rechts ^n toch? dan snap ik het in ieder geval 
The whole problem with the world is that fools and fanatics are always so certain of themselves, and wiser people so full of doubt


Helder, thanks 
The whole problem with the world is that fools and fanatics are always so certain of themselves, and wiser people so full of doubt


e^(x/n) de integraal ervoor is n * e^(x/n)
maar waarom? ik zou zelf denken 1 / ((x/n) + 1) * e^((x/n)+1)
Zucht, een paar weken niks aan wiskunde gedaan en het lijkt spontaan chinees
maar waarom? ik zou zelf denken 1 / ((x/n) + 1) * e^((x/n)+1)
Zucht, een paar weken niks aan wiskunde gedaan en het lijkt spontaan chinees
The whole problem with the world is that fools and fanatics are always so certain of themselves, and wiser people so full of doubt


Je bedoelt de primitieve ervan. Kijk eens goed wat er gebeurt bij differentieren: hebben we x^n of g^x?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


g^x => g^x/ln x ?
The whole problem with the world is that fools and fanatics are always so certain of themselves, and wiser people so full of doubt


Die ja, dan is het toch ook duidelijk dat je niet die macht met eentje moet ophogen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Jazeker, maar ik begrijp niet hoe ze aan n*e^(x/n) komen
The whole problem with the world is that fools and fanatics are always so certain of themselves, and wiser people so full of doubt


De functie die je hebt is (e^1/n)^x. Als je die zou differentiëren krijg je 1/n * e^(x/n).
Als je n*e^(x/n) differentieert, gaat het dus precies goed.
Als je n*e^(x/n) differentieert, gaat het dus precies goed.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Jouw uitbreiding van zeta(s) naar Re s > 0 definieert alvast een meromorfe uitbreiding van f(s) naar Re s > 0. Echter, dat ding zou polen kunnen hebben op de punten s waarvoor zeta(ks)=0. Nu heeft zeta(s) geen nulpunten voor Re s > 1: immers convergeert de Dirichletreeks voor 1/zeta(s) (= som mu(n) / n^s) absoluut en uniform op compacta voor Re s > 1, en kan dus geen polen hebben. Dus zeta(ks) heeft geen nulpunten voor Re(s)>1/k. Het open deel dat je kunt nemen is dan U = {s in C : Re s > 1/k, s != 1}.quote:Op maandag 27 april 2009 10:22 schreef teletubbies het volgende:
Hey,
Ik heb een vraag over de zeta-functie.
Ik zoek een "holomorfe uitbreiding" van de functie f(s):= zeta(s)/zeta(ks) waarbij k>=2 een geheel getal is. Deze uitbreiding heeft dan als domain een open deelverzameling van C die {s \in C| Re s >=1}\{1} bevat.
Voor zeta(s) heb ik al de holomorfe uitbreiding:
zeta(s)= 1/(s-1)+1/2 -s*int((x-[x]-1/2)x-1-s ), x=0..oo).
Deze geldt voor alle s in C met Re s >0, s != 1.
Ik zit nu vast met zeta(s)/zeta(ks).
Enig idee hoe het moet?
Alvast bedankt


Ik wil nog even de mensen hier bedanken, mede met hulp van jullie heb ik mijn twee wiskunde tentamens gehaald, analyse en lineaire algebra 
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Oh oke, ik zie het nu. Ik vergat dat er sprake was van absolute in uniforme convergentie. Maar voor de goeie orde lijkt het me goed om te weten wat voor rol deze twee precies spelen. De uniforme convergentie van de reeks holomorfe functies (som mu(n) /n^s, n=1...k)) zorgt ervoor dat de limiet 1/zeta(s) een holomorfe functie is.quote:Op maandag 27 april 2009 15:58 schreef thabit het volgende:
[..]
Jouw uitbreiding van zeta(s) naar Re s > 0 definieert alvast een meromorfe uitbreiding van f(s) naar Re s > 0. Echter, dat ding zou polen kunnen hebben op de punten s waarvoor zeta(ks)=0. Nu heeft zeta(s) geen nulpunten voor Re s > 1: immers convergeert de Dirichletreeks voor 1/zeta(s) (= som mu(n) / n^s) absoluut en uniform op compacta voor Re s > 1, en kan dus geen polen hebben. Dus zeta(ks) heeft geen nulpunten voor Re(s)>1/k. Het open deel dat je kunt nemen is dan U = {s in C : Re s > 1/k, s != 1}.
De absolute convergentie:.....wat voor rol speelt deze in deze redenering? Ik weet wel dat absolute convergentie nodig is om het inverse van zeta(s) te vinden (Dirichletreeksen samenstellen).
verlegen :)


Ik begreep het niet, vervolgens maakte ik wat andere sommen en nu begrijp ik het welquote:Op maandag 27 april 2009 15:04 schreef GlowMouse het volgende:
De functie die je hebt is (e^1/n)^x. Als je die zou differentiëren krijg je 1/n * e^(x/n).
Als je n*e^(x/n) differentieert, gaat het dus precies goed.
Als ik het goed begrijp is het bijv. bij e^3x dat als je differentieert er 3*e^3x ontstaat, en omdat er juist e^3x moet ontstaan zet je er 1/3 voor, en dan heb je dus de primitieve, namelijk 1/3 e^3x
Bij het differentiëren van de oorspronkelijke functie zou je 1/n * e^(x/n) krijgen, om er "1" van te maken doe je dus maal n (want n/n = 1)
The whole problem with the world is that fools and fanatics are always so certain of themselves, and wiser people so full of doubt


De absolute convergentie is hier misschien niet heel hard nodig, behalve inderdaad om aan te tonen dat je 1/zeta(s) ook als een Dirichletreeks kunt uitdrukken, of in het algemeen om makkelijk met reeksen te kunnen manipuleren. Maar dan nog heb je het alleen maar nodig voor Re(s) >> 0. Belangrijk is vooral de uniforme convergentie op compacta; dat toont namelijk aan dat de limiet ook weer holomorf is.quote:Op maandag 27 april 2009 20:43 schreef teletubbies het volgende:
[..]
Oh oke, ik zie het nu. Ik vergat dat er sprake was van absolute in uniforme convergentie. Maar voor de goeie orde lijkt het me goed om te weten wat voor rol deze twee precies spelen. De uniforme convergentie van de reeks holomorfe functies (som mu(n) /n^s, n=1...k)) zorgt ervoor dat de limiet 1/zeta(s) een holomorfe functie is.
De absolute convergentie:.....wat voor rol speelt deze in deze redenering? Ik weet wel dat absolute convergentie nodig is om het inverse van zeta(s) te vinden (Dirichletreeksen samenstellen).


Simpel grafentheorie probleempje waar ik op de een of andere manier niet uit kom .....
Zij G een vlakke graaf, en laat C een takkenverzameling zijn G, en stel dat het aantal gemeenschappelijke takken van C met elke minimale snede van G even is. Bewijs dat C de vereniging is van een aantal takdisjuncte kringen.
Ik zie wel eenvoudig in dat als C een kring is en S een minimale snede, dat C en S altijd een even aantal gemeenschappelijke takken moeten hebben. Maar de andere implicatie wil niet echt lukken....
Zij G een vlakke graaf, en laat C een takkenverzameling zijn G, en stel dat het aantal gemeenschappelijke takken van C met elke minimale snede van G even is. Bewijs dat C de vereniging is van een aantal takdisjuncte kringen.
Ik zie wel eenvoudig in dat als C een kring is en S een minimale snede, dat C en S altijd een even aantal gemeenschappelijke takken moeten hebben. Maar de andere implicatie wil niet echt lukken....
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Als je een punt van je graaf hebt, dan vormen de takken die aan dat punt vastzitten een minimale snede. Hieruit kun je afleiden dat C leeg is of een kring bevat. Haal je die kring weg uit C, dan houden we een verzameling over die nog steeds aan dezelfde voorwaarden voldoet. Zo kun je dus net zo lang kringen weghalen tot je niks meer overhoudt.


Zou iemand mij kunnen helpen?
Van een binomiaal verdeelde stochast X weet je dat de verwachtingswaarde 2 2/3 is. De standaardafwijking is 1 1/3.
Bereken P(X = 4).
E = np = 2 2/3 = 8/3
σ = wortel(npq) = 1 1/3 = 4/3
σ = npq = 16/9
np = 8/3
npq = 16/9
Ik weet niet hoe ik deze vergelijking verder op moet lossen:?
Van een binomiaal verdeelde stochast X weet je dat de verwachtingswaarde 2 2/3 is. De standaardafwijking is 1 1/3.
Bereken P(X = 4).
E = np = 2 2/3 = 8/3
σ = wortel(npq) = 1 1/3 = 4/3
σ = npq = 16/9
np = 8/3
npq = 16/9
Ik weet niet hoe ik deze vergelijking verder op moet lossen:?
ik doe wat ik wil dus als het je niet aanstaat heb je lekker dikke pech pipoo


Een dekpunt van een functie f: R pijl naar rechts R is een punt x element van R waarvoor geldt dat f(x)=x
Laat f: R pijl naar rechts gegeven zijn door f(x)=2*x-x^3. Bereken de dekpunten van f.
Dit is geen probleem gewoon de vgl x^3=x oplossen, levert de punten 0,1 en -1 op.
Bij de volgende vraag kom ik in de problemen.
Laat g: R pijl naar rechts R gegeven zijn door g(x)=2*x-x^3+epsilon. Laat zien dat als de absolute waarde van epsilon voldoende klein is, dat dan g evenveel dekpunten heeft als f. Maak de enigzins vage uitdrukking voldoende klein precies.
vraag c
Laat zien dat de dekpunten gevonden bij vraag b continu differentieerbare functies zijn van epsilon, en bereken hun afgeleides in het punt epsilon=0
Laat f: R pijl naar rechts gegeven zijn door f(x)=2*x-x^3. Bereken de dekpunten van f.
Dit is geen probleem gewoon de vgl x^3=x oplossen, levert de punten 0,1 en -1 op.
Bij de volgende vraag kom ik in de problemen.
Laat g: R pijl naar rechts R gegeven zijn door g(x)=2*x-x^3+epsilon. Laat zien dat als de absolute waarde van epsilon voldoende klein is, dat dan g evenveel dekpunten heeft als f. Maak de enigzins vage uitdrukking voldoende klein precies.
vraag c
Laat zien dat de dekpunten gevonden bij vraag b continu differentieerbare functies zijn van epsilon, en bereken hun afgeleides in het punt epsilon=0
-


Het gaat er dus om wanneer x-x³+epsilon drie nulpunten heeft. Je kunt gewoon kijken hoever het minimum nog omhoog kan en hoeveel het maximum nog omlaag.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja dat klopt. Maar wat bedoel je met maximum en minimum? Dat zie ik niet.quote:Op dinsdag 5 mei 2009 13:08 schreef GlowMouse het volgende:
Het gaat er dus om wanneer x-x³+epsilon drie nulpunten heeft. Je kunt gewoon kijken hoever het minimum nog omhoog kan en hoeveel het maximum nog omlaag.
-


Maak eens een plaatje van de x-x³ met x in [-2,2] en y in [-2, 2], je ziet dan precies wat er fout gaat als je de functie omhoog of omlaag verschuift. Dat idee gebruik je vervolgens om het exacte antwoord te vinden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Stel ik neem epsilon 0.3 dan zijn er nog steeds 3 dekpunten. Maar stel ik neem nu epsilon 0.5, dan zijn er geen 3 dekpunten meer. Dat begrijp ik. Maar ik zie nog steeds niet in hoe dit me verder helpt om de precieze epsilon te vinden.quote:Op dinsdag 5 mei 2009 13:34 schreef GlowMouse het volgende:
Maak eens een plaatje van de x-x³ met x in [-2,2] en y in [-2, 2], je ziet dan precies wat er fout gaat als je de functie omhoog of omlaag verschuift. Dat idee gebruik je vervolgens om het exacte antwoord te vinden.
-


Epsilon wordt van boven begrensd omdat het minimum anders te hoog komt te liggen. Het minimum heeft x-coordinaat -sqrt(3)/3 en dus y-coordinaat (-sqrt(3)/3)³-sqrt(3)/3 en dus maximaal sqrt(3)/3-(-sqrt(3)/3)³ omhoog.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Wacht even dit volg ik niet. Het is duidelijk dat epsilon begrends is. Maar wat hebben maxima en minima hier mee te maken?quote:Op dinsdag 5 mei 2009 13:43 schreef GlowMouse het volgende:
Epsilon wordt van boven begrensd omdat het minimum anders te hoog komt te liggen. Het minimum heeft x-coordinaat -sqrt(3)/3 en dus y-coordinaat (-sqrt(3)/3)³-sqrt(3)/3 en dus maximaal sqrt(3)/3-(-sqrt(3)/3)³ omhoog.
-


Heb je de grafiek wel voor je en zie je wat epsilon doet met het aantal nulpunten en wat het grensgeval is van 1 vs. 3 nulpunten?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik zie wat epsilon doet. maar ik zie het grensgeval niet.quote:Op dinsdag 5 mei 2009 13:53 schreef GlowMouse het volgende:
Heb je de grafiek wel voor je en zie je wat epsilon doet met het aantal nulpunten en wat het grensgeval is van 1 vs. 3 nulpunten?
-


Meer kan ik er toch niet van maken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoe ben je aan die epsilon gekomen? dat kun je toch wel uitleggen? Je ziet dat bij het kwartje niet valt bij. Maar als je gewoon uitlegt hoe je hebt gedaan dan zie ik het misschien wel. \Inplaats steeds weer vragen te stellen.quote:
-


Toch weer een vraag: wat denk je dat een positieve epsilon doet?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


een postieve epsilon verschuift de grafiek naar boven, en een negatieve epsilon verschuift hem naar beneden. En nu?quote:Op dinsdag 5 mei 2009 14:16 schreef GlowMouse het volgende:
Toch weer een vraag: wat denk je dat een positieve epsilon doet?
-


Nu als het minimum boven de x-as komt, heb je nog maar één nulpunt.quote:Op dinsdag 5 mei 2009 14:25 schreef gaussie het volgende:
[..]
een postieve epsilon verschuift de grafiek naar boven, en een negatieve epsilon verschuift hem naar beneden. En nu?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja en?quote:Op dinsdag 5 mei 2009 14:27 schreef GlowMouse het volgende:
[..]
Nu als het minimum boven de x-as komt, heb je nog maar één nulpunt.
-


Dat zal wel een grensgeval zijn. En nu houd ik erover op.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dit vind ik jammer. Andere mensen krijgen gewoon antwoord op hun vraag. Maar ik moet het zelf oplossen. Alsof ik het niet zelf heb geprobeerd. Als ik de uitwerking zie dan valt misschien het kwartje...quote:Op dinsdag 5 mei 2009 14:34 schreef GlowMouse het volgende:
[..]
Dat zal wel een grensgeval zijn. En nu houd ik erover op.
-


Regel 1 voor het leren van wiskunde:quote:Op dinsdag 5 mei 2009 14:40 schreef gaussie het volgende:
[..]
Als ik de uitwerking zie dan valt misschien het kwartje...
Kijk nooit naar de uitwerking (antwoordenboekje) voordat je een antwoord hebt.
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***


Snap jij de redenering achter het antwoord van glowmouse dan? Zo ja leg het aub uit want je ziet dat ik er gewoon niet uitkom als mij steeds weer vragen worden gesteld.quote:Op dinsdag 5 mei 2009 14:42 schreef Atlanticus het volgende:
[..]
Regel 1 voor het leren van wiskunde:
Kijk nooit naar de uitwerking (antwoordenboekje) voordat je een antwoord hebt.
-


Ik snap dat al niet. Bedoel je hier iets met limieten?quote:Maak de enigzins vage uitdrukking voldoende klein precies.
Er staat vast zo'n voorbeeld in je calculus boek.quote:vraag c
Laat zien dat de dekpunten gevonden bij vraag b continu differentieerbare functies zijn van epsilon, en bereken hun afgeleides in het punt epsilon=0
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***


De batterijen van mijn grafische rekenmachine waren leeg, en ik heb die batterijen toen vervangen voor nieuwe en nu loopt mijn GR gelijk vast als ik hem aanzet! Hetzelfde gebeurt als ik de oude batterijen er weer instop.. weet iemand hoe dit *snel* op te lossen is?? :[


Backupbatterij er ook een paar minuten uithalen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Gedaan.. maar als ik hem aanzet staat er nu TI-84 Plus 2.21 RAM cleared" en hij is nog steeds vastgelopen 


denk dat ik vraag b snap. De kritieke epsilon is de epsilon waar de lijn y=x de functie g(x) raakt. Dus het raakpunt. Hier worden 2 fixed points 1. Dat dus dat er dan maar 2 dekpunten zijn. Die epsilon vind je door gebruik te maken van de relatie tussen raaklijn en afgeleide. Dan vindt je je voor epsilon absoluut 2/3*sqrt(3) absoluut. Toch? Maar ik zit toch steeds vast bij vraag c. Kan iemand me daarbij helpen?
-


Heb het over deze vraag:
Een dekpunt van een functie f: R pijl naar rechts R is een punt x element van R waarvoor geldt dat f(x)=x
Laat f: R pijl naar rechts gegeven zijn door f(x)=2*x-x^3. Bereken de dekpunten van f.
Dit is geen probleem gewoon de vgl x^3=x oplossen, levert de punten 0,1 en -1 op.
Bij de volgende vraag kom ik in de problemen.
Laat g: R pijl naar rechts R gegeven zijn door g(x)=2*x-x^3+epsilon. Laat zien dat als de absolute waarde van epsilon voldoende klein is, dat dan g evenveel dekpunten heeft als f. Maak de enigzins vage uitdrukking voldoende klein precies.
vraag c
Laat zien dat de dekpunten gevonden bij vraag b continu differentieerbare functies zijn van epsilon, en bereken hun afgeleides in het punt epsilon=0
Een dekpunt van een functie f: R pijl naar rechts R is een punt x element van R waarvoor geldt dat f(x)=x
Laat f: R pijl naar rechts gegeven zijn door f(x)=2*x-x^3. Bereken de dekpunten van f.
Dit is geen probleem gewoon de vgl x^3=x oplossen, levert de punten 0,1 en -1 op.
Bij de volgende vraag kom ik in de problemen.
Laat g: R pijl naar rechts R gegeven zijn door g(x)=2*x-x^3+epsilon. Laat zien dat als de absolute waarde van epsilon voldoende klein is, dat dan g evenveel dekpunten heeft als f. Maak de enigzins vage uitdrukking voldoende klein precies.
vraag c
Laat zien dat de dekpunten gevonden bij vraag b continu differentieerbare functies zijn van epsilon, en bereken hun afgeleides in het punt epsilon=0
-


Bij epsilon = 2/3 sqrt(3) heb ik allang geen drie dekpunten meer. Je aanpak is een juiste, maar ik denk dat er bij de uitvoering ervan een fout wordt gemaakt. y=x en g(x) raken als 2-3x²=1 (afgeleiden aan elkaar gelijk), ofwel wanneer x = +/-sqrt(1/3). Dus op deze x-coordinaat gaan de problemen ontstaan.quote:Op dinsdag 5 mei 2009 19:01 schreef gaussie het volgende:
denk dat ik vraag b snap. De kritieke epsilon is de epsilon waar de lijn y=x de functie g(x) raakt. Dus het raakpunt. Hier worden 2 fixed points 1. Dat dus dat er dan maar 2 dekpunten zijn. Die epsilon vind je door gebruik te maken van de relatie tussen raaklijn en afgeleide. Dan vindt je je voor epsilon absoluut 2/3*sqrt(3) absoluut. Toch? Maar ik zit toch steeds vast bij vraag c. Kan iemand me daarbij helpen?
Ik gebruik dat 2x-x³+eps=x drie oplossingen heeft desda x-x³+eps drie nulpunten heeft.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat klopt epsilon = 2/3 sqrt(3) is de kritieke waarde. Als hij deze waarde aanneemt dan zijn er geen 3 dekpunten maar 2. Zolang epsilon kleiner is dan deze waarde hebben f en g hetzelfde aantal dekpunten. Daarmee is vraag b beantwoordt. Maar nu nog vraag c....quote:Op dinsdag 5 mei 2009 19:48 schreef GlowMouse het volgende:
[..]
Bij epsilon = 2/3 sqrt(3) heb ik allang geen drie dekpunten meer. Je aanpak is een juiste, maar ik denk dat er bij de uitvoering ervan een fout wordt gemaakt. y=x en g(x) raken als 2-3x²=1 (afgeleiden aan elkaar gelijk), ofwel wanneer x = +/-sqrt(1/3). Dus op deze x-coordinaat gaan de problemen ontstaan.
Ik gebruik dat 2x-x³+eps=x drie oplossingen heeft desda x-x³+eps drie nulpunten heeft.
-


|1.1| < 2/3sqrt(3), maar 2x-x³+1.1 en x snijden maar 1x.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op dinsdag 5 mei 2009 20:14 schreef GlowMouse het volgende:
|1.1| < 2/3sqrt(3), maar 2x-x³+1.1 en x snijden maar 1x.
Kwam dit nou uit een calculus boek?
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***


Inverse Laplace transformaties:
Ik kon niet uit de volgende opgave.
F(s) = 4s / ( s2-8s + 25)
Of zoals je wilt 4s * 1 / ( s2-8s + 25)
Noemer ontbinden kan naar (s-4)2 + 32
1 / ( (s-4)2 + 32 )
ofwel
(1/3) * 3 / ( (s-4)2 + 32 )
is naar te transformeren naar ( e4t * sin(3t) ) / 3 .. Maarja.. dan zit je nog met de factor 4s..dus dat werkt niet.
Waar gaat het mis?
Ik kon niet uit de volgende opgave.
F(s) = 4s / ( s2-8s + 25)
Of zoals je wilt 4s * 1 / ( s2-8s + 25)
Noemer ontbinden kan naar (s-4)2 + 32
1 / ( (s-4)2 + 32 )
ofwel
(1/3) * 3 / ( (s-4)2 + 32 )
is naar te transformeren naar ( e4t * sin(3t) ) / 3 .. Maarja.. dan zit je nog met de factor 4s..dus dat werkt niet.
Waar gaat het mis?


Laat V een deelverzameling van R^n zijn en f: R^m pijl R^n een continue functie. Laat verder x element van f^-1(V) een gegeven punt zijn, dat wil zeggen, een punt waarvoor geldt dat y=f(x) element van V. Bewijs dat als y inwendig punt is van V, dat dan x inwendig punt is van f^-1(V).
Bewijs met behulp van het resultaat van de bovenstaande vraag de volgende stelling: als f: R^m pijl R^n een continue functie is , en O deelverzameling van R^n een open verzameling, dan is f^-1(O) ook open.
Geen idee hoe ik moet beginnen....
Bewijs met behulp van het resultaat van de bovenstaande vraag de volgende stelling: als f: R^m pijl R^n een continue functie is , en O deelverzameling van R^n een open verzameling, dan is f^-1(O) ook open.
Geen idee hoe ik moet beginnen....
-


gaussie: wat je direct ziet bij het vraagstuk is dat je continuïteit van f echt nodig hebt. Dus ga daarmee verder. Een bewijs uit het ongerijmde is hier het eenvoudigst. Stel x is geen inwendig punt. Dan bestaat er een rijtje a_n in R^m dat geheel buiten f-invers(V) ligt met lim(n->inf)a_n = x. Door toepassing van het rijencriterium voor continue functies weten we dat lim(n->inf) f(a_n) = y. Maar f(a_n) ligt buiten V voor iedere n. Zie je waarom y geen inwendig punt kan zijn?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Wat bedoel je precies met f^-1 ? De inverse die niet hoeft te bestaan, of het origineel van de afbeelding? Ik ga van het laatste uit.quote:Op woensdag 6 mei 2009 18:18 schreef gaussie het volgende:
Laat V een deelverzameling van R^n zijn en f: R^m pijl R^n een continue functie. Laat verder x element van f^-1(V) een gegeven punt zijn, dat wil zeggen, een punt waarvoor geldt dat y=f(x) element van V. Bewijs dat als y inwendig punt is van V, dat dan x inwendig punt is van f^-1(V).
Als y een inwendig punt van V is dan is er een epsilon > 0 zodanig dat B(y,epsilon) (=alle punten met afstand kleiner dan epsilon tot y) die bevat is in V. Bij definitie van continuiteit is er nu een delta > 0 zodanig dat f(B(x,delta)) bevat is in B(y,epsilon). B(x,delta) is dus ook zeker bevat in f^-1(V) en daarom is x een inwendig punt.
Voor elke x in f^-1(O) is f(x) een inwendig punt van O (het is een open verzameling) en dus is x ook een inwendig punt volgens de voorgaande stelling en dus is bij definitie die hele verzameling open.quote:Bewijs met behulp van het resultaat van de bovenstaande vraag de volgende stelling: als f: R^m pijl R^n een continue functie is , en O deelverzameling van R^n een open verzameling, dan is f^-1(O) ook open.
Geen idee hoe ik moet beginnen....


Behalve dat bewijzen uit het ongerijmde lelijk zijn, ben ik er ook niet zo zeker van of je dat rijencriterium wel mag gebruiken. Het zou best wel eens kunnen zijn dat dat criterium bewezen moet worden met behulp van de gewenste stelling. En dat is dan vals spelen. Ik ben echter een beetje roestig geworden op dit gebied, dus ik ben er nu ook weer niet zo zeker van.quote:Op woensdag 6 mei 2009 19:05 schreef GlowMouse het volgende:
gaussie: wat je direct ziet bij het vraagstuk is dat je continuïteit van f echt nodig hebt. Dus ga daarmee verder. Een bewijs uit het ongerijmde is hier het eenvoudigst. Stel x is geen inwendig punt. Dan bestaat er een rijtje a_n in R^m dat geheel buiten f-invers(V) ligt met lim(n->inf)a_n = x. Door toepassing van het rijencriterium voor continue functies weten we dat lim(n->inf) f(a_n) = y. Maar f(a_n) ligt buiten V voor iedere n. Zie je waarom y geen inwendig punt kan zijn?


Niemand een idee.. dit zou een redelijk simpele opgave moeten zijn. Dus ik vraag me af, is hij wel op te lossen? Soortgelijke vragen kan ik verder ook nergens in boeken of dictaten terug vinden.. 


Volgens wikipedia geldt dat f'(t) in het tijddomein overeen komt met s.F(s)-f(0). Is jouw gezochte functie dan niet gewoon de afgeleide van je eerder genoemde functie (met een constante erbij)?quote:Op donderdag 7 mei 2009 00:57 schreef Robin__ het volgende:
Niemand een idee.. dit zou een redelijk simpele opgave moeten zijn. Dus ik vraag me af, is hij wel op te lossen? Soortgelijke vragen kan ik verder ook nergens in boeken of dictaten terug vinden..


Ik zie het nu. Thanks!quote:Op woensdag 6 mei 2009 19:18 schreef Wolfje het volgende:
[..]
Wat bedoel je precies met f^-1 ? De inverse die niet hoeft te bestaan, of het origineel van de afbeelding? Ik ga van het laatste uit.
Als y een inwendig punt van V is dan is er een epsilon > 0 zodanig dat B(y,epsilon) (=alle punten met afstand kleiner dan epsilon tot y) die bevat is in V. Bij definitie van continuiteit is er nu een delta > 0 zodanig dat f(B(x,delta)) bevat is in B(y,epsilon). B(x,delta) is dus ook zeker bevat in f^-1(V) en daarom is x een inwendig punt.
[..]
Voor elke x in f^-1(O) is f(x) een inwendig punt van O (het is een open verzameling) en dus is x ook een inwendig punt volgens de voorgaande stelling en dus is bij definitie die hele verzameling open.
-


Laat f,g : R pijl naar rechts R continu differentieerbare functies zijn, en laat gegeven zijn dat g(0)=0, f(1)=0 en f'(x) kleiner dan 0 en g'(x) > 0 voor alle x groter of gelijk aan 0. Beschouw de vergelijking:
f(x)=g(x)+a
Laat zien dat voor a=0 deze vergelijking een unieke oplossing x0 heeft.
geen idee...
f(x)=g(x)+a
Laat zien dat voor a=0 deze vergelijking een unieke oplossing x0 heeft.
geen idee...
-


Als je een plaatje maakt dan zie je eigenlijk direct dat het waar is. In dit geval blijkt het verstandig om te kijken naar de verschilfunctie f-g omdat de afgeleide daarvan zeker negatief is op [0,1]. Je weet dat (f-g)(0) > 0 en (f-g)(1) < 0 (een formeel bewijs hiervoor loopt via de middelwaardestelling) De tussenwaardestelling zegt nu de verschilfunctie tenminste één nulpunt heeft. Met de middelwaardestelling kun je laten zien dat er geen twee of meer nulpunten zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ok bedankt voor de uitleg.quote:Op donderdag 7 mei 2009 12:54 schreef GlowMouse het volgende:
Als je een plaatje maakt dan zie je eigenlijk direct dat het waar is. In dit geval blijkt het verstandig om te kijken naar de verschilfunctie f-g omdat de afgeleide daarvan zeker negatief is op [0,1]. Je weet dat (f-g)(0) > 0 en (f-g)(1) < 0 (een formeel bewijs hiervoor loopt via de middelwaardestelling) De tussenwaardestelling zegt nu de verschilfunctie tenminste één nulpunt heeft. Met de middelwaardestelling kun je laten zien dat er geen twee of meer nulpunten zijn.
-


Laat van f : R pijl naar rechts R bekend zijn dat f differentieerbaar is, dat f(0)=1 en dat f'(0) kleiner of gelijk is aan 1.
Als verder bekend is dat f concaaf is, laat zien dat f een nulpunt heeft; dat wil zeggen, laat zien dat er een a element van R is zodanig dat f(a)=0.
Als alleen maar bekend is dat f psuedo-concaaf is, volgt daar nog steeds uit dat f een nulpunt heeft? Zo ja , geef een bewijs, zo nee, geef een beargumenteerd tegenvoorbeeld.
Geef een voorbeeld van een functie f: R^2 pijl naar rechts R die niet convex is, maar wel quasi convex is.
Wat ik zelf heb uitgevogeld is het volgende:
- elke convexe functie is quasiconvex. Op wikipedia staat dat de floor functie quasiconvex is maar niet convex. Maar ik ben eigenlijk meer op zoek naar een simpelere voorbeeld.
Als verder bekend is dat f concaaf is, laat zien dat f een nulpunt heeft; dat wil zeggen, laat zien dat er een a element van R is zodanig dat f(a)=0.
Als alleen maar bekend is dat f psuedo-concaaf is, volgt daar nog steeds uit dat f een nulpunt heeft? Zo ja , geef een bewijs, zo nee, geef een beargumenteerd tegenvoorbeeld.
Geef een voorbeeld van een functie f: R^2 pijl naar rechts R die niet convex is, maar wel quasi convex is.
Wat ik zelf heb uitgevogeld is het volgende:
- elke convexe functie is quasiconvex. Op wikipedia staat dat de floor functie quasiconvex is maar niet convex. Maar ik ben eigenlijk meer op zoek naar een simpelere voorbeeld.
-


Tegenvoorbeeld: pak f(x) = 1+x, daarvoor geldt f is concaaf, f(0)=1 en f'(0) kleiner of gelijk is aan 1.
Ik neem even aan f'(0) <= -1.
Ik neem even aan f'(0) <= -1.
Tussenwaardestelling: f(1)-f(0) = f'(ksi) <= -1 (die laatste ongelijkheid volgt uit concaafheid, geen idee of je daar al een stelling over hebt gehad dus dat moet je wellicht nog bewijzen). Dus f(1) <= -1+f(0) = 0. Uit de middelwaardestelling volgt het gevraagde.quote:Op vrijdag 8 mei 2009 16:44 schreef gaussie het volgende:
Als verder bekend is dat f concaaf is, laat zien dat f een nulpunt heeft; dat wil zeggen, laat zien dat er een a element van R is zodanig dat f(a)=0.
Pseudo concaaf kan ik geen definitie over vinden en ken ik niet.quote:Als alleen maar bekend is dat f psuedo-concaaf is, volgt daar nog steeds uit dat f een nulpunt heeft? Zo ja , geef een bewijs, zo nee, geef een beargumenteerd tegenvoorbeeld.
De functie waarvan de grafiek eruit ziet als "sqrt(|x|) om de y-as gewikkeld" voldoet.quote:Geef een voorbeeld van een functie f: R^2 pijl naar rechts R die niet convex is, maar wel quasi convex is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb mijn wiskundeboek niet bij me, en kan het me even niet meer voor de geest halen.
Afgeleide van 3500/X = x^(-3500) of 3500x^(-1)?
[ Bericht 0% gewijzigd door Matthijs- op 11-05-2009 10:27:58 ]
Afgeleide van 3500/X = x^(-3500) of 3500x^(-1)?
[ Bericht 0% gewijzigd door Matthijs- op 11-05-2009 10:27:58 ]
Oh really?


3500/x = 3500∙x-1quote:Op maandag 11 mei 2009 10:21 schreef Matthijs- het volgende:
Ik heb mijn wiskundeboek niet bij me, en kan het me even niet meer voor de geest halen.
Afgeleide van 3500/X = x^(-3500) of 3500x^(-1)?
De beide suggesties die je doet voor de afgeleide zijn fout. En gebruik alsjeblieft het isgelijk teken correct, niet om stappen in je uitwerking aan te geven.


Mijn 2e suggestie was dus gewoon goed, alleen heb ik geen idee hoe ik op Fok! iets wat hoger plaats dus gaf ik het aan met een ^-teken.  Deze notatie was overigens puur even voor Fok!-use...
Deze notatie was overigens puur even voor Fok!-use...
Toch bedankt.
Toch bedankt.
Oh really?


Je snapt zijn tweede punt dus niet.quote:Op maandag 11 mei 2009 11:27 schreef Matthijs- het volgende:
Mijn 2e suggestie was dus gewoon goed, alleen heb ik geen idee hoe ik op Fok! iets wat hoger plaats dus gaf ik het aan met een ^-teken.Deze notatie was overigens puur even voor Fok!-use...
Toch bedankt.
3500/x is gelijk aan 3500∙x-1. De afgeleide van 3500/x is dus -3500∙x-2
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!


hallo mensen, een vraag over limieten.
ik moet voor mijn examen limieten kunnen vast stellen en volgens mijn leraar moest ik dan naar de standaard vormen toe werken.
nou is mijn vraag:
(4 + a/x )^x met x --> oneindig, wat is het limiet en hoe kom ik daar op?
de standaard vorm is
(1 + a/x)^x met limiet e^a
alvast bedankt!
[ Bericht 72% gewijzigd door GlowMouse op 11-05-2009 14:52:29 ]
ik moet voor mijn examen limieten kunnen vast stellen en volgens mijn leraar moest ik dan naar de standaard vormen toe werken.
nou is mijn vraag:
(4 + a/x )^x met x --> oneindig, wat is het limiet en hoe kom ik daar op?
de standaard vorm is
(1 + a/x)^x met limiet e^a
alvast bedankt!
[ Bericht 72% gewijzigd door GlowMouse op 11-05-2009 14:52:29 ]
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |