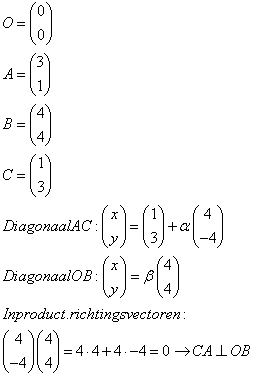SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



hoi,
ik moet voor een wiskunde po de naam geven van een ruimtelijk figuur, eentje heb ik al gevonden maar de andere zou ik echt niet weten.
even een korte beschrijving van het figuur:
het gaat om een afgeknotte piramide (4 hoeken) met daarop nog een piramide.
dat is de afgeknotte piramide
en deze zit er dan bovenop:
alvast bedankt!
ik moet voor een wiskunde po de naam geven van een ruimtelijk figuur, eentje heb ik al gevonden maar de andere zou ik echt niet weten.
even een korte beschrijving van het figuur:
het gaat om een afgeknotte piramide (4 hoeken) met daarop nog een piramide.
dat is de afgeknotte piramide
en deze zit er dan bovenop:
alvast bedankt!
no time to waste


Deze deelvraag is hiermee toch klaar? Want je toont aan door labmda=2/3 te kiezen dat het bewuste punt op de lijn ligt en dat was de vraag. Of doel je hiermee op de tweede vraag? Die is overigens nu wel gelukt.quote:Op donderdag 26 maart 2009 21:52 schreef Riparius het volgende:
Je weet ook uit de elementaire meetkunde dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1met het langste stuk aan de kant van het hoekpunt, dus voor λ = 2/3 zit je in het zwaartepunt. En inderdaad is a + 2/3∙(½∙b + ½∙c - a) = 1/3∙a + 1/3∙ b + 1/3∙c. Zo, nu mag je zelf weer even verder puzzelen ...
kloep kloep


Ja, de eerste deelvraag was in feite klaar en ik bedoelde inderdaad dat je nu zelf wel verder kon met de tweede deelvraag. Maar je zei hierboven ook dat λ = 2/3 voor jou uit de lucht kwam vallen terwijl dat natuurlijk niet zo is. Ik wilde even laten zien dat die waarde voor λ de bekende stelling weerspiegelt dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1.quote:Op vrijdag 27 maart 2009 17:53 schreef Borizzz het volgende:
[..]
Deze deelvraag is hiermee toch klaar? Want je toont aan door labmda=2/3 te kiezen dat het bewuste punt op de lijn ligt en dat was de vraag. Of doel je hiermee op de tweede vraag? Die is overigens nu wel gelukt.


Ja prima. Maar het is nu duidelijk. Maar het meetkundige verband had ik inderdaad al door. Ik heb nu wel even iets geleerd over het gebruik van lijnen die in vectornotatie staan.quote:Op vrijdag 27 maart 2009 18:08 schreef Riparius het volgende:
[..]
Ja, de eerste deelvraag was in feite klaar en ik bedoelde inderdaad dat je nu zelf wel verder kon met de tweede deelvraag. Maar je zei hierboven ook dat λ = 2/3 voor jou uit de lucht kwam vallen terwijl dat natuurlijk niet zo is. Ik wilde even laten zien dat die waarde voor λ de bekende stelling weerspiegelt dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1.
kloep kloep


Nog zoiets: een ruit en dan met vectoren laten zien dat diagonalen loodreacht staan.
Ik heb de ruit gedefinieerd met positievectoren a b c en d.
de beide diagonalen hebben dan richtingsvectoren c-a en d-b.
volgens mij gaat het er dan om dat je laat zien dat het inproduct van deze 2 richtingsvectoren 0 is.
dus (c-a)(d-b) =0 aantonen
levert mij (c-a)(d-b) = cd-cb-ad+ab = c(d-b) -a(d-b).
Maar dan ben ik er nog niet..
Ik heb de ruit gedefinieerd met positievectoren a b c en d.
de beide diagonalen hebben dan richtingsvectoren c-a en d-b.
volgens mij gaat het er dan om dat je laat zien dat het inproduct van deze 2 richtingsvectoren 0 is.
dus (c-a)(d-b) =0 aantonen
levert mij (c-a)(d-b) = cd-cb-ad+ab = c(d-b) -a(d-b).
Maar dan ben ik er nog niet..
kloep kloep


Een inproduct noteer ik als <x,y>. Bij een ruit zijn alle zijden even lang. Dus
<a-b, a-b> = <a-d, a-d> = <c-b, c-b> = <c-d, c-d>.
Als we de eerste gelijkheid uitwerken krijgen we
<a,a> - 2<a,b> + <b,b> = <a,a> - 2<a,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<a,b> - 2<a,d> = 2<a,b-d>
En bij de laatste gelijkheid krijgen we
<c,c> - 2<c,b> + <b,b> = <c,c> - 2<c,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<c,b-d>.
We zien dus <a,b-d> = <c,b-d> en als we dit naar 1 kant gooien staat er
<a-c, b-d> = <a, b-d> - <c,b-d> = 0.
<a-b, a-b> = <a-d, a-d> = <c-b, c-b> = <c-d, c-d>.
Als we de eerste gelijkheid uitwerken krijgen we
<a,a> - 2<a,b> + <b,b> = <a,a> - 2<a,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<a,b> - 2<a,d> = 2<a,b-d>
En bij de laatste gelijkheid krijgen we
<c,c> - 2<c,b> + <b,b> = <c,c> - 2<c,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<c,b-d>.
We zien dus <a,b-d> = <c,b-d> en als we dit naar 1 kant gooien staat er
<a-c, b-d> = <a, b-d> - <c,b-d> = 0.


Op die manier had ik het nog niet bekeken.
Maar ik had al een andere oplossing. Kan deze ook?
Een vierhoek heeft 4 gelijke zijden. stel vector a als een zijde en ook vector b als een zijde.
De diagonalen van deze vierhoek zijn dan (a+b) en (a-b).
Het inproduct van deze 2 is dan (a+b)(a-b) = a2 - b2.
Een eigenschap van vectoren is dat x2 = | x| 2.
dus er geldt dat (a+b)(a-b) = |a|2 - |b|2.
aangezien a en b dezelfde lengte voorstellen geldt (a+b)(a-b) = 0.
Maar ik had al een andere oplossing. Kan deze ook?
Een vierhoek heeft 4 gelijke zijden. stel vector a als een zijde en ook vector b als een zijde.
De diagonalen van deze vierhoek zijn dan (a+b) en (a-b).
Het inproduct van deze 2 is dan (a+b)(a-b) = a2 - b2.
Een eigenschap van vectoren is dat x2 = | x| 2.
dus er geldt dat (a+b)(a-b) = |a|2 - |b|2.
aangezien a en b dezelfde lengte voorstellen geldt (a+b)(a-b) = 0.
kloep kloep


Je gebruikt daar wel dat tegenover elkaar liggende diagonalen evenwijdig zijn. Ik neem aan dat dat niet in de definitie van een ruit zit?


Naja even de vraag goed herlezend: het ging om een vierhoek met evenlange zijden en tegenoverliggende zijden parallel.quote:Op vrijdag 27 maart 2009 21:19 schreef thabit het volgende:
Je gebruikt daar wel dat tegenover elkaar liggende diagonalen evenwijdig zijn. Ik neem aan dat dat niet in de definitie van een ruit zit?
kloep kloep


A street light is mounted at the top of a 15-ft-tall pole. A man 6ft tall walks away from the pole with a speed of 5 ft/s along a straight path. How fast is the tip of his shadow moving when he is 40ft from the pole?
Hoe bereken ik ook alweer waar de tip van his schaduw precies is? Dus niet het antwoord op de vraag, maar gewoon waar de tip van de schaduw is met betrekking tot de lantaarnpaal.
Hoe bereken ik ook alweer waar de tip van his schaduw precies is? Dus niet het antwoord op de vraag, maar gewoon waar de tip van de schaduw is met betrekking tot de lantaarnpaal.


Levensverzekeringswiskunde is een stom vak }:|
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen :o
Het antwoordenboek zegt dit:
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43 :N Wie heeft het verlossende antwoord?
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen :o
Het antwoordenboek zegt dit:
| 1 2 3 | 10.000 + p x ((503.387 – 167.324)/25.048) = 50.000 x (8.803,3/ 25.048) p = 564,43 |
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43 :N Wie heeft het verlossende antwoord?
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


Dit is niet goed voor mijn zelfvertrouwen, maar bedanktquote:Op zondag 29 maart 2009 19:05 schreef GlowMouse het volgende:
http://www.fi.uu.nl/toepassingen/02017/toepassing_wisweb.html
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


Ik vind het wel een mooie appletquote:Op zondag 29 maart 2009 19:06 schreef Maraca het volgende:
[..]
Dit is niet goed voor mijn zelfvertrouwen, maar bedankt
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


is het ookquote:
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


ik ben bezig met vergelijkingen oefenen voor statica, maar deze snap ik echt niet;
12/13A -A is gelijk aan 25/13 A
het zal vast heel makkelijk zijn maar...
12/13A -A is gelijk aan 25/13 A
het zal vast heel makkelijk zijn maar...


Moet dat geen 12/13A + A zijn?
12/13A + A = (12/13 + 1)A
En dan http://proto.thinkquest.nl/~klb045/h2-broptellen.html
12/13A + A = (12/13 + 1)A
En dan http://proto.thinkquest.nl/~klb045/h2-broptellen.html
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zondag 29 maart 2009 18:51 schreef Maraca het volgende:
Levensverzekeringswiskunde is een stom vak
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen
Het antwoordenboek zegt dit:
[ code verwijderd ]
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43Wie heeft het verlossende antwoord?
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
wordt
¤ 10.000 + p * 13,41675982 = 17572,....
wordt
p * 13,41675982 = 7572,....
en nu bijde kanten delen door 13,41.....
begrijpelijk ?
(vat dit niet persoonlijk op maar kon je dit nou echt niet


Wow, zo'n applet zoek ik al een tijdje. Thx.quote:
Zijn er ook applets waarmee je leert ingewikkelde stellingen te bewijzen?
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***