Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Iemand een idee hoe ik dit kan bewijzen?quote:Op donderdag 10 november 2011 18:49 schreef Alxander het volgende:
Consider [tex]A = \begin{pmatrix} 0 & 0 &0 &0 &0 &1\\
0 &0 &0 &0 &1&1\\
0 &1 &0 &0 &0 &0\\
1&1&0 &0 &0 &0\\
0 &0 &0 &1&0&0\\
0 &0 &1 & 1&0&0 \end{pmatrix} [/tex]
Is deze matrix primitief? Hij is niet primitief, maar hoe bewijs ik dat?
Heb hem inderdaad nu. Dankjewelquote:
Als je hem in 2x2 blokjes verdeelt, kun je misschien bewijzen met inductie dat er altijd maar één blokje per rij en één blokje per kolom niet-nul is?
!als ik 16a4-b4 tussen haakjes wil zetten waarom wordt het dan ( 4a2+ b2) (2a+b)(2a+b)?
waarom niet ( 4a2+ b2)(4a2+ b2)?
het is ( 4a2+ b2)(4a2- b2)
of ( 4a2+ b2)(2a - b)(2a + b)
ok sorry typfoutje ik bedoelde ookquote:
ken je merkwaardige producten: (a-b)(a+b) = ...
het is ( 4a2+ b2)(4a2- b2)
of ( 4a2+ b2)(2a - b)(2a + b)
maar als ik het antwoord zo laat staan is het ook goed? of moet ik het neerzetten als :
4a2+ b2)(2a-b)(2a+b)
Maar als dat ook goed is dan is er geen probleem verder.
Ik vind jouw antwoord eigenlijk zelfs nog netterquote:
Ok dank je wel. In mijn boek gaven ze als antwoord (4a2+ b2)(2a-b)(2a+b). En ik had het neergezet als (4a2+ b2)(4a2- b2).
Maar als dat ook goed is dan is er geen probleem verder.
, maar het is inderdaad precies hetzelfde.Ik denk dat het de bedoeling is dat je de uitdrukking zo ver mogelijk in factoren ontbindt. En dan is jouw antwoord weliswaar correct maar heb je niet alles gedaan wat je kunt doen (en verdien je dus ook niet alle punten als dit een proefwerkvraag zou zijn). Ik denk trouwens ook niet dat de opdracht luidde om 16a4 - b4 tussen haakjes te zetten, want dan krijg je (16a4 - b4) en dat zou wat al te gemakkelijk zijn.quote:
Ok dank je wel. In mijn boek gaven ze als antwoord (4a2+ b2)(2a-b)(2a+b). En ik had het neergezet als (4a2+ b2)(4a2- b2).
Maar als dat ook goed is dan is er geen probleem verder.
nee, de vraag was ontbind in factoren, was te lui om het op te zoeken. maar ik moet ze dus wel zo ver mogelijk uitwerken.quote:
[..]
Ik denk dat het de bedoeling is dat je de uitdrukking zo ver mogelijk in factoren ontbindt. En dan is jouw antwoord weliswaar correct maar heb je niet alles gedaan wat je kunt doen (en verdien je dus ook niet alle punten als dit een proefwerkvraag zou zijn). Ik denk trouwens ook niet dat de opdracht luidde om 16a4 - b4 tussen haakjes te zetten, want dan krijg je (16a4 - b4) en dat zou wat al te gemakkelijk zijn.
Ik ben bezig in het basisboek wiskunde om mijn wiskunde een beetje bij te spijkeren zodat ik mijn wiskundeboek waarover ik wel een tentamen heb beter begrijp. Maar daarin doen ze niet echt aan uitleg. En ik ben helaas niet zo'n wiskunde wonder. Ik heb dit op de havo allemaal wel gehad, maar dat is 8 jaar geleden en al heel ver weggezakt.
Ah zo. Ik dacht dat je in de eerste klassen van het middelbaar zat gezien de vraag. Het boek van Van de Craats vind ik inderdaad niet best. Voor een aantal onderwerpen is er wel betere uitleg te vinden op internet, gewoon een beetje zoeken.quote:
[..]
nee, de vraag was ontbind in factoren, was te lui om het op te zoeken. maar ik moet ze dus wel zo ver mogelijk uitwerken.
Ik ben bezig in het basisboek wiskunde om mijn wiskunde een beetje bij te spijkeren zodat ik mijn wiskundeboek waarover ik wel een tentamen heb beter begrijp. Maar daarin doen ze niet echt aan uitleg. En ik ben helaas niet zo'n wiskunde wonder. Ik heb dit op de havo allemaal wel gehad, maar dat is 8 jaar geleden en al heel ver weggezakt.
Geloof me, het boek van het HBO is zo mogelijk nog vager dan het boek van craats.quote:
[..]
Ah zo. Ik dacht dat je in de eerste klassen van het middelbaar zat gezien de vraag. Het boek van Van de Craats vind ik inderdaad niet best. Voor een aantal onderwerpen is er wel betere uitleg te vinden op internet, gewoon een beetje zoeken.
Het is een binomiaal kansexperiment en ik denk dat ik deze moet omzetten/benaderen naar een standaardnormale verdeling, klopt dit?
En heeft iemand een idee hoe dat moet?
Dank!
1 - stdnrml ( (52-50) / (sqrt 25) = 1 - stdnrml (0.4) = 0.34
klopt dit?
Inderdaad. De grap is dat als je "heel veel" binomiale experimenten doet, dat het dan bij benadering normaal verdeeld is. Dat is een toepassing van de centrale limietstelling: http://nl.wikipedia.org/wiki/Centrale_limietstelling .quote:
p(y100 >= 53) = 1 - p(y100<=52) wordt benaderd door 1 - stdnormaal ((52 - np )/ (sqrt (npq))) =
1 - stdnrml ( (52-50) / (sqrt 25) = 1 - stdnrml (0.4) = 0.34
klopt dit?
Wat is de context? Ik denk niet dat daar een algemene methode voor is.quote:
Hoe laat je zien hoeveel reflexieve en symmetrische relaties er zijn op een verzameling A met n elementen?
Er hoeft geen formeel bewijs voor gegeven te worden, meer een uitleg waarom het klopt wat ik zeg.quote:
[..]
Wat is de context? Ik denk niet dat daar een algemene methode voor is.
Er zijn volgens mij 2(1/2)n(n-1) relaties die reflexief en symmetrisch zijn, maar ik vind het erg moeilijk om dat op te schrijven.
Er zijn (n boven 2) paren van verschillende elementen. Elk paar kan wel of niet in de relatie zitten, dat zijn 2 mogelijkheden. Dus we hebben 2(n boven 2) van zulke relaties.quote:
Hoe laat je zien hoeveel reflexieve en symmetrische relaties er zijn op een verzameling A met n elementen?
Combinaties mag ik niet gebruiken, maar dit geeft me wel een idee om het op te schrijven:quote:
[..]
Er zijn (n boven 2) paren van verschillende elementen. Elk paar kan wel of niet in de relatie zitten, dat zijn 2 mogelijkheden. Dus we hebben 2(n boven 2) van zulke relaties.
R is reflexief, dus voor alle a in A geld (a,a) is in R. Daar valt verder niks te kiezen.
Stel we zetten a in de eerste positie neer, dan zijn er n-1 mogelijkheden voor een paar (a,b) zodat a is niet b. Dus zijn er n(n-1) paren van verschillende elementen.
Maar R is symmetrisch, dus als (a,b) erin zit, moet (b,a) er ook inzitten. Dus zijn er nog maar (1/2)n(n-1) paren van verschillende elementen waaruit we kunnen kiezen.
Elk paar kan er wel of niet inzitten, dus 2(1/2)n(n-1).
Alle symmetrische relaties zijn dan:
2(1/2)n^2 (n-1)
Omdat je nu ook nog de keuze hebt voor de n gelijke paren, dus zijn er (1/2)n2(n-1) paren, etc.
Toch?
Het totaal aantal relaties is 2n^2. Het aantal symmetrische relaties kan natuurlijk nooit groter zijn dan dat.quote:
Nog even een snelle vraag:
Alle symmetrische relaties zijn dan:
2(1/2)n^2 (n-1)
Omdat je nu ook nog de keuze hebt voor de n gelijke paren, dus zijn er (1/2)n2(n-1) paren, etc.
Toch?
Oeps..quote:Op zaterdag 12 november 2011 13:30 schreef thabit het volgende:
[..]
Het totaal aantal relaties is 2n^2. Het aantal symmetrische relaties kan natuurlijk nooit groter zijn dan dat.
Is het dan niet: 2(1/2)n(n+1)?
Want alle symmetrische paren met verschillende elementen zijn (1/2)n(n-1). Dan zijn er nog n paren over, namelijk alle paren van de vorm (a,a).
(1/2)n(n-1)+n=(1/2)n(n+1).
Stel xy = p² en yz = q²2 dan is xz = (pq/y)² . Om-
dat dit kwadraat een geheel getal is, is ook pq/y
geheel (!) en dus is xz een kwadraat van een
geheel getal.
[ Bericht 1% gewijzigd door Anoonumos op 12-11-2011 15:32:38 ]
Je maakt hier gebruik van het feit dat als het kwadraat van een rationaal getal geheel is, dat dan dat rationale getal geheel is. En dat is iets heel anders dan je hierboven beweerde.quote:
Hmm. Dat klopt niet inderdaad, maar dat is toch wat hier staat? Het gaat om het bewijzen van de transiviteit van de relatie x y <-> xy is een kwadraat( op Z):
Stel xy = p² en yz = q²2 dan is xz = (pq/y)² . Om-
dat dit kwadraat een geheel getal is, is ook pq/y
geheel (!) en dus is xz een kwadraat van een
geheel getal.
Ik heb momenteel een probleem. In mijn methode, getal en ruimte, wordt blijkbaar niet uitgelegd hoe je integralen en riemannsommen (de Sigma-notatie) uitrekent, slechts op je GR.
Hierbij de vraag: hoe moet ik uit het hoofd
en
uitrekenen?Riemannsommen worden in de praktijk alleen met de computer gebruikt om integralen uit te rekenen die "lastig" zijn. Als je een goede benadering wil met een Riemannsom dan moet je een hele kleinequote:
Al eerder gepost, alleen blijkbaar op de verkeerde plek!
Ik heb momenteel een probleem. In mijn methode, getal en ruimte, wordt blijkbaar niet uitgelegd hoe je integralen en riemannsommen (de Sigma-notatie) uitrekent, slechts op je GR.
Hierbij de vraag: hoe moet ik uit het hoofd [ afbeelding ] en
[ afbeelding ] uitrekenen?
Het kan natuurlijk wel met de hand. Neem bijvoorbeeld de eenvoudige functie f(x)=x (dan krijgen we ook niet zo'n moeilijke som). Stel dat we die willen integreren (met een Riemann som) van 0 tot 2. Neem nu een Delta x van bijvoorbeeld 0.1 (hoe kleiner je die neemt, hoe beter je benadering). Nu moeten we dus 20 termen gaan sommeren:
Nu is xk de x-waarde in het k-de interval. Maar in zo'n interval is f niet constant, dus laten we het punt nemen aan de linkerkant van ieder interval. Dan moeten we berekenen
Ik gebruik hier dus dat xk = 0.1k en de standaardformule voor een rekenkundige reeks.
We hebben dus berekend dat de oppervlakte onder de grafiek f(x)=x met x tussen 0 en 2 ongeveer 1.9 is. Omdat je in feite de oppervlakte van een eenvoudige driehoek berekent in dit geval, hadden we direct kunnen inzien dat de oppervlakte (exact) 2 is. (basis*hoogte /2 = 2*2/2=2).
Ik nam nu voor xn steeds het meest linker punt in een intervalletje. Dat is de waarde waar f zijn kleinste waarde aanneemt. Op deze manier hebben we dus met Riemannsommatie bepaald dat de oppervlakte minstens 1.9 is (dat klopt dus ook). Verder kan je ook op ieder interval het maximum bepalen van de functie en daarover sommeren, zodat je ook een bovengrens voor de integraal hebt. Als je je
Dit hele proces doe je eigenlijk alleen maar als je een lastige integraal hebt. Daarmee bedoelde ik een integraal die geen primitieve heeft. Een primitieve is het omgekeerde van een afgeleide. In andere woorden: als F de primitieve is van f, dan geldt F'=f. Als een functie wel een primietieve heeft dan kan je een integraal als volgt berekenen:
waarbij F dus weer de primitieve is van f.
Voorbeeld:
Ik gebruik hier dat
Helaas kan dit niet altijd. De functie f(x)=e^x² heeft bijvoorbeeld geen primitieve (d.w.z. je kan het niet uitdrukken in standaard functies als sin, log, exp, etc). Om toch een waarde te vinden voor je integraal kan je dan Riemannsommatie gebruiken.
Als je de bewijzen wil zien, zie: http://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus .
[ Bericht 0% gewijzigd door thenxero op 13-11-2011 14:21:53 ]
.Ik heb echter een klein probleem (waarschijnlijk een zeer simpele en 'domme' vraag, alleen ik zie hem op het moment niet).
Waarom is xk = 0.1k? Waarom verdwijnt de functie f(xk) en komt er slechts xk voor in de plaats als je voor Δx 0.1 neemt?
Als laatste stel vragen: waar komt de 20 vandaan (en waarom), en waarom vermenigvuldig je die met 19/2 (hoe komt 19/2 er überhaupt te staan)?
Probeer eens een tekening te maken bij het (eenvoudige) voorbeeld dat thenxzero uitwerkt. Het idee is dat je de 'oppervlakte onder de curve' (in dit geval een rechte lijn) over een bepaald interval (hier [0,2]) kunt benaderen door die oppervlakte in smalle verticale 'reepjes' te verdelen, en dan elk reepje bij benadering te beschouwen als een rechthoek, waarvan de oppervlakte uiteraard eenvoudig is te bepalen. De benadering wordt dan steeds beter naarmate de rechthoeken (reepjes) smaller worden. We nemen verticale reepjes, omdat de 'hoogte' van elk reepje (rechthoek) dan bij benadering de functiewaarde ter plaatse is, terwijl we de breedte van alle reepjes hetzelfde kunnen nemen (dat hoeft niet, maar is wel zo gemakkelijk). Als je nu het interval [0, 2] in bijvoorbeeld 20 gelijke stukjes (deelintervallen) verdeelt, dan heeft elk verticaal reepje dus een breedte van 0,1. Die twintig deelintervallen kun je voorstellen als [xk, xk+1] met xk = 0,1∙k. en k = 0..19.quote:
Bravo, geweldig uitgelegd! Te zeggen dat je uitleg goed was, zou een understatement zijn
Ik heb echter een klein probleem (waarschijnlijk een zeer simpele en 'domme' vraag, alleen ik zie hem op het moment niet).
Waarom is xk = 0.1k? Waarom verdwijnt de functie f(xk) en komt er slechts xk voor in de plaats als je voor Δx 0.1 neemt?
Als laatste stel vragen: waar komt de 20 vandaan (en waarom), en waarom vermenigvuldig je die met 19/2 (hoe komt 19/2 er überhaupt te staan)?
Alleen het is mij nog steeds niet duidelijk waarom de functie f(xk) plaats maakt voor de standaardformule xk = 0,1∙k. Immers: xk = 0,1∙k is alleen goed voor de x-coordinaten van de deelintervallen, niet de y-waarde/hoogte zoals f(xk).
Daarnaast is het mijn nog steeds onduidelijk waarom plotseling het sigma-teken met een 20 en 19/2 verwisselt wordt. Het is mij natuurlijk duidelijk dat 20 de hoeveelheid deelintervallen is enz enz, maar waarom de 20 dan te vermenigvuldigen met 19/2?
We zijn bezig met de functie f(x)=x. In het bijzonder geldt dus f(xk)=xk.quote:
Jazeker, zo ver was ik ook, toch bedankt voor het ophelderen van xk = 0,1∙k!
Alleen het is mij nog steeds niet duidelijk waarom de functie f(xk) plaats maakt voor de standaardformule xk = 0,1∙k. Immers: xk = 0,1∙k is alleen goed voor de x-coordinaten van de deelintervallen, niet de y-waarde/hoogte zoals f(xk).
Daarnaast is het mijn nog steeds onduidelijk waarom plotseling het sigma-teken met een 20 en 19/2 verwisselt wordt. Het is mij natuurlijk duidelijk dat 20 de hoeveelheid deelintervallen is enz enz, maar waarom de 20 dan te vermenigvuldigen met 19/2?
Wat betreft de sommatie, voor een rekenkundige rij geldt in het algemeen dat de som gelijk is aan het aantal termen gedeeld door twee, maal (de eerste term + de laatste term). In dit geval dus 20/2 * (0+19). Zie ook de wiki.
Bedankt voor het compliment
Ik wil graag het volgende berekenen.
Ik heb een bord van 5x5. Nu kan ik 1 steen op 25 verschillende plekken leggen. Nu wil ik graag weten hoeveel combinaties er zijn wanneer 2 stenen op het veld leg (antwoord weet ik al). De enigste twee regels die er zijn is dat de 2 stenen niet direct langs elkander mogen liggen. Hieronder zie je 2 voorbeelden. In de linker zijn er nog 22 mogelijkheden en in de rechter 20.
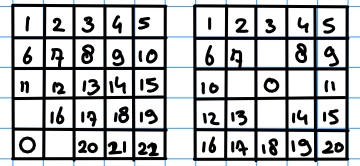
Nu wil ik dus weten op hoeveel combinaties er zijn als er 1 steen (25), 2 stenen (22*4 + 21*12 + 20*9 = 520), 3 stenen (???) op het veld liggen.
Is er een elegante methode om dit te berekenen?
En wat is regel 2?quote:Op zondag 13 november 2011 20:36 schreef Dale. het volgende:
Dringend vraagje mensen...
Ik wil graag het volgende berekenen.
Ik heb een bord van 5x5. Nu kan ik 1 steen op 25 verschillende plekken leggen. Nu wil ik graag weten hoeveel combinaties er zijn wanneer 2 stenen op het veld leg (antwoord weet ik al). De enigste twee regels die er zijn is dat de 2 stenen niet direct langs elkander mogen liggen. Hieronder zie je 2 voorbeelden. In de linker zijn er nog 22 mogelijkheden en in de rechter 20.
[ afbeelding ]
Nu wil ik dus weten op hoeveel combinaties er zijn als er 1 steen (25), 2 stenen (22*4 + 21*12 + 20*9 = 520), 3 stenen (???) op het veld liggen.
Is er een elegante methode om dit te berekenen?
Euh sorry 1 regelquote:
geen idee waarom ik 2 regels schreef. Maar iig, het aantal combo's is 8844 Gewoon die-hard alle mogelijkheden doorgenomen?quote:
[..]
Euh sorry 1 regel
Waarom wilde je dit berekenen trouwens?
Ik dacht zelf aan: construeer een rij zodat:
Ik heb nu moeite met het uitleggen dat sup V de limiet van de rij is. Ik dacht aan:
Weet iemand hoe ik dit goed op kan schrijven? Of kan ik dit wel zo zeggen?
Dat begrijp ik, omdat het gewoon niet klopt. Zie het tegenvoorbeeld van GlowMouse.quote:
V is een niet-lege , naar boven begrensde deelverzameling van. Ik wil een rij in V construeren zodat 1)
en 2) sup V is de limiet van de rij.
Ik dacht zelf aan: construeer een rij zodat:
Ik heb nu moeite met het uitleggen dat sup V de limiet van de rij is.
Het is heel goed mogelijk dat sup(V) de limiet is van je rij terwijl sup(V) zelf niet in V zit.quote:Ik dacht aan:vormen het interval
waarvan ik wel kan bewijzen dat sup V het supremum is. Ook weet ik niet of het vanzelfsprekend is dat
.
Weet iemand hoe ik dit goed op kan schrijven? Of kan ik dit wel zo zeggen?
Hoe dan?quote:
Op 1) sup V in Vquote:
Laat v0 = sup V. Construeer de rij v0 = v1 = v2 = ...
Deze rij heeft limiet sup V.
2) sup V niet in V. Laat v0 in V (Kan, V is niet leeg).
Sup V is een bovengrens van V. Voor elke vi in V geldt dus: (vi + supV)/2 < sup V, dus er is een v(i+1) in V met v(i + 1) > (vi + supV)/2. Construeer deze rij.
Sup V is de limiet van deze rij, want stel x is een kleinere bovengrens, dan:
(x+sup V)/2 < sup V dus er is een y in V met y > (x+supV)/2 > x. Tegenspraak.
Heb je er ook rekening mee gehouden dat je deelverzameling V van R geen interval hoeft te bevatten?quote:
Waarom bestaat dat element dan?quote:
Inderdaad niet volledig geformuleerd. Neem voor v(i+1) het kleinste element zo dat v(i + 1) > (vi + supV)/2. Zo had ik het bedacht.
Een open verzameling in R heeft bijvoorbeeld geen kleinste element. Dus als je begint met v0 en
[ Bericht 18% gewijzigd door thenxero op 20-11-2011 00:01:15 ]
jawelquote:
[..]
Een open verzameling in R heeft bijvoorbeeld geen kleinste element. Dus als je begint met v0 endan bestaat v1 al niet meer.
Nee, pak [0,1) en vi = 0.5-1/iquote:
Als je zegt dat v(i+1) > vi en v(i+1) is bevat in V, is dat dan niet al voldoende voor een constructie?
?quote:
never mindquote:
Dat kan. Nu moet je alleen nog laten zien dat die verzameling niet leeg is, dus dat er daadwerkelijk zo'n v_{i+1} is en dat de limiet sup V is. (daarvoor moet je dus nog wel een extra eis hebben voor de keuze van v_{i+1}, anders kan de limiet ook kleiner dan de bovengrens zijn zoals Glowmouse al aangaf).quote:
Heb je gelijk in.en anders weet ik het niet meer.
[ Bericht 4% gewijzigd door thenxero op 20-11-2011 00:37:31 ]
Dit gaat niet werken als je verzameling V slechts een eindig aantal elementen bevat (en dat kan).quote:
Heb je gelijk in.
Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.quote:
[..]
Dit gaat niet werken als je verzameling V slechts een eindig aantal elementen bevat (en dat kan).
Bedankt voor de kritische blik allen.
Precies dan is er geen probleem. Het lastige geval is als de sup buiten V ligt.quote:
[..]
Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.
Bedankt voor de kritische blik allen.
Ja, dat is waar. Maar je zou een constructie voor je rij {vn} moeten kunnen aangeven onafhankelijk van de aard van V en onafhankelijk van de vraag of sup(V) nu wel of geen element van V is, anders blijft het erg onelegant.quote:
[..]
Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.
Bedankt voor de kritische blik allen.
Gegeven is:
f(x) =
{ greatest integer function als x >= 0
{ least integer function als x < 0
Teken hiervan de grafiek, en beantwoord de vraag: "Why is f(x) called the integer part of x?"
---------------------------------
De grafiek tekenen is geen probleem, maar bij het beantwoorden van de vraag had ik in eerste instantie:
Mijn definitie 1: "f(x) is called the integer part of x, omdat de uitkomst ltijd een integer is voor elke waarde van x die je invult".
Echter, een andere definitie die ik kan geven (en die ik beter vind) is:
Mijn definitie 2: "stel ik vul x=2.14 in, dan is de uitkomst f(2.14) = 2. En voor x = -3.5 is de uitkomst f(-3.5) = -3. Dus f(x) is het integer gedeelte van x."
Het antwoord van het boek zegt:
Antwoord boek: "f(x) is called the integer part of x, becase |f(x)| is the largest integer that does not exceed x; i.e. |x| = |f(x)| + y, where 0 <= y < 1."
Ik heb moeite om het antwoord van het boek te begrijpen. Verder vind ik mijn definitie 2 beter dan definitie 1, maar is definitie 2 hetzelfde als het antwoord van het boek, maar dan anders geformuleerd?
M.a.w.; kan iemand mij het antwoord van het boek uitleggen, en aangeven of 'mijn definitie 2' hetzelfde qua betekenis is als het antwoord van het boek?
Bij voorbaat dank.
(p38 opg.32) -> Alle lezers: neger dit, dit is voor mijn eigen referentie
Het probleem met jouw definitie 2 is dat het een voorbeeld is. Je kan een voorbeeld geven van een definitie, maar de definitie zelf kan geen voorbeeld zijn. In plaats van die 2.14 en -3.5 moet je dus een algemene x>0 en x<0 nemen.quote:
Wat er met integer part van een getal x bedoeld wordt is het "gehele gedeelte" van dat getal. Dat is dus het grootste gehele getal dat kleiner of gelijk is aan x.
Als x>0, dan geldt dus
Oja, en definitie 1 is niet volledig. Als je de functie zou nemen f(x)=1 heb je ook een functie die altijd een geheel getal geeft voor iedere x. Maar dat is niet wat er bedoeld wordt met de "integer part of x".
[ Bericht 7% gewijzigd door thenxero op 20-11-2011 14:50:42 ]
Bedankt voor je hulp, echter, ik heb nog steeds moeite om het te begrijpen.
Ik snap dat bij x >= 0, dat f(x) <= x moet zijn, want bij x >= 0 geldt de greatest integer function (zoals gegeven in de opgave).
Zo ook begrij ik dat bij x < 0, dat f(x) >= x moet zijn, want bij x < 0 geldt weer de least integer function (wederom gegeven in de opgave).
Met enkele voorbeelden en waarden:
x >= 0 (greatest integer function) ........... dus f(x) <= x...................bv: x = 2.5, dan f(x) = 2.
x < 0 (least integer function)................... dus f(x) >= x...................bv: x = -3.5, dan f(x) = -3.
Dit is ook makkelijk te zien in de grafiek die ik moest schetsen.
Maar stel nu (wederom een voorbeeld):
voor x >= 0 ............. dus f(x) <=x.............. en x = y + f(x) met 0 <= y < 1. Stel ik vul voor y = 0.9 in (voldoet aan 0 <= y < 1) en voor x = 2.5. Dan krijg ik:
x = y + f(x) voor x >=0 waarbij geldt dat f(x) <= x, en met waardes wordt deze:
2.5 = 0.9 + 2, maar dit klopt toch niet meer, want als ik de 0.9 'naar links breng', krijg ik:
1.6 = 2 ????
Ik raak volledig in de war zodra de y bijgehaald wordt. Als ik waardes in vul, kom ik er niet uit. Hier raak ik dan ook in de knoop
Voorbeeld:
Als x = 3.15, dan f(x) = 3 en y = 0.15.
Dus:
3.15 = 3 + 0.15
x = f(x) + y
...als ik het zo lees is het inderdaad heel, heeeel erg logisch.Als het nou ook zo in het antwoord stond, zou dat een hoop tijd en moeite schelen..... Hartelijk dank voor je hulp, ik begrijp het nu.
[ Bericht 52% gewijzigd door thenxero op 21-11-2011 17:45:03 ]
zet je adblocker uit en/of leeg je browsercachequote:
Is al gelukt! (mbv. Excuses voor de dubbelpost maar mijn edit-knop werkt niet gek genoeg.
Het bovenhalfvlak is conform met de eenheidsschijf via de afbeelding z -> (z-i)/(z+i). De rand van de eenheidsschijf is de eenheidscirkel. Als we die afbeelding inverteren, dan krijgen we z -> i(z+1)/(1-z). Deze afbeelding beeldt de eenheidscirkel bijectief naar de projectieve lijn af. De verzameling punten behalve 1 wordt bijectief naar de reele lijn afgebeeld. Het punt 1 wordt afgebeeld naar het oneindige punt op de projectieve lijn. Ten opzichte van het bovenhalfvlak ligt dat punt oneindig ver verticaal omhoog. Alle verticale lijnen, die hyperbolisch ook lijnen zijn, gaan door dat randpunt.
ik heb een schattingslijn y^ en de echte lijn y.
Hoe zorg ik ervoor dat y^ de vorm van y krijgt?
een negatieve lineaire term + kwadratische positieve term?
Ik weet het niet meer.
*Naar aanleiding van mijn post in het SPSS topic*
Ik begrijp er geen reet van, want bij eigenlijk alles wat ik doe krijg ik een y = x lijn tussen de residuen en de afhankelijke variabel y. (wat dus niet mag..?)quote:
Met een lineaire term en een kwadratische term zou je een eind kunnen komen. Positief/negatief bepaalt de OLS schatter.
Zelfs al doe ik x^6 en doe ik de regressie..
u = x5-1
du = 5xdx
Nu deed ik een voorbeeld uit 't boek na met iets andere getallen maar die deden dit:
'iets'
= 'iets' * 1/13 u13 + C5x ......................................................................................... 5x
Maar wat moet ik in hemelsnaam voor dat 'iets' invullen .. volgens het antwoordenboek moest iets/5x 1/70 zijn mar als je dat terugrekent krijg je een onzinnig getal (1/13 * x = 1/70 » x = 5.3846 ... onzin)
Als je nu eens begint te bedenken dat je hebt:quote:Op woensdag 23 november 2011 20:53 schreef Sokz het volgende:
L'integrale
[ afbeelding ]
u = x5-1
du = 5xdx
Nu deed ik een voorbeeld uit 't boek na met iets andere getallen maar die deden dit:
'iets' [ afbeelding ] = 'iets' * 1/13 u13 + C
5x ......................................................................................... 5x
Maar wat moet ik in hemelsnaam voor dat 'iets' invullen .. volgens het antwoordenboek moest iets/5x 1/70 zijn mar als je dat terugrekent krijg je een onzinnig getal (1/13 * x = 1/70 » x = 5.3846 ... onzin)
(x4 - x9)(x5 - 1)12 = x4(1 - x5)(x5 - 1)12 = -x4(x5 - 1)13
Nu zie je meteen dat je kunt substitueren:
u = x5 - 1
Dan is:
du/dx = 5x4
En dus:
du = 5x4dx
En dus:
(-1/5)∙du = -x4∙dx
Verder hebben we u = -1 voor x = 0 en u = 0 voor x = 1. De Integraal wordt dan:
∫-10 (-1/5)∙u13du = (-1/5)∙∫-10 u13du
Ik zal de uitwerking even afmaken. We krijgen dan:quote:
Maar jij komt dus op ehm, 1/5 integr. en het antwoordenboek geeft 1/70 integr.
(-1/5)∙∫-10 u13du = (-1/5)∙[(1/14)∙u14]-10 = (-1/5)∙(0 - 1/14) = 1/70, en dat klopt uiteraard.
Express ln 0.25 in terms of ln 2 and ln 3.
Nou ben ik wel zover dat je e.e.a. kunt herschrijven als:
Het is vast heel simpel, maar ik loop vast op die 100 geloof ik. Kan iemand mij weer op weg helpen?
Wat enorm flauw. Ik heb me twee dagen uit de naad lopen schrijven om het in ln 2 én 3 uit te drukken. Zojuist -2 ln 2 ingevuld en voorwaar: "fantastic". Bedankt!
Mag ik dit ook schrijven als... (http://en.wikipedia.org/wiki/Summation#Notation)
Voor de goeie orde...
Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geïnterpreteerd worden.
Ja weet niet hoe je dat noemt als je zeg maar 'sommeerd' over conjunctie maar gewoon conjunctie dus? "Je conjuctie over de elementen van ..." klinkt nogal raar tegenover ... Je sommeert over de elemente van ..."quote:
Sommatie van conjuctie? Ik neem aan dat je gewoon conjunctie bedoelt van alle elementen in de gegeven verzamelingen.
Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geïnterpreteerd worden.
Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.
Waarom is Arg(1 + i) = pi / 4 ???
Ik kom namelijk uit op Arg 1 + i = 1, want tan arg(1 + i) = b / a = 1 / 1 = 1
Komt het doordat de argument Theta in RADIALEN uitgedrukt wordt?? Dus tan(pi / 4) = 1....klopt dit?
Maar dan zou ik tan-1 arg(w) moeten gebruiken toch?
In het boek staat als theorie:
If w = a + bi, where a = Re(w) != 0, then tan arg(w) = tan arg(a + bi) = b / a. (Dit snap ik allemaal)
Maar ik zit nu even in de knoop met wat tangens precies is, en wanneer je tangens gebruikt, en wanneer je tan-1 (inverse van tangens) gebruikt. Ik weet overigens dat tanx = sinx / cosx.
EDIT
Tan is een verhouding tussen sin en cos. Dus bij complexe getallen, geeft tan(arg(w)) de verhouding weer tussen sin(theta) en cos(theta). Indien deze verhouding 1 is, dan betekent dat de hoek (dus arg(w)) gelijk is aan pi/4.
Klopt dit?
[ Bericht 7% gewijzigd door NonameNogame op 26-11-2011 13:44:57 ]
Kijk ook eens naar http://en.wikipedia.org/w(...)ustration_modarg.svg
Dat heeft er waarschijnlijk mee te maken dat je dat laatste veel vaker hebt gehoord dan dat eerste.quote:
[..]
Ja weet niet hoe je dat noemt als je zeg maar 'sommeerd' over conjunctie maar gewoon conjunctie dus? "Je conjuctie over de elementen van ..." klinkt nogal raar tegenover ... Je sommeert over de elemente van ..."
anders kan schrijven? Is dat dan?quote:K*L-3/2
Of slaat dat nergens op?quote:K / (0.5*(sqrtL))
Bedankt voor jullie hulp alvast.
Je zou 'm zo kunnen schrijven:quote:Op zaterdag 26 november 2011 14:23 schreef Snuf. het volgende:
Zou iemand me uitkunnen leggen hoe ik de formule
[..]
anders kan schrijven? Is dat dan?
[..]
Of slaat dat nergens op?
Bedankt voor jullie hulp alvast.
quote:
Dankjulliewel, was even een beetje uit de wiskunde dus zag dit niet gelijkquote:
Kijk eens even hier en dan vooral dit plaatje. Voor a > 0 geldt Arg(a+bi) = arctan(b/a). Gebruik liever niet de (vooral Amerikaanse) notatie tan-1x voor arctan x.quote:
Vraag mbt complexe getallen.
Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.
Waarom is Arg(1 + i) = pi / 4 ???
Edit: ik zie net dat je boek beweert dat dit ook zou gelden voor a < 0. Maar dat klopt niet. Om te beginnen is arg(z) voor een complex getal z (ongelijk aan nul) slechts bepaald tot op een geheel veelvoud van 2π. Je kunt dus niet zeggen dat arg(1+i) gelijk is aan ¼π. Wat wél correct is, is dat arg(1+i) = ¼π + 2kπ, k ∈ Z.
Vooral in angelsaksische literatuur wordt vaak onderscheid gemaakt tussen arg(z) en Arg(z), waarbij met het laatste de zogeheten 'hoofdwaarde' van het argument van z wordt aangegeven. Hiermee wordt doorgaans de unieke waarde van arg(z) op het interval (-π, π] bedoeld. En zo kunnen we dus inderdaad zeggen dat Arg(1+i) = ¼π. Maar omdat arctan(b/a) voor a,b ∈ R (a ≠ 0) alleen waarden op het interval (-½π, ½π) aanneemt, kan Arg(a+bi) dus alleen gelijk zijn aan arctan (b/a) voor a > 0.
[ Bericht 16% gewijzigd door Riparius op 27-11-2011 20:02:38 ]
Ik heb bedacht dat
P(A<B<C) = P(A<B<C | A=min{A,B,C}) P(A=min{A,B,C}) = P(B<C | A=min{A,B,C}) P(A=min{A,B,C}),
maar weet niet hoe ik verder kan.
De verdeling van max{B,C} kun je zo bepalen, en dan zijn die kansen makkelijk uit te rekenen.
Dus max{B,C} is Exp(
edit: Thanks ik ben eruit
[ Bericht 18% gewijzigd door thenxero op 28-11-2011 16:23:12 ]
klopt dat?
Ja precies. Ik had het ook nog op mijn eigen manier uitgerekend en gebruikt dat {B<C} onafhankelijk is van {A=min{A,B,C}} en daar kwam hetzelfde uit.quote:
(domein D in R, en punt c in D, en f:D -> R continu in c)
Als
Ik heb geprobeerd te werken met de definitie van continuiteit en dan f(c) als epsilon maar hiermee liep ik vast. Weet iemand of dit toch goed gaat of misschien een andere manier?
Als f(x) groter gelijk f(c) dan dus ook f(x) > 0.
Als f(x) < f(c) dan moet gelden:
f(c) - f(x) < f(c) dus f(x) > 0.
Dus f(x) groter gelijk 0.
Is dit correct of mis ik iets?
Nee. De continuïteit van f in c houdt in dat er ook bij ε = f(c) > 0 een δ > 0 bestaat zodanig dat:quote:
Uit continuiteit volgt |f(x) - f(c)| < f(c) met f(c) > 0.
| f(x) - f(c) | < f(c) voor | x - c | < δ
Bedenk dat | f(x) - f(c) | = f(x) - f(c) voor f(x) ≥ f(c) en | f(x) - f(c) | = f(c) - f(x) voor f(x) ≤ f(c).quote:Als f(x) groter gelijk f(c) dan dus ook f(x) > 0.
Als f(x) < f(c) dan moet gelden:
f(c) - f(x) < f(c) dus f(x) > 0.
Riparius, Hartelijk dank voor je uitleg en links! Ik heb echter nog een aantal vraagjes, om te controleren of ik het helemaal snap:quote:
Ik moest Arg(z) berekenen, de modules bepalen, en z in r (= |z|) en theta herschrijven
Vraag 10)
Gegeven: z = -2 + i
Mijn uitwerking:
a = -2, b = 1
dus r = |z| = Wortel(a^2 + b^2) = Wortel(4 + 1) = Wortel(5);
En Arg(z) -----> arctan(1/-2). Antwoord gaf aan: Arg(z) = π - arctan(1/2).
Is dit omdat a < 0 en b >= 0, en er dus geldt: Arg(z) = arctan(b/a) + π ?? Zo ja, dan wordt het antwoord dat ik hiermee verkrijg Arg(z) < -π -----> en aangezien de principal argument bereik (-π, π] heeft, diende ik π hierbij op te tellen, en dus Arg(z) = π - arctan(1/2) te moeten doen? (zodat het uiteindelijke antwoord tussen het bereik (-π, π] komt te liggen, wat voldoet aan het bereik van de principal Argument)
Een 2e vraag met deze opgave: Uit het gegeven, blijkt dat a = -2. Waarom geeft het antwoord dan arctan(1 / 2) aan? (ipv arctan(1 / -2)).
Vraag 11)
Gegeven: z = -3 - 4i
Mijn uitwerking:
a = -3, b = -4
dus r = |z| = Wortel(a^2 + b^2) = Wortel(9+16) = 5
En Arg(z) -----> arctan(-4 / -3). Aangezien zowel a<0 en b<0, moet ik dus doen: Arg(z) = arctan(-4 / -3) - π
Maar arctan(-4 / -3) = 0.9272... -> Dit valt toch binnen de range (-π, π], en dus voldoet aan de range voor de principal Argument???
Het antwoord voor Arg(z) was overigens: Arg(z) = arctan(4/3) + π (waarom positieve a- en b-waarden en wordt er π BIJgeteld??? Zou je &pi niet AF moeten trekken? immers, a en b zijn beide kleiner dan 0, en in dat geval moet je &pi aftrekken, zoals aangegeven was op de wikipedia pagina)
Vraag 12)
Gegeven: z = 3 - 4i
Mijn uitwerking:
a = 3, b = -4
r = |z| = 5
En Arg(z) = arctan(-4 / 3) -----> omdat a > 0 , hoef ik hier geen π bij op te tellen.
Antwoord was: Arg(z) = - arctan(4 / 3) ......... Waarom b = positief nu? Kan dit?
Voor vraag 12, waarom b positief is en -arctan(b / a) geschreven wordt ipv arctan(-b / a), kan ik wel wat afleiden aan de hand van goniometrie en de eenheidscirkel (simpelweg zoals in vwo-stof wiskunde staat), namelijk:
sin(-x) = -sin(x).....Zoals in de afbeelding aangegeven:
Mijn vraag hierbij is....klopt mijn redenatie? Zo ja, dan snap ik waarom arctan(-4 / 3) herschreven kan worden in -arctan(4 / 3)
Vraag 12, deel 2)
De herschrijving van z in r (= |z|) en theta
Gegeven was: z = 3 -4i
Mijn uitwerking:
a = 3
b = -4
r = |z| = 5
Er geldt verder: sinθ = b / r ..... en ..... cosθ = a / r, dan b = r·sinθ en a = r·cosθ
Aangezien de algemene regel geldt: z = a + bi (in dit geval is b negatief), dus z = a + -bi, geldt:
z = r·cosθ + i·r·sinθ ---------> z = 5(cosθ - i·sinθ) (want b was negatief)
Antwoord luidt: z = 5(cosθ + i·sinθ)........... waarom??
Een vraag hierbij is o.a.: Hoe moet ik z = 3 - 4i nu zien, als z = a + bi (met b is negatief), of als z = a - bi (met b is positief) ??
------------------------------------
Mijn excuses voor de vele en lange vragen. Ik heb geen leraar 'bij de hand' en tevens is wiskunde niet mijn studie of een onderdeel ervan. Ik vind het echter behoorlijke leuk en interessant en ik doe aan zelfstudie. Nadeel is dat ik alles zelf uit moet zoeken zonder leraar. Vandaar het gebruik van dit forum.
Alvast enorm bedankt!!
[ Bericht 0% gewijzigd door NonameNogame op 29-11-2011 22:48:13 ]
Over het algemeen helpt het om aan poolcoördinaten te denken. Heb je een complex getal:quote:
[..]
Riparius, Hartelijk dank voor je uitleg en links! Ik heb echter nog een aantal vraagjes, om te controleren of ik het helemaal snap:
Ik moest Arg(z) berekenen, de modules bepalen, en z in r (= |z|) en theta herschrijven
Vraag 10)
Gegeven: z = -2 + i
Mijn uitwerking:
a = -2, b = 1
dus r = |z| = Wortel(a^2 + b^2) = Wortel(4 + 1) = Wortel(5);
En Arg(z) -----> arctan(1/-2). Antwoord gaf aan: Arg(z) = π - arctan(1/2).
(1) z = x + yi,
dan is het beeldpunt van dit getal in het complexe vlak het punt met coördinaten (x;y). Maar nu kun je de cartesische (rechthoekige) coördinaten van een punt ook omzetten naar poolcoördinaten. Heb je een punt P(x;y) dan moet je naar twee dingen kijken voor deze omzetting, namelijk de afstand OP = r (met de r van radius 'straal'), en de hoek die OP maakt met de positieve x-as. Stel dat we de positieve x-as over een hoek θ (uitgedrukt in radialen) moeten roteren om de (halve) lijn vanuit de oorsprong door punt P te krijgen, dan geldt voor de coördinaten van punt P(x;y):
(2) x = r∙cos θ
(3) y = r∙sin θ
En daar P(x;y) het beeldpunt is van ons complexe getal z = x + yi hebben we dus:
(4) z = r∙cosθ + i∙r∙sin θ = r(cos θ + i∙sin θ)
De poolcoördinaten van het beeldpunt P van z zijn dus (r;θ). Merk op dat we hier gewoonlijk i∙sin θ schrijven omdat sin θ∙i gemakkelijk aanleiding zou kunnen geven tot verwarring. Je kunt eenvoudig nagaan waarom (2) en (3) en dus ook (4) gelden, als je nog even terugdenkt aan de definitie van de sinus- en cosinusfunctie aan de hand van de eenheidscirkel. Noem je het snijpunt van lijnstuk OP of het verlengde daarvan met de eenheidscirkel P', dan zijn de coördinaten van dit punt P' per definitie (cos θ ; sin θ) omdat de cosinus en de sinus van θ gedefinieerd zijn als de x- resp. de y-coördinaat van het beeldpunt van (1;0) bij rotatie om de oorsprong over een hoek θ. En aangezien punt P het beeldpunt is van punt P' bij een meetkundige vermenigvuldiging ten opzichte van O met een factor r is het direct duidelijk dat de coördinaten van punt P dus inderdaad (r∙cos θ ; r∙sin θ) zijn.
Nu noemen we de afstand tot de oorsprong van het beeldpunt P(x;y) van het complexe getal z = x + yi de modulus (of: absolute waarde) van z, en geven we deze aan met abs(z) of |z|. Op grond van de stelling van Pythagoras is meteen duidelijk dat we hebben:
(5) |z| = √(x2 + y2)
De rotatiehoek θ heet het argument van z, en deze wordt aangegeven met arg(z). Maar nu is het zo dat we na een (extra) rotatie om de oorsprong over 2π radialen, hetzij met de wijzers van de klok mee (negatief) hetzij tegen de wijzers van de klok in (positief), weer op precies hetzelfde punt uitkomen. Daarom is arg(z) niet eenduidig bepaald, maar slechts tot op een geheel veelvoud van 2π.
Nu is het in de praktijk vaak nuttig om toch over 'het' argument van een complex getal te kunnen spreken, daarom heeft men bedacht dat je de rotatie van de positieve x-as (reële as) kunt beperken tot een halve slag linksom (positief, tegen de wijzers van de klok in),of een halve slag rechtsom (negatief, met de wijzers van de klok mee). Zo kunnen we het argument altijd uitdrukken als een hoek die ligt tussen -π en +π radialen.
Alleen: wat moeten we dan doen met punten op de negatieve reële as? Want voor de getallen waarvan het beeldpunt op de negatieve reële as ligt zou je dan nog steeds net zo goed kunnen zeggen dat het argument -π is als π. De conventie is dat we dan voor de getallen op de negatieve reële as de positieve waarde π nemen. Alles samengevat ligt de 'hoofdwaarde' van het argument dan altijd op het interval (-π,π]. Deze 'hoofdwaarde' van het argument van z wordt vooral in Amerikaanse boeken aangeduid als Arg(z), dus met een hoofdletter.
Je kunt de negatieve reële as nu een beetje vergelijken met de datumgrens op aarde: als je naar het westen reist, dan kom je gaandeweg in tijdzones waar het steeds een uur vroeger is, en als je naar het oosten reist dan kom je gaandeweg in tijdzones waar het steeds een uur later is. Maar omdat de aarde rond is, kom je dan als je naar het oosten reist uiteindelijk op een punt waar je ineens overgaat van GMT+12 uur naar GMT-12 uur. Je maakt dan een sprong van precies één dag terug in de tijd en als je dan verder blijft reizen in oostelijke richting blijf je steeds in tijdzones terecht komen waar het een uur later is. Zoiets hebben we nu ook met de 'hoofdwaarde' van het augment in het complexe vlak. Als we starten in het punt (1;0), dus het beeldpunt van het (reële) getal 1, en we roteren dit punt tegen de klok in, dan neemt het argument toe tot π en we op de negatieve reële as zitten. Maar zodra we verder roteren en de negatieve reële as zijn gepasseerd hebben we een sprong gemaakt waarbij het argument met 2π is verminderd. Draaien we dan verder tegen de wijzers van de klok in, dan blijft het argument toenemen vanaf -π tot we weer op het uitgangspunt (1;0) terug zijn, en dan is het (hoofd)argument weer 0.
Nu dan je vraag. Je wil Arg(-2 + i) berekenen, dus de 'hoofdwaarde' van het argument van -2 + i. Het eerste wat je dan altijd even moet doen (in gedachten) is de ligging van het beeldpunt van dit getal in het complexe vlak visualiseren. In dit geval gaat het om het punt met de coördinaten (-2;1), en dat punt ligt in het tweede kwadrant (meestal worden de kwadranten aangegeven met Romeinse cijfers, dus kwadrant II). Dan zie je meteen dat (a) Arg(-2 + i) positief moet zijn, want (-2;1) ligt in de bovenste helft van het vlak en (b) dat de waarde in ieder geval moet liggen tussen ½π en π. Pas als je dit bedacht hebt moet je gaan rekenen.
Laten we het punt (-2;1) waar het hier om gaat weer even P noemen. Maak je nu een schetsje, dan zie je dat lijnstuk OP een hoek θ maakt met de negatieve reële as (x-as) zodanig dat
(6) tan θ = 1 : 2 = ½
en dus is:
(7) θ = arctan(½)
Maar ja, we moeten niet de hoek van lijnstuk OP met de negatieve reële as hebben, maar de hoek met de positieve reële as, en die hoek is supplementair met hoek θ. Twee hoeken noemen we supplementair als ze samen een gestrekte hoek vormen, dus een hoek van 180 graden oftewel π radialen. Voor de gezochte hoek, en daarmee voor het 'hoofdargument' van het complexe getal -2 + i vinden we dus:
(8) Arg(-2 + i) = π - arctan(½)
Maar goed, waarom werkt het niet als we gewoon arctan(1/-2) nemen zoals jij deed? Nu, dat heeft te maken met het bereik van de arctan functie. De arctan functie is de inverse functie van de tangens functie, en die geeft de hoek aan (in radialen) waarvan de tangens gelijk is aan de gegeven waarde (hier -½). De aanduiding arctan is een afkorting van arcus tangens (met arcus 'boog' omdat een hoekmaat in radialen ook als een cirkelboog op de eenheidscirkel is op te vatten). Maar nu is de tangens evenals de sinus en de cosinus een periodieke functie en wel een periodieke functie met een periode π (dit in tegenstelling tot de sinus en cosinus die elk een periode 2π hebben). Omdat de tangens een periodieke functie is kunnen we dus ook niet spreken over 'de' hoek (of: rotatie) waarvan de tangens bijvoorbeeld -½ is, want er zijn oneindig veel hoeken (rotaties) waarbij de tangens -½ is, en deze hoeken (rotaties) verschillen allemaal een geheel veelvoud van π met elkaar. En dus moest men een keuze maken.
Nu is het zo dat de tangens van een hoek θ precies éénmaal alle waarden op R aanneemt als we θ het open interval (-½π, ½π) laten doorlopen, en dus kunnen we dit ook omkeren en zo bij elke x uit R precies één waarde θ op het interval (-½π, ½π) aanwijzen waarvoor geldt dat tan θ = x. We zeggen dan dat arctan x = θ. Met arctan x wordt dus bedoeld de hoek (in radialen) op het interval (-½π, ½π) waarvan de tangens gelijk is aan x. Zo is trouwens ook de notatie te verklaren: vroeger schreef men arc. tan. x (met puntjes, als afkorting) en bedoelde men hiermee 'de boog (arcus) waarvan de tangens x is'.
Maar goed, de arctan functie neemt dus op R alleen waarden aan op het interval (-½π, ½π) en dat verklaart waarom Arg(a + bi) niet gelijk kan zijn aan arctan(b/a) voor a < 0.
Zo kun je het beredeneren, maar het is om vergissingen te voorkomen beter om het altijd eerst even te visualiseren.quote:Is dit omdat a < 0 en b >= 0, en er dus geldt: Arg(z) = arctan(b/a) + π ?? Zo ja, dan wordt het antwoord dat ik hiermee verkrijg Arg(z) < -π -----> en aangezien de principal argument bereik (-π, π] heeft, diende ik π hierbij op te tellen, en dus Arg(z) = π - arctan(1/2) te moeten doen? (zodat het uiteindelijke antwoord tussen het bereik (-π, π] komt te liggen, wat voldoet aan het bereik van de principal Argument)
Dat is hopelijk duidelijk uit het bovenstaande. Ze zijn (impliciet) uitgegaan van de supplementaire hoek. Je zou het antwoord ook kunnen schrijven als π + arctan(1/-2) aangezien arctan(-x) = -arctan(x).quote:Een 2e vraag met deze opgave: Uit het gegeven, blijkt dat a = -2. Waarom geeft het antwoord dan arctan(1 / 2) aan? (ipv arctan(1 / -2)).
Grote verwarring. Zowel je eigen antwoord als het antwoord dat het boek geeft (als je dat juist hebt overgenomen) zijn niet correct. Wikipedia doet het wel goed. Het beeldpunt (-3;-4) van -3 - 4i ligt in kwadrant III, dus we kunnen meteen zeggen dat de hoofdwaarde van het argument moet liggen tussen -π en -½π, en dat zie ik niet in je antwoorden.quote:Vraag 11)
Gegeven: z = -3 - 4i
Mijn uitwerking:
a = -3, b = -4
dus r = |z| = Wortel(a^2 + b^2) = Wortel(9+16) = 5
En Arg(z) -----> arctan(-4 / -3). Aangezien zowel a<0 en b<0, moet ik dus doen: Arg(z) = arctan(-4 / -3) - π
Maar arctan(-4 / -3) = 0.9272... -> Dit valt toch binnen de range (-π, π], en dus voldoet aan de range voor de principal Argument???
Het antwoord voor Arg(z) was overigens: Arg(z) = arctan(4/3) + π (waarom positieve a- en b-waarden en wordt er π BIJgeteld??? Zou je &pi niet AF moeten trekken? immers, a en b zijn beide kleiner dan 0, en in dat geval moet je &pi aftrekken, zoals aangegeven was op de wikipedia pagina)
Dit antwoord is wel juist. Je maakt hier gebruik van arctan (-x) = -arctan x.quote:Vraag 12)
Gegeven: z = 3 - 4i
Mijn uitwerking:
a = 3, b = -4
r = |z| = 5
En Arg(z) = arctan(-4 / 3) -----> omdat a > 0 , hoef ik hier geen π bij op te tellen.
Antwoord was: Arg(z) = - arctan(4 / 3) ......... Waarom b = positief nu? Kan dit?
Je moet uitgaan van de tangensfunctie. Neem aan dat -½π < θ < ½π en stel tan θ = x. Dan is dus per definitie arctan x = θ. Maar omdat tan(-θ) = -tan θ en tan θ = x is dus tan(-θ) = -x en dus weer per definitie arctan(-x) = -θ. En dus geldt inderdaad arctan(-x) = -arctan x.quote:Voor vraag 12, waarom b positief is en -arctan(b / a) geschreven wordt ipv arctan(-b / a), kan ik wel wat afleiden aan de hand van goniometrie en de eenheidscirkel (simpelweg zoals in vwo-stof wiskunde staat), namelijk:
sin(-x) = -sin(x).....Zoals in de afbeelding aangegeven:
[ afbeelding ]
Mijn vraag hierbij is....klopt mijn redenatie? Zo ja, dan snap ik waarom arctan(-4 / 3) herschreven kan worden in -arctan(4 / 3)
Je introduceert hier zelf een minteken omdat je kennelijk uit wil gaan van een positieve hoek. Maar dat moet je (hier) niet doen, je kunt beter denken in termen van rotaties die zowel positief als negatief kunnen zijn. En dan heb je uitgaande van de positieve reële as aan een rotatie over een negatieve hoek tussen 0 en -½π voldoende om uit te komen op een punt in het vierde kwadrant. Formule (4) geldt altijd, ook voor negatieve rotaties, omdat immers de sinus en cosinusfuncties ook zo zijn gedefinieerd aan de hand van de eenheidscirkel.quote:Vraag 12, deel 2)
De herschrijving van z in r (= |z|) en theta
Gegeven was: z = 3 -4i
Mijn uitwerking:
a = 3
b = -4
r = |z| = 5
Er geldt verder: sinθ = b / r ..... en ..... cosθ = a / r, dan b = r·sinθ en a = r·cosθ
Aangezien de algemene regel geldt: z = a + bi (in dit geval is b negatief), dus z = a + -bi, geldt:
z = r·cosθ + i·r·sinθ ---------> z = 5(cosθ - i·sinθ) (want b was negatief)
Antwoord luidt: z = 5(cosθ + i·sinθ)........... waarom??
Dat is inderdaad de kern. Vroeger, in de 16e en ook in de 17e eeuw, toen men pas leerde 'rekenen met letters' had men grote moeite met het idee om een uitdrukking van de gedaante z = 3 - 4i te 'zien' als z = a + bi met a = 3 en b = -4, en nam men vaak aan dat de letters positieve grootheden voorstelden. En dus 'zag' men z = 3 - 4i als z = a - bi met a = 3 en b = 4. Dat kan, maar je moet het (hier) toch niet doen omdat je dan heel gauw in verwarring raakt met bijvoorbeeld het uitrekenen van het hoofdargument. We hebben hier Arg(3 - 4i) = arctan(-4/3) = -arctan(4/3).quote:Een vraag hierbij is o.a.: Hoe moet ik z = 3 - 4i nu zien, als z = a + bi (met b is negatief), of als z = a - bi (met b is positief) ??
Voor het uitrekenen van het hoofdargument van z = x + yi bestaat een formule die ook werkt als het beeldpunt op de imaginaire as of in de linkerhelft van het complexe vlak ligt (dus voor x ≤ 0), maar om dat te begrijpen moet je wel iets weten van goniometrie.
We hebben gezien dat arctan alleen waarden aanneemt op het interval (-½π, ½π) maar dat het 'hoofdargument' ligt op het interval (-π, π], en dat is nu precies het probleem. Als we nu de (mogelijke) waarde π voor het 'hoofdargument' (getallen op de negatieve reële as) even buiten beschouwing laten, dan is het interval (-π, π) dus precies tweemaal zo breed als het interval (-½π, ½π) waarin arctan ligt, en daar kunnen we wat mee doen. Laten we zeggen dat de gezochte hoofdwaarde Arg(z) van z = x + yi (y ≠ 0 voor x ≤ 0) gelijk is aan θ. Dan is dus -π < θ < π, en dus -½π < ½θ < ½π. Maar dit betekent dat:
(9) ½θ = arctan(tan ½θ) (-π < θ < π)
en dus:
(10) Arg(x + yi) = θ = 2∙arctan(tan ½θ) (-π < θ < π)
Als we nu tan ½θ uit kunnen drukken in cos θ = x/r en sin θ = y/r, dan hebben we dus Arg(x + yi) = θ. Hiervoor gaan we uit van de bekende formules voor de sinus en cosinus van de dubbele hoek:
(11a) sin 2α = 2∙sinα∙cos α
(11b) cos 2α = 2∙cos2α - 1
Uit (11b) krijgen we
(11c) 1 + cos 2α = 2∙cos2α
Deling van de leden van (11a) door de leden van (11c) geeft dan:
(11d) sin 2α /(1 + cos 2α) = tan α,
en door substitutie van α = ½θ en dus 2α = θ krijgen we dan:
(12) tan ½θ = sin θ /(1 + cos θ)
Substitutie van (12) in (10) geeft nu:
(13) Arg(x+ yi) = 2∙arctan(sin θ /(1 + cos θ))
en aangezien cos θ = x/r en sin θ = y/r levert substitutie hiervan in (13) na wat vereenvoudiging (vermenigvuldiging van de teller en noemer van het quotiënt met r):
(14) Arg(x + yi) = 2∙arctan(y/(r + x)) (y ≠ 0 voor x ≤ 0, r = √(x2 + y2))
Met deze formule kan ik bijvoorbeeld direct zeggen dat het 'hoofdargument' van -3 - 4i gelijk is aan 2∙arctan(-2), hetgeen overigens weer gelijk is aan arctan(4/3) - π zoals je gemakkelijk kunt controleren.
Er zijn nog andere manieren om (de hoofdwaarde van) het argument uit te rekenen die vooral toepasbaar zijn als je over een geschikt programma beschikt of bijvoorbeeld van WolframAlpha gebruik kunt maken. Je weet (hopelijk) dat bij vermenigvuldiging van twee complexe getallen de modulus van het product gelijk is aan het product van de moduli van de factoren en dat het argument gelijk is aan de som van de argumenten van de factoren modulo 2π. Vermenigvuldiging van een complex getal met cos θ + i∙sin θ is meetkundig te interpreteren als een rotatie van het beeldpunt van dat complexe getal om de oorsprong over een hoek θ. Je kunt dit vrij gemakkelijk inzien als je eerst beredeneert dat vermenigvuldiging van een complex getal met i meetkundig is te interpreteren als een rotatie over een rechte hoek oftewel ½π radialen in positieve zin (i.e. tegen de klok in). We hebben i(a + bi) = ai + bi2 = -b + ai. Als je nu de ligging van het beeldpunt (-b;a) van -b + ai ten opzichte van het originele beeldpunt (a;b) van a + bi bekijkt dan zie gemakkelijk (congruente driehoeken) dat vermenigvuldiging met i inderdaad een rotatie in positieve zin over een rechte hoek oftewel ½π rad representeert:
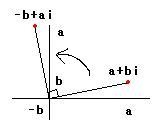
Heb je dit eenmaal gezien, dan is het niet moeilijk om te begrijpen (maak een tekening!) wat er gebeurt als je een complex getal a + bi vermenigvuldigt met cos θ + i∙sinθ. We kunnen het product opsplitsen in twee delen:
(15) (cos θ + i∙sinθ)(a + bi) = cos θ∙(a + bi) + (i∙sinθ)∙(a + bi) = cos θ∙(a + bi) + i∙(sinθ∙(a + bi))
De vermenigvuldiging van een complex getal a + bi met een reëel getal zoals (hier) cos θ of sin θ is niet zo spannend: dit komt overeen met een meetkundige vermenigvuldiging van het beeldpunt met die reële factor (of, zo je wil, de vermenigvuldiging van een vector met een scalar). Het beeldpunt van de vermenigvuldiging van een complex getal a + bi met een reëel getal ligt dus op dezelfde lijn door de oorsprong als het beeldpunt (a;b) van a + bi. Maar nu hebben we voor het product van a + bi met cos θ + i∙sinθ in het rechterlid van (15) twee componenten, waarvan de tweede component sinθ∙(a + bi) ook nog eens wordt vermenigvuldigd met i. En we hebben net gezien dat vermenigvuldiging met i meetkundig een rotatie tegen de klok in over een rechte hoek representeert. Als we nu lijnstukken tekenen vanuit de oorsprong naar de beeldpunten van elk van de beide complexe getallen cos θ∙(a + bi) en i∙(sinθ∙(a + bi)) in het rechterlid van (15) dan staan die lijnstukken dus loodrecht op elkaar. En dat betekent dat we de afstand van het beeldpunt van de som en daarmee de afstand (de modulus) van het gehele product in (15) eenvoudig kunnen berekenen met de stelling van Pythagoras. Aangezien cos2θ + sin2θ = 1 vinden we voor die afstand dan √(a2 + b2) zodat het beeldpunt van het product dus op dezelfde afstand van de oorsprong ligt als het beeldpunt (a;b) van a + bi zelf. Aan de modulus verandert dus niets door de vermenigvuldiging met cos θ + i∙sin θ zodat het beeldpunt van het product alleen is geroteerd ten opzichte van het beeldpunt (a;b) van a + bi. En aangezien het beeldpunt van de component cos θ∙(a + bi) langs dezelfde lijn ligt als het lijnstuk van de oorsprong naar het punt (a;b) en het beeldpunt van de component i∙(sinθ∙(a + bi)) = sinθ∙(-b + ai) op de lijn door de oorsprong loodrecht daarop, is direct in te zien dat vermenigvuldiging van een complex getal a + bi met cos θ + i∙sin θ correspondeert met een rotatie om de oorsprong van het beeldpunt (a;b) over een hoek θ.
Als je dit eenmaal inziet (en dit is fundamenteel) dan kun je hier aardige dingen mee doen. Als we het getal 1 = 1 + 0i vermenigvuldigen met cos α + i∙sin α dan is de uitkomst uiteraard cos α + i∙sin α en kunnen we zeggen dat het beeldpunt (1;0) van het getal 1 door deze vermenigvuldiging wordt geroteerd over een hoek α zodat het beeldpunt van het product uiteraard (cos α ; sin α) is. Dat is niet zo interessant, maar als we het getal cos α + i∙sin α nu weer met cos β + i∙sin β vermenigvuldigen, dan wordt het beeldpunt (cos α ; sin α) nog eens geroteerd over een hoek β. Maar dan is het beeldpunt (1;0) van het getal 1 dus uiteindelijk geroteerd over een hoek α + β, zodat we kunnen zeggen dat vermenigvuldiging met (cos α + i∙sin α)(cos β + i∙sin β) precies hetzelfde bewerkstelligt als een vermenigvuldiging met cos(α+β) + i∙sin(α+β). Zo komen we tot de conclusie dat geldt:
(16) cos(α+β) + i∙sin(α+β) = (cos α + i∙sin α)(cos β + i∙sin β)
Als je nu de haakjes in het rechterlid van (16) uitwerkt en de rekenregel i2 = -1 gebruikt, dan kun je dit schrijven als:
(17) cos(α+β) + i∙sin(α+β) = (cos α∙cos β - sin α∙sin β) + i∙(sin α∙cosβ + cos α∙sin β)
Maar nu zijn twee complexe getallen uitsluitend aan elkaar gelijk als zowel de reële delen als de imaginaire delen aan elkaar gelijk zijn, en dus volgt uit (17) dat:
(18a) cos(α+β) = cos α∙cos β - sin α∙sin β
(18b) sin(α+β) = sin α∙cosβ + cos α∙sin β
Dit zijn de bekende additietheorema's uit de elementaire goniometrie. Er bestaat dus een nauw verband tussen deze somformules en de vermenigvuldiging van complexe getallen.
Aangezien voor een natuurlijk getal n het verheffen tot de macht n van een getal neerkomt op een n maal herhaalde vermenigvuldiging, kun je op grond van (16) ook nog concluderen dat geldt:
(19) (cos θ + i∙sin θ)n = cos nθ + i∙sin nθ
Dit resultaat staat bekend als de formule van De Moivre. Je kunt deze formule bijvoorbeeld gebruiken om eenvoudig goniometrische identiteiten af te leiden voor de sinus en cosinus van een veelvoud van een hoek. Ook kun je deze formule gebruiken om alle oplossingen te vinden van de vergelijking zn = 1. Probeer dat eens uit voor bijvoorbeeld n = 5 en n = 6. Wat kun je zeggen over de beeldpunten van de complexe getallen die de oplossingen vormen van deze vergelijking?
De betrekking arg(z1z2) = arg(z1) + arg(z2) (mod 2π) die tot uitdrukking brengt dat bij vermenigvuldiging van twee complexe getallen de argumenten bij elkaar worden opgeteld (modulo 2π) doet je wellicht denken aan een soortgelijke betrekking bij logaritmen. De logaritme van het product van twee (positieve, reële) getallen is gelijk aan de som van de logaritmen van de factoren: log(ab) = log(a) + log(b). Nu zou je kunnen beginnen te vermoeden dat er wellicht een verband bestaat tussen logaritmen en het argument van complexe getallen. Welnu, dat is inderdaad het geval.
Het zou veel te ver voeren om hier een verantwoorde behandeling te geven van logaritmen van complexe getallen, maar ik zal toch proberen het verband tussen complexe logaritmen en het argument op een enigszins intuïtieve manier duidelijk te maken. Laten we eens aannemen dat het mogelijk is een zinnige betekenis toe te kennen aan een logaritme van een complex getal, waarbij ik even in het midden laat wat we ons daarbij zouden moeten voorstellen. Op grond van (16) hebben we dan:
(20) log(cos(α+β) + i∙sin(α+β)) = log((cos α + i∙sin α)(cos β + i∙sin β))
En omdat we mogen verwachten dat de logaritme van een product gelijk is aan de som van de logaritmen van de factoren zou dan ook moeten gelden:
(21) log(cos(α+β) + i∙sin(α+β)) = log(cos α + i∙sin α) + log(cos β + i∙sin β)
Nu kun je uit (21) opmaken dat de logaritme van een complex getal van de vorm cos θ + i∙sin θ kennelijk recht evenredig zou moeten zijn met θ, en dat is ook in overeenstemming met log(cos 0 + i∙sin 0) = log(1) = 0 voor θ = 0. Maar dan zou log(cos θ + i∙sin θ) dus gelijk moeten zijn aan θ maal een constante, en rijst onmiddellijk de vraag wat die constante dan is.
Laten we zeggen dat:
(22) z = cos θ + i∙sin θ en w = log(z),
zodat:
(23) w = log(cos θ + i∙sin θ)
Nu zou dus moeten gelden dat w recht evenredig is met θ, zodat er een constante c zou moeten zijn zodanig dat:
(24) w = c∙θ
Maar hoe vinden we die geheimzinnige constante c? Wel, als w = c∙θ dan moet gelden dw/dθ = c, zodat we de constante c zouden moeten kunnen vinden door de afgeleide dw/dθ te bepalen. En volgens de kettingregel hebben we dan:
(25) dw/dθ = dw/dz ∙ dz/dθ
Nu zouden we op grond van de afgeleide x-1 van de reële functie log(x) kunnen veronderstellen (en meer is dat niet op dit moment) dat voor w = log(z) evenzo moet gelden:
(26) dw/dz = z-1.
De bepaling van dz/dθ levert niet veel moeilijkheden op. De afgeleide van cos θ naar θ is -sin θ en de afgeleide van sin θ naar θ is cos θ. Maar nu is het je wellicht wel eens opgevallen dat je hebt:
(27a) d(cos t)/dt = cos(t + ½π) = -sin t
(27b) d(sin t)/dt = sin(t + ½π) = cos t
De verklaring hiervan is heel eenvoudig als je het even 'fysisch' bekijkt. Heb je een punt dat met een eenparige snelheid van 1 eenheid per seconde tegen de wijzers van de klok in langs de eenheidscirkel beweegt, te beginnen in het punt (1;0) op tijdstip t = 0, dan kun je de plaatsvector van dit punt schrijven als s(t) = cos(t)∙ex + sin(t)∙ey. De afgeleide s'(t) = v(t) = d(cos(t))/dt∙ex + d(sin(t))/dt∙ey is dan de snelheidsvector. Maar: we weten dat dit een vector moet zijn met lengte 1 die op ieder moment loodrecht staat op de plaatsvector, omdat de raaklijn aan een cirkel loodrecht staat op de straal naar het raakpunt. En omdat de beweging tegen de klok in gaat is v(t) een kwart slag in positieve zin gedraaid ten opzichte van s(t) en moet dus ook gelden v(t) = cos(t + ½π)∙ex + sin(t + ½π)∙ey, waaruit direct (27a) en (27b) volgen. Goed, zo hebben we dus:
(28) dz/dθ = cos(θ + ½π) + i∙sin(θ + ½π)
Maar nu weten we ook dat een rotatie over een hoek ½π beantwoordt aan een vermenigvuldiging met i, en dus kunnen we voor (28) schrijven:
(29) dz/dθ = i∙(cos θ + i∙sin θ) = i∙z
Uit (25), (26) en (29) volgt nu dat:
(30) dw/dθ = dw/dz ∙ dz/dθ = z-1 ∙ i∙z = i
We zien nu dat dw/dθ inderdaad een constante is, en deze evenredigheidsconstante c = dw/dθ is niets anders dan de imaginaire eenheid i. En dus volgt uit (23) en (24) dat kennelijk zou moeten gelden:
(31) log(cos θ + i∙sin θ) = i∙θ
Deze betrekking staat bekend als de formule van Cotes (1682-1716), die deze betrekking in 1714 als eerste publiceerde (zij het dat hij dit op een heel andere wijze had gevonden). Nu is er echter een probleem met (31) dat ook Cotes zich destijds niet heeft gerealiseerd. Als we in (31) θ vervangen door θ + 2kπ (k ∈ Ζ), dan krijgen we uiteraard:
(32) log(cos(θ + 2kπ) + i∙sin(θ + 2kπ)) = i∙(θ + 2kπ)
Maar nu zijn de sinus en cosinus periodieke functies met een periode 2π. En dus is cos(θ + 2kπ) = cos θ en sin(θ + 2kπ) = sin θ, zodat (32) wordt:
(33) log(cos θ + i∙sin θ) = i∙(θ + 2kπ), k ∈ Ζ
Dit betekent dat we kennelijk aan de logaritme van een complex getal geen eenduidige betekenis toe kunnen kennen: de logaritme van een complex getal is slechts bepaald tot op een geheel veelvoud van 2πi. Intuïtief is dit ook wel duidelijk uit (22). Het beeldpunt van z = cos θ + i∙sin θ bevindt zich op de eenheidscirkel, en als we θ met 2π laten toenemen of afnemen dan hebben we een volledig rondje gemaakt en bevinden we ons dus weer op hetzelfde punt, terwijl de evenredigheid van log(z) met θ zou impliceren dat de logaritme dan met 2πi zou moeten zijn toegenomen of afgenomen. Zo horen er bij elk beeldpunt van een complex getal op de eenheidscirkel dus oneindig veel waarden van log(z) die echter wel allemaal een geheel veelvoud van 2πi van elkaar verschillen.
Nemen we nu een complex getal z = x + yi ongelijk aan nul, dan weten we dat we dit altijd kunnen schrijven in de vorm z = r(cos θ + i∙sin θ) waarbij (r;θ) de poolcoördinaten zijn die corresponderen met het punt (x;y) en waarbij abs(z) = |z| = r en arg(z) = θ + 2kπ, k ∈ Ζ. Nu hebben we verder op grond van de regel log(ab) = log(a) + log(b) ook:
(34) log(z) = log(r(cos θ + i∙sin θ)) = log(r) + log(cos θ + i∙sin θ),
en dus vinden we met behulp van (33):
(35) log(z) = log |z| + i∙arg(z),
waaruit weer volgt:
(36) arg(z) = -i∙log(z/|z|)
Hier heb je dus nog een formule voor arg(z). Merk op dat we in (35) en (36) arg(z) hebben, dus niet de 'hoofdwaarde' Arg(z). Immers, log(z) is slechts bepaald tot op een geheel veelvoud van 2πi evenals arg(z) slechts bepaald is tot op een geheel veelvoud van 2π. Net als bij arg(z) is het bij log(z) vaak wenselijk om met een eenduidige waarde van log(z) te kunnen werken. De - voor de hand liggende - oplossing is dan om als 'hoofdwaarde' van log(z) de waarde te nemen die in (35) correspondeert met de 'hoofdwaarde' Arg(z) van arg(z). Deze conventie wordt onder meer gevolgd door WolframAlpha en de calculator van Google.
Nog even een voorbeeld. We hadden al gevonden dat we Arg(-3 - 4i) kunnen uitdrukken als arctan(4/3) - π en als 2∙arctan(-2). Maar nu zien we dat we Arg(-3 - 4i) met behulp van (36) ook uit kunnen drukken als de 'hoofdwaarde' van -i∙log((-3 - 4i)/5). Zo hebben we drie uitdrukkingen voor Arg(-3 -4i) die er op het eerste gezicht totaal verschillend uitzien, maar die toch echt hetzelfde resultaat opleveren, zoals je in WolframAlpha kunt controleren (link: 1, 2, 3). Overigens kun je in WolframAlpha ook eenvoudig arctan(-3,-4) invoeren om Arg(-3 - 4i) te berekenen (link: 4).
quote:------------------------------------
Mijn excuses voor de vele en lange vragen. Ik heb geen leraar 'bij de hand' en tevens is wiskunde niet mijn studie of een onderdeel ervan. Ik vind het echter behoorlijke leuk en interessant en ik doe aan zelfstudie. Nadeel is dat ik alles zelf uit moet zoeken zonder leraar. Vandaar het gebruik van dit forum.
Alvast enorm bedankt!!
[ Bericht 0% gewijzigd door Riparius op 09-12-2011 12:21:23 ]
"Suppose that the amplifier transfer function is given by G(s) = 1/(s+2). If the input signal to the amplifier is a sinewave with frequency of 10 Hz and with amplitude of 1, what is the amplitude of the output signal?"
De eerste stap die ik neem is:
G(s) = 1/(s+2)
G(I*omega) = 1/(I*omega+2)
En dan zit ik eigenlijk al vast. Ik weet dat de amplitude van de output abs(G(I*omega)) is. Maar hoe kan ik dit verder uitwerken?
• i staat voor Imaginair getal (had in mijn post een kleine i moeten zijn)
• i*omega(kleine letter) is volgens mij de frequentie
y''-y'-12y=0 with y(1)=0 and y'(1)=1
Krijg dan
(1) y(1)=Ae^(4)+Be^(-3)=0 en
(2) y'(1)=1=Ae^(4x+4)-Be^(3-3x)
Met A en B constanten die ik nu moet bepalen..
Dus als stelsel vergelijkingen:
Ae^4+Be^(-3) = 0
Ae^8+B = 1
Of: (bovenste maal e^3)
Ae^7+B=0
Ae^8+B=1
En toen zat ik vast
Ja en dan krijg je Ae^8-Ae^7=1, ofwel A=1/(e^8-e^7)quote:
Je kan volgens mij gewoon die laatste twee vergelijkingen van elkaar aftrekken, dan kan je A bepalen. Daarna kan je via één van de twee nog B bepalen.
Wat niet klopt..
De afgeleide van je functie klopt niet geloof ik. Je schrijft y'(1)=1=Ae^(4x+4)-Be^(3-3x), maar y' = 4Ae4x -3Be-3x, dus y'(1)=4Ae4 -3Be-3.quote:
[..]
Ja en dan krijg je Ae^8-Ae^7=1, ofwel A=1/(e^8-e^7)
Wat niet klopt..
Dit klopt natuurlijk niet 4Ae4x-3Be-3x =/= Ae4x+4-Be3-3x. Thanksquote:
[..]
De afgeleide van je functie klopt niet geloof ik. Je schrijft y'(1)=1=Ae^(4x+4)-Be^(3-3x), maar y' = 4Ae4x -3Be-3x, dus y'(1)=4Ae4 -3Be-3.
edit: Heb hem opgelost
[ Bericht 4% gewijzigd door Physics op 30-11-2011 19:00:47 ]
Echter heb ik het idee dat het antwoord andersom moet zijn.
Wie kan mij helpen?
Als je van onderaf -2 benadert is het dus -2.000...0001quote:
Ik heb de volgende formule met de volgende oplossing.
Echter heb ik het idee dat het antwoord andersom moet zijn.
[ afbeelding ]
Wie kan mij helpen?
Dus wat krijg je dan?
[ Bericht 2% gewijzigd door Physics op 01-12-2011 15:15:48 ]
Is dan pijltje naar boven van onder benaderen, en pijltje naar beneden van boven benaderen? Zo ja, dan staat het ergens anders fout in de uitwerkingen. Waardoor ik dus door de war ben geraakt.
Ja pijltje omhoog is van de onderkant benaderenquote:
dan krijg je -2,0000000000000001 + 2 = -0,0000000000000001
Is dan pijltje naar boven van onder benaderen, en pijltje naar beneden van boven benaderen? Zo ja, dan staat het ergens anders fout in de uitwerkingen. Waardoor ik dus door de war ben geraakt.
Klopt, ik bedoelde het begin/propedeuse van universiteit, wat natuurlijk ook afhankelijk is van de studie. Maar dan nog is het een erg breed spectrum met behulpzame filmpjesquote:
Op universitair niveau zijn er niet eens zo gek veel filmpjes. Gelukkig zijn er daarvoor weer diverse andere filmpjes, o.a. waarop hele colleges zijn opgenomen.
Hij heeft al ongeveer 120 filmpjes onder "Calculus", 90% daarvan is hoger dan VWO Wiskunde B niveau, dus dat is alsnog vrij veel
[ Bericht 1% gewijzigd door Thas op 01-12-2011 18:15:01 ]
Voor eerstejaars wiskunde vakken kan het nog best handig zijn ja. Ik heb het toen zelf gebruikt voor lineaire algebra.quote:
[..]
Klopt, ik bedoelde het begin/propedeuse van universiteit, wat natuurlijk ook afhankelijk is van de studie. Maar dan nog is het een erg breed spectrum met behulpzame filmpjes
Hij heeft al ongeveer 120 filmpjes onder "Calculus", 90% daarvan is hoger dan VWO Wiskunde B niveau, dus dat is alsnog vrij veel
Als je een tekenoverzicht van teller, noemer en f(x) (in die volgorde!!) onder elkaar had gezet, was het naar alle waarschijnlijkheid in 1 keer duidelijk gewordenquote:
Ik heb de volgende formule met de volgende oplossing.
Echter heb ik het idee dat het antwoord andersom moet zijn.
[ afbeelding ]
Wie kan mij helpen?
. T(f(x)): ++++++++++++2+++++++++++++
____________________________________
x......................................0..........................
N(f(x)): - - - - - - * +++++++++++++++++++
_____________________________________
x.......................(-2).......0.............................
f(x):
lim→0 - - - - - - - lim↓-∞ * lim↑∞ ++++++ 2 ++++++++++++ lim→0
__________________________________________________________
lim → -∞ ....................... -2 .........................0................................lim→∞
[ Bericht 5% gewijzigd door VanishedEntity op 01-12-2011 23:06:43 (formatting issues :') ) ]
Ooh nu zie ik het!quote:
[..]
Als je een tekenoverzicht van teller, noemer en f(x) (in die volgorde!!) onder elkaar had gezet, was het naar alle waarschijnlijkheid in 1 keer duidelijk geworden
T(f(x)): ++++++++++++2+++++++++++++
____________________________________
x......................................0..........................
N(f(x)): - - - - - - * +++++++++++++++++++
_____________________________________
x.......................(-2).......0.............................
f(x):
lim→0 - - - - - - - lim↓-∞ * lim↑∞ ++++++ 2 ++++++++++++ lim→0
__________________________________________________________
lim → -∞ ....................... -2 .........................0................................lim→∞
SPOILERwat staat daar?
T(f(x)) = de teller van f(x)
N(f(x)) = de noemer van f(x)
f(x) oftewel y; spreekt voor zich
* = y-waarde niet gedefinieerd voor de betreffende x-waarde.
lim = limiet
(-) ∞ = (min) oneindig met ↓, ↑, → om de limiet in kwestie van boven, van onderen resp. zonder specifieke richting te benaderen.
Boven de streep staan de tekens (plus of min), belangrijke functiewaarden, en * voor niet gedefinieerd, voor teller, noemer of f(x). Onder de streep staan de x-waarden die relevant zijn. De puntjes zijn er alleen om de formatting nog enigzins beschaafd te houden.
zie "tekenoverzicht" op wikipedia voor verdere uitleg.
[ Bericht 0% gewijzigd door VanishedEntity op 02-12-2011 05:10:27 ]
Ik dacht
E(max(A,B,C)) = E(max(A,B,C) | A<B<C) P(A<B<C) + E(max(A,B,C) | B<A<C) P(B<A<C) + ... + ...
en zo ga ik alle volgordes van A,B,C af. De kans P(A<B<C) heb ik al bepaald:
Alle andere benodigde kansen volgen hieruit door de letters A,B,C te verwisselen.
Verder weet je dat gegeven A<B<C dat max(A,B,C) = C. Dus E(max(A,B,C) | A<B<C) = E(C) = 1/lambda_C, etc. Dus op deze manier kan je die hele som berekenen.
Klopt dit en/of is er misschien een snellere methode?
[ Bericht 11% gewijzigd door thenxero op 03-12-2011 15:25:08 ]
Ik zou hem zo doen: definieer X = max{A,B}. Bepaal de verdeling van X. Dan definieer je Y = MAX{X,C}. Dan Y = max{A,B,C], en van Y is de verdeling makkelijk te bepalen.
Ja er zijn er inderdaad 6, maar ik had geen zin om alle permutaties uit te schrijven.quote:
Het eerste stuk klopt, maar er zijn wel zes permutaties. Als je weet dat A<B<C dan weet je meer over C, namelijk dat hij 'wel groot zal zijn'. Dus niet E(max(A,B,C) | A<B<C) = E(C).
Ik zou hem zo doen: definieer X = max{A,B}. Bepaal de verdeling van X. Dan definieer je Y = MAX{X,C}. Dan Y = max{A,B,C], en van Y is de verdeling makkelijk te bepalen.
Als je weet dat A<B<C dan weet je dat max(A,B,C)=C. Dus dan heb je wel E(max(A,B,C) | A<B<C) = E(C|A<B<C). Ik zie nu dat dat inderdaad niet hetzelfde is als E(C).
Het lijkt me niet handig om met maxima te gaan werken, want die hebben geen handige verdeling (in tegenstelling tot de minima). (vorige keer deden we dat verkeerd).
De verdeling van x is tochquote:
Het eerste stuk klopt, maar er zijn wel zes permutaties. Als je weet dat A<B<C dan weet je meer over C, namelijk dat hij 'wel groot zal zijn'. Dus niet E(max(A,B,C) | A<B<C) = E(C).
Ik zou hem zo doen: definieer X = max{A,B}. Bepaal de verdeling van X. Dan definieer je Y = MAX{X,C}. Dan Y = max{A,B,C], en van Y is de verdeling makkelijk te bepalen.
Bereken:
(a) P(A<B<C)
(b) P(A<B | max(A,B,C) = C)
(c) E(max{A,B,C} | A<B<C)
(d) E(max{A,B,C})
(a) en (b) heb ik nu, maar nu nog (c) en (d). Als je (c) hebt dan is (d) makkelijk, maar ik had (c) dus eerst fout gedaan.
E(max{A,B,C} | A<B<C) = E(C | A<B<C) = ??
Ik weet niet hoe ik dat kan vertalen in iets met verwachtingswaardes. Intuïtief zou ik denken dat E(X | X>t) = E(X) + t maar ik weet niet of dit klopt.
E(C | A<B<C) = E(C | A<C, B<C, A<B) = E(C | A<C, B<C) = E(C | A<C) + B = E(C) + A + B.
Maar daar gaat ook weer iets mis want vanwege de law of total expectation: E(C) = E(C) + E(A) + E(B).
n de gemiddelde levensduur (in uren) van gloeilampen met een betrouwbaarheid
van 95% schatten waarbij de totale lengte van het betrouwbaarheidsinterval niet
groter mag zijn dan 20 uur. Uit eerdere onderzoeken is reeds bekend dat de standaardafwijking
van de levensduren bij lampen van dit type gelijk is aan 60 uur.
De steekproefomvang n die voor dit schattingsprobleem nodig is, is gelijk aan:
______ (numerieke waarde).
het antwoord is 139.
weet iemand hoe je aan komt?
bvb
Ik heb de volgende functie: f(x,y)=x^½ y^⅕
Waarbij x≥0 en y≥0. Verder heb ik de constraint 3x+4y=11.
Je krijgt nu dus:
x^½ y^⅕ - λ(3x+4y-11)=0
F'(x)=0.5x^-0.5 y^0.2 -3λ
F'(y)=0.2y^-0.8 x^0.5 -4λ
Hoe verder?
F'(x)=0.5x^-0.5 y^0.2 -3λ = 0 en F'(y)=0.2y^-0.8 x^0.5 -4λ = 0 stellen,quote:Op zondag 4 december 2011 15:58 schreef TJV het volgende:
Hmm, zit wat te lezen over de Lagrangemultiplier maar snap er niet veel van.
Ik heb de volgende functie: f(x,y)=x^½ y^⅕
Waarbij x≥0 en y≥0. Verder heb ik de constraint 3x+4y=11.
Je krijgt nu dus:
x^½ y^⅕ - λ(3x+4y-11)=0
F'(x)=0.5x^-0.5 y^0.2 -3λ
F'(y)=0.2y^-0.8 x^0.5 -4λ
Hoe verder?
dan beiden in labdaa uitdrukken en dat aan elkaar gelijk stellen.
Dit oplossen in x = iets met y.
Die x of y invullen in de restrictie en daar is je oplossing.
http://www.wolframalpha.com/input/?i=max+x^0.5y^0.2+%2C+3x%2B4y%3D11
[ Bericht 4% gewijzigd door Fingon op 04-12-2011 16:55:35 ]
Ik kom bij F'(x) tot x^-0.5=-2y^-0.2 +6λ, klopt dat? Volgens mij doe ik iets ongelofelijk fout.quote:
[..]
F'(x)=0.5x^-0.5 y^0.2 -3λ = 0 en F'(y)=0.2y^-0.8 x^0.5 -4λ = 0 stellen,
dan beiden in labdaa uitdrukken en dat aan elkaar gelijk stellen.
Dit oplossen in x = iets met y.
Die x of y invullen in de restrictie en daar is je oplossing.
Als je die 2(F'(x) en F'(y) ) aan elkaar gelijk stelt zou eruit moeten komen y = 3x/10quote:
[..]
Ik kom bij F'(x) tot x^-0.5=-2y^-0.2 +6λ, klopt dat? Volgens mij doe ik iets ongelofelijk fout.
F'(x)=0.5x^-0.5 y^0.2 -3λ = 0 => λ = (1/6)*x^-0.5 y^0.2
F'(y)=0.2y^-0.8 x^0.5 -4λ = 0 => λ = (1/20)*y^-0.8 x^0.5
F'(λ) = -3x - 4y +11 = 0
Deze drie oplossen.
[ Bericht 5% gewijzigd door Fingon op 04-12-2011 17:03:50 ]
Nee, dat krijg je niet. Je definieert m.b.v. de Lagrange multiplier een Lagrange functie van drie je variabelen x,y, λ, als volgt:quote:
Hmm, zit wat te lezen over de Lagrangemultiplier maar snap er niet veel van.
Ik heb de volgende functie: f(x,y)=x^½ y^⅕
Waarbij x≥0 en y≥0. Verder heb ik de constraint 3x+4y=11.
Je krijgt nu dus:
x^½ y^⅕ - λ(3x+4y-11)=0
L(x,y,λ) = x½ y⅕ - λ(3x+4y-11)
Vervolgens moeten de drie partiële afgeleiden van deze functie naar x,y en λ nul zijn, wat dus drie vergelijkingen in drie onbekenden oplevert. Het is niet zo dat de functiewaarde zelf nul zou moeten zijn zoals jij beweert. Kijk even hier.
Bekende sigma, dusquote:
De ‘quality control manager’ wil op basis van een aselecte steekproef van omvang
n de gemiddelde levensduur (in uren) van gloeilampen met een betrouwbaarheid
van 95% schatten waarbij de totale lengte van het betrouwbaarheidsinterval niet
groter mag zijn dan 20 uur. Uit eerdere onderzoeken is reeds bekend dat de standaardafwijking
van de levensduren bij lampen van dit type gelijk is aan 60 uur.
De steekproefomvang n die voor dit schattingsprobleem nodig is, is gelijk aan:
______ (numerieke waarde).
het antwoord is 139.
weet iemand hoe je aan komt?
bvb
De lengte van dat interval is
Aha, snappie. Riparius ook bedankt. Nog eentje voor de checkcheckdubbelcheck?quote:
[..]
Als je die 2(F'(x) en F'(y) ) aan elkaar gelijk stelt zou eruit moeten komen y = 3x/10
F'(x)=0.5x^-0.5 y^0.2 -3λ = 0 => λ = (1/6)*x^-0.5 y^0.2
F'(y)=0.2y^-0.8 x^0.5 -4λ = 0 => λ = (1/20)*y^-0.8 x^0.5
F'(λ) = -3x - 4y +11 = 0
Deze drie oplossen.
C(x,y)=4x^2+4y^2+4xy+4 en de constraint=x+y=6
F'x=8x+4y-λ --> λ=8x+4y
F'y=8y=4x-λ --> λ=8y+4x
Klopt dat? Dat zou betekenen dat x=y en dan snap ik het niet meer.
Ok, we hebben gevonden dat x=y=3. Blij dat ik al zover kom, maar het antwoord heeft te maken met de shadow price. In mijn boek staat een uitleg waar ik niet uitkom, hoe reken ik dat kreng uit?
Hmm, ik lees dat de schaduwprijs de waarde van lambda is in het optimale punt. invoeren in bijvoorbeeld F'x geeft dan 36, klopt dat?SPOILERHele som is als volgt overigens:
A company produces x units of product A and y units of product B. The products are sold at prices pA=28 and pB=22. The total costs are given by
C(x,y)=4x^2+4y^2+4xy+4
Calculate the shadow price of the resources, given
x+y=6
[ Bericht 4% gewijzigd door TJV op 04-12-2011 17:33:17 ]
Waarom moet je delen door wortel 12 om de standaarddeviatie te krijgen? Dit kwam ik meerdere keren tegen, maar ik heb nergens gezien waarom dat zo is.
bedankt.
En de variantie is (b-a)² / 12. Dat kan je makkelijk bepalen met een momentgenererende functie.quote:
Omdat de standaarddeviatie de wortel van de variantie is.
Ok, maar ik bedoelde eigenlijk waarom "12".quote:
Omdat de standaarddeviatie de wortel van de variantie is.
Hoe zou jij de variantie willen uitrekenen?quote:
[..]
Ok, maar ik bedoelde eigenlijk waarom "12".
Ongelooflijk, wat een post! Hartelijk, hartelijk, hartelijk, hartelijk, hartelijk dank!!!! Ik stel het enorm op prijs en het heeft erg veel geholpen. Ik heb het zojuist goed bestudeerd en dingen goed in m'n gedachten voorgesteld. Ik heb het voor de zekerheid ook uitgeprint en als aantekening in m'n mapje gestopt. Je uitleg is uitstekend! Hartelijk dank voor de tijd en moeite!quote:
Je hebt tevens een grote interesse bij me opgewekt in complexe getallen. Ik kan het overgrote deel van je uitleg goed volgen als ik er goed voor ga zitten, maar ik merk dat ik oefening nodig heb om snel en goed met het onderwerp overweg te kunnen.
Ik zit er daarom aan te denken een boek aan te schaffen die specifiek over complexe getallen gaat en deze van het begin tot in de diepte behandeld, aangevuld met vele oefeningen.
Ken jij wellicht boeken over dit onderwerp die de theorie goed uitleggen en voldoende oefeningen/opgaven bevatten? (taal gaat bij voorkeur uit naar Engels, maar Nederlands is ook goed
). (Ik moet het echter volledig met zelfstudie doen, dus hoe gemakkelijker het boek te volgen is, des te beter. Het moet echter wel een universitaire boek zijn).Ik vind het knap dat je zoveel over het onderwerp weet! Ik wou dat ik ook je kennis had!
Studeer je wellicht wiskunde?Nogmaals hartelijk dank voor je zeer uitgebreide uitleg!
Misschien heb je hier wat aan: http://www.numbertheory.org/book/cha5.pdfquote:
quote:
[..]
Hoe zou jij de variantie willen uitrekenen?
Zo heb ik het gedaan. Ik ben nu een oefenboek aan het doorbladeren voor mijn tentamen, en een vergelijkbare opgave kwam ook nog eens voor:
Hier weer delen door wortel 12. Mij is echter totaal niet duidelijk waarom je dat doet (waarschijnlijk kom ik een of andere kennis tekort) of dit is een vaste formule
Ten eerste klopt die n-1 niet, dat moet een n zijn. Maar in dit geval hebben we niet eens een n. We hebben een continue stochast. Een integraal is dus op z'n plaats hier.quote:
[..]
[ afbeelding ]
Zo heb ik het gedaan. Ik ben nu een oefenboek aan het doorbladeren voor mijn tentamen, en een vergelijkbare opgave kwam ook nog eens voor:
[ afbeelding ]
Hier weer delen door wortel 12. Mij is echter totaal niet duidelijk waarom je dat doet (waarschijnlijk kom ik een of andere kennis tekort) of dit is een vaste formule
Oh ja bedankt, natuurlijk, dit is een continue variabelequote:
[..]
Ten eerste klopt die n-1 niet, dat moet een n zijn. Maar in dit geval hebben we niet eens een n. We hebben een continue stochast. Een integraal is dus op z'n plaats hier.
Maar waarom is het niet n-1 voor die formule van variantie? In al mijn boeken wordt n-1 gebruikt en niet n.
mensen die het verschil niet inzien tussen kansrekening en statistiekquote:
Het is toegestaan om een onderscheid te maken tussen s en sigma. De definitie daar is die van s. Voor sigma is een hele andere definitie, namelijk...
Als U ~ Uniform(a,b), danquote:
[..]
[ afbeelding ]
Zo heb ik het gedaan. Ik ben nu een oefenboek aan het doorbladeren voor mijn tentamen, en een vergelijkbare opgave kwam ook nog eens voor:
[ afbeelding ]
Hier weer delen door wortel 12. Mij is echter totaal niet duidelijk waarom je dat doet (waarschijnlijk kom ik een of andere kennis tekort) of dit is een vaste formule
Nu jij weer.
TE bepalen zoals hierboven getoond of kijk hier even bij moment-generating functions voor een andere manier.
Ik heb zelf ook nog een vraagje: Is deze Ito integraal correct berekend? (Bs is de Brownian motion).
Thanks, dan snap ik nu hoe hij in elkaar steekt.quote:
Hoe pak ik dit aan?
Ik begrijp niet wat je hier doet. Als B een functie is van s kun je ∫0t[B(s)]2∙dB schrijven als ∫0t[B(s)]2∙(dB/ds)∙ds = ∫0t[B(s)]2∙B'(s)∙ds, dus wat krijg je dan?quote:
Ik heb zelf ook nog een vraagje: Is deze Ito integraal correct berekend? (Bs is de Brownian motion).
[ afbeelding ]
Hoe zijn de begrippen 'taal' en L-formule bij jou gedefinieerd?quote:
Zij L een taal. Laat zien dat de cardinaliteit van {L-formules} gelijk aan max{ omega, |L|}.
Hoe pak ik dit aan?
B is ook een functie van omega, dus dat gaat niet op.quote:
[..]
Ik begrijp niet wat je hier doet. Als B een functie is van s kun je ∫0t[B(s)]2∙dB schrijven als ∫0t[B(s)]2∙(dB/ds)∙ds = ∫0t[B(s)]2∙B'(s)∙ds, dus wat krijg je dan?
Een taal bestaat uit constantes, functiesymbolen en relatiesymbolen.quote:
[..]
Hoe zijn de begrippen 'taal' en L-formule bij jou gedefinieerd?
Een L-formule is inductief gedefinieerd:
- (t=s) is een L-formule als t en s termen van L zijn
- R(t1,...,tn) is een L-formule als t1,...,tn termen zijn
- "vals" is een formule
- L-formules zijn gesloten onder implicatie, negatie, conjunctie, disjunctie en kwantificatie
Termen zijn constantes, variabelen, of functies van termen.
Ja, dat mag denk ik wel. Een formule is een rij symbolen; twee verschillende rijen symbolen definiëren twee verschillende formules.quote:
Ah dat is wel eenvoudig. Ik weet alleen niet of je vals /\ ... /\ vals als een andere formule kunt zien als vals... ze zijn immers equivalent.
Ik heb zelf ook een probleem waar ik niet uitkom. Als iemand me een zetje in de goede richting kan geven zou ik dat zeer op prijs stellen.
Gegeven is een functie
en een functiequote:f(a, x) = x5 + ax = y
Nu moet het mogelijk zijn om met de kettingregel de partiële afgeleiden van g te bepalen, gegeven dat g differentieerbaar is. Mijn plan was omquote:g(a, y) = x
op stellen, zodatquote:f2(a, x) = (a, x5) = (a, y)
En dan beide kanten te differentiëren en de linkerkant uit te werken met de kettingregel. Dit werkt echter niet omdat ik aan de linkerkant een rijvector krijgquote:g(f2(a, x)) = x
(het laatste is het product van een 1x2 matrix en een 2x2 matrix, wat als ik het goed heb weer een 1x2 matrix oplevert)quote:Dg(f(a, x)) = Dg(a, y)Df(a, x)
en aan de rechterkant een getal (of 1x1 matrix, als je wil):
Volgens mij is deze laatste stap trouwens niet correct (bijvoorbeeld omdat het niet duidelijk is waarvan ik precies de afgeleide neem over deze x, dus ik denk niet dat ik zomaar Dx = 1 mag stellen), maar dit was het enige wat ik kon bedenken.quote:Dx = 1
Baas! Ik moest even denken, maar nu valt alles op zijn plek. Zo simpel... Ik heb me er een beetje op zitten doodstaren! Super bedanktquote:
Je hebt. Differentieer nu beide kanten naar y.
(ik voel me vaak na een vraag in dit topic erg stom, en dit is geen uitzondering
)y*(dy/dx) = (d/dx)*(y2/2)
Kan iemand uitleggen waarom?
d/dx (y(x))² = 2y(x) * y'(x)
Ja vanaf die kant ben ik er nog niet uit, als je echter vanaf de andere kant werkt:quote:
Over je edit, integreren geeft (1/dx)*(y2/2)
d/dx 0.5y^2 = d/dy dy/dx 0.5y^2 = d(0.5y^2)/dy*dy/dx = y*dy/dx
Oh ja, stom. Zo is het wel duidelijk, maar andersom vind ik 't lastig om te zien.quote:
Dat is de kettingregel:
d/dx (y(x))² = 2y(x) * y'(x)
Bedankt. Goede tip.quote:
Var(Uniform) = (b-a)^2 / 12 dus Std = sqrt(Var) = b-a/12
TE bepalen zoals hierboven getoond of kijk hier even bij moment-generating functions voor een andere manier.
Ook bedankt, maar aangezien dit tentamen van mij, geloof het of niet, non-calculus is, ga ik er nu even niet op in (ik zit ook even niet in deze stof).quote:
[..]
Als U ~ Uniform(a,b), dan
Nu jij weer.
Klopt dit wel?quote:Conclusie: Based on the sample, you can be 90% confident that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
Verderop in het boek wordt namelijk gesteld:
Waarschijnlijk lees ik iets niet goed, maar zijn deze beweringen niet met elkaar in tegenspraak?quote:Let a and b represent the lower and upper boundaries of the 90% confidence
interval for the mean of the population. Is it correct to conclude that there is a
90% probability the true population mean lies between a and b? Explain your
answer.
A confidence interval does not describe the probability that any particular
interval constructed around the mean of a single sample will contain the actual
population mean. In this problem, it would be inaccurate to state that there is
a 90% probability the interval bounded below by a and above by b contains the
population mean.
De tekst in het tweede rondje klopt niet. Ze ronden daar af op 3 decimalen. Kijk je naar het vierde decimaal, zie je dat 1,64 de juiste afronding is op twee decimalen. Bedenk wel dat je door afronden geen echt 90% CI meer hebt.
Volgens mij bedoelen ze een wel heel subtiel verschil. Er is een kans van 90% dat een gevonden interval de ware E bevat. Er is geen kans van 90% dat het gevonden interval de ware E bevat.
Textueel gezien merk ik dat nu ook op. Toch knaagt er nog iets. Ik vind het verschil tussen deze twee opties niet helemaal overtuigend nog:quote:
Ik concludeer er zelf uit dat 'confidence' iets anders is dan 'probability'.
Based on the sample, you can be 90% confident that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
en
Based on the sample, there is a 90% probability that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
Het komt bij mij toch hetzelfde over. Als je zegt dat je ergens "zeker" over bent, dan impliceer je daarmee een bepaalde kans. Het kan natuurlijk ook zo zijn dat ik normaal taalgebruik en statisch taalgebruik door elkaar haal.
Maar als je dan een willekeurige steekproef daarvan neemt, dan is er toch een kans van 90% dat de ware mean daarin zit?quote:
Een 90% CI voor de mean is iets wat als je het 100 keer zou construeren op basis van 100 aselecte steekproeven, hij naar verwachting 90 keer de ware mean bevat.
Op wikipedia staat ook
enquote:A confidence interval does not predict that the true value of the parameter has a particular probability of being in the confidence interval given the data actually obtained.
Maar wat klopt er dan niet aan mijn beredenering?quote:A confidence interval with a particular confidence level is intended to give the assurance that, if the statistical model is correct, then taken over all the data that might have been obtained, the procedure for constructing the interval would deliver a confidence interval that included the true value of the parameter the proportion of the time set by the confidence level.
Om even mijn eigen vraag te beantwoorden. Wat er niet klopt aan mijn beredenering is dat je niet zomaar een willekeurige steekproef hebt, maar je hebt de steekproef waarmee je de CI berekend hebt. Ik denk dat het daar mis gaat.quote:
[..]
Maar wat klopt er dan niet aan mijn beredenering?
Het is allemaal heel subtiel. Ik vergelijk het met een dobbelsteen die je hebt gegooid maar waarvan je de ogen nog niet hebt gezien. Dan kun je niet meer zeggen dat de kans dat de 1 boven ligt 1/6de is.quote:
[..]
Maar als je dan een willekeurige steekproef daarvan neemt, dan is er toch een kans van 90% dat de ware mean daarin zit?
Dat het subtiel is is duidelijk, maar ik kan er nog steeds niet helemaal de vinger op leggen waarom het zo is.quote:
[..]
Het is allemaal heel subtiel. Ik vergelijk het met een dobbelsteen die je hebt gegooid maar waarvan je de ogen nog niet hebt gezien. Dan kun je niet meer zeggen dat de kans dat de 1 boven ligt 1/6de is.
Dat van die dobbelsteen snap ik wel. Als je hem gegooid hebt dan heeft ie een bepaalde waarde aangenomen in {1,...,6}. De waarde die hij aan heeft genomen heeft ie dus met kans 1 en de rest met kans 0. Als je gaat kijken (zonder voorkennis) heb je echter wel een kans van 1/6 dat je die 1 aantreft.
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
Volgens mij heeft het te maken met een misvatting die heerst. Zo denken mensen dat de kans op kop of munt met een eerlijke munt gelijk is aan respectievelijk 0.5 en 0.5. Toch is de kans slechts bij benadering 0.5 bij een heel groot aantal worpen, bijvoorbeeld 10.000. Zelfs dan zie je dat de proportie niet gelijk is aan 0.5.quote:
[..]
Als je gaat kijken (zonder voorkennis) heb je echter wel een kans van 1/6 dat je die 1 aantreft.
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
quote:4.3 Many tosses of a coin. The French naturalist Count Buffon (1707
1788) tossed a coin 4040 times. Result: 2048 heads, or proportion 2048/4040 =
0.5069 for heads.
Around 1900, the English statistician Karl Pearson heroically tossed a coin
24,000 times. Result: 12,012 heads, a proportion of 0.5005.
While imprisoned by the Germans duringWorldWar II, the South African
statistician John Kerrich tossed a coin 10,000 times. Result: 5067 heads, proportion
of heads 0.5067.
quote:Probability describes only what happens in the long
run. Most people expect chance outcomes to show more short-term regularity
than is actually true.
Introduction to the Practice of Statistics, p.238.
Het heeft ermee te maken dat als je het CI eenmaal hebt geconstrueerd, er geen kans meer aan te pas komt om de vraag te beantwoorden of hij de ware parameter bevat. Hij zit erin of hij zit er niet in.quote:
[..]
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
Dit bevestigt toch gewoon dat er variantie bestaat?quote:
[..]
Volgens mij heeft het te maken met een misvatting die heerst. Zo denken mensen dat de kans op kop of munt met een eerlijke munt gelijk is aan respectievelijk 0.5 en 0.5. Toch is de kans slechts bij benadering 0.5 bij een heel groot aantal worpen, bijvoorbeeld 10.000. Zelfs dan zie je dat de proportie niet gelijk is aan 0.5.
[..]
[..]
Ik snap nu de analogie. De parameter zit er inderdaad wel in met kans 1 of niet in met kans 1.quote:
[..]
Het heeft ermee te maken dat als je het CI eenmaal hebt geconstrueerd, er geen kans meer aan te pas komt om de vraag te beantwoorden of hij de ware parameter bevat. Hij zit erin of hij zit er niet in.
Net alsof je een muntje gooit in een afgesloten doos en je niets binnen die doos kan waarnemen. Als je dan het muntje gegooid hebt dan kan je niet meer spreken over 50% kans dat de munt kop is. Maar voor iemand die niet kan waarnemen hoe de munt is gevallen is op dat moment de kans wel 50% dat het kop zal blijken te zijn als je die doos open maakt. Zo is het volgens mij ook voor CI's: zolang je de werkelijke parameter niet kan waarnemen is de kans x % dat die parameter erin zal zitten op het moment dat je die parameter wel zou kunnen waarnemen.
Dus ik zie nog steeds niet waarom:
quote:A confidence interval does not predict that the true value of the parameter has a particular probability of being in the confidence interval given the data actually obtained.
Dit is de vraag. Nu is mijn vraag, welke formules (verdelingen) moet ik hiervoor gebruiken om het op te lossen?
Bij zo'n grote trekking en een redelijke kans ga je gewoon normaal benaderen. Laat X het aantal mensen zijn dat niet komt opdagen. X heeft verwachte waarde 215*0.12=25.8 en variantie 215*0.12*0.88=22.7. Dus als n groot is, heeft
Nu willen we weten de kans dat X<15. Met een correctie voor continuïteit wordt dit bij een normale benadering X<15.5.
Warren kraamt onzin uit. De kans dat je kop, danwel munt gooit is wel degelijk 0.5 bij een eerlijke munt. Dat je na 10000 worpen niet precies 5000x kop en 5000x munt hebt is weer een ander verhaal. Een kansexperiment geeft namelijk niet altijd de verwachtingswaarde, er bestaat ook nog zoiets als variantie..
Ja klopt, maar ik zag dat te laat. Sorry daarvoorquote:
Dat was al gezegd, en als je je adblocker uitzet dan kun je ook weer quoten.
, maar ook editten ging niet met adblocker aan.bedankt voor de tip!
Ik wilde het aan iemand uitleggen maar dat ging lastig.
Als het gemiddelde van een steekproef 30 is, wat zegt dat nu?
Het is enkel een theoretisch hulpmiddel om een beter beeld te krijgen hoe, in dit geval, de steekproef er ongeveer uit ziet toch?
Heeft iemand een mooie definitie voor het gemiddelde?
De eerste deelvraag is het berekenen van het aantal elementen in de verzameling
Het tweede deel vind ik lastiger: "Hoeveel elementen van orde 7 zijn er in
Ik weet wel wat de orde van n betekent (het aantal elementen dat je passeert wanneer je steeds n steeds verheft tot een hogere macht voordat je n weer bereikt, modulo 175), maar ik zie (naast brute force alle banen uitschrijven) geen handige manier om tot een antwoord te komen. Toch staan er voor zowel a als b 2 punten, dus kan het niet veel lastiger zijn dan de het berekenen van de Euler totient van 175, als in a.
[ Bericht 1% gewijzigd door Djoezt op 10-12-2011 21:10:27 ]
http://www.google.com/?q=definitie+gemiddeldequote:
Hele domme vraag, maar hoe zou je het "Gemiddelde" kunnen omschrijven?
Ik wilde het aan iemand uitleggen maar dat ging lastig.
Als het gemiddelde van een steekproef 30 is, wat zegt dat nu?
Het is enkel een theoretisch hulpmiddel om een beter beeld te krijgen hoe, in dit geval, de steekproef er ongeveer uit ziet toch?
Heeft iemand een mooie definitie voor het gemiddelde?
[ Bericht 1% gewijzigd door GlowMouse op 10-12-2011 21:07:50 ]
De orde van een element is altijd een deler van de orde van de groep.quote:
Een vraag over modulorekenen en groepen etc.
De eerste deelvraag is het berekenen van het aantal elementen in de verzameling- dit lukt me aardig (want
Het tweede deel vind ik lastiger: "Hoeveel elementen van orde 7 zijn er in?" Ik heb werkelijk geen flauw idee waar ik moet beginnen. Is er een formule die ik mis of over het hoofd heb gezien? Heeft iemand een tip?
Ik weet wel wat de orde van n betekent (het aantal elementen dat je passeert wanneer je steeds n steeds verheft tot een hogere macht voordat je n weer bereikt, modulo 175), maar ik zie (naast brute force alle banen uitschrijven) geen handige manier om tot een antwoord te komen. Toch staan er voor zowel a als b 2 punten, dus kan het niet veel lastiger zijn dan de het berekenen van de Euler totient van 175, als in a.
Dus de orde moet een deler zijn van 175, en aangezien 7 dat niet is zijn er geen elementen die orde 7 hebben? Oke!quote:
[..]
De orde van een element is altijd een deler van de orde van de groep.
Kan je verklaren waarom de orde van een elementen een deler moet zijn van de orde van de groep?
Nee, van 120.quote:
[..]
Dus de orde moet een deler zijn van 175?
Oke - waar komt dat uit voort?quote:
Ja, sorry daarvoor nog.quote:
Ik wil Warren quoten, maar blijkbaar wil de quoteknop dat niet, enfin:
Warren kraamt onzin uit. De kans dat je kop, danwel munt gooit is wel degelijk 0.5 bij een eerlijke munt. Dat je na 10000 worpen niet precies 5000x kop en 5000x munt hebt is weer een ander verhaal. Een kansexperiment geeft namelijk niet altijd de verwachtingswaarde, er bestaat ook nog zoiets als variantie..
Nog even een vraagje:
Het antwoord volgens het antwoordenmodel is c, maar volgens mij is het d.quote:10. Een bepaalde test is zodanig genormaliseerd dat het gemiddelde 100 is; de
populatievariantie is niet bekend. In een steekproef van 31 personen vinden
we een gemiddelde van 103; de standaarddeviatie is 6.28. We onderzoeken
de vraag of de personen uit een populatie afkomstig zijn met een gemiddelde
groter dan 100. Wat is het resultaat van de toets (geef het beste antwoord)?
a. We kunnen H0 niet verwerpen.
b. We kunnen H0 verwerpen met alfa = 0.05
c. We kunnen H0 verwerpen met alfa = 0.02
d. We kunnen H0 verwerpen met alfa = 0.01
Als ik de t-waarde opzoek bij 30 vrijheidsgraden bij een tail probability van 0.01 dan kom ik uit op 2.457.
t103 =
Daarnaast is de vraag slecht gesteld omdat je alpha kiest voordat je de toetsing uitvoert.
Je hebt gelijk, maar het komt uit een oud-tentamen, dus hier moet ik het helaas mee doen. Gezien het feit dat alleen de normale verdeling behandeld is, komt dit uit een normale verdeling.quote:
e. Dit kun je niet zeggen omdat je de onderliggende kansverdeling niet kent.
Daarnaast is de vraag slecht gesteld omdat je alpha kiest voordat je de toetsing uitvoert.
een normalisatie heeft niets met een normale verdeling te makenquote:
Eerste zin: een bepaalde test is [..] genormaliseerd. Dus een normale verdeling.
maar je doet alsof je ook de t-verdeling kentquote:
[..]
Je hebt gelijk, maar het komt uit een oud-tentamen, dus hier moet ik het helaas mee doen. Gezien het feit dat alleen de normale verdeling behandeld is, komt dit uit een normale verdeling.
Ik heb in mijn boek gelezen dat ik de t-verdeling kan gebruiken als de populatievariantie niet bekend is, en dat de steekproef uit 30 of minder personen bestaat.quote:
maar je doet alsof je ook de t-verdeling kent
Die is wel bekend; de standaarddeviatie is 6.28 staat in de opdracht.quote:
[..]
Ik heb in mijn boek gelezen dat ik de t-verdeling kan gebruiken als de populatievariantie niet bekend is, en dat de steekproef uit 30 of minder personen bestaat.
Dat is de STD van de steekproef. In de vraag staat "de populatievariantie is niet bekend. "quote:
[..]
Die is wel bekend; de standaarddeviatie is 6.28 staat in de opdracht.
Dank!quote:
. Of ja, nooit is overdreven, maar het huiswerk was 95% calculus.Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde puntenquote:
Prachtig, tentamen analyse bestaat voor 50% uit bewijzen, en we hebben nog nooit een bewijsopgave hoeven doen
en de 2e formulequote:The equation of a plane (points P are on the plane with normal N and point P3 on the plane) can be written as N dot (P - P3) = 0
The equation of the line (points P on the line passing through points P1 and P2) can be written as
P = P1 + u (P2 - P1)
The intersection of these two occurs when
N dot (P1 + u (P2 - P1)) = N dot P3
quote:A plane can also be represented by the equation
A x + B y + C z + D = 0
where all points (x,y,z) lie on the plane.
Substituting in the equation of the line through points P1 (x1,y1,z1) and P2 (x2,y2,z2)
P = P1 + u (P2 - P1)
gives
A (x1 + u (x2 - x1)) + B (y1 + u (y2 - y1)) + C (z1 + u (z2 - z1)) + D = 0
dus de vergelijking
De tweede formule is in feite hetzelfde, want
Voorbeeldje: stel dat je weet dat het punt (1,2,3) in het vlak ligt, en dat (4,5,6) een normaalvector van het vlak is. De vectoren die nu in het vlak liggen zijn de vectoren x=(x,y,z) die voldoen aan
Maar dit is alleen waar als de normaalvector mooi bij de oorsprong het vlak snijdt. Als het vlak niet door de oorsprong gaat, maar wel door het punt (1,2,3) zijn de vectoren x eigenlijk x=(x-1,y-2,z-3). De vectoren zijn dan namelijk het verschil tussen een punt in het vlak en het punt dat zeker in het vlak ligt.
Dan krijg je 4(x-1)+5(y-2)+6(z-3)=0, dus 4x+5y+6z=32.
Wat zijn dit voor rechtenpraktijken.quote:
[..]
Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde punten
Begin eens je quotes wat leesbaarder en correcter op te schrijven. En uit je vraagstelling proef ik een beetje dat je vooral een 'recept' wil hebben. Als je nu maar weet hoe je die formules in moet vullen dan ben je kennelijk tevreden. Maar dat is niet goed. Je moet begrijpen waarom die formules zijn zoals ze zijn en wat ze (meetkundig) voorstellen.quote:
Ben dus met wiskunde bezig. En nu heb ik een tweetal formules gekregen om een vector door een vlak te bereken. Echter snap ik niet helemaal hoe deze formules te gebruiken. Zou iemand misschien de formule in kunnen vullen met een voorbeeld zodat ik dit als referentie kan gebruiken? Bedankt alvast!
[..]
en de 2e formule
[..]
Eerste quote:
De vectorvergelijking van het bedoelde vlak V door punt P3 en loodrecht op vector n is:quote:The equation of a plane (points P are on the plane with normal N and point P3 on the plane) can be written as N dot (P - P3) = 0
The equation of the line (points P on the line passing through points P1 and P2) can be written as
P = P1 + u (P2 - P1)
The intersection of these two occurs when
N dot (P1 + u (P2 - P1)) = N dot P3
(1) V: n∙(p - p3) = 0
Hierbij stelt het eindpunt P van vector OP = p een willekeurig punt in het vlak V voor. Het is gemakkelijk in te zien waarom dit een vectorvoorstelling van het betreffende vlak is: als P in het vlak ligt, evenals het vaste punt P3, dan is de verschilvector OP - OP3 = p - p3 parallel aan lijnstuk PP3 in het vlak V, zodat deze verschilvector loodrecht op vector n staat en het inproduct van n en p - p3 dus gelijk is aan 0.
Tweede quote:
Om dit te begrijpen moet je weten hoe je de vectorvoorstelling (1) van een vlak V omzet in een vergelijking in cartesische coördinaten. Stel dat we hebben:quote:A plane can also be represented by the equation
A x + B y + C z + D = 0
where all points (x,y,z) lie on the plane.
Substituting in the equation of the line through points P1 (x1,y1,z1) and P2 (x2,y2,z2)
P = P1 + u (P2 - P1)
gives
A (x1 + u (x2 - x1)) + B (y1 + u (y2 - y1)) + C (z1 + u (z2 - z1)) + D = 0
(2) n = (a,b,c)
en:
(3) p3 = (x3,y3,z3)
en zij p = (x,y,z) weer de variabele vector. Dan volgt uit (1) dat het inproduct van n en p - p3 voor elke vector p = (x,y,z) met eindpunt in het betreffende vlak nul moet zijn, en dus:
(4) V: a(x - x3) + b(y - y3) + c(z - z3) = 0
Door het uitwerken van de haakjes breng je deze cartesische vergelijking voor het vlak V gemakkelijk in de standaardvorm:
(5) V: ax + by + cz + d = 0
Voor een lijn l door de punten P1 en P2 hebben we met de vaste vectoren OP1 = p1 en OP2 = p2 een vectorvoorstelling:
(6) l: p = p1 + μ∙(p2 - p1)
waarbij μ de verzameling reële getallen doorloopt. Ook dit is weer eenvoudig in te zien. Aangezien P1 en P2 op l liggen, is de verschilvector p2 - p1 parallel aan lijn l, zodat l': p = μ∙(p2 - p1) een vectorvoorstelling is van een lijn l' door de oorsprong en parallel aan l. Tellen we de vaste vector p1 hierbij op (hetgeen resulteert in een translatie langs lijnstuk OP1) dan krijgen we dus alle vectoren waarvan de eindpunten op lijn l liggen aangezien O op l' ligt en P1 op l ligt terwijl l' parallel is aan l. Schrijven we nu (6) in coördinaatvorm, dan hebben we:
(7) l: (x,y,z) = (x1 + μ(x2-x1), y1 + μ(y2-y1), z1 + μ(z2-z1))
Dit levert dus het volgende stelsel:
(8a) x = x1 + μ(x2-x1)
(8b) y = y1 + μ(y2-y1)
(8c) z = z1 + μ(z2-z1)
Substitutie van (8a), (8b) en (8c) in de cartesische vergelijking (5) van vlak V levert een lineaire vergelijking in μ op, die ons dus vertelt voor welke waarde van μ lijn l vlak V snijdt (als althans lijn l niet evenwijdig loopt aan vlak V of in vlak V ligt). Door terugsubstitueren van de aldus gevonden waarde van μ in (8a), (8b) en (8c) verkrijgen we dan de cartesische coördinaten van het snijpunt van lijn l met vlak V.
[ Bericht 0% gewijzigd door Riparius op 13-12-2011 07:29:19 ]
Herkauwen is iets voor koeien. En stamppot hoef je al helemaal niet te kauwen.quote:
[..]
Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde punten
"Er wordt gevraagd om de definitie van de definitie van de limiet waarbij x van boven d nadert voor de functie h(u), met de limiet R."
Dus lim h(u)=R (voor x->d+)
Alleen h is geen functie van x, dus moet die x geen u zijn?
[ Bericht 9% gewijzigd door Physics op 15-12-2011 17:01:45 ]
Als R een element is van de reële getallen, is h geen functie.quote:
Gegeven h: R->R en d,R elementen van de reële getallen.
Laat (an) de rij zijn met an de som van 1 naar n van (-1)k+1 ck.
Dan heb ik de volgende vragen:
1) De rij cn kan toch ook een nulrij zijn of uitkomen op een nulrij?
2) Is (an) een Cauchy-rij? En hoe kan ik dat bewijzen?
Ik had verkeerd gelezen, er stond d,R elementen van R met h:R->Rquote:
[..]
Als R een element is van de reële getallen, is h geen functie.
Lijkt me dat ze bedoelen lim h(x)=R (voor x->d+), anders is het niet zo'n spannende limietquote:
Gegeven h: R->R en d,R elementen van R.
"Er wordt gevraagd om de definitie van de definitie van de limiet waarbij x van boven d nadert voor de functie h(u), met de limiet R."
Dus lim h(u)=R (voor x->d+)
Alleen h is geen functie van x, dus moet die x geen u zijn?
.1) Het is toch gegeven dat (cn) een nulrij is?quote:
Gegeven (cn), een nulrij die dalend is.
Laat (an) de rij zijn met an de som van 1 naar n van (-1)k+1 ck.
Dan heb ik de volgende vragen:
1) De rij cn kan toch ook een nulrij zijn of uitkomen op een nulrij?
2) Is (an) een Cauchy-rij? En hoe kan ik dat bewijzen?
2)
Als j oneven is
Controleer dit even. Als het klopt moet je het hiermee kunnen bewijzen.
Ik heb een vraagje over kansrekening, waar ik niet uitkwam. Je hebt 500 appels waarvan er 10 rot zijn. De appels verdeel je over 20 dozen van elk 25 appels. Hoe groot is de kans dat je een doos kiest waarin geen enkele rotte appel zit?
Nu vond ik als antwoord (490 nCr 25)/(500 nCr 25). Dus het aantal mogelijkheden om 25 appels te kiezen uit de gave appels gedeeld door het totaal aantal mogelijkheden om 25 appels te kiezen uit de 500 appels. Dat betekent dus dat een doos vullen op een willekeurige manier gelijk staat aan één doos kiezen, maar ik zie niet waarom dat zo is. Is er iemand die mij dat helder kan uitleggen, misschien aan de hand van vergelijkingen?
(1) Beide zijden differentiëren naar x
F'=f=(lnt)^3
(2) d/dx (F(x^2+x)-F(x^2-x))
(3) f'(x)=ln(x^2+x)^3(2x+1)-(ln(x^2-x)^3(2x-1)
Klopt dat?
Ja. Je maakt in feite gebruik van een variant van de regel van Leibniz, zie ook hier (met een aardige anecdote van Feynman).quote:
Bepaal de afgeleide van f(x)=[ afbeelding ]
(1) Beide zijden differentiëren naar x
F'=f=(lnt)^3
(2) d/dx (F(x^2+x)-F(x^2-x))
(3) f'(x)=ln(x^2+x)^3(2x+1)-(ln(x^2-x)^3(2x-1)
Klopt dat?
Er zijn 500 nCr 25 manieren om 25 appels uit 500 te pakken waar de volgorde niet van belang is (het maakt niet uit of je een appel er eerder of later in doet, het gaat er alleen om of die wel of niet in de doos zit). Er zijn 490 nCr 25 manieren om dozen te maken waar géén rotte appels in zitten (want er zijn 500-10=490 niet-rotte appels). Als je een willekeurige doos pakt, dan is de kans dus (490 nCr 25)/(500 nCr 25) dat het er 1 is zonder rotte appels.quote:Op vrijdag 16 december 2011 13:53 schreef Dobbs het volgende:
Hoi, nieuw hier, mijn eerste post.
Ik heb een vraagje over kansrekening, waar ik niet uitkwam. Je hebt 500 appels waarvan er 10 rot zijn. De appels verdeel je over 20 dozen van elk 25 appels. Hoe groot is de kans dat je een doos kiest waarin geen enkele rotte appel zit?
Nu vond ik als antwoord (490 nCr 25)/(500 nCr 25). Dus het aantal mogelijkheden om 25 appels te kiezen uit de gave appels gedeeld door het totaal aantal mogelijkheden om 25 appels te kiezen uit de 500 appels. Dat betekent dus dat een doos vullen op een willekeurige manier gelijk staat aan één doos kiezen, maar ik zie niet waarom dat zo is. Is er iemand die mij dat helder kan uitleggen, misschien aan de hand van vergelijkingen?
Dat laatste is eigenlijk hetzelfde principe als dat je 10 knikkers hebt waarvan er 1 blauw is en 9 rood. Als je dan een willekeurige knikker pakt dan is de kans dat je dan een blauwe pakt 1/10.
Ik begrijp het, bedankt!quote:
[..]
Er zijn 500 nCr 25 manieren om 25 appels uit 500 te pakken waar de volgorde niet van belang is (het maakt niet uit of je een appel er eerder of later in doet, het gaat er alleen om of die wel of niet in de doos zit). Er zijn 490 nCr 25 manieren om dozen te maken waar géén rotte appels in zitten (want er zijn 500-10=490 niet-rotte appels). Als je een willekeurige doos pakt, dan is de kans dus (490 nCr 25)/(500 nCr 25) dat het er 1 is zonder rotte appels.
Dat laatste is eigenlijk hetzelfde principe als dat je 10 knikkers hebt waarvan er 1 blauw is en 9 rood. Als je dan een willekeurige knikker pakt dan is de kans dat je dan een blauwe pakt 1/10.
wacht, ik snap het al. (x+y) en x hebben geen gemeenschappelijke priemfactoren, en (x+y) en y ook niet, dus (x+y) heeft ook geen gemeenschappelijke priemfactoren met xy.
Thanks!
Ik was even in de war met het verschil tussen delen en gemeenschappelijke priemfactoren hebben.Ik kan het niet echt vinden in mijn boek en op Google..
Ik denk dat je wat meer context moet geven. Het heeft misschien te maken met een schatter die convergeert naar de werkelijke waarde als de tijd of je sample naar oneindig gaat.quote:
Kan iemand mij het principe van "in the long run" bij hypothese toetsen even uitleggen?
Ik kan het niet echt vinden in mijn boek en op Google..
dat als je 1 onderzoek hebt en je gevonden p-waarde is kleiner dan de alpha (0,05 bijvoorbeeld). Dan mag je niet zeggen dat je onderzoek met 95% zekerheid klopt (ofzo)quote:
[..]
Ik denk dat je wat meer context moet geven. Het heeft misschien te maken met een schatter die convergeert naar de werkelijke waarde als de tijd of je sample naar oneindig gaat.
Voor een vlakke representatie van een vlakke graaf is n het aantal knopen,
m het aantal takken en r het aantal gebieden. Wat is de kleinste waarde
die n − m + r kan aannemen?
Antwoord: Voor elke vlakke samenhangende graaf geldt n - m + r = 2. Ik vermoed dat dit ook het kleinste mogelijke waarde is. Als je een niet samenhangende graaf hebt, is die te verdelen in een aantal samenhangende grafen waarvoor voor elk van die grafen geldt n - m + r = 2.
Als je een samenhangende graaf toevoegt aan een groep samenhangende grafen, neemt het aantal gebieden met 1 minder toe dan het aantal gebieden van de nieuwe graaf, want de nieuwe graaf is bevat in een andere graaf en dan is zijn buitengebied een binnengebied van een andere graaf, of hij is niet bevat in een andere graaf en dan deelt hij het buitengebied. Dus als je een graaf toevoegt neemt n - m + r steeds met 1 toe, dus n - m + r is minstens 2, namelijk bij één samenhangende graaf.
Ik weet niet zeker of dat met het aantal gebieden goed geformuleerd is.
Ik heb nog geprobeerd om een tegenspraak af te leiden uit: stel dat n - m + r < 2, maar dat lukte mij nog niet.
Dan moet je even post #209 t/m #218 lezen van dit topic.quote:Op dinsdag 20 december 2011 18:35 schreef DuTank het volgende:
[..]
dat als je 1 onderzoek hebt en je gevonden p-waarde is kleiner dan de alpha (0,05 bijvoorbeeld). Dan mag je niet zeggen dat je onderzoek met 95% zekerheid klopt (ofzo)
De moeilijkheid zit erin dat j even en oneven kan zijn.quote:
[..]
1) Het is toch gegeven dat (cn) een nulrij is?
2)
Als j oneven is
Controleer dit even. Als het klopt moet je het hiermee kunnen bewijzen.
Maar ik heb het nu zo opgelost:
Eerst heb ik bewezen dat voor iedere m geldt: a2m=<an=<a2m+1 met n>2m+1.
En met dit volgt het vrij snel.
Bedankt!
Als je hebt: 2x • ln(x) - x = 0, hoe moet je dan verder? Wss is het iets heel simpels, maar ik heb me er zo op doodgestaard dat ik het niet zie.
Hopelijk kan iemand me helpen!
Dat was snelquote:
factoriseren, schrijf het als x(... - ...) = 0.
Ik snap hem nu, enorm bedankt!
s/sinds/omdatquote:Op woensdag 21 december 2011 18:10 schreef zoem het volgende:
Dan krijg je x=0 of x=exp(1/2). Let dan wel op dat x=0 geen valide antwoord is, sinds ln(0) niet bestaat.
Wat wil je nou zeggen? Het woordje sinds is misschien niet helemaal goed, maar dat komt omdat ik het Engels since gewend ben. Maar dit topic lijkt me niet de plek om over taalfouten te vallen?quote:
Op zich is je redenering goed, maar ik zou de waarde van n-m+r gewoon uitrekenen door n, m en r te schrijven als de som van de n_i, m_i en r_i van de samenhangende componenten.quote:
Klopt mijn antwoord op de volgende vraag?:
Voor een vlakke representatie van een vlakke graaf is n het aantal knopen,
m het aantal takken en r het aantal gebieden. Wat is de kleinste waarde
die n − m + r kan aannemen?
Antwoord: Voor elke vlakke samenhangende graaf geldt n - m + r = 2. Ik vermoed dat dit ook het kleinste mogelijke waarde is. Als je een niet samenhangende graaf hebt, is die te verdelen in een aantal samenhangende grafen waarvoor voor elk van die grafen geldt n - m + r = 2.
Als je een samenhangende graaf toevoegt aan een groep samenhangende grafen, neemt het aantal gebieden met 1 minder toe dan het aantal gebieden van de nieuwe graaf, want de nieuwe graaf is bevat in een andere graaf en dan is zijn buitengebied een binnengebied van een andere graaf, of hij is niet bevat in een andere graaf en dan deelt hij het buitengebied. Dus als je een graaf toevoegt neemt n - m + r steeds met 1 toe, dus n - m + r is minstens 2, namelijk bij één samenhangende graaf.
Ik weet niet zeker of dat met het aantal gebieden goed geformuleerd is.
Ik heb nog geprobeerd om een tegenspraak af te leiden uit: stel dat n - m + r < 2, maar dat lukte mij nog niet.
Ik heb een 3-plaatsige functie gedefinieerd. Als ik handmatig waarden invul doet ie precies wat ik wil, bijvoorbeeld f(1,2,3)=1. Maar als ik een vector X = [1,2,3] genereer dan geeft ie geen resultaat als ik f(X) (=f([1,2,3]) wil evalueren terwijl ik natuurlijk de output f(1,2,3) zou willen hebben. Ik wil dus eigenlijk een functie definiëren die wel arrays/vectors kan evalueren maar weet niet hoe.
Ben je er de hele tijd mee bezig zonder succes, post je het, en een minuut later vind je het opeens zelf.
[ Bericht 4% gewijzigd door thenxero op 24-12-2011 01:28:44 ]
Ik ben nog steeds benieuwd hoe je dat gedaan hebt, heb je die functie met 'inline' gedefinieerd of op een andere manier?quote:
Iemand hier met Matlab kennis?
Ik heb een 3-plaatsige functie gedefinieerd. Als ik handmatig waarden invul doet ie precies wat ik wil, bijvoorbeeld f(1,2,3)=1. Maar als ik een vector X = [1,2,3] genereer dan geeft ie geen resultaat als ik f(X) (=f([1,2,3]) wil evalueren terwijl ik natuurlijk de output f(1,2,3) zou willen hebben. Ik wil dus eigenlijk een functie definiëren die wel arrays/vectors kan evalueren maar weet niet hoe.
Ben je er de hele tijd mee bezig zonder succes, post je het, en een minuut later vind je het opeens zelf.
Eerst had ik zoiets als
function [C] = f(a,b,c)
if a==1 || b==2
x1=0;
else
x1=1;
...
etc etc
...
C = x1 + x2 + ...
Maar dat werkte niet. Dat heb ik veranderd in
function [C] = f(x)
if x(1)==1 || x(1)==2
x1=0;
else
x1=1;
...
etc etc
...
C = x1 + x2 + ...
Die functie heb ik gedefinieerd in een apart m-bestand.
[ Bericht 4% gewijzigd door thenxero op 24-12-2011 01:49:13 ]
Ik moest denken aan een normale continue differentieerbare functie.Die kan je erg makkelijk definiëren met http://www.mathworks.nl/help/techdoc/ref/inline.html
Voor jouw soort van functie moet je inderdaad een apart .m file aanmaken.
Maar volgens mij had je eerste methode gewoon moeten werken, op de manier dat jij het schrijft werkt het bij mij gewoon.
Maar nu je er toch bent even snel nog een vraag
.Ik heb een for-loop waarbij ik steeds een permutatie genereer en dus steeds die functie evalueer. Al die functiewaardes komen in een vector te staan. Daarna kijk ik welk vectorelement minimaal is. Maar ik wil ook de bijbehorende permutatie vinden waarbij dat minimum (of die minima) voorkomt. Hoe doe je zoiets?
Er zijn n steden en de afstand tussen stad i en stad j is bekend (i,j = 1; 2,...,n). De afstand tussen stad i en zichzelf is oneindig.
Je wilt een rondreis maken met een zo kort mogelijk afgelegde afstand. Je neemt de volgende beperkingen:
1) voor iedere stad is er precies één route naar die stad.
2) voor iedere stad is er precies één route naar een andere stad.
Dit model is nog niet correct.
Laat de route in plaats 1 beginnen en interpreteer
stad 1 wordt bezocht.
Toon aan dat het model wel correct is met deze extra beperking:
Mijn idee is dat het eerste model niet correct is omdat er meerdere kringen steden kunnen ontstaan, die niet met elkaar verbonden zijn en je zo dus niet elke stad kan bezoeken.
Mijn vraag is of je de extra beperking niet kan vervangen door alleen het geval dat
Dan komt de extra beperking neer op:
Dus stad i wordt eerder bezocht dan stad j als er een route van i naar j is. Vanwege beperkingen 1) en 2) is er een route tussen de laatste stad en stad 1. Ik zie niet hoe er dan nog iets mis kan gaan. Een andere kring dan de kring die plaats 1 bevat kan niet bestaan en losse steden ook niet vanwege beperkingen 1 en 2.
Is de beperking in het geval dat
Wat wordt er precies bedoeld met voorwaarden (1) en (2)? Is er 1 mogelijke route (bijv: je kan alleen in stad 4 komen vanuit stad 3) of neem je een enkele route (zodat je niet vaker in dezelfde stad komt) ?
Jouw vraag is daarmee beantwoordt, want x_ij is geen parameter. Maw je krijgt geen mixed integer probleem als je de aanwezigheid van een constraint conditioneert op de waarde van een variabele.
Het model is wel correct. Je kunt geen twee kringen krijgen; de notatie van die extra beperking laat dat niet toe.
Op universiteiten werkt iedereen morgen weer.quote:
Klopt, en bedankt.quote:
De vraag is erg onduidelijk omdat het begrip route niet gangbaar is. Ik vermoed dat je "er een route tussen stad i en j bestaat" moet lezen als "de weg van stad i naar j gebruikt wordt" (de volgorde i/j is belangrijk).
.| x + a | < b = -b < x + a <b ?
In mijn boek wordt dit als "regel" gegeven, maar ik wil het ook snappen.
| x + a | = b kan worden opgelost door
x + a = b en x + a = - b op te lossen. Ik dacht dus ook dit toe te passen op | x + a | < b. Kortom:
x + a < b en x + a < - b op te lossen. Maar hier kom ik niet op het juiste antwoord, omdat dat het ingelijkheidsteken bij beide dezelfde kant op wijst.
Bij voorbaat dank.
Je regel om |x+a|=b op te lossen is niet helemaal goed, je moet namelijk dan x+a=b en -(x+a)=b oplossen. Bij het gelijkheidsteken maakt dat niet uit, maar bij het >-teken klapt het teken om bij vermenigvuldiging met een negatief getal. Dan kom je wel op het goede antwoord.quote:
Kan iemand misschien toelichten waarom
| x + a | < b = -b < x + a <b ?
In mijn boek wordt dit als "regel" gegeven, maar ik wil het ook snappen.
| x + a | = b kan worden opgelost door
x + a = b en x + a = - b op te lossen. Ik dacht dus ook dit toe te passen op | x + a | < b. Kortom:
x + a < b en x + a < - b op te lossen. Maar hier kom ik niet op het juiste antwoord, omdat dat het ingelijkheidsteken bij beide dezelfde kant op wijst.
Bij voorbaat dank.
en