[Bèta wiskunde] Huiswerk- en vragentopic

Tja, bewijzen zijn er in alle soorten en maten, dus het zegt niets over moeilijkheidsgraad.

quote:

Op maandag 12 december 2011 23:21 schreef Physics het volgende:
Prachtig, tentamen analyse bestaat voor 50% uit bewijzen, en we hebben nog nooit een bewijsopgave hoeven doen . Of ja, nooit is overdreven, maar het huiswerk was 95% calculus.

Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde punten

Ben dus met wiskunde bezig. En nu heb ik een tweetal formules gekregen om een vector door een vlak te bereken. Echter snap ik niet helemaal hoe deze formules te gebruiken. Zou iemand misschien de formule in kunnen vullen met een voorbeeld zodat ik dit als referentie kan gebruiken? Bedankt alvast!

quote:

The equation of a plane (points P are on the plane with normal N and point P3 on the plane) can be written as N dot (P - P3) = 0

The equation of the line (points P on the line passing through points P1 and P2) can be written as
P = P1 + u (P2 - P1)

The intersection of these two occurs when
N dot (P1 + u (P2 - P1)) = N dot P3

en de 2e formule

quote:

A plane can also be represented by the equation
A x + B y + C z + D = 0

where all points (x,y,z) lie on the plane.

Substituting in the equation of the line through points P1 (x1,y1,z1) and P2 (x2,y2,z2)
P = P1 + u (P2 - P1)

gives
A (x1 + u (x2 - x1)) + B (y1 + u (y2 - y1)) + C (z1 + u (z2 - z1)) + D = 0

De eerste formule werkt met een inwendig product. Twee vectoren (in een inwendigproductruimte) staan loodrecht op elkaar als hun inwendig product nul is. De reden waarom dat het vlak weergeeft zie je in deze figuur:

dus de vergelijking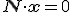 geeft alle vectoren x in het vlak.

De tweede formule is in feite hetzelfde, want


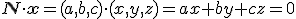
Voorbeeldje: stel dat je weet dat het punt (1,2,3) in het vlak ligt, en dat (4,5,6) een normaalvector van het vlak is. De vectoren die nu in het vlak liggen zijn de vectoren x=(x,y,z) die voldoen aan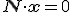 . Als je dat uitwerkt krijg je 4x+5y+6z=0.

Maar dit is alleen waar als de normaalvector mooi bij de oorsprong het vlak snijdt. Als het vlak niet door de oorsprong gaat, maar wel door het punt (1,2,3) zijn de vectoren x eigenlijk x=(x-1,y-2,z-3). De vectoren zijn dan namelijk het verschil tussen een punt in het vlak en het punt dat zeker in het vlak ligt.

Dan krijg je 4(x-1)+5(y-2)+6(z-3)=0, dus 4x+5y+6z=32.

quote:

Op maandag 12 december 2011 23:48 schreef Fingon het volgende:

[..]

Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde punten

Wat zijn dit voor rechtenpraktijken.

quote:

Op maandag 12 december 2011 23:51 schreef GeertJan88 het volgende:
Ben dus met wiskunde bezig. En nu heb ik een tweetal formules gekregen om een vector door een vlak te bereken. Echter snap ik niet helemaal hoe deze formules te gebruiken. Zou iemand misschien de formule in kunnen vullen met een voorbeeld zodat ik dit als referentie kan gebruiken? Bedankt alvast!

[..]

en de 2e formule

[..]

Begin eens je quotes wat leesbaarder en correcter op te schrijven. En uit je vraagstelling proef ik een beetje dat je vooral een 'recept' wil hebben. Als je nu maar weet hoe je die formules in moet vullen dan ben je kennelijk tevreden. Maar dat is niet goed. Je moet begrijpen waarom die formules zijn zoals ze zijn en wat ze (meetkundig) voorstellen.

Eerste quote:

quote:

The equation of a plane (points P are on the plane with normal N and point P3 on the plane) can be written as N dot (P - P3) = 0

The equation of the line (points P on the line passing through points P1 and P2) can be written as
P = P1 + u (P2 - P1)

The intersection of these two occurs when
N dot (P1 + u (P2 - P1)) = N dot P3

De vectorvergelijking van het bedoelde vlak V door punt P₃ en loodrecht op vector n is:

(1) V: n∙(p - p₃) = 0

Hierbij stelt het eindpunt P van vector OP = p een willekeurig punt in het vlak V voor. Het is gemakkelijk in te zien waarom dit een vectorvoorstelling van het betreffende vlak is: als P in het vlak ligt, evenals het vaste punt P₃, dan is de verschilvector OP - OP₃ = p - p₃ parallel aan lijnstuk PP₃ in het vlak V, zodat deze verschilvector loodrecht op vector n staat en het inproduct van n en p - p₃ dus gelijk is aan 0.

Tweede quote:

quote:

A plane can also be represented by the equation
A x + B y + C z + D = 0

where all points (x,y,z) lie on the plane.

Substituting in the equation of the line through points P1 (x1,y1,z1) and P2 (x2,y2,z2)
P = P1 + u (P2 - P1)

gives
A (x1 + u (x2 - x1)) + B (y1 + u (y2 - y1)) + C (z1 + u (z2 - z1)) + D = 0

Om dit te begrijpen moet je weten hoe je de vectorvoorstelling (1) van een vlak V omzet in een vergelijking in cartesische coördinaten. Stel dat we hebben:

(2) n = (a,b,c)

en:

(3) p₃ = (x₃,y₃,z₃)

en zij p = (x,y,z) weer de variabele vector. Dan volgt uit (1) dat het inproduct van n en p - p₃ voor elke vector p = (x,y,z) met eindpunt in het betreffende vlak nul moet zijn, en dus:

(4) V: a(x - x₃) + b(y - y₃) + c(z - z₃) = 0

Door het uitwerken van de haakjes breng je deze cartesische vergelijking voor het vlak V gemakkelijk in de standaardvorm:

(5) V: ax + by + cz + d = 0

Voor een lijn l door de punten P₁ en P₂ hebben we met de vaste vectoren OP₁ = p₁ en OP₂ = p₂ een vectorvoorstelling:

(6) l: p = p₁ + μ∙(p₂ - p₁)

waarbij μ de verzameling reële getallen doorloopt. Ook dit is weer eenvoudig in te zien. Aangezien P₁ en P₂ op l liggen, is de verschilvector p₂ - p₁ parallel aan lijn l, zodat l': p = μ∙(p₂ - p₁) een vectorvoorstelling is van een lijn l' door de oorsprong en parallel aan l. Tellen we de vaste vector p₁ hierbij op (hetgeen resulteert in een translatie langs lijnstuk OP₁) dan krijgen we dus alle vectoren waarvan de eindpunten op lijn l liggen aangezien O op l' ligt en P₁ op l ligt terwijl l' parallel is aan l. Schrijven we nu (6) in coördinaatvorm, dan hebben we:

(7) l: (x,y,z) = (x₁ + μ(x₂-x₁), y₁ + μ(y₂-y₁), z₁ + μ(z₂-z₁))

Dit levert dus het volgende stelsel:

(8a) x = x₁ + μ(x₂-x₁)
(8b) y = y₁ + μ(y₂-y₁)
(8c) z = z₁ + μ(z₂-z₁)

Substitutie van (8a), (8b) en (8c) in de cartesische vergelijking (5) van vlak V levert een lineaire vergelijking in μ op, die ons dus vertelt voor welke waarde van μ lijn l vlak V snijdt (als althans lijn l niet evenwijdig loopt aan vlak V of in vlak V ligt). Door terugsubstitueren van de aldus gevonden waarde van μ in (8a), (8b) en (8c) verkrijgen we dan de cartesische coördinaten van het snijpunt van lijn l met vlak V.

[ Bericht 0% gewijzigd door Riparius op 13-12-2011 07:29:19 ]

quote:

Op maandag 12 december 2011 23:48 schreef Fingon het volgende:

[..]

Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde punten

Herkauwen is iets voor koeien. En stamppot hoef je al helemaal niet te kauwen.

Twaal en Riparius echt top! Riparius je hebt gelijk en wil het ook graag begrijpen, ga met je uitleg aan de slag!!

Gegeven h: R->R en d,R elementen van R.

"Er wordt gevraagd om de definitie van de definitie van de limiet waarbij x van boven d nadert voor de functie h(u), met de limiet R."

Dus lim h(u)=R (voor x->d+)

Alleen h is geen functie van x, dus moet die x geen u zijn?

[ Bericht 9% gewijzigd door Physics op 15-12-2011 17:01:45 ]

quote:

Op woensdag 14 december 2011 11:33 schreef Physics het volgende:
Gegeven h: R->R en d,R elementen van de reële getallen.

Als R een element is van de reële getallen, is h geen functie.

Gegeven (c_n), een nulrij die dalend is.
Laat (a_n) de rij zijn met a_n de som van 1 naar n van (-1)^k+1 c_k.

Dan heb ik de volgende vragen:
1) De rij c_n kan toch ook een nulrij zijn of uitkomen op een nulrij?
2) Is (a_n) een Cauchy-rij? En hoe kan ik dat bewijzen?

quote:

Op woensdag 14 december 2011 16:54 schreef twaalf het volgende:

[..]

Als R een element is van de reële getallen, is h geen functie.

Ik had verkeerd gelezen, er stond d,R elementen van R met h:R->R

quote:

Op woensdag 14 december 2011 11:33 schreef Physics het volgende:
Gegeven h: R->R en d,R elementen van R.

"Er wordt gevraagd om de definitie van de definitie van de limiet waarbij x van boven d nadert voor de functie h(u), met de limiet R."

Dus lim h(u)=R (voor x->d+)

Alleen h is geen functie van x, dus moet die x geen u zijn?

Lijkt me dat ze bedoelen lim h(x)=R (voor x->d+), anders is het niet zo'n spannende limiet .

quote:

Op donderdag 15 december 2011 13:23 schreef Siddartha het volgende:
Gegeven (c_n), een nulrij die dalend is.
Laat (a_n) de rij zijn met a_n de som van 1 naar n van (-1)^k+1 c_k.

Dan heb ik de volgende vragen:
1) De rij c_n kan toch ook een nulrij zijn of uitkomen op een nulrij?
2) Is (a_n) een Cauchy-rij? En hoe kan ik dat bewijzen?

1) Het is toch gegeven dat (c_n) een nulrij is?
2)
Als j oneven is


Controleer dit even. Als het klopt moet je het hiermee kunnen bewijzen.

Hoi, nieuw hier, mijn eerste post.

Ik heb een vraagje over kansrekening, waar ik niet uitkwam. Je hebt 500 appels waarvan er 10 rot zijn. De appels verdeel je over 20 dozen van elk 25 appels. Hoe groot is de kans dat je een doos kiest waarin geen enkele rotte appel zit?

Nu vond ik als antwoord (490 nCr 25)/(500 nCr 25). Dus het aantal mogelijkheden om 25 appels te kiezen uit de gave appels gedeeld door het totaal aantal mogelijkheden om 25 appels te kiezen uit de 500 appels. Dat betekent dus dat een doos vullen op een willekeurige manier gelijk staat aan één doos kiezen, maar ik zie niet waarom dat zo is. Is er iemand die mij dat helder kan uitleggen, misschien aan de hand van vergelijkingen?

Bepaal de afgeleide van f(x)=

(1) Beide zijden differentiëren naar x
F'=f=(lnt)^3
(2) d/dx (F(x^2+x)-F(x^2-x))

(3) f'(x)=ln(x^2+x)^3(2x+1)-(ln(x^2-x)^3(2x-1)

Klopt dat?

quote:

Op vrijdag 16 december 2011 14:54 schreef Physics het volgende:
Bepaal de afgeleide van f(x)=[ afbeelding ]

(1) Beide zijden differentiëren naar x
F'=f=(lnt)^3
(2) d/dx (F(x^2+x)-F(x^2-x))

(3) f'(x)=ln(x^2+x)^3(2x+1)-(ln(x^2-x)^3(2x-1)

Klopt dat?

Ja. Je maakt in feite gebruik van een variant van de regel van Leibniz, zie ook hier (met een aardige anecdote van Feynman).

quote:

Op vrijdag 16 december 2011 13:53 schreef Dobbs het volgende:
Hoi, nieuw hier, mijn eerste post.

Ik heb een vraagje over kansrekening, waar ik niet uitkwam. Je hebt 500 appels waarvan er 10 rot zijn. De appels verdeel je over 20 dozen van elk 25 appels. Hoe groot is de kans dat je een doos kiest waarin geen enkele rotte appel zit?

Nu vond ik als antwoord (490 nCr 25)/(500 nCr 25). Dus het aantal mogelijkheden om 25 appels te kiezen uit de gave appels gedeeld door het totaal aantal mogelijkheden om 25 appels te kiezen uit de 500 appels. Dat betekent dus dat een doos vullen op een willekeurige manier gelijk staat aan één doos kiezen, maar ik zie niet waarom dat zo is. Is er iemand die mij dat helder kan uitleggen, misschien aan de hand van vergelijkingen?

Er zijn 500 nCr 25 manieren om 25 appels uit 500 te pakken waar de volgorde niet van belang is (het maakt niet uit of je een appel er eerder of later in doet, het gaat er alleen om of die wel of niet in de doos zit). Er zijn 490 nCr 25 manieren om dozen te maken waar géén rotte appels in zitten (want er zijn 500-10=490 niet-rotte appels). Als je een willekeurige doos pakt, dan is de kans dus (490 nCr 25)/(500 nCr 25) dat het er 1 is zonder rotte appels.
Dat laatste is eigenlijk hetzelfde principe als dat je 10 knikkers hebt waarvan er 1 blauw is en 9 rood. Als je dan een willekeurige knikker pakt dan is de kans dat je dan een blauwe pakt 1/10.

quote:

Op vrijdag 16 december 2011 16:21 schreef thenxero het volgende:

[..]

Er zijn 500 nCr 25 manieren om 25 appels uit 500 te pakken waar de volgorde niet van belang is (het maakt niet uit of je een appel er eerder of later in doet, het gaat er alleen om of die wel of niet in de doos zit). Er zijn 490 nCr 25 manieren om dozen te maken waar géén rotte appels in zitten (want er zijn 500-10=490 niet-rotte appels). Als je een willekeurige doos pakt, dan is de kans dus (490 nCr 25)/(500 nCr 25) dat het er 1 is zonder rotte appels.
Dat laatste is eigenlijk hetzelfde principe als dat je 10 knikkers hebt waarvan er 1 blauw is en 9 rood. Als je dan een willekeurige knikker pakt dan is de kans dat je dan een blauwe pakt 1/10.

Ik begrijp het, bedankt!

vast een domme vraag, maar waarom volgt uit gcd(x, y) = 1 dat gcd(x + y, xy) = 1?

relateer de delers van x+y en van xy eens aan de delers van x en van y.

tsja. Ik snap wel dat (x+y) x niet deelt en dat (x+y) y niet deelt...
wacht, ik snap het al. (x+y) en x hebben geen gemeenschappelijke priemfactoren, en (x+y) en y ook niet, dus (x+y) heeft ook geen gemeenschappelijke priemfactoren met xy.
Thanks! Ik was even in de war met het verschil tussen delen en gemeenschappelijke priemfactoren hebben.

Kan iemand mij het principe van "in the long run" bij hypothese toetsen even uitleggen?
Ik kan het niet echt vinden in mijn boek en op Google..

quote:

Op dinsdag 20 december 2011 13:47 schreef DuTank het volgende:
Kan iemand mij het principe van "in the long run" bij hypothese toetsen even uitleggen?
Ik kan het niet echt vinden in mijn boek en op Google..

Ik denk dat je wat meer context moet geven. Het heeft misschien te maken met een schatter die convergeert naar de werkelijke waarde als de tijd of je sample naar oneindig gaat.

quote:

Op dinsdag 20 december 2011 15:11 schreef thenxero het volgende:

[..]

Ik denk dat je wat meer context moet geven. Het heeft misschien te maken met een schatter die convergeert naar de werkelijke waarde als de tijd of je sample naar oneindig gaat.

dat als je 1 onderzoek hebt en je gevonden p-waarde is kleiner dan de alpha (0,05 bijvoorbeeld). Dan mag je niet zeggen dat je onderzoek met 95% zekerheid klopt (ofzo)