SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Baas! Ik moest even denken, maar nu valt alles op zijn plek. Zo simpel... Ik heb me er een beetje op zitten doodstaren! Super bedanktquote:Op dinsdag 6 december 2011 00:11 schreef twaalf het volgende:
Je hebt. Differentieer nu beide kanten naar y.
(ik voel me vaak na een vraag in dit topic erg stom, en dit is geen uitzondering
)
Ja vanaf die kant ben ik er nog niet uit, als je echter vanaf de andere kant werkt:quote:
Over je edit, integreren geeft (1/dx)*(y2/2)
d/dx 0.5y^2 = d/dy dy/dx 0.5y^2 = d(0.5y^2)/dy*dy/dx = y*dy/dx
Beneath the gold, bitter steel
Oh ja, stom. Zo is het wel duidelijk, maar andersom vind ik 't lastig om te zien.quote:
Dat is de kettingregel:
d/dx (y(x))² = 2y(x) * y'(x)
Bedankt. Goede tip.quote:
Var(Uniform) = (b-a)^2 / 12 dus Std = sqrt(Var) = b-a/12
TE bepalen zoals hierboven getoond of kijk hier even bij moment-generating functions voor een andere manier.
Ook bedankt, maar aangezien dit tentamen van mij, geloof het of niet, non-calculus is, ga ik er nu even niet op in (ik zit ook even niet in deze stof).quote:
[..]
Als U ~ Uniform(a,b), dan
Nu jij weer.
Ik heb trouwens nog een vraag.
Verderop in het boek wordt namelijk gesteld:
Klopt dit wel?quote:Conclusie: Based on the sample, you can be 90% confident that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
Verderop in het boek wordt namelijk gesteld:
Waarschijnlijk lees ik iets niet goed, maar zijn deze beweringen niet met elkaar in tegenspraak?quote:Let a and b represent the lower and upper boundaries of the 90% confidence
interval for the mean of the population. Is it correct to conclude that there is a
90% probability the true population mean lies between a and b? Explain your
answer.
A confidence interval does not describe the probability that any particular
interval constructed around the mean of a single sample will contain the actual
population mean. In this problem, it would be inaccurate to state that there is
a 90% probability the interval bounded below by a and above by b contains the
population mean.
Een 90% CI voor de mean is iets wat als je het 100 keer zou construeren op basis van 100 aselecte steekproeven, hij naar verwachting 90 keer de ware mean bevat.
De tekst in het tweede rondje klopt niet. Ze ronden daar af op 3 decimalen. Kijk je naar het vierde decimaal, zie je dat 1,64 de juiste afronding is op twee decimalen. Bedenk wel dat je door afronden geen echt 90% CI meer hebt.
De tekst in het tweede rondje klopt niet. Ze ronden daar af op 3 decimalen. Kijk je naar het vierde decimaal, zie je dat 1,64 de juiste afronding is op twee decimalen. Bedenk wel dat je door afronden geen echt 90% CI meer hebt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Erg leuk, die tekstballonnetjes. 
Volgens mij bedoelen ze een wel heel subtiel verschil. Er is een kans van 90% dat een gevonden interval de ware E bevat. Er is geen kans van 90% dat het gevonden interval de ware E bevat.
Volgens mij bedoelen ze een wel heel subtiel verschil. Er is een kans van 90% dat een gevonden interval de ware E bevat. Er is geen kans van 90% dat het gevonden interval de ware E bevat.
Bedankt voor jullie reacties.
Based on the sample, you can be 90% confident that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
en
Based on the sample, there is a 90% probability that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
Het komt bij mij toch hetzelfde over. Als je zegt dat je ergens "zeker" over bent, dan impliceer je daarmee een bepaalde kans. Het kan natuurlijk ook zo zijn dat ik normaal taalgebruik en statisch taalgebruik door elkaar haal.
Textueel gezien merk ik dat nu ook op. Toch knaagt er nog iets. Ik vind het verschil tussen deze twee opties niet helemaal overtuigend nog:quote:
Ik concludeer er zelf uit dat 'confidence' iets anders is dan 'probability'.
Based on the sample, you can be 90% confident that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
en
Based on the sample, there is a 90% probability that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
Het komt bij mij toch hetzelfde over. Als je zegt dat je ergens "zeker" over bent, dan impliceer je daarmee een bepaalde kans. Het kan natuurlijk ook zo zijn dat ik normaal taalgebruik en statisch taalgebruik door elkaar haal.
Maar als je dan een willekeurige steekproef daarvan neemt, dan is er toch een kans van 90% dat de ware mean daarin zit?quote:
Een 90% CI voor de mean is iets wat als je het 100 keer zou construeren op basis van 100 aselecte steekproeven, hij naar verwachting 90 keer de ware mean bevat.
Op wikipedia staat ook
enquote:A confidence interval does not predict that the true value of the parameter has a particular probability of being in the confidence interval given the data actually obtained.
Maar wat klopt er dan niet aan mijn beredenering?quote:A confidence interval with a particular confidence level is intended to give the assurance that, if the statistical model is correct, then taken over all the data that might have been obtained, the procedure for constructing the interval would deliver a confidence interval that included the true value of the parameter the proportion of the time set by the confidence level.
Om even mijn eigen vraag te beantwoorden. Wat er niet klopt aan mijn beredenering is dat je niet zomaar een willekeurige steekproef hebt, maar je hebt de steekproef waarmee je de CI berekend hebt. Ik denk dat het daar mis gaat.quote:
[..]
Maar wat klopt er dan niet aan mijn beredenering?
Het is allemaal heel subtiel. Ik vergelijk het met een dobbelsteen die je hebt gegooid maar waarvan je de ogen nog niet hebt gezien. Dan kun je niet meer zeggen dat de kans dat de 1 boven ligt 1/6de is.quote:
[..]
Maar als je dan een willekeurige steekproef daarvan neemt, dan is er toch een kans van 90% dat de ware mean daarin zit?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat het subtiel is is duidelijk, maar ik kan er nog steeds niet helemaal de vinger op leggen waarom het zo is.quote:
[..]
Het is allemaal heel subtiel. Ik vergelijk het met een dobbelsteen die je hebt gegooid maar waarvan je de ogen nog niet hebt gezien. Dan kun je niet meer zeggen dat de kans dat de 1 boven ligt 1/6de is.
Dat van die dobbelsteen snap ik wel. Als je hem gegooid hebt dan heeft ie een bepaalde waarde aangenomen in {1,...,6}. De waarde die hij aan heeft genomen heeft ie dus met kans 1 en de rest met kans 0. Als je gaat kijken (zonder voorkennis) heb je echter wel een kans van 1/6 dat je die 1 aantreft.
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
Je kunt zeggen dat ![\mathbb{P}([X_1,X_2]\ni \mu)=1-\alpha](https://forum.fok.nl/lib/mimetex.cgi?%5Cmathbb%7BP%7D%28%5BX_1%2CX_2%5D%5Cni%20%5Cmu%29%3D1-%5Calpha)
. Maar je kunt natuurlijk niet zeggen dat ![\mathbb{P}(\mu \in [x_1,x_2])=1-\alpha](https://forum.fok.nl/lib/mimetex.cgi?%5Cmathbb%7BP%7D%28%5Cmu%20%5Cin%20%5Bx_1%2Cx_2%5D%29%3D1-%5Calpha)
, let op het verschil tussen grote en kleine letters en de afwezigheid van stochasten..
Volgens mij heeft het te maken met een misvatting die heerst. Zo denken mensen dat de kans op kop of munt met een eerlijke munt gelijk is aan respectievelijk 0.5 en 0.5. Toch is de kans slechts bij benadering 0.5 bij een heel groot aantal worpen, bijvoorbeeld 10.000. Zelfs dan zie je dat de proportie niet gelijk is aan 0.5.quote:
[..]
Als je gaat kijken (zonder voorkennis) heb je echter wel een kans van 1/6 dat je die 1 aantreft.
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
quote:4.3 Many tosses of a coin. The French naturalist Count Buffon (1707
1788) tossed a coin 4040 times. Result: 2048 heads, or proportion 2048/4040 =
0.5069 for heads.
Around 1900, the English statistician Karl Pearson heroically tossed a coin
24,000 times. Result: 12,012 heads, a proportion of 0.5005.
While imprisoned by the Germans duringWorldWar II, the South African
statistician John Kerrich tossed a coin 10,000 times. Result: 5067 heads, proportion
of heads 0.5067.
quote:Probability describes only what happens in the long
run. Most people expect chance outcomes to show more short-term regularity
than is actually true.
Introduction to the Practice of Statistics, p.238.
Het heeft ermee te maken dat als je het CI eenmaal hebt geconstrueerd, er geen kans meer aan te pas komt om de vraag te beantwoorden of hij de ware parameter bevat. Hij zit erin of hij zit er niet in.quote:
[..]
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dit bevestigt toch gewoon dat er variantie bestaat?quote:
[..]
Volgens mij heeft het te maken met een misvatting die heerst. Zo denken mensen dat de kans op kop of munt met een eerlijke munt gelijk is aan respectievelijk 0.5 en 0.5. Toch is de kans slechts bij benadering 0.5 bij een heel groot aantal worpen, bijvoorbeeld 10.000. Zelfs dan zie je dat de proportie niet gelijk is aan 0.5.
[..]
[..]
Het verhaal van Warren is inderdaad ongerelateerd.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik snap nu de analogie. De parameter zit er inderdaad wel in met kans 1 of niet in met kans 1.quote:
[..]
Het heeft ermee te maken dat als je het CI eenmaal hebt geconstrueerd, er geen kans meer aan te pas komt om de vraag te beantwoorden of hij de ware parameter bevat. Hij zit erin of hij zit er niet in.
Net alsof je een muntje gooit in een afgesloten doos en je niets binnen die doos kan waarnemen. Als je dan het muntje gegooid hebt dan kan je niet meer spreken over 50% kans dat de munt kop is. Maar voor iemand die niet kan waarnemen hoe de munt is gevallen is op dat moment de kans wel 50% dat het kop zal blijken te zijn als je die doos open maakt. Zo is het volgens mij ook voor CI's: zolang je de werkelijke parameter niet kan waarnemen is de kans x % dat die parameter erin zal zitten op het moment dat je die parameter wel zou kunnen waarnemen.
Dus ik zie nog steeds niet waarom:
quote:A confidence interval does not predict that the true value of the parameter has a particular probability of being in the confidence interval given the data actually obtained.
Het percentage mensen dat terwijl ze een vlucht boeken maar niet gaan is 12%. Wat is de propability dat er geen passagier teleurgesteld hoeft te worden als een maatschappij 215 mensen boekt op een vliegtuig van 200?
Dit is de vraag. Nu is mijn vraag, welke formules (verdelingen) moet ik hiervoor gebruiken om het op te lossen?
Dit is de vraag. Nu is mijn vraag, welke formules (verdelingen) moet ik hiervoor gebruiken om het op te lossen?
Je moet aannemen dat de mensen hun beslissing om wel of niet te gaan onafhankelijk van elkaar nemen. Natuurlijk is dat niet zo, bijvoorbeeld als papa en mama niet gaan, gaan de kinderen ook niet. Dan heb je een binomiale situatie (wel of niet gaan) met 215 onafhankelijke trekkingen. We zijn geïnteresseerd in de kans dat er minder dan 15 successen zijn.
Bij zo'n grote trekking en een redelijke kans ga je gewoon normaal benaderen. Laat X het aantal mensen zijn dat niet komt opdagen. X heeft verwachte waarde 215*0.12=25.8 en variantie 215*0.12*0.88=22.7. Dus als n groot is, heeft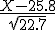
een standaardnormale verdeling.
Nu willen we weten de kans dat X<15. Met een correctie voor continuïteit wordt dit bij een normale benadering X<15.5.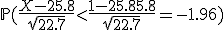
. Normaal gesproken moet je nu de kans opzoeken in een boek, maar -1.96 is een standaardwaarde waarvan de linkerstaart overeenkomt met een kans van 2.5%.
Bij zo'n grote trekking en een redelijke kans ga je gewoon normaal benaderen. Laat X het aantal mensen zijn dat niet komt opdagen. X heeft verwachte waarde 215*0.12=25.8 en variantie 215*0.12*0.88=22.7. Dus als n groot is, heeft
Nu willen we weten de kans dat X<15. Met een correctie voor continuïteit wordt dit bij een normale benadering X<15.5.
Ik wil Warren quoten, maar blijkbaar wil de quoteknop dat niet, enfin:
Warren kraamt onzin uit. De kans dat je kop, danwel munt gooit is wel degelijk 0.5 bij een eerlijke munt. Dat je na 10000 worpen niet precies 5000x kop en 5000x munt hebt is weer een ander verhaal. Een kansexperiment geeft namelijk niet altijd de verwachtingswaarde, er bestaat ook nog zoiets als variantie..
Warren kraamt onzin uit. De kans dat je kop, danwel munt gooit is wel degelijk 0.5 bij een eerlijke munt. Dat je na 10000 worpen niet precies 5000x kop en 5000x munt hebt is weer een ander verhaal. Een kansexperiment geeft namelijk niet altijd de verwachtingswaarde, er bestaat ook nog zoiets als variantie..
Dat was al gezegd, en als je je adblocker uitzet dan kun je ook weer quoten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja klopt, maar ik zag dat te laat. Sorry daarvoorquote:
Dat was al gezegd, en als je je adblocker uitzet dan kun je ook weer quoten.
, maar ook editten ging niet met adblocker aan.bedankt voor de tip!
Hele domme vraag, maar hoe zou je het "Gemiddelde" kunnen omschrijven?
Ik wilde het aan iemand uitleggen maar dat ging lastig.
Als het gemiddelde van een steekproef 30 is, wat zegt dat nu?
Het is enkel een theoretisch hulpmiddel om een beter beeld te krijgen hoe, in dit geval, de steekproef er ongeveer uit ziet toch?
Heeft iemand een mooie definitie voor het gemiddelde?
Ik wilde het aan iemand uitleggen maar dat ging lastig.
Als het gemiddelde van een steekproef 30 is, wat zegt dat nu?
Het is enkel een theoretisch hulpmiddel om een beter beeld te krijgen hoe, in dit geval, de steekproef er ongeveer uit ziet toch?
Heeft iemand een mooie definitie voor het gemiddelde?
Een vraag over modulorekenen en groepen etc.
De eerste deelvraag is het berekenen van het aantal elementen in de verzameling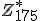
- dit lukt me aardig (want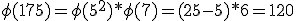 
Het tweede deel vind ik lastiger: "Hoeveel elementen van orde 7 zijn er in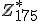
?" Ik heb werkelijk geen flauw idee waar ik moet beginnen. Is er een formule die ik mis of over het hoofd heb gezien? Heeft iemand een tip?
Ik weet wel wat de orde van n betekent (het aantal elementen dat je passeert wanneer je steeds n steeds verheft tot een hogere macht voordat je n weer bereikt, modulo 175), maar ik zie (naast brute force alle banen uitschrijven) geen handige manier om tot een antwoord te komen. Toch staan er voor zowel a als b 2 punten, dus kan het niet veel lastiger zijn dan de het berekenen van de Euler totient van 175, als in a.
[ Bericht 1% gewijzigd door Djoezt op 10-12-2011 21:10:27 ]
De eerste deelvraag is het berekenen van het aantal elementen in de verzameling
Het tweede deel vind ik lastiger: "Hoeveel elementen van orde 7 zijn er in
Ik weet wel wat de orde van n betekent (het aantal elementen dat je passeert wanneer je steeds n steeds verheft tot een hogere macht voordat je n weer bereikt, modulo 175), maar ik zie (naast brute force alle banen uitschrijven) geen handige manier om tot een antwoord te komen. Toch staan er voor zowel a als b 2 punten, dus kan het niet veel lastiger zijn dan de het berekenen van de Euler totient van 175, als in a.
[ Bericht 1% gewijzigd door Djoezt op 10-12-2011 21:10:27 ]
http://www.google.com/?q=definitie+gemiddeldequote:
Hele domme vraag, maar hoe zou je het "Gemiddelde" kunnen omschrijven?
Ik wilde het aan iemand uitleggen maar dat ging lastig.
Als het gemiddelde van een steekproef 30 is, wat zegt dat nu?
Het is enkel een theoretisch hulpmiddel om een beter beeld te krijgen hoe, in dit geval, de steekproef er ongeveer uit ziet toch?
Heeft iemand een mooie definitie voor het gemiddelde?
[ Bericht 1% gewijzigd door GlowMouse op 10-12-2011 21:07:50 ]
Maar laten we wel wezen, dat was natuurlijk al lang duidelijk.
De orde van een element is altijd een deler van de orde van de groep.quote:
Een vraag over modulorekenen en groepen etc.
De eerste deelvraag is het berekenen van het aantal elementen in de verzameling
Het tweede deel vind ik lastiger: "Hoeveel elementen van orde 7 zijn er in
Ik weet wel wat de orde van n betekent (het aantal elementen dat je passeert wanneer je steeds n steeds verheft tot een hogere macht voordat je n weer bereikt, modulo 175), maar ik zie (naast brute force alle banen uitschrijven) geen handige manier om tot een antwoord te komen. Toch staan er voor zowel a als b 2 punten, dus kan het niet veel lastiger zijn dan de het berekenen van de Euler totient van 175, als in a.
Dus de orde moet een deler zijn van 175, en aangezien 7 dat niet is zijn er geen elementen die orde 7 hebben? Oke!quote:
[..]
De orde van een element is altijd een deler van de orde van de groep.
Kan je verklaren waarom de orde van een elementen een deler moet zijn van de orde van de groep?
Nee, van 120.quote:
[..]
Dus de orde moet een deler zijn van 175?
Ja, sorry daarvoor nog.quote:
Ik wil Warren quoten, maar blijkbaar wil de quoteknop dat niet, enfin:
Warren kraamt onzin uit. De kans dat je kop, danwel munt gooit is wel degelijk 0.5 bij een eerlijke munt. Dat je na 10000 worpen niet precies 5000x kop en 5000x munt hebt is weer een ander verhaal. Een kansexperiment geeft namelijk niet altijd de verwachtingswaarde, er bestaat ook nog zoiets als variantie..
Nog even een vraagje:
Het antwoord volgens het antwoordenmodel is c, maar volgens mij is het d.quote:10. Een bepaalde test is zodanig genormaliseerd dat het gemiddelde 100 is; de
populatievariantie is niet bekend. In een steekproef van 31 personen vinden
we een gemiddelde van 103; de standaarddeviatie is 6.28. We onderzoeken
de vraag of de personen uit een populatie afkomstig zijn met een gemiddelde
groter dan 100. Wat is het resultaat van de toets (geef het beste antwoord)?
a. We kunnen H0 niet verwerpen.
b. We kunnen H0 verwerpen met alfa = 0.05
c. We kunnen H0 verwerpen met alfa = 0.02
d. We kunnen H0 verwerpen met alfa = 0.01
Als ik de t-waarde opzoek bij 30 vrijheidsgraden bij een tail probability van 0.01 dan kom ik uit op 2.457.
t103 =
e. Dit kun je niet zeggen omdat je de onderliggende kansverdeling niet kent.
Daarnaast is de vraag slecht gesteld omdat je alpha kiest voordat je de toetsing uitvoert.
Daarnaast is de vraag slecht gesteld omdat je alpha kiest voordat je de toetsing uitvoert.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je hebt gelijk, maar het komt uit een oud-tentamen, dus hier moet ik het helaas mee doen. Gezien het feit dat alleen de normale verdeling behandeld is, komt dit uit een normale verdeling.quote:
e. Dit kun je niet zeggen omdat je de onderliggende kansverdeling niet kent.
Daarnaast is de vraag slecht gesteld omdat je alpha kiest voordat je de toetsing uitvoert.
een normalisatie heeft niets met een normale verdeling te makenquote:
Eerste zin: een bepaalde test is [..] genormaliseerd. Dus een normale verdeling.
maar je doet alsof je ook de t-verdeling kentquote:
[..]
Je hebt gelijk, maar het komt uit een oud-tentamen, dus hier moet ik het helaas mee doen. Gezien het feit dat alleen de normale verdeling behandeld is, komt dit uit een normale verdeling.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb in mijn boek gelezen dat ik de t-verdeling kan gebruiken als de populatievariantie niet bekend is, en dat de steekproef uit 30 of minder personen bestaat.quote:
maar je doet alsof je ook de t-verdeling kent
Die is wel bekend; de standaarddeviatie is 6.28 staat in de opdracht.quote:
[..]
Ik heb in mijn boek gelezen dat ik de t-verdeling kan gebruiken als de populatievariantie niet bekend is, en dat de steekproef uit 30 of minder personen bestaat.
Dat is de STD van de steekproef. In de vraag staat "de populatievariantie is niet bekend. "quote:
[..]
Die is wel bekend; de standaarddeviatie is 6.28 staat in de opdracht.
Maar die kun je uitrekenen door 6.28 te kwadrateren. Dan is ze wel bekend. Zolang de vraag onduidelijk is, kun je daar toch gewoon gebruik van maken?
Prachtig, tentamen analyse bestaat voor 50% uit bewijzen, en we hebben nog nooit een bewijsopgave hoeven doen . Of ja, nooit is overdreven, maar het huiswerk was 95% calculus.
. Of ja, nooit is overdreven, maar het huiswerk was 95% calculus.
Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde puntenquote:
Prachtig, tentamen analyse bestaat voor 50% uit bewijzen, en we hebben nog nooit een bewijsopgave hoeven doen
Beneath the gold, bitter steel
Ben dus met wiskunde bezig. En nu heb ik een tweetal formules gekregen om een vector door een vlak te bereken. Echter snap ik niet helemaal hoe deze formules te gebruiken. Zou iemand misschien de formule in kunnen vullen met een voorbeeld zodat ik dit als referentie kan gebruiken? Bedankt alvast!
en de 2e formulequote:The equation of a plane (points P are on the plane with normal N and point P3 on the plane) can be written as N dot (P - P3) = 0
The equation of the line (points P on the line passing through points P1 and P2) can be written as
P = P1 + u (P2 - P1)
The intersection of these two occurs when
N dot (P1 + u (P2 - P1)) = N dot P3
quote:A plane can also be represented by the equation
A x + B y + C z + D = 0
where all points (x,y,z) lie on the plane.
Substituting in the equation of the line through points P1 (x1,y1,z1) and P2 (x2,y2,z2)
P = P1 + u (P2 - P1)
gives
A (x1 + u (x2 - x1)) + B (y1 + u (y2 - y1)) + C (z1 + u (z2 - z1)) + D = 0
De eerste formule werkt met een inwendig product. Twee vectoren (in een inwendigproductruimte) staan loodrecht op elkaar als hun inwendig product nul is. De reden waarom dat het vlak weergeeft zie je in deze figuur:
dus de vergelijking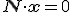
geeft alle vectoren x in het vlak.
De tweede formule is in feite hetzelfde, want
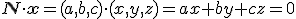
Voorbeeldje: stel dat je weet dat het punt (1,2,3) in het vlak ligt, en dat (4,5,6) een normaalvector van het vlak is. De vectoren die nu in het vlak liggen zijn de vectoren x=(x,y,z) die voldoen aan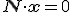. Als je dat uitwerkt krijg je 4x+5y+6z=0.
Maar dit is alleen waar als de normaalvector mooi bij de oorsprong het vlak snijdt. Als het vlak niet door de oorsprong gaat, maar wel door het punt (1,2,3) zijn de vectoren x eigenlijk x=(x-1,y-2,z-3). De vectoren zijn dan namelijk het verschil tussen een punt in het vlak en het punt dat zeker in het vlak ligt.
Dan krijg je 4(x-1)+5(y-2)+6(z-3)=0, dus 4x+5y+6z=32.
dus de vergelijking
De tweede formule is in feite hetzelfde, want
Voorbeeldje: stel dat je weet dat het punt (1,2,3) in het vlak ligt, en dat (4,5,6) een normaalvector van het vlak is. De vectoren die nu in het vlak liggen zijn de vectoren x=(x,y,z) die voldoen aan
Maar dit is alleen waar als de normaalvector mooi bij de oorsprong het vlak snijdt. Als het vlak niet door de oorsprong gaat, maar wel door het punt (1,2,3) zijn de vectoren x eigenlijk x=(x-1,y-2,z-3). De vectoren zijn dan namelijk het verschil tussen een punt in het vlak en het punt dat zeker in het vlak ligt.
Dan krijg je 4(x-1)+5(y-2)+6(z-3)=0, dus 4x+5y+6z=32.
Wat zijn dit voor rechtenpraktijken.quote:
[..]
Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde punten
Begin eens je quotes wat leesbaarder en correcter op te schrijven. En uit je vraagstelling proef ik een beetje dat je vooral een 'recept' wil hebben. Als je nu maar weet hoe je die formules in moet vullen dan ben je kennelijk tevreden. Maar dat is niet goed. Je moet begrijpen waarom die formules zijn zoals ze zijn en wat ze (meetkundig) voorstellen.quote:
Ben dus met wiskunde bezig. En nu heb ik een tweetal formules gekregen om een vector door een vlak te bereken. Echter snap ik niet helemaal hoe deze formules te gebruiken. Zou iemand misschien de formule in kunnen vullen met een voorbeeld zodat ik dit als referentie kan gebruiken? Bedankt alvast!
[..]
en de 2e formule
[..]
Eerste quote:
De vectorvergelijking van het bedoelde vlak V door punt P3 en loodrecht op vector n is:quote:The equation of a plane (points P are on the plane with normal N and point P3 on the plane) can be written as N dot (P - P3) = 0
The equation of the line (points P on the line passing through points P1 and P2) can be written as
P = P1 + u (P2 - P1)
The intersection of these two occurs when
N dot (P1 + u (P2 - P1)) = N dot P3
(1) V: n∙(p - p3) = 0
Hierbij stelt het eindpunt P van vector OP = p een willekeurig punt in het vlak V voor. Het is gemakkelijk in te zien waarom dit een vectorvoorstelling van het betreffende vlak is: als P in het vlak ligt, evenals het vaste punt P3, dan is de verschilvector OP - OP3 = p - p3 parallel aan lijnstuk PP3 in het vlak V, zodat deze verschilvector loodrecht op vector n staat en het inproduct van n en p - p3 dus gelijk is aan 0.
Tweede quote:
Om dit te begrijpen moet je weten hoe je de vectorvoorstelling (1) van een vlak V omzet in een vergelijking in cartesische coördinaten. Stel dat we hebben:quote:A plane can also be represented by the equation
A x + B y + C z + D = 0
where all points (x,y,z) lie on the plane.
Substituting in the equation of the line through points P1 (x1,y1,z1) and P2 (x2,y2,z2)
P = P1 + u (P2 - P1)
gives
A (x1 + u (x2 - x1)) + B (y1 + u (y2 - y1)) + C (z1 + u (z2 - z1)) + D = 0
(2) n = (a,b,c)
en:
(3) p3 = (x3,y3,z3)
en zij p = (x,y,z) weer de variabele vector. Dan volgt uit (1) dat het inproduct van n en p - p3 voor elke vector p = (x,y,z) met eindpunt in het betreffende vlak nul moet zijn, en dus:
(4) V: a(x - x3) + b(y - y3) + c(z - z3) = 0
Door het uitwerken van de haakjes breng je deze cartesische vergelijking voor het vlak V gemakkelijk in de standaardvorm:
(5) V: ax + by + cz + d = 0
Voor een lijn l door de punten P1 en P2 hebben we met de vaste vectoren OP1 = p1 en OP2 = p2 een vectorvoorstelling:
(6) l: p = p1 + μ∙(p2 - p1)
waarbij μ de verzameling reële getallen doorloopt. Ook dit is weer eenvoudig in te zien. Aangezien P1 en P2 op l liggen, is de verschilvector p2 - p1 parallel aan lijn l, zodat l': p = μ∙(p2 - p1) een vectorvoorstelling is van een lijn l' door de oorsprong en parallel aan l. Tellen we de vaste vector p1 hierbij op (hetgeen resulteert in een translatie langs lijnstuk OP1) dan krijgen we dus alle vectoren waarvan de eindpunten op lijn l liggen aangezien O op l' ligt en P1 op l ligt terwijl l' parallel is aan l. Schrijven we nu (6) in coördinaatvorm, dan hebben we:
(7) l: (x,y,z) = (x1 + μ(x2-x1), y1 + μ(y2-y1), z1 + μ(z2-z1))
Dit levert dus het volgende stelsel:
(8a) x = x1 + μ(x2-x1)
(8b) y = y1 + μ(y2-y1)
(8c) z = z1 + μ(z2-z1)
Substitutie van (8a), (8b) en (8c) in de cartesische vergelijking (5) van vlak V levert een lineaire vergelijking in μ op, die ons dus vertelt voor welke waarde van μ lijn l vlak V snijdt (als althans lijn l niet evenwijdig loopt aan vlak V of in vlak V ligt). Door terugsubstitueren van de aldus gevonden waarde van μ in (8a), (8b) en (8c) verkrijgen we dan de cartesische coördinaten van het snijpunt van lijn l met vlak V.
[ Bericht 0% gewijzigd door Riparius op 13-12-2011 07:29:19 ]
Herkauwen is iets voor koeien. En stamppot hoef je al helemaal niet te kauwen.quote:
[..]
Ach, het is gewoon herproduceren van wat op college is geweest dus als je dat maar stampt zijn dat gegarandeerde punten
Twaal en Riparius echt top! Riparius je hebt gelijk en wil het ook graag begrijpen, ga met je uitleg aan de slag!!
Gegeven h: R->R en d,R elementen van R.
"Er wordt gevraagd om de definitie van de definitie van de limiet waarbij x van boven d nadert voor de functie h(u), met de limiet R."
Dus lim h(u)=R (voor x->d+)
Alleen h is geen functie van x, dus moet die x geen u zijn?
[ Bericht 9% gewijzigd door Physics op 15-12-2011 17:01:45 ]
"Er wordt gevraagd om de definitie van de definitie van de limiet waarbij x van boven d nadert voor de functie h(u), met de limiet R."
Dus lim h(u)=R (voor x->d+)
Alleen h is geen functie van x, dus moet die x geen u zijn?
[ Bericht 9% gewijzigd door Physics op 15-12-2011 17:01:45 ]
Als R een element is van de reële getallen, is h geen functie.quote:
Gegeven h: R->R en d,R elementen van de reële getallen.
Gegeven (cn), een nulrij die dalend is.
Laat (an) de rij zijn met an de som van 1 naar n van (-1)k+1 ck.
Dan heb ik de volgende vragen:
1) De rij cn kan toch ook een nulrij zijn of uitkomen op een nulrij?
2) Is (an) een Cauchy-rij? En hoe kan ik dat bewijzen?
Laat (an) de rij zijn met an de som van 1 naar n van (-1)k+1 ck.
Dan heb ik de volgende vragen:
1) De rij cn kan toch ook een nulrij zijn of uitkomen op een nulrij?
2) Is (an) een Cauchy-rij? En hoe kan ik dat bewijzen?
Ik had verkeerd gelezen, er stond d,R elementen van R met h:R->Rquote:
[..]
Als R een element is van de reële getallen, is h geen functie.
Lijkt me dat ze bedoelen lim h(x)=R (voor x->d+), anders is het niet zo'n spannende limietquote:
Gegeven h: R->R en d,R elementen van R.
"Er wordt gevraagd om de definitie van de definitie van de limiet waarbij x van boven d nadert voor de functie h(u), met de limiet R."
Dus lim h(u)=R (voor x->d+)
Alleen h is geen functie van x, dus moet die x geen u zijn?
.
1) Het is toch gegeven dat (cn) een nulrij is?quote:
Gegeven (cn), een nulrij die dalend is.
Laat (an) de rij zijn met an de som van 1 naar n van (-1)k+1 ck.
Dan heb ik de volgende vragen:
1) De rij cn kan toch ook een nulrij zijn of uitkomen op een nulrij?
2) Is (an) een Cauchy-rij? En hoe kan ik dat bewijzen?
2)
Als j oneven is
Controleer dit even. Als het klopt moet je het hiermee kunnen bewijzen.
Hoi, nieuw hier, mijn eerste post.
Ik heb een vraagje over kansrekening, waar ik niet uitkwam. Je hebt 500 appels waarvan er 10 rot zijn. De appels verdeel je over 20 dozen van elk 25 appels. Hoe groot is de kans dat je een doos kiest waarin geen enkele rotte appel zit?
Nu vond ik als antwoord (490 nCr 25)/(500 nCr 25). Dus het aantal mogelijkheden om 25 appels te kiezen uit de gave appels gedeeld door het totaal aantal mogelijkheden om 25 appels te kiezen uit de 500 appels. Dat betekent dus dat een doos vullen op een willekeurige manier gelijk staat aan één doos kiezen, maar ik zie niet waarom dat zo is. Is er iemand die mij dat helder kan uitleggen, misschien aan de hand van vergelijkingen?
Ik heb een vraagje over kansrekening, waar ik niet uitkwam. Je hebt 500 appels waarvan er 10 rot zijn. De appels verdeel je over 20 dozen van elk 25 appels. Hoe groot is de kans dat je een doos kiest waarin geen enkele rotte appel zit?
Nu vond ik als antwoord (490 nCr 25)/(500 nCr 25). Dus het aantal mogelijkheden om 25 appels te kiezen uit de gave appels gedeeld door het totaal aantal mogelijkheden om 25 appels te kiezen uit de 500 appels. Dat betekent dus dat een doos vullen op een willekeurige manier gelijk staat aan één doos kiezen, maar ik zie niet waarom dat zo is. Is er iemand die mij dat helder kan uitleggen, misschien aan de hand van vergelijkingen?
Bepaal de afgeleide van f(x)=
(1) Beide zijden differentiëren naar x
F'=f=(lnt)^3
(2) d/dx (F(x^2+x)-F(x^2-x))
(3) f'(x)=ln(x^2+x)^3(2x+1)-(ln(x^2-x)^3(2x-1)
Klopt dat?
(1) Beide zijden differentiëren naar x
F'=f=(lnt)^3
(2) d/dx (F(x^2+x)-F(x^2-x))
(3) f'(x)=ln(x^2+x)^3(2x+1)-(ln(x^2-x)^3(2x-1)
Klopt dat?
Ja. Je maakt in feite gebruik van een variant van de regel van Leibniz, zie ook hier (met een aardige anecdote van Feynman).quote:
Bepaal de afgeleide van f(x)=[ afbeelding ]
(1) Beide zijden differentiëren naar x
F'=f=(lnt)^3
(2) d/dx (F(x^2+x)-F(x^2-x))
(3) f'(x)=ln(x^2+x)^3(2x+1)-(ln(x^2-x)^3(2x-1)
Klopt dat?
Er zijn 500 nCr 25 manieren om 25 appels uit 500 te pakken waar de volgorde niet van belang is (het maakt niet uit of je een appel er eerder of later in doet, het gaat er alleen om of die wel of niet in de doos zit). Er zijn 490 nCr 25 manieren om dozen te maken waar géén rotte appels in zitten (want er zijn 500-10=490 niet-rotte appels). Als je een willekeurige doos pakt, dan is de kans dus (490 nCr 25)/(500 nCr 25) dat het er 1 is zonder rotte appels.quote:Op vrijdag 16 december 2011 13:53 schreef Dobbs het volgende:
Hoi, nieuw hier, mijn eerste post.
Ik heb een vraagje over kansrekening, waar ik niet uitkwam. Je hebt 500 appels waarvan er 10 rot zijn. De appels verdeel je over 20 dozen van elk 25 appels. Hoe groot is de kans dat je een doos kiest waarin geen enkele rotte appel zit?
Nu vond ik als antwoord (490 nCr 25)/(500 nCr 25). Dus het aantal mogelijkheden om 25 appels te kiezen uit de gave appels gedeeld door het totaal aantal mogelijkheden om 25 appels te kiezen uit de 500 appels. Dat betekent dus dat een doos vullen op een willekeurige manier gelijk staat aan één doos kiezen, maar ik zie niet waarom dat zo is. Is er iemand die mij dat helder kan uitleggen, misschien aan de hand van vergelijkingen?
Dat laatste is eigenlijk hetzelfde principe als dat je 10 knikkers hebt waarvan er 1 blauw is en 9 rood. Als je dan een willekeurige knikker pakt dan is de kans dat je dan een blauwe pakt 1/10.
Ik begrijp het, bedankt!quote:
[..]
Er zijn 500 nCr 25 manieren om 25 appels uit 500 te pakken waar de volgorde niet van belang is (het maakt niet uit of je een appel er eerder of later in doet, het gaat er alleen om of die wel of niet in de doos zit). Er zijn 490 nCr 25 manieren om dozen te maken waar géén rotte appels in zitten (want er zijn 500-10=490 niet-rotte appels). Als je een willekeurige doos pakt, dan is de kans dus (490 nCr 25)/(500 nCr 25) dat het er 1 is zonder rotte appels.
Dat laatste is eigenlijk hetzelfde principe als dat je 10 knikkers hebt waarvan er 1 blauw is en 9 rood. Als je dan een willekeurige knikker pakt dan is de kans dat je dan een blauwe pakt 1/10.
relateer de delers van x+y en van xy eens aan de delers van x en van y.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
tsja. Ik snap wel dat (x+y) x niet deelt en dat (x+y) y niet deelt...
wacht, ik snap het al. (x+y) en x hebben geen gemeenschappelijke priemfactoren, en (x+y) en y ook niet, dus (x+y) heeft ook geen gemeenschappelijke priemfactoren met xy.
Thanks! Ik was even in de war met het verschil tussen delen en gemeenschappelijke priemfactoren hebben.
wacht, ik snap het al. (x+y) en x hebben geen gemeenschappelijke priemfactoren, en (x+y) en y ook niet, dus (x+y) heeft ook geen gemeenschappelijke priemfactoren met xy.
Thanks!
Ik was even in de war met het verschil tussen delen en gemeenschappelijke priemfactoren hebben.
Kan iemand mij het principe van "in the long run" bij hypothese toetsen even uitleggen?
Ik kan het niet echt vinden in mijn boek en op Google..
Ik kan het niet echt vinden in mijn boek en op Google..
Herb is the healing of a nation, alcohol is the destruction.
Ik denk dat je wat meer context moet geven. Het heeft misschien te maken met een schatter die convergeert naar de werkelijke waarde als de tijd of je sample naar oneindig gaat.quote:
Kan iemand mij het principe van "in the long run" bij hypothese toetsen even uitleggen?
Ik kan het niet echt vinden in mijn boek en op Google..
dat als je 1 onderzoek hebt en je gevonden p-waarde is kleiner dan de alpha (0,05 bijvoorbeeld). Dan mag je niet zeggen dat je onderzoek met 95% zekerheid klopt (ofzo)quote:
[..]
Ik denk dat je wat meer context moet geven. Het heeft misschien te maken met een schatter die convergeert naar de werkelijke waarde als de tijd of je sample naar oneindig gaat.
Herb is the healing of a nation, alcohol is the destruction.
Klopt mijn antwoord op de volgende vraag?:
Voor een vlakke representatie van een vlakke graaf is n het aantal knopen,
m het aantal takken en r het aantal gebieden. Wat is de kleinste waarde
die n − m + r kan aannemen?
Antwoord: Voor elke vlakke samenhangende graaf geldt n - m + r = 2. Ik vermoed dat dit ook het kleinste mogelijke waarde is. Als je een niet samenhangende graaf hebt, is die te verdelen in een aantal samenhangende grafen waarvoor voor elk van die grafen geldt n - m + r = 2.
Als je een samenhangende graaf toevoegt aan een groep samenhangende grafen, neemt het aantal gebieden met 1 minder toe dan het aantal gebieden van de nieuwe graaf, want de nieuwe graaf is bevat in een andere graaf en dan is zijn buitengebied een binnengebied van een andere graaf, of hij is niet bevat in een andere graaf en dan deelt hij het buitengebied. Dus als je een graaf toevoegt neemt n - m + r steeds met 1 toe, dus n - m + r is minstens 2, namelijk bij één samenhangende graaf.
Ik weet niet zeker of dat met het aantal gebieden goed geformuleerd is.
Ik heb nog geprobeerd om een tegenspraak af te leiden uit: stel dat n - m + r < 2, maar dat lukte mij nog niet.
Voor een vlakke representatie van een vlakke graaf is n het aantal knopen,
m het aantal takken en r het aantal gebieden. Wat is de kleinste waarde
die n − m + r kan aannemen?
Antwoord: Voor elke vlakke samenhangende graaf geldt n - m + r = 2. Ik vermoed dat dit ook het kleinste mogelijke waarde is. Als je een niet samenhangende graaf hebt, is die te verdelen in een aantal samenhangende grafen waarvoor voor elk van die grafen geldt n - m + r = 2.
Als je een samenhangende graaf toevoegt aan een groep samenhangende grafen, neemt het aantal gebieden met 1 minder toe dan het aantal gebieden van de nieuwe graaf, want de nieuwe graaf is bevat in een andere graaf en dan is zijn buitengebied een binnengebied van een andere graaf, of hij is niet bevat in een andere graaf en dan deelt hij het buitengebied. Dus als je een graaf toevoegt neemt n - m + r steeds met 1 toe, dus n - m + r is minstens 2, namelijk bij één samenhangende graaf.
Ik weet niet zeker of dat met het aantal gebieden goed geformuleerd is.
Ik heb nog geprobeerd om een tegenspraak af te leiden uit: stel dat n - m + r < 2, maar dat lukte mij nog niet.
Dan moet je even post #209 t/m #218 lezen van dit topic.quote:Op dinsdag 20 december 2011 18:35 schreef DuTank het volgende:
[..]
dat als je 1 onderzoek hebt en je gevonden p-waarde is kleiner dan de alpha (0,05 bijvoorbeeld). Dan mag je niet zeggen dat je onderzoek met 95% zekerheid klopt (ofzo)
De moeilijkheid zit erin dat j even en oneven kan zijn.quote:
[..]
1) Het is toch gegeven dat (cn) een nulrij is?
2)
Als j oneven is
Controleer dit even. Als het klopt moet je het hiermee kunnen bewijzen.
Maar ik heb het nu zo opgelost:
Eerst heb ik bewezen dat voor iedere m geldt: a2m=<an=<a2m+1 met n>2m+1.
En met dit volgt het vrij snel.
Bedankt!
Heyhey, ik had een vraagje!
Als je hebt: 2x • ln(x) - x = 0, hoe moet je dan verder? Wss is het iets heel simpels, maar ik heb me er zo op doodgestaard dat ik het niet zie.
Hopelijk kan iemand me helpen!
Als je hebt: 2x • ln(x) - x = 0, hoe moet je dan verder? Wss is het iets heel simpels, maar ik heb me er zo op doodgestaard dat ik het niet zie.
Hopelijk kan iemand me helpen!
factoriseren, schrijf het als x(... - ...) = 0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat was snelquote:
factoriseren, schrijf het als x(... - ...) = 0.
Ik snap hem nu, enorm bedankt!
Dan krijg je x=0 of x=exp(1/2). Let dan wel op dat x=0 geen valide antwoord is, sinds ln(0) niet bestaat.
s/sinds/omdatquote:Op woensdag 21 december 2011 18:10 schreef zoem het volgende:
Dan krijg je x=0 of x=exp(1/2). Let dan wel op dat x=0 geen valide antwoord is, sinds ln(0) niet bestaat.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wat wil je nou zeggen? Het woordje sinds is misschien niet helemaal goed, maar dat komt omdat ik het Engels since gewend ben. Maar dit topic lijkt me niet de plek om over taalfouten te vallen?quote:
Op zich is je redenering goed, maar ik zou de waarde van n-m+r gewoon uitrekenen door n, m en r te schrijven als de som van de n_i, m_i en r_i van de samenhangende componenten.quote:
Klopt mijn antwoord op de volgende vraag?:
Voor een vlakke representatie van een vlakke graaf is n het aantal knopen,
m het aantal takken en r het aantal gebieden. Wat is de kleinste waarde
die n − m + r kan aannemen?
Antwoord: Voor elke vlakke samenhangende graaf geldt n - m + r = 2. Ik vermoed dat dit ook het kleinste mogelijke waarde is. Als je een niet samenhangende graaf hebt, is die te verdelen in een aantal samenhangende grafen waarvoor voor elk van die grafen geldt n - m + r = 2.
Als je een samenhangende graaf toevoegt aan een groep samenhangende grafen, neemt het aantal gebieden met 1 minder toe dan het aantal gebieden van de nieuwe graaf, want de nieuwe graaf is bevat in een andere graaf en dan is zijn buitengebied een binnengebied van een andere graaf, of hij is niet bevat in een andere graaf en dan deelt hij het buitengebied. Dus als je een graaf toevoegt neemt n - m + r steeds met 1 toe, dus n - m + r is minstens 2, namelijk bij één samenhangende graaf.
Ik weet niet zeker of dat met het aantal gebieden goed geformuleerd is.
Ik heb nog geprobeerd om een tegenspraak af te leiden uit: stel dat n - m + r < 2, maar dat lukte mij nog niet.
Iemand hier met Matlab kennis?
Ik heb een 3-plaatsige functie gedefinieerd. Als ik handmatig waarden invul doet ie precies wat ik wil, bijvoorbeeld f(1,2,3)=1. Maar als ik een vector X = [1,2,3] genereer dan geeft ie geen resultaat als ik f(X) (=f([1,2,3]) wil evalueren terwijl ik natuurlijk de output f(1,2,3) zou willen hebben. Ik wil dus eigenlijk een functie definiëren die wel arrays/vectors kan evalueren maar weet niet hoe.
Ben je er de hele tijd mee bezig zonder succes, post je het, en een minuut later vind je het opeens zelf.
[ Bericht 4% gewijzigd door thenxero op 24-12-2011 01:28:44 ]
Ik heb een 3-plaatsige functie gedefinieerd. Als ik handmatig waarden invul doet ie precies wat ik wil, bijvoorbeeld f(1,2,3)=1. Maar als ik een vector X = [1,2,3] genereer dan geeft ie geen resultaat als ik f(X) (=f([1,2,3]) wil evalueren terwijl ik natuurlijk de output f(1,2,3) zou willen hebben. Ik wil dus eigenlijk een functie definiëren die wel arrays/vectors kan evalueren maar weet niet hoe.
Ben je er de hele tijd mee bezig zonder succes, post je het, en een minuut later vind je het opeens zelf.
[ Bericht 4% gewijzigd door thenxero op 24-12-2011 01:28:44 ]
Ik ben nog steeds benieuwd hoe je dat gedaan hebt, heb je die functie met 'inline' gedefinieerd of op een andere manier?quote:
Iemand hier met Matlab kennis?
Ik heb een 3-plaatsige functie gedefinieerd. Als ik handmatig waarden invul doet ie precies wat ik wil, bijvoorbeeld f(1,2,3)=1. Maar als ik een vector X = [1,2,3] genereer dan geeft ie geen resultaat als ik f(X) (=f([1,2,3]) wil evalueren terwijl ik natuurlijk de output f(1,2,3) zou willen hebben. Ik wil dus eigenlijk een functie definiëren die wel arrays/vectors kan evalueren maar weet niet hoe.
Ben je er de hele tijd mee bezig zonder succes, post je het, en een minuut later vind je het opeens zelf.
Beneath the gold, bitter steel
Het was een functie die gedefinieerd is op basis van if statements:
Eerst had ik zoiets als
function [C] = f(a,b,c)
if a==1 || b==2
x1=0;
else
x1=1;
...
etc etc
...
C = x1 + x2 + ...
Maar dat werkte niet. Dat heb ik veranderd in
function [C] = f(x)
if x(1)==1 || x(1)==2
x1=0;
else
x1=1;
...
etc etc
...
C = x1 + x2 + ...
Die functie heb ik gedefinieerd in een apart m-bestand.
[ Bericht 4% gewijzigd door thenxero op 24-12-2011 01:49:13 ]
Eerst had ik zoiets als
function [C] = f(a,b,c)
if a==1 || b==2
x1=0;
else
x1=1;
...
etc etc
...
C = x1 + x2 + ...
Maar dat werkte niet. Dat heb ik veranderd in
function [C] = f(x)
if x(1)==1 || x(1)==2
x1=0;
else
x1=1;
...
etc etc
...
C = x1 + x2 + ...
Die functie heb ik gedefinieerd in een apart m-bestand.
[ Bericht 4% gewijzigd door thenxero op 24-12-2011 01:49:13 ]
Ah een functie functie Ik moest denken aan een normale continue differentieerbare functie.
Die kan je erg makkelijk definiëren met http://www.mathworks.nl/help/techdoc/ref/inline.html
Voor jouw soort van functie moet je inderdaad een apart .m file aanmaken.
Maar volgens mij had je eerste methode gewoon moeten werken, op de manier dat jij het schrijft werkt het bij mij gewoon.
Ik moest denken aan een normale continue differentieerbare functie.Die kan je erg makkelijk definiëren met http://www.mathworks.nl/help/techdoc/ref/inline.html
Voor jouw soort van functie moet je inderdaad een apart .m file aanmaken.
Maar volgens mij had je eerste methode gewoon moeten werken, op de manier dat jij het schrijft werkt het bij mij gewoon.
Beneath the gold, bitter steel
Hmm vreemd dat ie het bij jou wel doet. Ik stopte steeds permutaties die door randperm(3) gegenereerd werden in de functie maar dat gaf geen antwoord.
Maar nu je er toch bent even snel nog een vraag
.
Ik heb een for-loop waarbij ik steeds een permutatie genereer en dus steeds die functie evalueer. Al die functiewaardes komen in een vector te staan. Daarna kijk ik welk vectorelement minimaal is. Maar ik wil ook de bijbehorende permutatie vinden waarbij dat minimum (of die minima) voorkomt. Hoe doe je zoiets?
Maar nu je er toch bent even snel nog een vraag
.Ik heb een for-loop waarbij ik steeds een permutatie genereer en dus steeds die functie evalueer. Al die functiewaardes komen in een vector te staan. Daarna kijk ik welk vectorelement minimaal is. Maar ik wil ook de bijbehorende permutatie vinden waarbij dat minimum (of die minima) voorkomt. Hoe doe je zoiets?
Het is me al gelukt met het commando find. Het is een hoop gepruts maar langzaam maar zeker ga ik vooruit.
Vraagje over besliskunde/modelleren.
Er zijn n steden en de afstand tussen stad i en stad j is bekend (i,j = 1; 2,...,n). De afstand tussen stad i en zichzelf is oneindig.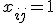
als er een route tussen stad i en j bestaat, en anders 0.
Je wilt een rondreis maken met een zo kort mogelijk afgelegde afstand. Je neemt de volgende beperkingen:
1) voor iedere stad is er precies één route naar die stad.
2) voor iedere stad is er precies één route naar een andere stad.
Dit model is nog niet correct.
Laat de route in plaats 1 beginnen en interpreteer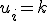
, wanneer plaats i als k-de stad vanuit
stad 1 wordt bezocht.
Toon aan dat het model wel correct is met deze extra beperking:
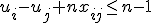voor alle 
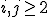en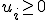 
en geheel voor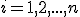 
Mijn idee is dat het eerste model niet correct is omdat er meerdere kringen steden kunnen ontstaan, die niet met elkaar verbonden zijn en je zo dus niet elke stad kan bezoeken.
Mijn vraag is of je de extra beperking niet kan vervangen door alleen het geval dat.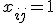
Dan komt de extra beperking neer op: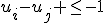
voor i en j groter dan 2.
Dus stad i wordt eerder bezocht dan stad j als er een route van i naar j is. Vanwege beperkingen 1) en 2) is er een route tussen de laatste stad en stad 1. Ik zie niet hoe er dan nog iets mis kan gaan. Een andere kring dan de kring die plaats 1 bevat kan niet bestaan en losse steden ook niet vanwege beperkingen 1 en 2.
Is de beperking in het geval dat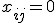
, namelijk 
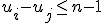, nodig?
Er zijn n steden en de afstand tussen stad i en stad j is bekend (i,j = 1; 2,...,n). De afstand tussen stad i en zichzelf is oneindig.
Je wilt een rondreis maken met een zo kort mogelijk afgelegde afstand. Je neemt de volgende beperkingen:
1) voor iedere stad is er precies één route naar die stad.
2) voor iedere stad is er precies één route naar een andere stad.
Dit model is nog niet correct.
Laat de route in plaats 1 beginnen en interpreteer
stad 1 wordt bezocht.
Toon aan dat het model wel correct is met deze extra beperking:
Mijn idee is dat het eerste model niet correct is omdat er meerdere kringen steden kunnen ontstaan, die niet met elkaar verbonden zijn en je zo dus niet elke stad kan bezoeken.
Mijn vraag is of je de extra beperking niet kan vervangen door alleen het geval dat
Dan komt de extra beperking neer op:
Dus stad i wordt eerder bezocht dan stad j als er een route van i naar j is. Vanwege beperkingen 1) en 2) is er een route tussen de laatste stad en stad 1. Ik zie niet hoe er dan nog iets mis kan gaan. Een andere kring dan de kring die plaats 1 bevat kan niet bestaan en losse steden ook niet vanwege beperkingen 1 en 2.
Is de beperking in het geval dat
Staat xij voor de afstand tussen stad i en j ?
Wat wordt er precies bedoeld met voorwaarden (1) en (2)? Is er 1 mogelijke route (bijv: je kan alleen in stad 4 komen vanuit stad 3) of neem je een enkele route (zodat je niet vaker in dezelfde stad komt) ?
Wat wordt er precies bedoeld met voorwaarden (1) en (2)? Is er 1 mogelijke route (bijv: je kan alleen in stad 4 komen vanuit stad 3) of neem je een enkele route (zodat je niet vaker in dezelfde stad komt) ?
De vraag is erg onduidelijk omdat het begrip route niet gangbaar is. Ik vermoed dat je "er een route tussen stad i en j bestaat" moet lezen als "de weg van stad i naar j gebruikt wordt" (de volgorde i/j is belangrijk).
Jouw vraag is daarmee beantwoordt, want x_ij is geen parameter. Maw je krijgt geen mixed integer probleem als je de aanwezigheid van een constraint conditioneert op de waarde van een variabele.
Het model is wel correct. Je kunt geen twee kringen krijgen; de notatie van die extra beperking laat dat niet toe.
Jouw vraag is daarmee beantwoordt, want x_ij is geen parameter. Maw je krijgt geen mixed integer probleem als je de aanwezigheid van een constraint conditioneert op de waarde van een variabele.
Het model is wel correct. Je kunt geen twee kringen krijgen; de notatie van die extra beperking laat dat niet toe.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Op universiteiten werkt iedereen morgen weer.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Klopt, en bedankt.quote:
De vraag is erg onduidelijk omdat het begrip route niet gangbaar is. Ik vermoed dat je "er een route tussen stad i en j bestaat" moet lezen als "de weg van stad i naar j gebruikt wordt" (de volgorde i/j is belangrijk).
.
Je hebt wel gelijk met dat je de constraint alleen voor x_ij=1 wilt laten gelden. Dit is een big-M constraint want voor x_ij=0 weet je dat er sowieso aan voldaan wordt). Cplex heeft ondersteuning indicator constraints: https://www-304.ibm.com/support/docview.wss?uid=swg21400084
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kan iemand misschien toelichten waarom
| x + a | < b = -b < x + a <b ?
In mijn boek wordt dit als "regel" gegeven, maar ik wil het ook snappen.
| x + a | = b kan worden opgelost door
x + a = b en x + a = - b op te lossen. Ik dacht dus ook dit toe te passen op | x + a | < b. Kortom:
x + a < b en x + a < - b op te lossen. Maar hier kom ik niet op het juiste antwoord, omdat dat het ingelijkheidsteken bij beide dezelfde kant op wijst.
Bij voorbaat dank.
| x + a | < b = -b < x + a <b ?
In mijn boek wordt dit als "regel" gegeven, maar ik wil het ook snappen.
| x + a | = b kan worden opgelost door
x + a = b en x + a = - b op te lossen. Ik dacht dus ook dit toe te passen op | x + a | < b. Kortom:
x + a < b en x + a < - b op te lossen. Maar hier kom ik niet op het juiste antwoord, omdat dat het ingelijkheidsteken bij beide dezelfde kant op wijst.
Bij voorbaat dank.
Je regel om |x+a|=b op te lossen is niet helemaal goed, je moet namelijk dan x+a=b en -(x+a)=b oplossen. Bij het gelijkheidsteken maakt dat niet uit, maar bij het >-teken klapt het teken om bij vermenigvuldiging met een negatief getal. Dan kom je wel op het goede antwoord.quote:
Kan iemand misschien toelichten waarom
| x + a | < b = -b < x + a <b ?
In mijn boek wordt dit als "regel" gegeven, maar ik wil het ook snappen.
| x + a | = b kan worden opgelost door
x + a = b en x + a = - b op te lossen. Ik dacht dus ook dit toe te passen op | x + a | < b. Kortom:
x + a < b en x + a < - b op te lossen. Maar hier kom ik niet op het juiste antwoord, omdat dat het ingelijkheidsteken bij beide dezelfde kant op wijst.
Bij voorbaat dank.
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
