SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Game onquote:Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
quote:Op donderdag 3 oktober 2013 22:57 schreef Johan_Haas_ het volgende:
(1-Y) * (ph/ (1-ph*HB) = Y* 1/HB Hoe vereenvoudig je dit door HB de functie te maken van Ph
Hoe kom je op HB = Y/ PH.
(1-y) * ph/(1-phHB)= y 1/Hb
Kan iemand me de stappen laten zien? Hoe kan ik breuken laten zien op het forum ?
Zo zou ik het in ieder geval doen.quote:
Stap drie is misschien niet helemaal netjes/duidelijk, ik heb daar Y meteen vermenigvuldigd met 1 - phHB.
Als je, zoals je zegt, bijvoorbeeld breuken wilt laten zien, dan kan je gebruik maken van de [tex][/tex] tags. Uitleg over wat je er zoal mee kunt, kun je in de link in de OP vinden.
[ Bericht 3% gewijzigd door jordyqwerty op 03-10-2013 23:42:42 ]
Snap alleen stap 1 naar 2 niet Voor de duidelijkheid 1 is de beginformule die naar 3 moet worden herleid
1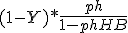
= 
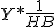
2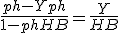
Wat doe je in deze stap?
Hardstikke bedankt trouwens! De breuken werken ook makkelijk hier
3 Uiteindelijke oplossing
HB =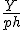
1
2
Wat doe je in deze stap?
Hardstikke bedankt trouwens! De breuken werken ook makkelijk hier
3 Uiteindelijke oplossing
HB =
a(1-b) = a-abquote:
Snap alleen stap 1 naar 2 niet
1
2
Wat doe je in deze stap?
Hardstikke bedankt trouwens!
Fervent tegenstander van het korps lasergamers.
Je vermenigvuldigd de termen met de teller.quote:
Snap alleen stap 1 naar 2 niet
1
2
Wat doe je in deze stap?
Hardstikke bedankt trouwens!
Voorbeelden ter illustratie;
Bedankt, snap het Nooit geweten dat dat zomaar kon, heb het met getallen nagerekend en het kan inderdaad gewoon en het klopt. Ik moet meer die ab regeltjes oefenen met breuken
Nooit geweten dat dat zomaar kon, heb het met getallen nagerekend en het kan inderdaad gewoon en het klopt. Ik moet meer die ab regeltjes oefenen met breuken
Hoe gaat deze kom hier na lang proberen niet uit. solving voor Ht+1
1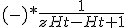
+ 
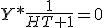
2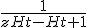
= 
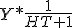
3 =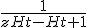 
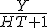
Hoe nu verder, stap 2 en 3 heb ik zelf gedaan. Als ik noemer nou gelijk maak, dus ZhT en - naar rechtsboven sleep, ?
Ga nu slapen en erover nadenken
uitkomst moet zijn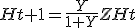
1
2
3
Hoe nu verder, stap 2 en 3 heb ik zelf gedaan. Als ik noemer nou gelijk maak, dus ZhT en - naar rechtsboven sleep, ?
Ga nu slapen en erover nadenken
uitkomst moet zijn
Dit is niet al te moeilijk om met de hand uit te rekenen. Als je het op een andere manier wilt doen, kan je gebruiken dat:quote:
2 23 > 3 13?
Hoe los je zoiets op zonder GR?
22 ≈ 31, maar
22 > 31, want 4 > 3 (1)
23 ≈ 32, maar
23 < 32, want 8 < 9 (2)
Met deze ongelijkheden kunnen we 'grotere' ongelijkheden makkelijk aantonen: als we bijvoorbeeld de eerste ongelijkheid tot de macht 10 nemen krijgen we de gelijkheid 220 > 310. Het verschil tussen deze twee gelijkheden is blijkbaar te groot, het lukt niet om 223 > 313 of 223 < 313 te laten zien. We hebben blijkbaar soortgelijke ongelijkheden nodig waar de twee- en de driemacht dichten bij elkaar zitten. Deze kunnen we proberen te maken door de al gevonden gelijkheden met elkaar te vermenigvuldigen:
We kunnen proberen de twee- en de driemacht dicht bij elkaar te krijgen door met ongelijkheid (1) te vermenigvuldigen als we een ongelijkheid van de vorm 2x < 3y hebben, en met ongelijkheid (2) als we een ongelijkheid van de vorm 2x > 3y hebben. We moeten de getallen 2x en 3y dan wel met de hand uitwerken, totdat we een combinatie van ongelijkheden vinden waaruit we 223 > 313 of 223 < 313 kunnen bewijzen.
Zo vinden we:
25 = 32 > 27 = 33 (3)
28 = 256 > 243 = 35 (4)
en omdat 23 = 8 + 8 + 5 + 2
kunnen we door ongelijkheid (4) achtereenvolgens te vermenigvuldigen met ongelijkheid (4), (3) en tenslotte (1), vinden:
223 > 314, wat nog een sterker resultaat is dan 223 > 313
(merk op: als a > b en c > d en a, b, c, d > 0, dan ac > bd. Dit bedoel ik met 'twee ongelijkheden vermenigvuldigen')
Dit is de enige manier die ik zo kan bedenken, en ik weet niet of dit echt veel makkelijker is dan gewoon de getallen uitrekenen. Het is wel zo dat hoe groter het verschil, hoe makkelijker de ongelijkheid aan is te tonen. (24 < 3100 is bijvoorbeeld door alleen formule (2) te gebruiken aan te tonen)
[ Bericht 4% gewijzigd door randomo op 05-10-2013 16:29:41 ]
Tja, da's een leuke. Ik zou het als volgt doen. Je weet dat √2 = 21/2 tussen 1,4 en 1,5 ligt, want 1,42 = 1,96 terwijl 1,52 = 2,25. Verder weet je ook dat √3 = 31/2 tussen 1,7 en 1,8 ligt, want 1,72 = 2,89 terwijl 1,82 = 3,24.quote:
2 23 > 3 13?
Hoe los je zoiets op zonder GR?
Nu heb je ook
25/2 = 22·21/2 = 4·21/2
en
33/2 = 31·31/2 = 3·31/2
Dus weten we nu dat
5,6 < 25/2 < 6,0
en
5,1 < 33/2 < 5,4
zodat
25/2 > 33/2
Hieruit volgt dat ook
(25/2)9 > (33/2)9
oftewel
222,5 > 313,5
En aangezien
223 > 222,5
heb je dus ook
223 > 313,5
En omdat ook
313,5 > 313
volgt dus inderdaad dat
223 > 313
QED
Nee. En weet je hoe dat komt? Omdat je geen flauw idee hebt van het rekenen met breuken. Dat had je op de lagere school moeten leren, maar dat is kennelijk - om welke reden dan ook - niet gebeurd. Ga daarom eerst deze cursus eens compleet doorwerken. Pas daarna heeft het zin om verder te gaan.quote:
Hoe gaat deze kom hier na lang proberen niet uit.
Ik volg de bèta topics nu al een aantal jaren, en ik denk altijd dat het niet gekker kan worden, maar ik moet spijtig genoeg steeds constateren dat ik me vergis. Wat je hier zegt is iets wat alleen de huidige sleep- en klikgeneratie zou kunnen bedenken.quote:Hoe nu verder, stap 2 en 3 heb ik zelf gedaan. Als ik noemer nou gelijk maak, dus ZhT en - naar rechtsboven sleep, ?
Nou nee. Je negeert om te beginnen het onderscheid tussen hoofdletters en kleine letters, en verder heb je kennelijk ook niet in de gaten dat de t hier zo te zien een index of parameter is en dat het er om gaat Ht+1 uit te drukken in Ht.quote:uitkomst moet zijn
Ik bedacht nadat ik jouw uiteenzetting had gelezen dat je hebt 25 > 33 dus (25)23/5 > (33)23/5 oftewel 223 > 313,8 > 313, QED. Nog eenvoudiger zal moeilijk gaan en dit is toch echt veel gemakkelijker dan uitrekenen.quote:
[..]
Dit is de enige manier die ik zo kan bedenken, en ik weet niet of dit echt veel makkelijker is dan gewoon de getallen uitrekenen.
Dat is wel een mooie ja! Om de een of andere reden dacht ik dat het makkelijker zou worden als ik alleen gehele getallen zou gebruiken, maar dat valt dus vies tegenquote:
[..]
Ik bedacht nadat ik jouw uiteenzetting had gelezen dat je hebt 25 > 33 dus (25)23/5 > (33)23/5 oftewel 223 > 313,8 > 313, QED. Nog eenvoudiger zal moeilijk gaan en dit is toch echt veel gemakkelijker dan uitrekenen.
Maar goed, die 223 en 313 uitrekenen is natuurlijk gewoon het simpel toepassen van een algoritme, terwijl het maar de vraag is of het afleiden van zoiets snel en elegant lukt.
Vast erg simpel tussen dit, maar:
stel ik heb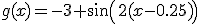
en ik moet aangeven hoe die uit de standaardgrafiek ontstaat
maakt het dan uit of ik eerst transleer of vermenigvuldig?
stel ik heb
maakt het dan uit of ik eerst transleer of vermenigvuldig?
De volgorde is niet bijzonder van belang zover ik weet, zolang je maar consistent bent zou ik zeggen.
Persoonlijk zou ik gaan voor sin(x)->sin(2x)->sin(2x-0.5)->sin(2x-0.5)-3
Dus een sinus die eerst 2 keer zo dun is, daarna een faseverschuiving ziet (ipv 0,0 zit het nulpunt op 0.5,0) Vervolgens schop je het hele ding drie omlaag.
Persoonlijk zou ik gaan voor sin(x)->sin(2x)->sin(2x-0.5)->sin(2x-0.5)-3
Dus een sinus die eerst 2 keer zo dun is, daarna een faseverschuiving ziet (ipv 0,0 zit het nulpunt op 0.5,0) Vervolgens schop je het hele ding drie omlaag.
Voor kleine exponenten lukt dit zeker. Voor m,n > 0 heb je immers 2m > 3n als m/n > log(3)/log(2) ≈ 1,585, dus is m = 5, n = 3 een goede keuze, want dan is m/n = 5/3 ≈ 1,667. En een hele goede keuze is dan m = 8, n = 5, want dan is m/n = 8/5 = 1,6. Maar het wordt lastiger bij grote exponenten en als de waarden van de machten dichter bij elkaar liggen. Als je uitsluitend met pen en papier zou willen nagaan of bijvoorbeeld 23162 nu groter of kleiner is dan 31995 dan zijn zelfs opa's logaritmentafels in vijf decimalen niet meer toereikend. En ik hoop niet dat je nu het advies blijft geven om het dan maar met de hand uit te rekenen omdat het algoritme zo lekker simpel is.quote:
[..]
Dat is wel een mooie ja! Om de een of andere reden dacht ik dat het makkelijker zou worden als ik alleen gehele getallen zou gebruiken, maar dat valt dus vies tegen
Maar goed, die 223 en 313 uitrekenen is natuurlijk gewoon het simpel toepassen van een algoritme, terwijl het maar de vraag is of het afleiden van zoiets snel en elegant lukt.
Ik weet niet wat je bedoelt met transleer/vermenigvuldig. Maar ik zou denken:quote:
Vast erg simpel tussen dit, maar:
stel ik heb
maakt het dan uit of ik eerst transleer of vermenigvuldig?
normale sin: f(x)=sin(x).
-3 betekent dat je evenwichtslijn bij -3 ligt. Dus als je +3 doet heb je sin(2(x-0.25)). Ik zie trouwens niet wat je hebt staan voor je amplitude. Die 2 geeft aan dat je grafiek/figuur naar links is gegaan met 2. Die -.25 betekent dat je grafiek naar rechts is gegaan met 0.25. Dus als je rekent met radialen/graden/etc kun je aangeven hoe die uit de normale grafiek is gekomen.
Ik geloof dat je dan de volgende variabele krijgt:
a= hier komt je amplitude, maar dit weet ik even niet...
b= -3 dit is de waarde voor je evenwichtslijn
c= 2pi/2 voor het verschuiven van de grafiek/dit heeft met de periode van je grafiek te maken, dus in jouw geval is pi 1 periode in je sinusgrafiek.
d=-.25 dit is de verschuiving naar rechts.
Riparius/Bram/iemand, kun jij mij verbeteren? Dit is training voor mezelf zodat ik de stof beter begrijp.
Amplitude is 1, immers de sinus zelf wordt nergens mee vermenigvuldigdquote:
Ik weet niet wat je bedoelt met transleer/vermenigvuldig. Maar ik zou denken:
Dat ligt eraan welke variable je voor welk aspect van zo'n sinusfunctie definieert. Het algemene geval wordt beschreven door f(x)=a+b*sin(c(x+d)). Hierin is:quote:
[..]
Ik weet niet wat je bedoelt met transleer/vermenigvuldig. Maar ik zou denken:
normale sin: f(x)=sin(x).
-3 betekent dat je evenwichtslijn bij -3 ligt. Dus als je +3 doet heb je sin(2(x-0.25)). Ik zie trouwens niet wat je hebt staan voor je amplitude. Die 2 geeft aan dat je grafiek/figuur naar links is gegaan met 2. Die -.25 betekent dat je grafiek naar rechts is gegaan met 0.25. Dus als je rekent met radialen/graden/etc kun je aangeven hoe die uit de normale grafiek is gekomen.
Ik geloof dat je dan de volgende variabele krijgt:
a= hier komt je amplitude, maar dit weet ik even niet...
b= -3 dit is de waarde voor je evenwichtslijn
c= 2pi/2 voor het verschuiven van de grafiek/dit heeft met de periode van je grafiek te maken, dus in jouw geval is pi 1 periode in je sinusgrafiek.
d=-.25 dit is de verschuiving naar rechts.
Riparius/Bram/iemand, kun jij mij verbeteren? Dit is training voor mezelf zodat ik de stof beter begrijp.
a = de verschuiving langs de y-as.
d = de verschuiving langs de x-as. LET OP!!: De eigenlijke verschuiving is het tegengestelde van de waarde d, oftewel, exact de andere kant van de x-as op.
b = de expansiefactor in de y-richting a.k.a. de verticale richting.
c = de, let op nu, compressiefactor in de x-richting a.k.a. de horizontale richting. Net als de parameter d in dezen is het effect op de grafiek exact het tegenovergestelde van de waarde b (compressie ipv van expansie met factor c).
EDIT: Ja die dubbele haken zijn belangrijk!! Vergelijk de translatie van sin(x+½π) tov sin(x) vergeleken met sin(2x+½π) tov sin(2x). De eerste twee zijn verschoven van elkaar met translatie T:(-½π,0,0), de laatste twee met translatie T:(-¼π,0,0). Dit omdat het argument (2x+½π) te schrijven valt als (2(x+¼π)).
[ Bericht 1% gewijzigd door VanishedEntity op 09-10-2013 19:50:00 ]
a = evenwichtsstand en dat is -3quote:
[..]
Ik weet niet wat je bedoelt met transleer/vermenigvuldig. Maar ik zou denken:
normale sin: f(x)=sin(x).
-3 betekent dat je evenwichtslijn bij -3 ligt. Dus als je +3 doet heb je sin(2(x-0.25)). Ik zie trouwens niet wat je hebt staan voor je amplitude. Die 2 geeft aan dat je grafiek/figuur naar links is gegaan met 2. Die -.25 betekent dat je grafiek naar rechts is gegaan met 0.25. Dus als je rekent met radialen/graden/etc kun je aangeven hoe die uit de normale grafiek is gekomen.
Ik geloof dat je dan de volgende variabele krijgt:
a= hier komt je amplitude, maar dit weet ik even niet...
b= -3 dit is de waarde voor je evenwichtslijn
c= 2pi/2 voor het verschuiven van de grafiek/dit heeft met de periode van je grafiek te maken, dus in jouw geval is pi 1 periode in je sinusgrafiek.
d=-.25 dit is de verschuiving naar rechts.
Riparius/Bram/iemand, kun jij mij verbeteren? Dit is training voor mezelf zodat ik de stof beter begrijp.
b= amplitude en dat is 1
c = periode = 2pi/2= pi
d= beginpunt = 1/4
maar dat was niet de vraag, vraag was om aan te tonen hoe de grafiek ontstaat uit de standaardgrafiek y=sin(x). (dus via pijltjes de transformaties aantonen)
Je hebtquote:
[..]
a = evenwichtsstand en dat is -3
b= amplitude en dat is 1
c = periode = 2pi/2= pi
d= beginpunt = 1/4
maar dat was niet de vraag, vraag was om aan te tonen hoe de grafiek ontstaat uit de standaardgrafiek y=sin(x). (dus via pijltjes de transformaties aantonen)
f(x) = sin(x)
en g(x) = -3 + sin(2x - 1/2)
Eerst transleer je de grafiek nog over (1/2, -3), en dan vermenigvuldig je f(x) t.o.v. de y-as met 1/2. Dat is dan g(x).
Fervent tegenstander van het korps lasergamers.
Voor welke waarde van q (uitgedrukt in r) is de onderstaande functie f(a, b) homogeen en wat is
de bijbehorende graad?
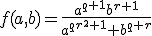
Ik heb geen idee hoe ik dit aan moet pakken, stel ik vul in (ta,tb):
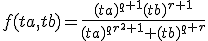
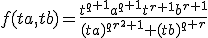
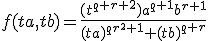
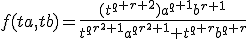
Verder (mocht dit goed zijn) kom ik niet. Iemand die me (verder) op weg kan helpen?
de bijbehorende graad?
Ik heb geen idee hoe ik dit aan moet pakken, stel ik vul in (ta,tb):
Verder (mocht dit goed zijn) kom ik niet. Iemand die me (verder) op weg kan helpen?
Kijk eerst eens naar de noemer. Dat is een homogeen polynoom alsquote:Op woensdag 9 oktober 2013 16:22 schreef jordyqwerty het volgende:
Voor welke waarde van q (uitgedrukt in r) is de onderstaande functie f(a, b) homogeen en wat is
de bijbehorende graad?
qr2 + 1 = q + r
Wat vind je dan voor q uitgedrukt in r?
qr2 + 1 = q + r
qr2 -q = r - 1
q(r2-1) = r - 1
q = (r-1)/(r2-1)
Begrijp ik goed dat als q deze 'waarde' heeft, de noemer dan homogeen is?
qr2 -q = r - 1
q(r2-1) = r - 1
q = (r-1)/(r2-1)
Begrijp ik goed dat als q deze 'waarde' heeft, de noemer dan homogeen is?
Ja, dan is de noemer uiteraard een homogeen polynoom in a en b, want dan zijn de termen toch van dezelfde graad? En dan ga je vervolgens naar de teller kijken. Maar vóór je dit doet moet je eerst de waarde die je voor q hebt gevonden nog verder herleiden.quote:
qr2 + 1 = q + r
qr2 -q = r - 1
q(r2-1) = r - 1
q = (r-1)/(r2-1)
Begrijp ik goed dat als q deze 'waarde' heeft, de noemer dan homogeen is?
1/(r+1) ?quote:
[..]
Ja, dan is de noemer uiteraard een homogeen polynoom in a en b, want dan zijn de termen toch van dezelfde graad? En dan ga je vervolgens naar de teller kijken. Maar vóór je dit doet moet je eerst de waarde die je voor q hebt gevonden nog verder herleiden.
Inderdaad. En als je nu q = 1/(r + 1) invult, wat wordt dan de graad van de term in de teller en wat is dan de graad van het polynoom in de noemer? Dus wat kun je nu zeggen over f(a,b) ?quote:
Die is er zeker, volgens mij in het MATH menu en dan FRAC (bij de TI-84)quote:
Vraag over gr,
is er een mode waarin je het antwoord ziet in breuken i.p.v. decimalen?
Dank je man!quote:
[..]
Die is er zeker, volgens mij in het MATH menu en dan FRAC (bij de TI-84)
Als je stelt dat qr2 +1 = q + r, mag je dan ook zeggen dat de graad van homogeniteit twee is? Tenzij r = 1 of -1quote:
[..]
Inderdaad. En als je nu q = 1/(r + 1) invult, wat wordt dan de graad van de term in de teller en wat is dan de graad van het polynoom in de noemer? Dus wat kun je nu zeggen over f(a,b) ?
Homogeniteit is eigenlijk toch gewoon als een functie volledig uit één macht bestaat? Bijvoorbeeld f(x) = 3x + 5x dan is hij homogeen met graad 1 en f(x) 3x^5 + 5x^5 dan is hij homogeen met graad 5?
In die gevallen wel jaquote:
Homogeniteit is eigenlijk toch gewoon als een functie volledig uit één macht bestaat? Bijvoorbeeld f(x) = 3x + 5x dan is hij homogeen met graad 1 en f(x) 3x^5 + 5x^5 dan is hij homogeen met graad 5?
Als q = 1/(r + 1) dan is q ongedefinieerd voor r = −1, maar niet voor r = 1, dan is q = ½. Maar voor r = 1 voldoet elke waarde van q aan q(r² − 1) = r − 1, terwijl voor r = −1 uiteraard geen enkele waarde van q aan deze betrekking kan voldoen. Ik heb het idee dat je gewoon met een schuin oog in het antwoordenboekje hebt zitten kijken zonder dat je begrijpt hoe dit antwoord is verkregen, want uit de betrekking qr² + 1 = q + r volgt an sich niet dat f(a,b) homogeen is van de graad 2 indien q = 1/(r + 1).quote:
[..]
Als je stelt dat qr2 +1 = q + r, mag je dan ook zeggen dat de graad van homogeniteit twee is? Tenzij r = 1 of -1
Je functie is homogeen van de graad k indien
f(ta,tb) = tk·f(a,b)
Bekijk nu de teller en de noemer eens apart. We definiëren nu
f(a,b) = g(a,b) / h(a,b)
met
g(a,b) = aq+1·br+1
en
h(a,b) = aqr²+1 + bq+r
De functie g(a,b) is sowieso homogeen, want je hebt g(ta,tb) = t(q+1)+(r+1)·g(a,b).
De functie h(a,b) is niet zonder meer homogeen, dat is immers alleen het geval als de machten van beide termen gelijk zijn, dus als qr² + 1 = q + r en dus q = 1/(r + 1) (r ≠ − 1).
Verder geldt: als g(a,b) homogeen is van de graad m en h(a,b) is homogeen van de graad n, dan is f(a,b) homogeen van de graad m − n, want dan is
f(ta,tb) = g(ta,tb) / h(ta,tb) = tm·g(a,b) / tn·h(a,b) = tm−n·(g(a,b)/h(a,b)) = tm−n·f(a,b)
Goed, we veronderstellen nu dat q = 1/(r + 1) (r ≠ −1). Voor de graad van homogeniteit m van de teller g(a,b) uitgedrukt in r vinden we dan
m = q + 1 + r + 1 = (r² + 3r + 3)/(r + 1)
En voor de graad van homogeniteit n van de noemer h(a,b) uitgedrukt in r hebben we dan
n = q + r = (r² + r + 1)/(r + 1)
De graad van homogeniteit m − n van f(a,b) is onfhankelijk van r, want uit m = q + r + 2 en n = q + r volgt direct dat m − n = 2.
Voila.
[ Bericht 0% gewijzigd door Riparius op 11-10-2013 11:21:55 ]
Nee, kijk even in Wikipedia.quote:
Homogeniteit is eigenlijk toch gewoon als een functie volledig uit één macht bestaat? Bijvoorbeeld f(x) = 3x + 5x dan is hij homogeen met graad 1 en f(x) 3x^5 + 5x^5 dan is hij homogeen met graad 5?
Ja heb ik gedaan maar wat ik eerder zei is feite toch wel waar het op neer komt? Alleen bedoel jij dat ik vergeet te vermelden dat het ook veralgemeend kan worden voor functies van meerdere veranderlijken, zoals f(x,y) = 19xy^3 + 14x^4 + 20(xy)^2 is een homogene functie van graad 4? Of zeg ik nou iets wat niet klopt?quote:
[ Bericht 0% gewijzigd door ulq op 11-10-2013 14:51:59 ]
Omdat je stelt qr2 + 1 = q + r, dacht ik dat je kon stellen q + r + 2 (volgt uit g) - (q+r) = 2.quote:
[..]
Als q = 1/(r + 1) dan is q ongedefinieerd voor r = −1, maar niet voor r = 1, dan is q = ½. Maar voor r = 1 voldoet elke waarde van q aan q(r² − 1) = r − 1, terwijl voor r = −1 uiteraard geen enkele waarde van q aan deze betrekking kan voldoen. Ik heb het idee dat je gewoon met een schuin oog in het antwoordenboekje hebt zitten kijken zonder dat je begrijpt hoe dit antwoord is verkregen, want uit de betrekking qr² + 1 = q + r volgt an sich niet dat f(a,b) homogeen is van de graad 2 indien q = 1/(r + 1).
Je functie is homogeen van de graad k indien
f(ta,tb) = tk·f(a,b)
Bekijk nu de teller en de noemer eens apart. We definiëren nu
f(a,b) = g(a,b) / h(a,b)
met
g(a,b) = aq+1·br+1
en
h(a,b) = aqr²+1 + bq+r
De functie g(a,b) is sowieso homogeen, want je hebt g(ta,tb) = t(q+1)+(r+1)·g(a,b).
De functie h(a,b) is niet zonder meer homogeen, dat is immers alleen het geval als de machten van beide termen gelijk zijn, dus als qr² + 1 = q + r en dus q = 1/(r + 1) (r ≠ − 1).
Verder geldt: als g(a,b) homogeen is van de graad m en h(a,b) is homogeen van de graad n, dan is f(a,b) homogeen van de graad m − n, want dan is
f(ta,tb) = g(ta,tb) / h(ta,tb) = tm·g(a,b) / tn·h(a,b) = tm−n·(g(a,b)/h(a,b)) = tm−n·f(a,b)
Goed, we veronderstellen nu dat q = 1/(r + 1) (r ≠ −1). Voor de graad van homogeniteit m van de teller g(a,b) uitgedrukt in r vinden we dan
m = q + 1 + r + 1 = (r² + 3r + 3)/(r + 1)
En voor de graad van homogeniteit n van de noemer h(a,b) uitgedrukt in r hebben we dan
n = q + r = (r² + r + 1)/(r + 1)
De graad van homogeniteit m − n van f(a,b) is onfhankelijk van r, want uit m = q + r + 2 en n = q + r volgt direct dat m − n = 2.
Voila.
Ik noemde de waardes 1 en - 1 omdat ik keek naar de niet verder vereenvoudigde (r-1)/(r2-1).
De functie is dus homogeen van graad 2 op voorwaarde dat r niet -1 (dan is hij niet homogeen).
Hartstikke bedankt voor je uitleg, een stuk helderder nu.
In het boek worden helaas vooral heel basale voorbeelden besproken (bijv. x2 + y2).
Dit klopt, maar de aanvulling is wel essentieel, want het vraagstuk van jordyqwerty ging over een functie van twee variabelen.quote:
[..]
Ja heb ik gedaan maar wat ik eerder zei is feite toch wel waar het op neer komt? Alleen bedoel jij dat ik vergeet te vermelden dat het ook veralgemeend kan worden voor functies van meerdere veranderlijken, zoals f(x,y) = 19xy^3 + 14x^4 + 20(xy)^2 is een homogene functie van graad 4? Of zeg ik nou iets wat niet klopt?
Iets heel anders. Op een tussentoets werd gevraagd of een functie op hetzelfde interval convex en concaaf kon zijn. Zo ja, moest je hier een voorbeeld voor geven.
Er stond niet expliciet bij of dat voorbeeld in de vorm van een functie met uitleg moest zijn, dus heb ik iets getekend. Ik heb genoteerd dat dat kan, mits er een buigpunt is (f'' = 0) en vervolgens een U (convex) verbonden met een ∩ (concaaf) en het buigpunt aangegeven.
In hoeverre is dat juist? Ik ben me er bewust van dat dit niet het meest verfijnde antwoord is.
Dan nog iets, stel je hebt een optimalisatieprobleem (voor de eenvoud van één variabele) en je moet binnen een gesloten interval (bijv. [2,6]) het maximum geven. Waarom is het dan verkeerd om de tweede afgeleide test te gebruiken om te kijken of de eindpunten 2 en 6 maxima of minima zijn?
Of is dat helemaal niet verkeerd?
Er stond niet expliciet bij of dat voorbeeld in de vorm van een functie met uitleg moest zijn, dus heb ik iets getekend. Ik heb genoteerd dat dat kan, mits er een buigpunt is (f'' = 0) en vervolgens een U (convex) verbonden met een ∩ (concaaf) en het buigpunt aangegeven.
In hoeverre is dat juist? Ik ben me er bewust van dat dit niet het meest verfijnde antwoord is.
Dan nog iets, stel je hebt een optimalisatieprobleem (voor de eenvoud van één variabele) en je moet binnen een gesloten interval (bijv. [2,6]) het maximum geven. Waarom is het dan verkeerd om de tweede afgeleide test te gebruiken om te kijken of de eindpunten 2 en 6 maxima of minima zijn?
Of is dat helemaal niet verkeerd?
Antwoord op je eerste vraag: Bedenk gewoon een functie waarvoor f ' '(x)=0 voor alle x. Alle functies van de vorm f(x)=ax+b voldoen hier uiteraard aan. Jouw voorbeeld klopt niet, want jouw functie is niet tegelijkertijd convex en concaaf op hetzelfde interval.quote:
Iets heel anders. Op een tussentoets werd gevraagd of een functie op hetzelfde interval convex en concaaf kon zijn. Zo ja, moest je hier een voorbeeld voor geven.
Er stond niet expliciet bij of dat voorbeeld in de vorm van een functie met uitleg moest zijn, dus heb ik iets getekend. Ik heb genoteerd dat dat kan, mits er een buigpunt is (f'' = 0) en vervolgens een U (convex) verbonden met een ∩ (concaaf) en het buigpunt aangegeven.
In hoeverre is dat juist? Ik ben me er bewust van dat dit niet het meest verfijnde antwoord is.
Dan nog iets, stel je hebt een optimalisatieprobleem (voor de eenvoud van één variabele) en je moet binnen een gesloten interval (bijv. [2,6]) het maximum geven. Waarom is het dan verkeerd om de tweede afgeleide test te gebruiken om te kijken of de eindpunten 2 en 6 maxima of minima zijn?
Of is dat helemaal niet verkeerd?
Tweede vraag: wat wil je met de tweede afgeleide doen op de randpunten?
Aha ok thanksquote:
[..]
Dit klopt, maar de aanvulling is wel essentieel, want het vraagstuk van jordyqwerty ging over een functie van twee variabelen.
Op het buigpunt ook niet?quote:
[..]
Antwoord op je eerste vraag: Bedenk gewoon een functie waarvoor f ' '(x)=0 voor alle x. Alle functies van de vorm f(x)=ax+b voldoen hier uiteraard aan. Jouw voorbeeld klopt niet, want jouw functie is niet tegelijkertijd convex en concaaf op hetzelfde interval.
Tweede vraag: wat wil je met de tweede afgeleide doen op de randpunten?
2: Kijken of het een minimum of maximum is, maar. ik begrijp dat die vlieger niet opgaat?
Kijk eens naar de definities van (strikt) convex en (strikt) concaaf. Die twee sluiten elkaar uit. Als je de eis van striktheid achterwege laat, dan kun je wel een functie hebben die zowel convex als concaaf is op hetzelfde interval, maar dat kan dan alleen een lineaire functie zijn op dat interval.quote:
Kijk eens naar de functie f: [2,6] → R gedefinieerd door f(x) = x3. Deze functie heeft een minimum bij x = 2 en een maximum bij x = 6 terwijl f''(2) en f''(6) beide positief zijn. Wat denk je daarvan?quote:2: Kijken of het een minimum of maximum is, maar. ik begrijp dat die vlieger niet opgaat?
Van wat ik weet is een functie strict convex als f'' > 0 en strict concaaf als f'' < 0. Daar komt = 0 bij zonder strictheid. In een buigpunt is f'' 0, dus ik dacht dat op dat punt de functie zowel convex als concaaf is (niet strict). Ik kijk zo even op mijn laptop naar de wikipedia pagina!quote:
[..]
Kijk eens naar de definities van (strikt) convex en (strikt) concaaf. Die twee sluiten elkaar uit. Als je de eis van striktheid achterwege laat, dan kun je wel een functie hebben die zowel convex als concaaf is op hetzelfde interval, maar dat kan dan alleen een lineaire functie zijn op dat interval.
[..]
Kijk eens naar de functie f: [2,6] → R gedefinieerd door f(x) = x3. Deze functie heeft een minimum bij x = 2 en een maximum bij x = 6 terwijl f''(2) en f''(6) beide positief zijn. Wat denk je daarvan?
.
2: Hm, lokaal minimum en maximum? Tweede afgeleide test is dus irrelevant voor randpunten?
Is 23162 nu groter of kleiner dan 31995?quote:
[..]
Voor kleine exponenten lukt dit zeker. Voor m,n > 0 heb je immers 2m > 3n als m/n > log(3)/log(2) ≈ 1,585, dus is m = 5, n = 3 een goede keuze, want dan is m/n = 5/3 ≈ 1,667. En een hele goede keuze is dan m = 8, n = 5, want dan is m/n = 8/5 = 1,6. Maar het wordt lastiger bij grote exponenten en als de waarden van de machten dichter bij elkaar liggen. Als je uitsluitend met pen en papier zou willen nagaan of bijvoorbeeld 23162 nu groter of kleiner is dan 31995 dan zijn zelfs opa's logaritmentafels in vijf decimalen niet meer toereikend. En ik hoop niet dat je nu het advies blijft geven om het dan maar met de hand uit te rekenen omdat het algoritme zo lekker simpel is.
Dit is toch niet te berekenen zonder rekenmachine?
1995a = 3162
a ~ 1.58
21.58< 3
Dus
23162< 31995
Of toch wel? Klopt bovenstaande?
[ Bericht 1% gewijzigd door wiskundenoob op 11-10-2013 23:52:39 ]
Ah! Hij (nouja, mijn uitleg) is niet convex (en concaaf) op hetzelfde interval omdat je die lijn niet kunt trekken tussen twee willekeurige punten zonder buiten het interval te komen. Klopt dat?quote:
[..]
Kijk eens naar de definities van (strikt) convex en (strikt) concaaf. Die twee sluiten elkaar uit. Als je de eis van striktheid achterwege laat, dan kun je wel een functie hebben die zowel convex als concaaf is op hetzelfde interval, maar dat kan dan alleen een lineaire functie zijn op dat interval.
[..]
Kijk eens naar de functie f: [2,6] → R gedefinieerd door f(x) = x3. Deze functie heeft een minimum bij x = 2 en een maximum bij x = 6 terwijl f''(2) en f''(6) beide positief zijn. Wat denk je daarvan?
Ik wist dat overigens, maar ik wist niet dat de hele functie convex en concaaf moet zijn op het gehele interval.
Jawel hoor, in principe is alles te berekenen zonder rekenmachine. Het is geen pretje, maar het kan. Met de calculator van Windows vind ik 23162/1995 = 2.9999998030641692219144189133716 ... zodat inderdaad 23162< 31995 maar dat kun je met bijvoorbeeld de logaritmentafels in 14 decimalen van Briggs uit 1624 ook concluderen. En die tafels zijn toch echt met de hand berekend. Dus ja, het kan.quote:Op vrijdag 11 oktober 2013 23:37 schreef wiskundenoob het volgende:
[..]
Is 23162 nu groter of kleiner dan 31995?
Dit is toch niet te berekenen zonder rekenmachine?
1995a = 3162
a ~ 1.58
21.58< 3
Dus
23162< 31995
Maar goed, vroeger kon men wel vaker dingen met de hand uitrekenen waarvan we nu soms nog niet weten hoe het is gedaan. Heel bekend is bijvoorbeeld dat Mersenne eens per brief aan Fermat vroeg of het getal 100895598169 priem was of niet. Fermat antwoordde nog dezelfde dag per kerende post dat dit getal niet priem is en dat dit getal het product is van 112303 en 898423 en dat elk van deze beide factoren priem is. Tot op de dag van vandaag weet niemand hoe hij dit zonder rekenmachine heeft gedaan. Het valt wel direct op dat je hebt 898423 = 8·112303 − 1, dus N = n(8n − 1) en daarmee 32N + 1 = (16n − 1)2 met n = 112303, maar ja ...
[ Bericht 4% gewijzigd door Riparius op 12-10-2013 02:49:56 ]
Een nieuwe.
Stel je hebt de functie:
f(x,y) = x3 + y3 - 9xy + 27
Verder is gegeven dat:
0 ≤ x ≤ 4 en 0 ≤ y ≤ 4
Gevraagd wordt om het maximum en minimum te vinden.
Eerst dus de stationaire punten vinden.
f'x(x,y) = 3x2 - 9y = 0
f'y(x,y) = 3y2 - 9x = 0
Y uitdrukken in x voor f'x(x,y)
9y = 3x2
y = (1/3)x2
Invoeren in f'y(x,y)
3((1/3)x2)2 - 9x = 0
3((1/9)x4) - 9x = 0
(1/3)x4 - 9x = 0
x4 - 27x = 0
x(x3 - 27) = 0
Waaruit volgt x = 0 of x = 3, omdat x = 0 een randpunt is, is x = 3 het enige stationaire punt. Bijbehorende y-waarde: (1/3)(3)2 = 3
Nu heb ik dus als mogelijk punt (3,3).
Ik snap nu niet hoe ik verder moet gaan, ofwel, wat ik met de randpunten moet doen (0 ≤ x ≤ 4 en 0 ≤ y ≤ 4).
In eerste instantie dacht ik dat ik door het invullen in de afgeleiden voor x en y de bijbehorende waardes kon vinden (bijvoorbeeld, welke waarde bij het punt x = 4 hoort), maar dat is niet zo/lijkt me onwaarschijnlijk.
Ik denk zelf dat ik iets moet doen met de originele functie f(x,y), maar wat? Als ik x = 0 invul, wat moet ik dan voor y invullen? Y kan immers tussen 0 en 4 liggen.
Stel je hebt de functie:
f(x,y) = x3 + y3 - 9xy + 27
Verder is gegeven dat:
0 ≤ x ≤ 4 en 0 ≤ y ≤ 4
Gevraagd wordt om het maximum en minimum te vinden.
Eerst dus de stationaire punten vinden.
f'x(x,y) = 3x2 - 9y = 0
f'y(x,y) = 3y2 - 9x = 0
Y uitdrukken in x voor f'x(x,y)
9y = 3x2
y = (1/3)x2
Invoeren in f'y(x,y)
3((1/3)x2)2 - 9x = 0
3((1/9)x4) - 9x = 0
(1/3)x4 - 9x = 0
x4 - 27x = 0
x(x3 - 27) = 0
Waaruit volgt x = 0 of x = 3, omdat x = 0 een randpunt is, is x = 3 het enige stationaire punt. Bijbehorende y-waarde: (1/3)(3)2 = 3
Nu heb ik dus als mogelijk punt (3,3).
Ik snap nu niet hoe ik verder moet gaan, ofwel, wat ik met de randpunten moet doen (0 ≤ x ≤ 4 en 0 ≤ y ≤ 4).
In eerste instantie dacht ik dat ik door het invullen in de afgeleiden voor x en y de bijbehorende waardes kon vinden (bijvoorbeeld, welke waarde bij het punt x = 4 hoort), maar dat is niet zo/lijkt me onwaarschijnlijk.
Ik denk zelf dat ik iets moet doen met de originele functie f(x,y), maar wat? Als ik x = 0 invul, wat moet ik dan voor y invullen? Y kan immers tussen 0 en 4 liggen.
Geen idee, je formulering is zo onduidelijk dat onmogelijk is te achterhalen wat je je hier precies bij voorstelt.quote:
[..]
Ah! Hij (nouja, mijn uitleg) is niet convex (en concaaf) op hetzelfde interval omdat je die lijn niet kunt trekken tussen twee willekeurige punten zonder buiten het interval te komen. Klopt dat?
Er werd duidelijk gevraagd naar een functie die zowel convex als concaaf moest zijn op hetzelfde interval. Jij maakte daarvan dat er werd gevraagd naar een functie die convex is op een deel van een interval maar concaaf op een ander deel van datzelfde interval. Maar dat is iets anders.quote:Ik wist dat overigens, maar ik wist niet dat de hele functie convex en concaaf moet zijn op het gehele interval.
Dan snap ik het, bedankt.quote:
[..]
Geen idee, je formulering is zo onduidelijk dat onmogelijk is te achterhalen wat je je hier precies bij voorstelt.
[..]
Er werd duidelijk gevraagd naar een functie die zowel convex als concaaf moest zijn op hetzelfde interval. Jij maakte daarvan dat er werd gevraagd naar een functie die convex is op een deel van een interval maar concaaf op een ander deel van datzelfde interval. Maar dat is iets anders.
Bepaal eerst de kritieke (stationaire) punten. Bepaal vervolgens voor elk gevonden stationair punt of het een locaal minimum of maximum is, of een zadelpunt. Bedenk eerst eens hoe je dat doet, of kijk eens in je dictaten of leerboeken.quote:
Een nieuwe.
Stel je hebt de functie:
f(x,y) = x3 + y3 - 9xy + 27
Verder is gegeven dat:
0 ≤ x ≤ 4 en 0 ≤ y ≤ 4
Gevraagd wordt om het maximum en minimum te vinden.
Er zijn drie typen punten waarbij globale minima of maxima van je functie op het beschouwde domein
V = {(x;y) ∈ R² | 0 ≤ x ≤ 4 ∧ 0 ≤ y ≤ 4}
kunnen worden bereikt, namelijk
1. Locale extrema bij inwendige punten van het vierkant V
2. Locale extrema op de randen van het vierkant V
3. Locale extrema bij de hoekpunten van het vierkant V
Bedenk nu zelf hoe je dit verder uitwerkt.
A = f''xx = 6xquote:
[..]
Bepaal eerst de kritieke (stationaire) punten. Bepaal vervolgens voor elk gevonden stationair punt of het een locaal minimum of maximum is, of een zadelpunt. Bedenk eerst eens hoe je dat doet, of kijk eens in je dictaten of leerboeken.
Er zijn drie typen punten waarbij globale minima of maxima van je functie op het beschouwde domein
V = {(x;y) ∈ R² | 0 ≤ x ≤ 4 ∧ 0 ≤ y ≤ 4}
kunnen worden bereikt, namelijk
1. Locale extrema bij inwendige punten van het vierkant V
2. Locale extrema op de randen van het vierkant V
3. Locale extrema bij de hoekpunten van het vierkant V
Bedenk nu zelf hoe je dit verder uitwerkt.
B = f''xy = -9
C =f''yy = 6y
(3,3)
Dus A > 0 en C > 0
AC - B2
324 - (-9)2 = 243
Dus AC - B2 > 0
Je hebt hier dus te maken met een minimum.
f(3,3) geeft 0 (27 + 27 - 81 + 27)
0 ≤ x ≤ 4 ∧ 0 ≤ y ≤ 4
f(0,y) = y3 + 27
De kleinst mogelijke waarde voor y is dan 0, dus (0,0) = 27
De grootst mogelijke waarde voor y is dan 4, dus (0,4) = 91
Is dit juist? Voordat ik verderga
Je moet hier wat aan je notatie doen, en je past ook het criterium voor een locaal minimum niet correct toe.quote:
[..]
A = f''xx = 6x
B = f''xy = -9
C =f''yy = 6y
(3,3)
Dus A > 0 en C > 0
AC - B2
324 - (-9)2 = 243
Dus AC - B2 > 0
Je hebt hier dus te maken met een minimum.
f(3,3) geeft 0 (27 + 27 - 81 + 27)
Het is niet nodig, en ook niet gebruikelijk, om primes te gebruiken voor de partiële afgeleiden van f(x,y) als je de notaties fx(x,y) en fy(x,y) gebruikt voor de partiële eerste afgeleiden. Er zijn overigens ook verschillende andere notaties zoals ∂f(x,y)/∂x resp. ∂f(x,y)/∂y of ∂f/∂x resp. ∂f/∂y of ∂z/∂x resp. ∂z/∂y als z = f(x,y). Ook gebruikt men wel indices, dus f1(x,y) resp. f2(x,y), dit om ambiguïteiten bij het samenstellen van functies met meerdere variabelen te vermijden. Voor de tweede partiële afgeleiden naar x resp. naar y kun je fxx(x,y) resp. fyy(x,y) gebruiken. Voor de gemengde partiële tweede afgeleiden heb je dan fxy(x,y) en fyx(x,y) maar helaas zijn deze notaties niet eenduidig. De meeste auteurs bedoelen met fxy(x,y) dat je eerst naar x differentieert en dan naar y, dus fxy = (fx)y, maar er zijn ook auteurs die ditzelfde nu juist noteren als fyx(x,y) om zo een overeenstemming te krijgen met de volgorde van de x en de y in de klassieke notatie ∂2f/∂y∂x = ∂/∂y(∂f/∂x). Nu is er een bekende stelling die zegt dat de gemengde partiële tweede afgeleiden onder bepaalde voorwaarden gelijk zijn, zodat dit in de praktijk meestal geen verwarring oplevert.
De determinant D(x,y) van de Hessiaan van f(x,y) is
D(x,y) = fxx(x,y)fyy(x,y) − (fxy(x,y))2
Als nu (xc;yc) een kritisch punt is van f(x,y), dus fx(xc,yc) = 0 en tevens fy(xc,yc) = 0, dan luidt de correcte (voldoende, maar niet noodzakelijke) voorwaarde voor een minimum dat D(xc,yc) > 0 en tevens fxx(xc,yc) > 0.
We hebben nu
f(x,y) = x3 + y3 − 9xy + 27
fx(x,y) = 3x2 − 9y
fy(x,y) = 3y2 − 9x
fxx(x,y) = 6x
fyy(x,y) = 6y
fxy(x,y) = −9
Om de kritische (oftewel stationaire) punten te bepalen moeten we eerst het stelsel fx(x,y) = 0, fy(x,y) = 0 oplossen. Dit levert niet één maar twee punten op, namelijk (0;0) en (3;3). Uit 3x2 − 9y = 0 volgt immers y = x2/3, en substitutie daarvan in 3y2 − 9x = 0 levert x(x3 − 27) = 0 en dus x = 0 of x = 3, en daarmee is ook y = 0 resp. y = 3.
Nu is fxx(0,0) = 0, fyy(0,0) = 0, fxy(0,0) = −9, en dus D(0,0) = 0 − (−9)2 = −81. Dat betekent dat (0;0) een zadelpunt is van f. Verder hebben we fxx(3,3) = 18, fyy(3,3) = 18, fxy(3,3) = −9, en dus D(3,3) = 182 − (−9)2 = 243. Aangezien ook fxx(3,3) > 0 betekent dit dat f(x,y) voor (x,y) = (3,3) een locaal minimum aanneemt. De waarde van dit locale minimum is f(3,3) = 0.
Nu gaan we de functiewaarden bekijken langs de vier zijden van het vierkant die de rand vormen van het domein van de functie. Hiervoor hebben we
f(x,0) = x3 + 27
f(x,4) = x3 − 36x + 91
f(0,y) = y3 + 27
f(4,y) = y3 − 36y + 91
Je ziet nu gemakkelijk dat fx(x,0) = 3x2 en fy(0,y) = 3y2 zodat f(x,0) stijgt voor x > 0 en f(0,y) stijgt voor y > 0. Als we dus in een rechte lijn van het punt (0;0) naar het punt (4;0) gaan, dan neemt de functiewaarde toe van f(0,0) = 27 tot f(4,0) = 91. Evenzo neemt de functiewaarde toe van f(0,0) = 27 tot f(0,4) = 91 wanneer we in een rechte lijn van het punt (0;0) naar het punt (0;4) gaan.
Maar hiermee zijn we er nog niet, want het vierkant heeft nog een vierde hoekpunt (4;4). Dus moeten we nu ook nog kijken wat er met de functiewaarde gebeurt als we vanuit hetzij het punt (0;4) hetzij het punt (4;0) in een rechte lijn naar het punt (4;4) gaan. Het is gemakkelijk te zien dat fx(x,4) = 3x2 − 36 een nulpunt heeft bij x = √12 = 2√3 en dat fx(x,4) negatief is voor 0 < x < 2√3 en positief voor x > 2√3. Evenzo is fy(4,y) = 3y2 − 36 negatief voor 0 < y < 2√2 en positief voor y > 2√3. De functiewaarde daalt dus eerst als we vanuit (0;4) in een rechte lijn naar (4;4) gaan, om in het punt (2√3;4) een minimum aan te nemen ter grootte van 2√3(12 − 36) + 91 = 91 − 48√3 (≈ 7,86). Vervolgens stijgt de functiewaarde weer, om dan uit te komen op 11 als we in het punt (4;4) zitten. Volkomen analoog daalt de functiewaarde eveneens van 91 tot 91 − 48√3 als we in een rechte lijn van het punt (4;0) naar het punt (4;2√3) gaan, om dan weer te stijgen tot 11 als we in een rechte lijn van het punt (4;2√3) naar het punt (4;4) gaan. De functiewaarde wordt niet negatief op de lijnstukken van (0;4) naar (4;4) en van (4;0) naar (4;4), zodat f(3,3) = 0 inderdaad het globale minimum blijft van de functie.
Conclusie:
De functie f: V → R gedefinieerd door V := { (x;y) ∈ R2 | 0 ≤ x ≤ 4 ∧ 0 ≤ y ≤ 4 } en f(x,y) := x3 + y3 − 9xy + 27 neemt op V een globaal minimum 0 aan in het punt (3;3) en een globaal maximum 91 in de punten (4;0) en (0;4).
Merk nog op dat de punten waar het globale minimum en maximum worden bereikt symmetrisch liggen ten opzichte van de lijn met vergelijking y = x. Dat was ook niet anders te verwachten aangezien f(x,y) symmetrisch is in x en y.
Bepaal x en y als
xy = 294
x+y = 54
Hoe reken je dit snel uit? Ik las hier ergens dat je de priemgetallen moet uitrekenen, maar ik kan het niet meer terugvinden.
294 = 2*3*7*7
54 = (7*7)+(2*3)
x= 49 en y= 6
xy = 294
x+y = 54
Hoe reken je dit snel uit? Ik las hier ergens dat je de priemgetallen moet uitrekenen, maar ik kan het niet meer terugvinden.
294 = 2*3*7*7
54 = (7*7)+(2*3)
x= 49 en y= 6
Opnieuw hartstikke bedankt.quote:
[..]
Je moet hier wat aan je notatie doen, en je past ook het criterium voor een locaal minimum niet correct toe.
Het is niet nodig, en ook niet gebruikelijk, om primes te gebruiken voor de partiële afgeleiden van f(x,y) als je de notaties fx(x,y) en fy(x,y) gebruikt voor de partiële eerste afgeleiden. Er zijn overigens ook verschillende andere notaties zoals ∂f(x,y)/∂x resp. ∂f(x,y)/∂y of ∂f/∂x resp. ∂f/∂y of ∂z/∂x resp. ∂z/∂y als z = f(x,y). Ook gebruikt men wel indices, dus f1(x,y) resp. f2(x,y), dit om ambiguïteiten bij het samenstellen van functies met meerdere variabelen te vermijden. Voor de tweede partiële afgeleiden naar x resp. naar y kun je fxx(x,y) resp. fyy(x,y) gebruiken. Voor de gemengde partiële tweede afgeleiden heb je dan fxy(x,y) en fyx(x,y) maar helaas zijn deze notaties niet eenduidig. De meeste auteurs bedoelen met fxy(x,y) dat je eerst naar x differentieert en dan naar y, dus fxy = (fx)y, maar er zijn ook auteurs die ditzelfde nu juist noteren als fyx(x,y) om zo een overeenstemming te krijgen met de volgorde van de x en de y in de klassieke notatie ∂2f/∂y∂x = ∂/∂y(∂f/∂x). Nu is er een bekende stelling die zegt dat de gemengde partiële tweede afgeleiden onder bepaalde voorwaarden gelijk zijn, zodat dit in de praktijk meestal geen verwarring oplevert.
De determinant D(x,y) van de Hessiaan van f(x,y) is
D(x,y) = fxx(x,y)fyy(x,y) − (fxy(x,y))2
Als nu (xc;yc) een kritisch punt is van f(x,y), dus fx(xc,yc) = 0 en tevens fy(xc,yc) = 0, dan luidt de correcte (voldoende, maar niet noodzakelijke) voorwaarde voor een minimum dat D(xc,yc) > 0 en tevens fxx(xc,yc) > 0.
We hebben nu
f(x,y) = x3 + y3 − 9xy + 27
fx(x,y) = 3x2 − 9y
fy(x,y) = 3y2 − 9x
fxx(x,y) = 6x
fyy(x,y) = 6y
fxy(x,y) = −9
Om de kritische (oftewel stationaire) punten te bepalen moeten we eerst het stelsel fx(x,y) = 0, fy(x,y) = 0 oplossen. Dit levert niet één maar twee punten op, namelijk (0;0) en (3;3). Uit 3x2 − 9y = 0 volgt immers y = x2/3, en substitutie daarvan in 3y2 − 9x = 0 levert x(x3 − 27) = 0 en dus x = 0 of x = 3, en daarmee is ook y = 0 resp. y = 3.
Nu is fxx(0,0) = 0, fyy(0,0) = 0, fxy(0,0) = −9, en dus D(0,0) = 0 − (−9)2 = −81. Dat betekent dat (0;0) een zadelpunt is van f. Verder hebben we fxx(3,3) = 18, fyy(3,3) = 18, fxy(3,3) = −9, en dus D(3,3) = 182 − (−9)2 = 243. Aangezien ook fxx(3,3) > 0 betekent dit dat f(x,y) voor (x,y) = (3,3) een locaal minimum aanneemt. De waarde van dit locale minimum is f(3,3) = 0.
Nu gaan we de functiewaarden bekijken langs de vier zijden van het vierkant die de rand vormen van het domein van de functie. Hiervoor hebben we
f(x,0) = x3 + 27
f(x,4) = x3 − 36x + 91
f(0,y) = y3 + 27
f(4,y) = y3 − 36y + 91
Je ziet nu gemakkelijk dat fx(x,0) = 3x2 en fy(0,y) = 3y2 zodat f(x,0) stijgt voor x > 0 en f(0,y) stijgt voor y > 0. Als we dus in een rechte lijn van het punt (0;0) naar het punt (4;0) gaan, dan neemt de functiewaarde toe van f(0,0) = 27 tot f(4,0) = 91. Evenzo neemt de functiewaarde toe van f(0,0) = 27 tot f(0,4) = 91 wanneer we in een rechte lijn van het punt (0;0) naar het punt (0;4) gaan.
Maar hiermee zijn we er nog niet, want het vierkant heeft nog een vierde hoekpunt (4;4). Dus moeten we nu ook nog kijken wat er met de functiewaarde gebeurt als we vanuit hetzij het punt (0;4) hetzij het punt (4;0) in een rechte lijn naar het punt (4;4) gaan. Het is gemakkelijk te zien dat fx(x,4) = 3x2 − 36 een nulpunt heeft bij x = √12 = 2√3 en dat fx(x,4) negatief is voor 0 < x < 2√3 en positief voor x > 2√3. Evenzo is fy(4,y) = 3y2 − 36 negatief voor 0 < y < 2√2 en positief voor y > 2√3. De functiewaarde daalt dus eerst als we vanuit (0;4) in een rechte lijn naar (4;4) gaan, om in het punt (2√3;4) een minimum aan te nemen ter grootte van 2√3(12 − 36) + 91 = 91 − 48√3 (≈ 7,86). Vervolgens stijgt de functiewaarde weer, om dan uit te komen op 11 als we in het punt (4;4) zitten. Volkomen analoog daalt de functiewaarde eveneens van 91 tot 91 − 48√3 als we in een rechte lijn van het punt (4;0) naar het punt (4;2√3) gaan, om dan weer te stijgen tot 11 als we in een rechte lijn van het punt (4;2√3) naar het punt (4;4) gaan. De functiewaarde wordt niet negatief op de lijnstukken van (0;4) naar (4;4) en van (4;0) naar (4;4), zodat f(3,3) = 0 inderdaad het globale minimum blijft van de functie.
Conclusie:
De functie f: V → R gedefinieerd door V := { (x;y) ∈ R2 | 0 ≤ x ≤ 4 ∧ 0 ≤ y ≤ 4 } en f(x,y) := x3 + y3 − 9xy + 27 neemt op V een globaal minimum 0 aan in het punt (3;3) en een globaal maximum 91 in de punten (4;0) en (0;4).
Merk nog op dat de punten waar het globale minimum en maximum worden bereikt symmetrisch liggen ten opzichte van de lijn met vergelijking y = x. Dat was ook niet anders te verwachten aangezien f(x,y) symmetrisch is in x en y.
Ik was reeds bekend met de notaties (en Young's theorem). In mijn boek worden echter wèl primes gebruikt voor partiële afgeleiden, desalniettemin zal ik er in het vervolg op letten.
Ik wist ook dat (0,0) zou volgen uit fx(x,y) = 0, fy(x,y) = 0, maar nam dit punt niet mee omdat het een randpunt is (bij f(x,0) = x3 + 27 en f(0,y) = y3 + 27 vind je dit punt ook), maar ik zal proberen zo volledig mogelijk te zijn.
Ik heb alleen deze som meegekregen om ermee te oefenen, dus ik ga nog even op zoek naar wat extra opdrachten.
Je motivatie om het punt (0;0) buiten beschouwing te laten omdat het randpunt is, is niet juist, immers ook in een randpunt kun je een extreme waarde hebben. Waar het om gaat is dat (0;0) een zadelpunt is.quote:
[..]
Opnieuw hartstikke bedankt.
Ik was reeds bekend met de notaties (en Young's theorem). In mijn boek worden echter wèl primes gebruikt voor partiële afgeleiden, desalniettemin zal ik er in het vervolg op letten.
Ik wist ook dat (0,0) zou volgen uit fx(x,y) = 0, fy(x,y) = 0, maar nam dit punt niet mee omdat het een randpunt is (bij f(x,0) = x3 + 27 en f(0,y) = y3 + 27 vind je dit punt ook), maar ik zal proberen zo volledig mogelijk te zijn.
Kijk hier eens voor wat (uitgewerkte) extra opgaven.quote:Ik heb alleen deze som meegekregen om ermee te oefenen, dus ik ga nog even op zoek naar wat extra opdrachten.
x en y zijn de oplossingen van de vergelijking (t-x)(t-y) = 0. Uitwerken geeft t2 - (x+y)t + xy = 0, ofwel t2 - 54t + 294 = 0.quote:
Bepaal x en y als
xy = 294
x+y = 54
Hoe reken je dit snel uit? Ik las hier ergens dat je de priemgetallen moet uitrekenen, maar ik kan het niet meer terugvinden.
294 = 2*3*7*7
54 = (7*7)+(2*3)
x= 49 en y= 6
Je rekenwerk klopt niet, waarschijnlijk bedoel je dat de som van de te vinden (gehele) getallen 55 moet zijn.quote:
Bepaal x en y als
xy = 294
x+y = 55
Het gaat niet om het 'uitrekenen' van priemgetallen maar het is de bedoeling dat je het product van de te vinden getallen ontbindt in factoren. Vervolgens verdeel je de gevonden priemfactoren over twee producten zodanig dat de som van deze producten gelijk is aan de gegeven som, en daarmee zijn de gevraagde (gehele) getallen gevonden.quote:Hoe reken je dit snel uit? Ik las hier ergens dat je de priemgetallen moet uitrekenen, maar ik kan het niet meer terugvinden.
quote:294 = 2*3*7*7
55 = (7*7)+(2*3)
x= 49 en y= 6
[ Bericht 0% gewijzigd door Riparius op 12-10-2013 15:38:55 ]
xy = 294 (1)quote:
Bepaal x en y als
xy = 294
x+y = 54
Hoe reken je dit snel uit? Ik las hier ergens dat je de priemgetallen moet uitrekenen, maar ik kan het niet meer terugvinden.
294 = 2*3*7*7
54 = (7*7)+(2*3)
x= 49 en y= 6
x + y = 54 (2)
Je kan nu bijvoorbeeld y schrijven als een functie van x:
y = 54 - x (3)
En dit vervolgens substitueren in (1)
Kan je dan verder?
Duidelijk. Bedankt voor de link, het wordt steeds helderder.quote:
[..]
Je motivatie om het punt (0;0) buiten beschouwing te laten omdat het randpunt is, is niet juist, immers ook in een randpunt kun je een extreme waarde hebben. Waar het om gaat is dat (0;0) een zadelpunt is.
[..]
Kijk hier eens voor wat (uitgewerkte) extra opgaven.
Ik weet niet of dit de juiste plek is om de vraag te stellen, maar misschien kan iemand me kort uitleg geven over het volgende (statistiek):
Welke test gebruik je om een relatie tussen twee variabelen (n.a.v. de H0 en HA) te onderzoeken naar aanleiding van alleen een kruistabel? Er mag verder geen gebruik van SPSS of andere programma's gemaakt worden. Het gaat me dus vooral om het kiezen van de juiste test hiervoor.
Welke test gebruik je om een relatie tussen twee variabelen (n.a.v. de H0 en HA) te onderzoeken naar aanleiding van alleen een kruistabel? Er mag verder geen gebruik van SPSS of andere programma's gemaakt worden. Het gaat me dus vooral om het kiezen van de juiste test hiervoor.
Nope, dan werk je dubbel, denk ik. Of bedoel je wat anders?quote:
[..]
xy = 294 (1)
x + y = 54 (2)
Je kan nu bijvoorbeeld y schrijven als een functie van x:
y = 54 - x (3)
En dit vervolgens substitueren in (1)
Kan je dan verder?
x(55-x)= 294
55x -x2 = 294
x2 -55x +294 = 0
Kan je x2 -55x +294 = 0 ontbinden in factoren?quote:
[..]
Nope, dan werk je dubbel, denk ik. Of bedoel je wat anders?
x(55-x)= 294
55x -x2 = 294
x2 -55x +294 = 0
Zoals Thabit hierboven al opmerkt zijn x en y de wortels van een vierkantsvergelijking, en door deze substitutie kom je op diezelfde vierkantsvergelijking uit, die je dan op één der bekende manieren kunt oplossen. Maar als je dan gaat proberen de vierkantsvergelijking door ontbinden in factoren op te lossen, dan ben je weer terug bij het oorspronkelijke vraagstuk om twee getallen te bepalen waarvan som en product zijn gegeven.quote:
[..]
xy = 294 (1)
x + y = 55 (2)
Je kan nu bijvoorbeeld y schrijven als een functie van x:
y = 55 - x (3)
En dit vervolgens substitueren in (1)
Kan je dan verder?
Je kunt het ook als volgt doen. We nemen het kwadraat van de som, dat is
(x + y)2 = 552 = 3025
Dit kwadraat verminderen we met het viervoud van het product, dit geeft
(x + y)2 − 4xy = 3025 − 4·294 = 1849
En aangezien (x + y)2 − 4xy = (x − y)2 hebben we dus
(x − y)2 = 1849
De vierkantswortel nemen geeft dan
x − y = 43
We hadden hier ook −43 kunnen nemen, maar we hebben aan één waarde voor het verschil genoeg, omdat het inverteren van het teken van het verschil neerkomt op het omwisselen van x en y. Optellen van som en verschil geeft nu
2x = (x + y) + (x − y) = 55 + 43 = 98, dus x = 49
En aftrekken van het verschil van de som geeft
2y = (x + y) − (x − y) = 55 − 43 = 12, dus y = 6
Dezelfde methode is ook te gebruiken om uitdrukkingen af te leiden voor de wortels van de algemene vierkantsvergelijking
ax2 + bx + c = 0 (a ≠ 0)
Zijn de wortels van deze vergelijking x1 en x2, dan is de vergelijking te schrijven als
a(x − x1)(x − x2) = 0
oftewel
ax2 − a(x1 + x2)x + ax1x2 = 0
zodat we door de coëfficiënten te vergelijken kunnen concluderen dat geldt
x1 + x2 = −b/a
en
x1x2 = c/a
Door nu op bovenstaande wijze x1 en x2 te bepalen uit de gegeven som −b/a en het gegeven product c/a kunnen we uitdrukkingen voor x1 en x2 in de coëfficiënten a, b en c van de vergelijking afleiden. Deze manier om de abc-formule af te leiden resp. een vierkantsvergelijking op te lossen wordt wel de methode van Harriot genoemd.
[ Bericht 0% gewijzigd door Riparius op 12-10-2013 17:47:31 ]
Dus:quote:
[..]
Als je de term anxn buiten haakjes haalt, dan heb je
P(x) = anxn(1 + (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
Nu moet je laten zien dat de uitdrukking tussen de haakjes positief is voor voldoend grote |x| en daarvoor heb je de driehoeksongelijkheid nodig.
[..]
De driehoeksongelijkheid ontleent haar naam uiteraard aan de meetkunde, maar je hebt ook betrekkingen tussen (de absolute waarden van) reële of complexe getallen die hiermee verband houden. Voor elk tweetal (reële of complexe) getallen a en b geldt
| a + b | ≤ | a | + | b |
Deze ongelijkheid kun je eenvoudig uitbreiden naar een willekeurig aantal termen, bijvoorbeeld
| a + b + c | ≤ | a | + | b | + | c |
Gebruik dit.
[..]
Dat vermoedde ik al. Dank voor de bevestiging.
P(x) = anxn(1 + (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
En volgens de driehoeksongelijkheid
|P(x)| = |anxn(1 + (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)| ≤ |anxn|(1 + |(an−1/an)x−1| + |(an−2/an)x−2| + ... + | (a1/an)x−(n−1)| + |(a0/an)x−n|)
En dus
|P(x)| / |anxn| ≤ 1 + |(an−1/an)x−1| + |(an−2/an)x−2| + ... + |(a1/an)x−(n−1)| + |(a0/an)x−n|
Dit mag omdat we door iets positiefs delen, dus het teken klapt niet om.
|P(x) / anxn| ≤ 1 + |(an−1/an)|·|x−1| + |(an−2/an)|·|x−2| + ... + |(a1/an)|·|x−(n−1)| + |(a0/an)|·|x−n|
En we weten dat |xk| = |x|k
|P(x) / anxn| ≤ 1 + |(an−1/an)|·|x|−1 + |(an−2/an)|·|x|−2 + ... + |(a1/an)|·|x|−(n−1) + |(a0/an)|·|x|−n
Als we dan nu de limiet voor |x| → ∞ nemen zien we dat de rechterkant van de uitdrukking 1 wordt.
Ik weet dat dit niet helemaal juist is. Riparius, zonder het bewijs compleet af te maken, kun je iets cursiveren waar ik wat mee moet doen of waar ik een fout bega? Het lijkt me onjuist om te concluderen dat
|P(x)| ≤ |anxn| voor |x| → ∞
En dus alleen de hoogste macht er feitelijk toe doet.
[ Bericht 1% gewijzigd door Amoeba op 12-10-2013 18:25:28 ]
Fervent tegenstander van het korps lasergamers.
Je kan dan net zo goed kwadraatafsplitsen of niet soms? Alles keer 4 eerst en dan uitwerken.quote:
[..]
Zoals Thabit hierboven al opmerkt zijn x en y de wortels van een vierkantsvergelijking, en door deze substitutie kom je op diezelfde vierkantsvergelijking uit, die je dan op één der bekende manieren kunt oplossen. Maar als je dan gaat proberen de vierkantsvergelijking door ontbinden in factoren op te lossen, dan ben je weer terug bij het oorspronkelijke vraagstuk om twee getallen te bepalen waarvan som en product zijn gegeven.
Je kunt het ook als volgt doen. We nemen het kwadraat van de som, dat is
(x + y)2 = 552 = 3025
Dit kwadraat verminderen we met het viervoud van het product, dit geeft
(x + y)2 − 4xy = 3025 − 4·294 = 1849
En aangezien (x + y)2 − 4xy = (x − y)2 hebben we dus
(x − y)2 = 1849
De vierkantswortel nemen geeft dan
x − y = 43
We hadden hier ook −43 kunnen nemen, maar we hebben aan één waarde voor het verschil genoeg, omdat het inverteren van het teken van het verschil neerkomt op het omwisselen van x en y. Optellen van som en verschil geeft nu
2x = (x + y) + (x − y) = 55 + 43 = 98, dus x = 49
En aftrekken van het verschil van de som geeft
2y = (x + y) − (x − y) = 55 − 43 = 12, dus y = 6
Dezelfde methode is ook te gebruiken om uitdrukkingen af te leiden voor de wortels van de algemene vierkantsvergelijking
ax2 + bx + c = 0 (a ≠ 0)
Zijn de wortels van deze vergelijking x1 en x2, dan is de vergelijking te schrijven als
a(x − x1)(x − x2) = 0
oftewel
ax2 − a(x1 + x2)x + ax1x2 = 0
zodat we door de coëfficiënten te vergelijken kunnen concluderen dat geldt
x1 + x2 = −b/a
en
x1x2 = c/a
Door nu op bovenstaande wijze x1 en x2 te bepalen uit de gegeven som −b/a en het gegeven product c/a kunnen we uitdrukkingen voor x1 en x2 in de coëfficiënten a, b en c van de vergelijking afleiden. Deze manier om de abc-formule af te leiden resp. een vierkantsvergelijking op te lossen wordt wel de methode van Harriot genoemd.
Je moet even begrijpen wat er gebeurt. Als x+y = a en xy = b gegeven is kun je i.p.v. een substitutie ook het verschil x-y uitrekenen. Riparius doet dit door zeer handig gebruik te maken van merkwaardige producten.quote:
[..]
Je kan dan net zo goed kwadraatafsplitsen of niet soms? Alles keer 4 eerst en dan uitwerken.
Fervent tegenstander van het korps lasergamers.
Uit | P(x)/anxn | ≤ 1 + ε voor een zekere ε > 0 volgt niet | P(x) | ≤ | anxn | want dan zou ε = 0 moeten zijn: tegenspraak. Overigens begrijp ik niet hoe je een ongelijkheid met | P(x) | wil gebruiken om aan te tonen dat P(x) een tegengesteld teken heeft voor een positieve en negatieve x met een voldoend grote absolute waarde (want dat is wat je aan moet tonen).quote:
[..]
Ik weet dat dit niet helemaal juist is. Riparius, zonder het bewijs compleet af te maken, kun je iets cursiveren waar ik wat mee moet doen of waar ik een fout bega? Het lijkt me onjuist om te concluderen dat
|P(x)| ≤ |anxn| voor |x| → ∞
En dus alleen de hoogste macht er feitelijk toe doet.
Ik dacht al dat het onjuist was.quote:
[..]
Uit | P(x)/anxn | ≤ 1 + ε voor een zekere ε > 0 volgt niet | P(x) | ≤ | anxn | want dan zou ε = 0 moeten zijn: tegenspraak.
Moet ik hieruit concluderen dat ik helemaal verkeerd denk?quote:Overigens begrijp ik niet hoe je een ongelijkheid met | P(x) | wil gebruiken om aan te tonen dat P(x) een tegengesteld teken heeft voor een positieve en negatieve x met een voldoend grote absolute waarde (want dat is wat je aan moet tonen).
Fervent tegenstander van het korps lasergamers.
Dat denk je dan weer goed.quote:
[..]
Ik dacht al dat het onjuist was.
[..]
Moet ik hieruit concluderen dat ik helemaal verkeerd denk?
Ik krijg er koppijn van. Hoe moet ik anders die driehoeksongelijkheid toepassen!?quote:
Fervent tegenstander van het korps lasergamers.
Wat is je precieze vraagstelling en wat heb je al behandeld over limieten?quote:
[..]
Ik krijg er koppijn van. Hoe moet ik anders die driehoeksongelijkheid toepassen!?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
quote:
[..]
Wat is je precieze vraagstelling en wat heb je al behandeld over limieten?
Hier komt hier op neer. Ik moet van Riparius bewijzen dat een polynoom van oneven graad ten minste één nulpunt in R heeft. Nu heb ik dat zo gedaan, maar dat is klaarblijkelijk te kort door de bocht.quote:
Zij P(x) een polynoom van de oneven graad met reële coëfficiënten. P(x) is continu op R.
zij P(x) = an•xn+an-1•xn-1+an-2•xn-2 .... +a0 met an, a0 ≠ 0 en n oneven.
lim(x -> ∞)(P(x)) = lim(x -> ∞)(anxn) = ∞ als an > 0 en -∞ als an < 0
lim(x -> -∞)(P(x)) = lim(x -> -∞)(anxn) = -∞ als an > 0 en ∞ als an < 0
Uit de tussenwaardestelling volgt dan dat er een waarde c bestaat zó dat P(c) = 0
Hmm?
Nu moet ik de driehoeksongelijkheid toepassen om aan te tonen dat P(x) van teken wisselt. En ik heb geen idee hoe ik dat anders moet doen dan op bovenstaande wijze.
Ik vraag niet om een complete uitwerking, FYI.
Over limieten, we hebben behandeld wat een limiet betekent, l'Hôpital, formele definitie van een limiet. Dat laatste minder uitvoerig trouwens. Een inleiding tot bij Calculus (C).
Fervent tegenstander van het korps lasergamers.
Hebben jullie al toevallig de middelwaardestelling behandeld?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Jazeker. Ook de tussenwaardestelling en de insluitstelling. De tussenwaardestelling pas ik trouwens in mijn quote toe.quote:
[..]
Hebben jullie al toevallig de middelwaardestelling behandeld?
Fervent tegenstander van het korps lasergamers.
Je bewijs totquote:
[..]
Jazeker. Ook de tussenwaardestelling en de insluitstelling. De tussenwaardestelling pas ik trouwens in mijn quote toe.
is goed. Je had namelijk niet hoeven delen. Je gaat als het goed is (hopelijk) nog al die formele regels krijgen voor limieten. Dus dat als de limieten van twee functies bestaat, dat dan de limiet van de product bestaat en dat limieten ongelijkheid behouden.
Maar volgens mij wil Riparius dat je de formele definities van limieten gebruikt om afschattingen te vinden, want je mag de tussenwaardestelling zo nog niet gebruiken.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Dat heb ik dus nog niet gehad, ofja, ik heb geen idee hoe ik het moet toepassen.quote:
[..]
Je bewijs tot
is goed. Je had namelijk niet hoeven delen. Je gaat als het goed is (hopelijk) nog al die formele regels krijgen voor limieten. Dus dat als de limieten van twee functies bestaat, dat dan de limiet van de product bestaat en dat limieten ongelijkheid behouden.
Maar volgens mij wil Riparius dat je de formele definities van limieten gebruikt om afschattingen te vinden, want je mag de tussenwaardestelling zo nog niet gebruiken.
Fervent tegenstander van het korps lasergamers.
Het was dus beter geweest om de limieten te nemen zonder de driehoeksongelijkheid en dan kun je vinden datquote:
Dan kun je de formele definitie gebruiken om op te schrijven dat
Stel dat x>0 en stel a_n is positief, kies dan epsilon= 0.5. Stel a_n is negatief, kies dan ook epsilon=2. (Hiermee weten we dus dat P(x)>0 voor a_n is positief en dat P(x)<0 voor a_n is negatief)
We kunnen dit op een analoge wijze doen voor limiet van x naar min oneindig, waarbij we aannemen dat x<0. Dus we vinden dat P(x)<0 voor a_n positief en P(x)>0 voor a_n negatief.
We kunnen de tussenwaardestelling gebruiken en bewijzen wat we wilden.
Maar ik ga nu even verder met mijn scriptie. Veel succes!
[ Bericht 1% gewijzigd door Mathemaat op 13-10-2013 12:14:31 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
In jouw tweede geval, stel dat an < 0. Je stelt epsilon gelijk aan 2:quote:
[..]
Het was dus beter geweest om de limieten te nemen zonder de driehoeksongelijkheid en dan kun je vinden dat
Dan kun je de formele definitie gebruiken om op te schrijven dat
We bekijken in dit limiet in het algemeen dat x>0. Stel a_n is positief, kies dan epsilon= 0.5. Stel a_n is negatief, kies dan epsilon=2. (Hiermee weten we dus dat P(x)>0, voor een x dat voldoet aan de limiet definitie)
We kunnen dit op een analoge wijze doen voor limiet van x naar min oneindig, waarbij dus in het algemeen geldt dat x<0. Dus we vinden dat P(x)<0 voor een x dat voldoet aan de limiet definitie van x naar min oneindig.
We kunnen de tussenwaardestelling gebruiken en bewijzen wat we wilden.
Maar ik ga nu even verder met mijn scriptie. Veel succes!
Je linkerterm wordt dan uiteraard positief, maar je rechterterm blijft negatief.
dus 0 ≤ P(x) ≤ iets negatiefs
Hoe kan dit?
[ Bericht 0% gewijzigd door Amoeba op 12-10-2013 23:25:58 ]
Fervent tegenstander van het korps lasergamers.
P(x) = anxn(1 + (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
Dus P(x) = anxn(1+f(x))
Met f(x) = (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
limx→∞f(x) = 0 want c/xk = 0 voor x→∞
En dan zal nu wel heel formeel dit gezegd moeten worden.
∀ε>0∃δ>0,∀x [0 < |x-c| < δ → |f(x) - L| < ε]
L = 0, dus kies ε = 1.
|f(x)| < 1
stel |x| > δ
dan
1+f(x) > 0
En dus positief. Dus die factor laat ik vanaf nu achterwege..
Stel a > δ
dan P(a) = anan
Weten we dat a>0, dus P(a) is negatief voor an < 0 en P(a) is positief voor an > 0.
Neem nu b < -δ
Dan P(b) is negatief voor an > 0 en P(b) is positief voor an < 0
En dan de tussenwaardestelling toepassen op de continu functie P(x) geeft dat er een c bestaat zodanig dat P(c) = 0
Het is niet compleet van mezelf. Voor de notatie met de ε,δ-methode heb ik wat hulp opgezocht, en geprobeerd in eigen notatie te formuleren, ik hoop dat ik dat goed heb gedaan.
[ Bericht 0% gewijzigd door Amoeba op 13-10-2013 02:24:46 ]
Dus P(x) = anxn(1+f(x))
Met f(x) = (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
limx→∞f(x) = 0 want c/xk = 0 voor x→∞
En dan zal nu wel heel formeel dit gezegd moeten worden.
∀ε>0∃δ>0,∀x [0 < |x-c| < δ → |f(x) - L| < ε]
L = 0, dus kies ε = 1.
|f(x)| < 1
stel |x| > δ
dan
1+f(x) > 0
En dus positief. Dus die factor laat ik vanaf nu achterwege..
Stel a > δ
dan P(a) = anan
Weten we dat a>0, dus P(a) is negatief voor an < 0 en P(a) is positief voor an > 0.
Neem nu b < -δ
Dan P(b) is negatief voor an > 0 en P(b) is positief voor an < 0
En dan de tussenwaardestelling toepassen op de continu functie P(x) geeft dat er een c bestaat zodanig dat P(c) = 0
Het is niet compleet van mezelf. Voor de notatie met de ε,δ-methode heb ik wat hulp opgezocht, en geprobeerd in eigen notatie te formuleren, ik hoop dat ik dat goed heb gedaan.
[ Bericht 0% gewijzigd door Amoeba op 13-10-2013 02:24:46 ]
Fervent tegenstander van het korps lasergamers.
Ow sorry, het is beter om het zo opgeschreven te houden:quote:
[..]
In jouw tweede geval, stel dat an < 0. Je stelt epsilon gelijk aan 2:
Je linkerterm wordt dan uiteraard positief, maar je rechterterm blijft negatief.
dus 0 ≤ P(x) ≤ iets negatiefs
Hoe kan dit?
Dan omdat a_n<0, slaan de ongelijktekens ook om, als je ermee vermenigvuldigt.
Ik heb de fouten eruit gepoetst!
[ Bericht 1% gewijzigd door Mathemaat op 13-10-2013 12:16:15 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Het is bijna goed, voor naar oneindig gebruik je overigens een andere limiet definitie. Maar één of andere reden heb je toch de juiste gebruikt in je uitwerking.quote:
P(x) = anxn(1 + (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
Dus P(x) = anxn(1+f(x))
Met f(x) = (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
limx→∞f(x) = 0 want c/xk = 0 voor x→∞
En dan zal nu wel heel formeel dit gezegd moeten worden.
∀ε>0∃δ>0,∀x [0 < |x-c| < δ → |f(x) - L| < ε]
L = 0, dus kies ε = 1.
|f(x)| < 1
stel |x| > δ
dan
1+f(x) > 0
En dus positief. Dus die factor laat ik vanaf nu achterwege..
Stel a > δ
dan P(a) = anan
Weten we dat a>0, dus P(a) is negatief voor an < 0 en P(a) is positief voor an > 0.
Neem nu b < -δ
Dan P(b) is negatief voor an > 0 en P(b) is positief voor an < 0
En dan de tussenwaardestelling toepassen op de continu functie P(x) geeft dat er een c bestaat zodanig dat P(c) = 0
Het is niet compleet van mezelf. Voor de notatie met de ε,δ-methode heb ik wat hulp opgezocht, en geprobeerd in eigen notatie te formuleren, ik hoop dat ik dat goed heb gedaan.
Het is niet netjes om nog een a of b te gebruiken. Het is beter om de gevallen van x af te gaan, voor wanneer het strikt positief of strikt negatief is.
[ Bericht 1% gewijzigd door Mathemaat op 13-10-2013 12:30:06 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Kun je daar iets meer over vertellen?quote:
[..]
Het is bijna goed, voor naar oneindig gebruik je overigens een andere limiet definitie. Maar één of andere reden heb je toch de juiste gebruikt in je uitwerking.
Dit begrijp ik niet.quote:Het is niet netjes om nog een a of b te gebruiken. Het is beter om de gevallen van x af te gaan, voor wanneer het strikt positief of strikt negatief is.
Dit wel.quote:Je hoeft overigens ook niet te zeggen dat |x|>delta.
Fervent tegenstander van het korps lasergamers.
Je x gaat naar oneindig, dus de voorwaarde wordt dan bijvoorbeeld geschreven alsquote:
[..]
Kun je daar iets meer over vertellen?
en niet als
Je kiest aparte letters a en b. Maar je kunt ook de gevallen afgaan van x, dus stel x is positief dan |x|=x en stel x is negatief dan |x|=-x. Dit maakt het lezen prettiger.quote:[..]
Dit begrijp ik niet.
[quote]
[ Bericht 5% gewijzigd door Mathemaat op 13-10-2013 12:30:23 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Volgens mij was die regel overbodig, althans, ik denk dat dat is wat je bedoelt?quote:
[..]
Je x gaat naar oneindig, dus de voorwaarde wordt dan bijvoorbeeld geschreven als,
en niet als
[..]
Je kiest aparte letters a en b. Maar je kunt ook de gevallen afgaan van x, dus stel x is positief dan |x|=x en stel x is negatief dan |x|=-x. Dit maakt het lezen prettiger.
[..]
Snap je dit wel?
Dus
//
P(x) = anxn(1 + (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
Dus P(x) = anxn(1+f(x))
Met f(x) = (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
limx→∞f(x) = 0 want c/xk = 0 voor x→∞
En dan zal nu wel heel formeel dit gezegd moeten worden.
∀ε>0∃δ>0,∀x [|x| > δ → |f(x) - L| < ε]
L = 0, dus kies ε = 1.
|f(x)| < 1
en dus
1+f(x) > 0
En dus positief. Dus die factor laat ik vanaf nu achterwege..
Stel x > δ
dan P(x) = anxn
Weten we dat a>0, dus P(x) is negatief voor an < 0 en P(x) is positief voor an > 0.
Neem nu x < -δ
Dan P(x) is negatief voor an > 0 en P(x) is positief voor an < 0
En dan de tussenwaardestelling toepassen op de continu functie P(x) geeft dat er een c bestaat zodanig dat P(c) = 0
Of zoiets als |x| > δ en |x| = x voor x>0 en |x| = -x voor x < 0
En dan hetzelfde riedeltje? Alhoewel ik nu even niet weet of het goed gaat met het teken..
Fervent tegenstander van het korps lasergamers.
Hier stond onzin...
[ Bericht 50% gewijzigd door Mathemaat op 13-10-2013 12:29:41 ]
[ Bericht 50% gewijzigd door Mathemaat op 13-10-2013 12:29:41 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Omdat de limiet bestaat is dat waar inderdaad. Dat moet ik goed onthouden.quote:
[..]
Ja, die regel is eigenlijk overbodig, maar dat heeft iets met logica te maken. Je bent vrij om het toch erbij te zetten, als je je fijner ermee voelt. Het heeft ermee te maken, dat omdat het uitspraak waar is, het gevolg waar is ongeacht de voorwaarden (hier is dat |x|>delta).
Dus je hoeft eigenlijk niets meer te doen met die delta.
Dus uhm, heb ik het laatste stuk nu wel juist opgeschreven?
Fervent tegenstander van het korps lasergamers.
Nee, vergeet wat ik net heb verteld, dat is onzin xDquote:
[..]
Omdat de limiet bestaat is dat waar inderdaad. Dat moet ik goed onthouden.
Dus uhm, heb ik het laatste stuk nu wel juist opgeschreven?
Je moet je |x|>delta kiezen, zodat het gevolg waar is. Het is het hele uitspraak dat waar is, dus ook ongeacht de voorwaardes. Maar je voorwaardes moeten waar zijn, zodat je gevolg waar is (hier maak je dus gebruik van dat het hele uitspraak waar is).
Jawel, het is goed. Ik moet gewoon meer koffie drinken
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Ik heb net een bakkie gehad. Goed, ga ik dit even netjes uitwerken in LaTeX.quote:
[..]
Nee, vergeet wat ik net heb verteld, dat is onzin xD
Je moet je |x|>delta kiezen, zodat het gevolg waar is. Het is het hele uitspraak dat waar is, dus ook ongeacht de voorwaardes. Maar je voorwaardes moeten waar zijn, zodat je gevolg waar is (hier maak je dus gebruik van dat het hele uitspraak waar is).
Jawel, het is goed. Ik moet gewoon meer koffie drinken
Fervent tegenstander van het korps lasergamers.
Goed zet er nog gelijk achter dat epsilon=1 ook dat je x kiest, zodat |x|>delta.quote:
[..]
Ik heb net een bakkie gehad. Goed, ga ik dit even netjes uitwerken in LaTeX.
Je moet ook nog in je limiet definite zetten dat je alle x kiest uit het domein van f. Nu staat er doodleuk voor alle x. Zet er ook expliciet bij dat je twee gevallen x (x groter dan nul en kleiner dan) gaat bekijken, voordat je dat begint te doen.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Komt goed.quote:
[..]
Goed zet er nog gelijk achter dat epsilon=1 ook dat je x kiest, zodat |x|>delta.
Je moet ook nog in je limiet definite zetten dat je alle x kiest uit het domein van f. Nu staat er doodleuk voor alle x. Zet er ook expliciet bij dat je twee gevallen x (x groter dan nul en kleiner dan) gaat bekijken, voordat je dat begint te doen.
Fervent tegenstander van het korps lasergamers.
Weer wat geleerdquote:
[..]
Zoals Thabit hierboven al opmerkt zijn x en y de wortels van een vierkantsvergelijking, en door deze substitutie kom je op diezelfde vierkantsvergelijking uit, die je dan op één der bekende manieren kunt oplossen. Maar als je dan gaat proberen de vierkantsvergelijking door ontbinden in factoren op te lossen, dan ben je weer terug bij het oorspronkelijke vraagstuk om twee getallen te bepalen waarvan som en product zijn gegeven.
Je kunt het ook als volgt doen. We nemen het kwadraat van de som, dat is
(x + y)2 = 552 = 3025
Dit kwadraat verminderen we met het viervoud van het product, dit geeft
(x + y)2 − 4xy = 3025 − 4·294 = 1849
En aangezien (x + y)2 − 4xy = (x − y)2 hebben we dus
(x − y)2 = 1849
De vierkantswortel nemen geeft dan
x − y = 43
We hadden hier ook −43 kunnen nemen, maar we hebben aan één waarde voor het verschil genoeg, omdat het inverteren van het teken van het verschil neerkomt op het omwisselen van x en y. Optellen van som en verschil geeft nu
2x = (x + y) + (x − y) = 55 + 43 = 98, dus x = 49
En aftrekken van het verschil van de som geeft
2y = (x + y) − (x − y) = 55 − 43 = 12, dus y = 6
Dezelfde methode is ook te gebruiken om uitdrukkingen af te leiden voor de wortels van de algemene vierkantsvergelijking
ax2 + bx + c = 0 (a ≠ 0)
Zijn de wortels van deze vergelijking x1 en x2, dan is de vergelijking te schrijven als
a(x − x1)(x − x2) = 0
oftewel
ax2 − a(x1 + x2)x + ax1x2 = 0
zodat we door de coëfficiënten te vergelijken kunnen concluderen dat geldt
x1 + x2 = −b/a
en
x1x2 = c/a
Door nu op bovenstaande wijze x1 en x2 te bepalen uit de gegeven som −b/a en het gegeven product c/a kunnen we uitdrukkingen voor x1 en x2 in de coëfficiënten a, b en c van de vergelijking afleiden. Deze manier om de abc-formule af te leiden resp. een vierkantsvergelijking op te lossen wordt wel de methode van Harriot genoemd.
Hoi allemaal,
Even een wiskundige vraag:
De intergraal van 5 tot 2 van lx-3l
Ik zelf kom uit op dit:
lx^2-3xl en dan invullen
l5^2-3*5l-l(2^2-3*2)l=12 maar het moet 5/2 zijn?
Alvast bedankt
Even een wiskundige vraag:
De intergraal van 5 tot 2 van lx-3l
Ik zelf kom uit op dit:
lx^2-3xl en dan invullen
l5^2-3*5l-l(2^2-3*2)l=12 maar het moet 5/2 zijn?
Alvast bedankt
Is er bij de Lagrange methode een systematische manier die altijd werkt voor het vinden van minima en maxima? Ik betrap mezelf er namelijk op dat ik soms in het wild begin te zoeken naar een minimum en maximum en dan slechts één van deze vind.
Zoals je de integraal nu berekent houd je geen rekening met de gevolgen van de absoluutstrepen voor de functie en de waarden waarvoor je de integraal evalueert. Waar ligt het nulpunt voor |x-3| en wat betekent dat voor de integraal?quote:
Hoi allemaal,
Even een wiskundige vraag:
De intergraal van 5 tot 2 van lx-3l
Ik zelf kom uit op dit:
lx^2-3xl en dan invullen
l5^2-3*5l-l(2^2-3*2)l=12 maar het moet 5/2 zijn?
Alvast bedankt
Je moet onthouden dat:quote:
Hoi allemaal,
Even een wiskundige vraag:
De intergraal van 5 tot 2 van lx-3l
Ik zelf kom uit op dit:
lx^2-3xl en dan invullen
l5^2-3*5l-l(2^2-3*2)l=12 maar het moet 5/2 zijn?
Alvast bedankt
|x-3| = x-3 voor x >= 3
en
|x-3| = -(x-3) voor x < 3
En zo kun je dus de integraal opdelen in 2 deelintegralen, en die kun je integreren.
Fervent tegenstander van het korps lasergamers.
Je verwart hierboven de definitie van limx → c f(x) = L met de definitie van limx → ∞ f(x) = L. Bovendien hield je er geen rekening mee dat limx → −∞ f(x) weer iets anders is dan limx → ∞ f(x).quote:
[..]
P(x) = anxn(1 + (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
Dus P(x) = anxn(1+ f(x))
Met f(x) = (an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n)
Het gebruik van de letters ε en δ om willekeurig klein te nemen positieve grootheden aan te duiden gaat terug op Cauchy, en men neemt aan dat hij deze letters heeft gekozen omdat de tegenhangers e en d uit het Latijnse alfabet de eerste letters zijn van de Franse woorden erreur en différence. Het idee bij limx→c f(x) = L is immers dat je de afwijking (: erreur) van f(x) van L kleiner kunt maken dan ε als je het verschil (: différence) van x met c kleiner maakt dan δ. De precieze definitie is overigens pas later gegeven door Weierstrass, die daarvoor ook de bekende notatie voor de absolute waarde met de verticale strepen invoerde, omdat hij deze nodig had om zijn definitie compact op te kunnen schrijven.
Met limx→∞ f(x) = L wordt bedoeld dat de afwijking (: erreur) van f(x) van L kleiner gemaakt kan worden dan een willekeurig klein te kiezen positieve grootheid ε als we x maar voldoende groot kiezen. En dus komt er aan de definitie van limx→∞ f(x) = L geen willekeurig klein te kiezen verschil van x met een vaste grootheid c te pas, en dus ook geen δ. De formele definitie van limx→∞ f(x) = L is dat er voor elke ε > 0 een X0 ∈ R bestaat zodanig dat |f(x) − L| < ε voor elke x > X0. Evenzo betekent limx→−∞ f(x) = L dat er voor elke ε > 0 een X0 ∈ R bestaat zodanig dat |f(x) − L| < ε voor elke x < X0.
Je hebt inmiddels gezien dat het voldoende is om aan te tonen dat in
P(x) = anxn(1+ f(x))
de waarde van |f(x)| tot nul nadert als we |x| steeds groter maken, maar het is niet handig om hier met de formele definities van limieten te werken, omdat je dan aan moet tonen dat zowel limx→∞ f(x) = 0 als limx→−∞ f(x) = 0. Bovendien hoef je helemaal niet zover te gaan: het is voldoende om aan te tonen dat er een X0 > 0 bestaat zodanig dat |f(x)| < 1 voor |x| > X0 want dan is −1 < f(x) < 1 en dus 0 < 1 + f(x) < 2, zodat P(x) = anxn(1+ f(x)) hetzelfde teken heeft als anxn voor |x| > X0. En dan heeft P(x) dus een tegengesteld teken voor x > X0 en voor x < −X0 aangezien n oneven is.
Welnu, met behulp van de driehoeksongelijkheid hebben we
(1) |(an−1/an)x−1 + (an−2/an)x−2 + ... + (a1/an)x−(n−1) + (a0/an)x−n| ≤ |(an−1/an)x−1| + |(an−2/an)x−2| + ... + |(a1/an)x−(n−1)| + |(a0/an)x−n|
Definieer nu
(2) A := |(an−1/an)| + |(an−2/an)| + ... + |(a1/an)| + |(a0/an)|
en merk op dat A > 0 aangezien we a0 ≠ 0 hebben verondersteld. Nu geldt verder voor |x| ≥ 1 en k ≥ 1 dat |x−k| ≤ |x−1|. Voor |x| ≥ 1 hebben we nu dus
(3) |(an−1/an)x−1| + |(an−2/an)x−2| + ... + |(a1/an)x−(n−1)| + |(a0/an)x−n| ≤ A·|x−1|
Zij nu X0 = max(1, A) en kies een r > X0. Dan geldt voor |x| = r dat |x| > 1 en tevens |x| > A zodat |x−1| < 1/A en dus A·|x−1| < 1. Uit de ongelijkheden (1) en (3) volgt nu dat |f(x)| < 1 voor |x| = r. Is nu an > 0 dan is P(r) > 0 en P(−r) < 0. Is daarentegen an < 0 dan is P(r) < 0 en P(−r) > 0. In beide gevallen bestaat er volgens de tussenwaardestelling een x0 ∈ [−r, r] zodanig dat P(x0) = 0, QED.
[ Bericht 0% gewijzigd door Riparius op 13-10-2013 20:34:57 ]
quote:
[..]
Zoals je de integraal nu berekent houd je geen rekening met de gevolgen van de absoluutstrepen voor de functie en de waarden waarvoor je de integraal evalueert. Waar ligt het nulpunt voor |x-3| en wat betekent dat voor de integraal?
Bedankt, is gelukt!quote:
[..]
Je moet onthouden dat:
|x-3| = x-3 voor x >= 3
en
|x-3| = -(x-3) voor x < 3
En zo kun je dus de integraal opdelen in 2 deelintegralen, en die kun je integreren.
Hoe vind je gemakkelijk de factoren van een getal?
Stel 75:
3,5 en 5 (priemgetallen)
Dan zijn de factoren dus 1, 75, 3, 25, 5 en 15.
Stel 1000:
2,2,2,5,5 en 5.
Hoe tel ik de factoren aan de hand van de priemgetallen?
Stel 75:
3,5 en 5 (priemgetallen)
Dan zijn de factoren dus 1, 75, 3, 25, 5 en 15.
Stel 1000:
2,2,2,5,5 en 5.
Hoe tel ik de factoren aan de hand van de priemgetallen?
Ik ga dit nog maar eens correct met limieten proberen op te schrijven. Een commentaar is dat ik onderscheid moet maken tussen de limx→∞ f(x) en limx→ -∞ f(x) en de limietvoorwaarde beter moet opschrijven.quote:
Kijk eens naar de Eulerfunctie. De Eulerfunctie geeft je alle getallen die copriem zijn met een getal. Daarvoor moet je wel de priemfactorontbinding weten. M.a.w. n - phi(n)quote:
Hoe vind je gemakkelijk de factoren van een getal?
Stel 75:
3,5 en 5 (priemgetallen)
Dan zijn de factoren dus 1, 75, 3, 25, 5 en 15.
Stel 1000:
2,2,2,5,5 en 5.
Hoe tel ik de factoren aan de hand van de priemgetallen?
Fervent tegenstander van het korps lasergamers.
Ok, ik zal even kijken. Ik dacht dat je het kon uitrekenen met kansrekening(oid).quote:
[..]
Ik ga dit nog maar eens correct met limieten proberen op te schrijven. Een commentaar is dat ik onderscheid moet maken tussen de limx→∞ f(x) en limx→ -∞ f(x) en de limietvoorwaarde beter moet opschrijven.
[..]
Kijk eens naar de Eulerfunctie. De Eulerfunctie geeft je alle getallen die copriem zijn met een getal. Daarvoor moet je wel de priemfactorontbinding weten.
Ik moet even corrigeren. De Eulerfunctie geeft je de hoeveelheid getallen die copriem zijn met een getal.quote:
[..]
Ok, ik zal even kijken. Ik dacht dat je het kon uitrekenen met kansrekening(oid).
Fervent tegenstander van het korps lasergamers.
Bedoel je hiermee het aantal factoren dat een getal heeft? Dat is exact wat ik wil berekenen.quote:
[..]
Ik moet even corrigeren. De Eulerfunctie geeft je de hoeveelheid getallen die copriem zijn met een getal.
De Functie van Euler geeft het aantal getallen dat Relatief priem met een ander getal is (dus dat er geen getal is dat beide deelt). Dat is denk ik niet wat je zoekt.quote:
[..]
Bedoel je hiermee het aantal factoren dat een getal heeft? Dat is exact wat ik wil berekenen.
Tot zover wat ik weet. Nu even logisch nadenken. Als je het aantal getallen zoekt dat een ander getal deelt, kun je dat getal eerst ontbinden in priemfactoren. Je vindt dan een reeks priemgetallen. Deze kun je met elkaar vermenigvuldigen om factoren van dat getal te vinden. Dat kan op een aantal manieren. Je gaat kijken hoeveel combinaties er mogelijk zijn met deze rij getallen waarbij volgorde niet van invloed is. Dat klinkt als een combinatie, inderdaad kansrekening. Al een idee hoe je verder zou moeten?
Overigens kan ik er compleet naast zitten, correct me if I'm wrong. Ik heb dit nl. niet gehad, maar probeer te beredeneren wat het zou kunnen zijn.
EDIT: Misschien dacht ik iets te moeilijk. Als Phi(n) het aantal getallen is dat geen deler gemeenschappelijk heeft, en je zoekt het aantal getallen dat wel een of meerde priemfactoren gemeenschappelijk heeft (en dus het aantal delers)... En n is het totaal aantal mogelijke delers Kan je daar dan iets mee? Ik denk dat dat is wat Amoebe probeerde te zeggen met de n-Phi(n) waarmee hij zijn post eindigde.
[ Bericht 1% gewijzigd door Aardappeltaart op 13-10-2013 18:40:42 ]
Wat ik heb:
Dit is dan het maximale totale oppervlakte.
Als je ervan uitgaat dat één punt ook een kubus is:
Dit is dan het minimale totale oppervlakte.
Klopt dit? Of denk ik nu gewoon te simpel?
Gist is liefde, gist is leven. Vooral in een vagijn.
Mensen die denken dat ze te simpel denken denken denk ik helemaal niet.quote:
[ afbeelding ]
Klopt dit? Of denk ik nu gewoon te simpel?
Ik zie in je opgave helemaal niet staan dat beide kubussen even groot zijn. Begin daar maar eens over na te denken.
@rezania; begin met definieren x1 en x2 voor kubus 1 en 2. Druk x2 uit in x1 en het totale volume. Nu kun je een functie maken die het totale opp weergeeft, op basis van x1, bereken dan de lokale minima en maxima tussen x1 = 0..2000^1/3
http://www.wolframalpha.c(...)000%5E%281%2F3%29%29
http://www.wolframalpha.c(...)000%5E%281%2F3%29%29
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl
Dus gewoon normaal optimaliseren eigenlijk, ik wist wel dat ik te makkelijk dacht.quote:
@rezania; begin met definieren x1 en x2 voor kubus 1 en 2. Druk x2 uit in x1 en het totale volume. Nu heb je een functie, bereken dan de lokale minima en maxima tussen x1 = 0..2000^1/3
http://www.wolframalpha.c(...)000%5E%281%2F3%29%29
quote:
[..]
Mensen die denken dat ze te simpel denken denken denk ik helemaal niet.
Ik zie in je opgave helemaal niet staan dat beide kubussen even groot zijn. Begin daar maar eens over na te denken.
Gist is liefde, gist is leven. Vooral in een vagijn.
http://www.wikihow.com/Find-How-Many-Factors-Are-in-a-Numberquote:
Bedoel je hiermee het aantal factoren dat een getal heeft? Dat is exact wat ik wil berekenen.
Nee, ik denk dat ik het fout heb. Lees dat artikel van Tochjo even door.quote:
[..]
Bedoel je hiermee het aantal factoren dat een getal heeft? Dat is exact wat ik wil berekenen.
Fervent tegenstander van het korps lasergamers.
Ah natuurlijk, dat kan ook.quote:
[..]
http://www.wikihow.com/Find-How-Many-Factors-Are-in-a-Number
Waarom is n-Phi(n) het dan niet? In ieder geval is de manier van dat artikel van Tochjo toch wel makkelijker dan n-Phi(n) of het optellen van combinaties wat ik voorstelde...quote:
[..]
Nee, ik denk dat ik het fout heb. Lees dat artikel van Tochjo even door.
Ik denk inderdaad dat hij dit bedoelt. Hij wil het totaal aantal delers van een positief geheel getal bepalen. En dat heeft niets met kansrekening te maken.quote:
[..]
http://www.wikihow.com/Find-How-Many-Factors-Are-in-a-Number
Voorbeeld: bereken het aantal delers van 1000.
Antwoord: we ontbinden 1000 eerst in priemfactoren. Dit geeft
1000 = 23·53
Het aantal delers van 1000 is dus (3 + 1)·(3 + 1) = 16.
Controle: de delers van 1000 zijn
1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000.
16 stuks inderdaad.
Stom hoor, uiteindelijk kom je gewoon weer op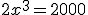 
uit en blijkt mijn vermoeden dus gewoon te kloppen.
Gist is liefde, gist is leven. Vooral in een vagijn.
Klopt helemaal, maar ja, als je alles met vermoedens aan kon tonen zou het geen wiskundetopic zijn he .
.
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl
Helaas niet nee.quote:
Klopt helemaal, maar ja, als je alles met vermoedens aan kon tonen zou het geen wiskundetopic zijn he
Gist is liefde, gist is leven. Vooral in een vagijn.
Niets stoms aan, vermoedens die je uit moet je wel kunnen bewijzen (of weerleggen natuurlijk).quote:
Stom hoor, uiteindelijk kom je gewoon weer op
Maar als dit vermoeden als stelling zou bestaan mocht je er toch wel gewoon vanuit gaan en was mijn eerste uitwerking correct?quote:
[..]
Niets stoms aan, vermoedens die je uit moet je wel kunnen bewijzen (of weerleggen natuurlijk).
Gist is liefde, gist is leven. Vooral in een vagijn.
Nee, zelf dat mag niet. Zoiets noemen ze een petitio principii, en dat is een doodzonde.quote:
[..]
Maar als dit vermoeden als stelling zou bestaan mocht je er toch wel gewoon vanuit gaan en was mijn eerste uitwerking correct?
phi(1000) = 400quote:
[..]
Ah natuurlijk, dat kan ook.
[..]
Waarom is n-Phi(n) het dan niet? In ieder geval is de manier van dat artikel van Tochjo toch wel makkelijker dan n-Phi(n) of het optellen van combinaties wat ik voorstelde...
1000 - 400 = 600
Dat is heel wat meer dan 16.
Fervent tegenstander van het korps lasergamers.
Misschien weet Riparius dat. Hoe druk je het aantal delers van 1000 uit als een vergelijking met daarin de eulerfunctie, of kan dit niet?
Of algemeen, het aantal delers van een integer getal n.
Of algemeen, het aantal delers van een integer getal n.
Fervent tegenstander van het korps lasergamers.
Maar waarom mag het dan bij meetkundig bewijzen wel? Daar moet je toch ook iets aantonen?quote:
[..]
Nee, zelf dat mag niet. Zoiets noemen ze een petitio principii, en dat is een doodzonde.
Gist is liefde, gist is leven. Vooral in een vagijn.
Lijkt me genoeg tegenbewijs ja, dankjewel. Interessante vraag of en hoe het wel zou kunnen, ik ben benieuwd!quote:
[..]
phi(1000) = 400
1000 - 400 = 600
Dat is heel wat meer dan 16.
Stellingen die je zelf bewezen hebt of bijvoorbeeld in de les bewezen zijn mag je gebruiken. Anderen niet. Toch?quote:
[..]
Maar waarom mag het dan bij meetkundig bewijzen wel? Daar moet je toch ook iets aantonen?
Ik denk dat jij een heel verkeerde voorstelling hebt van wat nu een wiskundig bewijs is. Je mag datgene wat je wil bewijzen nooit voor waar aannemen, want dan bewijs je uiteindelijk niets. Je ziet vaak dat mensen hiermee de mist in gaan als ze een bewijs met (volledige) inductie moeten geven.quote:
[..]
Maar waarom mag het dan bij meetkundig bewijzen wel? Daar moet je toch ook iets aantonen?
Ah ja, dan krijg je inderdaad een cirkelredenering.quote:
[..]
Ik denk dat jij een heel verkeerde voorstelling hebt van wat nu een wiskundig bewijs is. Je mag datgene wat je wil bewijzen nooit voor waar aannemen, want dan bewijs je uiteindelijk niets. Je ziet vaak dat mensen hiermee de mist in gaan als ze een bewijs met (volledige) inductie moeten geven.
Gist is liefde, gist is leven. Vooral in een vagijn.
Dat is inderdaad de gangbare Nederlandse term voor een petitio principii. Heb je deze limiet nog uitgewerkt?quote:
[..]
Ah ja, dan krijg je inderdaad een cirkelredenering.
Nee, ik liep op een gegeven moment steeds vast op die noemer en daarna heb ik er geen tijd meer aan besteed. Ik had andere prioriteiten.quote:
[..]
Dat is inderdaad de gangbare Nederlandse term voor een petitio principii. Heb je deze limiet nog uitgewerkt?
Gist is liefde, gist is leven. Vooral in een vagijn.
Hint: herschrijf de noemer alsquote:
[..]
Nee, ik liep op een gegeven moment steeds vast op die noemer en daarna heb ik er geen tijd meer aan besteed. Ik had andere prioriteiten.
x3·x−1·log(1 + x) = x3·log(1 + x)1/x
en gebruik dat
limx→0 (1 + x)1/x = e
zodat
limx→0 log(1 + x)1/x = log e = 1
Misschien morgen, ben voor vandaag wel klaar met wiskunde.quote:
[..]
Hint: herschrijf de noemer als
x3·x−1·log(1 + x) = x3·log(1 + x)1/x
en gebruik dat
limx→0 (1 + x)1/x = e
zodat
limx→0 log(1 + x)1/x = log e = 1
Gist is liefde, gist is leven. Vooral in een vagijn.
Het gaat uiteraard ook eenvoudig als je de formele definitie van een limiet en wat rekenregels voor limieten gebruikt. Voor k = 1 .. n heb jequote:
[..]
Ik ga dit nog maar eens correct met limieten proberen op te schrijven. Een commentaar is dat ik onderscheid moet maken tussen de limx→∞ f(x) en limx→ -∞ f(x) en de limietvoorwaarde beter moet opschrijven.
limx→∞ (an−k/an)x−k = 0
en
limx→−∞ (an−k/an)x−k = 0
(Bewijs dit aan de hand van de formele definitie van deze limieten). Aangezien de limiet van een som gelijk is aan de som van de limieten van de termen (mits deze bestaan) volgt dan direct dat
limx→∞ f(x) = 0
en
limx→−∞ f(x) = 0
In overeenstemming met de definitie van deze limieten bestaan er nu getallen X1, X2 ∈ R zodanig dat
|f(x)| < 1 voor x > X1
en
|f(x)| < 1 voor x < X2
Kies nu X0 = max(|X1|, |X2|), dan is X0 ≥ X1 en tevens −X0 ≤ X2 zodat |f(x)| < 1 voor |x| > X0.
Nog een vraagje over integreren:
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
Deze opgave komt me heel bekend voor. Toevallig ook econometrie?quote:
Nog een vraagje over integreren:
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
delers = factoren?quote:
[..]
Ik denk inderdaad dat hij dit bedoelt. Hij wil het totaal aantal delers van een positief geheel getal bepalen. En dat heeft niets met kansrekening te maken.
Voorbeeld: bereken het aantal delers van 1000.
Antwoord: we ontbinden 1000 eerst in priemfactoren. Dit geeft
1000 = 23·53
Het aantal delers van 1000 is dus (3 + 1)·(3 + 1) = 16.
Controle: de delers van 1000 zijn
1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000.
16 stuks inderdaad.
Of is er een verschil tussen NL en ENG?
Ja, jij weet niet toevallig hoe die moet?quote:Op zondag 13 oktober 2013 21:58 schreef Ensemble het volgende:
[..]
Deze opgave komt me heel bekend voor. Toevallig ook econometrie?
Nee, die lukte bij mij ook niet. Ook de practicumdocent kon hem niet uitleggen.quote:
[..]
Ja, jij weet niet toevallig hoe die moet?
Dus ben wel benieuwd hoe die moet.
Ik had trouwens precies hetzelfde als wat jij had.
Die docent moet eens wat creatiever worden. Het gaat uiteraard via partieel integreren, maar ook als je dat niet mag gebruiken en het uitsluitend via substitutie moet is het te doen. We gaan eerst de integrand een beetje herleiden.quote:Op zondag 13 oktober 2013 22:09 schreef Ensemble het volgende:
[..]
Nee, die lukte bij mij ook niet. Ook de practicumdocent kon hem niet uitleggen.
Dus ben wel benieuwd hoe die moet.
Ik had trouwens precies hetzelfde als wat jij had.
x(2x + 5)8 = ½·[2x(2x + 5)8] = ½·[(2x + 5 − 5)(2x + 5)8] = ½·[(2x + 5)(2x + 5)8 − 5(2x + 5)8] = ½·[(2x + 5)9 − 5(2x + 5)8] = ½·(2x + 5)9 − (5/2)·(2x + 5)8
Nu hebben we dus
∫ x(2x + 5)8dx = ∫ (½·(2x + 5)9 − (5/2)·(2x + 5)8)dx
Nu substitueren we
u = 2x + 5
zodat
du/dx = 2
en dus
dx = ½·du
Dan hebben we
∫ (½·(2x + 5)9 − (5/2)·(2x + 5)8)dx = ∫ (¼·u9 − (5/4)·u8)du = (1/40)·u10 − (5/36)·u9 + C = (1/40)·(2x + 5)10 − (5/36)·(2x + 5)9 + C
Deze uitkomst kunnen we weer herleiden door een factor (2x + 5)9 buiten haakjes te halen, en dan krijgen we uiteindelijk
∫ x(2x + 5)8dx = (2x + 5)9((1/20)·x − 1/72) + C
Edit: zoals hier terecht is opgemerkt is het nog veel eenvoudiger om te bedenken dat de substitutie u = 2x + 5 equivalent is met x = ½u − 5/2, waarmee direct ∫ (¼·u9 − (5/4)·u8)du wordt verkregen.
[ Bericht 26% gewijzigd door Riparius op 14-10-2013 23:25:38 ]
Gewoon productregel + kettingregel lijkt me?quote:
Nog een vraagje over integreren:
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
Met functie (1)=x en functie (2)=(2x+5)^8
En dan bij functie (2) de kettingregel toepassen.
Volgens de Nederlandse Wikipedia zijn deler en factor synoniemen.quote:
[..]
delers = factoren?
Of is er een verschil tussen NL en ENG?
Als je gaat differentiëren moet dat, of begrijp ik je niet goed?quote:
[..]
Gewoon productregel + kettingregel lijkt me?
Met functie (1)=x en functie (2)=(2x+5)^8
En dan bij functie (2) de kettingregel toepassen.
Oh ok nvm. Denk inderdaad dat die regels dan niet gelden voor integreren dan. Ik dacht ff een slim antwoord te gevenquote:
[..]
Als je gaat differentiëren moet dat, of begrijp ik je niet goed?
doe eensquote:
Nog een vraagje over integreren:
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
u = 2x + 5
du = 2dx
x = (u-5)/2
dan ∫x(2x+5)8dx = 1/4 ∫ (u-5)u8du
= 1/4(u10/10 - 5/9 u9) + C = u10/40 - 5/36 u9 + C
En dan x terug substitueren en je bent klaar.
= (2x+5)10/40 - 5/36 (2x+5)9 + C
Fervent tegenstander van het korps lasergamers.
Ik vind dit heel moeilijk, maar ik heb -zonder te spieken- een poging gedaan.quote:
[..]
Het gaat uiteraard ook eenvoudig als je de formele definitie van een limiet en wat rekenregels voor limieten gebruikt. Voor k = 1 .. n heb je
limx→∞ (an−k/an)x−k = 0
en
limx→−∞ (an−k/an)x−k = 0
(Bewijs dit aan de hand van de formele definitie van deze limieten).
f(x) = x-k met k ∈ N
dan
limx→∞ f(x) =0
als ∀ε>0∃x: [|f(x)| < ε] ,
dus |x-k| < ε
en
-ε < x-k < ε
voor x ≥ 1 geldt
0 ≤ x-k ≤ 1/x
dus -ε < 1/x
Dus kies x > -1/ε
En dan zit ik vast. Ik vind dit echt heel lastig. Ik moet een fout maken hierboven, maar waar zit die zonder dat je het hele bewijs hier neerknalt?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Zo gaat het ook inderdaad, maar ik vond mijn manier toch sneller.Fervent tegenstander van het korps lasergamers.
voor hierboven gekozen x
|x-k| < ε
geeft
|(-1/ε)-k| < ε
1/ε > 0, dus
|(-1/ε)-k| = |(1/ε)-k| = |εk| < ε
Lijkt me ook onzin.
|x-k| < ε
geeft
|(-1/ε)-k| < ε
1/ε > 0, dus
|(-1/ε)-k| = |(1/ε)-k| = |εk| < ε
Lijkt me ook onzin.
Fervent tegenstander van het korps lasergamers.
Het helpt wel als je de formele definitie van limx→∞ f(x) = 0 correct opschrijftquote:
[..]
Ik vind dit heel moeilijk, maar ik heb -zonder te spieken- een poging gedaan.
f(x) = x-k met k ∈ N
dan
limx→∞ f(x) =0
als ∀ε>0∃x: [|f(x)| < ε] ,
∀ε>0 ∃X∈R ∀x>X [ |f(x)| < ε ]
[snip]
Je maakte geen onderscheid tussen X en x. Voor elke ε > 0 moet er een X ∈ R bestaan zodanig dat voor elke x > X geldt |f(x)| < ε. Je moet dus een existentiebewijs leveren, en in het algemeen doe je dat bij een limiet als deze door te laten zien dat je voor elke ε > 0 zo'n X kunt construeren. Hier kun je gebruik maken van het feit dat x−k ≤ x−1 voor x ≥ 1 en k ≥ 1, maar dat hoeft niet.quote:En dan zit ik vast. Ik vind dit echt heel lastig. Ik moet een fout maken hierboven, maar waar zit die zonder dat je het hele bewijs hier neerknalt?
quote:Ja. Ik had er even niet bij stilgestaan dat je een lineaire substitutie gemakkelijk kunt inverteren.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Zo gaat het ook inderdaad, maar ik vond mijn manier toch sneller.
Dank. Ik ga hier morgenvroeg nog even over peinzen.quote:
[..]
Het helpt wel als je de formele definitie van limx→∞ f(x) = 0 correct opschrijft
∀ε>0 ∃X∈R ∀x>X [ |f(x)| < ε ]
[snip]
[..]
Je maakte geen onderscheid tussen X en x. Voor elke ε > 0 moet er een X ∈ R bestaan zodanig dat voor elke x > X geldt |f(x)| < ε. Je moet dus een existentiebewijs leveren, en in het algemeen doe je dat bij een limiet als deze door te laten zien dat je voor elke ε > 0 zo'n X kunt construeren. Hier kun je gebruik maken van het feit dat x−k ≤ x−1 voor x ≥ 1 en k ≥ 1, maar dat hoeft niet.
[..]
Ja. Ik had er even niet bij stilgestaan dat je een lineaire substitutie gemakkelijk kunt inverteren.
Fervent tegenstander van het korps lasergamers.
Maakt wolfram hier een dikke fout? -5(1+√2), 5(√2 -1)= -5+/- 5√2
[ Bericht 60% gewijzigd door wiskundenoob op 14-10-2013 19:45:14 ]
[ Bericht 60% gewijzigd door wiskundenoob op 14-10-2013 19:45:14 ]
Daar twijfel ik ten zeerste aan. Wat is je vergelijking precies, want dat is weer eens bepaald niet helder.Zoiets?quote:
Maakt wolfram hier een dikke fout? -5(1+√2), 5(√2 -1)= -5+/- 5√2
-5(1+√2), 5(√2 -1) = (-5-5√2), (5√2 -5)= -5+/- 5√2
Fervent tegenstander van het korps lasergamers.
Ja, die vergelijking bedoel ik.quote:
[..]
Daar twijfel ik ten zeerste aan. Wat is je vergelijking precies, want dat is weer eens bepaald niet helder.Zoiets?
-5(1+√2), 5(√2 -1) = (-5-5√2), (-5+5√2 )= -5+/- 5√2
Laat maar ik zie het al.
[ Bericht 6% gewijzigd door wiskundenoob op 14-10-2013 20:32:11 ]
Niets mis mee.quote:
[..]
http://www.wolframalpha.com/input/?i=x%5E2+%2B10x+-25+
Fervent tegenstander van het korps lasergamers.
Ik zou niet te hard roepen dat WolframAlpha geen fouten maakt, dat gebeurt namelijk wel, ook bij heel elementaire dingen. Kwam laatst nog iets tegen naar aanleiding van een vraag op het forum. Kijk hier eens naar. Zie jij de fout ook?quote:
[..]
Daar twijfel ik ten zeerste aan. Wat is je vergelijking precies, want dat is weer eens bepaald niet helder.Zoiets?
Ten eerste zijn er een oneindig aantal gehele oplossingen van deze ongelijkheid, ipv de 4 die genoemd worden.quote:
[..]
Ik zou niet te hard roepen dat WolframAlpha geen fouten maakt, dat gebeurt namelijk wel, ook bij heel elementaire dingen. Kwam laatst nog iets tegen naar aanleiding van een vraag op het forum. Kijk hier eens naar. Zie jij de fout ook?
En die tweede alternate form is volgens mij onjuist. Bij vermenigvuldiging met -1 klapt het ongelijkheidsteken om.
Fervent tegenstander van het korps lasergamers.
Exact.quote:Op dinsdag 15 oktober 2013 07:43 schreef Amoeba het volgende:
[..]
Ten eerste zijn er een oneindig aantal gehele oplossingen van deze ongelijkheid, ipv de 4 die genoemd worden.
En die tweede alternate form is volgens mij onjuist. Bij vermenigvuldiging met -1 klapt het ongelijkheidsteken om.
Trouwens nog bedankt voor je PM. Ik moet nog even een aantal dingen (woorden) opzoeken, maar kon het grotendeels wel volgen.quote:
Fervent tegenstander van het korps lasergamers.
Heeft iemand een idee welk wiskundeboek het meest geschikt is om je voor te bereiden op het staatsexamen wiB? Het lijkt me leuk om naast mijn studie wat extra's aan wiskunde te doen.
Ik had Pascal. Dat vond ik wel fijn werken, fijner dan G&T zonder leraar in ieder geval.quote:
Heeft iemand een idee welk wiskundeboek het meest geschikt is om je voor te bereiden op het staatsexamen wiB? Het lijkt me leuk om naast mijn studie wat extra's aan wiskunde te doen.
Gist is liefde, gist is leven. Vooral in een vagijn.
Ik gebruik basiswiskunde van Jan van de Craats, maar ik richt me op wiA-niveau. Volgens het boek beheers je wiB op vwo-niveau als je het volledige boek doorwerkt. Minpunten van dit boek: uitleg zeer beknopt en sommige onderwerpen, zoals kansrekening, komen weinig tot niet aan bod.quote:
Heeft iemand een idee welk wiskundeboek het meest geschikt is om je voor te bereiden op het staatsexamen wiB? Het lijkt me leuk om naast mijn studie wat extra's aan wiskunde te doen.
Ben je van plan het staatsexamen wiA te doen?quote:
[..]
Ik gebruik basiswiskunde van Jan van de Craats, maar ik richt me op wiA-niveau. Volgens het boek beheers je wiB op vwo-niveau als je het volledige boek doorwerkt. Minpunten van dit boek: uitleg zeer beknopt en sommige onderwerpen, zoals kansrekening, komen weinig tot niet aan bod.
Toevallig heb ik dat boek ook, maar niet nu bij me. Toen ik er een keer in gekeken heb leek het me wat meetkunde betreft, voor mij persoonlijk te beknopt. Ik heb dat niet meer gehad sinds 3 havo. Ik was toen ook verre van een gemotiveerde leerling en dan is een EM profiel makkelijk kiezen. Heb dit jaar wel vwo afgerond maar ik zou graag mezelf ook op andere vlakken wat meer ontwikkelen. Ik denk dat wiB goed mogelijk is om komend jaar staatsexamen in te doen. Een vak als natuurkunde lijkt me een stuk lastiger om zo snel op 'niveau' te komen. Misschien iets voor later!
Natuurkunde is makkelijker dan wiskunde B hoor, vooral omdat natuurkunde op het vwo niet veel meer is dan formules volgen, wat inzicht gebruiken en wat feitjes toepassen. Maar het is in totaal wel meer stof dan wiskunde B, omdat je wel al een deel van B hebt gehad natuurlijk (algebra voornamelijk).quote:
[..]
Ben je van plan het staatsexamen wiA te doen?
Toevallig heb ik dat boek ook, maar niet nu bij me. Toen ik er een keer in gekeken heb leek het me wat meetkunde betreft, voor mij persoonlijk te beknopt. Ik heb dat niet meer gehad sinds 3 havo. Ik was toen ook verre van een gemotiveerde leerling en dan is een EM profiel makkelijk kiezen. Heb dit jaar wel vwo afgerond maar ik zou graag mezelf ook op andere vlakken wat meer ontwikkelen. Ik denk dat wiB goed mogelijk is om komend jaar staatsexamen in te doen. Een vak als natuurkunde lijkt me een stuk lastiger om zo snel op 'niveau' te komen. Misschien iets voor later!
Gist is liefde, gist is leven. Vooral in een vagijn.
Daar komt het ook op neer, ik bedoel dat het langer duurt voordat je het goed onder de knie hebt omdat het relatief gezien meer stof is. Terwijl ik, als ik oude wisB examens bekijk een aantal sommen (meetkunde uitgezonderd) zo zou kunnen maken.quote:
[..]
Natuurkunde is makkelijker dan wiskunde B hoor, vooral omdat natuurkunde op het vwo niet veel meer is dan formules volgen, wat inzicht gebruiken en wat feitjes toepassen. Maar het is in totaal wel meer stof dan wiskunde B, omdat je wel al een deel van B hebt gehad natuurlijk (algebra voornamelijk).
Dat klopt, het enige wat je nog moet leren is integreren en meetkunde, dan kan je zo een wiskunde B examen maken.quote:
[..]
Daar komt het ook op neer, ik bedoel dat het langer duurt voordat je het goed onder de knie hebt omdat het relatief gezien meer stof is. Terwijl ik, als ik oude wisB examens bekijk een aantal sommen (meetkunde uitgezonderd) zo zou kunnen maken.
Gist is liefde, gist is leven. Vooral in een vagijn.
Grof gezien ja. Er zijn zat dingetjes waar wiB net een stukje verder gaat dan A (afgeleiden van exponenten en logaritmen e.d.). Niet moeilijk, maar wel rekening mee houdenquote:
[..]
Dat klopt, het enige wat je nog moet leren is integreren en meetkunde, dan kan je zo een wiskunde B examen maken.
Kom op, dat is gewoon een uitbreiding op wiskunde A, het is niks nieuws.quote:
[..]
Grof gezien ja. Er zijn zat dingetjes waar wiB net een stukje verder gaat dan A (afgeleiden van exponenten en logaritmen e.d.). Niet moeilijk, maar wel rekening mee houden
Gist is liefde, gist is leven. Vooral in een vagijn.
Dat zit ook gewoon in VWO wisk A, de laatste keer dat ik checkte.quote:
[..]
Grof gezien ja. Er zijn zat dingetjes waar wiB net een stukje verder gaat dan A (afgeleiden van exponenten en logaritmen e.d.). Niet moeilijk, maar wel rekening mee houden
Nee hoor, in Getal en Ruimte iig niet.Ben vorig jaar geen 5x of ln(3x+2) tegengekomen die je moest differentiëren.quote:
[..]
Dat zit ook gewoon in VWO wisk A, de laatste keer dat ik checkte.
Je hebt denk ik gelijk. Was even in de war.quote:
[..]
Nee hoor, in Getal en Ruimte iig niet.Ben vorig jaar geen 5x of ln(3x+2) tegengekomen die je moest differentiëren.
Log hoefde je ook niet te differentiëren, sinus, cosinus en tangens ook niet.quote:
[..]
Nee hoor, in Getal en Ruimte iig niet.Ben vorig jaar geen 5x of ln(3x+2) tegengekomen die je moest differentiëren.
Gist is liefde, gist is leven. Vooral in een vagijn.
Als objecten kleur hebben doordat ze licht/fotonen met een bepaalde golflengte absorberen, wat is waar te nemen als je geen licht hebt? Kun je dat uberhaupt waarnemen? Zwart is ook een kleur. Wat zie je dan? Transparante objecten?
Zwart een kleur hangt volgens mij van je definitie af(niet 100% zeker), maar het "zien van zwart" doe je eigenlijk niet. Het is de afwezigheid van licht. Daarom is het 's nachts "donker" (=zwart)quote:
Als objecten kleur hebben doordat ze licht/fotonen met een bepaalde golflengte absorberen, wat is waar te nemen als je geen licht hebt? Kun je dat uberhaupt waarnemen? Zwart is ook een kleur. Wat zie je dan? Transparante objecten?
@DefinitionX; je moet je vraag iets duidelijker stellen. Maar kijk eens hier: http://nl.wikipedia.org/wiki/Zwarte_straler
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl
Met je ogen is er dan niks waar te nemen, zwart is namelijk geen kleur maar een gebrek aan licht. Je ogen vangen geen licht op, dus iets is zwart.quote:
Als objecten kleur hebben doordat ze licht/fotonen met een bepaalde golflengte absorberen, wat is waar te nemen als je geen licht hebt? Kun je dat uberhaupt waarnemen? Zwart is ook een kleur. Wat zie je dan? Transparante objecten?
Maar dit is geloof ik het verkeerde bètatopic voor deze vraag.
Gist is liefde, gist is leven. Vooral in een vagijn.
Opnieuw geprobeerd, dit is wat ik heb:quote:
[..]
Aangezien je dit niet kon bedenken vraag ik me toch af hoe het verder met je toets is gegaan.
Ik heb nog wel een aardige oefening voor je:
[ afbeelding ]
En nee, hierbij mag je niet gebruik maken van de regel van l'Hôpital (die je toch niet kent).
Ik heb hem eerst herleid tot:
En toen ontbonden tot:
Die laatste limiet wordt 1, dus die is geen probleem. Die eerste en tweede daarentegen, die x3 zit gewoon in de weg. Tuurlijk, je kan x-3 voor de eerste groep zetten, maar dan deel je uiteindelijk nog steeds door nul, wat natuurlijk niet mag.
Gist is liefde, gist is leven. Vooral in een vagijn.
Die twee limieten tussen haakjes in je eerste factor zijn onbepaald, dus zo werkt het niet. Je moet de limiet van het quotiënt herschrijven als een product van limieten van quotiënten die elk wel bepaald zijn.quote:
[..]
Opnieuw geprobeerd, dit is wat ik heb:
Ik heb hem eerst herleid tot:
En toen ontbonden tot:
Die laatste limiet wordt 1, dus die is geen probleem. Die eerste en tweede daarentegen, die x3 zit gewoon in de weg. Tuurlijk, je kan x-3 voor de eerste groep zetten, maar dan deel je uiteindelijk nog steeds door nul, wat natuurlijk niet mag.
We hadden
( (1 − cos x)·sin x ) / ( x2·log(1 + x) )
al herschreven tot
( (1 − cos x)·sin x ) / ( x3·log(1 + x)1/x )
Nu zien we dat hier in ieder geval een factor sin x / x in zit, dus dit kunnen we weer herschrijven als
((1 − cos x) / x2) · (sin x / x) · (1 / log(1 + x)1/x)
De limieten van de tweede en de derde factor zijn gemakkelijk, die factoren gaan namelijk naar 1 voor x → 0. Nu moeten we dus alleen nog wat doen met de eerste factor. In de noemer hiervan staat x2, en aangezien limx→0 sin x / x = 1 zouden we in de teller graag iets hebben met het kwadraat van een sinus. Welnu, je kent je goniometrische identiteiten (toch?), dus dan denk je direct aan
cos 2α = 1 − 2·sin2α
Met α = ½x hebben we dan
1 − cos x = 1 − (1 − 2·sin2½x) = 2·sin2½x
Verder is x2 = 4·(½x)2 zodat
(1 − cos x)/x2 = 2·sin2½x / 4·(½x)2 = sin2½x / 2·(½x)2 = ½·(sin ½x / ½x)2
En dus hebben we
limx→0 ( (1 − cos x)·sin x ) / ( x2·log(1 + x) ) =
limx→0 ½ · (sin ½x / ½x)2· (sin x / x) · (1 / log(1 + x)1/x) = ½·12·1·1 = ½
[ Bericht 0% gewijzigd door Riparius op 16-10-2013 12:31:32 ]
Ah ja, cosinus herschrijven naar sinus, maar natuurlijk. Ik moet die identiteiten echt weer eens stampen, dat blijkt maar.quote:
[..]
Die twee limieten tussen haakjes in je eerste factor zijn onbepaald, dus zo werkt het niet. Je moet de limiet van het quotiënt herschrijven als een product van limieten van quotiënten die elk wel bepaald zijn.
We hadden
( (1 − cos x)·sin x ) / ( x2·log(1 + x) )
al herschreven tot
( (1 − cos x)·sin x ) / ( x3·log(1 + x)1/x )
Nu zien we dat hier in ieder geval een factor sin x / x in zit, dus dit kunnen we weer herschrijven als
((1 − cos x) / x2) · (sin x / x) · (1 / log(1 + x)1/x)
De limieten van de tweede en de derde factor zijn gemakkelijk, die factoren gaan namelijk naar 1 voor x → 0. Nu moeten we dus alleen nog wat doen met de eerste factor. In de noemer staat x2, en aangezien limx→0 sin x / x = 1 zouden we in te teller graag iets hebben met het kwadraat van een sinus. Welnu, je kent je goniometrische identiteiten (toch?), dus dan denk je direct aan
cos 2α = 1 − 2·sin2α
Met α = ½x hebben we dan
1 − cos x = 1 − (1 − 2·sin2½x) = 2·sin2½x
Verder is x2 = 4·(½x)2 zodat
(1 − cos x)/x2 = 2·sin2½x / 4·(½x)2 = sin2½x / 2·(½x)2 = ½·(sin ½x / ½x)2
En dus hebben we
limx→0 ( (1 − cos x)·sin x ) / ( x2·log(1 + x) ) =
limx→0 ½·(sin ½x / ½x)2· (sin x / x) · (1 / log(1 + x)1/x) = ½·12·1·1 = ½
En het stomme is, ik had die derde som, maar die schreef ik af als waardeloos omdat ik er niet aan dacht de cosinus te herschrijven naar sinus.
Gist is liefde, gist is leven. Vooral in een vagijn.
Waarschijnlijk komt nu de allerdomste idiootste vraag ooit:
Wat is de formule voor een klavertje 4 op de graph mode van mijn gr?
net google kwam ik er niet uit
Wat is de formule voor een klavertje 4 op de graph mode van mijn gr?
net google kwam ik er niet uit
Because you know i'm all about that ass
dankuzeer, maar als ik dit invoer op mijn ti krijg ik een rechte lijn vlak boven mijn x as?quote:
http://mathhelpforum.com/(...)lar-coordinates.html
Because you know i'm all about that ass
Stampen hoeft niet hoor. Neem mijn PDF eens goed door.quote:
[..]
Ah ja, cosinus herschrijven naar sinus, maar natuurlijk. Ik moet die identiteiten echt weer eens stampen, dat blijkt maar.
Tja ...quote:En het stomme is, ik had die derde som, maar die schreef ik af als waardeloos omdat ik er niet aan dacht de cosinus te herschrijven naar sinus.
Je moet de mode aanpassen, hij moeten plotten in een Oxy-vlak.quote:
[..]
Dankuzeer, maar als ik dit invoer op mijn ti krijg ik een rechte lijn vlak boven mijn x as?
Gist is liefde, gist is leven. Vooral in een vagijn.
dankquote:
[..]
Je moet de mode aanpassen, hij moeten plotten in een Oxy-vlak.
Nu ff proberen
Because you know i'm all about that ass
Voor welke waarde(n) van p heeft de vergelijking px2 + px + 2 = 0 geen oplossingen?
Met abc-formule? b-4ac < 0
Dus p = b en 4*1*2 = 8
p- 8 < 0
p < 8
Dus alle getallen kleiner dan 8 heeft geen oplossingen.
Maar het antwoord is 0 en 8.
Met abc-formule? b-4ac < 0
Dus p = b en 4*1*2 = 8
p- 8 < 0
p < 8
Dus alle getallen kleiner dan 8 heeft geen oplossingen.
Maar het antwoord is 0 en 8.
Zal ik morgen even doen, nu eerst slapen.quote:
[..]
Stampen hoeft niet hoor. Neem mijn PDF eens goed door.
[..]
Tja ...
Gist is liefde, gist is leven. Vooral in een vagijn.
Ja, duh, als p 0 is staat er 2. Dat wordt natuurlijk nooit 0...quote:
Voor welke waarde(n) van p heeft de vergelijking px2 + px + 2 = 0 geen oplossingen?
Met abc-formule? b-4ac < 0
Dus p = b en 4*1*2 = 8
p- 8 < 0
p < 8
Dus alle getallen kleiner dan 8 is kleiner.
Maar het antwoord is 0 en 8.
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl
Het is b^2 -4AC en dat moet kleiner zijn dan 0quote:
Voor welke waarde(n) van p heeft de vergelijking px2 + px + 2 = 0 geen oplossingen?
Met abc-formule? b-4ac < 0
Dus p = b en 4*1*2 = 8
p- 8 < 0
p < 8
Dus alle getallen kleiner dan 8 heeft geen oplossingen.
Maar het antwoord is 0 en 8.
Because you know i'm all about that ass
oh ja, maar hoe zit het met 8 dan?quote:
[..]
Ja, duh, als p 0 is staat er 2. Dat wordt natuurlijk nooit 0...
Ik kan het oxy vlak niet vinden op mn rekenmachine 
is dat een applet?
is dat een applet?
Because you know i'm all about that ass
p^2 is dan 8 dus p is dan -wortel 8 of wortel 8.quote:
[..]
oh ja, maar hoe zit het met 8 dan?
Because you know i'm all about that ass
Wacht eens even, sinus kwadraat plus cosinus kwadraat is 1. Jezus, die heb ik vanmiddag nog gebruikt. Wat slecht.
Jezus, die heb ik vanmiddag nog gebruikt. Wat slecht.
Gist is liefde, gist is leven. Vooral in een vagijn.
Pff, euh, al lang niet meer gebruikt zo'n GR.. Welke heb je?quote:
Ik kan het oxy vlak niet vinden op mn rekenmachine
http://www.math4all.nl/TI/TI83krom.html
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl
ti84 plus, maar de 83 is bijna identiekquote:
[..]
Pff, euh, al lang niet meer gebruikt zo'n GR.. Welke heb je?
http://www.math4all.nl/TI/TI83krom.html
thx
Because you know i'm all about that ass
Je berekent de discriminant verkeerd. Hier is a = p, b = p, c = 2, dus krijg jequote:
Voor welke waarde(n) van p heeft de vergelijking px2 + px + 2 = 0 geen oplossingen?
Met abc-formule? b-4ac < 0
Dus p = b en 4*1*2 = 8
p- 8 < 0
p < 8
Dus alle getallen kleiner dan 8 heeft geen oplossingen.
Maar het antwoord is 0 en 8.
D = b2 − 4ac = p2 − 4·p·2 = p2 − 8p
De voorwaarde waaronder de vierkantsvergelijking geen (reële) oplossingen heeft luidt dus
p2 − 8p < 0
Het 'juiste' antwoord dat je geeft is trouwens niet juist. Je moet eens leren je vragen en antwoorden correct op te schrijven, en niet in een soort telegramstijl waar vaak geen chocola van is te maken.
Lol im ging d
Ervan uit dat dat wel klopte haha. Nogeen vraagje: hoe laat ikde xasvan0 tot2 p lopen? Ik kan geenp vinden/:
Ervan uit dat dat wel klopte haha. Nogeen vraagje: hoe laat ikde xasvan0 tot2 p lopen? Ik kan geenp vinden/:
Because you know i'm all about that ass
Inderdaad. Ik neem aan dat je hiermee bedoelt dat je net ontdekt dat je bijquote:Op woensdag 16 oktober 2013 00:04 schreef Rezania het volgende:
Wacht eens even, sinus kwadraat plus cosinus kwadraat is 1.
(1 − cos x)/x2
ook teller en noemer met (1 + cos x) kunt vermenigvuldigen. Dan krijg je
sin2x / x2 · 1/(1 + cos x)
en zie je dus ook direct dat
limx→0 (1 − cos x)/x2 = limx→0 sin2x / x2 · 1/(1 + cos x) = 12 · 1/(1 + 1) = 1/2
Probeer deze eens:quote:
http://mathhelpforum.com/(...)lar-coordinates.html
r = sin4(4θ) + cos(5θ)
Ok, maar de vraag heb ik rechtstreeks gekopieerd.quote:
[..]
Je berekent de discriminant verkeerd. Hier is a = p, b = p, c = 2, dus krijg je
D = b2 − 4ac = p2 − 4·p·2 = p2 − 8p
De voorwaarde waaronder de vierkantsvergelijking geen (reële) oplossingen heeft luidt dus
p2 − 8p < 0
Het 'juiste' antwoord dat je geeft is trouwens niet juist. Je moet eens leren je vragen en antwoorden correct op te schrijven, en niet in een soort telegramstijl waar vaak geen chocola van is te maken.
p - 8 < 0
p < 8
Dus alle getallen onder 8 tot en met 0 leveren geen oplossingen op. Omdat negatieve p positieve p2 oplevert en ook -8(-p) positief wordt.
p ∈ (0,8)
Dit betekent zeker 0 tot en met 8.
Je uitleg is bijzonder onduidelijk. Dat moet echt beter als je ooit een examen denkt te gaan afleggen.quote:
[..]
Ok, maar de vraag heb ik rechtstreeks gekopieerd.
De voorwaarde die we hadden gevonden is
p2 − 8p < 0
Dit is een ongelijkheid in p, die je moet oplossen om te bepalen welke waarden van p hieraan voldoen. Om deze ongelijkheid op te lossen, los je eerst de vergelijking
p2 − 8p = 0
op. Dat is eenvoudig, want hier kun je p buiten haakjes halen. Dan vinden we
p = 0 ∨ p = 8
Nu maak je een tekenschema, en dan zie je dat p2 − 8p < 0 indien
0 < p < 8
In woorden: p moet liggen tussen 0 en 8.
Nee, dat betekent het niet. De notatie (0,8) duidt hier een open interval aan. Dat is een interval waarbij de eindpunten niet meedoen. Dit interval vatten we hier op als een verzameling getallen, namelijk de verzameling van alle reële getallen waarvoor geldt dat ze groter zijn dan 0 en tevens kleiner dan 8.quote:Dit betekent zeker 0 tot en met 8.
Het teken ∈ betekent '(is) element van' oftewel 'zit in', dus de notatie p ∈ (0,8) betekent dat p een element moet zijn van de verzameling van alle reële getallen die groter zijn dan 0 en tevens kleiner dan 8.
Over telegramstijl waar geen chocola van te maken is gesproken.quote:
Lol im ging d
Ervan uit dat dat wel klopte haha. Nogeen vraagje: hoe laat ikde xasvan0 tot2 p lopen? Ik kan geenp vinden/:
Fervent tegenstander van het korps lasergamers.
ja mn toetsenbord fliptequote:
[..]
Over telegramstijl waar geen chocola van te maken is gesproken.
Because you know i'm all about that ass
Ja, klopt.quote:
[..]
Inderdaad. Ik neem aan dat je hiermee bedoelt dat je net ontdekt dat je bij
(1 − cos x)/x2
ook teller en noemer met (1 + cos x) kunt vermenigvuldigen. Dan krijg je
sin2x / x2 · 1/(1 + cos x)
en zie je dus ook direct dat
limx→0 (1 − cos x)/x2 = limx→0 sin2x / x2 · 1/(1 + cos x) = 12 · 1/(1 + 1) = 1/2
Gist is liefde, gist is leven. Vooral in een vagijn.
In plaats van je post even op beschaafde wijze te wijzigen zodra je toetsenbord niet meer 'flipte' knal je er nog zo'n post erachteraan die gewoon pijn doet aan mijn ogen.quote:
Zonde.
Fervent tegenstander van het korps lasergamers.
quote:
[..]
Probeer deze eens:
r = sin4(4θ) + cos(5θ)
Jij/Amoeba hier toevallig nog een tip voor?quote:
Heeft iemand een idee welk wiskundeboek het meest geschikt is om je voor te bereiden op het staatsexamen wiB? Het lijkt me leuk om naast mijn studie wat extra's aan wiskunde te doen.
Wij gebruikten Getal en Ruimte op het vwo. Op zich niet onduidelijk, voldoende opgaven, wel een langzame opbouw. Verder denk ik dat Riparius het Basisboek Wiskunde aanbeveelt.quote:
[..]
[..]
Jij/Amoeba hier toevallig nog een tip voor?
Nog even gevonden met grote vriend Google.quote:
[..]
Iedereen die wiskunde wil leren (op welk niveau dan ook) heeft eigenlijk behoefte aan een goede en inspirerende docent (die dan ook echt lesgeeft en geen veredelde toezichthouder is) en die kan nooit helemaal worden vervangen door een boek c.q. zelfstudie. Maar als je niet de luxe hebt van een goede (privé)docent dan hoef je niet persé je toevlucht te nemen tot duistere bronnen. Ook op bijvoorbeeld YouTube kun je heel veel instructievideo's vinden waarin iemand een stukje wiskunde 'ouderwets' goed uitlegt. En als je een beetje een totaaloverzicht wil krijgen van bepaalde onderwerpen in historisch perspectief dan kan ik je de vrij toegankelijke videocolleges aanraden van Gresham College, bijvoorbeeld de colleges van Robin Wilson.
[ Bericht 25% gewijzigd door Amoeba op 16-10-2013 12:47:25 ]
Fervent tegenstander van het korps lasergamers.
Als je doelt op het plotten van een curve die als poolvoorstelling wordt gegeven, dan ja. Het wemelt van de online plotters, en sommige doen ook poolcoördinaten. Hier vind je een overzichtje, maar je kunt ook zelf even googelen, en dan vind je nog veel meer. De plaatjes die je zo krijgt zijn een stuk fraaier dan de plaatjes van welke GR dan ook, en bovendien kun je de plaatjes ook direct gebruiken in een werkstuk of zo.quote:
[..]
[..]
Jij hier toevallig nog een tip voor?
Om te zien wat je krijgt als je
r = sin44θ + cos 5θ
plot, zou je deze eens kunnen proberen. Hint: voer de poolvoorstelling in als
r = (sin(4*t))^4 + cos(5*t)
en zet onder Range of visible polar radii het maximum even op 3 of 4. Mooi hè?
Ik durf mijn schoen erom te verwedden dat hij op een tip voor een goed wiskundeboek doelde om een staatsexamen wiskunde B met succes af te ronden.
Fervent tegenstander van het korps lasergamers.
Niet helemaal. Mijn voorkeur gaat uit naar het Vlaamse boek Wiskundige basisvaardigheden waarvan net de derde druk is verschenen. Dit boek is ook in Nederland goed verkrijgbaar.quote:
[..]
Wij gebruikten Getal en Ruimte op het vwo. Op zich niet onduidelijk, voldoende opgaven, wel een langzame opbouw. Verder denk ik dat Riparius het Basisboek Wiskunde aanbeveelt.
[..]
Inderdaad. Jammer dat het linkje naar de lezingen van Robin Wilson niet meer goed werkt, wellicht omdat hij niet meer aan Gresham College is verbonden. Maar de video's van zijn lezingen staan nog gewoon op de site. Ik vond bijvoorbeeld deze lezing gehouden ter gelegenheid van de 300ste verjaardag van Leonhard Euler erg geslaagd, maar er zijn veel meer lezingen van Wilson die echt de moeite waard zijn.quote:Nog even gevonden met grote vriend Google.
Nu ja, als mensen binnenkort een eerstejaars op één schoen en één sok over de campus zien hinkelen, dat weten ze tenminste waarom ...quote:
Ik durf mijn schoen erom te verwedden dat hij op een tip voor een goed wiskundeboek doelde om een staatsexamen wiskunde B met succes af te ronden.
Ik zou mijn andere schoen ook thuis laten en gewoon voor hobbit spelen.quote:Op woensdag 16 oktober 2013 13:50 schreef Riparius het volgende:
[..]
Nu ja, als mensen binnenkort een eerstejaars op één schoen en één sok over de campus zien hinkelen, dat weten ze tenminste waarom ...
[ Bericht 0% gewijzigd door Amoeba op 16-10-2013 14:15:13 ]
Fervent tegenstander van het korps lasergamers.
Ik had het inderdaad over een wiskundeboek, maar ik ga hem zo eens plotten.quote:
[..]
Als je doelt op het plotten van een curve die als poolvoorstelling wordt gegeven, dan ja. Het wemelt van de online plotters, en sommige doen ook poolcoördinaten. Hier vind je een overzichtje, maar je kunt ook zelf even googelen, en dan vind je nog veel meer. De plaatjes die je zo krijgt zijn een stuk fraaier dan de plaatjes van welke GR dan ook, en bovendien kun je de plaatjes ook direct gebruiken in een werkstuk of zo.
Om te zien wat je krijgt als je
r = sin44θ + cos 5θ
plot, zou je deze eens kunnen proberen. Hint: voer de poolvoorstelling in als
r = (sin(4*t))^4 + cos(5*t)
en zet onder Range of visible polar radii het maximum even op 3 of 4. Mooi hè?
Het is an sich geen probleem of ik nu een maand langer of korter over de stof doe. Tuurlijk is het zo dat het in alle gevallen beter is om een degelijke docent aan je zijde te hebben. Maargoed, de geldboom wilt nog niet echt groeien.quote:
[..]
Wij gebruikten Getal en Ruimte op het vwo. Op zich niet onduidelijk, voldoende opgaven, wel een langzame opbouw. Verder denk ik dat Riparius het Basisboek Wiskunde aanbeveelt.
[..]
Nog even gevonden met grote vriend Google.
Overigens had ik zelf ook Getal en Ruimte toen ik wiskunde A deed. Maar daar was ik geen groot fan van, de hoofdstukken beginnen over het algemeen op een laag pitje (begrijpelijk), maar op het eind vond ik het vaak een tikkeltje onduidelijk worden en moest je het zelf maar uitzoeken.
Kan natuurlijk ook aan mij liggen, wiB versie kan heel anders zijn en het begon me pas te interesseren op het eind v/h jaar.
Ik kijk reeds al heel wat YT filmpjes, dus daar kan altijd een aanvulling op komenquote:
[..]
Niet helemaal. Mijn voorkeur gaat uit naar het Vlaamse boek Wiskundige basisvaardigheden waarvan net de derde druk is verschenen. Dit boek is ook in Nederland goed verkrijgbaar.
[..]
Inderdaad. Jammer dat het linkje naar de lezingen van Robin Wilson niet meer goed werkt, wellicht omdat hij niet meer aan Gresham College is verbonden. Maar de video's van zijn lezingen staan nog gewoon op de site. Ik vond bijvoorbeeld deze lezing gehouden ter gelegenheid van de 300ste verjaardag van Leonhard Euler erg geslaagd, maar er zijn veel meer lezingen van Wilson die echt de moeite waard zijn.
In hoeverre is dat basisboek geschikt voor een Nederlands examen wiB?
Heel geschikt, hoewel het niveau in Vlaanderen wat hoger ligt dan in Nederland. Anders dan het boek van Van de Craats is dit meer een echt leerboek, waarbij de stof per hoofdstuk wordt behandeld en pas aan het einde van ieder hoofdstuk opgaven worden gegeven. Als je het boek eens in wil kijken, dan kan dat hier.quote:
In hoeverre is dat basisboek geschikt voor een Nederlands examen wiB?
Riparius is er heilig van overtuigd dat het wiskundeonderwijs in Vlaanderen superieur is, dus prima geschikt voor een inferieur Nederlands staatsexamen.
Fervent tegenstander van het korps lasergamers.
Ik ben er toevallig al in aan het kijken. Ziet er tevens ook een stuk didactischer uit. Boek kost trouwens ook geen schijntje.quote:
[..]
Heel geschikt, hoewel het niveau in Vlaanderen wat hoger ligt dan in Nederland. Anders dan het boek van Van de Craats is dit meer een echt leerboek, waarbij de stof per hoofdstuk wordt behandeld en pas aan het einde van ieder hoofdstuk opgaven worden gegeven. Als je het boek eens in wil kijken ,dan kan dat hier.
Daar is nou ook niet veel voor nodig, ik bedoel kijk eens naar het wiskunde A examen van dit jaarquote:
Riparius is er heilig van overtuigd dat het wiskundeonderwijs in Vlaanderen superieur is, dus prima geschikt voor een inferieur Nederlands staatsexamen.
Dat is niet alleen een overtuiging, maar gemakkelijk te verifiëren door bijvoorbeeld leerplannen en de gebruikte boeken in het Nederlandse en Vlaamse secundaire onderwijs te vergelijken.quote:
Riparius is er heilig van overtuigd dat het wiskundeonderwijs in Vlaanderen superieur is, dus prima geschikt voor een inferieur Nederlands staatsexamen.
Ik heb inderdaad vernomen dat dit een aanfluiting moet zijn geweest. Ik heb dit jaar ook examen gedaan (geen Scheikunde en wiskunde - afgerond in 2012), dus met zat vrienden examens geëvalueerd die wiskunde A hebben gedaan.quote:
[..]
Daar is nou ook niet veel voor nodig, ik bedoel kijk eens naar het wiskunde A examen van dit jaar
Fervent tegenstander van het korps lasergamers.
Dit komt uit de herkansing van dit jaar.quote:
[..]
Ik heb inderdaad vernomen dat dit een aanfluiting moet zijn geweest. Ik heb dit jaar ook examen gedaan (geen Scheikunde en wiskunde - afgerond in 2012), dus met zat vrienden examens geëvalueerd die wiskunde A hebben gedaan.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
quote:
[..]
Dit komt uit de herkansing van dit jaar.Tja, de benodigde kennis gaat niet verder dan stof die vroeger in de tweede klas werd behandeld (het minimum of maximum van een kwadratische functie as² + bs + c wordt bereikt bij s = −b/2a, dus daar heb je geen differentiaalrekening voor nodig).SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Dit bevestigt nog maar eens wat Liesbeth van der Plas op haar website zegt over het niveau van het Nederlandse wiskunde onderwijs vroeger en nu. Ze rekent daar genadeloos af met de mythe dat uit PISA tests zou blijken dat Nederland het internationaal gezien zo goed doet. Ze analyseert ook Nederlandse examens uit 2009 en daaruit blijkt dat de benodigde kennis, zowel voor Wiskunde A als voor Wiskunde B, niet verder gaat dan de vroegere tweede klas stof. Ik heb deze website pas ontdekt, en ik moet zeggen dat het voor mij wel een eye opener was. Dat het er beroerd voor stond was mij natuurlijk al lang duidelijk gezien de vragen die hier sinds jaar en dag gesteld worden door scholieren en (beginnende) studenten, maar dat het zo dramatisch was, was mij niet bekend. Geen wonder dat bijna niemand meer in staat blijkt om bijvoorbeeld eenvoudige examenopgaven van de H.B.S. (een vijfjarige opleiding!) of het Gymnasium uit vroeger tijden op te lossen.
[ Bericht 0% gewijzigd door Riparius op 16-10-2013 15:48:20 ]
Klopt als een bus. In het examen van het eerste tijdvak moest je notabene een relatieve toename berekenen o.i.d. met heel gecompliceerde informatie (sarcasme). Snap best dat een som aan het begin niet de meest lastige hoeft te zijn maar er zijn grenzen. Ook mocht je een lineaire functie opstellen adhv twee xy coördinaten (rondom mij vonden mensen dat anders knap lastig), en verder waren bepaalde sommen op te lossen door het kennen van een merkwaardig product/het simpelweg opschrijven van de mogelijkheden.quote:
[..]
Tja, de benodigde kennis gaat niet verder dan stof die vroeger in de tweede klas werd behandeld (het minimum of maximum van een kwadratische functie as² + bs + c wordt bereikt bij s = −b/2a, dus daar heb je geen differentiaalrekening voor nodig).
Dit bevestigt nog maar wat Liesbeth van der Plas op haar website zegt over het niveau van het Nederlandse wiskunde onderwijs vroeger en nu. Ze rekent daar genadeloos af met de mythe dat uit PISA tests zou blijken dat Nederland het internationaal gezien zo goed doet. Ze analyseert ook Nederlandse examens uit 2009 en daaruit blijkt dat de benodigde kennis, zowel, voor Wiskunde A als voor Wiskunde B, niet verder gaat dan de vroegere tweede klas stof. Ik heb deze website pas ontdekt, en ik moet zeggen dat het voor mij wel een eye opener was. Dat het er beroerd voor stond was mij natuurlijk al lang duidelijk gezien de vragen die hier sinds jaar en dag gesteld worden door scholieren en (beginnende) studenten, maar dat het zo dramatisch was, was mij niet bekend. Geen wonder dat bijna niemand meer in staat blijkt om bijvoorbeeld eenvoudige examenopgaven van de H.B.S. (een vijfjarige opleiding!) of het Gymnasium uit vroeger tijden op te lossen.
Verder durf ik te wedden dat je het examen wel zou kunnen halen door een beetje logisch na te denken (je hoeft bijvoorbeeld geen genie te zijn om te bedenken dat de kans dat je 6 gooit met een dobbelsteen 1/6 is) en de differentiaalrekening te beheersen (en die is al niet bar uitgebreid).
Hoi, ik heb een kort vraagje.
Ik snap de werkwijze die ze gebruiken om van stap 1 naar stap 2 te komen niet (zie afbeelding). Ik zit nu al even te prutsen om op dezelfde uitdrukking uit te komen, maar mijn algebraïsche skills zijn helaas nog een beetje onderontwikkeld waardoor het me maar niet lukt. Zou iemand mij kunnen uitleggen wat de tussenstappen zijn om vanuit (1) naar (2) komen?
Bij voorbaat dank
Ik snap de werkwijze die ze gebruiken om van stap 1 naar stap 2 te komen niet (zie afbeelding). Ik zit nu al even te prutsen om op dezelfde uitdrukking uit te komen, maar mijn algebraïsche skills zijn helaas nog een beetje onderontwikkeld waardoor het me maar niet lukt. Zou iemand mij kunnen uitleggen wat de tussenstappen zijn om vanuit (1) naar (2) komen?
Bij voorbaat dank
quote:
[..]
Dit komt uit de herkansing van dit jaar.Ik dacht dat dit B was, ik schrok al.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Gist is liefde, gist is leven. Vooral in een vagijn.
Wat snap je precies niet? Het wordt gewoon uit elkaar getrokken.quote:Op woensdag 16 oktober 2013 16:10 schreef ulq het volgende:
Hoi, ik heb een kort vraagje.
Ik snap de werkwijze die ze gebruiken om van stap 1 naar stap 2 te komen niet (zie afbeelding). Ik zit nu al even te prutsen om op dezelfde uitdrukking uit te komen, maar mijn algebraïsche skills zijn helaas nog een beetje onderontwikkeld waardoor het me maar niet lukt. Zou iemand mij kunnen uitleggen wat de tussenstappen zijn om vanuit (1) naar (2) komen?
[ afbeelding ]
Bij voorbaat dank
quote:
Hoi, ik heb een kort vraagje.
Ik snap de werkwijze die ze gebruiken om van stap 1 naar stap 2 te komen niet (zie afbeelding). Ik zit nu al even te prutsen om op dezelfde uitdrukking uit te komen, maar mijn algebraïsche skills zijn helaas nog een beetje onderontwikkeld waardoor het me maar niet lukt. Zou iemand mij kunnen uitleggen wat de tussenstappen zijn om vanuit (1) naar (2) komen?
[ afbeelding ]
Bij voorbaat dank
Hier beginnen we dus mee, let op de -, die werken we eerst even weg.
Akkoord? Nou, dit kunnen we natuurlijk ook schrijven als:
Nu halen we in beide noemers de x^y naar boven:
Dat kunnen we vereenvoudigen tot:
Nu verplaatsen we de x weer van de teller naar de noemer:
En zo krijg je uiteindelijk:
Aha, wacht ff. Ik ben een beetje dom bezig inderdaad. Ik heb het nu nog een keer gedaan en het komt op hetzelfde uit, behalve dat de twee uitdrukkingen in (2) zijn omgewisseld. Het - teken staat dus voor de 2/(ln(x)x^(y-1)) en niet voor de y/(xln(x))quote:
[..]
Wat snap je precies niet? Het wordt gewoon uit elkaar getrokken.
Edit: oh sorry, ga nu ff eerst je andere reactie lezen.
Er in feite -1*(uitdrukking)quote:
[..]
Aha, wacht ff. Ik ben een beetje dom bezig inderdaad. Ik heb het nu nog een keer gedaan en het komt op hetzelfde uit, behalve dat de twee uitdrukkingen in (2) zijn omgewisseld. Het - teken staat dus voor de 2/(ln(x)x^(y-1)) en niet voor de y/(xln(x))
Edit: oh sorry, ga nu ff eerst je andere reactie lezen.
Je ziet dat er bij (1) een minteken voor de breuk als geheel staat. Bedenk nu eerst datquote:
Hoi, ik heb een kort vraagje.
Ik snap de werkwijze die ze gebruiken om van stap 1 naar stap 2 te komen niet (zie afbeelding). Ik zit nu al even te prutsen om op dezelfde uitdrukking uit te komen, maar mijn algebraïsche skills zijn helaas nog een beetje onderontwikkeld waardoor het me maar niet lukt. Zou iemand mij kunnen uitleggen wat de tussenstappen zijn om vanuit (1) naar (2) komen?
[ afbeelding ]
Bij voorbaat dank
En bedenk vervolgens dat
Nu zou je toch moeten zien hoe je verder kunt gaan. Het gelijk van Liesbeth wordt helaas alweer binnen enkele minuten na mijn vorige post bevestigd ...
Aha, thanks man. Ik liep gewoon een beetje te falen inderdaad. Er staat natuurlijk ook een - teken voor. Hij is inderdaad eigenlijk relatief ontzettend eenvoudig. En dan te bedenken dat ik er wel iets van 20 minuten mee heb zitten prutsenquote:
[..]
[ afbeelding ]
Hier beginnen we dus mee, let op de -, die werken we eerst even weg.
[ afbeelding ]
Akkoord? Nou, dit kunnen we natuurlijk ook schrijven als:
[ afbeelding ]
Nu halen we in beide noemers de x^y naar boven:
[ afbeelding ]
Dat kunnen we vereenvoudigen tot:
[ afbeelding ]
Nu verplaatsen we de x weer van de teller naar de noemer:
[ afbeelding ]
En zo krijg je uiteindelijk:
[ afbeelding ]
Zolang je het volgende week vrijdag maar niet verprutstquote:
[..]
Aha, thanks man. Ik liep gewoon een beetje te falen inderdaad. Er staat natuurlijk ook een - teken voor. Hij is inderdaad eigenlijk relatief ontzettend eenvoudig. En dan te bedenken dat ik er wel iets van 20 minuten mee heb zitten prutsen
Haha, ja ik weet ook niet helemaal waarom ik nou zo zat te kloten met deze opgave, normaal ben ik helemaal niet zo ontzettend slechtquote:
[..]
Zolang je het volgende week vrijdag maar niet verprutst
Ik had eerst 5 minuten nodig om te zien dat het antwoord uit 2 uitdrukkingen/breuken bestond ipv 1, waardoor ik in eerste instantie op iets heel anders uitkwam. Daarna begon ik te twijfelen of het wel zo was dat x^(y-1) gelijk was aan (x^-1)(x^y) omdat ik weer niet lekker uitkwam en toen dacht ik fuck it ik vraag het gewoon ff
Ik had voor de tweede toets wel een 7 trouwens
Laatst moesten we tentamensommen voorbereiden, ik hield het makkelijk maar wist dat veel mensen er de figuurlijke boot mee zouden ingaan (nml differentiëer x^x). Uiteindelijk is mijn som niet eens aan bod gekomen, omdat mijn mentor hem 'van te hoog niveau' achtte. Ik keek in het weekend naar een ouder tentamen, en jawel, bereken de elasticiteit van x^(2x)3^x (de formule voor elasticiteit is x/f(x) * f'(x)). Nou, succes als je dat nog nooit hebt gedaan.quote:
[..]
Je ziet dat er bij (1) een minteken voor de breuk als geheel staat. Bedenk nu eerst dat
En bedenk vervolgens dat
Nu zou je toch moeten zien hoe je verder kunt gaan. Het gelijk van Liesbeth wordt helaas alweer binnen enkele minuten na mijn vorige post bevestigd ...
[ Bericht 1% gewijzigd door jordyqwerty op 16-10-2013 16:43:42 ]
Oh, ok! Ik had de vergelijking door p gedeeld en hield niet rekening mee dat als p = 0 de discriminant nog steeds positief is!quote:
[..]
Je uitleg is bijzonder onduidelijk. Dat moet echt beter als je ooit een examen denkt te gaan afleggen.
De voorwaarde die we hadden gevonden is
p2 − 8p < 0
Dit is een ongelijkheid in p, die je moet oplossen om te bepalen welke waarden van p hieraan voldoen. Om deze ongelijkheid op te lossen, los je eerst de vergelijking
p2 − 8p = 0
op. Dat is eenvoudig, want hier kun je p buiten haakjes halen. Dan vinden we
p = 0 ∨ p = 8
Nu maak je een tekenschema, en dan zie je dat p2 − 8p < 0 indien
0 < p < 8
In woorden: p moet liggen tussen 0 en 8.
[..]
Nee, dat betekent het niet. De notatie (0,8) duidt hier een open interval aan. Dat is een interval waarbij de eindpunten niet meedoen. Dit interval vatten we hier op als een verzameling getallen, namelijk de verzameling van alle reële getallen waarvoor geldt dat ze groter zijn dan 0 en tevens kleiner dan 8.
Het teken ∈ betekent '(is) element van' oftewel 'zit in', dus de notatie p ∈ (0,8) betekent dat p een element moet zijn van de verzameling van alle reële getallen die groter zijn dan 0 en tevens kleiner dan 8.
Voor p = 0 vallen hier alle termen waarin de x voorkomt weg, zodat je dan geen vergelijking meer hebt. En als je geen (vierkants)vergelijking meer hebt kun je ook niet meer spreken van een discriminant.quote:
[..]
Oh, ok! Ik had de vergelijking door p gedeeld en hield er geen rekening mee dat als p = 0 de discriminant nog steeds positief is!
Oh ja... a mag niet gelijk aan 0 zijn.quote:
[..]
Voor p = 0 vallen hier alle termen waarin de x voorkomt weg, zodat je dan geen vergelijking meer hebt. En als je geen (vierkants)vergelijking meer hebt kun je ook niet meer spreken van een discriminant.
Nee, misschien wel wiskunde a tentamen bij de OU, maar dan moet ik wel de stof 100% beheersen. Ik weet alleen niet of dat lukt.quote:
[..]
Ben je van plan het staatsexamen wiA te doen?
[ Bericht 31% gewijzigd door wiskundenoob op 16-10-2013 19:13:04 ]
Toevallig anderen die Eureka gezien hebben? Is een programma over wiskunde, van Ionica Smeets (wiskundemeisjes) en Sofie van den Enk. Vorige aflevering ging over voetbal en wiskunde (o.a. grafentheorie op teams; verder veel kansrekening), die van vandaag over levensverwachting (o.a. correlatie en causaliteit, stochastische modellen). Misschien weinig nieuws voor de mensen hier, maar leuk gedaan.
Verhaal van de bommenwerper in de Tweede Wereldoorlog blijft mooi (Abraham Wald): men onderzocht eerst waar de vliegtuigen die terugkwamen, beschoten waren en versterkte die delen. Dat leek een slim idee, maar dat bleek weinig te helpen. De factoren met de grootste invloed (beschoten motor) kwamen niet aan het licht, want die vliegtuigen kwamen niet thuis.
Verhaal van de bommenwerper in de Tweede Wereldoorlog blijft mooi (Abraham Wald): men onderzocht eerst waar de vliegtuigen die terugkwamen, beschoten waren en versterkte die delen. Dat leek een slim idee, maar dat bleek weinig te helpen. De factoren met de grootste invloed (beschoten motor) kwamen niet aan het licht, want die vliegtuigen kwamen niet thuis.
Ik zal het dit weekend wel even terugkijken, klinkt best interessant.quote:
Toevallig anderen die Eureka gezien hebben? Is een programma over wiskunde, van Ionica Smeets (wiskundemeisjes) en Sofie van den Enk. Vorige aflevering ging over voetbal en wiskunde (o.a. grafentheorie op teams; verder veel kansrekening), die van vandaag over levensverwachting (o.a. correlatie en causaliteit, stochastische modellen). Misschien weinig nieuws voor de mensen hier, maar leuk gedaan.
Verhaal van de bommenwerper in de Tweede Wereldoorlog blijft mooi (Abraham Wald): men onderzocht eerst waar de vliegtuigen die terugkwamen, beschoten waren en versterkte die delen. Dat leek een slim idee, maar dat bleek weinig te helpen. De factoren met de grootste invloed (beschoten motor) kwamen niet aan het licht, want die vliegtuigen kwamen niet thuis.
Leuk programma. Zeker voor de leek die denkt dat je niks met wiskunde kanquote:
Toevallig anderen die Eureka gezien hebben? Is een programma over wiskunde, van Ionica Smeets (wiskundemeisjes) en Sofie van den Enk. Vorige aflevering ging over voetbal en wiskunde (o.a. grafentheorie op teams; verder veel kansrekening), die van vandaag over levensverwachting (o.a. correlatie en causaliteit, stochastische modellen). Misschien weinig nieuws voor de mensen hier, maar leuk gedaan.
Verhaal van de bommenwerper in de Tweede Wereldoorlog blijft mooi (Abraham Wald): men onderzocht eerst waar de vliegtuigen die terugkwamen, beschoten waren en versterkte die delen. Dat leek een slim idee, maar dat bleek weinig te helpen. De factoren met de grootste invloed (beschoten motor) kwamen niet aan het licht, want die vliegtuigen kwamen niet thuis.
. Geen diepe wiskundige analyses uiteraard, maar ze laten wel zien waar je wiskunde voor kan gebruiken en wat voor soort wiskunde er is. Daar hebben veel mensen helemaal geen beeld van.
Precies. Zou fijn zijn als 'de leek' dat wat meer zou zien. De artikelen die achter de beweringen schuilgaan zet Ionica overigens netjes op haar blog, interessant! Ik hoop ergens dat er meer dingen uit andere gebieden dan statistiek gaan komen. Dat de grafentheorie langskwam vond ik mooi. Benieuwd naar de rest!quote:
[..]
Leuk programma. Zeker voor de leek die denkt dat je niks met wiskunde kan
Gegeven zijn de vergelijkingen:
a+bλ = λ2
λa + b + (λ2 -1)c = λ2
2b - c = 0
Nu moet ik berekenen voor welke waardes van lambda dit stelsel géén oplossingen heeft. Het betreft hier een hoofdstuk uit Lineaire Algebra 1 dat de rang, inverses en determinanten van een matrix behandelt, dus ik denk dat ik daar de oplossing moet zoeken?
Ik zou dolgraag een determinant bepalen, maar het is geen vierkante matrix.. Iemand een tip zonder dit helemaal met de hand uit te moeten werken? Het lukt niet bepaald met vegen om een rij zonder variabelen te genereren.
a+bλ = λ2
λa + b + (λ2 -1)c = λ2
2b - c = 0
Nu moet ik berekenen voor welke waardes van lambda dit stelsel géén oplossingen heeft. Het betreft hier een hoofdstuk uit Lineaire Algebra 1 dat de rang, inverses en determinanten van een matrix behandelt, dus ik denk dat ik daar de oplossing moet zoeken?
Ik zou dolgraag een determinant bepalen, maar het is geen vierkante matrix.. Iemand een tip zonder dit helemaal met de hand uit te moeten werken? Het lukt niet bepaald met vegen om een rij zonder variabelen te genereren.
Fervent tegenstander van het korps lasergamers.
Dan denk ik dat het de bedoeling is dat je Rouché-Capelli gebruikt.quote:
Gegeven zijn de vergelijkingen:
a+bλ = λ2
λa + b + (λ2 -1)c = λ2
2b - c = 0
Nu moet ik berekenen voor welke waardes van lambda dit stelsel géén oplossingen heeft. Het betreft hier een hoofdstuk uit Lineaire Algebra 1 dat de rang, inverses en determinanten van een matrix behandelt, dus ik denk dat ik daar de oplossing moet zoeken?
Dat denk ik niet aangezien dit niet in het college behandeld is. Daarom begrijp ik er eigenlijk ook geen fluit van, en ik heb het toch al 3x doorgelezen vanaf Theorem 8.quote:
[..]
Dan denk ik dat het de bedoeling is dat je Rouché-Capelli gebruikt.
Fervent tegenstander van het korps lasergamers.
Goed, ik heb nu uitgevonden dat
rang(A) = rang(A|b) = 3 met λ ongelijk aan 1 of -1. Dit was eigenlijk exact opgave a,
Wat kan ik hier nu uit concluderen? Ik vermoed dat er voor een bepaalde lambda één unieke oplossing is.
rang(A) = rang(A|b) = 3 met λ ongelijk aan 1 of -1. Dit was eigenlijk exact opgave a,
Wat kan ik hier nu uit concluderen? Ik vermoed dat er voor een bepaalde lambda één unieke oplossing is.
Fervent tegenstander van het korps lasergamers.
Zou iemand dit uit kunnen leggen?
Bereken (bovenaan oneindig, onderaan 2) f(x)dx, f(x)=
Hoezo is de integraal van dit de rest lukt mij zelf wel. Alvast bedankt
Bereken (bovenaan oneindig, onderaan 2) f(x)dx, f(x)=
Hoezo is de integraal van dit de rest lukt mij zelf wel. Alvast bedankt
Je kan ook [ tex] gebruiken...quote:
Zou iemand dit uit kunnen leggen?
Bereken [ afbeelding ] (bovenaan oneindig, onderaan 2) f(x)dx, f(x)=[ afbeelding ]
Hoezo is de integraal van [ afbeelding ] dit [ afbeelding ] de rest lukt mij zelf wel. Alvast bedankt
-edit-
Kan jij
Lukt niet echtquote:
[..]
Je kan ook [ tex] gebruiken...
-edit-
Kan jijintegreren?
Ok weet je ook datquote:
-edit- vergeet trouwens niet de extra constante toe te voegen.
ah, stom van me, ja dat weet ik.quote:
[..]
Ok weet je ook daten
gewoon constanten zijn?
Ok dus hoe integreer jequote:
[..]
ah, stom van me, ja dat weet ik.
Ja dat had ik al gezegd.quote:
[..]
Hint:is gelijk aan
? Welke factoren zijn constant en welke is variabel?
2/e2x−4 = 2·e−2x+4 = 2·e4·e−2xquote:
Wat denk je daarvan?
Link trouwens niet naar plaatjes op wolframalpha.com, die linkjes blijven namelijk maar enkele minuten geldig.
Ik heb het uiteindelijk precies zo gedaan.quote:
[..]
2/e2x−4 = 2·e−2x+4 = 2·e4·e−2x
Wat denk je daarvan?
Link trouwens niet naar plaatjes op wolframalpha.com, die linkjes blijven namelijk maar enkele minuten geldig.
2/(e^(2x-4))=>2*(e^(2x-4)^-1)=>2e^-2x+4=>integraal is dus -1*e^(-2x+4)=-1/e^(2x-4)
Goed, ik zit nog steeds met hetzelfde probleem.quote:
[..]
Dan denk ik dat het de bedoeling is dat je Rouché-Capelli gebruikt.
De oplossingen a, b en c (in het dictaat staat x1, x2 en x3, maar dat is me nu te veel werk) worden gegeven door de regel van Cramer.
Als we hebben
Ax = b
met A alles (in een matrix) wat links van het =-teken staat, en b alles wat rechts van het =-teken staat, dan worden de oplossingen xi gegeven door
xi = det(Ai)/det(A)
Nou de determinant die weet ik. Onderdeel a van de opgave was om de inverse van A te bepalen voor iedere λ waarvoor A inverteerbaar is.
det(A) = 0 voor λ = 1 en λ = -1
Dus heeft het stelsel Ax = b dan alleen géén oplossingen voor λ = 1 en λ = -1
?
Fervent tegenstander van het korps lasergamers.
Dat klopt niet. Kies λ = 1, dan heb jequote:
[..]
Dus heeft het stelsel Ax = b dan alleen géén oplossingen voor λ = 1 en λ = -1
?
a + b = 1
a + b = 1
2b - c = 0
en dit stelsel heeft oneindig veel oplossingen.
We hebben die stelling van Rouché-Capelli nooit gehad.Ik had gevonden dat de rang van de grootst mogelijke vierkante submatrix 3 is, mits λ ongelijk aan 1 of -1.quote:
[..]
Dat klopt niet. Kies λ = 1, dan heb je
a + b = 1
a + b = 1
2b - c = 0
en dit stelsel heeft oneindig veel oplossingen.
Daaruit volgt volgens die stelling dat er één unieke oplossing is. Maar hoe vind ik dan voor welke waarde(n) van λ er nu géén oplossing is?
Fervent tegenstander van het korps lasergamers.
Dat klopt, voor λ² − 1 ≠ 0 heb je rank(A) = rank(A|b) = 3.quote:
[..]
We hebben die stelling van Rouché-Capelli nooit gehad. Ik had gevonden dat de rang van de grootst mogelijke vierkante submatrix 3 is, mits λ ongelijk aan 1 of -1.
Nee, dat zegt de stelling niet, je hebt het dus niet begrepen.quote:Daaruit volgt volgens die stelling dat er één unieke oplossing is.
Dat is het geval als rank(A) ≠ rank(A|b).quote:Maar hoe vind ik dan voor welke waarde(n) van λ er nu géén oplossing is?
http://en.wikipedia.org/wiki/Rouch%C3%A9%E2%80%93Capelli_theoremquote:
[..]
Dat klopt, voor λ² − 1 ≠ 0 heb je rank(A) = rank(A|b) = 3.
[..]
Nee, dat zegt de stelling niet, je hebt het dus niet begrepen.
if n = rank(A), the solution is unique,
otherwise there are infinite number of solutions.
Er geldt toch n = 3 (m.a.w. ik heb 3 variabelen)?
Waarom?quote:[..]
Dat is het geval als rank(A) ≠ rank(A|b).
Stelling 1 : Een stelsel Ax=b is oplosbaar, enkel en alleen indien rang[A] = rang[A|b]
http://nl.wikipedia.org/wiki/Stelsel_van_lineaire_vergelijkingen
Lijkt me wel duidelijk eigenlijk.
Maar rang(A) = rang(A|b) voor alle lambda ongelijk 1 of -1. Dus in feite hoef ik nu alleen nog maar naar de gevallen lambda = 1 en lambda = -1 te kijken?
Fervent tegenstander van het korps lasergamers.
Die e's deel je tegen elkaar weg, hoe wordt het vervolgens 2k/a. Ik begrijp wel dat je ze door elkaar deelt, volg niet hoe ze aan het antwoord komen.quote:
[..]
Je deelt de bovenste 2 vergelijkingen van het linkerstelsel gewoon op elkaar.
quote:
[..]
Die e's deel je tegen elkaar weg, hoe wordt het vervolgens 2k/a. Ik begrijp wel dat je ze door elkaar deelt, volg niet hoe ze aan het antwoord komen.
Kijk nou gewoon eens goed. Je hebtquote:
[..]
Die e's deel je tegen elkaar weg, hoe wordt het vervolgens 2k/a. Ik begrijp wel dat je ze door elkaar deelt, volg niet hoe ze aan het antwoord komen.
2·ea√k·√k = 4λ
ea√k·(a/2)·k-1/2 = 4λ
Dus
ea√k·(a/2)·k-1/2 = 2·ea√k·√k
en dus
(a/2)·k-1/2 = 2·√k
Zodat
a/2 = 2k
a = 4k
Oke ik snap 't. Bedankt voor de moeite, dit is voor mij een tentamenniveau som en ik kwam er niet uit.quote:
[..]
Kijk nou gewoon eens goed. Je hebt
2·ea√k·√k = 4λ
ea√k·(a/2)·k-1/2 = 4λ
Dus
ea√k·(a/2)·k-1/2 = 2·ea√k·√k
en dus
(a/2)·k-1/2 = 2·√k
Zodat
a/2 = 2k
a = 4k
En ABNORMAAL dom, ik liep dus de hele tijd vast omdat ik dacht dat k^(1/2)-k^(1/2) k^0=1 opleverde, maar door de deling wordt het natuurlijk k^((1/2--(1/2))=k^1.
Letterlijk een halfuur dom lopen doen over iets wat eigenlijk niet moeilijk was...
[ Bericht 13% gewijzigd door Scaletta op 20-10-2013 19:25:36 ]
Kan iemand mij vertellen, waarom deze 2 uitdrukkingen gelijk zijn? Dus hoe je van de eerste uitdrukking naar de tweede uitdrukking gaat?
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl
Ik heb een formule berekent dat gegeven een initial estimate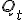 
, een aantal i.i.d. samples 
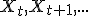en een reeks update rates 
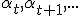een final estimate 
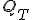maakt:
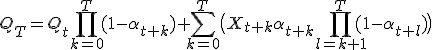
De intentie is dat het een estimate maakt voor de mean van een distributie waar de samples van afkomstig zijn.
De bias van deze estimate is simpel afgeleid, maar ik heb geen clou voor de variance. Dit komt doordat de update rate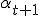
dependent is op alle vorige 
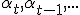en ook random variables kunnen zijn.
Iemand een suggestie hoe dit aan te pakken? Mijn reden om het algebraisch af te leiden is om verschillende invullingen van de update rates / samples leidt tot verschillende variance/biases.
// UPDATE:
Inmiddels heb ik iets weten te verzinnen. Extra detail: Qt is independent van Xt, Xt+1,... samples.
Herschrijf de bovenste equation als
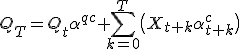
waar
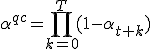, en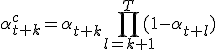 
Dan heb je dus een reeks random variables die gesummed moeten worden, tenzij de update rates ook stochastic zijn. Ik kom dan op de volgende variance:
![Var(Q_T) = E[\alpha^{qc}]^2 Var(Q_t) + E[Q_t]^2 Var(\alpha^{qc}) + Var(\alpha^{qc})Var(Q_t)](https://forum.fok.nl/lib/mimetex.cgi?Var%28Q_T%29%20%3D%20E%5B%5Calpha%5E%7Bqc%7D%5D%5E2%20Var%28Q_t%29%20%2B%20E%5BQ_t%5D%5E2%20Var%28%5Calpha%5E%7Bqc%7D%29%20%2B%20Var%28%5Calpha%5E%7Bqc%7D%29Var%28Q_t%29%20)
![+ \sum_{k=0}^T \bigl( E[\alpha_{t+k}^{c}]^2 Var(X_{t+k}) + E[X_{t+k}]^2 Var(\alpha_{t+k}^{c}) + Var(\alpha_{t+k}^{c}) Var(X_{t+k}) \bigr)](https://forum.fok.nl/lib/mimetex.cgi?%2B%20%5Csum_%7Bk%3D0%7D%5ET%20%5Cbigl%28%20E%5B%5Calpha_%7Bt%2Bk%7D%5E%7Bc%7D%5D%5E2%20Var%28X_%7Bt%2Bk%7D%29%20%2B%20E%5BX_%7Bt%2Bk%7D%5D%5E2%20Var%28%5Calpha_%7Bt%2Bk%7D%5E%7Bc%7D%29%20%2B%20Var%28%5Calpha_%7Bt%2Bk%7D%5E%7Bc%7D%29%20Var%28X_%7Bt%2Bk%7D%29%20%5Cbigr%29)
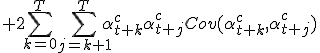
Kan iemand hier een blik op werpen en zeggen of dit misschien klopt?
[ Bericht 10% gewijzigd door koffiegast op 22-10-2013 15:27:40 ]
De intentie is dat het een estimate maakt voor de mean van een distributie waar de samples van afkomstig zijn.
De bias van deze estimate is simpel afgeleid, maar ik heb geen clou voor de variance. Dit komt doordat de update rate
Iemand een suggestie hoe dit aan te pakken? Mijn reden om het algebraisch af te leiden is om verschillende invullingen van de update rates / samples leidt tot verschillende variance/biases.
// UPDATE:
Inmiddels heb ik iets weten te verzinnen. Extra detail: Qt is independent van Xt, Xt+1,... samples.
Herschrijf de bovenste equation als
waar
Dan heb je dus een reeks random variables die gesummed moeten worden, tenzij de update rates ook stochastic zijn. Ik kom dan op de volgende variance:
Kan iemand hier een blik op werpen en zeggen of dit misschien klopt?
[ Bericht 10% gewijzigd door koffiegast op 22-10-2013 15:27:40 ]
Ik heb een vraag over directional derivatives.
Gevraagd wordt: op welk punt op de paraboloïde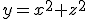
is het raakvlak parallel aan het vlak 
.
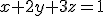Het raakvlak van de paraboloïde is dan dus:
.
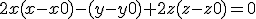Hoe moet ik nu verder gaan?
Gevraagd wordt: op welk punt op de paraboloïde
Het raakvlak van de paraboloïde is dan dus:
Hoe moet ik nu verder gaan?
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Herschrijf de vergelijking van je paraboloïde in de gedaantequote:
Ik heb een vraag over directional derivatives.
Gevraagd wordt: op welk punt op de paraboloïde
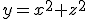
is het raakvlak parallel aan het vlak
Het raakvlak van de paraboloïde is dan dus:.
Hoe moet ik nu verder gaan?
F(x, y, z) = 0
Een normaalvector in een punt (x0,y0,z0) op dit vlak is nu
(∂F/∂x(x0,y0,z0), ∂F/∂y(x0,y0,z0), ∂F/∂z(x0,y0,z0)) = (2x0, −1, 2z0)
en deze vector moet dezelfde richting hebben als de normaalvector (1, 2, 3) van je vlak x + 2y + 3z = 1. Nu moet je het toch echt wel op kunnen lossen. Zie ook hier.
[ Bericht 2% gewijzigd door Riparius op 22-10-2013 17:46:19 ]
Bedankt voor je antwoord.quote:
[..]
Herschrijf de vergelijking van je paraboloïde in de gedaante
F(x,y,z) = 0
Een normaalvector in een punt (x0,y0,z0) op dit vlak is nu
(∂F/∂x(x0,y0,z0), ∂F/∂y(x0,y0,z0), ∂F/∂z(x0,y0,z0))
en deze vector moet dezelfde richting hebben als de normaalvector (1, 2, 3) van je vlak x + 2y + 3z = 1. Nu moet je het toch echt wel op kunnen lossen.
Dan krijg je dus:
normaalvector =
Dan bestaat er toch geen oplossing? Gezien welke waarden er ook worden gekozen, er geldt nooit , (2x0, -1, z0) = (1, 2, 3).
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Om te beginnen: gebruik ook subscript als je TeX gebruikt. Verder: zie mijn post hierboven voor de correcte vergelijking van het raakvlak.quote:
[..]
Bedankt voor je antwoord.
Dan krijg je dus:
normaalvector =
Dan bestaat er toch geen oplossing? Gezien welke waarden er ook worden gekozen, er geldt nooit (2x0, -1, 2z0) = (1, 2, 3).
Je vergist je als je meent dat er geen oplossing is. De normaalvectoren moeten in elkaars verlengde liggen, ze hoeven niet hetzelfde te zijn.
Oké, dan zal ik het maal een constante doen (c).quote:
[..]
Om te beginnen: gebruik ook subscript als je TeX gebruikt. Verder: zie mijn post hierboven voor de correcte vergelijking van het raakvlak.
Je vergist je als je meent dat er geen oplossing is. De normaalvectoren moeten in elkaars verlengde liggen, ze hoeven niet hetzelfde te zijn.
c(2x0, -1, 2z0) = (1, 2, 3)
c = 2 / -1 = -2.
dus:
-4x0 = 1
=> x0 = -1/4
-4z0 = 3
=> z0 = -3/4
dus het raakvlak van F(x) = 0 is parallel aan de vergelijking x + 2y + 3z = 1 in het punt P(-1/4, y0, -3/4), waarin y0 nog alles kan zijn. Correct?
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Nee, fout.quote:
[..]
Oké, dan zal ik het maal een constante doen (c).
c(2x0, -1, 2z0) = (1, 2, 3)
c = 2 / -1 = -2.
dus:
-4x0 = 1
=> x0 = -1/4
-4z0 = 3
=> z0 = -3/4
dus het raakvlak van F(x,y,z) = 0 is parallel aan het vlak met de vergelijking x + 2y + 3z = 1 in het punt P(-1/4, y0, -3/4), waarin y0 nog alles kan zijn. Correct?
Je gebruikt nu zomaar opeens y0 in plaats van z0.
Verder moet je nu y0 nog bepalen.
[ Bericht 2% gewijzigd door Riparius op 22-10-2013 18:12:37 ]
Excuus, ik heb het inmiddels verbeterd. Wat is verder mijn denkfout?quote:
[..]
Nee, fout.
Je gebruikt nu zomaar opeens y0 in plaats van z0.
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Het is zo goed, maar nu moet je y0 nog bepalen.quote:
[..]
Excuus, ik heb het inmiddels verbeterd. Wat is verder mijn denkfout?
Oké.
y0 = x02 + z02 = (-1/4)2 + (-3/4)2 = 1/16 + 9/16 = 10/16 = 5/8.
Dus P(1/4, 5/8, 3/4).
y0 = x02 + z02 = (-1/4)2 + (-3/4)2 = 1/16 + 9/16 = 10/16 = 5/8.
Dus P(1/4, 5/8, 3/4).
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Dat is het, behalve dat je nu weer je mintekens vergeet. Je moet echt netter gaan werken.quote:
Oké.
y0 = x02 + z02 = (-1/4)2 + (-3/4)2 = 1/16 + 9/16 = 10/16 = 5/8.
Dus P(−1/4, 5/8, −3/4).
Ik denk het wel, ik moest vooral even zien dat je met normaalvectoren moest werken.quote:
Je kunt dus stellen dat de vraag: 'wanneer is het raakvlak van F(x) parallel aan g(x) = c?' equivalent is aan de vraag: 'wanneer ligt de normaalvector van F(x) in het verlengde van de normaalvector van g(x) = c?'?
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Als je met g(x,y,z) = c een vergelijking van een plat vlak bedoelt, dan klopt dit. Twee vlakken die parallel zijn hebben immers ook normaalvectoren die parallel zijn. En: netter werken, je maakt voortdurend fouten met je notatie.quote:
[..]
Ik denk het wel, ik moest vooral even zien dat je met normaalvectoren moest werken.
Je kunt dus stellen dat de vraag: 'wanneer is het raakvlak aan F(x,y,z) = 0 parallel aan het vlak g(x,y,z) = c?' equivalent is aan de vraag: 'wanneer ligt de normaalvector van F(x,y,z) = 0 in het verlengde van de normaalvector van g(x,y,z) = c?'?
[ Bericht 4% gewijzigd door Riparius op 22-10-2013 18:34:01 ]
Ik heb een vraag over een vraagstuk waar ik eigenlijk nog niet klaar voor ben, maar ik wil een poging wagen. Gonio is een zwakke kant van mij, maar dat wil ik versterken.
Komt die: http://www2.cito.nl/vo/ex2013/VW-1025-a-13-1-o.pdf
Vraag 6 ( Toon uitgaande van de gelijkvormigheid van de driehoeken GCR en GPQ aan dat deze formule juist is.)
Ik stel dat:
alfa1= hoek dat gemaakt wordt door de sinus alfa1 = CR/CG
alfa2= hoek dat gemaakt wordt door sinus alfa2 = PQ/GP
CR = sin alfa 1
GP^2 = GQ^2 + PQ^2 = (cosalfa2)^2 + (sinalfa2)^2
en dus GP= cosalfa2 + sinalfa2
CG^2=GR^2 + CR^2 = (cosalfa1)^2 + (sinalfa1)^2
en dus CG=cosalfa1 + sinalfa1
Ik stel ook dat:
CR/CG=PQ/GP
Opdat:
PQ=(CR*GP)/CG
Opdat:
PQ=(sinalfa1 * cosalfa2 + sinalfa2)/(sinalfa1+cosalfa1)
Hierna loop ik vast....
Ik heb het geprobeerd zo netjes/begrijpbaar mogelijk neer te zetten.
Komt die: http://www2.cito.nl/vo/ex2013/VW-1025-a-13-1-o.pdf
Vraag 6 ( Toon uitgaande van de gelijkvormigheid van de driehoeken GCR en GPQ aan dat deze formule juist is.)
Ik stel dat:
alfa1= hoek dat gemaakt wordt door de sinus alfa1 = CR/CG
alfa2= hoek dat gemaakt wordt door sinus alfa2 = PQ/GP
CR = sin alfa 1
GP^2 = GQ^2 + PQ^2 = (cosalfa2)^2 + (sinalfa2)^2
en dus GP= cosalfa2 + sinalfa2
CG^2=GR^2 + CR^2 = (cosalfa1)^2 + (sinalfa1)^2
en dus CG=cosalfa1 + sinalfa1
Ik stel ook dat:
CR/CG=PQ/GP
Opdat:
PQ=(CR*GP)/CG
Opdat:
PQ=(sinalfa1 * cosalfa2 + sinalfa2)/(sinalfa1+cosalfa1)
Hierna loop ik vast....
Ik heb het geprobeerd zo netjes/begrijpbaar mogelijk neer te zetten.
-
[ Bericht 62% gewijzigd door Amoeba op 22-10-2013 19:53:22 ]
[ Bericht 62% gewijzigd door Amoeba op 22-10-2013 19:53:22 ]
Fervent tegenstander van het korps lasergamers.
Als eerste een tip, maak het jezelf en zeker anderen niet te moeilijk door een alfa1 en alfa2 te definieren wanneer er al een alfa in het probleem gebruikt wordt. gebruik dan een theta, of phi, of beta ofzo. Of maak er A en B van, dit is ook korter en dus duidelijker. Je zou ook tex-commando's kunnen gebruiken, maar aangezien je het eindexamen VWO aan het maken bent, heb je dit nog nooit gedaan waarschijnlijkquote:
Ik heb een vraag over een vraagstuk waar ik eigenlijk nog niet klaar voor ben, maar ik wil een poging wagen. Gonio is een zwakke kant van mij, maar dat wil ik versterken.
Komt die: http://www2.cito.nl/vo/ex2013/VW-1025-a-13-1-o.pdf
Vraag 6 ( Toon uitgaande van de gelijkvormigheid van de driehoeken GCR en GPQ aan dat deze formule juist is.)
Ik stel dat:
alfa1= hoek dat gemaakt wordt door de sinus alfa1 = CR/CG
alfa2= hoek dat gemaakt wordt door sinus alfa2 = PQ/GP
Naast een aantal elementaire fouten (quote:CR = sin alfa 1
GP^2 = GQ^2 + PQ^2 = (cosalfa2)^2 + (sinalfa2)^2
en dus GP= cosalfa2 + sinalfa2
CG^2=GR^2 + CR^2 = (cosalfa1)^2 + (sinalfa1)^2
en dus CG=cosalfa1 + sinalfa1
Ik stel ook dat:
CR/CG=PQ/GP
Opdat:
PQ=(CR*GP)/CG
Opdat:
PQ=(sinalfa1 * cosalfa2 + sinalfa2)/(sinalfa1+cosalfa1)
Hierna loop ik vast....
Ik heb het geprobeerd zo netjes/begrijpbaar mogelijk neer te zetten.
Je hebt die nieuwe hoeken namelijk helemaal niet nodig als je gelijkvormigheid goed gebruikt. Van een aantal punten is namelijk de (x,y) coordinaat gegeven. Als je die slim gebruikt moet je er ook uit kunnen komen.
Het eerste wat eruit springt:quote:
GP^2 = GQ^2 + PQ^2 = (cosalfa2)^2 + (sinalfa2)^2
en dus GP= cosalfa2 + sinalfa2
Als A2 + B2 = C2 (ongelijk aan 0) dan geldt niet dat C = A + B. Dat weet je hopelijk?
Heb deze vraag recent nog gemaakt. De kern zit hem erin dat je inderdaad de zijdes die overeenkomen door elkaar deelt. De zijdes zijn uit te drukken in een combinatie van de termen sin(alfa), cosinus(alfa) en 1. Kijk goed naar de vierkanten en de zijdes die bij de aangegeven hoeken alfa horen. Een aantal punten komen qua x of y coördinaat met elkaar overeen, bijvoorbeeld:
CR = YC - YR (zie plaatje)
YC = YT = ET = BE + BT= Sin(alfa)+ Cos(alfa) (Zie plaatje; gebruik het verband tussen een hoek alfa en de bijbehorende x en y coördinaat).
Overigens, hoever ben je dan al met je wiskunde? Je zegt dat je er niet aan toe bent.
Handig lijkt me:
- Meetkundige bewijzen / gelijkvormigheid;
- Goniometrische identiteiten;
- Poolcoördinaten: (verband tussen (straal, hoek) en (x,y) lijkt me 't overzicht voor je vereenvoudigen).
[ Bericht 1% gewijzigd door Aardappeltaart op 22-10-2013 20:00:40 ]
Volgens mij haal je hier de X en Y coordinaat door elkaarquote:
[..]
Het eerste wat eruit springt:
Als A2 + B2 = C2 dan geldt niet dat C = A + B. Dat weet je hopelijk?
Heb deze vraag recent nog gemaakt. De kern zit hem erin dat je inderdaad de zijdes die overeenkomen door elkaar deelt. De zijdes zijn uit te drukken in een combinatie van de termen sin(alfa), cosinus(alfa) en 1. Kijk goed naar de vierkanten en de zijdes die bij de aangegeven hoeken alfa horen. Een aantal punten komen qua x of y coördinaat met elkaar overeen, bijvoorbeeld:
CR = XC - XR (zie plaatje)
XC = XT = BE + TB = Sin(alfa)+ Cos(alfa) (Zie plaatje; gebruik het verband tussen een hoek alfa en de bijbehorende x en y coördinaat).
Overigens, hoever ben je dan al met je wiskunde? Je zegt dat je er niet aan toe bent.
Handig lijkt me:
- Meetkundige bewijzen / gelijkvormigheid;
- Goniometrische identiteiten;
- Poolcoördinaten: (verband tussen (straal, hoek) en (x,y) lijkt me 't overzicht voor je vereenvoudigen).
Bedankt. Ik heb het verbeterd. Het erge is, is dat dit soort haastige slordigheidsfouten weleens voorkomen in mijn toetsen. Daardoor zelden een 10.quote:
[..]
Volgens mij haal je hier de X en Y coordinaat door elkaar
Dank u veel beide. Ik dacht dat schuine zijde = verticale zijde + horizontale zijde, maar het is dus horizontale zijde = schijne zijde + verticale zijde. Stom van me.
Mijn voorkennis is wiskunde a, vwo, maar ik ben het nu stap voor stap aan het uitbreiden tot wiskunde b. Tot zover laatst nog met mijn prive wiskunde docent gehad over de eenheidscirkel, waar de sinus/cosinus zit , de cosinus/sinusregel de sinus functie en cosinus functie. Met dat laatste dus de amplitude/periode/evenwichtslijn/translaties/beginpunten.
Ik ga jullie uitleg nog even doorlezen en weer naar het vraagstuk kijken. Hoop dat ik hem dan wel zie, zoniet, dan zal ik hier weer posten met wat ik gedaan heb/waar ik vast zit.
Mijn voorkennis is wiskunde a, vwo, maar ik ben het nu stap voor stap aan het uitbreiden tot wiskunde b. Tot zover laatst nog met mijn prive wiskunde docent gehad over de eenheidscirkel, waar de sinus/cosinus zit , de cosinus/sinusregel de sinus functie en cosinus functie. Met dat laatste dus de amplitude/periode/evenwichtslijn/translaties/beginpunten.
Ik ga jullie uitleg nog even doorlezen en weer naar het vraagstuk kijken. Hoop dat ik hem dan wel zie, zoniet, dan zal ik hier weer posten met wat ik gedaan heb/waar ik vast zit.
Ik heb alleen nog niet gevonden waarom CR = cosα + sinα - 1
Verder is heel de opgave me eigenlijk wel gelukt.
Verder is heel de opgave me eigenlijk wel gelukt.
Fervent tegenstander van het korps lasergamers.
OF = sinα + cosα + 1
Lijkt me vrij helder.
∠GCR = π/2-α
DR' = QR = sin(π/2-α) = cos(α)
En dus
RH = sin(α)
En inderdaad
PQ = OF/GR * CR
GR = RH + GH = sin(α) + 1
En dan alleen CR nog ..
Lijkt me vrij helder.
∠GCR = π/2-α
DR' = QR = sin(π/2-α) = cos(α)
En dus
RH = sin(α)
En inderdaad
PQ = OF/GR * CR
GR = RH + GH = sin(α) + 1
En dan alleen CR nog ..
Fervent tegenstander van het korps lasergamers.
TE kan je uitdrukken in Sin(alfa)+Cos(alfa), zie mijn eerdere reply.quote:
Ik heb alleen nog niet gevonden waarom CR = cosα + sinα - 1
Verder is heel de opgave me eigenlijk wel gelukt.
CR = TE - GF
GF = 1, dat is gegeven
Vergelijk de y-coordinaat van G eens met die van Cquote:
OF = sinα + cosα + 1
Lijkt me vrij helder.
∠GCR = π/2-α
DR' = QR = sin(π/2-α) = cos(α)
En dus
RH = sin(α)
En inderdaad
PQ = OF/GR * CR
GR = RH + GH = sin(α) + 1
En dan alleen CR nog ..
Hoi, ik heb weer een (waarschijnlijk niet al te snuggere) vraag.
Ik snap precies wat ze hier doen bij het oplossen van deze opgave, ik had echter een andere manier in mijn gedachte.
Ik zou beide grondtallen met 3 vermenigvuldigen zodat je vervolgens 3 (links) en 27 (rechts) als grondtal krijgt. Vervolgens wordt de uitdrukking rechts 3^((3)(14x-11)) en links gewoon 3^(x^(2)+27x-64).
Je komt wanneer je dit doet echter niet goed uit. Waar ga ik de fout in?
Alvast bedankt
Ik snap precies wat ze hier doen bij het oplossen van deze opgave, ik had echter een andere manier in mijn gedachte.
Ik zou beide grondtallen met 3 vermenigvuldigen zodat je vervolgens 3 (links) en 27 (rechts) als grondtal krijgt. Vervolgens wordt de uitdrukking rechts 3^((3)(14x-11)) en links gewoon 3^(x^(2)+27x-64).
Je komt wanneer je dit doet echter niet goed uit. Waar ga ik de fout in?
Alvast bedankt
Je maakt hier weer de bekende Pippi Langkous fout, en dat valt me wel van je tegen. Het is niet handig om allerlei extra onbekenden in te gaan voeren, en aangezien de lengtes van de zijden van twee gelijkvormige driehoeken evenredig met elkaar zijn en de uitdrukking voor PQ die je gevraagd wordt te bewijzen zich eenvoudig als een evenredigheid laat herschrijven, ligt het wel érg voor de hand gebruik te maken van evenredigheden.quote:
Ik heb een vraag over een vraagstuk waar ik eigenlijk nog niet klaar voor ben, maar ik wil een poging wagen. Gonio is een zwakke kant van mij, maar dat wil ik versterken.
Komt die: http://www2.cito.nl/vo/ex2013/VW-1025-a-13-1-o.pdf
Vraag 6
Welnu, we hebben ΔPQG ∼ ΔCRG zodat
(1) PQ : QG = CR : RG
Nu is QR = SC = cos α en RH = CT = sin α en HG = EF = 1, zodat
(2) QG = QR + RH + HG = cos α + sin α + 1
Verder is TB = cos α en BE = sin α en HE = GF = 1, zodat
(3) CR = TH = TE − HE = TB + BE − HE = cos α + sin α − 1
En tenslotte is
(4) RG = RH + HG = CT + HG = sin α + 1
Op grond van (1) t/m (4) hebben we dus
(5) PQ : (cos α + sin α + 1) = (cos α + sin α − 1) : (sin α + 1)
En dus
(6) PQ = ((cos α + sin α − 1)·(cos α + sin α + 1))/(sin α + 1)
QED
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |