SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Hoe vind je gemakkelijk de factoren van een getal?
Stel 75:
3,5 en 5 (priemgetallen)
Dan zijn de factoren dus 1, 75, 3, 25, 5 en 15.
Stel 1000:
2,2,2,5,5 en 5.
Hoe tel ik de factoren aan de hand van de priemgetallen?
Stel 75:
3,5 en 5 (priemgetallen)
Dan zijn de factoren dus 1, 75, 3, 25, 5 en 15.
Stel 1000:
2,2,2,5,5 en 5.
Hoe tel ik de factoren aan de hand van de priemgetallen?
Ik ga dit nog maar eens correct met limieten proberen op te schrijven. Een commentaar is dat ik onderscheid moet maken tussen de limx→∞ f(x) en limx→ -∞ f(x) en de limietvoorwaarde beter moet opschrijven.quote:
Kijk eens naar de Eulerfunctie. De Eulerfunctie geeft je alle getallen die copriem zijn met een getal. Daarvoor moet je wel de priemfactorontbinding weten. M.a.w. n - phi(n)quote:Op zondag 13 oktober 2013 17:29 schreef wiskundenoob het volgende:
Hoe vind je gemakkelijk de factoren van een getal?
Stel 75:
3,5 en 5 (priemgetallen)
Dan zijn de factoren dus 1, 75, 3, 25, 5 en 15.
Stel 1000:
2,2,2,5,5 en 5.
Hoe tel ik de factoren aan de hand van de priemgetallen?
[ Bericht 0% gewijzigd door #ANONIEM op 13-10-2013 17:34:14 ]
Ok, ik zal even kijken. Ik dacht dat je het kon uitrekenen met kansrekening(oid).quote:Op zondag 13 oktober 2013 17:32 schreef Amoeba het volgende:
[..]
Ik ga dit nog maar eens correct met limieten proberen op te schrijven. Een commentaar is dat ik onderscheid moet maken tussen de limx→∞ f(x) en limx→ -∞ f(x) en de limietvoorwaarde beter moet opschrijven.
[..]
Kijk eens naar de Eulerfunctie. De Eulerfunctie geeft je alle getallen die copriem zijn met een getal. Daarvoor moet je wel de priemfactorontbinding weten.
Ik moet even corrigeren. De Eulerfunctie geeft je de hoeveelheid getallen die copriem zijn met een getal.quote:Op zondag 13 oktober 2013 17:34 schreef wiskundenoob het volgende:
[..]
Ok, ik zal even kijken. Ik dacht dat je het kon uitrekenen met kansrekening(oid).
Bedoel je hiermee het aantal factoren dat een getal heeft? Dat is exact wat ik wil berekenen.quote:
[..]
Ik moet even corrigeren. De Eulerfunctie geeft je de hoeveelheid getallen die copriem zijn met een getal.
De Functie van Euler geeft het aantal getallen dat Relatief priem met een ander getal is (dus dat er geen getal is dat beide deelt). Dat is denk ik niet wat je zoekt.quote:
[..]
Bedoel je hiermee het aantal factoren dat een getal heeft? Dat is exact wat ik wil berekenen.
Tot zover wat ik weet. Nu even logisch nadenken. Als je het aantal getallen zoekt dat een ander getal deelt, kun je dat getal eerst ontbinden in priemfactoren. Je vindt dan een reeks priemgetallen. Deze kun je met elkaar vermenigvuldigen om factoren van dat getal te vinden. Dat kan op een aantal manieren. Je gaat kijken hoeveel combinaties er mogelijk zijn met deze rij getallen waarbij volgorde niet van invloed is. Dat klinkt als een combinatie, inderdaad kansrekening. Al een idee hoe je verder zou moeten?
Overigens kan ik er compleet naast zitten, correct me if I'm wrong. Ik heb dit nl. niet gehad, maar probeer te beredeneren wat het zou kunnen zijn.
EDIT: Misschien dacht ik iets te moeilijk. Als Phi(n) het aantal getallen is dat geen deler gemeenschappelijk heeft, en je zoekt het aantal getallen dat wel een of meerde priemfactoren gemeenschappelijk heeft (en dus het aantal delers)... En n is het totaal aantal mogelijke delers Kan je daar dan iets mee? Ik denk dat dat is wat Amoebe probeerde te zeggen met de n-Phi(n) waarmee hij zijn post eindigde.
[ Bericht 1% gewijzigd door Aardappeltaart op 13-10-2013 18:40:42 ]
Wat ik heb:
Dit is dan het maximale totale oppervlakte.
Als je ervan uitgaat dat één punt ook een kubus is:
Dit is dan het minimale totale oppervlakte.
Klopt dit? Of denk ik nu gewoon te simpel?
Gist is liefde, gist is leven. Vooral in een vagijn.
Mensen die denken dat ze te simpel denken denken denk ik helemaal niet.quote:
[ afbeelding ]
Klopt dit? Of denk ik nu gewoon te simpel?
Ik zie in je opgave helemaal niet staan dat beide kubussen even groot zijn. Begin daar maar eens over na te denken.
@rezania; begin met definieren x1 en x2 voor kubus 1 en 2. Druk x2 uit in x1 en het totale volume. Nu kun je een functie maken die het totale opp weergeeft, op basis van x1, bereken dan de lokale minima en maxima tussen x1 = 0..2000^1/3
http://www.wolframalpha.c(...)000%5E%281%2F3%29%29
http://www.wolframalpha.c(...)000%5E%281%2F3%29%29
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl
Dus gewoon normaal optimaliseren eigenlijk, ik wist wel dat ik te makkelijk dacht.quote:
@rezania; begin met definieren x1 en x2 voor kubus 1 en 2. Druk x2 uit in x1 en het totale volume. Nu heb je een functie, bereken dan de lokale minima en maxima tussen x1 = 0..2000^1/3
http://www.wolframalpha.c(...)000%5E%281%2F3%29%29
quote:
[..]
Mensen die denken dat ze te simpel denken denken denk ik helemaal niet.
Ik zie in je opgave helemaal niet staan dat beide kubussen even groot zijn. Begin daar maar eens over na te denken.
Gist is liefde, gist is leven. Vooral in een vagijn.
http://www.wikihow.com/Find-How-Many-Factors-Are-in-a-Numberquote:
Bedoel je hiermee het aantal factoren dat een getal heeft? Dat is exact wat ik wil berekenen.
Nee, ik denk dat ik het fout heb. Lees dat artikel van Tochjo even door.quote:
[..]
Bedoel je hiermee het aantal factoren dat een getal heeft? Dat is exact wat ik wil berekenen.
Ah natuurlijk, dat kan ook.quote:
[..]
http://www.wikihow.com/Find-How-Many-Factors-Are-in-a-Number
Waarom is n-Phi(n) het dan niet? In ieder geval is de manier van dat artikel van Tochjo toch wel makkelijker dan n-Phi(n) of het optellen van combinaties wat ik voorstelde...quote:
[..]
Nee, ik denk dat ik het fout heb. Lees dat artikel van Tochjo even door.
Ik denk inderdaad dat hij dit bedoelt. Hij wil het totaal aantal delers van een positief geheel getal bepalen. En dat heeft niets met kansrekening te maken.quote:
[..]
http://www.wikihow.com/Find-How-Many-Factors-Are-in-a-Number
Voorbeeld: bereken het aantal delers van 1000.
Antwoord: we ontbinden 1000 eerst in priemfactoren. Dit geeft
1000 = 23·53
Het aantal delers van 1000 is dus (3 + 1)·(3 + 1) = 16.
Controle: de delers van 1000 zijn
1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000.
16 stuks inderdaad.
Stom hoor, uiteindelijk kom je gewoon weer op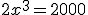 
uit en blijkt mijn vermoeden dus gewoon te kloppen.
Gist is liefde, gist is leven. Vooral in een vagijn.
Klopt helemaal, maar ja, als je alles met vermoedens aan kon tonen zou het geen wiskundetopic zijn he 
.
.
Zin in pizza? Simpel pizzarecept - Uitgebreid pizzarecept! - DIY pizzaschep - Bestron Alfredo Tuning - kookkompas.nl
Helaas niet nee.quote:
Klopt helemaal, maar ja, als je alles met vermoedens aan kon tonen zou het geen wiskundetopic zijn he
Gist is liefde, gist is leven. Vooral in een vagijn.
Niets stoms aan, vermoedens die je uit moet je wel kunnen bewijzen (of weerleggen natuurlijk).quote:
Stom hoor, uiteindelijk kom je gewoon weer op
Maar als dit vermoeden als stelling zou bestaan mocht je er toch wel gewoon vanuit gaan en was mijn eerste uitwerking correct?quote:
[..]
Niets stoms aan, vermoedens die je uit moet je wel kunnen bewijzen (of weerleggen natuurlijk).
Gist is liefde, gist is leven. Vooral in een vagijn.
Nee, zelf dat mag niet. Zoiets noemen ze een petitio principii, en dat is een doodzonde.quote:
[..]
Maar als dit vermoeden als stelling zou bestaan mocht je er toch wel gewoon vanuit gaan en was mijn eerste uitwerking correct?
phi(1000) = 400quote:
[..]
Ah natuurlijk, dat kan ook.
[..]
Waarom is n-Phi(n) het dan niet? In ieder geval is de manier van dat artikel van Tochjo toch wel makkelijker dan n-Phi(n) of het optellen van combinaties wat ik voorstelde...
1000 - 400 = 600
Dat is heel wat meer dan 16.
Misschien weet Riparius dat. Hoe druk je het aantal delers van 1000 uit als een vergelijking met daarin de eulerfunctie, of kan dit niet?
Of algemeen, het aantal delers van een integer getal n.
[ Bericht 13% gewijzigd door #ANONIEM op 13-10-2013 19:34:32 ]
Of algemeen, het aantal delers van een integer getal n.
[ Bericht 13% gewijzigd door #ANONIEM op 13-10-2013 19:34:32 ]
Maar waarom mag het dan bij meetkundig bewijzen wel? Daar moet je toch ook iets aantonen?quote:
[..]
Nee, zelf dat mag niet. Zoiets noemen ze een petitio principii, en dat is een doodzonde.
Gist is liefde, gist is leven. Vooral in een vagijn.
Lijkt me genoeg tegenbewijs ja, dankjewel. Interessante vraag of en hoe het wel zou kunnen, ik ben benieuwd!quote:
[..]
phi(1000) = 400
1000 - 400 = 600
Dat is heel wat meer dan 16.
Stellingen die je zelf bewezen hebt of bijvoorbeeld in de les bewezen zijn mag je gebruiken. Anderen niet. Toch?quote:
[..]
Maar waarom mag het dan bij meetkundig bewijzen wel? Daar moet je toch ook iets aantonen?
Ik denk dat jij een heel verkeerde voorstelling hebt van wat nu een wiskundig bewijs is. Je mag datgene wat je wil bewijzen nooit voor waar aannemen, want dan bewijs je uiteindelijk niets. Je ziet vaak dat mensen hiermee de mist in gaan als ze een bewijs met (volledige) inductie moeten geven.quote:
[..]
Maar waarom mag het dan bij meetkundig bewijzen wel? Daar moet je toch ook iets aantonen?
Ah ja, dan krijg je inderdaad een cirkelredenering.quote:
[..]
Ik denk dat jij een heel verkeerde voorstelling hebt van wat nu een wiskundig bewijs is. Je mag datgene wat je wil bewijzen nooit voor waar aannemen, want dan bewijs je uiteindelijk niets. Je ziet vaak dat mensen hiermee de mist in gaan als ze een bewijs met (volledige) inductie moeten geven.
Gist is liefde, gist is leven. Vooral in een vagijn.
Dat is inderdaad de gangbare Nederlandse term voor een petitio principii. Heb je deze limiet nog uitgewerkt?quote:
[..]
Ah ja, dan krijg je inderdaad een cirkelredenering.
Nee, ik liep op een gegeven moment steeds vast op die noemer en daarna heb ik er geen tijd meer aan besteed. Ik had andere prioriteiten.quote:
[..]
Dat is inderdaad de gangbare Nederlandse term voor een petitio principii. Heb je deze limiet nog uitgewerkt?
Gist is liefde, gist is leven. Vooral in een vagijn.
Hint: herschrijf de noemer alsquote:
[..]
Nee, ik liep op een gegeven moment steeds vast op die noemer en daarna heb ik er geen tijd meer aan besteed. Ik had andere prioriteiten.
x3·x−1·log(1 + x) = x3·log(1 + x)1/x
en gebruik dat
limx→0 (1 + x)1/x = e
zodat
limx→0 log(1 + x)1/x = log e = 1
Misschien morgen, ben voor vandaag wel klaar met wiskunde.quote:
[..]
Hint: herschrijf de noemer als
x3·x−1·log(1 + x) = x3·log(1 + x)1/x
en gebruik dat
limx→0 (1 + x)1/x = e
zodat
limx→0 log(1 + x)1/x = log e = 1
Gist is liefde, gist is leven. Vooral in een vagijn.
Het gaat uiteraard ook eenvoudig als je de formele definitie van een limiet en wat rekenregels voor limieten gebruikt. Voor k = 1 .. n heb jequote:
[..]
Ik ga dit nog maar eens correct met limieten proberen op te schrijven. Een commentaar is dat ik onderscheid moet maken tussen de limx→∞ f(x) en limx→ -∞ f(x) en de limietvoorwaarde beter moet opschrijven.
limx→∞ (an−k/an)x−k = 0
en
limx→−∞ (an−k/an)x−k = 0
(Bewijs dit aan de hand van de formele definitie van deze limieten). Aangezien de limiet van een som gelijk is aan de som van de limieten van de termen (mits deze bestaan) volgt dan direct dat
limx→∞ f(x) = 0
en
limx→−∞ f(x) = 0
In overeenstemming met de definitie van deze limieten bestaan er nu getallen X1, X2 ∈ R zodanig dat
|f(x)| < 1 voor x > X1
en
|f(x)| < 1 voor x < X2
Kies nu X0 = max(|X1|, |X2|), dan is X0 ≥ X1 en tevens −X0 ≤ X2 zodat |f(x)| < 1 voor |x| > X0.
Nog een vraagje over integreren:
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
Deze opgave komt me heel bekend voor. Toevallig ook econometrie?quote:
Nog een vraagje over integreren:
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
delers = factoren?quote:
[..]
Ik denk inderdaad dat hij dit bedoelt. Hij wil het totaal aantal delers van een positief geheel getal bepalen. En dat heeft niets met kansrekening te maken.
Voorbeeld: bereken het aantal delers van 1000.
Antwoord: we ontbinden 1000 eerst in priemfactoren. Dit geeft
1000 = 23·53
Het aantal delers van 1000 is dus (3 + 1)·(3 + 1) = 16.
Controle: de delers van 1000 zijn
1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000.
16 stuks inderdaad.
Of is er een verschil tussen NL en ENG?
Ja, jij weet niet toevallig hoe die moet?quote:Op zondag 13 oktober 2013 21:58 schreef Ensemble het volgende:
[..]
Deze opgave komt me heel bekend voor. Toevallig ook econometrie?
Nee, die lukte bij mij ook niet. Ook de practicumdocent kon hem niet uitleggen.quote:
[..]
Ja, jij weet niet toevallig hoe die moet?
Dus ben wel benieuwd hoe die moet.
Ik had trouwens precies hetzelfde als wat jij had.
Die docent moet eens wat creatiever worden. Het gaat uiteraard via partieel integreren, maar ook als je dat niet mag gebruiken en het uitsluitend via substitutie moet is het te doen. We gaan eerst de integrand een beetje herleiden.quote:Op zondag 13 oktober 2013 22:09 schreef Ensemble het volgende:
[..]
Nee, die lukte bij mij ook niet. Ook de practicumdocent kon hem niet uitleggen.
Dus ben wel benieuwd hoe die moet.
Ik had trouwens precies hetzelfde als wat jij had.
x(2x + 5)8 = ½·[2x(2x + 5)8] = ½·[(2x + 5 − 5)(2x + 5)8] = ½·[(2x + 5)(2x + 5)8 − 5(2x + 5)8] = ½·[(2x + 5)9 − 5(2x + 5)8] = ½·(2x + 5)9 − (5/2)·(2x + 5)8
Nu hebben we dus
∫ x(2x + 5)8dx = ∫ (½·(2x + 5)9 − (5/2)·(2x + 5)8)dx
Nu substitueren we
u = 2x + 5
zodat
du/dx = 2
en dus
dx = ½·du
Dan hebben we
∫ (½·(2x + 5)9 − (5/2)·(2x + 5)8)dx = ∫ (¼·u9 − (5/4)·u8)du = (1/40)·u10 − (5/36)·u9 + C = (1/40)·(2x + 5)10 − (5/36)·(2x + 5)9 + C
Deze uitkomst kunnen we weer herleiden door een factor (2x + 5)9 buiten haakjes te halen, en dan krijgen we uiteindelijk
∫ x(2x + 5)8dx = (2x + 5)9((1/20)·x − 1/72) + C
Edit: zoals hier terecht is opgemerkt is het nog veel eenvoudiger om te bedenken dat de substitutie u = 2x + 5 equivalent is met x = ½u − 5/2, waarmee direct ∫ (¼·u9 − (5/4)·u8)du wordt verkregen.
[ Bericht 26% gewijzigd door Riparius op 14-10-2013 23:25:38 ]
Gewoon productregel + kettingregel lijkt me?quote:
Nog een vraagje over integreren:
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
Met functie (1)=x en functie (2)=(2x+5)^8
En dan bij functie (2) de kettingregel toepassen.
Volgens de Nederlandse Wikipedia zijn deler en factor synoniemen.quote:
[..]
delers = factoren?
Of is er een verschil tussen NL en ENG?
Als je gaat differentiëren moet dat, of begrijp ik je niet goed?quote:
[..]
Gewoon productregel + kettingregel lijkt me?
Met functie (1)=x en functie (2)=(2x+5)^8
En dan bij functie (2) de kettingregel toepassen.
Oh ok nvm. Denk inderdaad dat die regels dan niet gelden voor integreren dan. Ik dacht ff een slim antwoord te gevenquote:
[..]
Als je gaat differentiëren moet dat, of begrijp ik je niet goed?
doe eensquote:
Nog een vraagje over integreren:
Hoe moet deze integraal met de substitutieregel:
x(2x+5)^8
Zelf:
U=2x+5
du=2
dx=0,5xdu
dan
0,5x(u)^8
Maar dit kan volgensmij niet want x en u door elkaar?
u = 2x + 5
du = 2dx
x = (u-5)/2
dan ∫x(2x+5)8dx = 1/4 ∫ (u-5)u8du
= 1/4(u10/10 - 5/9 u9) + C = u10/40 - 5/36 u9 + C
En dan x terug substitueren en je bent klaar.
= (2x+5)10/40 - 5/36 (2x+5)9 + C
[ Bericht 3% gewijzigd door #ANONIEM op 13-10-2013 22:55:30 ]
Ik vind dit heel moeilijk, maar ik heb -zonder te spieken- een poging gedaan.quote:
[..]
Het gaat uiteraard ook eenvoudig als je de formele definitie van een limiet en wat rekenregels voor limieten gebruikt. Voor k = 1 .. n heb je
limx→∞ (an−k/an)x−k = 0
en
limx→−∞ (an−k/an)x−k = 0
(Bewijs dit aan de hand van de formele definitie van deze limieten).
f(x) = x-k met k ∈ N
dan
limx→∞ f(x) =0
als ∀ε>0∃x: [|f(x)| < ε] ,
dus |x-k| < ε
en
-ε < x-k < ε
voor x ≥ 1 geldt
0 ≤ x-k ≤ 1/x
dus -ε < 1/x
Dus kies x > -1/ε
En dan zit ik vast. Ik vind dit echt heel lastig. Ik moet een fout maken hierboven, maar waar zit die zonder dat je het hele bewijs hier neerknalt?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Zo gaat het ook inderdaad, maar ik vond mijn manier toch sneller.
[ Bericht 0% gewijzigd door #ANONIEM op 13-10-2013 23:51:19 ]
voor hierboven gekozen x
|x-k| < ε
geeft
|(-1/ε)-k| < ε
1/ε > 0, dus
|(-1/ε)-k| = |(1/ε)-k| = |εk| < ε
Lijkt me ook onzin.
[ Bericht 19% gewijzigd door #ANONIEM op 14-10-2013 00:02:09 ]
|x-k| < ε
geeft
|(-1/ε)-k| < ε
1/ε > 0, dus
|(-1/ε)-k| = |(1/ε)-k| = |εk| < ε
Lijkt me ook onzin.
[ Bericht 19% gewijzigd door #ANONIEM op 14-10-2013 00:02:09 ]
Het helpt wel als je de formele definitie van limx→∞ f(x) = 0 correct opschrijftquote:
[..]
Ik vind dit heel moeilijk, maar ik heb -zonder te spieken- een poging gedaan.
f(x) = x-k met k ∈ N
dan
limx→∞ f(x) =0
als ∀ε>0∃x: [|f(x)| < ε] ,
∀ε>0 ∃X∈R ∀x>X [ |f(x)| < ε ]
[snip]
Je maakte geen onderscheid tussen X en x. Voor elke ε > 0 moet er een X ∈ R bestaan zodanig dat voor elke x > X geldt |f(x)| < ε. Je moet dus een existentiebewijs leveren, en in het algemeen doe je dat bij een limiet als deze door te laten zien dat je voor elke ε > 0 zo'n X kunt construeren. Hier kun je gebruik maken van het feit dat x−k ≤ x−1 voor x ≥ 1 en k ≥ 1, maar dat hoeft niet.quote:En dan zit ik vast. Ik vind dit echt heel lastig. Ik moet een fout maken hierboven, maar waar zit die zonder dat je het hele bewijs hier neerknalt?
quote:Ja. Ik had er even niet bij stilgestaan dat je een lineaire substitutie gemakkelijk kunt inverteren.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Zo gaat het ook inderdaad, maar ik vond mijn manier toch sneller.
Dank. Ik ga hier morgenvroeg nog even over peinzen.quote:
[..]
Het helpt wel als je de formele definitie van limx→∞ f(x) = 0 correct opschrijft
∀ε>0 ∃X∈R ∀x>X [ |f(x)| < ε ]
[snip]
[..]
Je maakte geen onderscheid tussen X en x. Voor elke ε > 0 moet er een X ∈ R bestaan zodanig dat voor elke x > X geldt |f(x)| < ε. Je moet dus een existentiebewijs leveren, en in het algemeen doe je dat bij een limiet als deze door te laten zien dat je voor elke ε > 0 zo'n X kunt construeren. Hier kun je gebruik maken van het feit dat x−k ≤ x−1 voor x ≥ 1 en k ≥ 1, maar dat hoeft niet.
[..]
Ja. Ik had er even niet bij stilgestaan dat je een lineaire substitutie gemakkelijk kunt inverteren.
Maakt wolfram hier een dikke fout? -5(1+√2), 5(√2 -1)= -5+/- 5√2
[ Bericht 60% gewijzigd door wiskundenoob op 14-10-2013 19:45:14 ]
[ Bericht 60% gewijzigd door wiskundenoob op 14-10-2013 19:45:14 ]
Daar twijfel ik ten zeerste aan. Wat is je vergelijking precies, want dat is weer eens bepaald niet helder.Zoiets?quote:
Maakt wolfram hier een dikke fout? -5(1+√2), 5(√2 -1)= -5+/- 5√2
-5(1+√2), 5(√2 -1) = (-5-5√2), (5√2 -5)= -5+/- 5√2
[ Bericht 5% gewijzigd door #ANONIEM op 14-10-2013 20:07:01 ]
Ja, die vergelijking bedoel ik.quote:
[..]
Daar twijfel ik ten zeerste aan. Wat is je vergelijking precies, want dat is weer eens bepaald niet helder.Zoiets?
-5(1+√2), 5(√2 -1) = (-5-5√2), (-5+5√2 )= -5+/- 5√2
Laat maar ik zie het al.
[ Bericht 6% gewijzigd door wiskundenoob op 14-10-2013 20:32:11 ]
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |