SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Game onquote:Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
quote:Op donderdag 3 oktober 2013 22:57 schreef Johan_Haas_ het volgende:
(1-Y) * (ph/ (1-ph*HB) = Y* 1/HB Hoe vereenvoudig je dit door HB de functie te maken van Ph
Hoe kom je op HB = Y/ PH.
(1-y) * ph/(1-phHB)= y 1/Hb
Kan iemand me de stappen laten zien? Hoe kan ik breuken laten zien op het forum ?
Zo zou ik het in ieder geval doen.quote:
Stap drie is misschien niet helemaal netjes/duidelijk, ik heb daar Y meteen vermenigvuldigd met 1 - phHB.
Als je, zoals je zegt, bijvoorbeeld breuken wilt laten zien, dan kan je gebruik maken van de [tex][/tex] tags. Uitleg over wat je er zoal mee kunt, kun je in de link in de OP vinden.
[ Bericht 3% gewijzigd door jordyqwerty op 03-10-2013 23:42:42 ]
Snap alleen stap 1 naar 2 niet Voor de duidelijkheid 1 is de beginformule die naar 3 moet worden herleid
1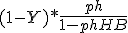
= 
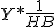
2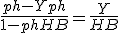
Wat doe je in deze stap?
Hardstikke bedankt trouwens! De breuken werken ook makkelijk hier
3 Uiteindelijke oplossing
HB =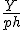
1
2
Wat doe je in deze stap?
Hardstikke bedankt trouwens! De breuken werken ook makkelijk hier
3 Uiteindelijke oplossing
HB =
a(1-b) = a-abquote:
Snap alleen stap 1 naar 2 niet
1
2
Wat doe je in deze stap?
Hardstikke bedankt trouwens!
Je vermenigvuldigd de termen met de teller.quote:
Snap alleen stap 1 naar 2 niet
1
2
Wat doe je in deze stap?
Hardstikke bedankt trouwens!
Voorbeelden ter illustratie;
Bedankt, snap het Nooit geweten dat dat zomaar kon, heb het met getallen nagerekend en het kan inderdaad gewoon en het klopt. Ik moet meer die ab regeltjes oefenen met breuken
Nooit geweten dat dat zomaar kon, heb het met getallen nagerekend en het kan inderdaad gewoon en het klopt. Ik moet meer die ab regeltjes oefenen met breuken
Hoe gaat deze kom hier na lang proberen niet uit. solving voor Ht+1
1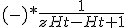
+ 
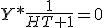
2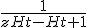
= 
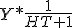
3 =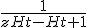 
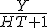
Hoe nu verder, stap 2 en 3 heb ik zelf gedaan. Als ik noemer nou gelijk maak, dus ZhT en - naar rechtsboven sleep, ?
Ga nu slapen en erover nadenken
uitkomst moet zijn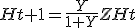
1
2
3
Hoe nu verder, stap 2 en 3 heb ik zelf gedaan. Als ik noemer nou gelijk maak, dus ZhT en - naar rechtsboven sleep, ?
Ga nu slapen en erover nadenken
uitkomst moet zijn
Dit is niet al te moeilijk om met de hand uit te rekenen. Als je het op een andere manier wilt doen, kan je gebruiken dat:quote:
2 23 > 3 13?
Hoe los je zoiets op zonder GR?
22 ≈ 31, maar
22 > 31, want 4 > 3 (1)
23 ≈ 32, maar
23 < 32, want 8 < 9 (2)
Met deze ongelijkheden kunnen we 'grotere' ongelijkheden makkelijk aantonen: als we bijvoorbeeld de eerste ongelijkheid tot de macht 10 nemen krijgen we de gelijkheid 220 > 310. Het verschil tussen deze twee gelijkheden is blijkbaar te groot, het lukt niet om 223 > 313 of 223 < 313 te laten zien. We hebben blijkbaar soortgelijke ongelijkheden nodig waar de twee- en de driemacht dichten bij elkaar zitten. Deze kunnen we proberen te maken door de al gevonden gelijkheden met elkaar te vermenigvuldigen:
We kunnen proberen de twee- en de driemacht dicht bij elkaar te krijgen door met ongelijkheid (1) te vermenigvuldigen als we een ongelijkheid van de vorm 2x < 3y hebben, en met ongelijkheid (2) als we een ongelijkheid van de vorm 2x > 3y hebben. We moeten de getallen 2x en 3y dan wel met de hand uitwerken, totdat we een combinatie van ongelijkheden vinden waaruit we 223 > 313 of 223 < 313 kunnen bewijzen.
Zo vinden we:
25 = 32 > 27 = 33 (3)
28 = 256 > 243 = 35 (4)
en omdat 23 = 8 + 8 + 5 + 2
kunnen we door ongelijkheid (4) achtereenvolgens te vermenigvuldigen met ongelijkheid (4), (3) en tenslotte (1), vinden:
223 > 314, wat nog een sterker resultaat is dan 223 > 313
(merk op: als a > b en c > d en a, b, c, d > 0, dan ac > bd. Dit bedoel ik met 'twee ongelijkheden vermenigvuldigen')
Dit is de enige manier die ik zo kan bedenken, en ik weet niet of dit echt veel makkelijker is dan gewoon de getallen uitrekenen. Het is wel zo dat hoe groter het verschil, hoe makkelijker de ongelijkheid aan is te tonen. (24 < 3100 is bijvoorbeeld door alleen formule (2) te gebruiken aan te tonen)
[ Bericht 4% gewijzigd door randomo op 05-10-2013 16:29:41 ]
Tja, da's een leuke. Ik zou het als volgt doen. Je weet dat √2 = 21/2 tussen 1,4 en 1,5 ligt, want 1,42 = 1,96 terwijl 1,52 = 2,25. Verder weet je ook dat √3 = 31/2 tussen 1,7 en 1,8 ligt, want 1,72 = 2,89 terwijl 1,82 = 3,24.quote:
2 23 > 3 13?
Hoe los je zoiets op zonder GR?
Nu heb je ook
25/2 = 22·21/2 = 4·21/2
en
33/2 = 31·31/2 = 3·31/2
Dus weten we nu dat
5,6 < 25/2 < 6,0
en
5,1 < 33/2 < 5,4
zodat
25/2 > 33/2
Hieruit volgt dat ook
(25/2)9 > (33/2)9
oftewel
222,5 > 313,5
En aangezien
223 > 222,5
heb je dus ook
223 > 313,5
En omdat ook
313,5 > 313
volgt dus inderdaad dat
223 > 313
QED
Nee. En weet je hoe dat komt? Omdat je geen flauw idee hebt van het rekenen met breuken. Dat had je op de lagere school moeten leren, maar dat is kennelijk - om welke reden dan ook - niet gebeurd. Ga daarom eerst deze cursus eens compleet doorwerken. Pas daarna heeft het zin om verder te gaan.quote:
Hoe gaat deze kom hier na lang proberen niet uit.
Ik volg de bèta topics nu al een aantal jaren, en ik denk altijd dat het niet gekker kan worden, maar ik moet spijtig genoeg steeds constateren dat ik me vergis. Wat je hier zegt is iets wat alleen de huidige sleep- en klikgeneratie zou kunnen bedenken.quote:Hoe nu verder, stap 2 en 3 heb ik zelf gedaan. Als ik noemer nou gelijk maak, dus ZhT en - naar rechtsboven sleep, ?
Nou nee. Je negeert om te beginnen het onderscheid tussen hoofdletters en kleine letters, en verder heb je kennelijk ook niet in de gaten dat de t hier zo te zien een index of parameter is en dat het er om gaat Ht+1 uit te drukken in Ht.quote:uitkomst moet zijn
Ik bedacht nadat ik jouw uiteenzetting had gelezen dat je hebt 25 > 33 dus (25)23/5 > (33)23/5 oftewel 223 > 313,8 > 313, QED. Nog eenvoudiger zal moeilijk gaan en dit is toch echt veel gemakkelijker dan uitrekenen.quote:
[..]
Dit is de enige manier die ik zo kan bedenken, en ik weet niet of dit echt veel makkelijker is dan gewoon de getallen uitrekenen.
Dat is wel een mooie ja! Om de een of andere reden dacht ik dat het makkelijker zou worden als ik alleen gehele getallen zou gebruiken, maar dat valt dus vies tegenquote:
[..]
Ik bedacht nadat ik jouw uiteenzetting had gelezen dat je hebt 25 > 33 dus (25)23/5 > (33)23/5 oftewel 223 > 313,8 > 313, QED. Nog eenvoudiger zal moeilijk gaan en dit is toch echt veel gemakkelijker dan uitrekenen.
Maar goed, die 223 en 313 uitrekenen is natuurlijk gewoon het simpel toepassen van een algoritme, terwijl het maar de vraag is of het afleiden van zoiets snel en elegant lukt.
Vast erg simpel tussen dit, maar:
stel ik heb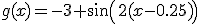
en ik moet aangeven hoe die uit de standaardgrafiek ontstaat
maakt het dan uit of ik eerst transleer of vermenigvuldig?
stel ik heb
maakt het dan uit of ik eerst transleer of vermenigvuldig?
De volgorde is niet bijzonder van belang zover ik weet, zolang je maar consistent bent zou ik zeggen.
Persoonlijk zou ik gaan voor sin(x)->sin(2x)->sin(2x-0.5)->sin(2x-0.5)-3
Dus een sinus die eerst 2 keer zo dun is, daarna een faseverschuiving ziet (ipv 0,0 zit het nulpunt op 0.5,0) Vervolgens schop je het hele ding drie omlaag.
Persoonlijk zou ik gaan voor sin(x)->sin(2x)->sin(2x-0.5)->sin(2x-0.5)-3
Dus een sinus die eerst 2 keer zo dun is, daarna een faseverschuiving ziet (ipv 0,0 zit het nulpunt op 0.5,0) Vervolgens schop je het hele ding drie omlaag.
Voor kleine exponenten lukt dit zeker. Voor m,n > 0 heb je immers 2m > 3n als m/n > log(3)/log(2) ≈ 1,585, dus is m = 5, n = 3 een goede keuze, want dan is m/n = 5/3 ≈ 1,667. En een hele goede keuze is dan m = 8, n = 5, want dan is m/n = 8/5 = 1,6. Maar het wordt lastiger bij grote exponenten en als de waarden van de machten dichter bij elkaar liggen. Als je uitsluitend met pen en papier zou willen nagaan of bijvoorbeeld 23162 nu groter of kleiner is dan 31995 dan zijn zelfs opa's logaritmentafels in vijf decimalen niet meer toereikend. En ik hoop niet dat je nu het advies blijft geven om het dan maar met de hand uit te rekenen omdat het algoritme zo lekker simpel is.quote:
[..]
Dat is wel een mooie ja! Om de een of andere reden dacht ik dat het makkelijker zou worden als ik alleen gehele getallen zou gebruiken, maar dat valt dus vies tegen
Maar goed, die 223 en 313 uitrekenen is natuurlijk gewoon het simpel toepassen van een algoritme, terwijl het maar de vraag is of het afleiden van zoiets snel en elegant lukt.
Ik weet niet wat je bedoelt met transleer/vermenigvuldig. Maar ik zou denken:quote:
Vast erg simpel tussen dit, maar:
stel ik heb
maakt het dan uit of ik eerst transleer of vermenigvuldig?
normale sin: f(x)=sin(x).
-3 betekent dat je evenwichtslijn bij -3 ligt. Dus als je +3 doet heb je sin(2(x-0.25)). Ik zie trouwens niet wat je hebt staan voor je amplitude. Die 2 geeft aan dat je grafiek/figuur naar links is gegaan met 2. Die -.25 betekent dat je grafiek naar rechts is gegaan met 0.25. Dus als je rekent met radialen/graden/etc kun je aangeven hoe die uit de normale grafiek is gekomen.
Ik geloof dat je dan de volgende variabele krijgt:
a= hier komt je amplitude, maar dit weet ik even niet...
b= -3 dit is de waarde voor je evenwichtslijn
c= 2pi/2 voor het verschuiven van de grafiek/dit heeft met de periode van je grafiek te maken, dus in jouw geval is pi 1 periode in je sinusgrafiek.
d=-.25 dit is de verschuiving naar rechts.
Riparius/Bram/iemand, kun jij mij verbeteren? Dit is training voor mezelf zodat ik de stof beter begrijp.
Amplitude is 1, immers de sinus zelf wordt nergens mee vermenigvuldigdquote:
Ik weet niet wat je bedoelt met transleer/vermenigvuldig. Maar ik zou denken:
Dat ligt eraan welke variable je voor welk aspect van zo'n sinusfunctie definieert. Het algemene geval wordt beschreven door f(x)=a+b*sin(c(x+d)). Hierin is:quote:
[..]
Ik weet niet wat je bedoelt met transleer/vermenigvuldig. Maar ik zou denken:
normale sin: f(x)=sin(x).
-3 betekent dat je evenwichtslijn bij -3 ligt. Dus als je +3 doet heb je sin(2(x-0.25)). Ik zie trouwens niet wat je hebt staan voor je amplitude. Die 2 geeft aan dat je grafiek/figuur naar links is gegaan met 2. Die -.25 betekent dat je grafiek naar rechts is gegaan met 0.25. Dus als je rekent met radialen/graden/etc kun je aangeven hoe die uit de normale grafiek is gekomen.
Ik geloof dat je dan de volgende variabele krijgt:
a= hier komt je amplitude, maar dit weet ik even niet...
b= -3 dit is de waarde voor je evenwichtslijn
c= 2pi/2 voor het verschuiven van de grafiek/dit heeft met de periode van je grafiek te maken, dus in jouw geval is pi 1 periode in je sinusgrafiek.
d=-.25 dit is de verschuiving naar rechts.
Riparius/Bram/iemand, kun jij mij verbeteren? Dit is training voor mezelf zodat ik de stof beter begrijp.
a = de verschuiving langs de y-as.
d = de verschuiving langs de x-as. LET OP!!: De eigenlijke verschuiving is het tegengestelde van de waarde d, oftewel, exact de andere kant van de x-as op.
b = de expansiefactor in de y-richting a.k.a. de verticale richting.
c = de, let op nu, compressiefactor in de x-richting a.k.a. de horizontale richting. Net als de parameter d in dezen is het effect op de grafiek exact het tegenovergestelde van de waarde b (compressie ipv van expansie met factor c).
EDIT: Ja die dubbele haken zijn belangrijk!! Vergelijk de translatie van sin(x+½π) tov sin(x) vergeleken met sin(2x+½π) tov sin(2x). De eerste twee zijn verschoven van elkaar met translatie T:(-½π,0,0), de laatste twee met translatie T:(-¼π,0,0). Dit omdat het argument (2x+½π) te schrijven valt als (2(x+¼π)).
[ Bericht 1% gewijzigd door VanishedEntity op 09-10-2013 19:50:00 ]
a = evenwichtsstand en dat is -3quote:
[..]
Ik weet niet wat je bedoelt met transleer/vermenigvuldig. Maar ik zou denken:
normale sin: f(x)=sin(x).
-3 betekent dat je evenwichtslijn bij -3 ligt. Dus als je +3 doet heb je sin(2(x-0.25)). Ik zie trouwens niet wat je hebt staan voor je amplitude. Die 2 geeft aan dat je grafiek/figuur naar links is gegaan met 2. Die -.25 betekent dat je grafiek naar rechts is gegaan met 0.25. Dus als je rekent met radialen/graden/etc kun je aangeven hoe die uit de normale grafiek is gekomen.
Ik geloof dat je dan de volgende variabele krijgt:
a= hier komt je amplitude, maar dit weet ik even niet...
b= -3 dit is de waarde voor je evenwichtslijn
c= 2pi/2 voor het verschuiven van de grafiek/dit heeft met de periode van je grafiek te maken, dus in jouw geval is pi 1 periode in je sinusgrafiek.
d=-.25 dit is de verschuiving naar rechts.
Riparius/Bram/iemand, kun jij mij verbeteren? Dit is training voor mezelf zodat ik de stof beter begrijp.
b= amplitude en dat is 1
c = periode = 2pi/2= pi
d= beginpunt = 1/4
maar dat was niet de vraag, vraag was om aan te tonen hoe de grafiek ontstaat uit de standaardgrafiek y=sin(x). (dus via pijltjes de transformaties aantonen)
Je hebtquote:
[..]
a = evenwichtsstand en dat is -3
b= amplitude en dat is 1
c = periode = 2pi/2= pi
d= beginpunt = 1/4
maar dat was niet de vraag, vraag was om aan te tonen hoe de grafiek ontstaat uit de standaardgrafiek y=sin(x). (dus via pijltjes de transformaties aantonen)
f(x) = sin(x)
en g(x) = -3 + sin(2x - 1/2)
Eerst transleer je de grafiek nog over (1/2, -3), en dan vermenigvuldig je f(x) t.o.v. de y-as met 1/2. Dat is dan g(x).
[ Bericht 6% gewijzigd door #ANONIEM op 08-10-2013 20:40:03 ]
Voor welke waarde van q (uitgedrukt in r) is de onderstaande functie f(a, b) homogeen en wat is
de bijbehorende graad?
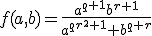
Ik heb geen idee hoe ik dit aan moet pakken, stel ik vul in (ta,tb):
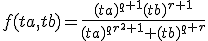
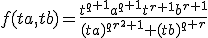
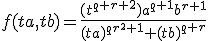
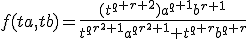
Verder (mocht dit goed zijn) kom ik niet. Iemand die me (verder) op weg kan helpen?
de bijbehorende graad?
Ik heb geen idee hoe ik dit aan moet pakken, stel ik vul in (ta,tb):
Verder (mocht dit goed zijn) kom ik niet. Iemand die me (verder) op weg kan helpen?
Kijk eerst eens naar de noemer. Dat is een homogeen polynoom alsquote:Op woensdag 9 oktober 2013 16:22 schreef jordyqwerty het volgende:
Voor welke waarde van q (uitgedrukt in r) is de onderstaande functie f(a, b) homogeen en wat is
de bijbehorende graad?
qr2 + 1 = q + r
Wat vind je dan voor q uitgedrukt in r?
qr2 + 1 = q + r
qr2 -q = r - 1
q(r2-1) = r - 1
q = (r-1)/(r2-1)
Begrijp ik goed dat als q deze 'waarde' heeft, de noemer dan homogeen is?
qr2 -q = r - 1
q(r2-1) = r - 1
q = (r-1)/(r2-1)
Begrijp ik goed dat als q deze 'waarde' heeft, de noemer dan homogeen is?
Ja, dan is de noemer uiteraard een homogeen polynoom in a en b, want dan zijn de termen toch van dezelfde graad? En dan ga je vervolgens naar de teller kijken. Maar vóór je dit doet moet je eerst de waarde die je voor q hebt gevonden nog verder herleiden.quote:
qr2 + 1 = q + r
qr2 -q = r - 1
q(r2-1) = r - 1
q = (r-1)/(r2-1)
Begrijp ik goed dat als q deze 'waarde' heeft, de noemer dan homogeen is?
1/(r+1) ?quote:
[..]
Ja, dan is de noemer uiteraard een homogeen polynoom in a en b, want dan zijn de termen toch van dezelfde graad? En dan ga je vervolgens naar de teller kijken. Maar vóór je dit doet moet je eerst de waarde die je voor q hebt gevonden nog verder herleiden.
Inderdaad. En als je nu q = 1/(r + 1) invult, wat wordt dan de graad van de term in de teller en wat is dan de graad van het polynoom in de noemer? Dus wat kun je nu zeggen over f(a,b) ?quote:
Die is er zeker, volgens mij in het MATH menu en dan FRAC (bij de TI-84)quote:
Vraag over gr,
is er een mode waarin je het antwoord ziet in breuken i.p.v. decimalen?
Dank je man!quote:
[..]
Die is er zeker, volgens mij in het MATH menu en dan FRAC (bij de TI-84)
Als je stelt dat qr2 +1 = q + r, mag je dan ook zeggen dat de graad van homogeniteit twee is? Tenzij r = 1 of -1quote:
[..]
Inderdaad. En als je nu q = 1/(r + 1) invult, wat wordt dan de graad van de term in de teller en wat is dan de graad van het polynoom in de noemer? Dus wat kun je nu zeggen over f(a,b) ?
Homogeniteit is eigenlijk toch gewoon als een functie volledig uit één macht bestaat? Bijvoorbeeld f(x) = 3x + 5x dan is hij homogeen met graad 1 en f(x) 3x^5 + 5x^5 dan is hij homogeen met graad 5?
In die gevallen wel jaquote:
Homogeniteit is eigenlijk toch gewoon als een functie volledig uit één macht bestaat? Bijvoorbeeld f(x) = 3x + 5x dan is hij homogeen met graad 1 en f(x) 3x^5 + 5x^5 dan is hij homogeen met graad 5?
Als q = 1/(r + 1) dan is q ongedefinieerd voor r = −1, maar niet voor r = 1, dan is q = ½. Maar voor r = 1 voldoet elke waarde van q aan q(r² − 1) = r − 1, terwijl voor r = −1 uiteraard geen enkele waarde van q aan deze betrekking kan voldoen. Ik heb het idee dat je gewoon met een schuin oog in het antwoordenboekje hebt zitten kijken zonder dat je begrijpt hoe dit antwoord is verkregen, want uit de betrekking qr² + 1 = q + r volgt an sich niet dat f(a,b) homogeen is van de graad 2 indien q = 1/(r + 1).quote:
[..]
Als je stelt dat qr2 +1 = q + r, mag je dan ook zeggen dat de graad van homogeniteit twee is? Tenzij r = 1 of -1
Je functie is homogeen van de graad k indien
f(ta,tb) = tk·f(a,b)
Bekijk nu de teller en de noemer eens apart. We definiëren nu
f(a,b) = g(a,b) / h(a,b)
met
g(a,b) = aq+1·br+1
en
h(a,b) = aqr²+1 + bq+r
De functie g(a,b) is sowieso homogeen, want je hebt g(ta,tb) = t(q+1)+(r+1)·g(a,b).
De functie h(a,b) is niet zonder meer homogeen, dat is immers alleen het geval als de machten van beide termen gelijk zijn, dus als qr² + 1 = q + r en dus q = 1/(r + 1) (r ≠ − 1).
Verder geldt: als g(a,b) homogeen is van de graad m en h(a,b) is homogeen van de graad n, dan is f(a,b) homogeen van de graad m − n, want dan is
f(ta,tb) = g(ta,tb) / h(ta,tb) = tm·g(a,b) / tn·h(a,b) = tm−n·(g(a,b)/h(a,b)) = tm−n·f(a,b)
Goed, we veronderstellen nu dat q = 1/(r + 1) (r ≠ −1). Voor de graad van homogeniteit m van de teller g(a,b) uitgedrukt in r vinden we dan
m = q + 1 + r + 1 = (r² + 3r + 3)/(r + 1)
En voor de graad van homogeniteit n van de noemer h(a,b) uitgedrukt in r hebben we dan
n = q + r = (r² + r + 1)/(r + 1)
De graad van homogeniteit m − n van f(a,b) is onfhankelijk van r, want uit m = q + r + 2 en n = q + r volgt direct dat m − n = 2.
Voila.
[ Bericht 0% gewijzigd door Riparius op 11-10-2013 11:21:55 ]
Nee, kijk even in Wikipedia.quote:
Homogeniteit is eigenlijk toch gewoon als een functie volledig uit één macht bestaat? Bijvoorbeeld f(x) = 3x + 5x dan is hij homogeen met graad 1 en f(x) 3x^5 + 5x^5 dan is hij homogeen met graad 5?
Ja heb ik gedaan maar wat ik eerder zei is feite toch wel waar het op neer komt? Alleen bedoel jij dat ik vergeet te vermelden dat het ook veralgemeend kan worden voor functies van meerdere veranderlijken, zoals f(x,y) = 19xy^3 + 14x^4 + 20(xy)^2 is een homogene functie van graad 4? Of zeg ik nou iets wat niet klopt?quote:
[ Bericht 0% gewijzigd door ulq op 11-10-2013 14:51:59 ]
Omdat je stelt qr2 + 1 = q + r, dacht ik dat je kon stellen q + r + 2 (volgt uit g) - (q+r) = 2.quote:
[..]
Als q = 1/(r + 1) dan is q ongedefinieerd voor r = −1, maar niet voor r = 1, dan is q = ½. Maar voor r = 1 voldoet elke waarde van q aan q(r² − 1) = r − 1, terwijl voor r = −1 uiteraard geen enkele waarde van q aan deze betrekking kan voldoen. Ik heb het idee dat je gewoon met een schuin oog in het antwoordenboekje hebt zitten kijken zonder dat je begrijpt hoe dit antwoord is verkregen, want uit de betrekking qr² + 1 = q + r volgt an sich niet dat f(a,b) homogeen is van de graad 2 indien q = 1/(r + 1).
Je functie is homogeen van de graad k indien
f(ta,tb) = tk·f(a,b)
Bekijk nu de teller en de noemer eens apart. We definiëren nu
f(a,b) = g(a,b) / h(a,b)
met
g(a,b) = aq+1·br+1
en
h(a,b) = aqr²+1 + bq+r
De functie g(a,b) is sowieso homogeen, want je hebt g(ta,tb) = t(q+1)+(r+1)·g(a,b).
De functie h(a,b) is niet zonder meer homogeen, dat is immers alleen het geval als de machten van beide termen gelijk zijn, dus als qr² + 1 = q + r en dus q = 1/(r + 1) (r ≠ − 1).
Verder geldt: als g(a,b) homogeen is van de graad m en h(a,b) is homogeen van de graad n, dan is f(a,b) homogeen van de graad m − n, want dan is
f(ta,tb) = g(ta,tb) / h(ta,tb) = tm·g(a,b) / tn·h(a,b) = tm−n·(g(a,b)/h(a,b)) = tm−n·f(a,b)
Goed, we veronderstellen nu dat q = 1/(r + 1) (r ≠ −1). Voor de graad van homogeniteit m van de teller g(a,b) uitgedrukt in r vinden we dan
m = q + 1 + r + 1 = (r² + 3r + 3)/(r + 1)
En voor de graad van homogeniteit n van de noemer h(a,b) uitgedrukt in r hebben we dan
n = q + r = (r² + r + 1)/(r + 1)
De graad van homogeniteit m − n van f(a,b) is onfhankelijk van r, want uit m = q + r + 2 en n = q + r volgt direct dat m − n = 2.
Voila.
Ik noemde de waardes 1 en - 1 omdat ik keek naar de niet verder vereenvoudigde (r-1)/(r2-1).
De functie is dus homogeen van graad 2 op voorwaarde dat r niet -1 (dan is hij niet homogeen).
Hartstikke bedankt voor je uitleg, een stuk helderder nu.
In het boek worden helaas vooral heel basale voorbeelden besproken (bijv. x2 + y2).
Dit klopt, maar de aanvulling is wel essentieel, want het vraagstuk van jordyqwerty ging over een functie van twee variabelen.quote:
[..]
Ja heb ik gedaan maar wat ik eerder zei is feite toch wel waar het op neer komt? Alleen bedoel jij dat ik vergeet te vermelden dat het ook veralgemeend kan worden voor functies van meerdere veranderlijken, zoals f(x,y) = 19xy^3 + 14x^4 + 20(xy)^2 is een homogene functie van graad 4? Of zeg ik nou iets wat niet klopt?
Iets heel anders. Op een tussentoets werd gevraagd of een functie op hetzelfde interval convex en concaaf kon zijn. Zo ja, moest je hier een voorbeeld voor geven.
Er stond niet expliciet bij of dat voorbeeld in de vorm van een functie met uitleg moest zijn, dus heb ik iets getekend. Ik heb genoteerd dat dat kan, mits er een buigpunt is (f'' = 0) en vervolgens een U (convex) verbonden met een ∩ (concaaf) en het buigpunt aangegeven.
In hoeverre is dat juist? Ik ben me er bewust van dat dit niet het meest verfijnde antwoord is.
Dan nog iets, stel je hebt een optimalisatieprobleem (voor de eenvoud van één variabele) en je moet binnen een gesloten interval (bijv. [2,6]) het maximum geven. Waarom is het dan verkeerd om de tweede afgeleide test te gebruiken om te kijken of de eindpunten 2 en 6 maxima of minima zijn?
Of is dat helemaal niet verkeerd?
Er stond niet expliciet bij of dat voorbeeld in de vorm van een functie met uitleg moest zijn, dus heb ik iets getekend. Ik heb genoteerd dat dat kan, mits er een buigpunt is (f'' = 0) en vervolgens een U (convex) verbonden met een ∩ (concaaf) en het buigpunt aangegeven.
In hoeverre is dat juist? Ik ben me er bewust van dat dit niet het meest verfijnde antwoord is.
Dan nog iets, stel je hebt een optimalisatieprobleem (voor de eenvoud van één variabele) en je moet binnen een gesloten interval (bijv. [2,6]) het maximum geven. Waarom is het dan verkeerd om de tweede afgeleide test te gebruiken om te kijken of de eindpunten 2 en 6 maxima of minima zijn?
Of is dat helemaal niet verkeerd?
Antwoord op je eerste vraag: Bedenk gewoon een functie waarvoor f ' '(x)=0 voor alle x. Alle functies van de vorm f(x)=ax+b voldoen hier uiteraard aan. Jouw voorbeeld klopt niet, want jouw functie is niet tegelijkertijd convex en concaaf op hetzelfde interval.quote:
Iets heel anders. Op een tussentoets werd gevraagd of een functie op hetzelfde interval convex en concaaf kon zijn. Zo ja, moest je hier een voorbeeld voor geven.
Er stond niet expliciet bij of dat voorbeeld in de vorm van een functie met uitleg moest zijn, dus heb ik iets getekend. Ik heb genoteerd dat dat kan, mits er een buigpunt is (f'' = 0) en vervolgens een U (convex) verbonden met een ∩ (concaaf) en het buigpunt aangegeven.
In hoeverre is dat juist? Ik ben me er bewust van dat dit niet het meest verfijnde antwoord is.
Dan nog iets, stel je hebt een optimalisatieprobleem (voor de eenvoud van één variabele) en je moet binnen een gesloten interval (bijv. [2,6]) het maximum geven. Waarom is het dan verkeerd om de tweede afgeleide test te gebruiken om te kijken of de eindpunten 2 en 6 maxima of minima zijn?
Of is dat helemaal niet verkeerd?
Tweede vraag: wat wil je met de tweede afgeleide doen op de randpunten?
Aha ok thanksquote:
[..]
Dit klopt, maar de aanvulling is wel essentieel, want het vraagstuk van jordyqwerty ging over een functie van twee variabelen.
Op het buigpunt ook niet?quote:
[..]
Antwoord op je eerste vraag: Bedenk gewoon een functie waarvoor f ' '(x)=0 voor alle x. Alle functies van de vorm f(x)=ax+b voldoen hier uiteraard aan. Jouw voorbeeld klopt niet, want jouw functie is niet tegelijkertijd convex en concaaf op hetzelfde interval.
Tweede vraag: wat wil je met de tweede afgeleide doen op de randpunten?
2: Kijken of het een minimum of maximum is, maar. ik begrijp dat die vlieger niet opgaat?
Kijk eens naar de definities van (strikt) convex en (strikt) concaaf. Die twee sluiten elkaar uit. Als je de eis van striktheid achterwege laat, dan kun je wel een functie hebben die zowel convex als concaaf is op hetzelfde interval, maar dat kan dan alleen een lineaire functie zijn op dat interval.quote:
Kijk eens naar de functie f: [2,6] → R gedefinieerd door f(x) = x3. Deze functie heeft een minimum bij x = 2 en een maximum bij x = 6 terwijl f''(2) en f''(6) beide positief zijn. Wat denk je daarvan?quote:2: Kijken of het een minimum of maximum is, maar. ik begrijp dat die vlieger niet opgaat?
Van wat ik weet is een functie strict convex als f'' > 0 en strict concaaf als f'' < 0. Daar komt = 0 bij zonder strictheid. In een buigpunt is f'' 0, dus ik dacht dat op dat punt de functie zowel convex als concaaf is (niet strict). Ik kijk zo even op mijn laptop naar de wikipedia pagina!quote:
[..]
Kijk eens naar de definities van (strikt) convex en (strikt) concaaf. Die twee sluiten elkaar uit. Als je de eis van striktheid achterwege laat, dan kun je wel een functie hebben die zowel convex als concaaf is op hetzelfde interval, maar dat kan dan alleen een lineaire functie zijn op dat interval.
[..]
Kijk eens naar de functie f: [2,6] → R gedefinieerd door f(x) = x3. Deze functie heeft een minimum bij x = 2 en een maximum bij x = 6 terwijl f''(2) en f''(6) beide positief zijn. Wat denk je daarvan?
.
2: Hm, lokaal minimum en maximum? Tweede afgeleide test is dus irrelevant voor randpunten?
Is 23162 nu groter of kleiner dan 31995?quote:
[..]
Voor kleine exponenten lukt dit zeker. Voor m,n > 0 heb je immers 2m > 3n als m/n > log(3)/log(2) ≈ 1,585, dus is m = 5, n = 3 een goede keuze, want dan is m/n = 5/3 ≈ 1,667. En een hele goede keuze is dan m = 8, n = 5, want dan is m/n = 8/5 = 1,6. Maar het wordt lastiger bij grote exponenten en als de waarden van de machten dichter bij elkaar liggen. Als je uitsluitend met pen en papier zou willen nagaan of bijvoorbeeld 23162 nu groter of kleiner is dan 31995 dan zijn zelfs opa's logaritmentafels in vijf decimalen niet meer toereikend. En ik hoop niet dat je nu het advies blijft geven om het dan maar met de hand uit te rekenen omdat het algoritme zo lekker simpel is.
Dit is toch niet te berekenen zonder rekenmachine?
1995a = 3162
a ~ 1.58
21.58< 3
Dus
23162< 31995
Of toch wel? Klopt bovenstaande?
[ Bericht 1% gewijzigd door wiskundenoob op 11-10-2013 23:52:39 ]
Ah! Hij (nouja, mijn uitleg) is niet convex (en concaaf) op hetzelfde interval omdat je die lijn niet kunt trekken tussen twee willekeurige punten zonder buiten het interval te komen. Klopt dat?quote:
[..]
Kijk eens naar de definities van (strikt) convex en (strikt) concaaf. Die twee sluiten elkaar uit. Als je de eis van striktheid achterwege laat, dan kun je wel een functie hebben die zowel convex als concaaf is op hetzelfde interval, maar dat kan dan alleen een lineaire functie zijn op dat interval.
[..]
Kijk eens naar de functie f: [2,6] → R gedefinieerd door f(x) = x3. Deze functie heeft een minimum bij x = 2 en een maximum bij x = 6 terwijl f''(2) en f''(6) beide positief zijn. Wat denk je daarvan?
Ik wist dat overigens, maar ik wist niet dat de hele functie convex en concaaf moet zijn op het gehele interval.
Jawel hoor, in principe is alles te berekenen zonder rekenmachine. Het is geen pretje, maar het kan. Met de calculator van Windows vind ik 23162/1995 = 2.9999998030641692219144189133716 ... zodat inderdaad 23162< 31995 maar dat kun je met bijvoorbeeld de logaritmentafels in 14 decimalen van Briggs uit 1624 ook concluderen. En die tafels zijn toch echt met de hand berekend. Dus ja, het kan.quote:Op vrijdag 11 oktober 2013 23:37 schreef wiskundenoob het volgende:
[..]
Is 23162 nu groter of kleiner dan 31995?
Dit is toch niet te berekenen zonder rekenmachine?
1995a = 3162
a ~ 1.58
21.58< 3
Dus
23162< 31995
Maar goed, vroeger kon men wel vaker dingen met de hand uitrekenen waarvan we nu soms nog niet weten hoe het is gedaan. Heel bekend is bijvoorbeeld dat Mersenne eens per brief aan Fermat vroeg of het getal 100895598169 priem was of niet. Fermat antwoordde nog dezelfde dag per kerende post dat dit getal niet priem is en dat dit getal het product is van 112303 en 898423 en dat elk van deze beide factoren priem is. Tot op de dag van vandaag weet niemand hoe hij dit zonder rekenmachine heeft gedaan. Het valt wel direct op dat je hebt 898423 = 8·112303 − 1, dus N = n(8n − 1) en daarmee 32N + 1 = (16n − 1)2 met n = 112303, maar ja ...
[ Bericht 4% gewijzigd door Riparius op 12-10-2013 02:49:56 ]
Een nieuwe.
Stel je hebt de functie:
f(x,y) = x3 + y3 - 9xy + 27
Verder is gegeven dat:
0 ≤ x ≤ 4 en 0 ≤ y ≤ 4
Gevraagd wordt om het maximum en minimum te vinden.
Eerst dus de stationaire punten vinden.
f'x(x,y) = 3x2 - 9y = 0
f'y(x,y) = 3y2 - 9x = 0
Y uitdrukken in x voor f'x(x,y)
9y = 3x2
y = (1/3)x2
Invoeren in f'y(x,y)
3((1/3)x2)2 - 9x = 0
3((1/9)x4) - 9x = 0
(1/3)x4 - 9x = 0
x4 - 27x = 0
x(x3 - 27) = 0
Waaruit volgt x = 0 of x = 3, omdat x = 0 een randpunt is, is x = 3 het enige stationaire punt. Bijbehorende y-waarde: (1/3)(3)2 = 3
Nu heb ik dus als mogelijk punt (3,3).
Ik snap nu niet hoe ik verder moet gaan, ofwel, wat ik met de randpunten moet doen (0 ≤ x ≤ 4 en 0 ≤ y ≤ 4).
In eerste instantie dacht ik dat ik door het invullen in de afgeleiden voor x en y de bijbehorende waardes kon vinden (bijvoorbeeld, welke waarde bij het punt x = 4 hoort), maar dat is niet zo/lijkt me onwaarschijnlijk.
Ik denk zelf dat ik iets moet doen met de originele functie f(x,y), maar wat? Als ik x = 0 invul, wat moet ik dan voor y invullen? Y kan immers tussen 0 en 4 liggen.
Stel je hebt de functie:
f(x,y) = x3 + y3 - 9xy + 27
Verder is gegeven dat:
0 ≤ x ≤ 4 en 0 ≤ y ≤ 4
Gevraagd wordt om het maximum en minimum te vinden.
Eerst dus de stationaire punten vinden.
f'x(x,y) = 3x2 - 9y = 0
f'y(x,y) = 3y2 - 9x = 0
Y uitdrukken in x voor f'x(x,y)
9y = 3x2
y = (1/3)x2
Invoeren in f'y(x,y)
3((1/3)x2)2 - 9x = 0
3((1/9)x4) - 9x = 0
(1/3)x4 - 9x = 0
x4 - 27x = 0
x(x3 - 27) = 0
Waaruit volgt x = 0 of x = 3, omdat x = 0 een randpunt is, is x = 3 het enige stationaire punt. Bijbehorende y-waarde: (1/3)(3)2 = 3
Nu heb ik dus als mogelijk punt (3,3).
Ik snap nu niet hoe ik verder moet gaan, ofwel, wat ik met de randpunten moet doen (0 ≤ x ≤ 4 en 0 ≤ y ≤ 4).
In eerste instantie dacht ik dat ik door het invullen in de afgeleiden voor x en y de bijbehorende waardes kon vinden (bijvoorbeeld, welke waarde bij het punt x = 4 hoort), maar dat is niet zo/lijkt me onwaarschijnlijk.
Ik denk zelf dat ik iets moet doen met de originele functie f(x,y), maar wat? Als ik x = 0 invul, wat moet ik dan voor y invullen? Y kan immers tussen 0 en 4 liggen.
Geen idee, je formulering is zo onduidelijk dat onmogelijk is te achterhalen wat je je hier precies bij voorstelt.quote:
[..]
Ah! Hij (nouja, mijn uitleg) is niet convex (en concaaf) op hetzelfde interval omdat je die lijn niet kunt trekken tussen twee willekeurige punten zonder buiten het interval te komen. Klopt dat?
Er werd duidelijk gevraagd naar een functie die zowel convex als concaaf moest zijn op hetzelfde interval. Jij maakte daarvan dat er werd gevraagd naar een functie die convex is op een deel van een interval maar concaaf op een ander deel van datzelfde interval. Maar dat is iets anders.quote:Ik wist dat overigens, maar ik wist niet dat de hele functie convex en concaaf moet zijn op het gehele interval.
