SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk-en-vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Ah ja, ik las het verkeerd. Ik neem aan dat n=2 en bewijs het in dat geval. Even proberen.
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm en algemener) gedefinieerd op p3!
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm en algemener) gedefinieerd op p3!
Niet helemaal equivalent: 0 deelt 0, maar 0/0 is niet gedefinieerd.quote:Op zondag 10 april 2011 16:53 schreef BasementDweller het volgende:
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm) gedefinieerd op p3!
Ik kom er echt niet uit...
Misschien toch wel
Klopt het dat E(X1² X2 + X1X2²) = 0?
[ Bericht 42% gewijzigd door BasementDweller op 10-04-2011 17:45:50 ]
Misschien toch wel
Klopt het dat E(X1² X2 + X1X2²) = 0?
[ Bericht 42% gewijzigd door BasementDweller op 10-04-2011 17:45:50 ]
Dat is uiteraard de bedoeling, anders is de opgave fout. Je wilde het echter met karakteristieke functies doen, in dat opzicht is E(X1² X2 + X1X2²) niet de juiste stap.
Ja dat is waar. Maar ik dacht misschien dat ik deze dan weer kan bewijzen met karakteristieke functies maar dat lukte me niet.quote:
Dat is uiteraard de bedoeling, anders is de opgave fout. Je wilde het echter met karakteristieke functies doen, in dat opzicht is E(X1² X2 + X1X2²) niet de juiste stap.
Je kan het derde moment van de som uitdrukken in karakteristieke functies, en de karakteristieke functie van de som van twee onafhankelijke stochasten in elk van beide.
Ah, ik heb gezegd f_X1+X2 = f_X1 f_X2, en dat ding 3x naar t gedifferentieerd. Na heel vaak de productregel van differentiëren toegepast te hebben komt het antwoord eruit. Bedankt.quote:
Je kan het derde moment van de som uitdrukken in karakteristieke functies, en de karakteristieke functie van de som van twee onafhankelijke stochasten in elk van beide.
Dat "heel vaak toepassen" daar bestaat ook een binomium voor:
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
Chique, bedankt.quote:Op zondag 10 april 2011 19:52 schreef thabit het volgende:
Dat "heel vaak toepassen" daar bestaat ook een binomium voor:
[ afbeelding ]
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
Om even terug naar trigonometrie te gaan: Klopt deze afleiding?
tan(x/2) = sinx / (1 + cosx)
stel sinx = p => arcsin(sinx) = x = arcsin(p)
tan(x/2) = p / (1 + SQRT(1-p2)
arctan(tan(x/2)) = arctan (p / (1 + SQRT(1-p2))
(x/2) = arctan (p / (1 + SQRT(1-p2))
x = 2 arctan (p / (1 + SQRT(1-p2))
backsub x = arcsin(p)
arcsin p = 2 arctan (p / (1 + SQRT(1-p2))
tan(x/2) = sinx / (1 + cosx)
stel sinx = p => arcsin(sinx) = x = arcsin(p)
tan(x/2) = p / (1 + SQRT(1-p2)
arctan(tan(x/2)) = arctan (p / (1 + SQRT(1-p2))
(x/2) = arctan (p / (1 + SQRT(1-p2))
x = 2 arctan (p / (1 + SQRT(1-p2))
backsub x = arcsin(p)
arcsin p = 2 arctan (p / (1 + SQRT(1-p2))
Da's enkel een kwestie van domeinrestrictie. En dat had je zelf al kunnen zien aan de wortelterm waarin x in [-1,1] moet liggen, anders is deze niet gedefinieerd. En laat [-1,1] nou net het complete domein van arcsin (en arccos) zijnquote:
Nee, arcsin(sin x) is niet x: als je bij x 2pi optelt, blijft z'n sinus immers hetzelfde.
[ Bericht 14% gewijzigd door VanishedEntity op 10-04-2011 20:57:17 ]
Ja, logisch dat je dan niet uitkomt, want je gaat voorbij aan de extra eis van domeinrestrictie die bij cyclometrische functies naar voren komt. 2pi valt niet binnen het domein [-1/2*pi;1/2*pi] voor sinx, en daarmee het bereik van arcsinx. Je zal eerst net zolang INT*2pi af moeten trekken totdat x, òf pi - x binnen [-1/2*pi;1/2*pi] komt te liggen.quote:
Vul maar x=2pi in: arcsin(sin 2pi) = 0, niet x.
Ola, ik zit ook even met een probleempje.
Als ik de volgende dubbele integraal oplos
I(a) = int(int(exp(-a(x+2*y)), y = x .. 1), x = 0 .. 1)
kom ik voor willekeurige a uit op
I(a) = (1/6)*(2*exp(-3*a)-3*exp(-2*a)+1)/a^2
vervolgens moet ik laten zien dat dit voor a=0 gelijk is aan een half, maar gezien je deelt door 0² heb je toch een ongedefinieerde oplossing, of ben ik nu een kiwi?
kusjes
Als ik de volgende dubbele integraal oplos
I(a) = int(int(exp(-a(x+2*y)), y = x .. 1), x = 0 .. 1)
kom ik voor willekeurige a uit op
I(a) = (1/6)*(2*exp(-3*a)-3*exp(-2*a)+1)/a^2
vervolgens moet ik laten zien dat dit voor a=0 gelijk is aan een half, maar gezien je deelt door 0² heb je toch een ongedefinieerde oplossing, of ben ik nu een kiwi?
kusjes
Omnia vincit amor, nos et cedamus amori
direct a invullen in de integraal dan kom je inderdaad uit op een half, maar de opdracht is vervolgens op I(a) voor willekeurige a te bepalen en dan komt de vraag op beide manieren overeen komen
Omnia vincit amor, nos et cedamus amori
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
vlogens mij wordt (x + h)^2 daar gewoon uitgeschrevenquote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Dus zonder haakjes 
Zie je het dan wel? Schrijf gewoon maar eens uit.
~Si vis amari, ama~
(x+h)2= x2+2xh+h2quote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Als je dit optelt met die -x2 krijg je 2xh+h2
Niet altijd serieus
Heb je wel eens gehoord van een merkwaardig product?quote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om de afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van x2 = 2x, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurt. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Eigenlijk niet.quote:
[..]
Heb je wel eens gehoord van een merkwaardig product?
Ik mis nogal wat algebraïsche kennis heb ik gemerkt. Ben er nu naar een het kijken. Erg verhelderend allemaal.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik ben nu wat aan het leren over o.a. modulorekenen, en er staan wat opdrachten bij. Ik kan maar niet uit deze komen:
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag.
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag
.
Finally, someone let me out of my cage
Het merkwaardig product dat je in je bepaling van de afgeleide van f(x) = x2 kunt gebruiken is:quote:
[..]
Eigenlijk niet.
(a + b)2 = a2 + 2ab + b2
Je kunt de juistheid van deze identiteit natuurlijk aantonen door de haakjes in het linkerlid weg te werken, maar het is meetkundig ook mooi in te zien dat dit klopt.
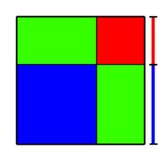
De oppervlakte van een vierkant met zijde a is a2 en de oppervlakte van een vierkant met zijde b is b2. Stel nu eens dat we een vierkant hebben met zijde (a + b), dan is de oppervlakte (a + b)2. Maar hoe staat deze oppervlakte nu in verband met die van de vierkanten met zijde a en zijde b? Ik heb even een plaatje gepikt uit de Franse Wikipedia:
Laten we aannemen dat het blauwe lijnstuk rechts van het vierkant een lengte a heeft, en het rode lijnstuk een lengte b. Dan is de totale zijde van het vierkant dus (a + b) en de totale oppervlakte van het vierkant dus (a + b)2. Maar je ziet dat de totale oppervlakte van het grote vierkant wordt gevormd door het blauwe vierkant (met oppervlakte a2), het rode vierkant (met oppervlakte b2), maar ook nog door de twee groene rechthoeken. Elk van die groene rechthoeken heeft een lengte a en een breedte b, en dus een oppervlakte ab. En omdat er twee van die rechthoeken zijn, moeten we bij a2 + b2 dus ook nog 2ab optellen om de oppervlakte van het grote vierkant te krijgen. En dat is precies wat het merkwaardig product hierboven zegt!
ok, laten we gewoon eens wat gaan rekenen en kijken hoever we komen:quote:
Ik ben nu wat aan het leren over o.a. modulorekenen, en er staan wat opdrachten bij. Ik kan maar niet uit deze komen:
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag
x2-3y2=1997
3y2=x2-1997
y2=(x2-1997)/3
Nu maken we de observatie dat als dit een oplossing heeft voor x en y gehele getallen, dan moet x2-1997 deelbaar zijn door 3. met andere woorden:
x2 = 1997 mod 3
Aan jou de vraag, waarom heeft dit geen oplossing?
Feitelijk is het dus zo dat X2 = 2X omdat het twee (blauwe) vierkanten vormt? Tenminste om het even eenvoudig te maken voor mezelf, want volgens mij klopt dat niet helemaal.quote:
[..]
... En dat is precies wat het merkwaardig product hierboven zegt!
[ Bericht 3% gewijzigd door Pipo1234 op 12-04-2011 12:34:29 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
x2 is sowieso niet gelijk aan 2x, de afgeleide van x2 is 2x. Dat is ook niet zo omdat het twee blauwe vierkanten vormt (los daarvan, er is maar één blauw vierkant), dat is slechts een tussenstap die je nodig hebt om de limiet op te lossen.quote:
[..]
Feitelijk is het dus zo dat X2 = 2X omdat het twee (blauwe) vierkanten vormt? Tenminste om het even eenvoudig te maken voor mezelf, want volgens mij klopt dat niet helemaal.
Het vierkant laat zien dat je (a+b)2 kunt schrijven als a2+2ab+b2. Als je dat invult in de limiet kom je uit op de oplossing
.Je moet het niet te simpel maken voor jezelf door stappen simpelweg over te slaan, dan klopt het niet meer.
The biggest argument against democracy is a five minute discussion with the average voter.
quote:
[..]
x2 is sowieso niet gelijk aan 2x, de afgeleide van x2 is 2x. Dat is ook niet zo omdat het twee blauwe vierkanten vormt (los daarvan, er is maar één blauw vierkant), dat is slechts een tussenstap die je nodig hebt om de limiet op te lossen.
Het vierkant laat zien dat je (a+b)2 kunt schrijven als a2+2ab+b2. Als je dat invult in de limiet kom je uit op de oplossing
Je moet het niet te simpel maken voor jezelf door stappen simpelweg over te slaan, dan klopt het niet meer.
Het is de afgeleide natuurlijk. Misschien probeer ik het inderdaad te simpel voor mezelf te maken.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Die merkwaardige producten is precies wat ik nodig had! Alleen nu heb ik er nog een vraag over. Als ik X3 heb en dan op h3 + 3x2h + 3xh2 uitkom, wat gebeurd er dan met die overtollige 3x van de laatste samenstelling? Als ik h wegstreep houd ik namelijk 3x over... en ik weet dat het antwoord 3x2 moet zijn.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik begrijp niet precies wat je bedoelt? Als ik het uitwerk kom ik uit op(h3 + 3x2h + 3xh2 + x3 - x3)/h. Als je dat uitwerkt komt het gewoon uit hoorquote:
Die merkwaardige producten is precies wat ik nodig had! Alleen nu heb ik er nog een vraag over. Als ik X3 heb en dan op h3 + 3x2h + 3xh2 uitkom, wat gebeurd er dan met die overtollige 3x van de laatste samenstelling? Als ik h wegstreep houd ik namelijk 3x over... en ik weet dat het antwoord 3x2 moet zijn.
. Misschien dat je vergeten bent om in het begin f(x+h) - f(x) te doen?
The biggest argument against democracy is a five minute discussion with the average voter.
Nee die formule heb ik ook. Ik probeer het te gebruiken voor een differentatie van X3. Bij X2 kom ik er door H weg te strepen. Maar bij X3 houd ik op de volgende manier 3X2 en 3X over: h3 + 3x2h + 3xh2 + x3 - x3)/hquote:
[..]
Ik begrijp niet precies wat je bedoelt? Als ik het uitwerk kom ik uit op(h3 + 3x2h + 3xh2 + x3 - x3)/h. Als je dat uitwerkt komt het gewoon uit hoor
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ah, nu begrijp ik het denk ik:quote:
[..]
ok, laten we gewoon eens wat gaan rekenen en kijken hoever we komen:
x2-3y2=1997
3y2=x2-1997
y2=(x2-1997)/3
Nu maken we de observatie dat als dit een oplossing heeft voor x en y gehele getallen, dan moet x2-1997 deelbaar zijn door 3. met andere woorden:
x2 = 1997 mod 3
Aan jou de vraag, waarom heeft dit geen oplossing?
x2 = 1997 mod 3
x2 = 2 mod 3
De enige manier om in modulo 3 verzameling 2 te krijgen is door 1 met 2 of 2 met 1 te vermenigvuldigen. Voor x2 is er us geen oplossing in gehele getallen.
Dit betekent als ik het goed begrijp ook dat x2 -2 nooit deelbaar is door 3, wat ik best opmerkelijk vind
.Dank voor de hulp
Finally, someone let me out of my cage
Ik denk dat je de limiet van h naar 0 vergeet. Je deelt een keer een h weg, zodat je h2 + 3xh + 3x2 overhoudt. De limiet van h naar 0 nemen zorgt er voor dat alleen de 3x2 overblijft.quote:
[..]
Nee die formule heb ik ook. Ik probeer het te gebruiken voor een differentatie van X3. Bij X2 kom ik er door H weg te strepen. Maar bij X3 houd ik op de volgende manier 3X2 en 3X over: h3 + 3x2h + 3xh2 + x3 - x3)/h
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?quote:Op dinsdag 12 april 2011 15:29 schreef freiss het volgende:
[..]
Ik denk dat je de limiet van h naar 0 vergeet. Je deelt een keer een h weg, zodat je h2 + 3xh + 3x2 overhoudt. De limiet van h naar 0 nemen zorgt er voor dat alleen de 3x2 overblijft.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Even tussendoor, snap je wat er bedoelt wordt met de limiet? Dat is namelijk wel redelijk belangrijk om dit echt te begrijpenquote:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
. Ik zal proberen uit te leggen wat er gebeurt, eerst heb je de limiet van (f(x+h) - f(x) )/h. Daarna schrijf je dit uit, in jouw geval krijg je dan de limiet van (h3 + 3x2h + 3xh2 + x3 - x3)/h. Eerst werk je dit uit, je deelt de h weg uit alle termen, je krijgt nu de limiet van h2 + 3x2 + 3xh. Nu ga je de limiet invullen, als h in deze uitdrukking naar nul gaat zullen alle termen nul worden behalve 3x2, dat is dus de uitkomst van dit probleem. Ik ben er in deze uitleg een beetje van uitgegaan dat je snapt wat de limiet is, als je dat niet snapt moet je dat maar even proberen op te zoeken of te vragen
.
The biggest argument against democracy is a five minute discussion with the average voter.
Differentiëren is geen 'wegstrepen'. Je bepaalt van een functie y = f(x) eerst het differentiequotiënt:quote:Op dinsdag 12 april 2011 15:58 schreef Pipo1234 het volgende:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
Δy/Δx = (f(x+h) - f(x))/((x+h) - x) = (f(x+h) - f(x))/h
Deze verhouding zegt iets over hoeveel de afhankelijke variabele y (i.e. de functiewaarde) verandert in verhouding tot een verandering van de onafhankelijke variabele x. Meetkundig kun je dit opvatten als de gemiddelde steilheid van de curve van f(x) over een klein intervalletje [x, x+h]. Door nu het intervalletje steeds kleiner te maken (en dus de limiet te bepalen als h naar 0 gaat) krijgen we dan de steilheid van de curve van f(x) c.q. de steilheid van de raaklijn aan de curve van f(x) in één bepaald punt. Die steilheid (en dus de afgeleide) is een maat voor de snelheid waarmee de waarde van f(x) op dat punt verandert.
Hebben we f(x) = x3, dan vinden we voor het differentiequotiënt:
(f(x+h) - f(x))/h = ((x+h)3 - x3)/h = (x3 + 3x2h + 3xh2 + h3 - x3)/h = 3x2 + 3xh + h2
Om nu de afgeleide f'(x) te vinden moet ik de limiet van dit differentiequotiënt bepalen voor h→ 0. Dus krijg ik:
f'(x) = lim h→0 (f(x+h) - f(x))/h = lim h→0 (3x2 + 3xh + h2) = 3x2
De beide termen 3xh en h2 naderen immers tot 0 als we h naar nul laten gaan, zodat 3x2 resulteert.
quote:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Bedankt voor alle antwoorden. Ik denk dat ik al begrijp wat ik fout heb gedaan. Ik moest het namelijk nog daar H delen, alleen had er niet bij stil gestaan dat dit voor het limiet noodzakelijk is.
De volgende benadering heb ik nu:
f(x) = x3
f'(x) = lim(h>0) (x+h)3 - (x)3 / h
f'(x) = lim(h>0) x3 + h3 - x3 / h
f'(x) = lim(h>0) x3 + h3 + 3x2h + 3xh2 - x3 / h (Volgens het merkwaardig product)
f'(x) = lim(h>0) h3 + 3x2h + 3xh2/ h (x3 - x3)
f'(x) = lim(h>0) h2 + 3x2 + 3xh (Gedeeld door h)
f'(x) = 3x2 (Limiet 0 is benaderd)
Mijn boek merkt trouwens op dat dit de beste maar moeilijkste methode is om te differentiëren. Is dat zo? Ik vind het voor uitvoerig, maar kan me wel voorstellen dat dit op een examen een beetje teveel van het goed is.
De volgende benadering heb ik nu:
f(x) = x3
f'(x) = lim(h>0) (x+h)3 - (x)3 / h
f'(x) = lim(h>0) x3 + h3 - x3 / h
f'(x) = lim(h>0) x3 + h3 + 3x2h + 3xh2 - x3 / h (Volgens het merkwaardig product)
f'(x) = lim(h>0) h3 + 3x2h + 3xh2/ h (x3 - x3)
f'(x) = lim(h>0) h2 + 3x2 + 3xh (Gedeeld door h)
f'(x) = 3x2 (Limiet 0 is benaderd)
Mijn boek merkt trouwens op dat dit de beste maar moeilijkste methode is om te differentiëren. Is dat zo? Ik vind het voor uitvoerig, maar kan me wel voorstellen dat dit op een examen een beetje teveel van het goed is.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
In grote lijnen klopt het zo, alleen nog een paar opmerkingenquote:
Bedankt voor alle antwoorden. Ik denk dat ik al begrijp wat ik fout heb gedaan. Ik moest het namelijk nog daar H delen, alleen had er niet bij stil gestaan dat dit voor het limiet noodzakelijk is.
De volgende benadering heb ik nu:
f(x) = x3
f'(x) = lim(h>0) (x+h)3 - (x)3 / h
f'(x) = lim(h>0) x3 + h3 - x3 / h
f'(x) = lim(h>0) x3 + h3 + 3x2h + 3xh2 - x3 / h (Volgens het merkwaardig product)
f'(x) = lim(h>0) h3 + 3x2h + 3xh2/ h (x3 - x3)
f'(x) = lim(h>0) h2 + 3x2 + 3xh (Gedeeld door h)
f'(x) = 3x2 (Limiet 0 is benaderd)
Mijn boek merkt trouwens op dat dit de beste maar moeilijkste methode is om te differentiëren. Is dat zo? Ik vind het voor uitvoerig, maar kan me wel voorstellen dat dit op een examen een beetje teveel van het goed is.
. Je zou wat meer haakjes mogen gebruiken voor de duidelijkheid, zoals je het nu doet is het voor jou en voor mij duidelijk, maar in een examen moet je ipv (x+h)3 - (x)3 / h toch echt ((x+h)3 - (x)3) / h schrijven. Verder vraag ik me af wat je precies tussen het eerste en tweede punt doet? Je haakjes zijn daar weg, maar je hebt ze nog niet uitgewerkt? Die stap kan je weglaten. Wat je boek zegt klopt, het is de beste manier, maar zoals je zelf al zegt, dit kan je in een examen niet iedere keer doen. Daarom zijn er regels voor het differentiëren, waarschijnlijk staan ze ook wel ergens in je boek in een volgende paragraaf, anders kan je hier even kijken
.
The biggest argument against democracy is a five minute discussion with the average voter.
Ik begrijp wat je bedoeld. Heb het even uitvoerig gedaan zodat het voor mezelf duidelijk is en voor anderen ook. Meer haakjes? Oké. Ik zal het proberen te onthouden. Ben er juist zuinig mee, omdat het er zo chaotisch uit gaat zien. Er staan trouwens regels op de volgende pagina's. Maar ik wil graag de basis beheersen, zodat ik weet waar het vandaan komt.quote:
[..]
In grote lijnen klopt het zo, alleen nog een paar opmerkingen
Wat je boek zegt klopt, het is de beste manier, maar zoals je zelf al zegt, dit kan je in een examen niet iedere keer doen. Daarom zijn er regels voor het differentiëren, waarschijnlijk staan ze ook wel ergens in je boek in een volgende paragraaf, anders kan je hier even kijken
Even nog een vraag hierover...
Hoe komt het dat bij een deling met x (dus 1/x2) een negatieve functie voortvloeit? Ik begrijp dat 1 delen door iets altijd een afname betekent als x hoger dan 1 is in ieder geval, maar welke stap zorgt daar voor. Mijn boek geeft totaal geen uitleg over dit onderwerp...
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik zou niet al te zuinig zijn met de haakjes, je kan er beter te veel dan te weinig hebbenquote:
[..]
Ik begrijp wat je bedoeld. Heb het even uitvoerig gedaan zodat het voor mezelf duidelijk is en voor anderen ook. Meer haakjes? Oké. Ik zal het proberen te onthouden. Ben er juist zuinig mee, omdat het er zo chaotisch uit gaat zien. Er staan trouwens regels op de volgende pagina's. Maar ik wil graag de basis beheersen, zodat ik weet waar het vandaan komt.
. Het ziet er misschien niet altijd even mooi uit, maar het is tenminste wel duidelijk. Verder is het heel goed dat je de basis wil beheersen, maar in een examen zal je nooit zo hoeven te differentiëren, dus als je snapt hoe het werkt zou ik verder gaan met die regels .Ik snap niet helemaal wat je bedoelt, wat bedoel je met een negatieve functie?quote:Even nog een vraag hierover...
The biggest argument against democracy is a five minute discussion with the average voter.
Je bedoelt dat de afgeleide negatief is?quote:
[..]
Even nog een vraag hierover...
Precies. f(x) = 1 / x2 wordt f'(x) = - (2 / x3)quote:
[..]
Je bedoelt dat de afgeleide negatief is?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je kan het zien als je de grafiek plot, 1/x2 is een dalende functie (als we even alleen naar positieve x kijken), van een dalende functie is de afgeleide negatief. Ik weet niet of je dat bedoelt?quote:
[..]
Precies. f(x) = 1 / x2 wordt f'(x) = - (2 / x3)
The biggest argument against democracy is a five minute discussion with the average voter.
Teken eens de grafiek van 1/x2.quote:
[..]
Precies. f(x) = 1 / x2 wordt f'(x) = - (2 / x3)
Vertel eens wat er met die grafiek gebeurt als je langs de x-as gaat: neemt de grafiek toe of af, hoe snel gaat die stijging/daling, etc.
Probeer aan de hand van dat verhaal het verloop van de afgeleide te vertellen.
Ik heb je eerdere posts bekeken:
Vertel liever eerst eens wat de afgeleide is?
De afgeleide van 1 / x2 of in het algemeen? Ik heb trouwens een grafiek uitgetekend en zie dat de rico steeds kleiner wordt. Dit klopt ook wanneer het vergeleken wordt met - (1/x3).quote:
[..]
Teken eens de grafiek van 1/x2.
Vertel eens wat er met die grafiek gebeurt als je langs de x-as gaat: neemt de grafiek toe of af, hoe snel gaat die stijging/daling, etc.
Probeer aan de hand van dat verhaal het verloop van de afgeleide te vertellen.
Ik heb je eerdere posts bekeken:
Vertel liever eerst eens wat de afgeleide is?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
De grafiek van 1/x2, vertel eerst eens wat daarmee gebeurt als je langs de x-as loopt.quote:
[..]
De afgeleide van 1 / x2 of in het algemeen? Ik heb trouwens een grafiek uitgetekend en zie dat de rico steeds kleiner wordt. Dit klopt ook wanneer het vergeleken wordt met - (1/x3).
Daarna vertel je wat er met de afgeleide gebeurt als je langs de x-as loopt.
De lijn loopt in een vrij scherp hoek omlaag en komt na 7 op een punt dat niet meer te tekenen is. Dus de formule geeft steeds kleinere waarden: 1, 0.25, 0.037, 0.0625, 0.04, 0.028, 0.0204.quote:
[..]
De grafiek van 1/x2, vertel eerst eens wat daarmee gebeurt als je langs de x-as loopt.
Daarna vertel je wat er met de afgeleide gebeurt als je langs de x-as loopt.
De afgeleide wordt ook steeds kleiner alleen dan wel in negatieve waarden: -1, -0.125, -0.037, -0.016, -0.008, -0.0046, -0.0029. Dat die waarden negatief zijn is logisch omdat de afname in een negatieve richting plaats vindt.
Als ik het goed begrijp is dus de afgeleide bij een afnemende waarde altijd negatief...?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
De grafiek van 1/x2 daalt als je langs de x-as naar rechts gaat, zoals je zelf ook zegt.quote:
[..]
De lijn loopt in een vrij scherp hoek omlaag en komt na 7 op een punt dat niet meer te tekenen is. Dus de formule geeft steeds kleinere waarden: 1, 0.25, 0.037, 0.0625, 0.04, 0.028, 0.0204.
De afgeleide wordt ook steeds kleiner alleen dan wel in negatieve waarden: -1, -0.125, -0.037, -0.016, -0.008, -0.0046, -0.0029. Dat die waarden negatief zijn is logisch omdat de afname in een negatieve richting plaats vindt.
Als ik het goed begrijp is dus de afgeleide bij een afnemende waarde altijd negatief...?
Wat je ook zou moeten opvallen, is dat die daling steeds langzamer gaat: In het begin neemt de grafiek een enorme duik, terwijl de grafiek wat later steeds een beetje afneemt.
Dus: De grafiek neemt constant af, maar de daling zelf neemt ook af.
De beschrijving van dit stijgen/dalen geven we weer met de afgeleide, de afgeleide in een punt is de 'rico'. De afgeleide geeft in elk punt weer hoe de grafiek gaat veranderen: Dalen of stijgen, en met welke snelheid.
Neem nu een punt op de grafiek 1/x2 dicht bij de oorsprong (dus dicht bij het punt x=0).
Je ziet aan de grafiek dat je met een kleine stap naar rechts, een grote daling gaat maken. Dus moet de afgeleide in dat punt:
-Negatief zijn: Want de grafiek neemt af, de rico van de grafiek in dat punt is negatief.
- Groot zijn: De afname/toename in dat punt is groot (in dit geval is het een afname, maar het kon net zo goed een toename zijn.)
Neem nu bijvoorbeeld x=12.
Dan zie je: De grafiek neemt in dat punt nog steeds af, is dus dalend. Maar de daling is nog maar heel klein. Dus de afgeleide ziet er zo uit:
-Negatief, want dalend
-Klein, want de afname/toename is klein
Nu weet je dus de rol van de afgeleide: Die beschrijft de richting van de grafiek (dalen of stijgen) en met hoeveel de grafiek stijgt of daalt( de absolute waarde van de afgeleide).
( Je gaf als afgeleide de functie : f ' (x)= -1/x3.
Bekijk die grafiek eens, en zie waarom die grafiek ook echt de afgeleide is van 1/x2.)
Kan iemand mij alsjeblieft met deze vragen helpen? Ik heb zelf al het één en ander geprobeerd maar ik kom er niet uit.
Op langere vluchten wil Hoogeland Air maaltijden serveren. Voor het leveren van de verpakte maaltijden komen twee leveranciers in aanmerking. Om de verpakte maaltijden te testen op houdbaarheid wordt van beide leveranciers een partij maaltijden gedurende langere tijd bewaard. Vervolgens wordt gekeken nar de fractie van elke partij die moet worden afgekeurd wegens te veel bacteriën.
De resultaten:
Leverancier 1: 96 van de 240 maaltijden moesten worden afgekeurd.
Leverancier 2: 144 van de 320 maaltijden moesten worden afgekeurd.
A.
Een betrouwbaarheidsinterval (confidence interval) voor de populatiefractie (population proportion) van maaltijden van leverancier 2 die moeten worden afgekeurd heeft als ondergrens 0,3835 en als bovengrens 0,5165. Bereken welke betrouwbaarheid hier gebruikt is (in procenten tot op 2 decimalen nauwkeurig).
B.
Toets of de proportie afgekeurde maaltijden verschilt voor beide leveranciers.
C.
Volgens 1 leverancier 1 is er met de geteste partij maaltijden iets misgegaan. Er wordt besloten om een nieuw onderzoek te doen naar de maaltijden van leverancier 1. Bereken hoe groot deze nieuwe steekproef moet worden, indien het 95%-betrouwbaarheidsinterval van de proportie afgekeurde maaltijden van leverancier 1 maximaal 0,06 breed mag worden (NB: breedte = 2x marge)
Alvast bedankt!
Op langere vluchten wil Hoogeland Air maaltijden serveren. Voor het leveren van de verpakte maaltijden komen twee leveranciers in aanmerking. Om de verpakte maaltijden te testen op houdbaarheid wordt van beide leveranciers een partij maaltijden gedurende langere tijd bewaard. Vervolgens wordt gekeken nar de fractie van elke partij die moet worden afgekeurd wegens te veel bacteriën.
De resultaten:
Leverancier 1: 96 van de 240 maaltijden moesten worden afgekeurd.
Leverancier 2: 144 van de 320 maaltijden moesten worden afgekeurd.
A.
Een betrouwbaarheidsinterval (confidence interval) voor de populatiefractie (population proportion) van maaltijden van leverancier 2 die moeten worden afgekeurd heeft als ondergrens 0,3835 en als bovengrens 0,5165. Bereken welke betrouwbaarheid hier gebruikt is (in procenten tot op 2 decimalen nauwkeurig).
B.
Toets of de proportie afgekeurde maaltijden verschilt voor beide leveranciers.
C.
Volgens 1 leverancier 1 is er met de geteste partij maaltijden iets misgegaan. Er wordt besloten om een nieuw onderzoek te doen naar de maaltijden van leverancier 1. Bereken hoe groot deze nieuwe steekproef moet worden, indien het 95%-betrouwbaarheidsinterval van de proportie afgekeurde maaltijden van leverancier 1 maximaal 0,06 breed mag worden (NB: breedte = 2x marge)
Alvast bedankt!
Hoever kom je met http://www.sigmazone.com/binomial_confidence_interval.htm ? En wat heb je al wel?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
A. p is X / N = 144 / 320 = 0.45
p ± m = 0.3835, 0.5165
m = z* x SEp
m = 0.0665
z* is onbekend daar ben je naar op zoek
SEp = (0.45(1-0.45)) / 320 = 0.0278
m / SEp = 0.0665/0.0278 = 2,3921
z* = 2,3921
oftewel het Confidence level zit tussen 98% en 99% volgens tabel D
maar het moet dus op 2 decimalen nauwkeurig dus ik zou niet weten wat dan te doen.
B. H0; p1=p2
Ha; p1p2
Z = (p1-p2)/SEdp
SEdp = p(1-p) (1/n1 + 1/n2) = 0.0423
p1 = x1/n1 = 0.4
p2 = x2/n2 = 0.45
p = (x1+x2)/(n1+n2) = 0.4286
n1 = 240
n2 = 320
Als je dan alles invult een Zwaarde van -1.1832
Dan kijk je in tabel A bij -1.19
Geeft een kans van 0.1170
Deze doe je keer 2, want het is een dubbelzijdige toets = 0.2340
En dan zit ik vast.
C. Hier heb ik eerlijk gezegd nog niet echt naar gekeken aangezien ik er al niet al
te veel vertrouwen meer in had
p ± m = 0.3835, 0.5165
m = z* x SEp
m = 0.0665
z* is onbekend daar ben je naar op zoek
SEp = (0.45(1-0.45)) / 320 = 0.0278
m / SEp = 0.0665/0.0278 = 2,3921
z* = 2,3921
oftewel het Confidence level zit tussen 98% en 99% volgens tabel D
maar het moet dus op 2 decimalen nauwkeurig dus ik zou niet weten wat dan te doen.
B. H0; p1=p2
Ha; p1p2
Z = (p1-p2)/SEdp
SEdp = p(1-p) (1/n1 + 1/n2) = 0.0423
p1 = x1/n1 = 0.4
p2 = x2/n2 = 0.45
p = (x1+x2)/(n1+n2) = 0.4286
n1 = 240
n2 = 320
Als je dan alles invult een Zwaarde van -1.1832
Dan kijk je in tabel A bij -1.19
Geeft een kans van 0.1170
Deze doe je keer 2, want het is een dubbelzijdige toets = 0.2340
En dan zit ik vast.
C. Hier heb ik eerlijk gezegd nog niet echt naar gekeken aangezien ik er al niet al
te veel vertrouwen meer in had
Dat gaat best goed.
A. Bij SEp vergeet je de wortel op te schrijven; 0.0278 klopt wel. Je moet dus geen tabel gebruiken maar wat nauwkeurigers. Met je rekenmachine zal het vast kunnen. Vergeet ook niet dat je tweezijdig toetst.
B. Je hebt geen significantieniveau gekozen. Gebruikelijk is alpha=0.05 of alpha=0.01. Omdat alpha < 0.2340 verwerp je H0 niet.
A. Bij SEp vergeet je de wortel op te schrijven; 0.0278 klopt wel. Je moet dus geen tabel gebruiken maar wat nauwkeurigers. Met je rekenmachine zal het vast kunnen. Vergeet ook niet dat je tweezijdig toetst.
B. Je hebt geen significantieniveau gekozen. Gebruikelijk is alpha=0.05 of alpha=0.01. Omdat alpha < 0.2340 verwerp je H0 niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dankje! Heb nu inderdaad A uitgevonden dat je dan kan doen met een functie genaamd 'Shadenorm' kom dan op een Confidence van 99,16% ?
En dat je deze testen ook allemaal uit kan voeren op je rekenmachine, wat natuurlijk een handig controleermiddel is dan.
Bij B is geen significantieniveau genoemd, dan moet je er dus zelf van één uitgaan?
Nu maar eens even bezig met C.
En dat je deze testen ook allemaal uit kan voeren op je rekenmachine, wat natuurlijk een handig controleermiddel is dan.
Bij B is geen significantieniveau genoemd, dan moet je er dus zelf van één uitgaan?
Nu maar eens even bezig met C
.
A. nee, ik zei nog dat je tweezijdig kijkt
B. klopt.
B. klopt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Jaa ik denk dat ik dan 0.0665/2 = 0.03325 --> 0.003325/0.0278 = 1.1960 moet doen dus mijn z* waarde wordt dan 1,1960 wat een Confidence-interval geeft van 88,42%?
Bepaal je een confidence interval mbv 0.0665 of ga je die 0.0665 opnieuw schatten? p(1-p) is het grootst als p=1/2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het is zo dat p ± m = (0.3835), (0.5165)
Waarbij p = 0.45 dus dan moet margin of error toch 0.0665 zijn?
m = z* x SEp waarbij je dus ook al SEp hebt = 0.0278
Dan lijkt het mij een kwestie van delen en de z* waarde vinden, wat zie ik dan over het hoofd?
Waarbij p = 0.45 dus dan moet margin of error toch 0.0665 zijn?
m = z* x SEp waarbij je dus ook al SEp hebt = 0.0278
Dan lijkt het mij een kwestie van delen en de z* waarde vinden, wat zie ik dan over het hoofd?
De p schat je natuurlijk adhv de nieuwe steekproef.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kan iemand de aangegeven stap in onderstaande som voor me verklaren?
Ik snap niet hoe je op de manier van uitschrijven van het gedeelte achter de pijl komt.
[ http://img94.imageshack.us/i/som25.png/ (copy/paste deze link) (copy/paste deze link) ]
Bij voorbaat dank, dat gaat me helpen met m'n tentamen morgen ;d
Ik snap niet hoe je op de manier van uitschrijven van het gedeelte achter de pijl komt.
[ http://img94.imageshack.us/i/som25.png/ (copy/paste deze link) (copy/paste deze link) ]
Bij voorbaat dank, dat gaat me helpen met m'n tentamen morgen ;d
Helpt het je als ik zeg dat (2-x)4=(2-x)*(2-x)3?quote:
Kan iemand de aangegeven stap in onderstaande som voor me verklaren?
Ik snap niet hoe je op de manier van uitschrijven van het gedeelte achter de pijl komt.
[ http://img94.imageshack.us/i/som25.png/ (copy/paste deze link) (copy/paste deze link) ]
Bij voorbaat dank, dat gaat me helpen met m'n tentamen morgen ;d
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
ik wilde net (2-x)^3 * (2-x) - (2-x)^3 *4x noemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Sorry maar ik snap niet wat je bedoelt..quote:
De p schat je natuurlijk adhv de nieuwe steekproef.
Ja, dat hielp! Super, bedankt. Ik miste deze koppeling even!quote:
[..]
Helpt het je als ik zeg dat (2-x)4=(2-x)*(2-x)3?
Ook bedankt voor het meedenken!quote:
ik wilde net (2-x)^3 * (2-x) - (2-x)^3 *4x noemen.
p = 0.45 komt van een oude steekproef. Als ik een nieuwe steekproef neem, vind ik een nieuwe p.quote:
[..]
Sorry maar ik snap niet wat je bedoelt..
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bepaal de afgeleide van f(x) = 1/x2 ook eens aan de hand van de definitie. Werk eerst het differentiequotiënt (f(x+h) - f(x))/h uit en neem dan de limiet voor h naar 0. Is meteen een goede algebra-oefening.quote:
[..]
Even nog een vraag hierover...
Welk boek gebruik je eigenlijk?
Maar jij hebt nu over C denk ik dan? Die had ik onderhand al gedaan en ik kwam dan op inderdaad een P nemen van 0,5 en dan doe je (Z*/2M)^2 --> (1.960/2x0.03)^2 = 1068 moet de nieuwe steekproef zijn. Ik zat nog met A ik snap niet wat daar nu het goede antwoord moet zijn en hoe die gevonden dient te worden?quote:
[..]
p = 0.45 komt van een oude steekproef. Als ik een nieuwe steekproef neem, vind ik een nieuwe p.
Daar gaat het mis. Bij die z hoort een kans (van overschreiding) van 0.0084. Dat geldt voor p+m. Bij p-m heb je z=-2,3921. Links daarvan zit ook een kans van 0.0084. Je krijgt dus 1-2*0.0084 = 98,32%.quote:z* = 2,3921
oftewel het Confidence level zit tussen 98% en 99% volgens tabel D
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh ik moest dus tabel A gebruiken super bedankt! Ik keek in tabel Dquote:
[..]
Daar gaat het mis. Bij die z hoort een kans (van overschreiding) van 0.0084. Dat geldt voor p+m. Bij p-m heb je z=-2,3921. Links daarvan zit ook een kans van 0.0084. Je krijgt dus 1-2*0.0084 = 98,32%.
Vraagje. In het basisboek wiskunde komt in hoofdstuk 1 dit stukje tekst voor:
Dit is dus het algoritme van Euclides. Natuurlijk zie ik dat het werkt, maar ik zie nog niet waarom. Is het bewijs eigenlijk eenvoudig (dat het al in hoofdstuk 1 gevraagd wordt) of is dit vrij gecompliceerd?quote:Een slim idee
Er is een methode om de ggd van twee getallen te bepalen waarbij priemontbindingen
niet nodig zijn, en die vaak veel sneller werkt. Het basisidee is dat de ggd van twee
getallen ook een deler moet zijn van het verschil van die twee getallen. Zie je ook
waarom dit zo is?
Zo moet ggd(4352, 4342) ook een deler zijn van 4352 4342 = 10. Het getal 10 heeft
alleen maar de priemdelers 2 en 5. Het is duidelijk dat 5 geen deler is van de beide
getallen, maar 2 wel, en dus geldt ggd(4352, 4342) = 2. Wie slim is kan zich door dit
idee te gebruiken veel rekenwerk besparen!
Het is vrij makkelijk. Als a een deler is, kun je de getallen schrijven als a*b en a*c. Wat kun je zeggen over het verschil?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je bedoelt dat b en c de getallen voorstellen waarvan de GGD gevraagd wordt?
Als het dat is, dan is het verschil van a*b en a*c het verschil tussen b en c maal de GGD...
Dus ik bedoel 30 en 12. verschil is 18, GGD = 6. 30*6 - 12*6 = 108. 108/6 = 18
Als het dat is, dan is het verschil van a*b en a*c het verschil tussen b en c maal de GGD...
Dus ik bedoel 30 en 12. verschil is 18, GGD = 6. 30*6 - 12*6 = 108. 108/6 = 18
Nee, dat bedoelt GlowMouse uiteraard niet, want b en c zijn niet hetzelfde als ab en ac.quote:
Je bedoelt dat b en c de getallen voorstellen waarvan de GGD gevraagd wordt?
Als het dat is, dan is het verschil van a*b en a*c het verschil tussen b en c maal de GGD...
Neem aan dat je twee natuurlijke getallen a en b hebt met a > b, die beiden een deler d hebben. Dan zijn er dus twee natuurlijke getallen m en n zodanig dat:
(1a) a = md
(1b) b = nd
En dan is dus:
(2) a - b = md - nd = (m - n)d,
zodat we kunnen concluderen dat d ook een deler is van (a - b).
Voor twee gebeurtenissen A en B geldt dat P(A|B) = P(B|A), beide ongelijk aan nul. Verder is de kans op gebeurtenis A gelijk aan 0.32. Bepaal de kans op gebeurtenis B.
Iemand enig idee welke regel ik hier überhaupt moet gebruiken?
Iemand enig idee welke regel ik hier überhaupt moet gebruiken?
P(A)P(B|A) = P(A en B)
P(B)P(A|B) = P(A en B)
die twee.
P(B)P(A|B) = P(A en B)
die twee.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja dus als A + B = A x B waarbij A = 0.32 ofzo?quote:
P(A)P(B|A) = P(A en B)
P(B)P(A|B) = P(A en B)
die twee.
en vergeet vooral niet te vermelden dat 1/x2 te schrijven is als x-2 .quote:
[..]
Bepaal de afgeleide van f(x) = 1/x2 ook eens aan de hand van de definitie. Werk eerst het differentiequotiënt (f(x+h) - f(x))/h uit en neem dan de limiet voor h naar 0. Is meteen een goede algebra-oefening.
Welk boek gebruik je eigenlijk?
dat is iets te kort door de bocht vrees ik..quote:
[..]
Ja dus als A + B = A x B waarbij A = 0.32 ofzo?
Zoals gezegd weten we dat
P(A|B) = P(B|A)
Hoe kun je dit gebruiken in:
P(A)P(B|A) = P(A en B)
P(B)P(A|B) = P(A en B)
Die notatie ken ik niet.quote:
[..]
Ja dus als A + B = A x B waarbij A = 0.32 ofzo?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
P(A)P(A|B) = P(B)P(A|B) = P(A en B) dus dan zou ik zeggen 0.32^2 = 0,1024?quote:
[..]
dat is iets te kort door de bocht vrees ik..
Zoals gezegd weten we dat
P(A|B) = P(B|A)
Hoe kun je dit gebruiken in:
P(A)P(B|A) = P(A en B)
P(B)P(A|B) = P(A en B)
Even een vraag tussendoor: Ik moet de functie f(x) = xWx - 3X differentieren. (W = Wortel)
Nu zit ik alleen met een probleem, want ik kan die eerste x niet plaatsen. De wortel en -3X krijg ik gedifferentieerd, waar die X kan ik nergens kwijt. Dit is wat ik nu heb: X.0,5X-0,5 - 3. Alleen wanneer ik dit controleer op mijn GR, dan klopt er geen snars van. Zonder de eerste X in de functie en afgeleide klopt het wel.
Nu zit ik alleen met een probleem, want ik kan die eerste x niet plaatsen. De wortel en -3X krijg ik gedifferentieerd, waar die X kan ik nergens kwijt. Dit is wat ik nu heb: X.0,5X-0,5 - 3. Alleen wanneer ik dit controleer op mijn GR, dan klopt er geen snars van. Zonder de eerste X in de functie en afgeleide klopt het wel.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
quote:
Even een vraag tussendoor: Ik moet de functie f(x) = xWx - 3X differentieren. (W = Wortel)
Nu zit ik alleen met een probleem, want ik kan die eerste x niet plaatsen. De wortel en -3X krijg ik gedifferentieerd, waar die X kan ik nergens kwijt. Dit is wat ik nu heb: X.0,5X-0,5 - 3. Alleen wanneer ik dit controleer op mijn GR, dan klopt er geen snars van. Zonder de eerste X in de functie en afgeleide klopt het wel.
Dan lukt het je vast
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Verrek... Is dit de regel in dergelijk samestellingen? Want die had ik niet verwacht.quote:
[..]
[ afbeelding ]
Dan lukt het je vast
Waar maak jij trouwens die formule mee?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
In dit geval wel, je kan overigens ook de productregel gebruiken voorquote:
[..]
Verrek... Is dit de regel in dergelijk samestellingen? Want die had ik niet verwacht.
Waar maak jij trouwens die formule mee?
Die formule heb ik opgemaakt met word, maar je kan ook LaTeX code gebruiken (http://www.forkosh.com/mimetextutorial.html) en die dan hier (http://betahw.mine.nu/index.php) invullen om vervolgens de formule op fok te kunnen plaatsen.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
0.32^2 = 0,1024 kan ik ook zo zeggen, dat is altijd waar. Maar je wilt P(B) weten. P(A)P(A|B) = P(B)P(B|A)quote:
[..]
P(A)P(A|B) = P(B)P(B|A) = P(A en B) dus dan zou ik zeggen 0.32^2 = 0,1024?
nu het gegeven gebruiken dat P(A|B) = P(B|A) (!= 0)
P(A)P(A|B) = P(B)P(A|B)
en nu weet je P(A)=0.32.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bedankt voor die handige link. Dat is wel erg handig aangezien ik Texmaker onder Ubuntu gebruik.quote:
[..]
... dan hier (http://betahw.mine.nu/index.php) invullen om vervolgens de formule op fok te kunnen plaatsen.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Kan iemand mij vertellen hoe ik de volgende vergelijking het makkelijkste oplos? Ik weet niet goed hoe ik machten moet aanpakken namelijk.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Deze valt ook met wat nadenken op te lossen ( je hebt een kwadraat, je moet op -1 uitkomen..), maar hier een methode:quote:
Kan iemand mij vertellen hoe ik de volgende vergelijking het makkelijkste oplos? Ik weet niet goed hoe ik machten moet aanpakken namelijk.
[ afbeelding ]
Haal -1 naar links zodat je
x2 -2x + 1=0
krijgt. Kijk dan of je kunt ontbinden in factoren. Probeer dit altijd als eerste, want dit heb je gewoon nodig.
In dit geval zie je dus dat je de functie zo kunt ontbinden:
(x-1)(x-1)=0
Dus kan je ook de oplossing gemakkelijk aflezen: x=1
Lukt dit niet, dan kun je dit toepassen.
Bedankt. Ik was intussen op hetzelfde onderwerp uitgekomen. Wanneer leer je dit soort algebraïsche dingen normaal eigenlijk op de middelbare school? Ik ken dit allemaal niet namelijk (en doe dus aan zelfstudie).quote:
[..]
Deze valt ook met wat nadenken op te lossen ( je hebt een kwadraat, je moet op -1 uitkomen..), maar hier een methode:
Haal -1 naar links zodat je
x2 -2x + 1=0
krijgt. Kijk dan of je kunt ontbinden in factoren. Probeer dit altijd als eerste, want dit heb je gewoon nodig.
In dit geval zie je dus dat je de functie zo kunt ontbinden:
(x-1)(x-1)=0
Dus kan je ook de oplossing gemakkelijk aflezen: x=1
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Dit leer je al vrij snel, ontbinden in factoren is de basis voor het oplossen van kwadratische functies.quote:
[..]
Bedankt. Ik was intussen op hetzelfde onderwerp uitgekomen. Wanneer leer je dit soort algebraïsche dingen normaal eigenlijk op de middelbare school? Ik ken dit allemaal niet namelijk (en doe dus aan zelfstudie).
Heb zeker niet goed opgelet in de MAVO.quote:
[..]
Dit leer je al vrij snel, ontbinden in factoren is de basis voor het oplossen van kwadratische functies.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Waarvoor doe je trouwens zelfstudie als ik vragen mag?quote:
[..]
Heb zeker niet goed opgelet in de MAVO.
Voor een BÈTA-studiequote:
[..]
Waarvoor doe je trouwens zelfstudie als ik vragen mag?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ja hoor. Gaat hartstikke goed. Vind het ook een leuk onderwerp, dus dat scheelt.quote:
[..]
Succes!
Lukt het nu trouwens beter met de afgeleide? Snap je nu wat de afgeleide is?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik heb een (simpel?) statistiek vraagje, waarbij je wat concepten nodig hebt die voor mij al een tijdje geleden zijn.
Stel, ik heb de verzameling reëele getallen R. Ik neem een eindige deelverzameling X en een eindige deelverzameling Y van R, waarbij het aantal elementen |X| van de verzameling X groter is dan het aantal elementen |Y| van de verzameling Y:
|X|>|Y|
Nu ga je een willekeurig getal in R genereren. Is de kans dat dit getal in X ligt nu groter dan in Y? Mijn gevoel zegt van niet, aangezien volgens mij zowel X als Y maat 0 hebben in R. Klopt deze naïeve redenatie?
En zou dit ook gelden als X en Y beide oneindig zijn, maar wel aftelbaar, met verschillende kardinaliteiten?
Stel, ik heb de verzameling reëele getallen R. Ik neem een eindige deelverzameling X en een eindige deelverzameling Y van R, waarbij het aantal elementen |X| van de verzameling X groter is dan het aantal elementen |Y| van de verzameling Y:
|X|>|Y|
Nu ga je een willekeurig getal in R genereren. Is de kans dat dit getal in X ligt nu groter dan in Y? Mijn gevoel zegt van niet, aangezien volgens mij zowel X als Y maat 0 hebben in R. Klopt deze naïeve redenatie?
En zou dit ook gelden als X en Y beide oneindig zijn, maar wel aftelbaar, met verschillende kardinaliteiten?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Dat is kansrekening, en je redenering met de kansmaat klopt. Beide kansen zijn 0. Ook bij aftelbare verzamelingen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Da's een snel antwoord, dank je welquote:Op zaterdag 16 april 2011 21:55 schreef GlowMouse het volgende:
Dat is kansrekening, en je redenering met de kansmaat klopt. Beide kansen zijn 0. Ook bij aftelbare verzamelingen.
Ik zal es opzoeken hoe je dit precies beredeneert
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Hallo,
Zij X1, X2, ... geometrische stochastische variabelen met parameter a. Zij N Fs verdeeld (Fs= first succes, d.w.z. p(X=k) = p (1-p)k-1). Stel dat alle stochastische variabelen onafhankelijk zijn en zet Y=X1 + ... + XN.
Ik moet laten zien dat Y geometrisch verdeeld is met een bepaalde parameter b die ik ook moet bepalen.
Ik denk dat ik kan gebruiken dat phiY (t) = gN(phiX(t)), waarbij phi staat voor de karakteristieke functie en g voor de kansgenererende functie.
Ik gebruik dat phiX(t) = a/(1-(1-a)eit) en de definitie van de kansgenererende functie: gN(t) = sum_{n=0}^{\infty} tn P(N=n) = sum_{n=0}^{\infty} tn p(1-p)n-1.
Als ik vervolgens phiX in gN(t) ga invullen dan krijg ik een best lelijke uitdrukking waaruit ik niet kan opmaken dat Y geometrisch verdeeld is. Klopt mijn aanpak een beetje of doe ik het verkeerd?
Alvast bedankt.
Zij X1, X2, ... geometrische stochastische variabelen met parameter a. Zij N Fs verdeeld (Fs= first succes, d.w.z. p(X=k) = p (1-p)k-1). Stel dat alle stochastische variabelen onafhankelijk zijn en zet Y=X1 + ... + XN.
Ik moet laten zien dat Y geometrisch verdeeld is met een bepaalde parameter b die ik ook moet bepalen.
Ik denk dat ik kan gebruiken dat phiY (t) = gN(phiX(t)), waarbij phi staat voor de karakteristieke functie en g voor de kansgenererende functie.
Ik gebruik dat phiX(t) = a/(1-(1-a)eit) en de definitie van de kansgenererende functie: gN(t) = sum_{n=0}^{\infty} tn P(N=n) = sum_{n=0}^{\infty} tn p(1-p)n-1.
Als ik vervolgens phiX in gN(t) ga invullen dan krijg ik een best lelijke uitdrukking waaruit ik niet kan opmaken dat Y geometrisch verdeeld is. Klopt mijn aanpak een beetje of doe ik het verkeerd?
Alvast bedankt.
De opgave was toch echt om te laten zien dat Y geometrisch verdeeld is.... Maar klopt mijn aanpak wel en heb jij op die manier laten zien dat Y negatief binomiaal verdeeld is?
edit: Volgens mij heb je er geen rekening mee gehouden dat N ook nog een stochastische variabele is...? Anders doe je inderdaad de karakteristieke functie van de geometrische verdeling tot de n-de macht en dan verkrijg je de karakteristieke functie voor de negatieve binomiale verdeling.
edit: Volgens mij heb je er geen rekening mee gehouden dat N ook nog een stochastische variabele is...? Anders doe je inderdaad de karakteristieke functie van de geometrische verdeling tot de n-de macht en dan verkrijg je de karakteristieke functie voor de negatieve binomiale verdeling.
Ah, N is een stochast. Dan had je beter P(N=k) kunnen schrijven.
Die aanpak werkt nog steeds, behalve dat je dan nog de N eruit moet sommeren (P(Y=k) = E(P(Y=k | N))quote:
edit: Volgens mij heb je er geen rekening mee gehouden dat N ook nog een stochastische variabele is...? Anders doe je inderdaad de karakteristieke functie van de geometrische verdeling tot de n-de macht en dan verkrijg je de karakteristieke functie voor de negatieve binomiale verdeling.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wat moet het nu uiteindelijk worden? En waarom? Want het lukt me zelfs niet om te vinden met mijn boek erbij.quote:
[..]
0.32^2 = 0,1024 kan ik ook zo zeggen, dat is altijd waar. Maar je wilt P(B) weten. P(A)P(A|B) = P(B)P(B|A)
nu het gegeven gebruiken dat P(A|B) = P(B|A) (!= 0)
P(A)P(A|B) = P(B)P(A|B)
en nu weet je P(A)=0.32.
Je hebt gelijk, typfoutje.quote:
Ah, N is een stochast. Dan had je beter P(N=k) kunnen schrijven.
Deze formule ken ik niet... Waar komt dat vandaan?quote:Die aanpak werkt nog steeds, behalve dat je dan nog de N eruit moet sommeren (P(Y=k) = E(P(Y=k | N))
edit: of staat E soms voor de som, en niet voor expected value?
Pak P(A)P(A|B) = P(B)P(A|B) en deel door P(A|B).quote:
[..]
Wat moet het nu uiteindelijk worden? En waarom? Want het lukt me zelfs niet om te vinden met mijn boek erbij.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
E is uiteraard expectation; http://en.wikipedia.org/wiki/Conditioning_%28probability%29quote:
Deze formule ken ik niet... Waar komt dat vandaan?
edit: of staat E soms voor de som, en niet voor expected value?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Die formule vind ik niet terug op die wikipagina.quote:
[..]
E is uiteraard expectation; http://en.wikipedia.org/wiki/Conditioning_%28probability%29
Ah, ik ken die formule wel alleen dan in een andere vorm. Nevermind...
Het idee is dus dat je het volgende doet:
P(y=k) = E(P(Y=k) | N) = E( [(N+k-1)nCr k] aN (1-a)k ),
om dat vervolgens met de definitie van de verwachtingswaarde te berekenen?
Dit wil ik wel proberen, maar dit heeft niks met mijn aanpak te maken en het wordt denk ik een erg omslachtige berekening. Heb je enig idee of er bij mijn methode iets mis ging?
P(y=k) = E(P(Y=k) | N) = E( [(N+k-1)nCr k] aN (1-a)k ),
om dat vervolgens met de definitie van de verwachtingswaarde te berekenen?
Dit wil ik wel proberen, maar dit heeft niks met mijn aanpak te maken en het wordt denk ik een erg omslachtige berekening. Heb je enig idee of er bij mijn methode iets mis ging?
Als je formules juist zijn, haal je een p/(1-p) voor de som en heb je een mooie meetkundige reeks. Dat is toch niet zo lelijk?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Klopt, valt nog wel mee. Dan krijg ik gN(t) = [p/(1-p)] * [(1-(t-tp)n)/(1-t+tp)]. Maar dan moet ik nog t->a/(1-(1-a)eit) gaan invullen en dat wordt niet leuk. Volgens mathematica komt er zo te zien niet het goede antwoord uit...quote:
Als je formules juist zijn, haal je een p/(1-p) voor de som en heb je een mooie meetkundige reeks. Dat is toch niet zo lelijk?
http://www.wolframalpha.c(...)C++++0%2C+Infinity}]
Om een willekeurig getal in R te genereren, moet je eerst een kansverdeling op R aangeven aan de hand waarvan je het willekeurige getal genereert.quote:
Nu ga je een willekeurig getal in R genereren.
In hoeverre is die kansverdeling van invloed op de eindconclusie?quote:
[..]
Om een willekeurig getal in R te genereren, moet je eerst een kansverdeling op R aangeven aan de hand waarvan je het willekeurige getal genereert.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
De invloed is er als niet elke waarde in R aangenomen kan worden.quote:
[..]
In hoeverre is die kansverdeling van invloed op de eindconclusie?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wel, er zijn kansverdelingen waarbij sommige elementen een positieve kans hebben.quote:
[..]
De invloed is er als niet elke waarde in R aangenomen kan worden.
Kun je een voorbeeld geven?quote:
[..]
Wel, er zijn kansverdelingen waarbij sommige elementen een positieve kans hebben.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
X={1,2}
Y = {2,3,4}
Definieer Z als:
- N(0,1) verdeeld met kans 0.5
- 1 met kans 0.5.
Dit soort gemengde continu/discrete verdelingen komt tevoorschijn bij censored regressiemodellen.
[ Bericht 6% gewijzigd door GlowMouse op 18-04-2011 09:37:04 ]
Y = {2,3,4}
Definieer Z als:
- N(0,1) verdeeld met kans 0.5
- 1 met kans 0.5.
Dit soort gemengde continu/discrete verdelingen komt tevoorschijn bij censored regressiemodellen.
[ Bericht 6% gewijzigd door GlowMouse op 18-04-2011 09:37:04 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik ben bezig met differentiëren volgens de quotiëntregel en nu kloppen mijn antwoorden allemaal, alleen is de vorm nog niet genoeg vereenvoudigd. Echter zou ik niet weten hoe/via welke methode ik van het antwoord op onderstaande formule de uiteindelijke formule krijg. Wie kan mij dit vertellen?
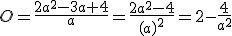
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik weet niet wat jij doet, maar ik zou je rekenregels omtrent breuken nog maar es goed doornemen
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Verrek. Hij is eenvoudiger dan ik had verwacht. Bedankt!quote:
[ afbeelding ]
Ik weet niet wat jij doet, maar ik zou je rekenregels omtrent breuken nog maar es goed doornemen
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
P(A)P(A|B) = 0.32 x 0.32quote:
[..]
Pak P(A)P(A|B) = P(B)P(A|B) en deel door P(A|B).
P(A|B) = 0.32
Dus (0.32 x 0.32) / 0.32 = 0.32?
In de vraag was niet gegeven dat P(A|B) = 0.32.quote:
[..]
P(A)P(A|B) = 0.32 x 0.32
P(A|B) = 0.32
Dus (0.32 x 0.32) / 0.32 = 0.32?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik weet het niet danquote:
[..]
In de vraag was niet gegeven dat P(A|B) = 0.32.
Het is echt heel simpel:quote:
P(A)P(B|A) = P(A en B)= P(B)P(A|B)
P(B|A)=P(A|B) geeft:
P(A)P(A|B) = P(B)P(A|B)
en dus
P(A)=P(B)
En het is gegeven dat P(A)=0.32, dus P(B)=0.32.
Som 1: 2(x2-3x-24)=16
1e stap: 2(x2-3x-10)=2
2e stap: x2-3x-10
A: 1
B: -3
C: -10
(3)2-(4x1x-10) = D= -360
Ik kom er dus niet uit, zoals je ziet
1e stap: 2(x2-3x-10)=2
2e stap: x2-3x-10
A: 1
B: -3
C: -10
(3)2-(4x1x-10) = D= -360
Ik kom er dus niet uit, zoals je ziet
Je wilt een kwadratische vergelijking oplossen?quote:
Som 1: 2(x2-3x-24)=16
1e stap: 2(x2-3x-10)=2
2e stap: x2-3x-10
A: 1
B: -3
C: -10
(3)2-(4x1x-10) = D= -360
Ik kom er dus niet uit, zoals je ziet
Ik zou eerst gezamelijke factoren wegdelen; hier is dat 2, dan krijg je
Dan haal je de 8 naar de andere kant, en krijg je
Nu kun je de ABC formule er op loslaten, met A=1, B=-3, C=-16 (mintekens niet vergeten!):
Zou zelf wel ff narekenen op rekenfouten
Je had natuurlijk ook gelijk de ABC formule op
kunnen loslaten (haken uitwerken, en de 16 naar links halen). Het eindantwoord is dan hetzelfde, zoals je zelf kunt checken.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Inderdaad Haus, kijk nog maar eens goed ...quote:
[..]
Zou zelf wel ff narekenen op rekenfouten
Ja, ik zie het al, -24-8 is plots -16 geworden, moet -32 zijn.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
De meeste mensen zijn risico avers, dit betekent dat ze liever 50 euro met zekerheid ontvangen dan 0 euro met kans een 0,5 en 100 euro met kans 0,5.
Het bedrag dat Klaas kan ontvangen hangt af van het toeval, bij de onderstaande vragen is de kansverdeling van de mogelijke bedragen gegeven. Als het gemiddelde van de kansverdelingen wordt weergegeven door µ en de standaarddeviatie door , dan is de waarde W die Klaas toekent aan het ontvangen bedrag gelijk aan: W = µ - 0,1 .
b) De kansvariabele (random-) X is binomiaal verdeeld met n = 4 en p = 0,6. Wat is de waarde (W) die Klaas toekent aan het te ontvangen bedrag 25X euro, m.a.w. bereken W(25X)?
np = 2,4
= 0.9798
Wat moet ik nu berekenen?
c) De kansvariabele Y is normaal verdeeld met gemiddelde µ en standaard deviatie . De waarde die Klaas toekent aan het te ontvangen bedrag Y euro is 45 (dus: W(Y)=45). Bovendien is er een kans van 10 procent dat Y groter is dan 100 euro. Bepaal µ en .
Kom tot InvNorm(0.9,45,100) = 173.16 en dan?
Het bedrag dat Klaas kan ontvangen hangt af van het toeval, bij de onderstaande vragen is de kansverdeling van de mogelijke bedragen gegeven. Als het gemiddelde van de kansverdelingen wordt weergegeven door µ en de standaarddeviatie door , dan is de waarde W die Klaas toekent aan het ontvangen bedrag gelijk aan: W = µ - 0,1 .
b) De kansvariabele (random-) X is binomiaal verdeeld met n = 4 en p = 0,6. Wat is de waarde (W) die Klaas toekent aan het te ontvangen bedrag 25X euro, m.a.w. bereken W(25X)?
np = 2,4
= 0.9798
Wat moet ik nu berekenen?
c) De kansvariabele Y is normaal verdeeld met gemiddelde µ en standaard deviatie . De waarde die Klaas toekent aan het te ontvangen bedrag Y euro is 45 (dus: W(Y)=45). Bovendien is er een kans van 10 procent dat Y groter is dan 100 euro. Bepaal µ en .
Kom tot InvNorm(0.9,45,100) = 173.16 en dan?
b) van X weet je dat mu=2,4 en sigma=0.98. Dan weet je dat ook van 25X, en dan kan je W berekenen.
c) 45 = mu - 0,1 sigma, en (100-sigma)/mu = invNorm(0.9). En dan oplossen.
c) 45 = mu - 0,1 sigma, en (100-sigma)/mu = invNorm(0.9). En dan oplossen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
B = 60 en 4.9 dus W = mu(60)- 0,1 x sigma(4,9) dus = 59,51quote:
b) van X weet je dat mu=2,4 en sigma=0.98. Dan weet je dat ook van 25X, en dan kan je W berekenen.
c) 45 = mu - 0,1 sigma, en (100-sigma)/mu = invNorm(0.9). En dan oplossen.
C = Snap niet wat ik moet doen kan je het antwoord vertellen aub, want heb morgen het tentamen
Bedankt voor al je hulp!
B 4,9 klopt niet, dat zou je hebben als je 25 ongecorreleerde X'en op zou tellen.
C reken invNorm(0.9) uit en je hebt twee vergelijkingen
C reken invNorm(0.9) uit en je hebt twee vergelijkingen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wie kan mij vertellen hoe ik deze vergelijking kan oplossen? Ontbinden in factoren lijkt mij namelijk niet te werken of ik maak een denkfout. Ik heb het antwoord overigens wel gevonden via mijn GRM, maar ik wil graag weten hoe het zou moeten.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Pak links en rechts de natuurlijke logaritme (dat is een strikt stijgende functie, dus daardoor introduceer je geen extra oplossingen).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Als je doet wat GlowMouse zegt vervalt de exponent en krijg je gewoon 2x = 1-x, -x naar links halen krijg je 3x = 1 -> x = 1/3quote:
Wie kan mij vertellen hoe ik deze vergelijking kan oplossen? Ontbinden in factoren lijkt mij namelijk niet te werken of ik maak een denkfout. Ik heb het antwoord overigens wel gevonden via mijn GRM, maar ik wil graag weten hoe het zou moeten.
[ afbeelding ]
Ik heb een vakantietaak (ja dat bestaat nog) voor wiskunde 
Ik heb vergelijkingen op te lossen naar y.
Bv. 2x+3y =2
3y=-2x=2
y=-2/3x +2/3
Weet iemand een online calculator voor dit?
Ik had een handige site wat dit betreft, maar die ben ik kwijt.
Ik heb vergelijkingen op te lossen naar y.
Bv. 2x+3y =2
3y=-2x=2
y=-2/3x +2/3
Weet iemand een online calculator voor dit?
Ik had een handige site wat dit betreft, maar die ben ik kwijt.
Deze vergelijkingen zijn dusdanig eenvoudig dat je meer tijd kwijt bent met het invoeren ervan en het overnemen van de uitwerkingen dan ze rechtstreeks met pen en papier te herleiden. Bovendien leer je er dan ook nog iets van, en dat zal toch wel de bedoeling zijn van die taak.quote:
Ik heb een vakantietaak (ja dat bestaat nog) voor wiskunde
Ik heb vergelijkingen op te lossen naar y.
Bv. 2x+3y =2
3y=-2x+2
y=-2/3x +2/3
Weet iemand een online calculator voor dit?
Ik had een handige site wat dit betreft, maar die ben ik kwijt.
http://www.wolframalpha.com/quote:
Ik heb een vakantietaak (ja dat bestaat nog) voor wiskunde
Ik heb vergelijkingen op te lossen naar y.
Bv. 2x+3y =2
3y=-2x=2
y=-2/3x +2/3
Weet iemand een online calculator voor dit?
Ik had een handige site wat dit betreft, maar die ben ik kwijt.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Bereken BC
Hoe kom ik hier uit?
Dingen die ik mag gebruiken zijn:
1. De stelling van Pythagoras
2. Gelijkvormige driehoeken (snavel- en zandloperfiguren)
3. Goniometrische verhoudingen in rechthoekige driehoeken
4. De 'zijde x hoogte' methode
5. De sinusregel
De uitkomst ligt rond de 60 centimeter.
Onvoldoende gegevens: je kan C willekeurig over de lijn BC verleggen en dan voldoet de configuratie nog altijd aan de gegevens.
Is hoek BAC niet toevallig 90 graden?quote:Op donderdag 21 april 2011 18:17 schreef verwarmingsbank het volgende:
[ afbeelding ]
Bereken BC
Hoe kom ik hier uit?
Dingen die ik mag gebruiken zijn:
1. De stelling van Pythagoras
2. Gelijkvormige driehoeken (snavel- en zandloperfiguren)
3. Goniometrische verhoudingen in rechthoekige driehoeken
4. De 'zijde x hoogte' methode
5. De sinusregel
De uitkomst ligt rond de 60 centimeter.
Nee, want dan zou BC langer zijn dan AB terwijl de vragensteller beweert dat BC ca. 60 cm zou moeten zijn.quote:
[..]
Is hoek BAC niet toevallig 90 graden?
Ik vind dit een boeiende vraag, alleen heb ik geen idee hoe ik moet beginnen.
Kan iemand me op weg helpen? Dan kan ik dan zien of ik genoeg intellect heb om het verder op te kunnen lossen
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Ik zou zowel positie als verplaatsing in poolcoördinaten uitdrukken, en dan kijken naar de lengte van de som.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Probeer eerst eens de kans te bepalen dat de muis van de tafel afloopt voor een gegeven afstand d van het vertrekpunt van de muis totaan het midelpunt van de tafel. Als de muis precies in het middelpunt van de tafel begint is die kans 0, want dan bereikt hij altijd juist de rand, ongeacht de richting. Als de muis daarentegen start vanaf een punt op de rand, dan is de kans om te eindigen op een punt buiten de tafel 2/3 aangezien alle richtingen even waarschijnlijk zijn en aangezien je dan een hoek hebt van 120 graden tussen de twee radii vanaf het punt op de rand van de tafel naar de snijpunten van de twee cirkels (de tafel met radius 1 meter en de actieradius van 1 meter van de muis vanaf het vertrekpunt op de rand van de tafel).quote:
[ afbeelding ]
Ik vind dit een boeiende vraag, alleen heb ik geen idee hoe ik moet beginnen.
Kan iemand me op weg helpen? Dan kan ik dan zien of ik genoeg intellect heb om het verder op te kunnen lossen
Bedankt voor je reactie, maar het is nog steeds niet goed. In het achterhoofd houden dat het antwoord: -4 of 7 moet zijn, komt deze berekening niet uit.quote:
[..]
Je wilt een kwadratische vergelijking oplossen?
[ afbeelding ]
Ik zou eerst gezamelijke factoren wegdelen; hier is dat 2, dan krijg je
[ afbeelding ]
Dan haal je de 8 naar de andere kant, en krijg je
[ afbeelding ]
Nu kun je de ABC formule er op loslaten, met A=1, B=-3, C=-16 (mintekens niet vergeten!):
[ afbeelding ]
Zou zelf wel ff narekenen op rekenfouten
Je had natuurlijk ook gelijk de ABC formule op
[ afbeelding ]
kunnen loslaten (haken uitwerken, en de 16 naar links halen). Het eindantwoord is dan hetzelfde, zoals je zelf kunt checken.
Ik had het volgende nog geprobeerd:
2(x2-3x-24)=16
2(x2-3x-10)=2^4
x2-3x-10=^4
En dan ABC....?
Of niet?
bedoel je met 2(x2-3x-24) soms 2^(x2-3x-24)?quote:
[..]
Bedankt voor je reactie, maar het is nog steeds niet goed. In het achterhoofd houden dat het antwoord: -4 of 7 moet zijn, komt deze berekening niet uit.
Ik had het volgende nog geprobeerd:
2(x2-3x-24)=16
2(x2-3x-10)=2^4
x2-3x-10=^4
En dan ABC....?
2^(x2-3x-24)=16quote:
[..]
bedoel je met 2(x2-3x-24) soms 2^(x2-3x-24)?
Of niet?
Ok, je had de functie al herleid totquote:
x2-3x-24=4
Dan is de post van Haushofer weer nuttig, want op die methode moet je dit oplossen.
Maar het kan natuurlijk ook zonder de ABC-formule, weet je wat ontbinden in factoren is?
[ Bericht 5% gewijzigd door Siddartha op 22-04-2011 12:26:22 ]
Middag,
Ben al een aantal weken bezig met het herkansen van vastgoed rekenen.
Hoop dat jullie me kunnen helpen, er zit een excel bestand in de bijlage, maar daar zit blijkbaar een fout in die ik er niet uit kan halen, weet iemand het?
http://img841.imageshack.us/i/excelk.jpg/ (copy/paste deze link)
Als je de fout zie, en je wil het excel bestand om het te checken dan kun je me ff pmen.
Ben al een aantal weken bezig met het herkansen van vastgoed rekenen.
Hoop dat jullie me kunnen helpen, er zit een excel bestand in de bijlage, maar daar zit blijkbaar een fout in die ik er niet uit kan halen, weet iemand het?
http://img841.imageshack.us/i/excelk.jpg/ (copy/paste deze link)
Als je de fout zie, en je wil het excel bestand om het te checken dan kun je me ff pmen.
Uhum ja het is misschien wat onduidelijk,
http://img855.imageshack.us/i/excel.jpg/ (copy/paste deze link)
Uploaded with http://imageshack.us (copy/paste deze link)
http://img855.imageshack.us/i/excel.jpg/ (copy/paste deze link)
Uploaded with http://imageshack.us (copy/paste deze link)
Waarde investering snap ik niet. Waarom is er in het eerste jaar geen waardevermeerdering?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Waarinvestering stijgt elk jaar met 2%, en in het 1ste jaar begin je met een start bedrag, die we gekregen hebben.
dan is er in het eerste jaar dus al een stijging.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Vraagje..
Ik heb een bankroll van 20,000, daarvan investeer ik 2.5% (500 dus). Op die 500 maak ik 5% winst, dus 25. Ofwel de return is 525. Bankroll na investering 1 is dus 20,025. Die 20,025 gaat dus via hetzelfde systeem weer in de cycle. Nu wil ik bepalen hoeveel mijn bankroll is na x cycles.
Ik heb een bankroll van 20,000, daarvan investeer ik 2.5% (500 dus). Op die 500 maak ik 5% winst, dus 25. Ofwel de return is 525. Bankroll na investering 1 is dus 20,025. Die 20,025 gaat dus via hetzelfde systeem weer in de cycle. Nu wil ik bepalen hoeveel mijn bankroll is na x cycles.
Je investeert steeds 5% van de 2.5% van het totale bedrag.
0,05 * 0,025 = 0,00125
Bedrag = 20000 * 1,00125 ^ aantal cycli
0,05 * 0,025 = 0,00125
Bedrag = 20000 * 1,00125 ^ aantal cycli
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Hey nog bedankt, ik heb hem vandaag gehaald bij de biebquote:
[..]
Er zijn legio boeken over getaltheorie geschreven, op alle mogelijke niveaus. Misschien is "Getaltheorie voor beginners" van Frits Beukers iets voor je?
, bevalt wel tot nu toe
Finally, someone let me out of my cage
Iemand die mij misschien wil helpen met uitleggen hoe ze hier van stap 3 naar stap 4 komen?
Het gaat om het ARDL model.
Het gaat om het ARDL model.
Ze herhalen het substitueren van y. De eerste term wordt delta*(1+theta1 + theta1² + ...), en dat is delta/(1-theta1).
In de rest zie je een patroontje dat ze met die som precies overnemen.
In de rest zie je een patroontje dat ze met die som precies overnemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe kun je makkelijk het kleinst gemeenschappelijke veelvoud vinden van bijvoorbeeld
. Is dat gewoon een kwestie van "proberen" tot dat je hem vindt?
Ik zou ontbinden in factoren. Het kgv moet deelbaar zijn door 8, a, b, a+2, en a²-b.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ok, zo.
8ab = 2*2*2*a*b
8ab+16b = 2*2*2*b(a+2)
En dan moet ik alles samenvoegen en dan krijg ik
Bedankt!
8ab = 2*2*2*a*b
8ab+16b = 2*2*2*b(a+2)
En dan moet ik alles samenvoegen en dan krijg ik
Bedankt!
Inderdaad, alleen krijg je nu bij bv. a=10 een onjuist antwoord.
Bijvoorbeeld met a=10 en b=1 moet je kgv(80, 96, 96) vinden, en dat is geen 80*96.
Bijvoorbeeld met a=10 en b=1 moet je kgv(80, 96, 96) vinden, en dat is geen 80*96.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
GlowMouse, nu ben ik in de war. Het KGV van 80,96,96 is idd geen 80*96, maar 480. Dus ik heb niet het KGV genomen? Ik dacht dat ik het goed had want dit kwam uit het antwoordenboekje:
Het 'probleem' is dat 8 en a-2 dezelfde factoren zijn. De vraag is of dat belangrijk is in dit geval, maar je zou dan dingen moeten uitsplitsen voor randgevallen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh zo, ik snap waarom je dan a=10 nam, maar volgens mij is dit niet echt belangrijk voor deze som. Bij een andere a zou het wel goed uitkomen lijkt het mij....
Zij (|R, Borel, lesbegue maat) een measure space, f:|R->|R measurable zodat u(x,t):=exp(xt)f(x) Lesbegue-integreerbaar is voor iedere t in (a,b), waarbij a,b in |R zitten. Is de Lesbegue-integraal van u(x,t) over x in |R differentieerbaar voor iedere t in (a,b)?
Als het zo is, dan is het voldoende om aan te tonen dat u(x,t) differentieerbaar is naar t, lesbegue integreerbaar is over x in |R, en dat de afgeleide kleiner of gelijk is aan een lesbegue integreerbare functie q(x). De eerste twee dingen zijn duidelijk, maar in welke richting moet ik denken voor die q(x)?
Alvast bedankt.
Als het zo is, dan is het voldoende om aan te tonen dat u(x,t) differentieerbaar is naar t, lesbegue integreerbaar is over x in |R, en dat de afgeleide kleiner of gelijk is aan een lesbegue integreerbare functie q(x). De eerste twee dingen zijn duidelijk, maar in welke richting moet ik denken voor die q(x)?
Alvast bedankt.
Ik zit met een differentiatie waar ik niet uitkom. Het gaat om een combinatie van de kettingregel met de productregel:
En daar krijg ik (i.c.m. de kettingregel) de volgende afgeleide uit:
Nu is de afgeleide verder in orde, maar zodra ik het ga vereenvoudigen raak ik ergens -120X kwijt. Ik snap niet waar het zit, want ik heb echt alles geprobeerd... Het moet volgens mij antwoordenboek het volgende worden (en dit lijkt ook te kloppen):
En daar krijg ik (i.c.m. de kettingregel) de volgende afgeleide uit:
Nu is de afgeleide verder in orde, maar zodra ik het ga vereenvoudigen raak ik ergens -120X kwijt. Ik snap niet waar het zit, want ik heb echt alles geprobeerd... Het moet volgens mij antwoordenboek het volgende worden (en dit lijkt ook te kloppen):
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Mis jij hem ook bij de linkerhelft?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ohh wacht te snel gerekend hij is wel goed.
(30-2x)^2 = 900 - 120x +4x^2
(x)(-4(30-2x) = -120x + 8x^2
(30-2x)^2 = 900 - 120x +4x^2
(x)(-4(30-2x) = -120x + 8x^2
Waar komt die eerste -120x vandaan? Ik zie namelijk alleen 900 (30^2) en 4x^2 (2x^2)quote:
Ohh wacht te snel gerekend hij is wel goed.
(30-2x)^2 = 900 - 120x +4x^2
(x)(-4(30-2x) = -120x + 8x^2
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
(30-2x)^2 = (30 - 2x) * (30 - 2x)quote:
[..]
Waar komt die eerste -120x vandaan? Ik zie namelijk alleen 900 (30^2) en 4x^2 (2x^2)
dus 30 * 30 = 900
30 * -2x = -60x
-2x * 30 = -60x
-2x * -2x = -4x^2
Het klopt toch echt. Het product van x, -4 en 30 in je tweede term is -120x. Overigens zou ik het niet zo opschrijven, je kunt beter niet de volgorde van de twee functies in je product omwisselen als je de afgeleide bepaalt, daarmee maak je het voor jezelf onnodig onoverzichtelijk. Verder is je gebruik van haakjes niet standaard, en dat komt de overzichtelijkheid ook niet ten goede.quote:
Ik zit met een differentiatie waar ik niet uitkom. Het gaat om een combinatie van de kettingregel met de productregel:
[ afbeelding ]
En daar krijg ik (i.c.m. de kettingregel) de volgende afgeleide uit:
[ afbeelding ]
Nu is de afgeleide verder in orde, maar zodra ik het ga vereenvoudigen raak ik ergens -120X kwijt. Ik snap niet waar het zit, want ik heb echt alles geprobeerd... Het moet volgens mij antwoordenboek het volgende worden (en dit lijkt ook te kloppen):
[ afbeelding ]
Ik besef nu (met dank aan voorgaande persoon) dat ik helemaal niet 30 keer -4 heb gedaan, maar alleen 30 keer 30 en 4 keer 4. Ik had dit kunnen weten.quote:
[..]
Het klopt toch echt. Het product van x, -4 en 30 in je tweede term is -120x. Overigens zou ik het niet zo opschrijven, je kunt beter niet de volgorde van de twee functies in je product omwisselen als je de afgeleide bepaalt, daarmee maak je het voor jezelf onnodig onoverzichtelijk. Verder is je gebruik van haakjes niet standaard, en dat komt de overzichtelijkheid ook niet ten goede.
Wat is er trouwens niet standaard aan de haakjes? Ik doe aan zelfstudie en sta open voor elke vorm van kritiek, aangezien ik dat amper krijg.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Haakjes dienen om volgordes van bewerkingen expliciet te maken resp. (zoals hier) om aan te geven dat twee of meer termen bij elkaar horen. Maar dan moet je dus niet (1) of (x) schrijven, daarbij is er namelijk maar één term tussen de haakjes en zijn de haakjes dus overbodig. Eventueel gebruik je een middenpunt (of bij gebrek daaraan een asterisk) om aan te geven dat er sprake is van een product, dus bijvoorbeeld x*-4*(30 - 2x).quote:
[..]
Ik besef nu (met dank aan voorgaande persoon) dat ik helemaal niet 30 keer -4 heb gedaan, maar alleen 30 keer 30 en 4 keer 4. Ik had dit kunnen weten.
Wat is er trouwens niet standaard aan de haakjes? Ik doe aan zelfstudie en sta open voor elke vorm van kritiek, aangezien ik dat amper krijg.
Oké op die manier. Bedankt voor het advies, ik zal het proberen te onthouden.quote:
[..]
Haakjes dienen om volgordes van bewerkingen expliciet te maken resp. (zoals hier) om aan te geven dat twee of meer termen bij elkaar horen. Maar dan moet je dus niet (1) of (x) schrijven, daarbij is er namelijk maar één term tussen de haakjes en zijn de haakjes dus overbodig. Eventueel gebruik je een middenpunt (of bij gebrek daaraan een asterisk) om aan te geven dat er sprake is van een product, dus bijvoorbeeld x*-4*(30 - 2x).
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Of nog netter is: -4x(30-2x). Als je eerst getallen schrijft en dan letters mag je het vermenigvuldigingsteken weglaten, maar dat wist je zo te zien alquote:
[..]
Oké op die manier. Bedankt voor het advies, ik zal het proberen te onthouden.
.
Stel ik wil x^3 x 2x + 2 opschrijven in factoren. Welke stappen zou ik dan kunnen nemen (het antwoord zou (x + 2)(x^2 2x + 1) moeten zijn.
Ik kan natuurlijk in dit in gedeelten oplossen:
x^3 + 2x + 2 = x(x^2-1) - 2(x-1) = x(x+1)(x-1) - 2(x-1)
Maar dan? Is het een kwestie van proberen?
[ Bericht 0% gewijzigd door Warren op 27-04-2011 14:19:53 ]
Ik kan natuurlijk in dit in gedeelten oplossen:
x^3 + 2x + 2 = x(x^2-1) - 2(x-1) = x(x+1)(x-1) - 2(x-1)
Maar dan? Is het een kwestie van proberen?
[ Bericht 0% gewijzigd door Warren op 27-04-2011 14:19:53 ]
Wat bedoel je met x^3 x 2x +2 en met (x+2)(x^2 2x +1)?quote:
Stel ik wil x^3 x 2x + 2 opschrijven in factoren. Welke stappen zou ik dan kunnen nemen (het antwoord zou (x + 2)(x^2 2x + 1) moeten zijn.
Ik kan natuurlijk in dit in gedeelten oplossen:
x^3 x 2x + 2 = x(x^2-1) - 2(x-1) = x(x+1)(x-1) - 2(x-1)
Maar dan? Is het een kwestie van proberen?
The biggest argument against democracy is a five minute discussion with the average voter.
Excuses.quote:
[..]
Wat bedoel je met x^3 x 2x +2 en met (x+2)(x^2 2x +1)?
Begin eens met dit te schrijven als:quote:
[..]
Excuses. [ afbeelding ] moet worden geschreven in factoren. Het antwoord zou moeten zijn [ afbeelding ]
x3 - 3x + 2
Je ziet nu vrij gemakkelijk door uitproberen dat x = -2 en x = 1 nulpunten zijn van deze veelterm, zodat deze dus deelbaar is door (x + 2) en door (x - 1). Voer dan een polynoomstaartdeling uit.
Ik moet van verschillende functies de extremen bepalen en het is de bedoeling dat ik dit uitreken. Echter weet ik niet of ik het nou echt moet uitrekenen, of dat het ook algebraïsch mag?
Stel dat ik een formule heb zoals: x^4 - 9x^2 hoe kan ik dan het beste de minimum/maximum vinden? Ik weet hoe het moet met de GRM, maar ik moet het dus ook kunnen berekenen?
Stel dat ik een formule heb zoals: x^4 - 9x^2 hoe kan ik dan het beste de minimum/maximum vinden? Ik weet hoe het moet met de GRM, maar ik moet het dus ook kunnen berekenen?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je hebt net het concept van de afgeleide geleerd, dit is waar de afgeleide van pas komt. De afgeleide geeft immers de helling van de functie aan, als de helling nul is, is er dus een minimum of een maximum (strikt genomen kan er ook een buigpunt zijn, maar daar zal ik niet verder over uitweiden). Wat je dus moet doen is de afgeleide gelijk stellen aan nul, dat geeft je de x-coördinaat van het maximum/minimum, en daarmee kan je ook de y-coördinaat vinden (invullen in de oorspronkelijke formule).quote:
Ik moet van verschillende functies de extremen bepalen en het is de bedoeling dat ik dit uitreken. Echter weet ik niet of ik het nou echt moet uitrekenen, of dat het ook algebraïsch mag?
Stel dat ik een formule heb zoals: x^4 - 9x^2 hoe kan ik dan het beste de minimum/maximum vinden? Ik weet hoe het moet met de GRM, maar ik moet het dus ook kunnen berekenen?
The biggest argument against democracy is a five minute discussion with the average voter.
Ik weet dat de plek waar de afgeleide 0 is, zich een extreme bevindt, echter vraag ik mij af of ik het terug moet rekenen of dat ik het via één of andere magische methode op de waarde moet komen (behalve door de vergelijking algebraïsch uit elkaar te trekken met de uitkomst nul).quote:
[..]
Je hebt net het concept van de afgeleide geleerd, dit is waar de afgeleide van pas komt. De afgeleide geeft immers de helling van de functie aan, als de helling nul is, is er dus een minimum of een maximum (strikt genomen kan er ook een buigpunt zijn, maar daar zal ik niet verder over uitweiden). Wat je dus moet doen is de afgeleide gelijk stellen aan nul, dat geeft je de x-coördinaat van het maximum/minimum, en daarmee kan je ook de y-coördinaat vinden (invullen in de oorspronkelijke formule).
Even een aanvulling, om mijn vraag iets duidelijker te maken. Ik heb de volgende afgeleide en via vier stappen kom ik op de waarde van X als Y = 0. Nu is alleen de vraag of dit de juiste methode is en hoe ik ervoor zorg dat ik alle extremen vind. (In dit geval -2, 0 en 2)?
[ Bericht 16% gewijzigd door Pipo1234 op 28-04-2011 20:15:22 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
dat klopt niet, f'(x) is geen 4x³. Daarnaast deel je ergens door x, wat als x=0?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Daar heb je inderdaad een goed punt... De methode werkte, maar ik wist even niet of het correct is.quote:
[ afbeelding ]
dat klopt niet, f'(x) is geen 4x³. Daarnaast deel je ergens door x, wat als x=0?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
een gevalletje abuse of notation dat slecht uitpakt dus....quote:
[ afbeelding ]
dat klopt niet, f'(x) is geen 4x³. Daarnaast deel je ergens door x, wat als x=0?
f '(x) = 4x³ - 18x
stel f '(x) = 0 => 4x³ - 18x = 0
x ( 4x2 - 18 ) = 0 =>
x = 0 OR 4x2 - 18 = 0
4x2 = 18
x2 = 4.5
x = SQRT(4.5) OR x = -SQRT(4.5)
4.5 = 9/2 = > SQRT(4.5) = SQRT(9/2) = 3/SQRT(2) = 3/2 * SQRT(2)
remember: SQRT(1/2) = 2-1/2 = 21/2 - 1 = SQRT(2) / 2
Het is de bedoeling dat ik de extremen van deze functie bepaal. Echter weet ik niet hoe ik bij de afgeleide de nulpunten moet bepalen, aangezien het niet om een gewone formule gaat. Kan iemand me even op weg helpen?
De afgeleide:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Een breuk is 0 als de teller 0 is en de noemer ongelijk aan 0 is. Je moet dan wel x³ + 3x + 2 = 0 oplossen, en dat is niet zo eenvoudig.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik zie het niet
(van regel 1 naar 2)Aha.. sin(A+B)=sinAcosB+cosAsinB
[ Bericht 13% gewijzigd door Alxander op 30-04-2011 18:55:05 ]
Geen huiswerk vraag maar gezien de bovenstaande post:
Snappen de meeste VWO wiskunde B/D'ers waarom bijvoorbeeld sin(A+B) gelijk staat aan SinACosB + CosASinB? Ik heb, dankzij falend onderwijs, nooit iets over sin/cos/tan gehad en zie vaak mensen met dit soort regels komen. Hoor je al die regels te snappen? Of is het een kwestie van de regels stampen en toepassen?
(Wil wellicht zelf Wiskunde B/D doen dus vraag dit uit interesse)
Snappen de meeste VWO wiskunde B/D'ers waarom bijvoorbeeld sin(A+B) gelijk staat aan SinACosB + CosASinB? Ik heb, dankzij falend onderwijs, nooit iets over sin/cos/tan gehad en zie vaak mensen met dit soort regels komen. Hoor je al die regels te snappen? Of is het een kwestie van de regels stampen en toepassen?
(Wil wellicht zelf Wiskunde B/D doen dus vraag dit uit interesse)
Ik heb het 1x uitgelegd gekregen met een cirkel erbij, en voor de rest is het alleen maar stampen jaquote:
Hoor je al die regels te snappen? Of is het een kwestie van de regels stampen en toepassen?
(of je GR propvol zetten met regels)Zie ook
[ Bericht 25% gewijzigd door #ANONIEM op 30-04-2011 23:45:58 ]
Wiskunde gaat over begrijpen, niet over stampen. Als je dat laatste doet of zelfs maar denkt dat je dat moet doen dan ben je verkeerd bezig. Dit neemt natuurlijk niet weg dat je een zekere routine moet verwerven en dat je een bepaalde parate kennis moet hebben. De additietheorema's uit de goniometrie horen daar zeker bij. Als je de formules voor cos(α+β) en sin(α+β) uit het hoofd kent dan kun je trouwens heel veel andere goniometrische identiteiten daar gemakkelijk uit afleiden, zodat het lonend is in ieder geval deze identiteiten te kennen. Overigens, als je iets van complexe getallen weet dan is het niet eens nodig de formules voor cos(α+β) en sin(α+β) uit het hoofd te kennen omdat je ze dan gemakkelijk af kunt leiden. Aangezien bij vermenigvuldiging van twee complexe getallen het argument van het product gelijk is aan de som van de argumenten van de factoren geldt:quote:
Geen huiswerk vraag maar gezien de bovenstaande post:
Snappen de meeste VWO wiskunde B/D'ers waarom bijvoorbeeld sin(A+B) gelijk staat aan SinACosB + CosASinB? Ik heb, dankzij falend onderwijs, nooit iets over sin/cos/tan gehad en zie vaak mensen met dit soort regels komen. Hoor je al die regels te snappen? Of is het een kwestie van de regels stampen en toepassen?
(Wil wellicht zelf Wiskunde B/D doen dus vraag dit uit interesse)
cos(α+β) + i∙sin(α+β) = (cos α + i∙sin α)(cos β + i∙sin β)
Uitwerken van de haakjes in het rechterlid en gelijkstellen van de reële en imaginaire delen in linker en rechterlid levert dan meteen de bekende identiteiten.
X = 5. Prima begrijp ik.
(het is X^-2, maar krijg dat niet voor elkaar)
Hoe bereken ik dit?
Zelfde voor deze...
Of niet?
x = 32 ^ (3/5)quote:
[ afbeelding ]
X = 5. Prima begrijp ik.
[ afbeelding ]
(het is X^-2, maar krijg dat niet voor elkaar)
Hoe bereken ik dit?
[ afbeelding ]
Zelfde voor deze...
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Ik heb ook nog steeds deze: 
Deze komt met tips van andere nog steeds met de ABC formule uit.
Ps. Alles tussen haakjes staat tot de macht to..
Deze komt met tips van andere nog steeds met de ABC formule uit.
Ps. Alles tussen haakjes staat tot de macht to..
Of niet?
16=2^4, hieruit volgt x^2-3x-24=4, dat wordt x^2-3x-28=0, ontbinden in factoren geeft (x+4)(x-7)=0, dat geeft als oplossingen x=-4 en x=7.quote:
Ik heb ook nog steeds deze: [ afbeelding ]
Deze komt met tips van andere nog steeds met de ABC formule uit.
Ps. Alles tussen haakjes staat tot de macht to..
The biggest argument against democracy is a five minute discussion with the average voter.
Ik vond wiskunde B zelf voor het grootste deel begrijpen, alleen bij de goniometrische formules kregen we zo'n overload (alle verdubbelingsformules, afgeleiden, somformules etc. moesten we kennen) dat het makkelijker was om uit je hoofd te leren dan om allemaal te beredeneren.quote:
Geen huiswerk vraag maar gezien de bovenstaande post:
Snappen de meeste VWO wiskunde B/D'ers waarom bijvoorbeeld sin(A+B) gelijk staat aan SinACosB + CosASinB? Ik heb, dankzij falend onderwijs, nooit iets over sin/cos/tan gehad en zie vaak mensen met dit soort regels komen. Hoor je al die regels te snappen? Of is het een kwestie van de regels stampen en toepassen?
(Wil wellicht zelf Wiskunde B/D doen dus vraag dit uit interesse)
(bij een wiskunde toets moest je dat wel allemaal in één keer weten, bij ons waren de wiskundetoetsen altijd vrij lang ten opzichte van de tijd die je ervoor had).
Verder was eigenlijk bijna alles begrijpen ipv leren, alleen bij differentiëren en integreren moesten we wat dingen echt leren voor zover ik me kan herinneren.
Finally, someone let me out of my cage
Heb zelf op de middelbare school niet echt bewijzen gehad van Goniometrische formules. Die formules van Mollweide/Simpson kwamen we overigens ook echt sporadisch tegen. Nu met mijn studie Econometrics kom ik ook weinig sinussen en cosinussen tegen, maar moest even mijn examentraining voorbereiden voor morgen..
Ik zit nu met iets waar ik finaal in vastloop. Ik moet van de volgende functie de afgeleide bepalen:
Tot zover geen probleem, namelijk:
Echter dien ik dan te bepalen bij welke waarde van p de vergelijking f' = 0 geen oplossing heeft en dan snap ik het even niet meer. Het antwoord is het bereik van de negatieve wortel van 2 keer 3 tot zijn positieve tegenhanger.
Ik moet van de volgende functie de afgeleide bepalen:Tot zover geen probleem, namelijk:
Echter dien ik dan te bepalen bij welke waarde van p de vergelijking f' = 0 geen oplossing heeft en dan snap ik het even niet meer. Het antwoord is het bereik van de negatieve wortel van 2 keer 3 tot zijn positieve tegenhanger.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
De discriminant is negatief in dit geval, dus er is geen oplossing. Maar het moet op één of andere manier toch op te lossen zijn? Hoe moet ik anders aan het antwoord komen?quote:
Wanneer heeft een kwadratische vergelijking geen oplossing?
Hint: discriminant
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Schrijf de discriminant eens uit, let daarbij op de pquote:
[..]
De discriminant is negatief in dit geval, dus er is geen oplossing. Maar het moet op één of andere manier toch op te lossen zijn? Hoe moet ik anders aan het antwoord komen?
.
The biggest argument against democracy is a five minute discussion with the average voter.
quote:
[..]
Schrijf de discriminant eens uit, let daarbij op de p
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ja dat zet me even aan het denken, aangezien ik de materie niet zo heel goed beheers.quote:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je weet de formule voor de discriminant? Die moet je nu toepassen op de formule die je eerder hebt gegeven. Schrijf deze eens op, en probeer voor jezelf te bedenken wat dit betekent.quote:
[..]
Ja dat zet me even aan het denken, aangezien ik de materie niet zo heel goed beheers.
The biggest argument against democracy is a five minute discussion with the average voter.
Het feit dat een kwadratische vergelijking geen oplossing heeft betekent niet dat jij het vraagstuk niet op kunt lossen, dat zijn twee heel verschillende dingen.quote:
[..]
De discriminant is negatief in dit geval, dus er is geen oplossing. Maar het moet op één of andere manier toch op te lossen zijn? Hoe moet ik anders aan het antwoord komen?
Een kwadratische veelterm in een variabele x heeft de algemene gedaante:
(1) ax2 + bx + c
Hierbij neem ik aan dat a,b en c reële grootheden zijn. Tevens mogen we a ongelijk aan nul veronderstellen, aangezien je anders geen kwadratische term zou hebben.
De discriminant D van deze kwadratische veelterm is:
(2) D = b2 - 4ac
De waarde van D is bepalend voor het aantal (reële) nulpunten van veelterm (1). Indien D negatief is, dan heeft (1) geen (reële) nulpunten.
De kwadratische veelterm die je nu hebt is:
(3) f'p(x) = 3x2 + 2px + 6
De vraag is nu voor welke waarde(n) van p f'p(x), en dus de kwadratische veelterm in (3), geen nulpunten heeft.
Uit een vergelijk van (3) met de algemene gedaante (1) van een kwadratische veelterm zie je dat hier geldt a = 3, b = 2p en c = 6. In overeenstemming met (2) is de discriminant van (3) dus:
(4) D = (2p)2 - 4*3*6 = 4p2 - 72
Het vraagstuk is nu herleid tot de vraag voor welke waarde(n) van p de uitdrukking 4p2 - 72 negatief is. Bedenk nu zelf eens hoe je deze laatste vraag oplost. Hint: bepaal eerst voor welke waarde(n) van p de uitdrukking 4p2 - 72 gelijk is aan nul.
Ik moet voor datastructuren een algoritme schrijven waar we te maken hebben met een recursieve functie:
f is gedefinieerd van 2 tot een zeker natuurlijk getal m>2:
f(2) = a
fn = fn-1 + ceiling(fn-1 / b)
(Waarin ceiling een functie is die afrondt naar het dichtbijzijnde natuurlijke getal dat gelijk aan of groter dan het argument is wat een zin)
Ik vroeg me af of je zo'n recursieve functie kunt benaderen met een niet-recursieve functie, dat zou namelijk erg kunnen helpen (hoewel het me onwaarschijnlijk lijkt dat dat de oplossing is die de docent voor ogen heeft, als het al kan)
f is gedefinieerd van 2 tot een zeker natuurlijk getal m>2:
f(2) = a
fn = fn-1 + ceiling(fn-1 / b)
(Waarin ceiling een functie is die afrondt naar het dichtbijzijnde natuurlijke getal dat gelijk aan of groter dan het argument is wat een zin)
Ik vroeg me af of je zo'n recursieve functie kunt benaderen met een niet-recursieve functie, dat zou namelijk erg kunnen helpen (hoewel het me onwaarschijnlijk lijkt dat dat de oplossing is die de docent voor ogen heeft, als het al kan)
Finally, someone let me out of my cage
fn is ongeveer fn-1 * (1 + 1/b). In elk geval zit het tussen fn-1 * (1 + 1/b) en fn-1 * (1 + 1/b) + 1. Dus fn zal ongeveer a * (1 + 1/b)n-2 zijn. Dat is in elk geval een ondergrens. Voor een bovengrens moet je de recursie fn = 1 + fn-1 * (1 + 1/b) oplossen. Dat doe je door eerst een c te vinden zdd deze vergelijking tot fn - c = (1 + 1/b) * (fn-1 - c) herleidt.
[ Bericht 25% gewijzigd door thabit op 04-05-2011 10:56:51 ]
[ Bericht 25% gewijzigd door thabit op 04-05-2011 10:56:51 ]
BETA-genieën; de volgende vraag. Echt superveel waardering als jullie hier zouden kunnen helpen.. ik heb geen flauw idee of ik dit goed doe..
[Blijkbaar staat fok.nl geen grote hoeveelheden spaties toe, bij de voorgestelde oplossingen moeten die spaties in de regels boven en onder 'SIGMA' er dus bij worden gedacht... Die regels waarin extra spaties moeten worden 'gedacht' zijn nu dikgedrukt]
Ik weet in principe wel hoe de som notatie werkt, en kan al zeg ik het zelf ook wel redelijk logisch nadenken, maar heb helaas nooit wiskunde B gehad, en loop nu toch echt goed vast. Ik zal eerst uitleggen waar ik een (sigma) som-formule voor wil hebben:
We hebben voor 5 mensen (i=5), over een periode van 10 jaar (t=10), waardes voor een bepaalde variabele genaamd A(i,t). Niet voor alle jaren is er voor iedere persoon een waarde van A bekend.
PART I
Nu wordt voor iedere persoon -individueel- de reeks A geïndexeerd. Laten we de nieuwe variabele IA(i,t) (IA = 'Index A') noemen. Per persoon wordt de gemiddelde waarde van A over de gehele periode gelijkgesteld aan 100. (Let op: aangezien dus niet voor alle personen over de gehele periode waardes van A bekend zijn, kun je de som van alle A-waardes van een bepaalde persoon niet simpelweg door 10 delen om het gemiddelde te krijgen. ~ik weet niet of delen door 'n' voldoet, of dat dat sigma-notatie-technisch incorrect is??)
PART II
Nadat de variabele IA(i,t) gecreëerd is, introduceren we de variabele B(t). B is gelijk aan een gewogen gemiddelde van de variabele IA in jaar t. De weights van IA(i,t) in B(t) hangen af van de waardes van weer een andere variabele: C(i,t). Als 'in jaar 5 de C-waarde voor persoon 1 gelijk is aan 8' (oftewel C(1,5)=8), en de som van alle C's in dat jaar gelijk is aan 80 (oftewel C(1,5)+C(2,5)+C(3,5)+...+C(10,5)=80), dan is het gewicht van IA(1,5) in B(5) 10% (=8/80).
Hopelijk is het probleem zo in ieder geval duidelijk (ik heb in ieder geval al veel vereenvoudigd...) De bedoeling is om uiteindelijk 1 som formule voor dit gehele verhaal te krijgen, maar het opsplitsen in twee problemen ligt hier uiteraard voor de hand en mag ook. (Uiteindelijk kunnen ze dan misschien nog worden samengevoegd, al wordt dan -ben ik bang- het een groot probleem dat sommige '"n's" betrekking hebben op i en andere op t)
OPLOSSING PART I
Mijn poging (geen flauw idee of dit correct is);
n
IA(i,t) = A(i,t) / { { SIGMA [ A(i,t) ] } / n } x 100
t=1
OPLOSSING PART II
Met betrekking tot PART II, klopt de formule zo??; (laat je vooral niet op het verkeerde been zetten door wat ik aan het doen ben, ik ben echt een leek..)
n n
B(t) = SIGMA [ IA(i,t) * { C(i,t) / SIGMA [ C(i,t) ] }
i=1 i=1
Klopt dat zo? Of zou ik bijvoorbeeld onder de tweede SIGMA niet 'i=1' maar gewoon 'i' moeten zetten (omdat het om een SIGMA binnen een SIGMA gaat)??
ALLES SAMENVOEGEN
Dan krijg je dit: probleem is nu alleen misschien dat sommige "n's" betrekking heb op i, en andere op t???
n n n
B(t) = SIGMA [ {{ A(i,t) / { { SIGMA [ A(i,t) ] } / n } x 100 }} * { C(i,t) / SIGMA [ C(i,t) ] }
i=1 t=1 i=1
Alvast heeeeeeeel erg veel dank en respect voor de slimmerik die dit weet op te lossen!
[Blijkbaar staat fok.nl geen grote hoeveelheden spaties toe, bij de voorgestelde oplossingen moeten die spaties in de regels boven en onder 'SIGMA' er dus bij worden gedacht... Die regels waarin extra spaties moeten worden 'gedacht' zijn nu dikgedrukt]
Ik weet in principe wel hoe de som notatie werkt, en kan al zeg ik het zelf ook wel redelijk logisch nadenken, maar heb helaas nooit wiskunde B gehad, en loop nu toch echt goed vast. Ik zal eerst uitleggen waar ik een (sigma) som-formule voor wil hebben:
We hebben voor 5 mensen (i=5), over een periode van 10 jaar (t=10), waardes voor een bepaalde variabele genaamd A(i,t). Niet voor alle jaren is er voor iedere persoon een waarde van A bekend.
PART I
Nu wordt voor iedere persoon -individueel- de reeks A geïndexeerd. Laten we de nieuwe variabele IA(i,t) (IA = 'Index A') noemen. Per persoon wordt de gemiddelde waarde van A over de gehele periode gelijkgesteld aan 100. (Let op: aangezien dus niet voor alle personen over de gehele periode waardes van A bekend zijn, kun je de som van alle A-waardes van een bepaalde persoon niet simpelweg door 10 delen om het gemiddelde te krijgen. ~ik weet niet of delen door 'n' voldoet, of dat dat sigma-notatie-technisch incorrect is??)
PART II
Nadat de variabele IA(i,t) gecreëerd is, introduceren we de variabele B(t). B is gelijk aan een gewogen gemiddelde van de variabele IA in jaar t. De weights van IA(i,t) in B(t) hangen af van de waardes van weer een andere variabele: C(i,t). Als 'in jaar 5 de C-waarde voor persoon 1 gelijk is aan 8' (oftewel C(1,5)=8), en de som van alle C's in dat jaar gelijk is aan 80 (oftewel C(1,5)+C(2,5)+C(3,5)+...+C(10,5)=80), dan is het gewicht van IA(1,5) in B(5) 10% (=8/80).
Hopelijk is het probleem zo in ieder geval duidelijk (ik heb in ieder geval al veel vereenvoudigd...) De bedoeling is om uiteindelijk 1 som formule voor dit gehele verhaal te krijgen, maar het opsplitsen in twee problemen ligt hier uiteraard voor de hand en mag ook. (Uiteindelijk kunnen ze dan misschien nog worden samengevoegd, al wordt dan -ben ik bang- het een groot probleem dat sommige '"n's" betrekking hebben op i en andere op t)
OPLOSSING PART I
Mijn poging (geen flauw idee of dit correct is);
n
IA(i,t) = A(i,t) / { { SIGMA [ A(i,t) ] } / n } x 100
t=1
OPLOSSING PART II
Met betrekking tot PART II, klopt de formule zo??; (laat je vooral niet op het verkeerde been zetten door wat ik aan het doen ben, ik ben echt een leek..)
n n
B(t) = SIGMA [ IA(i,t) * { C(i,t) / SIGMA [ C(i,t) ] }
i=1 i=1
Klopt dat zo? Of zou ik bijvoorbeeld onder de tweede SIGMA niet 'i=1' maar gewoon 'i' moeten zetten (omdat het om een SIGMA binnen een SIGMA gaat)??
ALLES SAMENVOEGEN
Dan krijg je dit: probleem is nu alleen misschien dat sommige "n's" betrekking heb op i, en andere op t???
n n n
B(t) = SIGMA [ {{ A(i,t) / { { SIGMA [ A(i,t) ] } / n } x 100 }} * { C(i,t) / SIGMA [ C(i,t) ] }
i=1 t=1 i=1
Alvast heeeeeeeel erg veel dank en respect voor de slimmerik die dit weet op te lossen!
MrMiguel, probeer er in word (of latex) iets fatsoenlijks van te maken en gooi dan hier een printscreen neer. Dit leest echt heel erg matig. Als je een mooie printscreen neerplempt wil ik me er wel over buigen.
//herschreven:
Het enige wat mijn paper erbij heeft is dat de phases een functie van de tijd zijn en als uitkomst naast 'delta Theta' (dus d Theta_i / d t)) nog een breuk '1/2pi' staan.
Kan helaas het paper niet op internet vinden...
Mijn issues zijn:
Hoe teken ik een lijn met behulp van phase/frequency/amplitude als de phase varieert? Tenminste, ik hoop dat ik Kuramoto goed doe :| bij mij gaan de phases steeds hoger en hoger.
voor de eerste 4 stappen, 6 oscillators diens phases op de tijdstippen:
0 1.4144 5.3829 6.9669
0 2.5284 6.2316 8.2936
5.1191 8.2058 10.1751 13.1296
5.6913 8.8670 10.6988 14.3709
0.7979 2.6108 5.2027 8.9379
5.7389 10.4320 13.0786 15.7821
Tenminste, in begin zijn ze nog zeer chaotisch, maar uiteindelijk is er een stabiel patroon, maar het fluctueert enorm nog altijd, terwijl in de paper het naar één lijn toe gaat (frequency tegenover tijd).
// nog een update:
als ze met allemaal dezelfde frequencies beginnen en de phases zijn schommelend, krijg ik alleen een rechte lijn als ik delta tijd iets van 0.001 of kleiner neem. Zodra ik verschillende frequencies probeer echter, krijg ik mega hoeveelheid schommelingen...
[ Bericht 12% gewijzigd door koffiegast op 04-05-2011 22:58:01 ]
Het enige wat mijn paper erbij heeft is dat de phases een functie van de tijd zijn en als uitkomst naast 'delta Theta' (dus d Theta_i / d t)) nog een breuk '1/2pi' staan.
Kan helaas het paper niet op internet vinden...
Mijn issues zijn:
Hoe teken ik een lijn met behulp van phase/frequency/amplitude als de phase varieert? Tenminste, ik hoop dat ik Kuramoto goed doe :| bij mij gaan de phases steeds hoger en hoger.
voor de eerste 4 stappen, 6 oscillators diens phases op de tijdstippen:
0 1.4144 5.3829 6.9669
0 2.5284 6.2316 8.2936
5.1191 8.2058 10.1751 13.1296
5.6913 8.8670 10.6988 14.3709
0.7979 2.6108 5.2027 8.9379
5.7389 10.4320 13.0786 15.7821
Tenminste, in begin zijn ze nog zeer chaotisch, maar uiteindelijk is er een stabiel patroon, maar het fluctueert enorm nog altijd, terwijl in de paper het naar één lijn toe gaat (frequency tegenover tijd).
// nog een update:
als ze met allemaal dezelfde frequencies beginnen en de phases zijn schommelend, krijg ik alleen een rechte lijn als ik delta tijd iets van 0.001 of kleiner neem. Zodra ik verschillende frequencies probeer echter, krijg ik mega hoeveelheid schommelingen...
[ Bericht 12% gewijzigd door koffiegast op 04-05-2011 22:58:01 ]
Hier een bewijsje.quote:Geen huiswerk vraag maar gezien de bovenstaande post:
Snappen de meeste VWO wiskunde B/D'ers waarom bijvoorbeeld sin(A+B) gelijk staat aan SinACosB + CosASinB? Ik heb, dankzij falend onderwijs, nooit iets over sin/cos/tan gehad en zie vaak mensen met dit soort regels komen. Hoor je al die regels te snappen? Of is het een kwestie van de regels stampen en toepassen?
(Wil wellicht zelf Wiskunde B/D doen dus vraag dit uit interesse)
http://www.khanacademy.or(...)cos-b?p=Trigonometry
http://www.khanacademy.or(...)sin-b?p=Trigonometry
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Die bewijzen met behulp van rechthoekige driehoeken vind ik niet fraai, omdat ze uitsluitend gelden voor scherpe hoeken α en β, terwijl er in de figuren bovendien vanuit wordt gegaan dat ook α+β een scherpe hoek is. De additietheorema's gelden echter voor willekeurige hoeken (rotaties), zowel positief als negatief. Er is een veel fraaier bewijs mogelijk met vectoren en de eenheidscirkel dat wél geldt voor willekeurige hoeken (rotaties), maar ik vind zo gauw geen webpagina waar dat goed wordt uitgelegd.quote:
[..]
Hier een bewijsje.
http://www.khanacademy.or(...)cos-b?p=Trigonometry
http://www.khanacademy.or(...)sin-b?p=Trigonometry
Dat lijkt maar zo. Als je, zoals op de middelbare school gebeurt, de goniometrische functies meetkundig definieert aan de hand van de eenheidscirkel, dan zou je eerst nog complexe getallen en de formules van De Moivre en Euler moeten behandelen (en afleiden) alvorens je daarmee dan de additietheorema's aantoont. Maar afgezien daarvan dat je dan didactisch een enorme omweg hebt gemaakt begeef je je dan in een cirkelredenering (no pun intended), want om te laten zien dat bij vermenigvuldiging van twee complexe getallen de argumenten optellen heb je dan ook al van de additietheorema's voor de cosinus en sinus gebruik gemaakt. Ik heb daar een hele tijd geleden op dit forum ook al eens op gewezen.quote:Op donderdag 5 mei 2011 09:17 schreef thenxero het volgende:
Ze zijn vrij makkelijk te bewijzen met de e-macht
Kan iemand mij verklaren waarom de afgeleide van x keer e^x = (1+x) keer e^x?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Pas de productregel toe om xex te differentiëren naar x en haal dan bij het resultaat ex buiten haakjes.quote:
Kan iemand mij verklaren waarom de afgeleide van x keer e^x gelijk is aan (1+x) keer e^x?
x keer ex keer (1) = 1x keer ex... waarom moet die ex eruit gehaald worden?quote:
[..]
Pas de productregel toe om xex te differentiëren naar x en haal dan bij het resultaat ex buiten haakjes.
Even iets tussendoor: Hoe kan ik van de wortel van 4,5 naar 1,5 keer de wortel van 2 komen? Aangezien het antwoord daarmee komt en het feitelijk hetzelfde is. Is het trouwens zo dat een negatieve wortel niet mag. Dus op de volgende wijze: -SRT(2) (en dus niet de wortel van een negatief getal).
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je kent de productregel? Deze toepassen op de functiequote:
[..]
x keer ex keer (1) = 1x keer ex... waarom moet die ex eruit gehaald worden?
quote:Even iets tussendoor: Hoe kan ik van de wortel van 4,5 naar 1,5 keer de wortel van 2 komen? Aangezien het antwoord daarmee komt en het feitelijk hetzelfde is.
Dat klopt, de wortel van een negatief getal bestaat niet (niet in de reële getallen in ieder geval).quote:Is het trouwens zo dat een negatieve wortel niet mag. Dus op de volgende wijze: -SRT(2) (en dus niet de wortel van een negatief getal).
The biggest argument against democracy is a five minute discussion with the average voter.
wordt enkel gedaan om het eenvoudiger op te schrijven e^x + x*e^x = e^x * (1+x)quote:
[..]
x keer ex keer (1) = 1x keer ex... waarom moet die ex eruit gehaald worden?
beetje hetzelfde als een breuk vereenvoudigen 2/4 is niet fout als antwoord maar toch schrijf je dan altijd 1/2 op
quote:Even iets tussendoor: Hoe kan ik van de wortel van 4,5 naar 1,5 keer de wortel van 2 komen?
Wortel van een negatief getal bestaat niet (enkel complex), maar je kan wel min de wortel van een positief getal hebben.quote:Aangezien het antwoord daarmee komt en het feitelijk hetzelfde is. Is het trouwens zo dat een negatieve wortel niet mag. Dus op de volgende wijze: -SRT(2) (en dus niet de wortel van een negatief getal).
niet: wortel(-4)
wel: - wortel(4)
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Bedankt voor alle verhelderende antwoorden! 
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Bedankt! Daar kan ik denk ik wel wat meequote:
fn is ongeveer fn-1 * (1 + 1/b). In elk geval zit het tussen fn-1 * (1 + 1/b) en fn-1 * (1 + 1/b) + 1. Dus fn zal ongeveer a * (1 + 1/b)n-2 zijn. Dat is in elk geval een ondergrens. Voor een bovengrens moet je de recursie fn = 1 + fn-1 * (1 + 1/b) oplossen. Dat doe je door eerst een c te vinden zdd deze vergelijking tot fn - c = (1 + 1/b) * (fn-1 - c) herleidt.
Finally, someone let me out of my cage
De formule van Euler kan ook eenvoudig bewezen worden met calculus en wat basisalgebra, zie http://en.wikipedia.org/wiki/Euler%27s_formula#Using_calculus .quote:
[..]
Dat lijkt maar zo. Als je, zoals op de middelbare school gebeurt, de goniometrische functies meetkundig definieert aan de hand van de eenheidscirkel, dan zou je eerst nog complexe getallen en de formules van De Moivre en Euler moeten behandelen (en afleiden) alvorens je daarmee dan de additietheorema's aantoont. Maar afgezien daarvan dat je dan didactisch een enorme omweg hebt gemaakt begeef je je dan in een cirkelredenering (no pun intended), want om te laten zien dat bij vermenigvuldiging van twee complexe getallen de argumenten optellen heb je dan ook al van de additietheorema's voor de cosinus en sinus gebruik gemaakt. Ik heb daar een hele tijd geleden op dit forum ook al eens op gewezen.
Het enige resultaat dat je daarvoor nodig hebt is dat d/dx e^ix = i e^ix.... Dit feit volgt direct uit de machtreeks van e^ix. We kunnen e^ix definiëren als die machtreeks, waardoor we ook geen kennis van Taylorreeksen nodig hebben.
Het enige wat je dus moet doen is e^ix definiëren als een machtreeks, toch? Op die manier zitten we niet in een cirkelredenering.
edit: ik bedenk me wel dat je nog uniforme convergentie moet aantonen om termgewijs te differentiëren, waardoor het toch wel iets gecompliceerder wordt. Niet echt stof voor de middelbare school. Aan de andere kant hebben ze bij mij op de middelbare school ook nooit aangetoond dat d/dx e^kx = k e^x voor reële k, dus ze zouden het ook gewoon als onbewezen stelling kunnen poneren.
Met die bewijzen voor de formule van Euler die in het Wikipedia artikel worden opgevoerd is ook van alles mis, lees de - inmiddels zeer omvangrijke - discussie er maar eens op na. Er is overigens een bewijs mogelijk zonder differentiaal- of integraalrekening uitgaande van een definitie van exp(z) als de limiet van (1 + z/n)n voor n naar oneindig, maar uitgerekend dat bewijs staat niet in het engelstalige Wikipedia artikel.quote:
[..]
De formule van Euler kan ook eenvoudig bewezen worden met calculus en wat basisalgebra, zie http://en.wikipedia.org/wiki/Euler%27s_formula#Using_calculus .
Toch wel, want als je exp(z) definieert aan de hand van een machtreeks, dan moet je wel aantonen dat die reeks convergeert voor elke z uit C.quote:Het enige resultaat dat je daarvoor nodig hebt is dat d/dx e^ix = i e^ix.... Dit feit volgt direct uit de machtreeks van e^ix. We kunnen e^ix definiëren als die machtreeks, waardoor we ook geen kennis van Taylorreeksen nodig hebben.
Inderdaad. En dan blijft didactisch het bezwaar dat je wel een enorme omweg maakt om de additietheorema's te bewijzen. Feitelijk moet je dan ook cos(z) en sin(z) definiëren als (exp(iz)+exp(-iz))/2 resp. (exp(iz)-exp(-iz))/2i waarmee de formule van Euler tot een tautologie wordt. Niet geschikt voor een elementaire behandeling van de goniometrie op school.quote:Het enige wat je dus moet doen is e^ix definiëren als een machtreeks, toch? Op die manier zitten we niet in een cirkelredenering.
edit: ik bedenk me wel dat je nog uniforme convergentie moet aantonen om termgewijs te differentiëren, waardoor het toch wel iets gecompliceerder wordt. Niet echt stof voor de middelbare school.
Nee, dan heb je een slechte docent gehad. Dit volgt onmiddellijk met behulp van de kettingregel.quote:Aan de andere kant hebben ze bij mij op de middelbare school ook nooit aangetoond dat d/dx e^kx = k e^x voor reële k, dus ze zouden het ook gewoon als onbewezen stelling kunnen poneren.
Dat je er een k voor zet komt inderdaad door de kettingregel, maar dat de afgeleide van e^x gelijk is aan e^x is bij mij nooit bewezen. Volgens mij werd e^x geïntroduceerd als lim (1+x/n)^n, en daarvoor zou dan toevallig gelden dat d/dx e^x = e^xquote:
Nee, dan heb je een slechte docent gehad. Dit volgt onmiddellijk met behulp van de kettingregel.
, maar dat is niet helemaal duidelijk.
quote:
[..]
Dat je er een k voor zet komt inderdaad door de kettingregel, maar dat de afgeleide van e^x gelijk is aan e^x is bij mij nooit bewezen. Volgens mij werd e^x geïntroduceerd als lim (1+x/n)^n, en daarvoor zou dan toevallig gelden dat d/dx e^x = e^x
Voorlaatste regel moet starten met limh→0
[ Bericht 3% gewijzigd door Nelis89 op 05-05-2011 21:35:36 ]
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
De elementaire behandelingen hiervan verschillen nogal. Soms wordt eerst ln x geïntroduceerd via de nog ontbrekende primitieve van x-1 en dan is ex uiteraard de inverse functie. Via de kettingregel is dan ook duidelijk dat ex zichzelf als afgeleide heeft. Het is ook mogelijk te beginnen met de afgeleide van glog x via de definitie van de afgeleide, dat dan aanleiding geeft (via een substitutie h = kx) tot het beschouwen van de limiet voor k→0 van (1+k)1/k, en daarmee de introductie van het getal e. De afgeleide van glog x blijkt dan x-1∙glog e te zijn, waarmee de speciale status van de natuurlijke logaritme ook meteen duidelijk wordt, immers voor g = e reduceert dit tot x-1. Daarna is de behandeling van de afgeleide van de exponentiële functie ax niet moeilijk meer en komt de bijzondere status van ex ook niet uit de lucht vallen.quote:
[..]
Dat je er een k voor zet komt inderdaad door de kettingregel, maar dat de afgeleide van e^x gelijk is aan e^x is bij mij nooit bewezen. Volgens mij werd e^x geïntroduceerd als lim (1+x/n)^n, en daarvoor zou dan toevallig gelden dat d/dx e^x = e^x
Je doet hier iets wat niet klopt. eh is niet gelijk aan lim h→0 (1+h) = 1.quote:
Om aannemelijk te maken dat limh→0 (eh - 1)/h = 1 zou je wel een substitutie eh - 1 = k en dus h = ln(1+k) kunnen gebruiken.
h is gedefineerd als 1/n dus klopt welquote:
[..]
Je doet hier iets wat niet klopt. eh is niet gelijk aan lim h→0 (1+h) = 1.
Om aannemelijk te maken dat limh→0 (eh - 1)/h = 1 zou je wel een substitutie eh - 1 = k en dus h = ln(1+k) kunnen gebruiken.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Nee, het klopt echt niet. eh is niet gelijk aan limh→0 (1+h) = 1, want dan zou eh gelijk zijn aan de constante 1 en dat is niet zo. Dit is slechte didactiek (en slechte wiskunde).quote:
[..]
h is gedefineerd als 1/n dus klopt wel
limh→0 eh = limh→0 (1+h)quote:
[..]
Nee, het klopt echt niet. eh is niet gelijk aan limh→0 (1+h) = 1, want dan zou eh gelijk zijn aan de constante 1 en dat is niet zo. Dit is slechte didactiek (en slechte wiskunde).
h = 1/n
limn→∞ e1/n = limn→∞ (1+1/n) = 1
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Dit is juist, maar het verandert niets aan mijn bezwaren. Wat je hierboven bij de bepaling van de afgeleide van ex doet is niet correct.quote:
[..]
limh→0 eh = limh→0 (1+h)
h = 1/n
limn→∞ e1/n = limn→∞ (1+1/n) = 1
Jaja, zit 1 keer een klein foutje in. Voorlaatste regel moet starten met lim h→0quote:
[..]
Dit is juist, maar het verandert niets aan mijn bezwaren. Wat je hierboven bij de bepaling van de afgeleide van ex doet is niet correct.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Nee, er zit een principieel probleem in je afleiding. Je vervangt in feite eh door 1 + h en probeert dat te legitimeren door erop te wijzen dat:quote:
[..]
Jaja, zit 1 keer een klein foutje in. Voorlaatste regel moet starten met lim h→0
lim h→0 eh = lim h→0 (1 + h) = 1.
Maar dit maakt de substitutie niet legitiem. Laat ik een tegenvoorbeeld geven. Ik kan ook zeggen dat geldt:
lim h→0 cos h = lim h→0 (1 + h) = 1.
Als ik nu jouw redenering volg, dan zou de limiet voor h→0 van (cos h - 1)/h dus evenzo gelijk zijn aan de limiet voor h→0 van (1 + h - 1)/h = h/h, oftewel 1. Maar dát klopt niet, want de limiet voor h→0 van (cos h - 1)/h is gelijk aan 0.
Nog maar een poging:
De volgende Matlab code heb ik geschreven:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | % per row een oscillator: frequency, amplitude en een phase. De eerste twee zijn in mijn model stimulus node en de overige 4 recognition. De phases van de recognition zijn random tussen [0,2pi] gekozen. T=[14,4,0; 21,4,0; 10,1,rand(1)*2*pi; 15,1,rand(1)*2*pi; 20,1,rand(1)*2*pi; 25,1,rand(1)*2*pi]; % Couplings, dus hoe ze met elkaar verbonden zijn. In mijn model, alles is met coupling 1 gekoppeld op de verbindingen tussen de stimulus na (die is 0) NS = 2; NR = 4; K = []; for i = 1:NS+NR M = []; for j = 1:NS+NR if (i<=NS && j <=NS && i ~= j) M = [M, 0]; else M = [M, 1]; end end K=[K; M]; end % Kuramoto's equation % wat in het plaatje staat. t=[0:0.01:0.5]; % delta T dus 0.01. pM = zeros(NS+NR,length(t)); % de differenties van pM for k = 1:length(t) tt = t(k); if tt == 0 for n = [1:NS+NR] pM(n,1) = T(n,3); % op het eerste tijdstip is het gewoon waar we mee begonnen end else for n = [1:NS+NR] uit = 0; for i=[1:NS+NR] uit = uit+T(n,2)*T(i,2)*K(i,n)*sin(pM(i,k-1) - pM(n,k-1)); % kuramoto binnen de sum end pM(n,k) = ((uit+T(n,1))/(2*pi))+pM(n,k); % alles opgeteld en een /(2*pi) erbij (in me paper) end end end xM = repmat(T(:,2),[1,length(t)]).*cos(pM); % hoe ze frequentie volgens de paper berekenen % xM = repmat(T(:,2),[1,length(t)]).*sin(repmat((2*pi*T(:,1)),[1,length(t)])+pM); % zou werken voor een lijn tekenen plot(t,xM(1,:),t,xM(2,:),t,xM(3,:),t,xM(4,:),t,xM(5,:),t,xM(6,:)) |
Dat de code niet efficient is boeit me niet zo, dat kan ik wel versnellen van zelf.
Wat het probleem atm is, is dat ik niets vergelijkbaars krijg zoals in mijn paper. Je hebt daar namelijk een frequentie (y) tegenover tijd (x) en binnen de halve seconde gaan alle lijnen naar elkaar. Mogelijk teken ik gewoon de lijnen niet goed... op het moment gaan de lijnen vanzelf wel interacteren, maar krijg je nog steeds duidelijk golven te zien, alhoewel stabiel.
Dit is echt een raadsel voor me: Wat is de afgeleide van ln(x)2? Ik weet dat de afgeleide van ln(x) = 1/x, maar deze krijg ik niet in beeld.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Kettingregel toepassen.quote:
Dit is echt een raadsel voor me: Wat is de afgeleide van ln(x)2? Ik weet dat de afgeleide van ln(x) = 1/x, maar deze krijg ik niet in beeld.
Dan krijg ik: 2 ln(x)... nou zie ik net dat dit wel een deel van antwoord is, maar niet alles.quote:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Twee mogelijkheden:quote:
Dit is echt een raadsel voor me: Wat is de afgeleide van ln(x)2? Ik weet dat de afgeleide van ln(x) gelijk is aan 1/x, maar deze krijg ik niet in beeld.
1. Schrijf ln(x)∙ln(x) en gebruik de productregel
2. Schrijf [ln(x)]2 en gebruik de kettingregel.
Die van de kettingregel is mijn niet helemaal duidelijk, maar met de productregel ben ik aan het goede antwoord gekomen.quote:
[..]
Twee mogelijkheden:
1. Schrijf ln(x)∙ln(x) en gebruik de productregel
2. Schrijf [ln(x)]2 en gebruik de kettingregel.
Bedankt!
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Begrijp je de kettingregel wel?quote:
[..]
Die van de kettingregel is mij niet helemaal duidelijk, maar met de productregel ben ik aan het goede antwoord gekomen.
Bedankt!
Het begin is inderdaad goed, maar wat je nog vergeet is de afgeleide van ln(x) zelf. De definitie van de kettingregel is:quote:
[..]
Dan krijg ik: 2 ln(x)... nou zie ik net dat dit wel een deel van antwoord is, maar niet alles.
Wat hier eigenlijk staat is dat je een deel van je functie gelijk stelt aan u. In dit geval zal dat worden u=ln(x), de functie wordt dan dus u2.
De afgeleide wordt nu de afgeleide van je functie met u maal de afgeleide van u zelf. De afgeleide van de functie met u is 2u, de afgeleide van u zelf is 1/x. Dit geeft dus 2u/x=2*ln(x)/x.
The biggest argument against democracy is a five minute discussion with the average voter.
Jahoor, alleen niet dusdanig dat ik deze zo kan differentiëren.quote:
Ik zie hem nu ook ja. Ik vergiste mij in de inhoud van u. Ik dacht namelijk dat u = x, maar in wezen is u natuurlijk ln(x). Beginnersfout zal ik maar zeggen.quote:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
En als ik nu zeg dat in overeenstemming met de kettingregel de afgeleide van [ln(x)]n gelijk is aan:quote:
[..]
Jahoor, alleen niet dusdanig dat ik deze zo kan differentiëren.
n∙[ln(x)]n-1∙x-1
Begrijp je het dan wel?
Dat zou uiteindelijk dus n*ln(x) / x worden, aangezien x negatief is en die n'en de afgeleide van de u vormen.quote:
[..]
En als ik nu zeg dat in overeenstemming met de kettingregel de afgeleide van [ln(x)]n gelijk is aan:
n∙[ln(x)]n-1∙x-1
Begrijp je het dan wel?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Nee, je begrijpt het dus duidelijk niet. En nee, x is niet negatief (dan is ln(x) niet reëel).quote:
[..]
Dat zou uiteindelijk dus n*ln(x) / x worden, aangezien x negatief is en die n'en de afgeleide van de u vormen.
Het idee van de kettingregel is dat je die gebruikt bij samengestelde functies, oftwel functies die op zichzelf weer een functie bevatten.quote:
[..]
Dat zou uiteindelijk dus n*ln(x) / x worden, aangezien x negatief is en die n'en de afgeleide van de u vormen.
In jouw geval is de functie van de form f(x) = x2. Echter, bij jou wordt geen x gekwadrateerd, maar een ln(x), wat op zichzelf ook weer een functie is.
De kettingregel zegt dan dat je eerst het feit negeert dat die ln(x) er staat en net doet alsof je een kwadratische formule moet differentieren.
Daarom krijg je in eerste instantie 2*ln(x) (2 in de macht ervoor, de macht wordt met 1 verkleind).
Vervolgens moet je nu nog wel kijken naar die ln(x), omdat we die in eerste instantie 'vergeten' zijn. Ter compensatie moeten we dan nog vermenigvuldigen met die ln(x) welke gelijk is aan 1/x.
Totaal krijgen we dus: 2ln(x) * 1/x = 2ln(x)/x
Ik zit met een een probleem met de rekenkundige rij. Het volgende:
Bij de rechter som heb ik:
70 x 68 + 0,5 x 70 x (70-1) x 7 = 21665 (is niet goed)
Bij de linker:
30 x 15 + 0,5 x 30 x (30-1) x 8 = 3930 (is ook niet goed)
Andere komen wel uit
Bij de rechter som heb ik:
70 x 68 + 0,5 x 70 x (70-1) x 7 = 21665 (is niet goed)
Bij de linker:
30 x 15 + 0,5 x 30 x (30-1) x 8 = 3930 (is ook niet goed)
Andere komen wel uit
Of niet?
Sn = N x A + 0,5 x N x (N -1) x Vquote:
Zijn er specifieke formules die je probeert toe te passen of doe je lukraak maar wat?
A = startwaarde
V = vaste verschil
N = aantal termen
Of niet?
60 termenquote:
Die linker klopt gewoon. En bij de rechter zou ik het aantal termen nog maar even natellen.
Klopt het antwoordenmodel dus niet..
Of niet?
Die is omdat je niet bij 11 begint maar bij 10. Bij de linker begin je bij 1 met tellen, daarom komt het daar mooi rond uitquote:
70-10 = 60
En die ene term komt van de 70e term?
.
The biggest argument against democracy is a five minute discussion with the average voter.
Je maakt het jezelf onnodig moeilijk. De som van een aantal opeenvolgende termen van een rekenkundige rij is gelijk aan het gemiddelde van de eerste en de laatste term vermenigvuldigd met het aantal termen.quote:
[..]
Sn = N x A + 0,5 x N x (N -1) x V
A = startwaarde
V = vaste verschil
N = aantal termen
Voor de linkersom hebben we dus:
((15+247)/2)*30 = 131*30 = 3930
En voor de rechtersom:
((68+488)/2)*61 = 278*61 = 16958
Heb je dit vraagstuk nog op kunnen lossen? Ik kom op 1/3 + (√3)/2π, wat neerkomt op ca. 60,9%. Ik vind het alleen geen goed idee de uitwerking te geven, omdat ik zag dat het vraagstuk deel uitmaakt van een Pythagoras Olympiade waarvan de inzendtermijn nog loopt tot 30 juni 2011.quote:
[ afbeelding ]
Ik vind dit een boeiende vraag, alleen heb ik geen idee hoe ik moet beginnen.
Kan iemand me op weg helpen? Dan kan ik dan zien of ik genoeg intellect heb om het verder op te kunnen lossen
Ben er nog niet aan toegekomen. Het komt idd uit dat boekje.quote:
[..]
Heb je dit vraagstuk nog op kunnen lossen? Ik kom op 1/3 + (√3)/2π, wat neerkomt op ca. 60,9%. Ik vind het alleen geen goed idee de uitwerking te geven, omdat ik zag dat het vraagstuk deel uitmaakt van een Pythagoras Olympiade waarvan de inzendtermijn nog loopt tot 30 juni 2011.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Leuke vraag, ik kom op hetzelfde antwoord.quote:
[..]
Heb je dit vraagstuk nog op kunnen lossen? Ik kom op 1/3 + (√3)/2π, wat neerkomt op ca. 60,9%. Ik vind het alleen geen goed idee de uitwerking te geven, omdat ik zag dat het vraagstuk deel uitmaakt van een Pythagoras Olympiade waarvan de inzendtermijn nog loopt tot 30 juni 2011.
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Fijn om te horen, dan vertrouw ik erop dat mijn uitwerking correct is (maar daar was ik toch al van overtuigd).quote:
[..]
Leuke vraag, ik kom op hetzelfde antwoord.
@Riparius
Je zou mij er plezier mee doen als je hier nog eens het bewijs zou plaatsen, of door een link te geven of door plaatjes in te scannen of met Paint of iets dergelijks zelf een bewijs te tekenen. Als je er eens tijd voor hebt natuurlijk.
Tja, dat is inderdaad een nadeel van dit bewijs.quote:Die bewijzen met behulp van rechthoekige driehoeken vind ik niet fraai, omdat ze uitsluitend gelden voor scherpe hoeken α en β, terwijl er in de figuren bovendien vanuit wordt gegaan dat ook α+β een scherpe hoek is. De additietheorema's gelden echter voor willekeurige hoeken (rotaties), zowel positief als negatief. Er is een veel fraaier bewijs mogelijk met vectoren en de eenheidscirkel dat wél geldt voor willekeurige hoeken (rotaties), maar ik vind zo gauw geen webpagina waar dat goed wordt uitgelegd.
Je zou mij er plezier mee doen als je hier nog eens het bewijs zou plaatsen, of door een link te geven of door plaatjes in te scannen of met Paint of iets dergelijks zelf een bewijs te tekenen. Als je er eens tijd voor hebt natuurlijk.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Hier staat een eenvoudig bewijs met vectoren, ik weet niet of dat ook het bewijs is wat Riparius bedoelde (het staat een stukje boven het tweede plaatje). Er is wel nog een ding wat ik niet zo snel zie, waarom is de cosinus van de hoek in dit bewijs gelijk aan cos(y-x)?quote:
@Riparius
[..]
Tja, dat is inderdaad een nadeel van dit bewijs.
Je zou mij er plezier mee doen als je hier nog eens het bewijs zou plaatsen, of door een link te geven of door plaatjes in te scannen of met Paint of iets dergelijks zelf een bewijs te tekenen. Als je er eens tijd voor hebt natuurlijk.
Edit: Ik zie het al, ik dacht dat x en y voor de x- en y-coördinaten stonden, maar ze staan gewoon voor de hoeken in dit geval.
The biggest argument against democracy is a five minute discussion with the average voter.
De stochastische vector (X,Y) is tweedimensionaal normaal verdeeld met gelijke varianties. Ik wil laten zien dat X+Y en X-Y onafhankelijke stochasten zijn.
Ik had al bedacht dat X+Y en X-Y normaal verdeeld zijn, omdat iedere lineaire combinatie van normaal verdeelde stochasten weer normaal verdeeld is. Sterker nog, X+Y is N(m1+m2, s1²+s2²) verdeeld en X-Y is N(m1-m2, s1²+s2²) verdeeld (si staat voor de standaard deviatie en mi voor het gemiddelde).
Ik kan dus de kansdichtheidsfunctie van zowel X+Y als X-Y opschrijven. Hoe kan ik de joint distributie van X+Y, X-Y bepalen? (met als doel te controleren of fX+Y,X-Y = fX+Y * fX-Y om zo te laten zien dat ze onafh zijn). Of is er een betere aanpak?
Ik had al bedacht dat X+Y en X-Y normaal verdeeld zijn, omdat iedere lineaire combinatie van normaal verdeelde stochasten weer normaal verdeeld is. Sterker nog, X+Y is N(m1+m2, s1²+s2²) verdeeld en X-Y is N(m1-m2, s1²+s2²) verdeeld (si staat voor de standaard deviatie en mi voor het gemiddelde).
Ik kan dus de kansdichtheidsfunctie van zowel X+Y als X-Y opschrijven. Hoe kan ik de joint distributie van X+Y, X-Y bepalen? (met als doel te controleren of fX+Y,X-Y = fX+Y * fX-Y om zo te laten zien dat ze onafh zijn). Of is er een betere aanpak?
Dat kan, gegeven de pdf van de vector (X,Y) mbv de jacobiaan, zie http://en.wikipedia.org/w(...)_change_of_variables
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hmm, bedankt. Ik heb het uiteindelijk maar met covariantie gedaan, dat lijkt me toch wat eenvoudiger .
.
Ik heb gekeken naar de random vector (X+Y,X-Y), welke jointly normally distributed is.quote:Op zondag 8 mei 2011 19:39 schreef GlowMouse het volgende:
http://en.wikipedia.org/w(...)ot_imply_independent
quote:Suppose two random variables X and Y are jointly normally distributed. That is the same as saying that the random vector (X, Y) has a multivariate normal distribution. It means that the joint probability distribution of X and Y is such that for any two constant (i.e., non-random) scalars a and b, the random variable aX + bY is normally distributed. In that case if X and Y are uncorrelated, i.e., their covariance cov(X, Y) is zero, then they are independent.
Als A en B elk afzonderlijk normaal verdeeld zijn, dan is de vector (A, B) niet automatisch jointly normally distributed, zoals je citaat al aangeeft.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik vond sommige andere leuker, bijvoorbeeld:quote:
[ afbeelding ]
Ik vind dit een boeiende vraag, alleen heb ik geen idee hoe ik moet beginnen.
Kan iemand me op weg helpen? Dan kan ik dan zien of ik genoeg intellect heb om het verder op te kunnen lossen
Ik heb nu ook het vak datastructuren, wat veel over algoritmes gaat. Daar wordt altijd een algoritme besproken in termen van best-case, average-case en worst-case. In deze vraag wordt gevraagd om het snelste algoritme (want dat is het als het ware) voor een probleem. Ik neem even aan dat hier gevraagd wordt om het algoritme met de beste worst-case performance (oh wat klink ik geleerdquote:Ernst heeft acht emmers: vier van het merk hamé en vier van het merk delta. Hoewel Ernst de emmers niet met het blote oog uit elkaar kan houden, weet hij dat een emmer van hamé in (bovenop) een emmer van delta past, maar niet andersom. Bovendien passen twee emmers van dezelfde soort natuurlijk wel in elkaar.Hoe kan Ernst in zo weinig mogelijk zetten alle emmers identificeren? Een zet bestaat uit het op elkaar zetten van twee emmers (geen stapeltjes); het uit elkaar halen van twee emmers mag zo vaak als je wilt.
).Stel dat je een mogelijke oplossing hebt voor dit of een dergelijk probleem. Is er dan een manier om dit te bewijzen, of moet je dit soort vraagstukken puur op intuïtie oplossen?
(Om dezelfde reden als Riparius zijn redenering bij zijn antwoord op de vraag over een muis op een tafel niet postte, post ik mijn antwoord nu niet: de vraag komt uit de Pytagoras olympiade en daarvoor kan men nog tot juni antwoorden opsturen)
Finally, someone let me out of my cage
Doet me denken aan deze post van je, die ik laatst bij het aanmaken van een reeks tegenkwam.quote:Op zondag 8 mei 2011 22:57 schreef thabit het volgende:
In de wiskunde is de bedoeling uiteraard dat je het bewijst, minibeer.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
In dit geval wel, ga maar na.quote:
Als A en B elk afzonderlijk normaal verdeeld zijn, dan is de vector (A, B) niet automatisch jointly normally distributed, zoals je citaat al aangeeft.
Ik begrijp dat men er in het algemeen naar streeft algoritmes te bewijzen, maar dat is toch niet altijd mogelijk? Als het wel mogelijk is, is er een bepaalde manier voor die vaak wordt toegepast?
Of, wat concreter, ik heb een vermoeden voor het probleem dat ik net postte. Kan ik op een makkelijke manier uitvogelen of het inderdaad de snelste manier is?
(voor zover ik weet kan je alleen ontkrachten dat het algoritme het snelst mogelijke is door een sneller algoritme te geven en van beide de performance te berekenen)
Sorry als ik veel vage vragen stel, als ik dingen niet goed begrijp vraag ik er soms maar wat op los
Of, wat concreter, ik heb een vermoeden voor het probleem dat ik net postte. Kan ik op een makkelijke manier uitvogelen of het inderdaad de snelste manier is?
(voor zover ik weet kan je alleen ontkrachten dat het algoritme het snelst mogelijke is door een sneller algoritme te geven en van beide de performance te berekenen)
Sorry als ik veel vage vragen stel, als ik dingen niet goed begrijp vraag ik er soms maar wat op los
Finally, someone let me out of my cage
In het algemeen is het bij algoritmen behoorlijk lastig om aan te tonen dat ze zo snel mogelijk zijn in het slechtste geval. Maar bij dit soort Pythagoraspuzzeltjes mag je ervan uitgaan dat het wel op een vrij eenvoudige manier kan.quote:
Ik begrijp dat men er in het algemeen naar streeft algoritmes te bewijzen, maar dat is toch niet altijd mogelijk? Als het wel mogelijk is, is er een bepaalde manier voor die vaak wordt toegepast?
Of, wat concreter, ik heb een vermoeden voor het probleem dat ik net postte. Kan ik op een makkelijke manier uitvogelen of het inderdaad de snelste manier is?
(voor zover ik weet kan je alleen ontkrachten dat het algoritme het snelst mogelijke is door een sneller algoritme te geven en van beide de performance te berekenen)
Sorry als ik veel vage vragen stel, als ik dingen niet goed begrijp vraag ik er soms maar wat op los
Het maken van een mooi plaatje (niet met Paint maar met iets als Cabri) laat ik graag aan anderen over omdat het prepareren van deze post mij al voldoende tijd kost, maar ook zonder plaatje zal het hopelijk duidelijk zijn. Vreemd genoeg kan ik nergens op het web een goede uiteenzetting vinden van het bewijs dat mij voor ogen staat.quote:
@Riparius
[..]
Je zou mij er plezier mee doen als je hier nog eens het bewijs zou plaatsen, of door een link te geven of door plaatjes in te scannen of met Paint of iets dergelijks zelf een bewijs te tekenen. Als je er eens tijd voor hebt natuurlijk.
Eerst wat inleidende opmerkingen over vectoren en de definitie van de sinus en cosinus aan de hand van de eenheidscirkel.
Kiezen we een punt O in het platte vlak en twee vectoren OA = a en OB = b die geen van beide de nulvector zijn en niet in elkaars verlengde liggen, dan kunnen we elke willekeurige andere vector OP = p in dat platte vlak uitdrukken als een lineaire combinatie van a en b, en wel op een eenduidige manier. Er is dan precies één geordend paar reële getallen (λ;μ) zodanig dat:
(1) p = λ∙a + μ∙b
We noemen de set {a, b} nu een basis voor de vectorruimte bestaande uit alle vectoren in het platte vlak. Het geordende paar (λ;μ) noemen we dan de coördinaten van vector p ten opzichte van de basis {a, b}.
Hebben we al een assenstelsel met cartesische coördinaten, dan vormen de vectoren met lengte één langs de positieve x-as resp. de positieve y-as de vectorbasis voor deze coördinaten. Aangezien deze vectoren een lengte één hebben spreken we van eenheidsvectoren en duiden we deze aan met ex resp. ey. De vectorbasis {ex , ey} wordt ook wel een orthonormale basis genoemd omdat de beide vectoren niet alleen een lengte één hebben maar tevens loodrecht op elkaar staan. Merk nog op dat de oriëntatie van het paar {ex, ey} zodanig is dat de eerste vector ex bij een rotatie over 90 graden in positieve zin (i.e. tegen de wijzers van de klok in) overgaat in de tweede vector ey.
Bij een elementaire behandeling worden de sinus en cosinus van een hoek in eerste instantie geïntroduceerd als verhoudingen tussen de rechthoekszijden en de schuine zijde (hypotenusa) in een rechthoekige driehoek. Aangezien de lengten van overeenkomstige zijden van gelijkvormige driehoeken evenredig met elkaar zijn, hangen deze verhoudingen uitsluitend af van de hoeken van de rechthoekige driehoek. De aldus geïntroduceerde begrippen sinus en cosinus hebben echter uitsluitend betekenis voor scherpe hoeken.
De zogeheten eenheidscirkel (een cirkel met middelpunt in de oorsprong van een cartesisch assenstelsel en met een straal één) maakt het nu mogelijk de begrippen sinus en cosinus uit te breiden naar willekeurige hoeken (rotaties), zowel in positieve zin (tegen de wijzers van de klok in) als in negatieve zin (met de wijzers van de klok mee).
Kiezen we een willekeurig punt P(xP; yP) op de eenheidscirkel, maar dan wel in het eerste kwadrant, en laten we vanuit P een loodlijn neer op de x-as, en noemen we het voetpunt van deze loodlijn Q, dan is driehoek OPQ een rechthoekige driehoek met een rechte hoek in hoekpunt Q en een hypotenusa OP.
Noemen we hoek QOP α, dan is de sinus van hoek α gelijk aan de overstaande rechthoekszijde QP gedeeld door de schuine zijde OP, dus:
(2) sin α = sin ∠QOP = QP : OP = yP : 1 = yP
En de cosinus van hoek α is gelijk aan de aanliggende rechthoekszijde OQ gedeeld door de schuine zijde OP, dus:
(3) cos α = cos ∠QOP = OQ : OP = xP : 1 = xP
We zien nu dat cos α en sin α gelijk zijn aan de coördinaten xP resp. yP van het punt P(xP;yP). Dit is uiteraard niet verrassend maar een direct gevolg van het feit dat de straal van de gekozen cirkel, en daarmee de lengte van de hypotenusa OP van driehoek OPQ, gelijk is aan één. Maar dit biedt wel een mogelijkheid om cos α en sin α betekenis te geven voor een willekeurige hoek (rotatie) α zowel in positieve als in negatieve zin.
Aangezien ∠QOP = α gaat het punt met coördinaten (1;0) over in punt P(xP;yP) bij een rotatie rond de oorprong over een hoek α. We kunnen nu afspreken (definiëren) dat we ook bij een rotatie om de oorsprong van punt (1;0) over een willekeurige hoek α de coördinaten xP en yP van het beeldpunt P(x P;yP) zullen beschouwen als de cosinus resp. de sinus van α. Anders gezegd, het punt met coördinaten (1;0) gaat bij een rotatie om de oorsprong over een willekeurige hoek α over in het punt met de coördinaten (cos α ; sin α).
Dan nu het bewijs van de additietheorema's. Het punt met coordinaten (1;0) is het eindpunt van de eenheidvector ex, en dus kunnen we het beeldpunt (cos α ; sin α) van (1;0) bij rotatie over een hoek α opvatten als het eindpunt van een vector ex' die het beeld is van vector ex bij een rotatie over een hoek α. Aldus hebben we:
(4) ex' = cos α∙ex + sin α∙ey
Nu gaat bij rotatie om de oorsprong over een (willekeurige) hoek α niet alleen de eenheidsvector ex over in een beeldvector ex', maar evenzo gaat de eenheidsvector ey over in een vector ey', zodat we kunnen zeggen dat de vectorbasis {ex, ey} bij rotatie over een hoek α overgaat in de (eveneens orthonormale) vectorbasis {ex', ey'}.
Nu hebben we middels (4) vector ex' uitgedrukt als een lineaire combinatie van ex en ey, maar we kunnen ook ey' uitdrukken in ex en ey. Dit gaat als volgt.
Bij rotatie om de oorsprong over een hoek van 90 graden tegen de wijzers van de klok in (i.e. in positieve zin) gaat vector ex over in vector ey en gaat vector ey over in vector -ex. Aldus kunnen we zeggen dat de vectorbasis {ex, ey} bij rotatie over 90 graden in positieve zin overgaat in de (eveneens orthonormale) vectorbasis {ey, -ex}. Kiezen we nu {ey, -ex} als basis waarbij de eerste vector ey van deze basis bij een rotatie over een hoek α overgaat in een beeldvector ey', dan geldt dus analoog aan (4) en conform de definitie van de cosinus en de sinus:
(5) ey' = cos α∙ey + sin α∙(-ex)
En aangezien sin α∙(-ex) = -sin α∙ex kunnen we hiervoor ook schrijven:
(6) ey' = cos α∙ey - sin α∙ex
Roteren we vervolgens vector ex' over een (willekeurige) hoek β en noemen we het beeld van ex' bij deze rotatie ex'', dan kunnen we ex'' op twee verschillende manieren uitdrukken in ex en ey.
Om te beginnen kunnen we bedenken dat ex' het beeld is van ex bij rotatie over een hoek α en dat ex'' weer het beeld is van ex' bij rotatie over een hoek β. Aldus is ex'' het beeld van ex bij rotatie over een hoek α+β, zodat naar analogie van (4) en in overeenstemming met de definitie van cosinus en sinus geldt:
(7) ex'' = cos(α+β)∙ex + sin(α+β)∙ey
We kunnen echter ex'' ook uitdrukken in de vectorbasis {ex', ey'}. Aangezien de eerste vector ex' van deze basis bij rotatie over een hoek β overgaat in ex'' geldt naar analogie van (4) en in overeenstemming met de definitie van cosinus en sinus:
(8) ex'' = cos β∙ex' + sin β∙ey'
Maar nu hadden we ex' en ey' al uitgedrukt in ex en ey. Substitutie van (4) en (6) in (8) levert:
(9) ex'' = cos β∙(cos α∙ex + sin α∙ey) + sin β∙(cos α∙ey - sin α∙ex)
Uitwerken van het rechterlid van (9) en hergroeperen van de termen met ex en ey geeft:
(10) ex'' = (cos α∙cos β - sin α∙sin β)∙ex + (sin α∙cos β + cos α∙sin β)∙ey
Nu weten we echter dat elke vector, en dus ook ex'', op precies één manier is uit te drukken als een lineaire combinatie van de basisvectoren {ex, ey}. Uit (7) en (10) volgt dus:
(11a) cos(α+β) = cos α∙cos β - sin α∙sin β
(11b) sin(α+β) = sin α∙cos β + cos α∙sin β
QED
Toegift: aangezien (11a) en (11b) gelden voor willekeurige rotaties in zowel positieve als negatieve zin en aangezien α-β = α+(-β) geldt ook:
(11a) cos(α-β) = cos α∙cos(-β) - sin α∙sin(-β)
(11b) sin(α-β) = sin α∙cos(-β) + cos α∙sin(-β)
Een rotatie van het punt (1;0) over een hoek -β is equivalent met een rotatie van het punt (1;0) over een hoek β gevolgd door een spiegeling in de x-as. En aangezien bij spiegeling in de x-as een punt met coördinaten (xP;yP) overgaat in een punt met coördinaten (xP;-yP) volgt dat geldt:
(12) cos(-β) = cos β en sin(-β) = -sin β
Substitutie van (12) in (11a) en (11b) levert dan:
(13a) cos(α-β) = cos α∙cos β + sin α∙sin β
(13b) sin(α-β) = sin α∙cos β - cos α∙sin β
[ Bericht 0% gewijzigd door Riparius op 09-05-2011 14:49:55 ]
Ik neem niet aan dat het de bedoeling is dat je in dat soort puzzels een bewijs geeft? Het is namelijk de enige vraag uit die links waarbij ik echt vastloop als ik een bewijs moet geven. Zie jij wel hoe het zou moeten dan?quote:
[..]
In het algemeen is het bij algoritmen behoorlijk lastig om aan te tonen dat ze zo snel mogelijk zijn in het slechtste geval. Maar bij dit soort Pythagoraspuzzeltjes mag je ervan uitgaan dat het wel op een vrij eenvoudige manier kan.
Finally, someone let me out of my cage
Ja, bij dit soort puzzels is altijd de bedoeling om een bewijs te geven, tenzij uit de vraagstelling heel duidelijk is dat dat niet hoeft. Als je daadwerkelijk de snelste methode hebt gevonden, dan is het in dit geval zelfs heel makkelijk te bewijzen dat het niet sneller kan.quote:
[..]
Ik neem niet aan dat het de bedoeling is dat je in dat soort puzzels een bewijs geeft? Het is namelijk de enige vraag uit die links waarbij ik echt vastloop als ik een bewijs moet geven. Zie jij wel hoe het zou moeten dan?
Jammer, dan ben ik gewoon aan het falenquote:
[..]
Ja, bij dit soort puzzels is altijd de bedoeling om een bewijs te geven, tenzij uit de vraagstelling heel duidelijk is dat dat niet hoeft. Als je daadwerkelijk de snelste methode hebt gevonden, dan is het in dit geval zelfs heel makkelijk te bewijzen dat het niet sneller kan.
Finally, someone let me out of my cage
ik denk dat ik het al wat beter begrijp, bedankt in ieder geval . Nog even kijken of ik een bewijs kan maken, als het lukt zal ik hem morgen wel ff posten.
. Nog even kijken of ik een bewijs kan maken, als het lukt zal ik hem morgen wel ff posten.
Finally, someone let me out of my cage
hallo,
Ik ben bezig met oefenen voor me wiskunde B examens en loop vast op het volgende:
In het correctie voorschrift staat dat je van "f'(x)=2cos x ⋅ (1+ sin x) + 2sin x ⋅cos x" dit "f'(x)=2cos x + 4cos x ⋅sin x" kan maken. Alleen ik weet niet hoe???
Ik ben bezig met oefenen voor me wiskunde B examens en loop vast op het volgende:
In het correctie voorschrift staat dat je van "f'(x)=2cos x ⋅ (1+ sin x) + 2sin x ⋅cos x" dit "f'(x)=2cos x + 4cos x ⋅sin x" kan maken. Alleen ik weet niet hoe???
heb je de haakjes om (1+sin x) al geprobeerd weg te werken?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja, dan krijg ik f'(x)=2cos x * 2cos x * sin x + 2sin x * cos x
En dat kan je ook schrijven als f'(x)=4cos x * sin x + 2sin x * cos x
En nu?
En dat kan je ook schrijven als f'(x)=4cos x * sin x + 2sin x * cos x
En nu?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |