SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk-en-vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Ah ja, ik las het verkeerd. Ik neem aan dat n=2 en bewijs het in dat geval. Even proberen.
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm en algemener) gedefinieerd op p3!
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm en algemener) gedefinieerd op p3!
Niet helemaal equivalent: 0 deelt 0, maar 0/0 is niet gedefinieerd.quote:Op zondag 10 april 2011 16:53 schreef BasementDweller het volgende:
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm) gedefinieerd op p3!
Ik kom er echt niet uit...
Misschien toch wel
Klopt het dat E(X1² X2 + X1X2²) = 0?
[ Bericht 42% gewijzigd door BasementDweller op 10-04-2011 17:45:50 ]
Misschien toch wel
Klopt het dat E(X1² X2 + X1X2²) = 0?
[ Bericht 42% gewijzigd door BasementDweller op 10-04-2011 17:45:50 ]
Dat is uiteraard de bedoeling, anders is de opgave fout. Je wilde het echter met karakteristieke functies doen, in dat opzicht is E(X1² X2 + X1X2²) niet de juiste stap.
Ja dat is waar. Maar ik dacht misschien dat ik deze dan weer kan bewijzen met karakteristieke functies maar dat lukte me niet.quote:
Dat is uiteraard de bedoeling, anders is de opgave fout. Je wilde het echter met karakteristieke functies doen, in dat opzicht is E(X1² X2 + X1X2²) niet de juiste stap.
Je kan het derde moment van de som uitdrukken in karakteristieke functies, en de karakteristieke functie van de som van twee onafhankelijke stochasten in elk van beide.
thanks thabit en basementdweller
Ah, ik heb gezegd f_X1+X2 = f_X1 f_X2, en dat ding 3x naar t gedifferentieerd. Na heel vaak de productregel van differentiëren toegepast te hebben komt het antwoord eruit. Bedankt.quote:
Je kan het derde moment van de som uitdrukken in karakteristieke functies, en de karakteristieke functie van de som van twee onafhankelijke stochasten in elk van beide.
Dat "heel vaak toepassen" daar bestaat ook een binomium voor:
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
Chique, bedankt.quote:Op zondag 10 april 2011 19:52 schreef thabit het volgende:
Dat "heel vaak toepassen" daar bestaat ook een binomium voor:
[ afbeelding ]
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
Om even terug naar trigonometrie te gaan: Klopt deze afleiding?
tan(x/2) = sinx / (1 + cosx)
stel sinx = p => arcsin(sinx) = x = arcsin(p)
tan(x/2) = p / (1 + SQRT(1-p2)
arctan(tan(x/2)) = arctan (p / (1 + SQRT(1-p2))
(x/2) = arctan (p / (1 + SQRT(1-p2))
x = 2 arctan (p / (1 + SQRT(1-p2))
backsub x = arcsin(p)
arcsin p = 2 arctan (p / (1 + SQRT(1-p2))
tan(x/2) = sinx / (1 + cosx)
stel sinx = p => arcsin(sinx) = x = arcsin(p)
tan(x/2) = p / (1 + SQRT(1-p2)
arctan(tan(x/2)) = arctan (p / (1 + SQRT(1-p2))
(x/2) = arctan (p / (1 + SQRT(1-p2))
x = 2 arctan (p / (1 + SQRT(1-p2))
backsub x = arcsin(p)
arcsin p = 2 arctan (p / (1 + SQRT(1-p2))
Da's enkel een kwestie van domeinrestrictie. En dat had je zelf al kunnen zien aan de wortelterm waarin x in [-1,1] moet liggen, anders is deze niet gedefinieerd. En laat [-1,1] nou net het complete domein van arcsin (en arccos) zijnquote:
Nee, arcsin(sin x) is niet x: als je bij x 2pi optelt, blijft z'n sinus immers hetzelfde.
[ Bericht 14% gewijzigd door VanishedEntity op 10-04-2011 20:57:17 ]
Ja, logisch dat je dan niet uitkomt, want je gaat voorbij aan de extra eis van domeinrestrictie die bij cyclometrische functies naar voren komt. 2pi valt niet binnen het domein [-1/2*pi;1/2*pi] voor sinx, en daarmee het bereik van arcsinx. Je zal eerst net zolang INT*2pi af moeten trekken totdat x, òf pi - x binnen [-1/2*pi;1/2*pi] komt te liggen.quote:
Vul maar x=2pi in: arcsin(sin 2pi) = 0, niet x.
Ola, ik zit ook even met een probleempje.
Als ik de volgende dubbele integraal oplos
I(a) = int(int(exp(-a(x+2*y)), y = x .. 1), x = 0 .. 1)
kom ik voor willekeurige a uit op
I(a) = (1/6)*(2*exp(-3*a)-3*exp(-2*a)+1)/a^2
vervolgens moet ik laten zien dat dit voor a=0 gelijk is aan een half, maar gezien je deelt door 0² heb je toch een ongedefinieerde oplossing, of ben ik nu een kiwi?
kusjes
Als ik de volgende dubbele integraal oplos
I(a) = int(int(exp(-a(x+2*y)), y = x .. 1), x = 0 .. 1)
kom ik voor willekeurige a uit op
I(a) = (1/6)*(2*exp(-3*a)-3*exp(-2*a)+1)/a^2
vervolgens moet ik laten zien dat dit voor a=0 gelijk is aan een half, maar gezien je deelt door 0² heb je toch een ongedefinieerde oplossing, of ben ik nu een kiwi?
kusjes
Omnia vincit amor, nos et cedamus amori
direct a invullen in de integraal dan kom je inderdaad uit op een half, maar de opdracht is vervolgens op I(a) voor willekeurige a te bepalen en dan komt de vraag op beide manieren overeen komen
Omnia vincit amor, nos et cedamus amori
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
vlogens mij wordt (x + h)^2 daar gewoon uitgeschrevenquote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Dus zonder haakjes 
Zie je het dan wel? Schrijf gewoon maar eens uit.
~Si vis amari, ama~
(x+h)2= x2+2xh+h2quote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Als je dit optelt met die -x2 krijg je 2xh+h2
Niet altijd serieus
Heb je wel eens gehoord van een merkwaardig product?quote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om de afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van x2 = 2x, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurt. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Eigenlijk niet.quote:
[..]
Heb je wel eens gehoord van een merkwaardig product?
Ik mis nogal wat algebraïsche kennis heb ik gemerkt. Ben er nu naar een het kijken. Erg verhelderend allemaal.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik ben nu wat aan het leren over o.a. modulorekenen, en er staan wat opdrachten bij. Ik kan maar niet uit deze komen:
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag.
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag
.
Finally, someone let me out of my cage
Het merkwaardig product dat je in je bepaling van de afgeleide van f(x) = x2 kunt gebruiken is:quote:
[..]
Eigenlijk niet.
(a + b)2 = a2 + 2ab + b2
Je kunt de juistheid van deze identiteit natuurlijk aantonen door de haakjes in het linkerlid weg te werken, maar het is meetkundig ook mooi in te zien dat dit klopt.
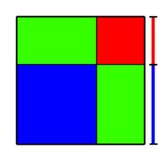
De oppervlakte van een vierkant met zijde a is a2 en de oppervlakte van een vierkant met zijde b is b2. Stel nu eens dat we een vierkant hebben met zijde (a + b), dan is de oppervlakte (a + b)2. Maar hoe staat deze oppervlakte nu in verband met die van de vierkanten met zijde a en zijde b? Ik heb even een plaatje gepikt uit de Franse Wikipedia:
Laten we aannemen dat het blauwe lijnstuk rechts van het vierkant een lengte a heeft, en het rode lijnstuk een lengte b. Dan is de totale zijde van het vierkant dus (a + b) en de totale oppervlakte van het vierkant dus (a + b)2. Maar je ziet dat de totale oppervlakte van het grote vierkant wordt gevormd door het blauwe vierkant (met oppervlakte a2), het rode vierkant (met oppervlakte b2), maar ook nog door de twee groene rechthoeken. Elk van die groene rechthoeken heeft een lengte a en een breedte b, en dus een oppervlakte ab. En omdat er twee van die rechthoeken zijn, moeten we bij a2 + b2 dus ook nog 2ab optellen om de oppervlakte van het grote vierkant te krijgen. En dat is precies wat het merkwaardig product hierboven zegt!
ok, laten we gewoon eens wat gaan rekenen en kijken hoever we komen:quote:
Ik ben nu wat aan het leren over o.a. modulorekenen, en er staan wat opdrachten bij. Ik kan maar niet uit deze komen:
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag
x2-3y2=1997
3y2=x2-1997
y2=(x2-1997)/3
Nu maken we de observatie dat als dit een oplossing heeft voor x en y gehele getallen, dan moet x2-1997 deelbaar zijn door 3. met andere woorden:
x2 = 1997 mod 3
Aan jou de vraag, waarom heeft dit geen oplossing?
Feitelijk is het dus zo dat X2 = 2X omdat het twee (blauwe) vierkanten vormt? Tenminste om het even eenvoudig te maken voor mezelf, want volgens mij klopt dat niet helemaal.quote:
[..]
... En dat is precies wat het merkwaardig product hierboven zegt!
[ Bericht 3% gewijzigd door Pipo1234 op 12-04-2011 12:34:29 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
x2 is sowieso niet gelijk aan 2x, de afgeleide van x2 is 2x. Dat is ook niet zo omdat het twee blauwe vierkanten vormt (los daarvan, er is maar één blauw vierkant), dat is slechts een tussenstap die je nodig hebt om de limiet op te lossen.quote:
[..]
Feitelijk is het dus zo dat X2 = 2X omdat het twee (blauwe) vierkanten vormt? Tenminste om het even eenvoudig te maken voor mezelf, want volgens mij klopt dat niet helemaal.
Het vierkant laat zien dat je (a+b)2 kunt schrijven als a2+2ab+b2. Als je dat invult in de limiet kom je uit op de oplossing
.Je moet het niet te simpel maken voor jezelf door stappen simpelweg over te slaan, dan klopt het niet meer.
The biggest argument against democracy is a five minute discussion with the average voter.
quote:
[..]
x2 is sowieso niet gelijk aan 2x, de afgeleide van x2 is 2x. Dat is ook niet zo omdat het twee blauwe vierkanten vormt (los daarvan, er is maar één blauw vierkant), dat is slechts een tussenstap die je nodig hebt om de limiet op te lossen.
Het vierkant laat zien dat je (a+b)2 kunt schrijven als a2+2ab+b2. Als je dat invult in de limiet kom je uit op de oplossing
Je moet het niet te simpel maken voor jezelf door stappen simpelweg over te slaan, dan klopt het niet meer.
Het is de afgeleide natuurlijk. Misschien probeer ik het inderdaad te simpel voor mezelf te maken.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Die merkwaardige producten is precies wat ik nodig had! Alleen nu heb ik er nog een vraag over. Als ik X3 heb en dan op h3 + 3x2h + 3xh2 uitkom, wat gebeurd er dan met die overtollige 3x van de laatste samenstelling? Als ik h wegstreep houd ik namelijk 3x over... en ik weet dat het antwoord 3x2 moet zijn.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik begrijp niet precies wat je bedoelt? Als ik het uitwerk kom ik uit op(h3 + 3x2h + 3xh2 + x3 - x3)/h. Als je dat uitwerkt komt het gewoon uit hoorquote:
Die merkwaardige producten is precies wat ik nodig had! Alleen nu heb ik er nog een vraag over. Als ik X3 heb en dan op h3 + 3x2h + 3xh2 uitkom, wat gebeurd er dan met die overtollige 3x van de laatste samenstelling? Als ik h wegstreep houd ik namelijk 3x over... en ik weet dat het antwoord 3x2 moet zijn.
. Misschien dat je vergeten bent om in het begin f(x+h) - f(x) te doen?
The biggest argument against democracy is a five minute discussion with the average voter.
Nee die formule heb ik ook. Ik probeer het te gebruiken voor een differentatie van X3. Bij X2 kom ik er door H weg te strepen. Maar bij X3 houd ik op de volgende manier 3X2 en 3X over: h3 + 3x2h + 3xh2 + x3 - x3)/hquote:
[..]
Ik begrijp niet precies wat je bedoelt? Als ik het uitwerk kom ik uit op(h3 + 3x2h + 3xh2 + x3 - x3)/h. Als je dat uitwerkt komt het gewoon uit hoor
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ah, nu begrijp ik het denk ik:quote:
[..]
ok, laten we gewoon eens wat gaan rekenen en kijken hoever we komen:
x2-3y2=1997
3y2=x2-1997
y2=(x2-1997)/3
Nu maken we de observatie dat als dit een oplossing heeft voor x en y gehele getallen, dan moet x2-1997 deelbaar zijn door 3. met andere woorden:
x2 = 1997 mod 3
Aan jou de vraag, waarom heeft dit geen oplossing?
x2 = 1997 mod 3
x2 = 2 mod 3
De enige manier om in modulo 3 verzameling 2 te krijgen is door 1 met 2 of 2 met 1 te vermenigvuldigen. Voor x2 is er us geen oplossing in gehele getallen.
Dit betekent als ik het goed begrijp ook dat x2 -2 nooit deelbaar is door 3, wat ik best opmerkelijk vind
.Dank voor de hulp
Finally, someone let me out of my cage
Ik denk dat je de limiet van h naar 0 vergeet. Je deelt een keer een h weg, zodat je h2 + 3xh + 3x2 overhoudt. De limiet van h naar 0 nemen zorgt er voor dat alleen de 3x2 overblijft.quote:
[..]
Nee die formule heb ik ook. Ik probeer het te gebruiken voor een differentatie van X3. Bij X2 kom ik er door H weg te strepen. Maar bij X3 houd ik op de volgende manier 3X2 en 3X over: h3 + 3x2h + 3xh2 + x3 - x3)/h
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?quote:Op dinsdag 12 april 2011 15:29 schreef freiss het volgende:
[..]
Ik denk dat je de limiet van h naar 0 vergeet. Je deelt een keer een h weg, zodat je h2 + 3xh + 3x2 overhoudt. De limiet van h naar 0 nemen zorgt er voor dat alleen de 3x2 overblijft.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Even tussendoor, snap je wat er bedoelt wordt met de limiet? Dat is namelijk wel redelijk belangrijk om dit echt te begrijpenquote:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
. Ik zal proberen uit te leggen wat er gebeurt, eerst heb je de limiet van (f(x+h) - f(x) )/h. Daarna schrijf je dit uit, in jouw geval krijg je dan de limiet van (h3 + 3x2h + 3xh2 + x3 - x3)/h. Eerst werk je dit uit, je deelt de h weg uit alle termen, je krijgt nu de limiet van h2 + 3x2 + 3xh. Nu ga je de limiet invullen, als h in deze uitdrukking naar nul gaat zullen alle termen nul worden behalve 3x2, dat is dus de uitkomst van dit probleem. Ik ben er in deze uitleg een beetje van uitgegaan dat je snapt wat de limiet is, als je dat niet snapt moet je dat maar even proberen op te zoeken of te vragen
.
The biggest argument against democracy is a five minute discussion with the average voter.
Differentiëren is geen 'wegstrepen'. Je bepaalt van een functie y = f(x) eerst het differentiequotiënt:quote:Op dinsdag 12 april 2011 15:58 schreef Pipo1234 het volgende:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
Δy/Δx = (f(x+h) - f(x))/((x+h) - x) = (f(x+h) - f(x))/h
Deze verhouding zegt iets over hoeveel de afhankelijke variabele y (i.e. de functiewaarde) verandert in verhouding tot een verandering van de onafhankelijke variabele x. Meetkundig kun je dit opvatten als de gemiddelde steilheid van de curve van f(x) over een klein intervalletje [x, x+h]. Door nu het intervalletje steeds kleiner te maken (en dus de limiet te bepalen als h naar 0 gaat) krijgen we dan de steilheid van de curve van f(x) c.q. de steilheid van de raaklijn aan de curve van f(x) in één bepaald punt. Die steilheid (en dus de afgeleide) is een maat voor de snelheid waarmee de waarde van f(x) op dat punt verandert.
Hebben we f(x) = x3, dan vinden we voor het differentiequotiënt:
(f(x+h) - f(x))/h = ((x+h)3 - x3)/h = (x3 + 3x2h + 3xh2 + h3 - x3)/h = 3x2 + 3xh + h2
Om nu de afgeleide f'(x) te vinden moet ik de limiet van dit differentiequotiënt bepalen voor h→ 0. Dus krijg ik:
f'(x) = lim h→0 (f(x+h) - f(x))/h = lim h→0 (3x2 + 3xh + h2) = 3x2
De beide termen 3xh en h2 naderen immers tot 0 als we h naar nul laten gaan, zodat 3x2 resulteert.
quote:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Bedankt voor alle antwoorden. Ik denk dat ik al begrijp wat ik fout heb gedaan. Ik moest het namelijk nog daar H delen, alleen had er niet bij stil gestaan dat dit voor het limiet noodzakelijk is.
De volgende benadering heb ik nu:
f(x) = x3
f'(x) = lim(h>0) (x+h)3 - (x)3 / h
f'(x) = lim(h>0) x3 + h3 - x3 / h
f'(x) = lim(h>0) x3 + h3 + 3x2h + 3xh2 - x3 / h (Volgens het merkwaardig product)
f'(x) = lim(h>0) h3 + 3x2h + 3xh2/ h (x3 - x3)
f'(x) = lim(h>0) h2 + 3x2 + 3xh (Gedeeld door h)
f'(x) = 3x2 (Limiet 0 is benaderd)
Mijn boek merkt trouwens op dat dit de beste maar moeilijkste methode is om te differentiëren. Is dat zo? Ik vind het voor uitvoerig, maar kan me wel voorstellen dat dit op een examen een beetje teveel van het goed is.
De volgende benadering heb ik nu:
f(x) = x3
f'(x) = lim(h>0) (x+h)3 - (x)3 / h
f'(x) = lim(h>0) x3 + h3 - x3 / h
f'(x) = lim(h>0) x3 + h3 + 3x2h + 3xh2 - x3 / h (Volgens het merkwaardig product)
f'(x) = lim(h>0) h3 + 3x2h + 3xh2/ h (x3 - x3)
f'(x) = lim(h>0) h2 + 3x2 + 3xh (Gedeeld door h)
f'(x) = 3x2 (Limiet 0 is benaderd)
Mijn boek merkt trouwens op dat dit de beste maar moeilijkste methode is om te differentiëren. Is dat zo? Ik vind het voor uitvoerig, maar kan me wel voorstellen dat dit op een examen een beetje teveel van het goed is.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
In grote lijnen klopt het zo, alleen nog een paar opmerkingenquote:
Bedankt voor alle antwoorden. Ik denk dat ik al begrijp wat ik fout heb gedaan. Ik moest het namelijk nog daar H delen, alleen had er niet bij stil gestaan dat dit voor het limiet noodzakelijk is.
De volgende benadering heb ik nu:
f(x) = x3
f'(x) = lim(h>0) (x+h)3 - (x)3 / h
f'(x) = lim(h>0) x3 + h3 - x3 / h
f'(x) = lim(h>0) x3 + h3 + 3x2h + 3xh2 - x3 / h (Volgens het merkwaardig product)
f'(x) = lim(h>0) h3 + 3x2h + 3xh2/ h (x3 - x3)
f'(x) = lim(h>0) h2 + 3x2 + 3xh (Gedeeld door h)
f'(x) = 3x2 (Limiet 0 is benaderd)
Mijn boek merkt trouwens op dat dit de beste maar moeilijkste methode is om te differentiëren. Is dat zo? Ik vind het voor uitvoerig, maar kan me wel voorstellen dat dit op een examen een beetje teveel van het goed is.
. Je zou wat meer haakjes mogen gebruiken voor de duidelijkheid, zoals je het nu doet is het voor jou en voor mij duidelijk, maar in een examen moet je ipv (x+h)3 - (x)3 / h toch echt ((x+h)3 - (x)3) / h schrijven. Verder vraag ik me af wat je precies tussen het eerste en tweede punt doet? Je haakjes zijn daar weg, maar je hebt ze nog niet uitgewerkt? Die stap kan je weglaten. Wat je boek zegt klopt, het is de beste manier, maar zoals je zelf al zegt, dit kan je in een examen niet iedere keer doen. Daarom zijn er regels voor het differentiëren, waarschijnlijk staan ze ook wel ergens in je boek in een volgende paragraaf, anders kan je hier even kijken
.
The biggest argument against democracy is a five minute discussion with the average voter.
Ik begrijp wat je bedoeld. Heb het even uitvoerig gedaan zodat het voor mezelf duidelijk is en voor anderen ook. Meer haakjes? Oké. Ik zal het proberen te onthouden. Ben er juist zuinig mee, omdat het er zo chaotisch uit gaat zien. Er staan trouwens regels op de volgende pagina's. Maar ik wil graag de basis beheersen, zodat ik weet waar het vandaan komt.quote:
[..]
In grote lijnen klopt het zo, alleen nog een paar opmerkingen
Wat je boek zegt klopt, het is de beste manier, maar zoals je zelf al zegt, dit kan je in een examen niet iedere keer doen. Daarom zijn er regels voor het differentiëren, waarschijnlijk staan ze ook wel ergens in je boek in een volgende paragraaf, anders kan je hier even kijken
Even nog een vraag hierover...
Hoe komt het dat bij een deling met x (dus 1/x2) een negatieve functie voortvloeit? Ik begrijp dat 1 delen door iets altijd een afname betekent als x hoger dan 1 is in ieder geval, maar welke stap zorgt daar voor. Mijn boek geeft totaal geen uitleg over dit onderwerp...
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik zou niet al te zuinig zijn met de haakjes, je kan er beter te veel dan te weinig hebbenquote:
[..]
Ik begrijp wat je bedoeld. Heb het even uitvoerig gedaan zodat het voor mezelf duidelijk is en voor anderen ook. Meer haakjes? Oké. Ik zal het proberen te onthouden. Ben er juist zuinig mee, omdat het er zo chaotisch uit gaat zien. Er staan trouwens regels op de volgende pagina's. Maar ik wil graag de basis beheersen, zodat ik weet waar het vandaan komt.
. Het ziet er misschien niet altijd even mooi uit, maar het is tenminste wel duidelijk. Verder is het heel goed dat je de basis wil beheersen, maar in een examen zal je nooit zo hoeven te differentiëren, dus als je snapt hoe het werkt zou ik verder gaan met die regels .Ik snap niet helemaal wat je bedoelt, wat bedoel je met een negatieve functie?quote:Even nog een vraag hierover...
The biggest argument against democracy is a five minute discussion with the average voter.
Je bedoelt dat de afgeleide negatief is?quote:
[..]
Even nog een vraag hierover...
Precies. f(x) = 1 / x2 wordt f'(x) = - (2 / x3)quote:
[..]
Je bedoelt dat de afgeleide negatief is?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je kan het zien als je de grafiek plot, 1/x2 is een dalende functie (als we even alleen naar positieve x kijken), van een dalende functie is de afgeleide negatief. Ik weet niet of je dat bedoelt?quote:
[..]
Precies. f(x) = 1 / x2 wordt f'(x) = - (2 / x3)
The biggest argument against democracy is a five minute discussion with the average voter.
Teken eens de grafiek van 1/x2.quote:
[..]
Precies. f(x) = 1 / x2 wordt f'(x) = - (2 / x3)
Vertel eens wat er met die grafiek gebeurt als je langs de x-as gaat: neemt de grafiek toe of af, hoe snel gaat die stijging/daling, etc.
Probeer aan de hand van dat verhaal het verloop van de afgeleide te vertellen.
Ik heb je eerdere posts bekeken:
Vertel liever eerst eens wat de afgeleide is?
De afgeleide van 1 / x2 of in het algemeen? Ik heb trouwens een grafiek uitgetekend en zie dat de rico steeds kleiner wordt. Dit klopt ook wanneer het vergeleken wordt met - (1/x3).quote:
[..]
Teken eens de grafiek van 1/x2.
Vertel eens wat er met die grafiek gebeurt als je langs de x-as gaat: neemt de grafiek toe of af, hoe snel gaat die stijging/daling, etc.
Probeer aan de hand van dat verhaal het verloop van de afgeleide te vertellen.
Ik heb je eerdere posts bekeken:
Vertel liever eerst eens wat de afgeleide is?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
De grafiek van 1/x2, vertel eerst eens wat daarmee gebeurt als je langs de x-as loopt.quote:
[..]
De afgeleide van 1 / x2 of in het algemeen? Ik heb trouwens een grafiek uitgetekend en zie dat de rico steeds kleiner wordt. Dit klopt ook wanneer het vergeleken wordt met - (1/x3).
Daarna vertel je wat er met de afgeleide gebeurt als je langs de x-as loopt.
De lijn loopt in een vrij scherp hoek omlaag en komt na 7 op een punt dat niet meer te tekenen is. Dus de formule geeft steeds kleinere waarden: 1, 0.25, 0.037, 0.0625, 0.04, 0.028, 0.0204.quote:
[..]
De grafiek van 1/x2, vertel eerst eens wat daarmee gebeurt als je langs de x-as loopt.
Daarna vertel je wat er met de afgeleide gebeurt als je langs de x-as loopt.
De afgeleide wordt ook steeds kleiner alleen dan wel in negatieve waarden: -1, -0.125, -0.037, -0.016, -0.008, -0.0046, -0.0029. Dat die waarden negatief zijn is logisch omdat de afname in een negatieve richting plaats vindt.
Als ik het goed begrijp is dus de afgeleide bij een afnemende waarde altijd negatief...?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
De grafiek van 1/x2 daalt als je langs de x-as naar rechts gaat, zoals je zelf ook zegt.quote:
[..]
De lijn loopt in een vrij scherp hoek omlaag en komt na 7 op een punt dat niet meer te tekenen is. Dus de formule geeft steeds kleinere waarden: 1, 0.25, 0.037, 0.0625, 0.04, 0.028, 0.0204.
De afgeleide wordt ook steeds kleiner alleen dan wel in negatieve waarden: -1, -0.125, -0.037, -0.016, -0.008, -0.0046, -0.0029. Dat die waarden negatief zijn is logisch omdat de afname in een negatieve richting plaats vindt.
Als ik het goed begrijp is dus de afgeleide bij een afnemende waarde altijd negatief...?
Wat je ook zou moeten opvallen, is dat die daling steeds langzamer gaat: In het begin neemt de grafiek een enorme duik, terwijl de grafiek wat later steeds een beetje afneemt.
Dus: De grafiek neemt constant af, maar de daling zelf neemt ook af.
De beschrijving van dit stijgen/dalen geven we weer met de afgeleide, de afgeleide in een punt is de 'rico'. De afgeleide geeft in elk punt weer hoe de grafiek gaat veranderen: Dalen of stijgen, en met welke snelheid.
Neem nu een punt op de grafiek 1/x2 dicht bij de oorsprong (dus dicht bij het punt x=0).
Je ziet aan de grafiek dat je met een kleine stap naar rechts, een grote daling gaat maken. Dus moet de afgeleide in dat punt:
-Negatief zijn: Want de grafiek neemt af, de rico van de grafiek in dat punt is negatief.
- Groot zijn: De afname/toename in dat punt is groot (in dit geval is het een afname, maar het kon net zo goed een toename zijn.)
Neem nu bijvoorbeeld x=12.
Dan zie je: De grafiek neemt in dat punt nog steeds af, is dus dalend. Maar de daling is nog maar heel klein. Dus de afgeleide ziet er zo uit:
-Negatief, want dalend
-Klein, want de afname/toename is klein
Nu weet je dus de rol van de afgeleide: Die beschrijft de richting van de grafiek (dalen of stijgen) en met hoeveel de grafiek stijgt of daalt( de absolute waarde van de afgeleide).
( Je gaf als afgeleide de functie : f ' (x)= -1/x3.
Bekijk die grafiek eens, en zie waarom die grafiek ook echt de afgeleide is van 1/x2.)
Kan iemand mij alsjeblieft met deze vragen helpen? Ik heb zelf al het één en ander geprobeerd maar ik kom er niet uit.
Op langere vluchten wil Hoogeland Air maaltijden serveren. Voor het leveren van de verpakte maaltijden komen twee leveranciers in aanmerking. Om de verpakte maaltijden te testen op houdbaarheid wordt van beide leveranciers een partij maaltijden gedurende langere tijd bewaard. Vervolgens wordt gekeken nar de fractie van elke partij die moet worden afgekeurd wegens te veel bacteriën.
De resultaten:
Leverancier 1: 96 van de 240 maaltijden moesten worden afgekeurd.
Leverancier 2: 144 van de 320 maaltijden moesten worden afgekeurd.
A.
Een betrouwbaarheidsinterval (confidence interval) voor de populatiefractie (population proportion) van maaltijden van leverancier 2 die moeten worden afgekeurd heeft als ondergrens 0,3835 en als bovengrens 0,5165. Bereken welke betrouwbaarheid hier gebruikt is (in procenten tot op 2 decimalen nauwkeurig).
B.
Toets of de proportie afgekeurde maaltijden verschilt voor beide leveranciers.
C.
Volgens 1 leverancier 1 is er met de geteste partij maaltijden iets misgegaan. Er wordt besloten om een nieuw onderzoek te doen naar de maaltijden van leverancier 1. Bereken hoe groot deze nieuwe steekproef moet worden, indien het 95%-betrouwbaarheidsinterval van de proportie afgekeurde maaltijden van leverancier 1 maximaal 0,06 breed mag worden (NB: breedte = 2x marge)
Alvast bedankt!
Op langere vluchten wil Hoogeland Air maaltijden serveren. Voor het leveren van de verpakte maaltijden komen twee leveranciers in aanmerking. Om de verpakte maaltijden te testen op houdbaarheid wordt van beide leveranciers een partij maaltijden gedurende langere tijd bewaard. Vervolgens wordt gekeken nar de fractie van elke partij die moet worden afgekeurd wegens te veel bacteriën.
De resultaten:
Leverancier 1: 96 van de 240 maaltijden moesten worden afgekeurd.
Leverancier 2: 144 van de 320 maaltijden moesten worden afgekeurd.
A.
Een betrouwbaarheidsinterval (confidence interval) voor de populatiefractie (population proportion) van maaltijden van leverancier 2 die moeten worden afgekeurd heeft als ondergrens 0,3835 en als bovengrens 0,5165. Bereken welke betrouwbaarheid hier gebruikt is (in procenten tot op 2 decimalen nauwkeurig).
B.
Toets of de proportie afgekeurde maaltijden verschilt voor beide leveranciers.
C.
Volgens 1 leverancier 1 is er met de geteste partij maaltijden iets misgegaan. Er wordt besloten om een nieuw onderzoek te doen naar de maaltijden van leverancier 1. Bereken hoe groot deze nieuwe steekproef moet worden, indien het 95%-betrouwbaarheidsinterval van de proportie afgekeurde maaltijden van leverancier 1 maximaal 0,06 breed mag worden (NB: breedte = 2x marge)
Alvast bedankt!
Hoever kom je met http://www.sigmazone.com/binomial_confidence_interval.htm ? En wat heb je al wel?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
A. p is X / N = 144 / 320 = 0.45
p ± m = 0.3835, 0.5165
m = z* x SEp
m = 0.0665
z* is onbekend daar ben je naar op zoek
SEp = (0.45(1-0.45)) / 320 = 0.0278
m / SEp = 0.0665/0.0278 = 2,3921
z* = 2,3921
oftewel het Confidence level zit tussen 98% en 99% volgens tabel D
maar het moet dus op 2 decimalen nauwkeurig dus ik zou niet weten wat dan te doen.
B. H0; p1=p2
Ha; p1p2
Z = (p1-p2)/SEdp
SEdp = p(1-p) (1/n1 + 1/n2) = 0.0423
p1 = x1/n1 = 0.4
p2 = x2/n2 = 0.45
p = (x1+x2)/(n1+n2) = 0.4286
n1 = 240
n2 = 320
Als je dan alles invult een Zwaarde van -1.1832
Dan kijk je in tabel A bij -1.19
Geeft een kans van 0.1170
Deze doe je keer 2, want het is een dubbelzijdige toets = 0.2340
En dan zit ik vast.
C. Hier heb ik eerlijk gezegd nog niet echt naar gekeken aangezien ik er al niet al
te veel vertrouwen meer in had
p ± m = 0.3835, 0.5165
m = z* x SEp
m = 0.0665
z* is onbekend daar ben je naar op zoek
SEp = (0.45(1-0.45)) / 320 = 0.0278
m / SEp = 0.0665/0.0278 = 2,3921
z* = 2,3921
oftewel het Confidence level zit tussen 98% en 99% volgens tabel D
maar het moet dus op 2 decimalen nauwkeurig dus ik zou niet weten wat dan te doen.
B. H0; p1=p2
Ha; p1p2
Z = (p1-p2)/SEdp
SEdp = p(1-p) (1/n1 + 1/n2) = 0.0423
p1 = x1/n1 = 0.4
p2 = x2/n2 = 0.45
p = (x1+x2)/(n1+n2) = 0.4286
n1 = 240
n2 = 320
Als je dan alles invult een Zwaarde van -1.1832
Dan kijk je in tabel A bij -1.19
Geeft een kans van 0.1170
Deze doe je keer 2, want het is een dubbelzijdige toets = 0.2340
En dan zit ik vast.
C. Hier heb ik eerlijk gezegd nog niet echt naar gekeken aangezien ik er al niet al
te veel vertrouwen meer in had
Dat gaat best goed.
A. Bij SEp vergeet je de wortel op te schrijven; 0.0278 klopt wel. Je moet dus geen tabel gebruiken maar wat nauwkeurigers. Met je rekenmachine zal het vast kunnen. Vergeet ook niet dat je tweezijdig toetst.
B. Je hebt geen significantieniveau gekozen. Gebruikelijk is alpha=0.05 of alpha=0.01. Omdat alpha < 0.2340 verwerp je H0 niet.
A. Bij SEp vergeet je de wortel op te schrijven; 0.0278 klopt wel. Je moet dus geen tabel gebruiken maar wat nauwkeurigers. Met je rekenmachine zal het vast kunnen. Vergeet ook niet dat je tweezijdig toetst.
B. Je hebt geen significantieniveau gekozen. Gebruikelijk is alpha=0.05 of alpha=0.01. Omdat alpha < 0.2340 verwerp je H0 niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dankje! Heb nu inderdaad A uitgevonden dat je dan kan doen met een functie genaamd 'Shadenorm' kom dan op een Confidence van 99,16% ?
En dat je deze testen ook allemaal uit kan voeren op je rekenmachine, wat natuurlijk een handig controleermiddel is dan.
Bij B is geen significantieniveau genoemd, dan moet je er dus zelf van één uitgaan?
Nu maar eens even bezig met C.
En dat je deze testen ook allemaal uit kan voeren op je rekenmachine, wat natuurlijk een handig controleermiddel is dan.
Bij B is geen significantieniveau genoemd, dan moet je er dus zelf van één uitgaan?
Nu maar eens even bezig met C
.
A. nee, ik zei nog dat je tweezijdig kijkt
B. klopt.
B. klopt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Jaa ik denk dat ik dan 0.0665/2 = 0.03325 --> 0.003325/0.0278 = 1.1960 moet doen dus mijn z* waarde wordt dan 1,1960 wat een Confidence-interval geeft van 88,42%?
Bepaal je een confidence interval mbv 0.0665 of ga je die 0.0665 opnieuw schatten? p(1-p) is het grootst als p=1/2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het is zo dat p ± m = (0.3835), (0.5165)
Waarbij p = 0.45 dus dan moet margin of error toch 0.0665 zijn?
m = z* x SEp waarbij je dus ook al SEp hebt = 0.0278
Dan lijkt het mij een kwestie van delen en de z* waarde vinden, wat zie ik dan over het hoofd?
Waarbij p = 0.45 dus dan moet margin of error toch 0.0665 zijn?
m = z* x SEp waarbij je dus ook al SEp hebt = 0.0278
Dan lijkt het mij een kwestie van delen en de z* waarde vinden, wat zie ik dan over het hoofd?
De p schat je natuurlijk adhv de nieuwe steekproef.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kan iemand de aangegeven stap in onderstaande som voor me verklaren?
Ik snap niet hoe je op de manier van uitschrijven van het gedeelte achter de pijl komt.
[ http://img94.imageshack.us/i/som25.png/ (copy/paste deze link) (copy/paste deze link) ]
Bij voorbaat dank, dat gaat me helpen met m'n tentamen morgen ;d
Ik snap niet hoe je op de manier van uitschrijven van het gedeelte achter de pijl komt.
[ http://img94.imageshack.us/i/som25.png/ (copy/paste deze link) (copy/paste deze link) ]
Bij voorbaat dank, dat gaat me helpen met m'n tentamen morgen ;d
Helpt het je als ik zeg dat (2-x)4=(2-x)*(2-x)3?quote:
Kan iemand de aangegeven stap in onderstaande som voor me verklaren?
Ik snap niet hoe je op de manier van uitschrijven van het gedeelte achter de pijl komt.
[ http://img94.imageshack.us/i/som25.png/ (copy/paste deze link) (copy/paste deze link) ]
Bij voorbaat dank, dat gaat me helpen met m'n tentamen morgen ;d
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
ik wilde net (2-x)^3 * (2-x) - (2-x)^3 *4x noemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Sorry maar ik snap niet wat je bedoelt..quote:
De p schat je natuurlijk adhv de nieuwe steekproef.
Ja, dat hielp! Super, bedankt. Ik miste deze koppeling even!quote:
[..]
Helpt het je als ik zeg dat (2-x)4=(2-x)*(2-x)3?
Ook bedankt voor het meedenken!quote:
ik wilde net (2-x)^3 * (2-x) - (2-x)^3 *4x noemen.
p = 0.45 komt van een oude steekproef. Als ik een nieuwe steekproef neem, vind ik een nieuwe p.quote:
[..]
Sorry maar ik snap niet wat je bedoelt..
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bepaal de afgeleide van f(x) = 1/x2 ook eens aan de hand van de definitie. Werk eerst het differentiequotiënt (f(x+h) - f(x))/h uit en neem dan de limiet voor h naar 0. Is meteen een goede algebra-oefening.quote:
[..]
Even nog een vraag hierover...
Welk boek gebruik je eigenlijk?
Maar jij hebt nu over C denk ik dan? Die had ik onderhand al gedaan en ik kwam dan op inderdaad een P nemen van 0,5 en dan doe je (Z*/2M)^2 --> (1.960/2x0.03)^2 = 1068 moet de nieuwe steekproef zijn. Ik zat nog met A ik snap niet wat daar nu het goede antwoord moet zijn en hoe die gevonden dient te worden?quote:
[..]
p = 0.45 komt van een oude steekproef. Als ik een nieuwe steekproef neem, vind ik een nieuwe p.
Daar gaat het mis. Bij die z hoort een kans (van overschreiding) van 0.0084. Dat geldt voor p+m. Bij p-m heb je z=-2,3921. Links daarvan zit ook een kans van 0.0084. Je krijgt dus 1-2*0.0084 = 98,32%.quote:z* = 2,3921
oftewel het Confidence level zit tussen 98% en 99% volgens tabel D
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh ik moest dus tabel A gebruiken super bedankt! Ik keek in tabel Dquote:
[..]
Daar gaat het mis. Bij die z hoort een kans (van overschreiding) van 0.0084. Dat geldt voor p+m. Bij p-m heb je z=-2,3921. Links daarvan zit ook een kans van 0.0084. Je krijgt dus 1-2*0.0084 = 98,32%.
Vraagje. In het basisboek wiskunde komt in hoofdstuk 1 dit stukje tekst voor:
Dit is dus het algoritme van Euclides. Natuurlijk zie ik dat het werkt, maar ik zie nog niet waarom. Is het bewijs eigenlijk eenvoudig (dat het al in hoofdstuk 1 gevraagd wordt) of is dit vrij gecompliceerd?quote:Een slim idee
Er is een methode om de ggd van twee getallen te bepalen waarbij priemontbindingen
niet nodig zijn, en die vaak veel sneller werkt. Het basisidee is dat de ggd van twee
getallen ook een deler moet zijn van het verschil van die twee getallen. Zie je ook
waarom dit zo is?
Zo moet ggd(4352, 4342) ook een deler zijn van 4352 4342 = 10. Het getal 10 heeft
alleen maar de priemdelers 2 en 5. Het is duidelijk dat 5 geen deler is van de beide
getallen, maar 2 wel, en dus geldt ggd(4352, 4342) = 2. Wie slim is kan zich door dit
idee te gebruiken veel rekenwerk besparen!
Het is vrij makkelijk. Als a een deler is, kun je de getallen schrijven als a*b en a*c. Wat kun je zeggen over het verschil?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je bedoelt dat b en c de getallen voorstellen waarvan de GGD gevraagd wordt?
Als het dat is, dan is het verschil van a*b en a*c het verschil tussen b en c maal de GGD...
Dus ik bedoel 30 en 12. verschil is 18, GGD = 6. 30*6 - 12*6 = 108. 108/6 = 18
Als het dat is, dan is het verschil van a*b en a*c het verschil tussen b en c maal de GGD...
Dus ik bedoel 30 en 12. verschil is 18, GGD = 6. 30*6 - 12*6 = 108. 108/6 = 18
Nee, dat bedoelt GlowMouse uiteraard niet, want b en c zijn niet hetzelfde als ab en ac.quote:
Je bedoelt dat b en c de getallen voorstellen waarvan de GGD gevraagd wordt?
Als het dat is, dan is het verschil van a*b en a*c het verschil tussen b en c maal de GGD...
Neem aan dat je twee natuurlijke getallen a en b hebt met a > b, die beiden een deler d hebben. Dan zijn er dus twee natuurlijke getallen m en n zodanig dat:
(1a) a = md
(1b) b = nd
En dan is dus:
(2) a - b = md - nd = (m - n)d,
zodat we kunnen concluderen dat d ook een deler is van (a - b).
Voor twee gebeurtenissen A en B geldt dat P(A|B) = P(B|A), beide ongelijk aan nul. Verder is de kans op gebeurtenis A gelijk aan 0.32. Bepaal de kans op gebeurtenis B.
Iemand enig idee welke regel ik hier überhaupt moet gebruiken?
Iemand enig idee welke regel ik hier überhaupt moet gebruiken?
P(A)P(B|A) = P(A en B)
P(B)P(A|B) = P(A en B)
die twee.
P(B)P(A|B) = P(A en B)
die twee.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja dus als A + B = A x B waarbij A = 0.32 ofzo?quote:
P(A)P(B|A) = P(A en B)
P(B)P(A|B) = P(A en B)
die twee.
en vergeet vooral niet te vermelden dat 1/x2 te schrijven is als x-2 .quote:
[..]
Bepaal de afgeleide van f(x) = 1/x2 ook eens aan de hand van de definitie. Werk eerst het differentiequotiënt (f(x+h) - f(x))/h uit en neem dan de limiet voor h naar 0. Is meteen een goede algebra-oefening.
Welk boek gebruik je eigenlijk?
dat is iets te kort door de bocht vrees ik..quote:
[..]
Ja dus als A + B = A x B waarbij A = 0.32 ofzo?
Zoals gezegd weten we dat
P(A|B) = P(B|A)
Hoe kun je dit gebruiken in:
P(A)P(B|A) = P(A en B)
P(B)P(A|B) = P(A en B)
Die notatie ken ik niet.quote:
[..]
Ja dus als A + B = A x B waarbij A = 0.32 ofzo?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
P(A)P(A|B) = P(B)P(A|B) = P(A en B) dus dan zou ik zeggen 0.32^2 = 0,1024?quote:
[..]
dat is iets te kort door de bocht vrees ik..
Zoals gezegd weten we dat
P(A|B) = P(B|A)
Hoe kun je dit gebruiken in:
P(A)P(B|A) = P(A en B)
P(B)P(A|B) = P(A en B)
Even een vraag tussendoor: Ik moet de functie f(x) = xWx - 3X differentieren. (W = Wortel)
Nu zit ik alleen met een probleem, want ik kan die eerste x niet plaatsen. De wortel en -3X krijg ik gedifferentieerd, waar die X kan ik nergens kwijt. Dit is wat ik nu heb: X.0,5X-0,5 - 3. Alleen wanneer ik dit controleer op mijn GR, dan klopt er geen snars van. Zonder de eerste X in de functie en afgeleide klopt het wel.
Nu zit ik alleen met een probleem, want ik kan die eerste x niet plaatsen. De wortel en -3X krijg ik gedifferentieerd, waar die X kan ik nergens kwijt. Dit is wat ik nu heb: X.0,5X-0,5 - 3. Alleen wanneer ik dit controleer op mijn GR, dan klopt er geen snars van. Zonder de eerste X in de functie en afgeleide klopt het wel.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
quote:
Even een vraag tussendoor: Ik moet de functie f(x) = xWx - 3X differentieren. (W = Wortel)
Nu zit ik alleen met een probleem, want ik kan die eerste x niet plaatsen. De wortel en -3X krijg ik gedifferentieerd, waar die X kan ik nergens kwijt. Dit is wat ik nu heb: X.0,5X-0,5 - 3. Alleen wanneer ik dit controleer op mijn GR, dan klopt er geen snars van. Zonder de eerste X in de functie en afgeleide klopt het wel.
Dan lukt het je vast
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Verrek... Is dit de regel in dergelijk samestellingen? Want die had ik niet verwacht.quote:
[..]
[ afbeelding ]
Dan lukt het je vast
Waar maak jij trouwens die formule mee?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
In dit geval wel, je kan overigens ook de productregel gebruiken voorquote:
[..]
Verrek... Is dit de regel in dergelijk samestellingen? Want die had ik niet verwacht.
Waar maak jij trouwens die formule mee?
Die formule heb ik opgemaakt met word, maar je kan ook LaTeX code gebruiken (http://www.forkosh.com/mimetextutorial.html) en die dan hier (http://betahw.mine.nu/index.php) invullen om vervolgens de formule op fok te kunnen plaatsen.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
0.32^2 = 0,1024 kan ik ook zo zeggen, dat is altijd waar. Maar je wilt P(B) weten. P(A)P(A|B) = P(B)P(B|A)quote:
[..]
P(A)P(A|B) = P(B)P(B|A) = P(A en B) dus dan zou ik zeggen 0.32^2 = 0,1024?
nu het gegeven gebruiken dat P(A|B) = P(B|A) (!= 0)
P(A)P(A|B) = P(B)P(A|B)
en nu weet je P(A)=0.32.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bedankt voor die handige link. Dat is wel erg handig aangezien ik Texmaker onder Ubuntu gebruik.quote:
[..]
... dan hier (http://betahw.mine.nu/index.php) invullen om vervolgens de formule op fok te kunnen plaatsen.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Kan iemand mij vertellen hoe ik de volgende vergelijking het makkelijkste oplos? Ik weet niet goed hoe ik machten moet aanpakken namelijk.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Deze valt ook met wat nadenken op te lossen ( je hebt een kwadraat, je moet op -1 uitkomen..), maar hier een methode:quote:
Kan iemand mij vertellen hoe ik de volgende vergelijking het makkelijkste oplos? Ik weet niet goed hoe ik machten moet aanpakken namelijk.
[ afbeelding ]
Haal -1 naar links zodat je
x2 -2x + 1=0
krijgt. Kijk dan of je kunt ontbinden in factoren. Probeer dit altijd als eerste, want dit heb je gewoon nodig.
In dit geval zie je dus dat je de functie zo kunt ontbinden:
(x-1)(x-1)=0
Dus kan je ook de oplossing gemakkelijk aflezen: x=1
Lukt dit niet, dan kun je dit toepassen.
Bedankt. Ik was intussen op hetzelfde onderwerp uitgekomen. Wanneer leer je dit soort algebraïsche dingen normaal eigenlijk op de middelbare school? Ik ken dit allemaal niet namelijk (en doe dus aan zelfstudie).quote:
[..]
Deze valt ook met wat nadenken op te lossen ( je hebt een kwadraat, je moet op -1 uitkomen..), maar hier een methode:
Haal -1 naar links zodat je
x2 -2x + 1=0
krijgt. Kijk dan of je kunt ontbinden in factoren. Probeer dit altijd als eerste, want dit heb je gewoon nodig.
In dit geval zie je dus dat je de functie zo kunt ontbinden:
(x-1)(x-1)=0
Dus kan je ook de oplossing gemakkelijk aflezen: x=1
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Dit leer je al vrij snel, ontbinden in factoren is de basis voor het oplossen van kwadratische functies.quote:
[..]
Bedankt. Ik was intussen op hetzelfde onderwerp uitgekomen. Wanneer leer je dit soort algebraïsche dingen normaal eigenlijk op de middelbare school? Ik ken dit allemaal niet namelijk (en doe dus aan zelfstudie).
Heb zeker niet goed opgelet in de MAVO.quote:
[..]
Dit leer je al vrij snel, ontbinden in factoren is de basis voor het oplossen van kwadratische functies.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Waarvoor doe je trouwens zelfstudie als ik vragen mag?quote:
[..]
Heb zeker niet goed opgelet in de MAVO.
Voor een BÈTA-studiequote:
[..]
Waarvoor doe je trouwens zelfstudie als ik vragen mag?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ja hoor. Gaat hartstikke goed. Vind het ook een leuk onderwerp, dus dat scheelt.quote:
[..]
Succes!
Lukt het nu trouwens beter met de afgeleide? Snap je nu wat de afgeleide is?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
