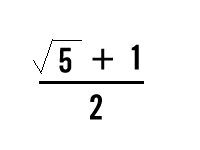SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier al je vragen met betrekking tot de vakken:
Wiskunde
Natuurkunde
Informatica
Scheikunde
Biologie
Algemene Natuurwetenschappen
Alles wat in de richting komt
Hierboven staan de vakken zoals ze op de middelbare school gegeven worden. Dit wil natuurlijk niet zeggen dat er hier geen ruimte is voor vragen van MBO, HBO of WO-niveau. Alle vragen die binnen het gebied van 'Bèta' vallen, kun je hier posten.
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
Hierboven staan de vakken zoals ze op de middelbare school gegeven worden. Dit wil natuurlijk niet zeggen dat er hier geen ruimte is voor vragen van MBO, HBO of WO-niveau. Alle vragen die binnen het gebied van 'Bèta' vallen, kun je hier posten.
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
You don't have to know why you do something to stop doing it. All you have to do is to take a close look at what you are actually doing and decide to stop doing it for that moment!"


Laatste post in het vorige topic..
quote:Op woensdag 19 april 2006 10:39 schreef Metalmeis het volgende:
*zucht*
Ik ben vandaag begonnen met mijn examenbundel voor wi-b1 door te nemen en loop nu al vast.
Ten eerste:
1/4e*x + b is de raaklijn van grafiek f(x). In (e, 1/2) zit een raakpunt.
Als 1/2 = 1/4e * e + b , waarom dan b=1/4 ?
Ten tweede:
Als f(x)= (lnx)^1/2 , waarom is de primitieve dan F(x) = x * ln x * x ??
Kan iemand me op weg helpen?
You don't have to know why you do something to stop doing it. All you have to do is to take a close look at what you are actually doing and decide to stop doing it for that moment!"


1) b is niet 1/4 maar 1/4 (2 - e^2)
2) klopt niet... de primitieve van ln(x)^(1/2) is erg lastig en valt buiten middelbare-schoolwiskunde. En de afgeleide van van F(x) = x^2 ln(x) is F'(x) = x + 2x ln(x)
2) klopt niet... de primitieve van ln(x)^(1/2) is erg lastig en valt buiten middelbare-schoolwiskunde. En de afgeleide van van F(x) = x^2 ln(x) is F'(x) = x + 2x ln(x)


Hey, ik heb een website gemaakt met frames enzo. Vrijwel alles goed gaat, behalve bij 1 of 2 pagina's, opeens komt de gevraagde pagina twee keer voor..
Ik heb gebruik gemaakt van javascript... kent iemand dat?
zou iemand mij willen helpen?
Ik heb gebruik gemaakt van javascript... kent iemand dat?
zou iemand mij willen helpen?
verlegen :)


Waarschijnlijk staat ergens wat code verkeerd bij de pagina's. Wat is de URL?quote:Hey, ik heb een website gemaakt met frames enzo. Vrijwel alles goed gaat, behalve bij 1 of 2 pagina's, opeens komt de gevraagde pagina twee keer voor..
Ik heb gebruik gemaakt van javascript... kent iemand dat?
Je kunt trouwens beter css, of als je dat teveel werk vindt, tabellen gebruiken, omdat pagina's met frames slecht te bookmarken zijn en zoekmachines het ook minder fijn vinden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Wat raar... Zo staat het toch echt in de antwoorden van mijn examenbundel.quote:Op woensdag 19 april 2006 11:37 schreef nlmark het volgende:
1) b is niet 1/4 maar 1/4 (2 - e^2)
2) klopt niet... de primitieve van ln(x)^(1/2) is erg lastig en valt buiten middelbare-schoolwiskunde. En de afgeleide van van F(x) = x^2 ln(x) is F'(x) = x + 2x ln(x)
Bovendien valt het niet buiten de middelbareschoolwiskunde, ik moet het echt kunnen.
Naja, dankjewel voor je hulp!


-edit dubbel.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Als f(x)= (lnx)^1/2 , waarom is de primitieve dan F(x) = x * ln x * x ??quote:Op woensdag 19 april 2006 12:51 schreef Metalmeis het volgende:
[..]
Wat raar... Zo staat het toch echt in de antwoorden van mijn examenbundel.
Bovendien valt het niet buiten de middelbareschoolwiskunde, ik moet het echt kunnen.
Naja, dankjewel voor je hulp!
Nou, differentieer F(x) es. Bedoel je F(x)=x2*ln(x)? Of x*ln(x2 ) ? Bij beide komt het niet uit namelijk; of jij ziet iets verkeerd of het staat er verkeerd. Maar je weet iig hoe je zoiets moet oplossen; gewoon F(x) differentieren. Daarvoor hoef je niet expliciet die functie te kunnen primitiveren.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Om welk examen (jaartal+tijdvak) en welke vraag gaat het?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


hier staat ie:
http://s39.yousendit.com/d.aspx?id=1Y5R7LXO5ZVO51PT1H567L2G1L
sommige menu-items verwijzen nergens naar toe.
wat ik eigenlijk wil, is dat als je via die menu een pagina opent, dat ie dus opent in die middelste frame en niet in die van links..
alvast thanx
http://s39.yousendit.com/d.aspx?id=1Y5R7LXO5ZVO51PT1H567L2G1L
sommige menu-items verwijzen nergens naar toe.
wat ik eigenlijk wil, is dat als je via die menu een pagina opent, dat ie dus opent in die middelste frame en niet in die van links..
alvast thanx
verlegen :)


| 1 2 | <frame name="head" src="home.htm" target="_self" scrolling="auto" noresize> |
In side.htm moet je alle links een target="head" meegeven (vreemde naam trouwens, voor het content-frame).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


oh zo... mm ik heb het net gedaan.. maar er is niet veel spannends veranderd :S:S
zou je die verbeterde site ff willen zetten op yousendit ?
zou je die verbeterde site ff willen zetten op yousendit ?
verlegen :)


Istie. In menu_tpl.js staat een extra variabele voor de link-target.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Vwo B wiskunde examenbundel 2005/2006.quote:Op woensdag 19 april 2006 13:18 schreef GlowMouse het volgende:
Om welk examen (jaartal+tijdvak) en welke vraag gaat het?
Het staat op een van de eerste bladzijden, onder het kopje "analyse" --> "wenteling".


oi oi , bedankt voor de site, al zit er een klein probleempje: als op het knopje; Producten klikt dan verschijnt er iets raars, maar normaal gesproken moet alleen een submenu verschijnen..
k zal het proberen te fixen..
thanx
k zal het proberen te fixen..
thanx
verlegen :)


I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Ik snap deze opdracht niet echt heeft iemand een idee hoe ik dit zou moeten aanpakken en misschien een aardig voorstel?
Ik moet minstens een dipeptide voorstellen, die uitgaande van de set van 20 natuurlijke aminozuren, staan hier: (http://www.science.uva.nl/onderwijs/nieuw/chem/webklasscheikunde/twintigaminozuren.htm) die volgens jou ook een zoete smaak moet hebben en komt dus in aanmerking als alternatieve zoetstof voor aspartaam.
De dipeptide schrijf je met de symbolen die in de tabel worden gebruikt (bijvoorbeeld aspartaam schrijf je als: Asp-Phe-OMe).
en Waarom denk je dat je voorgestelde dipeptide(n) zoet zou(den) kunnen smaken?
Ik hoop dat iemand mij kan helpen
Ik moet minstens een dipeptide voorstellen, die uitgaande van de set van 20 natuurlijke aminozuren, staan hier: (http://www.science.uva.nl/onderwijs/nieuw/chem/webklasscheikunde/twintigaminozuren.htm) die volgens jou ook een zoete smaak moet hebben en komt dus in aanmerking als alternatieve zoetstof voor aspartaam.
De dipeptide schrijf je met de symbolen die in de tabel worden gebruikt (bijvoorbeeld aspartaam schrijf je als: Asp-Phe-OMe).
en Waarom denk je dat je voorgestelde dipeptide(n) zoet zou(den) kunnen smaken?
Ik hoop dat iemand mij kan helpen


Die zijn ook niet foutloos.quote:Op woensdag 19 april 2006 12:51 schreef Metalmeis het volgende:
[..]
Wat raar... Zo staat het toch echt in de antwoorden van mijn examenbundel.
Verkapte tvp
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Bedankt voor de reactie, maar inmiddels heb ik het probleem opgelost denk ik. Ik ging er bij de Hannan-Rissanen procedure vanuit dat de absolute waarde van de AIC en SC zo klein mogelijk moesten zijn. Ik vermoed dat daar de fout zat en dat het dus gewoon om de 'echte' waarden gaat. Nu kom ik namelijk keurig op een ARMA(1,1) en een ARMA(1,0) model uit.quote:Op dinsdag 18 april 2006 21:39 schreef mrbombastic het volgende:
De methode van Hannan Rissanen ken ik niet, maar een ARIMA (7,1,8) model lijkt mij niet erg waarschijnlijk.
Edit: ik zit even in de helpfunctie van Eviews te kijken bij AIC en zie dat Eviews de AIC op een andere manier berekent dan dat ik gewend ben. Eviews gebruikt -2(l/T) +2(k/T) met l de loglikelihood, T het aantal waarnemingen en k het aantal parameters. Als je dus veel waarnemingen hebt, maakt het vrij weinig uit of je een extra parameter toevoegt.
De AIC die ik heb geleerd is -2*l +2(p+q+1) voor een ARMA(p,q) proces.
Als alternatief kun je kijken naar de AIC Corrected welke berekend wordt door -2*l+2n(p+q+1)/(n-p-q-2)


hier een vreemd probleem:
Stel je hebt een 7*7 vierkant getekend op een ruitjes papier.
het blokje van de hoek links onderaan krijgt de coordinaten (0,0)
het blokje van de hoek rechts onderaan krijgt de coordinaten (7,0)
en zo ga je de rest van de punten ook coordinaten geven..net als in een x,y assenstelsel.
Pak nu de vierkant (4,0) en de vierkant (4,4).
(dus het middelste blokje onder, en het middelste blokje van de hele vierkant.)
Nu moet je een lopen op de andere vierkanten van (4,0) naar (4,4), onderweg tel je het aantal blokjes waarop je liep. (je mag alleen door de zijden van de vierkanten lopen ..geen diagonaal gedoe).
Als je rechtstreeks loopt van beneden naar onder dan heb je gelopen over 4 blokjes ( zowel het begin blokje als het einde blokje tel je mee).
Mijn vraag is: hoe je ook loopt..dus links rechts boven naar beneden, heen en terug..je moet altijd over een even aantal blokjes lopen..
waarom is dat zo?
Stel je hebt een 7*7 vierkant getekend op een ruitjes papier.
het blokje van de hoek links onderaan krijgt de coordinaten (0,0)
het blokje van de hoek rechts onderaan krijgt de coordinaten (7,0)
en zo ga je de rest van de punten ook coordinaten geven..net als in een x,y assenstelsel.
Pak nu de vierkant (4,0) en de vierkant (4,4).
(dus het middelste blokje onder, en het middelste blokje van de hele vierkant.)
Nu moet je een lopen op de andere vierkanten van (4,0) naar (4,4), onderweg tel je het aantal blokjes waarop je liep. (je mag alleen door de zijden van de vierkanten lopen ..geen diagonaal gedoe).
Als je rechtstreeks loopt van beneden naar onder dan heb je gelopen over 4 blokjes ( zowel het begin blokje als het einde blokje tel je mee).
Mijn vraag is: hoe je ook loopt..dus links rechts boven naar beneden, heen en terug..je moet altijd over een even aantal blokjes lopen..
waarom is dat zo?
verlegen :)


Zie de vierkantjes als een schaakbord. Als je begint op een wit veld, kom je daarna altijd op een zwart veld, en van een zwart veld kom je altijd op een wit veld. Van een wit naar een wit veld kost je dus altijd 2k stapjes (waarbij k een geheel getal).
Zo'n aanpak heeft wel een naam, maar die weet ik helaas niet
Zo'n aanpak heeft wel een naam, maar die weet ik helaas niet
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedoel je: ln[x^(1/2)] of (ln[x])^(1/2) ??quote:Op donderdag 20 april 2006 10:45 schreef Metalmeis het volgende:
Nog 1 keertje.. Wie kan me helpen met de primitieve van ln(x)^(1/2)?
De eerste is namelijk niet zo moelijk (primiteve is (1/2)*(x*ln[x] - x) ), maar die tweede is inderdaad niet uit te schrijven in elementaire functies (zoals thabit zegt)
Theories come and theories go. The frog remains


hoe bewijs je dat eigenlijk???quote:Op donderdag 20 april 2006 14:39 schreef Bioman_1 het volgende:
[..]
Bedoel je: ln[x^(1/2)] of (ln[x])^(1/2) ??
De eerste is namelijk niet zo moelijk (primiteve is (1/2)*(x*ln[x] - x) ), maar die tweede is inderdaad niet uit te schrijven in elementaire functies (zoals thabit zegt)
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


exp(-x2/2) heeft geen primitieve in elementaire functies. De functie waar het hier om gaat is de inverse van exp(x2).


Weet iemand wat het nut is van poolvoorstellingen? Waar wordt het in de praktijk voor gebruikt? En weet iemand ook de formule bij een poolvoorstelling voor een driehoek? Daar kom ik ook maar niet uit.
Ten percent faster with a sturdier frame


Oke, dan de primitieve van ln(x)... Is die wel te berekenen?quote:Op donderdag 20 april 2006 14:39 schreef Bioman_1 het volgende:
[..]
Bedoel je: ln[x^(1/2)] of (ln[x])^(1/2) ??
De eerste is namelijk niet zo moelijk (primiteve is (1/2)*(x*ln[x] - x) ), maar die tweede is inderdaad niet uit te schrijven in elementaire functies (zoals thabit zegt)


Dat is x(ln x-1) (differentieer maar). Maar ook dat valt buiten de vwo-stof. Alles wat je voor vwo moet kunnen aan differentieren en integreren staat op de formulekaart.
Je bedoelt poolcoordinaten? Bijvoorbeeld om de normaalkromme te integreren. Vooral cirkels zijn handig om via poolcoordinaten te integreren, bij een hoekige vorm als een driehoek lijkt het me vooral onhandig.quote:Weet iemand wat het nut is van poolvoorstellingen? Waar wordt het in de praktijk voor gebruikt? En weet iemand ook de formule bij een poolvoorstelling voor een driehoek? Daar kom ik ook maar niet uit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja dat bedoel ik, bedankt. In mijn boek het heet trouwens poolvoorstellingen. Dus vandaar. Wat is een normaalkromme?quote:Op donderdag 20 april 2006 17:58 schreef GlowMouse het volgende:
Dat is x(ln x-1) (differentieer maar). Maar ook dat valt buiten de vwo-stof. Alles wat je voor vwo moet kunnen aan differentieren en integreren staat op de formulekaart.
[..]
Je bedoelt poolcoordinaten? Bijvoorbeeld om de normaalkromme te integreren. Vooral cirkels zijn handig om via poolcoordinaten te integreren, bij een hoekige vorm als een driehoek lijkt het me vooral onhandig.
Ten percent faster with a sturdier frame


Wiskundevraagje:
De functie:
f(x) = 1-x : 0 <= x <= 1
en 0: elders
moest bij a) dmv Fouriertransformatie getransformeerd worden, dit is me gelukt en het volgende antwoord kwam er uit:
Nu moet bij b) dmv de omkeerformule
bepaald worden.
Dat dit bepaald wordt door
kan ik ook nog wel volgen, maar nu geeft de uitwerking dat het eerste gedeelte even is en het 2e oneven ( cos en sin resp. ) en dat daardoor
vrij simpel opgelost kan worden.
Nu is mijn vraag: waarom wordt het oneven gedeelte weggelaten? De functie f(x) is niet even, noch oneven?
bvd.
De functie:
f(x) = 1-x : 0 <= x <= 1
en 0: elders
moest bij a) dmv Fouriertransformatie getransformeerd worden, dit is me gelukt en het volgende antwoord kwam er uit:
Nu moet bij b) dmv de omkeerformule
bepaald worden.
Dat dit bepaald wordt door
kan ik ook nog wel volgen, maar nu geeft de uitwerking dat het eerste gedeelte even is en het 2e oneven ( cos en sin resp. ) en dat daardoor
vrij simpel opgelost kan worden.
Nu is mijn vraag: waarom wordt het oneven gedeelte weggelaten? De functie f(x) is niet even, noch oneven?
bvd.


Nee, maar als je een oneven functie integreert van -oneindig naar +oneindig dan valt het negatieve stuk tegen het positieve stuk weg.


Volgens mij klopt dit niet, in zo'n (oneigenlijke) integraal hoeven de grenzen niet symmetrisch te lopen. De integraal van de oneven functie f(x) = x van -oneindig tot oneindig is dan ook niet gelijk aan 0. Dat geldt wel voor de zogenaamde 'hoofdwaarde', als je de grenzen dus symmetrisch laat lopen (bvb van -k tot k, dan de limiet voor k naar oneindig).quote:Op donderdag 20 april 2006 18:55 schreef thabit het volgende:
Nee, maar als je een oneven functie integreert van -oneindig naar +oneindig dan valt het negatieve stuk tegen het positieve stuk weg.


De integraal in die opgave convergeert absoluut, dus daar heb je dit soort problemen niet.quote:Op zaterdag 22 april 2006 18:33 schreef TomD het volgende:
[..]
Volgens mij klopt dit niet, in zo'n (oneigenlijke) integraal hoeven de grenzen niet symmetrisch te lopen. De integraal van de oneven functie f(x) = x van -oneindig tot oneindig is dan ook niet gelijk aan 0. Dat geldt wel voor de zogenaamde 'hoofdwaarde', als je de grenzen dus symmetrisch laat lopen (bvb van -k tot k, dan de limiet voor k naar oneindig).


Dat weet ik, ik had het ook niet over die opgave maar over
"als je een oneven functie integreert van -oneindig naar +oneindig dan valt het negatieve stuk tegen het positieve stuk weg"
hetgeen toch niet alleen over die opgave ging, maar over oneven functies in het algemeen - zo leek het toch. Het was verder dan ook maar enkel een aanvulling.
"als je een oneven functie integreert van -oneindig naar +oneindig dan valt het negatieve stuk tegen het positieve stuk weg"
hetgeen toch niet alleen over die opgave ging, maar over oneven functies in het algemeen - zo leek het toch. Het was verder dan ook maar enkel een aanvulling.


Ik ben weer wat aan het programmeren aan Stars en ik zit met een probleem, ik heb er al eens een topic over geopend:
Berekenen van een coordinaten grid
Zou iemand me hiermee kunnen helpen?
Berekenen van een coordinaten grid
Zou iemand me hiermee kunnen helpen?
Are you nuts??


Hoe krijg je die formules eigenlijk zo mooi in je post?quote:Op donderdag 20 april 2006 18:48 schreef pfaf het volgende:
Wiskundevraagje:
De functie:
f(x) = 1-x : 0 <= x <= 1
en 0: elders
moest bij a) dmv Fouriertransformatie getransformeerd worden, dit is me gelukt en het volgende antwoord kwam er uit:
[afbeelding]
Nu moet bij b) dmv de omkeerformule
[afbeelding]
bepaald worden.
Dat dit bepaald wordt door
[afbeelding]
kan ik ook nog wel volgen, maar nu geeft de uitwerking dat het eerste gedeelte even is en het 2e oneven ( cos en sin resp. ) en dat daardoor
[afbeelding]
vrij simpel opgelost kan worden.
Nu is mijn vraag: waarom wordt het oneven gedeelte weggelaten? De functie f(x) is niet even, noch oneven?
bvd.


Bij wiskunde speelt significantie geen rol. In de wiskunde geeft 3 exact dezelfde informatie als 3,00000 (in tegenstelling tot de natuur- en scheikunde, waar met 3 een getal tussen de 2,5 en 3,5 bedoeld wordt). Vaak moet je iets exact beantwoorden, wortel(3) kan dan bijvoorbeeld een antwoord zijn, terwijl dat bij natuur- en scheikunde altijd fout is. Wanneer je mag afronden staat dat in de vraag. In plaats van algebraïsch mag je het dan ook met je rekenmachine uitrekenen (zolang je de stapjes opschrijft).quote:Op zondag 23 april 2006 13:14 schreef Metalmeis het volgende:
Gaat er bij de eindexamens wiskunde eigenlijk gelet worden op significantie?
Weten jullie dat?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ok. Dat scheelt weer!quote:Op zondag 23 april 2006 13:18 schreef GlowMouse het volgende:
[..]
Bij wiskunde speelt significantie geen rol. In de wiskunde geeft 3 exact dezelfde informatie als 3,00000 (in tegenstelling tot de natuur- en scheikunde, waar met 3 een getal tussen de 2,5 en 3,5 bedoeld wordt). Vaak moet je iets exact beantwoorden, wortel(3) kan dan bijvoorbeeld een antwoord zijn, terwijl dat bij natuur- en scheikunde altijd fout is. Wanneer je mag afronden staat dat in de vraag. In plaats van algebraïsch mag je het dan ook met je rekenmachine uitrekenen (zolang je de stapjes opschrijft).


Gegeven is de cirkel (georth. assenstelsel) C:x²+y²+2x+4y=16 en een vast punt p(1,0). Door het middelpunt van die cirkel gaat een veranderlijke rechte A en door het vaste punt p gaan een rechte B loodrecht op de rechte A.
Zoek de meetkundige plaats van het snijpunt van die twee rechten, bepaal de aard van die meetkundige plaats, en de vergelijking van deze 2 rechten.
Iemand die me kan helpen?
Heb al gevonden dat het middelpunt van de cirkel [-1,-2] is.
Alvast bedankt!
Zoek de meetkundige plaats van het snijpunt van die twee rechten, bepaal de aard van die meetkundige plaats, en de vergelijking van deze 2 rechten.
Iemand die me kan helpen?
Heb al gevonden dat het middelpunt van de cirkel [-1,-2] is.
Alvast bedankt!


Ik heb ook een probleempje, me SPSS. Van 3 variabelen moet ik de Z-waarden uitrekenen;
Gebruik deze gemiddelden om voor deze drie variabelen de z-scores te berekenen. SPSS-opdracht: Transform>Compute
Omdat ik geen functie kon vinden om de z-waarde direct uit te rekenen (althans, CDFNORM oid geeft gewoon 1 als resultaat) heb ik dit al geprobeerd met de variabele dep95. Probleem is hier echter dat ik voor MEAN en SD twee 'arguments' moet geven. Als SPSS noob ben ik dus geheel de weg kwijt
(dep95 - MEAN(dep95)) / SD(dep95)
Dus iemand een tip/hint hoe ik toch de Z-waarden uitreken?
Gebruik deze gemiddelden om voor deze drie variabelen de z-scores te berekenen. SPSS-opdracht: Transform>Compute
Omdat ik geen functie kon vinden om de z-waarde direct uit te rekenen (althans, CDFNORM oid geeft gewoon 1 als resultaat) heb ik dit al geprobeerd met de variabele dep95. Probleem is hier echter dat ik voor MEAN en SD twee 'arguments' moet geven. Als SPSS noob ben ik dus geheel de weg kwijt
(dep95 - MEAN(dep95)) / SD(dep95)
Dus iemand een tip/hint hoe ik toch de Z-waarden uitreken?


tvp Misschien kan ik nog wat helpen op vwo5 niveau
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Ik heb ben met het onderzoeken van een tijdreeks. Eén van de mogelijke modellen is een ARMA(2,1) model. Nu vraag ik mij af, moet ik voor stationarity alleen kijken naar de individuele waarden van beide alfa's of ook naar een combinatie van beiden?
Dus alfa_i < 1 moet sowieso gelden, maar moet er ook iets in de geest van alfa_1 + alfa_2 < 1 gelden ofzo?
In mijn boek worden alleen maar ARMA(1,1) modellen besproken en heb je dit 'probleem' dus niet.
Dus alfa_i < 1 moet sowieso gelden, maar moet er ook iets in de geest van alfa_1 + alfa_2 < 1 gelden ofzo?
In mijn boek worden alleen maar ARMA(1,1) modellen besproken en heb je dit 'probleem' dus niet.


Hmm, heb ook nog wel een ander vraagje, gaat over het Markowitz model (financiering):
ik heb de functie:
f(w) = w'Qw
w is een vector met dimensie n en w'e=1 (met e een vector met allemaal éénen)
Q is een matrix met dimensie n*n,
Bovendien is Q een variantie-covariantie matrix (dus, Q'=Q).
Ik moet bewijzen dat f(w) >= 0, dus ik moet bewijzen dat Q positief semi definiet is.
Iemand enig idee hoe ik dat doe?
ik heb de functie:
f(w) = w'Qw
w is een vector met dimensie n en w'e=1 (met e een vector met allemaal éénen)
Q is een matrix met dimensie n*n,
Bovendien is Q een variantie-covariantie matrix (dus, Q'=Q).
Ik moet bewijzen dat f(w) >= 0, dus ik moet bewijzen dat Q positief semi definiet is.
Iemand enig idee hoe ik dat doe?


Daarvoor kijk je naar de determinanten van iedere principale deelmatrix. De getallen op de diagonaal van een covariantiematrix stellen varianties voor, dus die zijn zeker niet-negatief. Verder kun je gebruiken dat de matrix symmetrisch is.quote:Ik moet bewijzen dat f(w) >= 0, dus ik moet bewijzen dat Q positief semi definiet is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Mijn neefje vraagt mij om hulp voor een wiskunde opdracht dus ik dacht das een eitje
1 havo, ik heb de havo afgemaakt dus dat moet lukken
maja nou heeft hij een opdracht gekregen die ik nooit heb gehad in mijn hele havo tijd niet
dit is de opdracht:
MAAR
ik zoek een duidelijke manier om dit aan mijn neefje uit te leggen
ik ben te werk gegaan als volgt:
de website bekeken met hoe ze eruit zien die figuren
dit gedaan
- de naam van het lichaam
- bouwplaat (2 keer, ml 1 ongevouwen en 1 in elkaar gezet)
maja de regel van Euler??? ben aan het googlen en kwam bij dit
http://www.science.uva.nl(...)yllabus/node107.html
hehe toen begon het kraken in mijn hoofd alweer, leuk hahaha
maar hoe kan ik dit het simpelste uitleggen aan hem:
- het aantal vlakken, ribben en hoekpunten waarbij je laat zien dat de regel van Euler klopt.
- De berekening waarmee je het aantal hoekpunten en ribben kan uitrekenen als je vorm en aantal van de vlakken weet
en dat tekenen moet mij ook wel lukken, maar ook moet ik hem uitleggen hoe wat en waarom
de opdracht hoeft niet gemaakt te worden maar HOE leg ik het aan hem het makkelijkste uit (terwijl ik zelf geen genie ben in wiskunde)
1 havo, ik heb de havo afgemaakt dus dat moet lukken
maja nou heeft hij een opdracht gekregen die ik nooit heb gehad in mijn hele havo tijd niet
dit is de opdracht:
op zich moet mij dit wel lukken (denk ik)quote:Praktische Opdracht Klas 1
Moderne Wiskunde (7ed)
Hoofdstuk 7 Ruimtelijk bekeken
Platonische lichamen (Platonic solids) zijn regelmatige veelvlakken waarvan de zijvlakken regelmatig en onderling allemaal precies hetzelfde zijn (allemaal dezelfde driehoeken vierkanten of vijfhoeken. Er bestaan slechts 5 verschillende Platonische lichamen, namelijk het regelmatig viervlak, zesvlak (kubus), achtvlak twaalfvlak en twintig vlak.
Als je van een Platonisch lichaam er delen afzaagt, zodat de nieuwe zijvlakken die ontstaan alle weer regelmatig zijn dan krijg je een soort halfregelmatig veelvlak, die ook wel Archimedische lichamen (Archimedien Solid) worden genoemd. Er mogen in zo’n figuur dus best verschillende zijvlakken voorkomen, zolang ze maar regelmatig zijn.
Van alle Platonische lichamen (5) en Archimedische lichamen (13) kun je een afbeelding vinden op http://www.scienceu.com/geometry/facts/solids/handson.html
Met de muis kun je de lichamen draaien zodat je ziet dat ze van alle kanten bekeken er hetzelfde uitzien (in elk hoekpunt komen steeds op dezelfde manier de vlakken samen). Je kan ook van elk lichaams details opvragen zoals aantal vlakken, ribben en hoekpunten.
Op http://www.korthalsaltes.com/index.html kun je ook bouwplaten vinden.
OPDRACHT
Kies 1 van de 13 Archimedische lichamen uit en lever daarover het volgende in :
- de naam van het lichaam
- bouwplaat (2 keer, ml 1 ongevouwen en 1 in elkaar gezet)
- het aantal vlakken, ribben en hoekpunten waarbij je laat zien dat de regel van Euler klopt.
- De berekening waarmee je het aantal hoekpunten en ribben kan uitrekenen als je vorm en aantal van de vlakken weet.
- BONUS het bijbehorende Platonische lichaam in elkaar gezet, met daarop de zaaglijntjes getekend waarlangs je moet zagen om jouw Archimedisch lichaam te krijgen.
Andere links.
http://www.mathconsult.ch/showroom/unipoly/list-graph.html (nog meer ? alle 80)
http://www.wisfaq.nl/frame.htm?url=http://www.wisfaq.nl/pagina.asp?nummer=1365 (faq)
Woordenlijst
Polyhedra = veelvlakken
Solids = Lichamen (ruimtelijke figuren)
Faces = vlakken
Edges = ribben
Vertices = hoekpunten
MAAR
ik zoek een duidelijke manier om dit aan mijn neefje uit te leggen
ik ben te werk gegaan als volgt:
de website bekeken met hoe ze eruit zien die figuren
dit gedaan
- de naam van het lichaam
- bouwplaat (2 keer, ml 1 ongevouwen en 1 in elkaar gezet)
maja de regel van Euler??? ben aan het googlen en kwam bij dit
http://www.science.uva.nl(...)yllabus/node107.html
hehe toen begon het kraken in mijn hoofd alweer, leuk hahaha
maar hoe kan ik dit het simpelste uitleggen aan hem:
- het aantal vlakken, ribben en hoekpunten waarbij je laat zien dat de regel van Euler klopt.
- De berekening waarmee je het aantal hoekpunten en ribben kan uitrekenen als je vorm en aantal van de vlakken weet
en dat tekenen moet mij ook wel lukken, maar ook moet ik hem uitleggen hoe wat en waarom
de opdracht hoeft niet gemaakt te worden maar HOE leg ik het aan hem het makkelijkste uit (terwijl ik zelf geen genie ben in wiskunde)


Hij kan zich er beter zelf in verdiepen. Zo'n huiswerkopdracht krijgt hij niet voor niks. Bij wiskunde helpt het niets als je opdrachten uitgelegd krijgt, en huiswerk zelf maken is de enige manier om hem voor te bereiden. In plaats van alles te maken kun je hem ook vragen met specifieke vragen te komen.
Neem een convexe polyeder (bijvoorbeeld een kubus) en laat het de regel van Euler controleren (zie formule op je gevonden website). Het bewijs zou ik in dit geval achterwege laten.quote:- het aantal vlakken, ribben en hoekpunten waarbij je laat zien dat de regel van Euler klopt.
- De berekening waarmee je het aantal hoekpunten en ribben kan uitrekenen als je vorm en aantal van de vlakken weet
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik zit hier een beetje te tikken voor mijn werk en kom er niet op hoe het ook al weer heet als:
twee vloeistoffen(bloed & liquor) gemengd met elkaar op een papiertje/gaasje.
Bloed komt niet zo ver op het gaasje als liquor(vandaar de corona om het bloed op het gaasje) Maar hoe heet dat nu ook al weer???
Diffusie of zo iets?
twee vloeistoffen(bloed & liquor) gemengd met elkaar op een papiertje/gaasje.
Bloed komt niet zo ver op het gaasje als liquor(vandaar de corona om het bloed op het gaasje) Maar hoe heet dat nu ook al weer???
Diffusie of zo iets?


(papier)chromatografie? Je hebt een loopvloeistof, en je bloed loopt niet zo goed mee.....
You don't have to know why you do something to stop doing it. All you have to do is to take a close look at what you are actually doing and decide to stop doing it for that moment!"


ehm kan iemand mij deze even snel op een simpele manier laten zien
de rest lukt allemaal wel
de rest lukt allemaal wel
quote:- De berekening waarmee je het aantal hoekpunten en ribben kan uitrekenen als je vorm en aantal van de vlakken weet.


ik heb even snel een vraag.
in een elktrolyse reactie kan water ook als reductor of oxidator optreden.
moet water dan wel de sterktse reductor of oxidator zijn?
in een elktrolyse reactie kan water ook als reductor of oxidator optreden.
moet water dan wel de sterktse reductor of oxidator zijn?
Computer Says No


Hallo allemaal.
Ik heb een beetje veel moeite met het vak wiskunde (Ik ben er een tijd tussenuit geweest) en was benieuwd of iemand van jullie me zou kunnen helpen met het volgende:
Morgen heb ik een tentamen, o.a een onderwerp is `hypothese toetsen`.
De volgende dingen heb ik echter geen kaas van gegeten, ik weet alleen in heel lichte mate hoe je het toe moet passen:
1 Binomiale verdeling.
2 Standaardverdeling.
3 Standaardafwijking.
4 Variantie.
5 Etc.
Een vraag:
De kijkdichtheid van een televisiequiz bedraagt volgens de presentator 50%.
De voorzitter van de omroep beweert dat de kijkdichtheid 30% is.
Men onderzoekt dit en vind in een steekproef dat van de 100 mensen, 57 mensen de quiz nooit heeft gezien.
Het significantieniveau is 5%.
Is er op basis van de enquete-uitslag nog steeds voldoende reden om de presentator in het gelijk te stellen?
---------------------------------------------------------------------------------------------------------------
Antwoord:
Ik heb zelf H0, en H1 al gemaakt.
H0= 0,5
H1= 0,3
En nu weet ik het al niet meer???
Iemand die wel een idee heeft?
(Tip: we hebben wel een GR!)
Ik ben nu al erg dankbaar voor mogelijke antwoord
Ik heb een beetje veel moeite met het vak wiskunde (Ik ben er een tijd tussenuit geweest) en was benieuwd of iemand van jullie me zou kunnen helpen met het volgende:
Morgen heb ik een tentamen, o.a een onderwerp is `hypothese toetsen`.
De volgende dingen heb ik echter geen kaas van gegeten, ik weet alleen in heel lichte mate hoe je het toe moet passen:
1 Binomiale verdeling.
2 Standaardverdeling.
3 Standaardafwijking.
4 Variantie.
5 Etc.
Een vraag:
De kijkdichtheid van een televisiequiz bedraagt volgens de presentator 50%.
De voorzitter van de omroep beweert dat de kijkdichtheid 30% is.
Men onderzoekt dit en vind in een steekproef dat van de 100 mensen, 57 mensen de quiz nooit heeft gezien.
Het significantieniveau is 5%.
Is er op basis van de enquete-uitslag nog steeds voldoende reden om de presentator in het gelijk te stellen?
---------------------------------------------------------------------------------------------------------------
Antwoord:
Ik heb zelf H0, en H1 al gemaakt.
H0= 0,5
H1= 0,3
En nu weet ik het al niet meer???
Iemand die wel een idee heeft?
(Tip: we hebben wel een GR!)
Ik ben nu al erg dankbaar voor mogelijke antwoord
Ga eens naar www.thehungersite.com en klik elke dag een keer.


Dat klopt allemaal wel, maar volgens mij kan je niet aantonen dat een willekeurige covariantiematrix positief definiet is, dat is namelijk gewoon niet zo bij mijn weten.quote:Op dinsdag 25 april 2006 13:03 schreef GlowMouse het volgende:
[..]
Daarvoor kijk je naar de determinanten van iedere principale deelmatrix. De getallen op de diagonaal van een covariantiematrix stellen varianties voor, dus die zijn zeker niet-negatief. Verder kun je gebruiken dat de matrix symmetrisch is.
Inmiddels heb ik het probleem opgelost overigens! w'Qw valt te schrijven als een variantie, die dus zeker niet negatief is.


Ik zou zeggen dat een enquete over 100 mensen niet representatief is en dus niets zinnigs kan zeggen over wie er wel of geen gelijk heeftquote:Op dinsdag 25 april 2006 16:43 schreef vdo28 het volgende:
Hallo allemaal.
Ik heb een beetje veel moeite met het vak wiskunde (Ik ben er een tijd tussenuit geweest) en was benieuwd of iemand van jullie me zou kunnen helpen met het volgende:
Morgen heb ik een tentamen, o.a een onderwerp is `hypothese toetsen`.
De volgende dingen heb ik echter geen kaas van gegeten, ik weet alleen in heel lichte mate hoe je het toe moet passen:
1 Binomiale verdeling.
2 Standaardverdeling.
3 Standaardafwijking.
4 Variantie.
5 Etc.
Een vraag:
De kijkdichtheid van een televisiequiz bedraagt volgens de presentator 50%.
De voorzitter van de omroep beweert dat de kijkdichtheid 30% is.
Men onderzoekt dit en vind in een steekproef dat van de 100 mensen, 57 mensen de quiz nooit heeft gezien.
Het significantieniveau is 5%.
Is er op basis van de enquete-uitslag nog steeds voldoende reden om de presentator in het gelijk te stellen?
---------------------------------------------------------------------------------------------------------------
Antwoord:
Ik heb zelf H0, en H1 al gemaakt.
H0= 0,5
H1= 0,3
En nu weet ik het al niet meer???
Iemand die wel een idee heeft?
(Tip: we hebben wel een GR!)
Ik ben nu al erg dankbaar voor mogelijke antwoord


- De berekening waarmee je het aantal hoekpunten en ribben kan uitrekenen als je vorm en aantal van de vlakken weet.
dit is de enige die ik niet echt weet kan iemand mij daar mee helpen?
dit is de enige die ik niet echt weet kan iemand mij daar mee helpen?


Maar dat moet dus welquote:Op dinsdag 25 april 2006 16:56 schreef JedaiNait het volgende:
[..]
Ik zou zeggen dat een enquete over 100 mensen niet representatief is en dus niets zinnigs kan zeggen over wie er wel of geen gelijk heeft
Maar goed, ik moet weg.
Hopelijk kan ik vanavond nog even kijken.
Ga eens naar www.thehungersite.com en klik elke dag een keer.


Tel het aantal zijden van alle zijvlakken bij elkaar op. Omdat elke ribbe aan twee zijvlakken grenst, heb je op die manier tweemaal het aantal ribben. Delen door 2 levert dus het aantal ribben. Daarna pas je Euler toe om het aantal hoekpunten te bepalen.quote:Op dinsdag 25 april 2006 17:02 schreef Racing_X-Ray het volgende:
- De berekening waarmee je het aantal hoekpunten en ribben kan uitrekenen als je vorm en aantal van de vlakken weet.
dit is de enige die ik niet echt weet kan iemand mij daar mee helpen?


Vraag,
Ik heb al genoeg moeite om mijn vraag te formulieren, dus een antwoord erop krijgen zal nog wel lastiger worden.
Ik ga een onderzoek doen, ik gebruik A|B testing. Er komen een aantal respondenten die één bepaalde actie wel of niet uitvoeren.
Voorbeeld:
Ik heb 200 respondenten en 50 daarvan voeren de actie uit. Je zou dan zeggen dat de kans 25 procent is.
Maargoed als er slechts 4 respondenten zijn en één voert het uit. Dan is het ook 25 procent. Toch is het eerste voorbeeld "betrouwbaarder".
Wat ik wil bereiken is de kans een betrouwbaarheidspercentage geven afhankelijk van het aantal respondenten. Ik neig om de normaal verdeling te gebruiken. Ik snap alleen niks meer van de theorie die ik tien jaar geleden ooit eens op school heb geleerd.
Ik hoop dat de vraag duidelijk is
Erik
Ik heb al genoeg moeite om mijn vraag te formulieren, dus een antwoord erop krijgen zal nog wel lastiger worden.
Ik ga een onderzoek doen, ik gebruik A|B testing. Er komen een aantal respondenten die één bepaalde actie wel of niet uitvoeren.
Voorbeeld:
Ik heb 200 respondenten en 50 daarvan voeren de actie uit. Je zou dan zeggen dat de kans 25 procent is.
Maargoed als er slechts 4 respondenten zijn en één voert het uit. Dan is het ook 25 procent. Toch is het eerste voorbeeld "betrouwbaarder".
Wat ik wil bereiken is de kans een betrouwbaarheidspercentage geven afhankelijk van het aantal respondenten. Ik neig om de normaal verdeling te gebruiken. Ik snap alleen niks meer van de theorie die ik tien jaar geleden ooit eens op school heb geleerd.
Ik hoop dat de vraag duidelijk is
Erik


Ja.quote:ik heb even snel een vraag.
in een elktrolyse reactie kan water ook als reductor of oxidator optreden.
moet water dan wel de sterktse reductor of oxidator zijn?
Wat is er 0,5 en 0,5?quote:Ik heb zelf H0, en H1 al gemaakt.
H0= 0,5
H1= 0,3
Je hebt twee hypotheses die een dissectie moeten vormen. In H1 stop je altijd de alternatieve hypothese.
H0: μ>=0,50; H1: μ<0,50; α=0,05
TS: (F - 0,50) / SE(F)
RR: values < -z0,05 = -1,645
VAL: (0,43-0,50) / wortel(0,50²/100) = -1,4
Conclusie: Verwerp H0 niet.
Zolang het aantal respondenten maar groot genoeg is, zal de normale verdeling een goede benadering geven. Aan de hand van je steekproefdata kun je vervolgens een betrouwbaarheidsinterval bepalen waarin het gemiddeld aantal studenten dat iets invult zal liggen. Bij het bepalen gebruik je onder andere de variantie, die bij een grote steekproef kleiner is.quote:Wat ik wil bereiken is de kans een betrouwbaarheidspercentage geven afhankelijk van het aantal respondenten. Ik neig om de normaal verdeling te gebruiken. Ik snap alleen niks meer van de theorie die ik tien jaar geleden ooit eens op school heb geleerd.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt! Heb je hier misschien ook een voorbeeld bij?quote:[b]Op dinsdag 25 april 2006 22:42
...
Zolang het aantal respondenten maar groot genoeg is, zal de normale verdeling een goede benadering geven. Aan de hand van je steekproefdata kun je vervolgens een betrouwbaarheidsinterval bepalen waarin het gemiddeld aantal studenten dat iets invult zal liggen. Bij het bepalen gebruik je onder andere de variantie, die bij een grote steekproef kleiner is.


Hier ook een wiskundevraagje.
Ik ben net begonnen met integratie en ik heb het allemaal nog niet zo goed door.
Eén oefening lukt me echt niet:
ik moet de onbepaalde integraal berekenen van
tan2(4x)dx
(ik weet even niet hoe ik het helder kan voorstellen inclusief integraaltekentje enzo, sorry )
Ik heb hierbij twee mogelijkheden. Ik kan die tan2(4x) herschrijven, of de substitutiemethode toepassen (enige methodes die ik tot nu toe gezien heb).
Iemand enig idee hoe ik deze integraal moet oplossen?
Ik ben net begonnen met integratie en ik heb het allemaal nog niet zo goed door.
Eén oefening lukt me echt niet:
ik moet de onbepaalde integraal berekenen van
tan2(4x)dx
(ik weet even niet hoe ik het helder kan voorstellen inclusief integraaltekentje enzo, sorry )
Ik heb hierbij twee mogelijkheden. Ik kan die tan2(4x) herschrijven, of de substitutiemethode toepassen (enige methodes die ik tot nu toe gezien heb).
Iemand enig idee hoe ik deze integraal moet oplossen?


d/dx tan(x) = 1 + tan2x.quote:Op woensdag 26 april 2006 00:01 schreef vliegtuigje het volgende:
Hier ook een wiskundevraagje.
Ik ben net begonnen met integratie en ik heb het allemaal nog niet zo goed door.
Eén oefening lukt me echt niet:
ik moet de onbepaalde integraal berekenen van
tan2(4x)dx
(ik weet even niet hoe ik het helder kan voorstellen inclusief integraaltekentje enzo, sorry )
Ik heb hierbij twee mogelijkheden. Ik kan die tan2(4x) herschrijven, of de substitutiemethode toepassen (enige methodes die ik tot nu toe gezien heb).
Iemand enig idee hoe ik deze integraal moet oplossen?


hoooi!quote:Public Class Form1
Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click
Dim a, b, c, s As Double
opp(a, b, c)
End Sub
Private Function opp(ByVal a As Double, ByVal b As Double, ByVal c As Double)
Dim s As Double = (a + b + c) / 2
a = CDbl(TextBox1.Text)
b = CDbl(TextBox2.Text)
c = CDbl(TextBox3.Text)
Dim oppervlakte As Double
If a + b > c ora + c > b or a + c > b Then
oppervlakte = Math.Sqrt(s * (s - a) * (s - b) * (s - c))
Label1.Text = oppervlakte
Else
Throw New ArithmeticException("Er is een fout opgetreden")
End If
Return oppervlakte
End Function
End Class
nu ben ik bezig met een klein programma, de gebruiker voert in de lengtes van de zijden van de a,b,c en het programma rekent de oppervlakte van de driehoek.
Nu moet het een toepasselijke excpetion opgooien (en een foutmelding geven) wanneer de drie lengten geen driehoek kunnen vormen.
Ik moet ernaat ook een aanroepende methode schrijven die de exception opvangt..
Kan iemand me helpen?
Ik heb al iets zitten te typen maar.. er klopt niets van..
[ Bericht 0% gewijzigd door teletubbies op 26-04-2006 21:56:36 ]
verlegen :)


Als a de langste zijde is kan er geen driehoek zijn als: a>b+c .quote:Op woensdag 26 april 2006 20:34 schreef teletubbies het volgende:
[..]
hoooi!
nu ben ik bezig met een klein programma, de gebruiker voert in de lengtes van de zijden van de a,b,c en het programma rekent de oppervlakte van de driehoek.
Nu moet het een toepasselijke excpetion opgooien (en een foutmelding geven) wanneer de drie lengten geen driehoek kunnen vormen.
Ik moet ernaat ook een aanroepende methode schrijven die de exception opvangt..
Kan iemand me helpen?
Ik heb al iets zitten te typen maar.. er klopt niets van..
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Als a niet de langste zijde is ook nietquote:Op woensdag 26 april 2006 21:13 schreef Wackyduck het volgende:
[..]
Als a de langste zijde is kan er geen driehoek zijn als: a>b+c .
Maar dat is inderdaad wel een aardige, er zal nooit een driehoek ingevuld kunnen worden waarbij een van de zijden de langer is dan de andere twee zijden bij elkaar opgeteld.
"Dat is echt ontzettend zielig" ©


Als a de langste zijde is, en gelijk is aan b+c ook niet. Of als één van de zijden negatief is. Verder denk ik dat je de formule van Heron goed kunt gebruiken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik denk dat er een spatie tussen "or" en "a" moet. Waarom zijn if en then eigenlijk met hoofdletters en or niet?quote:If a + b > c ora + c > b or a + c > b Then


ja die or moet in feite apart staan Or..
maar zo'n feit geeft visual basic wel aan, ..
maar het gaat niet om de wiskundige kant..die kun je zo fixen..
het gaat om dat exception gedoe.. :S
ik heb een exception ' opgegooid' maar ik moet die nog afhandelen.. dus er moet iets gedaan worden met die exception... maar wat?:S
maar zo'n feit geeft visual basic wel aan, ..
maar het gaat niet om de wiskundige kant..die kun je zo fixen..
het gaat om dat exception gedoe.. :S
ik heb een exception ' opgegooid' maar ik moet die nog afhandelen.. dus er moet iets gedaan worden met die exception... maar wat?:S
verlegen :)


Vraagje over rekenregels.
Ik weet dat volgens nieuwe internationale regels dit ezelsbruggetje niet meer geldig is, maar waar stond 'Meneer Van Dale Wacht Op Antwoord' oorspronkelijk voor?
Mij is het volgens mij altijd geleerd als:
- optellen en aftrekken zijn gelijkwaardig (gewoon op volgorde zoals ze er staan uitrekenen)
- machtsverheffen en worteltrekken zijn niet gelijkwaardig
- vermenigvuldigen en delen zijn niet gelijkwaardig
Volgens de nieuwe regels zijn ook vermenigvuldigen en delen gelijkwaardig, en nu lees ik steeds meer over mensen die beweren dat dat met de 'meneer Van Dale' regel óók al zo was. Hoe zit het nu? In dit topic zijn de meningen ongeveer 50-50 verdeeld.
Ik weet dat volgens nieuwe internationale regels dit ezelsbruggetje niet meer geldig is, maar waar stond 'Meneer Van Dale Wacht Op Antwoord' oorspronkelijk voor?
Mij is het volgens mij altijd geleerd als:
- optellen en aftrekken zijn gelijkwaardig (gewoon op volgorde zoals ze er staan uitrekenen)
- machtsverheffen en worteltrekken zijn niet gelijkwaardig
- vermenigvuldigen en delen zijn niet gelijkwaardig
Volgens de nieuwe regels zijn ook vermenigvuldigen en delen gelijkwaardig, en nu lees ik steeds meer over mensen die beweren dat dat met de 'meneer Van Dale' regel óók al zo was. Hoe zit het nu? In dit topic zijn de meningen ongeveer 50-50 verdeeld.
Heeft Fok! verlaten, jeweetoch.


Vermenigvuldigen en delen zijn gelijkwaardig. In geval van twijfel kun je natuurlijk altijd haakjes gebruiken.


aftrekken bestaat officieel niet eens dus daar hoef je ook niet over na te denken.quote:Op donderdag 27 april 2006 13:05 schreef m021 het volgende:
Vraagje over rekenregels.
Ik weet dat volgens nieuwe internationale regels dit ezelsbruggetje niet meer geldig is, maar waar stond 'Meneer Van Dale Wacht Op Antwoord' oorspronkelijk voor?
Mij is het volgens mij altijd geleerd als:
- optellen en aftrekken zijn gelijkwaardig (gewoon op volgorde zoals ze er staan uitrekenen)
Het enige wat geld is vermenigvuldigen gaat voor optellen. De rest is vaak grafisch duidelijk
als je je wortelteken goed opschrijft is het duidelijk wat je eerst moet doen.quote:- machtsverheffen en worteltrekken zijn niet gelijkwaardig
idem met delen.
zoals ik al zei: het is grafisch vaak volkomen duidelijk en bij twijfel haakjes gebruiken
quote:- vermenigvuldigen en delen zijn niet gelijkwaardig
Volgens de nieuwe regels zijn ook vermenigvuldigen en delen gelijkwaardig, en nu lees ik steeds meer over mensen die beweren dat dat met de 'meneer Van Dale' regel óók al zo was. Hoe zit het nu? In dit topic zijn de meningen ongeveer 50-50 verdeeld.
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Ja, volgens de nieuwe regels wel. Maar was dat met MVDWOA ook al zo, is mijn vraag.quote:Op donderdag 27 april 2006 13:23 schreef thabit het volgende:
Vermenigvuldigen en delen zijn gelijkwaardig.
Op die manier kan je ook wel zeggen dat delen niet bestaat. Immers,quote:Op donderdag 27 april 2006 13:40 schreef McCarthy het volgende:
aftrekken bestaat officieel niet eens dus daar hoef je ook niet over na te denken.
x/y
is hetzelfde als
x * y-1
[ Bericht 38% gewijzigd door m021 op 27-04-2006 13:49:47 ]
Heeft Fok! verlaten, jeweetoch.


Ik heb een vraagje over Scheikunde:
Het gaat over reactie's kloppend maken, en aangezien sk mijn allerallerallerslechtste vak is snap ik er geen hol van
Hier komt de vraag:
Geef de reactievergelijking van de verbranding van:
C4H10 (g)
Dan is het antwoord: (DIT GEDEELTE WEET IK DUS NIET!)
2C4H10 (g) + O2 (g) --> 8CO2 + 10H2O (g)
Ik heb die cijfertjes ff naar beneden gedaan zodat jullie kunnen zien wat ik bedoel met dat kloppend maken met die nummers.
Heeft iemand een goeie duidelijke uitleg hoe ik dit zelf kan zien
help
BTW, ik zit in 3VWO dus geen moeilijke termen aub
Het gaat over reactie's kloppend maken, en aangezien sk mijn allerallerallerslechtste vak is snap ik er geen hol van
Hier komt de vraag:
Geef de reactievergelijking van de verbranding van:
C4H10 (g)
Dan is het antwoord: (DIT GEDEELTE WEET IK DUS NIET!)
2C4H10 (g) + O2 (g) --> 8CO2 + 10H2O (g)
Ik heb die cijfertjes ff naar beneden gedaan zodat jullie kunnen zien wat ik bedoel met dat kloppend maken met die nummers.
Heeft iemand een goeie duidelijke uitleg hoe ik dit zelf kan zien
help
BTW, ik zit in 3VWO dus geen moeilijke termen aub
Shoulder pads may come and go, but a BFF is forever O+


Gewoon tellen, het aantal C'tjes, H'tjes en O'tjes links van de pijl moet hetzelfde zijn als rechts van de pijl.


Hmm. En met een verbranding krijg je altijd CO2 en H2O?quote:Op donderdag 27 april 2006 15:19 schreef thabit het volgende:
Gewoon tellen, het aantal C'tjes, H'tjes en O'tjes links van de pijl moet hetzelfde zijn als rechts van de pijl.
Dus dan plant ik eerst de vergelijking (ofwathetookis) links en dan die CO2 en H2O aan de rechterkant.
En dan optellen?
C4 zijn dan 4 C's en met CO2 heb ik maar 1 C?
Shoulder pads may come and go, but a BFF is forever O+


mmm klopt. mara goed ik heb het opgelost..
er moest ergens staan
try
dit en dat..
catch ex as arithmetiqueexc...
dit en dat
thanx
er moest ergens staan
try
dit en dat..
catch ex as arithmetiqueexc...
dit en dat
thanx
verlegen :)


Ja, het enige dat je moet onthouden is dat een verbranding een reactie met zuurstof (O2) is en dat het reactieproductie van C, altijd CO2 is en dat van H altijd H2Oquote:Op donderdag 27 april 2006 15:24 schreef Nesle het volgende:
[..]
Hmm. En met een verbranding krijg je altijd CO2 en H2O?
Dus dan plant ik eerst de vergelijking (ofwathetookis) links en dan die CO2 en H2O aan de rechterkant.
En dan optellen?
C4 zijn dan 4 C's en met CO2 heb ik maar 1 C?
"MOLLUCK DU SCHEISS DRECKIGER BINGO SPIELER"


En met koolwaterstoffen (CxHx of CxHxOx) in het algemeen krijg je ook altijd CO2 en H2O.quote:Op donderdag 27 april 2006 19:11 schreef Molluck het volgende:
Ja, het enige dat je moet onthouden is dat een verbranding een reactie met zuurstof (O2) is en dat het reactieproductie van C, altijd CO2 is en dat van H altijd H2O
Heeft Fok! verlaten, jeweetoch.


Bedankt allemaal!
Ik ga morgen mijn proefwerk hopelijk goed maken
Cijfer volgt!
Ik ga morgen mijn proefwerk hopelijk goed maken
Cijfer volgt!
Shoulder pads may come and go, but a BFF is forever O+


Vraagje over Lie groepen. Ik weet dat de Liegroepen SU(n), O(n) etc, geschreven kunnen worden in termen van een eindige verzameling continu parameters. Is dit mogelijk voor alle Lie groepen of niet? En hoe zou je het kunnen bewijzen?
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Ik snap je vraag niet, Pietjuh. Kun je definieren wat je bedoelt met
quote:geschreven kunnen worden in termen van een eindige verzameling continu parameters.


Overkomt me wel vaker, maar waar, en wat was er fout?quote:@ GlowMouse
je zat er helemaal naast
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het is mischien ook een beetje slecht geformuleerdquote:Op vrijdag 28 april 2006 16:00 schreef thabit het volgende:
Ik snap je vraag niet, Pietjuh. Kun je definieren wat je bedoelt met
Neem als voorbeeld de Lie groep SO(3), die van de rotaties in 3 dimensies. Elk element U in SO(3) is te schrijven als U(a_1, a_2, a_3) = exp( a_1 L_1 + a_2 L_2 + a_3 L_3), waarbij de L_i de infinitesimale voortbrengers zijn van de groep. De a_i's zijn de continue parameters die het groepselement specificieren. Nu vraag ik me af of je voor een willekeurige Lie groep G je een element U in G ook kan schrijven als functie van een stel continue parameters en infinitesimale voortbrengers. Of geldt dat alleen maar voor Lie groepen die zijn afgeleid uit GL(n, K )?
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Wel Pietjuh, voor SL2(R) geldt dat de matrices met spoor < -2 niet in een eenparameter-ondergroep liggen. Het antwoord op je vraag is dus: nee.


Ok, dat is mooi om te weten
Er is ook een kleine verwarring met het begrip eenparameter-ondergroep. Is deze parameter een scalaire waarde of kan het ook een vector zijn? Want in het geval van SO(3) heb je duidelijk 3 parameters.
Er is ook een kleine verwarring met het begrip eenparameter-ondergroep. Is deze parameter een scalaire waarde of kan het ook een vector zijn? Want in het geval van SO(3) heb je duidelijk 3 parameters.
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


De formulevergelijking was fout ingevuldquote:Op vrijdag 28 april 2006 17:51 schreef GlowMouse het volgende:
[..]
Overkomt me wel vaker, maar waar, en wat was er fout?
maar dit hele gebeuren was niet nodig geweest hoorde ik dus.
Zie de schematische tekening van wijnsteenzuur en je ziet dat het tweewaardig is.
De rest weet ik niet meer precies maar dat sloeg weer op de uitwerking van dat ik als eerste had, alleen dan niet precies .