SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ah, natuurlijk. Maar is het niet ook zo dat omdat f(x) < g(x), voor alle x geldt dat c(x) := || f(x) - g(x) || > 0 en dus als als je p = min{ c(x) } neemt er dan een open bol met straal p rondom f(x) bestaat zodat voor ieder element y uit die bol geldt dat y < g(x)?quote:Op dinsdag 5 mei 2015 20:38 schreef thabit het volgende:
[..]
Als h(x) = f(x) - g(x), dan ben je dus op zoek naar het inverse beeld van ]-∞, 0[ onder h.
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
Als || f(x) - g(x) || > 0, dan zou het ook kunnen zijn dat f(x) > g(x).quote:Op dinsdag 5 mei 2015 21:31 schreef Diacetylmorfine het volgende:
[..]
Ah, natuurlijk. Maar is het niet ook zo dat omdat f(x) < g(x), voor alle x geldt dat c(x) := || f(x) - g(x) || > 0 en dus als als je p = min{ c(x) } neemt er dan een open bol met straal p rondom f(x) bestaat zodat voor ieder element y uit die bol geldt dat y < g(x)?
[ Bericht 100% gewijzigd door Quir op 05-05-2015 21:39:21 ]
"Social order at the expense of liberty is hardly a bargain."
Maar er is toch gegeven dat f(x) < g(x)?quote:
[..]
Als || f(x) - g(x) || > 0, dan zou het ook kunnen zijn dat f(x) > g(x).
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
Je kunt hier natuurlijk ook mooi gebruik maken van de residuenstelling voor r > 1. Je functie f(z) = 1/(z²+1) heeft een enkelvoudige pool z = i en je hebt Res(f(z), i) = 1/2i, zodat de integraal van f(z) langs de gesloten curve die bestaat uit het reële interval [−r, r] en de halve cirkel rond de oorsprong van r naar −r voor r > 1 gelijk is aan π. Maar de integraal van f(z) over het reële interval [−r, r] nadert ook tot π voor r → ∞ zodat de integraal van f(z) over de halve cirkel dus naar 0 moet gaan voor r → ∞. Zie je?quote:
[..]
Ah dat wist ik dan weer niet. M'n hoofd over zitten breken vanochtend.
Nee, want ik heb geen flauw idee wat de residuenstelling is. Echter stonden daar opgaven van in een voorbeeldtoets ter voorbereiding op een toets van vrijdag, zodat dat vandaag in het college behandeld moet worden. Dat wordt overigens gegeven door cabaretier Sjoerd Rienstra, ik weet niet of je bekend bent met de beste man.quote:
[..]
Je kunt hier natuurlijk ook mooi gebruik maken van de residuenstelling voor r > 1. Je functie f(z) = 1/(z²+1) heeft een enkelvoudige pool z = i en je hebt Res(f(z), i) = 1/2i, zodat de integraal van f(z) langs de gesloten curve die bestaat uit het reële interval [−r, r] en de halve cirkel rond de oorsprong van r naar −r voor r > 1 gelijk is aan π. Maar de integraal van f(z) over het reële interval [−r, r] nadert ook tot π voor r → ∞ zodat de integraal van f(z) over de halve cirkel dus naar 0 moet gaan voor r → ∞. Zie je?
Je hebt kennelijk nog niet veel aan complexe analyse gedaan, anders zou je begrijpen wat ik bedoel.quote:Op woensdag 6 mei 2015 00:23 schreef Amoeba het volgende:
[..]
Nee, want ik heb geen flauw idee wat de residuenstelling is. Echter stonden daar opgaven van in een voorbeeldtoets ter voorbereiding op een toets van vrijdag, zodat dat vandaag in het college behandeld moet worden. Dat wordt overigens gegeven door cabaretier Sjoerd Rienstra, ik weet niet of je bekend bent met de beste man.
We zitten pas 4 colleges gehad, en de eerste 2 waren niet zo boeiend.quote:
[..]
Je hebt kennelijk nog niet veel aan complexe analyse gedaan, anders zou je begrijpen wat ik bedoel.
Residues staan vandaag om 13:45 op het programma.Ik vind het vooral zonde dat je dan zo'n integraal probeert uit te rekenen maar dat dat niet eens schijnt te kunnen. Verder ook geen waarschuwing in het college dat daar zaken mis kunnen gaan enzo.
Je integraal is prima uit te rekenen, en dat kan op meerdere manieren, maar niet zoals jij het dacht te doen. Met de residuenstelling kan het zelfs uit het blote hoofd.quote:Op woensdag 6 mei 2015 00:39 schreef Amoeba het volgende:
[..]
We zitten pas 4 colleges gehad, en de eerste 2 waren niet zo boeiend.
Ik vind het vooral zonde dat je dan zo'n integraal probeert uit te rekenen maar dat dat niet eens schijnt te kunnen. Verder ook geen waarschuwing in het college dat daar zaken mis kunnen gaan enzo.
Ik vind de definitie van een residu al eng.quote:
[..]
Je integraal is prima uit te rekenen, en dat kan op meerdere manieren, maar niet zoals jij het dacht te doen. Met de residuenstelling kan het zelfs uit het blote hoofd.
Maar ik zie dat straks wel. Ik had de PC om andere redenen aangezet.
[ Bericht 5% gewijzigd door #ANONIEM op 06-05-2015 00:46:03 ]
Het is in feite gewoon de coëfficiënt a−1 van de Laurent expansie van de functie rond de pool in kwestie. Voor een enkelvoudige pool z = c hoef je dus alleen limz→c f(z)·(z−c) te bepalen, en dan vind je voor f(z) = 1/(z²+1) direct Res(f(z),i) = 1/2i.quote:
[..]
Ik vind de definitie van een residu al eng.
Ja dan snap ik 'm wel. Het bewijs van de stelling en het vinden van een residu daargelaten.quote:
[..]
Je kunt hier natuurlijk ook mooi gebruik maken van de residuenstelling voor r > 1. Je functie f(z) = 1/(z²+1) heeft een enkelvoudige pool z = i en je hebt Res(f(z), i) = 1/2i, zodat de integraal van f(z) langs de gesloten curve die bestaat uit het reële interval [−r, r] en de halve cirkel rond de oorsprong van r naar −r voor r > 1 gelijk is aan π. Maar de integraal van f(z) over het reële interval [−r, r] nadert ook tot π voor r → ∞ zodat de integraal van f(z) over de halve cirkel dus naar 0 moet gaan voor r → ∞. Zie je?
Maar waarom blijft die voorwaarde in een open omgeving van een dergelijk punt gelden?quote:
[..]
Maar er is toch gegeven dat f(x) < g(x)?
Is het je inmiddels wel compleet helder (inclusief bewijzen) na wat colleges van die komediant?quote:
[..]
Ja dan snap ik 'm wel. Het bewijs van de stelling en het vinden van een residu daargelaten.
Helemaal! Maar ik zal vast nog wel meer vragen hebben over complexe analyse. Ik vind het best een pittig vak.quote:
[..]
Is het je inmiddels wel compleet helder (inclusief bewijzen) na wat colleges van die komediant?
Weet je ook iets van partiële differentiaalvergelijkingen?
Hangt ervan af wat je precies wil weten. Je kunt je vraag hier natuurlijk altijd stellen. Als ik je er niet mee kan helpen dan wellicht iemand anders wel.quote:Op maandag 11 mei 2015 22:00 schreef Amoeba het volgende:
[..]
Helemaal! Maar ik zal vast nog wel meer vragen hebben over complexe analyse. Ik vind het best een pittig vak.
Weet je ook iets van partiële differentiaalvergelijkingen?
Heb ik net een vak over gehad! Dus stel je vraag maar, wie weet!quote:
[..]
Helemaal! Maar ik zal vast nog wel meer vragen hebben over complexe analyse. Ik vind het best een pittig vak.
Weet je ook iets van partiële differentiaalvergelijkingen?
Ik heb een vraagje over kansrekening.
Laat de stochasten X, Y onafhankelijk zijn en met een gelijke kans -1 / +1 aannemen. Zij Z=XY. Zijn X en Z onafhankelijk?
Het volgt dat f_{z}(z)=1/2*1/2=1/4 en f_{x}(x)=1/2. Onafhankelijkheid impliceert dat f_{zx}(zx)=f_{z}(z)*f_{x}(x), maar hier loop ik een beetje vast. Zou iemand mij een hint kunnen geven over hoe ik verder kan gaan?
Laat de stochasten X, Y onafhankelijk zijn en met een gelijke kans -1 / +1 aannemen. Zij Z=XY. Zijn X en Z onafhankelijk?
Het volgt dat f_{z}(z)=1/2*1/2=1/4 en f_{x}(x)=1/2. Onafhankelijkheid impliceert dat f_{zx}(zx)=f_{z}(z)*f_{x}(x), maar hier loop ik een beetje vast. Zou iemand mij een hint kunnen geven over hoe ik verder kan gaan?
Je f_z klopt nietquote:
Ik heb een vraagje over kansrekening.
Laat de stochasten X, Y onafhankelijk zijn en met een gelijke kans -1 / +1 aannemen. Zij Z=XY. Zijn X en Z onafhankelijk?
Het volgt dat f_{z}(z)=1/2*1/2=1/4 en f_{x}(x)=1/2. Onafhankelijkheid impliceert dat f_{zx}(zx)=f_{z}(z)*f_{x}(x), maar hier loop ik een beetje vast. Zou iemand mij een hint kunnen geven over hoe ik verder kan gaan?
P( Z = 1) = P(X=1,Y=1) + P(X = -1,Y=-1) = 1/4 + 1/4 = 1/2
En dan
P(Z = 1, X = 1) = P(Y = 1, X = 1) = 1/4 = P(Z = 1) * P(X = 1)
etc
Ik snap waarom mijn f_z niet klopt, maar dat betekent dan toch ook dat mijn f_x=f_y=1/2 niet kloppen? Immers, vanwege de onafhankelijkheid geldt dat f_z=f_x * f_y.quote:
[..]
Je f_z klopt niet
P( Z = 1) = P(X=1,Y=1) + P(X = -1,Y=-1) = 1/4 + 1/4 = 1/2
En dan
P(Z = 1, X = 1) = P(Y = 1, X = 1) = 1/4 = P(Z = 1) * P(X = 1)
etc
Nee Z is iets anders dan (X,Y) (de joint distribution van X en Y)quote:
[..]
vanwege de onafhankelijkheid geldt dat f_z=f_x * f_y.
onafhankelijkheid van X en Y zegt dat
P( X = x, Y = y) = P(X = x) P(Y = y)
dus
P(Z=1) = P(X = 1, Y = 1) + P(X = -1, Y = -1) = P(X = 1)P(Y = 1) + P(X = - 1)P(Y = -1) = 1/4 + 1/4 = 1/2
Aah op die manier! Duidelijk, bedankt!quote:
[..]
Nee Z is iets anders dan (X,Y)
onafhankelijkheid van X en Y zegt dat
P( X = x, Y = y) = P(X = x) P(Y = y)
dus
P(Z=1) = P(X = 1, Y = 1) + P(X = -1, Y = -1) = P(X = 1)P(Y = 1) + P(X = - 1)P(Y = -1) = 1/4 + 1/4 = 1/2
Wat een vreemde notatie. Meestal staat f voor een density functie.quote:
Ik heb een vraagje over kansrekening.
Laat de stochasten X, Y onafhankelijk zijn en met een gelijke kans -1 / +1 aannemen. Zij Z=XY. Zijn X en Z onafhankelijk?
Het volgt dat f_{z}(z)=1/2*1/2=1/4 en f_{x}(x)=1/2. Onafhankelijkheid impliceert dat f_{zx}(zx)=f_{z}(z)*f_{x}(x), maar hier loop ik een beetje vast. Zou iemand mij een hint kunnen geven over hoe ik verder kan gaan?
Ik weet niet of ik het hier moet vragen, maar weet iemand boeken of websites met calculus opgaven op hbo-niveau?
ROBODEMONS..................|:(
Ik gebruikte vroeger volgens mij Calculus van Stewart. Vond het een goede methode.quote:
Ik weet niet of ik het hier moet vragen, maar weet iemand boeken of websites met calculus opgaven op hbo-niveau?
kloep kloep
Weet iemand hoe je de extremen (extreme waarden) van |x^2-4| moet berekenen? Ik dacht er zelf aan om de functie te differentiëren en dan f'(x)=0 oplossen;
f'(x)=2x
0=2x
x=0
Echter staat in het antwoordenboek dat |x|=√x^2, dus f(x)=√(x^2 -4)^2 (kwadraat in de wortelfunctie)
Dit differentiëren ze dan en daar komt x=0, x=2 en x=-2 uit. Ik begrijp niet hoe dit precies in elkaar zit, zou iemand mij dit kunnen uitleggen?
f'(x)=2x
0=2x
x=0
Echter staat in het antwoordenboek dat |x|=√x^2, dus f(x)=√(x^2 -4)^2 (kwadraat in de wortelfunctie)
Dit differentiëren ze dan en daar komt x=0, x=2 en x=-2 uit. Ik begrijp niet hoe dit precies in elkaar zit, zou iemand mij dit kunnen uitleggen?
Die rechte strepen betekenen 'absolute waarde' oftewel de positieve waarde. |x| is uit te drukken als √ (x2) (immers, |2| = |-2| = √(22) = √((-2)2) en daarmee kun je je functie op de normale manier differentiëren, nulstellen etc.quote:
Weet iemand hoe je de extremen (extreme waarden) van |x^2-4| moet berekenen? Ik dacht er zelf aan om de functie te differentiëren en dan f'(x)=0 oplossen;
f'(x)=2x
0=2x
x=0
Echter staat in het antwoordenboek dat |x|=√x^2, dus f(x)=√(x^2 -4)^2 (kwadraat in de wortelfunctie)
Dit differentiëren ze dan en daar komt x=0, x=2 en x=-2 uit. Ik begrijp niet hoe dit precies in elkaar zit, zou iemand mij dit kunnen uitleggen?
Ik bekijk dit soort dingen meestal anders: de | | gaat ingrijpen op het punt waar je functie 0 is. Bij f(x) = x2-4 is dat bij x=2 en x=-2, dus daar zitten extreme waarden. De andere extreme waarde zit bij de top van de parabool, dus bij x=0.
Opinion is the medium between knowledge and ignorance (Plato)
Hartstikke bedankt! Ik begrijp dat |2| = |-2| en dat √(22) = √((-2)2), maar ik begrijp niet dat |x| = √(x2). Weet je waarom dit zo is?quote:
[..]
Die rechte strepen betekenen 'absolute waarde' oftewel de positieve waarde. |x| is uit te drukken als √ (x2) (immers, |2| = |-2| = √(22) = √((-2)2) en daarmee kun je je functie op de normale manier differentiëren, nulstellen etc.
Ik bekijk dit soort dingen meestal anders: de | | gaat ingrijpen op het punt waar je functie 0 is. Bij f(x) = x2-4 is dat bij x=2 en x=-2, dus daar zitten extreme waarden. De andere extreme waarde zit bij de top van de parabool, dus bij x=0.
Verder begrijp ik nu dat je ook naar de nulpunten moet kijken, omdat ze hier de minima zijn. Kun je trouwens alleen weten of de nulpunten extreme waarden zijn als je plot of kun je dit algebraïsch bepalen?
Edit: in het antwoordenboek wordt het heel anders (en moeilijker) uitgelegd, hier wordt de kettingregel gebruikt bij het differentiëren van de formule om zo op alle drie de waarden te komen. Moet je dat hier ook zo doen om op een correcte manier de uiterste waarden te berekenen of is jouw manier ook goed? (ik kan een foto maken als je niet begrijpt wat ik bedoel)
Komt door de definitie van de absolute waarde. |a| = a als a>0 en |a| = -a als a<0. Als je even bedenkt wat er gebeurt als je een getal eerst kwadrateert en daarna de wortel trekt (√(a2) dus) dan zie je snel genoeg dat dat hetzelfde is.quote:
[..]
Hartstikke bedankt! Ik begrijp dat |2| = |-2| en dat √(22) = √((-2)2), maar ik begrijp niet dat |x| = √(x2). Weet je waarom dit zo is?
In dit specifieke geval met de absolute waarde maakt het niet uit. Immers: of het was al een extremum van je functie zonder de absolute waarde, of het wordt het omdat op die plek de grafiek 'omklapt'.quote:Verder begrijp ik nu dat je ook naar de nulpunten moet kijken, omdat ze hier de minima zijn. Kun je trouwens alleen weten of de nulpunten extreme waarden zijn als je plot of kun je dit algebraïsch bepalen?
Ik snap wel wat je bedoelt. Als je duidelijk opschrijft wat je precies doet, voldoet mijn manier natuurlijk ook.quote:Edit: in het antwoordenboek wordt het heel anders (en moeilijker) uitgelegd, hier wordt de kettingregel gebruikt bij het differentiëren van de formule om zo op alle drie de waarden te komen. Moet je dat hier ook zo doen om op een correcte manier de uiterste waarden te berekenen of is jouw manier ook goed? (ik kan een foto maken als je niet begrijpt wat ik bedoel)
Opinion is the medium between knowledge and ignorance (Plato)
Nu begrijp ik het helemaal. Hartstikke bedankt voor de moeitequote:
[..]
Komt door de definitie van de absolute waarde. |a| = a als a>0 en |a| = -a als a<0. Als je even bedenkt wat er gebeurt als je een getal eerst kwadrateert en daarna de wortel trekt (√(a2) dus) dan zie je snel genoeg dat dat hetzelfde is.
[..]
In dit specifieke geval met de absolute waarde maakt het niet uit. Immers: of het was al een extremum van je functie zonder de absolute waarde, of het wordt het omdat op die plek de grafiek 'omklapt'.
[..]
Ik snap wel wat je bedoelt. Als je duidelijk opschrijft wat je precies doet, voldoet mijn manier natuurlijk ook.
!
Als dit echt zo is dan doet je antwoordenboekje iets wat niet klopt, je functie is namelijk niet differentieerbaar voor x = −2 en voor x = 2.quote:
[..]
Edit: in het antwoordenboek wordt het heel anders (en moeilijker) uitgelegd, hier wordt de kettingregel gebruikt bij het differentiëren van de formule om zo op alle drie de waarden te komen. Moet je dat hier ook zo doen om op een correcte manier de uiterste waarden te berekenen of is jouw manier ook goed? (ik kan een foto maken als je niet begrijpt wat ik bedoel)
Het is ook een kansdichtheidsfunctie. Er geldt dat voor alle waarden die x kan aannemen de kans van f_{x}(x)=(1/2)x(1/2)1-x. Merk op dat dit dus altijd 1/2 voor x=-1 en x=1.quote:
[..]
Wat een vreemde notatie. Meestal staat f voor een density functie.
Je hebtquote:Op zondag 17 mei 2015 14:47 schreef Goldenrush het volgende:
Bij de substitutiemethode x ln (x^2+1)dx = (1/2) ln (x^2+1)d(x^2+1)
Waar komt die (1/2) vandaan?
dus
en dus
Je voert hier een impliciete substutie uit. We kunnen precies hetzelfde ook doen met een expliciete substitutie
en dan is
dus
en dus
Om nu deze onbepaalde integraal verder uit te werken maak je gebruik van partiële integratie, waarbij je de integrand ln u opvat als het product van 1 en ln u, en dan vind je
Uiteindelijk krijgen we dus
Zie ook deze post van mij over het gebruik van de substitutieregel.
[ Bericht 1% gewijzigd door Riparius op 17-05-2015 16:31:55 ]
Wat je zegt klopt niet.quote:
[..]
Het is ook een kansdichtheidsfunctie. Er geldt dat voor alle waarden die x kan aannemen de kans van f_{x}(x)=(1/2)x(1/2)1-x. Merk op dat dit dus altijd 1/2 voor x=-1 en x=1.
Ten eerste is de functie die je daar opschrijft uberhaupt geen kansdichtheidsfunctie (want de integraal ervan is geen 1). Sterker nog, de integraal convergeert niet want er staat gewoon f_x(x)=1/2 voor alle x.
Ten tweede zijn er per definitie geen kansdichtheidsfuncties voor stochasten die discreet zijn (alleen voor continue stochasten).
En als jij claimt dat X en Y continu zijn, en het enige dat je weet is dat P(X=1)=P(Y=1) en P(X= -1) = P(Y= -1) (lees: 0 = 0 en 0 = 0, want continue stochasten nemen met kans 0 een specifieke waarde aan), dan is de vraagstelling bijzonder vreemd.
De normale notatie is voor discrete variabelen is P(X=x), of desnoods definieer je pX(x) := P(X = x). Ik denk dat jij met de definitie fX(x) := P(X = x) werkt, maar dat is geen standaard notatie.
Dit klopt natuurlijk niet, er bestaan ook discrete kansdichtheidsfuncties (discrete pdf's, ook die kunnen worden aangeduid als f_, dat is een notatiekwestie, Bain en Engelhardt doet dan bijv. ook). Merk op dat de f_{x}(x) wel naar 1 gaat, aangezien je moet sommeren over x in Im(X), i.e. x=1 en x=-1. Dat is natuurlijk 1/2+1/2=1. Bij discrete stochasten integreer je niet.quote:
[..]
Wat je zegt klopt niet.
Ten eerste is de functie die je daar opschrijft uberhaupt geen kansdichtheidsfunctie (want de integraal ervan is geen 1). Sterker nog, de integraal convergeert niet want er staat gewoon f_x(x)=1/2 voor alle x.
Ten tweede zijn er per definitie geen kansdichtheidsfuncties voor stochasten die discreet zijn (alleen voor continue stochasten).
En als jij claimt dat X en Y continu zijn, en het enige dat je weet is dat P(X=1)=P(Y=1) en P(X= -1) = P(Y= -1) (lees: 0 = 0 en 0 = 0, want continue stochasten nemen met kans 0 een specifieke waarde aan), dan is de vraagstelling bijzonder vreemd.
De normale notatie is voor discrete variabelen is P(X=x), of desnoods definieer je pX(x) := P(X = x). Ik denk dat jij met de definitie fX(x) := P(X = x) werkt, maar dat is geen standaard notatie.
Thenxero doelt erop dat die als kansmassafuncties worden aangeduid, denk ik.quote:
[..]
Dit klopt natuurlijk niet, er bestaan ook discrete kansdichtheidsfuncties (discrete pdf's, ook die kunnen worden aangeduid als f_, dat is een notatiekwestie, Bain en Engelhardt doet dan bijv. ook). Merk op dat de f_{x}(x) wel naar 1 gaat, aangezien je moet sommeren over x in Im(X), i.e. x=1 en x=-1. Dat is natuurlijk 1/2+1/2=1. Bij discrete stochasten integreer je niet.
Een korte en misschien stomme vraag:
Het gaat over de onderlinge ligging van een rechte op een assenstelsel.
Jullie kennen deze formule wel: a1/a2=b1/b2=c1/c2 Als dit klopt dan weet je dat de rechten samenvallend zijn. Maar wat nu als a1/a2=b1/b2Is niet gelijk aanc1c2? Wat weet je dan over de rechten?
k=a1 en L=a2 / k=b1 L=b2
Betekend dat rechte k en L dan samenvallend zijn en die 3de niet? Kon er geen concreet antwoord op vinden in mijn cursus en zou toch graag een bevestiging willen
Het gaat over de onderlinge ligging van een rechte op een assenstelsel.
Jullie kennen deze formule wel: a1/a2=b1/b2=c1/c2 Als dit klopt dan weet je dat de rechten samenvallend zijn. Maar wat nu als a1/a2=b1/b2Is niet gelijk aanc1c2? Wat weet je dan over de rechten?
k=a1 en L=a2 / k=b1 L=b2
Betekend dat rechte k en L dan samenvallend zijn en die 3de niet? Kon er geen concreet antwoord op vinden in mijn cursus en zou toch graag een bevestiging willen
Te kort.
[snip]quote:
Je vraag is zo goed als onbegrijpelijk. Leer eerst eens om een vraag correct en helder te formuleren. Als je letters voor grootheden introduceert dan moet je altijd duidelijk maken wat deze precies voorstellen. Misbruik ook niet het =-teken om zaken aan elkaar gelijk te stellen die niet aan elkaar gelijk kunnen zijn, zoals een naam van een rechte en een getal.
Waar kan ik deze tekens vinden? Op mijn toetsenbord in ieder geval niet...quote:
[..]
[snip]
Je vraag is zo goed als onbegrijpelijk. Leer eerst eens om een vraag correct en helder te formuleren. Als je letters voor grootheden introduceert dan moet je altijd duidelijk maken wat deze precies voorstellen. Misbruik ook niet het =-teken om zaken aan elkaar gelijk te stellen die niet aan elkaar gelijk kunnen zijn, zoals een naam van een rechte en een getal.
Te kort.
Welke tekens bedoel je? Je vraag is wederom volstrekt onduidelijk.quote:
[..]
Waar kan ik deze tekens vinden? Op mijn toetsenbord in ieder geval niet...
Bedankt voor de tip.quote:Op zaterdag 16 mei 2015 13:40 schreef Borizzz het volgende:
[..]
Ik gebruikte vroeger volgens mij Calculus van Stewart. Vond het een goede methode.
ROBODEMONS..................|:(
Hier gaan we dan:
k <-> a1.x + b1.y + c1 = 0
l <-> a2.x + b2.y + c2 = 0
a,b en c ∈ R (reële getallen)
Op die formule gebruik ik: ( / = breukstreep) a1/a2=b1/b2(=c1/cc)
Als al die 3 breuken gelijk zijn (c hebben we dus nu niet nodig) dan weten we dat de rechten samenvallend zijn. Maar in dit geval zijn alleen k en l gelijk, maar p (3de rechten, niet vermeld) niet.
betekend dit dat k en l samenvallend zijn en dat p ergens anders ligt? Of vallen alle rechten op een andere plek omdat de formule nu niet meer klopt.
Ik hoop dat dit wat duidelijk is
k <-> a1.x + b1.y + c1 = 0
l <-> a2.x + b2.y + c2 = 0
a,b en c ∈ R (reële getallen)
Op die formule gebruik ik: ( / = breukstreep) a1/a2=b1/b2(=c1/cc)
Als al die 3 breuken gelijk zijn (c hebben we dus nu niet nodig) dan weten we dat de rechten samenvallend zijn. Maar in dit geval zijn alleen k en l gelijk, maar p (3de rechten, niet vermeld) niet.
betekend dit dat k en l samenvallend zijn en dat p ergens anders ligt? Of vallen alle rechten op een andere plek omdat de formule nu niet meer klopt.
Ik hoop dat dit wat duidelijk is
Te kort.
OK. Dit is al een stuk duidelijker. Je hebt twee lineaire vergelijkingen in de variabelen x en y die elk een rechte voorstellen in een cartesisch assenstelsel. De reële getallen a1, b1, c1 zijn de coëfficiënten van de eerste vergelijking van een rechte die je k noemt en de reële getallen a2, b2, c2 zijn de coëfficiënten van de tweede vergelijking van een rechte die je l noemt.quote:
Hier gaan we dan:
k <-> a1.x + b1.y + c1 = 0
l <-> a2.x + b2.y + c2 = 0
a,b en c ∈ R (reële getallen)
Nee hoor, hier vergis je je in, c1 en c2 heb je ook nodig. Als je bijvoorbeeld hebtquote:Op die formule gebruik ik: ( / = breukstreep) a1/a2=b1/b2(=c1/cc)
Als al die 3 breuken gelijk zijn (c hebben we dus nu niet nodig) dan weten we dat de rechten samenvallend zijn.
k: 2x + 3y + 4 = 0
l: 4x + 6y + 7 = 0
dan vallen de rechten k en l niet samen. Het is eenvoudig in te zien waarom niet. Als we beide leden van de vergelijking van k met 2 vermenigvuldigen dan hebben we
k: 4x + 6y + 8 = 0
l: 4x + 6y + 7 = 0
Voor een gegeven punt met coördinaten (x, y) kan 4x + 6y echter nooit zowel −8 als −7 zijn, en dat betekent dat de rechten k en l dus geen enkel punt gemeen kunnen hebben, oftewel de lijnen k en l lopen in dit voorbeeld evenwijdig.
Als je een vraagstuk over drie rechten aan de orde wil stellen, dan moet je ook duidelijk maken wat die derde rechte dan is, anders is je vraag niet te beantwoorden.quote:Maar in dit geval zijn alleen k en l gelijk, maar p (3de rechte, niet vermeld) niet.
Nee, je vraag is nog steeds onduidelijk. Als je twee rechten hebt in een plat vlak, dan zijn er drie mogelijkheden, namelijk (1) de rechten snijden elkaar in één punt, (2) de rechten hebben geen punt gemeen en lopen evenwijdig, en (3) de rechten vallen geheel en al samen.quote:betekent dit dat k en l samenvallend zijn en dat p ergens anders ligt? Of vallen alle rechten op een andere plek omdat de formule nu niet meer klopt.
Ik hoop dat dit wat duidelijk is
De twee vergelijkingen van twee rechten vormen samen een stelsel in de variabelen x en y. Door dit stelsel op te lossen kun je vaststellen welk van de drie genoemde situaties zich voordoet. In geval (1) heeft je stelsel precies één oplossing, in geval (2) heeft je stelsel geen oplossing, en in geval (3) heeft je stelsel oneindig veel oplossingen.
Dag allen,
Op een of andere manier lukt het me niet om deze vergelijking algebraïsch op te lossen?
Heeft een van jullie enig idee?
Op een of andere manier lukt het me niet om deze vergelijking algebraïsch op te lossen?
Heeft een van jullie enig idee?
Verstand is de wiskunde van het gevoel.
Ik neem aan dat dat verticale streepje | geheel rechts een cursor is die dus niet tot de vergelijking behoort?quote:
Dag allen,
Op een of andere manier lukt het me niet om deze vergelijking algebraïsch op te lossen?
Heeft een van jullie enig idee?
[ afbeelding ]
Trek eerst eens 2 af van beide leden van je vergelijking, kun je dan de vergelijking wel verder oplossen?
Dat is niet het absoluut teken. Je moest een vergelijk opstellen met de volgende gegevens:quote:
Is die streep naast de 2 een absoluut teken? En waar is de andere dan?
Ik vind het raar dat ik hier niet uitkom op het goede antwoord.
Numeriek kwam ik uit op 2.66667 (2 2/3).
EDIT: AL GELUKT.
Ik vergat dat 1/2^0 = 1.
[ Bericht 2% gewijzigd door Integrationcalculus op 20-05-2015 20:02:39 (--) ]
Verstand is de wiskunde van het gevoel.
Het blijft onduidelijk wat je bedoelt doordat je notatie ambigu is. Als je hebtquote:
[..]
Dat is niet het absoluut teken. Je moest een vergelijk opstellen met de volgende gegevens:
[ afbeelding ]
Ik vind het raar dat ik hier niet uitkom op het goede antwoord.
Numeriek kwam ik uit op 2.66667 (2 2/3).
EDIT: AL GELUKT.
Ik vergat dat 1/2^0 = 1.
en het grondtal van je logaritme is 10, dan kom je uit op x = 8/3.
Je doet het vermoedelijk fout.quote:
[..]
EDIT: AL GELUKT.
Ik vergat dat 1/2^0 = 1.
Edit: Je bedoelt waarschijnlijk dat het grondtal 1/2 is. Ook dan kom je uit op x=8/3.
[ Bericht 8% gewijzigd door jungiaan op 20-05-2015 22:18:14 ]
Nee. Klaarblijkelijk kent niemand hier de software die je noemt en aangezien je vraag over die software gaat is dit een vraag die hier niet thuishoort.quote:
Ik moet binnenkort een rekenexamen voor toelating afleggen. In de voorbeeldtoets had ik 13/15 goed, behalve twee, en dat zijn deze 2:
Los de volgende vergelijking op: 5 (3 - x) = 3x + 4
Los de volgende ongelijkheid op: 313 4−> x
Ik heb geen idee hoe je deze ook al weer aanpakt, heb op internet gekeken ook maar kon niks vinden. Hoe doe je dit?
Los de volgende vergelijking op: 5 (3 - x) = 3x + 4
Los de volgende ongelijkheid op: 313 4−> x
Ik heb geen idee hoe je deze ook al weer aanpakt, heb op internet gekeken ook maar kon niks vinden. Hoe doe je dit?
“Advertising is based on one thing, happiness. Happiness is the smell of a new car. It’s a billboard on the side of the road that screams reassurance that whatever you are doing is okay. You are okay.”
-Don Draper
-Don Draper
Dit doe je met de zogenaamde balansmethode. Er staat een =-teken, dat betekent dat links en rechts "in evenwicht" zijn. Zo lang je links en rechts telkens hetzelfde optelt of aftrekt, of links en rechts vermenigvuldigt met dezelfde factor ongelijk 0, blijft de gelijkheid intact (nou ja, als je met 0 vermenigvuldigt blijft je gelijkheid ook wel kloppen, maar kun je je oplossing niet meer vinden).quote:Op zondag 24 mei 2015 12:56 schreef SherlockHolmes het volgende:
Los de volgende vergelijking op: 5 (3 - x) = 3x + 4
Oplossing:
5 (3-x) = 3x + 4
eerst de haakjes uitwerken
15 - 5x = 3x + 4
Alle termen met x naar de ene kant, dus links en rechts 3x aftrekken:
15 - 8x = 4
Alle termen zonder x naar de andere kant, dus links en rechts 15 aftrekken:
-8x = -11
Om te weten wat x is, links en rechts delen door -8:
x = 11/8.
Je andere vraag moet je even opnieuw (netjes) intypen, daar kan ik zo niks mee.
Opinion is the medium between knowledge and ignorance (Plato)
De andere was: 4 - 3x > 13quote:
[..]
Dit doe je met de zogenaamde balansmethode. Er staat een =-teken, dat betekent dat links en rechts "in evenwicht" zijn. Zo lang je links en rechts telkens hetzelfde optelt of aftrekt, of links en rechts vermenigvuldigt met dezelfde factor ongelijk 0, blijft de gelijkheid intact (nou ja, als je met 0 vermenigvuldigt blijft je gelijkheid ook wel kloppen, maar kun je je oplossing niet meer vinden).
Oplossing:
5 (3-x) = 3x + 4
eerst de haakjes uitwerken
15 - 5x = 3x + 4
Alle termen met x naar de ene kant, dus links en rechts 3x aftrekken:
15 - 8x = 4
Alle termen zonder x naar de andere kant, dus links en rechts 15 aftrekken:
-8x = -11
Om te weten wat x is, links en rechts delen door -8:
x = 11/8.
Je andere vraag moet je even opnieuw (netjes) intypen, daar kan ik zo niks mee.
Allereerst bedankt! Maar ik snap niet hoe je die haakjes werkwerkt. Opeens komt er -15, maar die 3 was nooit negatief, en nu opeens -15?
“Advertising is based on one thing, happiness. Happiness is the smell of a new car. It’s a billboard on the side of the road that screams reassurance that whatever you are doing is okay. You are okay.”
-Don Draper
-Don Draper
Naja ik kan niks overkopieren, hier is t:
“Advertising is based on one thing, happiness. Happiness is the smell of a new car. It’s a billboard on the side of the road that screams reassurance that whatever you are doing is okay. You are okay.”
-Don Draper
-Don Draper
Er staat geen -15quote:
[..]
De andere was: 4 - 3x > 13
Allereerst bedankt! Maar ik snap niet hoe je die haakjes werkwerkt. Opeens komt er -15, maar die 3 was nooit negatief, en nu opeens -15?
Vraag 14: Janneke heeft deze al voorgedaan, het exacte antwoord is x = 11/8. Zet nu de gewone breuk 11/8 eerst om in een decimale breuk, dat kun je hopelijk toch wel, zonder elektronische rekenhulpmiddelen?quote:
Naja ik kan niks overkopieren, hier is t:
[ afbeelding ]
Vraag 15: Laat eerst eens zien wat je hier hebt gedaan, licht elke stap toe én leg uit waarom je niet verder komt met deze opgave.
Nee dat zie ik nu, maar ik snap dus dat ze 5x3 heeft gedaan, en dan dat daar die 15 vandaan komt, maar opeens slaat er een 5 bij? 15-5x, waar komt die 5 vandaan?quote:
15 heb ik lang genoeg tevergeefs geprobeerd, ik heb alleen geen idee hoe je zo iets doet zonder dat er een '=' is, want je kan nu niets vergelijken.quote:
[..]
Vraag 14: Janneke heeft deze al voorgedaan, het exacte antwoord is x = 11/8. Zet nu de gewone breuk 11/8 eerst om in een decimale breuk, dat kun je hopelijk toch wel, zonder elektronische rekenhulpmiddelen?
Vraag 15: Laat eerst eens zien wat je hier hebt gedaan, licht elke stap toe én leg uit waarom je niet verder komt met deze opgave.
“Advertising is based on one thing, happiness. Happiness is the smell of a new car. It’s a billboard on the side of the road that screams reassurance that whatever you are doing is okay. You are okay.”
-Don Draper
-Don Draper
Als je deelt (of vermenigvuldigt) met -1 klapt het ongelijkheidsteken om.quote:
[..]
Nee dat zie ik nu, maar ik snap dus dat ze 5x3 heeft gedaan, en dan dat daar die 15 vandaan komt, maar opeens slaat er een 5 bij? 15-5x, waar komt die 5 vandaan?
[..]
15 heb ik lang genoeg tevergeefs geprobeerd, ik heb alleen geen idee hoe je zo iets doet zonder dat er een '=' is, want je kan nu niets vergelijken.
Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
Mag ik je, puur uit interesse, eens vragen waar de toelatingstest voor is?quote:
[..]
Nee dat zie ik nu, maar ik snap dus dat ze 5x3 heeft gedaan, en dan dat daar die 15 vandaan komt, maar opeens slaat er een 5 bij? 15-5x, waar komt die 5 vandaan?
Als je van 5 (3 - x) de haakjes wil 'uitwerken' dan moet je bedenken dat je eigenlijk een vermenigvuldiging maakt. Eigenlijk staat er: vijf keer de uitkomst van 'drie min x'.
Hierbij geldt, altijd, dat de vermenigvuldiging distributief is. Moeilijk woord, maar in een plaatje komt het hier op neer (hier wordt 2(p+7) uitgewerkt):
Jouw voorbeeld wordt dus 15 - 5x.
Niet veel anders dan het oplossen van een gelijkheid.quote:[..]
15 heb ik lang genoeg tevergeefs geprobeerd, ik heb alleen geen idee hoe je zo iets doet zonder dat er een '=' is, want je kan nu niets vergelijken.
Eerst even kijken wat er eigenlijk aan ons gevraagd wordt: we hebben een rechte lijn met formule y = 4 - 3x, en een getal, namelijk 13. Wanneer komt de lijn boven de 13 uit?
De balansmethode werkt ook hier. Het enige verschil is, dat je ongelijkheid omdraait als je vermenigvuldigt met een negatief getal. Om dit te demonstreren, bekijken we twee verschillende manieren van de balansmethode.
4 - 3x > 13
Alle termen met x staan al links, dus de termen zonder x naar rechts. Links en rechts 4 aftrekken:
-3x > 9
Delen door -3 (nu moet dus het teken worden omgekeerd)
x < -3. Klaar.
Of:
4 - 3x > 13
Alle termen met x naar rechts, dus links en rechts 3x optellen:
4 > 13 + 3x
Alle termen zonder x naar links, dus links en rechts 13 aftrekken:
-9 > 3x
Links en rechts delen door 3:
-3 > x
[ Bericht 22% gewijzigd door Janneke141 op 24-05-2015 21:55:15 ]
Opinion is the medium between knowledge and ignorance (Plato)
Vermenigvuldiging is distributief ten opzichte van optelling en aftrekking, dus je hebt in het algemeenquote:
[..]
Nee dat zie ik nu, maar ik snap dus dat ze 5x3 heeft gedaan, en dan dat daar die 15 vandaan komt, maar opeens slaat er een 5 bij? 15-5x, waar komt die 5 vandaan?
[..]
en
of, zo je wil
en
Voorbeeld: je hebt 8 bankbiljetten van 5 euro en je geeft 3 van die bankbiljetten uit. Hoeveel geld heb je dan nog over?
Nu zul je waarschijnlijk direct antwoorden dat je dan nog 25 euro over hebt, maar hoe reken je dat eigenlijk uit?
Er zijn in hoofdzaak twee manieren waarop je kunt redeneren. De eerste manier is dat je zegt: kijk, ik heb nog 8 − 3 = 5 biljetten over, dus dat is 5 × 5 = 25 euro. De tweede manier is dat je zegt: ik had eerst 8 × 5 = 40 euro en ik heb 3 × 5 = 15 euro uitgegeven, dus ik heb nog 40 − 15 = 25 euro over.
Uiteraard komen deze beide manieren op hetzelfde neer, oftewel, je hebt
of, zo je wil
Definieer eens wat volgens jou lang genoeg is? Twee minuten of zoiets? Ik heb niet het idee dat je veel moeite doet om na te denken.quote:15 heb ik lang genoeg tevergeefs geprobeerd, ik heb alleen geen idee hoe je zo iets doet zonder dat er een '=' is, want je kan nu niets vergelijken.
Bij een ongelijkheid als deze kun je in principe op dezelfde manier te werk gaan als bij een vergelijking: als je bij het linkerlid iets optelt of van het linkerlid iets aftrekt, dan moet je dat in het rechterlid ook doen (en omgekeerd, als je rechts iets optelt of aftrekt, dan moet je dat links ook doen). Verder kun je beide leden van een ongelijkheid met hetzelfde getal vermenigvuldigen, net als je dat bij een vergelijking kunt doen. Alleen moet je hier even opletten: als je beide leden van een ongelijkheid met een negatief getal vermenigvuldigt, dan klapt het ongelijkheidsteken om, dus > wordt dan < en < wordt dan >.
Je kunt deze opgave overigens ook beredeneren zonder de ongelijkheid formeel op te lossen. Links hebben we 4 − 3x, en dat moet groter zijn dan 13. Maar je weet dat als we iets positiefs aftrekken van 4, dat het dan alleen maar kleiner wordt, en dus zeker niet groter dan 13. Om van 4 naar 13 te komen moeten we er juist 9 bij optellen en aangezien optellen hetzelfde is als het aftrekken van het tegengestelde, moeten we dus −9 aftrekken van 4 om op 13 uit te komen:
Dat is het geval als die 3x in het linkerlid overeenkomt met −9, en dus x = −3 is. Maar nu moet de uitkomst van 4 − 3x groter zijn dan 13, en dus moeten we een nog negatiever getal van 4 aftrekken om op een resultaat groter dan 13 te komen, oftewel we moeten x < −3 hebben. Dit kun je gemakkelijk controleren. Als we bijvoorbeeld x = −4 nemen, dan krijgen we 4 − (−12) = 16, en dat is inderdaad groter dan 13.
[ Bericht 0% gewijzigd door Riparius op 25-05-2015 17:22:02 ]
quote:
[..]
Mag ik je, puur uit interesse, eens vragen waar de toelatingstest voor is?
Als je van 5 (3 - x) de haakjes wil 'uitwerken' dan moet je bedenken dat je eigenlijk een vermenigvuldiging maakt. Eigenlijk staat er: vijf keer de uitkomst van 'drie min x'.
Hierbij geldt, altijd, dat de vermenigvuldiging distributief is. Moeilijk woord, maar in een plaatje komt het hier op neer (hier wordt 2(p+7) uitgewerkt):
[ afbeelding ]
Jouw voorbeeld wordt dus 15 - 5x.
[..]
Niet veel anders dan het oplossen van een gelijkheid.
Eerst even kijken wat er eigenlijk aan ons gevraagd wordt: we hebben een rechte lijn met formule y = 4 - 3x, en een getal, namelijk 13. Wanneer komt de lijn boven de 13 uit?
De balansmethode werkt ook hier. Het enige verschil is, dat je ongelijkheid omdraait als je vermenigvuldigt met een negatief getal. Om dit te demonstreren, bekijken we twee verschillende manieren van de balansmethode.
4 - 3x > 13
Alle termen met x staan al links, dus de termen zonder x naar rechts. Links en rechts 4 aftrekken:
-3x > 9
Delen door -3 (nu moet dus het teken worden omgekeerd)
x < -3. Klaar.
Of:
4 - 3x > 13
Alle termen met x naar rechts, dus links en rechts 3x optellen:
4 > 13 + 3x
Alle termen zonder x naar links, dus links en rechts 13 aftrekken:
-9 > 3x
Links en rechts delen door 3:
-3 > x
He super allen, bedankt hoor! Echt.quote:
[..]
Vermenigvuldiging is distributief ten opzichte van optelling en aftrekking, dus je hebt in het algemeen
en
of, zo je wil
en
Voorbeeld: je hebt 8 bankbiljetten van 5 euro en je geeft 3 van die bankbiljetten uit. Hoeveel geld heb je dan nog over?
Nu zul je waarschijnlijk direct antwoorden dat je dan nog 25 euro over hebt, maar hoe reken je dat eigenlijk uit?
Er zijn in hoofdzaak twee manieren waarop je kunt redeneren. De eerste manier is dat je zegt: kijk, ik heb nog 8 − 3 = 5 biljetten over, dus dat is 5 × 5 = 25 euro. De tweede manier is dat je zegt: ik had eerst 8 × 5 = 40 euro en ik heb 3 × 5 = 15 euro uitgegeven, dus ik heb nog 40 − 15 = 25 euro over.
Uiteraard komen deze beide manieren op hetzelfde neer, oftewel, je hebt
of, zo je wil
[..]
Definieer eens wat volgens jou lang genoeg is? Twee minuten of zoiets? Ik heb niet het idee dat je veel moeite doet om na te denken.
Bij een ongelijkheid als deze kun je in principe op dezelfde manier te werk gaan als bij een vergelijking: als je bij het linkerlid iets optelt of van het linkerlid iets aftrekt, dan moet je dat in het rechterlid ook doen (en omgekeerd, als je rechts iets optelt of aftrekt, dan moet je dat links ook doen). Verder kun je beide leden van een ongelijkheid met hetzelfde getal vermenigvuldigen, net als je dat bij een vergelijking kunt doen. Alleen moet je hier even opletten: als je beide leden van een ongelijkheid met een negatief getal vermenigvuldigt, dan klapt het ongelijkheidsteken om, dus > wordt dan < en < wordt dan >.
Je kunt deze opgave overigens ook beredeneren zonder de ongelijkheid formeel op te lossen. Links hebben we 4 − 3x, en dat moet groter zijn dan 13. Maar je weet dat als we iets positiefs aftrekken van 4, dat het dan alleen maar kleiner wordt, en dus zeker niet groter dan 13. Om van 4 naar 13 te komen moeten we er juist 9 bij optellen en aangezien optellen hetzelfde is als het aftrekken van het tegengestelde, moeten we dus −9 aftrekken van 4 om op 13 uit te komen:
Dat is het geval als die 3x in het linkerlid overkomt met −9, en dus x = −3 is. Maar nu moet de uitkomst van 4 − 3x groter zijn dan 13, en dus moeten we een nog negatiever getal van 4 aftrekken om op een resultaat groter dan 13 te komen, oftewel we moeten x < −3 hebben. Dit kun je gemakkelijk controleren. Als we bijvoorbeeld x = −4 nemen, dan krijgen we 4 − (−12) = 16, en dat is inderdaad groter dan 13.
Ik heb sinds 1HAVO geen wiskunde gehad (nam pakket zonder wiskunde, echt debiel) en moet nu na 4 jaar dus alles ff opfrissen, ben alles helemaal vergeten.
@Janneke, de toets is voor een toelating voor opleiding Marketing!
Dank allen, ben weer een stuk verder nu. Super!
“Advertising is based on one thing, happiness. Happiness is the smell of a new car. It’s a billboard on the side of the road that screams reassurance that whatever you are doing is okay. You are okay.”
-Don Draper
-Don Draper
Ik heb nu nog veel van deze opgaven gemaakt, en ik snap ze ook daadwerkelijk. Hartelijk dank Riparius en Janneke141 
“Advertising is based on one thing, happiness. Happiness is the smell of a new car. It’s a billboard on the side of the road that screams reassurance that whatever you are doing is okay. You are okay.”
-Don Draper
-Don Draper
Okay!quote:
[..]
Heb ik net een vak over gehad! Dus stel je vraag maar, wie weet!
Het gaat me specifiek om 2a. We hebben een bewijs gezien voor de standaard vergelijkingen, dus du/dt = D*d^2u/dx^2. Nu hadden we *snap* de hint niet gelezen en dus inderdaad een transformatie toegepast met de gedachtekronkel dat f(x,t) = f(t).
Ergo zitten we nu een beetje vast aangezien we geen flauw benul hebben hoe we die ordering aantonen
Voor de liefhebber:
Op http://www.wereldwiskundeboeken.nl/ worden momenteel veel (oude, maar ook nieuwere) wiskundeboeken aangeboden voor een paar euro per stuk. Betreffen zowel Nederlandse, Duitse en Engelse boeken, die bij een antiquariaat stukken duurder zijn.
[ Bericht 1% gewijzigd door jungiaan op 27-05-2015 15:57:59 ]
Op http://www.wereldwiskundeboeken.nl/ worden momenteel veel (oude, maar ook nieuwere) wiskundeboeken aangeboden voor een paar euro per stuk. Betreffen zowel Nederlandse, Duitse en Engelse boeken, die bij een antiquariaat stukken duurder zijn.
[ Bericht 1% gewijzigd door jungiaan op 27-05-2015 15:57:59 ]
Voor kansrekening zit ik met de volgende opgave waar ik niet lekker uit kom, en ik hoop dat jullie mij erbij kunnen helpen.
Laat (X,Y) een gezamenlijke verdeling f(x,y) = 2x + 2y hebben voor 0<x<y<1. Vind de gezamenlijke verdeling voor (S,T) = (X,XY).
Met behulp van de pdf transformatiemethode kom ik uit op fs,t(s,t) = 2 + 2t*s^-2. Dit klopt, maar ik weet echt niet hoe ik de nieuwe domeinrestricties voor s en t op moet stellen.
Iemand?
Laat (X,Y) een gezamenlijke verdeling f(x,y) = 2x + 2y hebben voor 0<x<y<1. Vind de gezamenlijke verdeling voor (S,T) = (X,XY).
Met behulp van de pdf transformatiemethode kom ik uit op fs,t(s,t) = 2 + 2t*s^-2. Dit klopt, maar ik weet echt niet hoe ik de nieuwe domeinrestricties voor s en t op moet stellen.
Iemand?
Ik heb geen idee hoe ik het moet verwoorden, maar een lineaire vergelijking is een speciaal geval van een polynomiale vergelijking. Is er een klasse vergelijkingen waarvan polynomen een speciaal geval zijn? Ik kan wel dingen verzinnen, maar is er een canoniek antwoord?
Functies als een abstract idee. Dus f(x) = c?quote:
Ik heb geen idee hoe ik het moet verwoorden, maar een lineaire vergelijking is een speciaal geval van een polynomiale vergelijking. Is er een klasse vergelijkingen waarvan polynomen een speciaal geval zijn? Ik kan wel dingen verzinnen, maar is er een canoniek antwoord?
[ Bericht 0% gewijzigd door #ANONIEM op 29-05-2015 01:51:58 ]
Denk het niet. Ik denk nu aan polynomen verheven tot polynomen. Een polynoom heeft immers lineaire exponenten, dus een generalisatie extra zou polynomen verheffen tot polynomen.quote:
[..]
Functies als een abstract idee. Dus f(x) = c?
EDIT: Shit, dit zou wel erg logisch zijn gezien mijn doeleinde...
Oneindig vaak differentieerbare functies?quote:
Ik heb geen idee hoe ik het moet verwoorden, maar een lineaire vergelijking is een speciaal geval van een polynomiale vergelijking. Is er een klasse vergelijkingen waarvan polynomen een speciaal geval zijn? Ik kan wel dingen verzinnen, maar is er een canoniek antwoord?
Nice, nice, maar niet waarnaar ik op zoek ben. Polynomen verheven tot polynomen lijken voldoende. Ik wil aantonen dat iets altijd een bepaalde vorm heeft, dus zo specifiek mogelijk voor een zo sterk mogelijk resultaat.quote:
[..]
Oneindig vaak differentieerbare functies?
0 < x < y < 1 wordt 0 < s < t/s < 1quote:
Voor kansrekening zit ik met de volgende opgave waar ik niet lekker uit kom, en ik hoop dat jullie mij erbij kunnen helpen.
Laat (X,Y) een gezamenlijke verdeling f(x,y) = 2x + 2y hebben voor 0<x<y<1. Vind de gezamenlijke verdeling voor (S,T) = (X,XY).
Met behulp van de pdf transformatiemethode kom ik uit op fs,t(s,t) = 2 + 2t*s^-2. Dit klopt, maar ik weet echt niet hoe ik de nieuwe domeinrestricties voor s en t op moet stellen.
Iemand?
s < t/s geeft t > s2
t/s < 1 geeft t < s
dus 0 < s2 < t < s < 1
en inderdaad
Ik was hier best lang mee bezig omdat ik eerst t van s2 tot 1 had
Hallo,
Kan iemand mij met het volgende helpen:
Hoe (of met welke functie) kan ik schaalopbrengsten (constant/increasing/decreasing returns to scale) berekenen van een willekeurig bedrijf aan de hand van een jaarverslag?
Kan iemand mij met het volgende helpen:
Hoe (of met welke functie) kan ik schaalopbrengsten (constant/increasing/decreasing returns to scale) berekenen van een willekeurig bedrijf aan de hand van een jaarverslag?
Dit is het wiskunde topic hoor.quote:
Hallo,
Kan iemand mij met het volgende helpen:
Hoe (of met welke functie) kan ik schaalopbrengsten (constant/increasing/decreasing returns to scale) berekenen van een willekeurig bedrijf aan de hand van een jaarverslag?
Klopt maar wiskunde is hier een onderdeel van neem ik aan. Aangezien schaalopbrengsten een basisfunctie hebben (volgens mij) als de cobb douglas productie functie.quote:
Ik ben dus op zoek naar alfa, béta, L en K in jaarverslagen.... en dan komt wiskunde hierbij kijken..
Ik heb sowieso iets wiskundigs nodig om de returns to scale van een bedrijf aan de hand van jaarverslagen te kunnen berekenen, maar ik weet niet in hoeverre de cobb douglas functie juist is hiervoor?
[ Bericht 35% gewijzigd door RustCohle op 29-05-2015 20:13:46 ]
Ik kom niet helemaal uit opgave 1. Er wordt gevraagd om een expliciete oplosing w te construeren, dat is me gelukt.
Althans ik heb gevonden w = w(|x|) = -a|x|^2 + a, a in R en a = -1/(2d)
Inderdaad zien we dat voor |x| = 1 geldt w(|x|) = 0 (boundary condition) en voor de Laplace operator krijgen we:
en aangezien -a*2d = 1 verkrijgen we a = -1/(2d).
Enfin. Nu wordt er gevraagd om met 'multiples of w' aan te tonen dat: max |u| < C*Mf, ik snap niet helemaal hoe dat werkt. Wel hebben we een comparison principle gehad:
Even voor de structuur, voor u geldt:
voor c*w geldt, c > 0:
Als nu geldt dat f =< c op het domein en 0 =< 0 (triviaal waar) dan:
u =< c*w op het hele domein.
Nu geldt dat f < Mf dus als we c = Mf kiezen dan volgt:
u < Mf*g < Mf/(2d)
Mijn probleem is nu hoe ik dit vertaal naar de absoluutstrepen. Any tips?
[ Bericht 0% gewijzigd door #ANONIEM op 30-05-2015 18:28:02 ]
Super, bedankt voor de moeitequote:
[..]
0 < x < y < 1 wordt 0 < s < t/s < 1
s < t/s geeft t > s2
t/s < 1 geeft t < s
dus 0 < s2 < t < s < 1
en inderdaad
Ik was hier best lang mee bezig omdat ik eerst t van s2 tot 1 had
Jouw probleem is dat je niet weet welke formule je moet gebruiken voor je economische analyse, dat is vooral een economieprobleem. Met slechts de gegevens uit jaarverslagen zou je kunnen kijken hoe de totale kosten veranderen als de totale afzet verandert (i.e. nemen de kosten met een kleiner percentage toe dan de afzet, dan zijn er mogelijk economies of scale).quote:
[..]
Klopt maar wiskunde is hier een onderdeel van neem ik aan. Aangezien schaalopbrengsten een basisfunctie hebben (volgens mij) als de cobb douglas productie functie.
Antwoord voor diegenen die het boeit, je kunt het argument omdraaien. Kies nu w = -Mf, dan volgt dat u > -Mf/2d (Comparison principe)quote:
[ afbeelding ]
Ik kom niet helemaal uit opgave 1. Er wordt gevraagd om een expliciete oplosing w te construeren, dat is me gelukt.
Althans ik heb gevonden w = w(|x|) = -a|x|^2 + a, a in R en a = -1/(2d)
Inderdaad zien we dat voor |x| = 1 geldt w(|x|) = 0 (boundary condition) en voor de Laplace operator krijgen we:
en aangezien -a*2d = 1 verkrijgen we a = -1/(2d).
Enfin. Nu wordt er gevraagd om met 'multiples of w' aan te tonen dat: max |u| < C*Mf, ik snap niet helemaal hoe dat werkt. Wel hebben we een comparison principle gehad:
Even voor de structuur, voor u geldt:
voor c*w geldt, c > 0:
Als nu geldt dat f =< c op het domein en 0 =< 0 (triviaal waar) dan:
u =< c*w op het hele domein.
Nu geldt dat f < Mf dus als we c = Mf kiezen dan volgt:
u < Mf*g < Mf/(2d)
Mijn probleem is nu hoe ik dit vertaal naar de absoluutstrepen. Any tips?
En met waar ik al was krijg je dus dat max |u| < Mf/2d
Dat wilde ik zeggen maar leek me te obvious.quote:
[..]
Antwoord voor diegenen die het boeit, je kunt het argument omdraaien. Kies nu w = -Mf, dan volgt dat u > -Mf/2d (Comparison principe)
En met waar ik al was krijg je dus dat max |u| < Mf/2d
(en had niet helemaal gelezen)en ik wist niet of ik nou - u moest doen of - f en toen gaf ik op
Ja sorryquote:
[..]
Dat wilde ik zeggen maar leek me te obvious.
en ik wist niet of ik nou - u moest doen of - f en toen gaf ik op
normaal zie ik die geintjes altijd wel maar nu een keertje niet.
u onveranderd laten en c*w = -Mf*wquote:
[..]
Dat wilde ik zeggen maar leek me te obvious.
en ik wist niet of ik nou - u moest doen of - f en toen gaf ik op
Kut, toch nog verkeerd opgeschreven
Nais woensdag is de deadline dus kan nog terug vragen
[ Bericht 3% gewijzigd door #ANONIEM op 02-06-2015 02:45:07 ]
Nog een vraagje over kansrekening.
Zij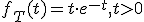
een continue stochast. Zij U een uniform verdeelde stochast op ![[0,1]](https://forum.fok.nl/lib/mimetex.cgi?%5B0%2C1%5D)
, onafhankelijk van T. Wat is de verdeling van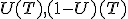 
. Ik zie hem alleen totaal niet. 
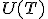moet nog wel lukken, maar hoe ik die laatste moet doen is mij niet duidelijk. Zou iemand mij een hint kunnen geven?
Zij
1 - U is ook uniform verdeeldquote:
Nog een vraagje over kansrekening.
Zij
Nee 1 - U heeft dezelfde verdeling als Uquote:
[..]
Metvoor 0<u<1 en 1 elders?
Edit: laat maar, dat lijkt me tamelijk onzinnig :p
Je kan laten zien dat P (1 - U ≤ x ) = x = P ( U ≤ x ) voor x in [0,1]
Dag lieve mensen 
De volgende vraag probeer ik op te lossen;
Van een bedrijf zijn de volgende omzet gegevens bekend:
2008 Januari 375
Februari 390
Maart 408
April 427
Mei 464
Juni 488
Juli 619
augustus 644
september 573
Oktober 542
november 457
december 385
2009 Januari 423
Februari 439
Maart 458
April 478
Mei 519
Echter kom ik er niet achter wat het gecentreerde voortschrijdend gemiddelde van 619 is.
Dit heb ik zelf uitgewerkt
ik weet dat ik over een beroerd handschrift beschik
De volgende vraag probeer ik op te lossen;
Van een bedrijf zijn de volgende omzet gegevens bekend:
2008 Januari 375
Februari 390
Maart 408
April 427
Mei 464
Juni 488
Juli 619
augustus 644
september 573
Oktober 542
november 457
december 385
2009 Januari 423
Februari 439
Maart 458
April 478
Mei 519
Echter kom ik er niet achter wat het gecentreerde voortschrijdend gemiddelde van 619 is.
Dit heb ik zelf uitgewerkt
ik weet dat ik over een beroerd handschrift beschik
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Wat lukt er niet danquote:
Dag lieve mensen
De volgende vraag probeer ik op te lossen;
Van een bedrijf zijn de volgende omzet gegevens bekend:
2008 Januari 375
Februari 390
Maart 408
April 427
Mei 464
Juni 488
Juli 619
augustus 644
september 573
Oktober 542
november 457
december 385
2009 Januari 423
Februari 439
Maart 458
April 478
Mei 519
Echter kom ik er niet achter wat het gecentreerde voortschrijdend gemiddelde van 619 is.
Dit heb ik zelf uitgewerkt
[ afbeelding ]
ik weet dat ik over een beroerd handschrift beschik
567.375 lijkt me
Daar kom ik ook op uit. Maar volgens oefententamen is het een van deze antwoordenquote:
[..]
Wat lukt er niet dan
567.375 lijkt me
Bepaal voor juli 2008 het gecentreerde voortschrijdende gemiddelde
a. 480
b. 481
c. 483
En het antwoord is A
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Het antwoord is C (ik heb de vraag gegoogled)quote:
[..]
Daar kom ik ook op uit. Maar volgens oefententamen is het een van deze antwoorden
Bepaal voor juli 2008 het gecentreerde voortschrijdende gemiddelde
a. 480
b. 481
c. 483
En het antwoord is A
Je moet blokken van lengte 12 gebruiken, niet van lengte 4
dus je krijgt
(375 + ... + 385 ) / 12 = 481
(390 + ... + 423 ) / 12 = 485
(481 + 485) / 2 = 483
Duidelijkquote:
[..]
Nee 1 - U heeft dezelfde verdeling als U
Je kan laten zien dat P (1 - U ≤ x ) = x = P ( U ≤ x ) voor x in [0,1]
Dus omdat (1-U) ~ U(0,1), kan ik schrijven dat (U(T),(1-U)(T))=(U(T),U(T)). Maar om die uit te rekenen, is het dan correct om te zeggen dat de verdeling van (U(T),U(T)) wordt gegeven door U(T)^2?
Oh ik dacht dat je U(T) en (1-U)(T) apart moest bepalenquote:
[..]
Duidelijk
Ik denk niet dat (U(T),(1-U)(T))=(U(T),U(T)) als verdeling omdat U en 1 - U niet independent zijn
Even kijken
