SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d


Weet het verder ook niet helaasquote:Op woensdag 3 juni 2015 19:40 schreef Holograph het volgende:
Nog een vraagje over kansrekening.
Zijeen continue stochast. Zij U een uniform verdeelde stochast op
, onafhankelijk van T. Wat is de verdeling van
. Ik zie hem alleen totaal niet.
moet nog wel lukken, maar hoe ik die laatste moet doen is mij niet duidelijk. Zou iemand mij een hint kunnen geven?
Regel van Bayesquote:Op donderdag 4 juni 2015 21:43 schreef Trias19 het volgende:
Dag iedereen,
Kan er iemand mij aub helpen met deze oefening? Het gaat over de voorwaardelijke kans en het lukt mij maar niet om dit op te lossen. Kan ik het ook oplossen met een boomdiagram?
Een psychotherapeut behandelt mensen met neurotische stoornissen meestal
(80%) met gesprekstherapie, terwijl voor psychotische stoornissen vaker een
combinatie van gedragstherapie en medicatie (70%) wordt toegepast. Indien
voor een bepaalde stoornis niet wordt gekozen voor de ene therapie, dan wordt
de andere toegepast. Stel dat 60% van de cliënten van deze psychotherapeut
worden behandeld voor een neurotische stoornis en 40% voor een psychotische
stoornis.
a) Als je nu weet dat de therapeut gesprekstherapie geeft aan een bepaalde cliënt,
hoe groot is dan de kans dat die lijdt aan een psychotische stoornis?
b) Stel dat je van 3 cliënten weet dat die gesprekstherapie krijgen, hoe groot is dan
de kans dat ze alle drie aan een psychose lijden?
Hier heb ik de gegevens opgesomt:
NS gespreksth =80%
PS gedragst & Med = 70%
NS = 60%
PS = 40%
[ Bericht 1% gewijzigd door Anoonumos op 04-06-2015 23:52:00 ]


Wilt er aub iemand mij zeggen of ik het juist oplos?
GT=gesprekstherapie, PS= psychotische stoornissen, NS = neurotische stoornis
Oplossing voor de eerste vraag : P(PS\GT) = (0,8* 0,4) / (0.8*0.4) + (0.3*0.6) = 0,64
Stoornissen:
NS= 0.6%
-GT =0.8%
-Niet GT = 0.2%
PS= 0.4%
-Gedrags & Med = 0.7%
- Niet Gedrags & Med = 0.3%
Hoe kan ik bij de vraag 2 die 3 cliënten selecteren? Hoe moet ik het opschrijven? P(..)
GT=gesprekstherapie, PS= psychotische stoornissen, NS = neurotische stoornis
Oplossing voor de eerste vraag : P(PS\GT) = (0,8* 0,4) / (0.8*0.4) + (0.3*0.6) = 0,64
Stoornissen:
NS= 0.6%
-GT =0.8%
-Niet GT = 0.2%
PS= 0.4%
-Gedrags & Med = 0.7%
- Niet Gedrags & Med = 0.3%
Hoe kan ik bij de vraag 2 die 3 cliënten selecteren? Hoe moet ik het opschrijven? P(..)


Waar je 0.8 het moet 0.3 staan (2 keer) en waar je 0.3 hebt moet 0.8 staanquote:Op vrijdag 5 juni 2015 22:41 schreef Trias19 het volgende:
Wilt er aub iemand mij zeggen of ik het juist oplos?
GT=gesprekstherapie, PS= psychotische stoornissen, NS = neurotische stoornis
Oplossing voor de eerste vraag : P(PS\GT) = (0,8* 0,4) / (0.8*0.4) + (0.3*0.6) = 0,64
P (PS | GT) = P (GT | PS) P (PS) / (P (GT | PS) P (PS) + P (GT | NS) P (NS)) = 0.3 * 0.4 / (0.3 * 0.4 + 0.8 * 0.6) = 0.2
Antwoord op B is dan het product van 3 keer de kans van antwoord A dus 0.23 = 0.008


Nee, dit had je gemakkelijk zelf kunnen inzien door jouw vermeende primitieve functie te differentiëren.quote:Op zaterdag 6 juni 2015 13:22 schreef rareziekte het volgende:
de primitieve van 2(1-x)^-(1/2) geeft -4(1-x)^(1/2) + c
is het niet 4?
Door juist te primitiveren. Tip: merk op dat er een coëfficiënt -1 voor x staat en ga dan nadenken over de kettingregel der differentiaalrekening.quote:


Ok, had die -x over het hoofd gezien, dankquote:Op zaterdag 6 juni 2015 14:16 schreef jungiaan het volgende:
[..]
Nee, dit had je gemakkelijk zelf kunnen inzien door jouw vermeende primitieve functie te differentiëren.
[..]
Door juist te primitiveren. Tip: merk op dat er een coëfficiënt -1 voor x staat en ga dan nadenken over de kettingregel der differentiaalrekening.


Bedankt, nu snap ik wat ik fout deed...quote:Op vrijdag 5 juni 2015 22:58 schreef Anoonumos het volgende:
[..]
Waar je 0.8 het moet 0.3 staan (2 keer) en waar je 0.3 hebt moet 0.8 staan
P (PS | GT) = P (GT | PS) P (PS) / (P (GT | PS) P (PS) + P (GT | NS) P (NS)) = 0.3 * 0.4 / (0.3 * 0.4 + 0.8 * 0.6) = 0.2
Antwoord op B is dan het product van 3 keer de kans van antwoord A dus 0.23 = 0.008


Ik probeer te bewijzen f(x)=1/sqrt(1-x2) geeft F(x)=arcsin(x)
Substitutie van x=sin(x) in f(x)dx geeft
1/sqrt(1-sin^2(t))dsin(t) = cos(t)/sqrt(1-sin^2(t))dt
Het boek neemt de noemer als sqrt cos^2(t)
Hoezo is 1-sin^2(t)=cos^2(t) ? Met de verdubbelingsformules kom ik er niet uit
[ Bericht 0% gewijzigd door rareziekte op 09-06-2015 19:00:31 ]
Substitutie van x=sin(x) in f(x)dx geeft
1/sqrt(1-sin^2(t))dsin(t) = cos(t)/sqrt(1-sin^2(t))dt
Het boek neemt de noemer als sqrt cos^2(t)
Hoezo is 1-sin^2(t)=cos^2(t) ? Met de verdubbelingsformules kom ik er niet uit
[ Bericht 0% gewijzigd door rareziekte op 09-06-2015 19:00:31 ]


cos^2(t) + sin^2(t) = 1 (eenheidscirkel en Pythagoras)quote:Op dinsdag 9 juni 2015 17:04 schreef rareziekte het volgende:
Ik probeer te bewijzen f(x)=1/sqrt(1-x2) geeft F(x)=arcsin(x)
Substitutie van x=sin(x) in f(x)dx geeft
1/sqrt(1-sin^2(t))dsin(t) = cos(t)/sqrt(1-sin^2(t))dt
Het boek neemt de noemer als sqrt cos^2(t)
Hoezo is 1-sin^(t)=cos^2(t) ? Met de verdubbelingsformules kom ik er niet uit
Dus het volgt direct dat 1 - sin^2(t)=cos^2(t).
Aangenomen dat je dat bedoelt (de typo).


Ah, dank. Stom. Jup, dat bedoelde ikquote:Op dinsdag 9 juni 2015 17:20 schreef Arthos het volgende:
[..]
cos^2(t) + sin^2(t) = 1 (eenheidscirkel en Pythagoras)
Dus het volgt direct dat 1 - sin^2(t)=cos^2(t).
Aangenomen dat je dat bedoelt (de typo).
Bij het berekenen van de oplossingen van een functie f(x) kom ik uiteindelijk uit op
-2x=-(1/2)pi + k2pi v 6x=-(1/2)pi+k2pi
Vervolgens geeft het boek
x= (1/4)pi + kpi v x=-(1/12)pi+k(1/3)pi
Waarom is het niet (1/4)pi - kpi?


k ranged over alle gehele getallen. In die context, is -kpi hetzelfde als +kpi.quote:Op dinsdag 9 juni 2015 19:10 schreef rareziekte het volgende:
[..]
Ah, dank. Stom. Jup, dat bedoelde ik
Bij het berekenen van de oplossingen van een functie f(x) kom ik uiteindelijk uit op
-2x=-(1/2)pi + k2pi v 6x=-(1/2)pi+k2pi
Vervolgens geeft het boek
x= (1/4)pi + kpi v x=-(1/12)pi+k(1/3)pi
Waarom is het niet (1/4)pi - kpi?
Immers, als x= (1/4)pi + kpi voor k=n, dan x= (1/4)pi - kpi voor k=-n. Als n een geheel getal is, is -n ook een geheel getal.
EDIT: Wauw, ik wist niet dat je kon TeXen hier. Maakt het leven makkelijker. Dus:
[ Bericht 8% gewijzigd door Arthos op 09-06-2015 21:58:48 ]


Als je vervolgens de oplossingen van die functie op domein [0,3pi] wilt geven neem je dusquote:Op dinsdag 9 juni 2015 19:29 schreef Arthos het volgende:
[..]
k ranged over alle gehele getallen. In die context, is -kpi hetzelfde als +kpi.
Immers, als x= (1/4)pi + kpi voor k=n, dan x= (1/4)pi - kpi voor k=-n. Als n een geheel getal is, is -n ook een geheel getal.
EDIT: Wauw, ik wist niet dat je kon TeXen hier. Maakt het leven makkelijker. Dus:
x=1/4 pi v x= (1/4pi) - -2*pi= 2 (1/4)pi ? Dan snap ik dat -kpi hier gelijk is aan +kpi
Bedankt.


Ik heb het idee dat je het nog niet begrijpt. Om te beginnen heeft een functie geen oplossingen. Je bedoelt waarschijnlijk de nulpunten van een functie f: [0, 3π] → R oftewel de oplossingen van een vergelijking f(x) = 0 op het interval [0, 3π]. Maar dan zijn er meer dan twee nulpunten van je functie f resp. oplossingen van je vergelijking f(x) = 0 op het interval [0, 3π].quote:Op woensdag 10 juni 2015 10:37 schreef rareziekte het volgende:
[..]
Als je vervolgens de oplossingen van die functie op domein [0,3pi] wilt geven neem je dus
x=1/4 pi v x= (1/4pi) - -2*pi= 2 (1/4)pi ? Dan snap ik dat -kpi hier gelijk is aan +kpi
Bedankt.


Kan iemand me helpen met de volgende opgave? X,Y onafhankelijk en standaard normaal verdeeld (dus gemiddelde 0, standaarddeviatie 1). We zoeken de kansdichtheid van 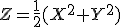 .
.
Als ik erop Google vind ik dingen over dat dit Chikwadraat verdeeld is ofzoiets, maar dat hebben we nog niet gehad. Hoe bepaal ik de kansdichtheid van Z? Alvast bedankt.
Verder loop ik vast op de marginale kansdichtheid fx van X bepalen, als X en Y gemeenschappelijk verdeeld zijn met:
![f_{X,Y}(x,y) := \frac{1}{2\pi \sqrt{1-\rho^2}} \cdot \exp\left[ - \frac{1}{2(1-\rho^2)}\left( x^2 + y^2 - 2\rho xy \right) \right]](https://forum.fok.nl/lib/mimetex.cgi?%20f_%7BX%2CY%7D%28x%2Cy%29%20%3A%3D%20%5Cfrac%7B1%7D%7B2%5Cpi%20%5Csqrt%7B1-%5Crho%5E2%7D%7D%20%5Ccdot%20%5Cexp%5Cleft%5B%20-%20%5Cfrac%7B1%7D%7B2%281-%5Crho%5E2%29%7D%5Cleft%28%20x%5E2%20%2B%20y%5E2%20-%202%5Crho%20xy%20%5Cright%29%20%5Cright%5D%20)
Dit komt neer op dit integreren over alle y. Ik krijg de volgende substitutie als hint:
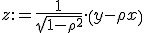
Als iemand me kan helpen met beide vragen, heel erg bedankt! Ik ben zo klaar met deze inleveropgave dat die integraal me niet lukt en bij die normale verdeling heb ik niet echt een idee hoe 't moet, vooral niet hoe ik moet beginnen.
[ Bericht 67% gewijzigd door Aardappeltaart op 10-06-2015 19:37:34 ]
Als ik erop Google vind ik dingen over dat dit Chikwadraat verdeeld is ofzoiets, maar dat hebben we nog niet gehad. Hoe bepaal ik de kansdichtheid van Z? Alvast bedankt.
Verder loop ik vast op de marginale kansdichtheid fx van X bepalen, als X en Y gemeenschappelijk verdeeld zijn met:
Dit komt neer op dit integreren over alle y. Ik krijg de volgende substitutie als hint:
Als iemand me kan helpen met beide vragen, heel erg bedankt! Ik ben zo klaar met deze inleveropgave dat die integraal me niet lukt en bij die normale verdeling heb ik niet echt een idee hoe 't moet, vooral niet hoe ik moet beginnen.
[ Bericht 67% gewijzigd door Aardappeltaart op 10-06-2015 19:37:34 ]


Sorry, ik bedoel een vergelijking in de vorm van cos(A)=cos(B), dat is geen functie idd. Er zijn dan twee oplossingen, maar ik wilde eigenlijk alleen zeker weten of bovenstaande oplossingen goed waren.quote:Op woensdag 10 juni 2015 17:17 schreef Riparius het volgende:
[..]
Ik heb het idee dat je het nog niet begrijpt. Om te beginnen heeft een functie geen oplossingen. Je bedoelt waarschijnlijk de nulpunten van een functie f: [0, 3π] → R oftewel de oplossingen van een vergelijking f(x) = 0 op het interval [0, 3π]. Maar dan zijn er meer dan twee nulpunten van je functie f resp. oplossingen van je vergelijking f(x) = 0 op het interval [0, 3π].


Als je wil weten of een bepaalde uitwerking of oplossing correct is, dan moet je wel het volledige vraagstuk posten, anders is je vraag onmogelijk te beantwoorden.quote:Op woensdag 10 juni 2015 20:33 schreef rareziekte het volgende:
[..]
Sorry, ik bedoel een vergelijking in de vorm van cos(A)=cos(B), dat is geen functie idd. Er zijn dan twee oplossingen, maar ik wilde eigenlijk alleen zeker weten of bovenstaande oplossingen goed waren.
Het is ook niet juist dat een vergelijking van de gedaante cos(A) = cos(B), waarin A en of B dan uitdrukkingen zijn in een onbekende, steeds twee oplossingen zou hebben. In het algemeen geldt wel het volgende:
Twee cosinussen zijn gelijk als de (rotatie)hoeken óf gelijk zijn óf tegengesteld, afgezien van een geheel veelvoud van 2π, dus
cos α = cos β ⇔ α = β + k·2π ∨ α = −β + k·2π, k ∈ Z
En ook geldt:
Twee sinussen zijn gelijk als de (rotatie)hoeken óf gelijk zijn óf supplementair, afgezien van een geheel veelvoud van 2π, dus
sin α = sin β ⇔ α = β + k·2π ∨ α = π − β + k·2π, k ∈ Z


Overigens is de tweede vraag ondertussen gelukt. Die met die som van kwadraten van normale verdeling helaas niet. Kan iemand helpen? Heel erg bedankt!!


Als je geen chi-squared verdeling hebt gehad wordt het lastig ben ik bangquote:Op donderdag 11 juni 2015 17:00 schreef Aardappeltaart het volgende:
Overigens is de tweede vraag ondertussen gelukt. Die met die som van kwadraten van normale verdeling helaas niet. Kan iemand helpen? Heel erg bedankt!!
Ze zullen niet verwachten dat je het zelf kan afleiden


Klopt dit qua conventies?:
• Als a = onsplitsbaar/atomair/geen verzameling (bijv a = integer 5), dan schrijf je a ∊ b
• Als a = (deel)verzameling (bijv. a = {2,4,9}), dan schrijf je a ⊆ b
• Als a = onsplitsbaar/atomair/geen verzameling (bijv a = integer 5), dan schrijf je a ∊ b
• Als a = (deel)verzameling (bijv. a = {2,4,9}), dan schrijf je a ⊆ b
graag op anoniem


Het verschil is idd of je het over een element hebt of over een deelverzameling.quote:Op donderdag 11 juni 2015 18:27 schreef topdeck het volgende:
Klopt dit qua conventies?:
• Als a = onsplitsbaar/atomair/geen verzameling (bijv a = integer 5), dan schrijf je a ∊ b
• Als a = (deel)verzameling (bijv. a = {2,4,9}), dan schrijf je a ⊆ b
Als
schrijven we:
en


Om te beginnen: ik ben tegen het gebruik van de notaties sin−1 en cos−1 voor arcsin resp. arccos, dus zal ik deze laatste notaties gebruiken. Als je wil weten waarom, dan moet je dit maar eens lezen.quote:Op donderdag 11 juni 2015 13:38 schreef GeorgeArArMartin het volgende:
[ afbeelding ]
Hoe kun je een dergelijke omschrijving uitvoeren?
Laten we zeggen dat
Dit impliceert dat
waarbij
Laten we tevens zeggen dat
Dit impliceert dat
waarbij
Goed, nu hebben we dus
waarbij uit (3) 0 ≤ α ≤ ½π en tevens (6) 0 ≤ β ≤ ½π volgt dat
Aangezien het domein van de arccos functie het interval [−1, 1] is en het bereik het interval [0, π] en deze functie strict monotoon dalend is, betekent dit dat er een unieke x ∈ [−1, 1] is zodanig dat
mits α ≥ β zodat α − β ≥ 0. Dan is ook
Om nu cos(α − β) en daarmee x te bepalen, maken we gebruik van de identiteit
Welnu, (2) sin α = 4/5 en (5) cos β = 12/13 kennen we al, dus nu moeten we alleen cos α en sin β nog bepalen. Dit is eenvoudig met behulp van de identiteit
Aangezien (3) 0 ≤ α ≤ ½π en tevens (6) 0 ≤ β ≤ ½π weten we dat cos α en sin β beiden niet negatief moeten zijn, en met behulp van (12) vinden we dan
en
Merk nu op dat sin α > sin β zodat inderdaad α > β waarmee α − β op het interval [0, ½π] ligt en daarmee binnen het bereik van de arccos functie.
Invullen van (2), (5), (13) en (14) in (11) geeft nu
en dus hebben we
zodat uit (7) en (16) inderdaad volgt dat
QED
Toegift: in de waarden cos α = 3/5, sin α = 4/5 en cos β = 12/13, sin β = 5/13 herkennen we de Pythagoreïsche tripletten (3, 4, 5) en (5, 12, 13). Nu is het zo dat het product van twee sommen van twee kwadraten van twee positieve gehele getallen steeds weer is te schrijven als een som van twee kwadraten van twee positieve gehele getallen, en wel op twee verschillende manieren, want we hebben
Vullen we nu in (18) en (19) a = 3, b = 4, c = 5, d = 12 in, dan krijgen we uit de Pythagoreïsche tripletten (3, 4, 5) en (5, 12, 13) twee nieuwe Pythagoreïsche tripletten (33, 56, 65) en (16, 63, 65), en nu herken je in het eerste van deze nieuwe tripletten de teller 56 en de noemer 65 van het quotiënt 56/65 in (17). De verklaring is dat de beide scherpe hoeken van een rechthoekige driehoek waarvan de zijden zich verhouden als (33, 56, 65) elk gelijk zijn aan een som resp. een verschil van twee scherpe hoeken van de rechthoekige driehoeken waarvan de zijden zich verhouden als (3, 4, 5) en (5, 12, 13), en datzelfde geldt voor een rechthoekige driehoek waarvan de zijden zich verhouden als (16, 63, 65).
Merk nog op dat we bij bovenstaande herleiding wegens (8) −½π ≤ α − β ≤ ½π ook hadden kunnen kiezen voor een herleiding tot een arcus sinus zonder daarbij te hoeven nagaan of werd voldaan aan α − β ≥ 0 aangezien de arcsin functie het interval [−½π, ½π] als bereik heeft. Daarvoor maken we gebruik van de identiteit voor sin(α − β) en dan vinden we sin(α − β) = 33/65 en dus
Hier zie je in de teller van het quotiënt 33/65 het getal 33 uit het Pythagoreïsche triplet (33, 56, 65) tevoorschijn komen, en dat is ook begrijpelijk, want uit (12) cos2φ + sin2φ = 1 volgt voor 0 ≤ φ ≤ ½π en als we cos φ = x stellen dat sin φ = √(1 − x2) en daarmee arccos(x) = arcsin(√(1 − x2)) voor 0 ≤ x ≤ 1. Zodoende is dus arccos(56/65) = arcsin(33/65) aangezien (56/65)2 + (33/65)2 = 1.
[ Bericht 0% gewijzigd door Riparius op 12-06-2015 05:18:06 ]


Wat is een handig geheugensteuntje om te onthouden:
sin(0π) = 0
sin(⅙π) = ½√1 = ½
sin(¼π) = ½√2
sin(⅓π) = ½√3
En nog een vraag: hoe kan je gemakkelijk inzien dat x = k*2π, x = ⅔π + k*2π, en x = -⅔π + k*2π herleid kunnen worden tot x = k*⅔π?
[ Bericht 0% gewijzigd door netchip op 11-06-2015 22:36:15 (typo) ]
sin(0π) = 0
sin(⅙π) = ½√1 = ½
sin(¼π) = ½√2
sin(⅓π) = ½√3
En nog een vraag: hoe kan je gemakkelijk inzien dat x = k*2π, x = ⅔π + k*2π, en x = -⅔π + k*2π herleid kunnen worden tot x = k*⅔π?
[ Bericht 0% gewijzigd door netchip op 11-06-2015 22:36:15 (typo) ]


Het is eenvoudiger om dit te onthouden als je de hoeken in graden uitdrukt, namelijk 0, 30, 45, 60 en 90 graden. Uiteraard moet je dan ook nog weten dat een gestrekte hoek, oftewel 180 graden, overeenkomt met π radialen. Een eenvoudig ezelsbruggetje: de sinus van de genoemde hoeken is nu achtereenvolgensquote:Op donderdag 11 juni 2015 22:07 schreef netchip het volgende:
Wat is een handig geheigensteuntje om te onthouden:
sin(0π) = 0
sin(⅙π) = ½√1 = ½
sin(¼π) = ½√2
sin(⅓π) = ½√3
½√0, ½√1, ½√2, ½√3, ½√4
en dus
0, ½, ½√2, ½√3, 1
en de cosinus van de genoemde hoeken krijg je achtereenvolgens door hetzelfde rijtje van rechts naar links op te schrijven.
Schets even een eenheidscirkel in een cartesisch assenstelsel en geef op de eenheidscirkel het punt aan dat je krijgt door het startpunt met coördinaten (1; 0) om de oorsprong te roteren over een hoek van +⅔π rad (positieve zin, dus tegen de klok in) en geef op de eenheidscirkel tevens het punt aan dat je krijgt door het startpunt met coördinaten (1; 0) om de oorsprong te roteren over een hoek van -⅔π rad (negatieve zin, dus met de klok mee).quote:En nog een vraag: hoe kan je gemakkelijk inzien dat x = k*2π, x = ⅔π + k*2π, en x = -⅔π + k*2π herleid kunnen worden tot x = k*⅔π?


Dat is inderdaad handig! Zo lukt het me wel om het te onthouden.quote:Op donderdag 11 juni 2015 22:32 schreef Riparius het volgende:
[..]
Het is eenvoudiger om dit te onthouden als je de hoeken in graden uitdrukt, namelijk 0, 30, 45, 60 en 90 graden. Uiteraard moet je dan ook nog weten dat een gestrekte hoek, oftewel 180 graden, overeenkomt met π radialen. Een eenvoudig ezelsbruggetje: de sinus van de genoemde hoeken is nu achtereenvolgens
½√0, ½√1, ½√2, ½√3, ½√4
en dus
0, ½, ½√2, ½√3, 1
en de cosinus van de genoemde hoeken krijg je achtereenvolgens door hetzelfde rijtje van rechts naar links op te schrijven.
Ja, dat zag ik later ook in mijn schets, maar dat moet je dan wel even net zien. Is er ook een manier om dit af te leiden uit de vergelijkingen voor x?quote:[..]
Schets even een eenheidscirkel in een cartesisch assenstelsel en geef op de eenheidscirkel het punt aan dat je krijgt door het startpunt met coördinaten (1; 0) om de oorsprong te roteren over een hoek van +⅔π rad (positieve zin, dus tegen de klok in) en geef op de eenheidscirkel tevens het punt aan dat je krijgt door het startpunt met coördinaten (1; 0) om de oorsprong te roteren over een hoek van -⅔π rad (negatieve zin, dus met de klok mee).


Je zou kunnen bedenken dat 3 · ⅔π = 2π, dan ben je er ook. De beeldpunten die we krijgen door het punt met coördinaten (1; 0) om de oorsprong te roteren over een hoek van +⅔π rad en over een hoek −⅔π rad hebben resp. de coördinaten (−½; ½√3) en (−½; −½√3). Los de vergelijking z3 = 1 maar eens op in C, zie je het verband?quote:Op donderdag 11 juni 2015 22:35 schreef netchip het volgende:
[..]
Dat is inderdaad handig! Zo lukt het me wel om het te onthouden.
[..]
Ja, dat zag ik later ook in mijn schets, maar dat moet je dan wel even net zien. Is er ook een manier om dit af te leiden uit de vergelijkingen voor x?


Het oplossen van vergelijkingen in C behandelen we aankomend jaar met wiskunde D, maar ik ga hier morgen zeker even naar kijken. Dan zie ik het verband misschien.quote:Op donderdag 11 juni 2015 22:43 schreef Riparius het volgende:
[..]
Je zou kunnen bedenken dat 3 · ⅔π = 2π, dan ben je er ook. De beeldpunten die we krijgen door het punt met coördinaten (1; 0) om de oorsprong te roteren over een hoek van +⅔π rad en over een hoek −⅔π rad hebben resp. de coördinaten (−½; ½√3) en (−½; −½√3). Los de vergelijking z3 = 1 maar eens op in C, zie je het verband?


Kent iemand een handig boek/pdf voor kegelsneden en analytische meetkunde? Ik heb het erg lang geleden gehad, maar het grootste deel is inmiddels weggezakt en ik vond het best een leuk onderdeel.


Ik kan je in ieder geval het Prisma Compendium Analytische meetkunde van C. van der Linden uit 1964 aanraden, waarin de vroegere stof van het middelbaar wordt behandeld. Dit boekje is niet meer nieuw te koop maar antiquarisch nog goed te vinden, bijvoorbeeld hier. Verder bijvoorbeeld dit Amerikaanse schoolboek van bijna een eeuw geleden. Oud, maar nog uitstekend leesbaar.quote:Op zaterdag 13 juni 2015 14:55 schreef GeorgeArArMartin het volgende:
Kent iemand een handig boek/pdf voor kegelsneden en analytische meetkunde? Ik heb het erg lang geleden gehad, maar het grootste deel is inmiddels weggezakt en ik vond het best een leuk onderdeel.


quote:Op zaterdag 13 juni 2015 20:02 schreef Riparius het volgende:
[..]
Ik kan je in ieder geval het Prisma Compendium Analytische meetkunde van C. van der Linden uit 1964 aanraden, waarin de vroegere stof van het middelbaar wordt behandeld. Dit boekje is niet meer nieuw te koop maar antiquarisch nog goed te vinden, bijvoorbeeld hier. Verder bijvoorbeeld dit Amerikaanse schoolboek van bijna een eeuw geleden. Oud, maar nog uitstekend leesbaar.
Opinion is the medium between knowledge and ignorance (Plato)


Kan iemand een goed boek/dictaat voor probability theory aanraden? Ik wil een beetje zelfstudie doen aangezien ik hier nooit vakken in heb gevolgd maar het zijdelings (uiteraard) wel tegenkom. Kan wel een dictaatje van een bachelorvak gebruiken, maar misschien hebben jullie een leuke tip?


Thanks! Ik probeer eerst het Amerikaans schoolboek uit, als ik het niveau aardig beheers zal ik het andere boek bestellen.quote:Op zaterdag 13 juni 2015 20:02 schreef Riparius het volgende:
[..]
Ik kan je in ieder geval het Prisma Compendium Analytische meetkunde van C. van der Linden uit 1964 aanraden, waarin de vroegere stof van het middelbaar wordt behandeld. Dit boekje is niet meer nieuw te koop maar antiquarisch nog goed te vinden, bijvoorbeeld hier. Verder bijvoorbeeld dit Amerikaanse schoolboek van bijna een eeuw geleden. Oud, maar nog uitstekend leesbaar.
Het komt ook voor in de D boeken van Getal en Ruimte, maar die moet ik binnenkort inleveren en als ik heel eerlijk ben, gaan ze er naar mijn mening niet diep genoeg op in.quote:Op zaterdag 13 juni 2015 20:09 schreef Janneke141 het volgende:
[..]Dat oude schoolboek, mooi! Die sla ik even op. Kegelsneden waren al geen examenstof meer toen ik examen deed, maar mijn docent was er nogal dol op dus deed er nog wel wat mee. Interessant.


Ik kwam laatst deze integraal tegen: 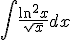
Ik dacht eraan om deze op te lossen d.m.v. partiële integratie.
u = ln2x
v' = 1/√x => v = 2√x
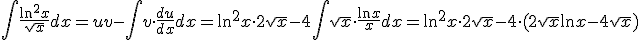
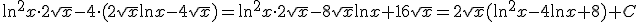
Klopt dit?
Ben ik zo op de goede weg? Ik zie niet helemaal hoe ik die laatste integraal zou moeten bepalen...
Edit: ik kan die √x en 1/x natuurlijk vereenvoudigen. Stom.
[ Bericht 6% gewijzigd door netchip op 16-06-2015 16:50:18 ]
Ik dacht eraan om deze op te lossen d.m.v. partiële integratie.
u = ln2x
v' = 1/√x => v = 2√x
Klopt dit?
Ben ik zo op de goede weg? Ik zie niet helemaal hoe ik die laatste integraal zou moeten bepalen...
Edit: ik kan die √x en 1/x natuurlijk vereenvoudigen. Stom.
[ Bericht 6% gewijzigd door netchip op 16-06-2015 16:50:18 ]


Weet iemand waar ik in de settings in m'n grafische rekenmachine kan uitzetten dat m'n rekenmachine op 0 decimalen afrond, nu rondt hij dus gewoon op hele getallen af. Erg hinderlijk, zelf al een kwartier gezocht maar kan 't niet vinden  Het gaat om een CASIO fx-9860GII
Het gaat om een CASIO fx-9860GII
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
-Harry Jekkers


Je kan 'm ook gewoon volledig resetten.quote:Op woensdag 17 juni 2015 16:21 schreef Nelvalhil het volgende:
Weet iemand waar ik in de settings in m'n grafische rekenmachine kan uitzetten dat m'n rekenmachine op 0 decimalen afrond, nu rondt hij dus gewoon op hele getallen af. Erg hinderlijk, zelf al een kwartier gezocht maar kan 't niet vindenHet gaat om een CASIO fx-9860GII


Het voordeel van een niet-grafisch rekenmachientje, de bediening is veel eenvoudiger.quote:Op woensdag 17 juni 2015 16:21 schreef Nelvalhil het volgende:
Weet iemand waar ik in de settings in m'n grafische rekenmachine kan uitzetten dat m'n rekenmachine op 0 decimalen afrond, nu rondt hij dus gewoon op hele getallen af. Erg hinderlijk, zelf al een kwartier gezocht maar kan 't niet vindenHet gaat om een CASIO fx-9860GII
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Option --> NUM --> RND uit mijn hoofd.quote:Op woensdag 17 juni 2015 16:21 schreef Nelvalhil het volgende:
Weet iemand waar ik in de settings in m'n grafische rekenmachine kan uitzetten dat m'n rekenmachine op 0 decimalen afrond, nu rondt hij dus gewoon op hele getallen af. Erg hinderlijk, zelf al een kwartier gezocht maar kan 't niet vindenHet gaat om een CASIO fx-9860GII
Daar moet die instelling staan.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Wat wordt er bedoeld met het monotoon gedrag bij een differentiaalvergelijking? Ik dacht altijd dat een functie dan een bepaald punt bereikt als x -> oneindig en begrensd wordt door een evenwichtsoplossing. Dus y(t) = a (dit is een evenwichtsoplossing) wanneer t-> oneindig, dan vertoont y(t) monotoon gedrag.


Wat is de beste manier om je voor te bereiden op een WO finance studie met weinig wiskundige voorkennis? Of afwachten tot ik de vakken heb en dan hard leren?


Heb het een tijd niet meer gedaan, dus het is een beetje weg. Het is een simpele:
wat nou bijv
0.05X + 0.02Y=0.03
Hoe bereken je X en Y uit?
Ik dacht eerst .03 naar links doen maar daarna ben ik het gewoon kwijt.
wat nou bijv
0.05X + 0.02Y=0.03
Hoe bereken je X en Y uit?
Ik dacht eerst .03 naar links doen maar daarna ben ik het gewoon kwijt.


Deze wordt altijd wel aangeraden voor wiskunde deficiënties weg te werken:quote:Op maandag 22 juni 2015 18:02 schreef dennis606 het volgende:
Wat is de beste manier om je voor te bereiden op een WO finance studie met weinig wiskundige voorkennis? Of afwachten tot ik de vakken heb en dan hard leren?
https://staff.fnwi.uva.nl/j.vandecraats/BasisboekWiskunde2HP.pdf
Volgens mij, als je twee onbekenden wilt oplossen heb je twee vergelijkingen nodig. Nu kan je weinig zinnigs zeggen over x en y. Misschien dat ik er naast zit hoor, want mijn wiskunde niveau is ook niet om over naar huis te schrijven.quote:Op maandag 22 juni 2015 20:47 schreef Doublepain het volgende:
Heb het een tijd niet meer gedaan, dus het is een beetje weg. Het is een simpele:
wat nou bijv
0.05X + 0.02Y=0.03
Hoe bereken je X en Y uit?
Ik dacht eerst .03 naar links doen maar daarna ben ik het gewoon kwijt.
Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game


Je kan X en Y niet uitrekenen uit één vergelijking, hiervoor heb je een (onafhankelijk) stelsel nodig. Je kan wel X uitdrukken in Y en andersom. Riparius of janneke zal wel een duidelijkere uitleg geven. Gaat het om een specifieke opgave?quote:Op maandag 22 juni 2015 20:47 schreef Doublepain het volgende:
Heb het een tijd niet meer gedaan, dus het is een beetje weg. Het is een simpele:
wat nou bijv
0.05X + 0.02Y=0.03
Hoe bereken je X en Y uit?
Ik dacht eerst .03 naar links doen maar daarna ben ik het gewoon kwijt.


je hebt inderdaad 2 vergelijkingen nodig om dat op te lossen. Nu zijn er oneindig veel antwoorden.quote:Op maandag 22 juni 2015 20:47 schreef Doublepain het volgende:
Heb het een tijd niet meer gedaan, dus het is een beetje weg. Het is een simpele:
wat nou bijv
0.05X + 0.02Y=0.03
Hoe bereken je X en Y uit?
Ik dacht eerst .03 naar links doen maar daarna ben ik het gewoon kwijt.
leef de leven


Bedankt! ik ga er mee aan de slagquote:Op maandag 22 juni 2015 21:20 schreef CapnIzzy het volgende:
[..]
Deze wordt altijd wel aangeraden voor wiskunde deficiënties weg te werken:
https://staff.fnwi.uva.nl/j.vandecraats/BasisboekWiskunde2HP.pdf
[..]
Volgens mij, als je twee onbekenden wilt oplossen heb je twee vergelijkingen nodig. Nu kan je weinig zinnigs zeggen over x en y. Misschien dat ik er naast zit hoor, want mijn wiskunde niveau is ook niet om over naar huis te schrijven.


quote:Op maandag 22 juni 2015 21:20 schreef CapnIzzy het volgende:
[..]
Deze wordt altijd wel aangeraden voor wiskunde deficiënties weg te werken:
https://staff.fnwi.uva.nl/j.vandecraats/BasisboekWiskunde2HP.pdf
[..]
Volgens mij, als je twee onbekenden wilt oplossen heb je twee vergelijkingen nodig. Nu kan je weinig zinnigs zeggen over x en y. Misschien dat ik er naast zit hoor, want mijn wiskunde niveau is ook niet om over naar huis te schrijven.
quote:Op maandag 22 juni 2015 21:47 schreef GeorgeArArMartin het volgende:
[..]
Je kan X en Y niet uitrekenen uit één vergelijking, hiervoor heb je een (onafhankelijk) stelsel nodig. Je kan wel X uitdrukken in Y en andersom. Riparius of janneke zal wel een duidelijkere uitleg geven. Gaat het om een specifieke opgave?
thx voor jullie reacties, Ik kom er alleen niet uit,quote:Op maandag 22 juni 2015 21:47 schreef RRuben het volgende:
[..]
je hebt inderdaad 2 vergelijkingen nodig om dat op te lossen. Nu zijn er oneindig veel antwoorden.
Het gaat om dit:
Ze vragen hoeveel liter zoutoplossing X en Y( in X zit 5% zout en Y 2% zout.) je nodig moet hebben om een bepaald aantal concentratie te krijgen, wat hier gaat om 3%,
Om 3% te krijgen heb je vergelijking 0.05X + 0.02Y nodig...


Is er gegeven hoeveel liter je van die 3%-oplossing moet krijgen? Want dan moet daar je tweede vergelijking uit komen.quote:Op maandag 22 juni 2015 22:17 schreef Doublepain het volgende:
[..]
[..]
[..]
thx voor jullie reacties, Ik kom er alleen niet uit,
Het gaat om dit:
Ze vragen hoeveel liter zoutoplossing X en Y( in X zit 5% zout en Y 2% zout.) je nodig moet hebben om een bepaald aantal concentratie te krijgen, wat hier gaat om 3%,
Om 3% te krijgen heb je vergelijking 0.05X + 0.02Y nodig...
Laten we voor het gemak even zeggen dat dit 1 liter is.
Dan geldt dat
X + Y = 1 (immers, de 2 oplossingen samen worden een liter)
en
0,05X + 0,02Y = 0,03 (let op; als je A liter oplossing wil krijgen, dan moet je het rechterlid nog met A vermenigvuldigen. Maar 3% van 1 liter is 0,03 liter voor het zout)
Omdat uit de eerste vergelijking volgt dat X = 1-Y, en we dat in de tweede kunnen substitueren, kom je uit op
0,05 (1-Y) + 0,02Y = 0,03
0,05 - 0,05Y + 0,02Y = 0,03
-0,03Y + 0,05 = 0,03
-0,03Y = -0,02
Y = 2/3
Je hebt dus 2/3 liter van oplossing Y nodig en 1/3 van oplossing X om tot de gewenste zoutoplossing te komen.
[ Bericht 5% gewijzigd door Janneke141 op 22-06-2015 23:43:59 ]
Opinion is the medium between knowledge and ignorance (Plato)


ff kort vraagje: Gaan bij matrices vermenigvuldigen, delen, etc. vóór optellen/aftrekken net als bij normale sommen? En kun je überhaupt matrices delen door een getal of door een ander matrix?
graag op anoniem


Volgens mij is de volgorde inderdaad hetzelfde.quote:Op dinsdag 23 juni 2015 15:36 schreef topdeck het volgende:
ff kort vraagje: Gaan bij matrices vermenigvuldigen, delen, etc. vóór optellen/aftrekken net als bij normale sommen? En kun je überhaupt matrices delen door een getal of door een ander matrix?
En delen door een getal is hetzelfde als vermenigvuldigen met het omgekeerde van dat getal. Laat A een matrix zijn en b een getal. Dan A/b=A*(1/b). Een matrix vermenigvuldigen met zo'n getal (scalair) is gewoon gedefinieerd.
Matrix delen is een goede vraag. Als we ook B en C matrices noemen, kan je de deling A/B=C definiëren als de unieke oplossing van A=BC. Hoe je die vindt en wanneer dit goed gaat is dan weer een andere vraag. Ik heb dit in ieder geval nog nooit gezien of hoeven doen.
Kom anders met wat voorbeelden over waar je over twijfelt?
[ Bericht 0% gewijzigd door Aardappeltaart op 23-06-2015 16:54:21 ]


thx ik loop nu niet vast met een som gelukkig. Ik heb het ook nagecheckt met een som en het klopt ook wat je zei over * / komt voor +-quote:Op dinsdag 23 juni 2015 15:46 schreef Aardappeltaart het volgende:
[..]
Volgens mij is de volgorde inderdaad hetzelfde.
En delen door een getal is hetzelfde als vermenigvuldigen met het omgekeerde van dat getal. Laat A een matrix zijn en b een getal. Dan A/b=A*(1/b). Een matrix vermenigvuldigen met zo'n getal (scalair) is gewoon gedefinieerd.
Matrix delen is een goede vraag. Als we ook C en D matrices noemen, kan je de deling A/B=C definiëren als de unieke oplossing van A=BC. Hoe je die vindt en wanneer dit goed gaat is dan weer een andere vraag. Ik heb dit in ieder geval nog nooit gezien of hoeven doen.
Kom anders met wat voorbeelden over waar je over twijfelt?
Over dat delen met andere matrices is niet zo belangrijk nu voor me, ik vroeg het me gewoon af
thx!
graag op anoniem


Weet je hoe je de inverse van een matrix bepaalt?quote:Op dinsdag 23 juni 2015 15:46 schreef Aardappeltaart het volgende:
Matrix delen is een goede vraag. Als we ook B en C matrices noemen, kan je de deling A/B=C definiëren als de unieke oplossing van A=BC. Hoe je die vindt en wanneer dit goed gaat is dan weer een andere vraag. Ik heb dit in ieder geval nog nooit gezien of hoeven doen.
Opinion is the medium between knowledge and ignorance (Plato)


Ja, hoezo? Ah wacht, A/B opvatten als A*Binv. Nee, dan heb ik al best veel 'matrixdelingen' uitgevoerd.quote:Op dinsdag 23 juni 2015 17:06 schreef Janneke141 het volgende:
[..]
Weet je hoe je de inverse van een matrix bepaalt?


We nemen 3 ballen zonder teruglegging
De kans op 2 zwarte en 1 witte bal is
In totaal zijn er 14 ballen waarvan 8 zwart en 6 wit. Hoe kan ik deze bewerking uitvoeren op mijn TI-83?
De kans op 2 zwarte en 1 witte bal is
In totaal zijn er 14 ballen waarvan 8 zwart en 6 wit. Hoe kan ik deze bewerking uitvoeren op mijn TI-83?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin


volgens mij kan je het niet helemaal in je rekenmachine zetten.quote:Op woensdag 24 juni 2015 15:19 schreef phpmystyle het volgende:
We nemen 3 ballen zonder teruglegging
De kans op 2 zwarte en 1 witte bal is
In totaal zijn er 14 ballen waarvan 8 zwart en 6 wit. Hoe kan ik deze bewerking uitvoeren op mijn TI-83?
leef de leven


P(ZZW) = 8/14 * 7/13 * 6/12 * 3 = 4/7 * 7/13 * 1/2 * 3.quote:Op woensdag 24 juni 2015 15:19 schreef phpmystyle het volgende:
We nemen 3 ballen zonder teruglegging
De kans op 2 zwarte en 1 witte bal is
In totaal zijn er 14 ballen waarvan 8 zwart en 6 wit. Hoe kan ik deze bewerking uitvoeren op mijn TI-83?
Volgens mij. Weet 't niet zeker.
[ Bericht 1% gewijzigd door netchip op 24-06-2015 16:23:15 ]


Je gebruikt combinaties en de productregel. P(zzw) = (8 nCr 2 * 6 nCr 1)/14 nCr 3 ≈ 0,461.quote:Op woensdag 24 juni 2015 15:19 schreef phpmystyle het volgende:
We nemen 3 ballen zonder teruglegging
De kans op 2 zwarte en 1 witte bal is
In totaal zijn er 14 ballen waarvan 8 zwart en 6 wit. Hoe kan ik deze bewerking uitvoeren op mijn TI-83?


De manier die ik hierboven heb gepost, werkt ook.quote:Op woensdag 24 juni 2015 16:47 schreef GeorgeArArMartin het volgende:
[..]
Je gebruikt combinaties en de productregel. P(zzw) = (8 nCr 2 * 6 nCr 1)/14 nCr 3 ≈ 0,461.


Het is dan ook hetzelfde principe.quote:Op woensdag 24 juni 2015 16:52 schreef netchip het volgende:
[..]
De manier die ik hierboven heb gepost, werkt ook.
Edit: Ik zie zojuist dat ik helemaal niet heb laten zien hoe ik aan het antwoord kom, wat minstens even belangrijk is.
OP, de kans op een gebeurtenis P(gebeurtenis) = P(G) = N(aantal gunstige uitkomsten)/N(totaal aantal uitkomsten); N is een ehm... telfunctie (ik weet niet of dat de juiste benaming is).
In dit geval gaat het op 2 gebeurtenissen, sleutelwoord: en. Hierom P(G1 en G2) = P(G1) * P(G2). Er zijn 8 zwarte knikkers, dus de kans dat je er exact 2 pakt is 8 nCr 2 / 14 nCr 2 omdat 14 nCr 2 het totaal aantal mogelijkheden is om 2 knikkers te pakken (rangschikking buiten beschouwing gelaten, anders gaat het om permutaties en dus nPr).
Maar je pakt nu 3 knikkers in totaal, dus N(totaal) = 14 nCr 3
Gunstige uitkomsten zijn 8 nCr 2 * 6 nCr 1. Delen op elkaar levert de uitkomst van mijn vorige post.
[ Bericht 38% gewijzigd door GeorgeArArMartin op 24-06-2015 18:16:51 ]


Thanks voor de duidelijk uitleg, als het goed is begrijp ik het nuquote:Op woensdag 24 juni 2015 16:55 schreef GeorgeArArMartin het volgende:
[..]
Het is dan ook hetzelfde principe.
Edit: Ik zie zojuist dat ik helemaal niet heb laten zien hoe ik aan het antwoord kom, wat minstens even belangrijk is.
OP, de kans op een gebeurtenis P(gebeurtenis) = P(G) = N(aantal gunstige uitkomsten)/N(totaal aantal uitkomsten); N is een ehm... telfunctie (ik weet niet of dat de juiste benaming is).
In dit geval gaat het op 2 gebeurtenissen, sleutelwoord: en. Hierom P(G1 en G2) = P(G1) * P(G2). Er zijn 8 zwarte knikkers, dus de kans dat je er exact 2 pakt is 8 nCr 2 / 14 nCr 2 omdat 14 nCr 2 het totaal aantal mogelijkheden is om 2 knikkers te pakken (rangschikking buiten beschouwing gelaten, anders gaat het om permutaties en dus nPr).
Maar je pakt nu 3 knikkers in totaal, dus N(totaal) = 14 nCr 3
Gunstige uitkomsten zijn 8 nCr 2 * 6 nCr 1. Delen op elkaar levert de uitkomst van mijn vorige post.
Nog een vraagje dan
BinomCdf werkt niet op mijn grafische rekenmachine.
Ik toets op mijn Gr eerst N,kans,onderwaarde,bovenwaarde. Maar ik krijg vervolgens een error ipv een antwoord. Enig idee?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin


Bij gebruik van Binomcdf voer jij een ondergrens en een bovengrens in. Bij de rekenmachines die ik ken kun je alleen een bovengrens invoeren en wordt de kans cumulatief vanaf 0 successen uitgerekend.
Het is afhankelijk van het type GR welke gegevens je moet invoeren.
Het is afhankelijk van het type GR welke gegevens je moet invoeren.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Heb een oude TI83quote:Op woensdag 24 juni 2015 19:02 schreef -J-D- het volgende:
Bij gebruik van Binomcdf voer jij een ondergrens en een bovengrens in. Bij de rekenmachines die ik ken kun je alleen een bovengrens invoeren en wordt de kans cumulatief vanaf 0 successen uitgerekend.
Het is afhankelijk van het type GR welke gegevens je moet invoeren.
Ik kan dus alleen maar N, P, bovengrens invoeren. Ipv N,P,ondergrens, bovengrens?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin


http://www.josgeerlings.n(...)0op%20de%20TI-83.docquote:Op woensdag 24 juni 2015 19:04 schreef phpmystyle het volgende:
[..]
Heb een oude TI83
Ik kan dus alleen maar N, P, bovengrens invoeren. Ipv N,P,ondergrens, bovengrens?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Thanks, heb'm doorgelezen en ik kan nu alles uitvoeren zolang er in het verhaal ''hoogstens'' gevraagd wordt. Echter als er een vraag komt zoals deze;quote:Op woensdag 24 juni 2015 19:31 schreef -J-D- het volgende:
[..]
http://www.josgeerlings.n(...)0op%20de%20TI-83.doc
Bereken de kans dat er minstens 7 en hoogstens 10 huishoudens van de 20 zijn die een
vaatwasser hebben.
a. 0,4556
b. 0,7353
c. 0,5304
N=2, P=0,50 Hoe kan ik dit nu berekenen met binomcdf?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin


Hoe je het met de GR doet weet ik ook niet (of ik weiger erover na te denken, dat zou ook kunnen), maar het is natuurlijk de kans op hoogstens 10 minus de kans op hoogstens 6.quote:Op woensdag 24 juni 2015 21:00 schreef phpmystyle het volgende:
[..]
Thanks, heb'm doorgelezen en ik kan nu alles uitvoeren zolang er in het verhaal ''hoogstens'' gevraagd wordt. Echter als er een vraag komt zoals deze;
Bereken de kans dat er minstens 7 en hoogstens 10 huishoudens van de 20 zijn die een
vaatwasser hebben.
a. 0,4556
b. 0,7353
c. 0,5304
N=2, P=0,50 Hoe kan ik dit nu berekenen met binomcdf?
Opinion is the medium between knowledge and ignorance (Plato)


N=20 overigens.quote:Op woensdag 24 juni 2015 21:03 schreef Janneke141 het volgende:
[..]
Hoe je het met de GR doet weet ik ook niet (of ik weiger erover na te denken, dat zou ook kunnen), maar het is natuurlijk de kans op hoogstens 10 minus de kans op hoogstens 6.
Maar ik heb het gedaan en het werkt. Dit soort geintjes krijg je meer op het tentamen, vaak even kwestie van combinaties proberen.
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin


En hoezo dit nu weer? Ben net begonnen met het leren van deze gekkigheid. Ik heb een oude TI-83 waar je geen ondergrens en bovengrens hebt bij binomcdf. dus als ik iets wil berekenen kan ik dat alleen op de oude manier doen. Dat ik daar vragen bij heb is logisch.quote:
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin


Nog één vraagje als het mag 
In een vaas zitten 7 blauwe knikkers, 8 rooie, en 5 groene.
Hoe groot is de kans dat ik 2 blauwe, 1 rooie en 1 groene pak?
In een vaas zitten 7 blauwe knikkers, 8 rooie, en 5 groene.
Hoe groot is de kans dat ik 2 blauwe, 1 rooie en 1 groene pak?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin


met of zonder teruglegging? En wat heb je al geprobeerd?quote:Op woensdag 24 juni 2015 23:10 schreef phpmystyle het volgende:
Nog één vraagje als het mag
In een vaas zitten 7 blauwe knikkers, 8 rooie, en 5 groene.
Hoe groot is de kans dat ik 2 blauwe, 1 rooie en 1 groene pak?
leef de leven


zonder;quote:Op woensdag 24 juni 2015 23:15 schreef RRuben het volgende:
[..]
met of zonder teruglegging? En wat heb je al geprobeerd?
Ik zou zeggen 7 boven 2 * 8 boven 1 * 5 boven 1/ 20 boven 4. Verder loop ik vast
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin


Je gebruikt gewoon exact dezelfde methode als netflix en ik hierboven hebben gebruikt.quote:Op woensdag 24 juni 2015 23:10 schreef phpmystyle het volgende:
Nog één vraagje als het mag
In een vaas zitten 7 blauwe knikkers, 8 rooie, en 5 groene.
Hoe groot is de kans dat ik 2 blauwe, 1 rooie en 1 groene pak?
P(bbrg) = 7 nCr 2 * 8 nCr 1 * 5 nCr 1/20 nCr 4
Edit: Waar loop je precies vast dan? Dit geeft namelijk gewoon de kans weer.


Gegeven is de parabool y2 = 2p(x-a)
De lijn 3x + y = 12 is de poollijn van het punt P(-2,2) t.o.v. de parabool.
Bereken a en p.
Ik dacht aan yPy = px + pxP
Dit levert 2y = p(x-a) + -2p; maar in het antwoordenboek staat 2y = p(x-a) + p(-2-a). Wat zie ik over het hoofd?
De lijn 3x + y = 12 is de poollijn van het punt P(-2,2) t.o.v. de parabool.
Bereken a en p.
Ik dacht aan yPy = px + pxP
Dit levert 2y = p(x-a) + -2p; maar in het antwoordenboek staat 2y = p(x-a) + p(-2-a). Wat zie ik over het hoofd?


Laten we eerst eens kijken naar de vergelijking van de poollijn van een punt P(xP; yP) ten opzichte van de parabool met vergelijkingquote:Op vrijdag 26 juni 2015 21:19 schreef GeorgeArArMartin het volgende:
Gegeven is de parabool y2 = 2p(x-a)
De lijn 3x + y = 12 is de poollijn van het punt P(-2,2) t.o.v. de parabool.
Bereken a en p.
Ik dacht aan yPy = px + pxP
Dit levert 2y = p(x-a) + -2p; maar in het antwoordenboek staat 2y = p(x-a) + p(-2-a). Wat zie ik over het hoofd?
(1) y2 = 2px
Vanuit een punt P buiten de parabool kunnen we twee raaklijnen k en l trekken aan de parabool, die de parabool raken in resp.de punten A en B. De rechte door de raakpunten A en B heet nu de poollijn van punt P ten opzichte van de parabool. Om de vergelijking van deze rechte door A en B te bepalen kunnen we als volgt te werk gaan.
De vergelijking van een rechte door punt P(xP; yP) met richtingscoëfficiënt m is te schrijven als
(2) y − yP = m(x − xP)
Als nu een rechte door punt P met richtingscoëfficiënt m een raaklijn is aan de parabool, dan is m gelijk aan het differentiaalquotiënt dy/dx = y' voor (1) in één van beide raakpunten. Impliciet differentiëren van beide leden van (1) naar x geeft
(3) 2yy' = 2p
en dus
(4) y' = p/y
als althans y ≠ 0. Merk op dat (1) een parabool voorstelt met de x-as als symmetrie-as en met de top in de oorsprong, zodat de y-as de raaklijn is aan de top van de parabool en y' dus inderdaad niet is gedefinieerd voor y = 0. Als (2) een raaklijn voorstelt aan de parabool met vergelijking (1) dan is m = y' = p/y en hebben we dus voor de coördinaten (x; y) van het raakpunt
(5) y − yP = (p/y)·(x − xP)
en daarmee
(6) y2 − yPy = p(x − xP)
Maar nu voldoen de coördinaten (x; y) van elk van beide raakpunten niet alleen aan (6) maar ook aan (1) aangezien de raakpunten immers op de parabool liggen, en door substitutie van (1) in (6) volgt dus dat voor de coördinaten (x; y) van elk van beide raakpunten geldt
(7) 2px − yPy = p(x − xP)
oftewel
(8) yPy = px + pxP
en aangezien een rechte is bepaald door twee punten is (8) dus inderdaad de gezochte vergelijking van de poollijn van het punt P(xP; yP) ten opzichte van de parabool met vergelijking y2 = 2px.
Nu de vergelijking van de poollijn van een punt P(xP; yP) ten opzichte van een parabool met vergelijking
(9) y2 = 2p(x − a)
De parabool met vergelijking (9) ligt a eenheden naar rechts (dat is: in de richting van de positieve x-as) verschoven ten opzichte van de parabool met vergelijking (1) omdat we in (9) immers de x-waarden steeds a eenheden groter moeten nemen om op dezelfde y-waarden uit te komen als in (1).
Laten we nu het geheel bestaande uit de parabool met vergelijking (9) en het punt P(xP; yP) eens a eenheden naar links (dat is: in de richting van de negatieve x-as) verschuiven. Dan gaat de parabool met vergelijking (9) over in de parabool met vergelijking (1) en gaat het punt P(xP; yP) over in een punt P'(xP − a; yP). Laten we nu verder de raaklijnen vanuit punt P' aan de parabool met vergelijking (1) k' en l' noemen en laten deze raaklijnen de parabool met vergelijking (1) raken in resp. de punten A' en B'. Dan is de rechte door A' en B' de poollijn van punt P'(xP − a; yP) ten opzichte van de parabool met vergelijking (1) en deze poollijn door A' en B' heeft dan in overeenstemming met (8) als vergelijking
(10) yPy = px + p(xP − a)
Verschuiven we nu het geheel bestaande uit de parabool met vergelijking (1), het punt P'(xP − a; yP) en de beide raaklijnen k' en l' vanuit P' aan de parabool met vergelijking (1) weer a eenheden naar rechts, dan gaat punt P' weer over in punt P en gaat de parabool met vergelijking (1) weer over in de parabool met vergelijking (9). Ook gaan de beide raaklijnen k' en l' vanuit punt P' daarbij over in raaklijnen k en l vanuit punt P aan de parabool met vergelijking (9) en de beide raakpunten A' en B' van de raaklijnen k' resp. l' aan de parabool met vergelijking (1) gaan daarbij over in raakpunten A resp. B van de raaklijnen k resp. l aan de parabool met vergelijking (9). Maar dat betekent dus niets anders dan dat bij deze verschuiving ook de poollijn van punt P' ten opzichte van de parabool met vergelijking (1) overgaat in de poollijn van punt P ten opzichte van de parabool met vergelijking (9).
Nu hebben we al de vergelijking (10) van de poollijn van P' ten opzichte van de parabool met vergelijking (1) en als we de lijn met vergelijking (10) a eenheden naar rechts verschuiven, dan moeten de x-waarden steeds a eenheden groter zijn om op dezelfde y-waarden uit te komen, zodat we dus een lijn krijgen met als vergelijking
(11) yPy = p(x − a) + p(xP − a)
en daarmee hebben we dan de gevraagde vergelijking van de poollijn van een punt P(xP; yP) ten opzichte van een parabool met als vergelijking y2 = 2p(x − a) gevonden.
Nu is de opgave uiteraard niet moeilijk meer. Substitutie van xP = −2 en yP = 2 in (11) geeft als vergelijking voor de poollijn van het punt (−2; 2) ten opzichte van de parabool met vergelijking (9) na wat herleiding
(12) −½px + y = −pa − p
en aangezien is gegeven dat de vergelijking van deze poollijn is
(13) 3x + y = 12
vinden we dat moet gelden
(14) −½p = 3
en tevens
(15) −pa − p = 12
waaruit volgt
(16) p = −6
en
(17) a = 1


Bedankt voor de uitgebreide uitleg, het is een stuk duidelijker nu. Ik merk dat dit soort dingetjes elke keer weer wegzakken. Het probleem is waarschijnlijk dat ik de "formules" heb geleerd in plaats van de afleiding ervan.


Oeps, dit moet in het statistiek topic!
[ Bericht 17% gewijzigd door Super-B op 30-06-2015 16:53:30 ]
[ Bericht 17% gewijzigd door Super-B op 30-06-2015 16:53:30 ]


Zou iemand aan mij kunnen uitleggen hoe ik zo'n vraagstuk moet oplossen? Ik weet wel wat Z-hoeken zijn, maar ik weet niet wat dit met gelijkvormige figuren te maken hebben. Hierdoor weet ik niet waarom de conclusie getrokken kan worden dat driehoek ABS ~ driehoek EDS. Verder snap ik wel waarom zijde AS en ES zich verhouden als 4 : 1, maar snap ik niet waarom zijde AS 4/5e deel is van zijde AE.


met Z-hoeken kom je erachter dat:quote:Op donderdag 2 juli 2015 00:01 schreef BrokenBoy het volgende:
Zou iemand aan mij kunnen uitleggen hoe ik zo'n vraagstuk moet oplossen? Ik weet wel wat Z-hoeken zijn, maar ik weet niet wat dit met gelijkvormige figuren te maken hebben. Hierdoor weet ik niet waarom de conclusie getrokken kan worden dat driehoek ABS ~ driehoek EDS. Verder snap ik wel waarom zijde AS en ES zich verhouden als 4 : 1, maar snap ik niet waarom zijde AS 4/5e deel is van zijde AE.
[ afbeelding ]
hoek SBA = hoek SDE
hoek SAB = hoek SED
Als twee driehoeken twee dezelfde hoeken hebben, dan zijn die twee driehoeken gelijkvormig, dus driehoek ABS ~ driehoek EDS. (Er zijn een paar gevallen waarbij 2 driehoeken gelijkvormig zijn, en die moet je gewoon leren)
Als AS:ES = 4:1 dan bestaat AE eigenlijk uit 5 keer ES. AS bestaat uit 4 keer ES (die verhouding). Dus AS is 4/5 van AE.
leef de leven


Hartstikke bedankt voor je reactiequote:Op donderdag 2 juli 2015 00:21 schreef RRuben het volgende:
[..]
met Z-hoeken kom je erachter dat:
hoek SBA = hoek SDE
hoek SAB = hoek SED
Als twee driehoeken twee dezelfde hoeken hebben, dan zijn die twee driehoeken gelijkvormig, dus driehoek ABS ~ driehoek EDS. (Er zijn een paar gevallen waarbij 2 driehoeken gelijkvormig zijn, en die moet je gewoon leren)
Als AS:ES = 4:1 dan bestaat AE eigenlijk uit 5 keer ES. AS bestaat uit 4 keer ES (die verhouding). Dus AS is 4/5 van AE.


Kan iemand mij het volgende uitleggen:
6 knikkers: 3 rode, 2 witte en 1 blauwe.
De knikkers worden steeds teruggelegd. In totaal worden 7 knikkers gepakt.
Wat is de kans op precies 2 rode knikkers:
P(rr r r r r r) = (3/6)2 * (3/6)5
Waarom moet dit nog vermenigvuldigd worden met 7 nCr 2 om tot het juiste antwoord te komen?
En
Wat is de kans op precies 5 rode knikkers en 2 witte knikkers?
P(rrrrr ww) = (3/6)5 * (2/6)2
Dit wordt vermenigvuldigd met 7 nCr 5, maar niet met 7 nCr 2. Waarom niet?
[ Bericht 1% gewijzigd door GeorgeArArMartin op 05-07-2015 09:47:34 ]
6 knikkers: 3 rode, 2 witte en 1 blauwe.
De knikkers worden steeds teruggelegd. In totaal worden 7 knikkers gepakt.
Wat is de kans op precies 2 rode knikkers:
P(rr r r r r r) = (3/6)2 * (3/6)5
Waarom moet dit nog vermenigvuldigd worden met 7 nCr 2 om tot het juiste antwoord te komen?
En
Wat is de kans op precies 5 rode knikkers en 2 witte knikkers?
P(rrrrr ww) = (3/6)5 * (2/6)2
Dit wordt vermenigvuldigd met 7 nCr 5, maar niet met 7 nCr 2. Waarom niet?
[ Bericht 1% gewijzigd door GeorgeArArMartin op 05-07-2015 09:47:34 ]


Sowieso,quote:Op zondag 5 juli 2015 09:34 schreef GeorgeArArMartin het volgende:
Kan iemand mij het volgende uitleggen:
6 knikkers: 3 rode, 2 witte en 1 blauwe.
De knikkers worden steeds teruggelegd. In totaal worden 7 knikkers gepakt.
Wat is de kans op precies 2 rode knikkers:
P(rr r r r r r) = (3/6)2 * (3/6)5
Waarom moet dit nog vermenigvuldigd worden met 7 nCr 2 om tot het juiste antwoord te komen?
En
Wat is de kans op precies 5 rode knikkers en 2 witte knikkers?
P(rrrrr ww) = (3/6)5 * (2/6)2
Dit wordt vermenigvuldigd met 7 nCr 5, maar niet met 7 nCr 2. Waarom niet?
Je moet nog extra vermenigvuldigen omdat de volgorde waarin je die rode knikkers pakt er niet toe doet. Jij hebt nu de waarschijnlijkheid bepaald van de reeks RR?????. Echter, de reeks ?????RR heeft dezelfde waarschijnlijkheid, bijv. En er zijn


Ah dat zag ik dus over het hoofd. Bedankt!quote:Op zondag 5 juli 2015 12:39 schreef Arthos het volgende:
[..]
Sowieso,, dus
.
Je moet nog extra vermenigvuldigen omdat de volgorde waarin je die rode knikkers pakt er niet toe doet. Jij hebt nu de waarschijnlijkheid bepaald van de reeks RR?????. Echter, de reeks ?????RR heeft dezelfde waarschijnlijkheid, bijv. En er zijnvan deze reeksen.


Weet iemand hoe ik de standaarddeviatie kan berekenen aan de hand van de volgende gegevens en vervolgens de volgende vragen kan beantwoorden?:
''Een bedrijf heeft geruime tijd de duur van telefoongesprekken van haar werknemers bijgehouden. Uit die gegevens bleek dat de gespreksduur van de telefoongesprekken een normale verdeling volgt waarbij de helft van de gesprekken langer dan 4 minuten duurden. Ook bleek dat slechts 6.68% van de gesprekken korter dan 3 minuten duurden''
1) Wat is de standaarddeviatie van de duur van telefoongesprekken?
2) Wat is de kans dat de totale duur van 4 aselekt getrokken telefoongesprekken korter is dan
12 minuten?
''Een bedrijf heeft geruime tijd de duur van telefoongesprekken van haar werknemers bijgehouden. Uit die gegevens bleek dat de gespreksduur van de telefoongesprekken een normale verdeling volgt waarbij de helft van de gesprekken langer dan 4 minuten duurden. Ook bleek dat slechts 6.68% van de gesprekken korter dan 3 minuten duurden''
1) Wat is de standaarddeviatie van de duur van telefoongesprekken?
2) Wat is de kans dat de totale duur van 4 aselekt getrokken telefoongesprekken korter is dan
12 minuten?


Met een TI-83 of hoger: Je weet dat het gemiddelde=modus=mediaan is 4 (minuten), want het is een normale verdeling, en die 4 wordt gegeven (de helft van de gesprekken ...)
Je vult in het formulescherm in
y1= normcdf(-10^99, 3, 4, x)
y2=0,0668
Je stelt je window in op [0 ; 0,8] en [0 ; 0,1] en zoekt met Trace, intersect het snijpunt, zo vind je de standaardeviatie.
Vier gesprekken achter elkaar, dan wordt het gemiddelde 4 x 4 minuten, en voor de standaarddeviatie pas je de wortel-n-wet toe, dus je vermenigvuldigt je gevonden standaarddeviatie met 2. Je zoekt uit met normcdf(-10^ 99, 12, 16, 2 * standaarddeviatie) wat de kans is op 4 gesprekken korter dan 12 minuten.
Met de Texas hoef je geen afgeronde standaarddeviatie in te voeren, want als je in het formulescherm x [enter] geeft, zie je dat de Texas voor x het getal van het gevonden snijpunt voor je vasthoudt, je kan die x dus ook in je formule gebruiken, want x blijft op die waarde staan tot je in het grafiekscherm een ander snijpunt zoekt, of iets anders met Trace doet.
Je vult in het formulescherm in
y1= normcdf(-10^99, 3, 4, x)
y2=0,0668
Je stelt je window in op [0 ; 0,8] en [0 ; 0,1] en zoekt met Trace, intersect het snijpunt, zo vind je de standaardeviatie.
Vier gesprekken achter elkaar, dan wordt het gemiddelde 4 x 4 minuten, en voor de standaarddeviatie pas je de wortel-n-wet toe, dus je vermenigvuldigt je gevonden standaarddeviatie met 2. Je zoekt uit met normcdf(-10^ 99, 12, 16, 2 * standaarddeviatie) wat de kans is op 4 gesprekken korter dan 12 minuten.
Met de Texas hoef je geen afgeronde standaarddeviatie in te voeren, want als je in het formulescherm x [enter] geeft, zie je dat de Texas voor x het getal van het gevonden snijpunt voor je vasthoudt, je kan die x dus ook in je formule gebruiken, want x blijft op die waarde staan tot je in het grafiekscherm een ander snijpunt zoekt, of iets anders met Trace doet.


Hallo,
Ik heb een vraag over een vraagstuk met betrekking tot Wiskunde A (kansrekenen):
Het vraagstuk, welke beantwoord moet worden met juist/onjuist (onder de opgave):
Dit is een kansboom:
Ik heb het volgende:
A = Deskundige voorspelt hoge index
B = Index is hoog
P(A | B) = 0,72
P(Ac | B c)
P(B) = 0,5
P(Bc) = 0,5
P(A) = 0,6
P(Ac) = 0,4
P(A | Bc) = 0,48
P(Ac | B) = 0,28
Wat doe ik fout? Het antwoord is ONJUIST, maar aangezien ik in mijn ingevulde kansboom uitkom op tweemaal 1000 (bij wel advies: 1000 en bij niet advies 1000), lijkt het mij niet meer dan logisch dat Frank niet bereid is om te betalen voor advies.. Maar ik doe dus iets fouts..
[ Bericht 10% gewijzigd door GeschiktX op 07-07-2015 18:24:43 ]
Ik heb een vraag over een vraagstuk met betrekking tot Wiskunde A (kansrekenen):
Het vraagstuk, welke beantwoord moet worden met juist/onjuist (onder de opgave):
Dit is een kansboom:
Ik heb het volgende:
A = Deskundige voorspelt hoge index
B = Index is hoog
P(A | B) = 0,72
P(Ac | B c)
P(B) = 0,5
P(Bc) = 0,5
P(A) = 0,6
P(Ac) = 0,4
P(A | Bc) = 0,48
P(Ac | B) = 0,28
Wat doe ik fout? Het antwoord is ONJUIST, maar aangezien ik in mijn ingevulde kansboom uitkom op tweemaal 1000 (bij wel advies: 1000 en bij niet advies 1000), lijkt het mij niet meer dan logisch dat Frank niet bereid is om te betalen voor advies.. Maar ik doe dus iets fouts..
[ Bericht 10% gewijzigd door GeschiktX op 07-07-2015 18:24:43 ]


Je vermenigvuldigt met de verkeerde bedragen bij het speculeren: als de index hoger is win je 4000 euro, en als de index lager is verlies je 2000 euro bij een inzet van 2000 euro. Nu reken je met 2000 winst bij hoge index en geen verlies bij lage index.quote:Op dinsdag 7 juli 2015 18:18 schreef GeschiktX het volgende:
Hallo,
Ik heb een vraag over een vraagstuk met betrekking tot Wiskunde A (kansrekenen):
Het vraagstuk, welke beantwoord moet worden met juist/onjuist (onder de opgave):
Dit is een kansboom:
[ afbeelding ]
[ afbeelding ]
[ afbeelding ]
Ik heb het volgende:
A = Deskundige voorspelt hoge index
B = Index is hoog
P(A | B) = 0,72
P(Ac | B c)
P(B) = 0,5
P(Bc) = 0,5
P(A) = 0,6
P(Ac) = 0,4
P(A | Bc) = 0,48
P(Ac | B) = 0,28
[ afbeelding ]
[ afbeelding ]
Wat doe ik fout? Het antwoord is ONJUIST, maar aangezien ik in mijn ingevulde kansboom uitkom op tweemaal 1000 (bij wel advies: 1000 en bij niet advies 1000), lijkt het mij niet meer dan logisch dat Frank niet bereid is om te betalen voor advies.. Maar ik doe dus iets fouts..
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!


Stel dat
dy/dt = t2 - ty + 0,25y2 - 0,25
Dan zoek ik de oplossingen, ik ga er eerst van uit dat de oplossing een lineaire functie is.
Stel dan dat de oplossing y = at + b geldt
dan is dy/dt = a
Dit substitueren we in dy/dt = t2 - ty + 0,25y2 - 0,25
Dit levert
a = t2 - t(at+b) + 0,25(at+b)2 - 0,25
a = t2 - at2 - bt + 0,25a2t2 + 0,5abt + 0,25b2 - 0,25
termen bij elkaar zoeken en binnen haakjes brengen
a = (1-a+0,25a2)t2 + (-b+0,5ab)t + 0,25b2 - 0,25
Deze vergelijking moet gelden voor elke waarde van t, maar hoe volgt daar het volgende uit:
1 - a + 0,25a2 = 0 ∧ -b + 0,5ab = 0 ∧ a = 0,25b2 - 0,25
Is het omdat ik y=at+b substitueer in de differentiaalvergelijking er dus een y=0 (assnede) moet bestaan?
Het komt nogal verwarrend over en ik heb erg veel moeite met dit visualiseren...
dy/dt = t2 - ty + 0,25y2 - 0,25
Dan zoek ik de oplossingen, ik ga er eerst van uit dat de oplossing een lineaire functie is.
Stel dan dat de oplossing y = at + b geldt
dan is dy/dt = a
Dit substitueren we in dy/dt = t2 - ty + 0,25y2 - 0,25
Dit levert
a = t2 - t(at+b) + 0,25(at+b)2 - 0,25
a = t2 - at2 - bt + 0,25a2t2 + 0,5abt + 0,25b2 - 0,25
termen bij elkaar zoeken en binnen haakjes brengen
a = (1-a+0,25a2)t2 + (-b+0,5ab)t + 0,25b2 - 0,25
Deze vergelijking moet gelden voor elke waarde van t, maar hoe volgt daar het volgende uit:
1 - a + 0,25a2 = 0 ∧ -b + 0,5ab = 0 ∧ a = 0,25b2 - 0,25
Is het omdat ik y=at+b substitueer in de differentiaalvergelijking er dus een y=0 (assnede) moet bestaan?
Het komt nogal verwarrend over en ik heb erg veel moeite met dit visualiseren...
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


Het linkerlid is constant, dus moet het rechterlid ook constant zijn. Voor elke waarde van t moet er rechts dus hetzelfde staan. Dat kan alleen als de coëfficiënten van t en t2 gelijk zijn aan 0. Dan is (1-a+0,25a2)t2 + (-b+0,5ab)t = 0 + 0 = 0 en houd je over a = 0,25b2 - 0,25.quote:a = (1-a+0,25a2)t2 + (-b+0,5ab)t + 0,25b2 - 0,25


O ja, totaal over het hoofd gezien. Bedankt!quote:Op woensdag 8 juli 2015 18:43 schreef Tochjo het volgende:
[..]
Het linkerlid is constant, dus moet het rechterlid ook constant zijn. Voor elke waarde van t moet er rechts dus hetzelfde staan. Dat kan alleen als de coëfficiënten van t en t2 gelijk zijn aan 0. Dan is (1-a+0,25a2)t2 + (-b+0,5ab)t = 0 + 0 = 0 en houd je over a = 0,25b2 - 0,25.


quote:Op dinsdag 7 juli 2015 18:18 schreef GeschiktX het volgende:
Hallo,
Ik heb een vraag over een vraagstuk met betrekking tot Wiskunde A (kansrekenen):
Het vraagstuk, welke beantwoord moet worden met juist/onjuist (onder de opgave):
Dit is een kansboom:
[ afbeelding ]
[ afbeelding ]
[ afbeelding ]
Ik heb het volgende:
A = Deskundige voorspelt hoge index
B = Index is hoog
P(A | B) = 0,72
P(Ac | B c)
P(B) = 0,5
P(Bc) = 0,5
P(A) = 0,6
P(Ac) = 0,4
P(A | Bc) = 0,48
P(Ac | B) = 0,28
[ afbeelding ]
[ afbeelding ]
Wat doe ik fout? Het antwoord is ONJUIST, maar aangezien ik in mijn ingevulde kansboom uitkom op tweemaal 1000 (bij wel advies: 1000 en bij niet advies 1000), lijkt het mij niet meer dan logisch dat Frank niet bereid is om te betalen voor advies.. Maar ik doe dus iets fouts..
Moet ik dan niet naar de pay-off kijken? Ik deed namelijk hoge index (4000) - investeringsbedrag (2000) = 2000quote:Op dinsdag 7 juli 2015 22:59 schreef freiss het volgende:
[..]
Je vermenigvuldigt met de verkeerde bedragen bij het speculeren: als de index hoger is win je 4000 euro, en als de index lager is verlies je 2000 euro bij een inzet van 2000 euro. Nu reken je met 2000 winst bij hoge index en geen verlies bij lage index.
Bij lage index (2000) - investering (2000) = 0


Ik ben niet zo bekend met de precieze methode, maar ik denk dat de opgave even beter moet lezenquote:Op woensdag 8 juli 2015 19:21 schreef GeschiktX het volgende:
[..]
[..]
Moet ik dan niet naar de pay-off kijken? Ik deed namelijk hoge index (4000) - investeringsbedrag (2000) = 2000
Bij lage index (2000) - investering (2000) = 0
hoge index (6000) - investeringsbedrag (2000) = 4000
lage index (0) - investeringsbedrag (2000) = -2000
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!


Omdat sin x een nulpunt heeft bij ieder geheel veelvoud van π?quote:Op vrijdag 10 juli 2015 16:14 schreef RRuben het volgende:
Ik snap alles behalve punt 3. Waarom staat daar k⋅π en niet k⋅2π?
Opinion is the medium between knowledge and ignorance (Plato)


Ohja! Hoe kan ik dat nou weer niet snappen, haha. Bedankt he!quote:Op vrijdag 10 juli 2015 16:17 schreef Janneke141 het volgende:
[..]
Omdat sin x een nulpunt heeft bij ieder geheel veelvoud van π?
leef de leven


Om hierop aan te sluiten, de periode van sin(ax) is gelijk aan 2π/a.Veel succes! Vergeet de dingetjes van de eenheidscirkel niet, mogelijk is het niet de bedoeling dat je die steeds op je GR intypt.quote:Op vrijdag 10 juli 2015 16:17 schreef Janneke141 het volgende:
[..]
Omdat sin x een nulpunt heeft bij ieder geheel veelvoud van π?


Denk aan de definities van de cosinus en de sinus aan de hand van de eenheidscirkel, dan zie je direct dat je het startpunt (1; 0) over een geheel aantal halve slagen om de oorsprong moet roteren om weer uit te komen op een punt waarvan de y-coördinaat nul is, zodat sin θ = 0 voor θ = kπ, k ∈ ℤ.quote:Op vrijdag 10 juli 2015 16:27 schreef RRuben het volgende:
[..]
Ohja! Hoe kan ik dat nou weer niet snappen, haha. Bedankt he!
Je kunt hier trouwens ook gebruik maken van de identiteit voor de sinus van de dubbele hoek, dan krijg je
sin x (1 + 2·cos x) = 0
sin x = 0 ∨ cos x = −½
x = kπ ∨ x = ⅔π + 2kπ ∨ x = −⅔π + 2kπ, k ∈ ℤ


ja thanks! Die tabel voor ainus en cosinus ken ik wel goed dus dat is het probleem niet.quote:Op vrijdag 10 juli 2015 16:33 schreef GeorgeArArMartin het volgende:
[..]
Om hierop aan te sluiten, de periode van sin(ax) is gelijk aan 2π/a.Veel succes! Vergeet de dingetjes van de eenheidscirkel niet, mogelijk is het niet de bedoeling dat je die steeds op je GR intypt.
leef de leven


ja ik snap het nuquote:Op vrijdag 10 juli 2015 16:41 schreef Riparius het volgende:
[..]
Denk aan de definities van de cosinus en de sinus aan de hand van de eenheidscirkel, dan zie je direct dat je het startpunt (1; 0) over een geheel aantal halve slagen om de oorsprong moet roteren om weer uit te komen op een punt waarvan de y-coördinaat nul is, zodat sin θ = 0 voor θ = kπ, k ∈ ℤ.
Je kunt hier trouwens ook gebruik maken van de identiteit voor de sinus van de dubbele hoek, dan krijg je
sin x (1 + 2·cos x) = 0
sin x = 0 ∨ cos x = −½
x = kπ ∨ x = ⅔π + 2kπ ∨ x = −⅔π + 2kπ, k ∈ ℤ
leef de leven


f(x) = cos(x)/(sin2(x) + 1)
Hoe kan ik F(x) bepalen? Ik weet wel dat als f(x) = 1/(x2+1), F(x) = arctan(x) + C ; maar wat doe ik met cos(x) in de teller?
Hoe kan ik F(x) bepalen? Ik weet wel dat als f(x) = 1/(x2+1), F(x) = arctan(x) + C ; maar wat doe ik met cos(x) in de teller?


cos(x) is de afgeleide van sin(x)quote:Op zaterdag 11 juli 2015 14:33 schreef GeorgeArArMartin het volgende:
f(x) = cos(x)/(sin2(x) + 1)
Hoe kan ik F(x) bepalen? Ik weet wel dat als f(x) = 1/(x2+1), F(x) = arctan(x) + C ; maar wat doe ik met cos(x) in de teller?
kettingregel en zo


Thanks!quote:Op zaterdag 11 juli 2015 14:48 schreef Anoonumos het volgende:
[..]
cos(x) is de afgeleide van sin(x)
kettingregel en zo
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |



 Op
Op