SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Klopt jaquote:Op dinsdag 18 december 2012 22:14 schreef twaalf het volgende:
Zo nu en dan is dat wel geinig om te zien in dit topic... staat er in de vraag 'los op met inklemmen' --> nee dat is flauwekul, zo gaan we het doen. Staat er in de vraag één klein detail verkeerd opgeschreven --> nee de vraag klopt niet en ik los hem ook niet op voor je.
(maar ook wel begrijpelijk soms)Ik ben het er inderdaad mee eens dat de huidige schoolboeken gebrekkig zijn qua voorbeelden. Toch werkt het didactisch denk ik beter als je het eerst aan de leerling over laat om te laten zien wat hij wel en niet snapt aan de vraag. Dan geef je een hint. En als het een rommeltje wordt dan geef je eventueel een complete uitwerking. Op die manier is het wat interactiever, en gaat de oplossing denk ik ook wat minder snel over het hoofd van de leerling heen.quote:
[..]
Tja, je zult ongetwijfeld hebben gemerkt dat ik nogal eens compete uitwerkingen of afleidingen post, en dat doe ik niet zonder reden, ik hoop namelijk dat de vragenstellers, maar mogelijk ook andere meelezers die het nodig hebben, daar iets van opsteken. Een helder uitgewerkt vraagstuk kan dienen als model om te imiteren en zo soortgelijke vraagstukken zelf te leren oplossen. In oudere schoolboeken zie je dan ook dat alle stof compleet wordt uitgelegd en dat werkt het beste. Maar omdat dat in de huidige schoolboeken niet niet meer gebeurt en er kennelijk ook geen les meer wordt gegeven krijg je mensen die het zelfs aan de meest basale vaardigheden ontbreekt en die ook niet in staat zijn om een uitwerking helder en correct op te schrijven, en dat is niet goed.
Dat doe ik ook wel, als ik er zin in heb en er tijd voor heb, maar dan zie je - helaas - toch vrij vaak dat je echt iedere stap er uit moet trekken en dan heb je al snel een half dozijn posts over iets wat in pakweg vijf regeltjes is op te schrijven. En dan heb je soms ook nog mensen die het spelletje gewoon niet mee willen spelen, maar die alleen een kant en klare oplossing van 'de som' willen hebben (ook al begrijpen ze die misschien niet eens) en die grof worden als ze merken dat ik ze zelf de oplossing wil laten vinden (ja, ik heb voorbeelden daarvan hier op FOK). Nu, ik zit er niet op te wachten om me te laten schofferen, dus dat is al een voldoende reden voor mij om niet te snel te beginnen met het geven van een hint als ik de indruk heb dat dat toch paarlen voor de zwijnen is.quote:
[..]
Klopt ja
[..]
Ik ben het er inderdaad mee eens dat de huidige schoolboeken gebrekkig zijn qua voorbeelden. Toch werkt het didactisch denk ik beter als je het eerst aan de leerling over laat om te laten zien wat hij wel en niet snapt aan de vraag. Dan geef je een hint. En als het een rommeltje wordt dan geef je eventueel een complete uitwerking. Op die manier is het wat interactiever, en gaat de oplossing denk ik ook wat minder snel over het hoofd van de leerling heen.
Ik denk dat menigeen (en ikzelf ook toen ik nog in de opleiding zat) jouw hulp erg waardeert. Ik ben er destijds stukken verder meegekomen in de complexe functietheorie, projectieve meetkunde en grafentheorie.quote:
[..]
Dat doe ik ook wel, als ik er zin in heb en er tijd voor heb, maar dan zie je - helaas - toch vrij vaak dat je echt iedere stap er uit moet trekken en dan heb je al snel een half dozijn posts over iets wat in pakweg vijf regeltjes is op te schrijven. En dan heb je soms ook nog mensen die het spelletje gewoon niet mee willen spelen, maar die alleen een kant en klare oplossing van 'de som' willen hebben (ook al begrijpen ze die misschien niet eens) en die grof worden als ze merken dat ik ze zelf de oplossing wil laten vinden (ja, ik heb voorbeelden daarvan hier op FOK). Nu, ik zit er niet op te wachten om me te laten schofferen, dus dat is al een voldoende reden voor mij om niet te snel te beginnen met het geven van een hint als ik de indruk heb dat dat toch paarlen voor de zwijnen is.
kloep kloep
Dat staat ook buiten kijf.quote:
[..]
Ik denk dat menigeen (en ikzelf ook toen ik nog in de opleiding zat) jouw hulp erg waardeert. Ik ben er destijds stukken verder meegekomen in de complexe functietheorie, projectieve meetkunde en grafentheorie.
Maar dat mag ook wel eens gezegd worden als ik lees dat er ook users zijn die hier totaal verkeerd mee om gaan.quote:
kloep kloep
Zeker, maar jij deed een wiskunde opleiding en was dus, naar ik aanneem, ook goed gemotiveerd. Ik doelde meer op mensen die niets met wiskunde hebben maar gewoon willen dat iemand anders even hun huiswerk maakt of die 's avonds laat (en bij voorkeur 's zondags) aan komen zetten met een opgave die de volgende ochtend ingeleverd moet worden of die de volgende ochtend een proefwerk hebben waar ze nog niets aan gedaan hebben. Meestal - maar niet altijd - is wel goed in te schatten of het zin heeft tijd in iemand te steken in de vorm van een uitgebreide uitleg of een dialoog over een vraagstuk.quote:
[..]
Ik denk dat menigeen (en ikzelf ook toen ik nog in de opleiding zat) jouw hulp erg waardeert. Ik ben er destijds stukken verder meegekomen in de complexe functietheorie, projectieve meetkunde en grafentheorie.
Ik zie het nu. Ik had moeten inzien dat de coefficieinten van f niet veranderen. Aangezien K een deelverzameling van E is, geldt automatisch dat f een polynoom over E is.quote:
[..]
Bekijk f=(x^2+1)(x^2-2) met coëfficiënten in. De splittingfield is dan
. De subfields, zodat
,
en
. Nu is het makkelijk inzien dat
de splittingfield van
,
en
is.
Een K-monomorfisme stuurt alle elementen uit K naar K en de uitbreidingselementen worden injectief naar de uitbreidingselementen gestuurd. Dus phi(E) is dan gewoon E en phi(E_1) is dan of E of E_1 of E_2 of, als ik de definitie van een K-monomorfisme goed begrepen heb.
-
Kan iemand mij uitleggen waarom de matrixvergelijking Ax=0 meerdere oplossingen heeft behalve x=0 als A niet reduceerbaar is tot de identiteitsmatrix?
In het boek staat dus dat er een niet triviale oplossing is als A niet reduceerbaar is tot I.
zijn er niet oneindig veel oplossingen? want als je A rij-reduceert en hij is niet reduceerbaar tot I, heb je toch meer variabelen dan vergelijkingen?
(A is een n x n matrix )
[ Bericht 3% gewijzigd door flopsies op 19-12-2012 00:22:15 ]
In het boek staat dus dat er een niet triviale oplossing is als A niet reduceerbaar is tot I.
zijn er niet oneindig veel oplossingen? want als je A rij-reduceert en hij is niet reduceerbaar tot I, heb je toch meer variabelen dan vergelijkingen?
(A is een n x n matrix )
[ Bericht 3% gewijzigd door flopsies op 19-12-2012 00:22:15 ]
Ja, er zijn dan oneindig veel oplossingen. Want als x een niet-triviale oplossing is, is cx ook een oplossing voor elke c.
Is dat niet jammer, om maar telkens voorgekauwde oplossingen te geven aan iedereen omdat sommige het verknald hebben bij je? Je zou, wanneer ze kwaad worden, ook gewoon kunnen negeren. Je hoeft ze uiteraard niet te helpen.quote:
[..]
Dat doe ik ook wel, als ik er zin in heb en er tijd voor heb, maar dan zie je - helaas - toch vrij vaak dat je echt iedere stap er uit moet trekken en dan heb je al snel een half dozijn posts over iets wat in pakweg vijf regeltjes is op te schrijven. En dan heb je soms ook nog mensen die het spelletje gewoon niet mee willen spelen, maar die alleen een kant en klare oplossing van 'de som' willen hebben (ook al begrijpen ze die misschien niet eens) en die grof worden als ze merken dat ik ze zelf de oplossing wil laten vinden (ja, ik heb voorbeelden daarvan hier op FOK). Nu, ik zit er niet op te wachten om me te laten schofferen, dus dat is al een voldoende reden voor mij om niet te snel te beginnen met het geven van een hint als ik de indruk heb dat dat toch paarlen voor de zwijnen is.
Eensquote:Op woensdag 19 december 2012 07:08 schreef Amoeba het volgende:
[..]
Is dat niet jammer, om maar telkens voorgekauwde oplossingen te geven aan iedereen omdat sommige het verknald hebben bij je? Je zou, wanneer ze kwaad worden, ook gewoon kunnen negeren. Je hoeft ze uiteraard niet te helpen.
Het punt is dat ik antwoorden niet alleen post voor de vragenstellers maar dat ik hoop of verwacht dat anderen daar ook wat aan hebben. Deze topicreeks heeft in verhouding tot het aantal (verschillende) posters vrij veel views, zodat je moet aannemen dat er ook veel passieve meelezers zijn die deze topicreeks kennelijk de moeite waard vinden. En daarnaast is het zo dat het meestal minder tijd kost om direct een oplossing in een paar regels netjes op te schrijven dan om alleen een hint te geven en vervolgens te gaan zitten afwachten wat de vragensteller daar mee doet en daar dan weer op te moeten reageren. Ik maak in principe in eerste instantie verder geen onderscheid tussen gekende onsympathieke en sympathieke posters, alleen de vraag is bepalend.quote:
[..]
Is dat niet jammer, om maar telkens voorgekauwde oplossingen te geven aan iedereen omdat sommige het verknald hebben bij je? Je zou, wanneer ze kwaad worden, ook gewoon kunnen negeren. Je hoeft ze uiteraard niet te helpen.
[ Bericht 0% gewijzigd door Riparius op 19-12-2012 23:10:38 ]
Ik heb een vraag die wellicht zeer makkelijk is voor veel mensen. Maar ik weet het dus niet zeker en aangezien ik al jaren van de middelbare school ben is het nogal weggezakt 
Stel je hebt 12 wedstrijden waarbij de uitkomst alleen winst en verlies kan zijn ( dus niet gelijk ).
Hoeveel verschillende combinaties zijn er dan mogelijk? Kan je dan de NcR formule ( 12C2 ) gebruiken wat dus 66 combinaties betekent? Of moet het op een andere manier?
Alvast bedankt iig.
Stel je hebt 12 wedstrijden waarbij de uitkomst alleen winst en verlies kan zijn ( dus niet gelijk ).
Hoeveel verschillende combinaties zijn er dan mogelijk? Kan je dan de NcR formule ( 12C2 ) gebruiken wat dus 66 combinaties betekent? Of moet het op een andere manier?
Alvast bedankt iig.
Stel je had maar 2 of 3 wedstrijden. Hoeveel zou het er dan zijn?quote:
Ik heb een vraag die wellicht zeer makkelijk is voor veel mensen. Maar ik weet het dus niet zeker en aangezien ik al jaren van de middelbare school ben is het nogal weggezakt
Stel je hebt 12 wedstrijden waarbij de uitkomst alleen winst en verlies kan zijn ( dus niet gelijk ).
Hoeveel verschillende combinaties zijn er dan mogelijk? Kan je dan de NcR formule ( 12C2 ) gebruiken wat dus 66 combinaties betekent? Of moet het op een andere manier?
Alvast bedankt iig.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Je vraag is te onduidelijk om te kunnen beantwoorden. Als je een soort totoformulier hebt, maar dan eentje met 12 wedstrijden en slechts twee kolommen, dan zijn er 212 = 4096 mogelijkheden voor de uitkomst van de 12 wedstrijden.quote:
Ik heb een vraag die wellicht zeer makkelijk is voor veel mensen. Maar ik weet het dus niet zeker en aangezien ik al jaren van de middelbare school ben is het nogal weggezakt
Stel je hebt 12 wedstrijden waarbij de uitkomst alleen winst en verlies kan zijn ( dus niet gelijk ).
Hoeveel verschillende combinaties zijn er dan mogelijk? Kan je dan de NcR formule ( 12C2 ) gebruiken wat dus 66 combinaties betekent? Of moet het op een andere manier?
Alvast bedankt iig.
Dank voor de reacties.quote:
Inderdaad is een beetje de vraag of TS over 12 identieke of unieke wedstrijden spreekt.
Ik doelde op 12 unieke wedstrijden met 2 uitkomst mogelijkheden. Dan zou ik de ''formule'' van Riparius moeten gebruiken, wat dus resulteert in 4096 mogelijkheden. Dat klinkt eigenlijk ook wel wat logischer.
Inderdaad. Snap je ook waarom dit zo is?quote:
[..]
Dank voor de reacties.
Ik doelde op 12 unieke wedstrijden met 2 uitkomst mogelijkheden. Dan zou ik de ''formule'' van Riparius moeten gebruiken, wat dus resulteert in 4096 mogelijkheden. Dat klinkt eigenlijk ook wel wat logischer.
Dankje hiervoor :-) Ik post niet zo heel vaak maar ik sla al jouw (uitgebreide) antwoorden (op vragen van anderen) op!quote:
[..]
Het punt is dat ik antwoorden niet alleen post voor de vragenstellers maar dat ik hoop of verwacht dat anderen daar ook wat aan hebben. Deze topicreeks heeft in verhouding tot het aantal (verschillende) posters vrij veel views, zodat je moet aannemen dat er ook veel passieve meelezers zijn die deze topicreeks kennelijk de moeite waard vinden. En daarnaast is het zo dat het meestal minder tijd kost om direct een oplossing in een paar regels netjes op te schrijven dan om alleen een hint te geven en vervolgens te gaan zitten wachten wat de vragensteller daar mee doet en daar dan weer op te moeten reageren. Ik maak in principe in eerste instantie verder geen onderscheid tussen gekende onsympathieke en sympathieke posters, alleen de vraag is bepalend.
Dank voor je reactie. Lees ook even mijn tip om posts optimaal leesbaar op te slaan en af te drukken.quote:
[..]
Dankje hiervoor :-) Ik post niet zo heel vaak maar ik sla al jouw (uitgebreide) antwoorden (op vragen van anderen) op!
Bij ons op school hebben ze echt zo'n versie van Word waarbij al die dingen niet werken. Het symbool voor een hoek wordt in een apart lettertype weergegeven, anders is het een vierkantje. Het leuke is dan dat 84pts dan overeenkomt met 12pts in Times New Roman. Om even ruwweg aan te geven dat je lay-out dan wel verknald is.quote:
[..]
Dank voor je reactie. Lees ook even mijn tip om posts optimaal leesbaar op te slaan en af te drukken.
Mijn docent vroeg adhv mijn concept PWS iets over 3 termen welke ik gebruikte, oblate en prolate sferoïden en sfeer als (wiskundig) synoniem voor het oppervlak van een bol. Dit is toch allemaal correct? Oblaat en prolaat geeft de vorm van de sferoïde aan, in een gefixeerd xyz-stelsel.
Je hebt toch zelf wel een computer met Microsoft Word (of anders Open Office, dat werkt ook)? Het teken ∠ (U+2220 ANGLE) zit inderdaad niet in Times New Roman of in Minion Pro, maar bijvoorbeeld wel in het (kosteloze) Linux Libertine dat kwalitatief ook heel goed is. Mixen van fonts is ook geen probleem, als je eerst alles in Linux Libertine zet en daarna alles weer terug in Minion Pro, dan blijven de tekens zoals ∠ die ontbreken in Minion Pro gewoon in Linux Libertine staan.quote:
[..]
Bij ons op school hebben ze echt zo'n versie van Word waarbij al die dingen niet werken. Het symbool voor een hoek wordt in een apart lettertype weergegeven, anders is het een vierkantje. Het leuke is dan dat 84pts dan overeenkomt met 12pts in Times New Roman. Om even ruwweg aan te geven dat je lay-out dan wel verknald is.
Dat zijn inderdaad allemaal courante termen, maar ik weet natuurlijk niet of je ze in je tekst ook correct gebruikt.quote:Mijn docent vroeg adhv mijn concept PWS iets over 3 termen welke ik gebruikte, oblate en prolate sferoïden en sfeer als (wiskundig) synoniem voor het oppervlak van een bol. Dit is toch allemaal correct? Oblaat en prolaat geeft de vorm van de sferoïde aan, in een gefixeerd xyz-stelsel.
Ik ben in het bezit van een computer ja, ik heb 't ding zelf in elkaar gestoken voor 3500 euro, ongeveer. 3 Samsung 2450BX op 2x de GTX580, om even een greep in de specificaties te doen.quote:
[..]
Je hebt toch zelf wel een computer met Microsoft Word (of anders Open Office, dat werkt ook)? Het teken ∠ (U+2220 ANGLE) zit inderdaad niet in Times New Roman of in Minion Pro, maar bijvoorbeeld wel in het (kosteloze) Linux Libertine dat kwalitatief ook heel goed is. Mixen van fonts is ook geen probleem, als je eerst alles in Linux Libertine zet en daarna alles weer terug in Minion Pro, dan blijven de tekens zoals ∠ die ontbreken in Minion Pro gewoon in Linux Libertine staan.
[..]
Dat zijn inderdaad allemaal courante termen, maar ik weet natuurlijk niet of je ze in je tekst ook correct gebruikt.
Ik geloof wel dat ik ze correct gebruik. Ik spreek over de projectie van een sfeer op een (tweedimensionaal) vlak.
De specs zeggen natuurlijk niets over de mogelijkheid om met Unicode te werken, dat is bij Windows al standaard vanaf XP geïntroduceerd eind 2001, en Linux is ook al heel lang op Unicode gebaseerd. Alleen duurt het kennelijk vele jaren voordat dat soort dingen een beetje doordringen tot sommige mensen. Anno 2012 zijn er nog hele volksstammen die blijven pielen met MS-DOS codes uit de jaren '80 van de vorige eeuw.quote:
[..]
Ik ben in het bezit van een computer ja, ik heb 't ding zelf in elkaar gestoken voor 3500 euro, ongeveer. 3 Samsung 2450BX op 2x de GTX580, om even een greep in de specificaties te doen.
Dat lijkt me correct, hoewel sfeer dacht ik in het Nederlands niet zo'n gebruikelijk woord is. In een document waarnaar je eerder linkte wordt gesproken van de projectie van een bol of de aardbol of het aardoppervlak op een plat vlak, het woord sfeer komt in dat hele document niet voor.quote:Ik geloof wel dat ik ze correct gebruik. Ik spreek over de projectie van een sfeer op een (tweedimensionaal) vlak.
Dit was ook zijn (principiële) bezwaar; het is geen gebruikelijk woord. Echter vond hij zinnen zoals "Echter is er genoeg materie in de diversiteit der cilindrische projecties om een vullend werkstuk te creëeren." onzinnig, te moeilijk en vooral niet doen. Even een opsomming van mijn zinnen waarin ik 'sfeer' gebruik:quote:
[..]
De specs zeggen natuurlijk niets over de mogelijkheid om met Unicode te werken, dat is bij Windows al standaard vanaf XP geïntroduceerd eind 2001, en Linux is ook al heel lang op Unicode gebaseerd. Alleen duurt het kennelijk vele jaren voordat dat soort dingen een beetje doordringen tot sommige mensen. Anno 2012 zijn er nog hele volksstammen die blijven pielen met MS-DOS codes uit de jaren '80 van de vorige eeuw.
[..]
Dat lijkt me correct, hoewel sfeer dacht ik in het Nederlands niet zo'n gebruikelijk woord is. In een document waarnaar je eerder linkte wordt gesproken van de projectie van een bol of de aardbol of het aardoppervlak op een plat vlak, het woord sfeer komt in dat hele document niet voor.
Ik wil echter maar een klein deel van dit onderwerp behandelen, namelijk de projecties van een sfeer op een tweedimensionaal vlak.
Nu behandel ik enkel de situaties waarvoor geldt dat het te projecteren oppervlak een sfeer betreft.
Beetje dubbelop, maar dit is beperking 1.
De cilindrische projectie beschrijft een methode om de sfeer af te beelden op een plat vlak met behulp van de cilinder.
Deze projecties zijn geen directe projecties van de sfeer op een mantel om de bol.
Op de kaart worden ook de grootcirkels, op een sfeer aangeduid met meridianen, als rechte lijnen weergegeven. (Deze zin ga ik wijzigen in het aardoppervlak, immers meridianen komen niet per definitie voor op een sfeer maar juist op het aardoppervlak oid..)
Stel dat we een willekeurig punt op de sfeer nemen,
Ik zou je natuurlijk een keer het document kunnen sturen, dat je het een keer doorleest wanneer je zin hebt. Ik moet eerst nog legio wijzingen en addities doorvoeren, dus nu nog niet. Ik stelde je hulp met de Mercatorprojectie zeer op prijs, dus misschien dat je nogmaals wat tijd voor me vrij kunt maken?
Ja, dat is ook mijn bezwaar. Je kunt je het beste houden aan de gebruikelijke terminologie in serieuze (wetenschappelijke) publicaties in het Nederlands over jouw specifieke onderwerp. Ik heb zelf de indruk dat het woord sfeer in het Nederlands vooral in een strict wiskundige contekst wordt gebruikt, zoals in het begrip Riemann-sfeer.quote:Op woensdag 19 december 2012 21:29 schreef Amoeba het volgende:
[..]
Dit was ook zijn (principiële) bezwaar; het is geen gebruikelijk woord.
Deze zin loopt niet lekker, is niet echt goed Nederlands, en klinkt ook wat te hoogdravend. Maak er iets van als de literatuur over de verschillende cilinderprojecties biedt voldoende materiaal voor een uitgebreid werkstuk.quote:Echter vond hij zinnen zoals "Echter is er genoeg materie in de diversiteit der cilindrische projecties om een vullend werkstuk te creëeren." onzinnig, te moeilijk en vooral niet doen.
Ik wil je werkstuk t.z.t. best doornemen, maar dat kan dan pas ruim na de feestdagen.quote:Even een opsomming van mijn zinnen waarin ik 'sfeer' gebruik:
Ik wil echter maar een klein deel van dit onderwerp behandelen, namelijk de projecties van een sfeer op een tweedimensionaal vlak.
Nu behandel ik enkel de situaties waarvoor geldt dat het te projecteren oppervlak een sfeer betreft.
Beetje dubbelop, maar dit is beperking 1.
De cilindrische projectie beschrijft een methode om de sfeer af te beelden op een plat vlak met behulp van de cilinder.
Deze projecties zijn geen directe projecties van de sfeer op een mantel om de bol.
Op de kaart worden ook de grootcirkels, op een sfeer aangeduid met meridianen, als rechte lijnen weergegeven. (Deze zin ga ik wijzigen in het aardoppervlak, immers meridianen komen niet per definitie voor op een sfeer maar juist op het aardoppervlak oid..)
Stel dat we een willekeurig punt op de sfeer nemen,
Ik zou je natuurlijk een keer het document kunnen sturen, dat je het een keer doorleest wanneer je zin hebt. Ik moet eerst nog legio wijzingen en addities doorvoeren, dus nu nog niet. Ik stelde je hulp met de Mercatorprojectie zeer op prijs, dus misschien dat je nogmaals wat tijd voor me vrij kunt maken?
Volgens deze URL: http://nl.wikipedia.org/wiki/Sfeer_(wiskunde) is aanname nog niet eens zo slecht. Je spreekt van een strikt wiskundige definitie, op zich wel een aardigheidje dat mijn werkstuk ook over een wiskundig onderwerp gaat. Nu even zonder satire, raad je het me aan om het te vervangen door boloppervlak, of iets in die trend? Of is het correct genoeg om te laten staan, afgezien van het dagelijkse gebruik?quote:
[..]
Ja, dat is ook mijn bezwaar. Je kunt je het beste houden aan de gebruikelijke terminologie in serieuze (wetenschappelijke) publicaties in het Nederlands over jouw specifieke onderwerp. Ik heb zelf de indruk dat het woord sfeer in het Nederlands vooral in een strict wiskundige contekst wordt gebruikt, zoals in het begrip Riemann-sfeer.
[..]
Deze zin loopt niet lekker, is niet echt goed Nederlands, en klinkt ook wat te hoogdravend. Maak er iets van als de literatuur over de verschillende cilinderprojecties biedt voldoende materiaal voor een uitgebreid werkstuk.
[..]
Ik wil je werkstuk t.z.t. best doornemen, maar dat kan dan pas ruim na de feestdagen.
Ik maak een aantekening. Ik houd van hoogdravende zinnen, maar ik zie zo even niet in wat er precies (taalkundig) niet goed aan is. Kun je dit nader toelichten?
Inderdaad, na de feestdagen pas. Het doel is om mijn werkstuk medio februari af te hebben, met mijn begeleidend docent heb ik afgesproken dat ik eind januari een conceptversie inlever, en ik loop ruim op schema. Onze laatste ontmoeting was dinsdag jongstleden, met de toen doorgenomen stof vond hij dat ik me op 80% bevond met voldoende vwo-diepgang.
Echter sprak hij ook over iets 'persoonlijks', vooral bij de stereografische projectie. Is het mogelijk dat ik de GPS coördinaten van (bijvoorbeeld) Eindhoven (E), Amsterdam(A) en Venlo (V) opzoek, uit deze coördinaten de hoek AEV afleidt, en dit bijvoorbeeld met een (Mercator)kaart van Nederland bevestig?
Ofwel, de hoek die deze 3 plaatsen met elkaar maken op het aardoppervlak is dus gelijk aan de hoek die loxodromen met elkaar maken, als ik het goed begrepen heb. Maar hoe haal ik deze hoek eruit?
Zo'n 'toepassing' moest ik gebruiken voor mijn presentatie/werkstuk om te laten zien dat mijn werkstuk authentiek is.
[ Bericht 0% gewijzigd door #ANONIEM op 19-12-2012 22:22:21 ]
Op grond van het artikel waarnaar je linkte en artikelen in de Nederlandse Wikipedia had ik de indruk dat het woord sfeer niet zo gebruikelijk is in Nederlandstalige publicaties over cartografie. Dat het een courante wiskundige term is weet ik ook wel, maar zoals gezegd kun je het beste aansluiting zoeken bij wat in de literatuur over jouw specifieke onderwerp gebruikelijk is, en dat zul je toch echt zelf na moeten gaan, ik ken de literatuur over cilindrische kaartprojecties niet.quote:
[..]
Volgens deze URL: http://nl.wikipedia.org/wiki/Sfeer_(wiskunde) is aanname nog niet eens zo slecht. Je spreekt van een strikt wiskundige definitie, op zich wel een aardigheidje dat mijn werkstuk ook over een wiskundig onderwerp gaat. Nu even zonder satire, raad je het me aan om het te vervangen door boloppervlak, of iets in die trend? Of is het correct genoeg om te laten staan, afgezien van het dagelijkse gebruik?
- materie in de diversiteit kun je zo niet laten staan, dat zou diversiteit in de materie moeten zijn, maar dan nog is het gebruik van het woord materie hier niet correct. Het woord materie wordt gebruikt in de fysica, en ook wel om het geheel aan te duiden van een bepaald onderwerp, zoals in: dit is een moeilijke materie. Materie duidt een niet-telbare kwantiteit aan, bij discrete (telbare) kwantiteiten gebruik je het woord materiaal. Je kunt bijvoorbeeld niet zeggen het NIOD heeft veel materie over de Tweede Wereldoorlog, dat moet zijn veel materiaal (of: veel documentatie).quote:Ik maak een aantekening. Ik houd van hoogdravende zinnen, maar ik zie zo even niet in wat er precies (taalkundig) niet goed aan is. Kun je dit nader toelichten?
- der klinkt hier wat archaïsch hoewel het niet fout is. Naamvallen van lidwoorden zijn wel courant in gezegdes en staande uitdrukkingen, en uiteraard in citaten van oudere teksten of titels van geraadpleegde oudere publicaties.
- een vullend werkstuk kun je zo niet laten staan, het gebruik van een actief deelwoord is hier in ieder geval fout. Het werkstuk zelf vult niets, jij stelt een werkstuk met een rijke inhoud in het vooruitzicht. Een goed gevuld werkstuk kan echter ook niet, dat klinkt als een blik rijk gevulde erwtensoep of iets anders uit een folder van de plaatselijke supermarkt.
- creëeren moet creëren zijn.
Dat lijkt me niet moeilijk, geografische coördinaten van plaatsen op aarde zijn gemakkelijk op te zoeken via Google Maps.quote:Inderdaad, na de feestdagen pas. Het doel is om mijn werkstuk medio februari af te hebben, met mijn begeleidend docent heb ik afgesproken dat ik eind januari een conceptversie inlever, en ik loop ruim op schema. Onze laatste ontmoeting was dinsdag jongstleden, met de toen doorgenomen stof vond hij dat ik me op 80% bevond met voldoende vwo-diepgang.
Echter sprak hij ook over iets 'persoonlijks', vooral bij de stereografische projectie. Is het mogelijk dat ik de GPS coördinaten van (bijvoorbeeld) Eindhoven (E), Amsterdam(A) en Venlo (V) opzoek, uit deze coördinaten de hoek AEV afleidt, en dit bijvoorbeeld met een (Mercatorkaart) van Nederland bevestig?
Daar mag je de komende tijd eens over gaan nadenken. Hiervoor heb je boldriehoeksmeting nodig. Op de site van het Nederlands schoolmuseum zijn voldoende boekjes te vinden over boldriehoeksmeting uit de tijd dat dat nog een schoolvak was.quote:Ofwel, de hoek die deze 3 plaatsen met elkaar maken op het aardoppervlak is dus gelijk aan de hoek die loxodromen met elkaar maken, als ik het goed begrepen heb. Maar hoe haal ik deze hoek eruit?
Ah zo, en daarom vraag je mij even om het op te lossen?quote:Zo'n 'toepassing' moest ik gebruiken voor mijn presentatie/werkstuk om te laten zien dat mijn werkstuk authentiek is.
[ Bericht 0% gewijzigd door Riparius op 19-12-2012 23:21:39 ]
Dit is geen hoogdravende zin hoor. Een zin is niet hoogdravend als de zin niet prettig leest. Schrijf je je werkstuk om gelezen te worden of niet?quote:
[..]
Ik maak een aantekening. Ik houd van hoogdravende zinnen, maar ik zie zo even niet in wat er precies (taalkundig) niet goed aan is. Kun je dit nader toelichten?
Boldriehoeksmeting, staat genoteerd.
Neen, niet direct oplossen, ik vroeg me af of dit mogelijk was. Prima opgelost zo
En er rijst direct een vraag op. Bij sferische trigonometrie worden lijnstukken vervangen door geodeten. Maar op mijn kaart zijn juist de loxodromen rechte lijnen, als ik dan de hoek op de kaart opmeet, moet die dan niet equivalent zijn aan de hoek de de loxodromen maken op de sfeer? Bij de bolmeetkunde gaat men juist met orthodromen werken, zo zegt het Wikipedia artikel.
Er staat slechts 1 vraag
[ Bericht 53% gewijzigd door #ANONIEM op 19-12-2012 23:48:09 ]
Neen, niet direct oplossen, ik vroeg me af of dit mogelijk was. Prima opgelost zo
En er rijst direct een vraag op. Bij sferische trigonometrie worden lijnstukken vervangen door geodeten. Maar op mijn kaart zijn juist de loxodromen rechte lijnen, als ik dan de hoek op de kaart opmeet, moet die dan niet equivalent zijn aan de hoek de de loxodromen maken op de sfeer? Bij de bolmeetkunde gaat men juist met orthodromen werken, zo zegt het Wikipedia artikel.
Er staat slechts 1 vraag
[ Bericht 53% gewijzigd door #ANONIEM op 19-12-2012 23:48:09 ]
Ah, op deze manier. Je had het over de hoek Amsterdam - Eindhoven - Venlo op het aardoppervlak, en dan denk ik toch automatisch aan een boldriehoek. Maar de zijden hiervan zijn inderdaad geen loxodromen. Als je ∠AEV op je kaartprojectie wil berekenen, dan bereken je eerst de cartesische coördinaten A(x1;y1), E(x2;y2) en V(x3;y3) van de drie punten op je kaart en dan kun je ∠AEV op de kaart berekenen. Bij een Mercatorprojectie is dit dan inderdaad de hoek tussen de loxodromen EA en EV.quote:
Boldriehoeksmeting, staat genoteerd.
Neen, niet direct oplossen, ik vroeg me af of dit mogelijk was. Prima opgelost zo
En er rijst direct een vraag op. Bij sferische trigonometrie worden lijnstukken vervangen door geodeten. Maar op mijn kaart zijn juist de loxodromen rechte lijnen, als ik dan de hoek op de kaart opmeet, moet die dan niet equivalent zijn aan de hoek de de loxodromen maken op de sfeer? Bij de bolmeetkunde gaat men juist met orthodromen werken, zo zegt het Wikipedia artikel.
Er staat slechts 1 vraag
Ik vroeg me af of het niet mogelijk was om dit andersom te doen, dus eerst de hoek die de loxodromen op het aardoppervlak met elkaar maken te berekenen met behulp van de bol, en dan een aha-momentje genereren door even heel intelligent met een Mercatorkaart aan te tonen dat dit juist is. Dat is wat mijn docent vroeg, althans. Het is natuurlijk ook gewoon 'goed' om eerst de Mercatorkaart hiervoor te gebruiken, en dan alsnog op basis van de bewezen conformiteit te stellen dat dit dan de hoek tussen loxodromen AE en EV moet zijn. Maar dan mis ik dat ziehiertada momentje waarmee ik in een klap de authenticiteit en de garantie op een goed cijfer veilig stel.quote:
[..]
Ah, op deze manier. Je had het over de hoek Amsterdam - Eindhoven - Venlo op het aardoppervlak, en dan denk ik toch automatisch aan een boldriehoek. Maar de zijden hiervan zijn inderdaad geen loxodromen. Als je ∠AEV op je kaartprojectie wil berekenen, dan bereken je eerst de cartesische coördinaten A(x1;y1), E(x2;y2) en V(x3;y3) van de drie punten op je kaart en dan kun je ∠AEV op de kaart berekenen. Bij een Mercatorprojectie is dit dan inderdaad de hoek tussen de loxodromen EA en EV.
Met authenticiteit bedoel ik natuurlijk dat ik het niet doodleuk van internet gekopieerd heb, maar er zelf ook moeite in gestoken heb en dergelijke. En beter gezegd, dat ik het bovenal begrepen heb.
Ik ga deze (na)middag beginnen aan het corrigeren van het werkstuk, heb nog flink wat kanttekeningen gekregen met kleine verbeterpuntjes, veelal taalkundig en wat gevraagde explicitering.
[ Bericht 0% gewijzigd door #ANONIEM op 20-12-2012 12:15:30 ]
thanks modje, maar gare layout van fok na edits ofzo 
[ Bericht 91% gewijzigd door #ANONIEM op 20-12-2012 13:34:50 ]
[ Bericht 91% gewijzigd door #ANONIEM op 20-12-2012 13:34:50 ]
En ik zat even na te denken over het bewijs van de equivalentie van de orthografische cilinderprojectie van Lambert.
Aangenomen dat voor een punt (λ;φ) geldt dat de cartesische coördinaten (x;y) luiden:
x = Rλ
y = Rsin(φ)
Als ik dan uitga van 'jouw methode' om aan te tonen dat het product van de schaalfactoren constant moet zijn om de equivalentie te bewijzen dan kom ik ongeveer op dit uit.
sh(λ;φ) = Δx/Δa
waarbij a de beweging over de bol is
Δx = RΔλ
Δa = Rcos(φ)*Δλ
Hierbij neem ik in acht dat de lengte v/d parallelcirkel gelijk is aan:
Rcosφ, waarbij φ de breedtegraad is.
ofwel sh(λ;φ) = Δx/Δa = (RΔλ)/(Rcos(φ)*Δλ) = 1/cosφ = secφ
Nu sv(λ;φ) = Δy/Δa, waarbij a wederom de beweging over de aardbol is, deze keer in verticale richting.
Δa = RΔλ
Alleen Δy vind ik moeilijk af te leiden. Ik kom wel op iets gaars uit dat:
Δy = R(tan(φ+Δφ) - tan(φ))
Of is dit dan weer niet algebraïsch te bewijzen, maar juist meetkundig? Ik las ergens iets dat het eenvoudig was om aan te tonen dat een smalle ring tussen 2 parallellen dezelfde oppervlakte op de kaart heeft als op de bol. Maar dit klopt toch niet, aangezien deze ring toch veel groter wordt, en niet smaller?
[ Bericht 0% gewijzigd door #ANONIEM op 20-12-2012 13:37:51 ]
Aangenomen dat voor een punt (λ;φ) geldt dat de cartesische coördinaten (x;y) luiden:
x = Rλ
y = Rsin(φ)
Als ik dan uitga van 'jouw methode' om aan te tonen dat het product van de schaalfactoren constant moet zijn om de equivalentie te bewijzen dan kom ik ongeveer op dit uit.
sh(λ;φ) = Δx/Δa
waarbij a de beweging over de bol is
Δx = RΔλ
Δa = Rcos(φ)*Δλ
Hierbij neem ik in acht dat de lengte v/d parallelcirkel gelijk is aan:
Rcosφ, waarbij φ de breedtegraad is.
ofwel sh(λ;φ) = Δx/Δa = (RΔλ)/(Rcos(φ)*Δλ) = 1/cosφ = secφ
Nu sv(λ;φ) = Δy/Δa, waarbij a wederom de beweging over de aardbol is, deze keer in verticale richting.
Δa = RΔλ
Alleen Δy vind ik moeilijk af te leiden. Ik kom wel op iets gaars uit dat:
Δy = R(tan(φ+Δφ) - tan(φ))
Of is dit dan weer niet algebraïsch te bewijzen, maar juist meetkundig? Ik las ergens iets dat het eenvoudig was om aan te tonen dat een smalle ring tussen 2 parallellen dezelfde oppervlakte op de kaart heeft als op de bol. Maar dit klopt toch niet, aangezien deze ring toch veel groter wordt, en niet smaller?
[ Bericht 0% gewijzigd door #ANONIEM op 20-12-2012 13:37:51 ]
Wat je hier doet klopt niet. Voor de orthografische cilinderprojectie van Lambert hebben we:quote:
En ik zat even na te denken over het bewijs van de equivalentie van de orthografische cilinderprojectie van Lambert.
x = s0∙R∙λ
y = s0∙R∙sin φ
De afbeelding in horizontale richting is hierbij hetzelfde als bij de Mercatorprojectie, en de formule voor de afbeelding in verticale richting had ik hier al afgeleid.
Voor de horizontale schaling sh(λ;φ) van een punt met geografische coördinaten (λ;φ) had ik verder hier al afgeleid dat we hebben:
sh(λ;φ) = s0∙sec φ
Nu de verticale schaalfactor sv(λ;φ) voor het punt met geografische coördinaten (λ;φ) bij de orthografische cilinderprojectie van Lambert. Voor de (georiënteerde) afstand a tot de evenaar gemeten langs een meridiaan hebben we a = R∙φ en dus da/dφ = R en dus dφ/da = 1/R. De verticale schaalfactor wordt dus:
sv(λ;φ) = dy/da = dy/dφ ∙ dφ/da = s0∙R∙cos φ ∙ (1/R) = s0∙cos φ
En voor het product van de horizontale en verticale schaalfactoren voor het punt met geografische coördinaten (λ;φ) hebben we dus:
sh(λ;φ)∙sv(λ;φ) = s0∙sec φ ∙ s0∙cos φ = s02
Het product van de horizontale en verticale schaalfactoren is dus onafhankelijk van λ en φ en daarmee een constante, zodat er sprake is van een equivalente oftewel oppervlaktegetrouwe projectie, QED.
Uiteraard kunnen we hetzelfde ook meetkundig bewijzen, en het aardige is dat dat al heel lang geleden is gedaan door Archimedes. Hij bewees namelijk dat de oppervlakte van een bolsegment gelijk is aan de oppervlakte van de projectie van dat bolsegment (of: bolschijf) op een omgeschreven cilinder van de bol als de as van de omgeschreven cilinder loodrecht op de snijvlakken van het bolsegment staat. Een consequentie hiervan is dat de oppervlakte van de gehele bol dus ook gelijk is aan de manteloppervlakte van de omgeschreven cilinder. Heb je een bol met straal r, dan heeft de mantel van de omgeschreven cilinder een omtrek 2πr en een hoogte 2r, zodat de oppervlakte van de bol dus gelijk is aan 2πr∙2r = 4πr2.quote:Of is dit dan weer niet algebraïsch te bewijzen, maar juist meetkundig? Ik las ergens iets dat het eenvoudig was om aan te tonen dat een smalle ring tussen 2 parallellen dezelfde oppervlakte op de kaart heeft als op de bol. Maar dit klopt toch niet, aangezien deze ring toch veel groter wordt, en niet smaller?
Je idee dat de oppervlakte van een gebied op aarde tussen twee parallellen niet gelijk zou zijn aan de projectie daarvan op een omgeschreven cilinder met de as loodrecht op de vlakken van de parallellen klopt gewoon niet. Denk daar maar eens over na.
Dit is veel minder eenvoudig dan je denkt, en omdat je al de mist ingaat met het berekenen van wat eenvoudige schaalfactoren denk ik dat je hier beter niet aan kunt beginnen. Ik heb wel een artikeltje voor je waar je eens naar zou kunnen kijken, maar de site van de MAA ligt momenteel plat, dus ik kan het artikel nu ook niet tevoorschijn toveren.quote:
[..]
Ik vroeg me af of het niet mogelijk was om dit andersom te doen, dus eerst de hoek die de loxodromen op het aardoppervlak met elkaar maken te berekenen met behulp van de bol, en dan een aha-momentje genereren door even heel intelligent met een Mercatorkaart aan te tonen dat dit juist is. Dat is wat mijn docent vroeg, althans.
Ik begrijp het, maar je krijgt niets voor niets.quote:Het is natuurlijk ook gewoon 'goed' om eerst de Mercatorkaart hiervoor te gebruiken, en dan alsnog op basis van de bewezen conformiteit te stellen dat dit dan de hoek tussen loxodromen AE en EV moet zijn. Maar dan mis ik dat ziehiertada momentje waarmee ik in een klap de authenticiteit en de garantie op een goed cijfer veilig stel.
Als je dingen van mij overneemt kopieer je ook van internet. Had je daar al eens bij stilgestaan?quote:Met authenticiteit bedoel ik natuurlijk dat ik het niet doodleuk van internet gekopieerd heb, maar er zelf ook moeite in gestoken heb en dergelijke. En beter gezegd, dat ik het bovenal begrepen heb.
quote:Ik ga deze (na)middag beginnen aan het corrigeren van het werkstuk, heb nog flink wat kanttekeningen gekregen met kleine verbeterpuntjes, veelal taalkundig en wat gevraagde explicitering.
Riparius; had jij een (hele) tijd terug een mooie post met een bewijs van 1+1 gelijk is aan 2?
Daar staat me iets van bij namelijk.
Oh, en bestaan er eigenlijk wel wiskunde vragen waar je geen antwoord op hebt? Zijn er gebieden in de wiskunde waar je minder affiniteit mee hebt?
Daar staat me iets van bij namelijk.
Oh, en bestaan er eigenlijk wel wiskunde vragen waar je geen antwoord op hebt? Zijn er gebieden in de wiskunde waar je minder affiniteit mee hebt?
kloep kloep
Dat was van Iblis. En nee, ik ben niet Iblis.quote:Op donderdag 20 december 2012 21:31 schreef Borizzz het volgende:
Riparius; had jij een (hele) tijd terug een mooie post met een bewijs van 1+1 gelijk is aan 2?
Daar staat me iets van bij namelijk.
Reken maar dat er vragen zijn waar ik geen antwoord op kan geven. Ik vind zelf dat ik maar betrekkelijk weinig wiskunde ken. En dat kan ook niet anders, want ik heb in een dictaat eens gelezen dat er veel meer wiskunde is dan in een mensenhoofd past. Vond ik wel een mooie gedachte.quote:Oh, en bestaan er eigenlijk wel wiskunde vragen waar je geen antwoord op hebt? Zijn er gebieden in de wiskunde waar je minder affiniteit mee hebt?
Oh was dat Iblis. Jammer dat hij er niet meer is. Ook aan hem heb ik destijds veel gehad.
Inderdaad een zeer mooie gedachte. Maar ook filosofisch van aard. Je bent nooit uitgeleerd in de wiskunde; er valt altijd weer iets nieuws te ontdekken. Schitterend toch?
Inderdaad een zeer mooie gedachte. Maar ook filosofisch van aard. Je bent nooit uitgeleerd in de wiskunde; er valt altijd weer iets nieuws te ontdekken. Schitterend toch?
kloep kloep
Ik bedoelde klakkeloos 1 op 1. Ik denk niet dat er van een vwo'er verwacht mag worden dat hij iets nieuws uitvindt, daar moet een promovendus zich maar mee bezighouden.quote:
[..]
Dit is veel minder eenvoudig dan je denkt, en omdat je al de mist ingaat met het berekenen van wat eenvoudige schaalfactoren denk ik dat je hier beter niet aan kunt beginnen. Ik heb wel een artikeltje voor je waar je eens naar zou kunnen kijken, maar de site van de MAA ligt momenteel plat, dus ik kan het artikel nu ook niet tevoorschijn toveren.
[..]
Ik begrijp het, maar je krijgt niets voor niets.
[..]
Als je dingen van mij overneemt kopieer je ook van internet. Had je daar al eens bij stilgestaan?
[..]
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt. Excuses, post gemist.Stel dat ik de 2 bovenste parallellen nabij de noordpool zou nemen, en de ring zou projecteren. Dan krijg je toch een omtrek (zie de rek op de orthografische projectie in horizontale richting) van 2piR? Dit terwijl de lengte van de parallel toch veel kleiner is, vanwege zijn geografische breedte.quote:Je idee dat de oppervlakte van een gebied op aarde tussen twee parallellen niet gelijk zou zijn aan de projectie daarvan op een omgeschreven cilinder met de as loodrecht op de vlakken van de parallellen klopt gewoon niet. Denk daar maar eens over na.
Daarom komt mij dit enigszins 'raar' voor.
En ik was al op de helft... En zo eenvoudig vind ik de afleiding van de verticale schaalfactor niet.Dit doet vrij weinig af aan een juist of onjuist antwoord Bram, sorry. Sterker nog, ik zou een 1/cos(x) = sec(x) zien als een vereenvoudiging, dus 'verplicht'. We laten x/x^2 toch ook niet staan wanneer we ook 1/x kunnen schrijven?quote:
Van ... = 1/cos(x) = sec(x) zou ik gewoon ... = 1/cos(x) of ... = sec(x) maken.
[ Bericht 7% gewijzigd door #ANONIEM op 20-12-2012 22:28:27 ]
Van ... = 1/cos(x) = sec(x) zou ik gewoon ... = 1/cos(x) of ... = sec(x) maken.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
quote:
Riparius; had jij een (hele) tijd terug een mooie post met een bewijs van 1+1 gelijk is aan 2?
Daar staat me iets van bij namelijk.
Oh, en bestaan er eigenlijk wel wiskunde vragen waar je geen antwoord op hebt? Zijn er gebieden in de wiskunde waar je minder affiniteit mee hebt?
quote:Op dinsdag 28 oktober 2008 22:20 schreef Iblis het volgende:
[..]
Neem de lege verzameling: {}. Definieer nu een recursieve relatie van een lijst waarbij we de opvolger van element k, zeg S(k), definiëren als S(k) = k ∪ {k}. Dan hebben we de volgende lijst: {}, {{}}, {{}, {{}} }, etc. Nu noemen we het eerste element 0. Het tweede 1, en het derde 2. Aldus construeren wij de natuurlijke getallen vanuit de lege verzameling. De symbolen gaan verder als 3, 4, 5, 6, 7, 8, 9, 10, maar dit is in feite arbitrair. Doch voor nu nemen we de gebruikelijke notatie aan.
Dan zijn er nog wat definities. Zij x een natuurlijk getal, en zijn y en z dit ook. Dan, x = x, x = y dan en slechts dan y = x, verder x = y en y = z, dan x = z en als laatste, als x een natuurlijk getal is en x = x', dan is x' ook een natuurlijk getal.
Voorts stipuleren we dat {} (noemen wij ook 0) een natuurlijk getal is, en dat S(k), waarbij k een natuurlijk getal is, ook een natuurlijk getal is. Verder nemen wij aan dat er geen k is zodanig dat S(k) = {}, en ook dat als S(x) = z, en S(y) = z, dat dan x = y. (Omgekeerd volgt natuurlijk direct uit de voorgaande axiomata).
Voor het gemak duiden we de verzameling van natuurlijke getallen aan met N, dan definiëren we + : N x N -> N, met als basisstap:
+(x, {}) = x (1)
En als recursie:
+(x, S(y)) = S(+(x, y)) (2)
Soms gebruiken we ook de infix-notatie en schrijven we derhalve x + y voor +(x, y).
Let op dat deze uiteenzetting niet helemaal formeel is, maar afdoende om het idee over te brengen.
Beschouw nu: 1 + 1, ofwel +({{}}, {{}}), dit voldoet niet aan (1), dus we moeten (2) toepassen, en dit zegt dat het gelijk is aan S(+({{}}, {})). De binnenste + kan nu weer nader beken worden, en deze voldoet wel aan (1). Dit geeft dat +({{}}, {}) gelijk is aan {{}}. Dat maakt dat de vergelijking vereenvoudigt tot S({{}}), wat per definitie van S gelijk is aan {{},{{}}}, of wel 2. QED.
Dit vanuit de set-theoretische constructie van de natuurlijke getallen, en de axiomata van Peano-Arithmetica. Een minstens zo elegant bewijs kan gegeven worden middels Church-numerals in de Lambda-calculus. Uiteindelijk komt het natuurlijk meer neer op een afspraak die wij maken hoe wij bepaalde verzamelingen (of lambda-functie-expressies) kort aanduiden met een cijfer, en de opvolgingsrelatie die wij daarin veronderstellen, dat volgt dat de som van 1 + 1 inderdaad gelijk is aan de opvolger van 1. Dit correspondeert redelijk met een discreet model van dingen in de werkelijkheid. Alhoewel je zou kunnen beargumenteren dat 1 druppel samen met 1 druppel weer één druppel is, en dat bovenstaande dit niet accuraat modelleert. Voor zulke vragen, in tegen stelling tot axiomatische afleidingen moet je denk ik in een WFL topic zijn, en je zou de Principia Mathematica er eens op na kunnen slaan.
[ Bericht 4% gewijzigd door #ANONIEM op 20-12-2012 22:08:19 ]
Ik ben ook wel benieuwd naar het bewijs van 1+1=2. Was dat wellicht met surreële getallen? Daarmee kan je dat soort "stellingen" wel bewijzen.
edit: oh ik zie nu dat ie hierboven al staat
[ Bericht 34% gewijzigd door thenxero op 20-12-2012 23:27:44 ]
edit: oh ik zie nu dat ie hierboven al staat
[ Bericht 34% gewijzigd door thenxero op 20-12-2012 23:27:44 ]
Dat moet je nooit zeggen. Don't sell yourself short. Ik moest toen ik dit las meteen denken aan de ontdekking van de toen 10-jarige Penny Drastik. Tot voor kort werd gedacht dat de minimale zijde van een vierkant dat je kunt verdelen in 5 rechthoekige driehoeken waarvan de zijden pythagoreïsche tripletten vormen een lengte 9000 moest hebben, maar Penny dacht daar toch anders over en kwam op de proppen met maar liefst 12 kleinere vierkanten die zich zo laten verdelen. Ze denkt ook dat het kleinste zo te verdelen vierkant een zijde 1248 moet hebben, en tot nu toe heeft niemand haar bevindingen kunnen weerleggen. Hier kun je er meer over lezen. Ook goed leesvoer voor achterlijke FOKkers die anno 2012 nog beweren dat wiskunde niets is voor meisjes.quote:
[..]
Ik bedoelde klakkeloos 1 op 1. Ik denk niet dat er van een vwo'er verwacht mag worden dat hij iets nieuws uitvindt, daar moet een promovendus zich maar mee bezighouden.
Je vergeet te bedenken dat het aardoppervlak niet parallel loopt aan de cilinder waarop je projecteert. Naarmate je dichter bij de polen komt, correspondeert met een vaste afstand in verticale richting op de projectie een steeds grotere afstand in verticale richting (langs een meridiaan) op het aardoppervlak.quote:Stel dat ik de 2 bovenste parallellen nabij de noordpool zou nemen, en de ring zou projecteren. Dan krijg je toch een omtrek (zie de rek op de orthografische projectie in horizontale richting) van 2piR? Dit terwijl de lengte van de parallel toch veel kleiner is, vanwege zijn geografische breedte.
Probeer maar eens met behulp van integraalrekening af te leiden dat de oppervlakte van een bolsegment inderdaad gelijk is aan de oppervlakte van de projectie van dat segment op een omgeschreven cilinder waarvan de as loodrecht staat op de snijvlakken van het bolsegment.
Aanwijzing: heb je de grafiek van een functie y = f(x) met f(x) ≥ 0 op een interval [a,b], dan is de manteloppervlakte van het omwentelingslichaam verkregen door de grafiek van f op het interval [a,b] rond de x-as te wentelen gelijk aan:
2π∙∫ab f(x)∙√(1 + (f'(x))2)dx
Kies een r > 0 en f(x) = √(r2 - x2) op [-r,r]. De grafiek van deze functie is uiteraard een halve cirkel met middelpunt in de oorsprong en straal r, zodat je bij wenteling om de x-as een bol krijgt met straal r. Je kunt nu integreren over een interval [p, p+h] met -r ≤ p < p+h ≤ r en dan zul je zien dat de oppervlakte van een bolsegment met hoogte h gelijk is aan 2πrh, en dus onafhankelijk van p en daarmee onafhankelijk van de positie van het segment in de bol.
De secans en cosecans worden tegenwoordig op het vasteland van Europa vrijwel niet meer gebruikt. In de VS (en in mindere mate in het Verenigd Koninkrijk) wel, en daar is een heel banale reden voor: meestal schrijft men daar sin-1x en cos-1x voor resp. arcsin x en arccos x, zodat de multiplicatieve inversen van sin x en cos x dus niet zo kunnen worden genoteerd en men daarom maar csc x en sec x handhaaft. Om dezelfde reden is de cotangens nog altijd 'populair' in de VS omdat men tan-1x schrijft voor arctan x. Uiteraard zou men er beter aan doen de misleidende notaties voor de inversen van de goniometrische functies (in 1813 geïntroduceerd door de Britse wiskundige en astronoom J.F.W. Herschel, 1792-1871) eindelijk eens af te schaffen.quote:Dit doet vrij weinig af aan een juist of onjuist antwoord Bram, sorry. Sterker nog, ik zou een 1/cos(x) = sec(x) zien als een vereenvoudiging, dus 'verplicht'. We laten x/x^2 toch ook niet staan wanneer we ook 1/x kunnen schrijven?
[ Bericht 1% gewijzigd door Riparius op 21-12-2012 03:56:26 ]
De geïnteresseerden in 1+1=2 kan ik aanraden om eens dit artikel te lezen. Het enige wat je nodig hebt is verzamelingen en een gezonde dosis logica. Daarmee worden getallen geconstrueerd waaruit allerlei basale eigenschappen zijn af te leiden. Ik vond het erg leuk om te lezenquote:
Ik ben ook wel benieuwd naar het bewijs van 1+1=2. Was dat wellicht met surreële getallen? Daarmee kan je dat soort "stellingen" wel bewijzen.
edit: oh ik zie nu dat ie hierboven al staat
.
Helaas denken ook veel meisjes dat nog.quote:Ook goed leesvoer voor achterlijke FOKkers die anno 2012 nog beweren dat wiskunde niets is voor meisjes.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik denk dat dit komt door de manier waarop wiskunde aan hen gepresenteerd wordt op het middelbaar onderwijs. Rijtjes sommen maken die uiteindelijk tot niets leiden. Als die Riparius zijn definitie van waardeloze wiskunde-educatie is, dan geef ik hem gelijk. Zeker in de eerste 4 jaar kom je binnen het vak wiskunde niets tegen dat je inspireert om verder te gaan. En daarnaast zal de diepgang ook wel missen, alhoewel je dat wel toe kunt schrijven aan het bovenstaande en iets van onwil.quote:
[..]
Helaas denken ook veel meisjes dat nog.
Riparius, ik ga je post nog een keer doornemen, vandaag weinig tijd. Knap wat Penny heeft gepresteerd, je hebt gelijk over mijn uitspraak.
Misschien hier iemand die hier uit komt?
Laat zien via het minimalisatie probleem
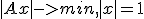
dat een eigenwaarde voor A bestaat.
(A een symmetrische n-bij-n matrix , x een kolomvector)
Laat zien via het minimalisatie probleem
dat een eigenwaarde voor A bestaat.
(A een symmetrische n-bij-n matrix , x een kolomvector)
ik snap je tex-code niet; wat is de doelfunctie, wat zijn de constraints, wat is het domein voor x, en wat is de optimale oplossing?
[ Bericht 36% gewijzigd door GlowMouse op 21-12-2012 14:08:12 ]
[ Bericht 36% gewijzigd door GlowMouse op 21-12-2012 14:08:12 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Mooie anekdotequote:
[..]
Dat moet je nooit zeggen. Don't sell yourself short. Ik moest toen ik dit las meteen denken aan de ontdekking van de toen 10-jarige Penny Drastik. Tot voor kort werd gedacht dat de minimale zijde van een vierkant dat je kunt verdelen in 5 rechthoekige driehoeken waarvan de zijden pythagoreïsche tripletten vormen een lengte 9000 moest hebben, maar Penny dacht daar toch anders over en kwam op de proppen met maar liefst 12 kleinere vierkanten die zich zo laten verdelen. Ze denkt ook dat het kleinste zo te verdelen vierkant een zijde 1248 moet hebben, en tot nu toe heeft niemand haar bevindingen kunnen weerleggen. Hier kun je er meer over lezen. Ook goed leesvoer voor achterlijke FOKkers die anno 2012 nog beweren dat wiskunde niets is voor meisjes.
Hoewel ik het idee heb dat sommige van de voorbeelden waar stellingen mee ontkracht worden meer een kwestie van geluk zijn (het geluk dat je bij toeval op zo'n voorbeeld stuit). (Hoewel hier dan weer minder van toepassing lijkt omdat dat meisje gelijk 12 tegenvoorbeelden heeft gevonden)
[ Bericht 3% gewijzigd door kutkloon7 op 21-12-2012 17:23:16 ]
Uhuh, bij dat soort problemen is het volgens mij vaak ook een beetje dat bijna niemand er meer serieus naar kijkt omdat het van te voren al onwaarschijnlijk lijkt dat je er verder mee komt. Maar ik bedoelde eigenlijk specifiek tegenvoorbeelden, en dan met name in de geometrie (maar in de getaltheorie bijvoorbeeld, speelt volgens mij precies hetzelfde).quote:
Het gebeurt wel vaker SES / Geniale student lost wiskundig probleem op
Jammer genoeg word ik van dat hele topic niet veel wijzer, en ik zie ook geen serieuze bronnen. Wat ik ervan begrijp is dat hij een differentiaalvergelijking exact heeft weten op te lossen die tot dan toe alleen numeriek kon worden opgelost. Ik zou zijn werk wel eens willen zien.quote:
Het gebeurt wel vaker SES / Geniale student lost wiskundig probleem op
Ik moet de kritieke punten vinden van deze formule:
f(x,y) = x^3+y*x^2-y^2-4*y
De x afgeleide is:
3*x^2 + 2*x*y
Deze is 0 bij (0,y) (-2,-6) en (2,-6)
De y afgeleide is:
x^2-2*y-4
Deze is 0 bij (-2,0) (2,0) (4,6) en (-4,6)
Dit levert echter geen kritieke punten op dus ik moet haast wel iets verkeerd doen bij de afgeleides.
Wie ziet de fout?
f(x,y) = x^3+y*x^2-y^2-4*y
De x afgeleide is:
3*x^2 + 2*x*y
Deze is 0 bij (0,y) (-2,-6) en (2,-6)
De y afgeleide is:
x^2-2*y-4
Deze is 0 bij (-2,0) (2,0) (4,6) en (-4,6)
Dit levert echter geen kritieke punten op dus ik moet haast wel iets verkeerd doen bij de afgeleides.
Wie ziet de fout?
When I get sad, I stop being sad and just be awesome instead.
Los eerst je stelsel fx(x,y) = 0, fy(x,y) = 0 eens fatsoenlijk op. Dan vind je (-4;6), (0;-2) en (1;-3/2).quote:Op vrijdag 21 december 2012 18:30 schreef MouzurX het volgende:
Ik moet de kritieke punten vinden van deze formule functie:
f(x,y) = x^3+y*x^2-y^2-4*y
De afgeleide naar x is:
3*x^2 + 2*x*y
Deze is 0 bij (0,y) (-2,-6) en (2,-6)
De afgeleide naar y is:
x^2-2*y-4
Deze is 0 bij (-2,0) (2,0) (4,6) en (-4,6)
Dit levert echter geen kritieke punten op dus ik moet haast wel iets verkeerd doen bij de afgeleides.
Wie ziet de fout?
Ah dus dan is (0,-2) een kritiek punt.quote:
[..]
Los eerst je stelsel fx(x,y) = 0, fy(x,y) = 0 eens fatsoenlijk op. Dan vind je (-4;6), (0;-2) en (1;-3/2).
When I get sad, I stop being sad and just be awesome instead.
Ik moet het uit mijn hoofd doen, het was een tentamenvraag.quote:
ik snap je tex-code niet; wat is de doelfunctie, wat zijn de constraints, wat is het domein voor x, en wat is de optimale oplossing?
De doelfunctie is |Ax|. Die moet geminimaliseerd worden onder de restrictie |x| = 1. Domein was niks bijzonders mee geloof ik, gewoon x element van (reëele getallen dimensie n). Optimale oplossing niet gegeven.
Zou je een duidelijk voorbeeld kunnen geven van een onjuist gebleken hypothese in de wiskunde waarbij de ontkrachting naar jouw idee puur een kwestie van 'geluk' of 'toeval' was? Een stelling kan overigens niet ontkracht worden als het bewijs deugdelijk is.quote:
[..]
Mooie anekdote
Hoewel ik het idee heb dat sommige van de voorbeelden waar stellingen mee ontkracht worden meer een kwestie van geluk zijn (het geluk dat je bij toeval op zo'n voorbeeld stuit). (Hoewel hier dan weer minder van toepassing lijkt omdat dat meisje gelijk 12 tegenvoorbeelden heeft gevonden)
Ik kon helaas ook geen goede bron vinden van wat hij nou precies gedaan had.quote:
[..]
Jammer genoeg word ik van dat hele topic niet veel wijzer, en ik zie ook geen serieuze bronnen. Wat ik ervan begrijp is dat hij een differentiaalvergelijking exact heeft weten op te lossen die tot dan toe alleen numeriek kon worden opgelost. Ik zou zijn werk wel eens willen zien.
Iedere matrix A heeft een complexe eigenwaarde. Dus ik denk dat er nog iets mist.quote:
[..]
Ik moet het uit mijn hoofd doen, het was een tentamenvraag.
De doelfunctie is |Ax|. Die moet geminimaliseerd worden onder de restrictie |x| = 1. Domein was niks bijzonders mee geloof ik, gewoon x element van (reëele getallen dimensie n). Optimale oplossing niet gegeven.
Nee, dat klopt uiteraardquote:
[..]
Zou je een duidelijk voorbeeld kunnen geven van een onjuist gebleken hypothese in de wiskunde waarbij de ontkrachting naar jouw idee puur een kwestie van 'geluk' of 'toeval' was? Een stelling kan overigens niet ontkracht worden als het bewijs deugdelijk is.
Ik zal zo eens kijken of ik mijn getaltheorieboek of dictaat een goed voorbeeld kan vinden, ik heb helaas niet zo'n uitstekend geheugen als jij voor dat soort dingen
.
Ik vraag me het volgende af (in verband met asymptotische stabiliteit van een systeem):
als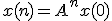
met x(n) een Nx1 matrix, A een NxN matrix en x(0) een Nx1 matrix (x is afhankelijk van de variabele n).
A is diagonaliseerbaar, dus ik kan schrijven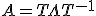
met T de matrix met in de kolommen de eigenvectoren van A, en 
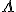de eigenwaardematrix.
Dus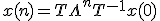
. Nu is gevraagd aan te tonen dat voor de limiet van n -> ∞ zal gelden dat x(n) -> 0 (de nulmatrix), als en slechts als de norm van alle eigenwaarden van A (dus alle diagonaalelementen van 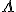) kleiner is dan één.
Het is simpel om te bewijzen dat als de norm van de eigenwaarden kleiner is dan één, dat dan x(n) -> 0, maar in de omgekeerde richting zie ik het niet direct.
Ik vermoed dat het echter niet zo moeilijk zal zijn.
[ Bericht 9% gewijzigd door yarnamc op 21-12-2012 23:16:19 ]
als
A is diagonaliseerbaar, dus ik kan schrijven
Dus
Het is simpel om te bewijzen dat als de norm van de eigenwaarden kleiner is dan één, dat dan x(n) -> 0, maar in de omgekeerde richting zie ik het niet direct.
Ik vermoed dat het echter niet zo moeilijk zal zijn.
[ Bericht 9% gewijzigd door yarnamc op 21-12-2012 23:16:19 ]
Probeer een bewijs uit het ongerijmde waarbij je voor x een eigenvector pakt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
http://tu-dresden.de/die_(...)eien/CommentsRay.pdfquote:
[..]
Jammer genoeg word ik van dat hele topic niet veel wijzer, en ik zie ook geen serieuze bronnen. Wat ik ervan begrijp is dat hij een differentiaalvergelijking exact heeft weten op te lossen die tot dan toe alleen numeriek kon worden opgelost. Ik zou zijn werk wel eens willen zien.
Hierin staat wat hij heeft gedaan (met commentaar van een aantal professoren)
In de laatste paragraaf staat dat hij eigenlijk niks nieuws heeft ontdekt, en zeker geen open probleem van Newton heeft opgelost. Zo zie je maar weer hoe de media werkt (en dat er geen wiskundigen werken).quote:
[..]
http://tu-dresden.de/die_(...)eien/CommentsRay.pdf
Hierin staat wat hij heeft gedaan (met commentaar van een aantal professoren)
Is A toevallig symmetrisch?quote:
[..]
Ik moet het uit mijn hoofd doen, het was een tentamenvraag.
De doelfunctie is |Ax|. Die moet geminimaliseerd worden onder de restrictie |x| = 1. Domein was niks bijzonders mee geloof ik, gewoon x element van (reëele getallen dimensie n). Optimale oplossing niet gegeven.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Aha dank je wel! Zo moet je het inderdaad doen, voor een eigenvector kom je dan uit dat zijn corresponderende eigenwaarde een modulus kleiner dan 1 heeft, en zo ga je ze allemaal af.quote:
Probeer een bewijs uit het ongerijmde waarbij je voor x een eigenvector pakt.
(ik merk nu op dat ik een klein beetje onnauwkeurig was in de formulering, de limiet moet gelden voor alle x(0))
Het kan sneller: neem aan dat er een eigenvector is met modulus >= 1.quote:
[..]
Aha dank je wel! Zo moet je het inderdaad doen, voor een eigenvector kom je dan uit dat zijn corresponderende eigenwaarde een modulus kleiner dan 1 heeft, en zo ga je ze allemaal af.
Ik denk dat je het antwoord in het Rayleigh quotient moet zoeken. Minimaliseren van ||Ax|| is hetzelfde als minimaliseren van het kwadraat ervan gedeeld door een constante: xTATAx / xTx. Dit is altijd groter dan de kleinste eigenwaarde van ATA, met gelijkheid desda x een eigenvector is horend bij de kleinste eigenwaarde.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik doe mijn profielwerkstuk over de chaostheorie en ben nu bezig met research doen naar de Lorenz Attractor. Ik stuitte op deze differentievergelijkingen:
Hoe zijn deze te schrijven als differentie vergelijkingen zoals die op de middelbare school worden geschreven? Dus bijvoorbeeld g(n)=3g(n-1) + 2 . Klopt dit:
x(n) = sigma * (y(n-1) - x(n-1))
y(n) = x(n-1) * (rho - x(n-1)) - y(n-1)
z(n) = x(n-1) * y(n-1) - beta * x(n-1)
Of mag dat niet zomaar tot die vorm herleid worden? Ben een beetje in de war omdat ik een differentievergelijking nog nooit zo geschreven heb zien maar het antwoord zal wel heel logisch zijn...
Hoe zijn deze te schrijven als differentie vergelijkingen zoals die op de middelbare school worden geschreven? Dus bijvoorbeeld g(n)=3g(n-1) + 2 . Klopt dit:
x(n) = sigma * (y(n-1) - x(n-1))
y(n) = x(n-1) * (rho - x(n-1)) - y(n-1)
z(n) = x(n-1) * y(n-1) - beta * x(n-1)
Of mag dat niet zomaar tot die vorm herleid worden? Ben een beetje in de war omdat ik een differentievergelijking nog nooit zo geschreven heb zien maar het antwoord zal wel heel logisch zijn...
Dit zijn differentiaalvergelijkingen, geen differentievergelijkingen.quote:
Ik doe mijn profielwerkstuk over de chaostheorie en ben nu bezig met research doen naar de Lorenz Attractor. Ik stuitte op deze differentievergelijkingen:
Ik heb nog een vraagje:
beschouw de differentievergelijking: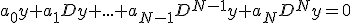
(de D staat voor de Delay operator: D(x(n)) = x(n-1), de n-de macht van D is de samenstelling van n delay operators).
Nu is er gegeven dat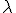
een meervoudige oplossing is van 
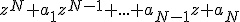, stel bijvoorbeeld met multipliciteit m.
Nu wordt er beweerd (vrij analoog als bij de homogene differentiaalvergelijking) dat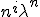
voor i = 0,1,...,m-1 oplossingen zijn van de differentievergelijking. Er wordt gevraagd dit te controleren via substitutie, maar dit lukt me niet direct :s.
Ik hoop dat iemand me kan helpen met het bovenstaande, misschien kan iemand ook dit oplossen (hoewel het moeilijk is om de volledige context te geven) : er wordt dan ook nog gesteld dat dit te controleren valt door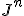
te berekenen, met J de Jordan-blok corresponderend met de meervoudige oplossing 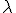. Je moet hierbij weten dat de differentievergelijking een systeem voorstelt, en dat lambda een meervoudige eigenwaarde is van de matrix A uit de ABCD-voorstelling (hiervan komt die veeltermvergelijking), omdat we het systeem bekijken vanuit het toestandsmodel.
Misschien komt dit voor iemand bekend voor en begrijpt hij wat ik met deze laatste paragraaf bedoel, anders zal ik al blij zijn als de eerste paragraaf opgelost wordt (een hint wat ik moet doen na de substitutie om van die vervelende (n-...)^i af te geraken zou heel handig zijn).
[ Bericht 15% gewijzigd door yarnamc op 23-12-2012 20:58:32 ]
beschouw de differentievergelijking:
Nu is er gegeven dat
Nu wordt er beweerd (vrij analoog als bij de homogene differentiaalvergelijking) dat
Ik hoop dat iemand me kan helpen met het bovenstaande, misschien kan iemand ook dit oplossen (hoewel het moeilijk is om de volledige context te geven) : er wordt dan ook nog gesteld dat dit te controleren valt door
Misschien komt dit voor iemand bekend voor en begrijpt hij wat ik met deze laatste paragraaf bedoel, anders zal ik al blij zijn als de eerste paragraaf opgelost wordt (een hint wat ik moet doen na de substitutie om van die vervelende (n-...)^i af te geraken zou heel handig zijn)
.[ Bericht 15% gewijzigd door yarnamc op 23-12-2012 20:58:32 ]
Aha ... ik had 'differential equations' te gauw vertaald naar differentievergelijkingen. Dat wordt nog even researchen!quote:
[..]
Dit zijn differentiaalvergelijkingen, geen differentievergelijkingen.
Je hebt in feite een rij {xn} die aan een N-de orde (hoofdletter!) homogene lineaire recursie met constante coëfficiënten moet voldoen. Substitutie van xn = zn levert dan een karakteristieke vergelijking P(z) = 0 op, waarbij P(z) een polynoom is in z van graad N (hoofdletter!). Is nu z = λ een (enkelvoudige) wortel van P(z) = 0, dan voldoet zoals bekend xn = λn aan de recursie. Is echter z = λ een meervoudige wortel van P(z) = 0 met multipliciteit m, dan kun je gebruik maken van het feit dat dan niet alleen P(λ) = 0 maar ook P(i)(λ) = 0 voor i = 1..(m-1) terwijl P(m)(λ) ≠ 0 (bewijs dit). Door te beginnen metquote:
Ik heb nog een vraagje:
beschouw de differentievergelijking:
Nu is er gegeven dat, stel bijvoorbeeld met multipliciteit m.
Nu wordt er beweerd (vrij analoog als bij de homogene differentiaalvergelijking) dat
∑j=0N ajzN+k-j = zk∙P(z), k ∈ N0
en telkens beide leden te differentiëren naar z en daarna weer te vermenigvuldigen met z kun je gemakkelijk zien dat
∑j=0N aj(N+k-j)iλN+k-j = 0 voor k ∈ N0, i = 1..(m-1)
zodat xn = ni∙λn met i = 1..(m-1) ook voldoet aan de recursie.
[ Bericht 0% gewijzigd door Riparius op 25-12-2012 17:55:37 ]
Weet iemand hier hoe je 'topological mixing' in het nederlands zegt? Heb het over dit:
http://en.wikipedia.org/w(...)g#Topological_mixing
en dan met name op de manier waarop het hier wordt uitgelegd, onder het subkopje 'Topological mixing':
http://en.wikipedia.org/wiki/Chaos_theory
Dus dat een gegeven regio in faseruimte na een bepaalde tijd altijd zal overlappen met een andere gegeven regio. Is daar een nederlandse term voor?
http://en.wikipedia.org/w(...)g#Topological_mixing
en dan met name op de manier waarop het hier wordt uitgelegd, onder het subkopje 'Topological mixing':
http://en.wikipedia.org/wiki/Chaos_theory
Dus dat een gegeven regio in faseruimte na een bepaalde tijd altijd zal overlappen met een andere gegeven regio. Is daar een nederlandse term voor?
In die vergelijkingen zijn x,y en z functies van t. rho, beta en sigma zijn parameters.quote:
Ik doe mijn profielwerkstuk over de chaostheorie en ben nu bezig met research doen naar de Lorenz Attractor. Ik stuitte op deze differentievergelijkingen:
[ afbeelding ]
Hoe zijn deze te schrijven als differentie vergelijkingen zoals die op de middelbare school worden geschreven? Dus bijvoorbeeld g(n)=3g(n-1) + 2 . Klopt dit:
x(n) = sigma * (y(n-1) - x(n-1))
y(n) = x(n-1) * (rho - x(n-1)) - y(n-1)
z(n) = x(n-1) * y(n-1) - beta * x(n-1)
Of mag dat niet zomaar tot die vorm herleid worden? Ben een beetje in de war omdat ik een differentievergelijking nog nooit zo geschreven heb zien maar het antwoord zal wel heel logisch zijn...
Is dit onderwerp niet te ambitieus voor een middelbare schoolleerling?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Kijk maar eens even hier (eenvoudig) en ook hier (uitgebreider, met historische achtergronden), dan moet het je wel duidelijk worden.quote:
Ik las ergens iets dat het eenvoudig was om aan te tonen dat een smalle ring tussen 2 parallellen dezelfde oppervlakte op de kaart heeft als op de bol. Maar dit klopt toch niet, aangezien deze ring toch veel groter wordt, en niet smaller?
Dat is knap gevonden! Dank je welquote:
[..]
Je hebt in feite een rij {xn} die aan een N-de orde (hoofdletter!) homogene lineaire recursie met constante coëfficiënten moet voldoen. Substutie van xn = zn levert dan een karakteristieke vergelijking P(z) = 0 op, waarbij P(z) een polynoom is in z van graad N (hoofdletter!). Is nu z = λ een (enkelvoudige) wortel van P(z) = 0, dan voldoet zoals bekend xn = λn aan de recursie. Is echter z = λ een meervoudige wortel van P(z) = 0 met multipliciteit m, dan kun je gebruik maken van het feit dat dan niet alleen P(λ) = 0 maar ook P(i)(λ) = 0 voor i = 1..(m-1) terwijl P(m)(λ) ≠ 0 (bewijs dit). Door te beginnen met
∑j=0N ajzN+k-j = zk∙P(z), k ∈ N0
en telkens beide leden te differentiëren naar z en daarna weer te vermenigvuldigen met z kun je gemakkelijk zien dat
∑j=0N aj(N+k-j)iλN+k-j = 0 voor k ∈ N0, i = 1..(m-1)
zodat xn = ni∙λn met i = 1..(m-1) ook voldoet aan de recursie.
Ik heb een vraag over het volgende lemma uit mijn leeswijzer functies en reeksen:
Neem n = p = 1 (en ik gebruikt y ipv dzeta xi, dat is wat makkelijker). Neem f(x) = x3. Dan is f totaal differentieerbaar (dit kan ik aantonen met de definitie, maar dat laat ik nu even achterwege).
Verder L(x) = Df (x) = 3x2. (dit staat in de laatste zin van het lemma, Df (x) is gewoon de afgeleide van f).
Dan komt de formule uit het lemma neer op:
x3 - y3 = 3x2(x-y)
Wat natuurlijk niet klopt. Doe ik iets verkeerd (klopt er een van mijn aannames niet?) of staat er iets verkeerd in het lemma?
[ Bericht 0% gewijzigd door kutkloon7 op 26-12-2012 21:55:23 ]
Neem n = p = 1 (en ik gebruikt y ipv dzeta xi, dat is wat makkelijker). Neem f(x) = x3. Dan is f totaal differentieerbaar (dit kan ik aantonen met de definitie, maar dat laat ik nu even achterwege).
Verder L(x) = Df (x) = 3x2. (dit staat in de laatste zin van het lemma, Df (x) is gewoon de afgeleide van f).
Dan komt de formule uit het lemma neer op:
x3 - y3 = 3x2(x-y)
Wat natuurlijk niet klopt. Doe ik iets verkeerd (klopt er een van mijn aannames niet?) of staat er iets verkeerd in het lemma?
[ Bericht 0% gewijzigd door kutkloon7 op 26-12-2012 21:55:23 ]
De verzameling lineaire afbeeldingen van Rn naar Rp. Dus ook wel de verzameling n bij p matrices met componenten uit R.quote:
Wat je verkeerd doet, is aannemen dat L over zijn hele domein gelijk is aan Df. De stelling zegt dat er een punt is, zodat L en Df in dat punt gelijk aan elkaar zijn. Er staat niets verkeerds in die stelling.quote:
Ik heb een vraag over het volgende lemma uit mijn leeswijzer functies en reeksen:
[ afbeelding ]
Neem n = p = 1 (en ik gebruikt y ipv dzeta xi, dat is wat makkelijker). Neem f(x) = x3. Dan is f totaal differentieerbaar (dit kan ik aantonen met de definitie, maar dat laat ik nu even achterwege).
Verder L(x) = Df (x) = 3x2. (dit staat in de laatste zin van het lemma, Df (x) is gewoon de afgeleide van f).
Dan komt de formule uit het lemma neer op:
x3 - y3 = 3x2(x-y)
Wat natuurlijk niet klopt. Doe ik iets verkeerd (klopt er een van mijn aannames niet?) of staat er iets verkeerd in het lemma?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Mathemaat heeft gelijk.
x3 - y3 = L(x)(x-y) voor elke x in X.
Dan geldt dus L(x) = x2 + xy + y2
Dus geldt L(y) = 3y2
x3 - y3 = L(x)(x-y) voor elke x in X.
Dan geldt dus L(x) = x2 + xy + y2
Dus geldt L(y) = 3y2
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
L(x) kan je opvatting als de helling tussen de punten f(x) en f(ksi) (makkelijkst om gewoon even in 1 dimensie te denken). De stelling zegt dus eigenlijk dat een functie differentieerbaar is in een punt desda de helling continu is in dat punt. Zo kan je het makkelijk begrijpen en onthouden.
Ik maakte inderdaad een denkfout, dank! Ik had om een of andere reden inderdaad niet goed door dat ze xi in het hele verhaal vast kiezen, it all makes sense nowquote:
[..]
Wat je verkeerd doet, is aannemen dat L over zijn hele domein gelijk is aan Df. De stelling zegt dat er een punt is, zodat L en Df in dat punt gelijk aan elkaar zijn. Er staat niets verkeerds in die stelling.
Ook dank Glowmouse en thenxzero, voor de extra uitleg.
Hallo, ik heb wiskunde A en krijg de abc-formule niet. Toch heb ik die nodig voor scheikunde. Ik moet bijv. dit oplossen:
Dit is dus de abc formule:
Kan iemand uitleggen hoe dit werkt in mijn situatie? (stap voor stap graag, ik heb alleen wiskunde A).
Dit is dus de abc formule:
Kan iemand uitleggen hoe dit werkt in mijn situatie? (stap voor stap graag, ik heb alleen wiskunde A).
Unbowed, Unbent, Unbroken.
Probeer eerst de op te lossen vergelijking in de vorm van de abc-formule te zetten. Het omschrijven van die vergelijking zou je met wiskunde A moeten kunnen.
Zo?
x^2 - 6,1*10^-10 * (0,01-x) = 0 Daarna haakjes wegwerken zodat:
1*x^2 + 6,1*10^-10*x + (-6.1*10^-12)
met a = 1
b = 6,1*10^-10
c= -6,1*10^-12
Oké, ik ga het even uitproberen om hem nu in die wortelvariant te zetten.
E: Waarschijnlijk doe ik iets fout. Ik krijg 1,26*10^-5, het antw. moet 2,5&10^-6 zijn.
E2: Het werkt wel, oké klaar, duidelijk. Bedankt.
[ Bericht 13% gewijzigd door BeyondTheGreen op 27-12-2012 13:50:18 ]
x^2 - 6,1*10^-10 * (0,01-x) = 0 Daarna haakjes wegwerken zodat:
1*x^2 + 6,1*10^-10*x + (-6.1*10^-12)
met a = 1
b = 6,1*10^-10
c= -6,1*10^-12
Oké, ik ga het even uitproberen om hem nu in die wortelvariant te zetten.
E: Waarschijnlijk doe ik iets fout. Ik krijg 1,26*10^-5, het antw. moet 2,5&10^-6 zijn.
E2: Het werkt wel, oké klaar, duidelijk.
Bedankt.[ Bericht 13% gewijzigd door BeyondTheGreen op 27-12-2012 13:50:18 ]
Unbowed, Unbent, Unbroken.
quote:
Zo?
x^2 - 6,1*10^-10 * (0,01-x) = 0 Daarna haakjes wegwerken zodat:
1*x^2 + 6,1*10^-10*x + (-6.1*10^-12)
met a = 1
b = 6,1*10^-10
c= -6,1*10^-12
Oké, ik ga het even uitproberen om hem nu in die wortelvariant te zetten.
E: Waarschijnlijk doe ik iets fout. Ik krijg 1,26*10^-5, het antw. moet 2,5&10^-6 zijn.
E2: Het werkt wel, oké klaar, duidelijk.
De ABC-formule is de manier om de 2 (complexe) nulpunten (ofwel f(x) = 0) van een tweedegraads polynoom exact te berekenen.quote:
Hallo, ik heb wiskunde A en krijg de abc-formule niet. Toch heb ik die nodig voor scheikunde. Ik moet bijv. dit oplossen:
[ afbeelding ]
Dit is dus de abc formule:
[ afbeelding ]
Kan iemand uitleggen hoe dit werkt in mijn situatie? (stap voor stap graag, ik heb alleen wiskunde A).
Wanneer geldt:
D > 0 : 2 reëele oplossingen
D=0 : 1 reëele oplossing, ofwel de top valt samen met de x-as
D<0 : 2 complexe oplossingen.
Bijvoorbeeld wanneer D = -9, dan geldt √D = √(-9) = √(i2)*√9 = i√9
i = √(-1)
D = b2 -4ac
Het is misschien wel nuttig om dit bewijs even te onderzoeken, maar ik neem aan dat je dit wel ergens op kunt snorren.
Geven ze dit tegenwoordig niet meer bij wisA?
nl.m.wikipedia.org/wiki/Wortelformule
Hier een afleiding van de formule.
Ik neem het door.quote:
[..]
Kijk maar eens even hier (eenvoudig) en ook hier (uitgebreider, met historische achtergronden), dan moet het je wel duidelijk worden.
Mijn excuses voor 'n laatste reactie. Loopt niet helemaal lekker thuis, knalt zover uit de pan dat het tot een scheiding van m'n ouders loopt en ik word daar flink in betrokken. Maar dat terzijde.
In de eerste post geeft hij aan dat je zelf even de gelijkvormigheid mag bewijzen. Ik heb het geheel correct wanneer ik stel dat aangezien AB een raaklijn in A is, de totale hoek A 90 graden is, en uit de driehoekensom dan volgt dat hoek BAC = hoek DCM en hoek BCA = hoek CDM = 90 graden?
Dus de driehoeken zijn gelijkvormig (hh).
Dit weekend meer. Ik moet
De vadsige koningen lezen, van Hugo Raes. Wat een grafboek is dat. Nederlandse literatuur 
(Met uitzonderingen uiteraard, Lijmen het Been 
en De Engelenmaker )[ Bericht 16% gewijzigd door #ANONIEM op 27-12-2012 18:43:38 ]
Deze notatie is prima tenzij er meer dan 1 onafhankelijke variabele in de vergelijking staat in welk geval je het als een partiële afgeleide moet weergeven met een teken wat lijkt op een a.quote:
Ik doe mijn profielwerkstuk over de chaostheorie en ben nu bezig met research doen naar de Lorenz Attractor. Ik stuitte op deze differentievergelijkingen:
[ afbeelding ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Als je de wortelformule gebruikt, bekijk dan ook even hoe die formule is afgeleid zodat je begrijpt wat je doet!quote:
Hallo, ik heb wiskunde A en krijg de abc-formule niet. Toch heb ik die nodig voor scheikunde. Ik moet bijv. dit oplossen:
[ afbeelding ]
Dit is dus de abc formule:
[ afbeelding ]
Kan iemand uitleggen hoe dit werkt in mijn situatie? (stap voor stap graag, ik heb alleen wiskunde A).
http://nl.wikipedia.org/wiki/Wortelformule
http://nl.wikipedia.org/wiki/Kwadraatsplitsen
Het is een simpele uitleg waarvoor je weinig basis nodig hebt, als je weet hoe je een eerstegraadsvergelijking kan oplossen dan zou je deze uitleg ook moeten kunnen volgen.
Kijk ook even naar de Engelstalige versie als je moeite hebt met iets te volgen.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik ben iemand die graag begrijpt wat ik doe, maar ik heb geen wiskunde B, doe drie VWO schooljaar in 1, en heb een tentamenweek na de kerstvakantie dus mijn prioriteit ligt daar niet. Toch bedankt, misschien kijk ik er nog eens naar.quote:
[..]
Als je de wortelformule gebruikt, bekijk dan ook even hoe die formule is afgeleid zodat je begrijpt wat je doet!
http://nl.wikipedia.org/wiki/Wortelformule
http://nl.wikipedia.org/wiki/Kwadraatsplitsen
Het is een simpele uitleg waarvoor je weinig basis nodig hebt, als je weet hoe je een eerstegraadsvergelijking kan oplossen dan zou je deze uitleg ook moeten kunnen volgen.
Kijk ook even naar de Engelstalige versie als je moeite hebt met iets te volgen.
Unbowed, Unbent, Unbroken.
Misschien een beetje opportunistisch om 3 schooljaren in een jaar af te willen ronden wanneer je het toepassen van de ABC-formule al niet volgt.quote:
[..]
Ik ben iemand die graag begrijpt wat ik doe, maar ik heb geen wiskunde B, doe drie VWO schooljaar in 1, en heb een tentamenweek na de kerstvakantie dus mijn prioriteit ligt daar niet. Toch bedankt, misschien kijk ik er nog eens naar.
Blame the system.quote:
[..]
Misschien een beetje opportunistisch om 3 schooljaren in een jaar af te willen ronden wanneer je het toepassen van de ABC-formule al niet volgt.
Vroeger leerde je in 1-MAVO of 2-MAVO de wortelformule te gebruiken.
Dit is uiteraard geen verwijt naar hem toe maar het doet de wenkbrauwen fronsen.
Dit is uiteraard geen verwijt naar hem toe maar het doet de wenkbrauwen fronsen.
In een kwartier tijd heb je het wel gelezen en begrepen als het goed is, het lijkt mij zinvol besteedde tijd.quote:
[..]
Ik ben iemand die graag begrijpt wat ik doe, maar ik heb geen wiskunde B, doe drie VWO schooljaar in 1, en heb een tentamenweek na de kerstvakantie dus mijn prioriteit ligt daar niet. Toch bedankt, misschien kijk ik er nog eens naar.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |