SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



De vraag staat er verkeerd, de rij waar het om gaat is an(-1)n. Als je an = (-1)n+1 pakt dan zie je dat jouw antwoord niet klopt.quote:Op dinsdag 4 december 2012 21:06 schreef kutkloon7 het volgende:
[..]
-edit: wacht even hoor, even wat beter kijken nog-
Als de limiet van de rij > 0 is, is de reeks sowieso niet convergent
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hier is zo geen chocola van te maken. Je praat over een reeks, maar geeft dan de notatie van een rij, en wat moet ik me bij die notatie voorstellen?quote:Op dinsdag 4 december 2012 20:49 schreef flopsies het volgende:
als je een alternerende reeks hebt zoals { (n+1)(-1)n } ,
Voor reeksen waarvan de termen alterneren heb je het criterium van Leibniz.
Als je een alternerende rij {an} hebt en een N zodanig dat
limn→∞ an = 0 ∧ ∀n>N |an+1| ≤ |an|
dan is de reeks ∑n=0 ∞ an convergent.
[ Bericht 0% gewijzigd door Riparius op 04-12-2012 21:26:01 ]


Hoezo, de reeks ∑n=0an heeft toch geen limiet als n naar oneindig gaat?quote:Op dinsdag 4 december 2012 21:12 schreef GlowMouse het volgende:
[..]
De vraag staat er verkeerd, de rij waar het om gaat is an(-1)n. Als je an = (-1)n+1 pakt dan zie je dat jouw antwoord niet klopt.


Klopt nog niet helemaal: je definieert an maar doet er vervolgens niks mee...
Ik snap ook niet helemaal wat je bedoelt: wil je nou weten of een specifieke reeks convergent is?
Ik snap ook niet helemaal wat je bedoelt: wil je nou weten of een specifieke reeks convergent is?


I see. Maar wat als de limiet van de rij (an) niet bestaat?quote:Op dinsdag 4 december 2012 21:06 schreef kutkloon7 het volgende:
[..]
-edit: wacht even hoor, even wat beter kijken nog-
Als de limiet van de rij > 0 is, is de reeks sowieso niet convergent
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dan bestaat de limiet van de bijbehorende reeks ook niet? (maar ik had het over het geval dat de limiet wel bestaat)quote:Op dinsdag 4 december 2012 21:28 schreef GlowMouse het volgende:
[..]
I see. Maar wat als de limiet van de rij (an) niet bestaat?


of dit de enige test is om te kijken of een alternerende reeks convergeert. Als de rij {an} niet voldoet
aan de voorwaarden die riparius ook heeft gepost, is de reeks ∑n=0 ∞ an dan sowieso NIET convergent? misschien een domme vraag maar ik wil het even zeker weten
aan de voorwaarden die riparius ook heeft gepost, is de reeks ∑n=0 ∞ an dan sowieso NIET convergent? misschien een domme vraag maar ik wil het even zeker weten


Het criterium van Leibniz is voldoende maar niet noodzakelijk voor convergentie van een reeks met alternerende termen. Beschouw bijvoorbeeld de rij {an} gedefinieerd door:quote:Op dinsdag 4 december 2012 21:34 schreef flopsies het volgende:
of dit de enige test is om te kijken of een alternerende reeks convergeert. Als de rij {an} niet voldoet
aan de voorwaarden die riparius ook heeft gepost, is de reeks ∑n=0 ∞ an dan sowieso NIET convergent? misschien een domme vraag maar ik wil het even zeker weten
an = ((-1)n+1∙|sin n|)/n2
Dan is |an| niet monotoon dalend terwijl ∑n=1 ∞ an toch convergeert.
[ Bericht 5% gewijzigd door Riparius op 04-12-2012 22:32:23 ]


Het criterium van Leibniz is wel sluitend voor alternerende, dalende reeksen. Als je alleen naar alternerende, dalende reeksen kijkt voldoet elke convergerende reeks aan het criterium en geen enkele niet-convergerende reeks.
Ik kom er nu net een tegen bij de inleveropgave voor functies en reeksen. We moeten de Fourier-coefficienten van de 2π-periodieke functie die op het interval [-π, π] gelijk is aan x2 bepalen.
Die blijkt gelijk te zijn aan (-1)k . 2/k2.
Om te bepalen of de bijbehorende Fourierreeks convergent is, moet je kijken of de som van al deze coefficienten convergeert. Ja dus, wat je aan kan tonen met Leibniz' criterium.
(er kunnen nog foutjes inzitten, ik ben er nog mee bezig )
)
[ Bericht 5% gewijzigd door kutkloon7 op 04-12-2012 23:58:12 ]
Ik kom er nu net een tegen bij de inleveropgave voor functies en reeksen. We moeten de Fourier-coefficienten van de 2π-periodieke functie die op het interval [-π, π] gelijk is aan x2 bepalen.
Die blijkt gelijk te zijn aan (-1)k . 2/k2.
Om te bepalen of de bijbehorende Fourierreeks convergent is, moet je kijken of de som van al deze coefficienten convergeert. Ja dus, wat je aan kan tonen met Leibniz' criterium.
(er kunnen nog foutjes inzitten, ik ben er nog mee bezig
[ Bericht 5% gewijzigd door kutkloon7 op 04-12-2012 23:58:12 ]


Ja, maar dat is niet in tegenspraak met wat ik hierboven beweer.quote:Op dinsdag 4 december 2012 23:53 schreef kutkloon7 het volgende:
Het criterium van Leibniz is wel sluitend voor alternerende, dalende reeksen. Als je alleen naar alternerende, dalende reeksen kijkt voldoet elke convergerende reeks aan het criterium en geen enkele niet-convergerende reeks.
Ik dacht dat de algemene term van de gedaante ((-1)k∙4∙cos kx)/k2 is. En dan nog een constante term π2/3 erbij.quote:Ik kom er nu net een tegen bij de inleveropgave voor functies en reeksen. We moeten de Fourier-coefficienten van de 2π-periodieke functie die op het interval [-π, π] gelijk is aan x2 bepalen.
Die blijkt gelijk te zijn aan (-1)k . 2/k2.
Inderdaad ... Vul trouwens eens x = 0 in, dan krijg je een alternerende reeks voor π2/12. Daarmee kun je gemakkelijk aantonen dat ∑k=1∞ 1/k2 = π2/6 (Bazel probleem).quote:Om te bepalen of de bijbehorende Fourierreeks convergent is, moet je kijken of de som van al deze coefficienten convergeert. Ja dus, wat je aan kan tonen met Leibniz' criterium.
(er kunnen nog foutjes inzitten, ik ben er nog mee bezig)


Uhuh, het was een aanvulling, geen verbeteringquote:Op woensdag 5 december 2012 00:14 schreef Riparius het volgende:
[..]
Ja, maar dat is niet in tegenspraak met wat ik hierboven beweer.
[..]
Ik dacht dat de algemene term van de gedaante ak = ((-1)k∙4∙cos kx)/k2 is. En dan nog een constante term π2/3 erbij.
[..]
Inderdaad ... Vul trouwens eens x = 0 in, dan krijg je een alternerende reeks voor π2/12. Daarmee kun je gemakkelijk aantonen dat ∑k=1∞ 1/k2 = π2/6 (Bazel probleem).
0 invullen is inderdaad een deel van de opgave.
Hm, ik ga er morgen nog maar even naar kijken denk ik... Volgens mij klopt het wel wat ik nu heb. Hoe kom je aan die algemene term?
In mijn dictaat staat dat de fourier coefficient gelijk is aan
En dat heb ik nagerekend, en dat lijkt te kloppen.
De constante term zou dan geloof ik 2/3π3 worden.
Ik heb wel complexe coefficienten gebruikt, misschien zit het hem daarin
[ Bericht 2% gewijzigd door kutkloon7 op 05-12-2012 00:35:20 ]


Ja, je had gelijk, ik ben eruit, het kwam inderdaad door die complexe coefficienten. Alleen die constante term heb ik nog wel anders.


Inderdaad, je moet natuurlijk twee complexe coëfficiënten ck en c-k hebben om de reële coëfficiënten ak = ck + c-k van de cosinustermen te krijgen.quote:Op woensdag 5 december 2012 00:27 schreef kutkloon7 het volgende:
[..]
Uhuh, het was een aanvulling, geen verbetering
0 invullen is inderdaad een deel van de opgave.
Hm, ik ga er morgen nog maar even naar kijken denk ik... Volgens mij klopt het wel wat ik nu heb. Hoe kom je aan die algemene term?
In mijn dictaat staat dat de fourier coefficient gelijk is aan
En dat heb ik nagerekend, en dat lijkt te kloppen.
De constante term zou dan geloof ik 2/3π3 worden.
Ik heb wel complexe coefficienten gebruikt, misschien zit het hem daarin


Ja, ik had nog niet helemaal door hoe dat precies werkte, ik werkte gewoon vanuit de uit het dictaat gegeven definities.quote:Op woensdag 5 december 2012 00:46 schreef Riparius het volgende:
[..]
Inderdaad, je moet natuurlijk twee complexe coëfficiënten ck en c-k hebben om de reële coëfficiënten ak = ck + c-k van de cosinustermen te krijgen.


Als je a0 berekent met de algemene integraal voor ak, dan moet je hiervan de helft nemen, de eerste term in de reeks geeft men daarom aan met ½a0. Dan krijg je dus π2/3 voor de constante term.quote:Op woensdag 5 december 2012 00:37 schreef kutkloon7 het volgende:
Ja, je had gelijk, ik ben eruit, het kwam inderdaad door die complexe coefficienten. Alleen die constante term heb ik nog wel anders.


Ja, wat ik de hele tijd al doe: de factor 1/2π vergeten, waardoor ik ook op π^3 uitkwam ipv π^2. Dank voor je hulp!quote:Op woensdag 5 december 2012 00:50 schreef Riparius het volgende:
[..]
Als je a0 berekent met de algemene integraal voor ak, dan moet je hiervan de helft nemen, de eerste term in de reeks geeft men daarom aan met ½a0. Dan krijg je dus π2/3 voor de constante term.


Je kunt je Fourier reeksen gemakkelijk controleren in WolframAlpha, zowel in goniometrische als in exponentiële vorm.quote:Op woensdag 5 december 2012 00:56 schreef kutkloon7 het volgende:
[..]
Ja, wat ik de hele tijd al doe: de factor 1/2π vergeten, waardoor ik ook op π^3 uitkwam ipv π^2. Dank voor je hulp!
Substitutie van x = 0 levert dan:
0 = π2/3 + 4∙(-1/12 + 1/22 - 1/32 + ...)
en dus:
∑k=1∞ (-1)k+1∙k-2 = π2/12
Nu is ook:
ζ(2) = ∑k=1∞ k-2 = ∑k=1∞ (-1)k+1∙k-2 + 2∙∑k=1∞ (2k)-2 = ∑k=1∞ (-1)k+1∙k-2 + ½∙∑k=1∞ k-2 = ∑k=1∞ (-1)k+1∙k-2 + ½∙ζ(2)
en dus:
ζ(2) = 2∙∑k=1∞ (-1)k+1∙k-2 = 2∙(π2/12) = π2/6


P(2*-(1/10)2a) = 0
Dus P = 0 v. 2*-(1/10)2a = 0; 2a = 0/x = 0 en blijft nul toch? Prof. / Lerares zegt a = 10 maar krijg maar niet door hoe ze daarop komt.
Dus P = 0 v. 2*-(1/10)2a = 0; 2a = 0/x = 0 en blijft nul toch? Prof. / Lerares zegt a = 10 maar krijg maar niet door hoe ze daarop komt.


Als je a=10 invult dan krijg je -4P=0, dus P=0...
Je hebt in feite een of andere constante c ongelijk aan nul, en de vgl c*P*a=0. Delen door c geeft P*a=0, dus P=0 of a=0.
Je hebt in feite een of andere constante c ongelijk aan nul, en de vgl c*P*a=0. Delen door c geeft P*a=0, dus P=0 of a=0.


Ja tot die conclusie kwam ik dus ook, hoe reflecteert dat zich tot deze vraag waarbij P=0 geen antwoord kan zijn (want wie verkoopt zijn product gratis?)
*Je krijgt dan P(4*-(1/10)2a = 0 volgens mij maar ik geloof dat je dan ook op P=0 of a=0 komt.
*Je krijgt dan P(4*-(1/10)2a = 0 volgens mij maar ik geloof dat je dan ook op P=0 of a=0 komt.


Okay voor duidelijk dan maar even hoofdletter P(rofit) = pi
dpi / da oplossen. = 4p - (1/10)2ap »» p(4 * (-1/10)2a)
Gelijkstellen aan 0 om a te vinden welke ik vervolgens in ga vullen in
dpi / dp zodat je p krijgt. (en dat leidt weer tot pi)
*d = ∂
dpi / da oplossen. = 4p - (1/10)2ap »» p(4 * (-1/10)2a)
Gelijkstellen aan 0 om a te vinden welke ik vervolgens in ga vullen in
dpi / dp zodat je p krijgt. (en dat leidt weer tot pi)
*d = ∂


Maak het allemaal niet zo moeilijk. Je hebt:quote:Op woensdag 5 december 2012 17:23 schreef Sokz het volgende:
Ja tot die conclusie kwam ik dus ook, hoe reflecteert dat zich tot deze vraag waarbij P=0 geen antwoord kan zijn (want wie verkoopt zijn product gratis?)
[ afbeelding ]
P(a,p) = 4ap + 50p -9p2 - (1/10)∙a2p -120
∂P/∂a = -(1/5)∙(a - 20)∙p
∂P/∂p = -a2/10 + 4a - 18p + 50
∂P/∂a = 0 geeft a = 20 of p = 0, maar je hebt P(a,0) = -120, dus dat valt af ook al omdat p = 0 niet realistisch is. Blijft over a = 20 en dan levert de voorwaarde ∂P/∂p = 0 op dat p = 5, en dan is P(20,5) = 105. Dan moet je eigenlijk nog wel netjes aantonen dat dit een lokaal maximum is, maar dat mag je zelf doen. Kijk ook even hier.


Zij 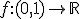 uniform continu. Toon aan dat
uniform continu. Toon aan dat  begrensd is.
begrensd is.
Kun je dit op een makkelijke manier bewijzen? Medestudenten en ik hadden bedacht dat je kunt aantonen dat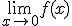 en
en 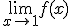 bestaan en zo een continue functie
bestaan en zo een continue functie ![f:[0,1]\rightarrow \mathbb{R}](https://forum.fok.nl/lib/mimetex.cgi?%20f%3A%5B0%2C1%5D%5Crightarrow%20%5Cmathbb%7BR%7D) kunt 'construeren': er is dan een stelling in het dictaat die zegt dat die functie (continu op een gesloten interval) begrensd is. We weten echter niet of dit correct is en het is behoorlijk lang en omslachtig. Heeft iemand een beter idee?
kunt 'construeren': er is dan een stelling in het dictaat die zegt dat die functie (continu op een gesloten interval) begrensd is. We weten echter niet of dit correct is en het is behoorlijk lang en omslachtig. Heeft iemand een beter idee?
Kun je dit op een makkelijke manier bewijzen? Medestudenten en ik hadden bedacht dat je kunt aantonen dat


Het kan veel simpeler. Pak uit de defintie op http://en.wikipedia.org/wiki/Uniform_continuity een willekeurige epsilon>0, dan komt daar een delta uitrollen. Kijk dan eens naar 1/delta (1/delta is interessant omdat delta minder dan 1/delta keer in het interval (0,1) past).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Kies ε = 1. Aangezien f uniform continu is op (0,1) bestaat er dan een δ > 0 zodanig dat | f(x) - f(y) | < ε = 1 voor elke x,y ∈ (0,1) met | x - y | < δ. Kies nu een positief geheel getal n0 > 1 zodanig dat 1/n0 < δ (i.e. n0 > 1/δ) en definieer xi = i/n0 voor i ∈ {1,...,n0-1}. Zij verder M een getal zodanig dat max(| f(xi) |, 1 ≤ i ≤ n0-1) < M - 1. Dan bestaat er voor elke x ∈ (0,1) een i ∈ {1,...,n0-1} zodanig dat | x - xi | < δ en dus | f(x) - f(xi) | < 1 zodat | f(x) | = | (f(x) - f(xi)) + f(xi) | ≤ | f(x) - f(xi) | + | f(xi) | < 1 + (M - 1) = M, QED.quote:Op donderdag 6 december 2012 20:12 schreef JWF het volgende:
Zijuniform continu. Toon aan dat
begrensd is.
Kun je dit op een makkelijke manier bewijzen? Medestudenten en ik hadden bedacht dat je kunt aantonen daten
bestaan en zo een continue functie
kunt 'construeren': er is dan een stelling in het dictaat die zegt dat die functie (continu op een gesloten interval) begrensd is. We weten echter niet of dit correct is en het is behoorlijk lang en omslachtig. Heeft iemand een beter idee?
[ Bericht 0% gewijzigd door Riparius op 07-12-2012 19:21:37 ]


[ Bericht 100% gewijzigd door Mathemaat op 07-12-2012 12:57:24 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


wat, dat f(x)=1/x begrensd is op (0,1)?quote:Op vrijdag 7 december 2012 12:47 schreef Mathemaat het volgende:
[..]
Ja, wat je zegt klopt. Je kunt het ook bewijzen voor continue functies.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Sorry, ik hield het door elkaar met het continue uitbreiden van reële functies op compacte domeinen.quote:Op vrijdag 7 december 2012 12:55 schreef GlowMouse het volgende:
[..]
wat, dat f(x)=1/x begrensd is op (0,1)?
[ Bericht 0% gewijzigd door Mathemaat op 07-12-2012 13:51:13 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


quote:Op donderdag 6 december 2012 21:05 schreef Riparius het volgende:
[..]
Kies ε = 1. Aangezien f uniform continu is op (0,1) bestaat er dan een δ > 0 zodanig dat | f(x) - f(y) | < ε = 1 voor elke x,y ∈ (0,1) met | x - y | < δ. Kies nu een positief geheel getal n0 > 1 zodanig dat 1/n0 < δ (i.e. n0 > 1/δ) en definieer xi = i/n0 voor i ∈ {1,...,n0-1}. Zij verder M een getal zodanig dat max(|(f(xi)|, 1 ≤ i ≤ n0-1) < M - 1. Dan bestaat er voor elke x ∈ (0,1) een i ∈ {1,...,n0-1} zodanig dat | x - xi | < δ en dus | f(x) - f(xi) | < 1 zodat | f(x) | = | (f(x) - f(xi)) + f(xi) | ≤ | f(x) - f(xi) | + | f(xi) | < 1 + (M - 1) = M, QED.
Dit idee laat ook mooi zien wat uniforme continuiteit betekent: waar je die delta intervalletjes ook plaatst, je hebt altijd een fluctuatie van hoogstens epsilon.quote:Op donderdag 6 december 2012 20:22 schreef GlowMouse het volgende:
Het kan veel simpeler. Pak uit de defintie op http://en.wikipedia.org/wiki/Uniform_continuity een willekeurige epsilon>0, dan komt daar een delta uitrollen. Kijk dan eens naar 1/delta (1/delta is interessant omdat delta minder dan 1/delta keer in het interval (0,1) past).


Ok, geen wiskunde dit maar hoe los los ik dit het handigst op uit 't hoofd? Iemand tips?
x : -6/8 = -14/35
-45/18 - 18/6 = x
x : -6/8 = -14/35
-45/18 - 18/6 = x


Dankjewel, heel helder. Ik zou dit zelf niet zomaar bedenken, maar ik heb wel het gevoel nu beter te begrijpen wat uniforme continuïteit inhoudt.quote:Op donderdag 6 december 2012 21:05 schreef Riparius het volgende:
Kies ε = 1. Aangezien f uniform continu is op (0,1) bestaat er dan een δ > 0 zodanig dat | f(x) - f(y) | < ε = 1 voor elke x,y ∈ (0,1) met | x - y | < δ. Kies nu een positief geheel getal n0 > 1 zodanig dat 1/n0 < δ (i.e. n0 > 1/δ) en definieer xi = i/n0 voor i ∈ {1,...,n0-1}. Zij verder M een getal zodanig dat max(|(f(xi)|, 1 ≤ i ≤ n0-1) < M - 1. Dan bestaat er voor elke x ∈ (0,1) een i ∈ {1,...,n0-1} zodanig dat | x - xi | < δ en dus | f(x) - f(xi) | < 1 zodat | f(x) | = | (f(x) - f(xi)) + f(xi) | ≤ | f(x) - f(xi) | + | f(xi) | < 1 + (M - 1) = M, QED.


Beide leden vermenigvuldigen met -6/8 = -3/4 en je hebt x = -3/4 ∙ -14/35 = 3/4 ∙ 2/7 = 6/28 = 3/14.quote:Op vrijdag 7 december 2012 18:21 schreef Maryn. het volgende:
Ok, geen wiskunde dit maar hoe los los ik dit het handigst op uit 't hoofd? Iemand tips?
x : -6/8 = -14/35
Breuken vereenvoudigen, x = -45/18 - 18/6 = -5/2 - 6/2 = -11/2.quote:-45/18 - 18/6 = x


"een uniform convergente reeks van exponentiële of circulaire functies convergeert, in het aangegeven gebied, naar een continue functie (waarom?)". Dit staat er, in verband met de uniforme convergentie van Fourierreeksen.
Iemand die ziet waarom dit zo is?
Iemand die ziet waarom dit zo is?


Het klassieke ε/3 trucje. Het bewijs staat vast wel ergens in de een of andere vorm in je leerboek, en anders moet je maar even hier kijken.quote:Op zaterdag 8 december 2012 17:31 schreef yarnamc het volgende:
"een uniform convergente reeks van exponentiële of circulaire functies convergeert, in het aangegeven gebied, naar een continue functie (waarom?)". Dit staat er, in verband met de uniforme convergentie van Fourierreeksen.
Iemand die ziet waarom dit zo is?


Stel je hebt een polynoom ![f \in \mathbb{Z}_p[x,y,z]](https://forum.fok.nl/lib/mimetex.cgi?f%20%5Cin%20%5Cmathbb%7BZ%7D_p%5Bx%2Cy%2Cz%5D) met p is priem en zodat
met p is priem en zodat 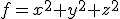 . Hoeveel oplossingen heeft f=0?
. Hoeveel oplossingen heeft f=0?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


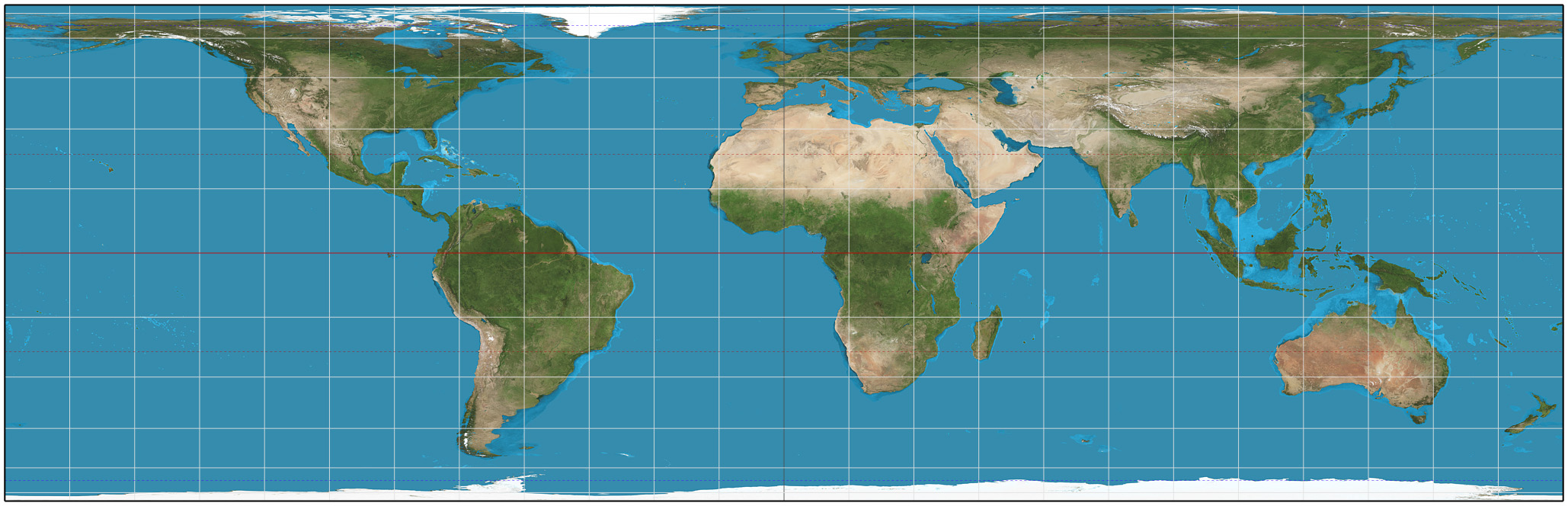
Komt een lastige. Ik ben bezig met de orthografische cilinderprojectie (van Johann Heinrich Lambert), nu wordt er gesteld dat dit een equivalente projectie is. Maar waaruit volgt dit precies? Stel dat ik de vraag krijg om dit uit te leggen, hoe zou ik dat dan in Godsnaam moeten beantwoorden?
Dit is de betreffende kaart.
Dit is de betreffende kaart.


Al gekeken op http://nl.wikipedia.org/wiki/Orthografische_cilinderprojectie?
Het volgt direct uit de formules.
Het volgt direct uit de formules.


Ja, maar ik zie even niet hoe. De formules afleiden (peanuts) ook al gedaan.quote:Op maandag 10 december 2012 02:03 schreef Dale. het volgende:
Al gekeken op http://nl.wikipedia.org/wiki/Orthografische_cilinderprojectie?
Het volgt direct uit de formules.


Uhmmm de eerste alinea?
quote:Die ontstaat door de aardbol af te beelden op een cilinder vanuit een punt op de omwentelingsas van de bol, zodanig dat de projectielijn loodrecht op de as staat.


Ik snap wat je hiermee bedoelt. Dit is hoe de projectie tot stand komt. Nu wil ik graag weten waarom de projectie equivalent is, en niet omdat 'dit toevallig zo is', nee, wat is de redenatie hierachter?quote:Op maandag 10 december 2012 12:36 schreef Dale. het volgende:
Uhmmm de eerste alinea?
[..]
[ afbeelding ]
Komt er nog een (wat eenvoudigere) meetkundige vraag bij.
Wanneer men dit document opent:
http://mail.vssd.nl/hlf/a028h02oud.pdf
Dan wordt op pagina 25 en 26 het bewijs dat een stereografische projectie conform is behandeld. Nu snap ik de hele godganse redenatie, op een puntje na. Bovenaan pagina 26 staat:
Angle(WRP) = Angle(WRA) = 90 graden
Waaruit volgt dit exact? Waarom is dit zo?


Angle(WRP) is me inmiddels duidelijk. Mag ik zeggen doordat de snijlijn van het raakvlaak aan P met het grondvlak NA snijdt in R, dat die snijlijn loodrecht op NA staat?


Waar staan die integralen van Riparius die hij een tijdje geleden ergens gepost had? Ik wou ze net gaan oplossen maar kan ze vreemd genoeg niet meer terugvinden.
@Amoeba: ik heb geen verstand van projecties, maar je hebt er steeds over dat die orthografische cilinderprojectie equivalent moet zijn. Maar je zegt niet waarmee die dan equivalent moet zijn.
@Amoeba: ik heb geen verstand van projecties, maar je hebt er steeds over dat die orthografische cilinderprojectie equivalent moet zijn. Maar je zegt niet waarmee die dan equivalent moet zijn.


Hier.quote:Op maandag 10 december 2012 16:28 schreef thenxero het volgende:
Waar staan die integralen van Riparius die hij een tijdje geleden ergens gepost had?


Equivalentie is hier een term voor oppervlaktegetrouwheid. Dat betekent dus dat het product van de schaalfactoren van de kaartprojectie in horizontale en in verticale richting in elk punt op de kaart constant moet zijn. Bij hoekgetrouwheid oftewel conformiteit moet daarentegen de verhouding van de schaalfactoren in verticale en horizontale richting voor elk punt op de kaart gelijk zijn aan één. Bij afbeelding van een bolvormig oppervlak op een plat vlak zijn equivalentie en conformiteit onverenigbaar.quote:Op maandag 10 december 2012 16:28 schreef thenxero het volgende:
@Amoeba: ik heb geen verstand van projecties, maar je hebt er steeds over dat die orthografische cilinderprojectie equivalent moet zijn. Maar je zegt niet waarmee die dan equivalent moet zijn.


De methode door te bewijzen (meetkundig) dat de hoek die 2 raaklijnen aan een bol maken equivalent is aan de hoek die de projecties van die lijnen met elkaar maken, is dat ook een sluitend bewijs? Immers, de hoek die 2 krommen maken is gelijk aan de hoek die hun raaklijnen maken.quote:Op maandag 10 december 2012 17:29 schreef Riparius het volgende:
[..]
Equivalentie is hier een term voor oppervlaktegetrouwheid. Dat betekent dus dat het product van de schaalfactoren van de kaartprojectie in horizontale en in verticale richting in elk punt op de kaart constant moet zijn. Bij hoekgetrouwheid oftewel conformiteit moet daarentegen de verhouding van de schaalfactoren in verticale en horizontale richting voor elk punt op de kaart gelijk zijn aan één. Bij afbeelding van een bolvormig oppervlak op een plat vlak zijn equivalentie en conformiteit onverenigbaar.


Bij een conforme projectie zoals de Mercatorprojectie zijn op ieder punt op de kaart de schaalfactoren in horizontale en in verticale richting gelijk. Omdat we willen dat de meridianen als verticale evenwijdige lijnen worden afgebeeld is de schaalfactor voor een punt op noorderbreedte of zuiderbreedte φ in horizontale richting dus 1/cos φ = sec φ maal de schaalfactor voor de evenaar, omdat een breedtecirkel op noorderbreedte of zuiderbreedte φ slechts een omtrek heeft van cos φ maal de omtrek van de evenaar.quote:Op maandag 10 december 2012 14:26 schreef Amoeba het volgende:
[..]
Ik snap wat je hiermee bedoelt. Dit is hoe de projectie tot stand komt. Nu wil ik graag weten waarom de projectie equivalent is, en niet omdat 'dit toevallig zo is', nee, wat is de redenatie hierachter?
Maar, vanwege de conformiteitseis moet de dan schaling in verticale richting voor een punt op noorderbreedte of zuiderbreedte φ ook sec φ maal de schaling voor de evenaar bedragen, en dus wordt de oppervlakte voor een punt op noorderbreedte of zuiderbreedte φ dan op de kaart geschaald met een factor sec2φ ten opzichte van de schaling van de oppervlakte op de kaartprojectie bij de evenaar.
Dus, om een voorbeeld te geven, op 60 graden noorderbreedte wordt de oppervlakte dan al opgeschaald met een factor sec2(π/3) = 4 ten opzichte van de schaling van een gebiedje op de evenaar.
Willen we nu echter een kaartprojectie waarbij de meridianen nog steeds als evenwijdige verticale lijnen worden afgebeeld maar die wel oppervlaktegetrouw is, dan hebben we voor een punt op noorderbreedte of zuiderbreedte φ nog steeds te maken met een horizontale schaling met dezelfde factor 1/cos φ = sec φ ten opzichte van de (horizontale) schaling van de evenaar, maar dan moeten we bij de verticale schaling gaan compenseren door te schalen met een factor cos φ, zodat het product van de horizontale en de verticale schalingen voor elk punt op de kaart, en daarmee dus de oppervlakteschaling constant blijft over de gehele kaart. En als je hebt:
dy/dφ = s0∙R∙cos φ
waarbij s0 de schaalfactor is waarmee de evenaar wordt afgebeeld, en R de straal is van de aarde, dan volgt door primitiveren dus dat we moeten hebben:
y = s0∙R∙sin φ
aangezien ook moet gelden y = 0 voor φ = 0. Begrijp je dit?