SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan ťťn of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan ťťn of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d


Niet echt huiswerk maar wel wiskunde/ statistiek dus kan vast ook wel hier.
Op Teletekst (en nu ook op de voorpagina) staat nu een bericht over een moordloze dag in New York, voor het eerst sinds mensheugenis. Dat wil ik nog wel geloven maar er staat ook dat er dit jaar (28 november) "nog maar" 366 moorden zijn gepleegd.
Er van uitgaande dat die 366 moorden willekeurig over het jaar worden gepleegd, hoe groot is de kans dat nu pas een moordloze dag optreedt? Er zijn zo'n 330 dagen geweest dit jaar en zijn die 366 moorden echt zo netjes daarover uitgesmeerd?
Oftewel: wie kan dit uitrekenen?
[ Bericht 10% gewijzigd door yoppybt op 28-11-2012 22:42:55 (Voorpagina erbij) ]
Op Teletekst (en nu ook op de voorpagina) staat nu een bericht over een moordloze dag in New York, voor het eerst sinds mensheugenis. Dat wil ik nog wel geloven maar er staat ook dat er dit jaar (28 november) "nog maar" 366 moorden zijn gepleegd.
Er van uitgaande dat die 366 moorden willekeurig over het jaar worden gepleegd, hoe groot is de kans dat nu pas een moordloze dag optreedt? Er zijn zo'n 330 dagen geweest dit jaar en zijn die 366 moorden echt zo netjes daarover uitgesmeerd?
Oftewel: wie kan dit uitrekenen?
[ Bericht 10% gewijzigd door yoppybt op 28-11-2012 22:42:55 (Voorpagina erbij) ]


366 moorden in 333 dagen geeft gemiddeld 1,1 moord per dag. De kans dat er 0 moorden zijn op een dag moet dus vrij groot zijn. Het bericht is duidelijk onzin.
Zij X het aantal moorden in een dag. Als je mag aannemen dat de moorden onafhankelijk zijn van elkaar en dat ze met een vaste rate plaatsvinden, dan kan je het modelleren met een Poisson verdeling. De kans dat er k moorden plaatsvinden op een dag is dan
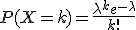
met lambda = 1/1.1.
Dus de kans op 0 moorden is P( X = 0 ) = e^(-1/1.1) = 0.4 = 40%.
De kans op 1 moord = 1.1 * e^(-1/1.1) = 36%
Kans op 2 moorden = 16%
Kans op minstens 3 moorden = 8%
Gemiddeld zijn er dus 0.4*365 = 146 moordvrije dagen per jaar (als je het gemiddelde van 1.1 mag doortrekken). Je hoeft geen statistiek toe te passen om te bedenken dat de kans dat er in tientallen jaren (om "sinds mensheugenis" nog maar bescheiden op te vatten) geen moordvrije dag geweest is nihil is.
[ Bericht 6% gewijzigd door thenxero op 28-11-2012 22:57:37 ]
Zij X het aantal moorden in een dag. Als je mag aannemen dat de moorden onafhankelijk zijn van elkaar en dat ze met een vaste rate plaatsvinden, dan kan je het modelleren met een Poisson verdeling. De kans dat er k moorden plaatsvinden op een dag is dan
met lambda = 1/1.1.
Dus de kans op 0 moorden is P( X = 0 ) = e^(-1/1.1) = 0.4 = 40%.
De kans op 1 moord = 1.1 * e^(-1/1.1) = 36%
Kans op 2 moorden = 16%
Kans op minstens 3 moorden = 8%
Gemiddeld zijn er dus 0.4*365 = 146 moordvrije dagen per jaar (als je het gemiddelde van 1.1 mag doortrekken). Je hoeft geen statistiek toe te passen om te bedenken dat de kans dat er in tientallen jaren (om "sinds mensheugenis" nog maar bescheiden op te vatten) geen moordvrije dag geweest is nihil is.
[ Bericht 6% gewijzigd door thenxero op 28-11-2012 22:57:37 ]


Goede uitleg thenxero. 
Als ik het dan goed begrijp is de kans op 330 moordloze dagen 0.6^330? (=10^-74, redelijk nihil inderdaad )
)
Als ik het dan goed begrijp is de kans op 330 moordloze dagen 0.6^330? (=10^-74, redelijk nihil inderdaad
gr gr


Je bedoelt denk ik dagen dat er juist wel een moord is. Iedere dag heb je 60% kans op minstens ťťn moord. Dus de kans dat op alle 330 dagen iedere dag minstens 1 moord is, is gelijk aan 0.6^330.quote:Op donderdag 29 november 2012 00:18 schreef Quyxz_ het volgende:
Goede uitleg thenxero.
Als ik het dan goed begrijp is de kans op 330 moordloze dagen 0.6^330? (=10^-74, redelijk nihil inderdaad)
Ze beweren dat dit sinds mensheugenis iedere dag een moord heeft plaatsgevonden in NY. Laten we voor "mensheugenis" maar even tien jaar pakken voor het gemak. Dan krijg je
De kans dat ik ergens op aarde een zandkorrel verstop en jij hem in ťťn keer aanwijst zonder voorkennis is miljarden malen groter.
[ Bericht 2% gewijzigd door thenxero op 29-11-2012 01:54:38 ]


Kijk eens aan, weer zo'n klassiek onderwerp. Ik heb net enige tijd geleden een artikel van Daniel Bernoulli (uit 1728) over lineaire recursieve rijen bestudeerd waarin onder meer de uitdrukking voor de algemene term van de rij van Fibonacci wordt afgeleid. Die formule is vernoemd naar Jacques Binet (1786-1856), maar de formule ťn de afleiding ervan waren al veel eerder bekend. Typisch gevalletje Stigler's law dus. De studie van lineaire recurrente rijen was een hot item in de eerste decennia van de 18e eeuw waar diverse wiskundigen zich mee bezig hielden, zoals verschillende leden van de familie Bernoulli, Pierre Rťmond de Montmort (1678-1719), Christian Goldbach (1690-1764), en ook de welbekende Abraham de Moivre (1667-1754).quote:Op woensdag 28 november 2012 20:50 schreef Amoeba het volgende:
Het wiskundeboek smijt weer eens met bewijzen. In het hoofdstuk 'Toepassing van complexe getallen' krijgen we nu te maken met complexe getallen i.c.m. recursieve formules. Bij het opstellen van een directe formule van een lineaire differentievergelijking van de tweede orde zijn blijkbaar complexe getallen heel nuttig. Goed, prima prima. Zij geven mij de aanpak om bij de formule
un=a*un-1+b*un-2
de substitutie un = gn door te voeren, dan te delen door gn-2 en dan de tweedegraadsvergelijking op te lossen. Wanneer geldt D<0, dan wordt de aanpak gegeven dat:
un = (Acos(nφ)+Bsin(nφ))gn met φ het argument van g1 en g de modulus van g1, waarbij g1 een van de oplossingen van de genoemde tweedegraadsvergelijking is. Maar waarom geldt deze aanpak/formule, is mijn vraag.
De oplossing van De Moivre werkte met wat we nu voortbrengende functies noemen, en splitsing daarvan in deelbreuken. Zo kan de algemene term van een lineaire recursieve rij worden geschreven als een lineaire combinatie van de algemene termen van een stel convergente meetkundige rijen waarvan de som gegeven is door elk van de lineaire partiŽle breuken van de voortbrengende functie. Maar deze methode om een gesloten uitdrukking te vinden voor de algemene term van een lineaire recursieve rij is betrekkelijk omslachtig, en is (anders dan thenxero suggereert) ook niet nodig om je vragen te beantwoorden. De methode met de zogeheten karakteristieke vergelijking (zoals voor het eerst gepubliceerd door Daniel Bernoulli, die evenwel spreekt van een aequatio primaria) is een stuk praktischer.
Laten we voor een goed begrip eerst eens kijken naar hťt schoolvoorbeeld van een tweede orde lineaire recursieve rij, de rij van Fibonacci (eigenlijk: Leonardo van Pisa, c.1170 - c.1250):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ...
Deze rij wordt, zoals bekend, gedefinieerd door het volgende recursieve voorschrift:
u0 = 0, u1 = 1, un = un-1 + un-2
Om nu een gesloten (niet recursieve) uitdrukking te vinden voor de algemene term un kun je beginnen met te bedenken dat op grond van het lineaire recursievoorschrift un = un-1 + un-2 elke lineaire combinatie van rijen die aan dit voorschrift voldoen ook weer aan dit voorschrift zal voldoen. Dus, als {an} en {bn} twee rijen zijn die voldoen dan zal een rij {cn} met cn = α∙an + β∙bn en met willekeurige constanten α en β ook voldoen aan het recursievoorschrift.
Goed, maar hoe vinden we nu een gesloten (niet recursieve) uitdrukking voor de termen van (alle) rijen die voldoen aan zo'n recursievoorschrift? Wel, om te beginnen is het duidelijk dat er geen rekenkundige rijen kunnen zijn die hier voldoen, want dan zou un - un-1 constant moeten zijn, en zou daarmee ook un-2 constant moeten zijn (i.e. onafhankelijk van n), en dat kan alleen als alle termen nul zijn. Maar dat is een triviale oplossing van het recursievoorschrift waar we niet naar op zoek zijn.
De volgende gedachte is om te proberen of er meetkundige rijen zijn die aan het recursievoorschrift voldoen. Laten we zeggen dat de reden van zo'n meetkundige rij λ is, dan moet voor de algemene term un dus gelden:
un = u0∙λn
Op grond van het recursievoorschrift un = un-1 + un-2 geldt dan:
u0∙λn = u0∙λn-1 + u0∙λn-2
Na herleiding van het rechterlid op nul en het buiten haakjes halen van de gemeenschappelijke factor u0∙λn-2 geeft dit:
u0∙λn-2∙(λ2 - λ - 1) = 0
Nu kan deze voorwaarde alleen gelden ongeacht de waarde van u0 en ongeacht de waarde van λ als de uitdrukking tussen haakjes nul is, dus:
λ2 - λ - 1 = 0
Dit is een vierkantsvergelijking met als oplossingen λ1 = (1 + √5)/2 en λ2 = (1 - √5)/2. Er zijn dus in ieder geval twee lineair onafhankelijke meetkundige rijen {an} en {bn} met reden λ1 resp. λ2 die voldoen aan de recursie un = un-1 + un-2. En aangezien elke lineaire combinatie hiervan ook voldoet hebben we dus in het algemeen:
un = α∙((1 + √5)/2)n + β∙((1 - √5)/2)n
Maar, hebben we hiermee nu wel alle mogelijke oplossingen voor de recursie un = un-1 + un-2 gevonden? Het antwoord is ja, want een rij die aan dit recursievoorschrift voldoet ligt volledig vast als twee opeenvolgende termen zijn gegeven, en door die in te vullen in bovenstaande uitdrukking voor de algemene term krijgen we twee lineaire vergelijkingen in α en β en daarmee ook de waarden van α en β die voldoen aan een gegeven specifieke rij.
Voor de rij van Fibonacci hebben we u0 = 0 en u1 = 1. Invullen hiervan in bovenstaande uitdrukking voor de algemene term levert:
α∙1 + β∙1 = 0, α∙((1 + √5)/2) + β∙((1 - √5)/2) = 1
Oplossen van dit stelsel geeft α = 1/√5 en β = -1/√5, zodat we dus als uitdrukking voor de algemene term un van de rij van Fibonacci krijgen:
Goed, we zien dat het oplossen van een tweede orde lineaire recursie (met constante en reŽle coŽfficiŽnten in het recursievoorschrift) leidt tot een vierkantsvergelijking met reŽle coŽfficiŽnten, en deze kan, zoals bekend, ook twee (toegevoegd) complexe wortels bezitten, namelijk als de discriminant van de vierkantsvergelijking negatief is. Nu begrijp je dus waarom het met deze methode kan gebeuren dat we als algemene term voor een tweede orde lineaire recursieve rij een uitdrukking krijgen waarin complexe getallen voorkomen, en dat terwijl de rij zelf uitsluitend uit reŽle getallen bestaat.
Natuurlijk rijst nu de vraag of het niet toch mogelijk is het gebruik van complexe getallen in de uitdrukking voor de algemene term van een tweede orde lineaire recursieve rij te vermijden, omdat de termen van de rij zelf immers reŽel zijn. Welnu, het antwoord op deze vraag luidt bevestigend, maar de manier waarop ligt niet zo voor de hand, en daarmee ben ik aangekomen bij je laatste vraag.
Het blijkt mogelijk om de uitdrukking voor de algemene term een tweede orde lineaire recursieve rij met complexe getallen om te schrijven naar een goniometrische vorm. Maar: waarom is dat zo? Wat hebben goniometrische functies te maken met een eenvoudige rij die voldoet aan een lineair tweede orde recursievoorschrift?
Een tipje van de sluier wordt al opgelicht als je kijkt naar bepaalde goniometrische identiteiten voor de sinus of cosinus van een veelvoud van een hoek. Om deze af te leiden begin ik even met de volgende formules van Simpson voor de som van twee sinussen of cosinussen die je uiteraard kent:
cos θ + cos φ = 2∙cos ½(θ + φ)∙cos ½(θ - φ)
sin θ + sin φ = 2∙sin ½(θ + φ)∙cos ½(θ - φ)
Deze identiteiten kun je, althans voor 0 < | θ - φ | < π, begrijpen als een eenvoudige consequentie van een stelling uit de elementaire meetkunde, als we ze als volgt herschrijven:
½(cos θ + cos φ) = cos ½(θ - φ)∙cos ½(θ + φ)
½(sin θ + sin φ) = cos ½(θ - φ)∙sin ½(θ + φ)
In woorden: het gemiddelde van de cosinussen of sinussen van twee hoeken is gelijk aan de cosinus resp. sinus van het gemiddelde van de hoeken, maar dan wel vermenigvuldigd met een schaalfactor die gelijk is aan de cosinus van het halve verschil tussen de hoeken.
Dat dit zo moet zijn is evident omdat een lijn door het middelpunt van een cirkel die een koorde van de cirkel middendoor deelt loodrecht op de koorde staat. Omgekeerd deelt een lijn door het middelpunt van een cirkel die een koorde van de cirkel loodrecht snijdt de koorde middendoor (Euclides, Elementen, boek III, stelling 3). Een equivalente formulering van deze stelling is dat een lijn door het middelpunt van een cirkel die een koorde van de cirkel middendoor deelt de bissectrice is van de middelpuntshoek die wordt omspannen door de koorde en dat omgekeerd de bissectrice van een middelpuntshoek in een cirkel de koorde die de middelpuntshoek omspant middendoor deelt. Hierbij is steeds te veronderstellen dat de koorde niet door het middelpunt van de cirkel gaat en dus zelf geen middellijn is.
Kies je (met 0 < | θ - φ | < π) twee punten op de eenheidscirkel met coŲrdinaten A(cos θ ; sin θ) en B(cos φ ; sin φ) dan heeft het midden M van de koorde AB die deze twee punten verbindt uiteraard de coŲrdinaten (½(cos θ + cos φ) ; ½(sin θ + sin φ)). Maar nu ligt M op de bissectrice van ∠AOB, en deze bissectrice snijdt de eenheidscirkel dus in het punt C(cos ½(θ + φ) ; sin ½(θ + φ)). En aangezien OM loodrecht staat op AB is OM : OC = OM : OA = cos ∠MOA = cos ½(θ - φ). Punt M is dus het beeld van punt C bij een meetkundige vermenigvuldiging ten opzichte van de oorsprong met een factor cos ½(θ - φ), zodat de coŲrdinaten van punt M ook gelijk zijn aan (cos ½(θ - φ)∙cos ½(θ + φ) ; cos ½(θ - φ)∙sin ½(θ + φ)), en dus is ½(cos θ + cos φ) = cos ½(θ - φ)∙cos ½(θ + φ) en tevens ½(sin θ + sin φ) = cos ½(θ - φ)∙sin ½(θ + φ).
Substitueer je in bovenstaande formules van Simpson θ = nψ en φ = (n-2)ψ, dan krijg je:
cos nψ + cos (n-2)ψ = 2∙cos (n-1)ψ∙cos ψ
sin nψ + sin (n-2)ψ = 2∙sin (n-1)ψ∙cos ψ
En dit kun je ook schrijven als:
cos nψ = 2∙cos ψ∙cos (n-1)ψ - cos (n-2)ψ
sin nψ = 2∙cos ψ∙sin (n-1)ψ - sin (n-2)ψ
Dit zijn recursieve betrekkingen voor de cosinus en sinus van een veelvoud van een hoek. Maar dat niet alleen, je ziet dat dit tweede orde recursieve betrekkingen zijn. Als we een rij hebben gedefinieerd door un = cos nψ ůf door un = sin nψ, dan voldoet deze rij op grond van bovenstaande recursieformules dus aan:
un = 2∙c∙un-1 - un-2
met c = cos ψ. Oefening: leid nu zelf aan de hand van deze recursieve betrekking gesloten (niet recursieve) uitdrukkingen af voor de algemene term un van deze rijen, zowel voor un = cos nψ als voor un = sin nψ.
Nu we zien waarom goniometrische rijen met als termen sinussen of cosinussen van opeenvolgende gehele veelvouden van een hoek altijd voldoen aan een tweede orde lineaire recursieve betrekking wordt het al wat inzichtelijker waarom er Łberhaupt goniometrische functies opduiken in de gesloten (niet recursieve) uitdrukkingen voor bepaalde rijen die voldoen aan een tweede orde lineaire recursieve betrekking.
Twee voor de hand liggende vragen zijn nu: (a) is het altijd mogelijk de uitdrukking voor de algemene term van een reŽle rij die voldoet aan een tweede orde lineaire recursie om te schrijven naar een goniometrische vorm wanneer de karakteristieke vergelijking twee (toegevoegd) complexe wortels heeft en (b) hoe kunnen we dat dan doen?
Het is inderdaad altijd mogelijk om de uitdrukking voor de algemene term un van een reŽle rij te herleiden tot een goniometrische vorm als de rij voldoet aan een tweede orde lineaire recursieve betrekking en de karakteristieke vergelijking twee (toegevoegd) complexe wortels heeft. Om dit te bewijzen gaan we uit van een reŽle rij met algemene term un die voldoet aan een tweede orde lineaire recursie en waarbij de karakteristieke vergelijking twee toegevoegd complexe wortels λ1 en λ2 heeft. De algemene oplossing voor de recursie is dan:
un = α∙λ1n + β∙λ2n
waarbij α en β constanten zijn, die in principe zowel reŽel als complex kunnen zijn. Nu weet je dat we complexe getallen ook in polaire vorm kunnen omzetten. Laten we zeggen dat:
λ1 = r(cos φ + i∙sinφ)
dan is:
λ2 = r(cos φ - i∙sinφ)
aangezien λ1 en λ2 elkaars geconjugeerde zijn. Nu weet je ook dat:
eiφ = cos φ + i∙sin φ
e-iφ = cos φ - i∙sin φ
zodat we hebben λ1 = r∙eiφ en λ2 = r∙e-iφ en we dus de uitdrukking voor de algemene term van onze rij kunnen schrijven als:
un = α∙rn∙einφ + β∙rn∙e-inφ
Introduceren we nu twee nieuwe parameters A en B als volgt:
A = α + β
Β = i(α - β)
dan hebben we dus:
α = ½(A - iB)
β = ½(A + iB)
en kunnen we de uitdrukking voor de algemene term van onze rij dus schrijven als:
un = ½(A - iB)∙rn∙einφ + ½(A + iB)∙rn∙e-inφ
oftewel:
un = A∙rn∙½∙(einφ + e-inφ) - B∙rn∙½∙i∙(einφ - e-inφ)
En aangezien:
cos nφ = (einφ + e-inφ)/2
sin nφ = (einφ - e-inφ)/2i
kunnen we de uitdrukking voor voor de algemene term van onze rij dus inderdaad schrijven als:
un = rn∙(A∙cos nφ + B∙sin nφ)
Maar hiermee zijn we er nog niet, want we hadden opgemerkt dat α en β, en dus ook A en B, in principe complexe grootheden kunnen zijn. Het is wel duidelijk dat als A en B reŽel zijn dat dan ook bovenstaande uitdrukking voor un reŽel is, maar nu moeten we het omgekeerde laten zien, namelijk dat A en B reŽel zijn als de termen van de rij reŽel zijn. Maar dit is niet moeilijk aan te tonen. Substitutie van n = 0 en n = 1 geeft:
u0 = A, u1 = A∙r∙cos φ + B∙r∙sin φ
Welnu, u0 is reŽel en dus is A ook reŽel en daarmee is A∙r∙cos φ ook reŽel. En aangezien u1 reŽel is en r∙sin φ reŽel is en tevens ongelijk aan nul omdat λ1 ≠ λ2 volgt dat B ook reŽel is.
Hiermee is dus aangetoond dat de algemene term van elke tweede orde lineaire recursieve rij met reŽle termen waarvan de karakteristieke vergelijking twee toegevoegd complexe wortels heeft kan worden uitgedrukt in de goniometrische gedaante un = rn∙(A∙cos nφ + B∙sin nφ) zonder gebruik van complexe getallen.
QED
[ Bericht 0% gewijzigd door Riparius op 01-12-2012 15:44:36 ]


Ik ga dit straks uitprinten en bestuderen. Betreffende de wet van Stigler, dat stukje stond ook in mijn boek, en ik dacht exact hetzelfde. Hartelijk dank voor je antwoord! Volgend uur weer wiskunde.


Grappig hoe Riparius overal een bewijs vandaan weet te toveren gebaseerd op goniometrie en meetkunde. Wist niet dat het ook zo kon.
Maar je verhaal is wel toegespitst op tweedegraads recurrente betrekkingen. Als je iets wil zeggen over het algemene geval (n-de graads) dan moet je denk ik wel echt met voortbrengende functies gaan werken. Correct?
Maar je verhaal is wel toegespitst op tweedegraads recurrente betrekkingen. Als je iets wil zeggen over het algemene geval (n-de graads) dan moet je denk ik wel echt met voortbrengende functies gaan werken. Correct?


Voor iedereen die mijn posts wil uitprinten nog wat tips: je kunt mijn tekst direct copy pasten in Microsoft Word en van daaruit goed leesbaar afdrukken, alle Unicode tekens en ook features zoals sub- en superscript en bold en italic blijven dan gewoon behouden. Als font kun je gewoon Times New Roman gebruiken, maar fraaier is bijvoorbeeld Minion Pro, dat wordt meegeleverd bij de kosteloze Adobe Reader. Aangezien vrijwel iedereen de Adobe Reader heeft, is dit font vrijwel zeker op je systeem aanwezig, maar moet je het alleen nog even toegankelijk maken, zie hier.quote:Op donderdag 29 november 2012 10:04 schreef Amoeba het volgende:
Ik ga dit straks uitprinten en bestuderen. Betreffende de wet van Stigler, dat stukje stond ook in mijn boek, en ik dacht exact hetzelfde. Hartelijk dank voor je antwoord! Volgend uur weer wiskunde.
[ Bericht 1% gewijzigd door Riparius op 30-11-2012 17:41:55 ]


Wat een baas hequote:Op donderdag 29 november 2012 14:50 schreef thenxero het volgende:
Grappig hoe Riparius overal een bewijs vandaan weet te toveren gebaseerd op goniometrie en meetkunde.
Maar verder vroeg ik ook expliciet om het bewijs voor een tweedegraads recursieve vergelijking.


De meetkunde gebruik ik hier alleen illustratief, maar ook om diepere verbanden te laten zien waaraan m.i. in het onderwijs veel te weinig aandacht wordt geschonken. Veel formules hebben een heel eenvoudige meetkundige interpretatie. Zo is de formule van Euler meetkundig te interpreteren als een consequentie van het feit dat een raaklijn aan een cirkel loodrecht staat op de straal naar het raakpunt. Evenzo zijn de formules van Simpson te interpreteren als een goniometrisch equivalent van een basale eigenschap van koorden in een cirkel, namelijk dat de middelloodlijn van een koorde samenvalt met de bissectrice van de middelpuntshoek die door de koorde wordt omspannen. En zo zijn er veel meer van dergelijke verbanden.quote:Op donderdag 29 november 2012 14:50 schreef thenxero het volgende:
Grappig hoe Riparius overal een bewijs vandaan weet te toveren gebaseerd op goniometrie en meetkunde. Wist niet dat het ook zo kon.
Nee. Als je een n-de orde lineaire recurrente betrekking hebt, dan levert die een n-de graads karakteristieke vergelijking op. De werkwijze blijft precies hetzelfde als bij tweedegraads recurrente betrekkingen, alleen zijn de betreffende hogeremachts vergelijkingen lastiger of (voor n > 4) in veel gevallen helemaal niet algebraÔsch op te lossen. Dat geldt trouwens evenzo bij het werken met voortbrengende functies. De voortbrengende functie van een n-de orde lineaire recurrente rij is een rationale functie waarvan de noemer een polynoom is van graad n, en als je dat in lineaire deelbreuken wil opsplitsen moet je dus evengoed de nulpunten bepalen van een n-de graads polynoom.quote:Maar je verhaal is wel toegespitst op tweedegraads recurrente betrekkingen. Als je iets wil zeggen over het algemene geval (n-de graads) dan moet je denk ik wel echt met voortbrengende functies gaan werken. Correct?
Verder blijft de werkwijze om complexe getallen in de gesloten uitdrukking voor de algemene term van een reŽle n-de orde recurrente rij te vermijden door het gebruik van goniometrische functies precies hetzelfde: complexe nulpunten van polynomen met reŽle coŽfficiŽnten treden namelijk altijd op als geconjugeerde paren en voor elk geconjugeerd paar kun je dus dezelfde werkwijze gebruiken als bij reŽle tweede orde lineaire recurrente rijen waarbij de karakteristieke vergelijking twee toegevoegd complexe wortels heeft.
[ Bericht 0% gewijzigd door Riparius op 29-11-2012 17:05:47 ]


Weet iemand of er zoiets is als een binas, maar dan voor (toegepaste) wiskunde? Ik bedoel een boek met formules, notaties en handigheidjes geordend naar onderwerp.
Bijvoorbeeld een overzicht van wiskundige symbolen en notatie, afgeleiden/integralen, kansdichtheden, (partiele) somrijen etc.
Maar ook zoiets als: a^n + b^n = (a-b)(a^n-1 + ba^n2 + ....+ b^n-1)
Ik heb de pagina van Wolfram in de OP wel gevonden maar dat is toch niet helemaal wat ik zoek. Naar mijn idee veelal "fundamentele" eigenschappen/operaties onder de lemma's. Dat zijn nou juist die dingen die ik wel kan onthouden indien ik ze nodig heb. Een goed voorbeeld is de voor- en achterflap van het boek Calculus: a complete course van Pearson education.
Achtergrondinformatie: Ik studeer Econometrie. Volgens mij heeft Wolfram meer een achterban in de natuurkunde/wiskunde (toch?), het zou kunnen dat ik de informatie daarom niet echt aansluit op mijn behoefte.
Bijvoorbeeld een overzicht van wiskundige symbolen en notatie, afgeleiden/integralen, kansdichtheden, (partiele) somrijen etc.
Maar ook zoiets als: a^n + b^n = (a-b)(a^n-1 + ba^n2 + ....+ b^n-1)
Ik heb de pagina van Wolfram in de OP wel gevonden maar dat is toch niet helemaal wat ik zoek. Naar mijn idee veelal "fundamentele" eigenschappen/operaties onder de lemma's. Dat zijn nou juist die dingen die ik wel kan onthouden indien ik ze nodig heb. Een goed voorbeeld is de voor- en achterflap van het boek Calculus: a complete course van Pearson education.
Achtergrondinformatie: Ik studeer Econometrie. Volgens mij heeft Wolfram meer een achterban in de natuurkunde/wiskunde (toch?), het zou kunnen dat ik de informatie daarom niet echt aansluit op mijn behoefte.


Bij dit soort hogere orde diff vergl. komt het moment van geklungel bij het omschrijven naar (lapda +1)^3 op de 2e alinea, hoe pak je zoiets nu goed aan...
Blues ain't nothing but a good man feeling bad...


Dit is alvast fout. Je bedoelt:quote:Op vrijdag 30 november 2012 15:54 schreef synthesix het volgende:
Weet iemand of er zoiets is als een binas, maar dan voor (toegepaste) wiskunde? Ik bedoel een boek met formules, notaties en handigheidjes geordend naar onderwerp.
Bijvoorbeeld een overzicht van wiskundige symbolen en notatie, afgeleiden/integralen, kansdichtheden, (partiele) somrijen etc.
Maar ook zoiets als: a^n + b^n = (a-b)(a^n-1 + ba^n2 + ....+ b^n-1)
an - bn = (a - b)∙∑k=1n an-kbk-1
De som an + bn heeft een factor (a + b) als n oneven is, bijvoorbeeld:
a3 + b3 = (a + b)(a2 - ab + b2)
Is n even en groter dan 2, dan kun je an + bn wel ontbinden in reŽle kwadratische factoren met het cirkeltheorema van Cotes, bijvoorbeeld:
a4 + b4 = (a2 + √2∙ab + b2)(a2 - √2∙ab + b2)
Lastig, want ik weet niet wat je allemaal nodig denkt te hebben. Een klassieker is het handboek van Abramowitz en Stegun. Dit is rechtenvrij en op verschillende plaatsen als PDF te downloaden, zie het Wikipedia artikel over dit boek. Overigens is dit handboek inmiddels vervangen door de NIST Digital Library of Mathematical Functions.quote:Ik heb de pagina van Wolfram in de OP wel gevonden maar dat is toch niet helemaal wat ik zoek. Naar mijn idee veelal "fundamentele" eigenschappen/operaties onder de lemma's. Dat zijn nou juist die dingen die ik wel kan onthouden indien ik ze nodig heb. Een goed voorbeeld is de voor- en achterflap van het boek Calculus: a complete course van Pearson education.
Achtergrondinformatie: Ik studeer Econometrie. Volgens mij heeft Wolfram meer een achterban in de natuurkunde/wiskunde (toch?), het zou kunnen dat ik de informatie daarom niet echt aansluit op mijn behoefte.


@Riparius Oeps, typo. Bedoelde inderdaad 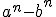

Je laatste link helpt me al een eind op weg, thanks!
Nu ik er zo over nadenk gaat het eigenlijk met name om dingen die je in een basiscursus calculus leert, en die je later in je studie wel een nodig hebt voor bewijzen oid. Maar dan zo weinig dat je het niet onthoud, en niet zo triviaal dat je het zelf wel kunt bedenken als het nodig hebt.
Om wat voorbeelden te geven van dingen die ik de laatste paar maanden nog op moest zoeken en waarvan ik sommige nu alweer vergeten ben:'):
- Det[A] berekenen mbv de determinaten van submatrixen, wat was ook al weer het teken van de cofactoren
-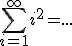
- Variabelen transformatie van (x,y) naar (u,v) in een dubbele integraal. Gebruik je dan de Jacobiaan van (u,v) in (x,y) of van (x,y) in (u,v)?
- cos(x-y) = cosxcosy + sinxsiny
Snap je een beetje wat ik bedoel? Ik kan me haast niet voorstellen dat dat ik de enige ben die dat heeft.
Je laatste link helpt me al een eind op weg, thanks!
Nu ik er zo over nadenk gaat het eigenlijk met name om dingen die je in een basiscursus calculus leert, en die je later in je studie wel een nodig hebt voor bewijzen oid. Maar dan zo weinig dat je het niet onthoud, en niet zo triviaal dat je het zelf wel kunt bedenken als het nodig hebt.
Om wat voorbeelden te geven van dingen die ik de laatste paar maanden nog op moest zoeken en waarvan ik sommige nu alweer vergeten ben:'):
- Det[A] berekenen mbv de determinaten van submatrixen, wat was ook al weer het teken van de cofactoren
-
- Variabelen transformatie van (x,y) naar (u,v) in een dubbele integraal. Gebruik je dan de Jacobiaan van (u,v) in (x,y) of van (x,y) in (u,v)?
- cos(x-y) = cosxcosy + sinxsiny
Snap je een beetje wat ik bedoel? Ik kan me haast niet voorstellen dat dat ik de enige ben die dat heeft.


Klopt, ik google die dingen meestal gewoon. Maar er zijn ook vrij veel van dat soort formules, dus ik weet niet of zo'n lijst echt overzichtelijk zou zijn. Het makkelijkste is om de formules die jij vaak vergeet voor jezelf op te schrijvenquote:Op vrijdag 30 november 2012 19:36 schreef synthesix het volgende:
@Riparius Oeps, typo. Bedoelde inderdaad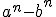
Je laatste link helpt me al een eind op weg, thanks!
Nu ik er zo over nadenk gaat het eigenlijk met name om dingen die je in een basiscursus calculus leert, en die je later in je studie wel een nodig hebt voor bewijzen oid. Maar dan zo weinig dat je het niet onthoud, en niet zo triviaal dat je het zelf wel kunt bedenken als het nodig hebt.
Om wat voorbeelden te geven van dingen die ik de laatste paar maanden nog op moest zoeken en waarvan ik sommige nu alweer vergeten ben:'):
- Det[A] berekenen mbv de determinaten van submatrixen, wat was ook al weer het teken van de cofactoren
-
- Variabelen transformatie van (x,y) naar (u,v) in een dubbele integraal. Gebruik je dan de Jacobiaan van (u,v) in (x,y) of van (x,y) in (u,v)?
- cos(x-y) = cosxcosy + sinxsiny
Snap je een beetje wat ik bedoel? Ik kan me haast niet voorstellen dat dat ik de enige ben die dat heeft.


De Jacobiaan voor de transformatie van (x,y) naar (u,v) is gemakkelijk in symbolische vorm te onthouden:quote:Op vrijdag 30 november 2012 19:36 schreef synthesix het volgende:
@Riparius Oeps, typo. Bedoelde inderdaad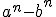
Je laatste link helpt me al een eind op weg, thanks!
Nu ik er zo over nadenk gaat het eigenlijk met name om dingen die je in een basiscursus calculus leert, en die je later in je studie wel eens nodig hebt voor bewijzen oid. Maar dan zo weinig dat je het niet onthoudt, en niet zo triviaal dat je het zelf wel kunt bedenken als het nodig hebt.
Om wat voorbeelden te geven van dingen die ik de laatste paar maanden nog op moest zoeken en waarvan ik sommige nu alweer vergeten ben:'):
- Det[A] berekenen mbv de determinaten van submatrixen, wat was ook al weer het teken van de cofactoren
-
- Variabelen transformatie van (x,y) naar (u,v) in een dubbele integraal. Gebruik je dan de Jacobiaan van (u,v) in (x,y) of van (x,y) in (u,v)?
- cos(x-y) = cosxcosy + sinxsiny
Snap je een beetje wat ik bedoel? Ik kan me haast niet voorstellen dat dat ik de enige ben die dat heeft.
dxdy = ∂(x,y)/∂(u,v) ∙ dudv
En voor goniometrische identiteiten kan ik je mijn PDF aanbevelen. Hopelijk vergeet je ze dan nooit meer.
Voor wat meer elementaire zaken kan ik je het Vademecum van de wiskunde van Otto Teller aanraden (Prisma pocket nr. 1033). Ik weet niet of dit nog nieuw verkrijgbaar is, maar tweedehands is het vast niet moeilijk te vinden.
[ Bericht 0% gewijzigd door Riparius op 30-11-2012 20:59:25 ]


Ik heb helaas colleges moeten missen en de documentatie van het vak wat ik nu volg is vrij bagger. Nu wil ik graag wat meer achtergrond van de gegeven onderwerpen in: http://www.2shared.com/do(...)jd__tweede_coll.html. Als iemand goede bronnen heeft hoor ik het graag.
* Ito calculus (lemma, diffusie)
* Stochastische dynamische optimalisatie
* Merton's portfolio problem
* Ito calculus (lemma, diffusie)
* Stochastische dynamische optimalisatie
* Merton's portfolio problem


Omdat het een orde drie diff. vergelijking is zonder triviale coŽfficiŽnten (geen nullen), wordt de algemene oplossing opgespannen door een basis van dimensie 3 (dus de algemene oplossing bestaat uit drie termen). In dit geval zijn dat dus die e-machten. Je vult die e-macht in (dit is ťťn van je basiselementen) en vindt daarmee alle mogelijke lambda's. Als n lambda's dezelfde waarde hebben, dan hebben de bijbehorende n basiselementen respectievelijk 1,x,x^2,...,x^(n-1) in de factorisatie van de coŽfficiŽnten zitten.quote:Op vrijdag 30 november 2012 16:52 schreef GoodGawd het volgende:
Bij dit soort hogere orde diff vergl. komt het moment van geklungel bij het omschrijven naar (lapda +1)^3 op de 2e alinea, hoe pak je zoiets nu goed aan...
[ afbeelding ]
Ben ik begrijpelijk?
Hier staat uitgelegd hoe je tot de algemene oplossing komt:
http://en.wikipedia.org/w(...)onstant_coefficients
Het stomme van diff. vergelijkingen is dat je gewoon de algemene oplossing uit je hoofd moet kennen.
[ Bericht 0% gewijzigd door Mathemaat op 02-12-2012 14:20:05 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Dank.
[ Bericht 94% gewijzigd door GoodGawd op 01-12-2012 21:55:38 ]
[ Bericht 94% gewijzigd door GoodGawd op 01-12-2012 21:55:38 ]
Blues ain't nothing but a good man feeling bad...


Niet helemaal: als λ0 een wortel is met multipliciteit n van de karakteristieke vergelijking van een lineaire homogene differentiaalvergelijking met constante coŽfficiŽnten, dan is xn∙exp(λ0∙x) geen oplossing van de differentiaalvergelijking.quote:Op zaterdag 1 december 2012 10:17 schreef Mathemaat het volgende:
Als n lambda's dezelfde waarde hebben, dan hebben de bijbehorende n basiselementen respectievelijk 1,x,x^2,...,x^n in de factorisatie van de coŽfficiŽnten zitten.


[ Bericht 100% gewijzigd door Mathemaat op 02-12-2012 14:20:13 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Ben ik het helemaal mee eens!quote:Op donderdag 29 november 2012 16:58 schreef Riparius het volgende:
[..]
De meetkunde gebruik ik hier alleen illustratief, maar ook om diepere verbanden te laten zien waaraan m.i. in het onderwijs veel te weinig aandacht wordt geschonken. Veel formules hebben een heel eenvoudige meetkundige interpretatie. Zo is de formule van Euler meetkundig te interpreteren als een consequentie van het feit dat een raaklijn aan een cirkel loodrecht staat op de straal naar het raakpunt. Evenzo zijn de formules van Simpson te interpreteren als een goniometrisch equivalent van een basale eigenschap van koorden in een cirkel, namelijk dat de middelloodlijn van een koorde samenvalt met de bissectrice van de middelpuntshoek die door de koorde wordt omspannen. En zo zijn er veel meer van dergelijke verbanden.
[...]
Riparius, schrijf je voor je werk ook weleens dingen over wiskunde? Je bent er erg bedreven in moet ik zeggen
[ Bericht 0% gewijzigd door kutkloon7 op 02-12-2012 19:59:58 ]


- Protterquote:Op zaterdag 1 december 2012 00:21 schreef Physics het volgende:
Ik heb helaas colleges moeten missen en de documentatie van het vak wat ik nu volg is vrij bagger. Nu wil ik graag wat meer achtergrond van de gegeven onderwerpen in: http://www.2shared.com/do(...)jd__tweede_coll.html. Als iemand goede bronnen heeft hoor ik het graag.
* Ito calculus (lemma, diffusie)
* Stochastische dynamische optimalisatie
* Merton's portfolio problem
- Shreve & Karatzas


Trouwens, misschien een aanrader voor mensen die geÔnteresseerd zijn, maar geen bronnen hebben:
http://webmovies.science.uu.nl/
Opgenomen wiskunde colleges van de UU, misschien wat voor jou Amoeba? Omdat je aangaf niet te kunnen wachten om te beginnen met een studie wiskunde (meen ik me te herinneren).
(ik ben zelf ook van plan om ze te gaan gebruiken, goed om te leren voor een herkansing, vooruit te leren of als je gewoon je geheugen wil opfrissen)
http://webmovies.science.uu.nl/
Opgenomen wiskunde colleges van de UU, misschien wat voor jou Amoeba? Omdat je aangaf niet te kunnen wachten om te beginnen met een studie wiskunde (meen ik me te herinneren).
(ik ben zelf ook van plan om ze te gaan gebruiken, goed om te leren voor een herkansing, vooruit te leren of als je gewoon je geheugen wil opfrissen)


Alles wat je interessant vindt. Alles wat in die lijst onder Functies en Reeksen staat zijn eerstejaarsvakken. Calculus en analyse zijn denk ik het boeiendst om te volgen (infi a is een beetje basic misschien). Lineaire algebra B is wel boeiend, maar ik vond de manier waarop het gegeven werd wat te abstract (alleen maar theorie, amper toepassingen).quote:
Ik vind alleen uit een boek dingen leren altijd zo droog, een college is een wat makkelijkere manier om dingen te leren (je snapt wat sneller hoe de docenten naar de dingen kijken). Als je de opgenomen colleges en een boek of dictaat (deze staan vaak ook wel op internet) hebt is dit volgens mij een prima manier om het vak een beetje door te krijgen.
Voor mij werkt het in ieder geval beter als ik het zo leer in mijn vrije tijd dan dat ik het vak echt volg


Ik heb een vraagje wat betreft Matlab. Ik heb de volgende ODE:
Nu wil ik dit simpel oplossen in Matlab met de 'dsolve-functie.' http://www.mathworks.nl/help/symbolic/dsolve.html
Ik vul de vergelijking in op deze manier, waar volgens mij niet veel mis mee is:
syms k L
dsolve('k*D2x=-x*(L-x)' , 'x(0)=0' , 'x(L)=0')
Nu geeft hij als antwoord slechts ans=0. Dit is natuurlijk niet de bedoeling. Weet iemand hoe ik een beter antwoord kan krijgen. Heeft het er iets te maken dat ik ook de eigenwaarde moet opgeven?
Nu wil ik dit simpel oplossen in Matlab met de 'dsolve-functie.' http://www.mathworks.nl/help/symbolic/dsolve.html
Ik vul de vergelijking in op deze manier, waar volgens mij niet veel mis mee is:
syms k L
dsolve('k*D2x=-x*(L-x)' , 'x(0)=0' , 'x(L)=0')
Nu geeft hij als antwoord slechts ans=0. Dit is natuurlijk niet de bedoeling. Weet iemand hoe ik een beter antwoord kan krijgen. Heeft het er iets te maken dat ik ook de eigenwaarde moet opgeven?
gr gr


Als ik je linkje doorlees, dan denk ik dat je D2u moet schrijven, niet D2x, want u is je afhankelijke variabele, niet x: Any character immediately following a differentiation operator is a dependent variable. En dan natuurlijk ook u(0) en u(L) schrijven. Overigens gaan dit soort dingen gemakkelijk in WolframAlpha.quote:Op maandag 3 december 2012 13:43 schreef Quyxz_ het volgende:
Ik heb een vraagje wat betreft Matlab. Ik heb de volgende ODE:
[ afbeelding ]
Nu wil ik dit simpel oplossen in Matlab met de 'dsolve-functie.' http://www.mathworks.nl/help/symbolic/dsolve.html
Ik vul de vergelijking in op deze manier, waar volgens mij niet veel mis mee is:
syms k L
dsolve('k*D2x=-x*(L-x)' , 'x(0)=0' , 'x(L)=0')
Nu geeft hij als antwoord slechts ans=0. Dit is natuurlijk niet de bedoeling. Weet iemand hoe ik een beter antwoord kan krijgen. Heeft het er iets te maken dat ik ook de eigenwaarde moet opgeven?


Ah bedankt!quote:Op maandag 3 december 2012 13:54 schreef Riparius het volgende:
[..]
Als ik je linkje doorlees, dan denk ik dat je D2u moet schrijven, niet D2x, want u is je afhankelijke variabele, niet x: Any character immediately following a differentiation operator is a dependent variable. En dan natuurlijk ook u(0) en u(L) schrijven. Overigens gaan dit soort dingen gemakkelijk in WolframAlpha.
Ik heb het nu ook uit Matlab gekregen door even goed naar de afhankelijke en onafhankelijke variabelen te kijken. Blijkbaar gebruikt deze functie t als standaard onafhankelijke variabele, dus ik heb het nu zo ingevuld:
dsolve('k*D2x=-t*(L-t)' , 'x(0)=0' , 'x(L)=0')
Nu krijg ik hetzelfde antwoord als WA.
gr gr


Zo kan het ook, maar zoals je het eerst deed had je x zowel als afhankelijke als als onafhankelijke variabele, en dan is het nogal wiedes dat het niet werkt.quote:Op maandag 3 december 2012 14:01 schreef Quyxz_ het volgende:
[..]
Ah bedankt!
Ik heb het nu ook uit Matlab gekregen door even goed naar de afhankelijke en onafhankelijke variabelen te kijken. Blijkbaar gebruikt deze functie t als standaard onafhankelijke variabele, dus ik heb het nu zo ingevuld:
dsolve('k*D2x=-t*(L-t)' , 'x(0)=0' , 'x(L)=0')
Nu krijg ik hetzelfde antwoord als WA.


Ik ga er naar kijken.quote:Op zondag 2 december 2012 21:13 schreef kutkloon7 het volgende:
[..]
Alles wat je interessant vindt. Alles wat in die lijst onder Functies en Reeksen staat zijn eerstejaarsvakken. Calculus en analyse zijn denk ik het boeiendst om te volgen (infi a is een beetje basic misschien). Lineaire algebra B is wel boeiend, maar ik vond de manier waarop het gegeven werd wat te abstract (alleen maar theorie, amper toepassingen).
Ik vind alleen uit een boek dingen leren altijd zo droog, een college is een wat makkelijkere manier om dingen te leren (je snapt wat sneller hoe de docenten naar de dingen kijken). Als je de opgenomen colleges en een boek of dictaat (deze staan vaak ook wel op internet) hebt is dit volgens mij een prima manier om het vak een beetje door te krijgen.
Voor mij werkt het in ieder geval beter als ik het zo leer in mijn vrije tijd dan dat ik het vak echt volg
Infi A, wat behandelt dat precies? Beetje beginselen differentiaal/integraalrekening (limieten?)


Gewoon middelbare school stof in feite maar dan hier en daar net wat verder. Heel veel dingen ben je waarschijnlijk al tegen gekomen in wisB of wisD. DifferentiŽren, integreren, substitutieregel voor integralen, partiŽel integreren, simpele limietjes (zonder strikte bewijzen: bewijzen met limieten zitten in Analyse A), Taylorreeks, injectieve/surjectieve/bijectieve functies, gewone differentiaalvergelijkingen, continue functies, ... . Dat is ongeveer wat ik me kan herinnerenquote:Op maandag 3 december 2012 21:13 schreef Amoeba het volgende:
[..]
Ik ga er naar kijken.
Infi A, wat behandelt dat precies? Beetje beginselen differentiaal/integraalrekening (limieten?)


Op de webpagina van de docent staat een linkje naar een dictaat, maar ze zijn zo te zien nu overgestapt op het Engelstalige boek Calculus, A Complete Course van Adams & Essex. Dat is een pil van ruim 1000 bladzijden. Hier verbaas ik me wel een beetje over, want dat boek is meer bedoeld voor opleidingen waarbij wiskunde geen hoofdzaak is maar wel wordt toegepast.quote:Op maandag 3 december 2012 21:13 schreef Amoeba het volgende:
[..]
Ik ga er naar kijken.
Infi A, wat behandelt dat precies? Beetje beginselen differentiaal/integraalrekening (limieten?)


Ja, verder wat over taylorreeksen, en hoe en hoe goed je functie daarmee benadert. Verder wat begin in differentiaalvergelijkingen. Dictaat is hier te vinden. Voor infi B gebruikten we een boek, dat was helaas wat minder overzichtelijk.quote:Op maandag 3 december 2012 21:13 schreef Amoeba het volgende:
[..]
Ik ga er naar kijken.
Infi A, wat behandelt dat precies? Beetje beginselen differentiaal/integraalrekening (limieten?)
Edit: O, dit was dus allemaal al gezegd
Ik zie nu dat er op de site van hogendijk ook wat extra opgaven (zogenaamde marsopgaven, je kreeg een mars als je ze goed oploste


Vrij simpele vraag lijkt mij.
Ik weet niet precies waar ik dit moet plaatsen maar probeer het maar op GC.
De vraag is:
Legoland is gebouw op een schaal van 1:25
Hoe groot is de oppervlakte van een terein op Legoland, dat in werkelijkheid precies 1/16de hectare is.
De oppervlakte van legoland is dan ... vierkante meter.
Ik zou denken 10000 vierkante meter / 16 / 25 = 25 m2 maar dat klopt niet.
Iemand die hier het antwoord wel weet want ik kan zo niet verder. Heb alles ook al gegoogled.
Vraag 2
Legoland is gebouwd op een schaal van 1:25
de inhoud van een nagebouwde vloeistoftank is 3,2 liter
wat is de inhoud van de ECHTE tank in liters
Ik kom hier echt niet uit. En heb van dit deel ook geen antwoorden.
Ik weet niet precies waar ik dit moet plaatsen maar probeer het maar op GC.
De vraag is:
Legoland is gebouw op een schaal van 1:25
Hoe groot is de oppervlakte van een terein op Legoland, dat in werkelijkheid precies 1/16de hectare is.
De oppervlakte van legoland is dan ... vierkante meter.
Ik zou denken 10000 vierkante meter / 16 / 25 = 25 m2 maar dat klopt niet.
Iemand die hier het antwoord wel weet want ik kan zo niet verder. Heb alles ook al gegoogled.
Vraag 2
Legoland is gebouwd op een schaal van 1:25
de inhoud van een nagebouwde vloeistoftank is 3,2 liter
wat is de inhoud van de ECHTE tank in liters
Ik kom hier echt niet uit. En heb van dit deel ook geen antwoorden.


oppervlakte is in 2 dimensies, inhoud in 3 dimensies.
Wil je dus de oppervlakte van een schaalmodel weten, moet je 2 keer delen door de schaal. zowel voor de "x" richting als voor de "y" richting.
vb: anders ga je van een vierkant naar een rechthoek waarvan 1 zijde nog steeds even lang is ipv een kleiner vierkant.
Voor inhoud zelfs een 3e keer voor de "z" richting.
Wil je dus de oppervlakte van een schaalmodel weten, moet je 2 keer delen door de schaal. zowel voor de "x" richting als voor de "y" richting.
vb: anders ga je van een vierkant naar een rechthoek waarvan 1 zijde nog steeds even lang is ipv een kleiner vierkant.
Voor inhoud zelfs een 3e keer voor de "z" richting.
U kunt hier adverteren voor maar §10 per maand. Neem contact op via PM.


Onderaan de kettingbreuk beginnen: 3 + 1/4 = 12/4 + 1/4 = 13/4. Nu het omgekeerde nemen, dat is 4/13, en hier 2 bij optellen. Dat geeft 2 + 4/13 = 26/13 + 4/13 = 30/13. Weer het omgekeerde nemen, dat is 13/30. Hier tenslotte 1 bij optellen en we krijgen 1 + 13/30 = 30/30 + 13/30 = 43/30. Dit is echt lagere school werk.quote:Op dinsdag 4 december 2012 17:37 schreef Miraculously het volgende:
Op de ťťn of andere manier kom ik niet uit deze vraag..
[ afbeelding ]
Ik moet op [ afbeelding ] uitkomen


Bedankt, maar dit heb ik nooit op de lagere of middelbare school gehad.quote:Op dinsdag 4 december 2012 17:56 schreef Riparius het volgende:
[..]
Onderaan de kettingbreuk beginnen: 3 + 1/4 = 12/4 + 1/4 = 13/4. Nu het omgekeerde nemen, dat is 4/13, en hier 2 bij optellen. Dat geeft 2 + 4/13 = 26/13 + 4/13 = 30/13. Weer het omgekeerde nemen, dat is 13/30. Hier tenslotte 1 bij optellen en we krijgen 1 + 13/30 = 30/30 + 13/30 = 43/30. Dit is echt lagere school werk.


Eigenlijk wel, maar je hebt er nooit stil bij gestaan. Je moet consequent de regenregels, die altijd zo intuÔtief leken, gebruiken en die heb je wel geleerd.quote:Op dinsdag 4 december 2012 18:04 schreef Miraculously het volgende:
[..]
Bedankt, maar dit heb ik nooit op de lagere of middelbare school gehad.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Het is ook al even geleden dat ik dit soort dingen uit mijn hoofd gedaan heb, ik heb sinds de middelbare school immers alleen maar een rekenmachine gebruikt..quote:Op dinsdag 4 december 2012 18:06 schreef Mathemaat het volgende:
[..]
Eigenlijk wel, maar je hebt er nooit stil bij gestaan. Je moet consequent de regenregels, die altijd zo intuÔtief leken, gebruiken en die heb je wel geleerd.


Een rekenmachine kan dit ook niet als je het niet volgens de rekenregels invoert. Het is niet erg dat je het niet kon, dat is niet het punt dat ik wil maken.quote:Op dinsdag 4 december 2012 18:12 schreef Miraculously het volgende:
[..]
Het is ook al even geleden dat ik dit soort dingen uit mijn hoofd gedaan heb, ik heb sinds de middelbare school immers alleen maar een rekenmachine gebruikt..
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


als je een alternerende rij { an } hebt met an = (n+1)(-1)n ,
(sommatie van n=0 tot oneindig) (n+1)(-1)n zal convergent zijn als de rij {an} voldoet aan bepaalde voorwaarden
anan+1 <0 voor n>een positief getal.
|an+1|<=an voor n>een positief getal.
lim n->oneindig an = 0
als de rij hier niet aan voldoet, is (sommatie van n=0 tot oneindig) (n+1)(-1)n dan sowieso niet convergent?
[ Bericht 4% gewijzigd door flopsies op 04-12-2012 21:24:27 ]
(sommatie van n=0 tot oneindig) (n+1)(-1)n zal convergent zijn als de rij {an} voldoet aan bepaalde voorwaarden
anan+1 <0 voor n>een positief getal.
|an+1|<=an voor n>een positief getal.
lim n->oneindig an = 0
als de rij hier niet aan voldoet, is (sommatie van n=0 tot oneindig) (n+1)(-1)n dan sowieso niet convergent?
[ Bericht 4% gewijzigd door flopsies op 04-12-2012 21:24:27 ]


-edit: wacht even hoor, even wat beter kijken nog-quote:Op dinsdag 4 december 2012 20:49 schreef flopsies het volgende:
als je een alternerende reeks hebt zoals { (n+1)(-1)n } ,
(sommatie van n=0 tot oneindig) (n+1)(-1)n (en andere alternerende reeksen) zal convergent zijn als de reeks voldoet aan bepaalde voorwaarden
anan+1 <0 voor n>een positief getal.
|an+1|<=an voor n>een positief getal.
lim n->oneindig an = 0
als de reeks hier niet aan voldoet, is (sommatie van n=0 tot oneindig) (n+1)(-1)n dan sowieso niet convergent?
Als de limiet van de rij > 0 is, is de reeks sowieso niet convergent


De vraag staat er verkeerd, de rij waar het om gaat is an(-1)n. Als je an = (-1)n+1 pakt dan zie je dat jouw antwoord niet klopt.quote:Op dinsdag 4 december 2012 21:06 schreef kutkloon7 het volgende:
[..]
-edit: wacht even hoor, even wat beter kijken nog-
Als de limiet van de rij > 0 is, is de reeks sowieso niet convergent
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hier is zo geen chocola van te maken. Je praat over een reeks, maar geeft dan de notatie van een rij, en wat moet ik me bij die notatie voorstellen?quote:Op dinsdag 4 december 2012 20:49 schreef flopsies het volgende:
als je een alternerende reeks hebt zoals { (n+1)(-1)n } ,
Voor reeksen waarvan de termen alterneren heb je het criterium van Leibniz.
Als je een alternerende rij {an} hebt en een N zodanig dat
limn→∞ an = 0 ∧ ∀n>N |an+1| ≤ |an|
dan is de reeks ∑n=0 ∞ an convergent.
[ Bericht 0% gewijzigd door Riparius op 04-12-2012 21:26:01 ]


Hoezo, de reeks ∑n=0an heeft toch geen limiet als n naar oneindig gaat?quote:Op dinsdag 4 december 2012 21:12 schreef GlowMouse het volgende:
[..]
De vraag staat er verkeerd, de rij waar het om gaat is an(-1)n. Als je an = (-1)n+1 pakt dan zie je dat jouw antwoord niet klopt.


Klopt nog niet helemaal: je definieert an maar doet er vervolgens niks mee...
Ik snap ook niet helemaal wat je bedoelt: wil je nou weten of een specifieke reeks convergent is?
Ik snap ook niet helemaal wat je bedoelt: wil je nou weten of een specifieke reeks convergent is?


I see. Maar wat als de limiet van de rij (an) niet bestaat?quote:Op dinsdag 4 december 2012 21:06 schreef kutkloon7 het volgende:
[..]
-edit: wacht even hoor, even wat beter kijken nog-
Als de limiet van de rij > 0 is, is de reeks sowieso niet convergent
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dan bestaat de limiet van de bijbehorende reeks ook niet? (maar ik had het over het geval dat de limiet wel bestaat)quote:Op dinsdag 4 december 2012 21:28 schreef GlowMouse het volgende:
[..]
I see. Maar wat als de limiet van de rij (an) niet bestaat?


of dit de enige test is om te kijken of een alternerende reeks convergeert. Als de rij {an} niet voldoet
aan de voorwaarden die riparius ook heeft gepost, is de reeks ∑n=0 ∞ an dan sowieso NIET convergent? misschien een domme vraag maar ik wil het even zeker weten
aan de voorwaarden die riparius ook heeft gepost, is de reeks ∑n=0 ∞ an dan sowieso NIET convergent? misschien een domme vraag maar ik wil het even zeker weten


Het criterium van Leibniz is voldoende maar niet noodzakelijk voor convergentie van een reeks met alternerende termen. Beschouw bijvoorbeeld de rij {an} gedefinieerd door:quote:Op dinsdag 4 december 2012 21:34 schreef flopsies het volgende:
of dit de enige test is om te kijken of een alternerende reeks convergeert. Als de rij {an} niet voldoet
aan de voorwaarden die riparius ook heeft gepost, is de reeks ∑n=0 ∞ an dan sowieso NIET convergent? misschien een domme vraag maar ik wil het even zeker weten
an = ((-1)n+1∙|sin n|)/n2
Dan is |an| niet monotoon dalend terwijl ∑n=1 ∞ an toch convergeert.
[ Bericht 5% gewijzigd door Riparius op 04-12-2012 22:32:23 ]


Het criterium van Leibniz is wel sluitend voor alternerende, dalende reeksen. Als je alleen naar alternerende, dalende reeksen kijkt voldoet elke convergerende reeks aan het criterium en geen enkele niet-convergerende reeks.
Ik kom er nu net een tegen bij de inleveropgave voor functies en reeksen. We moeten de Fourier-coefficienten van de 2π-periodieke functie die op het interval [-π, π] gelijk is aan x2 bepalen.
Die blijkt gelijk te zijn aan (-1)k . 2/k2.
Om te bepalen of de bijbehorende Fourierreeks convergent is, moet je kijken of de som van al deze coefficienten convergeert. Ja dus, wat je aan kan tonen met Leibniz' criterium.
(er kunnen nog foutjes inzitten, ik ben er nog mee bezig )
)
[ Bericht 5% gewijzigd door kutkloon7 op 04-12-2012 23:58:12 ]
Ik kom er nu net een tegen bij de inleveropgave voor functies en reeksen. We moeten de Fourier-coefficienten van de 2π-periodieke functie die op het interval [-π, π] gelijk is aan x2 bepalen.
Die blijkt gelijk te zijn aan (-1)k . 2/k2.
Om te bepalen of de bijbehorende Fourierreeks convergent is, moet je kijken of de som van al deze coefficienten convergeert. Ja dus, wat je aan kan tonen met Leibniz' criterium.
(er kunnen nog foutjes inzitten, ik ben er nog mee bezig
[ Bericht 5% gewijzigd door kutkloon7 op 04-12-2012 23:58:12 ]


Ja, maar dat is niet in tegenspraak met wat ik hierboven beweer.quote:Op dinsdag 4 december 2012 23:53 schreef kutkloon7 het volgende:
Het criterium van Leibniz is wel sluitend voor alternerende, dalende reeksen. Als je alleen naar alternerende, dalende reeksen kijkt voldoet elke convergerende reeks aan het criterium en geen enkele niet-convergerende reeks.
Ik dacht dat de algemene term van de gedaante ((-1)k∙4∙cos kx)/k2 is. En dan nog een constante term π2/3 erbij.quote:Ik kom er nu net een tegen bij de inleveropgave voor functies en reeksen. We moeten de Fourier-coefficienten van de 2π-periodieke functie die op het interval [-π, π] gelijk is aan x2 bepalen.
Die blijkt gelijk te zijn aan (-1)k . 2/k2.
Inderdaad ... Vul trouwens eens x = 0 in, dan krijg je een alternerende reeks voor π2/12. Daarmee kun je gemakkelijk aantonen dat ∑k=1∞ 1/k2 = π2/6 (Bazel probleem).quote:Om te bepalen of de bijbehorende Fourierreeks convergent is, moet je kijken of de som van al deze coefficienten convergeert. Ja dus, wat je aan kan tonen met Leibniz' criterium.
(er kunnen nog foutjes inzitten, ik ben er nog mee bezig)


Uhuh, het was een aanvulling, geen verbeteringquote:Op woensdag 5 december 2012 00:14 schreef Riparius het volgende:
[..]
Ja, maar dat is niet in tegenspraak met wat ik hierboven beweer.
[..]
Ik dacht dat de algemene term van de gedaante ak = ((-1)k∙4∙cos kx)/k2 is. En dan nog een constante term π2/3 erbij.
[..]
Inderdaad ... Vul trouwens eens x = 0 in, dan krijg je een alternerende reeks voor π2/12. Daarmee kun je gemakkelijk aantonen dat ∑k=1∞ 1/k2 = π2/6 (Bazel probleem).
0 invullen is inderdaad een deel van de opgave.
Hm, ik ga er morgen nog maar even naar kijken denk ik... Volgens mij klopt het wel wat ik nu heb. Hoe kom je aan die algemene term?
In mijn dictaat staat dat de fourier coefficient gelijk is aan
En dat heb ik nagerekend, en dat lijkt te kloppen.
De constante term zou dan geloof ik 2/3π3 worden.
Ik heb wel complexe coefficienten gebruikt, misschien zit het hem daarin
[ Bericht 2% gewijzigd door kutkloon7 op 05-12-2012 00:35:20 ]


Ja, je had gelijk, ik ben eruit, het kwam inderdaad door die complexe coefficienten. Alleen die constante term heb ik nog wel anders.


Inderdaad, je moet natuurlijk twee complexe coŽfficiŽnten ck en c-k hebben om de reŽle coŽfficiŽnten ak = ck + c-k van de cosinustermen te krijgen.quote:Op woensdag 5 december 2012 00:27 schreef kutkloon7 het volgende:
[..]
Uhuh, het was een aanvulling, geen verbetering
0 invullen is inderdaad een deel van de opgave.
Hm, ik ga er morgen nog maar even naar kijken denk ik... Volgens mij klopt het wel wat ik nu heb. Hoe kom je aan die algemene term?
In mijn dictaat staat dat de fourier coefficient gelijk is aan
En dat heb ik nagerekend, en dat lijkt te kloppen.
De constante term zou dan geloof ik 2/3π3 worden.
Ik heb wel complexe coefficienten gebruikt, misschien zit het hem daarin


Ja, ik had nog niet helemaal door hoe dat precies werkte, ik werkte gewoon vanuit de uit het dictaat gegeven definities.quote:Op woensdag 5 december 2012 00:46 schreef Riparius het volgende:
[..]
Inderdaad, je moet natuurlijk twee complexe coŽfficiŽnten ck en c-k hebben om de reŽle coŽfficiŽnten ak = ck + c-k van de cosinustermen te krijgen.


Als je a0 berekent met de algemene integraal voor ak, dan moet je hiervan de helft nemen, de eerste term in de reeks geeft men daarom aan met ½a0. Dan krijg je dus π2/3 voor de constante term.quote:Op woensdag 5 december 2012 00:37 schreef kutkloon7 het volgende:
Ja, je had gelijk, ik ben eruit, het kwam inderdaad door die complexe coefficienten. Alleen die constante term heb ik nog wel anders.


Ja, wat ik de hele tijd al doe: de factor 1/2π vergeten, waardoor ik ook op π^3 uitkwam ipv π^2. Dank voor je hulp!quote:Op woensdag 5 december 2012 00:50 schreef Riparius het volgende:
[..]
Als je a0 berekent met de algemene integraal voor ak, dan moet je hiervan de helft nemen, de eerste term in de reeks geeft men daarom aan met Ĺa0. Dan krijg je dus π2/3 voor de constante term.


Je kunt je Fourier reeksen gemakkelijk controleren in WolframAlpha, zowel in goniometrische als in exponentiŽle vorm.quote:Op woensdag 5 december 2012 00:56 schreef kutkloon7 het volgende:
[..]
Ja, wat ik de hele tijd al doe: de factor 1/2π vergeten, waardoor ik ook op π^3 uitkwam ipv π^2. Dank voor je hulp!
Substitutie van x = 0 levert dan:
0 = π2/3 + 4∙(-1/12 + 1/22 - 1/32 + ...)
en dus:
∑k=1∞ (-1)k+1∙k-2 = π2/12
Nu is ook:
ζ(2) = ∑k=1∞ k-2 = ∑k=1∞ (-1)k+1∙k-2 + 2∙∑k=1∞ (2k)-2 = ∑k=1∞ (-1)k+1∙k-2 + ½∙∑k=1∞ k-2 = ∑k=1∞ (-1)k+1∙k-2 + ½∙ζ(2)
en dus:
ζ(2) = 2∙∑k=1∞ (-1)k+1∙k-2 = 2∙(π2/12) = π2/6


P(2*-(1/10)2a) = 0
Dus P = 0 v. 2*-(1/10)2a = 0; 2a = 0/x = 0 en blijft nul toch? Prof. / Lerares zegt a = 10 maar krijg maar niet door hoe ze daarop komt.
Dus P = 0 v. 2*-(1/10)2a = 0; 2a = 0/x = 0 en blijft nul toch? Prof. / Lerares zegt a = 10 maar krijg maar niet door hoe ze daarop komt.


Als je a=10 invult dan krijg je -4P=0, dus P=0...
Je hebt in feite een of andere constante c ongelijk aan nul, en de vgl c*P*a=0. Delen door c geeft P*a=0, dus P=0 of a=0.
Je hebt in feite een of andere constante c ongelijk aan nul, en de vgl c*P*a=0. Delen door c geeft P*a=0, dus P=0 of a=0.


Ja tot die conclusie kwam ik dus ook, hoe reflecteert dat zich tot deze vraag waarbij P=0 geen antwoord kan zijn (want wie verkoopt zijn product gratis?)
*Je krijgt dan P(4*-(1/10)2a = 0 volgens mij maar ik geloof dat je dan ook op P=0 of a=0 komt.
*Je krijgt dan P(4*-(1/10)2a = 0 volgens mij maar ik geloof dat je dan ook op P=0 of a=0 komt.


Okay voor duidelijk dan maar even hoofdletter P(rofit) = pi
dpi / da oplossen. = 4p - (1/10)2ap ĽĽ p(4 * (-1/10)2a)
Gelijkstellen aan 0 om a te vinden welke ik vervolgens in ga vullen in
dpi / dp zodat je p krijgt. (en dat leidt weer tot pi)
*d = ∂
dpi / da oplossen. = 4p - (1/10)2ap ĽĽ p(4 * (-1/10)2a)
Gelijkstellen aan 0 om a te vinden welke ik vervolgens in ga vullen in
dpi / dp zodat je p krijgt. (en dat leidt weer tot pi)
*d = ∂


Maak het allemaal niet zo moeilijk. Je hebt:quote:Op woensdag 5 december 2012 17:23 schreef Sokz het volgende:
Ja tot die conclusie kwam ik dus ook, hoe reflecteert dat zich tot deze vraag waarbij P=0 geen antwoord kan zijn (want wie verkoopt zijn product gratis?)
[ afbeelding ]
P(a,p) = 4ap + 50p -9p2 - (1/10)∙a2p -120
∂P/∂a = -(1/5)∙(a - 20)∙p
∂P/∂p = -a2/10 + 4a - 18p + 50
∂P/∂a = 0 geeft a = 20 of p = 0, maar je hebt P(a,0) = -120, dus dat valt af ook al omdat p = 0 niet realistisch is. Blijft over a = 20 en dan levert de voorwaarde ∂P/∂p = 0 op dat p = 5, en dan is P(20,5) = 105. Dan moet je eigenlijk nog wel netjes aantonen dat dit een lokaal maximum is, maar dat mag je zelf doen. Kijk ook even hier.


Zij 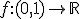 uniform continu. Toon aan dat
uniform continu. Toon aan dat  begrensd is.
begrensd is.
Kun je dit op een makkelijke manier bewijzen? Medestudenten en ik hadden bedacht dat je kunt aantonen dat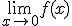 en
en 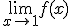 bestaan en zo een continue functie
bestaan en zo een continue functie ![f:[0,1]\rightarrow \mathbb{R}](https://forum.fok.nl/lib/mimetex.cgi?%20f%3A%5B0%2C1%5D%5Crightarrow%20%5Cmathbb%7BR%7D) kunt 'construeren': er is dan een stelling in het dictaat die zegt dat die functie (continu op een gesloten interval) begrensd is. We weten echter niet of dit correct is en het is behoorlijk lang en omslachtig. Heeft iemand een beter idee?
kunt 'construeren': er is dan een stelling in het dictaat die zegt dat die functie (continu op een gesloten interval) begrensd is. We weten echter niet of dit correct is en het is behoorlijk lang en omslachtig. Heeft iemand een beter idee?
Kun je dit op een makkelijke manier bewijzen? Medestudenten en ik hadden bedacht dat je kunt aantonen dat


Het kan veel simpeler. Pak uit de defintie op http://en.wikipedia.org/wiki/Uniform_continuity een willekeurige epsilon>0, dan komt daar een delta uitrollen. Kijk dan eens naar 1/delta (1/delta is interessant omdat delta minder dan 1/delta keer in het interval (0,1) past).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Kies ε = 1. Aangezien f uniform continu is op (0,1) bestaat er dan een δ > 0 zodanig dat | f(x) - f(y) | < ε = 1 voor elke x,y ∈ (0,1) met | x - y | < δ. Kies nu een positief geheel getal n0 > 1 zodanig dat 1/n0 < δ (i.e. n0 > 1/δ) en definieer xi = i/n0 voor i ∈ {1,...,n0-1}. Zij verder M een getal zodanig dat max(| f(xi) |, 1 ≤ i ≤ n0-1) < M - 1. Dan bestaat er voor elke x ∈ (0,1) een i ∈ {1,...,n0-1} zodanig dat | x - xi | < δ en dus | f(x) - f(xi) | < 1 zodat | f(x) | = | (f(x) - f(xi)) + f(xi) | ≤ | f(x) - f(xi) | + | f(xi) | < 1 + (M - 1) = M, QED.quote:Op donderdag 6 december 2012 20:12 schreef JWF het volgende:
Zijuniform continu. Toon aan dat
begrensd is.
Kun je dit op een makkelijke manier bewijzen? Medestudenten en ik hadden bedacht dat je kunt aantonen daten
bestaan en zo een continue functie
kunt 'construeren': er is dan een stelling in het dictaat die zegt dat die functie (continu op een gesloten interval) begrensd is. We weten echter niet of dit correct is en het is behoorlijk lang en omslachtig. Heeft iemand een beter idee?
[ Bericht 0% gewijzigd door Riparius op 07-12-2012 19:21:37 ]


[ Bericht 100% gewijzigd door Mathemaat op 07-12-2012 12:57:24 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


wat, dat f(x)=1/x begrensd is op (0,1)?quote:Op vrijdag 7 december 2012 12:47 schreef Mathemaat het volgende:
[..]
Ja, wat je zegt klopt. Je kunt het ook bewijzen voor continue functies.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Sorry, ik hield het door elkaar met het continue uitbreiden van reŽle functies op compacte domeinen.quote:Op vrijdag 7 december 2012 12:55 schreef GlowMouse het volgende:
[..]
wat, dat f(x)=1/x begrensd is op (0,1)?
[ Bericht 0% gewijzigd door Mathemaat op 07-12-2012 13:51:13 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


quote:Op donderdag 6 december 2012 21:05 schreef Riparius het volgende:
[..]
Kies ε = 1. Aangezien f uniform continu is op (0,1) bestaat er dan een δ > 0 zodanig dat | f(x) - f(y) | < ε = 1 voor elke x,y ∈ (0,1) met | x - y | < δ. Kies nu een positief geheel getal n0 > 1 zodanig dat 1/n0 < δ (i.e. n0 > 1/δ) en definieer xi = i/n0 voor i ∈ {1,...,n0-1}. Zij verder M een getal zodanig dat max(|(f(xi)|, 1 ≤ i ≤ n0-1) < M - 1. Dan bestaat er voor elke x ∈ (0,1) een i ∈ {1,...,n0-1} zodanig dat | x - xi | < δ en dus | f(x) - f(xi) | < 1 zodat | f(x) | = | (f(x) - f(xi)) + f(xi) | ≤ | f(x) - f(xi) | + | f(xi) | < 1 + (M - 1) = M, QED.
Dit idee laat ook mooi zien wat uniforme continuiteit betekent: waar je die delta intervalletjes ook plaatst, je hebt altijd een fluctuatie van hoogstens epsilon.quote:Op donderdag 6 december 2012 20:22 schreef GlowMouse het volgende:
Het kan veel simpeler. Pak uit de defintie op http://en.wikipedia.org/wiki/Uniform_continuity een willekeurige epsilon>0, dan komt daar een delta uitrollen. Kijk dan eens naar 1/delta (1/delta is interessant omdat delta minder dan 1/delta keer in het interval (0,1) past).


Ok, geen wiskunde dit maar hoe los los ik dit het handigst op uit 't hoofd? Iemand tips?
x : -6/8 = -14/35
-45/18 - 18/6 = x
x : -6/8 = -14/35
-45/18 - 18/6 = x


Dankjewel, heel helder. Ik zou dit zelf niet zomaar bedenken, maar ik heb wel het gevoel nu beter te begrijpen wat uniforme continuÔteit inhoudt.quote:Op donderdag 6 december 2012 21:05 schreef Riparius het volgende:
Kies ε = 1. Aangezien f uniform continu is op (0,1) bestaat er dan een δ > 0 zodanig dat | f(x) - f(y) | < ε = 1 voor elke x,y ∈ (0,1) met | x - y | < δ. Kies nu een positief geheel getal n0 > 1 zodanig dat 1/n0 < δ (i.e. n0 > 1/δ) en definieer xi = i/n0 voor i ∈ {1,...,n0-1}. Zij verder M een getal zodanig dat max(|(f(xi)|, 1 ≤ i ≤ n0-1) < M - 1. Dan bestaat er voor elke x ∈ (0,1) een i ∈ {1,...,n0-1} zodanig dat | x - xi | < δ en dus | f(x) - f(xi) | < 1 zodat | f(x) | = | (f(x) - f(xi)) + f(xi) | ≤ | f(x) - f(xi) | + | f(xi) | < 1 + (M - 1) = M, QED.


Beide leden vermenigvuldigen met -6/8 = -3/4 en je hebt x = -3/4 ∙ -14/35 = 3/4 ∙ 2/7 = 6/28 = 3/14.quote:Op vrijdag 7 december 2012 18:21 schreef Maryn. het volgende:
Ok, geen wiskunde dit maar hoe los los ik dit het handigst op uit 't hoofd? Iemand tips?
x : -6/8 = -14/35
Breuken vereenvoudigen, x = -45/18 - 18/6 = -5/2 - 6/2 = -11/2.quote:-45/18 - 18/6 = x


"een uniform convergente reeks van exponentiŽle of circulaire functies convergeert, in het aangegeven gebied, naar een continue functie (waarom?)". Dit staat er, in verband met de uniforme convergentie van Fourierreeksen.
Iemand die ziet waarom dit zo is?
Iemand die ziet waarom dit zo is?


Het klassieke ε/3 trucje. Het bewijs staat vast wel ergens in de een of andere vorm in je leerboek, en anders moet je maar even hier kijken.quote:Op zaterdag 8 december 2012 17:31 schreef yarnamc het volgende:
"een uniform convergente reeks van exponentiŽle of circulaire functies convergeert, in het aangegeven gebied, naar een continue functie (waarom?)". Dit staat er, in verband met de uniforme convergentie van Fourierreeksen.
Iemand die ziet waarom dit zo is?


Stel je hebt een polynoom ![f \in \mathbb{Z}_p[x,y,z]](https://forum.fok.nl/lib/mimetex.cgi?f%20%5Cin%20%5Cmathbb%7BZ%7D_p%5Bx%2Cy%2Cz%5D) met p is priem en zodat
met p is priem en zodat 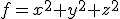 . Hoeveel oplossingen heeft f=0?
. Hoeveel oplossingen heeft f=0?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Komt een lastige. Ik ben bezig met de orthografische cilinderprojectie (van Johann Heinrich Lambert), nu wordt er gesteld dat dit een equivalente projectie is. Maar waaruit volgt dit precies? Stel dat ik de vraag krijg om dit uit te leggen, hoe zou ik dat dan in Godsnaam moeten beantwoorden?
Dit is de betreffende kaart.
Dit is de betreffende kaart.


Al gekeken op http://nl.wikipedia.org/wiki/Orthografische_cilinderprojectie?
Het volgt direct uit de formules.
Het volgt direct uit de formules.


Ja, maar ik zie even niet hoe. De formules afleiden (peanuts) ook al gedaan.quote:Op maandag 10 december 2012 02:03 schreef Dale. het volgende:
Al gekeken op http://nl.wikipedia.org/wiki/Orthografische_cilinderprojectie?
Het volgt direct uit de formules.


Uhmmm de eerste alinea?
quote:Die ontstaat door de aardbol af te beelden op een cilinder vanuit een punt op de omwentelingsas van de bol, zodanig dat de projectielijn loodrecht op de as staat.


Ik snap wat je hiermee bedoelt. Dit is hoe de projectie tot stand komt. Nu wil ik graag weten waarom de projectie equivalent is, en niet omdat 'dit toevallig zo is', nee, wat is de redenatie hierachter?quote:Op maandag 10 december 2012 12:36 schreef Dale. het volgende:
Uhmmm de eerste alinea?
[..]
[ afbeelding ]
Komt er nog een (wat eenvoudigere) meetkundige vraag bij.
Wanneer men dit document opent:
http://mail.vssd.nl/hlf/a028h02oud.pdf
Dan wordt op pagina 25 en 26 het bewijs dat een stereografische projectie conform is behandeld. Nu snap ik de hele godganse redenatie, op een puntje na. Bovenaan pagina 26 staat:
Angle(WRP) = Angle(WRA) = 90 graden
Waaruit volgt dit exact? Waarom is dit zo?


Angle(WRP) is me inmiddels duidelijk. Mag ik zeggen doordat de snijlijn van het raakvlaak aan P met het grondvlak NA snijdt in R, dat die snijlijn loodrecht op NA staat?


Waar staan die integralen van Riparius die hij een tijdje geleden ergens gepost had? Ik wou ze net gaan oplossen maar kan ze vreemd genoeg niet meer terugvinden.
@Amoeba: ik heb geen verstand van projecties, maar je hebt er steeds over dat die orthografische cilinderprojectie equivalent moet zijn. Maar je zegt niet waarmee die dan equivalent moet zijn.
@Amoeba: ik heb geen verstand van projecties, maar je hebt er steeds over dat die orthografische cilinderprojectie equivalent moet zijn. Maar je zegt niet waarmee die dan equivalent moet zijn.


Hier.quote:Op maandag 10 december 2012 16:28 schreef thenxero het volgende:
Waar staan die integralen van Riparius die hij een tijdje geleden ergens gepost had?


Equivalentie is hier een term voor oppervlaktegetrouwheid. Dat betekent dus dat het product van de schaalfactoren van de kaartprojectie in horizontale en in verticale richting in elk punt op de kaart constant moet zijn. Bij hoekgetrouwheid oftewel conformiteit moet daarentegen de verhouding van de schaalfactoren in verticale en horizontale richting voor elk punt op de kaart gelijk zijn aan ťťn. Bij afbeelding van een bolvormig oppervlak op een plat vlak zijn equivalentie en conformiteit onverenigbaar.quote:Op maandag 10 december 2012 16:28 schreef thenxero het volgende:
@Amoeba: ik heb geen verstand van projecties, maar je hebt er steeds over dat die orthografische cilinderprojectie equivalent moet zijn. Maar je zegt niet waarmee die dan equivalent moet zijn.


De methode door te bewijzen (meetkundig) dat de hoek die 2 raaklijnen aan een bol maken equivalent is aan de hoek die de projecties van die lijnen met elkaar maken, is dat ook een sluitend bewijs? Immers, de hoek die 2 krommen maken is gelijk aan de hoek die hun raaklijnen maken.quote:Op maandag 10 december 2012 17:29 schreef Riparius het volgende:
[..]
Equivalentie is hier een term voor oppervlaktegetrouwheid. Dat betekent dus dat het product van de schaalfactoren van de kaartprojectie in horizontale en in verticale richting in elk punt op de kaart constant moet zijn. Bij hoekgetrouwheid oftewel conformiteit moet daarentegen de verhouding van de schaalfactoren in verticale en horizontale richting voor elk punt op de kaart gelijk zijn aan ťťn. Bij afbeelding van een bolvormig oppervlak op een plat vlak zijn equivalentie en conformiteit onverenigbaar.


Bij een conforme projectie zoals de Mercatorprojectie zijn op ieder punt op de kaart de schaalfactoren in horizontale en in verticale richting gelijk. Omdat we willen dat de meridianen als verticale evenwijdige lijnen worden afgebeeld is de schaalfactor voor een punt op noorderbreedte of zuiderbreedte φ in horizontale richting dus 1/cos φ = sec φ maal de schaalfactor voor de evenaar, omdat een breedtecirkel op noorderbreedte of zuiderbreedte φ slechts een omtrek heeft van cos φ maal de omtrek van de evenaar.quote:Op maandag 10 december 2012 14:26 schreef Amoeba het volgende:
[..]
Ik snap wat je hiermee bedoelt. Dit is hoe de projectie tot stand komt. Nu wil ik graag weten waarom de projectie equivalent is, en niet omdat 'dit toevallig zo is', nee, wat is de redenatie hierachter?
Maar, vanwege de conformiteitseis moet de dan schaling in verticale richting voor een punt op noorderbreedte of zuiderbreedte φ ook sec φ maal de schaling voor de evenaar bedragen, en dus wordt de oppervlakte voor een punt op noorderbreedte of zuiderbreedte φ dan op de kaart geschaald met een factor sec2φ ten opzichte van de schaling van de oppervlakte op de kaartprojectie bij de evenaar.
Dus, om een voorbeeld te geven, op 60 graden noorderbreedte wordt de oppervlakte dan al opgeschaald met een factor sec2(π/3) = 4 ten opzichte van de schaling van een gebiedje op de evenaar.
Willen we nu echter een kaartprojectie waarbij de meridianen nog steeds als evenwijdige verticale lijnen worden afgebeeld maar die wel oppervlaktegetrouw is, dan hebben we voor een punt op noorderbreedte of zuiderbreedte φ nog steeds te maken met een horizontale schaling met dezelfde factor 1/cos φ = sec φ ten opzichte van de (horizontale) schaling van de evenaar, maar dan moeten we bij de verticale schaling gaan compenseren door te schalen met een factor cos φ, zodat het product van de horizontale en de verticale schalingen voor elk punt op de kaart, en daarmee dus de oppervlakteschaling constant blijft over de gehele kaart. En als je hebt:
dy/dφ = s0∙R∙cos φ
waarbij s0 de schaalfactor is waarmee de evenaar wordt afgebeeld, en R de straal is van de aarde, dan volgt door primitiveren dus dat we moeten hebben:
y = s0∙R∙sin φ
aangezien ook moet gelden y = 0 voor φ = 0. Begrijp je dit?