SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
ik snap je tex-code niet; wat is de doelfunctie, wat zijn de constraints, wat is het domein voor x, en wat is de optimale oplossing?
[ Bericht 36% gewijzigd door GlowMouse op 21-12-2012 14:08:12 ]
[ Bericht 36% gewijzigd door GlowMouse op 21-12-2012 14:08:12 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Mooie anekdotequote:Op donderdag 20 december 2012 23:37 schreef Riparius het volgende:
[..]
Dat moet je nooit zeggen. Don't sell yourself short. Ik moest toen ik dit las meteen denken aan de ontdekking van de toen 10-jarige Penny Drastik. Tot voor kort werd gedacht dat de minimale zijde van een vierkant dat je kunt verdelen in 5 rechthoekige driehoeken waarvan de zijden pythagoreďsche tripletten vormen een lengte 9000 moest hebben, maar Penny dacht daar toch anders over en kwam op de proppen met maar liefst 12 kleinere vierkanten die zich zo laten verdelen. Ze denkt ook dat het kleinste zo te verdelen vierkant een zijde 1248 moet hebben, en tot nu toe heeft niemand haar bevindingen kunnen weerleggen. Hier kun je er meer over lezen. Ook goed leesvoer voor achterlijke FOKkers die anno 2012 nog beweren dat wiskunde niets is voor meisjes.
Hoewel ik het idee heb dat sommige van de voorbeelden waar stellingen mee ontkracht worden meer een kwestie van geluk zijn (het geluk dat je bij toeval op zo'n voorbeeld stuit). (Hoewel hier dan weer minder van toepassing lijkt omdat dat meisje gelijk 12 tegenvoorbeelden heeft gevonden)
[ Bericht 3% gewijzigd door kutkloon7 op 21-12-2012 17:23:16 ]
Uhuh, bij dat soort problemen is het volgens mij vaak ook een beetje dat bijna niemand er meer serieus naar kijkt omdat het van te voren al onwaarschijnlijk lijkt dat je er verder mee komt. Maar ik bedoelde eigenlijk specifiek tegenvoorbeelden, en dan met name in de geometrie (maar in de getaltheorie bijvoorbeeld, speelt volgens mij precies hetzelfde).quote:
Het gebeurt wel vaker SES / Geniale student lost wiskundig probleem op
Jammer genoeg word ik van dat hele topic niet veel wijzer, en ik zie ook geen serieuze bronnen. Wat ik ervan begrijp is dat hij een differentiaalvergelijking exact heeft weten op te lossen die tot dan toe alleen numeriek kon worden opgelost. Ik zou zijn werk wel eens willen zien.quote:
Het gebeurt wel vaker SES / Geniale student lost wiskundig probleem op
Ik moet de kritieke punten vinden van deze formule:
f(x,y) = x^3+y*x^2-y^2-4*y
De x afgeleide is:
3*x^2 + 2*x*y
Deze is 0 bij (0,y) (-2,-6) en (2,-6)
De y afgeleide is:
x^2-2*y-4
Deze is 0 bij (-2,0) (2,0) (4,6) en (-4,6)
Dit levert echter geen kritieke punten op dus ik moet haast wel iets verkeerd doen bij de afgeleides.
Wie ziet de fout?
f(x,y) = x^3+y*x^2-y^2-4*y
De x afgeleide is:
3*x^2 + 2*x*y
Deze is 0 bij (0,y) (-2,-6) en (2,-6)
De y afgeleide is:
x^2-2*y-4
Deze is 0 bij (-2,0) (2,0) (4,6) en (-4,6)
Dit levert echter geen kritieke punten op dus ik moet haast wel iets verkeerd doen bij de afgeleides.
Wie ziet de fout?
When I get sad, I stop being sad and just be awesome instead.
Los eerst je stelsel fx(x,y) = 0, fy(x,y) = 0 eens fatsoenlijk op. Dan vind je (-4;6), (0;-2) en (1;-3/2).quote:Op vrijdag 21 december 2012 18:30 schreef MouzurX het volgende:
Ik moet de kritieke punten vinden van deze formule functie:
f(x,y) = x^3+y*x^2-y^2-4*y
De afgeleide naar x is:
3*x^2 + 2*x*y
Deze is 0 bij (0,y) (-2,-6) en (2,-6)
De afgeleide naar y is:
x^2-2*y-4
Deze is 0 bij (-2,0) (2,0) (4,6) en (-4,6)
Dit levert echter geen kritieke punten op dus ik moet haast wel iets verkeerd doen bij de afgeleides.
Wie ziet de fout?
Ah dus dan is (0,-2) een kritiek punt.quote:
[..]
Los eerst je stelsel fx(x,y) = 0, fy(x,y) = 0 eens fatsoenlijk op. Dan vind je (-4;6), (0;-2) en (1;-3/2).
When I get sad, I stop being sad and just be awesome instead.
Ik moet het uit mijn hoofd doen, het was een tentamenvraag.quote:
ik snap je tex-code niet; wat is de doelfunctie, wat zijn de constraints, wat is het domein voor x, en wat is de optimale oplossing?
De doelfunctie is |Ax|. Die moet geminimaliseerd worden onder de restrictie |x| = 1. Domein was niks bijzonders mee geloof ik, gewoon x element van (reëele getallen dimensie n). Optimale oplossing niet gegeven.
Zou je een duidelijk voorbeeld kunnen geven van een onjuist gebleken hypothese in de wiskunde waarbij de ontkrachting naar jouw idee puur een kwestie van 'geluk' of 'toeval' was? Een stelling kan overigens niet ontkracht worden als het bewijs deugdelijk is.quote:Op vrijdag 21 december 2012 17:14 schreef kutkloon7 het volgende:
[..]
Mooie anekdote
Hoewel ik het idee heb dat sommige van de voorbeelden waar stellingen mee ontkracht worden meer een kwestie van geluk zijn (het geluk dat je bij toeval op zo'n voorbeeld stuit). (Hoewel hier dan weer minder van toepassing lijkt omdat dat meisje gelijk 12 tegenvoorbeelden heeft gevonden)
Ik kon helaas ook geen goede bron vinden van wat hij nou precies gedaan had.quote:
[..]
Jammer genoeg word ik van dat hele topic niet veel wijzer, en ik zie ook geen serieuze bronnen. Wat ik ervan begrijp is dat hij een differentiaalvergelijking exact heeft weten op te lossen die tot dan toe alleen numeriek kon worden opgelost. Ik zou zijn werk wel eens willen zien.
Iedere matrix A heeft een complexe eigenwaarde. Dus ik denk dat er nog iets mist.quote:
[..]
Ik moet het uit mijn hoofd doen, het was een tentamenvraag.
De doelfunctie is |Ax|. Die moet geminimaliseerd worden onder de restrictie |x| = 1. Domein was niks bijzonders mee geloof ik, gewoon x element van (reëele getallen dimensie n). Optimale oplossing niet gegeven.
Nee, dat klopt uiteraardquote:
[..]
Zou je een duidelijk voorbeeld kunnen geven van een onjuist gebleken hypothese in de wiskunde waarbij de ontkrachting naar jouw idee puur een kwestie van 'geluk' of 'toeval' was? Een stelling kan overigens niet ontkracht worden als het bewijs deugdelijk is.
Ik zal zo eens kijken of ik mijn getaltheorieboek of dictaat een goed voorbeeld kan vinden, ik heb helaas niet zo'n uitstekend geheugen als jij voor dat soort dingen
.
Ik vraag me het volgende af (in verband met asymptotische stabiliteit van een systeem):
als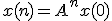
met x(n) een Nx1 matrix, A een NxN matrix en x(0) een Nx1 matrix (x is afhankelijk van de variabele n).
A is diagonaliseerbaar, dus ik kan schrijven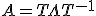
met T de matrix met in de kolommen de eigenvectoren van A, en 
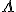de eigenwaardematrix.
Dus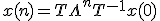
. Nu is gevraagd aan te tonen dat voor de limiet van n -> ∞ zal gelden dat x(n) -> 0 (de nulmatrix), als en slechts als de norm van alle eigenwaarden van A (dus alle diagonaalelementen van 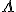) kleiner is dan één.
Het is simpel om te bewijzen dat als de norm van de eigenwaarden kleiner is dan één, dat dan x(n) -> 0, maar in de omgekeerde richting zie ik het niet direct.
Ik vermoed dat het echter niet zo moeilijk zal zijn.
[ Bericht 9% gewijzigd door yarnamc op 21-12-2012 23:16:19 ]
als
A is diagonaliseerbaar, dus ik kan schrijven
Dus
Het is simpel om te bewijzen dat als de norm van de eigenwaarden kleiner is dan één, dat dan x(n) -> 0, maar in de omgekeerde richting zie ik het niet direct.
Ik vermoed dat het echter niet zo moeilijk zal zijn.
[ Bericht 9% gewijzigd door yarnamc op 21-12-2012 23:16:19 ]
Probeer een bewijs uit het ongerijmde waarbij je voor x een eigenvector pakt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
http://tu-dresden.de/die_(...)eien/CommentsRay.pdfquote:
[..]
Jammer genoeg word ik van dat hele topic niet veel wijzer, en ik zie ook geen serieuze bronnen. Wat ik ervan begrijp is dat hij een differentiaalvergelijking exact heeft weten op te lossen die tot dan toe alleen numeriek kon worden opgelost. Ik zou zijn werk wel eens willen zien.
Hierin staat wat hij heeft gedaan (met commentaar van een aantal professoren)
In de laatste paragraaf staat dat hij eigenlijk niks nieuws heeft ontdekt, en zeker geen open probleem van Newton heeft opgelost. Zo zie je maar weer hoe de media werkt (en dat er geen wiskundigen werken).quote:
[..]
http://tu-dresden.de/die_(...)eien/CommentsRay.pdf
Hierin staat wat hij heeft gedaan (met commentaar van een aantal professoren)
Is A toevallig symmetrisch?quote:
[..]
Ik moet het uit mijn hoofd doen, het was een tentamenvraag.
De doelfunctie is |Ax|. Die moet geminimaliseerd worden onder de restrictie |x| = 1. Domein was niks bijzonders mee geloof ik, gewoon x element van (reëele getallen dimensie n). Optimale oplossing niet gegeven.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Aha dank je wel! Zo moet je het inderdaad doen, voor een eigenvector kom je dan uit dat zijn corresponderende eigenwaarde een modulus kleiner dan 1 heeft, en zo ga je ze allemaal af.quote:
Probeer een bewijs uit het ongerijmde waarbij je voor x een eigenvector pakt.
(ik merk nu op dat ik een klein beetje onnauwkeurig was in de formulering, de limiet moet gelden voor alle x(0))
Het kan sneller: neem aan dat er een eigenvector is met modulus >= 1.quote:
[..]
Aha dank je wel! Zo moet je het inderdaad doen, voor een eigenvector kom je dan uit dat zijn corresponderende eigenwaarde een modulus kleiner dan 1 heeft, en zo ga je ze allemaal af.
Ik denk dat je het antwoord in het Rayleigh quotient moet zoeken. Minimaliseren van ||Ax|| is hetzelfde als minimaliseren van het kwadraat ervan gedeeld door een constante: xTATAx / xTx. Dit is altijd groter dan de kleinste eigenwaarde van ATA, met gelijkheid desda x een eigenvector is horend bij de kleinste eigenwaarde.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik doe mijn profielwerkstuk over de chaostheorie en ben nu bezig met research doen naar de Lorenz Attractor. Ik stuitte op deze differentievergelijkingen:
Hoe zijn deze te schrijven als differentie vergelijkingen zoals die op de middelbare school worden geschreven? Dus bijvoorbeeld g(n)=3g(n-1) + 2 . Klopt dit:
x(n) = sigma * (y(n-1) - x(n-1))
y(n) = x(n-1) * (rho - x(n-1)) - y(n-1)
z(n) = x(n-1) * y(n-1) - beta * x(n-1)
Of mag dat niet zomaar tot die vorm herleid worden? Ben een beetje in de war omdat ik een differentievergelijking nog nooit zo geschreven heb zien maar het antwoord zal wel heel logisch zijn...
Hoe zijn deze te schrijven als differentie vergelijkingen zoals die op de middelbare school worden geschreven? Dus bijvoorbeeld g(n)=3g(n-1) + 2 . Klopt dit:
x(n) = sigma * (y(n-1) - x(n-1))
y(n) = x(n-1) * (rho - x(n-1)) - y(n-1)
z(n) = x(n-1) * y(n-1) - beta * x(n-1)
Of mag dat niet zomaar tot die vorm herleid worden? Ben een beetje in de war omdat ik een differentievergelijking nog nooit zo geschreven heb zien maar het antwoord zal wel heel logisch zijn...
Dit zijn differentiaalvergelijkingen, geen differentievergelijkingen.quote:
Ik doe mijn profielwerkstuk over de chaostheorie en ben nu bezig met research doen naar de Lorenz Attractor. Ik stuitte op deze differentievergelijkingen:
Ik heb nog een vraagje:
beschouw de differentievergelijking: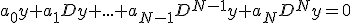
(de D staat voor de Delay operator: D(x(n)) = x(n-1), de n-de macht van D is de samenstelling van n delay operators).
Nu is er gegeven dat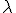
een meervoudige oplossing is van 
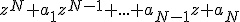, stel bijvoorbeeld met multipliciteit m.
Nu wordt er beweerd (vrij analoog als bij de homogene differentiaalvergelijking) dat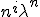
voor i = 0,1,...,m-1 oplossingen zijn van de differentievergelijking. Er wordt gevraagd dit te controleren via substitutie, maar dit lukt me niet direct :s.
Ik hoop dat iemand me kan helpen met het bovenstaande, misschien kan iemand ook dit oplossen (hoewel het moeilijk is om de volledige context te geven) : er wordt dan ook nog gesteld dat dit te controleren valt door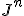
te berekenen, met J de Jordan-blok corresponderend met de meervoudige oplossing 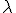. Je moet hierbij weten dat de differentievergelijking een systeem voorstelt, en dat lambda een meervoudige eigenwaarde is van de matrix A uit de ABCD-voorstelling (hiervan komt die veeltermvergelijking), omdat we het systeem bekijken vanuit het toestandsmodel.
Misschien komt dit voor iemand bekend voor en begrijpt hij wat ik met deze laatste paragraaf bedoel, anders zal ik al blij zijn als de eerste paragraaf opgelost wordt (een hint wat ik moet doen na de substitutie om van die vervelende (n-...)^i af te geraken zou heel handig zijn).
[ Bericht 15% gewijzigd door yarnamc op 23-12-2012 20:58:32 ]
beschouw de differentievergelijking:
Nu is er gegeven dat
Nu wordt er beweerd (vrij analoog als bij de homogene differentiaalvergelijking) dat
Ik hoop dat iemand me kan helpen met het bovenstaande, misschien kan iemand ook dit oplossen (hoewel het moeilijk is om de volledige context te geven) : er wordt dan ook nog gesteld dat dit te controleren valt door
Misschien komt dit voor iemand bekend voor en begrijpt hij wat ik met deze laatste paragraaf bedoel, anders zal ik al blij zijn als de eerste paragraaf opgelost wordt (een hint wat ik moet doen na de substitutie om van die vervelende (n-...)^i af te geraken zou heel handig zijn)
.[ Bericht 15% gewijzigd door yarnamc op 23-12-2012 20:58:32 ]
Aha ... ik had 'differential equations' te gauw vertaald naar differentievergelijkingen. Dat wordt nog even researchen!quote:
[..]
Dit zijn differentiaalvergelijkingen, geen differentievergelijkingen.
Je hebt in feite een rij {xn} die aan een N-de orde (hoofdletter!) homogene lineaire recursie met constante coëfficiënten moet voldoen. Substitutie van xn = zn levert dan een karakteristieke vergelijking P(z) = 0 op, waarbij P(z) een polynoom is in z van graad N (hoofdletter!). Is nu z = λ een (enkelvoudige) wortel van P(z) = 0, dan voldoet zoals bekend xn = λn aan de recursie. Is echter z = λ een meervoudige wortel van P(z) = 0 met multipliciteit m, dan kun je gebruik maken van het feit dat dan niet alleen P(λ) = 0 maar ook P(i)(λ) = 0 voor i = 1..(m-1) terwijl P(m)(λ) ≠ 0 (bewijs dit). Door te beginnen metquote:
Ik heb nog een vraagje:
beschouw de differentievergelijking:
Nu is er gegeven dat, stel bijvoorbeeld met multipliciteit m.
Nu wordt er beweerd (vrij analoog als bij de homogene differentiaalvergelijking) dat
∑j=0N ajzN+k-j = zk∙P(z), k ∈ N0
en telkens beide leden te differentiëren naar z en daarna weer te vermenigvuldigen met z kun je gemakkelijk zien dat
∑j=0N aj(N+k-j)iλN+k-j = 0 voor k ∈ N0, i = 1..(m-1)
zodat xn = ni∙λn met i = 1..(m-1) ook voldoet aan de recursie.
[ Bericht 0% gewijzigd door Riparius op 25-12-2012 17:55:37 ]
Weet iemand hier hoe je 'topological mixing' in het nederlands zegt? Heb het over dit:
http://en.wikipedia.org/w(...)g#Topological_mixing
en dan met name op de manier waarop het hier wordt uitgelegd, onder het subkopje 'Topological mixing':
http://en.wikipedia.org/wiki/Chaos_theory
Dus dat een gegeven regio in faseruimte na een bepaalde tijd altijd zal overlappen met een andere gegeven regio. Is daar een nederlandse term voor?
http://en.wikipedia.org/w(...)g#Topological_mixing
en dan met name op de manier waarop het hier wordt uitgelegd, onder het subkopje 'Topological mixing':
http://en.wikipedia.org/wiki/Chaos_theory
Dus dat een gegeven regio in faseruimte na een bepaalde tijd altijd zal overlappen met een andere gegeven regio. Is daar een nederlandse term voor?
In die vergelijkingen zijn x,y en z functies van t. rho, beta en sigma zijn parameters.quote:
Ik doe mijn profielwerkstuk over de chaostheorie en ben nu bezig met research doen naar de Lorenz Attractor. Ik stuitte op deze differentievergelijkingen:
[ afbeelding ]
Hoe zijn deze te schrijven als differentie vergelijkingen zoals die op de middelbare school worden geschreven? Dus bijvoorbeeld g(n)=3g(n-1) + 2 . Klopt dit:
x(n) = sigma * (y(n-1) - x(n-1))
y(n) = x(n-1) * (rho - x(n-1)) - y(n-1)
z(n) = x(n-1) * y(n-1) - beta * x(n-1)
Of mag dat niet zomaar tot die vorm herleid worden? Ben een beetje in de war omdat ik een differentievergelijking nog nooit zo geschreven heb zien maar het antwoord zal wel heel logisch zijn...
Is dit onderwerp niet te ambitieus voor een middelbare schoolleerling?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Kijk maar eens even hier (eenvoudig) en ook hier (uitgebreider, met historische achtergronden), dan moet het je wel duidelijk worden.quote:
Ik las ergens iets dat het eenvoudig was om aan te tonen dat een smalle ring tussen 2 parallellen dezelfde oppervlakte op de kaart heeft als op de bol. Maar dit klopt toch niet, aangezien deze ring toch veel groter wordt, en niet smaller?
Dat is knap gevonden! Dank je welquote:
[..]
Je hebt in feite een rij {xn} die aan een N-de orde (hoofdletter!) homogene lineaire recursie met constante coëfficiënten moet voldoen. Substutie van xn = zn levert dan een karakteristieke vergelijking P(z) = 0 op, waarbij P(z) een polynoom is in z van graad N (hoofdletter!). Is nu z = λ een (enkelvoudige) wortel van P(z) = 0, dan voldoet zoals bekend xn = λn aan de recursie. Is echter z = λ een meervoudige wortel van P(z) = 0 met multipliciteit m, dan kun je gebruik maken van het feit dat dan niet alleen P(λ) = 0 maar ook P(i)(λ) = 0 voor i = 1..(m-1) terwijl P(m)(λ) ≠ 0 (bewijs dit). Door te beginnen met
∑j=0N ajzN+k-j = zk∙P(z), k ∈ N0
en telkens beide leden te differentiëren naar z en daarna weer te vermenigvuldigen met z kun je gemakkelijk zien dat
∑j=0N aj(N+k-j)iλN+k-j = 0 voor k ∈ N0, i = 1..(m-1)
zodat xn = ni∙λn met i = 1..(m-1) ook voldoet aan de recursie.
Ik heb een vraag over het volgende lemma uit mijn leeswijzer functies en reeksen:
Neem n = p = 1 (en ik gebruikt y ipv dzeta xi, dat is wat makkelijker). Neem f(x) = x3. Dan is f totaal differentieerbaar (dit kan ik aantonen met de definitie, maar dat laat ik nu even achterwege).
Verder L(x) = Df (x) = 3x2. (dit staat in de laatste zin van het lemma, Df (x) is gewoon de afgeleide van f).
Dan komt de formule uit het lemma neer op:
x3 - y3 = 3x2(x-y)
Wat natuurlijk niet klopt. Doe ik iets verkeerd (klopt er een van mijn aannames niet?) of staat er iets verkeerd in het lemma?
[ Bericht 0% gewijzigd door kutkloon7 op 26-12-2012 21:55:23 ]
Neem n = p = 1 (en ik gebruikt y ipv dzeta xi, dat is wat makkelijker). Neem f(x) = x3. Dan is f totaal differentieerbaar (dit kan ik aantonen met de definitie, maar dat laat ik nu even achterwege).
Verder L(x) = Df (x) = 3x2. (dit staat in de laatste zin van het lemma, Df (x) is gewoon de afgeleide van f).
Dan komt de formule uit het lemma neer op:
x3 - y3 = 3x2(x-y)
Wat natuurlijk niet klopt. Doe ik iets verkeerd (klopt er een van mijn aannames niet?) of staat er iets verkeerd in het lemma?
[ Bericht 0% gewijzigd door kutkloon7 op 26-12-2012 21:55:23 ]
De verzameling lineaire afbeeldingen van Rn naar Rp. Dus ook wel de verzameling n bij p matrices met componenten uit R.quote:
Wat je verkeerd doet, is aannemen dat L over zijn hele domein gelijk is aan Df. De stelling zegt dat er een punt is, zodat L en Df in dat punt gelijk aan elkaar zijn. Er staat niets verkeerds in die stelling.quote:
Ik heb een vraag over het volgende lemma uit mijn leeswijzer functies en reeksen:
[ afbeelding ]
Neem n = p = 1 (en ik gebruikt y ipv dzeta xi, dat is wat makkelijker). Neem f(x) = x3. Dan is f totaal differentieerbaar (dit kan ik aantonen met de definitie, maar dat laat ik nu even achterwege).
Verder L(x) = Df (x) = 3x2. (dit staat in de laatste zin van het lemma, Df (x) is gewoon de afgeleide van f).
Dan komt de formule uit het lemma neer op:
x3 - y3 = 3x2(x-y)
Wat natuurlijk niet klopt. Doe ik iets verkeerd (klopt er een van mijn aannames niet?) of staat er iets verkeerd in het lemma?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Mathemaat heeft gelijk.
x3 - y3 = L(x)(x-y) voor elke x in X.
Dan geldt dus L(x) = x2 + xy + y2
Dus geldt L(y) = 3y2
x3 - y3 = L(x)(x-y) voor elke x in X.
Dan geldt dus L(x) = x2 + xy + y2
Dus geldt L(y) = 3y2
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
L(x) kan je opvatting als de helling tussen de punten f(x) en f(ksi) (makkelijkst om gewoon even in 1 dimensie te denken). De stelling zegt dus eigenlijk dat een functie differentieerbaar is in een punt desda de helling continu is in dat punt. Zo kan je het makkelijk begrijpen en onthouden.
Ik maakte inderdaad een denkfout, dank! Ik had om een of andere reden inderdaad niet goed door dat ze xi in het hele verhaal vast kiezen, it all makes sense nowquote:
[..]
Wat je verkeerd doet, is aannemen dat L over zijn hele domein gelijk is aan Df. De stelling zegt dat er een punt is, zodat L en Df in dat punt gelijk aan elkaar zijn. Er staat niets verkeerds in die stelling.
Ook dank Glowmouse en thenxzero, voor de extra uitleg.
Hallo, ik heb wiskunde A en krijg de abc-formule niet. Toch heb ik die nodig voor scheikunde. Ik moet bijv. dit oplossen:
Dit is dus de abc formule:
Kan iemand uitleggen hoe dit werkt in mijn situatie? (stap voor stap graag, ik heb alleen wiskunde A).
Dit is dus de abc formule:
Kan iemand uitleggen hoe dit werkt in mijn situatie? (stap voor stap graag, ik heb alleen wiskunde A).
Unbowed, Unbent, Unbroken.
Probeer eerst de op te lossen vergelijking in de vorm van de abc-formule te zetten. Het omschrijven van die vergelijking zou je met wiskunde A moeten kunnen.
Zo?
x^2 - 6,1*10^-10 * (0,01-x) = 0 Daarna haakjes wegwerken zodat:
1*x^2 + 6,1*10^-10*x + (-6.1*10^-12)
met a = 1
b = 6,1*10^-10
c= -6,1*10^-12
Oké, ik ga het even uitproberen om hem nu in die wortelvariant te zetten.
E: Waarschijnlijk doe ik iets fout. Ik krijg 1,26*10^-5, het antw. moet 2,5&10^-6 zijn.
E2: Het werkt wel, oké klaar, duidelijk. Bedankt.
[ Bericht 13% gewijzigd door BeyondTheGreen op 27-12-2012 13:50:18 ]
x^2 - 6,1*10^-10 * (0,01-x) = 0 Daarna haakjes wegwerken zodat:
1*x^2 + 6,1*10^-10*x + (-6.1*10^-12)
met a = 1
b = 6,1*10^-10
c= -6,1*10^-12
Oké, ik ga het even uitproberen om hem nu in die wortelvariant te zetten.
E: Waarschijnlijk doe ik iets fout. Ik krijg 1,26*10^-5, het antw. moet 2,5&10^-6 zijn.
E2: Het werkt wel, oké klaar, duidelijk.
Bedankt.[ Bericht 13% gewijzigd door BeyondTheGreen op 27-12-2012 13:50:18 ]
Unbowed, Unbent, Unbroken.
quote:
Zo?
x^2 - 6,1*10^-10 * (0,01-x) = 0 Daarna haakjes wegwerken zodat:
1*x^2 + 6,1*10^-10*x + (-6.1*10^-12)
met a = 1
b = 6,1*10^-10
c= -6,1*10^-12
Oké, ik ga het even uitproberen om hem nu in die wortelvariant te zetten.
E: Waarschijnlijk doe ik iets fout. Ik krijg 1,26*10^-5, het antw. moet 2,5&10^-6 zijn.
E2: Het werkt wel, oké klaar, duidelijk.
De ABC-formule is de manier om de 2 (complexe) nulpunten (ofwel f(x) = 0) van een tweedegraads polynoom exact te berekenen.quote:
Hallo, ik heb wiskunde A en krijg de abc-formule niet. Toch heb ik die nodig voor scheikunde. Ik moet bijv. dit oplossen:
[ afbeelding ]
Dit is dus de abc formule:
[ afbeelding ]
Kan iemand uitleggen hoe dit werkt in mijn situatie? (stap voor stap graag, ik heb alleen wiskunde A).
Wanneer geldt:
D > 0 : 2 reëele oplossingen
D=0 : 1 reëele oplossing, ofwel de top valt samen met de x-as
D<0 : 2 complexe oplossingen.
Bijvoorbeeld wanneer D = -9, dan geldt √D = √(-9) = √(i2)*√9 = i√9
i = √(-1)
D = b2 -4ac
Het is misschien wel nuttig om dit bewijs even te onderzoeken, maar ik neem aan dat je dit wel ergens op kunt snorren.
Geven ze dit tegenwoordig niet meer bij wisA?
nl.m.wikipedia.org/wiki/Wortelformule
Hier een afleiding van de formule.
Ik neem het door.quote:
[..]
Kijk maar eens even hier (eenvoudig) en ook hier (uitgebreider, met historische achtergronden), dan moet het je wel duidelijk worden.
Mijn excuses voor 'n laatste reactie. Loopt niet helemaal lekker thuis, knalt zover uit de pan dat het tot een scheiding van m'n ouders loopt en ik word daar flink in betrokken. Maar dat terzijde.
In de eerste post geeft hij aan dat je zelf even de gelijkvormigheid mag bewijzen. Ik heb het geheel correct wanneer ik stel dat aangezien AB een raaklijn in A is, de totale hoek A 90 graden is, en uit de driehoekensom dan volgt dat hoek BAC = hoek DCM en hoek BCA = hoek CDM = 90 graden?
Dus de driehoeken zijn gelijkvormig (hh).
Dit weekend meer. Ik moet
De vadsige koningen lezen, van Hugo Raes. Wat een grafboek is dat. Nederlandse literatuur 
(Met uitzonderingen uiteraard, Lijmen het Been 
en De Engelenmaker )[ Bericht 16% gewijzigd door #ANONIEM op 27-12-2012 18:43:38 ]
Deze notatie is prima tenzij er meer dan 1 onafhankelijke variabele in de vergelijking staat in welk geval je het als een partiële afgeleide moet weergeven met een teken wat lijkt op een a.quote:
Ik doe mijn profielwerkstuk over de chaostheorie en ben nu bezig met research doen naar de Lorenz Attractor. Ik stuitte op deze differentievergelijkingen:
[ afbeelding ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Als je de wortelformule gebruikt, bekijk dan ook even hoe die formule is afgeleid zodat je begrijpt wat je doet!quote:
Hallo, ik heb wiskunde A en krijg de abc-formule niet. Toch heb ik die nodig voor scheikunde. Ik moet bijv. dit oplossen:
[ afbeelding ]
Dit is dus de abc formule:
[ afbeelding ]
Kan iemand uitleggen hoe dit werkt in mijn situatie? (stap voor stap graag, ik heb alleen wiskunde A).
http://nl.wikipedia.org/wiki/Wortelformule
http://nl.wikipedia.org/wiki/Kwadraatsplitsen
Het is een simpele uitleg waarvoor je weinig basis nodig hebt, als je weet hoe je een eerstegraadsvergelijking kan oplossen dan zou je deze uitleg ook moeten kunnen volgen.
Kijk ook even naar de Engelstalige versie als je moeite hebt met iets te volgen.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik ben iemand die graag begrijpt wat ik doe, maar ik heb geen wiskunde B, doe drie VWO schooljaar in 1, en heb een tentamenweek na de kerstvakantie dus mijn prioriteit ligt daar niet. Toch bedankt, misschien kijk ik er nog eens naar.quote:
[..]
Als je de wortelformule gebruikt, bekijk dan ook even hoe die formule is afgeleid zodat je begrijpt wat je doet!
http://nl.wikipedia.org/wiki/Wortelformule
http://nl.wikipedia.org/wiki/Kwadraatsplitsen
Het is een simpele uitleg waarvoor je weinig basis nodig hebt, als je weet hoe je een eerstegraadsvergelijking kan oplossen dan zou je deze uitleg ook moeten kunnen volgen.
Kijk ook even naar de Engelstalige versie als je moeite hebt met iets te volgen.
Unbowed, Unbent, Unbroken.
Misschien een beetje opportunistisch om 3 schooljaren in een jaar af te willen ronden wanneer je het toepassen van de ABC-formule al niet volgt.quote:
[..]
Ik ben iemand die graag begrijpt wat ik doe, maar ik heb geen wiskunde B, doe drie VWO schooljaar in 1, en heb een tentamenweek na de kerstvakantie dus mijn prioriteit ligt daar niet. Toch bedankt, misschien kijk ik er nog eens naar.
Blame the system.quote:Op vrijdag 28 december 2012 00:18 schreef Amoeba het volgende:
[..]
Misschien een beetje opportunistisch om 3 schooljaren in een jaar af te willen ronden wanneer je het toepassen van de ABC-formule al niet volgt.
Vroeger leerde je in 1-MAVO of 2-MAVO de wortelformule te gebruiken. 
Dit is uiteraard geen verwijt naar hem toe maar het doet de wenkbrauwen fronsen.
Dit is uiteraard geen verwijt naar hem toe maar het doet de wenkbrauwen fronsen.
In een kwartier tijd heb je het wel gelezen en begrepen als het goed is, het lijkt mij zinvol besteedde tijd.quote:
[..]
Ik ben iemand die graag begrijpt wat ik doe, maar ik heb geen wiskunde B, doe drie VWO schooljaar in 1, en heb een tentamenweek na de kerstvakantie dus mijn prioriteit ligt daar niet. Toch bedankt, misschien kijk ik er nog eens naar.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
