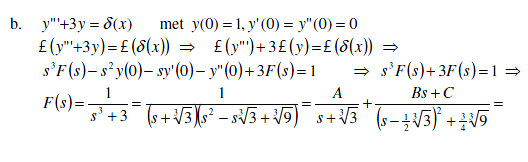SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Het is niet voor niets dat we het grondtal van de logaritme als superscript noteren, dus 5log 3. Gebruik dan ook superscript. Een hele tijd geleden was er hier een warrige discussie over een opgave met logaritmen waarbij alle misverstanden bleken te berusten op het feit dat de oorspronkelijke vragensteller te beroerd was geweest het grondtal even te superscripten. Let daar dus op.quote:Op zondag 25 maart 2012 17:51 schreef ulq het volgende:
Dus mijn vraag is: wat klopt er niet of wat doe ik fout?
De wiskunde hierachter is:quote:
Er staat 5*log(3). Voor 5log3 moet je log3/log5 intypen.
5log3 is de oplossing van 5^x = 3.
Neem van de vergelijking aan beide kanten een willekeurige logaritme (geldt dus ook voor de 10-log die op je rekenmachine zit):
log(5^x) = log(3)
x * log(5) = log(3)
x = log(3)/log(5)
Als je het op deze manier nagaat vergeet je ook niet of je nou log(3)/log(5) of log(5)/log(3) moet doen.
Ik kom niet uit deze analyse 2 vraag:
Beschouw de afbeelding H = 1/2 (x²y² + x²z² + y²z²)
Beschouw een deeltje dat zich beweegt door het vlak V = {x + 2y + 3z = 6} en dat zich bevindt
in het punt (1,1,1) in V.
Bepaal de richting waarin het deeltje moet bewegen om H zo sterk mogelijk te laten toenemen.
Mijn poging:
De gradient geeft de richting aan waarin de stijging het grootste is, grad H(1,1,1) = (2,2,2)
Het deeltje moet in V blijven, dus als (u1,u2,u3) de richting is dan
(1+ u1) + 2(1 + u2) + 3(1+u3) = 6
dus u1 + 2u2 + 3u3 = 0.
Hoe bepaal ik nu de richting m.b.v. deze twee voorwaarden?
Beschouw de afbeelding H = 1/2 (x²y² + x²z² + y²z²)
Beschouw een deeltje dat zich beweegt door het vlak V = {x + 2y + 3z = 6} en dat zich bevindt
in het punt (1,1,1) in V.
Bepaal de richting waarin het deeltje moet bewegen om H zo sterk mogelijk te laten toenemen.
Mijn poging:
De gradient geeft de richting aan waarin de stijging het grootste is, grad H(1,1,1) = (2,2,2)
Het deeltje moet in V blijven, dus als (u1,u2,u3) de richting is dan
(1+ u1) + 2(1 + u2) + 3(1+u3) = 6
dus u1 + 2u2 + 3u3 = 0.
Hoe bepaal ik nu de richting m.b.v. deze twee voorwaarden?
volgende keer een keuze maken, topic openen of hier posten, niet allebei
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik denk dat je de orthogonale projectie van de gradient op het vlak moet bepalen.quote:
Ik kom niet uit deze analyse 2 vraag:
Beschouw de afbeelding H = 1/2 (x²y² + x²z² + y²z²)
Beschouw een deeltje dat zich beweegt door het vlak V = {x + 2y + 3z = 6} en dat zich bevindt
in het punt (1,1,1) in V.
Bepaal de richting waarin het deeltje moet bewegen om H zo sterk mogelijk te laten toenemen.
Mijn poging:
De gradient geeft de richting aan waarin de stijging het grootste is, grad H(1,1,1) = (2,2,2)
Het deeltje moet in V blijven, dus als (u1,u2,u3) de richting is dan
(1+ u1) + 2(1 + u2) + 3(1+u3) = 6
dus u1 + 2u2 + 3u3 = 0.
Hoe bepaal ik nu de richting m.b.v. deze twee voorwaarden?
oja, dank je.quote:
[..]
De wiskunde hierachter is:
5log3 is de oplossing van 5^x = 3.
Neem van de vergelijking aan beide kanten een willekeurige logaritme (geldt dus ook voor de 10-log die op je rekenmachine zit):
log(5^x) = log(3)
x * log(5) = log(3)
x = log(3)/log(5)
Als je het op deze manier nagaat vergeet je ook niet of je nou log(3)/log(5) of log(5)/log(3) moet doen.
dat zie je ook gelijk doordat log(x)/log(3) stijgend is in x en log(3)/log(x) dalendquote:
vergeet je ook niet of je nou log(3)/log(5) of log(5)/log(3) moet doen.
er zijn heel veel unbounded rays, wat is 'zo sterk mogelijk'?quote:
Bepaal de richting waarin het deeltje moet bewegen om H zo sterk mogelijk te laten toenemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Waar de richtingsafgeleide maximaal is zou ik zeggen. Daar gaat het hoofdstuk in ieder geval over.quote:
[..]
dat zie je ook gelijk doordat log(x)/log(3) stijgend is in x en log(3)/log(x) dalend
[..]
er zijn heel veel unbounded rays, wat is 'zo sterk mogelijk'?
Orthogonale projectie van de gradient op V zou moeten werken, maar het is niet iets wat we hebben behandeld bij dit vak.
Je kunt ook x substitueren uit de vergelijking voor H, dan heb je nog maar twee variabelen en geen restrictie.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bestudeer even deze oude post van mij om te zien hoe je de coördinaten van het voetpunt van een loodlijn vanuit een punt op een vlak bepaalt.quote:
[..]
Waar de richtingsafgeleide maximaal is zou ik zeggen. Daar gaat het hoofdstuk in ieder geval over.
Orthogonale projectie van de gradient op V zou moeten werken, maar het is niet iets wat we hebben behandeld bij dit vak.
Edit: ik kom voor jouw opgave op (u1, u2, u3) = (4/7, 1/7, -2/7).
[ Bericht 2% gewijzigd door Riparius op 25-03-2012 19:50:18 ]
Ah, ik heb hem. Bij een andere opgave moest je berekenen in welke richting in het vlak de richtingsafgeleide 0 was, en de maximale toename staat hier dan loodrecht op. Ik krijg dan hetzelfde antwoord als Riparius. Bedankt.
Los de volgende diff verglijking op:
Dit is een stukje van de uitwerking, maar volgens mij is het fout? ze hebben die -s2 weggelaten, want y (0) = 1 dus waar is die opeens gebleven?
Dit is een stukje van de uitwerking, maar volgens mij is het fout? ze hebben die -s2 weggelaten, want y (0) = 1 dus waar is die opeens gebleven?
Blues ain't nothing but a good man feeling bad...
Ik snap de volgende vraag niet:
In de tabel staan de percentages van vijf leeftijdsklassen van de totale Nederlandse bevolking vermeld.
0-19 31,5
20-44 37,2
45-64 19,9
65-79 9,3
>80 2,1
Geef de mediaan
Het antwoordenboek zegt door middel van interpolatie 32,4.
Hoe doe ik dit?
In de tabel staan de percentages van vijf leeftijdsklassen van de totale Nederlandse bevolking vermeld.
0-19 31,5
20-44 37,2
45-64 19,9
65-79 9,3
>80 2,1
Geef de mediaan
Het antwoordenboek zegt door middel van interpolatie 32,4.
Hoe doe ik dit?
Formule mediaan:
X = L + ( nl / nl + nr ) * Sm
19 + (20 / (19 + 35)) * 36 = 32.3333
X = L + ( nl / nl + nr ) * Sm
19 + (20 / (19 + 35)) * 36 = 32.3333
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Blues ain't nothing but a good man feeling bad...
Huh?quote:
Formule mediaan:
X = L + ( nl / nl + nr ) * Sm
19 + (20 / (19 + 35)) * 36 = 32.3333
niemandquote:
Los de volgende diff verglijking op:
Dit is een stukje van de uitwerking, maar volgens mij is het fout? ze hebben die -s2 weggelaten, want y (0) = 1 dus waar is die opeens gebleven?
[ afbeelding ]
?
Blues ain't nothing but a good man feeling bad...
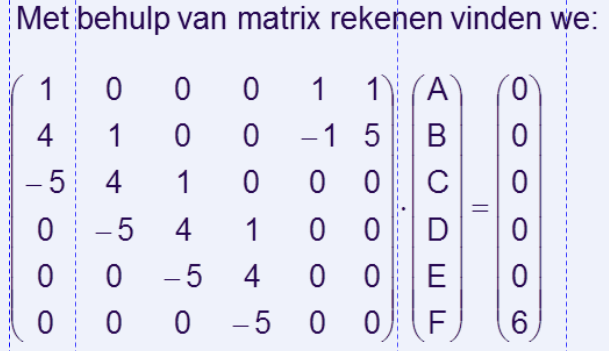
Iemand verstand van GRM TI-83 rekenmachine?
Ik deed die matrices eerst met de hand maar word nu wel beetje groot..
Ik voer dit in op mijn GRM, die hele meut onder [A] en die kolom rechts onder matrix [B]
Maar hoe moet ik die twee matrices vermenigvuldigen zodat ik de onbekende A B C etc kom te weten?
Ik deed die matrices eerst met de hand maar word nu wel beetje groot..
Ik voer dit in op mijn GRM, die hele meut onder [A] en die kolom rechts onder matrix [B]
Maar hoe moet ik die twee matrices vermenigvuldigen zodat ik de onbekende A B C etc kom te weten?
Blues ain't nothing but a good man feeling bad...
De resultaatvector, dus die (0, 0, 0, 0, 0, 6)t, voorvermenigvuldigen met de inverse van die (grote) matrix.quote:
Iemand verstand van GRM TI-83 rekenmachine?
[ afbeelding ]
Ik deed die matrices eerst met de hand maar word nu wel beetje groot..
Ik voer dit in op mijn GRM, die hele meut onder [A] en die kolom rechts onder matrix [B]
Maar hoe moet ik die twee matrices vermenigvuldigen zodat ik de onbekende A B C etc kom te weten?
[ Bericht 0% gewijzigd door kutkloon7 op 29-03-2012 18:52:46 ]
Ik hoopte dat iemand me met het volgende kon helpen:
Dit komt uit een dictaat voor complexe analyse:
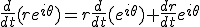
En er geldt
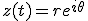
(Oftewel, z is een complexe functie van t, en z is uitgedrukt als e-macht)
Waarom geldt dit? Ik heb geprobeerd hetzelfde resultaat te krijgen met de kettingregel voor meerdere variabelen:
Dit komt uit een dictaat voor complexe analyse:
En er geldt
(Oftewel, z is een complexe functie van t, en z is uitgedrukt als e-macht)
Waarom geldt dit? Ik heb geprobeerd hetzelfde resultaat te krijgen met de kettingregel voor meerdere variabelen:
SPOILER: Maar ik ben erachter dat ik iets onzinnigs deed :')Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Ik zal wel iets fout doen, aangezien ik de kettingregel voor meerdere variabelen nooit helemaal goed begrepen heb... Maar waar? Ik hoop dat iemand me wat verder kan helpen
Edit: Ik zie al wat ik fout doe, ik druk namelijk functies in elkaar uit en ga er daar één van differentiëren, wat me niet echt nuttig lijkt.
Het lijkt gewoon te kloppen, ze werken alleen de d/dt van de exponent niet uit.
Het is overigens handiger om te zeggen dat
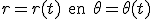
Dan ben je nooit mis met de variabelnamen.
Het is overigens handiger om te zeggen dat
Dan ben je nooit mis met de variabelnamen.
Ja dat snap ik, maar ik snap niet wat voor handelingen je daarvoor moet doen in de GRquote:Op donderdag 29 maart 2012 18:30 schreef kutkloon7 het volgende:
[..]
De resultaatvector, dus die (0, 0, 0, 0, 0, 6)t, voorvermenigvuldigen met de inverse van die (grote) matrix.
-edit-
heb handboek van GR maar gedownload
Got it, oh het is echt super simpel T_T
[ Bericht 6% gewijzigd door GoodGawd op 29-03-2012 19:47:52 ]
Blues ain't nothing but a good man feeling bad...
Je zou wat meer context moeten geven, want als dit werkelijk zo in je dictaat staat denk ik dat je dictaat niet helemaal netjes is. Als je een voorstelling r = r(θ) in poolcoördinaten hebt van een contour waarlangs je wil integreren (want ik vermoed dat dat de bedoeling is) dan kun je werken met z(θ) = r(θ)∙eiθ als parametervoorstelling van je contour en dan is dus θ, niet t, je onafhankelijke variabele. Gaat het soms om een afleiding van de integraalformule van Cauchy?quote:
Ik hoopte dat iemand me met het volgende kon helpen:
Dit komt uit een dictaat voor complexe analyse:
En er geldt
(Oftewel, z is een complexe functie van t, en z is uitgedrukt als e-macht)
quote:
Bedankt! (en ! dat ik het niet zag, misschien moet ik weer wat meer aan differentiëren en integreren doen...)Het gaat om de afleiding van een planeetbaan met complexe analyse (als ik het goed begrepen heb)quote:
[..]
Je zou wat meer context moeten geven, want als dit werkelijk zo in je dictaat staat denk ik dat je dictaat niet helemaal netjes is. Als je een voorstelling r = r(θ) in poolcoördinaten hebt van een contour waarlangs je wil integreren (want ik vermoed dat dat de bedoeling is) dan kun je werken met z(θ) = r(θ)∙eiθ als parametervoorstelling van je contour en dan is dus θ, niet t, je onafhankelijke variabele. Gaat het soms om een afleiding van de integraalformule van Cauchy?
http://people.math.gatech.edu/~cain/winter99/ch2.pdf (bladzijde 2)
Voor de geïntresseerden, het hele dictaat complexe analyse is daar te downloaden. Het is een vak dat ik volgend jaar ga doen, en ik heb gemerkt dat je van te voren inlezen in vakken echt enorm scheelt. Heeft ook met motivatie te maken, als ik een vak heb is het opeens een verplichting in plaats van een keuze, waardoor mijn motivatie blijkbaar enorm daalt
.
Ik zie het, het gaat om een afleiding van de eerste wet van Kepler met behulp van het complexe vlak. Meestal doet men dat met vectoranalyse. Als je dat eens wil zien, en dan meteen ook een afleiding van de perkenwet en de periodenwet (2e en 3e wet van Kepler) dan moet je het einde van dit dictaat eens doornemen.quote:
[..]
[..]
Het gaat om de afleiding van een planeetbaan met complexe analyse (als ik het goed begrepen heb)
http://people.math.gatech.edu/~cain/winter99/ch2.pdf (bladzijde 2)
Voor de geïntresseerden, het hele dictaat complexe analyse is daar te downloaden. Het is een vak dat ik volgend jaar ga doen, en ik heb gemerkt dat je van te voren inlezen in vakken echt enorm scheelt. Heeft ook met motivatie te maken, als ik een vak heb is het opeens een verplichting in plaats van een keuze, waardoor mijn motivatie blijkbaar enorm daalt
Het dictaat waar je naar verwijst heb ik wel eens vaker gezien. Mijn bezwaar tegen de meeste inleidingen (zoals ook hoofdstuk 1 van het dictaat waar je naar verwijst) is dat de behandeling niet erg veel inzicht geeft. Zo wordt meestal gebruik gemaakt van de additietheorema's uit de goniometrie om aan te tonen dat argumenten optellen (modulo 2π) bij vermenigvuldiging van twee complexe getallen, terwijl het nu juist veel inzichtelijker is om dit om te keren en te laten zien dat de additietheorema's van de goniometrie op een eenvoudige wijze volgen uit bepaalde eigenschappen van complexe getallen. Op die manier breng je studenten veel meer inzicht bij door te laten zien dat oude bekende resultaten dankzij de complexe getallen in een heel nieuw daglicht komen te staan. Zie hiervoor ook hoofdstuk III van het genoemde dictaat. Verder komt de formule van Euler vaak uit de lucht vallen doordat men min of meer out of the blue eit definieert als cos t + i∙sin t. Ook dit is didactisch (en historisch) helemaal fout, want voor iemand die net kennis maakt met complexe getallen is het totaal niet evident wat een complexe e-macht nu met cirkels en goniometrie heeft te maken. Dat kan uiteraard ook anders worden gedaan, zoals ik hier onlangs nog heb uiteengezet.
Er zijn heel wat dictaten over complexe analyse vrij beschikbaar op het web, en ik denk dat daar betere tussen zitten dan het dictaat waar je hier zelf naar verwijst. Probeer bijvoorbeeld eens dit of dit. Of dit, in het Nederlands.
[ Bericht 0% gewijzigd door Riparius op 30-03-2012 01:36:40 ]
Hulde! Vooral voor het nederlandse dictaat, dat vind ik eerlijk gezegd nog altijd een stuk makkelijker lezen dan engelse teksten.quote:
[..]
Ik zie het, het gaat om een afleiding van de eerste wet van Kepler met behulp van het complexe vlak. Meestal doet men dat met vectoranalyse. Als je dat eens wil zien, en dan meteen ook een afleiding van de perkenwet en de periodenwet (2e en 3e wet van Kepler) dan moet je het einde van dit dictaat eens doornemen.
Het dictaat waar je naar verwijst heb ik wel eens vaker gezien. Mijn bezwaar tegen de meeste inleidingen (zoals ook hoofdstuk 1 van het dictaat waar je naar verwijst) is dat de behandeling niet erg veel inzicht geeft. Zo wordt meestal gebruik gemaakt van de additietheorema's uit de goniometrie om aan te tonen dat argumenten optellen (modulo 2π) bij vermenigvuldiging van twee complexe getallen, terwijl het nu juist veel inzichtelijker is om dit om te keren en te laten zien dat de additietheorema's van de goniometrie op een eenvoudige wijze volgen uit bepaalde eigenschappen van complexe getallen. Op die manier breng je studenten veel meer inzicht bij door te laten zien dat oude bekende resultaten dankzij de complexe getallen in een heel nieuw daglicht komen te staan. Zie hiervoor ook hoofdstuk III van het genoemde dictaat. Verder komt de formule van Euler vaak uit de lucht vallen doordat men min of meer out of the blue eit definieert als cos t + i∙sin t. Ook dit is didactisch (en historisch) helemaal fout, want voor iemand die net kennis maakt met complexe getallen is het totaal niet evident wat een complexe e-macht nu met cirkels en goniometrie heeft te maken. Dat kan uiteraard ook anders worden gedaan, zoals ik hier onlangs nog heb uiteengezet.
Er zijn heel wat dictaten over complexe analyse vrij beschikbaar op het web, en ik denk dat daar betere tussen zitten dan het dictaat waar je hier zelf naar verwijst. Probeer bijvoorbeeld eens dit of dit. Of dit, in het Nederlands.
Ik ben het overigens totaal eens met je betoog over het definiëren van eit als cos t + i sin t. In mijn dictaat infinitesimaalrekening (wat eigenlijk gewoon calculus moet heten
) werden de taylorreeksen vergeleken, wat wel een ok manier is, maar de manier die jij gebruikt vind ik veel didactisch verantwoorder (veel hoogleraren zouden er nog wat van kunnen leren...).
Ik heb een vraagje over het toetsen van een hypothese.
Er is een opgave:
Volgens Hans kijkt de Nederlander gemiddeld minstens 28,4 uur per week naar de tv. Een medewerker van reclamebureau 'de Ster' trekt deze bewering in twijfel. Een aselecte steekproef van 30 personen levert het gemiddelde 27,6 uur op. Onderzoek of je het bij een significantieniveau 2,5% eens kunt zijn met de uitspraak van 'de Ster'. Ga er vanuit dat de tijd die een Nederlander per week naar de tv kijkt normaal verdeeld is met sigma=2,4.
Nu snap ik dat je de nulhypothese op 28,4 uur stelt, en de alternatieve hypothese op <28,4 omdat het steekproefgemiddelde lager is dan mu, en je dus linkszijdig moet toetsen.
Nu is er een andere opgave:
Een medicijn is verkrijgbaar in tabletvorm. Het werkzame aandeel X in een tablet is normaal verdeeld met een gemiddelde van 4 mg en een standaardafwijking van 0,12 mg. Het medicijn helpt als het werkzame aandeel per tablet tussen 3,8 mg en 4,2 mg ligt.
Er vinden regelmatig controles plaats om te kijken of de gemiddelde hoeveelheid inderdaad 4 mg is. Een steekproef van 50 tabletten levert een gemiddelde van 3,95 mg werkzame stof op. Toets of hieruit volgt dat dit gemiddelde niet significant afwijkt van 4 mg met alpha = 0,05.
Volgens de uitwerkingen wordt hier tweezijdig getoetst, maar als je naar de vorige opgave kijkt, waarbij je linkszijdig toets doordat het steekproefgemiddelde lager is dan mu, waarom doe je dat hier dan ook niet? 3,95 is minder dan 4 en dus kan je toch linkszijdig toetsen??
Alvast bedankt.
Er is een opgave:
Volgens Hans kijkt de Nederlander gemiddeld minstens 28,4 uur per week naar de tv. Een medewerker van reclamebureau 'de Ster' trekt deze bewering in twijfel. Een aselecte steekproef van 30 personen levert het gemiddelde 27,6 uur op. Onderzoek of je het bij een significantieniveau 2,5% eens kunt zijn met de uitspraak van 'de Ster'. Ga er vanuit dat de tijd die een Nederlander per week naar de tv kijkt normaal verdeeld is met sigma=2,4.
Nu snap ik dat je de nulhypothese op 28,4 uur stelt, en de alternatieve hypothese op <28,4 omdat het steekproefgemiddelde lager is dan mu, en je dus linkszijdig moet toetsen.
Nu is er een andere opgave:
Een medicijn is verkrijgbaar in tabletvorm. Het werkzame aandeel X in een tablet is normaal verdeeld met een gemiddelde van 4 mg en een standaardafwijking van 0,12 mg. Het medicijn helpt als het werkzame aandeel per tablet tussen 3,8 mg en 4,2 mg ligt.
Er vinden regelmatig controles plaats om te kijken of de gemiddelde hoeveelheid inderdaad 4 mg is. Een steekproef van 50 tabletten levert een gemiddelde van 3,95 mg werkzame stof op. Toets of hieruit volgt dat dit gemiddelde niet significant afwijkt van 4 mg met alpha = 0,05.
Volgens de uitwerkingen wordt hier tweezijdig getoetst, maar als je naar de vorige opgave kijkt, waarbij je linkszijdig toets doordat het steekproefgemiddelde lager is dan mu, waarom doe je dat hier dan ook niet? 3,95 is minder dan 4 en dus kan je toch linkszijdig toetsen??
Alvast bedankt.
Het levende bewijs dat drugs en intelligentie prima samengaan.
>> de alternatieve hypothese op <28,4 omdat het steekproefgemiddelde lager is dan mu, en je dus linkszijdig moet toetsen.
Dit klopt niet, je moet tweezijdig toetsen. Met jouw argument komt een tweezijdige toets nooit voor.
Dit klopt niet, je moet tweezijdig toetsen. Met jouw argument komt een tweezijdige toets nooit voor.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hmm, ja daar heb je gelijk in, nu ben ik helemaal verward.quote:
>> de alternatieve hypothese op <28,4 omdat het steekproefgemiddelde lager is dan mu, en je dus linkszijdig moet toetsen.
Dit klopt niet, je moet tweezijdig toetsen. Met jouw argument komt een tweezijdige toets nooit voor.
Dit is de uitwerking volgens de uitgever trouwens.
Er wordt dus duidelijk linkszijdig getoetst.
Het levende bewijs dat drugs en intelligentie prima samengaan.
Ik geef wel eens wisk A bijles en het is me soms ook een raadsel waarom ze een enkelzijdige toets gebruiken, zoals hier. Ik zou hier ook de tweezijdige toets genomen hebben.
Ja, in de les leren ze je aan dat door de bewering van iemand anders die de nulhypothese in twijfel trekt je links of rechtszijdig toetst, en in het boek doen ze het dan soms op basis van het steekproefgemiddelde, maar soms ook niet. Erg verwarrend.
Het levende bewijs dat drugs en intelligentie prima samengaan.
Zo hoort het ook, als er stond "Een medewerker van reclamebureau 'de Ster' trekt deze bewering in twijfel en denkt dat er minder gekeken wordt.", moest je wel linkszijdig toetsen.quote:
Ja, in de les leren ze je aan dat door de bewering van iemand anders die de nulhypothese in twijfel trekt je links of rechtszijdig toetst, en in het boek doen ze het dan soms op basis van het steekproefgemiddelde, maar soms ook niet. Erg verwarrend.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Gewoon haakjes wegwerken en integreren, dan zie je het vanzelf.quote:Op vrijdag 6 april 2012 22:23 schreef Dale. het volgende:
http://www.wolframalpha.com/input/?i=int+%281-x%2Fa%29%5E2xdx
Waar komt de a^2 ook alweer vandaan
Stel je hebt
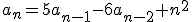
met a_0=0 en a_1=1. Die wil ik oplossen.
De karakteristieke vgl heeft als oplossingen 3 en 2. Met de beginwaardes a_0 en a_1 vind je dan dat
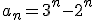de oplossing is van de homogene vergelijking.
Nu zoek ik een particuliere oplossing van de inhomogene vgl. Definieer
.
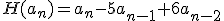Volgens de docent moet je dan als particuliere oplossing iets nemen wat "lijkt" op het inhomogene deel; n^2 in dit geval. Maar
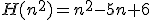
krijg ik niet gelijk aan n^2 voor algemene n. Dus wat nu ?
met a_0=0 en a_1=1. Die wil ik oplossen.
De karakteristieke vgl heeft als oplossingen 3 en 2. Met de beginwaardes a_0 en a_1 vind je dan dat
Nu zoek ik een particuliere oplossing van de inhomogene vgl. Definieer
Volgens de docent moet je dan als particuliere oplossing iets nemen wat "lijkt" op het inhomogene deel; n^2 in dit geval. Maar
krijg ik niet gelijk aan n^2 voor algemene n. Dus wat nu ?
Probeer eens een algemeen polynoom van graad 2.quote:
Stel je hebt
met a_0=0 en a_1=1. Die wil ik oplossen.
De karakteristieke vgl heeft als oplossingen 3 en 2. Met de beginwaardes a_0 en a_1 vind je dan dat
Nu zoek ik een particuliere oplossing van de inhomogene vgl. Definieer
Volgens de docent moet je dan als particuliere oplossing iets nemen wat "lijkt" op het inhomogene deel; n^2 in dit geval. Maar
krijg ik niet gelijk aan n^2 voor algemene n. Dus wat nu ?
Oja, dat werkt. Thanks.quote:
[..]
Probeer eens een algemeen polynoom van graad 2.
Hey weet iemand hier een beetje een duidelijke definitie van een 'Primitieve functie' en waarom zo'n functie belangrijk is in de integraalrekening? Ik kan nergens echt een duidelijke definitie vinden op het internet, alleen dat het het eigenlijk 'de omgekeerde afgeleide' is van een functie, oftewel dat een normale functie de afgeleide is van een Primitieve functie. Ik heb het boek waar het in zou moeten staan ook niet
Maar waarom is dit belangrijk bij integralen? En wat is het nou eigenlijk, ik vind het namelijk een beetje raar om van een normale functie de omgekeerde afgeleide te nemen. Dan zou een bepaalde x voor de normale functie een soort van de richtingcoëfficent zijn van de Primitieve functie in dat punt x? Ik snap het nog niet helemaal.
THnx!!
Maar waarom is dit belangrijk bij integralen? En wat is het nou eigenlijk, ik vind het namelijk een beetje raar om van een normale functie de omgekeerde afgeleide te nemen. Dan zou een bepaalde x voor de normale functie een soort van de richtingcoëfficent zijn van de Primitieve functie in dat punt x? Ik snap het nog niet helemaal.
THnx!!
Hmmm...
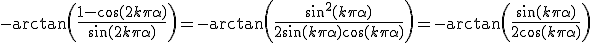
Klopt toch? Boek zegt dat het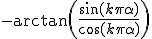
moet zijn. Foutje toch? Of maak ik nou een fout 
Klopt toch? Boek zegt dat het
SPOILER: Voor mensen die de indentiteiten niet kennenOm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
quote:
Hmmm...
Klopt toch? Boek zegt dat hetDe tweede identiteit in de spoiler klopt niet.SPOILER: Voor mensen die de indentiteiten niet kennenOm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
quote:
[..]
De tweede identiteit in de spoiler klopt niet.
, bedankt!
Is dit een altijd kloppende definitie? Das wel een stuk helderder.quote:
Een primitieve functie geeft de oppervlakte onder een grafiek van f(x).
Behalve dat hier maar weer eens uit blijkt hoe beroerd het huidige onderwijs is, vind ik het vreemd dat je deze vraag stelt. Ik heb dit namelijk onlangs nog uiteengezet, nota bene in een topic dat je zelf had geopend en waarin je naderhand ook nog hebt gereageerd.quote:
Hey weet iemand hier een beetje een duidelijke definitie van een 'Primitieve functie' en waarom zo'n functie belangrijk is in de integraalrekening? Ik kan nergens echt een duidelijke definitie vinden op het internet, alleen dat het het eigenlijk 'de omgekeerde afgeleide' is van een functie, oftewel dat een normale functie de afgeleide is van een Primitieve functie. Ik heb het boek waar het in zou moeten staan ook niet
Maar waarom is dit belangrijk bij integralen? En wat is het nou eigenlijk, ik vind het namelijk een beetje raar om van een normale functie de omgekeerde afgeleide te nemen. Dan zou een bepaalde x voor de normale functie een soort van de richtingcoëfficent zijn van de Primitieve functie in dat punt x? Ik snap het nog niet helemaal.
THnx!!
Ooh sorry man, had ik allemaal niet gelezen, veel te lang stuk en niet bruikbaar voor mijn vraag. Maar klopt dit:quote:
[..]
Behalve dat hier maar weer eens uit blijkt hoe beroerd het huidige onderwijs is, vind ik het vreemd dat je deze vraag stelt. Ik heb dit namelijk onlangs nog uiteengezet, nota bene in een topic dat je zelf had geopend en waarin je naderhand ook nog hebt gereageerd.
???quote:
Een primitieve functie geeft de oppervlakte onder een grafiek van f(x).
Het stuk is niet te lang, jij bent te lui om het te lezen.quote:
[..]
Ooh sorry man, had ik allemaal niet gelezen, veel te lang stuk en niet bruikbaar voor mijn vraag.
Lees het stuk nu maar, dan leer je nog wat. En nee, in zijn algemeenheid klopt het niet, omdat oppervlakten niet negatief zijn maar de waarde van een bepaalde integraal wel negatief kan zijn. Bovendien is een primitieve van een functie slechts tot op een constante bepaald.quote:Maar klopt dit:
[..]
???
Dat stuk beantwoord precies jouw vraag. Als je iets echt wil snappen dan moet je er altijd moeite voor doen. Niks is gratis.quote:
[..]
Ooh sorry man, had ik allemaal niet gelezen, veel te lang stuk en niet bruikbaar voor mijn vraag.
Nee, daar gaat het niet om. In dat topic ging het over logaritmen, wat dat precies waren. Gewoon een heel laag niveau vraag. Vervolgens zei Riparius dat het onderwijs zo slecht was e.d. en was hij met zo'n andere wiskundige aan het praten. Dat stuk wat hij daar plaatste had eigenlijk niks te maken met het topic, vandaar heb ik het ook niet helemaal doorgelezen.quote:
[..]
Dat stuk beantwoord precies jouw vraag. Als je iets echt wil snappen dan moet je er altijd moeite voor doen. Niks is gratis.
Bram had in dat topic dezelfde vraag als jij nu hier stelt. Riparius legt uit waaromquote:
[..]
Nee, daar gaat het niet om. In dat topic ging het over logaritmen, wat dat precies waren. Gewoon een heel laag niveau vraag. Vervolgens zei Riparius dat het onderwijs zo slecht was e.d. en was hij met zo'n andere wiskundige aan het praten. Dat stuk wat hij daar plaatste had eigenlijk niks te maken met het topic, vandaar heb ik het ook niet helemaal doorgelezen.
waarbij F de primitieve van f is (dit geldt alleen onder de bepaalde voorwaarden). Die identiteit is natuurlijk erg handig als je integralen wil berekenen.
Bijna, maar niet helemaal. Want in een integraal wordt oppervlakte boven de x-as positief gerekend, maar oppervlakte onder de x-as negatief.quote:
Ok maar het klopt dus wel dat := Oppervlakte van interval [a,b] tussen de x-as en f(x)
toch? ^^
Als f dus een niet-negatieve functie is op [a,b] dan heb je gelijk.
Ok dankje dan snap ik het allemaal opzich wel. Alleen snap ik het nut van een primitieve functie nog niet helemaal, maar dat is ook geen vereiste voor mijn niveau.quote:
[..]
Bijna, maar niet helemaal. Want in een integraal wordt oppervlakte boven de x-as positief gerekend, maar oppervlakte onder de x-as negatief.
Als f dus een niet-negatieve functie is op [a,b] dan heb je gelijk.
Thnx!
Het nut is juist wel duidelijk: je kan op die manier integralen berekenen. Als je de reden wil weten waarom het zo werkt, dan moet je Riparius' post erop nalezen.quote:
[..]
Ok dankje dan snap ik het allemaal opzich wel. Alleen snap ik het nut van een primitieve functie nog niet helemaal, maar dat is ook geen vereiste voor mijn niveau.
Thnx!
klopt, de toepassing weet ik nu, ik snap alleen nog niet waarom dat zo werkt, oftewel waarom :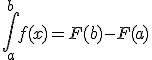
maar ik zal dat stukkie idd nog wel ff lezen.
maar ik zal dat stukkie idd nog wel ff lezen.
Hallon, ik heb weer eens een vraag en aangezien ik hier altijd prima geholpen wordt, stel ik mijn vraag hier nog maar een keer. Ik ben het boek A=B aan het lezen. Op bladzijde 55 (65 in het bestand) zit een stukje wat ik niet helemaal begrijp. Men probeert hier de som
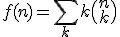
te evalueren. Ik zal voor de eenvoudigheid doen wat ze daar ook dan, maar dan met de som
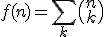
Eerst wordt de functie waarover gesommeerd wordt bekeken, daar wordt dit de sommand/summand genoemd:
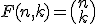
Dan wordt er gezocht naar een recurrente betrekking waaraan de sommand voldoet, bijvoorbeeld:
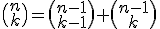
dus ook:
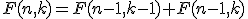
Dan wordt hiervan de sommatie over alle integers k genomen:
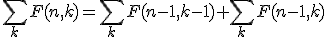
en omdat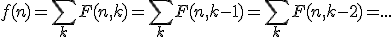
kunnen we dit vereenvoudigen naar:
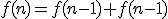
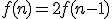
dus als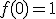
is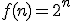
de oplossing van deze vergelijking. Ik geloof dat ik dit op zich begrijp, maar als ik het goed begrijp is dit nog steeds een oneindige som (een sommatie over alle integers k). Ik begrijp het nut hier niet zo van, volgens mij heb je liever een formule voor een eindige sommatie. Het viel me ook op dat je met het binomium van Newton natuurlijk gelijk kan inzien dat
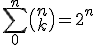
Wat natuurlijk een veel nuttigere formule is, en waar ook nog eens hetzelfde uitkomt, maar over een sommatie met eindige grenzen. Om tot deze oplossing te komen kan je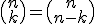
gebruiken, maar in het algemeen lijkt het me dat je niet zoiets kan toepassen. Bovendien kan je dan te maken hebben met negatieve faculteiten, waarvan ik niet weet of dat een probleem is (?).
Begrijp ik het goed en is deze methode alleen bruikbaar om oneindige sommen te evalueren?
[ Bericht 0% gewijzigd door kutkloon7 op 08-04-2012 23:21:43 ]
te evalueren. Ik zal voor de eenvoudigheid doen wat ze daar ook dan, maar dan met de som
Eerst wordt de functie waarover gesommeerd wordt bekeken, daar wordt dit de sommand/summand genoemd:
Dan wordt er gezocht naar een recurrente betrekking waaraan de sommand voldoet, bijvoorbeeld:
dus ook:
Dan wordt hiervan de sommatie over alle integers k genomen:
en omdat
kunnen we dit vereenvoudigen naar:
dus als
is
Wat natuurlijk een veel nuttigere formule is, en waar ook nog eens hetzelfde uitkomt, maar over een sommatie met eindige grenzen. Om tot deze oplossing te komen kan je
Begrijp ik het goed en is deze methode alleen bruikbaar om oneindige sommen te evalueren?
[ Bericht 0% gewijzigd door kutkloon7 op 08-04-2012 23:21:43 ]
ik mis de integrator (dx) in alle integralen hierboven
De faculteit is alleen voor niet-negatieve gehele getallen gedefinieerd, maar je zou de gamma-functie kunnen gebruiken om de definitie uit te breiden naar negatieve getallen.
De faculteit is alleen voor niet-negatieve gehele getallen gedefinieerd, maar je zou de gamma-functie kunnen gebruiken om de definitie uit te breiden naar negatieve getallen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat zal niet gaan werken. De Gamma-functie is immers singulier voor negatieve gehele getallen.quote:
De faculteit is alleen voor niet-negatieve gehele getallen gedefinieerd, maar je zou de gamma-functie kunnen gebruiken om de definitie uit te breiden naar negatieve getallen.
De hele tijd dx schrijven is voor beginnersquote:
ik mis de integrator (dx) in alle integralen hierboven
wacht maar tot je iets anders tegenkomt als een Riemann-integraalquote:
[..]
De hele tijd dx schrijven is voor beginners
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bij lebesgue integralen zet ik ook niet de hele tijd de maat en variabele neerquote:
[..]
wacht maar tot je iets anders tegenkomt als een Riemann-integraal
. Dan is het uit de context meestal ook wel duidelijk welke maat je gebruikt en wat je variabele is.
quote:
De som is eindig, want (n boven k) is 0 voor k > n.
Ik begrijp nu nog steeds niet zo goed wat precies het 'bereik' van de integraalsommatie is. Zou je kunnen zeggen dat f(n) de som is van alle f(n, k) waar k alle aanneemt zodat f(n, k) gedefinieerd is?quote:
De faculteit is alleen voor niet-negatieve gehele getallen gedefinieerd, maar je zou de gamma-functie kunnen gebruiken om de definitie uit te breiden naar negatieve getallen.
Dit lijkt me wel een logisch, volgens mij zijn de resultaten dan nog steeds geldig
.[ Bericht 1% gewijzigd door kutkloon7 op 09-04-2012 17:13:11 ]
welke integraal?quote:
[..]
[..]
Ik begrijp nu nog steeds niet zo goed wat precies het 'bereik' van de integraal is.
de notatie is heel sloppy, en dat kun je op 2 manieren 'oplossen':quote:Zou je kunnen zeggen dat f(n) de som is van alle f(n, k) waar k alle waarden aanneemt zodat waarvoor f(n, k) gedefinieerd is?
Dit lijkt me wel een logisch, volgens mij zijn de resultaten dan nog steeds geldig
- f(n,k) = 0 stellen voor alle rare k
- de sommatie netter opschrijven en aangeven wat k mag zijn
en bij een Riemann-Stieltjes-integraal?quote:
[..]
Bij lebesgue integralen zet ik ook niet de hele tijd de maat en variabele neer
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
True, had ik gemist.quote:
[..]
Lees nog eens de laatste alinea van blz. 19 van je tekst. Lijkt me toch vrij duidelijk.
Maar, even for the record, de recurrentievergelijking
Een dergelijke recurrente betrekking gebruik je niet om f(n) te berekenen voor n = 0, dus ik zie je probleem niet zo.quote:Op maandag 9 april 2012 18:08 schreef kutkloon7 het volgende:
[..]
True, had ik gemist.
Maar, even for the record, de recurrentievergelijkingklopt dus niet voor de randgevallen, als je bijvoorbeeld n = k = 0 gebruikt. Deels hierdoor raakte ik een beetje in de war.
Nouja, omdat je uiteindelijk die recurrente betrekking gebruikt om een formule voor de sommatie te krijgen, leek het me raar dat die recurrente betrekking niet voor alle termen in de sommatie klopt. Maar het is nu helemaal duidelijk, dank.quote:
[..]
Een dergelijke recurrente betrekking gebruik je niet om f(n) te berekenen voor n = 0, dus ik zie je probleem niet zo.
In het voorbeeld dat je hierboven uitwerkt leid je af dat f(n) = 2∙f(n-1), maar daar volgt niet uit dat f(0) = 1, dat haal je namelijk - impliciet - uit je definitie van f(n). Je functie f(n) is alleen gedefinieerd voor niet-negatieve gehele waarden van n en je recurrente betrekking is dus alleen geldig voor n > 0.quote:
[..]
Nouja, omdat je uiteindelijk die recurrente betrekking gebruikt om een formule voor de sommatie te krijgen, leek het me raar dat die recurrente betrekking niet voor alle termen in de sommatie klopt. Maar het is nu helemaal duidelijk, dank.
Kan iemand mij iets uitleggen over wiskundige economie? Zit hier al een tijd op te puzzelen, maar kom er niet uit.
Hoe kun je laten zien dat wanneer de preferentierelatie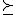
strict convex is, x* uniek is.
Ik dacht aan tx1 + (1-t)x0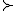
x0 , dat hieruit volgt tx1 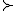tx0, maar denk niet dat je zon preferentierelatie als vergelijking mag gebruiken, daarom denk ik dat dit niet goed is.
Iemand die op deze vraag het juiste antwoord weet.
En wanneer de preferentierelatie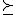 convex is, x* niet per definitie uniek is.
Hier heb ik al helemaal geen benul van
Iemand die hier een antwoord op weet?
Bedankt vast!
Hoe kun je laten zien dat wanneer de preferentierelatie
Ik dacht aan tx1 + (1-t)x0
Iemand die op deze vraag het juiste antwoord weet.
En wanneer de preferentierelatie
Hier heb ik al helemaal geen benul van
Iemand die hier een antwoord op weet?
Bedankt vast!
Het klinkt als iets wat in 2 regels op te lossen is; het probleem is alleen dat ik dat economische jargon niet ken.
Zonder definitie van x* is het een beetje lastig. Ik neem aan dat x* het meest geprefereerde goed is.
Laat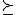
een strict convexe preferentie op S. Stel x* en y* zijn beide optimaal (dus x* 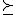z en y*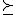z voor elke z in S) met x* != y*.
Pak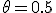
, dan 0.5x* + 0.5y*
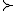x*, tegenspraak (omdat S convex is).
Laat
Pak
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Wat gaat er fout? Grenzen kloppen niet? Moeten de grenzenzijn? Omdat
eigenlijk afhangt van
en
en niet alleen
functie... Met de grenzen
en
?
z ligt tussen 0 en z=1-y-x (gewoon z isoleren uit de gegeven formule van het vlak)
Dan blijft er voor y de bovengrens y=1-x over (projectie op y-x vlak)
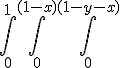
Dan blijft er voor y de bovengrens y=1-x over (projectie op y-x vlak)
Kijk eerst maar eens na of je de integrand wel goed hebt overgenomen. WolframAlpha kan jouw integraal niet berekenen met 0 als ondergrens voor x, en daar is een goede reden voor ...quote:
Ja precies ik geloof namelijk dat je nog steeds iets krijgt metquote:
[..]
Kijk eerst maar eens na of je de integrand wel goed hebt overgenomen. WolframAlpha kan jouw integraal niet berekenen met 0 als ondergrens voor x, en daar is een goede reden voor ...
Wat heb je zelf al geprobeerd?quote:
Zou iemand mij hier mee kunnen helpen, ik kom er echt niet uit:
[ afbeelding ]
Kom je uit geen van alle?
~Si vis amari, ama~
Vraag a twijfel ik of ik het goed heb:quote:
[..]
Wat heb je zelf al geprobeerd?
Kom je uit geen van alle?
en b kom ik echt helemaal niet uit
Je hebt niet de pdf van de poissonverdeling, en ik weet niet wat een Q-matrix is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik begrijp dat als je 2 convergerende sequences hebt in R1 die convergeren, het product (zowel als de som) van die 2 sequences convergeert. Nu vraag ik me dus af, geldt dit voor alle Rn, als in, kan je ook zeggen dat als je 2 convergerende sequences hebt in R10, dat het product van die 2 sequences dan ook convergeert?
Edit: Hmm, ik realiseer me net dat er natuurlijk geen vaste definitie is voor het "product" in dat geval. Ik probeer wel even verder
Edit: Hmm, ik realiseer me net dat er natuurlijk geen vaste definitie is voor het "product" in dat geval. Ik probeer wel even verder
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Voor de som is het zeker waar. Stel dat je n-dimensionale rijenquote:
Ik begrijp dat als je 2 convergerende sequences hebt in R1 die convergeren, het product (zowel als de som) van die 2 sequences convergeert. Nu vraag ik me dus af, geldt dit voor alle Rn, als in, kan je ook zeggen dat als je 2 convergerende sequences hebt in R10, dat het product van die 2 sequences dan ook convergeert?
Edit: Hmm, ik realiseer me net dat er natuurlijk geen vaste definitie is voor het "product" in dat geval. Ik probeer wel even verder
Als "product" zou je inproduct of uitproduct (of misschien nog wat anders leuks) kunnen nemen en het weer nagaan.
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
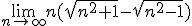
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.
Dit kan op heel veel manieren. Een manier is n=1/h invullen; dan gaat h dus van boven naar 0. Een andere manier is (wortel(a)-wortel(b))(wortel(a)+wortel(b)) = a-b gebruiken.quote:
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.
Ik neem aan dat er een n mist onder het kwadraat.quote:
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.
Nu kan je nog laten zien dat de eerste en tweede factor allebei naar 1 gaan.
De uitdrukking vermenigvuldigen met (√(n2+1) + √(n2-1))/(√(n2+1) + √(n2-1)) (=1) en gebruik maken van het merkwaardig product (a-b)(a+b) = a2 - b2. Dan in de resulterende breuk teller en noemer door n (= √(n2)) delen.quote:
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.
quote:
[..]
Dit kan op heel veel manieren. Een manier is n=1/h invullen; dan gaat h dus van boven naar 0. Een andere manier is (wortel(a)-wortel(b))(wortel(a)+wortel(b)) = a-b gebruiken.
quote:
[..]
Ik neem aan dat er een n mist onder het kwadraat.
Nu kan je nog laten zien dat de eerste en tweede factor allebei naar 1 gaan.
Dank, het is duidelijk nu. Ik moet nog wat meer oefenen met die dingen denk ik (hoewel de meeste andere limieten van het proeftentamen me wel lukten). Na thabit's post was ik er bijna uit, alleen beschouwde ikquote:
[..]
De uitdrukking vermenigvuldigen met (√(n2+1) + √(n2-1))/(√(n2+1) + √(n2-1)) (=1) en gebruik maken van het merkwaardig product (a-b)(a+b) = a2 - b2. Dan in de resulterende breuk teller en noemer door n (= √(n2)) delen.
Herleiding geeft 2/(√(1 + 1/n2) + √(1 - 1/n2)) en de limiet hiervan voor n →∞ is 2/(1 + 1) = 1.quote:
[..]
[..]
[..]
Dank, het is duidelijk nu. Ik moet nog wat meer oefenen met die dingen denk ik (hoewel de meeste andere limieten van het proeftentamen me wel lukten). Na thabit's post was ik er bijna uit, alleen beschouwde ikmaar even als standaardlimiet (waardoor ik dus wel gewoon een stap miste).
Gebruikquote:
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.
oftewel
[ Bericht 0% gewijzigd door Mathemaat op 14-04-2012 20:44:04 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
[ Bericht 100% gewijzigd door Mathemaat op 14-04-2012 20:53:02 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Ik kom er niet uit door de 2de -.
Ik moet de afgeleiden functie uitrekenen van: f(x)= -3x3 - (4x2 - x + 6 )
Kan iemand mij helpen hiermee?
Ik moet de afgeleiden functie uitrekenen van: f(x)= -3x3 - (4x2 - x + 6 )
Kan iemand mij helpen hiermee?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |