[Bèta wiskunde] Huiswerk- en vragentopic

woensdag 11 april 2012 @ 00:19:47 #181

zoem

zoemt

z ligt tussen 0 en z=1-y-x (gewoon z isoleren uit de gegeven formule van het vlak)
Dan blijft er voor y de bovengrens y=1-x over (projectie op y-x vlak)

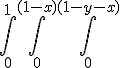
$\int_0^1\int_0^{(1-x)}\int_0^{(1-y-x)}$

woensdag 11 april 2012 @ 02:42:28 #182

Riparius

quote:
Op woensdag 11 april 2012 00:04 schreef Dale. het volgende:

Wat gaat er fout?

Kijk eerst maar eens na of je de integrand wel goed hebt overgenomen. WolframAlpha kan jouw integraal niet berekenen met 0 als ondergrens voor x, en daar is een goede reden voor ...

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 11 april 2012 @ 10:01:29 #183

Dale.

quote:
Op woensdag 11 april 2012 02:42 schreef Riparius het volgende:

[..]

Kijk eerst maar eens na of je de integrand wel goed hebt overgenomen. WolframAlpha kan jouw integraal niet berekenen met 0 als ondergrens voor x, en daar is een goede reden voor ...

Ja precies ik geloof namelijk dat je nog steeds iets krijgt met $\ln$ over 0 en 1 en $\ln(0)$ is niet gedefinieerd. Maar ik heb de integraal goed overgenomen. Misschien gewoon fout in 't oud tentamen.

donderdag 12 april 2012 @ 15:28:56 #184

dynamiet

Zou iemand mij hier mee kunnen helpen, ik kom er echt niet uit:

donderdag 12 april 2012 @ 15:42:16 #185

FedExpress

quote:
Op donderdag 12 april 2012 15:28 schreef dynamiet het volgende:
Zou iemand mij hier mee kunnen helpen, ik kom er echt niet uit:
[ afbeelding ]

Wat heb je zelf al geprobeerd?
Kom je uit geen van alle?

~Si vis amari, ama~

donderdag 12 april 2012 @ 16:43:04 #186

dynamiet

quote:
Op donderdag 12 april 2012 15:42 schreef FedExpress het volgende:

[..]

Wat heb je zelf al geprobeerd?
Kom je uit geen van alle?

Vraag a twijfel ik of ik het goed heb:

en b kom ik echt helemaal niet uit

donderdag 12 april 2012 @ 17:08:26 #187

GlowMouse

l'état, c'est moi

Je hebt niet de pdf van de poissonverdeling, en ik weet niet wat een Q-matrix is.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

donderdag 12 april 2012 @ 20:03:42 #188

Thas

Ik begrijp dat als je 2 convergerende sequences hebt in R¹ die convergeren, het product (zowel als de som) van die 2 sequences convergeert. Nu vraag ik me dus af, geldt dit voor alle Rⁿ, als in, kan je ook zeggen dat als je 2 convergerende sequences hebt in R¹⁰, dat het product van die 2 sequences dan ook convergeert?

Edit: Hmm, ik realiseer me net dat er natuurlijk geen vaste definitie is voor het "product" in dat geval. Ik probeer wel even verder

vrijdag 13 april 2012 @ 00:49:27 #189

thenxero

quote:
Op donderdag 12 april 2012 20:03 schreef Thas het volgende:
Ik begrijp dat als je 2 convergerende sequences hebt in R¹ die convergeren, het product (zowel als de som) van die 2 sequences convergeert. Nu vraag ik me dus af, geldt dit voor alle Rⁿ, als in, kan je ook zeggen dat als je 2 convergerende sequences hebt in R¹⁰, dat het product van die 2 sequences dan ook convergeert?

Edit: Hmm, ik realiseer me net dat er natuurlijk geen vaste definitie is voor het "product" in dat geval. Ik probeer wel even verder

Voor de som is het zeker waar. Stel dat je n-dimensionale rijen $((a_k^1,...,a_k^n))_k$ en $((b_k^1,...,b_k^n))_k$ hebt die convergeren naar de vectors a resp. b. De somrij
$((b_k^1+a_k^1,...,b_k^n+a_k^n))$ kan je per coördinaat beschouwen. Je weet dat iedere coördinaat convergeert (want dat kan je beschouwen als R^1), dus ook de totale vector (ga na).

Als "product" zou je inproduct of uitproduct (of misschien nog wat anders leuks) kunnen nemen en het weer nagaan.

vrijdag 13 april 2012 @ 14:36:12 #190

kutkloon7

Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
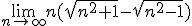
$\lim_{n \rightarrow \infty}{n(\sqrt{n^2+1}-\sqrt{n^2-1})}$
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.

vrijdag 13 april 2012 @ 15:32:18 #191

thabit

quote:
Op vrijdag 13 april 2012 14:36 schreef kutkloon7 het volgende:
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
$\lim_{n \rightarrow \infty}{n(\sqrt{n^2+1}-\sqrt{n^2-1})}$
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.

Dit kan op heel veel manieren. Een manier is n=1/h invullen; dan gaat h dus van boven naar 0. Een andere manier is (wortel(a)-wortel(b))(wortel(a)+wortel(b)) = a-b gebruiken.

vrijdag 13 april 2012 @ 15:34:09 #192

thenxero

quote:
Op vrijdag 13 april 2012 14:36 schreef kutkloon7 het volgende:
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
$\lim_{n \rightarrow \infty}{n(\sqrt{n^2+1}-\sqrt{n^2-1})}$
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.

Ik neem aan dat er een n mist onder het kwadraat.

$n(\sqrt{n^2+1}-\sqrt{n^2-1}) =n(\sqrt{n^2+1}-\sqrt{n^2-1})\cdot\frac{\sqrt{n^2+1}}{\sqrt{n^2+1}}= \frac{n}{\sqrt{n^2+1}}\cdot(n^2+1-\sqrt{n^4-1})$
Nu kan je nog laten zien dat de eerste en tweede factor allebei naar 1 gaan.

vrijdag 13 april 2012 @ 16:03:21 #193

Riparius

quote:
Op vrijdag 13 april 2012 14:36 schreef kutkloon7 het volgende:
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
$\lim_{n \rightarrow \infty}{n(\sqrt{n^2+1}-\sqrt{n^2-1})}$
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.

De uitdrukking vermenigvuldigen met (√(n²+1) + √(n²-1))/(√(n²+1) + √(n²-1)) (=1) en gebruik maken van het merkwaardig product (a-b)(a+b) = a² - b². Dan in de resulterende breuk teller en noemer door n (= √(n²)) delen.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

vrijdag 13 april 2012 @ 16:09:51 #194

kutkloon7

quote:
Op vrijdag 13 april 2012 15:32 schreef thabit het volgende:

[..]

Dit kan op heel veel manieren. Een manier is n=1/h invullen; dan gaat h dus van boven naar 0. Een andere manier is (wortel(a)-wortel(b))(wortel(a)+wortel(b)) = a-b gebruiken.

quote:
Op vrijdag 13 april 2012 15:34 schreef thenxero het volgende:

[..]

Ik neem aan dat er een n mist onder het kwadraat.

$n(\sqrt{n^2+1}-\sqrt{n^2-1}) =n(\sqrt{n^2+1}-\sqrt{n^2-1})\cdot\frac{\sqrt{n^2+1}}{\sqrt{n^2+1}}= \frac{n}{\sqrt{n^2+1}}\cdot(n^2+1-\sqrt{n^4-1})$
Nu kan je nog laten zien dat de eerste en tweede factor allebei naar 1 gaan.

quote:
Op vrijdag 13 april 2012 16:03 schreef Riparius het volgende:

[..]

De uitdrukking vermenigvuldigen met (√(n²+1) + √(n²-1))/(√(n²+1) + √(n²-1)) (=1) en gebruik maken van het merkwaardig product (a-b)(a+b) = a² - b². Dan in de resulterende breuk teller en noemer door n (= √(n²)) delen.

Dank, het is duidelijk nu. Ik moet nog wat meer oefenen met die dingen denk ik (hoewel de meeste andere limieten van het proeftentamen me wel lukten). Na thabit's post was ik er bijna uit, alleen beschouwde ik $\lim_{n \rightarrow \infty}\frac{\sqrt{n^2 \pm 1}}{n}=1$ maar even als standaardlimiet (waardoor ik dus wel gewoon een stap miste).

vrijdag 13 april 2012 @ 16:20:13 #195

Riparius

quote:
Op vrijdag 13 april 2012 16:09 schreef kutkloon7 het volgende:

[..]

[..]

[..]

Dank, het is duidelijk nu. Ik moet nog wat meer oefenen met die dingen denk ik (hoewel de meeste andere limieten van het proeftentamen me wel lukten). Na thabit's post was ik er bijna uit, alleen beschouwde ik $\lim_{n \rightarrow \infty}\frac{\sqrt{n^2 \pm 1}}{n}=1$ maar even als standaardlimiet (waardoor ik dus wel gewoon een stap miste).

Herleiding geeft 2/(√(1 + 1/n²) + √(1 - 1/n²)) en de limiet hiervan voor n →∞ is 2/(1 + 1) = 1.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zaterdag 14 april 2012 @ 20:35:16 #196

Mathemaat

quote:
Op vrijdag 13 april 2012 14:36 schreef kutkloon7 het volgende:
Kan iemand me uitleggen hoe je de volgende limiet kan berekenen?
$\lim_{n \rightarrow \infty}{n(\sqrt{n^2+1}-\sqrt{n^2-1})}$
Wolfram alpha zegt dat er 1 uitkomt, maar kan niet laten zien met welke stappen je dit in kan zien.

Gebruik

$a-b=\frac{a^2-b^2}{a+b},$
$\lim_{n \rightarrow \infty}{\frac{1}{n}}=0,$

oftewel

$\lim_{n \rightarrow \infty}{n(\sqrt{n^2+1}-\sqrt{n^2-1})}=\lim_{n \rightarrow \infty}{n\frac{n^2+1-n^2+1}{\sqrt{n^2+1}+sqrt{n^2-1}}}=\lim_{n \rightarrow \infty}{\frac{2}{\sqrt{1+1/n^2}+\sqrt{1-1/n^2}}}=1.$

[ Bericht 0% gewijzigd door Mathemaat op 14-04-2012 20:44:04 ]

Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.

zaterdag 14 april 2012 @ 20:40:33 #197

thenxero

Je bent niet de eerste met de oplossing

zaterdag 14 april 2012 @ 20:43:06 #198

Mathemaat

[ Bericht 100% gewijzigd door Mathemaat op 14-04-2012 20:53:02 ]

Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.

maandag 16 april 2012 @ 18:08:58 #199

pocketplayer09

Ik kom er niet uit door de 2de -.

Ik moet de afgeleiden functie uitrekenen van: f(x)= -3x³ - (4x² - x + 6 )

Kan iemand mij helpen hiermee?

maandag 16 april 2012 @ 18:11:50 #200

zoem

zoemt

Met het gegeven dat 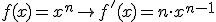$f(x) = x^n \rightarrow f'(x)= n \cdot x^{n-1}$ moet het wel te doen zijn toch?

De eerste term wordt dan: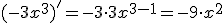 $(-3x^3)'=-3\cdot3x^{3-1}=-9\cdot x^2$

De andere 3 termen mag je zelf proberen

maandag 16 april 2012 @ 18:17:30 #201

pocketplayer09

quote:
Op maandag 16 april 2012 18:11 schreef zoem het volgende:
Met het gegeven dat $f(x) = x^n \rightarrow f'(x)= n \cdot x^{n-1}$ moet het wel te doen zijn toch?

De eerste term wordt dan: $(-3x^3)'=-3\cdot3x^{3-1}=-9\cdot x^2$

De andere 3 termen mag je zelf proberen

Dankje voor het meedenken!, maar het gaatt om de - voor het eerste haakje. Wat moet ik daar precies mee doen?

maandag 16 april 2012 @ 18:22:34 #202

zoem

zoemt

Je kunt deze vergelijking zelfs zonder de haakjes weg te werken al differentiëren, omdat er alleen min één voor de haakjes staat (en geen variabele). Als je dat niet fijn vindt kun je de haakjes eerst wegwerken, maar het uiteindelijke antwoord zal hier hetzelfde blijven. Daarna kwestie van bovenstaande regel toepassen.

maandag 16 april 2012 @ 18:22:51 #203

Riparius

quote:
Op maandag 16 april 2012 18:17 schreef pocketplayer09 het volgende:

[..]

Dankje voor het meedenken, maar het gaat om de - voor het eerste haakje. Wat moet ik daar precies mee doen?

Schaam je, dit is brugklas werk. Als je de haakjes wegwerkt krijg je:

f(x) = -3x³ - 4x² + x - 6

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 17 april 2012 @ 20:23:27 #204

GivanildoVieiraDeSouza

Reken de elasticiteit van substitutie tussen y en x
F(x,y)= 2x^5 + 3y^5
Ik weet de formule van elasticiteit = ryx (y/x)
waarbij ryx (=Marginal rate of substitution) = F1' (x,y) / F2' (x,y) = (10x^4 + 3y^5) / (2x^5 + 15y^4) = 5x^-1 +0,2y
Maar dat is dus de MRS en nu weet ik niet hoe ik tot de Elasticiteit van substitutie kom gewoon 5x^-1 +0,2y vermenigvuldigen met (y/x) of zo iets ?

donderdag 19 april 2012 @ 10:54:45 #205

Warren

Kan iemand mij een hint geven hoe ik deze moet oplossen? Ik heb geprobeerd om die eerste vergelijking te delen door die tweede, maar ik komt er niet uit doordat p q en r in de eerste staan. Iemand een idee?

[ Bericht 1% gewijzigd door Warren op 19-04-2012 11:04:06 ]

donderdag 19 april 2012 @ 11:22:11 #206

kutkloon7

quote:
Op donderdag 19 april 2012 10:54 schreef Warren het volgende:
[ afbeelding ]

Kan iemand mij een hint geven hoe ik deze moet oplossen? Ik heb geprobeerd om die eerste vergelijking te delen door die tweede, maar ik komt er niet uit doordat p q en r in de eerste staan. Iemand een idee?

Als je naar de deling kijkt, kan je aan de eerste twee termen al zien wat uit de deling moet komen (als deze 'uitkomt', dus als er geen rest overblijft of een breuk in de deling komt). Er moet namelijk gelden:
(ax + b)(x³ + 3x²) = (x⁴ + 4x³ + rest)
Waar in de rest alleen termen staan waar de exponent van x 2 of lager is en (ax + b) de uitkomst van de deling is.

Als je eenmaal weet wat eruit moet komen, kan bedenken welke getallen er voor p, q en r ingevuld moeten worden, en kan je dus ook p(q + r) berekenen.

donderdag 19 april 2012 @ 11:23:45 #207

freiss

Hertog Jan :9~

quote:
Op donderdag 19 april 2012 10:54 schreef Warren het volgende:
[ afbeelding ]

Kan iemand mij een hint geven hoe ik deze moet oplossen? Ik heb geprobeerd om die eerste vergelijking te delen door die tweede, maar ik komt er niet uit doordat p q en r in de eerste staan. Iemand een idee?

Je kunt hier een staartdeling uitvoeren.

x³+3x²+9x+3 / x⁴+4x³+6px²+4qx + r \

Je ziet dat de tweede (derdegraads) vergelijking in ieder geval x keer in de eerste (vierdegraads) vergelijking past, dus je vermenigvuldigt de tweede vergelijking met x en trekt dit van de eerste vergelijking af:
x⁴+4x³+6px²+4qx + r
x⁴+3x³+9x²+3x
----------------------------------------------------------- -
x³ + (6p-9)x² + (4q-3)x + r

In deze vergelijking past nog precies een keer de tweede vergelijking, en aangezien de twee vergelijkingen deelbaar waren, komt er geen rest uit. Je weet dus nu dat (6p-9)=3, (4q-3)=9 en r=3.

HJ 14-punt-gift.
Lijst met rukmateriaal!

donderdag 19 april 2012 @ 11:27:15 #208

kutkloon7

Ik zie het antwoord dat volgens mij goed is er overigens niet bijstaan.
Edit: O, wel, ik kan niet rekenen of ben dyslectisch

donderdag 19 april 2012 @ 11:39:30 #209

Warren

quote:
Op donderdag 19 april 2012 11:23 schreef freiss het volgende:

[..]

Je kunt hier een staartdeling uitvoeren.

x³+3x²+9x+3 / x⁴+4x³+6px²+4qx + r \

Je ziet dat de tweede (derdegraads) vergelijking in ieder geval x keer in de eerste (vierdegraads) vergelijking past, dus je vermenigvuldigt de tweede vergelijking met x en trekt dit van de eerste vergelijking af:
x⁴+4x³+6px²+4qx + r
x⁴+3x³+9x²+3x
----------------------------------------------------------- -
x³ + (6p-9)x² + (4q-3)x + r

In deze vergelijking past nog precies een keer de tweede vergelijking, en aangezien de twee vergelijkingen deelbaar waren, komt er geen rest uit. Je weet dus nu dat (6p-9)=3, (4q-3)=9 en r=3.

Bedankt, en de rest is een kwestie van invullen q = 3, p = 2 en r = 3. 2(3+3) = 12.

donderdag 19 april 2012 @ 13:49:45 #210

hello_moto1992

Vraagje over statistiek: als je mbv de z-statistic een p-value uitrekent, zegt deze dan wat over de kans dat de nulhypothese waar is?

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs