SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



pi *a*b reduceert gewoon tot pi*r^2 (de bol wordt in de richting van de z-as uitgerekt door c)quote:Op zaterdag 17 maart 2012 23:58 schreef thabit het volgende:
Maakt het überhaupt iets uit dat daar een c staat? Het is toch alleen maar een schalingsfactor?


Weet iemand hoe je T=27•0,4^t•(3-0,4^2t) herleidt tot de vorm T=a•g^t+b•h^t ?
"Nibnub. A name to remember."


Wat je dan nog kan schrijven als:quote:Op zondag 18 maart 2012 12:18 schreef Anoonumos het volgende:
Dus eerst de haakjes uitwerken en dan gebruiken dat
Gebruikmakende van
[ Bericht 0% gewijzigd door Nelis89 op 18-03-2012 14:36:38 ]
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Fixedquote:Op zondag 18 maart 2012 14:33 schreef Riparius het volgende:
[..]
Het antwoord van Nelis89 klopt niet, want 0,43 = 0,064.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Ik ben mijn wiskunde aan het oppoetsen en me langzaam door een dik wiskunde boek aan het werken.
Ik kom echter bij het volgende voorbeeld niet verder:
Maar daarna wordt me het spoor bijster. Waar komt die "+ 2k + 1" vandaan, en waar komt daarna de "+ 1 + (2k - 6)" vandaan?
Ik begrijp waarom de uitdrukking altijd waar is voor elke n ≥ 8, ik volg alleen de redenering en de inductie niet.
Als dit niet de juiste plek is voor mijn vraag, dan hoor ik het wel!

Ik kom echter bij het volgende voorbeeld niet verder:
Ik kan het nog net volgen tot: (k + 1)2 = k2 + 2k + 1 > ....quote:Bewijs dat n2 > 7n + 1 for alle n >= 8
Oplossing: Het resultaat is waar wanneer n = 8, want 82 = 64 en 7 * 8 + 1 = 57. Veronderstel dat het waar is voor iedere n wanneer k ≥ 8, dat wil zeggen k2 > 7k + 1
(k + 1)2 = k2 + 2k + 1 > (7k + 1) + 2k + 1 = 7(k + 1) + 1 + (2k - 6)
Omdat k ≥ 8, is 2k - 6 een natuurlijk nummer, en de laatste uitdrukking boven is groter dan 7(k + 1). De inductie stap is geverifiëerd, en dus is het resultaat waar voor alle n ≥ 8.
(vrij vertaald uit het Engels uit Discrete Mathematics van Normal L. Biggs)
Maar daarna wordt me het spoor bijster. Waar komt die "+ 2k + 1" vandaan, en waar komt daarna de "+ 1 + (2k - 6)" vandaan?
Ik begrijp waarom de uitdrukking altijd waar is voor elke n ≥ 8, ik volg alleen de redenering en de inductie niet.
Als dit niet de juiste plek is voor mijn vraag, dan hoor ik het wel!


Uit de kut van tante Sjaan!quote:Op maandag 19 maart 2012 21:28 schreef RedVampire het volgende:
Ik ben mijn wiskunde aan het oppoetsen en me langzaam door een dik wiskunde boek aan het werken.
Ik kom echter bij het volgende voorbeeld niet verder:
[..]
Ik kan het nog net volgen tot: (k + 1)2 = k2 + 2k + 1 > ....
Maar daarna wordt me het spoor bijster. Waar komt die "+ 2k + 1" vandaan, en waar komt daarna de "+ 1 + (2k - 6)" vandaan?
Je gebruikt hier k2 > 7k + 1; dat mag je doen omdat dat de inductiehypothese is.


Ik heb het een beetje herschreven en verduidelijkt:
quote:Bewijs dat n² > 7n + 1 for alle n >= 8
Oplossing: Het resultaat is waar wanneer n = 8, want 82 = 64 en 7 * 8 + 1 = 57. Veronderstel dat het waar is voor een k ≥ 8, dat wil zeggen k² > 7k + 1. (Hiermee willen we aantonen dat het ook geldt voor k+1). Dan
(k + 1)² = k² + 2k + 1
> (7k + 1) + 2k + 1 (vanwege de inductiehypothese: k² > 7k + 1)
= 7(k + 1) + 1 + (2k - 6) (herschrijven)
Omdat k ≥ 8, is 2k - 6>0, dus de laatste uitdrukking boven is groter dan 7(k + 1). De inductie stap is geverifiëerd, en dus is het resultaat waar voor alle n ≥ 8.
(vrij vertaald uit het Engels uit Discrete Mathematics van Normal L. Biggs)


Dus als ik het goed begrijpt, volg je de volgende stappen:quote:Op maandag 19 maart 2012 22:24 schreef thenxero het volgende:
Ik heb het een beetje herschreven en verduidelijkt:
[..]
1. schrijf de (k + 1)2 uit
2. voeg het verschil tussen k2 en (k + 1)2 bij 7k + 1
3. herschrijf je die functie naar het format 7(k + 1) + 1 + ...
De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?


En dus ook vanaf k = 8.quote:Op maandag 19 maart 2012 22:57 schreef RedVampire het volgende:
[..]
De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?


Wat je met stap 2 bedoelt is nogal vaag. Ik heb het idee dat je inductie nog niet helemaal snapt.quote:Op maandag 19 maart 2012 22:57 schreef RedVampire het volgende:
[..]
Dus als ik het goed begrijpt, volg je de volgende stappen:
1. schrijf de (k + 1)2 uit
2. voeg het verschil tussen k2 en (k + 1)2 bij 7k + 1
3. herschrijf je die functie naar het format 7(k + 1) + 1 + ...
De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?
Het idee van inductie is dat je een uitspraak P bewijst vanaf een 'basis' (in dit geval n=8). Dan stel je dat dat P(k) waar is (dat heet de inductiehypothese), en dan laat je zien dat P(k+1) waar is. Als dat lukt, dan heb je bewezen dat het waar is voor iedere n groter dan de basis. Want uit het geval n=8 volgt het voor n=9, daaruit weer voor n=10, etc, als een soort domino-effect.
In dit specifieke neem je voor P(n) de uitspraak n² > 7n + 1. Dan bewijs je P(8), en stel je dat P(k) : k² > 7k + 1waar is (dat is je inductiehypothese). Je wil laten zien dat P(k+1) ook waar is, oftewel (k+1)² > 7(k+1) + 1. Dat doe je door (k+1)² uit te werken, je inductiehypothese te gebruiken, en te herschrijven. Dan zie je dat inderdaad (k + 1)² > 7(k + 1) + 1 + (2k - 6) > 7(k+1)+1, omdat (2k-6)>0 voor k>8. We bekijken k>8, omdat we het willen bewijzen voor k >= 8 (en k=8 is al bewezen). Dat het ook al geldt vanaf k=4 is fijn, maar dat heb je niet eens nodig.


Je hebt gelijk, ik heb inderdaad wat moeite met het concept. Ik snapte het met de voorgaande voorbeelden wel, die begonnen met sommatie waar dan een functie voor was gegeven en die je dan voor k=1 en k=k+1 moest bewijzen dat die functie de sommatie correct beschreef.quote:Op maandag 19 maart 2012 23:44 schreef thenxero het volgende:
[..]
Wat je met stap 2 bedoelt is nogal vaag. Ik heb het idee dat je inductie nog niet helemaal snapt.
Het idee van inductie is dat je een uitspraak P bewijst vanaf een 'basis' (in dit geval n=8). Dan stel je dat dat P(k) waar is (dat heet de inductiehypothese), en dan laat je zien dat P(k+1) waar is. Als dat lukt, dan heb je bewezen dat het waar is voor iedere n groter dan de basis. Want uit het geval n=8 volgt het voor n=9, daaruit weer voor n=10, etc, als een soort domino-effect.
In dit specifieke neem je voor P(n) de uitspraak n² > 7n + 1. Dan bewijs je P(8), en stel je dat P(k) : k² > 7k + 1waar is (dat is je inductiehypothese). Je wil laten zien dat P(k+1) ook waar is, oftewel (k+1)² > 7(k+1) + 1. Dat doe je door (k+1)² uit te werken, je inductiehypothese te gebruiken, en te herschrijven. Dan zie je dat inderdaad (k + 1)² > 7(k + 1) + 1 + (2k - 6) > 7(k+1)+1, omdat (2k-6)>0 voor k>8. We bekijken k>8, omdat we het willen bewijzen voor k >= 8 (en k=8 is al bewezen). Dat het ook al geldt vanaf k=4 is fijn, maar dat heb je niet eens nodig.
Maar begrijp ik je nu goed dat de eerste stap in de inductie heeft bewezen waar het punt ligt dat k2 groter wordt dan 7k + 1, en dat de k+1 stap in deze heeft bewezen dat de k2 tegenover 7k + 1 alsmaar groter wordt?


Nee, niet helemaal. Je hebt niet bewezen dat n=8 het kleinste getal is waar de uitspraak waar wordt (maar dat is natuurlijk wel eenvoudig na te gaan door n=7 in te vullen en te concluderen dat de uitspraak onwaar wordt). Je hebt wel al bewezen dat de uitspraak waar is vanaf n=8.quote:Op dinsdag 20 maart 2012 00:07 schreef RedVampire het volgende:
[..]
Je hebt gelijk, ik heb inderdaad wat moeite met het concept. Ik snapte het met de voorgaande voorbeelden wel, die begonnen met sommatie waar dan een functie voor was gegeven en die je dan voor k=1 en k=k+1 moest bewijzen dat die functie de sommatie correct beschreef.
Maar begrijp ik je nu goed dat de eerste stap in de inductie heeft bewezen waar het punt ligt dat k2 groter wordt dan 7k + 1
Probeer dit eens helder te formuleren.quote:en dat de k+1 stap in deze heeft bewezen dat de k2 tegenover 7k + 1 alsmaar groter wordt?


Nee, k = k + 1 is onmogelijk, dus zo moet je het om te beginnen al niet formuleren. De gedachte achter een bewijs met inductie is dat je eerst laat zien dat de te bewijzen uitspraak geldt voor de startwaarde (in jouw geval dus n = 8) en dat je vervolgens laat zien dat de juistheid van de uitspraak voor een natuurlijk getal n = k + 1 volgt uit de juistheid van de uitspraak voor een zekere n = k. Uiteraard mag je niet beginnen met te stellen, zoals je hierboven doet, dat de uitspraak waar is voor elke n ≥ 8, want dat is een petitio principii, d.w.z. dan neem je datgene wat je wil bewijzen al op voorhand voor waar aan, en dan bewijs je dus niets.quote:Op dinsdag 20 maart 2012 00:07 schreef RedVampire het volgende:
[..]
Je hebt gelijk, ik heb inderdaad wat moeite met het concept. Ik snapte het met de voorgaande voorbeelden wel, die begonnen met sommatie waar dan een functie voor was gegeven en die je dan voor k=1 en k=k+1 moest bewijzen dat die functie de sommatie correct beschreef.
Het helpt als je je stappen helder opschrijft, bijvoorbeeld als volgt. We hebben al gezien datquote:[cut crap]
(1) n2 > 7n + 1
geldt voor n = 8. We nemen nu aan dat (1) geldt voor een zekere n = k ≥ 8, dus:
(2) k2 > 7k + 1
Tellen we bij beide leden van (2) 2k + 1 op dan hebben we:
(3) k2 + 2k + 1 > 9k + 2
En dus:
(4) (k + 1)2 > 9k + 2
Nu geldt ook:
(5) 9k + 2 = 7(k + 1) + 1 + (2k - 6)
En aangezien 2k - 6 > 0 voor k ≥ 8 volgt uit (5) dat ook geldt:
(6) 9k + 2 > 7(k + 1) + 1
Op grond van de ongelijkheden (4) en (6) hebben we nu:
(7) (k + 1)2 > 7(k + 1) + 1
Maar (7) betekent niets anders dan dat (1) geldt voor n = k + 1. Uit (2), i.e. de juistheid van (1) voor n = k, volgt dus (7) en daarmee de juistheid van (1) voor n = k + 1. Tezamen met de juistheid van (1) voor n = 8 impliceert dit dat (1) juist is voor elk natuurlijk getal n ≥ 8, QED.
[ Bericht 0% gewijzigd door Riparius op 20-03-2012 01:44:59 ]


Bedankt voor de uitleg allemaal, het begint allemaal een beetje duidelijker te worden. Ik denk dat het tijd wordt om de opgaven in het boek even verder uit te werken, ik denk dat het dan vanzelf allemaal helemaal duidelijker wordt.
Ik begrijp nu tenminste hoe ik dit soort probleem moet aanpakken!

Ik begrijp nu tenminste hoe ik dit soort probleem moet aanpakken!


Hoop dat hier iemand mij kan helpen. De vraag waar ik niet uitkom is de volgende
Let A be a nonempty set, and let I be a nonempty set. Assume for all i in I A( i ) is a sigma-
algebra of A, then Intersection of all A( i ) is a sigma-algebra of A.
Het is logisch dat A en de empty set in de intersection zullen zitten maar de andere condities zou ik niet kunnen laten zien. Iemand een idee?
Let A be a nonempty set, and let I be a nonempty set. Assume for all i in I A( i ) is a sigma-
algebra of A, then Intersection of all A( i ) is a sigma-algebra of A.
Het is logisch dat A en de empty set in de intersection zullen zitten maar de andere condities zou ik niet kunnen laten zien. Iemand een idee?


Stel 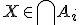 ,
,
dan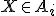 voor alle
voor alle 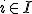 (definitie doorsnede),
(definitie doorsnede),
dus ook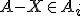 voor alle
voor alle 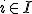 (definitie algebra),
(definitie algebra),
dus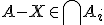 (definitie doorsnede).
(definitie doorsnede).
En hetzelfde voor de andere voorwaarde.
dan
dus ook
dus
En hetzelfde voor de andere voorwaarde.


weet iemand hoe je hier makkelijk a en b uit kan halen?
3/(1+a) + 103/(1+b)^2 = 100.41
9/(1+a) + 109/(1+b)^2 = 104.32
Het lukt me om het op te lossen door eerst te schrijven in de vorm a = , en dan a te substituten voor b, maar dat duurt veel te lang.
3/(1+a) + 103/(1+b)^2 = 100.41
9/(1+a) + 109/(1+b)^2 = 104.32
Het lukt me om het op te lossen door eerst te schrijven in de vorm a = , en dan a te substituten voor b, maar dat duurt veel te lang.


Vermenigvuldig beide leden van je eerste vergelijking met 3 en trek dan de leden van de tweede vergelijking af van de leden van de eerste vergelijking, zodat je een vergelijking in uitsluitend b overhoudt. Als je alleen in de antwoorden geïnteresseerd bent, kun je natuurlijk WolframAlpha gebruiken.quote:Op zaterdag 24 maart 2012 16:17 schreef Klonker het volgende:
weet iemand hoe je hier makkelijk a en b uit kan halen?
3/(1+a) + 103/(1+b)^2 = 100.41
9/(1+a) + 109/(1+b)^2 = 104.32
Het lukt me om het op te lossen door eerst te schrijven in de vorm a = , en dan a te substituten voor b, maar dat duurt veel te lang.


Bedankt!quote:Op zaterdag 24 maart 2012 16:46 schreef Riparius het volgende:
[..]
Vermenigvuldig beide leden van je eerste vergelijking met 3 en trek dan de leden van de tweede vergelijking af van de leden van de eerste vergelijking, zodat je een vergelijking in uitsluitend b overhoudt. Als je alleen in de antwoorden geïnteresseerd bent, kun je natuurlijk WolframAlpha gebruiken.


Even een vraagje over logaritmen.
Ik had dus het idee dat een logaritme van getal X met grondtal Y eigenlijk gewoon het getal is waarmee je Y moet verheffen om X te krijgen.
log(3)=0,477...
en 10^0,477
Dit klopt vooralsnog dus. Maar als ik een ander grondtal als 10 of e wil invoeren klopt het niet meer. Hier bijvoorbeeld:
5log(3)=2,386...
terwijl 5^2,386 niet gelijk is aan 5
Dus mijn vraag is: wat klopt er niet of wat doe ik fout?
Bij voorbaat dank!
Ik had dus het idee dat een logaritme van getal X met grondtal Y eigenlijk gewoon het getal is waarmee je Y moet verheffen om X te krijgen.
log(3)=0,477...
en 10^0,477
Dit klopt vooralsnog dus. Maar als ik een ander grondtal als 10 of e wil invoeren klopt het niet meer. Hier bijvoorbeeld:
5log(3)=2,386...
terwijl 5^2,386 niet gelijk is aan 5
Dus mijn vraag is: wat klopt er niet of wat doe ik fout?
Bij voorbaat dank!


Er staat 5*log(3). Voor 5log3 moet je log3/log5 intypen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


aight ok bedanktquote:Op zondag 25 maart 2012 17:57 schreef GlowMouse het volgende:
Er staat 5*log(3). Voor 5log3 moet je log3/log5 intypen.
