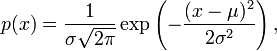SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Beta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Wiskundig inhoudelijk:
http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
OP
[ Bericht 4% gewijzigd door GlowMouse op 22-06-2009 21:03:55 ]
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Wiskundig inhoudelijk:
OP
[ Bericht 4% gewijzigd door GlowMouse op 22-06-2009 21:03:55 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Stelling: Als A > 1 en a ≤ A^-n voor alle positieve gehele getallen n, dan a ≤ 0.
(dit volgt uit het Archimedische postulaat)\
Bewijs?
(dit volgt uit het Archimedische postulaat)\
Bewijs?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
En FIPO is verboden?quote:Op donderdag 18 juni 2009 19:08 schreef Iblis het volgende:
Voor de docent van automatic_ en andere geïnteresseerden:
Het filmpje is wel uitermate geestig, als je van Britse humor houdt. 8 en 9 = Classified.
GO LANCE !!!
Hoe is je Archimedes postulaat precies geformuleerd in je boek? Ik ken het vooral als geometrisch axioma.quote:Op donderdag 18 juni 2009 19:02 schreef Washington het volgende:
Stelling: Als A > 1 en a ≤ A^-n voor alle positieve gehele getallen n, dan a ≤ 0.
(dit volgt uit het Archimedische postulaat)\
Bewijs?
Soms moet het kunnen toch?quote:Op donderdag 18 juni 2009 19:17 schreef .txt het volgende:
En FIPO is verboden?
Het filmpje is wel uitermate geestig, als je van Britse humor houdt. 8 en 9 = Classified.
Ik dacht er vooral aan omdat 45 miljard het grootste nummer is in dat filmpje, dat zou de problemen van 264 oplossen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Schrijf A = 1 + A', dan is A' > 0. Er geldt voor positieve gehele n dat An >= 1+nA' (met inductie makkelijk in te zien of ook door (1+A')n uit te werken met het binomium van Newton).quote:Op donderdag 18 juni 2009 19:02 schreef Washington het volgende:
Stelling: Als A > 1 en a ≤ A^-n voor alle positieve gehele getallen n, dan a ≤ 0.
(dit volgt uit het Archimedische postulaat)\
Bewijs?
Stel a > 0. Bekijk dan b=1/a. Kies een n > b / A'. Dan is An >= 1+nA' > 1+b > b, dus A-n < 1/b = a.
Archimedes postulaat: Voor elk getal a, bestaat er een geheel getaal k zodat a < k.
Hieruit volgt dus die eerder gepostte stelling.
Hieruit volgt dus die eerder gepostte stelling.
Dat is idd ook ongeveer de uitwerking in mijn boek.quote:Op donderdag 18 juni 2009 19:23 schreef thabit het volgende:
[..]
Schrijf A = 1 + A', dan is A' > 0. Er geldt voor positieve gehele n dat An >= 1+nA' (met inductie makkelijk in te zien of ook door (1+A')n uit te werken met het binomium van Newton).
Stel a > 0. Bekijk dan b=1/a. Kies een n > b / A'. Dan is An >= 1+nA' > 1+b > b, dus A-n < 1/b = a.
Toch wel lastig om zelf op dat bewijs te komen.
Hallo, wil iemand me helpen met volgende differentiaalvergelijking op te lossen (naar y=...) ? Ik geraak er niet aan uit...
(y+1)dx + √(x) dx = 0
Bedankt !!!
(y+1)dx + √(x) dx = 0
Bedankt !!!
Ik mis een dyquote:
Hallo, wil iemand me helpen met volgende differentiaalvergelijking op te lossen (naar y=...) ? Ik geraak er niet aan uit...
(y+1)dx + √(x) dx = 0
Bedankt !!!
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ja, maar wist niet zeker of ik zo goed zat. Hoe kun je dan die dx naar het rechterlid brengen? Krijg je dan:quote:Op donderdag 18 juni 2009 20:02 schreef thabit het volgende:
dy/(y+1) + dx/wortel(x) = 0, had je die stap al?
dy/(y+1) = - dx/wortel(x) ??
Ja natuurlijk kan dat, gewoon aan beide kanten -dx/wortel(x) doen.quote:Op donderdag 18 juni 2009 20:09 schreef DeborahL het volgende:
[..]
ja, maar wist niet zeker of ik zo goed zat. Hoe kun je dan die dx naar het rechterlid brengen? Krijg je dan:
dy/(y+1) = - dx/wortel(x) ??
"Reality is an illusion created by a lack of alcohol."
Ok; het is me gelukt! Bedankt!!quote:Op donderdag 18 juni 2009 20:16 schreef Dzy het volgende:
[..]
Ja natuurlijk kan dat, gewoon aan beide kanten -dx/wortel(x) doen.
Mooi.quote:
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Hoi! Ik heb het gehaald! 
Of naja, ik heb 7 fouten en je mag er 8 hebben, dus hopelijk gaat hij niets in mijn nadeel veranderen.
Nog bedankt voor de hulp!
Of naja, ik heb 7 fouten en je mag er 8 hebben, dus hopelijk gaat hij niets in mijn nadeel veranderen.
Nog bedankt voor de hulp!
"It's good to be open-minded, but not so open that your brains fall out."
Y(k) + Y(k-1) - 2Y(k-2) = k^2
(k, k-1, k-2 moet in subscript staan)
Ik krijg voor Y(k) = C1(-2)^k + C2 + (k^3)/6 + (7k^2)/18
Kan iemand controleren of dit correct is?
Hoe kan ik bovenstaande dv in Maple invoeren?
Google isn't very helpfull...
(k, k-1, k-2 moet in subscript staan)
Ik krijg voor Y(k) = C1(-2)^k + C2 + (k^3)/6 + (7k^2)/18
Kan iemand controleren of dit correct is?
Hoe kan ik bovenstaande dv in Maple invoeren?
Google isn't very helpfull...
"The name is Bond, James Bond"
Je kunt hem gewoon invullen natuurlijk, en dan kom je links niet op k² uit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wat moet ik eigenlijk voor Y(k) substituren om een particuliere oplossing te vinden?quote:Op zaterdag 20 juni 2009 01:11 schreef GlowMouse het volgende:
Je kunt hem gewoon invullen natuurlijk, en dan kom je links niet op k² uit.
Y(k) = Ak^2 + Bk + c gaf de vorige oplossing.
Ik kom er echt niet meer uit...
[ Bericht 3% gewijzigd door James.Bond op 20-06-2009 03:29:27 ]
"The name is Bond, James Bond"
Om te beginnen: je vergelijking Y(k) + Y(k-1) - 2Y(k-2) = k2 is geen differentiaalvergelijking. Je kunt direct zien dat Y(k) slechts tot op een constante bepaald kan zijn, want die constante valt weg als je Y(k) en Y(k-1) bij elkaar optelt en hier vervolgens weer tweemaal Y(k-2) van aftrekt. Ook is het duidelijk dat Y(k) geen kwadratisch polynoom in k kan zijn, omdat dan de termen met k2 tegen elkaar wegvallen in Y(k) + Y(k-1) - 2Y(k-2), zodat dit niet gelijk zou kunnen zijn aan k2. Als echter Y(k) een polynoom in k van de derde graad is, dan zullen evenzo de termen met k3 tegen elkaar wegvallen, zodat er een kwadratische veelterm in k overblijft. Je kunt daarom uitgaan van:quote:Op zaterdag 20 juni 2009 03:23 schreef James.Bond het volgende:
[..]
Wat moet ik eigenlijk voor Y(k) substituren om een particuliere oplossing te vinden?
Y(k) = Ak^2 + Bk + c gaf de vorige oplossing.
Ik kom er echt niet meer uit...
Y(k) = Ak3 + Bk2 + Ck + D
Herschrijf nu eerst Y(k-1) en Y(k-2) als derdegraadspolynomen in k, waarbij dan de coëfficiënten lineaire uitdrukkingen in A, B, C en D zijn. Schrijf dan Y(k) + Y(k-1) - 2Y(k-2) als polynoom in k. Hierbij vallen zoals gezegd de termen met k3 tegen elkaar weg, evenals de constante D. Je hebt dan een kwadratische veelterm in k, waarbij de drie coëfficiënten lineaire uitdrukkingen zijn in A, B en C. Door gelijkstelling met het rechterlid k2 krijg je aldus drie lineaire vergelijkingen in de drie onbekenden A, B en C, en dit stelsel vergelijkingen kun je eenvoudig oplossen. Als je het goed doet, zou je uit moeten komen op:
A = 1/9, B = 7/18, C = 19/54
Daarmee is dan de gevraagde uitdrukking van Y(k) in k gevonden.
[ Bericht 0% gewijzigd door Riparius op 20-06-2009 06:38:00 ]
Mijn dank is groot, hartelijk dank!!quote:Op zaterdag 20 juni 2009 05:56 schreef Riparius het volgende:
[..]
Om te beginnen: je vergelijking Y(k) + Y(k-1) - 2Y(k-2) = k2 is geen differentiaalvergelijking. Je kunt direct zien dat Y(k) slechts tot op een constante bepaald kan zijn, want die constante valt weg als je Y(k) en Y(k-1) bij elkaar optelt en hier vervolgens weer tweemaal Y(k-2) van aftrekt. Ook is het duidelijk dat Y(k) geen kwadratisch polynoom in k kan zijn, omdat dan de termen met k2 tegen elkaar wegvallen in Y(k) + Y(k-1) - 2Y(k-2), zodat dit niet gelijk zou kunnen zijn aan k2. Als echter Y(k) een polynoom in k van de derde graad is, dan zullen evenzo de termen met k3 tegen elkaar wegvallen, zodat er een kwadratische veelterm in k overblijft. Je kunt daarom uitgaan van:
Y(k) = Ak3 + Bk2 + Ck + D
Herschrijf nu eerst Y(k-1) en Y(k-2) als derdegraadspolynomen in k, waarbij dan de coëfficiënten lineaire uitdrukkingen in A, B, C en D zijn. Schrijf dan Y(k) + Y(k-1) - 2Y(k-2) als polynoom in k. Hierbij vallen zoals gezegd de termen met k3 tegen elkaar weg, evenals de constante D. Je hebt dan een kwadratische veelterm in k, waarbij de drie coëfficiënten lineaire uitdrukkingen zijn in A, B en C. Door gelijkstelling met het rechterlid k2 krijg je aldus drie lineaire vergelijkingen in de drie onbekenden A, B en C, en dit stelsel vergelijkingen kun je eenvoudig oplossen. Als je het goed doet, zou je uit moeten komen op:
A = 1/9, B = 7/18, C = 19/54
Daarmee is dan de gevraagde uitdrukking van Y(k) in k gevonden.
"The name is Bond, James Bond"
Normaalgesproken vermenigvuldig je je poging voor een particuliere oplossing met k als hij niet lukt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De vraag is nog niet gesteld maar ik heb niet voor niets zitten typen terwijl er een topic op slot ging, dus ik geef het antwoord alvast 
Ik denk dat je moet beginnen met het weten hoe je de inhoud van een kegel en een piramide uitrekent. De formule voor de inhoud van een piramide is :
1/3 * hoogte * (oppervlakte grondvlak)
Het maakt niet uit hoeveel hoeken het grondvlak heeft. Een kegel is te beschouwen als een piramide waarvan het grondvlak een oneindig aantal hoeken heeft, en dus kan dezelfde formule worden gebruikt voor het uitrekenen van de inhoud van een kegel.
Omdat de kegel twee keer zo hoog is als de piramide, moet het oppervlak van het grondvlak van de piramide twee keer zo groot zijn als het oppervlak van het grondvlak van de kegel: Op = 2*Ok
Op is het oppervlak van een vierkant en Ok het oppervlak van een cirkel. Ik neem aan dat je weet hoe je het oppervlak van een vierkant en een cirkel moet uitrekenen en daarmee de opgave dus kan oplossen.
[ Bericht 0% gewijzigd door #ANONIEM op 20-06-2009 23:27:18 ]
Ik denk dat je moet beginnen met het weten hoe je de inhoud van een kegel en een piramide uitrekent. De formule voor de inhoud van een piramide is :
1/3 * hoogte * (oppervlakte grondvlak)
Het maakt niet uit hoeveel hoeken het grondvlak heeft. Een kegel is te beschouwen als een piramide waarvan het grondvlak een oneindig aantal hoeken heeft, en dus kan dezelfde formule worden gebruikt voor het uitrekenen van de inhoud van een kegel.
Omdat de kegel twee keer zo hoog is als de piramide, moet het oppervlak van het grondvlak van de piramide twee keer zo groot zijn als het oppervlak van het grondvlak van de kegel: Op = 2*Ok
Op is het oppervlak van een vierkant en Ok het oppervlak van een cirkel. Ik neem aan dat je weet hoe je het oppervlak van een vierkant en een cirkel moet uitrekenen en daarmee de opgave dus kan oplossen.
[ Bericht 0% gewijzigd door #ANONIEM op 20-06-2009 23:27:18 ]
hij is gelijk weg gebleven
niet te veel voorkauwen he, als je vwo doet moet je aan de hand van dat soort verhaaltje dit soort dingen zelf kunnen opstellen, of in ieder geval een poging doen vind ik.
niet te veel voorkauwen he, als je vwo doet moet je aan de hand van dat soort verhaaltje dit soort dingen zelf kunnen opstellen, of in ieder geval een poging doen vind ik.
ik heb ook een vraag...
Een piramide en een kegel hebben dezelfde inhoud. De kegel is twee keer zo hoog als de piramide. De straal van het grondvlak van de kegel is 4cm. Het grondvlak van de piramide is een vierkant. Bereken de lengte van de zijde van dit vierkant op één decimaal nauwkeurig.
Een piramide en een kegel hebben dezelfde inhoud. De kegel is twee keer zo hoog als de piramide. De straal van het grondvlak van de kegel is 4cm. Het grondvlak van de piramide is een vierkant. Bereken de lengte van de zijde van dit vierkant op één decimaal nauwkeurig.
Begin eens met het opstellen van twee formules voor de inhoud van beide figuren.
Probeer daarna het gegeven erin te verwerken dat de kegel 2x zo hoog is als een piramide.
Maak mbv beide formules een vergelijking.
Succes
Probeer daarna het gegeven erin te verwerken dat de kegel 2x zo hoog is als een piramide.
Maak mbv beide formules een vergelijking.
Succes
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Begin eens met twee posts boven je te kijken.quote:Op zondag 21 juni 2009 10:24 schreef ikhebhulpnodigmetwiskunde het volgende:
ik heb ook een vraag...
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
De normale verdeling
Help me!
Hoe moet ik dit aanpakken, volgens mij begrijp ik de vraagstelling niet helemaal.
1. Bepaal indien Z~N(0,1) :
a. P (0 < z < 1,93)
b. P (-1,55 < z < 1,20)
c. P (-2,20 < z < 0)
d. P (-2,20 < z < -1,20)
e. P (1,5 < z < 2,5)
Help me!
Hoe moet ik dit aanpakken, volgens mij begrijp ik de vraagstelling niet helemaal.
1. Bepaal indien Z~N(0,1) :
a. P (0 < z < 1,93)
b. P (-1,55 < z < 1,20)
c. P (-2,20 < z < 0)
d. P (-2,20 < z < -1,20)
e. P (1,5 < z < 2,5)
bier
Je hebt een Normaal verdeelde kansvariabele Z met een mu van 0 en een standaarddeviatie van 1 (dit is de standaardnormale verdeling). Nu moet je een 5-tal kansen berekenen. De kleine z is hoever hij van de mu afzit bij de standaard normale verdeling. Voor 1a wil je dus weten wat de kans is dat de variabele op een waarde tussen 0 en 1.93 valt, dit kun je met je rekenmachine of via een tabel uitzoeken. Het is alleen rechts van mu, maar wel bijna alles ernaast, ik gok dat het zo'n 47% is.quote:Op zondag 21 juni 2009 16:44 schreef italiaan1987 het volgende:
De normale verdeling
Help me!
Hoe moet ik dit aanpakken, volgens mij begrijp ik de vraagstelling niet helemaal.
1. Bepaal indien Z~N(0,1) :
a. P (0 < z < 1,93)
b. P (-1,55 < z < 1,20)
c. P (-2,20 < z < 0)
d. P (-2,20 < z < -1,20)
e. P (1,5 < z < 2,5)
"Reality is an illusion created by a lack of alcohol."
Dat is wel een hele vreemde omschrijving hoor. Italiaan1987 moet zich inlezen en uitzoeken wat een CDF is.quote:
[..]
Je hebt een Normaal verdeelde kansvariabele Z met een mu van 0 en een standaarddeviatie van 1 (dit is de standaardnormale verdeling). Nu moet je een 5-tal kansen berekenen. De kleine z is hoever hij van de mu afzit bij de standaard normale verdeling. Voor 1a wil je dus weten wat de kans is dat de variabele op een waarde tussen 0 en 1.93 valt, dit kun je met je rekenmachine of via een tabel uitzoeken. Het is alleen rechts van mu, maar wel bijna alles ernaast, ik gok dat het zo'n 47% is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ok misschien niet helemaal handig uitgelegd.. maar goed. Hier is een plaatje:quote:Op zondag 21 juni 2009 17:23 schreef GlowMouse het volgende:
[..]
Dat is wel een hele vreemde omschrijving hoor. Italiaan1987 moet zich inlezen en uitzoeken wat een CDF is.
http://www.wiswijzer.nl/bestanden/q1443img7.gif
Hier is de kans van -infinite tot een bepaalde z 0.25. Bij die bovenste vraag werk je vanuit het midden tot z.
"Reality is an illusion created by a lack of alcohol."
Eerst moet je een tabel opsnorren, b.v. zo een, maar die staat ook ergens in je boek, als het goed is. Je moet verder even de klok-curve in gedachten houden, zoals deze:quote:
snap het nog steeds niet.
Kan iemand misschien 1tje voordoen ofzo ?
In jouw geval geldt dat μ = 0, en σ = 1, dus je kunt de waarden op de x-as als -3, -2, -1, 0, 1, 2, 3 zien. Met behulp van die grafiek kun je nu kansen uitrekenen voor de waarde van z door de oppervlakte onder die grafiek te berekenen. B.v. de kans dat z >= 0 is 50%, immers, vanaf 0 naar rechts is 50% van de oppervlakte van de grafiek (de totale oppervlakte onder de grafiek is overigens 1). Dat z >= -1 is 50% + 34.1% zoals je in het plaatje ziet, dus 84.1%, dat z >= 1 is echter 50% - 34.1% = 15.9%.
Nou, omdat het wat lastig is om die waarden uit te rekenen gebruik je een tabel om de oppervlakte af te lezen. Nemen we je eerste som:
a. P (0 < z < 1,93)
We moeten dus de oppervlakte weten in feite van het donkerblauwe gedeelte rechts van het midden, en bijna het gehele stukje ernaast (voor P(0 < z < 2.0) was het antwoord natuurlijk 34.1% + 13.6 = 47.7% geweest). We kijken nu even goed naar de tabel die ik gaf, die zegt dat het de oppervlakte van -oo tot z geeft. En inderdaad zien we voor 0.000 dat Z = 50%. Voor z = 1.93 zoek je eerst de juiste rij op, die vind je bij 1.9, dan kijk je in de 4e kolom (voor 1.93) en vind je: 0.9732. Nu, 0.9732 - 0.5 = 0.4732, dus je antwoord op 'a' is 47.3%.
Voor 'b' moet je even bedenken dat de grafiek symmetrisch is, dus 'links' van -1.55 zit evenveel als er rechts van +1.55 zit (en dat is 1 - wat er links van +1.55 zit).
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja, schrijf het eens uit:quote:
Is (n+1)! = (n+1)n! ??? Dit staat in mijn aantekeningen, maar ik snap het niet...
(n + 1)! = (n + 1)*n*(n-1) * ... * 1
En:
n! = n * (n - 1) * ... * 1
Dus ja, (n + 1)! = (n + 1)*n!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Of, maar dat is natuurlijk geen bewijs, doch het kan je wel helpen, vul het eens in: 5! = 5 * 4 * 3 * 2 * 1 = 5 * 4!.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Is de OP niet wat gedateerd nu er voor wiskunde een apart topic is en verder een beta overig?
tevens is dit, voor de scherperen onder jullie een verkapte TVP.quote:Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Wiskunde
Natuurkunde
Informatica
Scheikunde
Biologie
Algemene Natuurwetenschappen
... en alles wat verder in de richting komt.
kloep kloep
Waar zie jij die OP?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Oh ja! De wiki moet even aangepast worden dus! Want daar had ik het vandaan gehaald!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Oh ja! Schande!quote:
Oh ja! De wiki moet even aangepast worden dus! Want daar had ik het vandaan gehaald!
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Er zouden nog wel wat meer aanpassingen gemaakt mogen worden aan de OP. Waarom alleen die verwijzingen naar Wolfram, terwijl er naar mijn idee toch betere sites zijn voor bijv. integratie?quote:Op maandag 22 juni 2009 20:59 schreef Iblis het volgende:
Oh ja! De wiki moet even aangepast worden dus! Want daar had ik het vandaan gehaald!
Iblis heeft het uitgelegd, maar om het ook maar een beetje nauwkeurig uit te rekenen heb je een rekenmachine nodig. Dus met welk apparaat/programma probeer je het op te lossen en wat heb je met dit apparaat geprobeerd om tot het antwoord te komen.quote:Op zondag 21 juni 2009 20:11 schreef italiaan1987 het volgende:
snap het nog steeds niet.
Kan iemand misschien 1tje voordoen ofzo ?
Jesus hates you.
Ik heb een algemene vraag:
Is het verstandig om Wiskunde te studeren en daarnaast 20 tot 30 uur per week werken?
Is het verstandig om Wiskunde te studeren en daarnaast 20 tot 30 uur per week werken?
Als je geen behoefte hebt aan een sociaal leven, of als je het niet erg vindt langer over je studie te doen wel.quote:Op dinsdag 23 juni 2009 12:43 schreef Washington het volgende:
Ik heb een algemene vraag:
Is het verstandig om Wiskunde te studeren en daarnaast 20 tot 30 uur per week werken?
Op dinsdag 23 augustus 2011 23:18 schreef problematiQue het volgende:
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Als ik daardoor langer over m'n studie doe, is het dus niet verstandig.quote:Op dinsdag 23 juni 2009 12:50 schreef Gebraden_Wombat het volgende:
[..]
Als je geen behoefte hebt aan een sociaal leven, of als je het niet erg vindt langer over je studie te doen wel.
Maar zijn er hier mensen die werken en Wiskunde studeren, en alle vakken halen?
Wat zijn je plannen, welk niveau en welke richting wil je doen?
"Reality is an illusion created by a lack of alcohol."
Universitair en binnen de gestelde tijd.quote:Op dinsdag 23 juni 2009 12:55 schreef Dzy het volgende:
Wat zijn je plannen, welk niveau en welke richting wil je doen?
Nouja, ik denk dat het wel pittig wordt, dat het wel te doen is maar vooral ook aan jezelf ligt, qua inzicht en inzet.
"Reality is an illusion created by a lack of alcohol."
Ok. Nja, het komt vast wel goed. Als het toch te druk blijkt te worden kan ik altijd ontslag nemen.
Als ik goed voorbereid het eerste jaar in ga, zal ik vast nog wel een tijdje kunnen werken.
Als ik goed voorbereid het eerste jaar in ga, zal ik vast nog wel een tijdje kunnen werken.
Ik. En als je er voor wil werken is het goed te combineren. Goed plannen en je aan je eigen afspraken houden, dan lukt het best wel.quote:Op dinsdag 23 juni 2009 12:54 schreef Washington het volgende:
[..]
Als ik daardoor langer over m'n studie doe, is het dus niet verstandig.
Maar zijn er hier mensen die werken en Wiskunde studeren, en alle vakken halen?
Door een goede planning hou ik ook tijd over voor andere leuke dingen!
kloep kloep
Ik vind het lastig om de afgeleide te bepalen. Dit kan zeker niet met behulp van de GR of wel?
-je webicon was te groot, niet terugplaatsen-
Doorgaans niet nauwkeurig, alhoewel sommige GR's het wel kunnen. Overigens is het voor de rest van je wiskundige leven, al was het maar op de middelbare school, wel beter om het wel te kunnen. Hier kunnen mensen je wel uitleg geven, als je docent er niet veel van bakt.quote:
Ik vind het lastig om de afgeleide te bepalen. Dit kan zeker niet met behulp van de GR of wel?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Volgens mij kan de GR het in elk geval niet algebraïsch. Afgeleides bepalen is iets wat je toch echt ooit zelf moet kunnen. Maar wat voor afgeleides precies, misschien kunnen we je hier wel helpen.quote:
Ik vind het lastig om de afgeleide te bepalen. Dit kan zeker niet met behulp van de GR of wel?
Op dinsdag 23 augustus 2011 23:18 schreef problematiQue het volgende:
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
GR? Grrr... Er zijn sites waar je een afgeleide kunt laten bepalen, deze bijvoorbeeld (hint voor Glowmouse: staat niet in de OP). Maar wat vind je precies lastig? Om wat voor functies gaat het? Het is natuurlijk wel de bedoeling dat je de afgeleiden van een aantal standaardfuncties gewoon uit het blote hoofd kent, evenals de gangbare regels voor het bepalen van de afgeleide van een som, verschil, product of quotiënt van twee functies, en de samenstelling van twee functies (kettingregel).quote:Op dinsdag 23 juni 2009 16:49 schreef ikvalopdikkewijven het volgende:
Ik vind het lastig om de afgeleide te bepalen. Dit kan zeker niet met behulp van de GR of wel?
Hint voor Riparius: OP staat in een wiki.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Heel erg bedankt ik begin het te snappenquote:Op zondag 21 juni 2009 20:24 schreef Iblis het volgende:
[..]
Eerst moet je een tabel opsnorren, b.v. zo een, maar die staat ook ergens in je boek, als het goed is. Je moet verder even de klok-curve in gedachten houden, zoals deze:
[ afbeelding ]
In jouw geval geldt dat μ = 0, en σ = 1, dus je kunt de waarden op de x-as als -3, -2, -1, 0, 1, 2, 3 zien. Met behulp van die grafiek kun je nu kansen uitrekenen voor de waarde van z door de oppervlakte onder die grafiek te berekenen. B.v. de kans dat z >= 0 is 50%, immers, vanaf 0 naar rechts is 50% van de oppervlakte van de grafiek (de totale oppervlakte onder de grafiek is overigens 1). Dat z >= -1 is 50% + 34.1% zoals je in het plaatje ziet, dus 84.1%, dat z >= 1 is echter 50% - 34.1% = 15.9%.
Nou, omdat het wat lastig is om die waarden uit te rekenen gebruik je een tabel om de oppervlakte af te lezen. Nemen we je eerste som:
a. P (0 < z < 1,93)
We moeten dus de oppervlakte weten in feite van het donkerblauwe gedeelte rechts van het midden, en bijna het gehele stukje ernaast (voor P(0 < z < 2.0) was het antwoord natuurlijk 34.1% + 13.6 = 47.7% geweest). We kijken nu even goed naar de tabel die ik gaf, die zegt dat het de oppervlakte van -oo tot z geeft. En inderdaad zien we voor 0.000 dat Z = 50%. Voor z = 1.93 zoek je eerst de juiste rij op, die vind je bij 1.9, dan kijk je in de 4e kolom (voor 1.93) en vind je: 0.9732. Nu, 0.9732 - 0.5 = 0.4732, dus je antwoord op 'a' is 47.3%.
Voor 'b' moet je even bedenken dat de grafiek symmetrisch is, dus 'links' van -1.55 zit evenveel als er rechts van +1.55 zit (en dat is 1 - wat er links van +1.55 zit).
bier
Klein vraagje:
Zijn er truukjes of stappen om grote wortels in de standaardvorm te zetten?
Dat 'wortel 54', '3 wortel 6' is, daar heb ik niet zo'n moeite mee natuurlijk, maar zijn er misschien wat handigheden om bijvoorbeeld 'wortel 288' snel uit te rekenen. Ik weet dat je gewoon wat kunt proberen en schrijven totdat je het gevonden hebt maar omdat ik het snel moet kunnen toepassen vraag ik het me af.
Dank u
Zijn er truukjes of stappen om grote wortels in de standaardvorm te zetten?
Dat 'wortel 54', '3 wortel 6' is, daar heb ik niet zo'n moeite mee natuurlijk, maar zijn er misschien wat handigheden om bijvoorbeeld 'wortel 288' snel uit te rekenen. Ik weet dat je gewoon wat kunt proberen en schrijven totdat je het gevonden hebt maar omdat ik het snel moet kunnen toepassen vraag ik het me af.
Dank u
Gewoon ontbinden in factoren en op grond daarvan bepalen wat het grootste kwadraat is dat het getal deelt.quote:Op woensdag 24 juni 2009 11:44 schreef BellieB het volgende:
Klein vraagje:
Zijn er truukjes of stappen om grote wortels in de standaardvorm te zetten?
Dat 'wortel 54', '3 wortel 6' is, daar heb ik niet zo'n moeite mee natuurlijk, maar zijn er misschien wat handigheden om bijvoorbeeld 'wortel 288' snel uit te rekenen. Ik weet dat je gewoon wat kunt proberen en schrijven totdat je het gevonden hebt maar omdat ik het snel moet kunnen toepassen vraag ik het me af.
Dank u
Ontbinden in priemfactoren wil nog weleens helpen. Vervolgens moet je alle paren buiten haakjes halen.quote:Op woensdag 24 juni 2009 11:44 schreef BellieB het volgende:
Klein vraagje:
Zijn er truukjes of stappen om grote wortels in de standaardvorm te zetten?
Dat 'wortel 54', '3 wortel 6' is, daar heb ik niet zo'n moeite mee natuurlijk, maar zijn er misschien wat handigheden om bijvoorbeeld 'wortel 288' snel uit te rekenen. Ik weet dat je gewoon wat kunt proberen en schrijven totdat je het gevonden hebt maar omdat ik het snel moet kunnen toepassen vraag ik het me af.
Dank u
54 = 2 * 3 * 3 * 3 = 3 wortel(2*3) = 3 wortel(6)
Jesus hates you.
Ok. Cool.quote:Op dinsdag 23 juni 2009 16:34 schreef Borizzz het volgende:
[..]
Ik. En als je er voor wil werken is het goed te combineren. Goed plannen en je aan je eigen afspraken houden, dan lukt het best wel.
Door een goede planning hou ik ook tijd over voor andere leuke dingen!
Ik weet prima hoe je de buigpunten moet berekenen, maar ik weet niet hoe je dan moet zien of ze van hol naar bol gaan of andersom... Iemand?
Probeer dit zelf eens te beredeneren. Als je (van links naar rechts beschouwd) overgaat van bol naar hol, dan heeft de steilheid van de curve (dus de eerste afgeleide) een minimum in het buigpunt. De afgeleide van de afgeleide oftewel de tweede afgeleide is dan nul in het buigpunt, maar wat kun je zeggen over de hogere afgeleiden?quote:Op woensdag 24 juni 2009 15:57 schreef codemss het volgende:
Ik weet prima hoe je de buigpunten moet berekenen, maar ik weet niet hoe je dan moet zien of ze van hol naar bol gaan of andersom... Iemand?
quote:Op woensdag 24 juni 2009 23:32 schreef codemss het volgende:
ik zou het niet weten
maar bedankt voor je antwoord
GO LANCE !!!
Als ik een symmetrische matrix heb met a=c en b=0, wat voor een kegelsnede heb ik dan?
Klopt het dat het dan een ellips is?!
Klopt het dat het dan een ellips is?!
kloep kloep
Waarom dan perse een cirkel? je krijgt dan toch ax2 +ay2=k.quote:Op donderdag 25 juni 2009 16:08 schreef thabit het volgende:
Dan heb je een cirkel (en dus een ellips).
ok, of het zit zo:
ax2+ay2=k.
schrijf je om tot
x2+ay2=k/a en dan is het idd een cirkel.
kloep kloep
laat de formule f(x) om de y-as wentelen en bereken inhoud. f(x)=ln(x)^2
Ik krijg hem niet eens naar de x= vorm. Weet iemand hoe je deze som oplost?
Ik krijg hem niet eens naar de x= vorm. Weet iemand hoe je deze som oplost?
Heb je ook nog een domein?quote:
laat de formule f(x) om de y-as wentelen en bereken inhoud. f(x)=ln(x)^2
Ik krijg hem niet eens naar de x= vorm. Weet iemand hoe je deze som oplost?
Anders is je antwoord volgens mij gewoon oneindig.
gr gr
Je kunt een 'formule' niet om de y-as laten wentelen. Nu ja, het kan wel, maar dat is niet wat er wordt bedoeld. Iets minder onbeholpen taalgebruik mag wel. Wiskunde is een exact vak, en hoewel taal dat niet is, is nauwkeurig formuleren toch wel een vereiste bij wiskunde.quote:Op donderdag 25 juni 2009 22:55 schreef Zwavel-Zuur het volgende:
laat de formule f(x) om de y-as wentelen en bereken inhoud. f(x)=ln(x)^2
Geef eens de oorspronkelijke en complete tekst van de opgave.quote:Ik krijg hem niet eens naar de x= vorm. Weet iemand hoe je deze som oplost?
En is 't ln(x)2 of misschien toch ln(x2), beide kan op zich…, maar die jij geeft is volgens mij wel wat lastiger.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het probleem is dat ik de opgave niet bij me heb. Daarom ga ik eerder ook niet het domein. Wat natuurlijk verreist is. Ik zal nog eens goed zoeken naar het opgavevel.
Hij zal het lijnstuk {(x,y) | y=f(x), 0<x<=2} wel om de y-as willen wentelen.quote:
[..]
Je kunt een 'formule' niet om de y-as laten wentelen. Nu ja, het kan wel, maar dat is niet wat er wordt bedoeld. Iets minder onbeholpen taalgebruik mag wel. Wiskunde is een exact vak, en hoewel taal dat niet is, is nauwkeurig formuleren toch wel een vereiste bij wiskunde.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Maar moet je niet gewoon de integraal uitrekenen over het domein en dat dan maal (pi * r²) te doen? Met 2 als straal in dit geval.
edit: o nee toch niet hier waren bepaalde formules voor geloof ik, die ik alweer vergeten ben
edit: o nee toch niet
hier waren bepaalde formules voor geloof ik, die ik alweer vergeten ben
gr gr
Is het dan wel goed als je zegt dat je "de integraal van de functie f(x) = ... " wilt wentelen om de y-as op het domein a,b ?quote:Op donderdag 25 juni 2009 23:02 schreef Riparius het volgende:
[..]
Je kunt een 'formule' niet om de y-as laten wentelen. Nu ja, het kan wel, maar dat is niet wat er wordt bedoeld. Iets minder onbeholpen taalgebruik mag wel. Wiskunde is een exact vak, en hoewel taal dat niet is, is nauwkeurig formuleren toch wel een vereiste bij wiskunde.
[..]
Geef eens de oorspronkelijke en complete tekst van de opgave.
Indien je dat bedoelt?
je r is f-1(y).quote:
Maar moet je niet gewoon de integraal uitrekenen over het domein en dat dan maal (pi * r²) te doen? Met 2 als straal in dit geval.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ook ik had het anders in mijn hoofd.
f(x)=ln2(x)
a) G is het gebied, begrensd door de X-as, de Y-as, de grafiek van f en de rechte lijn y=2
bereken algebraïsch de oppervlakte van G.
b) Bereken algebraisch de inhoud van het lichaam dat onstaan door G te wentelen om de Y-as.
Uit b) kom ik niet uit.
f(x)=ln2(x)
a) G is het gebied, begrensd door de X-as, de Y-as, de grafiek van f en de rechte lijn y=2
bereken algebraïsch de oppervlakte van G.
b) Bereken algebraisch de inhoud van het lichaam dat onstaan door G te wentelen om de Y-as.
Uit b) kom ik niet uit.
ln(x) = sqrt(y)
x = exp(sqrt(y)).
b is integraal van 0 t/m 2 van pi*exp(sqrt(y))^2 dy.
x = exp(sqrt(y)).
b is integraal van 0 t/m 2 van pi*exp(sqrt(y))^2 dy.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, dat klopt nog niet helemaal ... y is je onafhankelijke variabele, dus het interval waarover je integreert is niet [0,2].quote:Op donderdag 25 juni 2009 23:18 schreef GlowMouse het volgende:
ln(x) = sqrt(y)
x = exp(sqrt(y)).
b is integraal van 0 t/m 2 van pi*exp(sqrt(y))^2 dy.
Een primitieve van e√y is 2(√y - 1)e√y. Maar bedenk dat je een primitieve moet vinden van het kwadraat van e√y ...quote:Op donderdag 25 juni 2009 23:24 schreef Zwavel-Zuur het volgende:
Maar ik zie niet hoe die kunt primitiveren? deze bedoel ik dan exp(sqrt(y)).
[ Bericht 10% gewijzigd door Riparius op 25-06-2009 23:43:20 ]
quote:
[..]
Nee, dat klopt nog niet helemaal ... y is je onafhankelijke variabele, dus het interval waarover je integreert is niet [0,2].
quote:
Ook ik had het anders in mijn hoofd.
f(x)=ln2(x)
a) G is het gebied, begrensd door de X-as, de Y-as, de grafiek van f en de rechte lijn y=2
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Op het gebied vanaf het snijpunt van y=2 met f(x) tot f(x)=0 is de maximale y-waarde geen 2, maar f(x).quote:
Of zit dat al in de formule verwerkt?
edit: ik blijf wel weer weg uit dit topic
gr gr
Ja, hetgeen je zei klopt wel, maar dat was pas het geval nadat Zwavel-Zuur zijn post had ge-edit en de complete opgave had gegeven.quote:
Volgens mij is het wel gewoon [0.2], want de grafiek verandert toch niet? Ik snap niet helemaal wat je bedoelt. De lijn y=2 geeft toch aan tot waar hij gaat?
Deze klopt nu dan wel of niet, exp(sqrt(y))?
Deze klopt nu dan wel of niet, exp(sqrt(y))?
Correct, maar dat gegeven (de lijn y = 2) had je er eerst niet bij staan.quote:Op donderdag 25 juni 2009 23:43 schreef Zwavel-Zuur het volgende:
Volgens mij is het wel gewoon [0.2], want de grafiek verandert toch niet? Ik snap niet helemaal wat je bedoelt. De lijn y=2 geeft toch aan tot waar hij gaat?
Ok ik begin het te snappen. Maar hoe kom je op deze primitieve 2(√y - 1)e√y? Voor de rest gewoon simpel oplossen. Welke methodes heb je gebruikt om daar te komen? Partieel integreren?
Het simpelste is een beetje trial and error. Je weet dat ey zichzelf als primitieve heeft, dus 'probeer' je als primitieve van e√y eerst e√y. Bepaal daarvan de afgeleide, en je ziet dan wel hoe je moet 'corrigeren'. Maar ga je hier nu niet blind op staren, want je hebt voor de bepaling van het volume van het omwentelingslichaam een primitieve van het kwadraat van deze functie nodig.quote:Op donderdag 25 juni 2009 23:56 schreef Zwavel-Zuur het volgende:
Ok ik begin het te snappen. Maar hoe kom je op deze primitieve 2(√y - 1)e√y? Voor de rest gewoon simpel oplossen. Welke methodes heb je gebruikt om daar te komen? Partieel integreren?
Edit: Ik zie dat je alweer vertrokken bent (vanwege de storingen op FOK?), maar ik heb het volume van het bedoelde omwentelingslichaam even uitgerekend en kom op:
π∙((√2 - ½)∙e2√2 + ½)
Numeriek is dat 50,163 ...
[ Bericht 7% gewijzigd door Riparius op 26-06-2009 00:35:27 ]
Over een half jaar begin ik met mijn laatste wiskunde vak "getaltheorie". Omdat ik me ook voor dit vak voor 100% wil inzetten zou ik graag wat tips hebben om een goede start te maken. Bijv een boek ofzo waarin ik de beginselen kan leren? Iemand tips?
Vakinhouden zijn:
-basistheorie rondom ggd, kgv, priemgetallen, Euler-phi-functie en kan deze theorie in opgaven gebruiken;
-modulovergelijkingen en stelsels modulovergelijkingen systematisch oplossen o.a. met behulp van de Chinese reststelling;
-kan de stellingen van Wilson, Fermat, Euler e n de kwadratische reciprociteitsstelling in opgaven toepassen;
-kent de achtergronden uit de getaltheorie bij het RSA-cryptosysteem, hij kan ook in RSA communiceren en omgaan met een digitale handtekening.
-leert toepassingen van de getaltheorie: geheim delen, geboortedag vaststellen, digitaal tossen, ISBN-nummers controleren, n-proeven.
Vakinhouden zijn:
-basistheorie rondom ggd, kgv, priemgetallen, Euler-phi-functie en kan deze theorie in opgaven gebruiken;
-modulovergelijkingen en stelsels modulovergelijkingen systematisch oplossen o.a. met behulp van de Chinese reststelling;
-kan de stellingen van Wilson, Fermat, Euler e n de kwadratische reciprociteitsstelling in opgaven toepassen;
-kent de achtergronden uit de getaltheorie bij het RSA-cryptosysteem, hij kan ook in RSA communiceren en omgaan met een digitale handtekening.
-leert toepassingen van de getaltheorie: geheim delen, geboortedag vaststellen, digitaal tossen, ISBN-nummers controleren, n-proeven.
kloep kloep
Er is een boek "Getaltheorie voor beginners" (oid), geschreven door Frits Beukers. Misschien is dat iets voor je.
Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...
kloep kloep
Ik heb het nog even nagekeken en je moet dus de prrimitieven van e^2wortel(y) hebben. Hoe ben je daar dan gekomen? Want daar strand ik de hele tijd.
In dat geval raad ik je "De Telduivel" aan.quote:Op vrijdag 26 juni 2009 11:00 schreef Borizzz het volgende:
Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...
Je bent bijna afgestudeerd wiskundige? Als je dan geen beginner bent… Dan moet het boek wel heel raar geschreven zijn.quote:
Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik geef alleen maar weer wat ze ons verteld hebbenquote:Op vrijdag 26 juni 2009 11:06 schreef Iblis het volgende:
[..]
Je bent bijna afgestudeerd wiskundige? Als je dan geen beginner bent… Dan moet het boek wel heel raar geschreven zijn.
... Maar ach ik schaf ze allebei wel aan!
kloep kloep
Wel, de oppervlakte van een cirkel is pi * r2 waarbij r de straal is, die in dit geval gelijk is aan de functiewaarde.quote:Op vrijdag 26 juni 2009 11:02 schreef Zwavel-Zuur het volgende:
Ik heb het nog even nagekeken en je moet dus de prrimitieven van e^2wortel(y) hebben. Hoe ben je daar dan gekomen? Want daar strand ik de hele tijd.
Je bedoelt dat boek van Enzensberger? Ik dacht dat dit voor beginners in de wiskunde was?! Is dit boek inleidend voor getaltheorie dan?quote:Op vrijdag 26 juni 2009 11:06 schreef thabit het volgende:
[..]
In dat geval raad ik je "De Telduivel" aan.
kloep kloep
't Is een boek voor kinderen die geen wiskunde kunnen. Maar ik ben bang dat er toch weinig materiaal is te vinden dat qua niveau strikt tussen 'De telduivel' en 'Getaltheorie voor beginners' ligt.quote:Op vrijdag 26 juni 2009 11:10 schreef Borizzz het volgende:
[..]
Je bedoelt dat boek van Enzensberger? Ik dacht dat dit voor beginners in de wiskunde was?! Is dit boek inleidend voor getaltheorie dan?
Je kunt ook eens naar je universiteitsbibliotheek gaan, daar heb je natuurlijk genoeg boeken van b.v. Springer, zoals A course in number theory and cryptography. Nu zijn die Springerboeken soms best compact geschreven, maar als je met je laatste vak bezig bent moet dat toch te doen zijn. En als er dan eentje is die je bevalt, dan kun je 't kopen.
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:46:47 ]
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:46:47 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
http://nl.wikipedia.org/wiki/Centrale_limietstellingquote:Op vrijdag 26 juni 2009 14:12 schreef Washington het volgende:
Kan iemand mij vertellen waarom de functie voor een klokgrafiek zo is?
[ afbeelding ]
Heb de wiskundetitels op die Russische site even bekeken en zie bij de niet-Russische titels toch veel bekende namen zoals Gauss, Hermite, Galois, Lagrange ... Al die titels zijn public domain omdat de auteurs al langer dan 70 jaar geleden zijn overleden. Dat is volkomen legaal. Russische titels zijn inderdaad wel recenter, maar ik weet niet hoe het in Rusland met auteursrecht zit. Overigens kun je ook op archive.org legaal terecht voor ingescande oudere titels. Heb daar bijvoorbeeld boeken gevonden van Cajori die mij interesseerden. Voor recente titels kun je beter even op - kijken. Zie daar al enkele dozijnen titels over getaltheorie staan. Meestal djvu formaat (wat ik zelf erg prettig vind werken).quote:Op vrijdag 26 juni 2009 11:34 schreef Iblis het volgende:
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:47:10 ]
Als het een vertaling betreft echter, dan wordt het auteursrecht van die vertaling gegeven op het moment dat die vertaling gemaakt is. Maar b.v. Knuth staat er ook op, en dat is echt niet legaal, ook genoeg werken die in 2000 zijn gepubliceerd.quote:
Heb de wiskundetitels op die Russische site even bekeken en zie bij de niet-Russische titels toch veel bekende namen zoals Gauss, Hermite, Galois, Lagrange ... Al die titels zijn public domain omdat de auteurs al langer dan 70 jaar geleden zijn overleden. Dat is volkomen legaal. Russische titels zijn inderdaad wel recenter, maar ik weet niet hoe het in Rusland met auteursrecht zit.
Jup, er zijn meer wegen die naar illegale werken leiden. De bibliotheek vind ik zelf nog het handigst echter.quote:Overigens kun je ook op archive.org legaal terecht voor ingescande oudere titels. Heb daar bijvoorbeeld boeken gevonden van Cajori die mij interesseerden. Voor recente titels kun je beter even op - kijken. Zie daar al enkele dozijnen titels over getaltheorie staan. Meestal djvu formaat (wat ik zelf erg prettig vind werken).
Maar soms heeft iemand een werk als z'n persoonlijke bezit geclaimd lijkt het wel en is het niet in de bieb te vinden.[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:47:26 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Iblis toch, dat ik juist jou sites zie noemen met auteursrechtelijk beschermd materiaal.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja, noemen, niet linken.quote:Op vrijdag 26 juni 2009 17:48 schreef GlowMouse het volgende:
Iblis toch, dat ik juist jou sites zie noemen met auteursrechtelijk beschermd materiaal.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
We leven niet meer in 1989 dat je als je de naam van een BBS had nog niks kon zonder telefoonnummer; met dank aan zoekmachines liggen een naam en een url dicht bij elkaar; niet meer doen dus.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Stel je moet een parametrisatie maken van de doorsnijding van de cilinder (x-1)2 + y2=1 met het vlak y+z=1.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.
kloep kloep
Nee, want je kunt x niet tegelijk als parameter gebruiken ... Ik zou inderdaad zeggen x = 1 + cos t, y = sin t, z = 1 - sin t, 0 ≤ t < 2π.quote:Op zaterdag 27 juni 2009 21:55 schreef Borizzz het volgende:
Stel je moet een parametrisatie maken van de doorsnijding van de cilinder (x-1)2 + y2=1 met het vlak y+z=1.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
Lijkt me niet handig, maar dat hangt er ook van af wat je vervolgens met die parametervoorstelling wil gaan doen.quote:2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.
Hoe kom je bij 1) aan z? de keuze van x en y kan ik wel volgen. Verder logisch uiteraard dat je een andere parameter t dan x neemt.
kloep kloep
Je hebt y+z = 1, aangezien y= sin(t) moet z dus wel 1 - sin(t) zijn.
"Reality is an illusion created by a lack of alcohol."
D de driehoek is die (0,0) , (1,0) en (0,1) als hoekpunten heeft
Zijn de grenzen: 0 < x < 1 en 0 < y < (1-x) ??
[ Bericht 99% gewijzigd door motorbloempje op 01-09-2013 21:25:17 ]
"The name is Bond, James Bond"
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Thnx, wist niet hoe ik LaTeX werkend kon krijgenquote:Op zondag 28 juni 2009 17:59 schreef GlowMouse het volgende:
[..]
http://betahw.mine.nu/index.php
en substitueer z=x²
"The name is Bond, James Bond"
Ja, het lijkt me ook handig als je de integratievolgorde omwisselt.quote:
Zijn de grenzen: 0 < x < 1 en 0 < y < (1-x) ??
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
