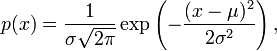SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Er is een boek "Getaltheorie voor beginners" (oid), geschreven door Frits Beukers. Misschien is dat iets voor je.


Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...
kloep kloep


Ik heb het nog even nagekeken en je moet dus de prrimitieven van e^2wortel(y) hebben. Hoe ben je daar dan gekomen? Want daar strand ik de hele tijd.


In dat geval raad ik je "De Telduivel" aan.quote:Op vrijdag 26 juni 2009 11:00 schreef Borizzz het volgende:
Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...


Je bent bijna afgestudeerd wiskundige? Als je dan geen beginner bent… Dan moet het boek wel heel raar geschreven zijn.quote:Op vrijdag 26 juni 2009 11:00 schreef Borizzz het volgende:
Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik geef alleen maar weer wat ze ons verteld hebbenquote:Op vrijdag 26 juni 2009 11:06 schreef Iblis het volgende:
[..]
Je bent bijna afgestudeerd wiskundige? Als je dan geen beginner bent… Dan moet het boek wel heel raar geschreven zijn.
kloep kloep


Wel, de oppervlakte van een cirkel is pi * r2 waarbij r de straal is, die in dit geval gelijk is aan de functiewaarde.quote:Op vrijdag 26 juni 2009 11:02 schreef Zwavel-Zuur het volgende:
Ik heb het nog even nagekeken en je moet dus de prrimitieven van e^2wortel(y) hebben. Hoe ben je daar dan gekomen? Want daar strand ik de hele tijd.


Je bedoelt dat boek van Enzensberger? Ik dacht dat dit voor beginners in de wiskunde was?! Is dit boek inleidend voor getaltheorie dan?quote:Op vrijdag 26 juni 2009 11:06 schreef thabit het volgende:
[..]
In dat geval raad ik je "De Telduivel" aan.
kloep kloep


't Is een boek voor kinderen die geen wiskunde kunnen. Maar ik ben bang dat er toch weinig materiaal is te vinden dat qua niveau strikt tussen 'De telduivel' en 'Getaltheorie voor beginners' ligt.quote:Op vrijdag 26 juni 2009 11:10 schreef Borizzz het volgende:
[..]
Je bedoelt dat boek van Enzensberger? Ik dacht dat dit voor beginners in de wiskunde was?! Is dit boek inleidend voor getaltheorie dan?


Je kunt ook eens naar je universiteitsbibliotheek gaan, daar heb je natuurlijk genoeg boeken van b.v. Springer, zoals A course in number theory and cryptography. Nu zijn die Springerboeken soms best compact geschreven, maar als je met je laatste vak bezig bent moet dat toch te doen zijn. En als er dan eentje is die je bevalt, dan kun je 't kopen.
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:46:47 ]
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:46:47 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


http://nl.wikipedia.org/wiki/Centrale_limietstellingquote:Op vrijdag 26 juni 2009 14:12 schreef Washington het volgende:
Kan iemand mij vertellen waarom de functie voor een klokgrafiek zo is?
[ afbeelding ]


Heb de wiskundetitels op die Russische site even bekeken en zie bij de niet-Russische titels toch veel bekende namen zoals Gauss, Hermite, Galois, Lagrange ... Al die titels zijn public domain omdat de auteurs al langer dan 70 jaar geleden zijn overleden. Dat is volkomen legaal. Russische titels zijn inderdaad wel recenter, maar ik weet niet hoe het in Rusland met auteursrecht zit. Overigens kun je ook op archive.org legaal terecht voor ingescande oudere titels. Heb daar bijvoorbeeld boeken gevonden van Cajori die mij interesseerden. Voor recente titels kun je beter even op - kijken. Zie daar al enkele dozijnen titels over getaltheorie staan. Meestal djvu formaat (wat ik zelf erg prettig vind werken).quote:Op vrijdag 26 juni 2009 11:34 schreef Iblis het volgende:
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:47:10 ]


Als het een vertaling betreft echter, dan wordt het auteursrecht van die vertaling gegeven op het moment dat die vertaling gemaakt is. Maar b.v. Knuth staat er ook op, en dat is echt niet legaal, ook genoeg werken die in 2000 zijn gepubliceerd.quote:Op vrijdag 26 juni 2009 14:36 schreef Riparius het volgende:
Heb de wiskundetitels op die Russische site even bekeken en zie bij de niet-Russische titels toch veel bekende namen zoals Gauss, Hermite, Galois, Lagrange ... Al die titels zijn public domain omdat de auteurs al langer dan 70 jaar geleden zijn overleden. Dat is volkomen legaal. Russische titels zijn inderdaad wel recenter, maar ik weet niet hoe het in Rusland met auteursrecht zit.
Jup, er zijn meer wegen die naar illegale werken leiden. De bibliotheek vind ik zelf nog het handigst echter.quote:Overigens kun je ook op archive.org legaal terecht voor ingescande oudere titels. Heb daar bijvoorbeeld boeken gevonden van Cajori die mij interesseerden. Voor recente titels kun je beter even op - kijken. Zie daar al enkele dozijnen titels over getaltheorie staan. Meestal djvu formaat (wat ik zelf erg prettig vind werken).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:47:26 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Iblis toch, dat ik juist jou sites zie noemen met auteursrechtelijk beschermd materiaal.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja, noemen, niet linken.quote:Op vrijdag 26 juni 2009 17:48 schreef GlowMouse het volgende:
Iblis toch, dat ik juist jou sites zie noemen met auteursrechtelijk beschermd materiaal.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


We leven niet meer in 1989 dat je als je de naam van een BBS had nog niks kon zonder telefoonnummer; met dank aan zoekmachines liggen een naam en een url dicht bij elkaar; niet meer doen dus.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Stel je moet een parametrisatie maken van de doorsnijding van de cilinder (x-1)2 + y2=1 met het vlak y+z=1.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.
kloep kloep


Nee, want je kunt x niet tegelijk als parameter gebruiken ... Ik zou inderdaad zeggen x = 1 + cos t, y = sin t, z = 1 - sin t, 0 ≤ t < 2π.quote:Op zaterdag 27 juni 2009 21:55 schreef Borizzz het volgende:
Stel je moet een parametrisatie maken van de doorsnijding van de cilinder (x-1)2 + y2=1 met het vlak y+z=1.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
Lijkt me niet handig, maar dat hangt er ook van af wat je vervolgens met die parametervoorstelling wil gaan doen.quote:2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.


Hoe kom je bij 1) aan z? de keuze van x en y kan ik wel volgen. Verder logisch uiteraard dat je een andere parameter t dan x neemt.
kloep kloep


Je hebt y+z = 1, aangezien y= sin(t) moet z dus wel 1 - sin(t) zijn.
"Reality is an illusion created by a lack of alcohol."


D de driehoek is die (0,0) , (1,0) en (0,1) als hoekpunten heeft
Zijn de grenzen: 0 < x < 1 en 0 < y < (1-x) ??
[ Bericht 99% gewijzigd door motorbloempje op 01-09-2013 21:25:17 ]
"The name is Bond, James Bond"


eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Thnx, wist niet hoe ik LaTeX werkend kon krijgenquote:Op zondag 28 juni 2009 17:59 schreef GlowMouse het volgende:
[..]
http://betahw.mine.nu/index.php
en substitueer z=x˛
"The name is Bond, James Bond"


Ja, het lijkt me ook handig als je de integratievolgorde omwisselt.quote:Op zondag 28 juni 2009 17:55 schreef James.Bond het volgende:
Zijn de grenzen: 0 < x < 1 en 0 < y < (1-x) ??
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0