SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
En die k^2 wordt dus k^10. Dat kan zomaar in de breuk gestopt worden?quote:Op dinsdag 7 november 2017 16:34 schreef Janneke141 het volgende:
[..]
Het minteken zou je kunnen zien als een vermenigvuldiging met -1. en (-1)^5 = -1, dus blijf je een minteken houden.
Had er geen vijfde maar een zesde macht gestaan dan was het minteken verdwenen, aangezien (-1)^6 = 1.
Crack the following and we will get back to you: !1!llssod000;;
Je weet ook datquote:
Wat zijn de tussenstappen hier en waarom?
Dus schrijf
Dan gebruik je de regel voor vermenigvuldigen:
Dan werk je alle losse termen uit:
En dan combineer je alles weer:
Bedankt, dit heeft me geholpen!quote:Op dinsdag 7 november 2017 16:40 schreef Alrac4 het volgende:
[..]
Je weet ook dat.
Dus schrijfals
Dan gebruik je de regel voor vermenigvuldigen:
Dan werk je alle losse termen uit:
En dan combineer je alles weer:
nog 1 vraagje. waarom kan er eigenlijk nog een 1 komen na de '-' als er al een getal staat? in dit geval een getal kleiner dan 1.
Crack the following and we will get back to you: !1!llssod000;;
Eeh, omdat je een getal zo vaak als je wil met 1 kan vermenigvuldigen zonder dat er iets verandert?quote:Op dinsdag 7 november 2017 16:45 schreef _--_ het volgende:
[..]
Bedankt, dit heeft me geholpen!
nog 1 vraagje. waarom kan er eigenlijk nog een 1 komen na de '-' als er al een getal staat? in dit geval een getal kleiner dan 1.
Opinion is the medium between knowledge and ignorance (Plato)
Het is dus altijd zo dat je na een '-' een 1 moet zetten als je een opgave dergelijk moet oplossen?quote:
[..]
Eeh, omdat je een getal zo vaak als je wil met 1 kan vermenigvuldigen zonder dat er iets verandert?
Crack the following and we will get back to you: !1!llssod000;;
Er moet niks. Je kan ook concluderen dat een oneven macht van een minteken altijd een minteken oplevert, en een even macht niet.quote:
[..]
Het is dus altijd zo dat je na een '-' een 1 moet zetten als je een opgave dergelijk moet oplossen?
Opinion is the medium between knowledge and ignorance (Plato)
Bedankt voor de hulpquote:
[..]
Er moet niks. Je kan ook concluderen dat een oneven macht van een minteken altijd een minteken oplevert, en een even macht niet.
Crack the following and we will get back to you: !1!llssod000;;
Je kunt het minteken ook bij de 2, de k^2 of zelfs bij de 3 zetten. Als je de 5e macht dan uitwerkt zie je dat je uiteindelijk een minteken overhoudt. Zoals Janneke al zegt kom het er uiteindelijk op neer dat oneven machten van een minteken een minteken opleveren, terwijl even machten een plusteken geven.quote:
[..]
Het is dus altijd zo dat je na een '-' een 1 moet zetten als je een opgave dergelijk moet oplossen?
quote:
[..]
Je kunt het minteken ook bij de 2, de k^2 of zelfs bij de 3 zetten. Als je de 5e macht dan uitwerkt zie je dat je uiteindelijk een minteken overhoudt. Zoals Janneke al zegt kom het er uiteindelijk op neer dat oneven machten van een minteken een minteken opleveren, terwijl even machten een plusteken geven.
Crack the following and we will get back to you: !1!llssod000;;
Gewoon gebruik maken van de bekende rekenregels voor breuken en voor machten:quote:
Wat zijn de tussenstappen hier en waarom?
Jow bedankt!quote:
[..]
Gewoon gebruik maken van de bekende rekenregels voor breuken en voor machten:
Crack the following and we will get back to you: !1!llssod000;;
Deze notaties, hoe krijg ik die makkelijk vanaf m`n toetsenbord op het beeld?quote:
[..]
Je weet ook dat
Dus schrijf
Dan gebruik je de regel voor vermenigvuldigen:
Dan werk je alle losse termen uit:
En dan combineer je alles weer:
Alt + ... invoer, of in een word document eerst intypen/gebruik maken?
Met LaTex door [tex] tagjes.quote:
[..]
Deze notaties, hoe krijg ik die makkelijk vanaf m`n toetsenbord op het beeld?
Alt + ... invoer, of in een word document eerst intypen/gebruik maken?
Het is eenvoudiger dan het lijkt. Werk deze vijf blogs eens door.quote:
[..]
Bedankt, heb er even vluchtig naar gekeken, dat heb je zo te zien niet even onder de knie.
Ga ik doen, merciquote:
[..]
Het is eenvoudiger dan het lijkt. Werk deze vijf blogs eens door.
Kan iemand de logica uitleggen van de log2 term in Shannon-entropie? Moest dit gebruiken om de purity van een set uit te rekenen maar kan de log niet plaatsen
https://nl.m.wikipedia.org/wiki/Entropie_(informatietheorie)
https://nl.m.wikipedia.org/wiki/Entropie_(informatietheorie)
Is wel verdomd handig. Ik wist niet dat FOK! LaTex faciliteerde overigens.quote:
[..]
Bedankt, heb er even vluchtig na gekeken, dat heb je zo te zien niet even onder de knie.
[i]Put me on a pedestal and I'll only disappoint you
Tell me I'm exceptional and I promise to exploit you
Give me all your money and I'll make some origami honey
I think you're a joke but I don't find you very funny[/i]
Tell me I'm exceptional and I promise to exploit you
Give me all your money and I'll make some origami honey
I think you're a joke but I don't find you very funny[/i]
Omdat ze informatie uitdrukken in aantal bits als ik er zo even kort naar kijk.quote:
Kan iemand de logica uitleggen van de log2 term in Shannon-entropie? Moest dit gebruiken om de purity van een set uit te rekenen maar kan de log niet plaatsen
https://nl.m.wikipedia.org/wiki/Entropie_(informatietheorie)
Edit:
Ik heb even in de Engelstalige wiki gespiekt en het concept is best interessant.
Het betreft een maat voor de 'voorspelbaarheid' van een (discrete) stochast. Het volgende voorbeeld is denk ik wel duidelijk:
Now consider the example of a coin toss. Assuming the probability of heads is the same as the probability of tails, then the entropy of the coin toss is as high as it could be. This is because there is no way to predict the outcome of the coin toss ahead of time: if we have to choose, the best we can do is predict that the coin will come up heads, and this prediction will be correct with probability 1/2. Such a coin toss has one bit (reken maar eens na) of entropy since there are two possible outcomes that occur with equal probability, and learning the actual outcome contains one bit of information. In contrast, a coin toss using a coin that has two heads and no tails has zero entropy since the coin will always come up heads, and the outcome can be predicted perfectly.
[ Bericht 41% gewijzigd door #ANONIEM op 13-11-2017 20:17:33 ]
Toch wonderlijk dat ze dat zo op de Engelstalige wiki vermelden.quote:
.
"The world will note that the first atomic bomb was dropped on Hiroshima, a military base."
quote:
[..]
Toch wonderlijk dat ze dat zo op de Engelstalige wiki vermelden.
Heb nu een vak Stochastics 2 en kom er echt niet uit. Misschien iemand hier 
Een of andere leuke variant op Polya's Urn model:
We hebben een aantal boxen met label {1,..,n}. Zij X_0 het aantal rode ballen in box 0.
In iedere box zitten m ballen. De verdeling van aantal ballen in box i+1 komt zo tot stand: uit box i wordt m keer 1 bal getrokken (met terugleggen) en het resultaat wordt in box i+1 bijgeplaatst.
Dus:
In alle boxen zitten uiteindelijk m ballen. Dit spel gaat door tot Xn = 0 of Xn = m, in dat geval is de staart van de serie triviaal. Dus zij T_0, T_m gedefinieerd als de hitting time van de event X_n = 0 resp X_n = m, dus per definitie: T_0 = inf{ n s.t. X_n = 0}
Gevraagd:
Bereken Pr(T_0 < T_m | X_0 = k)
Het vak gaat nogal over martingale theory dus in die richting word ik ook geacht te zoeken.
Nu is E[ X_{n+1} | X_0, .. , X_n] = m* (X_n/m) = X_n, dus X = (X_n)n>0 zelf een martingale.
Maar hier loop ik een beetje vast. Ik heb het idee dat ik X als een random walk op (-k, m-k) kan zien, maar dat is het dan ook.
[ Bericht 0% gewijzigd door #ANONIEM op 10-12-2017 22:19:44 ]
Een of andere leuke variant op Polya's Urn model:
We hebben een aantal boxen met label {1,..,n}. Zij X_0 het aantal rode ballen in box 0.
In iedere box zitten m ballen. De verdeling van aantal ballen in box i+1 komt zo tot stand: uit box i wordt m keer 1 bal getrokken (met terugleggen) en het resultaat wordt in box i+1 bijgeplaatst.
Dus:
In alle boxen zitten uiteindelijk m ballen. Dit spel gaat door tot Xn = 0 of Xn = m, in dat geval is de staart van de serie triviaal. Dus zij T_0, T_m gedefinieerd als de hitting time van de event X_n = 0 resp X_n = m, dus per definitie: T_0 = inf{ n s.t. X_n = 0}
Gevraagd:
Bereken Pr(T_0 < T_m | X_0 = k)
Het vak gaat nogal over martingale theory dus in die richting word ik ook geacht te zoeken.
Nu is E[ X_{n+1} | X_0, .. , X_n] = m* (X_n/m) = X_n, dus X = (X_n)n>0 zelf een martingale.
Maar hier loop ik een beetje vast. Ik heb het idee dat ik X als een random walk op (-k, m-k) kan zien, maar dat is het dan ook.
[ Bericht 0% gewijzigd door #ANONIEM op 10-12-2017 22:19:44 ]
Is er een manier waarop je opdracht 22a, 24a en 24b kan berekenen? Wat ik doe nu is simpel invullen en raden totdat het klopt. Ik heb niet echt een berekening zeg maar.
Crack the following and we will get back to you: !1!llssod000;;
Ja, dat kan. Het zou me ook niet verbazen als er een paar pagina's eerder of later in dat boek uitgelegd staat hoe je dat moet doen.
"The world will note that the first atomic bomb was dropped on Hiroshima, a military base."
Dat staat er dus niet. Hoe moet ik 2 aparte variabelen dan berekenen?quote:
Ja, dat kan. Het zou me ook niet verbazen als er een paar pagina's eerder of later in dat boek uitgelegd staat hoe je dat moet doen.
Crack the following and we will get back to you: !1!llssod000;;
Bij 22a is gegeven dat er een lineair verband bestaat tussen C en t, namelijkquote:Op zaterdag 9 december 2017 17:38 schreef _--_ het volgende:
[ afbeelding ]
Is er een manier waarop je opdracht 22a, 24a en 24b kan berekenen? Wat ik doe nu is simpel invullen en raden totdat het klopt. Ik heb niet echt een berekening zeg maar.
waarbij a en b constantes zijn. Om nu a en b te bepalen maken we gebruik van de gegevens uit het tabelletje. We hebben twee onbekenden a en b, en dus hebben we ook twee vergelijkingen in a en b nodig om deze eenduidig te kunnen bepalen. Uit het tabelletje lezen we af dat C = 10 als t = 2. Invullen in de betrekking C = at + b geeft
Ook lezen we uit het tabelletje af dat C = 50 als t = 6. Deze waarden weer invullen in de betrekking C = at + b geeft
Nu hebben we twee (lineaire) vergelijkingen in de twee onbekenden a en b. Deze vergelijkingen vormen samen een stelsel, en dit stelsel kunnen we oplossen. We herschrijven om te beginnen de vergelijkingen even in een gestandaardiseerde vorm zodanig dat de onbekenden a en b in het linkerlid komen te staan en de coëfficiënten van de a vóór de a en dan hebben we
Om dit stelsel op te lossen is het het eenvoudigst om de leden van de eerste vergelijking af te trekken van de leden van de tweede vergelijking. Uit bovenstaande twee vergelijkingen volgt immers dat moet gelden
en dus
zodat
Nu we de waarde van a kennen, kunnen we deze invullen in één van onze twee vergelijkingen. Invullen van a = 10 in de eerste vergelijking 2a + b = 10 geeft
en zo vinden we
Nu de waarden a = 10 en b = −10 gevonden zijn kennen we ook de betrekking tussen C en t, namelijk
Je kunt dit uiteraard controleren door de waarden van t uit het tabelletje in te vullen, en deze betrekking levert dan inderdaad de bijbehorende waarden van C.
Los nu zelf opgave 24 op deze manier op. Je krijgt bij deze opgave weer een lineair stelsel van twee vergelijkingen, maar nu met p en q als onbekenden.
Heel erg bedankt. Ik zie nu in hoe het werkt.quote:
[..]
Bij 22a is gegeven dat er een lineair verband bestaat tussen C en t, namelijk
waarbij a en b constantes zijn. Om nu a en b te bepalen maken we gebruik van de gegevens uit het tabelletje. We hebben twee onbekenden a en b, en dus hebben we ook twee vergelijkingen in a en b nodig om deze eenduidig te kunnen bepalen. Uit het tabelletje lezen we af dat C = 10 als t = 2. Invullen in de betrekking C = at + b geeft
Ook lezen we uit het tabelletje af dat C = 50 als t = 6. Deze waarden weer invullen in de betrekking C = at + b geeft
Nu hebben we twee (lineaire) vergelijkingen in de twee onbekenden a en b. Deze vergelijkingen vormen samen een stelsel, en dit stelsel kunnen we oplossen. We herschrijven om te beginnen de vergelijkingen even in een gestandaardiseerde vorm zodanig dat de onbekenden a en b in het linkerlid komen te staan en de coëfficiënten van de a vóór de a en dan hebben we
Om dit stelsel op te lossen is het het eenvoudigst om de leden van de eerste vergelijking af te trekken van de leden van de tweede vergelijking. Uit bovenstaande twee vergelijkingen volgt immers dat moet gelden
en dus
zodat
Nu we de waarde van a kennen, kunnen we deze invullen in één van onze twee vergelijkingen. Invullen van a = 10 in de eerste vergelijking 2a + b = 10 geeft
en zo vinden we
Nu de waarden a = 10 en b = −10 gevonden zijn kennen we ook de betrekking tussen C en t, namelijk
Je kunt dit uiteraard controleren door de waarden van t uit het tabelletje in te vullen, en deze betrekking levert dan inderdaad de bijbehorende waarden van C.
Los nu zelf opgave 24 op deze manier op. Je krijgt bij deze opgave weer een lineair stelsel van twee vergelijkingen, maar nu met p en q als onbekenden.
Crack the following and we will get back to you: !1!llssod000;;
Inmiddels wel. Nogmaals X=(X_n) was een martingale op de versie van Polya's Urn op de pagina hiervoor. In box 0 k rode ballen uit m totaal, daar werden dan steeds ballen uit getrokken (met terugleggen) en het resultaat werd in de volgende box getrokken, recursief dus.quote:
Op Enfin, omdat tau = min{T_0, T_m} zelf ook weer een hitting time is volgt uit Optional Stopping Theorem dat E[X_tau] = E[X_0] = k.
De verwachting van X_tau is natuurlijk sommeren over een zeer beperkte state space (namelijk {0,m}), dus E[X_tau] = k = p*0 + (1-p)*m, waar p = Pr(T_0 < T_m | X_0 = k), de gevraagde waarde.
Dit oplossen levert Pr(T_0 < T_m | X_0 = k) = 1-k/m.
To whom it may concern. Het nagaan van bijv. de eisen voor OST is niet zo ingewikkeld.
[ Bericht 2% gewijzigd door #ANONIEM op 10-12-2017 22:49:40 ]
[tex]^{3}log(5-x) - ^{3}log(2x+4)=1
[/tex]
Hoe los je dit op? Ik heb er doormiddel van een rekenregel een breuk van gemaakt (alleen het stukje tussenhaakjes). Maar dan is die breuk niet te vereenvoudigen.
[/tex]
Hoe los je dit op? Ik heb er doormiddel van een rekenregel een breuk van gemaakt (alleen het stukje tussenhaakjes). Maar dan is die breuk niet te vereenvoudigen.
Crack the following and we will get back to you: !1!llssod000;;
3 log 3 is toch geen 3?quote:
Het linkerlid is te schrijven alsen het rechterlid is te schrijven als
. Daaruit volgt
.
Crack the following and we will get back to you: !1!llssod000;;
Even een tip: je moet op FOK geen enter gebruiken tussen je TeX tags, want de parser die FOK gebruikt kan daar niet mee overweg. Daarom werkte je TeX code hierboven niet.quote:
En je hebt inderdaad
maar dat is precies wat je nodig hebt, want je wil het rechterlid van je vergelijking herschrijven als een logaritme met grondtal 3.
Aha ik snap het al. Daarna pas je de regel g^log(x)=c is x=g^cquote:
[..]
Even een tip: je moet op FOK geen enter gebruiken tussen je TeX tags, want de parser die FOK gebruikt kan daar niet mee overweg. Daarom werkte je TeX code hierboven niet.
En je hebt inderdaad
maar dat is precies wat je nodig hebt, want je wil het rechterlid van je vergelijking herschrijven als een logaritme met grondtal 3.
Crack the following and we will get back to you: !1!llssod000;;
Dat is de definitie van een logaritme: de logaritme van een getal is de exponent waartoe je een vast getal (het grondtal) moet verheffen om dat getal te verkrijgen. De regel die je toepast bij het oplossen van je vergelijking is dat twee grootheden met dezelfde logaritme (met hetzelfde grondtal) aan elkaar gelijk zijn. Dus, uitquote:
[..]
Aha ik snap het al. Daarna pas je de regel toe dat g^log(x)=c equivalent is met x=g^c
volgt
Bedankt, Riparius.quote:
[..]
Dat is de definitie van een logaritme: de logaritme van een getal is de exponent waartoe je een vast getal (het grondtal) moet verheffen om dat getal te verkrijgen. De regel die je toepast bij het oplossen van je vergelijking is dat twee grootheden met dezelfde logaritme (met hetzelfde grondtal) aan elkaar gelijk zijn. Dus, uit
volgt
Crack the following and we will get back to you: !1!llssod000;;
Hoi, ik had een vraag over een praktisch probleem die ik moet onderzoeken. Het probleem is als volgt: https://imgur.com/Vfpl0Vm
De plattegrond: https://imgur.com/a/6lSls
Het gaat om het gebied wat omsloten wordt door:
aan de noordzijde: Wateringsevest en Nieuwe Plantage
aan de westzijde: Phoenixstraat en Westvest
aan de oostzijde: de Delftsche Vliet
aan de zuidzijde: de Delftsche Vliet en Kolk
Het is dus de bedoeling dat dit probleem met behulp van een wiskundig model moet worden opgelost. Ik vroeg me af of iemand me kan helpen welk wiskundige modellen geschikt zijn om dit probleem op te lossen. Alvast bedankt !
De plattegrond: https://imgur.com/a/6lSls
Het gaat om het gebied wat omsloten wordt door:
aan de noordzijde: Wateringsevest en Nieuwe Plantage
aan de westzijde: Phoenixstraat en Westvest
aan de oostzijde: de Delftsche Vliet
aan de zuidzijde: de Delftsche Vliet en Kolk
Het is dus de bedoeling dat dit probleem met behulp van een wiskundig model moet worden opgelost. Ik vroeg me af of iemand me kan helpen welk wiskundige modellen geschikt zijn om dit probleem op te lossen. Alvast bedankt !
Het is meer een optimalisatieprobleem wat je op kan lossen met linear programming. Zoek uit wat zo'n sneeuwruimer per uur zo'n beetje qua afstand haalt en maak een soort grid. Je geeft strafpunten voor overlappende routes en/of aantal sneeuwruimers en minimaliseert die penalty functions.quote:
Hoi, ik had een vraag over een praktisch probleem die ik moet onderzoeken. Het probleem is als volgt: https://imgur.com/Vfpl0Vm
De plattegrond: https://imgur.com/a/6lSls
Het gaat om het gebied wat omsloten wordt door:
aan de noordzijde: Wateringsevest en Nieuwe Plantage
aan de westzijde: Phoenixstraat en Westvest
aan de oostzijde: de Delftsche Vliet
aan de zuidzijde: de Delftsche Vliet en Kolk
Het is dus de bedoeling dat dit probleem met behulp van een wiskundig model moet worden opgelost. Ik vroeg me af of iemand me kan helpen welk wiskundige modellen geschikt zijn om dit probleem op te lossen. Alvast bedankt !
Kijk bijv eens naar AIMMS
[ Bericht 0% gewijzigd door #ANONIEM op 24-12-2017 05:16:33 ]
Weet iemand hoe ik dit plattegrond beschikbaar kan krijgen zonder straatnamen etc? :
https://imgur.com/a/AQWCL
En wat de standaardschaal is van zo'n plattegrond? In google maps komt 1,7 cm overeen met 200m. Maar ik weet niet of ik die schaal ook voor deze plattegrond kan hanteren.
https://imgur.com/a/AQWCL
En wat de standaardschaal is van zo'n plattegrond? In google maps komt 1,7 cm overeen met 200m. Maar ik weet niet of ik die schaal ook voor deze plattegrond kan hanteren.
Denk eens simpel. Tel het aantal kruispunten (en eindpunten) en definieer een graaf (V,E) met punten vi, i = 1,..,n met n = #kruispunten. Nu, [vi, vj] zit in E desda als het aanliggende kruispunten zijn. Het zal even tijd zijn om deze adjacency matrix te construeren, maar dan heb je ook wat. Ik neem aan dat je wilt dat je sneeuwruimers een aaneensluitende route krijgen, anders kun je gewoon een simpel algoritme gebruiken.quote:
Weet iemand hoe ik dit plattegrond beschikbaar kan krijgen zonder straatnamen etc? :
https://imgur.com/a/AQWCL
En wat de standaardschaal is van zo'n plattegrond? In google maps komt 1,7 cm overeen met 200m. Maar ik weet niet of ik die schaal ook voor deze plattegrond kan hanteren.
Vervolgens geef je iedere kant e in E een gewicht c(e) mee, ofwel de totale hoeveelheid werk (uitgedrukt in uren voor één sneeuwruimer), nogmaals, dat gaat even wat tijd kosten dus ik neem aan dat je hiervoor betaald wordt.
Daarna is het een kwestie van dat probleem linear programmeren, in bijvoorbeeld AIMMS.
Wat betreft je andere vraag, je kan beter direct met de hand uitzoeken hoe lang die straten zijn via Google maps, althans eentje want dan weet je ook direct de schaal.
https://www.iculture.nl/t(...)n-hemelsbreed-meten/
[ Bericht 1% gewijzigd door #ANONIEM op 12-01-2018 21:42:06 ]
Dat is inderdaad de methode die ik in gedachte had. Heb hier al een begin gemaakt:quote:
[..]
Denk eens simpel. Tel het aantal kruispunten (en eindpunten) en definieer een graaf (V,E) met punten vi, i = 1,..,n met n = #kruispunten. Nu, [vi, vj] zit in E desda als het aanliggende kruispunten zijn. Het zal even tijd zijn om deze adjacency matrix te construeren, maar dan heb je ook wat. Ik neem aan dat je wilt dat je sneeuwruimers een aaneensluitende route krijgen, anders kun je gewoon een simpel algoritme gebruiken.
Vervolgens geef je iedere kant e in E een gewicht c(e) mee, ofwel de totale hoeveelheid werk (uitgedrukt in uren voor één sneeuwruimer), nogmaals, dat gaat even wat tijd kosten dus ik neem aan dat je hiervoor betaald wordt.
Daarna is het een kwestie van dat probleem linear programmeren, in bijvoorbeeld AIMMS.
Wat betreft je andere vraag, je kan beter direct met de hand uitzoeken hoe lang die straten zijn via Google maps, althans eentje want dan weet je ook direct de schaal.
https://www.iculture.nl/t(...)n-hemelsbreed-meten/
https://imgur.com/a/Xnyqo
Wat ik in gedachte had was om tussen 2 punten de tijd te noteren die een sneeuwruimer nodig heeft om van A naar B te gaan. Vervolgens met een algoritme, bijvoorbeeld het kortste pad algoritme kijken waar de sneeuwruimer eindigt na 1 uur sneeuw ruimen. Het eindpunt van sneeuwruimer 1 is het startpunt van sneeuwruimer 2. Op die manier heel de plattegrond af gaan. Voor alle straten die zijn overgeslagen stuur ik aan het eind een extra sneeuwruimer die deze laatste straten wegruimt.
Dat kan. Maar ik denk dat een arbitrair beginpunt ook wel te doen is.quote:
[..]
Dat is inderdaad de methode die ik in gedachte had. Heb hier al een begin gemaakt:
https://imgur.com/a/Xnyqo
Wat ik in gedachte had was om tussen 2 punten de tijd te noteren die een sneeuwruimer nodig heeft om van A naar B te gaan. Vervolgens met een algoritme, bijvoorbeeld het kortste pad algoritme kijken waar de sneeuwruimer eindigt na 1 uur sneeuw ruimen. Het eindpunt van sneeuwruimer 1 is het startpunt van sneeuwruimer 2. Op die manier heel de plattegrond af gaan. Voor alle straten die zijn overgeslagen stuur ik aan het eind een extra sneeuwruimer die deze laatste straten wegruimt.
Maar het is uiteindelijk de bedoeling dat ik aangeef hoeveel sneeuwruimers er in totaal nodig zijn. Ik ben dan van plan om ergens bovenin inderdaad ook gewoon random te beginnen, en vanuit daar het algoritme toepassen. Of bedoel je dat niet?quote:
[..]
Dat kan. Maar ik denk dat een arbitrair beginpunt ook wel te doen is.
Nee. Sterker nog, er is iets fundamenteel mis met je idee.quote:
[..]
Maar het is uiteindelijk de bedoeling dat ik aangeef hoeveel sneeuwruimers er in totaal nodig zijn. Ik ben dan van plan om ergens bovenin inderdaad ook gewoon random te beginnen, en vanuit daar het algoritme toepassen. Of bedoel je dat niet?
Even een kleine kanttekening, ik ben niet zo thuis in algoritmen (andere tak van sport) of optimalisatie in het algemeen, maar dit algoritme is niet zo effectief. Je zou een beginpunt kunnen definiëren (logischerwijs op de aanrijroute van de sneeuwruimers) maar daarna kom je niet verder dan een shortest path boom, ofwel je weet de kortste paden van punt X naar Y voor alle X,Y in je netwerk, maar dat geeft je geen 'route' zeg maar. Je moet nog steeds een tweede punt 'kiezen'.
En hoe je dat dan weer doet ..
[ Bericht 3% gewijzigd door #ANONIEM op 12-01-2018 22:13:57 ]
Hmm.. hoezo zou het mij geen route opleveren? Ik heb één random beginpunt(en om te optimaliseren zou ik dit beginpunt telkens kunnen wijzigen) en vanuit dit beginpunt laat ik sneeuwruimer 1 vertrekken. Doormiddel van het kortste pad algoritme kan ik zien waar hij eindigt nadat hij een uur is bezig geweest. Dit eindpunt is het startpunt van sneeuwruimer 2. Die kiest zijn route op dezelfde wijze zoals sneeuwruimer 1 dat heeft gedaan. Op die manier heeft elk sneeuwruimer zijn eigen route die hij kan doorlopen.quote:
[..]
Nee. Sterker nog, er is iets fundamenteel mis met je idee.
Even een kleine kanttekening, ik ben niet zo thuis in algoritmen (andere tak van sport) of optimalisatie in het algemeen, maar dit algoritme is niet zo effectief. Je zou een beginpunt kunnen definiëren (logischerwijs op de aanrijroute van de sneeuwruimers) maar daarna kom je niet verder dan een shortest path boom, ofwel je weet de kortste paden van punt X naar Y voor alle X,Y in je netwerk, maar dat geeft je geen 'route' zeg maar. Je moet nog steeds een tweede punt 'kiezen'.
En hoe je dat dan weer doet ..
Jazeker kan dat, maar dan moet je nog steeds een eindpunt 'kiezen'. En daarnaast geeft het volgen van zo'n algoritme nog steeds de complicatie dat je dezelfde weg meerdere keren schoon gaat maken.quote:
[..]
Hmm.. hoezo zou het mij geen route opleveren? Ik heb één random beginpunt(en om te optimaliseren zou ik dit beginpunt telkens kunnen wijzigen) en vanuit dit beginpunt laat ik sneeuwruimer 1 vertrekken. Doormiddel van het kortste pad algoritme kan ik zien waar hij eindigt nadat hij een uur is bezig geweest. Dit eindpunt is het startpunt van sneeuwruimer 2. Die kiest zijn route op dezelfde wijze zoals sneeuwruimer 1 dat heeft gedaan. Op die manier heeft elk sneeuwruimer zijn eigen route die hij kan doorlopen.
Nog een tipje, je probleem is equivalent met het 'Route inspection problem' of Chinese Postbodeprobleem. Het goede nieuws is dat het probleem gelukkig niet NP hard is. Op de Engelstalige wiki kun je veel vinden over een mogelijk algoritme.
[ Bericht 2% gewijzigd door #ANONIEM op 12-01-2018 22:35:57 ]
Ah super, dan zal ik daar naar gaan kijken. Maar een eis die ik dan stel aan het kortste pad algoritme is dat wegen die al geruimd zijn, niet nog is doorlopen mogen worden tenzij niet anders kan.quote:
[..]
Jazeker kan dat, maar dan moet je nog steeds een eindpunt 'kiezen'. En daarnaast geeft het volgen van zo'n algoritme nog steeds de complicatie dat je dezelfde weg meerdere keren schoon gaat maken.
Nog een tipje, je probleem is equivalent met het 'Route inspection problem' of Chinese Postbodeprobleem. Het goede nieuws is dat het probleem gelukkig niet NP hard is. Op de Engelstalige wiki kun je veel vinden over een mogelijk algoritme.
[ Bericht 4% gewijzigd door ronaldoo12 op 12-01-2018 22:49:59 ]
Nogmaals, het is een algoritme om de minimale afstand tussen 2 arbitraire punten in een netwerk te bepalen inclusief route, niet een route die alle punten in het netwerk aandoet.quote:
[..]
Ah super, dan zal ik daar naar gaan kijken. Maar een eis die ik dan stel aan het kortste pad algoritme is dat wegen die al geruimd zijn, niet nog is doorlopen mogen worden tenzij niet anders kan.
En als je iets verzint om dat geheugen in te bouwen ga je wel een rekenkundig gedrocht krijgen en blijft van je argument dat je 'cover route' minimaal is weinig over.
Ik heb hier de graaf af van de plattegrond van Delft:
https://imgur.com/a/pihW7
Ik wil dus nu het Chinese postbode algoritme op toepassen maar ik loop een beetje vast met hoe ik het best mijn grafen kan opsplitsen. Ik neem aan dat de sneeuwruimers sneeuw ruimen met een snelheid van 3 km/u. De gemeente Delft wilt nu 3 dingen weten:
1. Het aantal sneeuwruimers dat nodig is om de binnenstad van Delft binnen een uur te ruimen.
2. Het startpunt van elk van deze sneeuwruimers.
3. De route die de sneeuwruimers moeten afleggen.
Ik denk dat al deze drie punten prima te bepalen zijn met het Chinese postbode algoritme. Ik heb zelf bedacht om grafen te maken met een gewicht van maximaal 2800m zodat er 200m speling overblijft voor de wegen die dubbel moeten worden bewandeld. Ik weet alleen niet of dit ideaal is.
https://imgur.com/a/pihW7
Ik wil dus nu het Chinese postbode algoritme op toepassen maar ik loop een beetje vast met hoe ik het best mijn grafen kan opsplitsen. Ik neem aan dat de sneeuwruimers sneeuw ruimen met een snelheid van 3 km/u. De gemeente Delft wilt nu 3 dingen weten:
1. Het aantal sneeuwruimers dat nodig is om de binnenstad van Delft binnen een uur te ruimen.
2. Het startpunt van elk van deze sneeuwruimers.
3. De route die de sneeuwruimers moeten afleggen.
Ik denk dat al deze drie punten prima te bepalen zijn met het Chinese postbode algoritme. Ik heb zelf bedacht om grafen te maken met een gewicht van maximaal 2800m zodat er 200m speling overblijft voor de wegen die dubbel moeten worden bewandeld. Ik weet alleen niet of dit ideaal is.
Dat hoef jij niet te doen, dat doet het algoritme voor je.quote:
Ik heb hier de graaf af van de plattegrond van Delft:
https://imgur.com/a/pihW7
Ik wil dus nu het Chinese postbode algoritme op toepassen maar ik loop een beetje vast met hoe ik het best mijn grafen kan opsplitsen.
Ik neem aan dat je kennis hebt van graaftheorie? Een beschrijving (van de simpele versie) van je probleem wordt hier gegeven: https://en.wikipedia.org/(...)#Undirected_solution
De versie die jij probeert op te lossen is het meer algemene k-Chinese postman probleem.
Waarom zou je meerdere grafen willen maken?quote:Ik neem aan dat de sneeuwruimers sneeuw ruimen met een snelheid van 3 km/u. De gemeente Delft wilt nu 3 dingen weten:
1. Het aantal sneeuwruimers dat nodig is om de binnenstad van Delft binnen een uur te ruimen.
2. Het startpunt van elk van deze sneeuwruimers.
3. De route die de sneeuwruimers moeten afleggen.
Ik denk dat al deze drie punten prima te bepalen zijn met het Chinese postbode algoritme. Ik heb zelf bedacht om grafen te maken met een gewicht van maximaal 2800m zodat er 200m speling overblijft voor de wegen die dubbel moeten worden bewandeld. Ik weet alleen niet of dit ideaal is.
WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.
Arguing on the Internet is like running in the Special Olympics.
Omdat ik voor ieder sneeuwruimer moet bepalen welk route hij moet bewandelen. Elk sneeuwruimer krijgt dus zijn eigen graaf toegewezen. Daarnaast mag de afstand die hij beloopt niet groter zijn dan 3000m omdat dat de afstand is die hij aflegt binnen 1 uur.quote:
[..]
Dat hoef jij niet te doen, dat doet het algoritme voor je.
Ik neem aan dat je kennis hebt van graaftheorie? Een beschrijving (van de simpele versie) van je probleem wordt hier gegeven: https://en.wikipedia.org/(...)#Undirected_solution
De versie die jij probeert op te lossen is het meer algemene k-Chinese postman probleem.
[..]
Waarom zou je meerdere grafen willen maken?
Je kunt dit probleem niet zomaar opsplitsen in kleinere deelproblemen aangezien de oplossing voor een sneeuwruimer afhankelijk is van de oplossingen voor andere sneeuwruimers.quote:
[..]
Omdat ik voor ieder sneeuwruimer moet bepalen welk route hij moet bewandelen. Elk sneeuwruimer krijgt dus zijn eigen graaf toegewezen. Daarnaast mag de afstand die hij beloopt niet groter zijn dan 3000m omdat dat de afstand is die hij aflegt binnen 1 uur.
Voor wat voor soort vak is deze opdracht? Heb je kennis van graaftheorie en van algoritmes?
WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.
Arguing on the Internet is like running in the Special Olympics.
Voor een wiskundig praktijkopdracht, een project is 't. Heb wel wat kennis van graaftheorie en algoritmes maar niet gigantisch veel. Ik heb nu bijna de afstand van elk zijde bepaald. Het is voor mij 't belangrijkste dat ik met een oplossing kom, dat dit niet de meest ideale is maakt me niet heel veel uit. Het Chinese postbode algoritme schijnt hier heel goed bij te passen. Ik wil er nu alleen nog voor zorgen dat ik dit algoritme zo goed mogelijk toepas.quote:
[..]
Je kunt dit probleem niet zomaar opsplitsen in kleinere deelproblemen aangezien de oplossing voor een sneeuwruimer afhankelijk is van de oplossingen voor andere sneeuwruimers.
Voor wat voor soort vak is deze opdracht? Heb je kennis van graaftheorie en van algoritmes?
Je hebtquote:
Hoe herleid ik 2(4-a)^2-1/3(4-a)^3-1/2a(4-a)^2?
Je kunt beginnen met te bedenken dat je drie termen hebt die een factor (4−a)² gemeen hebben, en deze gemene factor kun je buiten haakjes halen, dan krijgen we
Na uitwerken van ⅓(4−a) geeft dit
en dus
Nu kun je bedenken dat 2/3 = 4/6. Halen we dus bij (⅔ − ⅙a) een factor ⅙ buiten haakjes, dan hebben we (⅔ − ⅙a) = ⅙(4 − a) zodat we krijgen
oftewel
That's all.
[ Bericht 0% gewijzigd door Riparius op 18-01-2018 18:59:45 ]
Helder, bedankt. Toch weer twee handige dingen geleerd.quote:
[..]
Je hebt
Je kunt beginnen met te bedenken dat je drie termen hebt die een factor (4−a)² gemeen hebben, en deze gemene factor kun je buiten haakjes halen, dan krijgen we
Na uitwerken van ⅓(4−a) geeft dit
en dus
Nu kun je bedenken dat 2/3 = 4/6. Halen we dus bij (⅔ − ⅙a) een factor ⅙ buiten haakjes, dan hebben we (⅔ − ⅙a) = ⅙(4 − a) zodat we krijgen
oftewel
That's all.
Ook zoiets getuigt weer van weinig inzicht, want de oplossing van je probleem was nou net per definitie de optimale.quote:
[..]
Voor een wiskundig praktijkopdracht, een project is 't. Heb wel wat kennis van graaftheorie en algoritmes maar niet gigantisch veel. Ik heb nu bijna de afstand van elk zijde bepaald. Het is voor mij 't belangrijkste dat ik met een oplossing kom, dat dit niet de meest ideale is maakt me niet heel veel uit. Het Chinese postbode algoritme schijnt hier heel goed bij te passen. Ik wil er nu alleen nog voor zorgen dat ik dit algoritme zo goed mogelijk toepas.
Een oplossing van het Chinese Postbode Probleem is zo'n Euclidean Tour, dat zou inderdaad een route voor één sneeuwruimer geven die je dan vervolgens kunt splitten in afzonderlijke routes.
Klopt het is inmiddels gelukt(Y).quote:
[..]
Ook zoiets getuigt weer van weinig inzicht, want de oplossing van je probleem was nou net per definitie de optimale.
Een oplossing van het Chinese Postbode Probleem is zo'n Euclidean Tour, dat zou inderdaad een route voor één sneeuwruimer geven die je dan vervolgens kunt splitten in afzonderlijke routes.
Ik vroeg me af of iemand me kan helpen met dit algoritme vertalen naar eenvoudig Nederlandse taal:
https://imgur.com/a/oZUYt
De eerste stap: Geef A het label (-,0). Houdt dit in dat A verbonden is met (geen knopen, 0 takken) Op die manier?
https://imgur.com/a/oZUYt
De eerste stap: Geef A het label (-,0). Houdt dit in dat A verbonden is met (geen knopen, 0 takken) Op die manier?
Nee de afstand van A naar A is 0. Dijkstra's algoritme vindt het kortste pad volgens de volgende methode.quote:
Ik vroeg me af of iemand me kan helpen met dit algoritme vertalen naar eenvoudig Nederlandse taal:
https://imgur.com/a/oZUYt
De eerste stap: Geef A het label (-,0). Houdt dit in dat A verbonden is met (geen knopen, 0 takken) Op die manier?
Kijk naar alle buren u van A en bereken d(u,a)
Daarna naar alle buren x van u en bereken d(x,u) + d(a,u), stel dat x meerdere malen voorkomt. Als d(x,v) als eens berekend was voor een bepaalde v kies dan de minimum afstand van de twee (dus of de kortste route van A naar x via v of u gaat).
Bij een gelijke afstand wordt altijd uniform gekozen.
Dit gaat door tot Z gevonden is en Dijkstra's algoritme vindt, inderdaad, de kortste afstand van A naar Z.
Dit werkt in ieder geval voor een verbonden graaf. Als je dit programmeert zet je alle afstanden in het begin naar +∞, omdat null en een Real niet zo goed vergelijken.
[ Bericht 2% gewijzigd door #ANONIEM op 21-01-2018 13:20:54 ]
Ik heb ook vraag.
Even een paar opmerkingen, de dimensie van X is mogelijk oneindig, B(X) is de ruimte van alle begrensde, lineare operatoren op X, p(T) is de resolvent set en o(T) is het spectrum.
a,b,c,d heb ik eigenlijk zo goed als bewezen. Het bewijs van e) gaat in grote lijnen zo (volgens contradictie)
Dus D' = D intersection p(T) is niet leeg, maar ook niet gelijk aan D.
Kies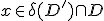
(dus in de boundary van D')
Het idee is nu om uit 3d te concluderen dat dit niet kan, dus het euvel is nu om het bestaan van een rij (xn) aan te tonen met limiet x en uit d) te halen dat x in D' zit. Dat is een consequentie van het volgende argument:
D' is open.
Dus dat betekent o.a. direct dat x niet in p(T) zit, waaruit direct de tegenspraak volgt, immers volgens d) betekent de rij in D' naar x dat x wel in p(T) zit.
Waarom is D' open? Volgens mij is p(T) gesloten in D, D zelf is open dus ik zie niet zo snel waarom die intersection ook open is.
[ Bericht 0% gewijzigd door #ANONIEM op 22-01-2018 19:10:15 ]
Even een paar opmerkingen, de dimensie van X is mogelijk oneindig, B(X) is de ruimte van alle begrensde, lineare operatoren op X, p(T) is de resolvent set en o(T) is het spectrum.
a,b,c,d heb ik eigenlijk zo goed als bewezen. Het bewijs van e) gaat in grote lijnen zo (volgens contradictie)
Dus D' = D intersection p(T) is niet leeg, maar ook niet gelijk aan D.
Kies
Het idee is nu om uit 3d te concluderen dat dit niet kan, dus het euvel is nu om het bestaan van een rij (xn) aan te tonen met limiet x en uit d) te halen dat x in D' zit. Dat is een consequentie van het volgende argument:
D' is open.
Dus dat betekent o.a. direct dat x niet in p(T) zit, waaruit direct de tegenspraak volgt, immers volgens d) betekent de rij in D' naar x dat x wel in p(T) zit.
Waarom is D' open? Volgens mij is p(T) gesloten in D, D zelf is open dus ik zie niet zo snel waarom die intersection ook open is.
[ Bericht 0% gewijzigd door #ANONIEM op 22-01-2018 19:10:15 ]
Ik zit zelf niet zo in de functionaalanalyse, maar ik zou denken dat je (c) kunt gebruiken daarvoor.
Ik heb even wat rondgevraagd en een van de eigenschappen van p(T) is dat het altijd een open subset van C is, en eindige intersecties van opens zijn weer open, dus topologisch gezien zit het dan wel juist. Ik zie alleen mijn eigen logische fout helaas nog niet zo in als ik zeg dat p(T) gesloten is in D.quote:
Ik zit zelf niet zo in de functionaalanalyse, maar ik zou denken dat je (c) kunt gebruiken daarvoor.
Analysevakken zijn over het algemeen de moeilijkste wiskundevakken (in ieder geval qua tentamen), aangezien mijn major in de richting van stochastiek is en ik een aantal keuzevakken uit andere tracks moet hebben kies ik meestal die analysevakken zoals Partial Differential Equations, Topologie, Functionaal Analyse, etc. Dat je qua curriculum in ieder geval nog kan zeggen dat je het jezelf niet te makkelijk hebt gemaakt.
Iedereen op de TU/e kan tegenwoordig een bachelor Applied Mathematics krijgen terwijl je bijna de helft van je vakken bij andere faculteiten mag volgen.
[ Bericht 3% gewijzigd door #ANONIEM op 22-01-2018 21:20:22 ]
Dat is ook niet fout. Het is zowel open als gesloten in D, dus de doorsnede is heel D of leeg.quote:
[..]
Ik heb even wat rondgevraagd en een van de eigenschappen van p(T) is dat het altijd een open subset van C is, en eindige intersecties van opens zijn weer open, dus topologisch gezien zit het dan wel juist. Ik zie alleen mijn eigen logische fout helaas nog niet zo in als ik zeg dat p(T) gesloten is in D.
Ja klopt, een andere manier om eigenlijk op te merken dat er een contradictie is. Had ik natuurlijk wel moeten weten dat die ook open is.quote:
[..]
Dat is ook niet fout. Het is zowel open als gesloten in D, dus de doorsnede is heel D of leeg.
Surjectiviteit impliceert dat λ - T een open mapping is.quote:
Maar is dat bij (c) niet een open conditie op λ?
Kun je daaruit concluderen dat p(T) open is?
Ik heb overigens een dictaat/boek waarin een lemma staat dat p(T) een open subset is, het bewijs laat zien dat er een power series representation van de resolvent bestaat die convergent is op een open subset van C rondom een punt in p(T).
Als je dat weet moet p(T) wel open zijn aangezien een topologie gesloten is onder willekeurige verenigingen
[ Bericht 8% gewijzigd door #ANONIEM op 22-01-2018 22:07:14 ]
Heeft iemand enig idee waar ik een zo simpel mogelijke bewijs kan vinden dat het argument dat Fermatgetallen alleen uit priemgetallen bestaat ontkracht? Behalve dat je het manueel invult.
Crack the following and we will get back to you: !1!llssod000;;
Of moet ik wat anders formuleren om te bewijzen omdat de post hierboven een beetje obvious is .
.
Crack the following and we will get back to you: !1!llssod000;;
Misschien dit: Bewijs of Fermatgetallen na n=5 geen priemgetallen meer bevat.
Crack the following and we will get back to you: !1!llssod000;;
Het bewijs dat niet alle Fermatgetallen priemgetallen zijn, lever je door er een te vinden die niet priem is. Dat is gebeurd, nummer 5.quote:
Heeft iemand enig idee waar ik een zo simpel mogelijke bewijs kan vinden dat het argument dat Fermatgetallen alleen uit priemgetallen bestaat ontkracht? Behalve dat je het manueel invult.
Het bewijs dat ze voor n>5 allemaal niet-priem zijn is volgens mij nooit geleverd. Maar leef je uit.
Opinion is the medium between knowledge and ignorance (Plato)
Ik heb eens een globaal kijkje gedaan op Wikipedia maar daar worden voor bewijzen allemaal tekens gebruikt die ik bij lange na niet heb gehad.quote:
[..]
Vergis ik mij, of is dat bewijs nooit geleverd?
https://en.wikipedia.org/wiki/Fermat_number CTRL + F "proof"
Ik weet wel dat dat vage tekentje netto betekent. Maar wat heeft dat hiermee te maken?
Crack the following and we will get back to you: !1!llssod000;;
Sorry het blijk dat ik me vergis. Bij fermatgetallen is n=4 het grootste priemgetal.
Crack the following and we will get back to you: !1!llssod000;;
Het grootste bekende priemgetal.quote:
Sorry het blijk dat ik me vergis. Bij fermatgetallen is n=4 het grootste priemgetal.
Opinion is the medium between knowledge and ignorance (Plato)
Om alles te verduidelijken: Ik heb getallentheorie op school en om m'n cijfer wat omhoog te halen is het de bedoeling om je eigen opdracht te maken wat betreft getallentheorie. Nu probeer ik wat informatie te werven.
Crack the following and we will get back to you: !1!llssod000;;
Nu even terug. Wat kan je bewijzen wat betreft Fermatgetallen. (en een beetje op mijn niveau 
)
)
Crack the following and we will get back to you: !1!llssod000;;
Dat ze niet allemaal priem zijn. P5 schijnt deelbaar te zijn door 641.quote:
Nu even terug. Wat kan je bewijzen wat betreft Fermatgetallen.
Opinion is the medium between knowledge and ignorance (Plato)
Dat is zeg maar te simpel.quote:
[..]
Dat ze niet allemaal priem zijn. P5 schijnt deelbaar te zijn door 641.
"vraag 1: Bewijs dat niet alle Fermatgetallen priem zijn"
Antwoord: N=5
Okay dat was kort door de bocht. Ik kan in de opdracht ook verwerken dat ze moeten bewijzen dat het ook echt geen priem is.
Crack the following and we will get back to you: !1!llssod000;;
Tja.
Als je bewijst dat ze voor n>5 allemaal niet-priem zijn dan denk ik net dat je je nog erg druk hoeft te maken over je cijfer.
Als je bewijst dat ze voor n>5 allemaal niet-priem zijn dan denk ik net dat je je nog erg druk hoeft te maken over je cijfer.
Opinion is the medium between knowledge and ignorance (Plato)
En dan misschien vraag 1c. "Bereken de grootst gemene deler van n=5 en n=6"quote:
Tja.
Als je bewijst dat ze voor n>5 allemaal niet-priem zijn dan denk ik net dat je je nog erg druk hoeft te maken over je cijfer.
Ohhh ik word enthousiast.
Crack the following and we will get back to you: !1!llssod000;;
Ik gok dat die 1 is.quote:
[..]
En dan misschien vraag 1c. "Bereken het grootst gemene deler van n=5 en n=6"
Opinion is the medium between knowledge and ignorance (Plato)
GGD(65537, 4294967297)
Welke wiskundige wilt een gokje wagen?
op internet gedaan en het is 1. Wat leuk dit.
Welke wiskundige wilt een gokje wagen?
op internet gedaan en het is 1. Wat leuk dit.
Crack the following and we will get back to you: !1!llssod000;;
Even een tip: zoek iets eenvoudigers. De voorbeelden die je geeft leveren niet het idee op dat je weet waar je over praat.quote:
GGD(65537, 4294967297)
Welke wiskundige wilt een gokje wagen?
65537 is priem, dus je hoeft voor het grote getal maar 1 deler uit te proberen.
Misschien wel leuk om te bewijzen dat Fn geen deler is van Fn+1.
Opinion is the medium between knowledge and ignorance (Plato)
Ben ik ook zojuist achter gekomen. Ik had het verkeerde getal gekopieerd. Nu wil ik n=5 en n=6 doen maar n=6 is zo'n groot getal dat dat gewoon niet gaat lukken. Dus dat gedoe met de GGD kan de prullenbak al in.quote:
[..]
Even een tip: zoek iets eenvoudigers. De voorbeelden die je geeft leveren niet het idee op dat je weet waar je over praat.
65537 is priem, dus je hoeft voor het grote getal maar 1 deler uit te proberen.
Misschien wel leuk om te bewijzen dat Fn geen deler is van Fn+1.
En bedankt voor je tip. Ik ga het bekijken
Crack the following and we will get back to you: !1!llssod000;;
Getaltheorie.quote:
Om alles te verduidelijken: Ik heb getallentheorie op school en om m'n cijfer wat omhoog te halen is het de bedoeling om je eigen opdracht te maken wat betreft getallentheorie. Nu probeer ik wat informatie te werven.
Omg, het is mijn computer toch gelukt.
Maar helaas geen interessant getal.
Crack the following and we will get back to you: !1!llssod000;;
Ik zal je vast een geheimpje verklappen: de GGD van ieder paar Fermatgetallen is 1. Bewijs daarvan zal wel een stap te ver zijn, dus probeer eerst maar eens te bewijzen wat ik suggereerde in #289.quote:
[ afbeelding ]
Omg, het is mijn computer toch gelukt.
Maar helaas geen interessant getal.
Opinion is the medium between knowledge and ignorance (Plato)
Met het algoritme van Euclides kun je heel snel ggd's van nog veel grotere getallen uitrekenenquote:
[ afbeelding ]
Omg, het is mijn computer toch gelukt.
Maar helaas geen interessant getal.
Als het getal groot is heb je met het algoritme van Euclides toch ellenlange berekeningen? Vooral met zulke getallen.quote:
[..]
Met het algoritme van Euclides kun je heel snel ggd's van nog veel grotere getallen uitrekenen
Crack the following and we will get back to you: !1!llssod000;;
Nee hoor, getallen van duizenden cijfers zijn voor de computer geen enkel probleem.quote:
[..]
Als het getal groot is heb je met het algoritme van Euclides toch ellenlange berekeningen? Vooral met zulke getallen.
Een inkoppertje.quote:1a. Vul in n=5 en zoek uit of het resulterende Fermatgetal een priemgetal is met behulp van het getal 4487 en het algoritme van Euclides.
[ Bericht 0% gewijzigd door _--_ op 07-03-2018 22:09:19 ]
Crack the following and we will get back to you: !1!llssod000;;
Bedoel je overigens niet F(n+1)? Want ik twijfel nu of je het nou hebt over het 1 bijtellen bij een Fermatgetal of bij de n.quote:
[..]
Even een tip: zoek iets eenvoudigers. De voorbeelden die je geeft leveren niet het idee op dat je weet waar je over praat.
65537 is priem, dus je hoeft voor het grote getal maar 1 deler uit te proberen.
Misschien wel leuk om te bewijzen dat Fn geen deler is van Fn+1.
bijvoorbeeld: 65537 + 1 of 4 + 1?
Crack the following and we will get back to you: !1!llssod000;;
Heb nu dit en ik zit nu een beetje in de knel. 
Heb nu dit en ik zit nu een beetje in de knel.
Crack the following and we will get back to you: !1!llssod000;;
Als het een deler is weet je in ieder geval dat die fractie een postief natuurlijk getal is. Zoek met deze informatie nu naar een contradictie.quote:
[ afbeelding ] Heb nu dit en ik zit nu een beetje in de knel.
