SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Hoeft toch ook niet, stel er is een functiequote:Op maandag 29 september 2014 13:15 schreef t4rt4rus het volgende:
[..]
Omdat er niet gezegd wordt dat a van P afhangt.
Als dat trouwens wel zo is, doe je de productregel ook nog eens fout ook.
En je begint met "en vervolgens de productregel", maar zegt niet dat je de afgeleide aan het nemen bent.
Leer nou eens duidelijk beschrijven wat je aan het doen bent.
y = z² g²
Dan zou je om de afgeleide te bepalen toch ook gewoon de productregel toepassen..
Dat hangt ervan af wat z en g zijn. In jouw voorbeeld is ea een constante en dus is de productregel niet nodig. Als er in plaats van ea het getal 37 had gestaan, wat zou je dan doen?quote:
[..]
Hoeft toch ook niet, stel er is een functie
y = z² g²
Dan zou je om de afgeleide te bepalen toch ook gewoon de productregel toepassen..
Opinion is the medium between knowledge and ignorance (Plato)
Zou ik maar net als Riparius maar gewoon de oplossing geven in plaats van vragen te stellen of je het snapt?
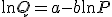
Express Q as a function of P, and show that dQ / dP = -bQ/P
We kunnen dit heel makkelijk oplossen door gebruik te maken van impliciet differentiëren.
Neem de afgeleide naar P aan beide kanten
![\frac{d}{dP}\ln{Q} = \frac{d}{dP}[a -b \ln{P}]](https://forum.fok.nl/lib/mimetex.cgi?%5Cfrac%7Bd%7D%7BdP%7D%5Cln%7BQ%7D%20%3D%20%5Cfrac%7Bd%7D%7BdP%7D%5Ba%20-b%20%5Cln%7BP%7D%5D)
,
dan krijgen we
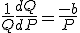
En daaruit volgt dan dat
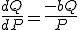
Echter moet dit dus expliciet opgelost worden
We hebben
,
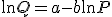dit is equivalent aan
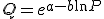
vereenvoudigen geeft
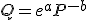
Nemen we hiervan de afgeleide naar P, dan krijgen we
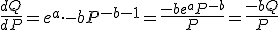Q.E.D.
[ Bericht 43% gewijzigd door t4rt4rus op 29-09-2014 13:46:01 ]
Express Q as a function of P, and show that dQ / dP = -bQ/P
We kunnen dit heel makkelijk oplossen door gebruik te maken van impliciet differentiëren.
Neem de afgeleide naar P aan beide kanten
dan krijgen we
En daaruit volgt dan dat
Echter moet dit dus expliciet opgelost worden
We hebben
dit is equivalent aan
vereenvoudigen geeft
Nemen we hiervan de afgeleide naar P, dan krijgen we
[ Bericht 43% gewijzigd door t4rt4rus op 29-09-2014 13:46:01 ]
Ow.. dan zou ik gewoon het volgende doen:quote:
[..]
Dat hangt ervan af wat z en g zijn. In jouw voorbeeld is ea een constante en dus is de productregel niet nodig. Als er in plaats van ea het getal 37 had gestaan, wat zou je dan doen?
-bea P -b-1
Want de constante telt niet mee.
[ Bericht 2% gewijzigd door RustCohle op 29-09-2014 13:28:56 ]
Wat is de variabele in je uitdrukking waarnaar je differentieert? a, b, e of p?quote:
[..]
Ow.. dan zou ik gewoon het volgende doen:
-bea P -b-1
Want de constante telt niet mee.
Opinion is the medium between knowledge and ignorance (Plato)
P denk ik.quote:
[..]
Wat is de variabele in je uitdrukking waarnaar je differentieert? a, b, e of p?
Inderdaad, want de rest zijn allemaal constanten. Maar in je post differentieer je naar b.quote:
Nu nog eens proberen, maar dan naar p. En let op: het is een exponentiële functie.Oeps.
Opinion is the medium between knowledge and ignorance (Plato)
Volgens mij deed hij het nu goed.quote:
[..]
Inderdaad, want de rest zijn allemaal constanten. Maar in je post differentieer je naar b.
Nu nog eens proberen, maar dan naar p. En let op: het is een exponentiële functie.
Differentieren naar P.
-bea P -b-1quote:
[..]
Inderdaad, want de rest zijn allemaal constanten. Maar in je post differentieer je naar b.
Nu nog eens proberen, maar dan naar p. En let op: het is een exponentiële functie.
Ahumquote:
[..]
Volgens mij deed hij het nu goed.
Differentieren naar P.
Zelf even slecht gelezen. Sorry...
Klopt inderdaad.quote:
Opinion is the medium between knowledge and ignorance (Plato)
Hoe zou ik nu kunnen beweren dat dQ / dP = -bQ / Pquote:
[..]
Ahum
Zelf even slecht gelezen. Sorry...
[..]
Klopt inderdaad.
Want k heb nu al in principe dQ / dP uitgedrukt toch?
Zie hierquote:
[..]
Hoe zou ik nu kunnen beweren dat dQ / dP = -bQ / P
Want k heb nu al in principe dQ / dP uitgedrukt toch?
Opinion is the medium between knowledge and ignorance (Plato)
Deze overgang is mij niet geheel duidelijk? Wat heb je gedaan om daar Q te krijgen en ea en P-b weg te krijgen?quote:
Zou ik maar net als Riparius maar gewoon de oplossing geven in plaats van vragen te stellen of je het snapt?
Express Q as a function of P, and show that dQ / dP = -bQ/P
We kunnen dit heel makkelijk oplossen door gebruik te maken van impliciet differentiëren.
Neem de afgeleide naar P aan beide kanten
dan krijgen we
En daaruit volgt dan dat
Echter moet dit dus expliciet opgelost worden
We hebben
dit is equivalent aan
Dit vereenvoudigen geeft
Nemen we hiervan de afgeleide naar P, dan krijgen we[/b] Q.E.D.
quote:
[..]
Deze overgang is mij niet geheel duidelijk? Wat heb je gedaan om daar Q te krijgen en ea en P-b weg te krijgen?
Kijk naar de regel er boven...quote:
[..]
Ja dat heb ik begrepen, maar ik bedoel dus van die één na laatste naar -bQ/P
Ik voel me nu wel heel dom..quote:
[..]
*
Nemen we hiervan de afgeleide naar PQ.E.D.
-edit-, maakt dit het duidelijk?
Dank
Ik ga maar even een kwartiertje pauzeren. Ik ben al sinds 07.00 bezig met wiskunde.
quote:
[..]
''According to Herman Wold, the demand Q for butter in Stockholm during the period 1925-1937 was related to the price by P by the equation Q * p1/2 = 38. Find dQ/dP by implicit differentiation. Check the answer by using a different method to compute the derivative. ''
Ik kwam uit op:quote:
[..]
Geen idee wat je in je vorige post aan het doen was.
Maar je moet dusimpliciet differentiëren.
De eerste stap is dan
Kan jij nu verder?
Q' * P 1/2 + Q1/2P -1/2
Maar daar blijft het dan bij, want ik heb geen idee...
Uitquote:
Als
(-1/b) * ea/b Q -1 -1/b
Hoe kan ik het verder herschrijven tot :
(-1/b)P / Q?
kun je halen dat
Jouw uitdrukking was
Klaar.
Opinion is the medium between knowledge and ignorance (Plato)
Hoe kan ik x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)] herschrijven om zodoende een getallenlijn te kunnen maken ?
Ik kan een getallenlijn maken zonder x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)] te herschrijven. Wat is de opdracht?quote:
x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)]
Opinion is the medium between knowledge and ignorance (Plato)
Nja ik moet het kunnen he.quote:
[..]
Ik kan een getallenlijn maken zonder x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)] te herschrijven. Wat is de opdracht?
Ik moet weten wanneer de functie f increast en wanneer die decreast.. En in mijn vorige post staat dus de afgeleide (die ik heb bepaald) van de originele functie..
Ik zou graag willen weten hoe ik het kan herschrijven of hoe ik een getallenlijn kan maken van zo'n lange afgeleide althans ingewikkelde. Als ik er een breuk van maak is het voor mij makkelijk om een getallenlijn te maken.
Ik zie de overgang niet?quote:
[..]
Uit
kun je halen dat
Jouw uitdrukking was
[tex]= -(\frac{1}{b}) e^{a/b} Q^{-1/b}Q^{-1}[/tex]
[tex]= -(\frac{1}{b}) P Q^{-1}[/tex]
Klaar.
Gebruik deze:quote:
Deze uitdrukking voor P staat letterlijk in de één na laatste regel.
Opinion is the medium between knowledge and ignorance (Plato)
quote:
[..]
Gebruik deze:
Deze uitdrukking voor P staat letterlijk in de één na laatste regel.
x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)]
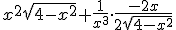
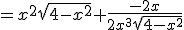
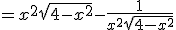
Waar heeft de uitdrukking z - 1/z nulpunten?
Waar heeft de uitdrukking z - 1/z nulpunten?
Opinion is the medium between knowledge and ignorance (Plato)
Het was 1/3x³ he..quote:
x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)]
Waar heeft de uitdrukking z - 1/z nulpunten?
Ik heb geen idee.
Dat staat niet in je post. En mijn glazen bol is al een tijdje stuk.quote:
Mocht je je afvragen waarom ik die vraag stel, ik vervang x^2worteldinges even door 'z', en dan staat er z-1/z. Je zoekt nulpunten, en dus is het wel handig om te weten waar z-1/z nulpunten heeft. Kun je daarna je x^2worteldinges er weer inplakken.quote:Ik heb geen idee.
Opinion is the medium between knowledge and ignorance (Plato)
Ik zou van die z - 1/zquote:
[..]
Dat staat niet in je post. En mijn glazen bol is al een tijdje stuk.
[..]
Mocht je je afvragen waarom ik die vraag stel, ik vervang x^2worteldinges even door 'z', en dan staat er z-1/z. Je zoekt nulpunten, en dus is het wel handig om te weten waar z-1/z nulpunten heeft. Kun je daarna je x^2worteldinges er weer inplakken.
Die heb ik even niet gezien. Edit 'm maar snel weg.quote:
[..]
Ik zou van die z - 1/z
*Oeps*
Opinion is the medium between knowledge and ignorance (Plato)
Klote wiskunde.. Heb geen ideequote:
[..]
Die heb ik even niet gezien. Edit 'm maar snel weg.
Ik zoek waarde(n) van z waarvoor z - 1/z = 0, oftewel z = 1/z. Eigenlijk vind ik dat je meteen moet zien dat alleen 1 en -1 hun eigen omgekeerde zijn, maar zo niet dan gebruik je de technieken die je hiervoor kent.quote:
[..]
Klote wiskunde.. Heb geen idee
Een vergelijking met breuken maak je in vrijwel alle gevallen overzichtelijker door links en rechts te vermenigvuldigen met die noemer. Alleen even opletten dat je niet per ongeluk met 0 vermenigvuldigt en er daardoor allerlei ongewenste oplossingen bij krijgt, maar dat is hier niet het geval.
Dus:
z - 1/z = 0 <=> z2-1 = 0 <=> z2 = 1 <=> z = 1 of z = -1.
Dus je afgeleide is gelijk aan 0 als x2√(4-x2) = ± 1
Opinion is the medium between knowledge and ignorance (Plato)
hmmm als ik het zo bekijk heel makkelijk, maar in het antwoordenboek is het niet genoeg om te berekenen wanneer de afgeleide 0 is maar wanneer die stijgt en daalt en dat is:quote:
[..]
Ik zoek waarde(n) van z waarvoor z - 1/z = 0, oftewel z = 1/z. Eigenlijk vind ik dat je meteen moet zien dat alleen 1 en -1 hun eigen omgekeerde zijn, maar zo niet dan gebruik je de technieken die je hiervoor kent.
Een vergelijking met breuken maak je in vrijwel alle gevallen overzichtelijker door links en rechts te vermenigvuldigen met die noemer. Alleen even opletten dat je niet per ongeluk met 0 vermenigvuldigt en er daardoor allerlei ongewenste oplossingen bij krijgt, maar dat is hier niet het geval.
Dus:
z - 1/z = 0 <=> z2-1 = 0 <=> z2 = 1 <=> z = 1 of z = -1.
Dus je afgeleide is gelijk aan 0 als x2√(4-x2) = ± 1
Stijging: [-W3, W3]
Daling: [-2, -W3]
Het is je wellicht opgevallen dat ik vrijwel nooit volledige antwoorden geef, maar de vraagstellers een stukje op weg help. Dat in een poging om de user na te laten denken over de achtereenvolgende stappen om een probleem op te lossen, en een handje te helpen als iemand vastloopt bij een bepaalde stap.quote:Op maandag 29 september 2014 15:25 schreef BroodjeKebab het volgende:
[..]
hmmm als ik het zo bekijk heel makkelijk, maar in het antwoordenboek is het niet genoeg om te berekenen wanneer de afgeleide 0 is maar wanneer die stijgt en daalt en dat is:
Stijging: [-W3, W3]
Daling: [-2, -W3]
Het denkpatroon zou er in dit voorbeeld als volgt uit kunnen zien:
- Ik heb een of andere functie f.
- Ik wil weten wanneer die stijgt en daalt.
- Daar kan een afgeleide functie mij wat over vertellen
- Dus ik differentieer mijn functie f en vind dus f'
- Als f'>0 dan stijgt f, als f'<0 dan daalt f. Dus eerst wil ik weten wanneer f'=0
- Dus ik stel mijn f' gelijk aan 0 en vind wat oplossingen
- Die oplossingen verdelen het domein van f in een paar stukken.
- Van ieder stuk weet ik dat f op dat hele stuk stijgend - of op dat hele stuk dalend is. Was het namelijk niet zo, dan zou f' in dat stuk nog ergens 0 moeten worden en dat was ie niet.
- Dus ik zoek van ieder interval uit of f daar stijgt of daalt
- Dat kan ik doen door f te visualiseren, of door bepaalde waarden uit het gevraagde stuk in f' in te vullen en te kijken of dat groter of kleiner dan 0 is.
- Nu heb ik de gezochte info bij elkaar en teken ik mijn getallenlijn.
Ik schrijft het nu bewust overdreven uitgebreid op. En toch is het heel belangrijk om, vóórdat je überhaupt begint te pennen en te rekenen, eerst zo'n stappenplan te maken. Dan weet je waar je moet beginnen en waar je moet eindigen - en of je de gestelde vraag wel beantwoordt.
Bijkomend voordeel in dit topic is dat het dan iets makkelijker te specificeren is bij welke stap je nu vastloopt.
Opinion is the medium between knowledge and ignorance (Plato)
Daar ben je docente voor toch.quote:
[..]
Het is je wellicht opgevallen dat ik vrijwel nooit volledige antwoorden geef, maar de vraagstellers een stukje op weg help. Dat in een poging om de user na te laten denken over de achtereenvolgende stappen om een probleem op te lossen, en een handje te helpen als iemand vastloopt bij een bepaalde stap.
Het denkpatroon zou er in dit voorbeeld als volgt uit kunnen zien:
- Ik heb een of andere functie f.
- Ik wil weten wanneer die stijgt en daalt.
- Daar kan een afgeleide functie mij wat over vertellen
- Dus ik differentieer mijn functie f en vind dus f'
- Als f'>0 dan stijgt f, als f'<0 dan daalt f. Dus eerst wil ik weten wanneer f'=0
- Dus ik stel mijn f' gelijk aan 0 en vind wat oplossingen
- Die oplossingen verdelen het domein van f in een paar stukken.
- Van ieder stuk weet ik dat f op dat hele stuk stijgend - of op dat hele stuk dalend is. Was het namelijk niet zo, dan zou f' in dat stuk nog ergens 0 moeten worden en dat was ie niet.
- Dus ik zoek van ieder interval uit of f daar stijgt of daalt
- Dat kan ik doen door f te visualiseren, of door bepaalde waarden uit het gevraagde stuk in f' in te vullen en te kijken of dat groter of kleiner dan 0 is.
- Nu heb ik de gezochte info bij elkaar en teken ik mijn getallenlijn.
Ik schrijft het nu bewust overdreven uitgebreid op. En toch is het heel belangrijk om, vóórdat je überhaupt begint te pennen en te rekenen, eerst zo'n stappenplan te maken. Dan weet je waar je moet beginnen en waar je moet eindigen - en of je de gestelde vraag wel beantwoordt.
Bijkomend voordeel in dit topic is dat het dan iets makkelijker te specificeren is bij welke stap je nu vastloopt.
Je methode is goed hoor door steeds een tip te geven ipv het volledige antwoord.
Die stappenplan heb ik idd ook in mijn hoofd. Ik weet tot dusverre dat op zowel x = -1 als op x = 1 een nulpunt wordt bereikt ofwel een maximum/minimum. Voor en na -1/+1 is er sprake van of een daling of een stijging.. maar dan loop ik dus vast en kan ik uren staren zonder dat het licht brand..quote:
[..]
Het is je wellicht opgevallen dat ik vrijwel nooit volledige antwoorden geef, maar de vraagstellers een stukje op weg help. Dat in een poging om de user na te laten denken over de achtereenvolgende stappen om een probleem op te lossen, en een handje te helpen als iemand vastloopt bij een bepaalde stap.
Het denkpatroon zou er in dit voorbeeld als volgt uit kunnen zien:
- Ik heb een of andere functie f.
- Ik wil weten wanneer die stijgt en daalt.
- Daar kan een afgeleide functie mij wat over vertellen
- Dus ik differentieer mijn functie f en vind dus f'
- Als f'>0 dan stijgt f, als f'<0 dan daalt f. Dus eerst wil ik weten wanneer f'=0
- Dus ik stel mijn f' gelijk aan 0 en vind wat oplossingen
- Die oplossingen verdelen het domein van f in een paar stukken.
- Van ieder stuk weet ik dat f op dat hele stuk stijgend - of op dat hele stuk dalend is. Was het namelijk niet zo, dan zou f' in dat stuk nog ergens 0 moeten worden en dat was ie niet.
- Dus ik zoek van ieder interval uit of f daar stijgt of daalt
- Dat kan ik doen door f te visualiseren, of door bepaalde waarden uit het gevraagde stuk in f' in te vullen en te kijken of dat groter of kleiner dan 0 is.
- Nu heb ik de gezochte info bij elkaar en teken ik mijn getallenlijn.
Ik schrijft het nu bewust overdreven uitgebreid op. En toch is het heel belangrijk om, vóórdat je überhaupt begint te pennen en te rekenen, eerst zo'n stappenplan te maken. Dan weet je waar je moet beginnen en waar je moet eindigen - en of je de gestelde vraag wel beantwoordt.
Bijkomend voordeel in dit topic is dat het dan iets makkelijker te specificeren is bij welke stap je nu vastloopt.
Dit is niet waar. Waar kwam mijn z ook weer vandaan?quote:
Ik weet tot dusverre dat op zowel x = -1 als op x = 1 een nulpunt wordt bereikt ofwel een maximum/minimum.
Opinion is the medium between knowledge and ignorance (Plato)
x2√(4-x2)quote:
[..]
Dit is niet waar. Waar kwam mijn z ook weer vandaan?
Maar het was 1/3x³ dus moet het geen
3x2√(4-x2)
zijn
Dan zou het wordenquote:
[..]
x2√(4-x2)
Maar het was 1/3x³ dus moet het geen
3x2√(4-x2)
zijn
en vraag je je dus af wanneer z-1/(3z)=0. Dat is als z2=1/3, oftewel z=±√(1/3).
Je afgeleide functie heeft dus nulpunten als
x2√(4-x2)=√(1/3) of als
x2√(4-x2)=-√(1/3)
Opinion is the medium between knowledge and ignorance (Plato)
We gaan beide ergens de fout in want we moeten uitkomen op -W3 of W3 (?)quote:
[..]
Dan zou het worden
en vraag je je dus af wanneer z-1/(3z)=0. Dat is als z2=1/3, oftewel z=±√(1/3).
Je afgeleide functie heeft dus nulpunten als
x2√(4-x2)=√(1/3) of als
x2√(4-x2)=-√(1/3)
Ik denk dat het bepalen van je afgeleide niet klopt, dus eigenlijk al in je eerste post over dit vraagstuk. Want vanquote:
[..]
We gaan beide ergens de fout in want we moeten uitkomen op -W3 of W3 (?)
x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)]
is √3 (of -√3) helemaal geen nulpunt.
Van x²√(4-x²) + 1/3x³ * -2x/[2√(4-x²)] trouwens ook niet. Weet je zeker dat het niet moet zijn
x²√(4-x²) + 3/x³ * -2x/[2√(4-x²)] ?
Opinion is the medium between knowledge and ignorance (Plato)
In het antwoordenboek staat immers:quote:
[..]
Ik denk dat het bepalen van je afgeleide niet klopt, dus eigenlijk al in je eerste post over dit vraagstuk. Want van
x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)]
is √3 (of -√3) helemaal geen nulpunt.
[-W3, W3] Increase
[-2, -W3] decrease
Dus moeten √3 en -√3 nulpunten zijn van de afgeleide, en -2 is de grens van het domein. Maar van de afgeleide die jij hier neerzet, zijn √3 en -√3 geen nulpunten dus je afgeleide klopt niet.quote:
[..]
In het antwoordenboek staat immers:
[-W3, W3] Increase
[-2, -W3] decrease
Opinion is the medium between knowledge and ignorance (Plato)
Het antwoordenboek zegt:quote:
[..]
Ik denk dat het bepalen van je afgeleide niet klopt, dus eigenlijk al in je eerste post over dit vraagstuk. Want van
x²√(4-x²) + 1/x³ * -2x/[2√(4-x²)]
is √3 (of -√3) helemaal geen nulpunt.
Van x²√(4-x²) + 1/3x³ * -2x/[2√(4-x²)] trouwens ook niet. Weet je zeker dat het niet moet zijn
x²√(4-x²) + 3/x³ * -2x/[2√(4-x²)] ?
f'(x) =
x²√(4-x²) + 1/3x² * -2x / 2√(4-x²)
ook wel.. ;
4x² (3 - x²) / 3√(4-x²)
Dus je afgeleide klopte niet.quote:
[..]
Het antwoordenboek zegt:
f'(x) =
x²√(4-x²) + 1/3x² * -2x / 2√(4-x²)
ook wel.. ;
4x² (3 - x²) / 3√(4-x²)
Opinion is the medium between knowledge and ignorance (Plato)
Owww!quote:
[..]
Dus je afgeleide klopte niet.
Ben ik nou gek of niet? Ik denk zelf toch echt steeds dat het moet resulteren naar b * 1/x en dus b/x ipv b.. als afgeleide..
Het gaat in jouw plaatje niet over een afgeleide. Er staat een gelijkheid waar ze links en rechts de natuurlijke logaritme op loslaten.quote:
[ afbeelding ]
Ben ik nou gek of niet? Ik denk zelf toch echt steeds dat het moet resulteren naar b * 1/x en dus b/x ipv b.. als afgeleide..
Opinion is the medium between knowledge and ignorance (Plato)
Oeps.. Plaatje uploaden ging mis..quote:
[..]
Het gaat in jouw plaatje niet over een afgeleide. Er staat een gelijkheid waar ze links en rechts de natuurlijke logaritme op loslaten.
Beter dan de in rood geschreven tekst die ernaast staat kan ik het eigenlijk ook niet uitleggen.
Substitueer ln x = u en differentieer daarna naar u.
Substitueer ln x = u en differentieer daarna naar u.
Opinion is the medium between knowledge and ignorance (Plato)
Dat heb ik begrepen. Vind het alleen frappant.. Aangezien de afgeleide van een ln functie altijd 1 / .. is.. Dat ln A weggaat begrijp ik sowieso (omdat het een constante is.)quote:
Beter dan de in rood geschreven tekst die ernaast staat kan ik het eigenlijk ook niet uitleggen.
Substitueer ln x = u en differentieer daarna naar u.
Na de substitutie staat er geen ln-functie meer.quote:
[..]
Dat heb ik begrepen. Vind het alleen frappant.. Aangezien de afgeleide van een ln functie altijd 1 / .. is..
Opinion is the medium between knowledge and ignorance (Plato)
Ja maar stel je hebtquote:
[..]
Na de substitutie staat er geen ln-functie meer.
2x + ln x
Dan is de afgeleide toch
2 + 1/x
je kan toch niet zomaar zeggen dat het 2 is omdat ln x ookwel u kan zijn en dan dy/du toepassen waardoor je dus 2 hebt..
Het is bekend dat de formule: p / D(p) * dD(p)/dp gebruikt moet worden om de elasticiteit te berekenen.
Stel nou dat ik dit wil berekenen voor de functie:
xp eax
Dan pas ik p / D(p) * dD(p)/dp toe, alleen in dit geval:
x / D(x) * dD(x)/dx , dus :
[ x/xp eax ] * (pxp-1 eax + xp aeax )
x * (pxp-1 eax + xp aeax ) / xp eax
Hoe doe ik het wegstrepen hier?
Ik zelf streepte de eax en xp weg en dit leverde mij het volgende op:
x * pxp-1
Stel nou dat ik dit wil berekenen voor de functie:
xp eax
Dan pas ik p / D(p) * dD(p)/dp toe, alleen in dit geval:
x / D(x) * dD(x)/dx , dus :
[ x/xp eax ] * (pxp-1 eax + xp aeax )
x * (pxp-1 eax + xp aeax ) / xp eax
Hoe doe ik het wegstrepen hier?
Ik zelf streepte de eax en xp weg en dit leverde mij het volgende op:
x * pxp-1
Je leidt hier af naar ln x, niet naar x.quote:
[..]
Dat heb ik begrepen. Vind het alleen frappant.. Aangezien de afgeleide van een ln functie altijd 1 / .. is.. Dat ln A weggaat begrijp ik sowieso (omdat het een constante is.)
Het is voor je begrip van de techniek van belang dat je weet wat je precies doet. 'Wegstrepen' is natuurlijk geen toegestane handeling - wat doe je nu precies in je poging om de uitdrukking te herschrijven? Wat gebeurt er met die eax?quote:
[ Bericht 0% gewijzigd door Janneke141 op 29-09-2014 19:47:06 ]
Opinion is the medium between knowledge and ignorance (Plato)
Die kunnen weg, omdat er in de twee termen (in de teller) eax staat en in de noemer.quote:
[..]
Het is voor je begrip van de techniek van belang wat je weet wat je precies doet. 'Wegstrepen' is natuurlijk geen toegestane handeling - wat doe je nu precies in je poging om de uitdrukking te herschrijven? Wat gebeurt er met die eax?
Dat klopt. Dus wat doe je ermee?quote:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Opinion is the medium between knowledge and ignorance (Plato)
quote:
[..]
Dat klopt. Dus wat doe je ermee?Die kun je delen door e^axSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
OK, nu we weten wat we eigenlijk aan het doen zijn (volgende keer gewoon in je eerste post netjes opschrijven!) gaan we kijken hoe dat dan werkt:quote:
x * (pxp-1 eax + xp aeax ) / xp eax
= pxp eax + xp+1 aeax ) / xp eax
= xp eax(p + ax) / xp eax
Nu in teller en noemer delen door xp eax, en er blijft (p+ax) over.
Opinion is the medium between knowledge and ignorance (Plato)
Wat doe je in het tweede waardoor die x * weggaat en waarom verdwijnt die p-1 en komt er een +1 te staan?quote:
[..]
OK, nu we weten wat we eigenlijk aan het doen zijn (volgende keer gewoon in je eerste post netjes opschrijven!) gaan we kijken hoe dat dan werkt:
x * (pxp-1 eax + xp aeax ) / xp eax
= pxp eax + xp+1 aeax ) / xp eax
= xp eax(p + ax) / xp eax
Nu in teller en noemer delen door xp eax, en er blijft (p+ax) over.
Op het einde; zie ik het ook niet..? Hoe moet ik die vermenigvuldiging zien?
(.....) * (....) of alleen die e^ax * (p + ax) .. en dan die x^p op het einde?
Ik kan het niet 'zien' in één keer... Ik zie wel de deling op het eind door x^p en e^ax.
Ooit van vermenigvuldigingen gehoord?quote:
[..]
Wat doe je in het tweede waardoor die x * weggaat en waarom verdwijnt die p-1 en komt er een +1 te staan?
Jaquote:
[..]
Ooit van vermenigvuldigingen gehoord?
Dat hoeft ook niet, daarom schrijf ik tussenstappen op. Wen jezelf ook aan om dat te doen en om vooral niet teveel in één stap te willen doen.quote:Ik kan het niet 'zien' in één keer...
De haakjes uitwerken; er staat iets van de vorm a(b+c) en dat schrijf ik als ab+ac. Bedenk daarbij dat x*xp-1 = xpquote:
[..]
Wat doe je in het tweede waardoor die x * weggaat en waarom verdwijnt die p-1 en komt er een +1 te staan?
Als het uit zou maken had ik het wel anders opgeschreven.quote:Op het einde; zie ik het ook niet..? Hoe moet ik die vermenigvuldiging zien?
(.....) * (....) of alleen die e^ax * (p + ax) .. en dan die x^p op het einde?
Er staat iets van de vorm a*b*(c+d). Dat kun je maar op één manier lezen.
Opinion is the medium between knowledge and ignorance (Plato)
Het feit dat je je erover verbaast bewijst nu juist dat je het niet begrijpt.quote:
[..]
Dat heb ik begrepen. Vind het alleen frappant..
Opmerkingen als deze laten zien dat je alleen maar probeert 'regeltjes' toe te passen zonder echt te begrijpen wat het allemaal voorstelt. OllieWilliams had hier een correcte opmerking die je waarschijnlijk niet hebt begrepen.quote:Aangezien de afgeleide van een ln functie altijd 1 / .. is..
Je hebtquote:Dat ln A weggaat begrijp ik sowieso (omdat het een constante is.)
Nu stellen we
en ook
Dan is
en dus
Nu zetten we ln y weer terug in de plaats van z en zetten we ln x weer terug in de plaats van u, en zie, we hebben
Je moet echt deze post van mij eens goed bestuderen.
Ik heb even de Leibniz notatie posts van Riparius gelezen, ik heb het wel begrepen, maar ben toch lichtelijk verward geworden.. en dan is het om hoe de regel werkt, want praktisch gezien begrijp ik dat wel als ik letters en getallen zie, maar in notatievorm ben ik nog lichtelijk verward..
Stel je hebt
d F(x) / dx ofwel F'(x) waarbij F(x) = f(x) * g(x)
Waarom is de afgeleide dan:
f'(x) * g(x) + f(x) * g'(x)
en niet:
f'(x) * x' * g(x) + f(x) * g'(x) * x
Want
dY / dI = F'(Y) dY/dI + 1 als Y = f(Y) + I
Stel je hebt
d F(x) / dx ofwel F'(x) waarbij F(x) = f(x) * g(x)
Waarom is de afgeleide dan:
f'(x) * g(x) + f(x) * g'(x)
en niet:
f'(x) * x' * g(x) + f(x) * g'(x) * x
Want
dY / dI = F'(Y) dY/dI + 1 als Y = f(Y) + I
Ik ben eindelijk bij de laatste bladzijde gekomen die ik moet kennen voor het deeltentamen en ja hoor... ik begrijp de laatste bladzijde niet.
Hier worden de theorie tot dan toe in een 'economisch' voorbeeld genomen
Groen is wat ik begrijp en rood wat ik niet begrijp.
Hier worden de theorie tot dan toe in een 'economisch' voorbeeld genomen
Groen is wat ik begrijp en rood wat ik niet begrijp.
Je snapt toch dat een product niet hetzelfde is als een som?quote:
Ik heb even de Leibniz notatie posts van Riparius gelezen, ik heb het wel begrepen, maar ben toch lichtelijk verward geworden.. en dan is het om hoe de regel werkt, want praktisch gezien begrijp ik dat wel als ik letters en getallen zie, maar in notatievorm ben ik nog lichtelijk verward..
Stel je hebt
d F(x) / dx ofwel F'(x) waarbij F(x) = f(x) * g(x)
Waarom is de afgeleide dan:
f'(x) * g(x) + f(x) * g'(x)
en niet:
f'(x) * x' * g(x) + f(x) * g'(x) * x
Want
dY / dI = F'(Y) dY/dI + 1 als Y = f(Y) + I
Je hebt eerder de tip gekregen om niet zomaar scans/foto's met rode strepen te plaatsen, maar om nauwkeuriger aan te geven wat je niet begrijpt.quote:
Groen is wat ik begrijp en rood wat ik niet begrijp.
Wat begrijp je niet, de vraagstelling of de uitwerking? Welke stappen heb je al gezet? Hoe zou je het probleem zelf aanpakken en waar is dat anders dan de antwoorden in het boek?
Dan wordt het voor de mensen hier wat eenvoudiger om een functioneel en enigszins beknopt antwoord te geven.
Even een vraagje tussendoor, krijg je colleges en/of werkcolleges over deze stof?
Opinion is the medium between knowledge and ignorance (Plato)
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |