[Bèta wiskunde] Huiswerk- en vragentopic

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
pi_108608682
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.

Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!

Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).

Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...

OP
  Moderator / Redactie Sport / Devops donderdag 1 maart 2012 @ 23:15:31 #2
176766 zoem
zoemt
pi_108608729
Even recapituleren:
quote:
0s.gif Op donderdag 1 maart 2012 23:02 schreef Paxcon het volgende:
Wtf wat vaag allemaal. Ik heb dit vorig jaar wel eens gehad maar zo ingewikkeld met die formules kan het toch niet zijn?

Voor een normale afgeleide kun je gewoon zeggen je doet de macht keer het voorste getal en trekt 1 van die macht af en dat is de afgeleide? En dat In komt me ook totaal onbekend voor.
quote:
2s.gif Op donderdag 1 maart 2012 23:10 schreef zoem het volgende:
Dat is helemaal geen rare formule eigenlijk, hij is alleen wat minder bekend. De regel die jij noemt is eigenlijk een versimpelde variant van die formule. Pas het maar eens toe op bijvoorbeeld x3:

(x^3)' = x^3 (1\cdot \frac{3}{x} + 0 \cdot ln x) = 3x^2
quote:
0s.gif Op donderdag 1 maart 2012 23:13 schreef thenxero het volgende:

[..]

Er is toch niks ingewikkelds aan. Eigenlijk is het nog makkelijker: als je de afgeleide neemt hoef je er alleen maar ln(a) bij te zetten :P .
pi_108608771
Ik snap het echt niet :D

Welke formule krijg je met x = -2 ingevuld?
  Moderator / Redactie Sport / Devops donderdag 1 maart 2012 @ 23:17:40 #4
176766 zoem
zoemt
pi_108608828
f(x)'=3^xln3
f(-2)'=3^{-2}ln3 = 0.122
pi_108608853
Oke wat in hemelsnaam is dat In. Iets met logaritme?
  Moderator / Redactie Sport / Devops donderdag 1 maart 2012 @ 23:19:02 #6
176766 zoem
zoemt
pi_108608893
ln is inderdaad het logaritme.
pi_108608909
Staat ook gewoon op je rekenmachine hoor, zo'n ln knop :P
pi_108608977
Ohja, ik zie het :') Dan krijg ik inderdaad het goede antwoord. Toch moet het voor m'n gevoel nog anders kunnen maar zo ben ik tijdelijk uit de brand denk ik :D Dankjullie :)
pi_108609227
quote:
0s.gif Op donderdag 1 maart 2012 23:20 schreef Paxcon het volgende:
Ohja, ik zie het :') Dan krijg ik inderdaad het goede antwoord. Toch moet het voor m'n gevoel nog anders kunnen maar zo ben ik tijdelijk uit de brand denk ik :D Dankjullie :)
Je kan ook de functie plotten, en dan je dy/dx functie nemen, en 2 invullen. Dan hoef je die afgeleide niet eens te kennen, en heb je direct een numerieke benadering.
pi_108609312
quote:
0s.gif Op donderdag 1 maart 2012 23:26 schreef thenxero het volgende:

[..]

Je kan ook de functie plotten, en dan je dy/dx functie nemen, en 2 invullen. Dan hoef je die afgeleide niet eens te kennen, en heb je direct een numerieke benadering.
In dit hoofdstuk staat inderdaad uitleg over dy/dx...

Ik ga het even uitzoeken..
pi_108609518
Nouja laat maar ik snap er echt geen zak van
pi_108609979
Als je een TI hebt: Plot de functie, druk op 2nd + calc. Ga naar dy/dx. Druk op 2 en dan op enter.

(zo uit mijn hoofd)
pi_108759542
te vroeg..
pi_108760543
Ik heb

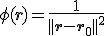
\phi(\mathbf{r}) = \frac{1}{||\mathbf{r} - \mathbf{r}_0||^2}

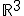met \mathbf{r} vector in \mathbb{R}^3. Nu moet ik de afgeleide bepalen ervan.

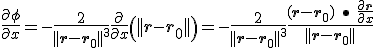
\frac{\partial \phi}{\partial x} = -\frac{2}{||\mathbf{r} - \mathbf{r}_0||^3}\frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right) = -\frac{2}{||\mathbf{r} - \mathbf{r}_0||^3}\frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||}

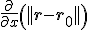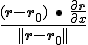Kan iemand mij die laatste stap uitleggen? Waarom \frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right) dus \frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||} is.
pi_108761061
En sticky!
Ja doei.
pi_108762362
Ow, Sticky/Open :') oops!
Ja doei.
pi_108762460
quote:
7s.gif Op maandag 5 maart 2012 21:40 schreef Dale. het volgende:
Ik heb

\phi(\mathbf{r}) = \frac{1}{||\mathbf{r} - \mathbf{r}_0||^2}

met \mathbf{r} vector in \mathbb{R}^3. Nu moet ik de afgeleide bepalen ervan.

\frac{\partial \phi}{\partial x} = -\frac{2}{||\mathbf{r} - \mathbf{r}_0||^3}\frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right) = -\frac{2}{||\mathbf{r} - \mathbf{r}_0||^3}\frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||}

Kan iemand mij die laatste stap uitleggen? Waarom \frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right) dus \frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||} is.
Als ||...|| staat voor de Euclidische norm, dan kan je het gewoon uitschrijven als wortel en dan differentiëren.
pi_108763587
quote:
7s.gif Op maandag 5 maart 2012 21:40 schreef Dale. het volgende:

Kan iemand mij die laatste stap uitleggen? Waarom \frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right) dus \frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||} is.
Laten we zeggen dat r = (x,y,z) en r0 = (x0,y0,z0). Wat is dan het inproduct van r - r0 en ∂r/∂x ?
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_108763837
Ik zoek het aantal partities van n in drie positieve getallen a,b,c (dus a+b+c=n), met de restricties dat a<b+1 en b<c, met behulp van een genererende functie.

De genererende functie voor a is (x + x^2 + ... + x^b) (want a neemt waardes aan tussen 1 en b),
voor b: (x^a + x^2 + ... + x^(c-1))
voor c: (x^(b+1) + ... + x^n)

Die drie functies kan ik met elkaar vermenigvuldigen. Maar als je dan kijkt naar de coëfficiënt van x^n, die dan het aantal partities van n zou moeten geven, dan is die afhankelijk van de "gekozen" a,b,c, terwijl die juist variabel zijn. Dus ik zit in de knoop.... Moet ik misschien nog sommeren over alle paren a,b,c?
pi_108767978
quote:
0s.gif Op maandag 5 maart 2012 22:29 schreef thenxero het volgende:
Ik zoek het aantal partities van n in drie positieve getallen a,b,c (dus a+b+c=n), met de restricties dat a<b+1 en b<c, met behulp van een genererende functie.

De genererende functie voor a is (x + x^2 + ... + x^b) (want a neemt waardes aan tussen 1 en b),
voor b: (x^a + x^2 + ... + x^(c-1))
voor c: (x^(b+1) + ... + x^n)

Die drie functies kan ik met elkaar vermenigvuldigen. Maar als je dan kijkt naar de coëfficiënt van x^n, die dan het aantal partities van n zou moeten geven, dan is die afhankelijk van de "gekozen" a,b,c, terwijl die juist variabel zijn. Dus ik zit in de knoop.... Moet ik misschien nog sommeren over alle paren a,b,c?
Je kan de genererendevoortbrengende functies natuurlijk niet van elkaar afhankelijk laten zijn. Dus je moet niet iets doen met "voortbrengende functie van a = (uitdrukking in b)".

Je kan het als volgt bekijken: het gaat om ongeordende drietallen getallen (a, b, c), waarvan de twee kleinste gelijk mogen zijn, maar de grootste niet gelijk mag zijn aan een van de andere twee. Dit is gemakkelijk in bijectie met de drietallen getallen (a, b, c) zonder restricties op de grootste (trek gewoon 1 van de grootste af).

Hopelijk kom je nu verder met deze hint. ;).
pi_108768126
quote:
0s.gif Op maandag 5 maart 2012 22:07 schreef thenxero het volgende:

[..]

Als ||...|| staat voor de Euclidische norm, dan kan je het gewoon uitschrijven als wortel en dan differentiëren.
Ja klopt. En idd had het gewoon moeten uitschrijven (maar was een beetje lui :P, dacht dat er van allerlei zooi zou uitkomen hahaha) was een makkelijke integraal eigenlijk. De tussenstap had achteraf best mogen weggelaten worden eigenlijk.
pi_108768827
quote:
0s.gif Op dinsdag 6 maart 2012 00:01 schreef thabit het volgende:

[..]

Je kan de genererendevoortbrengende functies natuurlijk niet van elkaar afhankelijk laten zijn. Dus je moet niet iets doen met "voortbrengende functie van a = (uitdrukking in b)".

Je kan het als volgt bekijken: het gaat om ongeordende drietallen getallen (a, b, c), waarvan de twee kleinste gelijk mogen zijn, maar de grootste niet gelijk mag zijn aan een van de andere twee. Dit is gemakkelijk in bijectie met de drietallen getallen (a, b, c) zonder restricties op de grootste (trek gewoon 1 van de grootste af).

Hopelijk kom je nu verder met deze hint. ;).
Slim. Hiermee lukt het wel :) . Bedankt!
pi_108787719
Even een korte vraag m.b.t. het Leontief model (matrixen).

Wat is de uitkomst van?
http://imageshack.us/photo/my-images/860/deelvanvraag5c.png/ (copy/paste deze link)

Wanneer ik dit stukje begrijp kan ik weer verder, het is een deel van het antwoord op een oefententamenvraag waarvan deze (sub)vraag een hele punt waard is, dus hulp wordt zeker op prijs gesteld!

Alvast bedankt.
  dinsdag 6 maart 2012 @ 17:21:58 #25
75592 GlowMouse
l'état, c'est moi
pi_108788076
Een matrix maal zijn inverse is, vanwege de definitie van de inverse, gelijk aan de eenheidsmatrix.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_108788403
Ik vermoedde het al maar misde de theorie, bedankt voor de snelle bevestiging :)
pi_108830261
Ik heb moeite met het bewijzen dat een gelijkvormigheid een bijectie is.
Een gelijkvormigheid is een niet-constante afbeelding f: R² -> R² die verhoudingen van afstanden invariant laat: voor alle viertallen punten a,b,c,d in R² met a !=b en c !=d geldt:
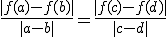
\frac{|f(a) - f(b)|}{|a-b|} = \frac{|f(c) - f(d)|}{|c-d|}

Ik weet niet hoe ik de surjectiviteit kan bewijzen. Ik heb het idee dat een gelijkvormigheid een samenstelling is van een isometrie en een schaalfunctie, maar dit concreet maken is nog niet gelukt. Heeft iemand een tip?
pi_108830474
quote:
0s.gif Op woensdag 7 maart 2012 18:10 schreef Anoonumos het volgende:
Ik heb moeite met het bewijzen dat een gelijkvormigheid een bijectie is.
Een gelijkvormigheid is een niet-constante afbeelding f: R² -> R² die verhoudingen van afstanden invariant laat: voor alle viertallen punten a,b,c,d in R² met a !=b en c !=d geldt:
\frac{|f(a) - f(b)|}{|a-b|} = \frac{|f(c) - f(d)|}{|c-d|}

Ik weet niet hoe ik de surjectiviteit kan bewijzen. Ik heb het idee dat een gelijkvormigheid een samenstelling is van een isometrie en een schaalfunctie, maar dit concreet maken is nog niet gelukt. Heeft iemand een tip?
De verhouding is gegeven en is niet 0 want de afbeelding is niet-constant. Als je nu f door die verhouding deelt, dan krijg je een isometrie.
pi_108929691
Hoi!

Weet niet of dit hier hoort, maar ik heb een SPSS vraag. Het is dus de bedoeling dat ik dat voor Research Seminar data verwerk. Leuk, want ik snap er de ballen van. Mijn vraag is als volgt:

Ik heb meerdere keren verschillende items waar ik een construct/variabele van maak. Dat gaat goed. Echter, die items meten de antwoorden van een vraag met een likert-schaal van 1 tot en met 5. En zo nu en dan zit er een 0 tussen. Dat lijkt mij een missing variable. Als ik dat in de variable view aanmerk als missing (Missing > discrete =0), 'ziet' spss wel de missing data wanneer ik Analyze>Descripte>Frequencies doe. Echter, (en hier komt het probleem) verschijnen er dan gaten in mijn construct, precies daar waar in de items een 0 voorkomt. Dus een nul in mijn item betekent een . in mijn construct. Staan er enkel items met correcte antwoorden dan staat er wel netjes een cijfer.

Wat doe ik fout en hoe dit op te lossen?

Bedankt!
  zaterdag 10 maart 2012 @ 01:28:22 #30
75592 GlowMouse
l'état, c'est moi
pi_108929855
Het SPSS topic #4 - Syntaxen verder.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_108974829
Ik moet een basis van de deelruimte van R4 geven waarvoor geldt:
x1+x2-x3+x4=0
Dit lukt me wel door drie vectoren te kiezen die aan deze vergelijking voldoen, en vervolgens te testen of deze onafhankelijk zijn, maar ik hoopte eigenlijk dat er een betere/snellere manier was, weet iemand dat misschien?
pi_108975038
quote:
14s.gif Op zaterdag 10 maart 2012 01:28 schreef GlowMouse het volgende:
Het SPSS topic #4 - Syntaxen verder.
Excuus en bedankt
  zondag 11 maart 2012 @ 17:39:46 #33
120139 freiss
Hertog Jan :9~
pi_108976845
quote:
2s.gif Op zondag 11 maart 2012 16:44 schreef kutkloon7 het volgende:
Ik moet een basis van de deelruimte van R4 geven waarvoor geldt:
x1+x2-x3+x4=0
Dit lukt me wel door drie vectoren te kiezen die aan deze vergelijking voldoen, en vervolgens te testen of deze onafhankelijk zijn, maar ik hoopte eigenlijk dat er een betere/snellere manier was, weet iemand dat misschien?
Je kunt door de vergelijking bekijken die drie vectoren slim kiezen, door bijvoorbeeld x1 altijd de waarde 1 te geven, en dan twee van de andere variabelen 0 te zetten. Zo zie je bijvoorbeeld dat [1,-1,0,0], [1,0,1,0] en [1,0,0,1] aan de vergelijkingen voldoen. Omdat de eerste vector de enige van deze vectoren is die in de x2 richting werkt, moet deze onafhankelijk zijn van de andere twee vectoren. Ditzelfde argument geldt ook voor de tweede en derde vector (voor resp. x3 en x4), dus moeten ze onafhankelijk zijn, dus is het een basis.
HJ 14-punt-gift.
Lijst met rukmateriaal!
pi_108980737
quote:
14s.gif Op zondag 11 maart 2012 17:39 schreef freiss het volgende:

[..]

Je kunt door de vergelijking bekijken die drie vectoren slim kiezen, door bijvoorbeeld x1 altijd de waarde 1 te geven, en dan twee van de andere variabelen 0 te zetten. Zo zie je bijvoorbeeld dat [1,-1,0,0], [1,0,1,0] en [1,0,0,1] aan de vergelijkingen voldoen. Omdat de eerste vector de enige van deze vectoren is die in de x2 richting werkt, moet deze onafhankelijk zijn van de andere twee vectoren. Ditzelfde argument geldt ook voor de tweede en derde vector (voor resp. x3 en x4), dus moeten ze onafhankelijk zijn, dus is het een basis.
Logisch en duidelijk ^O^ (hoewel de laatste vector volgens mij niet klopt)
pi_108992863
Als je al één vector hebt, kun je een extra vergelijking opstellen over orthogonaliteit met de eerste vector. Daarna nog een vergelijking voor orthogonaliteit met de tweede.
pi_109065753


Wie kan mij helpen met dit integraal?
AJAX AMSTERDAM!
pi_109066073
quote:
0s.gif Op dinsdag 13 maart 2012 21:18 schreef bloodysunday het volgende:
[ afbeelding ]

Wie kan mij helpen met deze integraal?
Herschrijf de integrand als 10∙t-5/2.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109100312
quote:
0s.gif Op dinsdag 13 maart 2012 21:25 schreef Riparius het volgende:

[..]

Herschrijf de integrand als 10∙t-5/2.
Inderdaad, sqrt(t) = t^0,5 dus staat er t^2,5 onder de deelstreep.

Daarna krijg je

1/(1+2,5) t^3,5

En dan vul je 'm in.
pi_109103719
quote:
6s.gif Op woensdag 14 maart 2012 19:30 schreef hello_moto1992 het volgende:

[..]

Inderdaad, sqrt(t) = t^0,5 dus staat er t^2,5 onder de deelstreep.

Daarna krijg je

1/(1+2,5) t^3,5

En dan vul je 'm in.
Nee, dit klopt niet.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
  Moderator / Redactie Sport / Devops woensdag 14 maart 2012 @ 20:54:04 #40
176766 zoem
zoemt
pi_109105236
Je vergeet het minteken mee te nemen. En mensen gebruik de [ tex] tag nou eens :o

\int{\frac{10}{t^2 \sqrt{t}}dt}=\int{\frac{10}{t^{2,5}}dt}=\int{10\cdot t^{-2,5}dt}=[\frac{10}{-1,5}\cdot t^{-1,5}]^9_4=[-\frac{10}{1,5 t\sqrt{t}}]^9_4

Wtf, nu werkt mn tex niet meer _O-
pi_109107529
Hoe werkt die [tex] dan?

Ik heb nu de formule

5/x^2=9

Ik schrijf dan

5 ʃ 1/x^2 + 1/9

5 ʃ x^-2 + 1/9

5 ʃ 1/-1 x^-1 + 1/9
5/-1 1/x + 5/9
5/-x + 5/9

Volgens mij is dit compleet fout? Help!
Ik snap helemaal niks van het integreren met breuken.
AJAX AMSTERDAM!
  woensdag 14 maart 2012 @ 21:37:55 #42
75592 GlowMouse
l'état, c'est moi
pi_109107589
ik mis dx, en zie niet hoe je van een formule naar een integraal gaat
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_109107773
quote:
0s.gif Op woensdag 14 maart 2012 21:36 schreef bloodysunday het volgende:
Hoe werkt die (...) dan?

Ik heb nu de formule

5/x^2=9

Ik schrijf dan

5 ʃ 1/x^2 + 1/9

5 ʃ x^-2 + 1/9

5 ʃ 1/-1 x^-1 + 1/9
5/-1 1/x + 5/9
5/-x + 5/9

Volgens mij is dit compleet fout? Help!
Ik snap helemaal niks van het integreren met breuken.
Integreren met breuken is niet veel anders dan integreren van 'gewone' machten, als je in de gaten houdt dat 1/x^n = x^{-n} .

Hoe je van die formule naar je integraal gaat is me echter ook niet helemaal duidelijk.
The biggest argument against democracy is a five minute discussion with the average voter.
pi_109107951
Mijn formule is ʃ 5 / x^2 + 9 dx
Ik haal die 5 buiten het integraal, waardoor je de formule 1 / x^2+9 overhoud.
Ik krijg dan x^-2 + 9^-1.
Dan 1/-1 x^-1 + 9^-1.
Daarna ben ik een beetje het spoort bijster.
AJAX AMSTERDAM!
  Moderator / Redactie Sport / Devops woensdag 14 maart 2012 @ 21:44:23 #45
176766 zoem
zoemt
pi_109107995
quote:
0s.gif Op woensdag 14 maart 2012 21:36 schreef bloodysunday het volgende:
Hoe werkt die [ tex] dan?
De tags zijn [ tex] en [/tex]

http://en.wikibooks.org/wiki/LaTeX/Mathematics

Veelgebruikte TeX voor wiskunde:
wortel \sqrt{...}
integraal \int{...}
breuk \frac{teller}{noemer}
productteken \cdot
superscript a^{superscript}
subscript a_{subscript}
pi_109108062
Ah, deze is wat ingewikkelder inderdaad. Je primitieve wordt iets van \arctan u.
pi_109108132
quote:
0s.gif Op woensdag 14 maart 2012 21:45 schreef twaalf het volgende:
Ah, deze is wat ingewikkelder inderdaad. Je primitieve wordt iets van \arctan u.
Dat arctan u zie ik vaker, maar waar haal ik die rekenregels vandaan?
AJAX AMSTERDAM!
  Moderator / Redactie Sport / Devops woensdag 14 maart 2012 @ 21:48:59 #48
176766 zoem
zoemt
pi_109108320
quote:
0s.gif Op woensdag 14 maart 2012 21:43 schreef bloodysunday het volgende:
Mijn formule is ʃ 5 / x^2 + 9 dx
Ik haal die 5 buiten het integraal, waardoor je de formule 1 / x^2+9 overhoud.
Ik krijg dan x^-2 + 9^-1.
Dan 1/-1 x^-1 + 9^-1.
Daarna ben ik een beetje het spoort bijster.
Als je de 5 buiten de integraal haalt, moet je zorgen dat de term 9 ook door 5 gedeeld wordt. Anders klopt je vergelijking niet meer.

\int{\frac{5}{x^2}+9}=5\cdot\int{\frac{1}{x^2}+\frac{9}{5}}
pi_109108339
Je weet dat
\int \frac{dx}{1+x^2}=\arctan x+c
Dus jouw integraal
\int \frac{dx}{9+x^2}=\frac{1}{9}\int \frac{dx}{1+(x/3)^2}
Nu substitueren u=x/3, dan volgt dx=3du;
\frac{1}{9}\int \frac{3du}{1+u^2}=\frac{1}{3}\int \frac{du}{1+u^2}=\frac{1}{3}\arctan u + c=\frac{1}{3}\arctan (x/3)+c
pi_109108729
Het is 5 / (x^2 + 9). dx
AJAX AMSTERDAM!
pi_109108815
Dan moet je het antwoord nog met 5 vermenigvuldigen :).
The biggest argument against democracy is a five minute discussion with the average voter.
pi_109108817
wat M.rak zegt
pi_109109148
Wat doet mn studie me aan :(
AJAX AMSTERDAM!
pi_109109667
Ik snap het stuk tot het substitueren. Ik snap alleen de stap naar die 3du niet.
AJAX AMSTERDAM!
  Moderator / Redactie Sport / Devops woensdag 14 maart 2012 @ 22:11:44 #55
176766 zoem
zoemt
pi_109109871
Je wilt ervoor zorgen dat de x/3 weg is, zodat je de integraalregel kan toepassen. Dus dan vervang je x/3 door u. Maar dat kan alleen als je dx ook naar du omrekent: u=x/3 -> afgeleide nemen -> du = dx/3 -> dx = 3du. Vervang dx door 3du en dan kun je de integraal uitrekenen.

De grenzen moet je inderdaad ook omrekenen, zoals Riparius zegt.
pi_109109876
quote:
0s.gif Op woensdag 14 maart 2012 22:08 schreef bloodysunday het volgende:
Ik snap het stuk tot het substitueren. Ik snap alleen de stap naar die 3du niet.
Krijg je wel les? En heb je wel een boek of dictaat? Dan zou de substitutieregel voor de integraalrekening toch uitgelegd moeten zijn. En vergeet niet dat je bij een bepaalde integraal ook de integratiegrenzen aan moet passen als je verder rekent met een nieuwe variabele.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109110096
quote:
0s.gif Op woensdag 14 maart 2012 22:11 schreef Riparius het volgende:

[..]

Krijg je wel les? En heb je wel een boek of dictaat? Dan zou de substitutieregel voor de integraalrekening toch uitgelegd moeten zijn. En vergeet niet dat je bij een bepaalde integraal ook de integratiegrenzen aan moet passen als je verder rekent met een nieuwe variabele.
Les gehad, werd ik niet veel wijzer van. Heb een boek, maar dat staat vol fouten dus dat schiet lekker op :')
AJAX AMSTERDAM!
pi_109110392
quote:
2s.gif Op woensdag 14 maart 2012 22:11 schreef zoem het volgende:
Je wilt ervoor zorgen dat de x/3 weg is, zodat je de integraalregel kan toepassen. Dus dan vervang je x/3 door u. Maar dat kan alleen als je dx ook naar du omrekent: u=x/3 -> afgeleide nemen -> du = dx/3 -> dx = 3du. Vervang dx door 3du en dan kun je de integraal uitrekenen.

De grenzen moet je inderdaad ook omrekenen, zoals Riparius zegt.
Ja ok natuurlijk. thx
AJAX AMSTERDAM!
pi_109110513
quote:
0s.gif Op woensdag 14 maart 2012 22:14 schreef bloodysunday het volgende:

[..]

Les gehad, werd ik niet veel wijzer van. Heb een boek, maar dat staat vol fouten dus dat schiet lekker op :')
Welk boek is dat, als ik vragen mag?

Je kunt natuurlijk zelf op zoek gaan naar een beter leerboek. Of kijk eens in Wikipedia.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109110613
quote:
0s.gif Op woensdag 14 maart 2012 22:18 schreef bloodysunday het volgende:

[..]

Ja ok natuurlijk. thx
Als je het nog lastig vindt helpt dit filmpje misschien:
Indefinite Integration (part IV)
Indefinite Integration (part IV)
Daar kan je eventueel ook andere delen van bekijken, mocht je daar problemen mee hebben :P.
The biggest argument against democracy is a five minute discussion with the average voter.
pi_109110617
quote:
0s.gif Op woensdag 14 maart 2012 22:14 schreef bloodysunday het volgende:

[..]

Les gehad, werd ik niet veel wijzer van. Heb een boek, maar dat staat vol fouten dus dat schiet lekker op :')
Check haar filmpjes

U-Substitution Example 7
U-Substitution Example 7

:9~
pi_109112700
quote:
0s.gif Op woensdag 14 maart 2012 22:21 schreef thenxero het volgende:

[..]

Check haar filmpjes

U-Substitution Example 7
U-Substitution Example 7

:9~
Je droomt er zeker van dat ze jou het squeeze theorem nog eens persoonlijk komt uitleggen?
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109116678
quote:
0s.gif Op woensdag 14 maart 2012 22:51 schreef Riparius het volgende:

[..]

Je droomt er zeker van dat ze jou het squeeze theorem nog eens persoonlijk komt uitleggen?
Mwa, ik zou het in ieder geval niet weigeren.
pi_109121618
quote:
0s.gif Op woensdag 14 maart 2012 22:20 schreef Riparius het volgende:

[..]

Welk boek is dat, als ik vragen mag?

Je kunt natuurlijk zelf op zoek gaan naar een beter leerboek. Of kijk eens in Wikipedia.
Toegepaste Wiskunde voor het Hoger Onderwijs.
AJAX AMSTERDAM!
pi_109122260
Op een tentamen stond een keer de volgende vraag:

Je hebt 90 meter hekwerk. Het hek moet aan 1 zijde open zijn. Bepaal de maximale oppervlakte.
Wat voor formule moet je hier bij opzetten.

De oppervlakte is lxb maar aangezien je 1 zijde minder hebt moet het (lxb)-l zijn ofzo?
AJAX AMSTERDAM!
pi_109122977
quote:
0s.gif Op donderdag 15 maart 2012 10:31 schreef bloodysunday het volgende:
Op een tentamen stond een keer de volgende vraag:

Je hebt 90 meter hekwerk. Het hek moet aan 1 zijde open zijn. Bepaal de maximale oppervlakte.
Wat voor formule moet je hier bij opzetten.

De oppervlakte is lxb maar aangezien je 1 zijde minder hebt moet het (lxb)-l zijn ofzo?
duidelijke vraagstelling!
www.wiskunde.tk
  Moderator / Redactie Sport / Devops donderdag 15 maart 2012 @ 10:52:51 #67
176766 zoem
zoemt
pi_109122979
quote:
0s.gif Op donderdag 15 maart 2012 10:31 schreef bloodysunday het volgende:
Op een tentamen stond een keer de volgende vraag:

Je hebt 90 meter hekwerk. Het hek moet aan 1 zijde open zijn. Bepaal de maximale oppervlakte.
Wat voor formule moet je hier bij opzetten.

De oppervlakte is lxb maar aangezien je 1 zijde minder hebt moet het (lxb)-l zijn ofzo?
Wat jij doet kan niet; je trekt een lengte van een oppervlakte af. Let op je dimensies ;)

Stel eerst de formule voor de oppervlakte op. Aangenomen dat het een rechthoekig vlak is, kun je het volgende zeggen: De rechthoek heeft vier zijdes, waarvan er eentje open is. De twee zijdes die grenzen aan de opening noem je x. Voor de zijde tegenover de opening bliijft dan 90-2x over van het 90m hekwerk. Oppervlakte is lengte maal breedte:

A = x \cdot (90-2x) = 90x - 2x^2

Het maximum vind je door de eerste afgeleide naar x te nemen en deze gelijk te stellen aan 0.

A'=90 - 4x = 0 \rightarrow 4x=90 \rightarrow x = \frac{90}{4} = 22,5m

[edit]
Inderdaad, ik ben vergeten het uiteindelijke antwoord te geven.

A(x=22,5) = 90\cdot22,5 - 2\cdot 22,5^2 = 1012,5m^2

quote:
1s.gif Op donderdag 15 maart 2012 10:52 schreef JoPiDo het volgende:
duidelijke vraagstelling!
Hoezo is het niet duidelijk? Het enige wat niet expliciet gegeven is, is dat het een rechthoek moet zijn.

[ Bericht 12% gewijzigd door zoem op 15-03-2012 15:02:31 ]
pi_109130672
quote:
2s.gif Op donderdag 15 maart 2012 10:52 schreef zoem het volgende:

[..]

Hoezo is het niet duidelijk? Het enige wat niet expliciet gegeven is, is dat het een rechthoek moet zijn.
Inderdaad. Maar de vragensteller citeert de opgave kennelijk uit het hoofd, bij de oorspronkelijke opgave zal er wel bij hebben gestaan dat het ging om een rechthoekig terrein. Vaak was dat dan een terrein dat langs het water lag of zo.

Je moet trouwens nog wel even het gevraagde antwoord geven: de maximaal af te rasteren oppervlakte bedraagt 1012,5 m². Vroeger waren dit gewone algebra opgaven die je geacht werd zonder differentiaalrekening op te kunnen lossen. De uitdrukking voor de oppervlakte is middels kwadraatafsplitsing te schrijven als A = 1012,5 - 2(x - 22,5)² zodat direct duidelijk is dat het maximum van 1012,5 m² bereikt wordt bij x = 22,5 m aangezien het kwadraat hier niet negatief kan zijn.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109137822
Nee dit was een zon beetje de vraag.
AJAX AMSTERDAM!
pi_109139236
quote:
0s.gif Op donderdag 15 maart 2012 18:30 schreef bloodysunday het volgende:
Nee dit was een zo'n beetje de vraag.
Dat kan ik me niet voorstellen, tenzij het een hele slechte docent was. Want stel dat we het hek in een halve cirkel plaatsen, of dat we het hek twee zijden van een gelijkzijdige driehoek laten vormen, of de twee rechthoekszijden van een rechthoekige driehoek, dan kun je zonder nadere gegevens net zo goed volhouden dat het hek 'aan één zijde open' is.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109211826
Ik heb een vraag over kansrekenen:
Een gezamenlijke kansdichtheid:
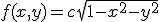
f(x,y) = c \sqrt{1 - x^2 - y^2}
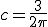
normaliseren geeft c =\frac{3}{2\pi}
Nu zoek ik de marginale kansdichtheden.
Ik zag dit als plakjes snijden uit de bol, en wilde dan de oppervlakte van die plakjes bepalen. Alleen is f(x,y) geen echte bol. Hoe kan ik dit nu aanpakken?
Voor de andere vragen gebruikte ik poolcoordinaten om te integreren, maar ik weet niet of je daar de marginale kansdichtheden uit kon halen.
pi_109217727
Het is een ellips(oïde), de oppervlakte van een 'plakje' wordt gegeven door 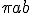\pi a b, waarin a en b de halve assen zijn. Voor gegeven x kun je a en b uitrekenen.
pi_109218267
quote:
0s.gif Op zaterdag 17 maart 2012 23:29 schreef twaalf het volgende:
Het is een ellips(oïde), de oppervlakte van een 'plakje' wordt gegeven door \pi a b, waarin a en b de halve assen zijn. Voor gegeven x kun je a en b uitrekenen.

Het is toch gewoon een bol?
Sorry je hebt gelijk, die c gooit roet in het eten.
pi_109218636
Maakt het überhaupt iets uit dat daar een c staat? Het is toch alleen maar een schalingsfactor?
pi_109218781
Het is gelukt. Je kon ook uitgaan van een bol en dan normaliseren, maar nu snap ik het beter. Bedankt.
pi_109218795
quote:
0s.gif Op zaterdag 17 maart 2012 23:58 schreef thabit het volgende:
Maakt het überhaupt iets uit dat daar een c staat? Het is toch alleen maar een schalingsfactor?
pi *a*b reduceert gewoon tot pi*r^2 (de bol wordt in de richting van de z-as uitgerekt door c)
pi_109226551
Weet iemand hoe je T=27•0,4^t•(3-0,4^2t) herleidt tot de vorm T=a•g^t+b•h^t ?
"Nibnub. A name to remember."
pi_109227410
27 \cdot 0.4^t \cdot (3 - 0.4^{2t})
= 27 \cdot 0.4^t \cdot 3 - 27 \cdot 0.4^t \cdot 0.4^{2t}
= 81 \cdot 0.4^t - 27 \cdot 0.4 ^{2t + t}
= 81 \cdot 0.4^t - 27 \cdot 0.4 ^{3t}
Dus eerst de haakjes uitwerken en dan gebruiken dat x^a \cdot x^b = x^{a+b}
pi_109227660
quote:
0s.gif Op zondag 18 maart 2012 12:18 schreef Anoonumos het volgende:
27 \cdot 0.4^t \cdot (3 - 0.4^{2t})
= 27 \cdot 0.4^t \cdot 3 - 27 \cdot 0.4^t \cdot 0.4^{2t}
= 81 \cdot 0.4^t - 27 \cdot 0.4 ^{2t + t}
= 81 \cdot 0.4^t - 27 \cdot 0.4 ^{3t}
Dus eerst de haakjes uitwerken en dan gebruiken dat x^a \cdot x^b = x^{a+b}
Wat je dan nog kan schrijven als:
= 81 \cdot 0.4^t - 27 \cdot 0.064 ^t

Gebruikmakende van x^{a \cdot b} = (x^a)^b

[ Bericht 0% gewijzigd door Nelis89 op 18-03-2012 14:36:38 ]
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
pi_109228406
Het klopt, bedankt Anoonumos & Nelis89 :)
"Nibnub. A name to remember."
pi_109232599
quote:
0s.gif Op zondag 18 maart 2012 12:53 schreef Nibnub het volgende:
Het klopt, bedankt Anoonumos & Nelis89 :)
Het antwoord van Nelis89 klopt niet, want 0,43 = 0,064.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109232700
quote:
0s.gif Op zondag 18 maart 2012 14:33 schreef Riparius het volgende:

[..]

Het antwoord van Nelis89 klopt niet, want 0,43 = 0,064.
Fixed
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
pi_109290700
Ik ben mijn wiskunde aan het oppoetsen en me langzaam door een dik wiskunde boek aan het werken.

Ik kom echter bij het volgende voorbeeld niet verder:

quote:
Bewijs dat n2 > 7n + 1 for alle n >= 8

Oplossing: Het resultaat is waar wanneer n = 8, want 82 = 64 en 7 * 8 + 1 = 57. Veronderstel dat het waar is voor iedere n wanneer k ≥ 8, dat wil zeggen k2 > 7k + 1

(k + 1)2 = k2 + 2k + 1 > (7k + 1) + 2k + 1 = 7(k + 1) + 1 + (2k - 6)

Omdat k ≥ 8, is 2k - 6 een natuurlijk nummer, en de laatste uitdrukking boven is groter dan 7(k + 1). De inductie stap is geverifiëerd, en dus is het resultaat waar voor alle n ≥ 8.

(vrij vertaald uit het Engels uit Discrete Mathematics van Normal L. Biggs)
Ik kan het nog net volgen tot: (k + 1)2 = k2 + 2k + 1 > ....

Maar daarna wordt me het spoor bijster. Waar komt die "+ 2k + 1" vandaan, en waar komt daarna de "+ 1 + (2k - 6)" vandaan?

Ik begrijp waarom de uitdrukking altijd waar is voor elke n ≥ 8, ik volg alleen de redenering en de inductie niet.

Als dit niet de juiste plek is voor mijn vraag, dan hoor ik het wel!

:)
pi_109291024
quote:
0s.gif Op maandag 19 maart 2012 21:28 schreef RedVampire het volgende:
Ik ben mijn wiskunde aan het oppoetsen en me langzaam door een dik wiskunde boek aan het werken.

Ik kom echter bij het volgende voorbeeld niet verder:

[..]

Ik kan het nog net volgen tot: (k + 1)2 = k2 + 2k + 1 > ....

Maar daarna wordt me het spoor bijster. Waar komt die "+ 2k + 1" vandaan, en waar komt daarna de "+ 1 + (2k - 6)" vandaan?
Uit de kut van tante Sjaan!

Je gebruikt hier k2 > 7k + 1; dat mag je doen omdat dat de inductiehypothese is.
pi_109294126
Ik heb het een beetje herschreven en verduidelijkt:

quote:
Bewijs dat n² > 7n + 1 for alle n >= 8

Oplossing: Het resultaat is waar wanneer n = 8, want 82 = 64 en 7 * 8 + 1 = 57. Veronderstel dat het waar is voor een k ≥ 8, dat wil zeggen k² > 7k + 1. (Hiermee willen we aantonen dat het ook geldt voor k+1). Dan

(k + 1)² = k² + 2k + 1
> (7k + 1) + 2k + 1 (vanwege de inductiehypothese: k² > 7k + 1)
= 7(k + 1) + 1 + (2k - 6) (herschrijven)

Omdat k ≥ 8, is 2k - 6>0, dus de laatste uitdrukking boven is groter dan 7(k + 1). De inductie stap is geverifiëerd, en dus is het resultaat waar voor alle n ≥ 8.

(vrij vertaald uit het Engels uit Discrete Mathematics van Normal L. Biggs)
pi_109295700
quote:
0s.gif Op maandag 19 maart 2012 22:24 schreef thenxero het volgende:
Ik heb het een beetje herschreven en verduidelijkt:

[..]

Dus als ik het goed begrijpt, volg je de volgende stappen:
1. schrijf de (k + 1)2 uit
2. voeg het verschil tussen k2 en (k + 1)2 bij 7k + 1
3. herschrijf je die functie naar het format 7(k + 1) + 1 + ...

De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?
pi_109297035
quote:
0s.gif Op maandag 19 maart 2012 22:57 schreef RedVampire het volgende:

[..]

De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?
En dus ook vanaf k = 8.
pi_109297310
quote:
0s.gif Op maandag 19 maart 2012 22:57 schreef RedVampire het volgende:

[..]

Dus als ik het goed begrijpt, volg je de volgende stappen:
1. schrijf de (k + 1)2 uit
2. voeg het verschil tussen k2 en (k + 1)2 bij 7k + 1
3. herschrijf je die functie naar het format 7(k + 1) + 1 + ...

De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?
Wat je met stap 2 bedoelt is nogal vaag. Ik heb het idee dat je inductie nog niet helemaal snapt.

Het idee van inductie is dat je een uitspraak P bewijst vanaf een 'basis' (in dit geval n=8). Dan stel je dat dat P(k) waar is (dat heet de inductiehypothese), en dan laat je zien dat P(k+1) waar is. Als dat lukt, dan heb je bewezen dat het waar is voor iedere n groter dan de basis. Want uit het geval n=8 volgt het voor n=9, daaruit weer voor n=10, etc, als een soort domino-effect. ;)

In dit specifieke neem je voor P(n) de uitspraak n² > 7n + 1. Dan bewijs je P(8), en stel je dat P(k) : k² > 7k + 1waar is (dat is je inductiehypothese). Je wil laten zien dat P(k+1) ook waar is, oftewel (k+1)² > 7(k+1) + 1. Dat doe je door (k+1)² uit te werken, je inductiehypothese te gebruiken, en te herschrijven. Dan zie je dat inderdaad (k + 1)² > 7(k + 1) + 1 + (2k - 6) > 7(k+1)+1, omdat (2k-6)>0 voor k>8. We bekijken k>8, omdat we het willen bewijzen voor k >= 8 (en k=8 is al bewezen). Dat het ook al geldt vanaf k=4 is fijn, maar dat heb je niet eens nodig.
pi_109298120
quote:
0s.gif Op maandag 19 maart 2012 23:44 schreef thenxero het volgende:

[..]

Wat je met stap 2 bedoelt is nogal vaag. Ik heb het idee dat je inductie nog niet helemaal snapt.

Het idee van inductie is dat je een uitspraak P bewijst vanaf een 'basis' (in dit geval n=8). Dan stel je dat dat P(k) waar is (dat heet de inductiehypothese), en dan laat je zien dat P(k+1) waar is. Als dat lukt, dan heb je bewezen dat het waar is voor iedere n groter dan de basis. Want uit het geval n=8 volgt het voor n=9, daaruit weer voor n=10, etc, als een soort domino-effect. ;)

In dit specifieke neem je voor P(n) de uitspraak n² > 7n + 1. Dan bewijs je P(8), en stel je dat P(k) : k² > 7k + 1waar is (dat is je inductiehypothese). Je wil laten zien dat P(k+1) ook waar is, oftewel (k+1)² > 7(k+1) + 1. Dat doe je door (k+1)² uit te werken, je inductiehypothese te gebruiken, en te herschrijven. Dan zie je dat inderdaad (k + 1)² > 7(k + 1) + 1 + (2k - 6) > 7(k+1)+1, omdat (2k-6)>0 voor k>8. We bekijken k>8, omdat we het willen bewijzen voor k >= 8 (en k=8 is al bewezen). Dat het ook al geldt vanaf k=4 is fijn, maar dat heb je niet eens nodig.
Je hebt gelijk, ik heb inderdaad wat moeite met het concept. Ik snapte het met de voorgaande voorbeelden wel, die begonnen met sommatie waar dan een functie voor was gegeven en die je dan voor k=1 en k=k+1 moest bewijzen dat die functie de sommatie correct beschreef.

Maar begrijp ik je nu goed dat de eerste stap in de inductie heeft bewezen waar het punt ligt dat k2 groter wordt dan 7k + 1, en dat de k+1 stap in deze heeft bewezen dat de k2 tegenover 7k + 1 alsmaar groter wordt?
pi_109298524
quote:
0s.gif Op dinsdag 20 maart 2012 00:07 schreef RedVampire het volgende:

[..]

Je hebt gelijk, ik heb inderdaad wat moeite met het concept. Ik snapte het met de voorgaande voorbeelden wel, die begonnen met sommatie waar dan een functie voor was gegeven en die je dan voor k=1 en k=k+1 moest bewijzen dat die functie de sommatie correct beschreef.

Maar begrijp ik je nu goed dat de eerste stap in de inductie heeft bewezen waar het punt ligt dat k2 groter wordt dan 7k + 1
Nee, niet helemaal. Je hebt niet bewezen dat n=8 het kleinste getal is waar de uitspraak waar wordt (maar dat is natuurlijk wel eenvoudig na te gaan door n=7 in te vullen en te concluderen dat de uitspraak onwaar wordt). Je hebt wel al bewezen dat de uitspraak waar is vanaf n=8.

quote:
en dat de k+1 stap in deze heeft bewezen dat de k2 tegenover 7k + 1 alsmaar groter wordt?
Probeer dit eens helder te formuleren.
pi_109300410
quote:
0s.gif Op dinsdag 20 maart 2012 00:07 schreef RedVampire het volgende:

[..]

Je hebt gelijk, ik heb inderdaad wat moeite met het concept. Ik snapte het met de voorgaande voorbeelden wel, die begonnen met sommatie waar dan een functie voor was gegeven en die je dan voor k=1 en k=k+1 moest bewijzen dat die functie de sommatie correct beschreef.
Nee, k = k + 1 is onmogelijk, dus zo moet je het om te beginnen al niet formuleren. De gedachte achter een bewijs met inductie is dat je eerst laat zien dat de te bewijzen uitspraak geldt voor de startwaarde (in jouw geval dus n = 8) en dat je vervolgens laat zien dat de juistheid van de uitspraak voor een natuurlijk getal n = k + 1 volgt uit de juistheid van de uitspraak voor een zekere n = k. Uiteraard mag je niet beginnen met te stellen, zoals je hierboven doet, dat de uitspraak waar is voor elke n ≥ 8, want dat is een petitio principii, d.w.z. dan neem je datgene wat je wil bewijzen al op voorhand voor waar aan, en dan bewijs je dus niets.
quote:
[cut crap]

Het helpt als je je stappen helder opschrijft, bijvoorbeeld als volgt. We hebben al gezien dat

(1) n2 > 7n + 1

geldt voor n = 8. We nemen nu aan dat (1) geldt voor een zekere n = k ≥ 8, dus:

(2) k2 > 7k + 1

Tellen we bij beide leden van (2) 2k + 1 op dan hebben we:

(3) k2 + 2k + 1 > 9k + 2

En dus:

(4) (k + 1)2 > 9k + 2

Nu geldt ook:

(5) 9k + 2 = 7(k + 1) + 1 + (2k - 6)

En aangezien 2k - 6 > 0 voor k ≥ 8 volgt uit (5) dat ook geldt:

(6) 9k + 2 > 7(k + 1) + 1

Op grond van de ongelijkheden (4) en (6) hebben we nu:

(7) (k + 1)2 > 7(k + 1) + 1

Maar (7) betekent niets anders dan dat (1) geldt voor n = k + 1. Uit (2), i.e. de juistheid van (1) voor n = k, volgt dus (7) en daarmee de juistheid van (1) voor n = k + 1. Tezamen met de juistheid van (1) voor n = 8 impliceert dit dat (1) juist is voor elk natuurlijk getal n ≥ 8, QED.

[ Bericht 0% gewijzigd door Riparius op 20-03-2012 01:44:59 ]
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109303638
Bedankt voor de uitleg allemaal, het begint allemaal een beetje duidelijker te worden. Ik denk dat het tijd wordt om de opgaven in het boek even verder uit te werken, ik denk dat het dan vanzelf allemaal helemaal duidelijker wordt.

Ik begrijp nu tenminste hoe ik dit soort probleem moet aanpakken!

:)
pi_109429816
Hoop dat hier iemand mij kan helpen. De vraag waar ik niet uitkom is de volgende

Let A be a nonempty set, and let I be a nonempty set. Assume for all i in I A( i ) is a sigma-
algebra of A, then Intersection of all A( i ) is a sigma-algebra of A.
Het is logisch dat A en de empty set in de intersection zullen zitten maar de andere condities zou ik niet kunnen laten zien. Iemand een idee?
pi_109434868
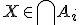Stel X\in \bigcap A_i,
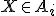dan X\in A_i voor alle 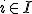i\in I (definitie doorsnede),
dus ook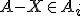 A-X\in A_i voor alle 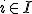i\in I (definitie algebra),
dus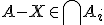 A-X\in\bigcap A_i (definitie doorsnede).

En hetzelfde voor de andere voorwaarde.
pi_109464135
weet iemand hoe je hier makkelijk a en b uit kan halen?

3/(1+a) + 103/(1+b)^2 = 100.41

9/(1+a) + 109/(1+b)^2 = 104.32

Het lukt me om het op te lossen door eerst te schrijven in de vorm a = , en dan a te substituten voor b, maar dat duurt veel te lang.
pi_109464823
quote:
0s.gif Op zaterdag 24 maart 2012 16:17 schreef Klonker het volgende:
weet iemand hoe je hier makkelijk a en b uit kan halen?

3/(1+a) + 103/(1+b)^2 = 100.41

9/(1+a) + 109/(1+b)^2 = 104.32

Het lukt me om het op te lossen door eerst te schrijven in de vorm a = , en dan a te substituten voor b, maar dat duurt veel te lang.
Vermenigvuldig beide leden van je eerste vergelijking met 3 en trek dan de leden van de tweede vergelijking af van de leden van de eerste vergelijking, zodat je een vergelijking in uitsluitend b overhoudt. Als je alleen in de antwoorden geïnteresseerd bent, kun je natuurlijk WolframAlpha gebruiken.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_109464984
quote:
0s.gif Op zaterdag 24 maart 2012 16:46 schreef Riparius het volgende:

[..]

Vermenigvuldig beide leden van je eerste vergelijking met 3 en trek dan de leden van de tweede vergelijking af van de leden van de eerste vergelijking, zodat je een vergelijking in uitsluitend b overhoudt. Als je alleen in de antwoorden geïnteresseerd bent, kun je natuurlijk WolframAlpha gebruiken.
Bedankt!
pi_109497620
Even een vraagje over logaritmen.

Ik had dus het idee dat een logaritme van getal X met grondtal Y eigenlijk gewoon het getal is waarmee je Y moet verheffen om X te krijgen.

log(3)=0,477...
en 10^0,477

Dit klopt vooralsnog dus. Maar als ik een ander grondtal als 10 of e wil invoeren klopt het niet meer. Hier bijvoorbeeld:

5log(3)=2,386...
terwijl 5^2,386 niet gelijk is aan 5

Dus mijn vraag is: wat klopt er niet of wat doe ik fout?

Bij voorbaat dank!
  zondag 25 maart 2012 @ 17:57:28 #99
75592 GlowMouse
l'état, c'est moi
pi_109497904
Er staat 5*log(3). Voor 5log3 moet je log3/log5 intypen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_109497979
quote:
0s.gif Op zondag 25 maart 2012 17:57 schreef GlowMouse het volgende:
Er staat 5*log(3). Voor 5log3 moet je log3/log5 intypen.
aight ok bedankt
actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
[Bèta wiskunde] Huiswerk- en vragentopic
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')