[Bèta wiskunde] Huiswerk- en vragentopic

donderdag 1 maart 2012 @ 23:14:15 #1

thenxero

Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.

Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!

Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).

Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...

_OP

Moderator / Redactie Sport / Devops donderdag 1 maart 2012 @ 23:15:31 #2

zoem

zoemt

Even recapituleren:

quote:
Op donderdag 1 maart 2012 23:02 schreef Paxcon het volgende:
Wtf wat vaag allemaal. Ik heb dit vorig jaar wel eens gehad maar zo ingewikkeld met die formules kan het toch niet zijn?

Voor een normale afgeleide kun je gewoon zeggen je doet de macht keer het voorste getal en trekt 1 van die macht af en dat is de afgeleide? En dat In komt me ook totaal onbekend voor.

quote:
Op donderdag 1 maart 2012 23:10 schreef zoem het volgende:
Dat is helemaal geen rare formule eigenlijk, hij is alleen wat minder bekend. De regel die jij noemt is eigenlijk een versimpelde variant van die formule. Pas het maar eens toe op bijvoorbeeld x³:

$(x^3)' = x^3 (1\cdot \frac{3}{x} + 0 \cdot ln x) = 3x^2$

quote:
Op donderdag 1 maart 2012 23:13 schreef thenxero het volgende:

[..]

Er is toch niks ingewikkelds aan. Eigenlijk is het nog makkelijker: als je de afgeleide neemt hoef je er alleen maar ln(a) bij te zetten .

donderdag 1 maart 2012 @ 23:16:32 #3

#ANONIEM

Ik snap het echt niet

Welke formule krijg je met x = -2 ingevuld?

Moderator / Redactie Sport / Devops donderdag 1 maart 2012 @ 23:17:40 #4

zoem

zoemt

$f(x)'=3^xln3$
$f(-2)'=3^{-2}ln3 = 0.122$

donderdag 1 maart 2012 @ 23:18:15 #5

#ANONIEM

Oke wat in hemelsnaam is dat In. Iets met logaritme?

Moderator / Redactie Sport / Devops donderdag 1 maart 2012 @ 23:19:02 #6

zoem

zoemt

Dat is de natuurlijke logaritme.

donderdag 1 maart 2012 @ 23:19:08 #7

twaalf

ln is inderdaad het logaritme.

donderdag 1 maart 2012 @ 23:19:28 #8

thenxero

Staat ook gewoon op je rekenmachine hoor, zo'n ln knop

donderdag 1 maart 2012 @ 23:20:59 #9

#ANONIEM

Ohja, ik zie het

Dan krijg ik inderdaad het goede antwoord. Toch moet het voor m'n gevoel nog anders kunnen maar zo ben ik tijdelijk uit de brand denk ik

Dankjullie

donderdag 1 maart 2012 @ 23:26:45 #10

thenxero

quote:
Op donderdag 1 maart 2012 23:20 schreef Paxcon het volgende:
Ohja, ik zie het Dan krijg ik inderdaad het goede antwoord. Toch moet het voor m'n gevoel nog anders kunnen maar zo ben ik tijdelijk uit de brand denk ik Dankjullie

Je kan ook de functie plotten, en dan je dy/dx functie nemen, en 2 invullen. Dan hoef je die afgeleide niet eens te kennen, en heb je direct een numerieke benadering.

donderdag 1 maart 2012 @ 23:28:31 #11

#ANONIEM

quote:
Op donderdag 1 maart 2012 23:26 schreef thenxero het volgende:

[..]

Je kan ook de functie plotten, en dan je dy/dx functie nemen, en 2 invullen. Dan hoef je die afgeleide niet eens te kennen, en heb je direct een numerieke benadering.

In dit hoofdstuk staat inderdaad uitleg over dy/dx...

Ik ga het even uitzoeken..

donderdag 1 maart 2012 @ 23:33:52 #12

#ANONIEM

Nouja laat maar ik snap er echt geen zak van

donderdag 1 maart 2012 @ 23:44:45 #13

thenxero

Als je een TI hebt: Plot de functie, druk op 2nd + calc. Ga naar dy/dx. Druk op 2 en dan op enter.

(zo uit mijn hoofd)

maandag 5 maart 2012 @ 21:24:30 #14

Dale.

te vroeg..

maandag 5 maart 2012 @ 21:40:50 #15

Dale.

Ik heb

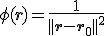
$\phi(\mathbf{r}) = \frac{1}{||\mathbf{r} - \mathbf{r}_0||^2}$

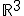met $\mathbf{r}$ vector in $\mathbb{R}^3$ . Nu moet ik de afgeleide bepalen ervan.

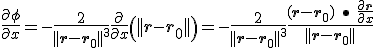
$\frac{\partial \phi}{\partial x} = -\frac{2}{||\mathbf{r} - \mathbf{r}_0||^3}\frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right) = -\frac{2}{||\mathbf{r} - \mathbf{r}_0||^3}\frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||}$

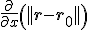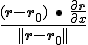Kan iemand mij die laatste stap uitleggen? Waarom $\frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right)$ dus $\frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||}$ is.

maandag 5 maart 2012 @ 21:47:36 #16

motorbloempje

#Anoniem

En sticky!

Ja doei.

maandag 5 maart 2012 @ 22:06:24 #17

motorbloempje

#Anoniem

Ow, Sticky/Open

oops!

Ja doei.

maandag 5 maart 2012 @ 22:07:49 #18

thenxero

quote:
Op maandag 5 maart 2012 21:40 schreef Dale. het volgende:
Ik heb

$\phi(\mathbf{r}) = \frac{1}{||\mathbf{r} - \mathbf{r}_0||^2}$

met $\mathbf{r}$ vector in $\mathbb{R}^3$ . Nu moet ik de afgeleide bepalen ervan.

$\frac{\partial \phi}{\partial x} = -\frac{2}{||\mathbf{r} - \mathbf{r}_0||^3}\frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right) = -\frac{2}{||\mathbf{r} - \mathbf{r}_0||^3}\frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||}$

Kan iemand mij die laatste stap uitleggen? Waarom $\frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right)$ dus $\frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||}$ is.

Als ||...|| staat voor de Euclidische norm, dan kan je het gewoon uitschrijven als wortel en dan differentiëren.

maandag 5 maart 2012 @ 22:25:06 #19

Riparius

quote:
Op maandag 5 maart 2012 21:40 schreef Dale. het volgende:

Kan iemand mij die laatste stap uitleggen? Waarom $\frac{\partial}{\partial x}\left(||\mathbf{r} - \mathbf{r}_0||\right)$ dus $\frac{(\mathbf{r}-\mathbf{r}_0) \ \bullet \ \frac{\partial \mathbf{r}}{\partial x}}{||\mathbf{r} - \mathbf{r}_0||}$ is.

Laten we zeggen dat r = (x,y,z) en r₀ = (x₀,y₀,z₀). Wat is dan het inproduct van r - r₀ en ∂r/∂x ?

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

maandag 5 maart 2012 @ 22:29:14 #20

thenxero

Ik zoek het aantal partities van n in drie positieve getallen a,b,c (dus a+b+c=n), met de restricties dat a<b+1 en b<c, met behulp van een genererende functie.

De genererende functie voor a is (x + x^2 + ... + x^b) (want a neemt waardes aan tussen 1 en b),
voor b: (x^a + x^2 + ... + x^(c-1))
voor c: (x^(b+1) + ... + x^n)

Die drie functies kan ik met elkaar vermenigvuldigen. Maar als je dan kijkt naar de coëfficiënt van x^n, die dan het aantal partities van n zou moeten geven, dan is die afhankelijk van de "gekozen" a,b,c, terwijl die juist variabel zijn. Dus ik zit in de knoop.... Moet ik misschien nog sommeren over alle paren a,b,c?

dinsdag 6 maart 2012 @ 00:01:13 #21

thabit

quote:
Op maandag 5 maart 2012 22:29 schreef thenxero het volgende:
Ik zoek het aantal partities van n in drie positieve getallen a,b,c (dus a+b+c=n), met de restricties dat a<b+1 en b<c, met behulp van een genererende functie.

De genererende functie voor a is (x + x^2 + ... + x^b) (want a neemt waardes aan tussen 1 en b),
voor b: (x^a + x^2 + ... + x^(c-1))
voor c: (x^(b+1) + ... + x^n)

Die drie functies kan ik met elkaar vermenigvuldigen. Maar als je dan kijkt naar de coëfficiënt van x^n, die dan het aantal partities van n zou moeten geven, dan is die afhankelijk van de "gekozen" a,b,c, terwijl die juist variabel zijn. Dus ik zit in de knoop.... Moet ik misschien nog sommeren over alle paren a,b,c?

Je kan de genererendevoortbrengende functies natuurlijk niet van elkaar afhankelijk laten zijn. Dus je moet niet iets doen met "voortbrengende functie van a = (uitdrukking in b)".

Je kan het als volgt bekijken: het gaat om ongeordende drietallen getallen (a, b, c), waarvan de twee kleinste gelijk mogen zijn, maar de grootste niet gelijk mag zijn aan een van de andere twee. Dit is gemakkelijk in bijectie met de drietallen getallen (a, b, c) zonder restricties op de grootste (trek gewoon 1 van de grootste af).

Hopelijk kom je nu verder met deze hint.

dinsdag 6 maart 2012 @ 00:05:42 #22

Dale.

quote:
Op maandag 5 maart 2012 22:07 schreef thenxero het volgende:

[..]

Als ||...|| staat voor de Euclidische norm, dan kan je het gewoon uitschrijven als wortel en dan differentiëren.

Ja klopt. En idd had het gewoon moeten uitschrijven (maar was een beetje lui

, dacht dat er van allerlei zooi zou uitkomen hahaha) was een makkelijke integraal eigenlijk. De tussenstap had achteraf best mogen weggelaten worden eigenlijk.

dinsdag 6 maart 2012 @ 00:34:48 #23

thenxero

quote:
Op dinsdag 6 maart 2012 00:01 schreef thabit het volgende:

[..]

Je kan de genererendevoortbrengende functies natuurlijk niet van elkaar afhankelijk laten zijn. Dus je moet niet iets doen met "voortbrengende functie van a = (uitdrukking in b)".

Je kan het als volgt bekijken: het gaat om ongeordende drietallen getallen (a, b, c), waarvan de twee kleinste gelijk mogen zijn, maar de grootste niet gelijk mag zijn aan een van de andere twee. Dit is gemakkelijk in bijectie met de drietallen getallen (a, b, c) zonder restricties op de grootste (trek gewoon 1 van de grootste af).

Hopelijk kom je nu verder met deze hint. .

Slim. Hiermee lukt het wel

. Bedankt!

dinsdag 6 maart 2012 @ 17:12:04 #24

Forzes

Even een korte vraag m.b.t. het Leontief model (matrixen).

Wat is de uitkomst van?
http://imageshack.us/photo/my-images/860/deelvanvraag5c.png/ (copy/paste deze link)

Wanneer ik dit stukje begrijp kan ik weer verder, het is een deel van het antwoord op een oefententamenvraag waarvan deze (sub)vraag een hele punt waard is, dus hulp wordt zeker op prijs gesteld!

Alvast bedankt.

dinsdag 6 maart 2012 @ 17:21:58 #25

GlowMouse

l'état, c'est moi

Een matrix maal zijn inverse is, vanwege de definitie van de inverse, gelijk aan de eenheidsmatrix.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

dinsdag 6 maart 2012 @ 17:30:44 #26

Forzes

Ik vermoedde het al maar misde de theorie, bedankt voor de snelle bevestiging

woensdag 7 maart 2012 @ 18:10:57 #27

Anoonumos

Ik heb moeite met het bewijzen dat een gelijkvormigheid een bijectie is.
Een gelijkvormigheid is een niet-constante afbeelding f: R² -> R² die verhoudingen van afstanden invariant laat: voor alle viertallen punten a,b,c,d in R² met a !=b en c !=d geldt:
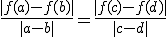
$\frac{|f(a) - f(b)|}{|a-b|} = \frac{|f(c) - f(d)|}{|c-d|}$

Ik weet niet hoe ik de surjectiviteit kan bewijzen. Ik heb het idee dat een gelijkvormigheid een samenstelling is van een isometrie en een schaalfunctie, maar dit concreet maken is nog niet gelukt. Heeft iemand een tip?

woensdag 7 maart 2012 @ 18:17:05 #28

thabit

quote:
Op woensdag 7 maart 2012 18:10 schreef Anoonumos het volgende:
Ik heb moeite met het bewijzen dat een gelijkvormigheid een bijectie is.
Een gelijkvormigheid is een niet-constante afbeelding f: R² -> R² die verhoudingen van afstanden invariant laat: voor alle viertallen punten a,b,c,d in R² met a !=b en c !=d geldt:
$\frac{|f(a) - f(b)|}{|a-b|} = \frac{|f(c) - f(d)|}{|c-d|}$

Ik weet niet hoe ik de surjectiviteit kan bewijzen. Ik heb het idee dat een gelijkvormigheid een samenstelling is van een isometrie en een schaalfunctie, maar dit concreet maken is nog niet gelukt. Heeft iemand een tip?

De verhouding is gegeven en is niet 0 want de afbeelding is niet-constant. Als je nu f door die verhouding deelt, dan krijg je een isometrie.

zaterdag 10 maart 2012 @ 01:17:44 #29

Meneerik2

Hoi!

Weet niet of dit hier hoort, maar ik heb een SPSS vraag. Het is dus de bedoeling dat ik dat voor Research Seminar data verwerk. Leuk, want ik snap er de ballen van. Mijn vraag is als volgt:

Ik heb meerdere keren verschillende items waar ik een construct/variabele van maak. Dat gaat goed. Echter, die items meten de antwoorden van een vraag met een likert-schaal van 1 tot en met 5. En zo nu en dan zit er een 0 tussen. Dat lijkt mij een missing variable. Als ik dat in de variable view aanmerk als missing (Missing > discrete =0), 'ziet' spss wel de missing data wanneer ik Analyze>Descripte>Frequencies doe. Echter, (en hier komt het probleem) verschijnen er dan gaten in mijn construct, precies daar waar in de items een 0 voorkomt. Dus een nul in mijn item betekent een . in mijn construct. Staan er enkel items met correcte antwoorden dan staat er wel netjes een cijfer.

Wat doe ik fout en hoe dit op te lossen?

Bedankt!

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs