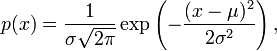SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Er is een boek "Getaltheorie voor beginners" (oid), geschreven door Frits Beukers. Misschien is dat iets voor je.
Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...
kloep kloep
Ik heb het nog even nagekeken en je moet dus de prrimitieven van e^2wortel(y) hebben. Hoe ben je daar dan gekomen? Want daar strand ik de hele tijd.
In dat geval raad ik je "De Telduivel" aan.quote:Op vrijdag 26 juni 2009 11:00 schreef Borizzz het volgende:
Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...
Je bent bijna afgestudeerd wiskundige? Als je dan geen beginner bent… Dan moet het boek wel heel raar geschreven zijn.quote:Op vrijdag 26 juni 2009 11:00 schreef Borizzz het volgende:
Ja, dat boek heb ik ook gezien, maar daarvan wordt ons verteld dat het een veel te hoog instap niveau heeft...
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik geef alleen maar weer wat ze ons verteld hebbenquote:Op vrijdag 26 juni 2009 11:06 schreef Iblis het volgende:
[..]
Je bent bijna afgestudeerd wiskundige? Als je dan geen beginner bent… Dan moet het boek wel heel raar geschreven zijn.
... Maar ach ik schaf ze allebei wel aan!
kloep kloep
Wel, de oppervlakte van een cirkel is pi * r2 waarbij r de straal is, die in dit geval gelijk is aan de functiewaarde.quote:Op vrijdag 26 juni 2009 11:02 schreef Zwavel-Zuur het volgende:
Ik heb het nog even nagekeken en je moet dus de prrimitieven van e^2wortel(y) hebben. Hoe ben je daar dan gekomen? Want daar strand ik de hele tijd.
Je bedoelt dat boek van Enzensberger? Ik dacht dat dit voor beginners in de wiskunde was?! Is dit boek inleidend voor getaltheorie dan?quote:Op vrijdag 26 juni 2009 11:06 schreef thabit het volgende:
[..]
In dat geval raad ik je "De Telduivel" aan.
kloep kloep
't Is een boek voor kinderen die geen wiskunde kunnen. Maar ik ben bang dat er toch weinig materiaal is te vinden dat qua niveau strikt tussen 'De telduivel' en 'Getaltheorie voor beginners' ligt.quote:Op vrijdag 26 juni 2009 11:10 schreef Borizzz het volgende:
[..]
Je bedoelt dat boek van Enzensberger? Ik dacht dat dit voor beginners in de wiskunde was?! Is dit boek inleidend voor getaltheorie dan?
Je kunt ook eens naar je universiteitsbibliotheek gaan, daar heb je natuurlijk genoeg boeken van b.v. Springer, zoals A course in number theory and cryptography. Nu zijn die Springerboeken soms best compact geschreven, maar als je met je laatste vak bezig bent moet dat toch te doen zijn. En als er dan eentje is die je bevalt, dan kun je 't kopen.
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:46:47 ]
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:46:47 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
http://nl.wikipedia.org/wiki/Centrale_limietstellingquote:Op vrijdag 26 juni 2009 14:12 schreef Washington het volgende:
Kan iemand mij vertellen waarom de functie voor een klokgrafiek zo is?
[ afbeelding ]
Heb de wiskundetitels op die Russische site even bekeken en zie bij de niet-Russische titels toch veel bekende namen zoals Gauss, Hermite, Galois, Lagrange ... Al die titels zijn public domain omdat de auteurs al langer dan 70 jaar geleden zijn overleden. Dat is volkomen legaal. Russische titels zijn inderdaad wel recenter, maar ik weet niet hoe het in Rusland met auteursrecht zit. Overigens kun je ook op archive.org legaal terecht voor ingescande oudere titels. Heb daar bijvoorbeeld boeken gevonden van Cajori die mij interesseerden. Voor recente titels kun je beter even op - kijken. Zie daar al enkele dozijnen titels over getaltheorie staan. Meestal djvu formaat (wat ik zelf erg prettig vind werken).quote:Op vrijdag 26 juni 2009 11:34 schreef Iblis het volgende:
Overigens is er ook een website, - genaamd (Russisch voor e-Book) die vrij veel electronische wiskundeboeken hebben, vele gescand. Sommige PDF, sommige DJVU. De legaliteit van die site vind ik wat twijfelachtig (vandaar geen link).
[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:47:10 ]
Als het een vertaling betreft echter, dan wordt het auteursrecht van die vertaling gegeven op het moment dat die vertaling gemaakt is. Maar b.v. Knuth staat er ook op, en dat is echt niet legaal, ook genoeg werken die in 2000 zijn gepubliceerd.quote:
Heb de wiskundetitels op die Russische site even bekeken en zie bij de niet-Russische titels toch veel bekende namen zoals Gauss, Hermite, Galois, Lagrange ... Al die titels zijn public domain omdat de auteurs al langer dan 70 jaar geleden zijn overleden. Dat is volkomen legaal. Russische titels zijn inderdaad wel recenter, maar ik weet niet hoe het in Rusland met auteursrecht zit.
Jup, er zijn meer wegen die naar illegale werken leiden. De bibliotheek vind ik zelf nog het handigst echter.quote:Overigens kun je ook op archive.org legaal terecht voor ingescande oudere titels. Heb daar bijvoorbeeld boeken gevonden van Cajori die mij interesseerden. Voor recente titels kun je beter even op - kijken. Zie daar al enkele dozijnen titels over getaltheorie staan. Meestal djvu formaat (wat ik zelf erg prettig vind werken).
Maar soms heeft iemand een werk als z'n persoonlijke bezit geclaimd lijkt het wel en is het niet in de bieb te vinden.[ Bericht 0% gewijzigd door GlowMouse op 26-06-2009 17:47:26 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Iblis toch, dat ik juist jou sites zie noemen met auteursrechtelijk beschermd materiaal.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja, noemen, niet linken.quote:Op vrijdag 26 juni 2009 17:48 schreef GlowMouse het volgende:
Iblis toch, dat ik juist jou sites zie noemen met auteursrechtelijk beschermd materiaal.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
We leven niet meer in 1989 dat je als je de naam van een BBS had nog niks kon zonder telefoonnummer; met dank aan zoekmachines liggen een naam en een url dicht bij elkaar; niet meer doen dus.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Stel je moet een parametrisatie maken van de doorsnijding van de cilinder (x-1)2 + y2=1 met het vlak y+z=1.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.
kloep kloep
Nee, want je kunt x niet tegelijk als parameter gebruiken ... Ik zou inderdaad zeggen x = 1 + cos t, y = sin t, z = 1 - sin t, 0 ≤ t < 2π.quote:Op zaterdag 27 juni 2009 21:55 schreef Borizzz het volgende:
Stel je moet een parametrisatie maken van de doorsnijding van de cilinder (x-1)2 + y2=1 met het vlak y+z=1.
Vlg mij zijn er dan 2 mogelijkheden:
1. De doorsnijding is een ellips; als je die projecteert op het xy vlak krijg je een cirkel met middelpunt (1,0). Dan kies je x=cos(x)+1 en y=sin(x). Verder rekenen voor z. Klopt dit?
Lijkt me niet handig, maar dat hangt er ook van af wat je vervolgens met die parametervoorstelling wil gaan doen.quote:2. Kun je niet beter x=t kiezen, dan wordt y=+/- sqrt(-t2+2t). Ook weer doorrekenen voor z. Ik zoek ff een handigheidje.
Hoe kom je bij 1) aan z? de keuze van x en y kan ik wel volgen. Verder logisch uiteraard dat je een andere parameter t dan x neemt.
kloep kloep
Je hebt y+z = 1, aangezien y= sin(t) moet z dus wel 1 - sin(t) zijn.
"Reality is an illusion created by a lack of alcohol."
D de driehoek is die (0,0) , (1,0) en (0,1) als hoekpunten heeft
Zijn de grenzen: 0 < x < 1 en 0 < y < (1-x) ??
[ Bericht 99% gewijzigd door motorbloempje op 01-09-2013 21:25:17 ]
"The name is Bond, James Bond"
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Thnx, wist niet hoe ik LaTeX werkend kon krijgenquote:Op zondag 28 juni 2009 17:59 schreef GlowMouse het volgende:
[..]
http://betahw.mine.nu/index.php
en substitueer z=x²
"The name is Bond, James Bond"
Ja, het lijkt me ook handig als je de integratievolgorde omwisselt.quote:
Zijn de grenzen: 0 < x < 1 en 0 < y < (1-x) ??
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus eerst integreren naar y van 0 .. (1-x) en daarna dat hele geval integreren naar x van 0 .. 1?quote:Op zondag 28 juni 2009 18:12 schreef GlowMouse het volgende:
[..]
Ja, het lijkt me ook handig als je de integratievolgorde omwisselt.
Stel dat er dit staat:
Moet ik hierboven de integratievolgorde dan ook omwisselen?
[ Bericht 27% gewijzigd door motorbloempje op 01-09-2013 21:25:22 ]
"The name is Bond, James Bond"
Probeer gewoon, en als het niet lukt is het vroeg genoeg om de volgorde om te draaien.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Als ik het me goed herinner, dan moest je met dit soort dingen altijd van binnen naar buiten werken.
kloep kloep
Ja uiteraard, maar je hebt ook nog de stelling van Fubini.quote:
Als ik het me goed herinner, dan moest je met dit soort dingen altijd van binnen naar buiten werken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
MENSEN! Ik ben met wiskunde kansberekening bezig en ik heb een brandende vraag want ik kom er niet uit!
Dit is de vraag:
Ik heb een bak met 100 speciale Hi-Rel bouten. Helaas voldoet 10% hiervan niet aan de gestelde kwaliteitseisen. Ik pak geheel willekeurig 8 bouten uit de bak.
Bereken de kans dat er tussen deze acht hooguit 1 afgekeurde bout zit.
Dat is het antwoord. Maar ik snap niet hoe ze die dingen tussen de haakjes berekenen?
Op wikipedia zag ik dit:
Maar dat kan niet, want 90 faculteit bijvoorbeeld is zo'n groot getal dat je GRM een error geeft!
Dus wie weet dit?
Dit is de vraag:
Ik heb een bak met 100 speciale Hi-Rel bouten. Helaas voldoet 10% hiervan niet aan de gestelde kwaliteitseisen. Ik pak geheel willekeurig 8 bouten uit de bak.
Bereken de kans dat er tussen deze acht hooguit 1 afgekeurde bout zit.
Dat is het antwoord. Maar ik snap niet hoe ze die dingen tussen de haakjes berekenen?
Op wikipedia zag ik dit:
Maar dat kan niet, want 90 faculteit bijvoorbeeld is zo'n groot getal dat je GRM een error geeft!
Dus wie weet dit?
Blues ain't nothing but a good man feeling bad...
Als je goed kijkt dan zie je na de tweede gelijkheid dat je 90! niet uit hoeft te rekenen. Veel rekenmachines hebben bovendien een nCr-toets.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je moet dan 10C1 x 90C7 delen door 100C8
De C zit gewoon op je rekenmachine (nCr)
De C zit gewoon op je rekenmachine (nCr)
"It's good to be open-minded, but not so open that your brains fall out."
Oh man briljant, als het om de functies gaan in de rekenmachine ben ik echt een noob.quote:Op maandag 29 juni 2009 22:20 schreef automatic_ het volgende:
Je moet dan 10C1 x 90C7 delen door 100C8
De C zit gewoon op je rekenmachine (nCr)
Waar gebruik je nPr voor als ik vragen mag?
Blues ain't nothing but a good man feeling bad...
Dit is het enige wat ik goed kanquote:
[..]
Oh man briljant, als het om de functies gaan in de rekenmachine ben ik echt een noob.
"It's good to be open-minded, but not so open that your brains fall out."
Dat is het nadeel van de GR! Je kunt natuurlijk vereenvoudigen. Begin eens met (90 boven 8), dat is:
En (100 boven 8) is:
Deel je die op elkaar (Delen door een breuk is vermenigvuldigen met het omgekeerde, streep dan 8! weg), dan krijg je:
Nu zie je dat dit hetzelfde is als:
En dat kun je waarschijnlijk wel intypen (je kunt natuurlijk nog verder vereenvoudigen als je wilt).
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:25:29 ]
En (100 boven 8) is:
Deel je die op elkaar (Delen door een breuk is vermenigvuldigen met het omgekeerde, streep dan 8! weg), dan krijg je:
Nu zie je dat dit hetzelfde is als:
En dat kun je waarschijnlijk wel intypen (je kunt natuurlijk nog verder vereenvoudigen als je wilt).
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:25:29 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja en ik leg wat uit! Ben je nu trots op mij?quote:
"It's good to be open-minded, but not so open that your brains fall out."
Ik had een rekenmachine die als de ! het niet deed, de nCr het ook niet deed.quote:
Als je goed kijkt dan zie je na de tweede gelijkheid dat je 90! niet uit hoeft te rekenen. Veel rekenmachines hebben bovendien een nCr-toets.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja, je overtreft mijn verwachtingen.quote:
[..]
Ja en ik leg wat uit! Ben je nu trots op mij?
Batterijen op?quote:Op maandag 29 juni 2009 22:27 schreef Iblis het volgende:
[..]
Ik had een rekenmachine die als de ! het niet deed, de nCr het ook niet deed.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kijk nog eens goed naar de uitwerking die je er zelf bij geeft. Het gaat om quotiënten met binomiaalcoëfficiënten in de teller en in de noemer, dus wat kun je met die breuken doen?quote:Op maandag 29 juni 2009 22:16 schreef GoodGawd het volgende:
MENSEN! Ik ben met wiskunde kansberekening bezig en ik heb een brandende vraag want ik kom er niet uit!
Dit is de vraag:
Ik heb een bak met 100 speciale Hi-Rel bouten. Helaas voldoet 10% hiervan niet aan de gestelde kwaliteitseisen. Ik pak geheel willekeurig 8 bouten uit de bak.
Bereken de kans dat er tussen deze acht hooguit 1 afgekeurde bout zit.
[ afbeelding ]
Dat is het antwoord. Maar ik snap niet hoe ze die dingen tussen de haakjes berekenen?
Op wikipedia zag ik dit:
[ afbeelding ]
Maar dat kan niet, want 90 faculteit bijvoorbeeld is zo'n groot getal dat je GRM een error geeft!
Dus wie weet dit?
F5'en?quote:
[..]
Kijk nog eens goed naar de uitwerking die je er zelf bij geeft. Het gaat om quotiënten met binomiaalcoëfficiënten in de teller en in de noemer, dus wat kun je met die breuken doen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Inderdaad, hét grote nadeel van Firefox en dan tegelijk veel tabbladen open hebben staan en met (heel) andere dingen bezig zijn. Mea culpa.quote:
En trouwens met die normal pdf en normal cdf en binomal pdf, cdf etc etc.
Het is mij altijd een raadsel geweest wanneer ik nou die cdf of die pdf moest nemen?
Het is mij altijd een raadsel geweest wanneer ik nou die cdf of die pdf moest nemen?
Blues ain't nothing but a good man feeling bad...
ff snel:
De C in CDF staat voor cumulatief. Dit betekent dat het een gebied bestrijkt. De binomcdf van 2 is daarmee de kans op 0, 1 of 2 keer succes. ( je krijgt dus de kans P(x<=2))
PDF rekent echter maar één mogelijkheid uit. De binompdf van 2 is dus puur en alleen de kans dat je 2 keer succes hebt in je reeks experimenten. (Je berekent dus de kans P(X=2))
De C in CDF staat voor cumulatief. Dit betekent dat het een gebied bestrijkt. De binomcdf van 2 is daarmee de kans op 0, 1 of 2 keer succes. ( je krijgt dus de kans P(x<=2))
PDF rekent echter maar één mogelijkheid uit. De binompdf van 2 is dus puur en alleen de kans dat je 2 keer succes hebt in je reeks experimenten. (Je berekent dus de kans P(X=2))
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Ik heb een kromme K in parametervoorstelling gegeven door:
y = f(t) = t3/(t2-1)
en
x = g(t) = t2/(t2-1)
gevraagd wordt om dit beestje te onderzoeken. Dus snijpunten met de coordinaatassen, punten waarin helling plat of loodrecht is, limietwaarden en horizontale en vertikale asympoten opsporen. Niet bijster moeilijk dus. Totdat ze scheve asymptoten gaan vragen. OK, dat zal dan grotendeels op dezelfde manier gaan als voor standaard y=f(x) functies, maw bereken de afgeleide dy/dx en bereken vervolgens de limietwaarde van dy/dx voor x naar + of - oneindig. Dit geeft de a-factor (rico dus) voor de tweeterm ax+b die de asymptoot beschijft. Uit ( f(x) - (ax + b) ) is met een hoop gegoochel dan de intercept b te berekenen. Vertaald naar parametercurven betekent dit dus (dy/dt)/(dx/dt) = dy/dx berekenen en limietwaarden van dy/dx voor t naar + of - oneindig berekenen. a heb ik dus al gevonden, maar die b-term loop ik mee te k*tten; ik kan geen uitdrukking K(t) - (at+b) vinden die op ( f(x) - (ax + b) ) lijkt. Any suggestions?
y = f(t) = t3/(t2-1)
en
x = g(t) = t2/(t2-1)
gevraagd wordt om dit beestje te onderzoeken. Dus snijpunten met de coordinaatassen, punten waarin helling plat of loodrecht is, limietwaarden en horizontale en vertikale asympoten opsporen. Niet bijster moeilijk dus. Totdat ze scheve asymptoten gaan vragen. OK, dat zal dan grotendeels op dezelfde manier gaan als voor standaard y=f(x) functies, maw bereken de afgeleide dy/dx en bereken vervolgens de limietwaarde van dy/dx voor x naar + of - oneindig. Dit geeft de a-factor (rico dus) voor de tweeterm ax+b die de asymptoot beschijft. Uit ( f(x) - (ax + b) ) is met een hoop gegoochel dan de intercept b te berekenen. Vertaald naar parametercurven betekent dit dus (dy/dt)/(dx/dt) = dy/dx berekenen en limietwaarden van dy/dx voor t naar + of - oneindig berekenen. a heb ik dus al gevonden, maar die b-term loop ik mee te k*tten; ik kan geen uitdrukking K(t) - (at+b) vinden die op ( f(x) - (ax + b) ) lijkt. Any suggestions?
je hebt dy/dx = -0.5(t³-3t).
Ik snap alleen niet waarom je t naar +/- oneindig wilt laten gaan.
Ik snap alleen niet waarom je t naar +/- oneindig wilt laten gaan.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Denk daar nog over na, dan kom je uiteindelijk op twee waarden van a. We onderzoeken a=1.quote:
Ik snap alleen niet waarom je t naar +/- oneindig wilt laten gaan.
Dan geldt voor die asymptoot dat lim(t->1) t³/(t²-1) - t²/(t²-1) - b = 0
dus lim(t->1) t²(t-1)/(t²-1) = b
dus lim(t->1) t²/(t+1) = b
dus b=1/2.
[ Bericht 0% gewijzigd door GlowMouse op 30-06-2009 14:06:44 (puntjes ingevuld) ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Is denk ik macht der gewoonte; vanwege mijn ervaringen met scheve asymptoten voor y=f(x) functies wordt die oplossingsstrategie getriggerd in mn kop.quote:Op dinsdag 30 juni 2009 13:44 schreef GlowMouse het volgende:
je hebt dy/dx = -0.5(t³-3t).
Ik snap alleen niet waarom je t naar +/- oneindig wilt laten gaan.
Maar goed, dan laat ik t alleen van boven naar 1, van onder naar 1, van boven naar -1 en van onder naar -1 gaan. krijg je idd 1 en -1 voor de hellingen van die twee scheve asymptoten. Maar het berekenen van de intercept dus maar niet.
Van boven / van onder maakt niet uit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus als ik het goed begrijp stel je dusquote:Op dinsdag 30 juni 2009 13:52 schreef GlowMouse het volgende:
[..]
Denk daar nog over na, dan kom je uiteindelijk op twee waarden van a. We onderzoeken a=1.
Dan geldt voor die asymptoot dat lim(t-> ...) t³/(t²-1) - t²/(t²-1) - b = 0
dus lim(t-> ...) t²(t-1)/(t²-1) = b
dus lim(t->...) t²/(t+1) = b
dus b=1/2.
y - ax - b = 0
y - ax = b
f(t) - a*g(t) = b
f(t) - 1*g(t) = b OF f(t) - (-1)*g(t) = b
en ga je daarmee verder rekenen?
Je kunt ook een vergelijking geven voor de kromme: x3 - xy2 + y2 = 0. Daaruit kun je e.e.a. ook makkelijk afleiden.
gevonden!!quote:
weer twee dingen geleerd:
-in tegenstelling tot functies y=f(x) hoeft de parameter niet naar (-)oneindig te lopen voor een scheve asymptoot
-voor scheve asymptoten is recht-toe-recht-aan invullen van y - ax - b = 0 voldoende
quote:
Je kunt ook een vergelijking geven voor de kromme: x3 - xy2 + y2 = 0. Daaruit kun je e.e.a. ook makkelijk afleiden.
hoe kom je erop?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
???quote:Op dinsdag 30 juni 2009 14:17 schreef thabit het volgende:
Je kunt ook een vergelijking geven voor de kromme: x3 - xy2 + y2 = 0. Daaruit kun je e.e.a. ook makkelijk afleiden.
ik zie het verband met mijn parametervoorstelling niet
De vergelijking is waar voor iedere tquote:
[..]
???
ik zie het verband met mijn parametervoorstelling niet [ afbeelding ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
maar hoe in godsnaam schud je zoiets zo snel uit je mouw.quote:Op dinsdag 30 juni 2009 14:30 schreef GlowMouse het volgende:
[..]
De vergelijking is waar voor iedere t
*kijkt nog eens met heel grote ogen
OK, recht-toe-recht-aan invullen is natuurlijk geen kunst, maar ik geloof dat ik er nu ook een patroon in begin te zien. Iets met tot de kleinste gemeenschappelijke macht van t verheffen van teller en noemer.
[ Bericht 17% gewijzigd door ErictheSwift op 30-06-2009 15:31:10 ]
Wat ik zelf handig vind hier is om met projectieve coordinaten te werken. Je krijgt dan een parametervoorstellingquote:
(X : Y : Z) = (T2U : T3 : T2U - U3)
Als je nu een vergelijking wilt vinden dan moet je bijvoorbeeld de term U3 wegwerken in de Z coordinaat. U komt alleen nog voor bij X, dus krijg je iets met X3 = T6U3. Om het weg te kunnen werken moet je Z dus met T6 = Y2 vermenigvuldigen. Zo vind je
X3 + Y2Z = T8U = XY2. In affiene coordinaten:
x3 + y2 = xy2
Voor de geinteresseerden:
In het algemeen kun je zulke vergelijkingen met Groebnerbases vinden. We hebben de ring Q[t, 1/(t2-1)] = Q[t, z] / (z(t2 - 1)). Tussen de elementen t2z en t3z willen we alle relaties vinden. Als je nu op de ring Q[x,y,z,t] een monoomordening definieert waarin elk monoom in enkel x en y kleiner is dan de rest, dan kun je de relaties uit een Groebnerbasis voor het ideaal (tz - 1, x - t2z, y - t3z) afleiden.
Nu een codevoorbeeld met het wiskundepakket SAGE:
En we zien de vergelijking als laatste element van de rij.
In het algemeen kun je zulke vergelijkingen met Groebnerbases vinden. We hebben de ring Q[t, 1/(t2-1)] = Q[t, z] / (z(t2 - 1)). Tussen de elementen t2z en t3z willen we alle relaties vinden. Als je nu op de ring Q[x,y,z,t] een monoomordening definieert waarin elk monoom in enkel x en y kleiner is dan de rest, dan kun je de relaties uit een Groebnerbasis voor het ideaal (tz - 1, x - t2z, y - t3z) afleiden.
Nu een codevoorbeeld met het wiskundepakket SAGE:
| 1 2 3 4 | sage: I = (z*(t^2-1) - 1, x - z*t^2, y - z*t^3) * R sage: I.groebner_basis() [t^2 + x^2 + x - y^2, t*x - y, t*y + x^2 - y^2, z - x + 1, x^3 - x*y^2 + y^2] |
En we zien de vergelijking als laatste element van de rij.
Je hebt factoranalyse en discriminantanalyse. Maar nu is de vraag of de factoranalyse discriminantfuncties heeft. Ik kom er echt niet uit, ik kan bij factoranalyse geen discriminantfuncties ontdekken...
EDIT: Ik haal nu volgens mij alles door elkaar. Kan iemand aangeven wat de verschillen/overeenkomsten zijn tussen de factoren (uit de factoranalyse) en de discriminantfunctie uit de discriminantanalyse? Ik denk dat ik de stof dan makkelijker kan bestuderen. Ik kan hierover niets op internet of in het boek vinden.
[ Bericht 44% gewijzigd door James.Bond op 30-06-2009 21:24:47 ]
EDIT: Ik haal nu volgens mij alles door elkaar. Kan iemand aangeven wat de verschillen/overeenkomsten zijn tussen de factoren (uit de factoranalyse) en de discriminantfunctie uit de discriminantanalyse? Ik denk dat ik de stof dan makkelijker kan bestuderen. Ik kan hierover niets op internet of in het boek vinden.
[ Bericht 44% gewijzigd door James.Bond op 30-06-2009 21:24:47 ]
"The name is Bond, James Bond"
Je moet even iets meer uitleggen over jouw probleem wil je hier antwoord krijgen lijkt me.quote:Op dinsdag 30 juni 2009 20:43 schreef James.Bond het volgende:
Je hebt factoranalyse en discriminantanalyse. Maar nu is de vraag of de factoranalyse discriminantfuncties heeft. Ik kom er echt niet uit, ik kan bij factoranalyse geen discriminantfuncties ontdekken...
kloep kloep
Ik heb mijn post aangepast, hopelijk kun je er wat mee.quote:Op dinsdag 30 juni 2009 21:22 schreef Borizzz het volgende:
[..]
Je moet even iets meer uitleggen over jouw probleem wil je hier antwoord krijgen lijkt me.
"The name is Bond, James Bond"
En kan dit ook allemaal met het handje, of ben je op de brute kracht van een CPU aangewezen?quote:Op dinsdag 30 juni 2009 15:41 schreef thabit het volgende:
Voor de geinteresseerden:
In het algemeen kun je zulke vergelijkingen met Groebnerbases vinden. We hebben de ring Q[t, 1/(t2-1)] = Q[t, z] / (z(t2 - 1)). Tussen de elementen t2z en t3z willen we alle relaties vinden. Als je nu op de ring Q[x,y,z,t] een monoomordening definieert waarin elk monoom in enkel x en y kleiner is dan de rest, dan kun je de relaties uit een Groebnerbasis voor het ideaal (tz - 1, x - t2z, y - t3z) afleiden.
Nu een codevoorbeeld met het wiskundepakket SAGE:
[ code verwijderd ]
En we zien de vergelijking als laatste element van de rij.
Wat Thabit doet is echte wiskunde, maar in dit geval kun je ook met elementaire algebra de vergelijking van de curve uit de parametervoorstellingen afleiden, heb je alleen die CPU tussen je oren voor nodig.quote:Op dinsdag 30 juni 2009 23:25 schreef ErictheSwift het volgende:
[..]
En kan dit ook allemaal met het handje, of ben je op de brute kracht van een CPU aangewezen?
Je hebt:
(1) x = t2/(t2 -1)
(2) y = t3/(t2 - 1)
Je ziet nu meteen dat geldt y = tx, oftewel:
(3) t = y/x
Substitutie van (3) in (1) levert dan na uitwerking x3 - xy2 + y2 = 0.
ik had het eigenlijk over die groebner basis, of dat ook met het handje te doen was, want het wikipedia artikel had het erover dat die basis vooral in computational algebra gebruikt wordt. Maar OK, 2 polynoomstaartdelingen uitvoeren en gelijk stellen werkt hier ook.quote:Op dinsdag 30 juni 2009 23:43 schreef Riparius het volgende:
[..]
Wat Thabit doet is echte wiskunde, maar in dit geval kun je ook met elementaire algebra de vergelijking van de curve uit de parametervoorstellingen afleiden, heb je alleen die CPU tussen je oren voor nodig.
Je hebt:
(1) x = t2/(t2 -1)
(2) y = t3/(t2 - 1)
Je ziet nu meteen dat geldt y = tx, oftewel:
(3) t = y/x
Substitutie van (3) in (1) levert dan na uitwerking x3 - xy2 + y2 = 0.
Meestal zijn Groebnerbasisberekeningen te ingewikkeld om met de hand uit te voeren (de looptijd is in het slechtste geval dubbelexponentieel als ik me niet vergis), maar in dit specifieke voorbeeld is dat geen enkel probleem. 't Is zelfs wel illustratief om dat gewoon eens een keertje te doen, dan zie je wat er gebeurt.
Mijn vraag is:
[2n boven sigma]Sigma[k=1 onder sigma] (-1) ^ k . k = n
Met n positief en geheel. Bewijs dit.
(Dus je krijgt -1 + 2 -3 + 4 -5 + ... + 2n, afwisselend een min-teken en plus-teken)
[2n boven sigma]Sigma[k=1 onder sigma] (-1) ^ k . k = n
Met n positief en geheel. Bewijs dit.
(Dus je krijgt -1 + 2 -3 + 4 -5 + ... + 2n, afwisselend een min-teken en plus-teken)
\sigma typen. Of \varsigma als je de andere sigma wilt.quote:
Hoe krijg ik een sigma-teken in die site van GlowMouse?
En als je de hoofdletter wilt \Sigma. De truc is echter om LaTeX te leren, althans, wat wiskunde notatie betreft, ik zoek dat even voor je op!Wat jij wilt is dus dit:
En ik heb dat zo getypt:
| 1 |
Hmm, ik kan nog niet echt een handige guide vinden.
[ Bericht 27% gewijzigd door motorbloempje op 01-09-2013 21:25:38 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Een inductiebewijs lijkt me overigens goed te doen, heb je dat al geprobeerd?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Hier kan ik wel wat mee. En dat bedoel ik idd.quote:Op woensdag 1 juli 2009 14:32 schreef Iblis het volgende:
[..]
\sigma typen. Of \varsigma als je de andere sigma wilt.
Wat jij wilt is dus dit:
[ afbeelding ]
En ik heb dat zo getypt:
[ code verwijderd ]
Hmm, ik kan nog niet echt een handige guide vinden.
Daar heb ik bar weinig ervaring mee. Met sigma's ben ik ook slecht.quote:Op woensdag 1 juli 2009 14:39 schreef Iblis het volgende:
Een inductiebewijs lijkt me overigens goed te doen, heb je dat al geprobeerd?
Ik weet wel ongeveer wat ik wil, maar weet niet hoe ik het moet uitwerken.
Hier is een tutorial: http://www.forkosh.com/mimetextutorial.html
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Wat wil je dan?quote:
[..]
Daar heb ik bar weinig ervaring mee. Met sigma's ben ik ook slecht.
Ik weet wel ongeveer wat ik wil, maar weet niet hoe ik het moet uitwerken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Nu, dan heb je twee zaken nodig: Een basisgeval, en een inductiehypothese. Kun je die formuleren?quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
n=1 is mijn basisgeval. Ik heb laten zien dat dit klopt.
Nu n + 1:
Zo? Maar wat nu?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:25:44 ]
Nu n + 1:
Zo? Maar wat nu?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:25:44 ]
Nu treedt je inductiehypothese in werking. De truc is namelijk, en dat is essentieel, dat je nu wilt bewijzen dat als het geldt voor n dat het dán ook geldt voor n + 1. Dus bij deze stap wil je het voor n + 1 bewijzen, maar dan mag je dus aannemen dat het voor n inderdaad geldt. Als je dat gegeven toepast, dan kun je de som vereenvoudigen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
We beginnen dus hiermee:
En splitsen nu de som, de laatste twee termen halen we eruit, om het zo te zeggen:
Nu echter kun je je inductie-hypothese toepassen. Je neemt namelijk aan dat voor n de gelijkheid al geldt, dus je kunt nu stellen dat je:
kunt toepassen, dat doen we dus, en we krijgen daarom:
Dat kunnen we even uitwerken:
Dus:
n + 1 = n + 1
Dat klopt.
Kortom, je hebt nu bewezen dat als het voor n geldt, dat het dan ook voor n+1 geldt. Met het basisgeval, n = 1, is nu je bewijs rond. Immers uit dit basisgeval en bovenstaande volgt dat het ook voor n = 2 geldt, en daar weer uit voor n = 3, enzovoort.
[ Bericht 0% gewijzigd door motorbloempje op 01-09-2013 21:25:48 ]
En splitsen nu de som, de laatste twee termen halen we eruit, om het zo te zeggen:
Nu echter kun je je inductie-hypothese toepassen. Je neemt namelijk aan dat voor n de gelijkheid al geldt, dus je kunt nu stellen dat je:
kunt toepassen, dat doen we dus, en we krijgen daarom:
Dat kunnen we even uitwerken:
Dus:
n + 1 = n + 1
Dat klopt.
Kortom, je hebt nu bewezen dat als het voor n geldt, dat het dan ook voor n+1 geldt. Met het basisgeval, n = 1, is nu je bewijs rond. Immers uit dit basisgeval en bovenstaande volgt dat het ook voor n = 2 geldt, en daar weer uit voor n = 3, enzovoort.
[ Bericht 0% gewijzigd door motorbloempje op 01-09-2013 21:25:48 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Waar ik van een uitdrukking met som-teken naar n - (2n + 1) + (2n + 2) ga?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Dat is hele truc van inductief bewijzen. Je zet een inductiebewijs namelijk zo op:
1) Basisstap (voor n = 1)
2) Inductiestap: Als het voor n geldt, dan geldt het ook voor n + 1.
(2) is dus de crux. Je zou ook kunnen zeggen: Aangenomen dat het voor n geldt, dán geldt het ook voor n + 1. In het bewijs voor stap 2 kun je dus aannemen dat de gelijkheid in het geval van n al geldt. En dat is wat ik doe.
Ik heb dus deze uitdrukking:
Mijn aanname is dat:
inderdaad geldt. En als ik dat toepas, dan krijg ik:
n - (2n + 1) + (2n + 2)
Dat lijkt misschien een beetje raar, want hoe heb ik nu echt wat bewezen? Zit ik niet gewoon aan te nemen wat ik moet bewijzen? Het antwoord daarop is Nee maar dat is alleen omdat je stap (1) hebt. Stap (2) op zich is niet voldoende als bewijs.
Want ik heb alleen nog maar bewezen dat als het voor een zekere n geldt (ik kan het niet vaak genoeg zeggen) dat het dan ook voor (n + 1) geldt. Dus stel het geldt voor n = 10, dan ook voor n = 11. (En dus dan ook voor n = 12).
En daarom heb ik stap 1 nodig. Dat is namelijk je beginnetje. Dan zeg je: Aha, kijk, het geldt inderdaad voor n = 1, dus mag ik op basis van (2) concluderen dat het voor n = 2 geldt. En dan kan mag ik op basis van (2) concluderen dat het voor n = 3 geldt, en zo kun je doorgaan natuurlijk.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:25:54 ]
1) Basisstap (voor n = 1)
2) Inductiestap: Als het voor n geldt, dan geldt het ook voor n + 1.
(2) is dus de crux. Je zou ook kunnen zeggen: Aangenomen dat het voor n geldt, dán geldt het ook voor n + 1. In het bewijs voor stap 2 kun je dus aannemen dat de gelijkheid in het geval van n al geldt. En dat is wat ik doe.
Ik heb dus deze uitdrukking:
Mijn aanname is dat:
inderdaad geldt. En als ik dat toepas, dan krijg ik:
n - (2n + 1) + (2n + 2)
Dat lijkt misschien een beetje raar, want hoe heb ik nu echt wat bewezen? Zit ik niet gewoon aan te nemen wat ik moet bewijzen? Het antwoord daarop is Nee maar dat is alleen omdat je stap (1) hebt. Stap (2) op zich is niet voldoende als bewijs.
Want ik heb alleen nog maar bewezen dat als het voor een zekere n geldt (ik kan het niet vaak genoeg zeggen) dat het dan ook voor (n + 1) geldt. Dus stel het geldt voor n = 10, dan ook voor n = 11. (En dus dan ook voor n = 12).
En daarom heb ik stap 1 nodig. Dat is namelijk je beginnetje. Dan zeg je: Aha, kijk, het geldt inderdaad voor n = 1, dus mag ik op basis van (2) concluderen dat het voor n = 2 geldt. En dan kan mag ik op basis van (2) concluderen dat het voor n = 3 geldt, en zo kun je doorgaan natuurlijk.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:25:54 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ah okay. Heel helder uitgelegd.
Maar je zegt dus
omdat je 2n + 2 hebt ?
[ Bericht 2% gewijzigd door motorbloempje op 01-09-2013 21:25:58 ]
Maar je zegt dus
omdat je 2n + 2 hebt ?
[ Bericht 2% gewijzigd door motorbloempje op 01-09-2013 21:25:58 ]
Ja, ik haal een paar termen uit dat somteken dus:
Dat doe ik natuurlijk expres zo, zodat ik die vervanging daarna makkelijk kan toepassen. Ik zou er ook eentje meer of minder uit kunnen halen, maar ja, dat is niet handig.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:26:00 ]
Dat doe ik natuurlijk expres zo, zodat ik die vervanging daarna makkelijk kan toepassen. Ik zou er ook eentje meer of minder uit kunnen halen, maar ja, dat is niet handig.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:26:00 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Als je 'm nog niet gedaan hebt:
Is ook een klassieker om met volledige inductie te bewijzen. Kun je kijken of je het begrepen hebt.
[ Bericht 0% gewijzigd door motorbloempje op 01-09-2013 21:26:03 ]
Is ook een klassieker om met volledige inductie te bewijzen. Kun je kijken of je het begrepen hebt.
[ Bericht 0% gewijzigd door motorbloempje op 01-09-2013 21:26:03 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik zou er dan nog wel een k bij typen.quote:Op woensdag 1 juli 2009 16:05 schreef Iblis het volgende:
Als je 'm nog niet gedaan hebt:
[ afbeelding ]
Is ook een klassieker om met volledige inductie te bewijzen. Kun je kijken of je het begrepen hebt.
Gefikst!quote:
[..]
Ik zou er dan nog wel een k bij typen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Dank voor het beantwoorden van mijn vraag met die nCR! Ik heb mijn toets met een 8,8 gehaald en heb daarmee mijn propedeuse in de zak
Blues ain't nothing but a good man feeling bad...
P !quote:Op woensdag 1 juli 2009 19:03 schreef GoodGawd het volgende:
Dank voor het beantwoorden van mijn vraag met die nCR! Ik heb mijn toets met een 8,8 gehaald en heb daarmee mijn propedeuse in de zak
Gefeliciteerd.
GO LANCE !!!
Ik zou het heel anders aanpakken. Die factor (-1)k zorgt alleen voor een alternerend teken van de termen van je som, en het aantal termen is bovendien steeds even. Je kunt de som dan ook eenvoudig herschrijven als het verschil van twee sommen van rekenkundige rijen en vervolgens de gangbare somformule voor rekenkundige rijen toepassen.quote:Op woensdag 1 juli 2009 14:41 schreef Washington het volgende:
[..]
Daar heb ik bar weinig ervaring mee. Met sigma's ben ik ook slecht.
Ik weet wel ongeveer wat ik wil, maar weet niet hoe ik het moet uitwerken.
Hoi!
Ik heb even een vraag over modulorekenen, wat waarschijnlijk heel simpel is
Als vraag heb ik:
Bereken de rest van 2^100 modulo 7. Tip: 2³ modulo 7 = 1
en
Wat is de rest van 2 * 10^10 modulo 97
Zelf heb ik al wat geprobeerd, maar ik zie niet hoe je bijvoorbeeld van die 2³ modulo 7 naar het antwoord van 2^100 modulo 7 kan komen.
Alvast bedankt!
Ik heb even een vraag over modulorekenen, wat waarschijnlijk heel simpel is
Als vraag heb ik:
Bereken de rest van 2^100 modulo 7. Tip: 2³ modulo 7 = 1
en
Wat is de rest van 2 * 10^10 modulo 97
Zelf heb ik al wat geprobeerd, maar ik zie niet hoe je bijvoorbeeld van die 2³ modulo 7 naar het antwoord van 2^100 modulo 7 kan komen.
Alvast bedankt!
