[Bèta wiskunde] Huiswerk- en vragentopic.

woensdag 21 januari 2015 @ 21:02:50 #176

Alrac4

quote:
Op woensdag 21 januari 2015 21:00 schreef CapnIzzy het volgende:
Hoi,

kort vraagje tussendoor: ik kan mijzelf niet meer herinneren hoe je ln weg werkt in een vergelijking .

11.64 = ln(4*I)

Hoe krijg ik hier I vrij?

Weet je nog wat je krijgt als je e^ln(x) berekent?

woensdag 21 januari 2015 @ 21:03:35 #177

CapnIzzy

Geef aye voor de kapitein

quote:
Op woensdag 21 januari 2015 21:02 schreef Alrac4 het volgende:

[..]

Weet je nog wat je krijgt als je e^ln(x) berekent?

O ja, thanks

. Deed telkens maal e

, moet inderdaad e^ zijn

Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game

woensdag 21 januari 2015 @ 21:06:09 #178

PausNicolaas

quote:
Op woensdag 21 januari 2015 20:58 schreef Borizzz het volgende:
Dat is de Latex-code. Moet ik mij ook nog eens in gaan verdiepen als ik tijd heb.
Paus: volgens mij pas jij de theorie van partieel integreren gewoon niet goed toe. Op hhofstede.nl en math4all.nl wordt dat wel uitgelegd

Volgens mij doe ik het perfect.
Dat werd net hierboven ook al gezegd.

En de formule komt rechtstreeks uit mijn boek.

'Ego te absolvo peccatis tuis in nomine patris et filii et spiritus sancti.'

woensdag 21 januari 2015 @ 21:09:26 #179

Riparius

quote:
Op woensdag 21 januari 2015 20:07 schreef PausNicolaas het volgende:

[..]

Yes, dat had ik gezien.

f * g' = f * g - (f ' *g)

Zoals ik dat probeerde, kreeg ik een enorm lange functie waar ik uiteindelijk niks mee op schoot.

Bij partieel integreren is het altijd zaak dat je de integrand op een geschikte en handige manier schrijft als het product van een functie en een afgeleide van een andere functie. De regel voor partieel integreren bij onbepaalde integralen luidt

$\int f(x)g'(x){\rm d}x \,=\, f(x)g(x) \,-\, \int f'(x)g(x){\rm d}x$

Zie ook hier.

Gevraagd wordt nu

$\int \frac{\ln\,x}{(x\,+\,1)^2}\mathrm{d}x$

te bepalen. We kunnen hier kiezen

$f(x)\,=\,\ln\,x$

zodat

$f'(x)\,=\,\frac{1}{x}$

en

$g'(x)\,=\,\frac{1}{(x\,+\,1)^2}$

zodat we kunnen nemen

$g(x)\,=\,-\,\frac{1}{x\,+\,1}$

We krijgen dan

$\int \frac{\ln\,x}{(x\,+\,1)^2}\mathrm{d}x\,=\,-\,\frac{\ln\,x}{x\,+\,1}\,-\,\int -\,\frac{1}{x(x\,+\,1)}\mathrm{d}x\,=\,-\,\frac{\ln\,x}{x\,+\,1}\,+\,\int \frac{1}{x(x\,+\,1)}\mathrm{d}x$

Nu moeten we de integraal in het rechterlid nog bepalen. Dat kunnen we doen door de integrand op te splitsen in partiële breuken. We willen hebben

$\frac{1}{x(x\,+\,1)}\,=\,\frac{A}{x}\,+\,\frac{B}{x\,+\,1}$

waarbij we dan A en B moeten bepalen. Dit doen we door beide leden van deze gelijkheid te vermenigvuldigen met x(x+1), dan krijgen we

$1\,=\,A(x\,+\,1)\,+\,Bx$

oftewel

$1\,=\,(A\,+\,B)x\,+\, A$

waaruit we af kunnen lezen dat A + B = 0 en A = 1 moet zijn, en waaruit volgt dat B = −1. Zo hebben we dus

$\frac{1}{x(x\,+\,1)}\,=\,\frac{1}{x}\,-\,\frac{1}{x\,+\,1}$

en daarmee

$\int \frac{1}{x(x\,+\,1)}\mathrm{d}x\,=\,\int \left(\frac{1}{x}\,-\,\frac{1}{x\,+\,1}\right)\mathrm{d}x\,=\,\ln\, x \,-\, \ln(x\,+\,1)\,+\,C$

Invullen hiervan in bovenstaande betrekking voor de integraal van ln(x)/(x+1)² geeft dan

$\int \frac{\ln\,x}{(x\,+\,1)^2}\mathrm{d}x\,=\,-\,\frac{\ln\,x}{x\,+\,1}\,+\,\ln\,x\,-\,\ln(x\,+\,1)\,+\,C$

Nu kunnen we dit nog vereenvoudigen, want we hebben immers

$-\,\frac{\ln\,x}{x\,+\,1}\,+\,\ln\,x\,=\,-\,\frac{\ln\,x}{x\,+\,1}\,+\,\frac{(x\,+\,1)\ln\,x}{x\,+\,1}\,=\,\frac{x\ln\,x}{x\,+\,1}$

zodat we uiteindelijk krijgen

$\int \frac{\ln\,x}{(x\,+\,1)^2}\mathrm{d}x\,=\,\frac{x\ln\,x}{x\,+\,1}\,-\,\ln(x\,+\,1)\,+\,C$

That's all.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 21 januari 2015 @ 21:10:21 #180

Mathemaat

quote:
Op woensdag 21 januari 2015 19:07 schreef PausNicolaas het volgende:

[..]

Ik heb al 6 jaar wiskunde gehad, en moet met deze studie blijkbaar nog meer wiskunde hebben.

Maar goed, zou jij deze kunnen :
---------------------------
ln(x)
_______________
(x+1)²
---------------------------

Het is een integraal he (dus zo'n kringetje ernaast).

$\int \frac{\log(x)}{(x+1)^2} dx = -\frac{\log(x)}{x+1} +\int \frac{1}{x(x+1)} dx= -\frac{\log(x)}{x+1} +\int \frac{1}{x} dx - \int \frac{1}{x+1} dx = -\frac{\log(x)}{x+1} + \log(x)-\log(x+1) + \text{constante}$

Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.

woensdag 21 januari 2015 @ 21:16:09 #181

PausNicolaas

quote:
Op woensdag 21 januari 2015 21:09 schreef Riparius het volgende:

[..]

Bij partieel integreren is het altijd zaak dat je de integrand op een geschikte en handige manier schrijft als het product van een functie en een afgeleide van een andere functie. De regel voor partieel integreren bij onbepaalde integralen luidt

$\int f(x)g'(x){\rm d}x \,=\, f(x)g(x) \,-\, \int f'(x)g(x){\rm d}x$

Zie ook hier.

Gevraagd wordt nu

$\int \frac{\ln\,x}{(x\,+\,1)^2}\mathrm{d}x$

te bepalen. We kunnen hier kiezen

$f(x)\,=\,\ln\,x$

zodat

$f'(x)\,=\,\frac{1}{x}$

en

$g'(x)\,=\,\frac{1}{(x\,+\,1)^2}$

zodat we kunnen nemen

$g(x)\,=\,-\,\frac{1}{x\,+\,1}$

We krijgen dan

$\int \frac{\ln\,x}{(x\,+\,1)^2}\mathrm{d}x\,=\,-\,\frac{\ln\,x}{x\,+\,1}\,-\,\int -\,\frac{1}{x(x\,+\,1)}\mathrm{d}x\,=\,-\,\frac{\ln\,x}{x\,+\,1}\,+\,\int \frac{1}{x(x\,+\,1)}\mathrm{d}x$

Nu moeten we de integraal in het rechterlid nog bepalen. Dat kunnen we doen door de integrand op te splitsen in partiële breuken. We willen hebben

$\frac{1}{x(x\,+\,1)}\,=\,\frac{A}{x}\,+\,\frac{B}{x\,+\,1}$

waarbij we dan A en B moeten bepalen. Dit doen we door beide leden van deze gelijkheid te vermenigvuldigen met x(x+1), dan krijgen we

$1\,=\,A(x\,+\,1)\,+\,Bx$

oftewel

$1\,=\,(A\,+\,B)x\,+\, A$

waaruit we af kunnen lezen dat A + B = 0 en A = 1 moet zijn, en waaruit volgt dat B = −1. Zo hebben we dus

$\frac{1}{x(x\,+\,1)}\,=\,\frac{1}{x}\,-\,\frac{1}{x\,+\,1}$

en daarmee

$\int \frac{1}{x(x\,+\,1)}\mathrm{d}x\,=\,\int \left(\frac{1}{x}\,-\,\frac{1}{x\,+\,1}\right)\mathrm{d}x\,=\,\ln\, x \,-\, \ln(x\,+\,1)\,+\,C$

Invullen hiervan in bovenstaande betrekking voor de integraal van ln(x)/(x+1)² geeft dan

$\int \frac{\ln\,x}{(x\,+\,1)^2}\mathrm{d}x\,=\,-\,\frac{\ln\,x}{x\,+\,1}\,+\,\ln\,x\,-\,\ln(x\,+\,1)\,+\,C$

Nu kunnen we dit nog vereenvoudigen, want we hebben immers

$-\,\frac{\ln\,x}{x\,+\,1}\,+\,\ln\,x\,=\,-\,\frac{\ln\,x}{x\,+\,1}\,+\,\frac{(x\,+\,1)\ln\,x}{x\,+\,1}\,=\,\frac{x\ln\,x}{x\,+\,1}$

zodat we uiteindelijk krijgen

$\int \frac{\ln\,x}{(x\,+\,1)^2}\mathrm{d}x\,=\,\frac{x\ln\,x}{x\,+\,1}\,-\,\ln(x\,+\,1)\,+\,C$

That's all.

The master himself!

Precies wat ik nodig had

Duidelijker kan het niet

'Ego te absolvo peccatis tuis in nomine patris et filii et spiritus sancti.'

woensdag 21 januari 2015 @ 21:16:13 #182

Andijvie_

quote:
Op woensdag 21 januari 2015 21:02 schreef Borizzz het volgende:

[..]

Helpt partieel integreren ook jou niet verder?

Nee begrijp er geen ruk van. Heb een blackout.. desondanks overmorgen een toets.

woensdag 21 januari 2015 @ 22:04:04 #183

Super-B

Goedenavond wiskundigen,

Ik heb aanstaande vrijdag een wiskunde toets en op dit moment ben ik wat oude toetsen aan het oefenen. Echter ben ik een vraag tegengekomen waar ik niet uitkom en hopelijk kan iemand mij hierbij helpen. Het onderwerp betreft: lineair programmeren.

Ik heb de grafiek getekend en ik kom tot de conclusie dat x − y ≤ 2 rechts van de doelfunctie ligt, −4x + 2y ≤ 2 links van de doelfunctie en −x + y ≤ 3 de doelfunctie snijdt op x=3, y=6.

woensdag 21 januari 2015 @ 22:08:05 #184

Riparius

quote:
Op woensdag 21 januari 2015 20:03 schreef Andijvie_ het volgende:
[ afbeelding ]

Deze integraal kun je gemakkelijk behandelen met een impliciete substitutie. Bedenk dat je hebt

$\frac{\mathrm{d}(x^{10}\,-\,7)}{\mathrm{d}x}\,=\,10x^9$

en dus

$\mathrm{d}(x^{10}\,-\,7)\,=\,10x^9\mathrm{d}x$

en dus

$200\cdot\mathrm{d}(x^{10}\,-\,7)\,=\,2000x^9\mathrm{d}x$

zodat

$\int 2000x^9(x^{10}\,-\,7)^{99}\mathrm{d}x\,=\,\int 200(x^{10}\,-\,7)^{99}\mathrm{d}(x^{10}\,-\,7)\,=\,200\cdot\frac{1}{100}(x^{10}\,-\,7)^{100}\,+\,C\,=\,2\cdot(x^{10}\,-\,7)^{100}\,+\,C$

Als de techniek van een substitutie en een impliciete substitutie bij de integraalrekening je nog niet duidelijk is, dan kan ik je aanbevelen dit eens goed door te nemen.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 21 januari 2015 @ 22:11:48 #185

Andijvie_

quote:
Op woensdag 21 januari 2015 22:08 schreef Riparius het volgende:

[..]

Deze integraal kun je gemakkelijk behandelen met een impliciete substitutie. Bedenk dat je hebt

$\frac{\mathrm{d}(x^{10}\,-\,7)}{\mathrm{d}x}\,=\,10x^9$

en dus

$\mathrm{d}(x^{10}\,-\,7)\,=\,10x^9\mathrm{d}x$

en dus

$200\cdot\mathrm{d}(x^{10}\,-\,7)\,=\,2000x^9\mathrm{d}x$

zodat

$\int 2000x^9(x^{10}\,-\,7)^{99}\mathrm{d}x\,=\,\int 200(x^{10}\,-\,7)^{99}\mathrm{d}(x^{10}\,-\,7)\,=\,200\cdot\frac{1}{100}(x^{10}\,-\,7)^{100}\,+\,C\,=\,2\cdot(x^{10}\,-\,7)^{100}\,+\,C$

Als de techniek van een substitutie en een impliciete substitutie bij de integraalrekening je nog niet duidelijk is, dan kan ik je aanbevelen dit eens goed door te nemen.

De meester, Riparius. Hoe zou je het doen zonder impliciete substitutie, maar met u en du?

woensdag 21 januari 2015 @ 22:37:20 #186

Riparius

quote:
Op woensdag 21 januari 2015 22:11 schreef Andijvie_ het volgende:

[..]

De meester, Riparius. Hoe zou je het doen zonder impliciete substitutie, maar met u en du?

Eigenlijk hetzelfde. Je substitueert

$u\,=\,x^{10}\,-\,7$

zodat

$\frac{\mathrm{d}u}{\mathrm{d}x}\,=\,10x^9$

en dus

$\mathrm{d}u\,=\,10x^9\mathrm{d}x$

en daarmee

$200\cdot\mathrm{d}u\,=\,2000x^9\mathrm{d}x$

zodat we krijgen

$\int 2000x^9(x^{10}\,-\,7)^{99}\mathrm{d}x\,=\,\int 200u^{99}\mathrm{d}u\,=\,200\cdot\frac{1}{100}u^{100}\,+\,C\,=\,2u^{100}\,+\,C\,=\,2(x^{10}\,-\,7)^{100}\,+\,C$

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 21 januari 2015 @ 22:39:15 #187

Janneke141

Green, green grass of home

quote:
Op woensdag 21 januari 2015 22:04 schreef Super-B het volgende:
Goedenavond wiskundigen,

Ik heb aanstaande vrijdag een wiskunde toets en op dit moment ben ik wat oude toetsen aan het oefenen. Echter ben ik een vraag tegengekomen waar ik niet uitkom en hopelijk kan iemand mij hierbij helpen. Het onderwerp betreft: lineair programmeren.

[ afbeelding ]

Ik heb de grafiek getekend en ik kom tot de conclusie dat x − y ≤ 2 rechts van de doelfunctie ligt, −4x + 2y ≤ 2 links van de doelfunctie en −x + y ≤ 3 de doelfunctie snijdt op x=3, y=6.

Hoe teken je de doelfunctie?

Opinion is the medium between knowledge and ignorance (Plato)

woensdag 21 januari 2015 @ 22:58:13 #188

Super-B

quote:
Op woensdag 21 januari 2015 22:39 schreef Janneke141 het volgende:

[..]

Hoe teken je de doelfunctie?

Met stippellijnen. De budgetconstraint teken ik als een doorgetrokken streep. Overigens schrijf ik zowel de doelfuncties als de budgetconstraint om naar y =.... en dan begin ik met tekenen.

woensdag 21 januari 2015 @ 23:05:01 #189

Riparius

quote:
Op woensdag 21 januari 2015 20:48 schreef RustCohle het volgende:
Hoi allemaal,

Ik heb weer eens een vraag en hoop weer voor de zoveelste keer uit de brand geholpen te worden:

Hoe kan ik de volgende integralen degelijk opschrijven om het te kunnen integreren?:

[ afbeelding ]

[ afbeelding ]

Je moet eens goed nakijken of je de opgaven wel correct hebt overgenomen. Bij de eerste integraal moet je een vrij lastige breuksplitsing uitvoeren en je derde integraal convergeert niet.

Bij de integrand van je eerste integraal kun je in de teller een factor x en in de noemer een factor 2x⁴ buiten haakjes halen, en aangezien x² + 2x + 1 = (x + 1)² wordt de integrand dan

$\frac{3x\,+\,2}{2x^3(x\,+\,1)^2}\,=\,\frac{1}{x^3}\,-\,\frac{1}{2x^2}\,+\,\frac{1}{2(x\,+\,1)^2}$

Bij de integrand van de tweede integraal kun je bedenken dat 2x² + 4x − 6 = 2(x + 3)(x − 1) zodat de integrand eenvoudig wordt

$2x\,+\,6$

althans voor x ≠ 1. Je hebt hier dus een oneigenlijke integraal, aangezien je integreert over het interval [−1, 1].

De derde integraal zou je kunnen behandelen met een substitutie u = ln x, maar zoals gezegd convergeert deze integraal niet.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 21 januari 2015 @ 23:06:18 #190

Janneke141

Green, green grass of home

quote:
Op woensdag 21 januari 2015 22:58 schreef Super-B het volgende:

[..]

Met stippellijnen. De budgetconstraint teken ik als een doorgetrokken streep. Overigens schrijf ik zowel de doelfuncties als de budgetconstraint om naar y =.... en dan begin ik met tekenen.

Wat ik bedoel is dat je je doelfunctie helemaal niet kan tekenen, omdat je daarmee zo moet 'schuiven' dat deze een maximale waarde bereikt.

Het lichtpaarse gebied is het gebied dat omsloten wordt door de voorwaarden. De groene lijn hoort bij 4x-2y=16, de rode lijn hoort bij 4x-2y=24. Omdat het paarse gebied naar rechts niet begrensd wordt, kun je de lijn horend bij de doelfunctie zo ver naar rechts schuiven als je zelf wil; 4x-2y kan oneindig groot worden zonder buiten het gebied te komen.

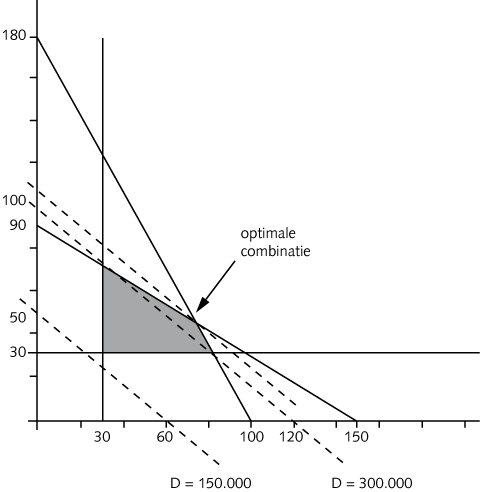
Ter vergelijking een plaatje bij een wel-oplosbaar lineair programmeren-probleem: het gebied in het onderstaande plaatje is wel begrensd. De stippellijnen horen bij de doelfunctie; deze wordt zo verschoven zodat deze op een hoekje van het gebied terecht komt, en heeft daar zijn maximum binnen de voorwaarden. Dat kan in jouw voorbeeld niet, omdat het toegestane gebied niet eindig is.

Opinion is the medium between knowledge and ignorance (Plato)

woensdag 21 januari 2015 @ 23:46:53 #191

Super-B

quote:
Op woensdag 21 januari 2015 23:06 schreef Janneke141 het volgende:

[..]

Wat ik bedoel is dat je je doelfunctie helemaal niet kan tekenen, omdat je daarmee zo moet 'schuiven' dat deze een maximale waarde bereikt.

[ afbeelding ]

Het lichtpaarse gebied is het gebied dat omsloten wordt door de voorwaarden. De groene lijn hoort bij 4x-2y=16, de rode lijn hoort bij 4x-2y=24. Omdat het paarse gebied naar rechts niet begrensd wordt, kun je de lijn horend bij de doelfunctie zo ver naar rechts schuiven als je zelf wil; 4x-2y kan oneindig groot worden zonder buiten het gebied te komen.

Ter vergelijking een plaatje bij een wel-oplosbaar lineair programmeren-probleem: het gebied in het onderstaande plaatje is wel begrensd. De stippellijnen horen bij de doelfunctie; deze wordt zo verschoven zodat deze op een hoekje van het gebied terecht komt, en heeft daar zijn maximum binnen de voorwaarden. Dat kan in jouw voorbeeld niet, omdat het toegestane gebied niet eindig is.
[ afbeelding ]

Hartstikke bedankt! Veel duidelijker dan het antwoordenmodel! Enige vraag dat, vanuit mijn kant, rest is het volgende:

Waarom zit het paarse gebied tussen de twee budgetconstraints en nietrechts van de laatste budgetconstraint(meest rechtse)? Want dat paarse gebied staat nu boven de meest rechtse budgetconstraint.

[ Bericht 0% gewijzigd door Super-B op 22-01-2015 00:15:01 ]

donderdag 22 januari 2015 @ 21:17:33 #192

netchip

Zijn integratie door substitutie, partiële integratie en integratie door breuksplitsing onderdeel van het VWO Wiskunde B programma? Ik zou mij hier namelijk graag in verdiepen, maar voordat ik dubbelwerk doe, zou ik dit graag willen weten.

Heeft iemand een goed boek hierover, trouwens? Misschien moeten we een boekenlijst in de OP plaatsen.

vrijdag 23 januari 2015 @ 00:01:09 #193

Novermars

quote:
Op donderdag 22 januari 2015 21:17 schreef netchip het volgende:
Zijn integratie door substitutie, partiële integratie en integratie door breuksplitsing onderdeel van het VWO Wiskunde B programma? Ik zou mij hier namelijk graag in verdiepen, maar voordat ik dubbelwerk doe, zou ik dit graag willen weten.

Heeft iemand een goed boek hierover, trouwens? Misschien moeten we een boekenlijst in de OP plaatsen.

Nee, enkel een keuze-onderwerp. En elk elementair calculusboek.

vrijdag 23 januari 2015 @ 11:19:40 #194

mary1995

Van het gewicht van schoolboeken van een school in Friesland is bekend: het gemiddelde is 103 g met een standaarddeviatie van 22 g. De verdeling is bij benadering 'normaal', hetgeen inhoudt dat bepaalde vuistregels opgaan. Er wordt een steekproef van 1869 schoolboeken genomen.
Bij hoeveel % van de schoolboeken zal volgens de vuistregels het gewicht tussen 81 en 125 g liggen?

Hint: ga na hoeveel standaarddeviaties 81 en 125 van het gemiddelde liggen.

Antwoord is 68%

Ik heb alleen geen flauw idee hoe ze hierop komen. Ik heb ook geen idee hoe ik moet beginnen. Zouden jullie mij hiermee willen helpen? dat zou heel fijn zijn!

vrijdag 23 januari 2015 @ 11:27:21 #195

Anoonumos

quote:
Op vrijdag 23 januari 2015 11:19 schreef mary1995 het volgende:
Van het gewicht van schoolboeken van een school in Friesland is bekend: het gemiddelde is 103 g met een standaarddeviatie van 22 g. De verdeling is bij benadering 'normaal', hetgeen inhoudt dat bepaalde vuistregels opgaan. Er wordt een steekproef van 1869 schoolboeken genomen.
Bij hoeveel % van de schoolboeken zal volgens de vuistregels het gewicht tussen 81 en 125 g liggen?

Hint: ga na hoeveel standaarddeviaties 81 en 125 van het gemiddelde liggen.

Antwoord is 68%

Ik heb alleen geen flauw idee hoe ze hierop komen. Ik heb ook geen idee hoe ik moet beginnen. Zouden jullie mij hiermee willen helpen? dat zou heel fijn zijn!

Gemiddelde is 103
Standaarddeviatie is 22

103 + 22 = 125
103 - 22 = 81

En één van die vuistregels van de normaalverdeling is dat 68% van de gemeten waardes een standaarddeviatie of minder van het gemiddelde afwijken.

vrijdag 23 januari 2015 @ 11:45:27 #196

CapnIzzy

Geef aye voor de kapitein

[ Bericht 100% gewijzigd door CapnIzzy op 23-01-2015 11:49:18 ]

Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game

vrijdag 23 januari 2015 @ 11:50:06 #197

CapnIzzy

Geef aye voor de kapitein

quote:
Op vrijdag 23 januari 2015 11:19 schreef mary1995 het volgende:
Van het gewicht van schoolboeken van een school in Friesland is bekend: het gemiddelde is 103 g met een standaarddeviatie van 22 g. De verdeling is bij benadering 'normaal', hetgeen inhoudt dat bepaalde vuistregels opgaan. Er wordt een steekproef van 1869 schoolboeken genomen.
Bij hoeveel % van de schoolboeken zal volgens de vuistregels het gewicht tussen 81 en 125 g liggen?

Hint: ga na hoeveel standaarddeviaties 81 en 125 van het gemiddelde liggen.

Antwoord is 68%

Ik heb alleen geen flauw idee hoe ze hierop komen. Ik heb ook geen idee hoe ik moet beginnen. Zouden jullie mij hiermee willen helpen? dat zou heel fijn zijn!

Misschien dat dit helpt:

Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game

vrijdag 23 januari 2015 @ 13:06:30 #198

defineaz

In mijn kansrekening boek wordt de convolutie van F en G gedefinieerd als
(F * G)(a) = ∫ F(a - y) dG(y)

wat voor continue F en G overeenkomt met
(F * G)(a) = ∫ F(a - y) g(y) dy

met g(y) = G'(y)

Dit is natuurlijk niet de normale definitie van convolutie (zoals ik hem bij andere vakken heb geleerd):
(F * G)(a) = ∫ F(a - y) G(y) dy

in de definitie uit het boek wordt dus van G de afgeleide genomen (wat normaal niet het geval is)

(wat context: er wordt gesteld dat als X en Y twee onafhankelijke random variabelen zijn met distributies F en G, de distributie van de som F * G is. het boek gebruikt vaak de distribution F ipv de probablility density function. als je de pdf's f en g zou gebruiken zou je volgens mij wel hebben dat de pdf van X + Y gelijk is aan f * g, als je dus de standaard definitie van convolutie gebruikt)

Is deze definitie van convolutie gebruikelijk in de kansrekening? Ik kan er zo snel geen andere voorbeelden van vinden.

vrijdag 23 januari 2015 @ 13:10:09 #199

mary1995

quote:
Op vrijdag 23 januari 2015 11:27 schreef Anoonumos het volgende:

[..]

Gemiddelde is 103
Standaarddeviatie is 22

103 + 22 = 125
103 - 22 = 81

En één van die vuistregels van de normaalverdeling is dat 68% van de gemeten waardes een standaarddeviatie of minder van het gemiddelde afwijken.

quote:
Op vrijdag 23 januari 2015 11:50 schreef CapnIzzy het volgende:

[..]

Misschien dat dit helpt:

[ afbeelding ]

Ik begrijp hem! Beide bedankt voor de hulp! Is toch simpeler dan ik dacht

vrijdag 23 januari 2015 @ 17:59:43 #200

thenxero

quote:
Op vrijdag 23 januari 2015 13:06 schreef defineaz het volgende:
In mijn kansrekening boek wordt de convolutie van F en G gedefinieerd als
(F * G)(a) = ∫ F(a - y) dG(y)

wat voor continue F en G overeenkomt met
(F * G)(a) = ∫ F(a - y) g(y) dy

met g(y) = G'(y)

Dit is natuurlijk niet de normale definitie van convolutie (zoals ik hem bij andere vakken heb geleerd):
(F * G)(a) = ∫ F(a - y) G(y) dy

in de definitie uit het boek wordt dus van G de afgeleide genomen (wat normaal niet het geval is)

(wat context: er wordt gesteld dat als X en Y twee onafhankelijke random variabelen zijn met distributies F en G, de distributie van de som F * G is. het boek gebruikt vaak de distribution F ipv de probablility density function. als je de pdf's f en g zou gebruiken zou je volgens mij wel hebben dat de pdf van X + Y gelijk is aan f * g, als je dus de standaard definitie van convolutie gebruikt)

Is deze definitie van convolutie gebruikelijk in de kansrekening? Ik kan er zo snel geen andere voorbeelden van vinden.

(F * G)(a) = ∫ F(a - y) dG(y) is de standaard definitie van convolutie in de kansrekening. De integraal is een Stieltjes integraal. Als G absoluut continu is (dat is wat anders dan 'gewoon' continu) dan kan je gebruikten dat dG(y) = g(y)dy om het als gewone Riemann/Lebesgue integraal te schrijven (dit is in feite de Radon-Nikodym stelling). Maar soms heb je geen absolute continuïteit, en dus geen pdf's, en dan moet je het wel opschrijven op de Stieltjes manier. Vandaar dat deze definitie gangbaar is in de kansrekening.

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs